A New Macro-Element for Predicting the Behavior of Masonry Structures under In-Plane Cyclic Loading
Abstract
1. Introduction
2. The DFM for In-Plane Loads
2.1. Stiffness of the Struts
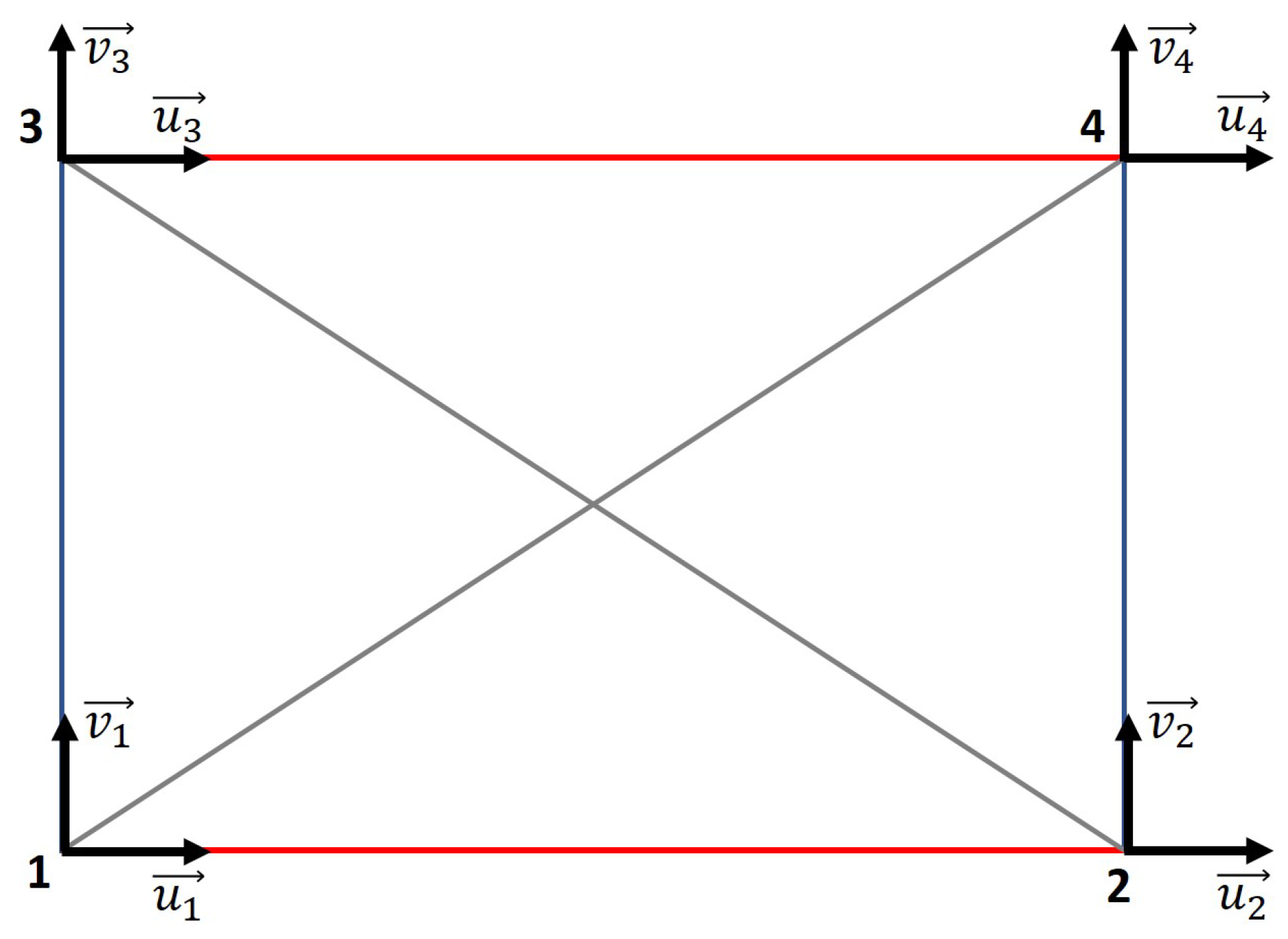
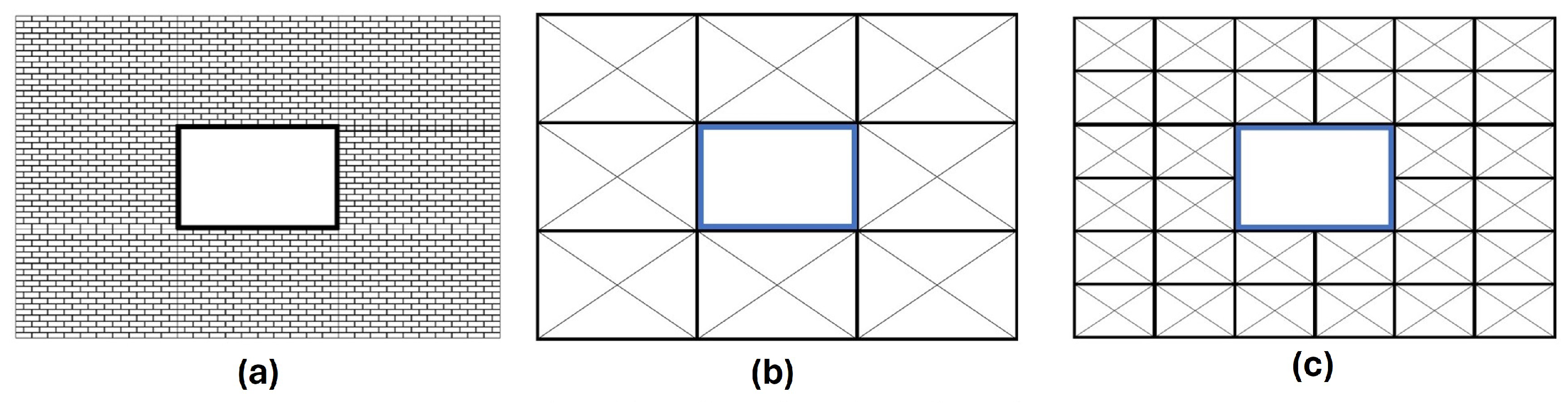
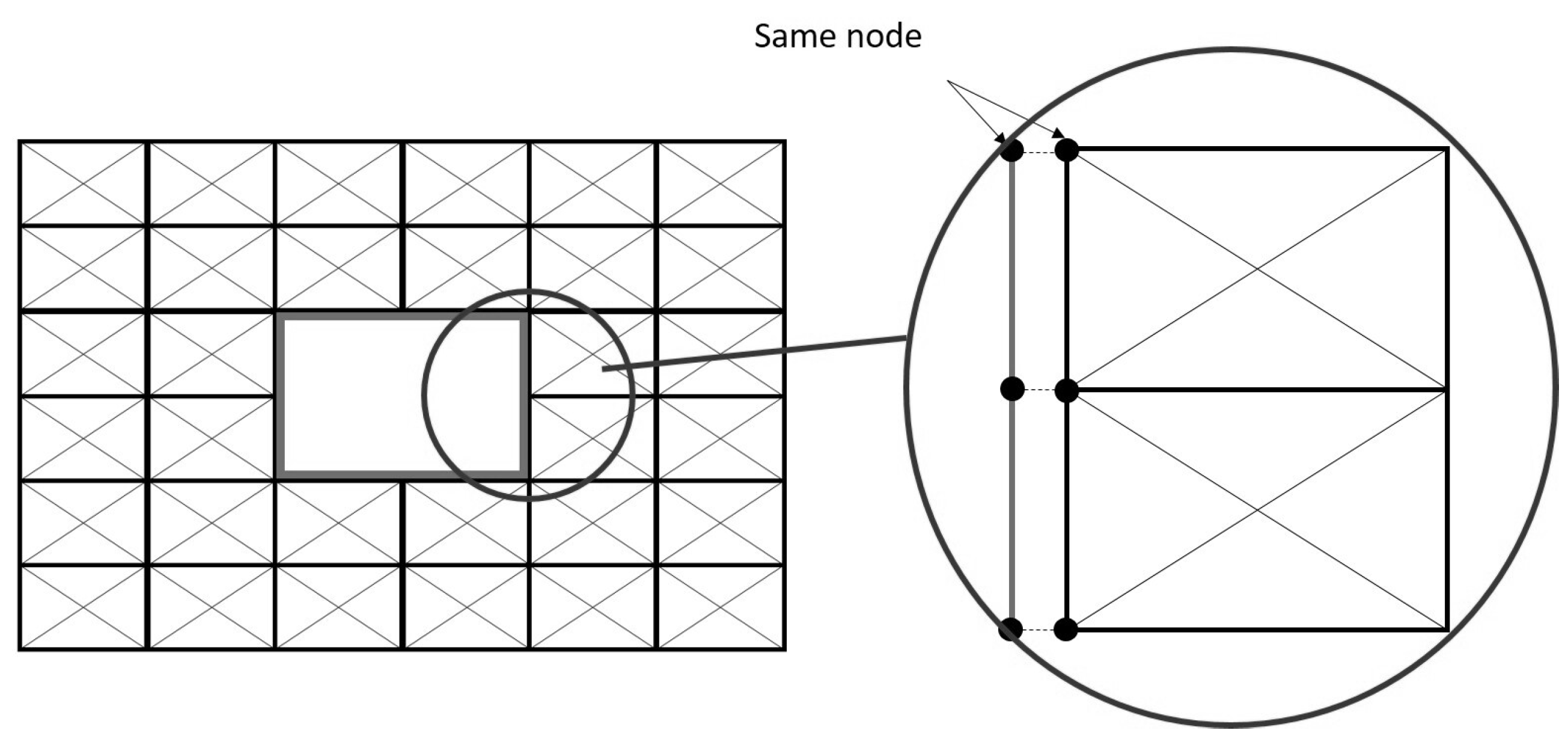
2.2. Macro-Element Discretization
2.3. Shear Strength of the DFM
- Diagonal cracking:
- Shear/sliding:
2.4. Inelastic Behavior of the DFM
2.4.1. Damage in One Direction
- 1.
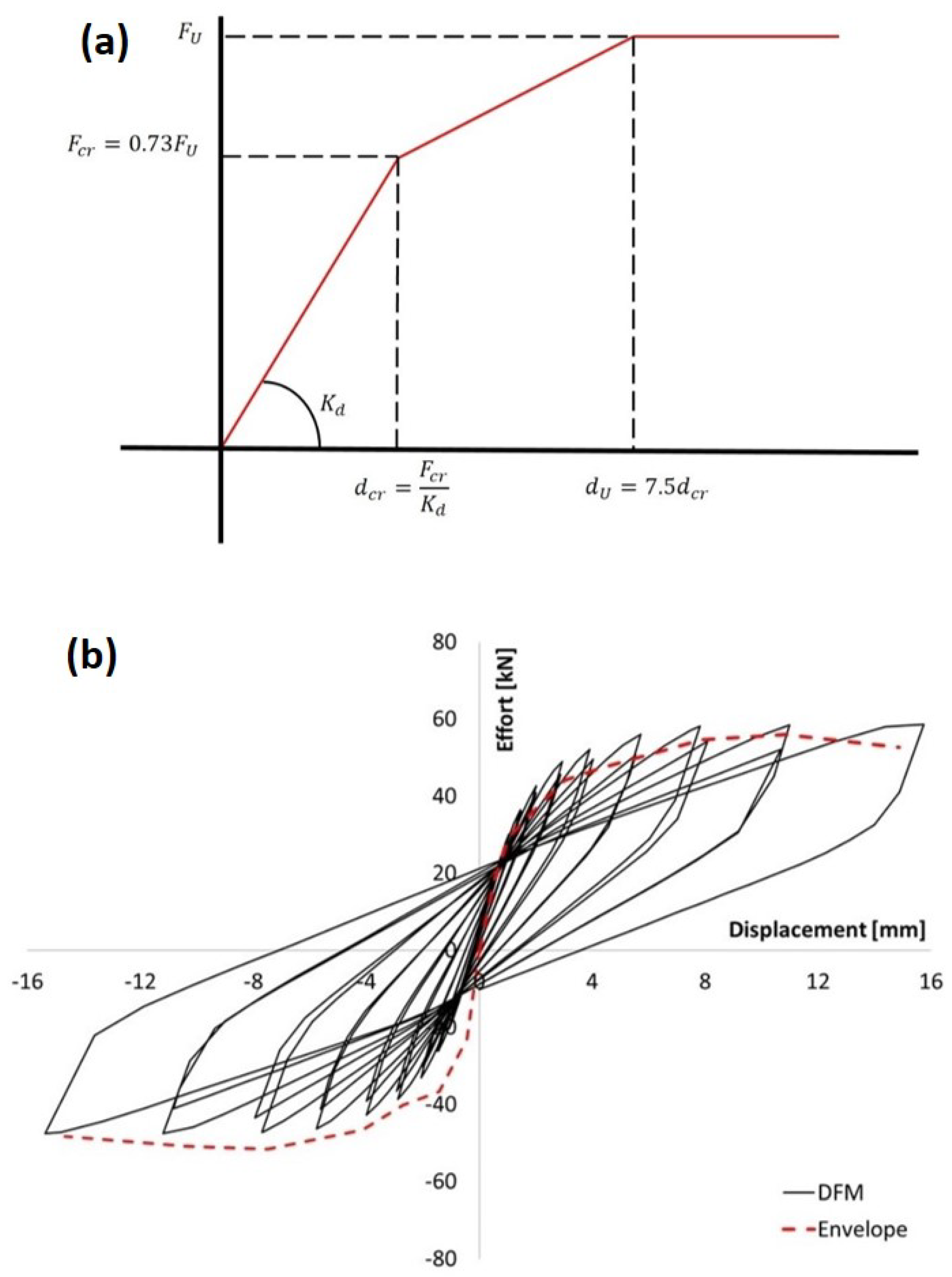
- From point B, the unloading occurs with initial stiffness, . This behavior occurs until the force is reached at point C in Figure 4.
- 2.
- After point C, the stiffness decreases, corresponding to the opening of the cracks produced by the solicitation in this direction. Since the modeled masonry portion has not been damaged in the other excitation direction, the point targeted by the constitutive law is the point of ordinate - on the envelope curve; see point D in Figure 4. After this point, the DFM follows the behavior of the envelope curve.
2.4.2. Damage in Both Directions
- 1.
- From point F, the unloading takes place with the initial stiffness, , as from point B. The branch FG is described exactly as the branch BC.
- 2.
- After reaching point G, the following branch is not defined like the branch CD. Since the modeled masonry portion has already been damaged in the opposite direction, some cracks remain open due to the reloading. Thus, two phenomena occur on the branch GH: the closing of cracks in one direction and the reopening of cracks in the other direction. Note = is the displacement at force in the other direction.
- 3.
- Depending on the mode of failure that occurs, the last part of the curve is defined differently.
- At point H, the masonry exhibits damaged stiffness until the ultimate force, , is recovered. Therefore, point I in Figure 4 is different from point B. After point I, one follows the envelope curve again. This type of behavior occurs if the failure is along a bed joint.
- If the failure is along the wall portion diagonally, the masonry has softening behavior due to cyclic damage. The ultimate force at displacement is no longer , but with 1. The value is chosen as the new maximum of the envelop curve as shown in Figure 4 with the branch HI’. After point I’, the new definition of the envelope curve is followed.
2.5. Parameters of the Hysteresis Constitutive Model
- if
- if
3. Wall with an Opening
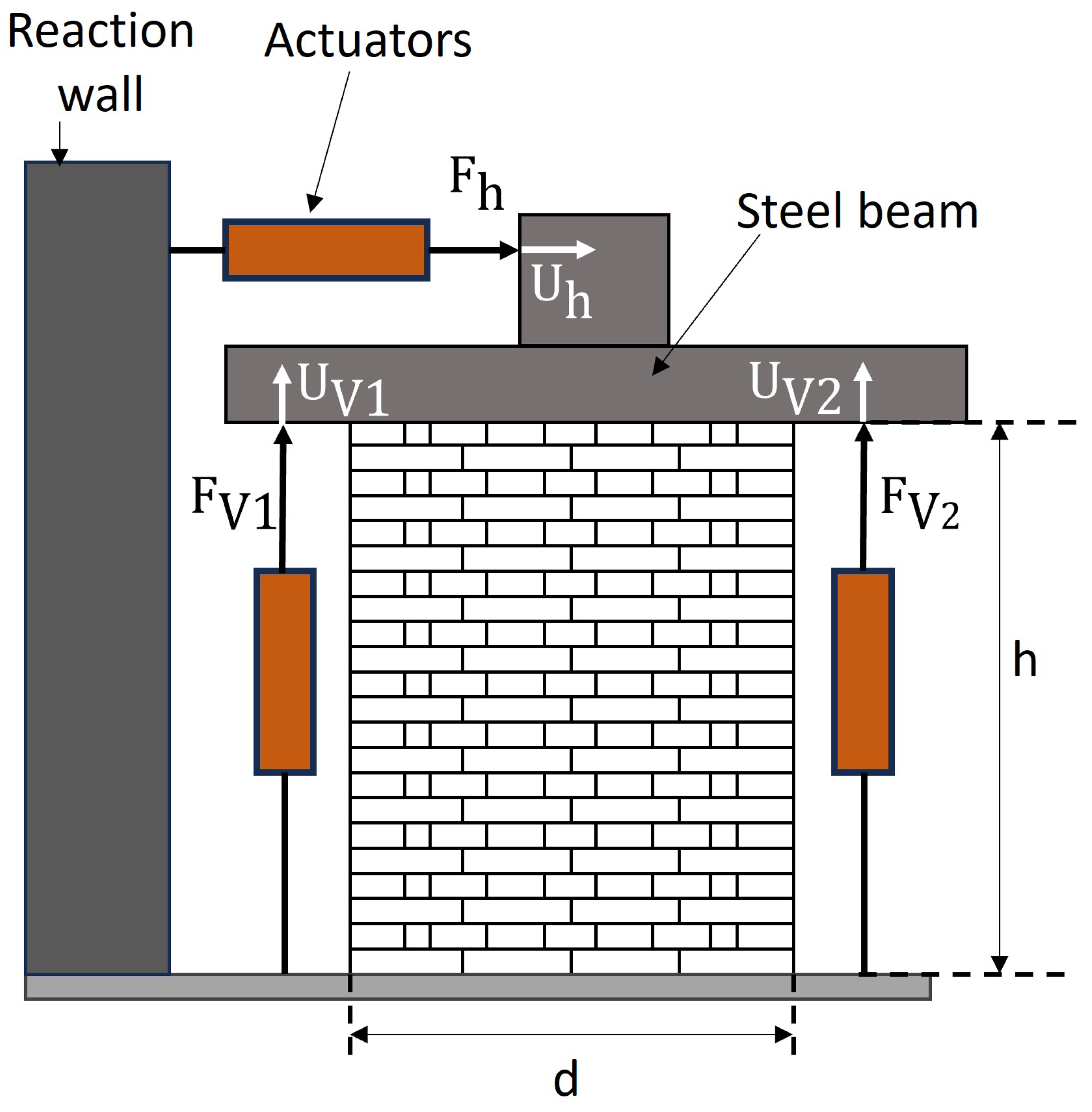
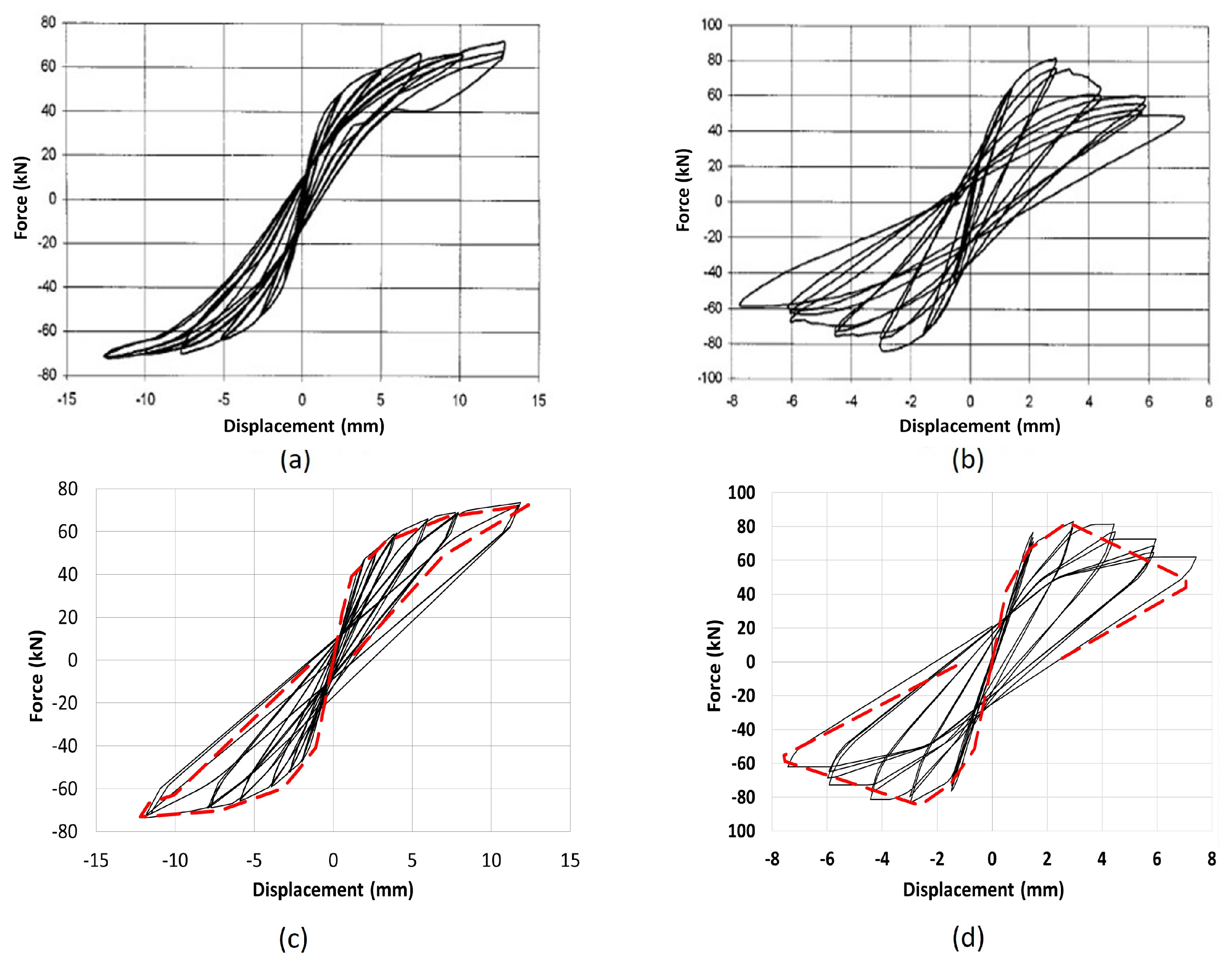
4. Validation of the Macro-Element Model
4.1. URM Piers
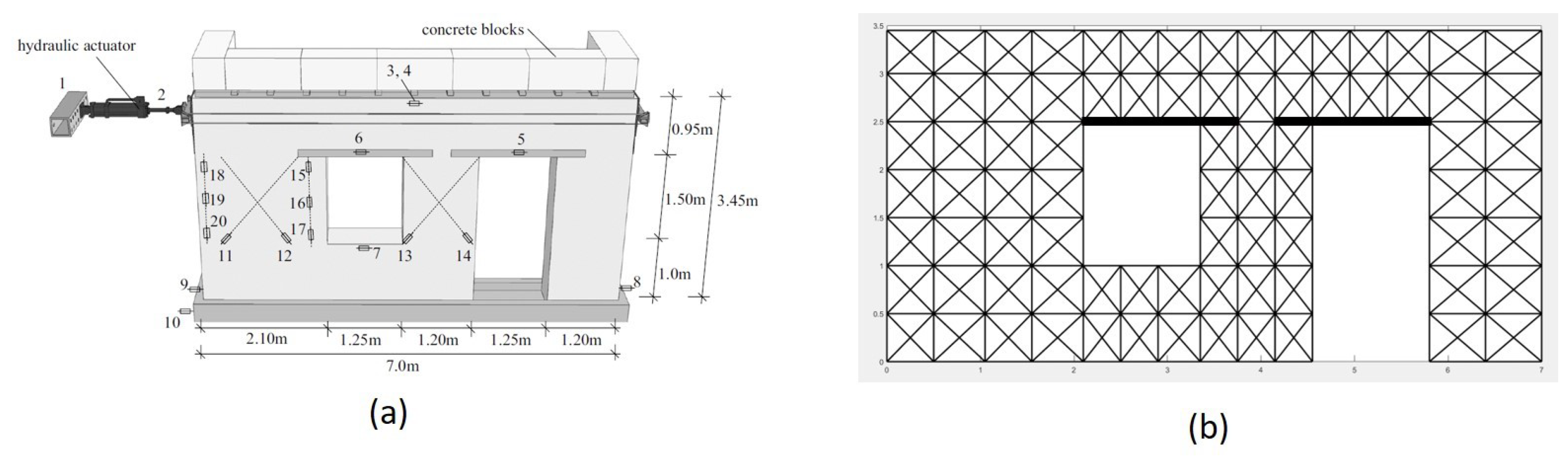
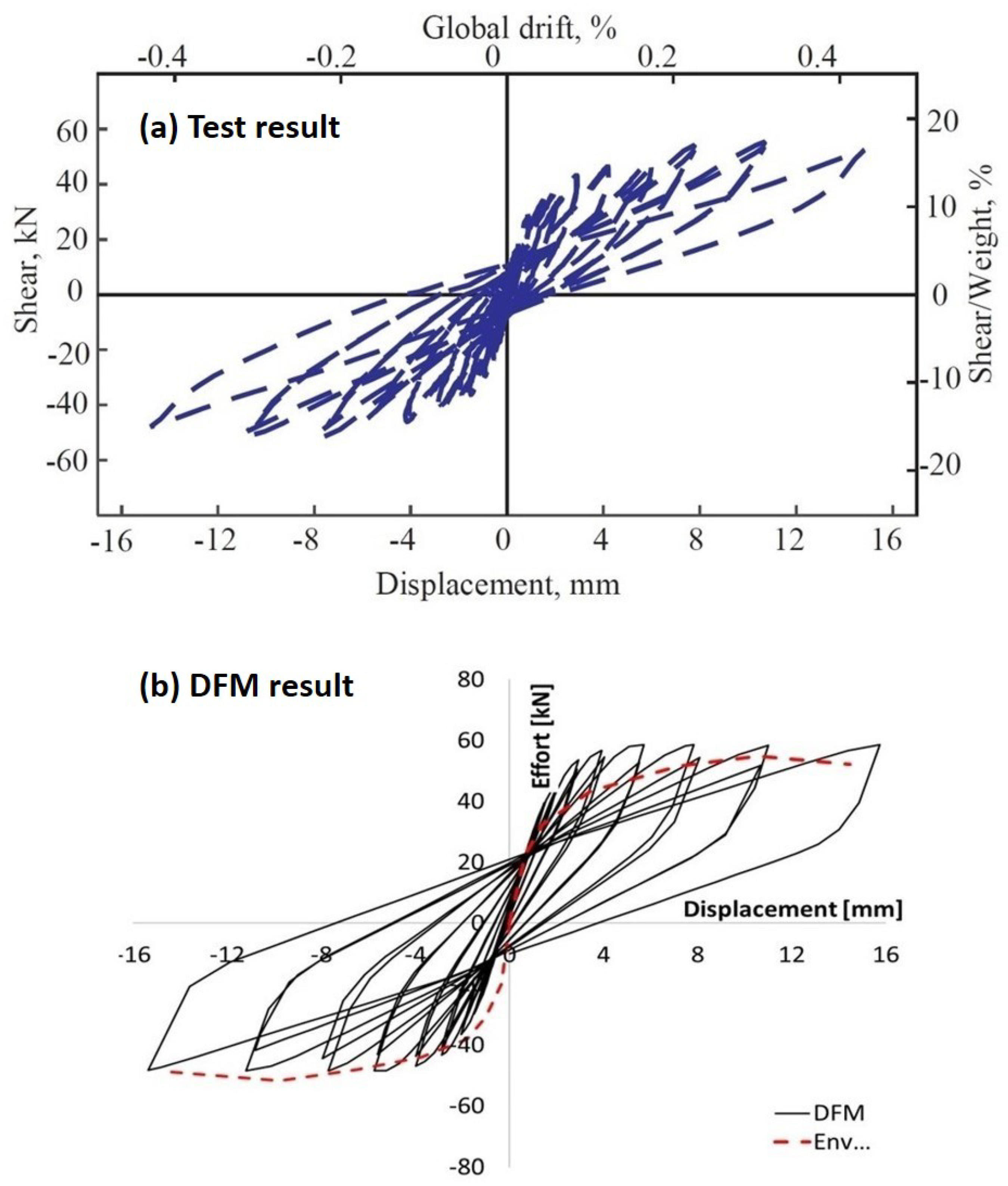
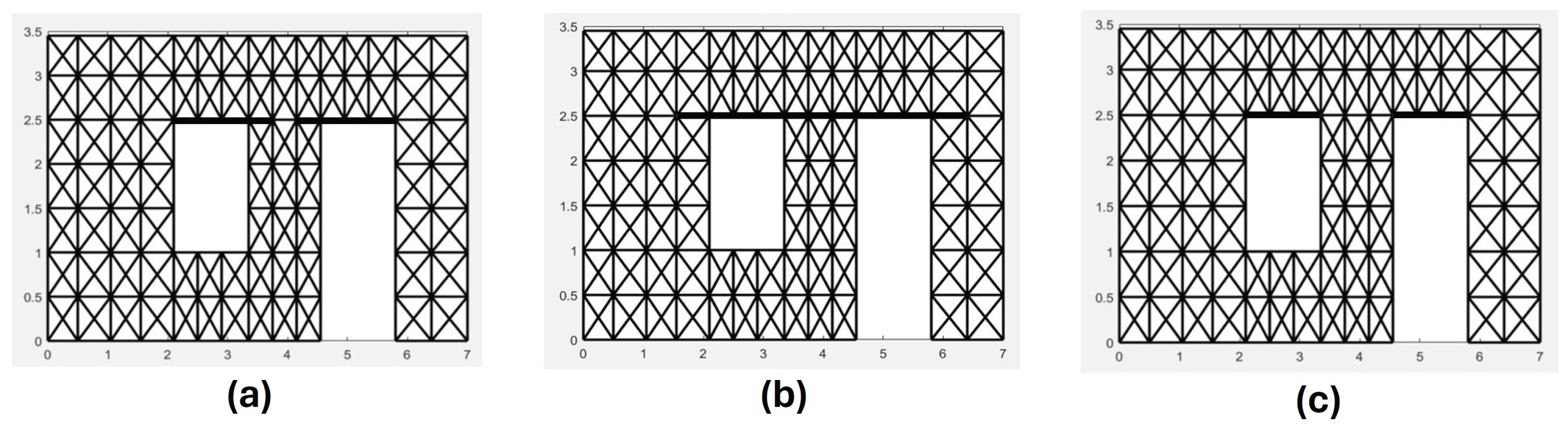
4.2. Wide Walls with Openings
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| List of abbreviations | |
| CSM | composite spring method |
| DFM | deformable frame model |
| DM-MVLEM | double-modified multiple vertical-line-element method |
| DOF | degrees of freedom |
| EFM | equivalent frame model |
| ESM | equivalent strut model |
| MFE | macro-frame element |
| MP | multi-pier |
| MVLEM | multiple vertical-line-element method |
| RBSM | rigid body spring model |
| REM | rigid element model |
| RMEM | rigid macro-element model |
| SAM | simplified analysis of masonry |
| UM | unified method |
| URM | unreinforced masonry |
| List of symbols | |
| b | parameter accounting for the element slenderness |
| bdiag | new definition of the parameter b used for the DFM |
| c | masonry cohesion |
| masonry cohesion as proposed by Mann and Muller | |
| dmax | maximum displacement reached in the opposite direction by the DFM diagonal strut |
| du | displacement at the ultimate strength of the DFM diagonal strut |
| Em | masonry Young modulus |
| ft | masonry tensile strength |
| Fu | ultimate strength of the DFM diagonal strut |
| Fv | vertical force applied on the macro-element |
| fv,1 | masonry shear strength for the diagonal cracking failure |
| fv,2 | masonry shear strength for shear-sliding failure |
| Gm | masonry shear modulus |
| Hb | brick height |
| helem | macro-element height |
| hinf | height of the area of influence of a horizontal strut |
| hm | height of the considered masonry part |
| Kd | DFM diagonal strut initial stiffness |
| Kd,i | initial stiffness of the diagonal strut i |
| Kh | DFM horizontal strut in-plane stiffness |
| Kv | DFM vertical strut in-plane stiffness |
| Lb | brick length |
| lelem | DFM width |
| linf | width of the area of influence of a vertical strut |
| lm | width of the considered masonry part |
| tm | thickness of the considered masonry part |
| ud | longitudinal elongation of the diagonal strut |
| uv | vertical displacement of the top nodes of the DFM |
| parameter accounting for the cyclic damage in the masonry | |
| parameter accounting for the cyclic shear behavior of masonry | |
| parameter accounting for plasticity in the hysteretic behavior | |
| strain tensor | |
| angle of the macro-element diagonal strut with the horizontal axis | |
| vertical stress applied on the macro-element | |
| Stress tensor | |
| masonry Poisson’s ratio | |
| lintel Poisson’s ratio | |
| coefficient of friction of masonry | |
| coefficient of friction of masonry as proposed by Mann and Muller | |
| masonry density | |
| lintel density | |
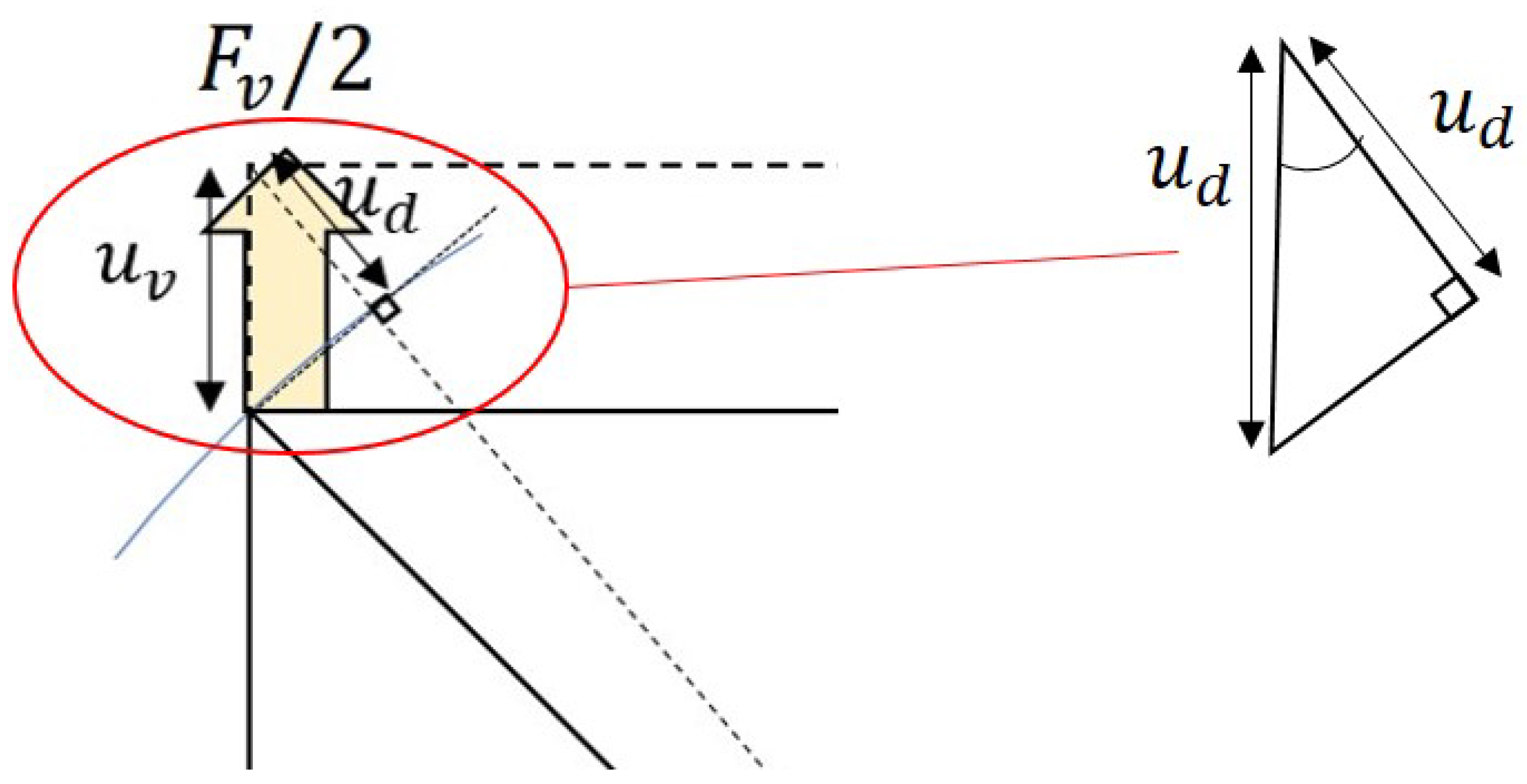
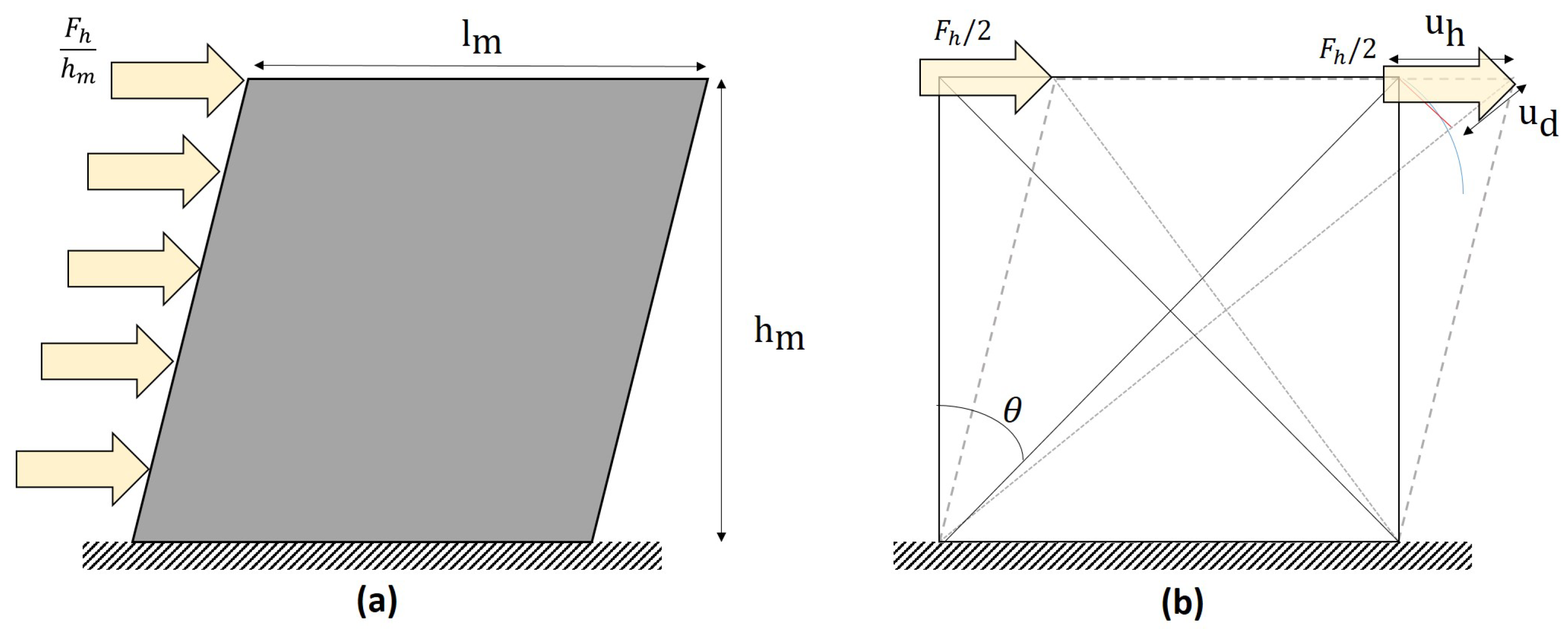
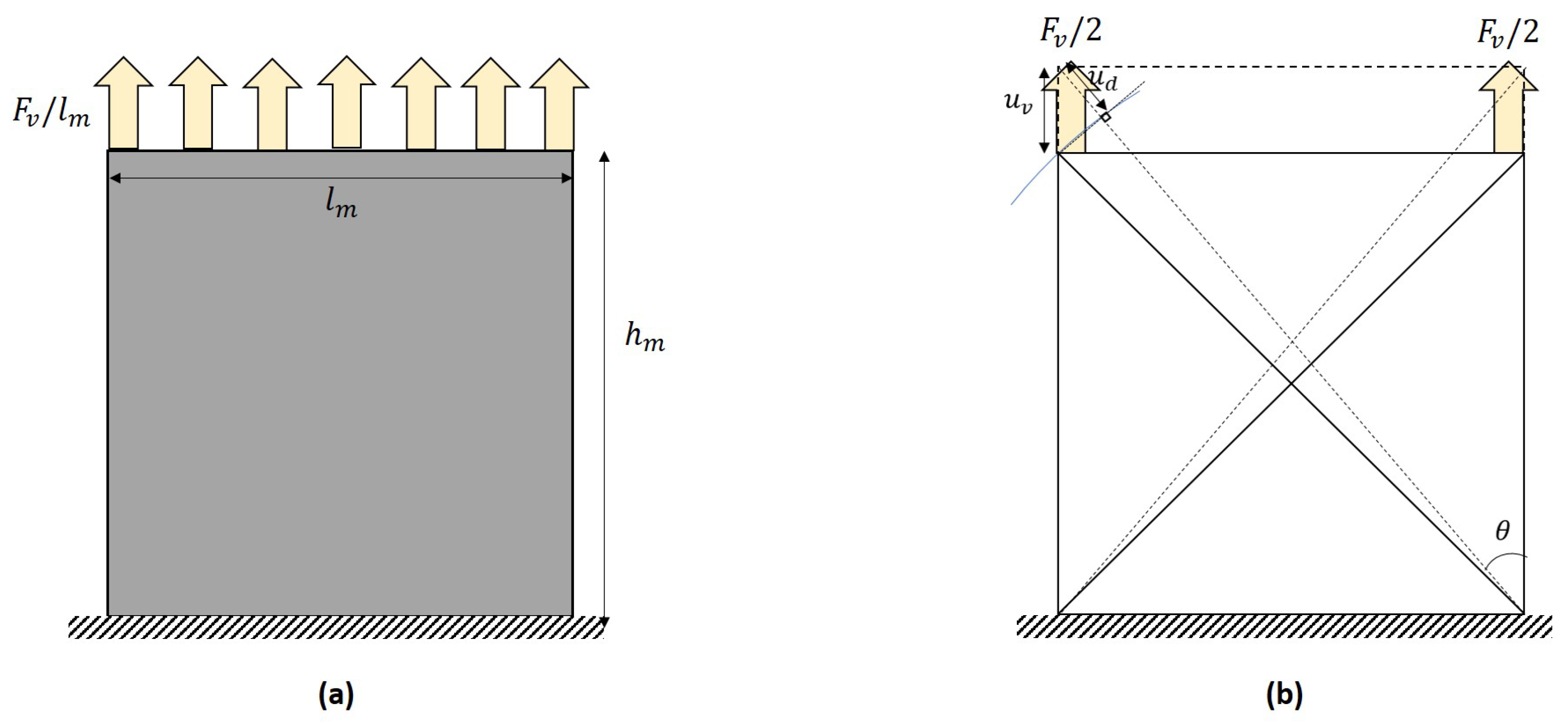
Appendix A. Definition of the Rigidity of the Struts
Appendix A.1. Vertical Loading
Appendix A.2. Shear Loading
References
- Zucchini, A.; Lourenço, P. A micro-mechanical model for the homogenisation of masonry. Int. J. Solids Struct. 2002, 39, 3233–3255. [Google Scholar] [CrossRef]
- Casolo, S. Modelling in-plane micro-structure of masonry walls by rigid elements. Int. J. Solids Struct. 2004, 41, 3625–3641. [Google Scholar] [CrossRef]
- Gambarotta, L.; Lagomarsino, S. Damage models for the seismic response of brick masonry shear walls. Part I: The mortar joint model and its applications. Earthq. Eng. Struct. Dyn. 1997, 26, 423–439. [Google Scholar] [CrossRef]
- Crisafulli, F.J. Seismic Behaviour of Reinforced Concrete Structures with Masonry Infills. Ph.D. Thesis, University of Canterbury, Christchurch, New Zealand, 1997. [Google Scholar]
- Panagiotakos, T.; Fardis, M. Seismic response of infilled RC frames structures. In Proceedings of the 11th World Conference on Earthquake Engineering, Acapulco, Mexico, 23–28 June 1996. Number 225. [Google Scholar]
- Combescure, D. Modélisation du Comportement Sous Chargement Sismique des Structures de Bâtiment Comportant des Murs de Remplissage en Maçonnerie. Ph.D. Thesis, Châtenay-Malabry, Paris, France, 1996. [Google Scholar]
- Pirsaheb, H.; Moradi, M.J.; Milani, G. A Multi-Pier MP procedure for the non-linear analysis of in-plane loaded masonry walls. Eng. Struct. 2020, 212, 110534. [Google Scholar] [CrossRef]
- Xu, H.; Gentilini, C.; Yu, Z.; Wu, H.; Zhao, S. A unified model for the seismic analysis of brick masonry structures. Constr. Build. Mater. 2018, 184, 733–751. [Google Scholar] [CrossRef]
- Shabani, A.; Kioumarsi, M. A novel macroelement for seismic analysis of unreinforced masonry buildings based on MVLEM in OpenSees. J. Build. Eng. 2022, 49, 104019. [Google Scholar] [CrossRef]
- Lagomarsino, S.; Penna, A.; Galasco, A.; Cattari, S. TREMURI program: An equivalent frame model for the nonlinear seismic analysis of masonry buildings. Eng. Struct. 2013, 56, 1787–1799. [Google Scholar] [CrossRef]
- EN1998-1; Eurocode 8: Design of Structures for Earthquake Resistance-Part 1: General Rules, Seismic Actions and Rules for Buildings. Technical Report; European Committee for Standardization: Brussels, Belgium, 2004.
- FEMA. Prestandard and Commentary for the Seismic Rehabilitation of Buildings (FEMA 356); Technical Report; Federal Emergency Management Agency: Washington, DC, USA, 2000. [Google Scholar]
- Tomazevic, M.; Weiss, P. A rational, experimentally based method for the verification of earthquake resistance of masonry buildings. Proceedings of Fourth US National Conference on Earthquake Engineering, Palm Springs, CA, USA, 20–24 May 1990; Volume 2, pp. 349–359. [Google Scholar]
- Tomazevic, M. The Computer Program POR, Report ZRMK; Technical Report; Institute for Testing and Research in Materials and Structures: Ljubljiana, Slovenia, 2016. [Google Scholar]
- POR2000. Structural and Seismic Calculation and Analysis of Masonry Structures. Newsoft. 2023. Available online: https://www.newsoft-eng.it/software/por-2000 (accessed on 10 February 2024).
- Braga, F.; Liberatore, D.; Spera, G. A computer program for the seismic analysis of complex masonry buildings. In Proceedings of the Computer Methods in Structural Masonry-4: Fourth International Symposium; CRC Press: Boca Raton, FL, USA, 1998; Volume 4, p. 309. [Google Scholar]
- Magenes, G.; Della Fontana, A. Simplified non-linear seismic analysis of masonry buildings. Proc. Br. Mason. Soc. 1998, 8, 190–195. [Google Scholar]
- Magenes, G. A method for pushover analysis in seismic assessment of masonry buildings. In Proceedings of the 12th World Conference on Earthquake Engineering, Auckland, New Zealand, 30 January–4 February 2000; Volume 42. [Google Scholar]
- Pasticier, L.; Amadio, C.; Fragiacomo, M. Non-linear seismic analysis and vulnerability evaluation of a masonry building by means of the SAP2000 V. 10 code. Earthq. Eng. Struct. Dyn. 2008, 37, 467–485. [Google Scholar] [CrossRef]
- Salonikios, T.; Karakostas, C.; Lekidis, V.; Anthoine, A. Comparative inelastic pushover analysis of masonry frames. Eng. Struct. 2003, 25, 1515–1523. [Google Scholar] [CrossRef]
- Rinaldin, G.; Amadio, C.; Macorini, L. A macro-model with nonlinear springs for seismic analysis of URM buildings. Earthq. Eng. Struct. Dyn. 2016, 45, 2261–2281. [Google Scholar] [CrossRef]
- Gambarotta, L.; Lagomarsino, S. Sulla risposta dinamica di pareti in muratura. In Atti del Convegno Nazionale “La Meccanica delle Murature tra Teoria e Progetto”; Pitagora Editrice: Messina, Italy, 1996; pp. 18–20. [Google Scholar]
- Gambarotta, L.; Lagomarsino, S. Computational models for the seismic response of damaging structures. In Proceedings of the US-Italian Workshop on Seismic Evaluation and Retrofit, New York, NY, USA, 12–13 December 1996; p. 45. [Google Scholar]
- Kolozvari, K.; Orakcal, K.; Wallace, J.W. New opensees models for simulating nonlinear flexural and coupled shear-flexural behavior of RC walls and columns. Comput. Struct. 2018, 196, 246–262. [Google Scholar] [CrossRef]
- Esmaeiltabar, P.; Vaseghi, J.; Khosravi, H. Nonlinear macro modeling of slender reinforced concrete shear walls. Struct. Concr. 2019, 20, 899–910. [Google Scholar] [CrossRef]
- Quagliarini, E.; Maracchini, G.; Clementi, F. Uses and limits of the Equivalent Frame Model on existing unreinforced masonry buildings for assessing their seismic risk: A review. J. Build. Eng. 2017, 10, 166–182. [Google Scholar] [CrossRef]
- Casolo, S.; Pena, F. Rigid element model for in-plane dynamics of masonry walls considering hysteretic behaviour and damage. Earthq. Eng. Struct. Dyn. 2007, 36, 1029–1048. [Google Scholar] [CrossRef]
- Casolo, S.; Pena, F. Modelling micro-structure aspects of masonry walls by a simplified approach. WIT Trans. Built Environ. 2003, 66, 10. [Google Scholar]
- Casolo, S. Macroscale modelling of microstructure damage evolution by a rigid body and spring model. J. Mech. Mater. Struct. 2009, 4, 551–570. [Google Scholar] [CrossRef]
- Caliò, I.; Marletta, M.; Pantò, B. A simplified model for the evaluation of the seismic behaviour of masonry buildings. In Proceedings of the 10th International Conference on Civil, Structural and Environmental Engineering Computing, Rome, Italy, 30 August–2 September 2005; Civil-Comp Press: Stirlingshire, UK, 2005; Volume 195. [Google Scholar]
- Pantò, B.; Raka, E.; Cannizzaro, F.; Camata, G.; Caddemi, S.; Spacone, E.; Caliò, I. Numerical macro-modeling of unreinforced masonry structures: A critical appraisal. In Proceedings of the Fifteenth International Conference on Civil, Structural and Environmental Engineering Computing, Prague, Czech Republic, 1–4 September 2015; Civil-Comp Press: Stirlingshire, UK, 2015. [Google Scholar]
- Caliò, I.; Pantò, B. A macro-element modelling approach of Infilled Frame Structures. Comput. Struct. 2014, 143, 91–107. [Google Scholar] [CrossRef]
- Pantò, B.; Caliò, I.; Lourenço, P.B. A 3D discrete macro-element for modelling the out-of-plane behaviour of infilled frame structures. Eng. Struct. 2018, 175, 371–385. [Google Scholar] [CrossRef]
- Pantò, B.; Rossi, P.P. A new macromodel for the assessment of the seismic response of infilled RC frames. Earthq. Eng. Struct. Dyn. 2019, 48, 792–817. [Google Scholar] [CrossRef]
- Turnšek, V.; Čačovič, F. Some experimental results on the strength of brick masonry walls. In Proceedings of the 2nd International Brick Masonry Conference, Stoke-on-Trent, UK, 12–15 April 1970; pp. 149–156. [Google Scholar]
- Mann, W.; Müller, H. Failure of Shear-Stressed Masonry: An Enlarged Theory, Tests and Application to Shear Walls. Proc. Br. Ceram. Soc. 1982, 30, 223–235. [Google Scholar]
- Decret, D. Numerical Model for the Assessment of the Seismic Vulnerability of Traditional Masonry Structures with Seismic Bands. Ph.D. Thesis, Université Grenoble Alpes, Grenoble, France, 2021. [Google Scholar]
- Anthoine, A.; Magonette, G.; Magenes, G. Shear-compression testing and analysis of brick masonry walls. In Proceedings of the 10th European Conference on Earthquake Engineering, Vienna, Austria, 28 August–2 September 1994; Volume 3, pp. 1657–1662. [Google Scholar]
- Gambarotta, L.; Lagomarsino, S. Damage models for the seismic response of brick masonry shear walls. Part II: The continuum model and its applications. Earthq. Eng. Struct. Dyn. 1997, 26, 441–462. [Google Scholar] [CrossRef]
- Caliò, I.; Marletta, M.; Pantò, B. A new discrete element model for the evaluation of the seismic behaviour of unreinforced masonry buildings. Eng. Struct. 2012, 40, 327–338. [Google Scholar] [CrossRef]
- Reyes, J.C.; Yamin, L.E.; Hassan, W.M.; Sandoval, J.D.; Gonzalez, C.D.; Galvis, F.A. Shear behavior of adobe and rammed earth walls of heritage structures. Eng. Struct. 2018, 174, 526–537. [Google Scholar] [CrossRef]
- Reyes, J.C.; Smith-Pardo, J.P.; Yamin, L.E.; Galvis, F.A.; Sandoval, J.D.; Gonzalez, C.D.; Correal, J.F. In-plane seismic behavior of full-scale earthen walls with openings retrofitted with timber elements and vertical tensors. Bull. Earthq. Eng. 2019, 17, 4193–4215. [Google Scholar] [CrossRef]
- Grange, S. ATL4S, a Tool and Language for Simplified Structural Solution Strategy; Technical Report; GEOMAS INSA-Lyon: Villeurbanne, France, 2016. [Google Scholar]
- Petrovčič, S.; Kilar, V. Seismic failure mode interaction for the equivalent frame modeling of unreinforced masonry structures. Eng. Struct. 2013, 54, 9–22. [Google Scholar] [CrossRef]
- Magenes, G.; Calvi, G.M. In-plane seismic response of brick masonry walls. Earthq. Eng. Struct. Dyn. 1997, 26, 1091–1112. [Google Scholar] [CrossRef]
- Sandoval Triana, J.D. Estudio Experimental y Modelación del Comportamiento de Estructuras en Adobe. Master’s Thesis, Uniandes, Bogotá, Colombia, 2018. [Google Scholar]




| Stiffness | ||
|---|---|---|
| Young modulus a | 2.1 GPa | |
| Shear modulus a | 420 MPa | |
| Shear strength | ||
| Tensile strength b | 0.345 MPa | |
| Cohesion c | c | 0.23 MPa |
| Coefficient of friction c | 0.43 | |
| Masonry density a | 1750 kg·m−3 | |
| Brick length c | 120 mm | |
| Brick height c | 55 mm |
| High wall | 0.9885–0.99 | 0.82 | 0.6 |
| Small wall | 0.9438–0.9446 | 0.53 | 0.3 |
| Stiffness | ||
|---|---|---|
| Young modulus b | 200 MPa | |
| Poisson’s ratio b | 0.15 | |
| Shear Strength | ||
| Tensile strength a | 27.5 kPa | |
| Cohesion a | c | 15 kPa |
| Friction coefficient a | 0.86 | |
| Masonry density a | 1850 kg·m−3 | |
| Properties of Lintels | ||
| Young modulus c | 9 GPa | |
| Poisson’s ratio c | 0.2 | |
| Section b | 15 × 15 cm2 | |
| Lintel density c | 700 kg·m−3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Decret, D.; Malecot, Y.; Sieffert, Y.; Vieux-Champagne, F.; Daudeville, L. A New Macro-Element for Predicting the Behavior of Masonry Structures under In-Plane Cyclic Loading. Buildings 2024, 14, 768. https://doi.org/10.3390/buildings14030768
Decret D, Malecot Y, Sieffert Y, Vieux-Champagne F, Daudeville L. A New Macro-Element for Predicting the Behavior of Masonry Structures under In-Plane Cyclic Loading. Buildings. 2024; 14(3):768. https://doi.org/10.3390/buildings14030768
Chicago/Turabian StyleDecret, Damien, Yann Malecot, Yannick Sieffert, Florent Vieux-Champagne, and Laurent Daudeville. 2024. "A New Macro-Element for Predicting the Behavior of Masonry Structures under In-Plane Cyclic Loading" Buildings 14, no. 3: 768. https://doi.org/10.3390/buildings14030768
APA StyleDecret, D., Malecot, Y., Sieffert, Y., Vieux-Champagne, F., & Daudeville, L. (2024). A New Macro-Element for Predicting the Behavior of Masonry Structures under In-Plane Cyclic Loading. Buildings, 14(3), 768. https://doi.org/10.3390/buildings14030768








