Abstract
This paper focuses on the response of reticulated shell structures under oblique impact loads, with a departure from the traditional emphasis on vertical impact loads. These structures are typically utilised in large-span spaces such as iconic buildings and large venues. The study begins by establishing a numerical simulation method for reticulated shell structures subjected to oblique impact loads, which is then validated against existing experimental results. Building on this verified method, the research delves into the effects of varying impactor mass, velocity, and initial kinetic energy on the reticulated shell structure under oblique impacts, as well as the influence of different oblique impact angles. The study extensively examines the failure modes of the structure, node displacements in the structure, and variations in member stress under different impactor parameters. It further investigates how these parameters influence the maximum impact bearing capacity, impact duration, energy dissipation capability, and response forms of the structures, analyzing the reasons behind these effects. The findings offer valuable insights for further research and practical engineering design of reticulated shell structures.
1. Introduction
Reticulated shell structures form the basis for numerous practical engineering applications and novel, reasonable architectural structures. Additionally, they are widely exploited for their beautiful shape and the ability to distribute forces in a uniform manner, which refers to the even spread of stresses primarily under vertical loads. These structures are also designed to resist horizontal loads effectively, and special considerations are considered to manage local effects and stress concentrations around openings. Reticulated shells are often the structures of local landmark buildings. However, frequent terrorist attacks and military activities have brought attention to the impact resistance of architectural structures; large-span space buildings are mostly national and regional landmark buildings, which can easily become targets of terrorist and military attacks and suffer from external impact, resulting in immeasurable losses. In this context, studying the impact resistance of long-span space structures is of great political and economic significance.
Before studying the dynamic response of structures under an impact load, the mechanical properties of materials under high-speed impact should be defined. Cowper and Symonds [1] proposed the C-S constitutive model, which provides the relationship between material stress and strain rate. This piecewise-linear plasticity model can effectively characterise the dynamic mechanical behaviour of metal materials; thus, it is widely used in the field of structural impact resistance. Johnson and Cook [2] proposed the J-C constitutive model, which comprehensively considers the influence of large strain, large stress, and high temperature on metal materials under high-speed impact. Paul [3] proposed an elastoplastic constitutive model that is suitable for wide strain rates and temperature ranges. This model was adapted to characterise the dynamic mechanical behaviour of steel and has been successfully applied to low-carbon steel ES, DP600, and TRIP700. However, the parameters of this model are coupled with each other and difficult to calibrate. This bottleneck restricts the application of this model to a wide range of materials. Based on the above research analysis, the current research on the dynamic mechanical properties of materials is relatively mature, among which the Cowper-Symonds constitutive model and the Johnson-Cook constitutive model are widely used in the field of structural impact resistance.
The dynamic response of structural components to impact loads is a critical area of research in structural engineering. In the realm of metallic components, Al-Thairy et al. [4], Liang et al. [5,6], Li et al. [7], and Xiang et al. [8] have contributed significantly. Their research spans from the numerical simulation of steel columns under impact to the assessment of energy absorption in dimpled steel sheets and the analysis of impact resistance in steel parking structure columns. For non-metallic components, Bambach et al. [9], Wang et al. [10], Goswami et al. [11], Lee et al. [12], Li et al. [13], and Li et al. [14] have provided valuable insights. Their work includes the exploration of concrete-filled steel beams, ULCC-filled pipe-in-pipe composites, concrete slab shear failure, steel plate-concrete composite walls, and the dynamic performance of concrete beams, among others. The dynamic analysis of light weight structures is also being studied; Slimane et al. [15] suggested using a bilayer ceramic/aluminum honeycomb sandwich panel (HSP) for spacecraft shielding against orbital debris, showing improved resistance compared to monolayer concepts through modelling and experiments; Sun et al. [16] studied the impact response of a composite structure consisting of a metal-packaged ceramic interlayer and an ultra-high molecular weight polyethylene (UHMWPE) laminate through a ballistic test and numerical simulation. Additionally, the influence of impact angles is a crucial aspect; Yang et al. [17] simulated the circular steel tube response to lateral impact. It analysed factors such as impact angle, energy, and failure modes, finding that impact forces depended on angle and velocity, while failure modes were energy-driven. This research has illuminated how impact angles affect the forces and failure modes in structural components, which is vital for the design and safety of structures.
Recent years have witnessed a significant focus on the dynamic response of large-span space structures under various impact loads. Gupta et al. [18,19,20,21] conducted in-depth studies on thin-walled spherical aluminium shells, examining deformation modes under axial compression and impact loads, thereby laying a foundation for understanding the collapse behaviour of metallic shells. Fan et al. [22,23,24] contributed by proposing an efficient method for solving impact problems using finite element analysis, identifying four distinct failure modes in reticulated domes. Zhi et al. [25,26] expanded this research to the safety and protective measures of single-layer reticulated domes under various loads, including impact and seismic forces. Their work was complemented by Zhai et al. [27], who focused on blast resistance strategies for dome structures. Wang et al. [28,29], Ma et al. [30,31], and Hu et al. [32] furthered the understanding of dynamic responses, failure modes, and energy mechanisms in reticulated shell structures and hemispherical shell systems under impact loads. This line of inquiry was continued by Su et al. [33], who studied the dynamic response of long-span reticulated shells under external explosion loads. The research scope was broadened by Zhi et al. [34], Ma et al. [35], and Nazari et al. [36], who investigated the dynamic behaviour of reticulated domes and double-layer domes under various impact scenarios. Wu et al. [37], Deepshikha et al. [38], and Pilarska et al. [39] contributed by examining multi-point impacts, roof-substructure interactions, and seismic effects on dome structures. Xu et al. [40,41] focused on the impact response of spherical reticulated shell structures and plane cable-membrane structures, respectively, exploring the effects of various factors on dynamic response and failure modes. Rossot et al. [42] conducted studies on geodesic domes and composite materials under impact, enhancing the understanding of structural behaviour under different loading conditions. Gou et al. [43] and Shen et al. [44] explored the dynamic behaviour of welded spherical joints and mesh shells and the impact resistance of large-span net shell structures, respectively, using advanced numerical methods and experimental techniques to assess the effects of combined loads and material properties on structural response. This body of work collectively enhances our understanding of the dynamic behaviour of these critical structures, guiding future designs towards greater resilience against impact loads.
In the current landscape of research, studies on the performance of steel structures under oblique impact loads predominantly focus on individual components [17]. Notably, the mass, velocity, initial kinetic energy, and impact angle of the impactor play a crucial role in influencing the dynamic response of reticulated shell structures [44]. However, most existing research on these structures’ centres around vertical and horizontal impacts, with limited exploration into the effects of oblique impacts. This study investigated the dynamic response and failure modes of reticulated shell structures under oblique impact loads. Utilizing a numerically simulated method, which was validated through experimental data, we examined the dynamic responses of these structures under different oblique impact loads on a plumb surface and assessed the influence of the impactor parameters on their dynamic behaviour. Our investigation first identified and analysed two distinct failure modes—unpenetrated and penetrative—and their energy dissipation capacity. Further, we delved into the intricacies of node displacements and internal member stresses, particularly noting their correlation with proximity to the impact point. A pivotal aspect of our research was the assessment of how variations in the oblique impact angle affected the structure’s response. Finally, our findings provided insights for optimising the design and reinforcement of reticulated shell structures.
2. Experimental Verification
2.1. Finite Element Modelling
This study was mainly conducted using numerical simulation. To verify the accuracy of the numerical simulation method, the impact test results of existing reticulated shell structures [40] were selected for verification. The test-verified model was a Kiewitt6 (K6) single-layer spherical reticulated shell (see Figure 1) with a span of 1800 mm and a vector span ratio of 1/9.2307. The reticulated shell member had a round tube section with an outer diameter of 14 mm and a wall thickness of 2 mm. The boundary conditions of the model were three-directional fixed hinge supports. The relevant material properties of the Q235B steel adopted in steel reticulated shells are listed in Table 1. The drop weight in the test was 100.5 kg, and drop hammer heights of 8 mm and 10 mm were used to simulate the elastic impact test, while a drop hammer height of 3.2 m was used to simulate the destructive impact test.
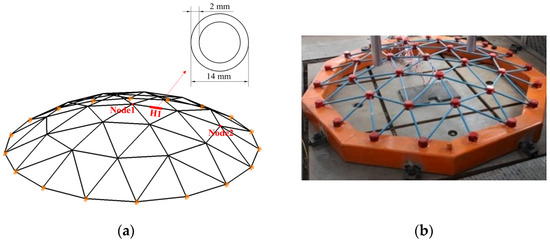
Figure 1.
Schematic diagram of the reticulated shell: (a) Simulation; (b) Experiment in literature [40].

Table 1.
Parameters of Q235B steel.
In this study, numerical simulation analysis was performed using the common finite element software, ABAQUS version 6.1.4. As the members in the reticulated shell structure were subjected to bending moment, shear, and tensile forces at the same time, B33 from the ABAQUS element library was used for the simulation, and for the impactor, a discrete rigid body was chosen for the simulation, which could effectively avoid the problem of inaccurate friction caused by the rigid body mesh being too rough. The mesh size of the latticed shell was determined to be 15 mm. The finite element analysis utilised in this study employed an explicit time integration scheme to address the time-dependent dynamic response. The time step size was determined through a series of trials based on the stability of the time-history curve, ensuring numerical stability and accuracy throughout the simulation process. Meanwhile, the contact between the reticulated shell and impact body was considered. The contact type between the impactor and the reticulated shell structure was implemented using ABAQUS’s advanced algorithms for general contact, which involved sophisticated tracking of the contact surface as opposed to simpler node-to-surface methods. The contact properties were divided into tangential and normal behaviour; the tangential behaviour was a penalty function method with a friction coefficient of 0.15, which was implemented to accurately simulate the resistance generated at the contact interface during impact; in the normal direction, an augmented Lagrangian contact formulation, known as “hard contact” in ABAQUS, was used to accurately simulate the interaction. Moreover, the simulation accounted for large displacement effects, ensuring that the non-linear deformation behaviour of the shell structure under loading was accurately captured. Furthermore, material damping effects have been considered; these dissipative phenomena were directly incorporated within the constitutive laws chosen for the simulation. The C-S constitutive model [1] was adopted to simulate the reticulated shell material. The expression of the model is shown in Equation (1).
where is the effective strain rate; is the yield stress with a constant strain rate ; and are the strain rate parameters, taken as 5 and 40 [45] for low-carbon steel, respectively; is the material yield strength; is the effective plastic strain; is the Yong’s modulus; and is the strain-hardening modulus.
2.2. Verification of the Numerical Simulation Method
The experimental data were obtained from the literature [40], such as time-history curves, axial stress, and displacements. The experimental and numerical comparisons of the axial stresses in H1 when the height of the drop hammer was 8 and 10 mm are displayed in Figure 2. Obviously, the numerical results were in accordance with the experimental results. Table 2 quantitatively analyses the stress in H1 obtained from experimental and numerical investigations. Note that the minus sign in Table 2 denotes that member H1 is in compression. As it can be seen, the differences between the experimental and numerical results were around 5.0% and 4.7% for the cases of 8 mm and 10 mm drop hammer heights, respectively. Thus, it was accurate to investigate the behaviour of single-layer reticulated shells under impact loading by using numerical analysis.

Figure 2.
Time-history curve of H1 with different drop hammer heights: (a) 8 mm; (b) 10 mm.

Table 2.
Comparison of H1 axial stress between the experimental and numerical stress in H1.
Figure 3 shows the failure mode obtained by numerical simulation of the reticulated shell when the impact height was 3.2 m. It could be observed that the failure mode of the reticulated shell was concave in the middle, which was in good agreement with the experimental results provided in reference [40]. The comparisons of the vertical displacement results for typical nodes are listed in Table 3. In this study, the direction of displacement was defined as vertical. Clearly, the displacement of the vertex was significantly larger than that of the other nodes under an impact load. The greater the distance from the vertex, the smaller the node displacement; this was consistent with the failure mode in Figure 3. Table 3 shows that even for the destructive impact experiment, the finite element analysis showed good accuracy.

Figure 3.
Failure modes for the destructive impact simulation of the reticulated shell structure: (a) Simulation; (b) Experiment in literature [40].

Table 3.
Comparison of displacements for typical nodes under 3.2-m impact.
3. Impact Response of Reticulated Shell Structures under Oblique Impact Load
3.1. Analytical Model
The feasibility of using the ABAQUS software to analyse the impact response of the K6 reticulated shell structure was verified in the previous section. Practically, the impact load is not always along the normal direction of the reticulated shell surface but may form a certain angle with the normal direction of the surface (i.e., oblique impact). Therefore, this study focused on the impact response of K6 reticulated shell structures under oblique impact loads. Regarding the reticulated shell structure designed in this study, its span was 60 m, the vector span ratio was 0.22, the division frequency was six, and it was simply supported. The outer diameter and wall thickness of the radial member were 168 mm and 6 mm, respectively; the outer diameter and wall thickness of the circumferential member were 140 mm and 5 mm, respectively; and the outer diameter and wall thickness of the oblique member were 100 mm and 5 mm, respectively. The yield strength of the adopted steel was 235 MPa, and the failure strain was 0.25. The constitutive model of steel adopted the C-S constitutive model [1]. Figure 4a,b show the geometric and finite-element models of the reticulated shell structure, respectively. The numerical simulation method was carried out as described in Section 2.

Figure 4.
Structural models of the reticulated shells: (a) Geometric model; (b) Finite element model.
When studying the impact response of a reticulated shell structure, the deformation characteristics of the structure and the failure of the member need to be considered. In this study, the impact response of a reticulated shell structure was determined by analyzing the change in displacement of the reticulated shell node under an impact load and the change in axial stress of the bar member. For convenience, part of the reticulated shell nodes and members are numbered in Figure 4a, in which node 3 is the application point of the impact load. For the analysis in this section, the impact angle (i.e., the angle between the impact direction and horizontal plane) was set to 66.25°. The local angle between the tangential plane of the structures and the horizontal plane was 23.75°. Table 4 presents the range of values for two parameters, namely the mass and velocity of the impactor. Specifically, a large number of cases (56 in total, generated by combining 7 masses with 8 velocities) were created to simulate the uncertainty of impact loads in real-life scenarios. Additionally, the kinetic energy of the impactor, ranging from 6.25 × 103 J to 1.25 × 1010 J, is considered. Based on these cases, the distribution of failure modes in shell structures was investigated.

Table 4.
Distribution of mass and velocity of the impactor.
3.2. Failure Mode
3.2.1. Unpenetrated Failure
The impact deformation process of the reticulated shell structure under the impactor for unpenetrated failure is shown in Figure 5. When the impactor acted on the reticulated shell structure, the contact member deformed, and the deformation range gradually expanded until the structure failed. The failure feature was that the impactor did not penetrate the reticulated shell structure during impact failure. For unpenetrated failure, the reticulated shell member potentially may not break. It should be noted that the difference between (c) Gradual deformation and (d) Final state is that (c) Gradual deformation indicated the structure had not yet reached a stable state, and there were still vibrations in the members and nodes, but (d) Final state indicated the structure had reached a static state. Figure 6 shows the deformation of the reticulated shell structure under different impact masses and velocities. When the impact mass was 20 t and the velocity was 10 m/s (kinetic energy = 1 × 106 J), only a local depression occurred in the reticulated shell structure. When the impact mass was 5 t and the velocity was 50 m/s (kinetic energy = 6.25 × 106 J), the depression range increased significantly. When the impact mass was 100 t, and velocity was 20 m/s (kinetic energy = 2 × 109 J), the overall structure was deformed. The observed failure modes in the reticulated shell structure demonstrated a clear correlation with the kinetic energy of the impact. Higher kinetic energies, resulting from either increased mass or velocity, tended to cause more extensive deformation and damage, highlighting the kinetic energy of the impactor and determining the severity of the impact on the structure.
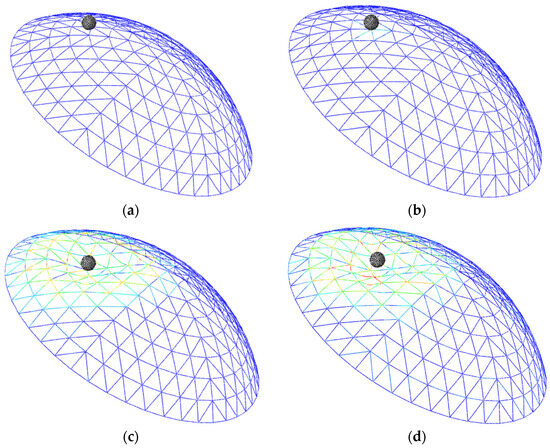
Figure 5.
Deformation process of the reticulated shell structure experiencing unpenetrated failure: (a) Original state; (b) Beginning of contact; (c) Gradual deformation; (d) Final state.
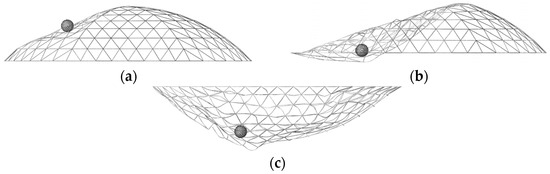
Figure 6.
Typical failure modes of unpenetrated failure: (a) 20 t, 10 m/s; (b) 5 t, 50 m/s; (c) 100 t, 20 m/s.
The time-history curves of the kinetic energy of the impactor in the entire impact process under the three failure modes shown in Figure 6. can be used to analyse the mechanism behind these modes; these curves are shown in Figure 7. When the impact mass was 20 t and the velocity was 10 m/s, the corresponding initial kinetic energy was at a minimum of approximately 1 × 106 J. If the initial kinetic energy of the impactor was small, the reticulated shell structure would undergo local depression deformation when unpenetrated failure occurred. Additionally, when the structure was damaged, the kinetic energy corresponding to the impactor remained constant. Accordingly, the energy change rates of the impactor under the three situations were calculated as 96.06, 99.45, and 99.13%, respectively, and this part of the changed energy was absorbed by the reticulated shell structure. It can also be seen that the slope of the kinetic energy time course curve can reflect the impact duration accurately. The kinetic energy time-history curve in Figure 7c changed from a convex function at the beginning to a concave function, with the slope smaller than Figure 7a,b at each time point. The slope of Figure 7b was also larger than Figure 7a at each time point, so the magnitude of the impact duration relationship is: (c) > (a) > (b). It can be observed from Figure 6 and Figure 7 that the reticulated shell structure exhibited a local bending response under impact with a mass of 20 t and a velocity of 10 m/s, and the structure exhibited an overall bending/shear response with a mass of 5 t and a velocity of 50 m/s. The energy change rate of the structure exhibiting an overall bending/shear response (99.45) is significantly larger than that of the structure exhibiting a local bending response (96.06). Meanwhile, the impact duration of structures that exhibited an overall bending/shear response was shorter than that of structures exhibiting a local bending response. It could be concluded that the energy dissipation capacity of the reticulated shell structure varies significantly with the form of response, which is influenced by the combination of impact mass and velocity.
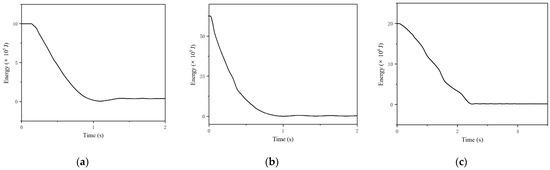
Figure 7.
Time-history curve for kinetic energy under different impact parameters for unpenetrated failure: (a) 20 t, 10 m/s; (b) 5 t, 50 m/s; (c) 100 t, 20 m/s.
Figure 8 and Figure 9 show the time-history curves of the displacement and axial stress, respectively, of the typical nodes and members experiencing unpenetrated failure. Figure 8 shows that when the weight of the impactor is 20 t and the impact velocity is 10 m/s, only nodes 2, 3, and 4 exhibited obvious displacements, and the maximum displacement is roughly 4.5 m. When the weight was 100 t and the impact velocity was 20 m/s, the seven typical nodes exhibit obvious displacements, and the maximum displacement was approximately 27 m. By comparing the displacement amplitudes of each node in Figure 8, it can be found that the magnitude of the displacement amplitudes of each node is (c) > (b) > (a), and the magnitude of the initial kinetic energy of the impactor is (c) > (b) > (a). Therefore, it can be concluded that the displacement amplitude of the node is positively correlated with the initial kinetic energy of the impactor for unpenetrated failure. Furthermore, comparisons of deformation patterns of structures were conducted: the structure exhibiting a local bending response, as shown in Figure 8a, showed localised deformations (nodes 1, 2, and 4); for the structure exhibiting an overall bending/shear response, as shown in Figure 8b, the deformations were more uniform and distributed over a larger area (nodes 1 to 6). Comparing the members’ axial stress of structures exhibiting different responses, it was found that for structures exhibiting a local bending response, as shown in Figure 9a, only a few members (member R2) experienced significant stress during the impact duration; for structures exhibiting an overall bending/shear response, as shown in Figure 9b, most selected members exhibited significant axial stress. This phenomenon can also explain why the structures exhibiting an overall bending/shear response had a stronger energy dissipation capacity. By comparing Figure 8 and Figure 9 and considering the relationship between the nodes and members shown in Figure 4, it is inferred that the stress variation law of the members is consistent with the deformation law. For example, in Figure 9a, the axial stress of member R2 is the highest, and R2 corresponds to nodes 2 and 3, as shown in Figure 4. Therefore, the displacements of nodes 2 and 3 in Figure 8a are also the largest.

Figure 8.
Time-history curve of displacement of typical nodes experiencing unpenetrated failure: (a) 20 t, 10 m/s; (b) 5 t, 50 m/s; (c) 100 t, 20 m/s.
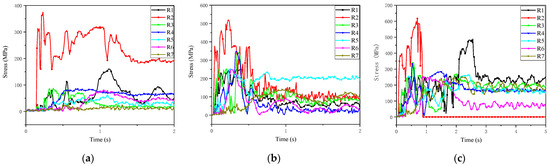
Figure 9.
Time-history curve of axial stress of typical bars experiencing unpenetrated failure: (a) 20 t, 10 m/s; (b) 5 t, 50 m/s; (c) 100 t, 20 m/s.
3.2.2. Penetrated Failure
The deformation process of the reticulated shell structure experiencing penetration failure under the impactor is shown in Figure 10. When the reticulated shell structure was subjected to an impact load, the structure diffused around the impact point as the center, resulting in both deformation and the members near the impact point breaking. In contrast to unpenetrated failure, the failure characteristics of penetrated failure included the reticulated shell member breaking and the impactor penetrating the reticulated shell structure. Depending on the impact parameters, different types of penetrated failure modes may occur in reticulated shell structures. Figure 11 shows several typical penetrated failure modes of reticulated shell structures under different impact masses and velocities: when the impact mass was 50 t and the velocity was 50 m/s (kinetic energy = 6.25 × 107 J), the reticulated shell structure experienced wide-ranging depression under impact; when the impact mass was 50 t and the velocity was 150 m/s (kinetic energy = 5.62 × 108 J), the reticulated shell structure was partially damaged under impact; when the impact mass was 50 t and the velocity was 500 m/s (kinetic energy = 6.25 × 109 J), the reticulated shell structure exhibited local penetration, and there was almost no deformation in the non-impact area.
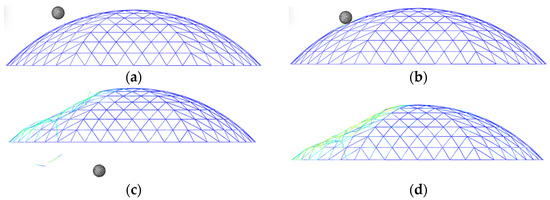
Figure 10.
Deformation process of reticulated shell structure experiencing penetrated failure: (a) Original state; (b) Beginning of contact; (c) Gradual deformation; (d) Final state.
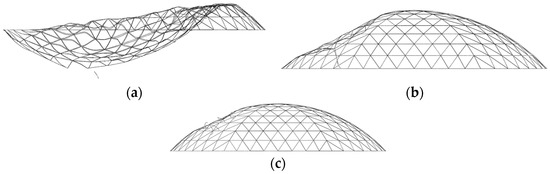
Figure 11.
Typical failure modes of penetrated failure: (a) 50 t, 50 m/s; (b) 50 t, 150 m/s; (c) 50 t, 500 m/s.
Figure 12 shows the kinetic energy-time history curves of the reticulated shell structure experiencing penetrated failure under different impact parameters. The larger the initial impact velocity of the impactor, the faster its energy attenuation. When the initial impact velocity was 50 m/s, it took approximately 1 s to decay to a stable value. When the initial impact kinetic energies were 6.25 × 107, 5.63 × 108, and 6.25 × 109 J, the energy change rates of the shell structure before and after contact with the impactor were 23.97, 1.48, and 0.24%, and the corresponding dissipated energy values were 15.0 × 106, 8.3 × 106, and 15.0 × 106 J. It could be found that the dissipated energy values were relatively close. This was because the impactor penetrated the reticulated shell structure during the penetration failure. This indicated that for structures with penetration failure, the kinetic energy of the impactor has exceeded their energy dissipation capacities; the energy change rate naturally decreased as the kinetic energy of the impactor increased.
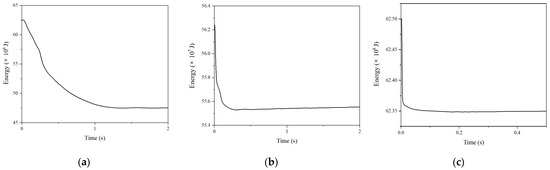
Figure 12.
Kinetic energy-time history curve under different impact parameters for penetrated failure: (a) 50 t, 50 m/s; (b) 50 t, 150 m/s; (c) 50 t, 500 m/s.
Figure 13 and Figure 14 show the time-history curves of the displacement and axial stress of the typical nodes and members when the reticulated shell structure is experiencing penetrated failure. When the impact rate was 500 m/s, node 3 was damaged. Therefore, the displacement time-history curve of node 3 is not shown in Figure 13c. The greater the initial impact velocity of the impactor, the shorter the impact failure time of the reticulated shell structure. When the initial impact velocity was 50 m/s, the longest time required for completion of the impact was approximately 2 s. In Figure 13a, for the impactor with an initial kinetic energy of 6.25 × 107 J, the deformations were uniform and distributed over a large area, and the structure exhibited an overall bending/shear response as the part structures with unpenetrated failure. In Figure 13b, for the impactor with an initial kinetic energy of 5.63 × 108 J, node 3, which was in contact with the impactor, underwent a significant displacement, and other nodes experienced small and fluctuating displacements or not. This was because the structure exhibited a local bending response. When the initial kinetic energy of the impactor was 6.25 × 109 J, as displayed in Figure 13c, the impactor instantly penetrated the structure. The node in contact with the impactor was destroyed within 0.02 s; the other nearby nodes all experienced significant deformation in a short period of time. This is because the structure dissipated a large amount of energy in a short time and exhibited local penetration. Figure 14 shows that all three impactors caused fracture failure of the member of the reticulated shell structure, which is also consistent with the failure mode shown in Figure 11. The structure, as displayed in Figure 14a, exhibited an overall bending/shear response, and most of the selected members participated in the dynamic load-carrying process. The structure displayed in Figure 14b exhibited a local bending response, and member R2 participated in the dynamic load-carrying process together with the nearby members. The structure displayed in Figure 14c exhibited local penetration, and fewer members participated in the dynamic load-carrying process except member R2.
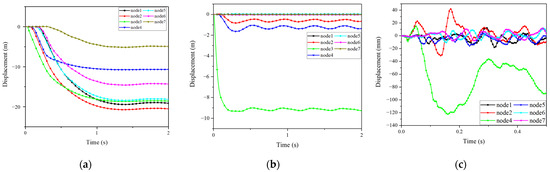
Figure 13.
Time-history curve of displacement of typical nodes experiencing penetrated failure: (a) 50 t, 50 m/s; (b) 50 t, 150 m/s; (c) 50 t, 500 m/s.
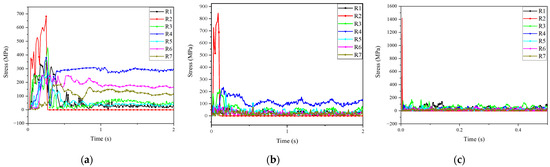
Figure 14.
Time-history curve of axial stress of typical members experiencing penetrated failure: (a) 50 t, 50 m/s; (b) 50 t, 150 m/s; (c) 50 t, 500 m/s.
4. Comparative Analysis of the Dynamic Response of Reticulated Shell Structure at Different Impact Angles
In the previous section, the K6 single-layer spherical reticulated shell structure was subjected to an oblique impact at 66.25° under various working conditions. Its failure modes were divided into two types, and the dynamic response characteristics of each failure mode were studied. Owing to the great uncertainties in practically using impactors, studying only the impact in the inclined direction at 66.25° is far from sufficient. Therefore, in this section, we have considered the impact angle of the impactor as the variable and have selected 15, 30, 45, 60, and 75° on the plumb surface as the impact angles to study the effect of the impact angle on the dynamic response of K6 single-layer spherical reticulated shell structures.
4.1. Influence of Oblique Impact Angle on Impact Response of Reticulated Shell Structure Experiencing Unpenetrated Failure
In this section, we focused on the effects of an oblique impact angle using a selected impact mass of 20 t and an impact velocity of 10 m/s (kinetic energy = 1 × 106 J). Table 5 lists the impact duration, maximum impact force, and energy transfer rate for the reticulated shell structure at various impact angles. To quantitatively assess the influence of the impact angle, we introduced the coefficient of variation (CoV), a measure that represents the ratio of the standard deviation to the mean of a data set, providing insight into the data’s dispersion. Our calculations revealed that the CoV for impact duration, maximum impact force, and energy transfer rate were 0.028, 0.054, and 0.168, respectively. These findings suggested that the impact angle had a negligible impact on the duration and force of the impact, but it had a substantial role in determining the rate of energy transfer.

Table 5.
Impact duration, maximum impact force, and energy transfer rate at various impact angles for unpenetrated failure.
Figure 15 shows the deformation of the reticulated shell structure experiencing unpenetrated failure at different oblique impact angles. Generally, under the six impact angles analysed here, the reticulated shell structures exhibited depression deformation near the impact point, and they all exhibited the overall bending/shear response. When the oblique impact angle was 15°, the impactor reversely bounced back after impacting the reticulated shell structure and did not contact the reticulated shell structure, as shown in Figure 15a. When the oblique impact angle was greater than 15°, the impactor did not bounce back but was in continuous contact with the reticulated shell structure. Accordingly, at this angle, the lowest energy transfer rate was only 56.9%, as listed in Table 5.
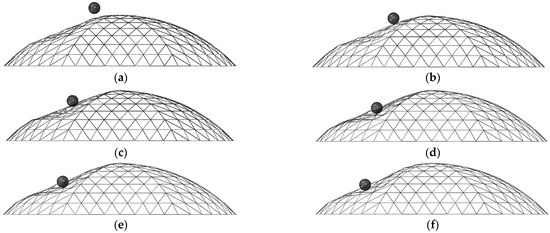
Figure 15.
Deformation under unpenetrated failure at different impact angles: (a) 15°; (b) 30°; (c) 45°; (d) 60°; (e) 66.25°; (f) 75°.
Figure 16 shows the impact force-time history curves and kinetic energy-time history curves when the reticulated shell structure is not penetrated at different impact angles. The time-history curves of the impact force at different angles exhibited the same trend (Figure 16a), but the energy transfer rate gradually increased with an increase in the impact angle (Figure 16b). When the oblique impact angle exceeded 45°, the energy transfer rate reached 90%, and the structure had a close energy transfer rate under oblique impact with different impact angles. It could be concluded that when the oblique impact angle is greater than 45 °, its impact on the energy dissipation capacity of the structure is limited.
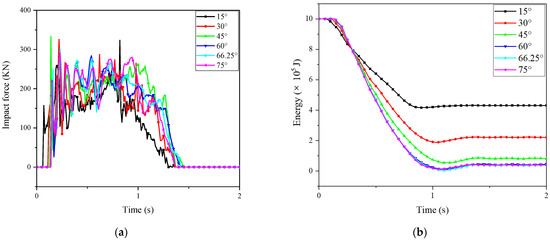
Figure 16.
Time-history curve of impact force and kinetic energy at different impact angles for unpenetrated failure: (a) time-history curve of impact force; (b) time-history curve of kinetic energy.
Figure 17 shows the displacement-time history curves of typical nodes of the reticulated shell structure experiencing unpenetrated failure at different oblique impact angles. The oblique impact angle had a significant influence on the node displacement. The displacement of the typical nodes was generally greater at an impact angle greater than 60° than at an angle less than 60°. Referring to the energy transfer rate shown in Table 5, node displacement is positively correlated with the energy transfer rate. This is because structures that exhibit similar responses typically have energy dissipation capacities that are positively correlated with the extent of their structural deformations.

Figure 17.
Displacement-time history curves of typical nodes experiencing unpenetrated failure at different impact angles: (a) node 1; (b) node 2; (c) node 3; (d) node 4; (e) node 5; (f) node 6; (g) node 7.
Figure 18 shows the time-history curves of the axial stress of a typical bar experiencing unpenetrated failure at different oblique impact angles. The typical bar did not break under different impact angles in this section. The stress of member R2 was the largest, and that of member R7 was the smallest. This was because R2 was close to the position of the impactor. It could be observed that the sensitivity of members positioned differently within the structure to impacts at various angles was not uniform. For instance, for member R3, the impact at a 75° angle was of greater concern. Meanwhile, member R1 was particularly susceptible to failure when subjected to an impact at a 45° angle, warranting closer attention due to its heightened vulnerability at this specific angle. This variability in response underscores the importance of considering the angle of impact in the structural analysis of each individual member.
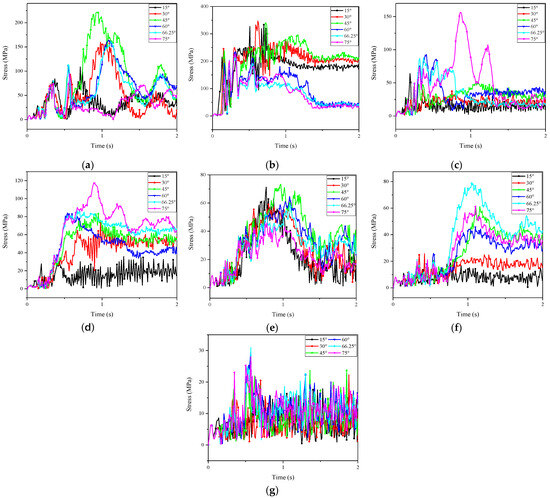
Figure 18.
Stress-time history curve of a typical member under different impact angles: (a) R1; (b) R2; (c) R3; (d) R4; (e) R5; (f) R6; (g) R7.
4.2. Influence of Oblique Impact Angle on Impact Response of Reticulated Shell Structure Experiencing Penetrated Failure
In the previous section, the unpenetrated failure of reticulated shell structures at different oblique impact angles was studied. In this section, the impact angle on the impact response of the penetrated failure was studied. Similar to the previous section, this section also considered impact angles of 15, 30, 45, 60, 66.25, and 75°. In the analysis in this section, the mass of the impactor was 50 t, and the impact velocity was 200 m/s (kinetic energy = 1 × 109 J). Table 6 lists the impact duration, maximum impact force, and energy transfer rate at different oblique impact angles. The closer the impact angle was to 45°, the greater the impact force. Regardless of the impact angle, the energy transfer rate of the structure experiencing penetration failure studied in this section was small. In several cases listed in Table 6, the energy transfer rate is approximately 1%, which is significantly lower than the rates under unpenetrated failure shown in Table 5. It could be calculated that the CoV for the duration of impact, maximum impact force, and energy transfer rate were 0.259, 0.489, and 0.094, respectively. It could be seen that, in contrast to unpenetrated failure, the impact angle had a greater influence on the duration of impact and maximum impact force but a smaller impact on the energy transfer rate.

Table 6.
Impact duration, maximum impact force, and energy transfer rate at various impact angles for penetrated failure.
Figure 19 shows the failure modes of the reticulated shell structure when penetration failure occurs at different oblique impact angles. In the six cases shown in Figure 19, the reticulated shell structures all have depressions near the impact point. It could be observed that the oblique impact angles of the impactor did not change the response form of the structures, and these structures all exhibited a local bending response. However, from the failure modes, it could be found that when the angle is 30 or 45°, the impact areas on the structures were more dispersed compared to other impact angles. This dispersed force distribution helped to reduce local stress concentration and explained the phenomenon that the maximum impact force with these angles is greater, especially for the oblique impact angle of 45°.

Figure 19.
Deformation under penetrated failure at different impact angles: (a) 15°; (b) 30°; (c) 45°; (d) 60°; (e) 66.25°; (f) 75°.
Figure 20 shows the impact force-time history curves and kinetic energy-time history curves when penetrated failure occurs in the reticulated shell structure at different impact angles. As shown in Figure 20a, the impact force at all angles decreases to zero within 0.05 s, indicating that the impactor instantly penetrated the reticulated shell structure. It was found that the maximum impact force on the structure occurred when the impact angle is 45 °. It could be observed in Figure 20b that the oblique impact angles had a slight impact on the energy change rate, while a small angle could only bring a small improvement in the energy change rate.

Figure 20.
Time-history curve of impact force and kinetic energy at different impact angles for penetrated failure: (a) time-history curve of impact force; (b) time-history curve of kinetic energy.
Figure 21 shows the displacement-time history curves of typical nodes in the case of penetrated failure at different impact angles. In several cases analysed in this section, node 3 was damaged under impact. Therefore, the displacement-time history of node 3 is not shown in Figure 22. Generally, when the oblique angle is less than 45°, the displacement deformation of the point is relatively large, maintaining consistency with the larger energy transfer rate in Table 6 and Figure 20b. Figure 22 shows the maximum stress of typical bars at different oblique impact angles. Obviously, under the six impact angles shown in Figure 19, member R2 experienced fracture failure. It could be observed from Figure 22b that, compared to larger impact angles, when the impact angle is less than 45 °, the maximum impact force of the structure is greater, but the stresses of the member R3, which was in contact with the impactor, are relatively smaller. This indicated that, under these angles of impact, the structure could effectively distribute the impact force to other members of the structure.

Figure 21.
Displacement-time history curves of typical nodes experiencing penetrated failure at different impact angles: (a) node 1; (b) node 2; (c) node 4; (d) node 5; (e) node 6; (f) node 7.
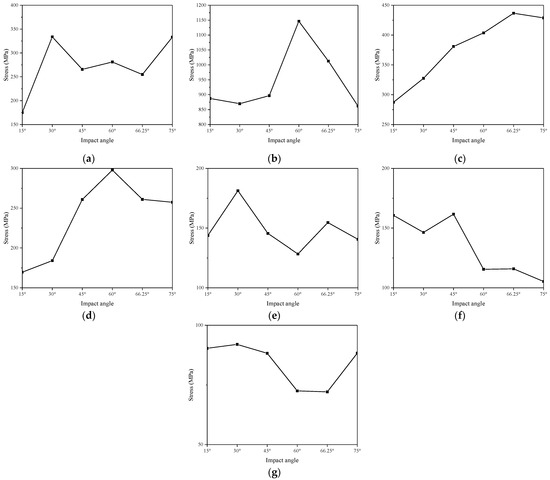
Figure 22.
Maximum stress curve of a typical member under different impact angles: (a) R1; (b) R2; (c) R3; (d) R4; (e) R5; (f) R6; (g) R7.
5. Conclusions
In this study, based on the experimentally verified numerical simulation method, a series of studies on the impact response of reticulated shell structures under oblique loads were conducted. The main conclusions are as follows:
- The failure modes of the reticulated shell structure under oblique impact loads were divided into two types: unpenetrated and penetrated failure modes. In the case of unpenetrated failure, most of the impact energy was absorbed by the reticulated shell structure; the structures always exhibited a local bending response for the impactor with a small initial kinetic energy and an overall bending/shear response for the impactor with a large one. In the case of penetrated failure, only a small part of the impact energy was absorbed by the reticulated shell structure; the structures exhibited an overall bending/shear response or local penetration, depending on the initial kinetic energy of the impactor.
- For the reticulated shell structure experiencing unpenetrated failure mode, the oblique impact angle had a quite limited effect on the impact duration and maximum impact force, but had an important effect on the energy dissipation capacity of the structures, especially for the oblique impact angle less than 60°. When the impact angle exceeded 60°, the energy change rates of the structure remained consistently above 90%, and the influence of the oblique impact angle on the energy change rate was limited.
- For the reticulated shell structure experiencing penetrated failure mode, the oblique impact angle had a slight effect on the energy change rate of the structure. However, it played an important part in the maximum impact force of the structures. Compared to other angles, the structure exhibits the greatest impact force at an oblique impact angle of 45°. It was noteworthy that the impact angle had a relatively limited influence on the response mode of the structures experiencing both unpenetrated and penetrated failure modes.
This study delved into the impact of various oblique impact angles on reticulated shell structures. The findings could offer valuable insights for practical engineering applications, particularly in the design of reticulated shell structures. These insights could guide engineers in better designing these structures, considering the oblique impact angles, to enhance their performance and resilience in real-world scenarios.
Author Contributions
Conceptualisation, P.L.; methodology, G.C. and H.W.; software, H.L. and B.J.; validation, G.C. and L.K.; formal analysis, G.C. and H.L.; investigation, L.K.; resources, L.K.; data curation, H.L. and B.J.; writing—original draft, G.C. and H.L.; writing—review and editing, P.L., G.C. and H.W.; visualisation, H.L.; supervision, H.W. and B.J.; project administration, P.L. and B.J.; funding acquisition, P.L. and H.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China, grant number 51890902, the Natural Science Foundation of Shandong Province, grant number ZR2020QE244, and the Science and Technology Program of the Housing and Urban-Rural Development Department of Shandong Province, grant number 2021-K5-16.
Data Availability Statement
The original contributions presented in the study are included in the article.
Conflicts of Interest
Author Lu Ke was employed by the company Chongqing Jinyeshi Industrial Co., Ltd. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Cowper, G.R.; Symonds, P.S. Strain-harding and strain-rate effects in the impact loading of cantilever beams. Small Bus. Econ. 1957, 31, 235–263. [Google Scholar] [CrossRef]
- Johnson, G.R.; Cook, W.H. A constitutive model and data for metals subjected to large strains, high strain rates and high temperature. In Proceedings of the 7th International Symposium on Ballistics, Hague, The Netherlands, 19–21 April 1983. [Google Scholar]
- Paul, S.K. Predicting the flow behavior of metals under different strain rate and temperature through phenomenological modeling. Comput. Mater. Sci. 2012, 65, 91–99. [Google Scholar] [CrossRef]
- Al-Thairy, H.; Wang, Y.C. A numerical study of the behaviour and failure modes of axially compressed steel columns subjected to transverse impact. Int. J. Impact Eng. 2011, 39, 732–744. [Google Scholar] [CrossRef]
- Liang, C.; Wang, C.J.; Nguyen, V.B.; English, M.; Mynors, D. Experimental and numerical study on crashworthiness of cold-formed dimpled steel columns. Thin Walled Struct. 2017, 112, 83–91. [Google Scholar] [CrossRef]
- Liang, C.; Wang, C.J.; English, M.; Mynors, D. Behaviour of cold-formed dimpled columns under lateral impact. Eng. Struct. 2018, 163, 167–176. [Google Scholar] [CrossRef]
- Li, W.; Gu, Y.Z.; Han, L.H.; Zhao, X.L. Behaviour of grout-filled double-skin steel tubular T-joint subjected to low-velocity impact. Thin Walled Struct. 2019, 144, 106270. [Google Scholar] [CrossRef]
- Xiang, S.; He, Y.J.; Zhou, X.H. Behaviour and failure modes of steel parking structure column under transverse impact. Thin Walled Struct. 2021, 167, 108163. [Google Scholar] [CrossRef]
- Bambach, M.R.; Jama, H.; Zhao, X.L.; Grzebieta, R.H. Hollow and concrete filled steel hollow sections under transverse impact load. Eng. Struct. 2008, 30, 2859–2870. [Google Scholar] [CrossRef]
- Wang, Y.; Qian, X.D.; Liw, J.Y.R.; Zhang, M.H. Experimental behavior of cement filled pipe-in-pipe composite structures under transverse impact. Int. J. Impact Eng. 2014, 72, 1–16. [Google Scholar] [CrossRef]
- Goswami, A.; Adhikary, S.D.; Li, B. Predicting the punching shear failure of concrete slabs under low velocity impact loading. Eng. Struct. 2019, 184, 37–51. [Google Scholar] [CrossRef]
- Lee, K.K.; Shin, J.W.; Kim, K.S.; Varma, A. Local responses of steel-plate composite walls subjected to impact loads: Intermediate scale tests. Eng. Struct. 2020, 206, 110131. [Google Scholar] [CrossRef]
- Li, H.W.; Chen, W.S.; Huang, Z.J.; Hao, H.; Ngo, T.T.; Pham, T.M.; Yeoh, K.J. Dynamic response of monolithic and precast concrete joint with wet connections under impact loads. Eng. Struct. 2022, 250, 113434. [Google Scholar] [CrossRef]
- Li, L.; Wang, H.W.; Wu, J.; Du, X.L.; Zhang, X.Y.; Yao, Y.L. Experimental and numerical investigation on impact dynamic performance of steel fiber reinforced concrete beams at elevated temperatures. J. Build. Eng. 2022, 47, 103841. [Google Scholar] [CrossRef]
- Slimane, S.A.; Slimane, A.S.; Guelailia, A.; Boudjemai, A.; Kebdani, S.; Smahat, A.; Mouloud, D. Hypervelocity impact on honeycomb structure reinforced with bi-layer ceramic/aluminum factsheets used for spacecraft shielding. Mech. Adv. Mater. Struct. 2022, 29, 4487–4505. [Google Scholar] [CrossRef]
- Shen, Y.; Lin, L.; Tang, P.; Xu, T. Impact Dynamic Response of Spherical Net Shells: Finite Element-Based Computational Analysis Investigating the Influence of Dynamic Constitutive Models. Buildings 2023, 13, 1849. [Google Scholar] [CrossRef]
- Yang, Q.F.; Zhang, R. Analysis of lateral impact resistance performance of LS-DYNA round steel pipes. Low Temp. Archit. Technol. 2014, 36, 38–41. [Google Scholar] [CrossRef]
- Gupta, N.K.; Venkatesh. Experimental and numerical studies of dynamic axial compression of thin walled spherical shells. Int. J. Impact Eng. 2004, 30, 1225–1240. [Google Scholar] [CrossRef]
- Gupta, N.K.; Mohamed Sheriff, N.R.; Velmurugan. Experimental and numerical investigations into collapse behaviour of thin spherical shells under drop hammer impact. Int. J. Solids Struct. 2007, 44, 3136–3155. [Google Scholar] [CrossRef]
- Gupta, N.K.; Mohamed Sheriff, N.R.; Velmurugan. Analysis of collapse behaviour of combined geometry metallic shells under axial impact. Int. J. Impact Eng. 2008, 35, 731–741. [Google Scholar] [CrossRef]
- Gupta, N.K.; Mohamed Sheriff, N.R.; Velmurugan. Experimental and theoretical studies on buckling of thin spherical shells under axial loads. Int. J. Mech. Sci. 2008, 50, 422–432. [Google Scholar] [CrossRef]
- Fan, F.; Wang, D.Z.; Zhi, X.D.; Shen, S.Z. Failure modes for single-layer reticulated domes under impact loads. Trans. Tianjin Univ. 2008, 14, 545–550. [Google Scholar] [CrossRef]
- Wang, D.; Zhi, X.; Fan, F.; Shen, S. Failure process and energy transmission for single-layer reticulated domes under impact loads. Trans. Tianjin Univ. 2008, 14, 551–557. [Google Scholar] [CrossRef]
- Fan, F.; Wang, F.D.; Zhi, X.D.; Shen, S.Z. Failure modes of reticulated domes subjected to impact and the judgment. Thin Walled Struct. 2010, 48, 143–149. [Google Scholar] [CrossRef]
- Zhi, X.D.; Fan, F.; Shen, S.Z. Elasto-plastic instability of single-layer reticulated shells under dynamic actions. Thin Walled Struct. 2010, 48, 837–845. [Google Scholar] [CrossRef]
- Zhi, X.; Wang, D.; Fan, F. Cost-effectiveness of protective measures for single-layer reticulated domes subject to impact loading. Int. J. Steel Struct. 2012, 12, 311–319. [Google Scholar] [CrossRef]
- Zhai, X.M.; Wang, Y.H.; Huang, M. Performance and protection approach of single-layer reticulated dome subjected to blast loading. Thin Walled Struct. 2013, 73, 57–67. [Google Scholar] [CrossRef]
- Wang, D.Z.; Fan, F.; Zhi, X.D.; Dai, J.W. Failure modes and characteristics of dynamic response for reticulated shells under impact. Eng. Mech. 2014, 31, 180–189. [Google Scholar] [CrossRef]
- Wang, D.Z.; Zhi, X.D.; Fan, F.; Lin, L. The energy-based failure mechanism of reticulated domes subjected to impact. Thin Walled Struct. 2017, 119, 356–370. [Google Scholar] [CrossRef]
- Ma, J.L.; Fan, F.; Wu, C.Q.; Zhi, X.D. Counter-intuitive collapse of single-layer reticulated domes subject to interior blast loading. Thin Walled Struct. 2015, 96, 130–138. [Google Scholar] [CrossRef]
- Ma, X.; Wang, X. Dynamic stability of single-layer reticulated shell structures subjected to impact loads. J. Vib. Shock 2015, 34, 119–124. [Google Scholar] [CrossRef]
- Hu, J.X.; Lu, G.Y.; Yang, H.W.; Yu, T.X.; Xu, J. Dynamic response of internally nested hemispherical shell system to impact loading. Thin Walled Struct. 2017, 120, 29–37. [Google Scholar] [CrossRef]
- Su, Q.Q.; Zhai, X.M. Dynamic response of single-layer reticulated shell with explosion-protection wall under blast loading. Thin Walled Struct. 2018, 127, 389–401. [Google Scholar] [CrossRef]
- Zhi, X.D.; Qi, S.B.; Fan, F.; Zhai, X.M. Experimental and numerical investigations of a single-layer reticulated dome subjected to external blast loading. Eng. Struct. 2018, 176, 103–114. [Google Scholar] [CrossRef]
- Ma, X.; Wang, X.; Bao, C.; Lu, H.; Yang, W. Dynamic Response Analysis and Model Test Research on K6 Single-Layer Spherical Reticulated Shells Subjected to Impact Load. Int. J. Steel Struct. 2019, 19, 1446–1453. [Google Scholar] [CrossRef]
- Nazari, E.; Shekastehband, B. Failure behavior of double-layer-domes subjected to impact. Int. J. Struct. Stab. Dyn. 2021, 21, 2150015. [Google Scholar] [CrossRef]
- Wu, C.; Yang, Y.; Gou, B.; Wu, J. Research on a multi-point impact test of single-layer spherical reticulated shell. J. Constr. Steel Res. 2021, 186, 106897. [Google Scholar] [CrossRef]
- Deepshikha, N.; Keita, I.; Yuki, T.; Ben, S. Higher mode effects of multistorey substructures on the seismic response of double-layered steel grid shell domes. Eng. Struct. 2021, 243, 112677. [Google Scholar] [CrossRef]
- Pilarska, D.; Maleska, T. Numerical analysis of steel geodesic dome under seismic excitations. Materials 2021, 14, 4493. [Google Scholar] [CrossRef]
- Xu, T.L.; Lin, L.; Zhi, X.D.; Fan, F. Experimental study on the impact resistance of single-layer spherical reticulated shell roof panels. Structures 2022, 45, 23–38. [Google Scholar] [CrossRef]
- Xu, J.H.; Zhang, Y.Y.; Zhao, Q.C.; Zhang, L.L. Experiment and simulation analysis on dynamic response of plane cable-membrane structure under impact load. Thin Walled Struct. 2022, 171, 108814. [Google Scholar] [CrossRef]
- Rossot, D.; Machado, R.D.; Barbieri, N.; de Lima, K.F. Experimental and Numerical Study of a Geodesic Dome Under Static and Dynamic Loads and the Influence of Nodal Connections. Exp. Tech. 2022, 46, 823–834. [Google Scholar] [CrossRef]
- Gou, B.L.; Wang, X.L.; Wu, C. Experimental and numerical study on the behavior of single-layer spherical reticulated shells under the combined action of temperature and impact load. Thin Walled Struct. 2023, 182, 110333. [Google Scholar] [CrossRef]
- Wu, C.; Yang, Y.P.; Wang, R.H. Performance of Reticulated Shells under Different Impact Angles. J. Vib. Control 2021, 41, 7–12. [Google Scholar] [CrossRef]
- Zhang, Y.H.; Chen, C.H.; Zhu, X. Ballistic performance of Q235 steel plate subjected to impact by middle and high velocity projectiles. Ship Sci. Technol. 2017, 39, 52–54. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).