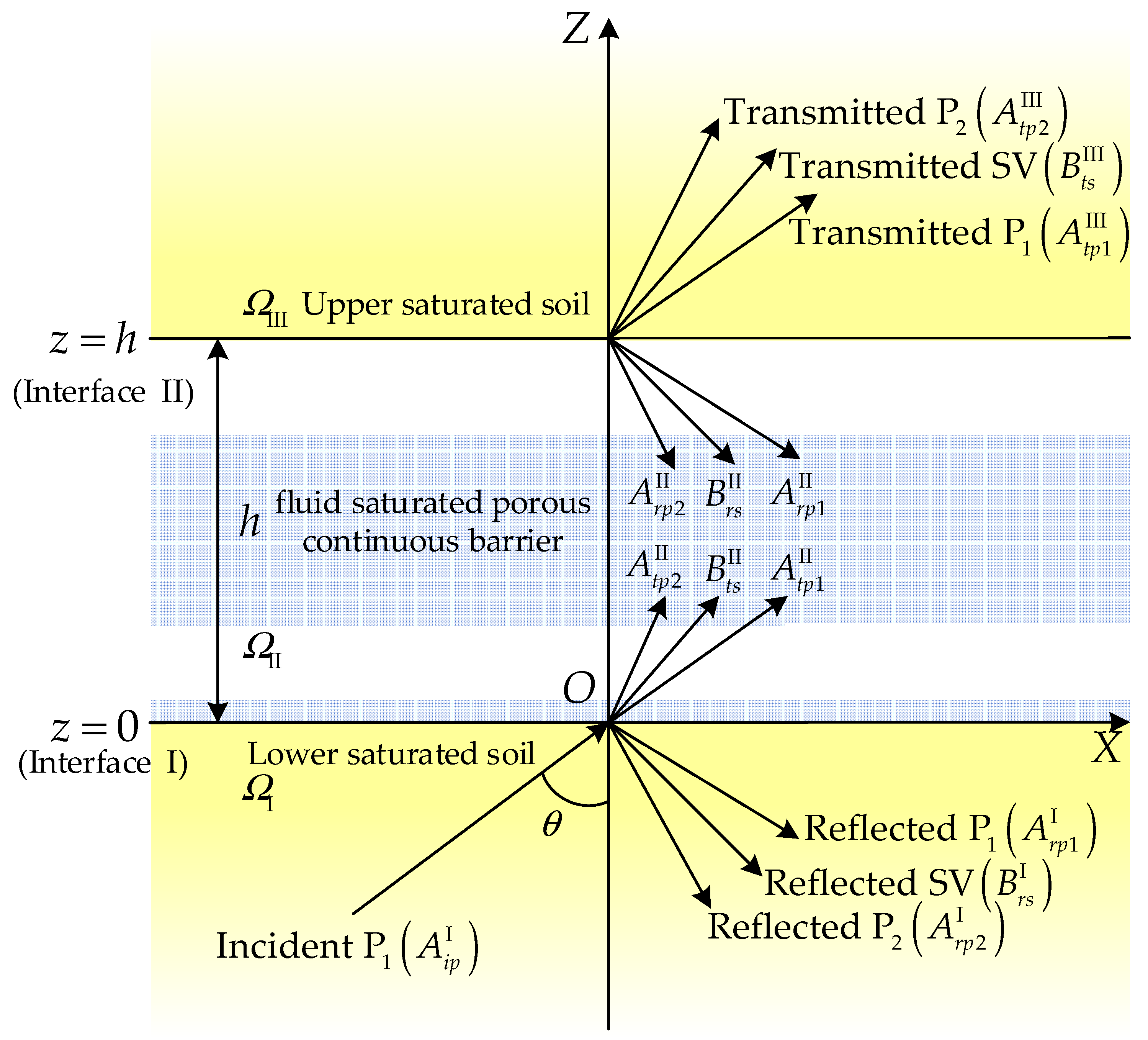
1. Introduction
With the accelerated process of modern infrastructure construction, the environmental pollution problems caused by artificial vibrations in industrial production, transportation, and building construction are becoming more and more prominent, such as in the foundations of power machines, traffic load (underground traffic, high-speed rail, light rail, etc.), and building construction processes (blasting, piling, ramming, etc.), which have a significant impact on the adjacent buildings, underground pipelines, and precision instruments and equipment, as well as on people’s living and working environments the working environment of people’s lives. Compared with the contingency, unpredictability, and great destructiveness of earthquakes [
1], the hazards produced by artificial vibrations are not so obvious and seldom attract people’s attention, but they are persistent, cyclical, and long-lasting, and are closely related to people’s daily production and life; excessive vibration will have different degrees of physiological and psychological impacts on the human body [
2]. Previous studies have shown that vibration can directly affect the quality of the human environment, leading to the increased annoyance of the residents and seriously endangering human health [
3]; vibration can as well cause low-frequency micro-vibration and secondary noise pollution in existing urban complexes and cultural relics [
4,
5,
6], and can also attenuate the service life of precision instruments [
7]. The foundation is the main medium connecting the vibration source and the vibration receptor, and setting vibration isolation barriers (air trench, filled trench, wave barrier plate, row of piles, etc.) in the foundation can effectively control the vibration. Therefore, analyzing the propagation process of elastic waves through vibration isolation barriers in foundations is of great practical significance for practical engineering applications.
At present, domestic and foreign scholars have conducted research on the isolation performance of barriers from the perspectives of barrier material composition, barrier structure type, and foundation material characteristics. Zhang et al. [
7] compared the vibration isolation effects of ceramic-filled continuous and discontinuous barriers, as well as sand-filled continuous and discontinuous barriers, using full-scale experiments and numerical simulation methods. The results showed that regardless of whether the fillers were lightweight or heavy materials, continuous barriers had better vibration isolation effects compared to discontinuous barriers. Zhou et al. [
8] proposed a liquid-saturated porous wave barrier based on fluid–solid coupling in a liquid-saturated porous medium and placed this barrier on a single-phase elastic foundation. The Fourier series expansion method was used to compare and analyze the vibration isolation effects of the single-phase solid wave barrier and the liquid-saturated porous wave barrier. The results showed that the liquid-saturated porous wave barrier has a better vibration reduction effect and designability. Xu et al. [
9] proposed a composite isolation barrier made of water-filled concrete and studied the isolation effect of the composite barrier on P
1-wave in a saturated soil foundation. The results showed that the isolation effect of the barrier first decreased and then increased with the increase in incident angle. Li et al. [
10] used Comsol to establish a finite element analysis model for multiple empty ditches in a saturated foundation with an overlying single-phase elastic layer. They studied the far-field vibration isolation effects of multi-ditch barriers with equal and unequal ditch depths, inclined ditch walls, and continuous undulating terrain barriers under different water levels, taking into account the effect of water in the ditch. Ma and Shu established a double-layer wave resistance plate calculation model [
11] and a composite multi-layer wave resistance plate calculation model [
12,
13] for an unsaturated soil foundation, and they calculated the reflection and transmission amplitude ratios of S-waves passing through the double-layer wave resistance plate calculation model and of P
1-waves and S-waves passing through the composite multi-layer wave resistance plate calculation model, respectively. The study showed that the wave impedance ratio and the shear modulus of the wave resistance plate have a significant impact on the transmission/reflection coefficient. Li et al. [
14] analyzed the wave field of plane P-wave and SV-wave incidence in unsaturated soil rock systems based on the wave characteristics of unsaturated porous media. Jiang et al. [
15] derived an analytical solution for the vertical displacement of the ground surface after P-wave incidence from the bedrock into an unsaturated soil site and subsequently passed through a wave resistance plate.
In the above research on barrier isolation, the foundation is often simplified as a single and uniform elastic medium. However, due to the influence of geological structure and stress history, natural soil typically exhibits irregular layered distribution in space [
16,
17,
18,
19,
20,
21,
22,
23,
24,
25,
26,
27,
28,
29,
30,
31]. Gao et al. [
17] established a layered foundation model with wave barrier plates and analyzed the effects of upper soft and lower hard soil layers and upper hard and lower soft soil layers on wave barrier plates. The results showed that the foundation layering parameters had a significant impact on the vibration isolation effect of wave barrier plates. Xu Ping [
18] studied the reflection and transmission of the P
1-wave at the interface when incident from quasi saturated soil to elastic soil layers. Chen et al. [
19] studied the reflection and transmission of S-waves at the interface of layered unsaturated soil foundation models. Corredor et al. [
20] studied the reflection and transmission coefficients of highly permeable and compliant porous layers when plane waves were incident in a porous elastic half space. Wang et al. [
22] studied the reflection and transmission of plane elastic waves at the interface of a layered dual porous medium model, taking into account the influence of local fluid flow. Yuan et al. [
23] used a 2.5-dimensional finite element method to compare and analyze the isolation effect of hollow trenches in homogeneous saturated soil and layered saturated soil under moving loads. The results showed that the soil interface affects the reflection and transmission of waves, thereby affecting the isolation effect of hollow trenches. Ba et al. [
24] used a 2.5-dimensional indirect boundary element method to establish a coupled dynamic system, namely, layered saturated foundation–track–empty ditch, and studied the isolation performance of the empty ditch on the moving load of trains in the layered saturated foundation. Liu et al. [
25] established a layered elastic foundation model with empty ditch using a Comsol simulation physical field and studied the effects of changes in the density, elastic modulus, and Poisson’s ratio of the upper and lower soil layers on soil vibration response. Yang et al. used the stiffness matrix method to derive the analytical solution for the dynamic response of a long tunnel in a horizontally layered saturated porous elastic formation under the action of inclined SV-waves. The results showed that SV-waves induced greater tunnel internal forces than the P
1-wave. It is worth noting that the above research on barrier isolation in layered soil only focuses on isolation barriers composed of single-phase media and does not involve research on fluid-saturated porous media barriers in layered soil. However, studies have shown that the fluid structure coupling in fluid-saturated porous media structures can cause energy dissipation and attenuation during vibration, which has a similar damping effect [
9].
In summary, previous studies on the isolation performance of barriers have mostly focused on a single and uniform foundation soil, while layered soil is the more common state in nature. Moreover, in coastal areas and below groundwater levels, simplifying soil to saturated soil is closer to reality. Meanwhile, the vast majority of studies simulate isolation barriers as single-phase elastic media, while there is little research on fluid-saturated porous media materials as isolation barriers. Therefore, the propagation characteristics of fluid-saturated porous continuous barriers in layered saturated soil deserve further analysis. This paper, in its study of an analytical solution for the amplitude ratio of the reverse transmission of the P1-wave after passing through a fluid-saturated porous continuous barrier in layered saturated soil, is based on Biot’s saturated porous medium wave theory and Snell’s law. Through numerical examples, the differences in the propagation characteristics of the fluid-saturated porous continuous barrier in layered saturated soil, homogeneous saturated soil, and layered single-phase soil are analyzed, as well as the influence of changes in physical and mechanical parameters of the fluid-saturated porous continuous barrier on the reflection amplitude ratio under layered saturated soil foundation conditions.
3. Wave Equation of Saturated Porous Media
Biot [
34,
35,
36] systematically investigated the deformation mechanisms of compression and shear waves in saturated porous media and the propagation of body waves in them. He applied continuum mechanics to fluid-saturated porous two-phase media, considering the stress–strain and motion of the fluid and solid skeleton, respectively, as well as the complex inertial and viscous coupling between the two phases. The study shows that in macroscopically isotropic and homogeneous porous continuous media with interconnected pores, there generally exist two kinds of compression waves (i.e., fast compression wave, also known as the P
1-wave; and slow compression wave, also known as the P
2-wave) and one kind of shear wave, and the three kinds of waves are dispersive and attenuating. Among them, the P
1-wave is in-phase, and its nature is comparable with the longitudinal wave in single-phase medium; the slow longitudinal wave is in-phase, and the energy attenuation is very fast, which is similar to the diffusion phenomenon or the heat-conduction phenomenon.
According to Biot’s saturated porous media theory [
34,
35,
36], the governing equation of the dynamic response problem of homogeneous linear elastic saturated porous media is as follows:
where
and
are, respectively, the displacement of solid skeleton in saturated porous media and the relative displacement of fluid relative to the solid skeleton;
and
denote the Lame constant of a solid skeleton with saturated porous medium;
and
denote the Biot parameter
,
, where
,
, and
are the bulk modulus of the solid skeleton, solid particle, and pore fluid, respectively;
is the mass density of the mixture medium, where
is the porosity;
and
are, respectively, the density of the solid phase and the liquid phase;
is the fluid viscosity coefficient; and
is the permeability coefficient.
According to the Helmholtz vector decomposition principle, the displacement vector
and
can be represented by the displacement potential function as follows:
where
and
are scalar potential functions in the solid skeleton and fluid, respectively; and
and
are vector potential functions in the solid skeleton and fluid, respectively.
5. Numerical Calculation and Analysis
5.1. Verification and Comparative Analysis
In order to verify the rationality of the solution method presented in this paper, the soil layer porosity of the calculation model in this paper is set to 0 to simulate the interface effect model of the P-wave between the single-phase elastic medium, saturated porous medium, and single-phase elastic medium [
37], which is consistent with the model in the literature [
37]. The same material parameters as those in reference [
37] were taken in the verification calculation, as shown in
Table 1 and
Table 2.
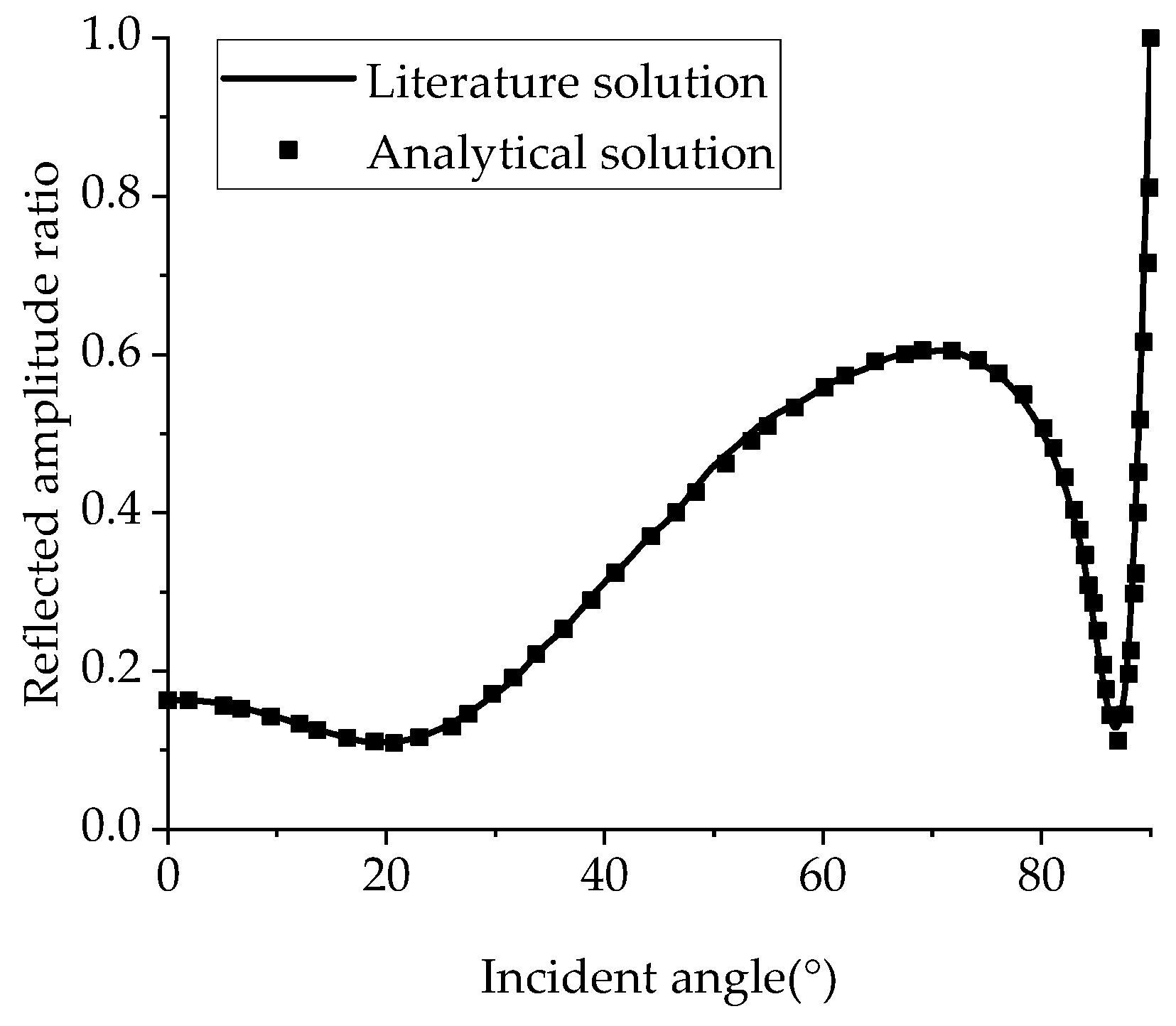
Figure 2 shows the relationship between the reflection amplitude ratio of the P
1-wave and the incidence angle when the P-wave is incident on a fluid-saturated porous continuous barrier model with a thickness of 2 m in layered single-phase soil at an incident frequency of 30 Hz. It can be seen from the figure that the calculated results of the solution in this paper are highly consistent with those in the literature, indicating the rationality of the method in this paper.
Figure 3 shows the contrast curve between the P
1-wave reflection amplitude ratio and the incident angle of the fluid-saturated porous continuous barrier in stratified saturated soil and single-phase soil, where the barrier thickness is 2 m, the barrier porosity is 0.2, the upper saturated soil porosity is 0.18, and the lower saturated soil porosity is 0.30. This paper considers the frequency = 30 Hz, which is within the significant frequency range of the traffic environment vibration [
4]. In the single-phase ground-based model, the reflection amplitude ratio of the P
1-wave decreases with the increase in the incidence angle and reaches the minimum value near 21°. Then, it increases with the increase in the incidence angle and reaches a local maximum near 70°. When the incidence angle is from 70° to 87°, the reflection amplitude ratio of the P
1-wave decreases rapidly with the increase in the incidence angle. It then increases rapidly as the incidence angle increases, reaching a maximum value of 1 at an incidence angle of 90°. In the layered saturated ground-based model, the reflection amplitude ratio of the P
1-wave first decreases with the increase in the incidence angle, reaches the minimum value near 40°, then rapidly increases with the increase in the incidence angle and slowly increases, reaching the maximum value of 1 when the incidence angle is 90°. In the homogeneous saturated ground model, the reflection amplitude ratio of P
1-wave increases with the increase in the incidence angle and reaches a local maximum near 70°. When the incidence angle is from 70° to 87°, the reflection amplitude ratio of the P
1-wave decreases rapidly with the increase in the incidence angle. It then increases rapidly as the incidence angle increases, reaching a maximum value of 1 at an incidence angle of 90°. It can be seen from
Figure 3 that the presence of fluid changes the trend of the reflection amplitude ratio with the incidence angle.
5.2. Influence of Barrier Thickness
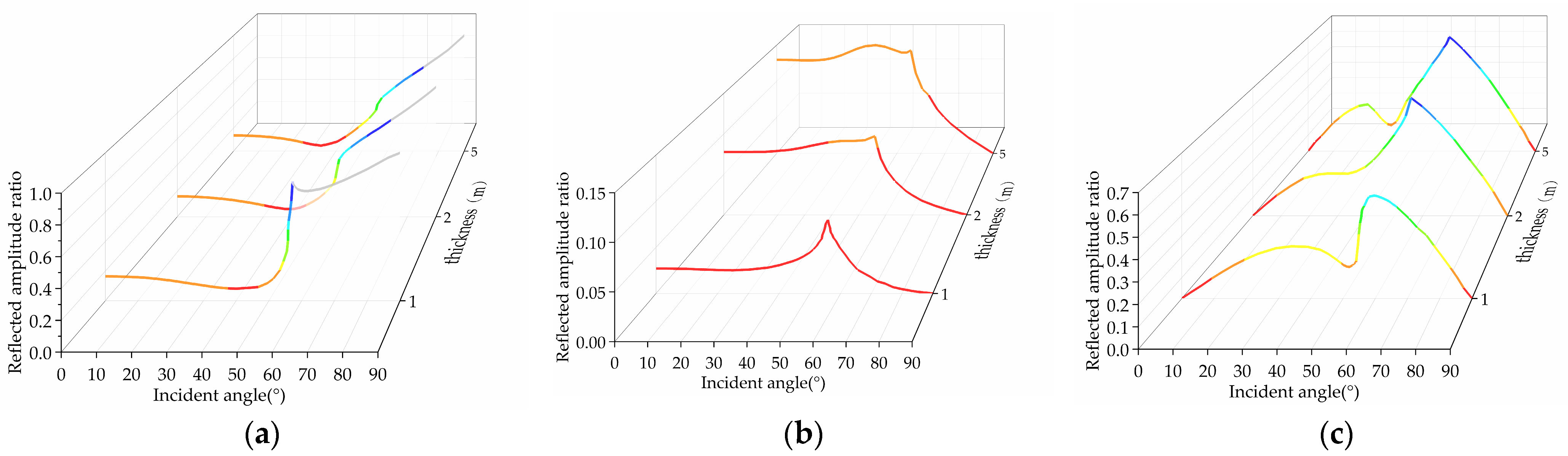
The change curves of the reflection amplitude ratios of the P
1-, P
2-, and SV-waves, incidence angle, and barrier thickness are shown in
Figure 4, where the barrier thickness is 1 m, 2 m, and 5 m, respectively. From the perspective of energy conservation, the more reflection, the less transmission [
11], and the energy transmitted by the P
1-, P
2-, and SV-waves to the upper saturated soil after passing through the fluid-saturated porous continuous barrier will be dissipated and attenuated. The amplitude ratio of the three reflected waves varies with the incidence angle, and the influence of the barrier thickness on the reflection amplitude ratio is discussed below. It can be seen from
Figure 4 that the reflection curve is discontinuous, that there are two critical angles, and that the magnitude of the critical angles is closely related to the barrier thickness.
(1) The reflection amplitude ratio of the P1-wave first decreases with the increase in the incidence angle, reaches the minimum value near 40°, then rapidly increases with the increase in the incidence angle, slowly increases near 60°, and reaches 1 when the incidence angle is 90°; at this time, there is only a reflected P1-wave, no reflected P2-wave and SV-wave. When the incidence angle is 0°, there is no reflected SV-wave. For the P1-wave, the position of the critical angle is affected by the thickness of the barrier and moves to the left as the thickness increases.
(2) The reflection amplitude ratio of the P2-wave increases slowly with the increase in the incidence angle, reaches a maximum value around 60°, and then decreases rapidly and reaches 0 when the incidence angle is 90°. For the P2-wave, the reflection amplitude ratio increases with the increase in barrier thickness.
(3) The reflection amplitude ratio of the SV-wave starts from 0 at the time of vertical incidence and gradually increases to a local maximum with the increase in the incidence angle, then gradually decreases to a local minimum; then, it rapidly increases to another local maximum and finally rapidly decreases and reaches 0 when the incidence angle is 90°. For the SV-wave, the position of the critical angle is affected by the thickness of the barrier and moves to the left with the increase in thickness. Compared with the P1-wave, the SV-wave is more affected by the change in barrier thickness.
5.3. Influence of Barrier Porosicty
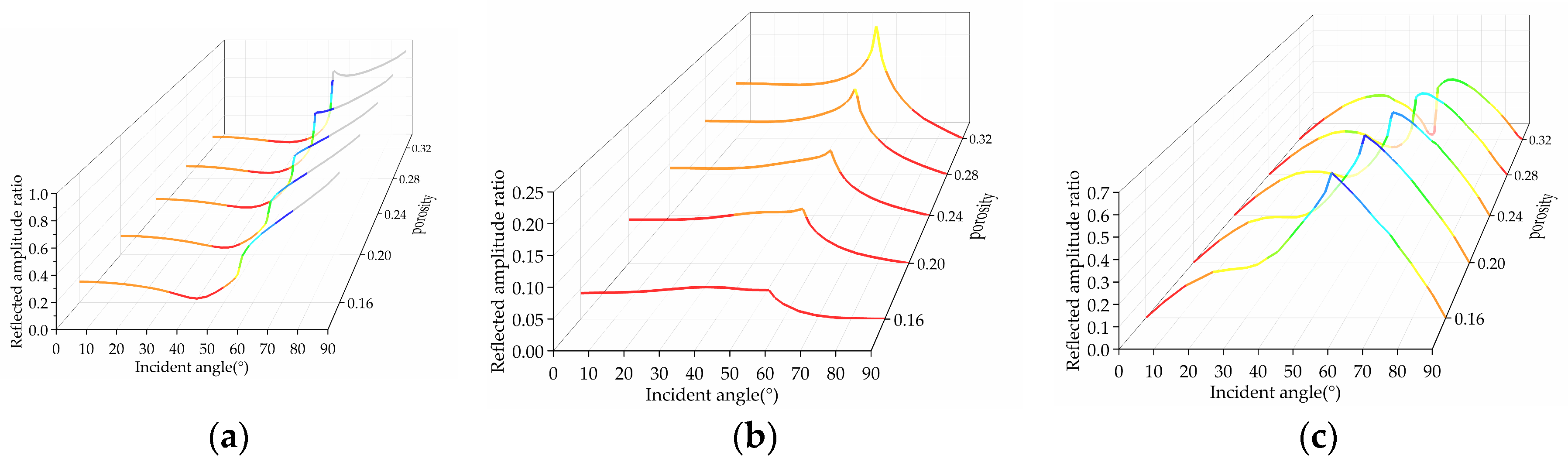
The change curves of the reflection amplitude ratio of the P
1-, P
2-, and SV-waves with the incidence angle and barrier porosity are shown in
Figure 5, where the porosity is 0.16, 0.20, 0.24, 0.28, and 0.32, respectively.
(1) When the incidence angle is small, the reflection amplitude ratio of the P1-wave first decreases with the increase in the incidence angle, reaches the minimum value near 40°, then rapidly increases with the increase in the incidence angle, slowly increases again near 60°, and reaches 1 when the incidence angle is 90°. For the P1-wave, the position of the critical angle is affected by the barrier porosity and moves to the left with the increase in porosity.
(2) The reflection amplitude ratio of the P2-wave increases slowly with the increase in the incidence angle, reaches a maximum value around 60°, and then decreases rapidly and reaches 0 when the incidence angle is 90°. For the P2-wave, the reflection amplitude ratio increases with the increase in porosity, which is affected by the change of barrier porosity.
(3) The reflection amplitude ratio of the SV-wave starts from 0 at the time of vertical incidence and gradually increases to a local maximum with the increase in the incidence angle, then gradually decreases to a local minimum; then, it rapidly increases to another local maximum and finally rapidly decreases and reaches 0 when the incidence angle is 90°. For the SV-wave, the position of the critical angle is affected by porosity and moves to the right with the increase in porosity, but the reflection amplitude ratio does not change significantly with the increase in porosity at small angle incidence.
6. Conclusions
Based on Biot’s wave theory of saturated porous media and Snell’s law, this paper studies the analytical solution of the inverse transmitted wave amplitude ratio of the P1-wave passing through a fluid-saturated porous continuous barrier in layered saturated soil and compares it with the solution of the existing the P-wave effect model at the interface of elastic media-saturated coarse-interlayer elastic medium, which verifies the rationality of the proposed method. Numerical examples were used to analyze the difference in propagation characteristics of the fluid-saturated porous continuous barrier in layered saturated soil and homogeneous saturated soil in layered single-phase soil, as well as the influence of changes in thickness and porosity in the fluid-saturated porous continuous barrier on the reflection amplitude ratio under the condition of a layered saturated soil foundation. The research results reveal the following:
(1) According to the model of stratified single-phase soil, stratified saturated soil and homogeneous saturated soil, the presence of fluid changes the trend of reflection amplitude ratio with incident angle, the dissipation of solid skeleton energy seriously affects the propagation of shear wave, but has little effect on the propagation of compression waves.
(2) In the stratified single-phase ground-based model, under the low frequency excitation, the reflection coefficient changes steadily and remains at 0.25, the frequency is small, the wavelength is large, the barrier thickness is relatively thin layer, and there is no wave mode conversion at vertical incidence. When the wavelength thickness is extremely small, the reflection coefficient approaches zero, and most of the energy is transferred to the lower medium.
(3) In the stratification single-phase ground-based model, the impact of incident angle on reflection coefficient is reflected in the impact on the wave pattern. When incident waves are incident at different angles, wave pattern conversion will occur.
(4) The change of incidence angle has great influence on the P1-, P2-, and SV-wave. The reflection amplitude ratio of the P2- and SV-waves increases first and then decreases with the increase in incident angle, while the reflection amplitude ratio of the P1-wave decreases first and then increases. When the incidence angle is 0°, there is no SV-wave; when the incidence angle is 90°, there are no P2- and SV-waves.
(5) The change in barrier thickness and porosity has great influence on the P1-, P2-, and SV-waves. The SV-wave is more affected by the change in barrier thickness; the P2-wave is more affected by the change of barrier porosity. The higher the barrier thickness and porosity, the higher the reflection amplitude ratio.
(6) In layered saturated soil foundation, the incident angle has a large influence on the vibration isolation effect of vibration isolation barriers. When incident at a small angle, the reflected amplitude ratio of the P1-wave decreases and then increases with the increase in the thickness, the P2-wave increases with the increase in the thickness, and the SV-wave increases and then decreases and finally increases with the increase in the thickness. When incident at a large angle, the reflected amplitude ratio of the P1-wave decreases with the increase in the thickness, and the reflected amplitude ratios of the P2-wave and SV-wave increase with the increase in the thickness. The reflection amplitude ratio of the P1-wave decreases with the increase in thickness for large angle incidence and increases for the P2- and SV-waves with the increase in thickness. When incident at a small angle, the reflection amplitude ratio of the P1-wave decreases with the increase in porosity, the P2-wave increases with the increase in porosity, and SV-wave increases and then decreases with the increase on porosity. When incident at a large angle, the reflection amplitude ratios of the P1- and P2-waves increase with the increase in porosity, and the P2- and SV-wave decrease with the increase in porosity. Therefore, the angle of the vibration isolation barrier should be selected reasonably and appropriately when vibration isolation is carried out in engineering applications.