Green Residential Building Design Scheme Optimization Based on the Orthogonal Experiment EWM-TOPSIS
Abstract
1. Introduction
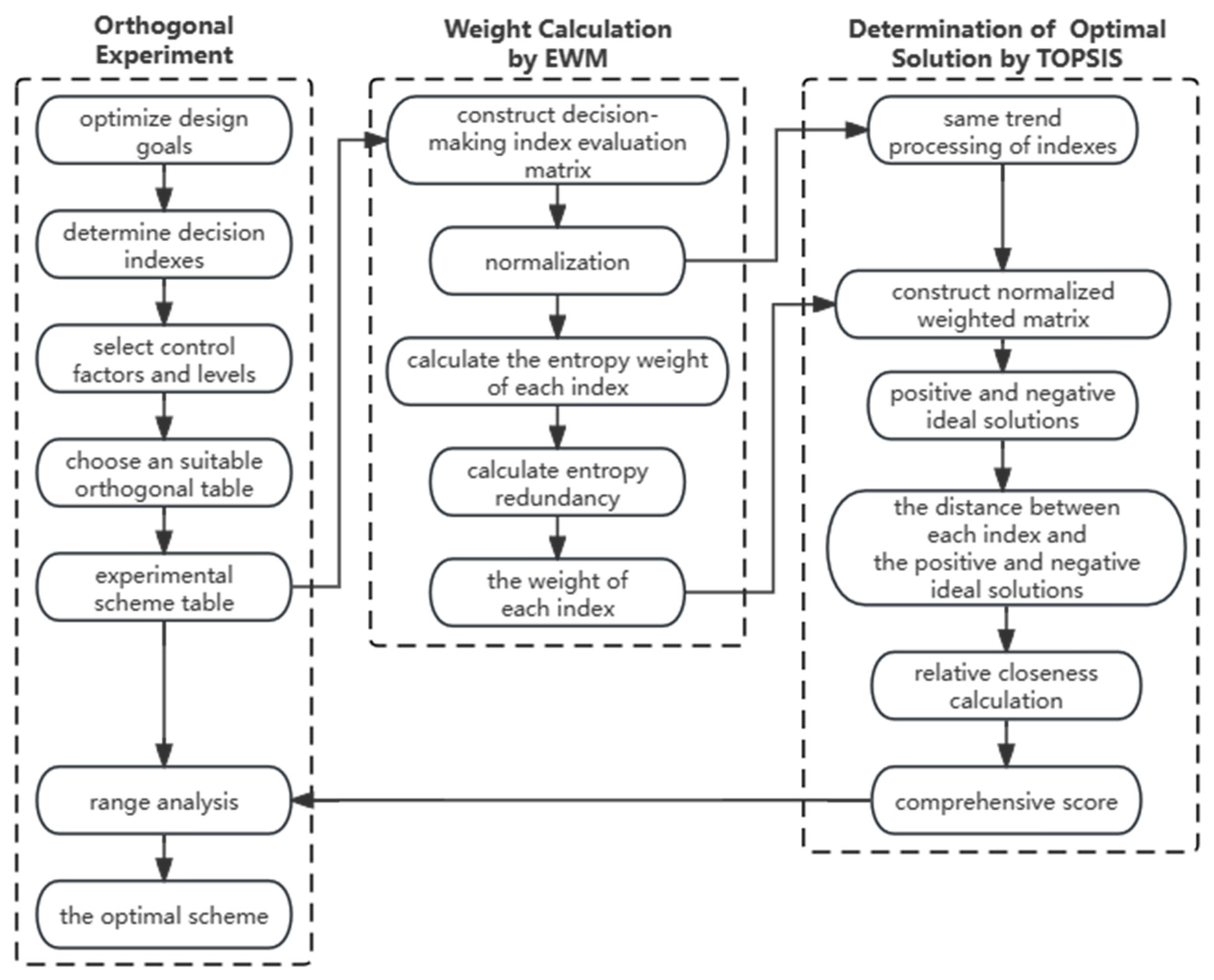
2. Design of Scheme Optimization
2.1. Principle of Orthogonal Experiment
- (1)
- Obtain the orthogonal experimental scheme and the evaluation index of the merits and demerits of each plan.
- (2)
- Calculate the sum Kl of the evaluation indexes of the scheme when the factor is at level l:where is the comprehensive score, as shown in Formula (16).
- (3)
- Calculate the mean of Kl:where r is the number of orthogonal experimental repetitions for the factor at level l.
- (4)
- Obtain the range value, which is used to rank the influence degree of factors. The larger the range value, the greater the influence of the control factor on the design scheme:
2.2. Determination of Decision-Making Index Weights Based on EWM
- (1)
- Assume that there are green building evaluation schemes and decision-making indexes, and a decision-making index evaluation matrix with rows and columns is constructed.
- (2)
- Normalize each element of the evaluation matrix. Indexes with larger values that are more beneficial to the decision-making goal are called the positive indexes, and vice versa are the negative indexes. Obtain the normalized matrix :Positive index:Negative index:
- (3)
- Calculate the entropy weight of the index:where . Satisfy .
- (4)
- Calculate the entropy redundancy (coefficient of variation) :
- (5)
- Calculate the weights based on the entropy redundancy :
2.3. Construction of Decision-Making Model Based on TOPSIS
- (1)
- Construct an initial judgment matrix and process the original data with the same trend.The initial judgment matrix is constructed the same as in step (1) of the EWM. The TOPSIS method requires that all indexes have consistent directions. It is common to distinguish between positive indexes and negative indexes in the data and convert negative indexes into positive indexes (that is, data positive processing). The reciprocal method is used for absolutely negative indexes, and the difference method is used for relatively negative indexes [24].
- (2)
- Make the indexes dimensionless, eliminate the influences of different index measurement units, and obtain the standard matrix :
- (3)
- Via the EWM, the weight of an index was determined to be . As such, the index weight matrix is as follows:
- (4)
- Construct a weighted decision matrix :where , , is the weighted value of the scheme and the evaluation index; and is the weight of the evaluation index.
- (5)
- Determine the positive ideal scheme and the negative ideal scheme . By analyzing the weighted decision matrix, the best value and the worst value of the green building multi-objective optimization design decision-making objective can be obtained. The specific calculation formula is as follows:where is a subset of positive indexes, and is a subset of negative indexes.
- (6)
- Calculate the distance between each index value and the positive and negative ideal scheme values. Comparing the scheme designed using orthogonal experiments with the best optimization scheme and the worst optimization scheme can be calculated using the following formula:where is the distance from the target to the optimal target, and is the distance from the target to the worst target.
- (7)
- Calculate the relative closeness of each index value:where was used as the final comprehensive score, and the goals were sorted according to the size of to form the basis for decision making, thereby determining the optimal scheme. When , , indicating that the scheme was the worst solution. When , it meant that the scheme was optimal. The evaluation schemes were sorted in ascending order according to the value of . A greater value of indicated that the scheme was better. The scheme with the largest value of was the best evaluation scheme.
3. Case Analysis
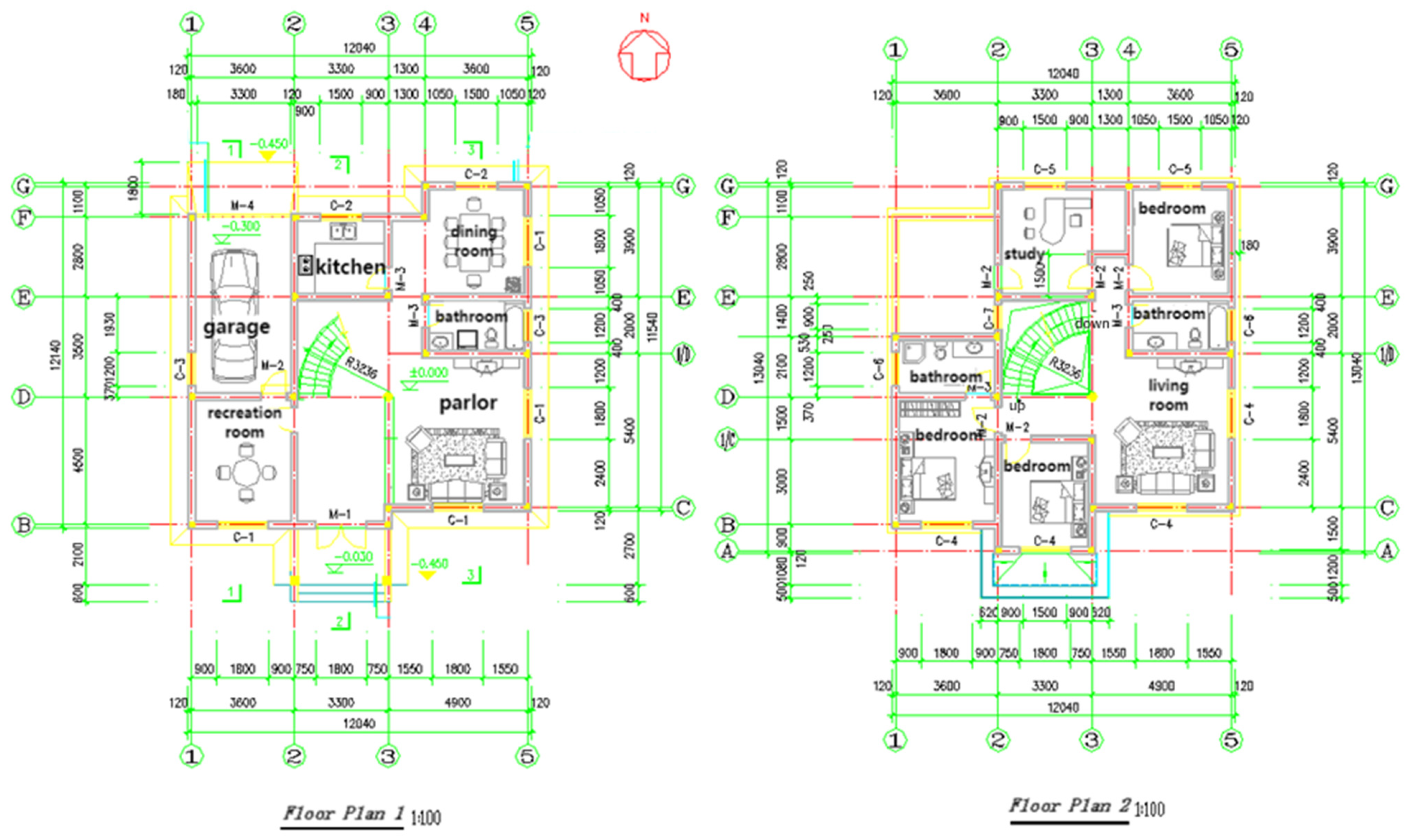
3.1. Case Overview
3.2. Orthogonal Experimental Analysis
3.2.1. Determination of Control Factors
3.2.2. Orthogonal Experimental Analysis Results of Design Scheme
3.3. Optimized Design Based on EWM-TOPSIS Model
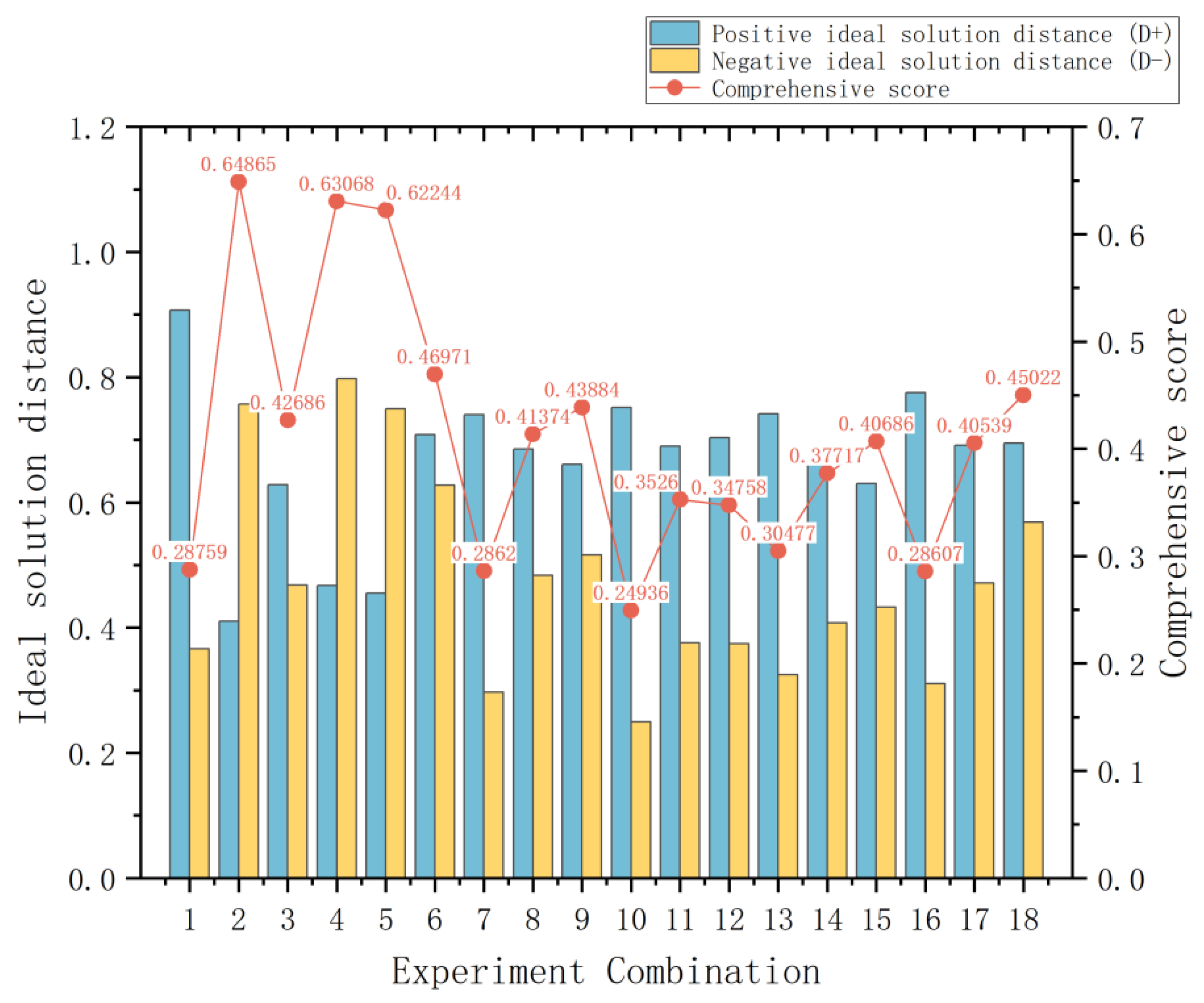
3.4. Result Analysis
4. Discussion
4.1. For the Method Model
4.2. For the Case
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Li, X.; Damartzis, T.; Stadler, Z.; Moret, S.; Meier, B.; Friedl, M.; Maréchal, F. Decarbonization in complex energy systems: A study on the feasibility of carbon neutrality for Switzerland in 2050. Front. Energy Res. 2020, 8, 549615. [Google Scholar] [CrossRef]
- Wu, Z.; Jiang, M.; Cai, Y.; Wang, H.; Li, S. What hinders the development of green building? An investigation of China. Int. J. Environ. Res. Public Health 2019, 16, 3140. [Google Scholar] [CrossRef] [PubMed]
- Xue, S.; Zhu, J.; Wang, L.; Wang, S.; Xu, X. Research on dissipative structure of China’s green building industry system based on Brusselator model. Environ. Impact Assess. Rev. 2023, 103, 107284. [Google Scholar] [CrossRef]
- Xue, S.; Na, J.; Wang, L.; Wang, S.; Xu, X. The Outlook of Green Building Development in China during the “Fourteenth Five-Year Plan” Period. Int. J. Environ. Res. Public Health 2023, 20, 5122. [Google Scholar] [CrossRef] [PubMed]
- Kibert, C.J. Sustainable Construction: Green Building Design and Delivery; John Wiley & Sons: Hoboken, NJ, USA, 2016; pp. 12–79. [Google Scholar]
- Robichaud, L.B.; Anantatmula, V.S. Greening project management practices for sustainable construction. J. Manag. Eng. 2011, 27, 48–57. [Google Scholar] [CrossRef]
- Doan, D.T.; Ghaffarianhoseini, A.; Naismith, N.; Zhang, T.; Ghaffarianhoseini, A.; Tookey, J. A critical comparison of green building rating systems. Build. Environ. 2017, 123, 243–260. [Google Scholar] [CrossRef]
- GB50189-2015; Design Standard for Energy Efficiency of Public Buildings. Beijing Institute of Architectural Design Co., Ltd.: Beijing, China, 2015.
- GB5003-2013; Standard for Daylighting Design of Buildings. Ministry of Housing and Urban-Rural Development of the People’s Republic of China: Beijing, China, 2013.
- Wu, H. Building Energy-Saving Automatic Design System Based on BIM and Grey Taguchi Method. Master’s Thesis, Southwest Jiaotong University, Chengdu, China, 2018. [Google Scholar]
- Cai, J.; Zhang, Z.; Shi, P.; He, Q. Research on risk evaluation of green building design based on fuzzy multi-hierarchical gray method. J. Hefei Univ. Technol. (Nat. Sci.) 2015, 38, 968–972+983. [Google Scholar]
- Yu, H.; Chen, J. Research on the Risk Chain of Green Building Projects under EPC Mode Based on SEM. Sci. Technol. Manag. Res. 2021, 41, 199–205. [Google Scholar]
- Zhang, J.; Zhao, H.; Li, Z.; Guo, Z. Evaluation of Greenness of Green Buildings Based on Carbon Emissions. Kybernetes 2023, 52, 4645–4667. [Google Scholar] [CrossRef]
- Eti, S.; Dinçer, H.; Yüksel, S.; Uslu, Y.D.; Gökalp, Y.; Kalkavan, H.; Mikhaylov, A.; Pinter, G. Determination of priority criteria in green building transformation: An analysis on the service industry. Res. Glob. 2023, 7, 100164. [Google Scholar] [CrossRef]
- Jamaludin, F.A.B.; Li, J. Research on low-carbon evaluation of green buildings based on the whole life cycle theory. SN Appl. Sci. 2023, 5, 262. [Google Scholar] [CrossRef]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Ching-Lai, H.; Yoon, K. Multiple Attribute Decision Making: Methods and Applications; CRC Press: Calabasas, CA, USA, 1981; pp. 11–13. [Google Scholar]
- Xu, J. Research on Low Energy of Rural Residential Buildings in The Cold Regions Based on Traditional Wisdom Construction. Master’s Thesis, Harbin Institute of Technology, Harbin, China, 2016. [Google Scholar]
- Liu, Y. The Research of Daylighting and Energy Consumption on Office Building. Master’s Thesis, Tianjin University, Tianjin, China, 2008. [Google Scholar]
- Mao, H.J.; Shu, M.; Li, C.; Zhang, B.J. Optimization design for beam structures of rail weld CNC fine milling machine based on Ansys Workbench. Appl. Mech. Mater. 2015, 716–717, 817–824. [Google Scholar] [CrossRef]
- Wang, X.; Liu, W.; Chen, C.; Zhang, Y. Rotor position optimization of a hybrid configuration UAV based on orthogonal experiment. Adv. Aeronaut. Sci. Eng. 2013, 1–12. Available online: http://kns.cnki.net/kcms/detail/61.1479.V.20231101.1323.002.html (accessed on 23 November 2023).
- Tao, M. Research on Risk Evaluation System of Green Building Developer Based on Entropy Weight TOPSIS. Master’s Thesis, Guangzhou University, Guangzhou, China, 2020. [Google Scholar]
- Liu, J. Research on Evaluating Model of Energy-Saving Reconstruction for Historic Office Building—A Case Study in Tianjin. Master’s Thesis, Tianjin University, Tianjin, China, 2017. [Google Scholar]
- Gao, Y.; Wang, J.; Shi, D. Implementation of weighted TOPSIS method comprehensive evaluation in Excel. Chin. J. Health Stat. 2007, 24, 428–429. [Google Scholar]
- GB50068-2018; Unified Standard for Reliability Design of Building Structures. Ministry of Housing and Urban-Rural Development of the People’s Republic of China: Beijing, China, 2018.
- JGJ 134; Design Standard for Energy Efficiency of Residential Buildings in Hot Summer and Cold Winter Zone. Ministry of Housing and Urban-Rural Development of the People’s Republic of China: Beijing, China, 2010.
- Zou, Y.; Zhao, W.; Zhong, R. The spatial distribution of green buildings in China: Regional imbalance, economic fundamentals, and policy incentives. Appl. Geogr. 2017, 88, 38–47. [Google Scholar] [CrossRef]
- GB50378-2019; Assessment Standard for Green Buildings. Ministry of Housing and Urban-Rural Development of the People’s Republic of China: Beijing, China, 2019.
- Xu, F.; Liu, Q. Building energy consumption optimization method based on convolutional neural network and BIM. Alex. Eng. J. 2023, 77, 407–417. [Google Scholar] [CrossRef]
- Guo, K.; Li, Q.; Zhang, L.; Wu, X. BIM-based green building evaluation and optimization: A case study. J. Clean. Prod. 2021, 320, 128824. [Google Scholar] [CrossRef]
- Zhang, S.; Hu, L.; Zhu, M.; Shi, J. Economic Benefit Evaluation of the Assembled Green Roof: Taking the Teaching Building of Hefei Experimental School as an Example. J. Shenyang Jianzhu Univ. (Soc. Sci.) 2022, 24, 592–597. [Google Scholar]
- Gao, B.; Li, X.; Shen, L. Design Optimization of Green Building Schematic Plan Based on Comprehensive Performance Analysis. Constr. Econ. 2014, 378, 90–94. [Google Scholar]
- Xu, X.; Xu, P.; Zhu, J.; Liu, J.; Xue, Q. How to minimize the embodied environmental impact of green building envelope? An automatic optimization method. Environ. Impact Assess. Rev. 2022, 93, 106732. [Google Scholar] [CrossRef]
- Ding, Z.; Chen, W.; Hu, T.; Xu, X. Evolutionary double attention-based long short-term memory model for building energy prediction: Case study of a green building. Appl. Energy 2021, 288, 116660. [Google Scholar] [CrossRef]
- Bansal, N.K.; Hauser, G.; Minke, G. Passive Building Design. A Handbook of Natural Climatic Control; Elsevier Science BV: Amsterdam, The Netherlands, 1994; pp. 35–46. [Google Scholar]
- Li, F.; Zhang, J.; Liu, Y.; Wang, Y.; Qian, Y. Research on Green Building Technology Application Strategies—An Example of Three-Star Green High-Rise Office Building in Hot Summer and Cold Winter Region. Green Build. 2023, 15, 44–46. [Google Scholar]
- GB20376-2012; Design Code for Heating Ventilation and Air Conditioning of Civil Buildings. China Academy of Building Research: Beijing, China, 2012.
- Eddy, K.; Bradley, N. Green BIM; China Architecture & Building Press: Beijing, China, 2016; pp. 150–189. [Google Scholar]
- Fu, X.; Shen, S.G.; Yin, J. Study on Green Low Carbon Building Design Based on Photovoltaic Power Generation Technology. Appl. Mech. Mater. 2012, 193, 239–242. [Google Scholar] [CrossRef]
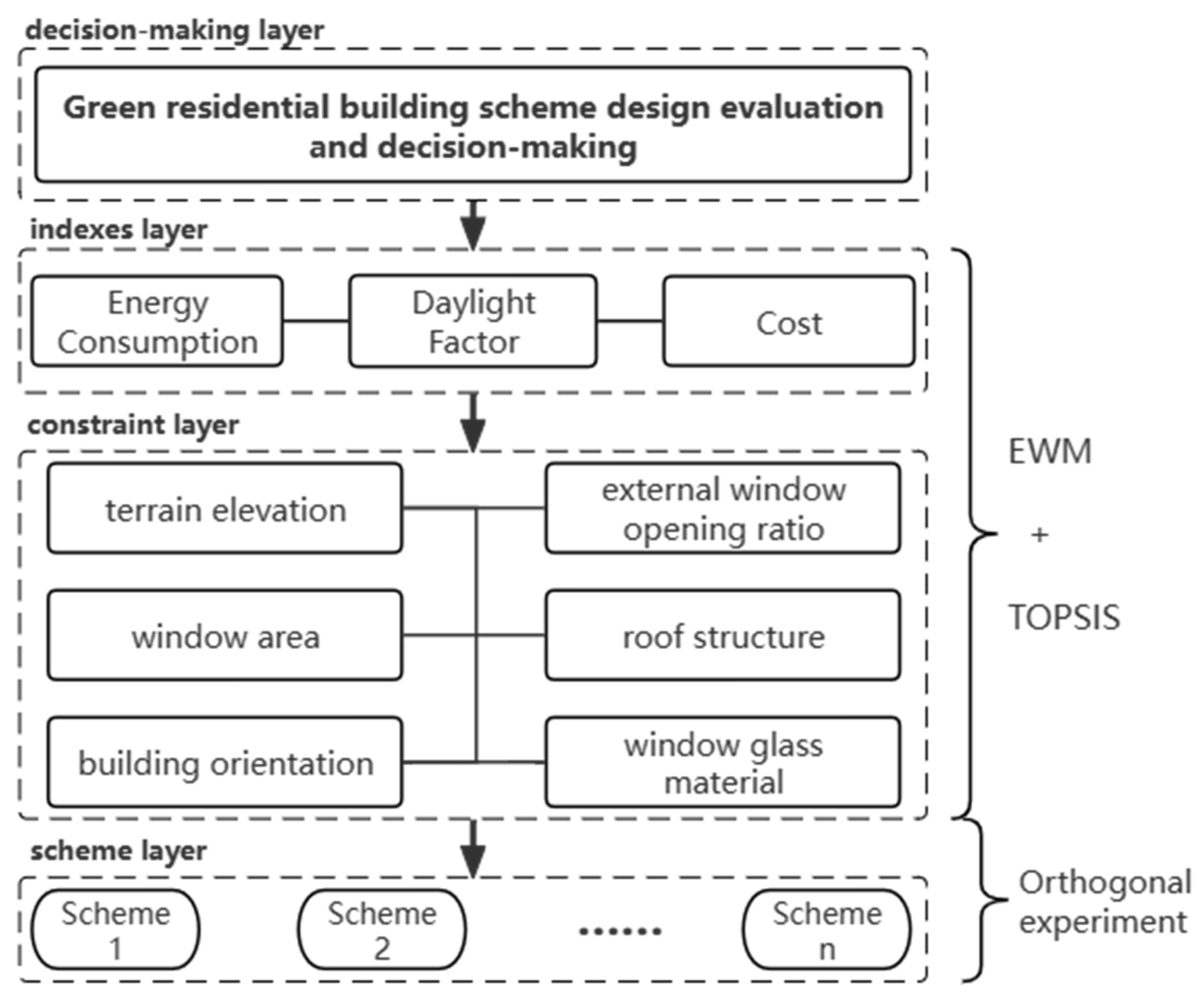
| Green Building Multi-Objective Optimization Design Scheme | ||||
|---|---|---|---|---|
| Design Parameters | No. | Level 1 | Level 2 | Level 3 |
| Terrain elevation | A | 5 | 15 | 25 |
| Window area | B | 900 × 200 | 1200 × 1500 | 1500 × 1800 |
| Building orientation | C | 160° | 170° | 180° |
| External window opening ratio | D | 40% | 45% | 50% |
| Roof structure | E | Roof structure 1 | Roof structure 2 | Roof structure 3 |
| Window glass material | F | Ordinary glass | Double-layer insulated glass | Vacuum glass |
| No. | Combination * | A | B | C | D | E | F |
|---|---|---|---|---|---|---|---|
| 1 | A1B1C1D1E1F1 | 5 | 900 × 1200 | 160° | 40% | E1 | F1 |
| 2 | A1B2C2D2E2F2 | 5 | 1200 × 1500 | 170° | 45% | E2 | F2 |
| 3 | A1B3C3D3E3F3 | 5 | 1500 × 1800 | 180° | 50% | E3 | F3 |
| 4 | A2B1C1D2E2F2 | 15 | 900 × 1200 | 160° | 45% | E2 | F3 |
| 5 | A2B2C2D3E3F1 | 15 | 1200 × 1500 | 170° | 50% | E3 | F1 |
| 6 | A2B3C3D1E1F2 | 15 | 1500 × 1800 | 180° | 40% | E1 | F2 |
| 7 | A3B1C2D1E3F2 | 25 | 900 × 1200 | 170° | 40% | E3 | F2 |
| 8 | A3B2C3D2E1F3 | 25 | 1200 × 1500 | 180° | 45% | E1 | F3 |
| 9 | A3B3C1D3E2F1 | 25 | 1500 × 1800 | 160° | 50% | E2 | F1 |
| 10 | A1B1C3D3E2F2 | 5 | 900 × 1200 | 180° | 50% | E2 | F2 |
| 11 | A1B2C1D1E3F3 | 5 | 1200 × 1500 | 160° | 40% | E3 | F3 |
| 12 | A1B3C2D2E1F1 | 5 | 1500 × 1800 | 170° | 45% | E1 | F1 |
| 13 | A2B1C2D3E1F3 | 15 | 900 × 1200 | 170° | 50% | E1 | F3 |
| 14 | A2B2C3D1E2F1 | 15 | 1200 × 1500 | 180° | 40% | E2 | F1 |
| 15 | A2B3C1D2E3F2 | 15 | 1500 × 1800 | 160° | 45% | E3 | F2 |
| 16 | A3B1C3D2E3F1 | 25 | 900 × 1200 | 180° | 45% | E3 | F1 |
| 17 | A3B2C1D3E1F2 | 25 | 1200 × 1500 | 160° | 50% | E1 | F2 |
| 18 | A3B3C2D1E2F3 | 25 | 1500 × 1800 | 170° | 40% | E2 | F3 |
| Energy Consumption Analysis Using GBS | |
|---|---|
| Location | Nanjing |
| Weather station | 538,562 |
| Floor area | 299 m2 |
| Exterior wall area | 364 m2 |
| Average lighting power | 9.69 W/m2 |
| Exterior window proportions | 0.14 |
| Electricity cost | USD 0.09/kWh |
| Fuel cost | USD 0.78/g calorie |
| EUI of electricity | 215 kWh/sm/yr |
| EUI of fuel | 35 kWh/sm/yr |
| Total EUI | 809 kWh/sm/yr |
| Life cycle electricity consumption | 1,924,258 kWh |
| Life cycle fuel consumption | 314,728 MJ |
| Life cycle energy cost | USD 83,094 |
| Range of Daylight Factor | Area that Meets Level IV Standards | |
|---|---|---|
| (From–to) | Within (%) | Above (%) |
| 2–4 | 0.48 | 52.7 |
| 4–6 | 0 | 52.17 |
| 6–8 | 0 | 51.63 |
| 8–10 | 0 | 50.03 |
| 10–12 | 0.05 | 47.35 |
| 12–14 | 0.95 | 40.94 |
| 14–16 | 2.83 | 40.39 |
| 16–18 | 4.74 | 37.45 |
| 18–20 | 4.28 | 34.78 |
| Experimental Combination | Energy Consumption (kwh) | Daylight Factor (%) | Cost (USD Thousand) |
|---|---|---|---|
| A1B1C1D1E1F1 | 1,924,258 | 53.18 | 29.5 |
| A1B2C2D2E2F2 | 917,639 | 58.19 | 40.1 |
| A1B3C3D3E3F3 | 1,469,207 | 63.64 | 49.6 |
| A2B1C1D2E2F2 | 856,507 | 54.83 | 36.9 |
| A2B2C2D3E3F1 | 918,293 | 59.51 | 45.8 |
| A2B3C3D1E1F2 | 1,850,214 | 67.59 | 26.3 |
| A3B1C2D1E3F2 | 1,714,876 | 56.79 | 37.4 |
| A3B2C3D2E1F3 | 1,771,765 | 66.06 | 37.1 |
| A3B3C1D3E2F1 | 1,714,432 | 67.69 | 40.0 |
| A1B1C3D3E2F2 | 1,641,766 | 56.45 | 44.6 |
| A1B2C1D1E3F3 | 1,680,125 | 57.59 | 33.3 |
| A1B3C2D2E1F1 | 1,738,423 | 59.48 | 34.2 |
| A2B1C2D3E1F3 | 1,771,155 | 58.83 | 36.4 |
| A2B2C3D1E2F1 | 1,721,112 | 61.4 | 34.8 |
| A2B3C1D2E3F2 | 1,654,524 | 63.35 | 38.3 |
| A3B1C3D2E3F1 | 1,827,978 | 60.75 | 40.1 |
| A3B2C1D3E1F2 | 1,786,188 | 62.82 | 31.0 |
| A3B3C2D1E2F3 | 1,808,409 | 68.64 | 34.6 |
| No. | Factors | Comprehensive Score | |||||
|---|---|---|---|---|---|---|---|
| A | B | C | D | E | F | ||
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0.28759 |
| 2 | 1 | 2 | 2 | 2 | 2 | 2 | 0.64865 |
| 3 | 1 | 3 | 3 | 3 | 3 | 3 | 0.42686 |
| 4 | 2 | 1 | 1 | 2 | 2 | 2 | 0.63068 |
| 5 | 2 | 2 | 2 | 3 | 3 | 1 | 0.62244 |
| 6 | 2 | 3 | 3 | 1 | 1 | 2 | 0.46971 |
| 7 | 3 | 1 | 2 | 1 | 3 | 2 | 0.2862 |
| 8 | 3 | 2 | 3 | 2 | 1 | 3 | 0.41374 |
| 9 | 3 | 3 | 1 | 3 | 2 | 1 | 0.43884 |
| 10 | 1 | 1 | 3 | 3 | 2 | 2 | 0.24936 |
| 11 | 1 | 2 | 1 | 1 | 3 | 3 | 0.3526 |
| 12 | 1 | 3 | 2 | 2 | 1 | 1 | 0.34758 |
| 13 | 2 | 1 | 2 | 3 | 1 | 3 | 0.30477 |
| 14 | 2 | 2 | 3 | 1 | 2 | 1 | 0.37717 |
| 15 | 2 | 3 | 1 | 2 | 3 | 2 | 0.40686 |
| 16 | 3 | 1 | 3 | 2 | 3 | 1 | 0.28607 |
| 17 | 3 | 2 | 1 | 3 | 1 | 2 | 0.40539 |
| 18 | 3 | 3 | 2 | 1 | 2 | 3 | 0.45022 |
| K1 | 2.313 | 2.045 | 2.522 | 2.223 | 2.229 | 2.36 | |
| K2 | 2.812 | 2.82 | 2.66 | 2.734 | 2.795 | 2.466 | |
| K3 | 2.28 | 2.54 | 2.223 | 2.448 | 2.381 | 2.579 | |
| 0.385 | 0.341 | 0.42 | 0.371 | 0.371 | 0.393 | ||
| 0.469 | 0.47 | 0.443 | 0.456 | 0.466 | 0.411 | ||
| 0.38 | 0.423 | 0.37 | 0.408 | 0.397 | 0.43 | ||
| R | 0.089 | 0.129 | 0.073 | 0.085 | 0.094 | 0.037 | |
| Number of experimental replicates per level | 6 | 6 | 6 | 6 | 6 | 6 | |
| Optimal level | A2 | B2 | C2 | D2 | E2 | F3 | |
| Influence degree of factor | B > E > A > D > C > F | ||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, H.; An, Y.-c. Green Residential Building Design Scheme Optimization Based on the Orthogonal Experiment EWM-TOPSIS. Buildings 2024, 14, 452. https://doi.org/10.3390/buildings14020452
Chen H, An Y-c. Green Residential Building Design Scheme Optimization Based on the Orthogonal Experiment EWM-TOPSIS. Buildings. 2024; 14(2):452. https://doi.org/10.3390/buildings14020452
Chicago/Turabian StyleChen, Honghua, and Yun-ce An. 2024. "Green Residential Building Design Scheme Optimization Based on the Orthogonal Experiment EWM-TOPSIS" Buildings 14, no. 2: 452. https://doi.org/10.3390/buildings14020452
APA StyleChen, H., & An, Y.-c. (2024). Green Residential Building Design Scheme Optimization Based on the Orthogonal Experiment EWM-TOPSIS. Buildings, 14(2), 452. https://doi.org/10.3390/buildings14020452





