Optimal Cost Design of RC T-Shaped Combined Footings
Abstract
1. Introduction
2. Mathematical Models
2.1. Minimum Contact Surface
2.2. Minimum Cost Design
2.2.1. Moments
2.2.2. Bending Shears
2.2.3. Punching Shears
2.2.4. Objective Function for Minimum Cost
2.2.5. Constraint Functions
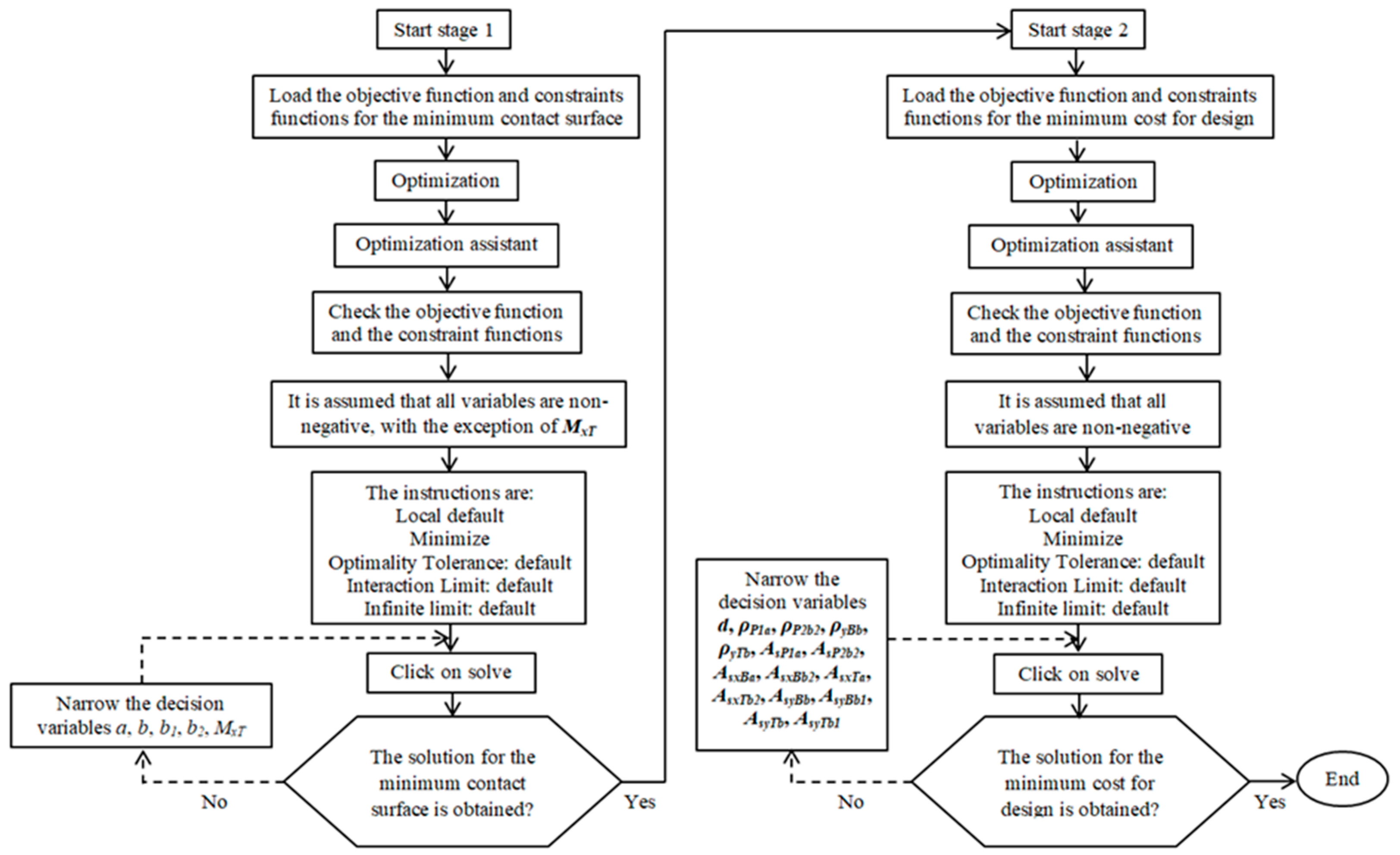
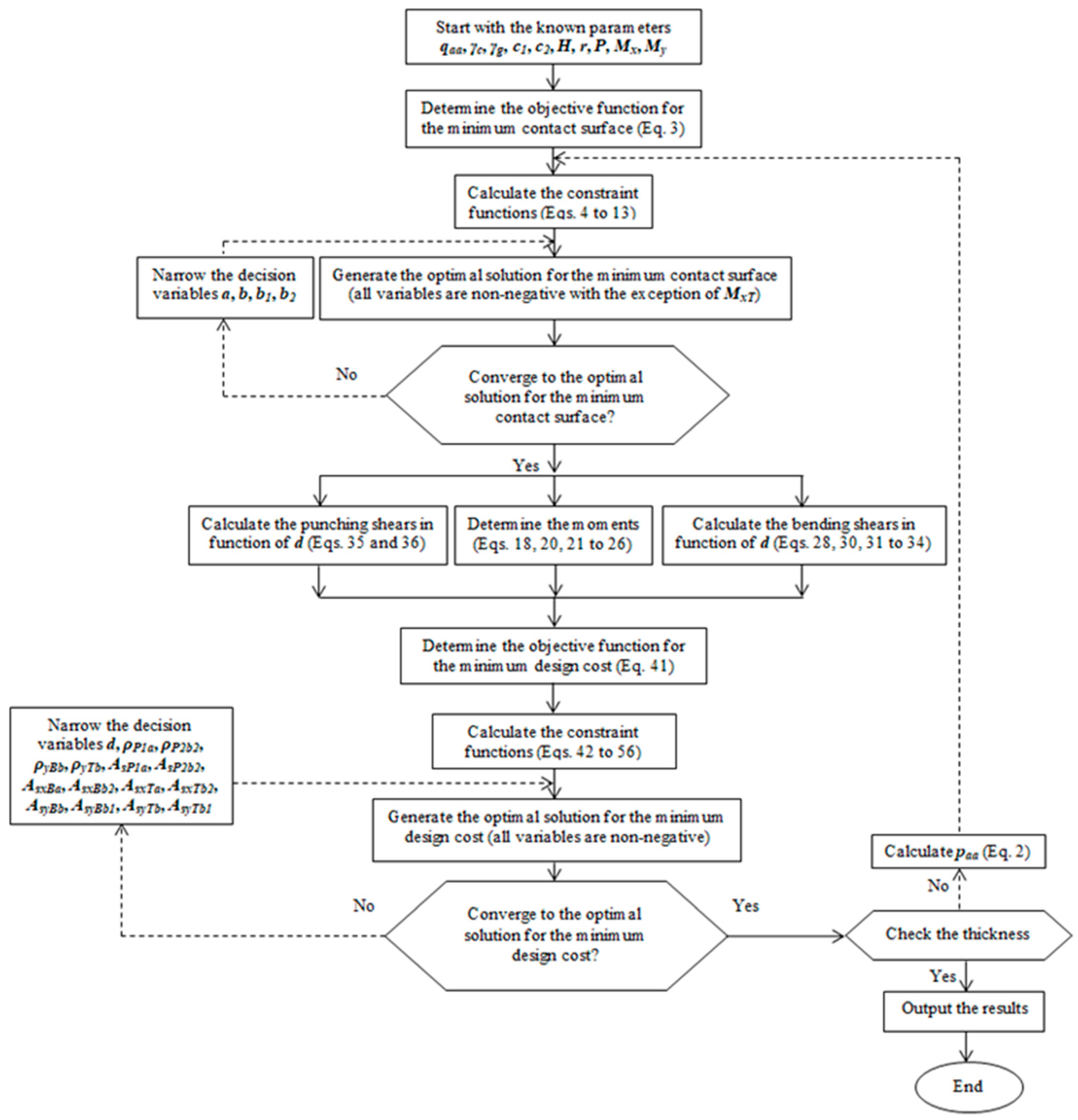
3. Numerical Problems
- First iteration: Stage 1. Start with the minimum thickness of t = 25 cm; therefore, d = 17 cm, since the ACI proposes a minimum of r = 7.5 cm (here, it is assumed r = 8 cm). With the known data, the minimum area is obtained. Subsequently, the dimensions of the footing are proposed (a, b, b1 and b2), and the properties of the footing are obtained (yt, S, Ix and Iy).
- First iteration: Stage 2. Now, the factored resultant force and the factored resultant moments are obtained (Ru, MuxT and MuyT). The moments, the bending shears as a function of d and the punching shears as a function of d that act are then determined. With all these data, the minimum cost of the footing is determined.
- Second iteration: Stage 1. Now, as the thickness of the footing has increased, the same procedure as in the first iteration of stage 1 is developed.
- Second iteration: Stage 2. The same procedure as in the first iteration of stage 2 is developed.
- Final iteration: Stage 1. Now, with the adjusted dimensions of the second iteration of stage 1, it is developed to determine the minimum area and the pressures acting on the footing (Results section).
- Final iteration: Stage 2. Now, with the adjusted dimensions of the second iteration of stage 2, it is developed to determine the effective depth, the percentage of reinforcing steel, the reinforcing steel area, and the optimal cost design of the footing (Results section).
4. Results and Discussion
5. Conclusions
- The minimum contact surface and the optimal cost design of the T-shaped combined footings in this paper are more accurate and converge faster.
- The optimal cost design of rectangular combined footings presented in this paper is more accurate than that presented by Velázquez-Santillán et al. [15], because the moments Mx1 and Mx2 acting on the footing are not considered in the analysis for the minimum contact surface and the lowest design cost [15].
- If the moment about the X axis is zero, the resultant force is located at the center of gravity of the footing.
- Minimum cost design for other types of foundations using the optimization process to include sustainability considerations, such as minimizing environmental impact or carbon footprint.
- Minimum surface for RC T-shaped combined footings assuming that the foundation area is partially supported.
- Minimum cost for RC T-shaped combined footings assuming that the foundation area is partially supported.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Vrecl-Kojc, H. The anchored pile wall optimization using NLP approach. Acta Geotech. Slov. 2005, 2, 5–11. Available online: http://fgserver3.fg.um.si/journal-ags/pdfs/AGS_2005-2_article_1.pdf (accessed on 16 April 2024).
- Wang, Y.; Kulhawy, F.H. Economic design optimization of foundation. J. Geotech. Geoenviron. 2008, 134, 1097–1105. [Google Scholar] [CrossRef]
- Kortnik, J. Optimization of the high safety pillars for the underground excavation of natural stone blocks. Acta Geotech. Slov. 2009, 6, 61–73. Available online: http://www.dlib.si/details/URN:NBN:SI:doc-P6YIXYXG (accessed on 28 April 2024).
- Wang, Y. Reliability-based economic design optimization of spread foundations. J. Geotech. Geoenviron. 2009, 135, 954–959. [Google Scholar] [CrossRef]
- Chagoyén, E.; Negrín, A.; Cabrera, M.; López, L.; Padrón, N. Diseño óptimo de cimentaciones superficiales rectangulares. Formulación. Rev. Constr. 2009, 8, 60–71. Available online: http://www.redalyc.org/articulo.oa?id=127619798006 (accessed on 6 May 2024).
- Basudhar, P.K.; Dey, A.; Mondal, A.S. Optimal cost-analysis and design of circular footings. Int. J. Eng. Technol. Innov. 2012, 2, 243–264. Available online: http://ojs.imeti.org/index.php/IJETI/article/view/73/104 (accessed on 16 May 2024).
- Rizwan, M.; Alam, B.; Rehman, F.U.; Masud, N.; Shahzada, K.; Masud, T. Cost Optimization of Combined Footings Using Modified Complex Method of Box. Int. J. Adv. Struct. Geotech. Eng. 2012, 1, 24–28. [Google Scholar]
- Jagodnik, V.; Jelenić, G.; Arbanas, Ž. On the application of a mixed finite element approach to beam-soil interaction. Acta Geotech. Slov. 2013, 10, 14–27. Available online: http://www.dlib.si/details/URN:NBN:SI:doc-48QPPGCW (accessed on 21 June 2024).
- Al-Ansari, M.S. Structural cost of optimized reinforced concrete isolated footing. Int. Schol. Sci. Res. Innov. 2013, 7, 290–297. Available online: https://zenodo.org/record/1080444/files/13071.pdf?download=1 (accessed on 28 June 2024).
- Jelusic, P.; Zlender, B. Soil-nail wall stability analysis using ANFIS. Acta Geotech. Slov. 2013, 10, 35–48. Available online: http://www.dlib.si/details/URN:NBN:SI:doc-JPKHM66L (accessed on 22 July 2024).
- Al-Ansari, M.S. Cost of reinforced concrete paraboloid shell footing. Int. J. Struct. Analys. Des. 2013, 1, 111–119. Available online: http://journals.theired.org/journals/paper/details/4470.html (accessed on 29 July 2024).
- Sadoğlu, E. Design optimization for symmetrical gravity retaining walls. Acta Geotech. Slov. 2014, 11, 61–73. Available online: http://www.dlib.si/details/URN:NBN:SI:doc-ROBPWX51 (accessed on 21 August 2024).
- El-Sakhawy, N.R.; Salem, T.N.; Al-Tuhamy, A.A.; El_Latief, A.A. Experimental study for the optimization of foundation shapes on soft soil. Egypt. Int. J. Eng. Sci. Technol. 2016, 21, 24–32. [Google Scholar] [CrossRef]
- Ukritchon, B.; Keawsawasvong, S. A practical method for the optimal design of continuous footing using ant-colony optimization. Acta Geotech. Slov. 2016, 13, 45–55. Available online: https://www.dlib.si/details/URN:NBN:SI:DOC-2K2QA1HZ (accessed on 22 August 2024).
- Velázquez-Santillán, F.; Luévanos-Rojas, A.; López-Chavarría, S.; Medina-Elizondo, M.; Sandoval-Rivas, S. Numerical experimentation for the optimal design for reinforced concrete rectangular combined footings. Adv. Comput. Des. 2018, 3, 49–69. [Google Scholar] [CrossRef]
- Luévanos-Rojas, A.; López-Chavarría, S.; Medina-Elizondo, M. A new model for T-shaped combined footings Part I: Optimal dimensioning. Geomech. Eng. 2018, 14, 51–60. [Google Scholar] [CrossRef]
- Luévanos-Rojas, A.; López-Chavarría, S.; Medina-Elizondo, M. A new model for T-shaped combined footings Part II: Mathematical model for design. Geomech. Eng. 2018, 14, 61–69. [Google Scholar] [CrossRef]
- Nigdeli, S.M.; Bekdas, G.; Yang, X.-S. Metaheuristic Optimization of Reinforced Concrete Footings. KSCE J. Civ. Eng. 2018, 22, 4555–4563. Available online: https://link.springer.com/article/10.1007/s12205-018-2010-6 (accessed on 24 August 2024). [CrossRef]
- Islam, M.S.; Rokonuzzaman, M. Optimized design of foundations: An application of genetic algorithms. Aust. J. Civil. Eng. 2018, 16, 46–52. [Google Scholar] [CrossRef]
- Rawat, S.; Mittal, R.K. Optimization of eccentrically loaded reinforced-concrete isolated footings. Pract. Period. Struct. Des. Constr. 2018, 23, 06018002. [Google Scholar] [CrossRef]
- Chaudhuri, P.; Maity, D. Cost optimization of rectangular RC footing using GA and UPSO. Soft Comput. 2020, 24, 709–721. [Google Scholar] [CrossRef]
- Nawaz, M.N.; Ali, A.S.; Jaffar, S.T.A.; Jafri, T.H.; Oh, T.-M.; Abdallah, M.; Karam, S.; Azab, M. Cost-Based Optimization of Isolated Footing in Cohesive Soils Using Generalized Reduced Gradient Method. Buildings 2022, 12, 1646. [Google Scholar] [CrossRef]
- Waheed, J.; Azam, R.; Riaz, M.R.; Shakeel, M.; Mohamed, A.; Ali, E. Metaheuristic-Based Practical Tool for Optimal Design of Reinforced Concrete Isolated Footings: Development and Application for Parametric Investigation. Buildings 2022, 12, 471. [Google Scholar] [CrossRef]
- Nigdeli, S.M.; Bekdas, G. The Investigation of Optimization of Eccentricity in Reinforced Concrete Footings. In Proceedings of 7th International Conference on Harmony Search. Soft Comput. Appl. 2022, 140, 207–215. [Google Scholar]
- Kashani, A.R.; Camp, C.V.; Akhani, M.; Ebrahimi, S. Optimum design of combined footings using swarm intelligence-based algorithms. Adv. Eng. Soft. 2022, 169, 103140. [Google Scholar] [CrossRef]
- Aishwarya, K.M.; Balaji, N.C. Analysis and design of eccentrically loaded corner combined footing for rectangular columns. In Proceedings of the International Conference on Advances in Sustainable Construction Materials, Guntur, India, 18–19 March 2022. [Google Scholar] [CrossRef]
- López-Machado, N.A.; Perez, G.; Castro, C.; Perez, J.C.V.; López-Machado, L.J.; Alviar-Malabet, J.D.; Romero-Romero, C.A.; Guerrero-Cuasapaz, D.P.; Montesinos-Machado, V.V. A Structural Design Comparison Between Two Reinforced Concrete Regular 6-Level Buildings using Soil-Structure Interaction in Linear Range. Ing. Inv. 2022, 42, e86819. [Google Scholar] [CrossRef]
- Komolafe, O.O.; Balogun, I.O.; Abiodun, U.O. Comparison of square and circular isolated pad foundations in cohesionless soils. Arid Zone J. Eng. Technol. Environ. 2023, 17, 197–210. Available online: https://www.ajol.info/index.php/azojete/article/view/243597 (accessed on 24 August 2024).
- Ekbote, A.G.; Nainegali, L. Study on Closely Spaced Asymmetric Footings Embedded in a Reinforced Soil Medium. Ing. Inv. 2023, 43, e101082. [Google Scholar] [CrossRef]
- Solorzano, G.; Plevris, V. Optimum Design of RC Footings with Genetic Algorithms According to ACI 318-19. Buildings 2022, 10, 110. [Google Scholar] [CrossRef]
- Chaabani, W.; Remadna, M.S.; Abu-Farsakh, M. Numerical Modeling of the Ultimate Bearing Capacity of Strip Footings on Reinforced Sand Layer Overlying Clay with Voids. Infrastructures 2023, 8, 3. [Google Scholar] [CrossRef]
- Gnananandarao, T.; Onyelowe, K.; Khatri, V.N.; Dutta, R.K. Performance of T-shaped skirted footings resting on sand. Int. J. Min. Geo.-Eng. (IJMGE) 2023, 57, 65–71. Available online: https://civilica.com/doc/1625762/ (accessed on 24 August 2024).
- Shaaban, M.Q.; Al-kuaity, A.S.; Aliakbar, M.R.M. Simple function to find base pressure under triangular and trapezoidal footing with two eccentric loads. Open Eng. 2023, 13, 20220458. [Google Scholar] [CrossRef]
- Al-Ansari, M.S.; Afzal, M.S. Structural analysis and design of irregular shaped footings subjected to eccentric loading. Eng. Rep. 2021, 3, e12283. [Google Scholar] [CrossRef]
- Ranadive, R.; Mahiyar, H.K. An Experimental Study of Rectangular T-Shaped Footing Subjected to Dynamic Load. Int. J. Sci. Eng. Technol. 2015, 3, 179–188. Available online: https://www.ijset.in/wp-content/uploads/2016/01/10.2348.ijset1115179.pdf (accessed on 24 August 2024).
- Khare, P.A.; Thakare, S.W. Performance of T-shaped Footing on Layered Sand. Int. J. Innov. Res. Sci. Eng. Technol. 2017, 6, 9462–9469. Available online: https://www.ijirset.com/upload/2017/may/284_60_Performance.pdf (accessed on 24 August 2024).
- Sivanantham, P.; Selvan, S.S.; Srinivasan, S.K.; Gurupatham, B.G.A.; Roy, K. Influence of Infill on Reinforced Concrete Frame Resting on Slopes under Lateral Loading. Buildings 2023, 13, 289. [Google Scholar] [CrossRef]
- Helis, R.; Mansouri, T.; Abbeche, K. Behavior of a Circular Footing resting on Sand Reinforced with Geogrid and Grid Anchors. Eng. Technol. Appl. Sci. Res. 2023, 13, 10165–10169. [Google Scholar] [CrossRef]
- ACI 318-19; Building Code Requirements for Structural Concrete and Commentary. American Concrete Institute: Farmington Hills, MI, USA, 2019.
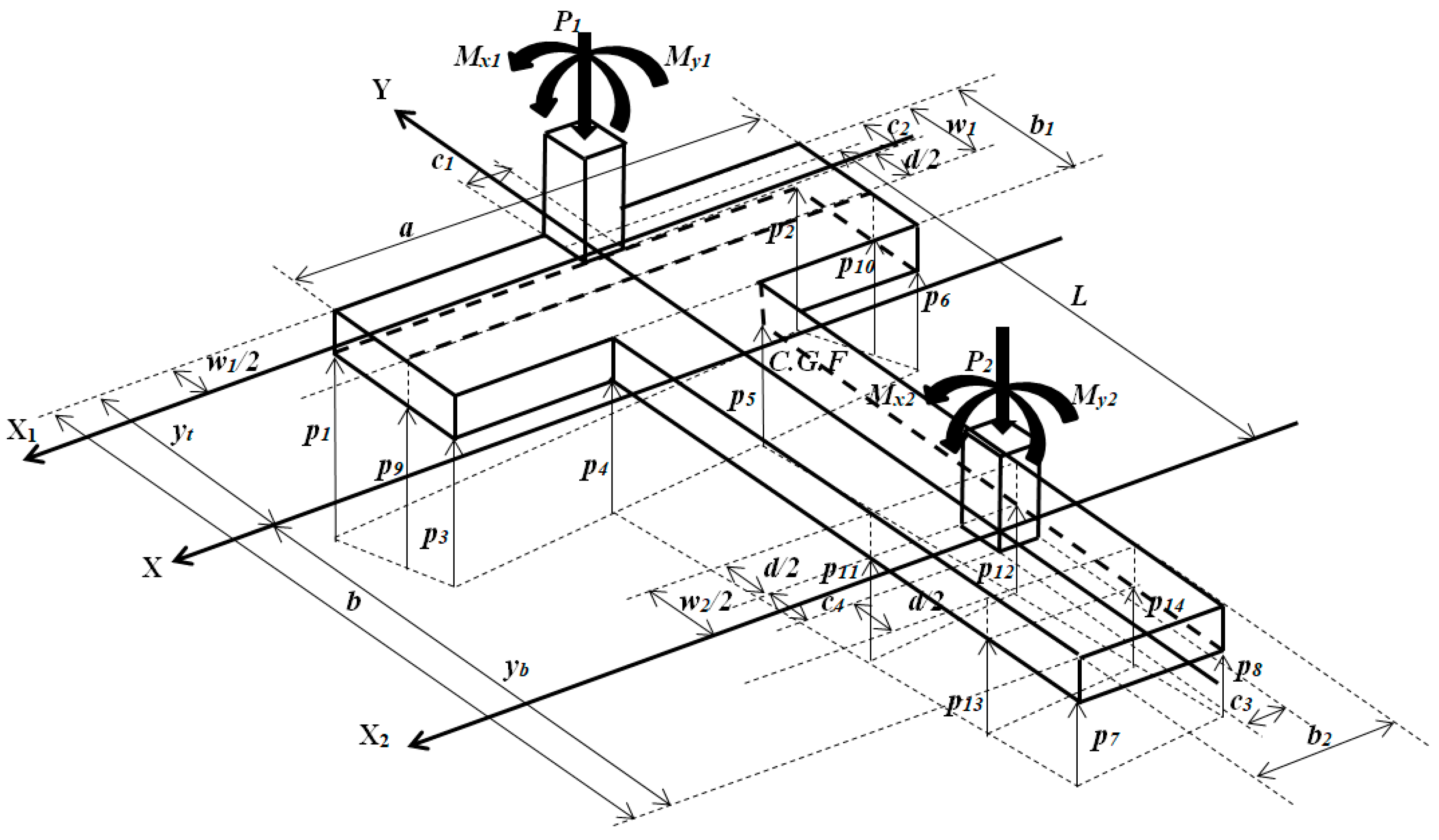
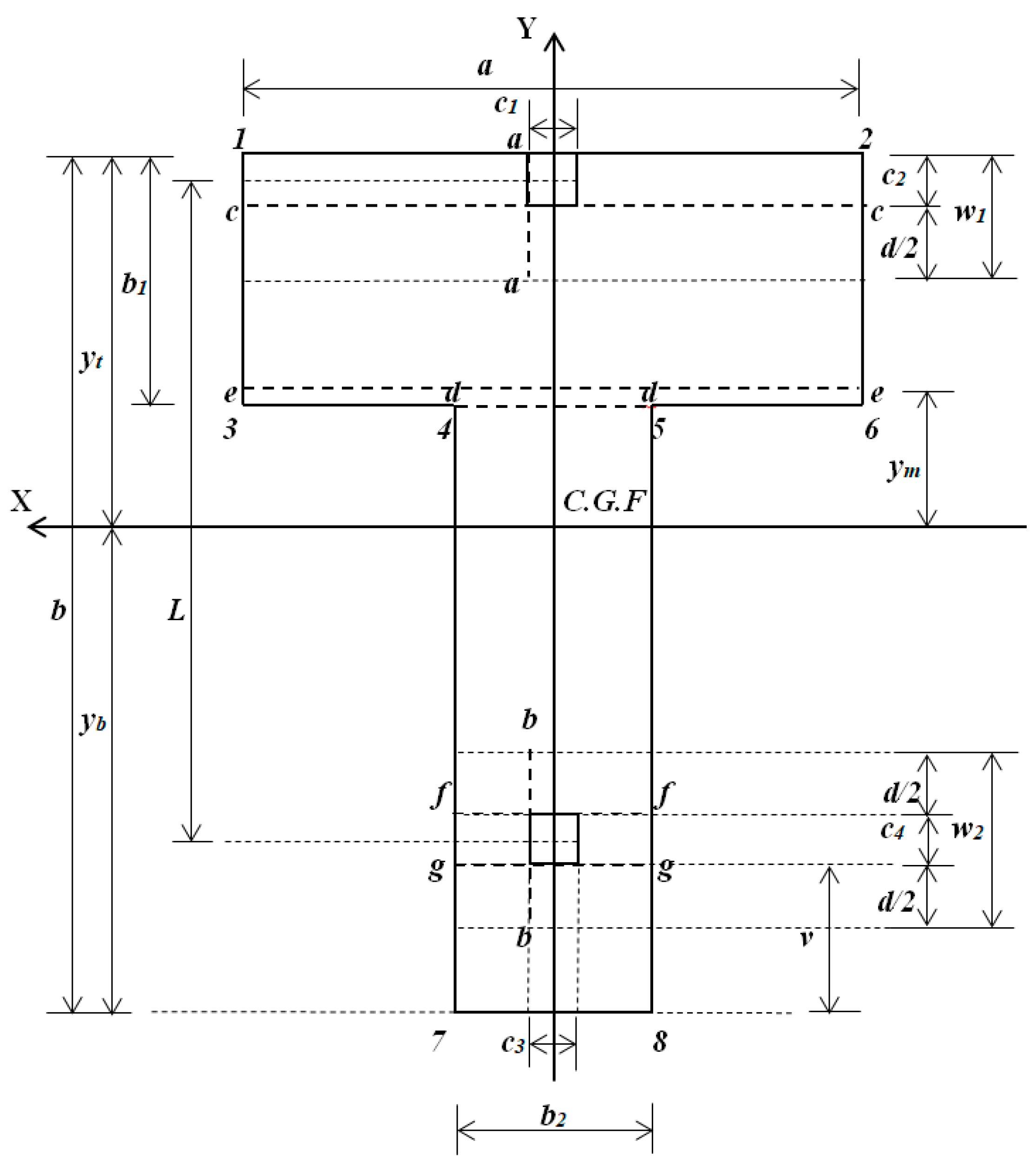
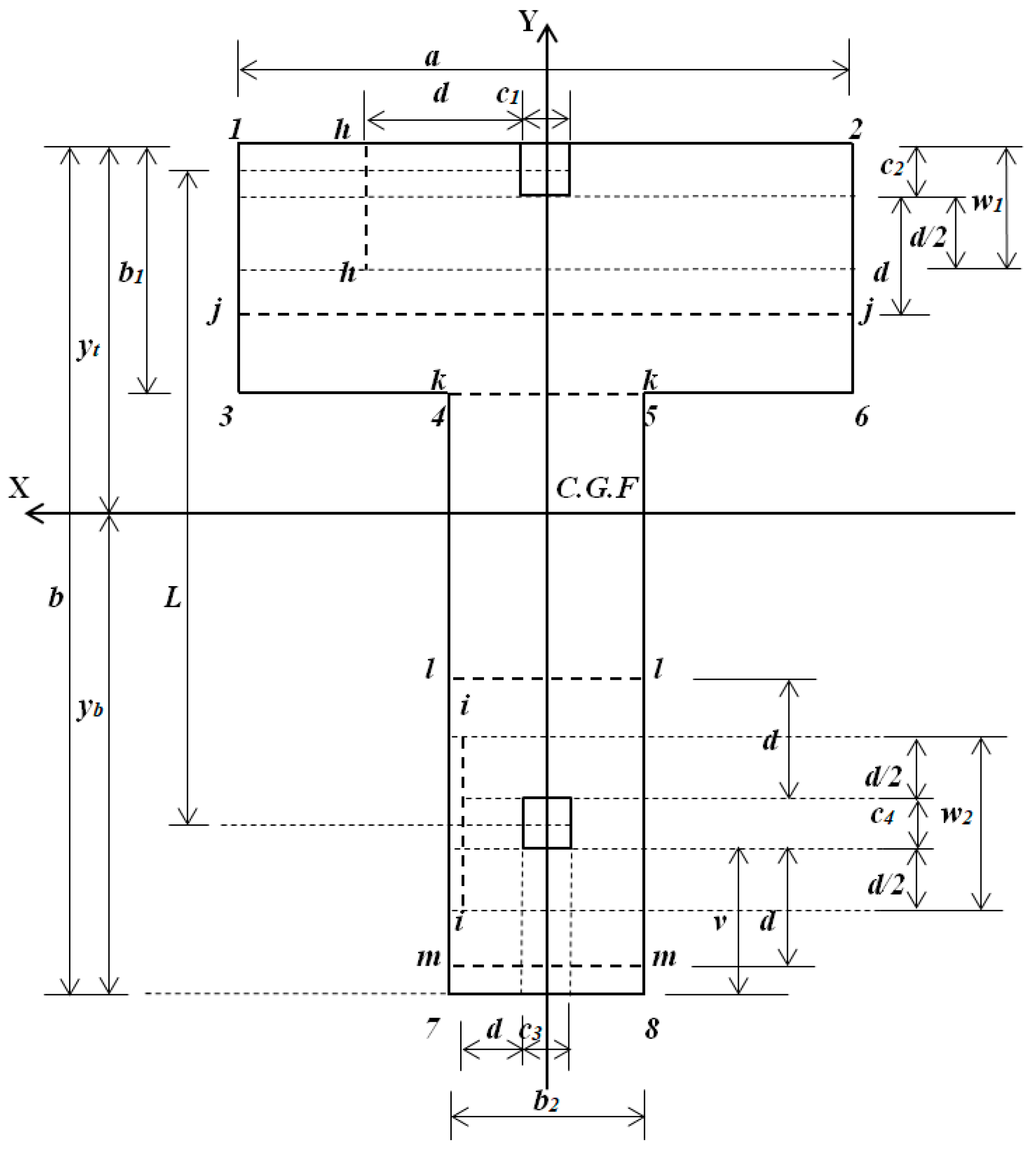
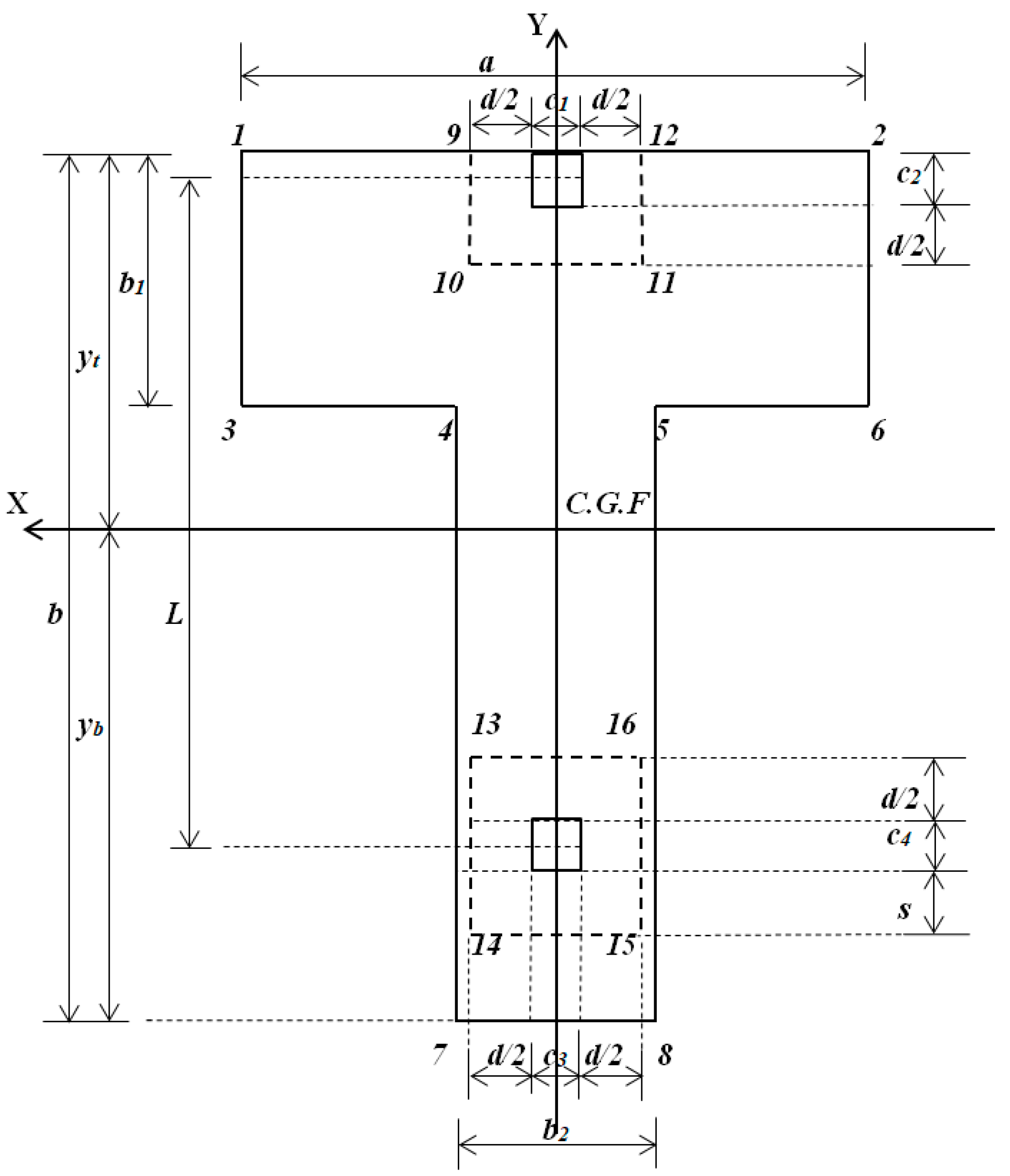
| Pressures pn (kN/m2) | p1 | p2 | p3 | p4 | p5 | p6 | p7 | p8 |
|---|---|---|---|---|---|---|---|---|
| Coordinates | x1 = a/2 | x2 = −a/2 | x3 = a/2 | x4 = b2/2 | x5 = −b2/2 | x6 = −a/2 | x7 = b2/2 | x8 = −b2/2 |
| y1 = yt | y2 = yt | y3 = yt − b1 | y4 = yt − b1 | y5 = yt − b1 | y6 = yt − b1 | y7 = −yb | y8 = −yb |
| Pressures pn (kN/m2) | Pressures Due to P1 pn (kN/m2) | Pressures Due to P2 pn (kN/m2) | ||||||
|---|---|---|---|---|---|---|---|---|
| p1 | p2 | p9 | p10 | p11 | p12 | p13 | p14 | |
| Coordinates | x1 = a/2 | x2 = −a/2 | x9 = a/2 | x10 = −a/2 | x11 = b2/2 | x12 = −b2/2 | x13 = b2/2 | x14 = −b2/2 |
| y1 = w1/2 | y2 = w1/2 | y9 = −w1/2 | y10 = −w1/2 | y11 = w2/2 | y12 = w2/2 | y13 = −w2/2 | y14 = −w2/2 | |
| Column | PD kN | PL kN | MDx kN-m | MLx kN-m | MDy kN-m | MLy kN-m |
|---|---|---|---|---|---|---|
| 1 | 600 | 600 | 160 | 140 | 120 | 80 |
| 2 | 500 | 500 | 80 | 70 | 120 | 80 |
| First Iteration: Stage 1 | ||||||||||||||||
| paa | t | d | MxT | a | b | b1 | b2 | p1 | p2 | p3 | p4 | p5 | p6 | p7 | p8 | Smin |
| (kN/m2) | (cm) | (cm) | (kN-m) | (m) | (kN/m2) | (m2) | ||||||||||
| 217.50 | 25.00 | 17.00 | 0 | 2.92 | 6.40 | 3.69 | 1.50 | 217.75 | 78.86 | 217.75 | 184.02 | 112.59 | 78.86 | 184.02 | 112.59 | 14.83 |
| Proposed dimensions and properties: a = 3.00 m, b = 6.40 m, b1 = 3.70 m, b2 = 1.50 m, yt = 2.71 m, S = 15.15 m2, Ix = 45.51 m4, Iy = 9.08 m4 | ||||||||||||||||
| First iteration: Stage 2 | ||||||||||||||||
| MuxT | d | ρP1a | ρP2b2 | ρyBb | ρyTb | AsP1a | AsP2b2 | AsxBa | AsxBb2 | AsxTa | AsxTb2 | AsyBb | AsyBb1 | AsyTb | AsyTb1 | Cmin |
| (kN-m) | (cm) | (cm2) | ||||||||||||||
| −59.23 | 87.50 | 0.00333 | 0.00333 | 0.00333 | 0.00588 | 24.42 | 24.42 | 45.08 | 29.33 | 58.27 | 42.52 | 43.75 | 23.62 | 77.21 | 23.62 | 27.61Cc |
| Second iteration: Stage 1 | ||||||||||||||||
| paa | t | d | MxT | a | b | b1 | b2 | p1 | p2 | p3 | p4 | p5 | p6 | p7 | p8 | Smin |
| (kN/m2) | (cm) | (cm) | (kN-m) | (m) | (kN/m2) | (m2) | ||||||||||
| 211.00 | 100 | 92.00 | 0 | 2.97 | 6.40 | 3.80 | 1.50 | 211.00 | 79.06 | 211.00 | 178.40 | 111.66 | 79.06 | 178.40 | 111.66 | 15.17 |
| Proposed dimensions and properties: a = 3.00 m, b = 6.40 m, b1 = 3.80 m, b2 = 1.50 m, yt = 2.72 m, S = 15.30 m2, Ix = 45.67 m4, Iy = 9.28 m4 | ||||||||||||||||
| Second iteration: Stage 2 | ||||||||||||||||
| MuxT | d | ρP1a | ρP2b2 | ρyBb | ρyTb | AsP1a | AsP2b2 | AsxBa | AsxBb2 | AsxTa | AsxTb2 | AsyBb | AsyBb1 | AsyTb | AsyTb1 | Cmin |
| (kN-m) | (cm) | (cm2) | ||||||||||||||
| −27.69 | 88.04 | 0.00333 | 0.00333 | 0.00333 | 0.00583 | 24.66 | 24.66 | 46.91 | 27.89 | 58.64 | 41.20 | 44.02 | 23.77 | 76.97 | 23.77 | 27.92Cc |
| First Iteration: Stage 1 | ||||||||||||||||
| paa | t | d | MxT | a | b | b1 | b2 | p1 | p2 | p3 | p4 | p5 | p6 | p7 | p8 | Smin |
| (kN/m2) | (cm) | (cm) | (kN-m) | (m) | (kN/m2) | (m2) | ||||||||||
| 217.50 | 25.00 | 17.00 | 3.26 | 4.74 | 6.40 | 1.00 | 2.00 | 217.75 | 65.70 | 217.75 | 173.76 | 109.59 | 65.65 | 173.48 | 109.30 | 15.54 |
| Proposed dimensions and properties: a = 4.80 m, b = 6.40 m, b1 = 1.00 m, b2 = 2.00 m, yt = 2.72 m, S = 15.60 m2, Ix = 60.67 m4, Iy = 12.82 m4 | ||||||||||||||||
| First iteration: Stage 2 | ||||||||||||||||
| MuxT | d | ρP1a | ρP2b2 | ρyBb | ρyTb | AsP1a | AsP2b2 | AsxBa | AsxBb2 | AsxTa | AsxTb2 | AsyBb | AsyBb1 | AsyTb | AsyTb1 | Cmin |
| (kN-m) | (cm) | (cm2) | ||||||||||||||
| −28.62 | 85.38 | 0.00441 | 0.00333 | 0.00333 | 0.00371 | 31.15 | 23.53 | 2.66 | 70.28 | 15.37 | 82.99 | 56.92 | 43.03 | 63.41 | 43.03 | 27.43Cc |
| Second iteration: Stage 1 | ||||||||||||||||
| paa | t | d | MxT | a | b | b1 | b2 | p1 | p2 | p3 | p4 | p5 | p6 | p7 | p8 | Smin |
| (kN/m2) | (cm) | (cm) | (kN-m) | (m) | (kN/m2) | (m2) | ||||||||||
| 211.45 | 95 | 87.00 | −51.39 | 4.91 | 6.40 | 1.00 | 2.00 | 210.67 | 64.87 | 211.45 | 168.24 | 108.92 | 65.71 | 172.77 | 113.45 | 15.71 |
| Proposed dimensions and properties: a = 5.00 m, b = 6.40 m, b1 = 1.00 m, b2 = 2.00 m, yt = 2.69 m, S = 15.80 m2, Ix = 61.66 m4, Iy = 14.02 m4 | ||||||||||||||||
| Second iteration: Stage 2 | ||||||||||||||||
| MuxT | d | ρP1a | ρP2b2 | ρyBb | ρyTb | AsP1a | AsP2b2 | AsxBa | AsxBb2 | AsxTa | AsxTb2 | AsyBb | AsyBb1 | AsyTb | AsyTb1 | Cmin |
| (kN-m) | (cm) | (cm2) | ||||||||||||||
| −114.99 | 86.38 | 0.00448 | 0.00333 | 0.00333 | 0.00360 | 32.16 | 23.95 | 2.61 | 71.02 | 15.55 | 83.96 | 57.58 | 46.64 | 62.20 | 46.64 | 27.99Cc |
| First Iteration: Stage 1 | ||||||||||||||||
| paa | t | d | MxT | a | b | b1 | b2 | p1 | p2 | p3 | p4 | p5 | p6 | p7 | p8 | Smin |
| (kN/m2) | (cm) | (cm) | (kN-m) | (m) | (kN/m2) | (m2) | ||||||||||
| 217.50 | 25.00 | 17.00 | 651.51 | 3.29 | 6.40 | 1.70 | 2.50 | 217.75 | 99.77 | 199.85 | 185.73 | 96.00 | 81.88 | 136.10 | 46.37 | 17.34 |
| Proposed dimensions and properties: a = 3.30 m, b = 6.40 m, b1 = 1.70 m, b2 = 2.50 m, yt = 3.02 m, S = 17.36 m2, Ix = 61.86 m4, Iy = 11.21 m4 | ||||||||||||||||
| First iteration: Stage 2 | ||||||||||||||||
| MuxT | d | ρP1a | ρP2b2 | ρyBb | ρyTb | AsP1a | AsP2b2 | AsxBa | AsxBb2 | AsxTa | AsxTb2 | AsyBb | AsyBb1 | AsyTb | AsyTb1 | Cmin |
| (kN-m) | (cm) | (cm2) | ||||||||||||||
| 896.97 | 74.63 | 0.00412 | 0.00333 | 0.00333 | 0.00433 | 23.79 | 19.23 | 12.45 | 52.75 | 22.84 | 63.14 | 62.19 | 10.75 | 80.73 | 10.75 | 27.55Cc |
| Second iteration: Stage 1 | ||||||||||||||||
| paa | t | d | MxT | a | b | b1 | b2 | p1 | p2 | p3 | p4 | p5 | p6 | p7 | p8 | Smin |
| (kN/m2) | (cm) | (cm) | (kN-m) | (m) | (kN/m2) | (m2) | ||||||||||
| 212.35 | 85 | 77.00 | 594.19 | 3.43 | 6.40 | 1.64 | 2.50 | 212.35 | 95.29 | 196.80 | 180.95 | 95.59 | 79.74 | 135.98 | 50.62 | 17.53 |
| Proposed dimensions and properties: a = 3.50 m, b = 6.40 m, b1 = 1.70 m, b2 = 2.50 m, yt = 2.97 m, S = 17.70 m2, Ix = 63.51 m4, Iy = 12.19 m4 | ||||||||||||||||
| Second iteration: Stage 2 | ||||||||||||||||
| MuxT | d | ρP1a | ρP2b2 | ρyBb | ρyTb | AsP1a | AsP2b2 | AsxBa | AsxBb2 | AsxTa | AsxTb2 | AsyBb | AsyBb1 | AsyTb | AsyTb1 | Cmin |
| (kN-m) | (cm) | (cm2) | ||||||||||||||
| 768.82 | 76.51 | 0.00413 | 0.00333 | 0.00333 | 0.00407 | 24.74 | 19.96 | 12.64 | 53.95 | 23.41 | 64.73 | 63.76 | 13.77 | 77.84 | 13.77 | 28.42Cc |
| First Iteration: Stage 1 | ||||||||||||||||
| paa | t | d | MxT | a | b | b1 | b2 | p1 | p2 | p3 | p4 | p5 | p6 | p7 | p8 | Smin |
| (kN/m2) | (cm) | (cm) | (kN-m) | (m) | (kN/m2) | (m2) | ||||||||||
| 217.50 | 25.00 | 17.00 | 1050.00 | 2.88 | 6.40 | - | - | 217.75 | 127.48 | - | - | - | - | 111.03 | 20.76 | 18.45 |
| Proposed dimensions and properties: a = 2.90 m, b = 6.40 m, yt = 3.20 m, S = 18.56 m2, Ix = 63.35 m4, Iy = 13.01 m4 | ||||||||||||||||
| First iteration: Stage 2 | ||||||||||||||||
| MuxT | d | ρP1a | ρP2b2 | ρyBb | ρyTb | AsP1a | AsP2b2 | AsxBa | AsxBb2 | AsxTa | AsxTb2 | AsyBb | AsyBb1 | AsyTb | AsyTb1 | Cmin |
| (kN-m) | (cm) | (cm2) | ||||||||||||||
| 1464.00 | 70.24 | 0.00415 | 0.00358 | 0.00333 | 0.00592 | 21.92 | 18.87 | 61.92 | - | 80.92 | - | 67.90 | - | 12.06 | - | 29.97Cc |
| Second iteration: Stage 1 | ||||||||||||||||
| paa | t | d | MxT | a | b | b1 | b2 | p1 | p2 | p3 | p4 | p5 | p6 | p7 | p8 | Smin |
| (kN/m2) | (cm) | (cm) | (kN-m) | (m) | (kN/m2) | (m2) | ||||||||||
| 212.80 | 80 | 72.00 | 1050.00 | 2.94 | 6.40 | - | - | 212.80 | 125.91 | - | - | - | - | 108.10 | 21.21 | 18.80 |
| Proposed dimensions and properties: a = 3.00 m, b = 6.40 m, yt = 3.20 m, S = 19.20 m2, Ix = 65.54 m4, Iy = 14.40 m4 | ||||||||||||||||
| Second iteration: Stage 2 | ||||||||||||||||
| MuxT | d | ρP1a | ρP2b2 | ρyBb | ρyTb | AsP1a | AsP2b2 | AsxBa | AsxBb2 | AsxTa | AsxTb2 | AsyBb | AsyBb1 | AsyTb | AsyTb1 | Cmin |
| (kN-m) | (cm) | (cm2) | ||||||||||||||
| 1464.00 | 71.43 | 0.00414 | 0.00356 | 0.00333 | 0.00551 | 22.38 | 19.25 | 62.81 | - | 82.28 | - | 71.42 | - | 11.81 | - | 31.03Cc |
| Sides of the Footing m | Soil Pressure on the Footing at Each Vertex kN/m2 | Smin m2 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| a | b | b1 | b2 | p1 | p2 | p3 | p4 | p5 | p6 | p7 | p8 | |
| Case 1: t = 100 cm, qaa = 211.00 kN/m2, MxT = −15.49 kN-m | ||||||||||||
| 3.00 | 6.40 | 3.80 | 1.50 | 207.52 | 78.22 | 208.81 | 176.48 | 111.84 | 79.51 | 177.36 | 112.72 | 15.30 |
| Case 2: t = 95 cm, qaa = 211.45 kN/m2, MxT = −77.85 kN-m | ||||||||||||
| 5.00 | 6.40 | 1.00 | 2.00 | 207.19 | 64.50 | 208.45 | 165.65 | 108.57 | 65.77 | 172.47 | 115.39 | 15.80 |
| Case 3: t = 85 cm, qaa = 212.35 kN/m2, MxT = 553.45 kN-m | ||||||||||||
| 3.50 | 6.40 | 1.70 | 2.50 | 207.62 | 92.81 | 192.80 | 176.40 | 94.39 | 77.99 | 135.45 | 53.44 | 17.70 |
| Case 4: t = 80 cm, qaa = 212.80 kN/m2, MxT = 1050.00 kN-m | ||||||||||||
| 3.00 | 6.40 | 6.40 | 3.00 | 207.52 | 124.19 | 104.98 | 104.98 | 21.65 | 21.65 | 104.98 | 21.65 | 19.20 |
| Case | Mua kN-m | Mub kN-m | Muc kN-m | Mud kN-m | ym m | Mue kN-m | Muf kN-m | Mug kN-m |
|---|---|---|---|---|---|---|---|---|
| 1 | 582.16 | 224.06 | −704.06 | −2123.21 | −0.07 * | −2429.38 | −47.72 | 0 |
| 2 | 1008.43 | 319.74 | −675.93 | −1283.65 | −0.18 ** | −1966.06 | −40.00 | 0 |
| 3 | 689.39 | 412.34 | −693.66 | −1908.80 | 0.19 ** | −2170.32 | −47.98 | 0 |
| 4 | 582.16 | 503.29 | −1369.06 | –– | 0.41 | −3033.87 | −49.94 | 0 |
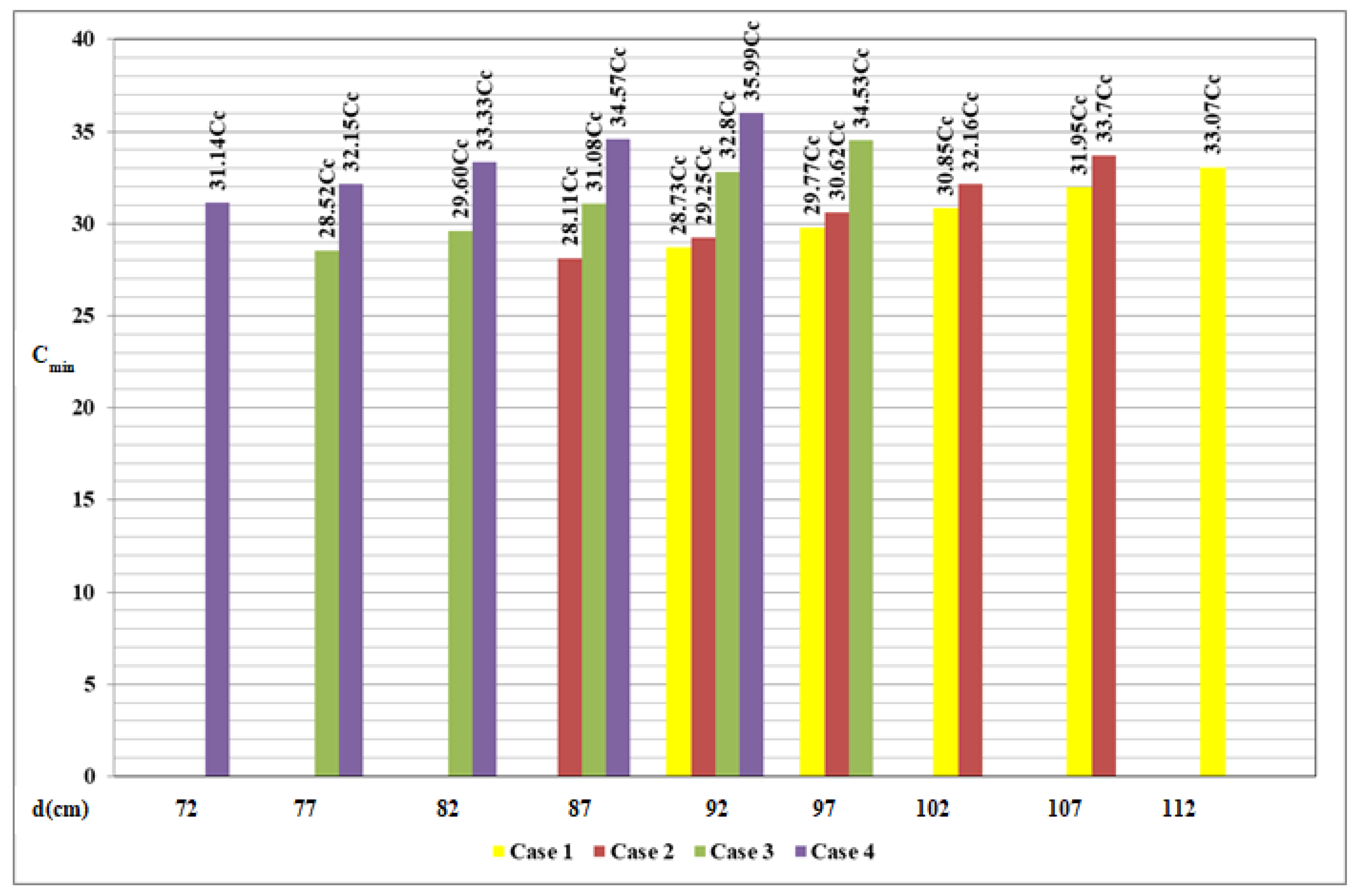
| Effective Depth d cm | Reinforcing Steel Areas cm2 | Cmin | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| AsP1a | AsP2b2 | AsxBa | AsxBb2 | AsxTa | AsxTb2 | AsyBb | AsyBb1 | AsyTb | AsyTb1 | ||
| Case 1: t = 100 cm, ρP1a = 0.0033333, ρP2b2 = 0.0033333, ρPyBb = 0.0033333, ρPyTb = 0.0053119 | |||||||||||
| 92.00 | 26.37 | 26.37 | 48.69 | 28.81 | 61.27 | 43.06 | 46.00 | 24.84 | 73.30 | 24.84 | 28.73Cc |
| Case 2: t = 95 cm, ρP1a = 0.0043918, ρP2b2 = 0.0033333, ρPyBb = 0.0033333, ρPyTb = 0.0035472 | |||||||||||
| 87.00 | 31.90 | 24.21 | 25.84 | 71.49 | 15.66 | 84.56 | 58.00 | 46.98 | 61.72 | 46.98 | 28.11Cc |
| Case 3: t = 85 cm, ρP1a = 0.0040647, ρP2b2 = 0.0033333, ρPyBb = 0.0033333, ρPyTb = 0.0040163 | |||||||||||
| 77.00 | 24.57 | 20.15 | 12.68 | 54.26 | 23.56 | 65.14 | 64.17 | 13.86 | 77.31 | 13.86 | 28.52Cc |
| Case 4: t = 80 cm, ρP1a = 0.0040545, ρP2b2 = 0.0034871, ρPyBb = 0.0033333, ρPyTb = 0.0054209 | |||||||||||
| 72.00 | 22.19 | 19.08 | 63.24 | –– | 82.94 | –– | 72.00 | –– | 11.71 | –– | 31.14Cc |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Moreno-Landeros, V.M.; Luévanos-Rojas, A.; Santiago-Hurtado, G.; López-León, L.D.; Olguin-Coca, F.J.; López-León, A.L.; Landa-Gómez, A.E. Optimal Cost Design of RC T-Shaped Combined Footings. Buildings 2024, 14, 3688. https://doi.org/10.3390/buildings14113688
Moreno-Landeros VM, Luévanos-Rojas A, Santiago-Hurtado G, López-León LD, Olguin-Coca FJ, López-León AL, Landa-Gómez AE. Optimal Cost Design of RC T-Shaped Combined Footings. Buildings. 2024; 14(11):3688. https://doi.org/10.3390/buildings14113688
Chicago/Turabian StyleMoreno-Landeros, Victor Manuel, Arnulfo Luévanos-Rojas, Griselda Santiago-Hurtado, Luis Daimir López-León, Francisco Javier Olguin-Coca, Abraham Leonel López-León, and Aldo Emelio Landa-Gómez. 2024. "Optimal Cost Design of RC T-Shaped Combined Footings" Buildings 14, no. 11: 3688. https://doi.org/10.3390/buildings14113688
APA StyleMoreno-Landeros, V. M., Luévanos-Rojas, A., Santiago-Hurtado, G., López-León, L. D., Olguin-Coca, F. J., López-León, A. L., & Landa-Gómez, A. E. (2024). Optimal Cost Design of RC T-Shaped Combined Footings. Buildings, 14(11), 3688. https://doi.org/10.3390/buildings14113688






