Numerical Methods for Topological Optimization of Wooden Structural Elements
Abstract
1. Introduction
2. Test Equipment
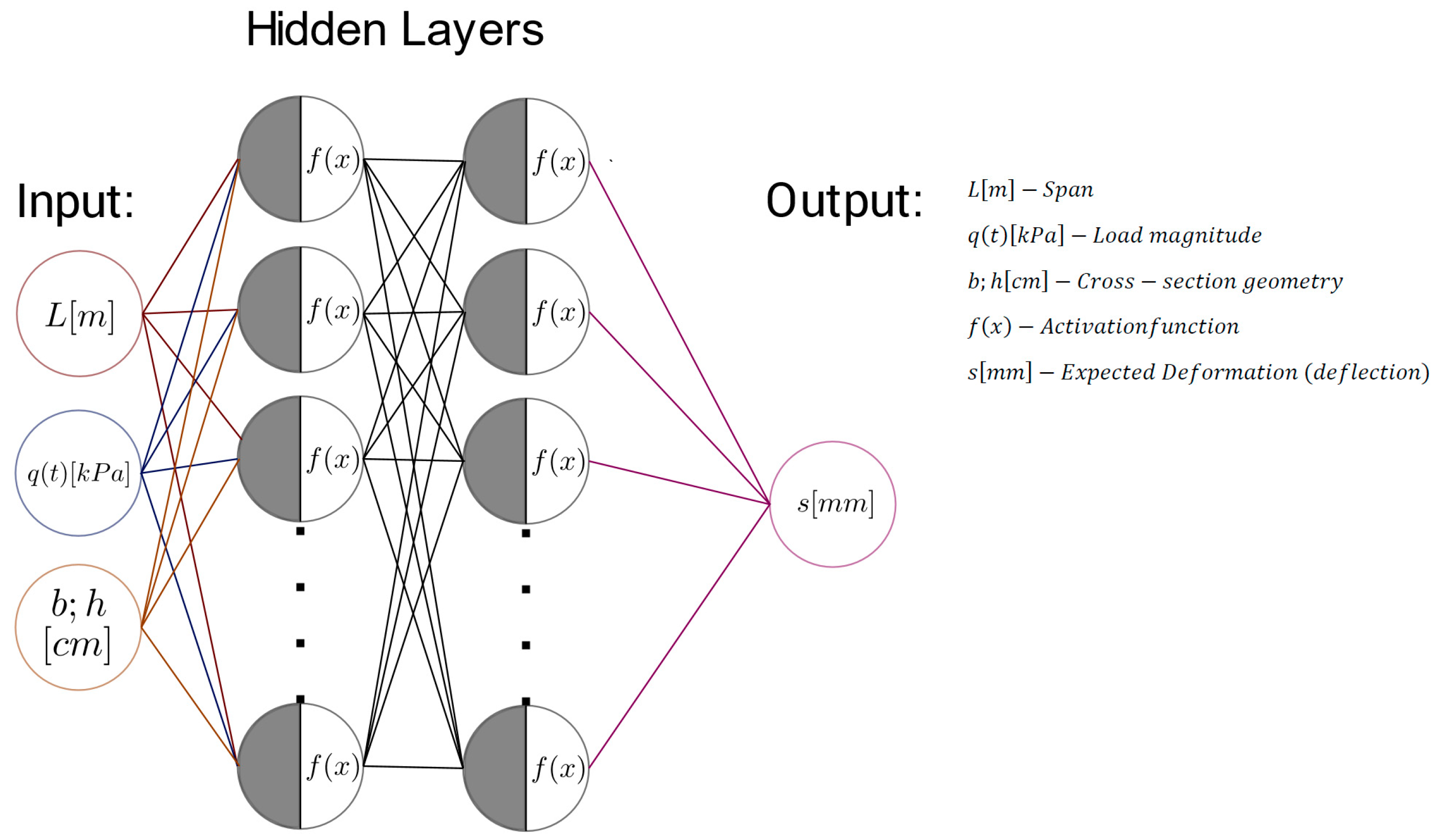
3. Numerical Modeling and Methods
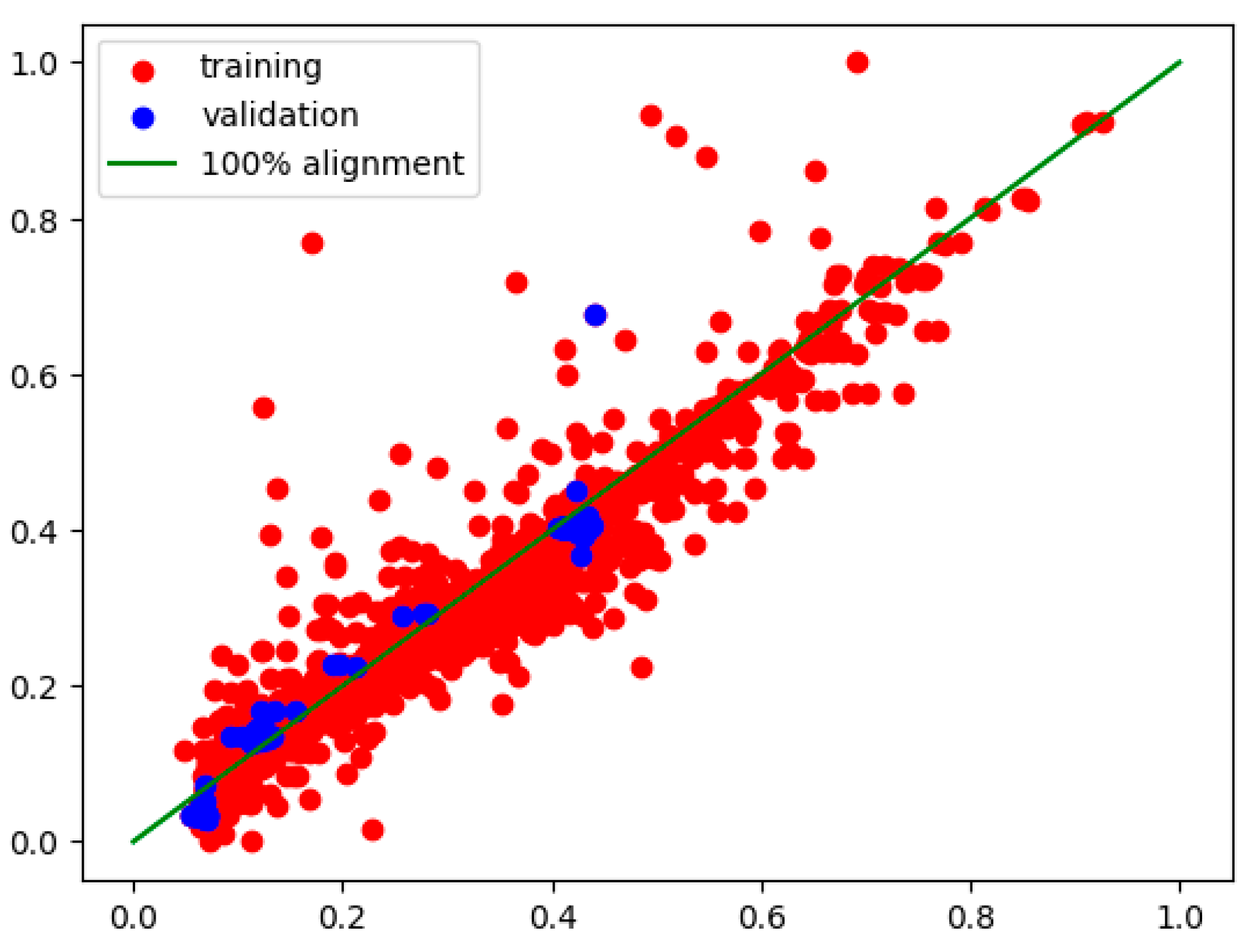
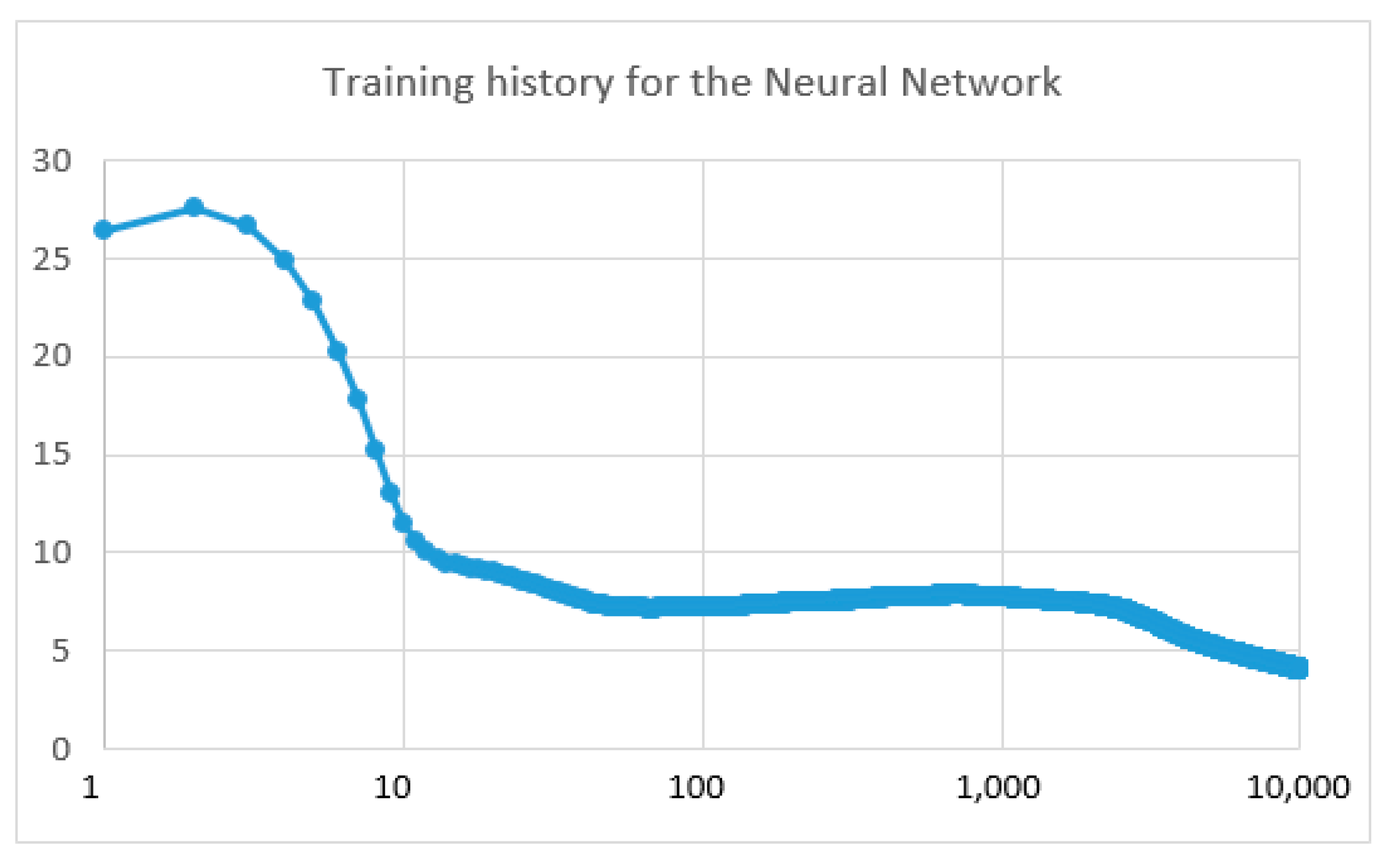
4. Results
- Planar symmetry with respect to the vertical plane perpendicular to the longitudinal axis of the beam in the center of gravity;
- Planar symmetry with respect to the horizontal median plane;
- Polar symmetry with respect to the center of gravity of the beam.
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Mayencourt, P.; Mueller, C. Structural Optimization of Cross-laminated Timber Panels in One-way Bending. Structures 2019, 18, 48–59. [Google Scholar] [CrossRef]
- Mayencourt, P.; Mueller, C. Structural Optimization and Digital Fabrication of Timber Beams. IABSE Symp. Rep. 2017, 108, 153–154. [Google Scholar] [CrossRef]
- Skaržauskaitė, M.; Aleksandraviciute-Sviaziene, A.; Kovaite, K.; Gulevičiūtė, G.; Skarzauskiene, A. Innovating Civil Engineering: Strategies for Fostering Stakeholder Engagement in the Circular Economy. Eur. Conf. Innov. Entrep. 2024, 19, 416–424. [Google Scholar] [CrossRef]
- Lobos Calquin, D.; Mata, R.; Correa, C.; Nuñez, E.; Bustamante, G.; Caicedo, N.; Blanco Fernandez, D.; Díaz, M.; Pulgar-Rubilar, P.; Roa, L. Implementation of Building Information Modeling Technologies in Wood Construction: A Review of the State of the Art from a Multidisciplinary Approach. Buildings 2024, 14, 584. [Google Scholar] [CrossRef]
- De Vito, A.F., Jr.; Vicente, W.M.; Xie, Y.M. Topology optimization applied to the core of structural engineered wood product. Structures 2023, 48, 1567–1575. [Google Scholar] [CrossRef]
- Du, H.; Xu, R.; Liu, P.; Yuan, S.; Wei, Y. Experimental and theoretical evaluation of inclined screws in glued laminated bamboo and timber-concrete composite beams. J. Build. Eng. 2024, 91, 109579. [Google Scholar] [CrossRef]
- Jaaranen, J.; Fink, G. A finite element simulation approach for glued-laminated timber beams using continuum-damage model and sequentially linear analysis. Eng. Struct. 2024, 304, 117679. [Google Scholar] [CrossRef]
- Pech, S.; Kandler, G.; Lukacevic, M.; Füss, J. Metamodel assisted optimization of glued laminated timber beams by using metaheuristic algorithms. Eng. Appl. Artif. Intell. 2019, 79, 129–141. [Google Scholar] [CrossRef]
- Christoforo, A.; de Moraes, M.; Fraga, I.; Pereira Junior, W.; Lahr, F. Computational Intelligence Applied in Optimal Design of Wooden Plane Trusses. Eng. Agríc. 2022, 42, e20210123. [Google Scholar] [CrossRef]
- Vicente, W.; Picelli, R.; Pavanello, R.; Xie, Y. Topology Optimization of Periodic Structures for Coupled Acoustic-Structure Systems. In Proceedings of the VII European Congress on Computational Methods in Applied Sciences and Engineering, Crete, Greece, 5–10 June 2016. [Google Scholar]
- Boado Cuartero, B.; Pérez-Álvarez, J.; Roibas, E. Material Characterization of High-Performance Polymers for Additive Manufacturing (AM) in Aerospace Mechanical Design. Aerospace 2024, 11, 748. [Google Scholar] [CrossRef]
- Zheng, H. A review on the topology optimization of the fiber-reinforced composite structures. Aerosp. Technic Technol. 2021, 54–72. [Google Scholar] [CrossRef]
- Anciferov, S.; Karachevceva, A.; Sychyov, E.; Litvishko, A. Topological optimization of design elements of a robotic cell. Bull. Belgorod State Technol. Univ. Named After V. G. Shukhov 2023, 8, 93–102. [Google Scholar] [CrossRef]
- Ding, Y.-M.; Wang, Y.-C.; Zhang, S.-X.; Yan, Z. Exploring the topological sector optimization on quantum computers. Phys. Rev. Appl. 2024, 22, 034031. [Google Scholar] [CrossRef]
- Méndez, D.; Garcia Cena, C.; Bedolla-Martinez, D.; González, A. Innovative Metaheuristic Optimization Approach with a Bi-Triad for Rehabilitation Exoskeletons. Sensors 2024, 24, 2231. [Google Scholar] [CrossRef] [PubMed]
- Osakpolor, O.; Jimu, H.; Odion, D. Optimization Techniques for Maximizing Energy Harvested in Solar-Powered Wearable Medical Devices. Int. J. Wearable Device 2024, 171. [Google Scholar]
- Peto, M.; García-Ávila, J.; Rodriguez, C.; Siller, H.; Silva, J.; Ramirez-Cedillo, E. Review on structural optimization techniques for additively manufactured implantable medical devices. Front. Mech. Eng. 2024. [Google Scholar] [CrossRef]
- Lin, K.; He, Y.; Yang, Y.; Xiong, L. From Topology Optimization to Complex Digital Architecture: A New Methodology for Architectural Morphology Generation. Adv. Civil Eng. 2021, 2021, 1–13. [Google Scholar] [CrossRef]
- Korus, K.; Salamak, M.; Jasiński, M. Optimization of geometric parameters of arch bridges using visual programming FEM components and genetic algorithm. Eng. Struct. 2021, 241, 112465. [Google Scholar] [CrossRef]
- Milner, R. A study of the strength of glued laminated timber. Aust. J. Struct. Eng. 2018, 16, 256–265. [Google Scholar] [CrossRef]
- Kravanja, S.; Žula, T. Optimization of a single-storey timber building structure. Int. J. Comput. Methods Exp. Meas. 2021, 9, 126–140. [Google Scholar] [CrossRef]
- Simón-Portela, M.; Villar-García, J.R.; Vidal-López, P.; Rodríguez-Robles, D. Enhancing Sustainable Construction: Optimization Tool for Glulam Roof Structures According to Eurocode 5. Sustainability 2024, 16, 3514. [Google Scholar] [CrossRef]
- Ochieng, D. Kiu Publication Extension. Introduction to Lightweight Structures: A Review and Analysis of Topological Optimization Methods and Applications. Res. Invent. J. Eng. Phys. Sci. 2024, 3, 9–15. [Google Scholar]
- Fedchikov, V. Topological optimization methods in the design of metal structures of buildings. E3S Web Conf. 2024, 533, 02023. [Google Scholar] [CrossRef]
- Li, H.; Gao, L.; Li, H.; Li, X.; Tong, H. Full-scale topology optimization for fiber-reinforced structures with continuous fiber paths. Comput. Methods Appl. Mech. Eng. 2021, 377, 113668. [Google Scholar] [CrossRef]
- Wellershoff, F.; Baudisch, R.; Posavec, M. Design optimization of glued-laminated timber freeform strcutrues with multi-objective constraints. In Proceedings of the IASS Annual Symposium 2017 Interfaces: Architecture, Engineering, Science, Hamburg, Germany, 25–28 September 2017. [Google Scholar]
- Simón-Portela, M.; Villar-García, J.R.; Rodríguez-Robles, D.; Vidal-López, P. Optimization of Glulam Regular Double-Tapered Beams for Agroforestry Constructions. Appl. Sci. 2023, 13, 5731. [Google Scholar] [CrossRef]
- Stanić, A.; Hudobivnik, B.; Brank, B. Economic-design optimization of cross laminated timber plates with ribs. Compos. Struct. 2016, 154, 527–537. [Google Scholar] [CrossRef]
- Wenhao, R. Prediction and optimization of civil engineering material properties based on artificial intelligence. Appl. Comput. Eng. 2024, 51, 298–312. [Google Scholar] [CrossRef]
- Taye, M.M. Understanding of Machine Learning with Deep Learning: Architectures, Workflow, Applications and Future Directions. Computers 2023, 12, 91. [Google Scholar] [CrossRef]
- Park, H.I.; Cho, C. Neural Network Model for Predicting the Resistance of Driven Piles. Mar. Georesour. Geotechnol. 2010, 28, 324–344. [Google Scholar] [CrossRef]
- Nauata, N.; Hosseini, S.; Chang, K.-H.; Chu, H.; Cheng, C.-Y.; Furukawa, Y. House-GAN++: Generative Adversarial Layout Refinement Network towards Intelligent Computational Agent for Professional Architect. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021; pp. 13632–13641. [Google Scholar]
- Livas, C.; Ekevad, M.; Öhman, M. Experimental analysis of passively and actively reinforced glued-laminated timber with focus on ductility. Wood Mater. Sci. Eng. 2020, 17, 129–137. [Google Scholar] [CrossRef]
- EN 14080:2013; Timber Structures—Glued Laminated Timber and Glued Solid Timber—Requirements. European Committee for Standardization (CEN): Brussels, Belgium, 2013.
- Gong, Y.; Chen, X.; Ren, H.; Liu, B.; Zhang, H.; Wang, Y. Theoretical and experimental studies on the bending properties of glued laminated timber manufactured with Chinese fir. Structures 2024, 68, 107149. [Google Scholar] [CrossRef]
- Tapusi, D.; Andronic, A.; Tufan, N.; Teodorescu, I.; Erbasu, R. Development of a generator of glued laminated timber elements sections using artificial intelligence. In Proceedings of the XXIVth International Multidisciplinary Scientific GeoConference Surveying, Geology and Mining, Ecology and Management, SGEM 2024, Albena, Bulgaria, 29 June–8 July 2024. [Google Scholar]


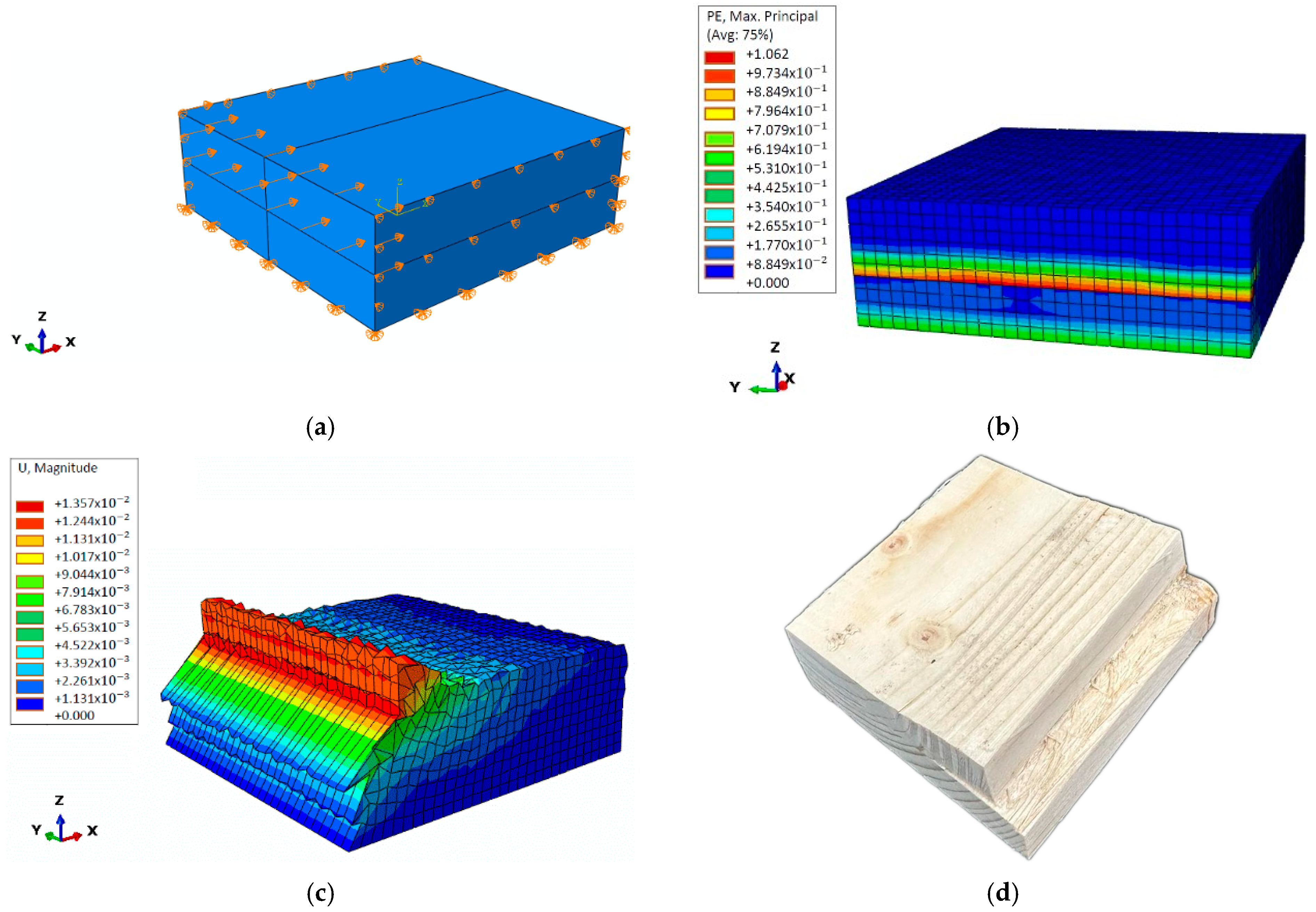
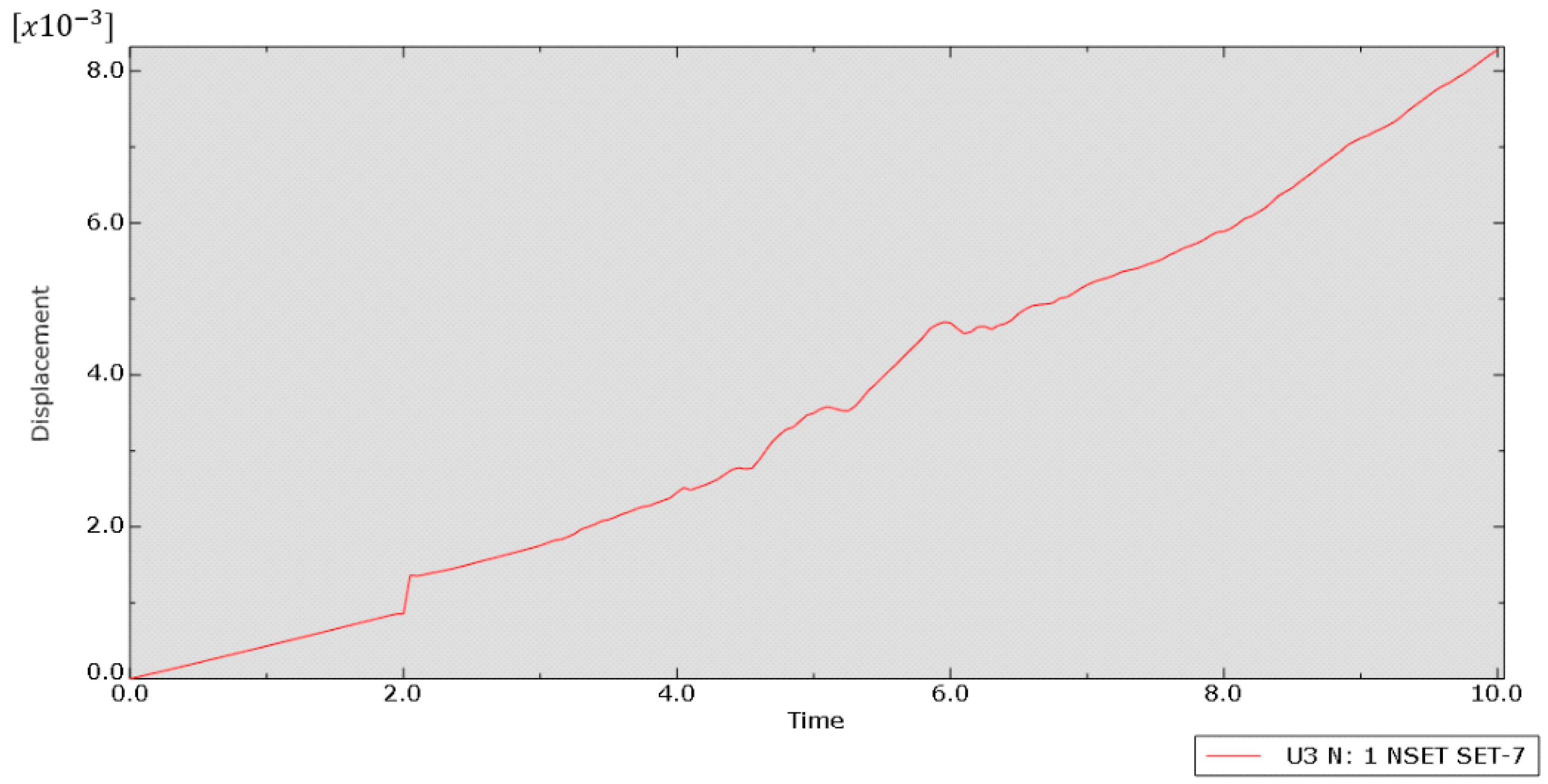
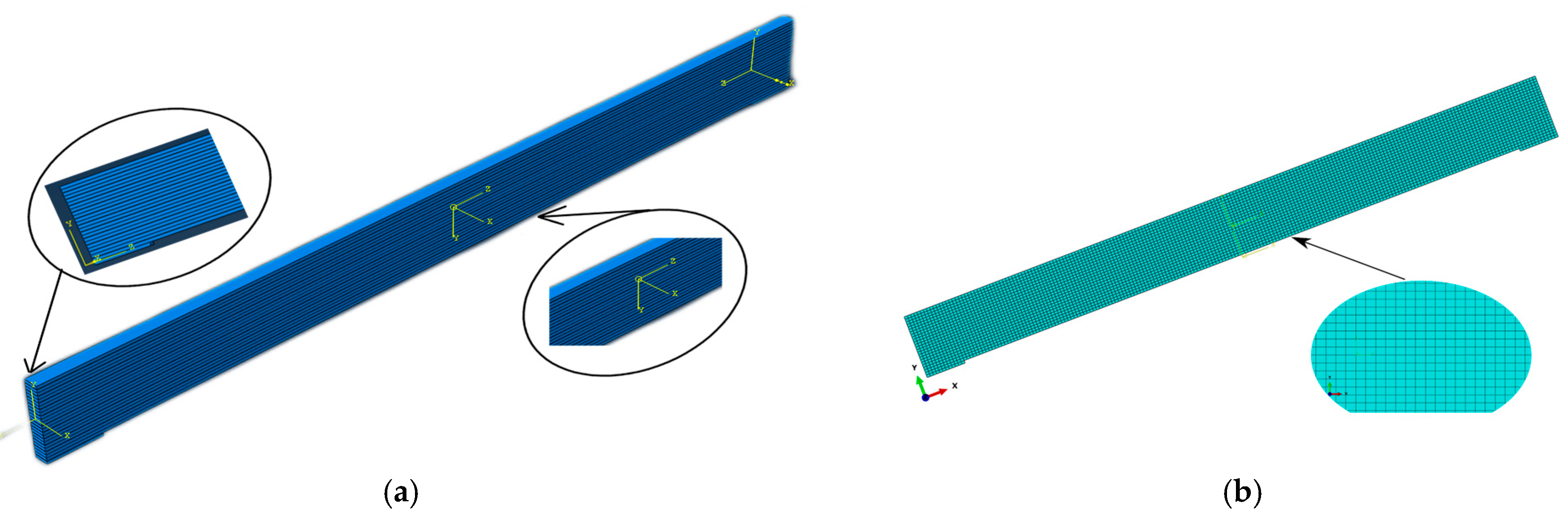
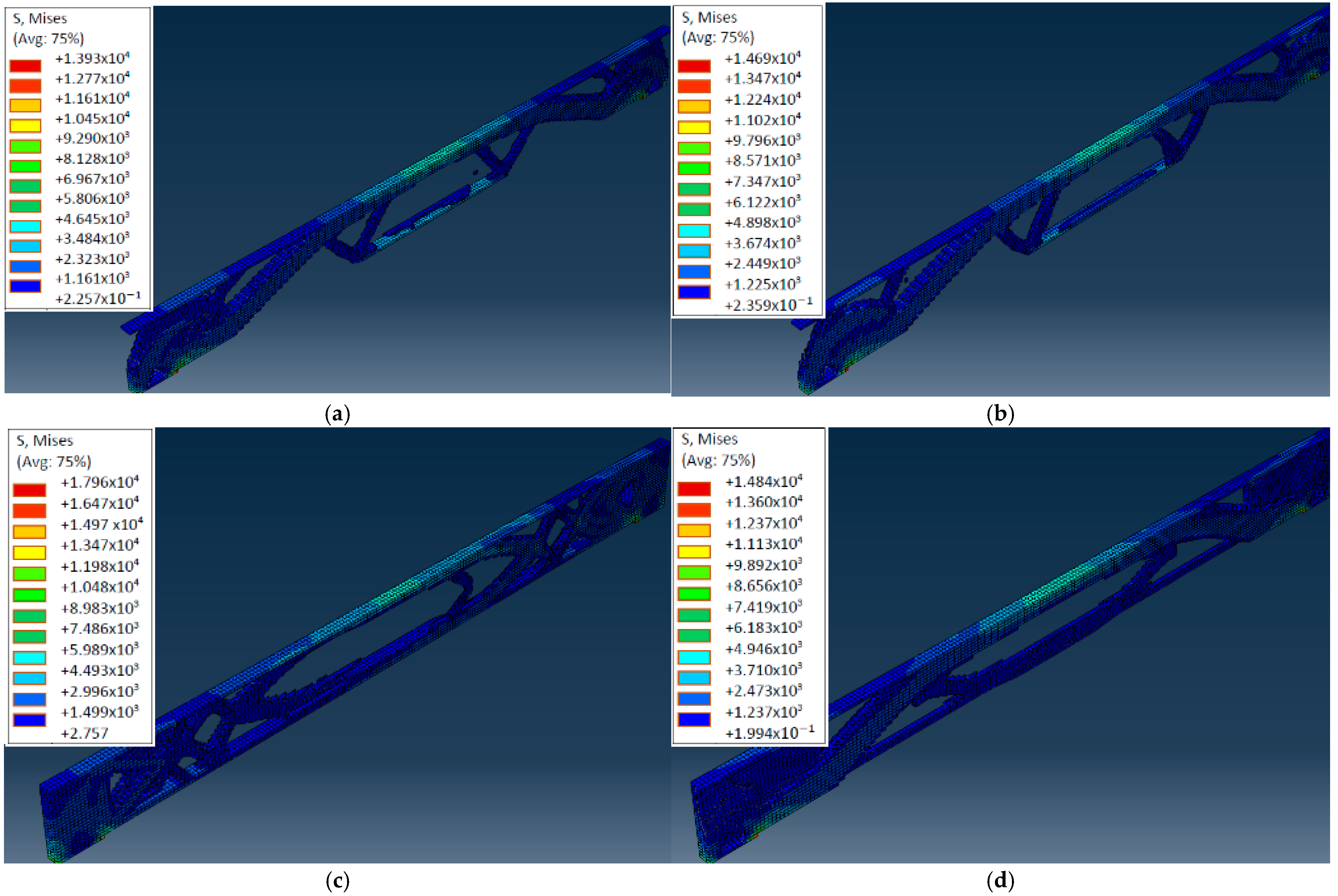
| Test Number | Test Specimen Sample Size (w × h − L) | Average Strength Value |
|---|---|---|
| Traction parallel to the fibers | 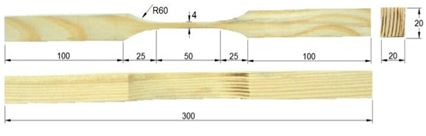 | ft = 93.61 N/mm2 |
| Compression parallel to the fibers |  | fc = 40.85 N/mm2 |
| Bending |  | finc = 79.58 N/mm2 |
| Type of Element | Dimensions | Pitch |
|---|---|---|
| Beam length (L) | from 4 to 8 m | 10 cm |
| Beam width (W) | From 65 cm to 1.65 m | 5 cm |
| Beam span | from 3 to 5 m | 50 cm |
| Thickness of a plank | 4 cm | - |
| Length of the support area | 20 cm, 30 cm and 40 cm | - |
| Parameter | Minimum Value | Δ |
|---|---|---|
| Beam length (L) | 4.0 | 2.2 |
| Beam span | 3.0 | 2.0 |
| Beam width (W) | 0.065 | 0.1 |
| Optimization constraint | 0 | 2 |
| Deflection | 0.019020382 | 0.029697631 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Țăpuși, D.; Sabău, A.-D.; Savu, A.-A.; Erbașu, R.-I.; Teodorescu, I. Numerical Methods for Topological Optimization of Wooden Structural Elements. Buildings 2024, 14, 3672. https://doi.org/10.3390/buildings14113672
Țăpuși D, Sabău A-D, Savu A-A, Erbașu R-I, Teodorescu I. Numerical Methods for Topological Optimization of Wooden Structural Elements. Buildings. 2024; 14(11):3672. https://doi.org/10.3390/buildings14113672
Chicago/Turabian StyleȚăpuși, Daniela, Andrei-Dan Sabău, Adrian-Alexandru Savu, Ruxandra-Irina Erbașu, and Ioana Teodorescu. 2024. "Numerical Methods for Topological Optimization of Wooden Structural Elements" Buildings 14, no. 11: 3672. https://doi.org/10.3390/buildings14113672
APA StyleȚăpuși, D., Sabău, A.-D., Savu, A.-A., Erbașu, R.-I., & Teodorescu, I. (2024). Numerical Methods for Topological Optimization of Wooden Structural Elements. Buildings, 14(11), 3672. https://doi.org/10.3390/buildings14113672







