Seismic Responses and Overturning Resistance Capacity of Base-Isolated Structures Under the Influence of Pounding Interactions with Adjacent Structures

Abstract

Seismic accelerations and interlayer displacements can be reduced by Laminated Rubber Bearings (LRBs) efficiently. Isolators would amplify the displacement of the superstructure by extending the natural period, thereby reducing acceleration and seismic damage. However, as a result, the risk of pounding with adjacent structures would be raised. This study investigated the seismic responses and overturning resistance capacity of base-isolated structures subjected to pounding against an adjacent structure. Parameter studies were conducted to evaluate the effects of gap size, pounding stiffness, and horizontal stiffness of the isolation layer. Results show that poundings are characterized by intense, short forces causing acceleration spikes, amplifying the overturning coefficient and risk. The overturning risk initially decreases then increases with gap size under pulse-like earthquakes, while wider gaps mitigate effects during non-pulse events. Increased pounding stiffness intensifies poundings, heightening vulnerability. The structure’s overturning resistance initially improves with increased horizontal stiffness of the isolation layer but declines excessively with further stiffness increase.

1. Introduction

The Laminated Rubber Bearing (LRB) has been proven to be an effective device in significantly reducing structural acceleration and inter-story displacement. By diminishing the stiffness of the isolation layer, the natural period of the structure was extended, thereby mitigating its acceleration and inter-story displacement responses under seismic loads [1].

While it has been observed that isolators can amplify the displacement of the superstructure, this amplification is inherent to the extension of the natural period, which is beneficial for suppressing acceleration responses. The potential for pounding with adjacent structures is influenced by multiple factors, including the displacement amplification, but also the stiffness and damping characteristics of the adjacent structures, their separation distance, and the overall system’s dynamic response under seismic excitation. Polycarpou found that poundings during strong earthquakes can significantly impact seismic isolation effectiveness in buildings if the clearance was exceeded, causing increased floor accelerations, inter-story deflections, and higher deformation modes [2]. Polycarpou and Komodromos’ studies on pounding effects on seismically isolated buildings showed that even with sufficient gaps to prevent base poundings, deformations in superstructures can still lead to poundings with adjacent buildings [3]. Research investigating the potential impacts of earthquake-induced poundings on the overall dynamic behavior of seismically isolated buildings has shown that these buildings may come into contact with adjacent structures at upper levels, and the extent of the impact severity is dependent on both the dynamic characteristics of the adjacent buildings and the specific features of the earthquake itself [4]. The results of work on seismic responses of adjacent buildings supported on different or similar base systems considering impacts between bases and superstructures indicate that the pounding-involved responses of the buildings depend mainly on the type of structural base systems and on the structural parameters of both buildings [5]. It is concluded that the normalized base shear, bearing, and top floor displacement increase due to impact with adjacent isolated structure [6]. Amplification of buildings’ drift and the top deck acceleration of the isolated structure were observed when pounding was considered, with a profound effect of the stiffness of the adjacent buildings on the value of the impact they impose on the superstructure [7]. Majdi et al. found that adjacent isolated structures might collapse under extreme earthquakes, influenced by their proximity, height difference, and isolator displacement capacity. Furthermore, tall isolated structures negatively impact adjacent shorter ones [8]. Sadeghi et al. studied the effects of superstructure and isolator flexibility on the pounding and seismic performance of adjacent isolated buildings using 3D models. They discovered that increasing isolator flexibility and reducing superstructure flexibility worsened the buildings’ performance under pounding [9]. Yaghmaei and Panjehbashi assessed the damage of adjacent steel building frames of varying heights under multiple ground motions, considering base isolation and repeated earthquakes; they reported that base isolators significantly reduce damage compared to fixed-base buildings [10]. The effect of the seismic pounding of moat walls on the response of buildings isolated by Triple Friction Pendulum Bearing (TFPB) was investigated by Shakouri et al. [11]. Mavronicola and Polycarpou discovered that pounding has especially detrimental effects on base-isolated buildings, significantly enhancing their peak inter-story deflections, which can increase the potential for structural damage [12]. It has been demonstrated that pounding significantly increases building responses; peak accelerations of upper stories are amplified due to poundings, but increasing the gap size can reduce these effects [13]. The effects of one structure pounding against adjacent structures and the seismic response of the base-isolated structure were analyzed by Liu et al.; their results indicate that the structural response increases with pounding, and significant amplifications of the story shear force, velocity, and acceleration were observed [14]. Movahhed et al. demonstrated the pulse of acceleration caused by structural pounding [15].

Numerous scholars have proposed solutions to mitigate the potential adverse effects of pounding on structures. Hubballi and Jangid’s experimental and parametric studies on base-isolated frame structures with expansion gaps revealed that mitigating materials in the gaps are more effective at reducing pounding for similar frequency combinations compared to dissimilar-frequency frame setups [16]. Farghaly and Kontoni evaluated methods of reducing the risk of pounding between adjacent twin high-rise buildings and found that the PTMD method between two adjacent RC twin high-rise buildings is an efficient method in mitigating the earthquake-induced pounding risk [17]. The study by Khatami et al. shows that thicker, stiffer, and more numerous rubber bumpers reduce peak impact force during earthquakes, effectively protecting base-isolated buildings from pounding [18]. Du et al. proposed a complete pounding force model; they found that contact stiffness is more sensitive than contact damping to the isolation layer deformation [19]. Du et al.’s shake table tests showed that combining soft limiter stiffness with a reserved gap effectively limits base displacement in base-isolated buildings, without harming the superstructure [20]. Stefani et al. studied how varying gap size affects the response of an SDOF structure excited by harmonic base acceleration [21]. Mazza and Labernarda proposed magnetic damping to reduce structural pounding effects between adjacent buildings [22]. Changing the dynamic characteristics of base-isolation devices significantly impacts the pounding behavior of adjacent buildings, as the period of the isolator bearing alters the fundamental period of the superstructure, as demonstrated by Kandemir’s work [23]. Zhang found that VE material can mitigate the structural pounding between adjacent structures [24]. Song et al. used a tuned-inerter damper (TID) system to mitigate the potential pounding and unseating damages between adjacent bridge structures under severe earthquakes; it was found that the TID system can provide a good alternative to control the excessive relative motions between adjacent bridge structures [25]. Huang et al. also reported that equipping a TID can reduce the required width of the isolation joint to avoid pounding between the isolation layer and the moat wall [26]. Ebrahimi et al. found that adding viscous dampers to the isolation system balanced the behavior of the structure considering pounding phenomena under near-field pulse-type records [27]. Antoniou et al. proposed and verified the seismic performance of a novel passive vibration isolation and damping device termed Extended KDamper (EKD); they found that the deck’s pounding with the abutments reduced the maximum attained deck drift [28]. Rayegani and Nouri tried to use a magnetorheological damper as a smart dissipating device in isolated buildings to mitigate seismic pounding; they found that it can prevent the pounding of the building and improve the structure’s behavior [29]. Domenico et al. proposed and experimentally investigated a base isolation combining low-friction curved surface sliders and hysteretic gap dampers to improve the seismic performance of structures subjected to poundings [30]. Zargar et al. proposed and experimentally evaluated the gap damper to reduce displacement demands to avoid structural pounding and its negative effect [31,32]. It should be noted that the potential for pounding between adjacent structures is not exclusively limited to tall buildings, and pounding can occur in any scenario involving two or more structures, regardless of their height. The use of an active control device is another method to eliminate unnecessary displacement, and methods have been used to design an active control system. A comprehensive design method for base-isolated buildings utilizing LQR control has been developed, estimating the maximum required control force via the control-force spectrum [33]. Chen et al. have presented a spectrum-based design method for constructing an equivalent linear model of an active nonlinear system, and the effectiveness of this method is demonstrated through a design example [34]. A new method for estimating the maximum response and maximum control force in high-rise base-isolated buildings equipped with active structural control was also proposed, aiming to simplify the conventional complex design procedure [35]. Furthermore, a straightforward method for estimating the maximum displacement responses and maximum control force for active base-isolation systems was reported, which is easily understandable for structural designers [36].

However, most of the current research on pounding between adjacent structures has primarily focused on analyzing its effects on their dynamic responses (including acceleration, interlayer displacement, etc.), with limited attention given to investigating the overturning resistance capacity of seismic isolation structures when subjected to pounding with neighboring structures. Moreover, newly constructed structures may also be exposed to extreme earthquakes, which significantly increases the potential for poundings due to design complexities or unforeseen circumstances. In addition, gaps originally reserved for non-isolated structures may be insufficient to prevent pounding when fixed-base structures are retrofitted into isolated ones. Therefore, the likelihood of pounding occurring increases. Given that seismic isolation bearings inherently have limited tensile strength, ensuring the proper functioning of these bearings and the overturning resistance capacity of seismic isolation structures is of utmost importance. Consequently, investigations on the overturning resistance capacity of seismic isolation structures under pounding conditions hold significant value in enhancing the overall structural safety and stability.

To this end, the overturning resistance capacity of base-isolated structures subjected to pounding with adjacent structures was investigated. The influences of gap size, pounding stiffness, and horizontal stiffness of the isolation story on the overturning resistance of the base-isolated structure were also evaluated through parameter studies.

2. Modeling of the System

2.1. Dynamic Equation of the System

Structures designed for isolation are typically frame structures. Therefore, the shear-type and bilinear model of the superstructure can be employed in the numerical analysis.

When a base-isolated structure is constructed adjacent to a fixed-base structure, as shown in Figure 1, the dynamic equation of the system can be formulated as Equation (1a,b).

$$\left[{\mathit{M}}^{\mathit{L}}\right]\left\{{\ddot{\mathit{x}}}^L\right\}+\left[{\mathit{C}}^{\mathit{L}}\right]\left\{{\dot{\mathit{x}}}^L\right\}+\left[{\mathit{K}}^{\mathit{L}}\right]\left\{{\mathit{x}}^L\right\}+\left[\mathit{F}\right]=\left[{\mathit{M}}^{\mathit{L}}\right]\left\{{\ddot{\mathit{x}}}_g\right\}$$

(1a)

$$\left[{\mathit{M}}^{\mathit{R}}\right]\left\{{\ddot{\mathit{x}}}^R\right\}+\left[{\mathit{C}}^{\mathit{R}}\right]\left\{{\dot{\mathit{x}}}^R\right\}+\left[{\mathit{K}}^{\mathit{R}}\right]\left\{{\mathit{x}}^R\right\}-\left[\mathit{F}\right]=\left[{\mathit{M}}^{\mathit{R}}\right]\left\{{\ddot{\mathit{x}}}_g\right\}$$

(1b)

$\left[{\mathit{M}}^{\mathit{L}}\right]$, $\left[{\mathit{C}}^{\mathit{L}}\right]$, $\left[{\mathit{K}}^{\mathit{L}}\right]$, and $\left\{{\mathit{x}}^L\right\}$ represent the mass, damping, and stiffness matrices, respectively, pertaining to the left structure in the given system. These matrices can be expressed as Equations (2)–(4), and $\left[{\mathit{M}}^{\mathit{R}}\right]$, $\left[{\mathit{C}}^{\mathit{R}}\right]$, $\left[{\mathit{K}}^{\mathit{R}}\right]$, and $\left\{{\mathit{x}}^R\right\}$ represent the mass, damping, and stiffness matrices, respectively, pertaining to the right structure in the given system.

$$\left[{\mathit{M}}^{\mathit{L}}\right]=\left[\begin{array}{ccc}{m}_1^L& & \\ & \ddots & \\ & & m_n^L\end{array}\right]$$

(2)

$${\mathit{K}}^{\mathit{L}}=\left[\begin{array}{ccccc}{k}_1^L{+k}_2^L& {-k}_2^L& & & \\ {-k}_2^L& k_2^L{+k}_3^L& & & \\ & {-k}_3^L& \ddots & & \\ & & \ddots & & \\ & & \ddots & {-k}_{n-1}^L& \\ & & & k_{n-1}^L{+k}_n^L& {-k}_n^L\\ & & & {-k}_n^L& k_n^L\end{array}\right]$$

(3)

$${\mathit{C}}^{\mathit{L}}=\left[\begin{array}{ccccc}{c}_1^L{+c}_2^L& {-c}_2^L& & & \\ {-c}_2^L& c_2^L{+c}_3^L& & & \\ & {-c}_3^L& \ddots & & \\ & & \ddots & & \\ & & \ddots & {-c}_{n-1}^L& \\ & & & c_{n-1}^L{+c}_n^L& {-c}_n^L\\ & & & {-c}_n^L& c_n^L\end{array}\right]$$

(4)

where $\left[\mathit{F}\right]$ represents the pounding force vector matrix. In this work, which discusses adjacent structures at the same elevation level, pounding can be found when the relative displacement between the two structures reaches a pre-defined threshold at the corresponding story level.

A six-story base-isolated building located in the Tibetan Qiang Autonomous Prefecture of Ngawa, Sichuan Province, China, was selected (the parameters of the building are summarized in

Table 1. Parameters of the building.

Story	Height (mm)	Mass (106 kg)	Stiffness (106 N/mm)	Story Yield Force (106 N)
6	4100	0.232	0.231	1.722
5	4500	2.079	1.266	10.358
4	3900	2.171	1.494	10.594
3	3900	2.184	1.676	11.884
2	3900	2.515	1.740	12.338
1	4200	2.006	1.576	11.989

). Both the building and its FPB were designed in accordance with China’s seismic design codes, utilizing a total of 40 friction pendulum bearings with an equivalent radius of 4 m. A fixed-base non-isolated structure with identical floor parameters was considered as the adjacent structure with a gap of 0.2 m based on China’s seismic design codes.

In this work, the KOKJ RECORD (obtained by the KJMA station during the Kobe earthquake in 1995) and the IMEA record (obtained by the El Centro Array station during the Imperial Valley earthquake in 1940) were selected based on the following reasons: their representativeness of distinct geological conditions and seismic activity characteristics and their applicability in structural seismic analysis for assessing a wide range of seismic responses, all of which contribute to a more comprehensive and reliable analysis of structural performance. And the accelerograms and response spectra of the IMEA and KOKJ earthquake records are presented in Figure 2.

2.2. Calculation of Pounding Force

In simulating pounding forces, although various computational models exist, the nonlinear viscoelastic model stands out for its innovative approach of dividing the pounding process into the approach period and restitution period, effectively addressing the inaccuracies of traditional models in simulating energy dissipation patterns during pounding, thereby achieving higher simulation accuracy. Furthermore, the parameters of pounding forces in this model can be based on previous experimental results, further ensuring the accuracy of calculations.

The nonlinear viscoelastic model proposed (as shown in Figure 3) by Jankowski for calculating structural pounding forces [37,38] has been proven to be highly accurate and stable in simulating poundings between adjacent buildings and has therefore gained widespread acceptance and application [39,40].

The pounding force can be obtained as Equation (5):

$$F\left(t\right)=\left\{\begin{array}{c}{k}_{\mathrm{P}}{\delta }^{1.5}\left(t\right)+c_{\mathrm{P}}\left(t\right)\dot{\delta }\left(t\right)\begin{array}{cc}& \dot{\delta }\left(t\right)>0(\mathrm{a}\mathrm{p}\mathrm{p}\mathrm{r}\mathrm{o}\mathrm{a}\mathrm{c}\mathrm{h}\mathrm{p}\mathrm{e}\mathrm{r}\mathrm{i}\mathrm{o}\mathrm{d})\end{array}\\ k_{\mathrm{P}}{\delta }^{1.5}\left(t\right)\begin{array}{cc}& \dot{\delta }\left(t\right)\le 0\end{array}(\mathrm{r}\mathrm{e}\mathrm{s}\mathrm{t}\mathrm{i}\mathrm{t}\mathrm{u}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}\mathrm{p}\mathrm{e}\mathrm{r}\mathrm{i}\mathrm{o}\mathrm{d})\end{array}\right.$$

(5)

where $\delta$ is the penetration displacement between stories, k_P is the pounding stiffness, and $c_{\mathrm{P}}\left(t\right)$ is the damping parameter, which can be obtained from Equation (6).

$$c_{\mathrm{P}}\left(t\right)=2{\displaystyle \frac{-\mathrm{l}\mathrm{n}e}{\sqrt{{\pi }^2+{\left(\mathrm{l}\mathrm{n}e\right)}^2}}}\sqrt{k_{\mathrm{P}}\sqrt{\delta \left(t\right)}{\displaystyle \frac{m_1{m}_2}{m_1{+m}_2}}}$$

(6)

where e is the coefficient of restitution.

Pounding stiffness is determined by considering multiple factors, including structural materials, interface characteristics, loading conditions, and geometric dimensions. This can be achieved through theoretical calculations based on contact mechanics theories, experimental testing using scaled models or full-scale structures, or the utilization of empirical formulas derived from past data and engineering experience. In this paper, the pounding parameters for steel towers from the literature are adopted, taking into account that the structure is similar to the one validated in the work of Jankowski [38]. It is important to note that these parameters have been verified to have good accuracy.

2.3. Evaluation of Overturning Resistance of Isolated Structure

Since the bearing has almost no tensile resistance, the overturning resistance moment of the structure is entirely generated by the gravity of the superstructure. The overturning resistance moment of the structure can be expressed as Equation (7):

$$M_R\left(t\right)={0.5m}_{\mathrm{b}}g{L}_{\mathrm{b}}\left(t\right)+{\sum }_{i=1}^n{m}_{i}g{L}_i\left(t\right)$$

(7)

where $h_i$ is the floor height of the ith floor and $L_i$ is the distance between the centroid and the overturn point.

The overturning moment of the structure is composed of the bending moments generated by the inertia forces of each floor level, which act on the overturning point and can be expressed as Equation (8):

$$M\left(t\right)={m_{\mathrm{b}}\ddot{x}}_{\mathrm{b}}\left(t\right)h_{\mathrm{b}}+{\sum }_{i=1}^n{m}_i{\ddot{x}}_i\left(t\right)h_i$$

(8)

Equation (9) presents the critical prerequisite for guaranteeing a structure’s stability and preventing overturn.

$$M\left(t\right)\le M_R\left(t\right)$$

(9)

To evaluate the potential overturning risk of the isolated structure, the coefficient of overturning resistance, denoted as $\beta$, is introduced as Equation (10):

$$\beta ={\left({\displaystyle \frac{M\left(t\right)}{M_R\left(t\right)}}\right)}_{\mathrm{m}\mathrm{a}\mathrm{x}}$$

(10)

The prevention of overturning is ensured when β is less than 1, and it becomes increasingly evident that the isolated structure’s risk of overturning escalates as β increases, ultimately leading to the structure’s overturn when β reaches a value of 1.

3. Seismic Response of the Structures

3.1. Dynamic Response of the Structures

Pounding between the structures will inevitably occur when the relative displacement between adjacent structural stories decreases below the gap. The pounding is primarily and notably manifested as the generation of immense pounding forces, whose magnitudes often far exceed the shear forces between stories in non-pounding conditions.

Figure 4 depicts the time-history curves of the pounding forces experienced by the structure excited by different earthquake records. It is evident that the colossal magnitude of the pounding forces is remarkable. Taking the result of the system subjected to the KOKJ earthquake record as an example, two significant poundings within a specific period can be observed between the top stories of adjacent structures. The maximum pounding forces were 4.4 × 10⁷ kN and 1.9 × 10⁷ kN, respectively. Furthermore, when the pounding occurred on the fifth story, which has a more substantial mass, the pounding force generated during the first pounding soared even higher, reaching 1.4 × 10⁸ kN, underscoring the influence of mass on pounding intensity.

On the other hand, the duration of these poundings is extremely short, which is particularly evident in the two poundings caused by the KOKJ earthquake recorded on the top stories of the structure. The durations of these two poundings were confined to short periods of 0.012 s and 0.014 s, respectively, emphasizing the instantaneous nature of the pounding phenomenon and the high intensity of the pounding forces.

When short-duration but extremely large pounding force is applied to the structure, significant acceleration pulses in the floor where the pounding occurs can be found.

The acceleration time-history curves of the structure’s top story are depicted in Figure 5; it becomes evident that the acceleration experienced during pounding far surpasses that observed in the absence of pounding. This is a direct consequence of the pounding force generating a discernible and substantial acceleration pulse at the top story of the structure.

Moreover, this acceleration pulse stands out prominently compared to the accelerations recorded at other moments during the seismic event. While seismic activity undoubtedly elicits dynamic responses and variations in acceleration within the structure, the nature and duration of its effects differ significantly from those of pounding. Seismic load typically propagates in a more gradual and sustained manner, gradually building up energy over time. In contrast, pounding forces are characterized by their instantaneous onset and immense magnitude, resulting in a sudden and pronounced acceleration pulse.

Figure 6 shows the variation in the acceleration envelope along the height direction of the structure. It can be seen that when the structure is subjected to KOKJ and IMEA earthquake records, significant structural poundings are observed on the sixth, fifth, and fourth stories. The pounding on these stories directly led to a sharp increase in acceleration on corresponding stories. When the structure is subjected to KOKJ, the acceleration levels of the three stories are relatively low, maintaining around 0.7 g, 0.5 g, and 0.4 g, respectively, under normal circumstances without pounding. However, once pounding occurs, it is immediate, causing a drastic change in the maximum acceleration values of these stories. The maximum acceleration of the sixth story has soared from the original 0.7 g to an astonishing 19.3 g, an increase of 2841.1%, which visually reflects the extreme effect of poundings on the structural dynamic characteristics. The fifth story also suffered heavy damage, with the maximum acceleration surging from 0.5 g to 6.8 g, an increase of 1390.7%. The acceleration of the fourth story also increased from 0.4 g to 5.7 g, an increase of 1181.6%. When the structure is subjected to the IMEA seismic record, the acceleration of the sixth, fifth, and fourth stories increases sharply from 0.6 g, 0.5 g, and 0.5 g without pounding to 8.8 g, 3.7 g, and 3.5 g, with an increase of 1766.4%, 777.7%, and 824.9%, respectively. This further emphasizes the significant influence of poundings on structural acceleration responses.

The variations in acceleration within the structure are frequently accompanied by substantial fluctuations in displacement, as depicted in Figure 7, which showcases the displacement envelope of the structure along its height. This figure underscores that the pounding-induced acceleration pulse not only signifies an abrupt velocity change within the structure at the moment of pounding but also vigorously propels the structure to undergo considerable displacement in the direction of the pounding force. Notably, in the vicinity of or directly at the point of pounding, the displacement of the seismic isolation structure experiences a marked increase under the influence of the pounding force.

Taking the result of the system subjected to the KOKJ earthquake record as a case study, when this earthquake record is applied to the structure, it can be observed that the displacements of the sixth, fifth, and fourth floors, which were 0.100 m, 0.0998 m, and 0.0709 m, respectively, without pounding, escalate dramatically to 0.295 m, 0.286 m, and 0.275 m upon the occurrence of pounding. This phenomenon arises due to the fact that when the structural displacement is positive, meaning that the direction of structural movement aligns with that of the pounding force, the pounding significantly accelerates the structure, resulting in larger displacements. Conversely, when the structural displacement is negative, signifying movement towards the fixed end, the pounding force introduces an acceleration pulse opposite to the direction of motion, thereby diminishing the displacement of the structure in that direction (see Figure 8).

Furthermore, the pounding triggers a sharp change in the acceleration pulse within the structure, leading to a significant increase in displacement along the direction of the pounding force. This chain reaction may ultimately cause structural yielding in areas that were originally designed to remain elastic, altering the overall mechanical behavior and response characteristics of the structure.

To visualize this complex process, Figure 9 presents the variation in inter-story shear force between the fifth and fourth floors of the structure. In the absence of pounding, the presence of advanced seismic isolation techniques enables the superstructure to effectively absorb and disperse seismic energy, maintaining small relative motions between floors, preventing yielding, and ensuring the structure remains in an elastic state.

However, upon the occurrence of pounding, the dynamics of the affected floors drastically change. The acceleration of these floors increases significantly, disrupting the previous dynamical equilibrium. This surge in acceleration intensifies inter-story relative motions, resulting in a sharp rise in inter-story shear forces, far exceeding levels observed under non-pounding conditions. In extreme cases, such as when the system is subjected to a strong earthquake like the KOKJ earthquake record, inter-story displacements can become substantial enough to surpass the elastic limit of the structural materials, triggering yielding in the floors. Yielding signifies the transition of the structure from a recoverable elastic phase to an irreversible plastic phase, posing a significant threat to the overall safety and subsequent seismic performance of the structure.

3.2. Potential Overturning Risk of Isolated Structure

Owing to their almost complete lack of tensile strength, ensuring that the structure possesses sufficient resistance to overturning is a crucial prerequisite for its safety and stability. The core of this overturning resistance capability lies in using the self-weight of the superstructure to generate the necessary gravitational bending moment to effectively resist the overturning moment caused by floor acceleration due to external factors such as earthquakes. However, a significant acceleration pulse is generated when pounding occurs, which greatly increases the overturning moment experienced by the system, making the isolated structure face a higher risk of overturning.

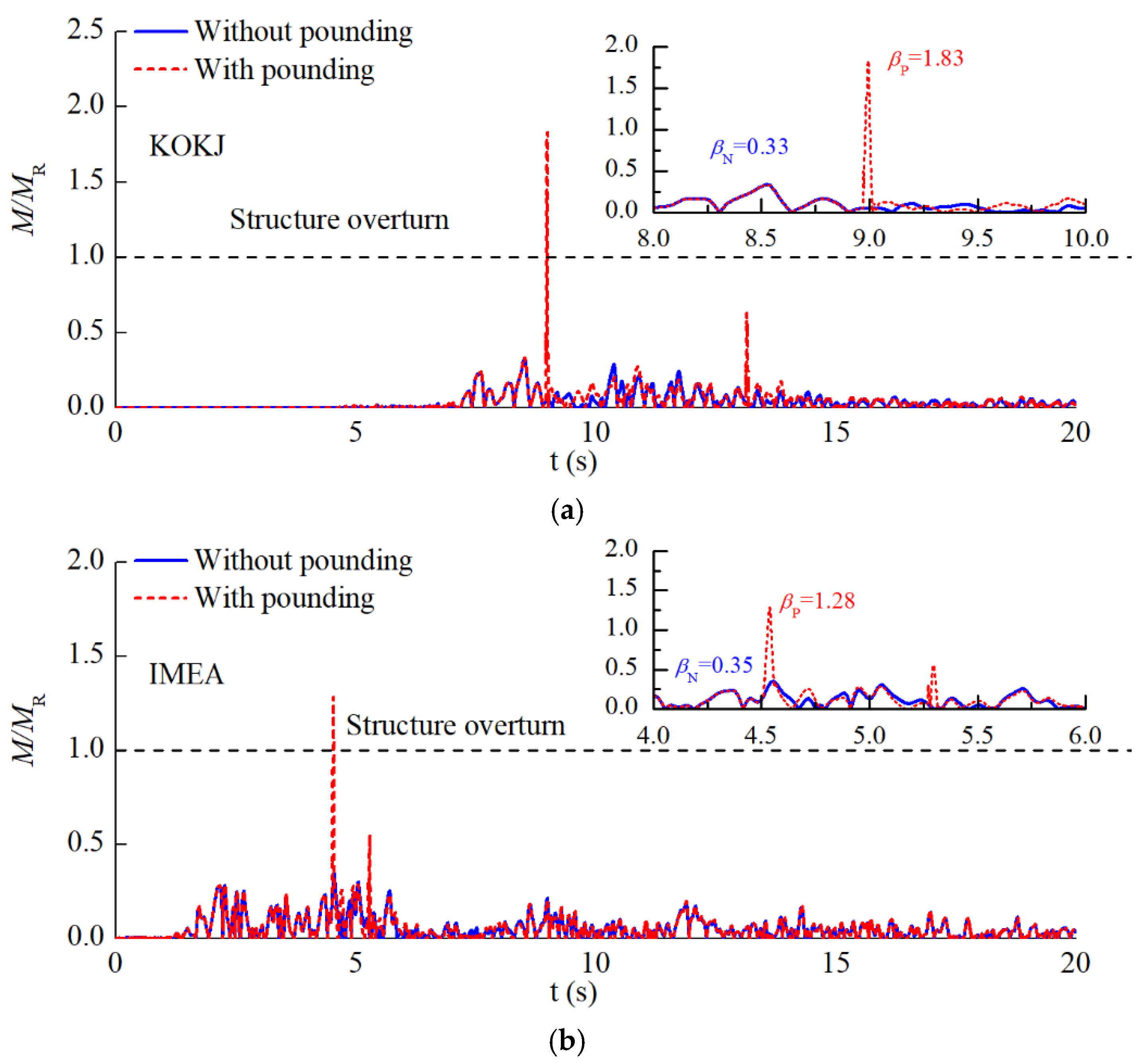
Figure 10 shows the time-history curve of the ratio of overturning bending moment to overturning resistance bending moment of the isolated structure during the pounding process. It can be clearly seen from the figure that after each pounding, the overturning bending moment will increase in a pulse-like manner, which directly leads to the risk of overturning of the structure. Specifically, this ratio increased sharply from 0.33 and 0.35 in the pounding-free state to 1.83 and 1.28, with increases of up to 454.5% and 265.7% when the system was excited by the KOKJ and IMEA seismic records, respectively. This fully demonstrates that even structures with sufficient overturning resistance capabilities may overturn under the impact of poundings.

The primary principle of seismic isolation technology lies in reducing the dynamic response by extending the structural period. However, the velocity pulses carried by pulse-like seismic waves can induce significant displacement responses in structures, resulting in higher strength and ductility requirements for structures proximal to fault lines. Consequently, the maximum absolute acceleration of the superstructure and the maximum displacement of the isolation layer in base-isolated structures experience considerable increases compared to those under conventional earthquakes when the structures were subjected the pulse-like earthquakes. This suggests that during poundings, structures subjected to pulse-like earthquakes possess greater velocities and more kinetic energy requiring dissipation through poundings. As a result, larger pounding forces emerge between structures, leading to a more pronounced weakening of their overturning resistance capacity.

Additionally, it is important to note that the more the pounding occurs, the more detrimental it is to the overturning resistance capability of the isolated structure. This is because the weakening effect of the pounding on the structural overturning performance is essentially the moment created by the pounding force at the overturning point. Consequently, under the same conditions, the higher the floor, the greater the overturning bending moment generated by the pounding, and the more prone the structure is to overturning. Furthermore, poundings are more likely to occur at higher floors due to the deformation characteristics of the isolated structure and adjacent structures. This further underscores the severity of the damage inflicted on the overturning resistance capability of the structure by poundings between the isolated structure and adjacent structures.

4. Parametric Study

The weakening of the overturning resistance of the isolated structure caused by poundings occurs because of the acceleration pulse generated by the pounding force on the structure. The magnitude of the pounding force is related to the velocity of the floor at the time of pounding, the properties of the contact section, and the constraints imposed on the structure. This section will employ a parametric study approach to investigate the influence of these parameters on the overturning resistance of the isolation structure when pounding is taken into consideration.

4.1. Gap Size

The relationship between gap size and pounding events depends on a multitude of factors. A smaller gap size accelerates the occurrence of pounding primarily because the threshold distance that needs to be traversed by external forces to initiate impact would be reduced. This early contact would result in a potentially higher frequency of impacts, as the system vibrates more frequently in response to fluctuations.

However, the magnitude of the pounding force generated during these impacts is not solely determined by the gap size. This phenomenon stems from the fact that, in addition to the precise moment of impact, the velocities of the adjacent structures during the impact are of paramount importance. The higher the velocities, the greater the amount of energy that must be dissipated through the impact, thereby generating more intense impact forces. The gap between the structures solely determines the timing of the impact, yet it is insufficient to dictate the velocities at which the structures collide.

An acceleration pulse would be caused by pounding, and the velocity and displacement responses are also influenced. It should be noted that the dynamic responses of the entire system are determined by the damping mechanisms and the stiffness of the structures. A more rigid system may experience larger forces due to less energy dissipation and a more significant acceleration pulse, while a more flexible system may absorb some of the impact energy through deformation, reducing the acceleration pulse.

Figure 11 presents a comprehensive analysis of the pounding force time history for isolated structures subjected to varying gap sizes. Specifically, distinct pounding patterns emerge based on the gap dimension when the structure is subjected to the IMEA earthquake record. With gap values of 0.10 m, 0.15 m, and 0.20 m, the structure experiences four, two, and two poundings, respectively. Notably, the peak pounding forces recorded are 3.0 × 10⁷ N, 5.1 × 10⁷ N, and 4.4 × 10⁷ N, indicating that the most intense pounding occurs when the gap is set at 0.15 m; it is implied that the relative velocity between the two floors of the structure during pounding is maximum among the cases.

Conversely, when the same structure is excited by the IMEA seismic wave, the pounding dynamics shift. The number of poundings increases to six, three, and two for the respective gap sizes, but the peak pounding forces diminish to 2.7 × 10⁷ N, 2.6 × 10⁷ N, and 1.9 × 10⁷ N. This observation underscores a trend where a larger gap size correlates with a reduced pounding force, suggesting that the optimal gap dimension for mitigating severe impacts may vary depending on the specific seismic loading conditions. The pounding force applied to the structure generates an acceleration pulse on the floors (as shown in Figure 12), resulting in a corresponding pounding response from the structure itself.

In summary, the intricacies of gap size’s influence on pounding frequency and intensity underscore the importance of meticulous design considerations to balance the need for timely responses with the risk of excessive pounding forces in seismic-resistant structures.

Figure 13 illustrates the trend of the structural overturning coefficient varying with the gap size. The structural overturning coefficient peaks at 2.98 when the gap is set at 0.14 m and subjected to the KOKJ earthquake record, indicating the highest risk of overturning at this point. Prior to this threshold, the overturning coefficient increases as the gap size enlarges, signifying a gradual decline in structural stability and an intensifying potential threat of overturning. However, once the gap value surpasses this critical value, the overturning coefficient begins to decrease, and the risk of overturning gradually diminishes. It is noteworthy that in most pounding scenarios, the overturning coefficient of the structure exceeds 1, explicitly pointing to poundings as the primary cause of structural overturning. Only when the gap size exceeds 0.24 m can the structure avoid the fate of overturning.

In contrast, when the structure is subjected to the IMEA seismic wave, the trend of the overturning coefficient changes significantly. As the gap size increases, the overturning coefficient steadily decreases. Notably, when the gap value surpasses 0.22 m, even in the event of pounding, the structure remains stable, avoiding the risk of overturning.

4.2. Pounding Stiffness

The magnitude of pounding forces is also significantly influenced by the pounding stiffness. A higher pounding stiffness results in the generation of greater pounding forces by the structure. For the purpose of discussion, the pounding stiffness ratio is defined as per Equation (11).

$${\eta }_{PS}={\displaystyle \frac{k_p^{\prime }}{k_{\mathrm{P}}}}$$

(11)

where ${\eta }_{PS}$ is pounding stiffness ratio; $k_{\mathrm{P}}$ and $k_p^{\prime }$ are the pounding stiffness for steel–steel structures and the pounding stiffness discussed in this section, respectively.

The pounding stiffness directly influences the magnitude of pounding force at the moment of impact, as well as the mechanism of energy dissipation during the pounding process. According to the principles of pounding mechanics, pounding force increases as pounding stiffness increases; as a result, more intense acceleration pulses in the structure can be found. Consequently, the structure’s resistance to overturning would be reduced.

Nevertheless, it is crucial to note that during pounding, the primary mechanism of energy dissipation is through material damping. Larger pounding forces lead to higher velocities, accelerating the process of energy dissipation. Simultaneously, a structure with a higher velocity enhances its own energy-dissipating process through damping. Considering that the total energy that needs to be dissipated during the entire pounding process remains constant, the duration of the pounding inevitably decreases.

Therefore, an increase in pounding stiffness directly leads to a significant enhancement in the force generated during the pounding, as displayed in Figure 14. This heightened pounding force not only imposes a more violent impact on the structure but also triggers a more intense acceleration pulse (see Figure 15). This intensification of the acceleration pulse, in turn, propels the overturning coefficient of the structure upwards, ultimately weakening its resistance to overturning (see Figure 16).

Furthermore, Figure 14 illustrates that as pounding stiffness increases, the duration of the pounding event shortens. This observation underscores that under higher pounding stiffness, the pounding reaches its peak within a shorter timeframe, ultimately contributing to the escalation of the structure’s overturning coefficient, as shown in Figure 16.

It is particularly noteworthy that in most cases, when the overturning coefficient surpasses the critical value of 1, it signifies that the structure has already overturned. This fact provides compelling evidence of the severe detrimental impact of poundings on the overturning resistance capacity of structures (Figure 16).

4.3. Horizontal Stiffness of Isolation Story

The horizontal stiffness ratio of the isolation story is defined as Equation (12) for discussion:

$${\eta }_{HS}={\displaystyle \frac{k_b^{\prime }}{k_{\mathrm{b}}}}$$

(12)

where ${\eta }_{HS}$ is the horizontal stiffness ratio of the isolation story; $k_{\mathrm{b}}$ and $k_b^{\prime }$ denote the horizontal stiffness of the isolation story discussed in this section.

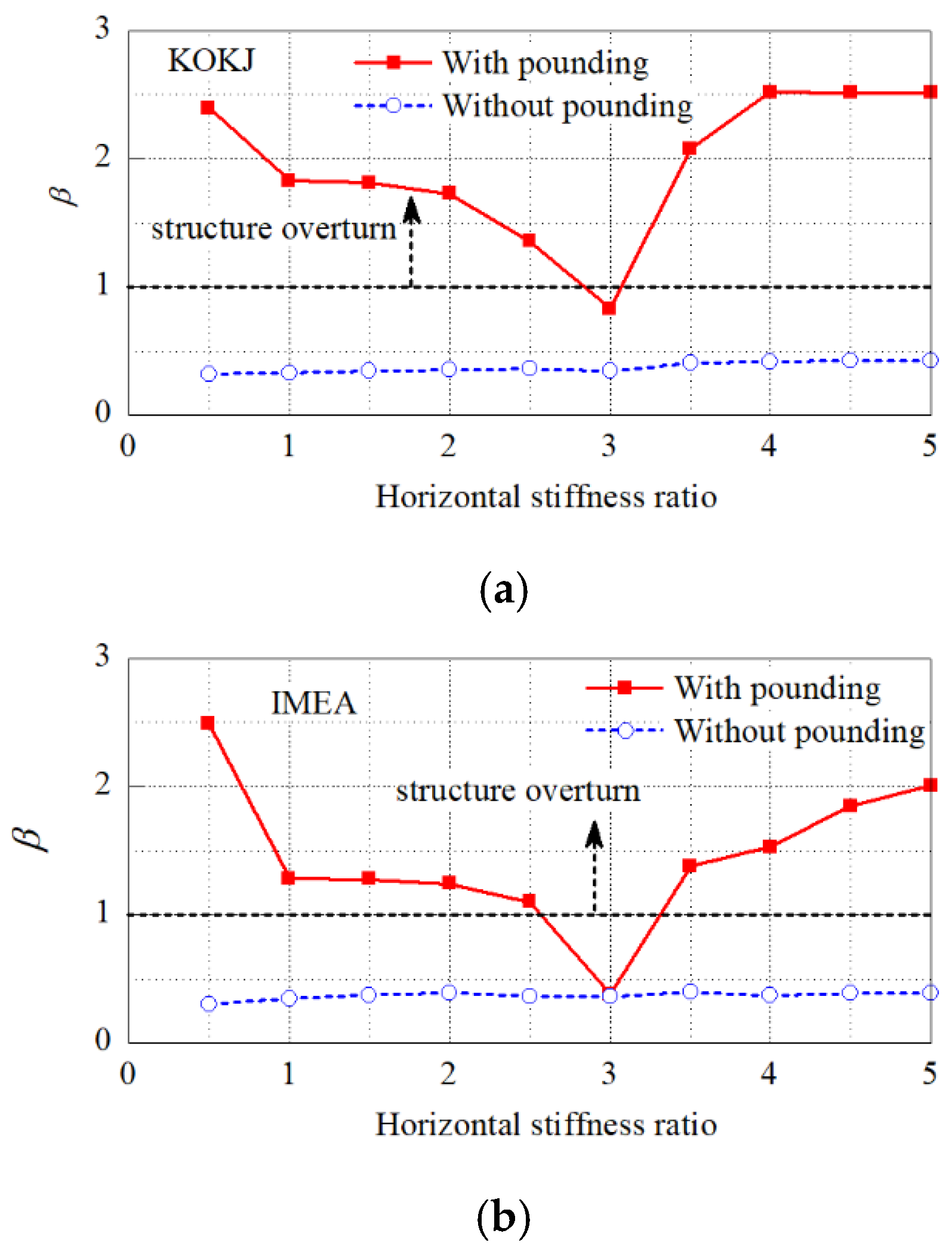
Given that the interlayer stiffness of the superstructure is significantly greater than the horizontal stiffness of the isolation story, the isolated structure can be approximately simplified as a single-degree-of-freedom (SDOF) system consisting solely of the horizontal stiffness of the isolation story and the mass of the superstructure. Therefore, the horizontal stiffness of the isolation story essentially determines the period of the structure, which directly influence its seismic dynamic response.

Based on the isolation mechanism of isolation bearings, a smaller horizontal stiffness of the isolation story can prolong the period of the structure, which is conducive to reducing the acceleration responses. However, it is important to note that when the period of the structure is similar to the dominant period of the seismic wave, the acceleration response of the structure will be significantly amplified, potentially intensifying poundings and severely compromising the overturning resistance of the isolated structure. Consequently, the occurrence of such a scenario should be avoided in the design of isolated structures.

Figure 17 illustrates the pounding force time-history curve at the top of the structure. It can be observed that structures with varying horizontal stiffnesses in their isolation layers experience poundings at different times. As the horizontal stiffness of the isolation layer decreases, the structural period is effectively extended, resulting in larger displacements. Consequently, when considering pounding effects, earlier poundings between adjacent structures and an increased number of poundings can lead to larger pounding forces and more significant acceleration impulses imparted on the structure throughout the seismic event (see Figure 18).

As the horizontal stiffness of the isolation layer increases, the structural period correspondingly shortens. The dynamic response of the structure becomes more pronounced when the structural period gradually approaches the dominant period of the seismic wave, leading to more intense poundings and subsequently generating stronger acceleration pulses. As a result, the overturning resistance of the structure is reduced. Subsequently, as the horizontal stiffness of the isolation layer continues to increase, the structural period further shortens and gradually moves away from the dominant period of the seismic wave. The structural response is reduced, and the pulse acceleration generated by the poundings also decreases, reducing the negative impact on the overturning resistance of the structure and thereby enhancing its overturning resistance. Therefore, a trend of the overturning coefficient first decreasing and then increasing can be observed (see Figure 19).

5. Discussions

It is demonstrated that the overturning resistance capacity of base-isolated structures is important, given that isolation bearings cannot be tensile. Therefore, not only must conventional seismic responses such as acceleration, velocity, and inter-story displacement under design conditions be addressed, but attention must also be paid to the overturning performance of these structures.

The overturning resistance capacity of base-isolated structures can be reduced by pounding interactions with adjacent structures. This emphasizes the importance of considering pounding effects during both the retrofitting of existing buildings and the new construction of base-isolated structures. In particular, the reduced displacement between adjacent fixed-end structures contrasts sharply with the large displacement of the isolated structure under earthquake loads when converting non-isolated structures into base-isolated ones. This disparity can significantly increase the risk of pounding, and it necessitates careful assessment.

Furthermore, measures should be taken to mitigate the detrimental impacts of pounding on structural overturning resistance capacity. For instance, the gap should be smaller than the threshold to minimize pounding risks, and suitable materials with lower pounding stiffness for interfaces between adjacent structures can suppress structural poundings.

Additionally, the parameters utilized in this paper are all sourced from the existing literature. Variations in structural parameters may lead to deviations in the results; therefore, further experiments need to be conducted to study this in more detail.

6. Conclusions

The overturning resistance capacity of base-isolated structures subjected to pounding with adjacent structures based on evaluations of pounding forces, structural dynamic responses, and overturning resistance capacity was investigated. The influences of gap size, pounding stiffness, and the horizontal stiffness of the isolation story on the overturning resistance of the base-isolated structure were also evaluated. The following conclusions can be drawn:

(1)

Pounding between the base-isolated and adjacent structures is characterized by short but intense forces, resulting in significant acceleration pulses in the structures, which would amplify the overturning coefficient and increase the risk of structural overturning.

(2)

The risk of overturning first decreases and then increases as the gap size increases when the system is subjected to pulse-like earthquake motions, but larger gap sizes mitigate the pounding effects when the system is excited by non-pulse-like earthquakes.

(3)

An increase in pounding stiffness intensifies pounding, which amplifies the vulnerability of the structure to overturning.

(4)

The structure’s overturning resistance initially improves with an increase in the horizontal stiffness of the isolation story but subsequently declines as this stiffness continues to increase.

(5)

The gap originally designed for fixed-base structures may be insufficient when existing structures are renovated into isolation structures. It is necessary to fully consider the dynamic characteristics of adjacent structures and reserve a sufficient gap when conducting isolation design for existing structures to avoid poundings.