A Mesoscopic Approach for the Numerical Simulation of a Mass Concrete Structure Construction Using Post-Cooling Systems
Abstract
1. Introduction
2. Numerical Modeling
2.1. Mass Concrete
2.2. Post-Cooling System
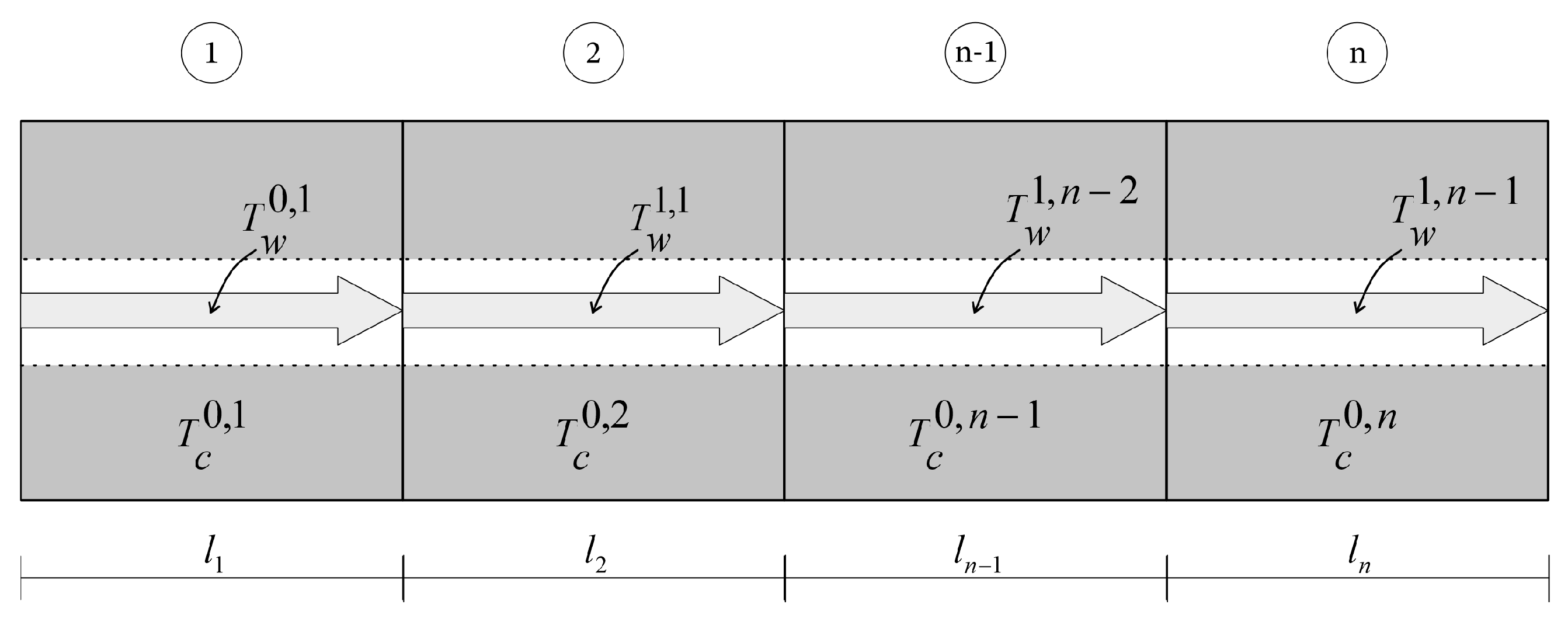
2.3. Layered Construction
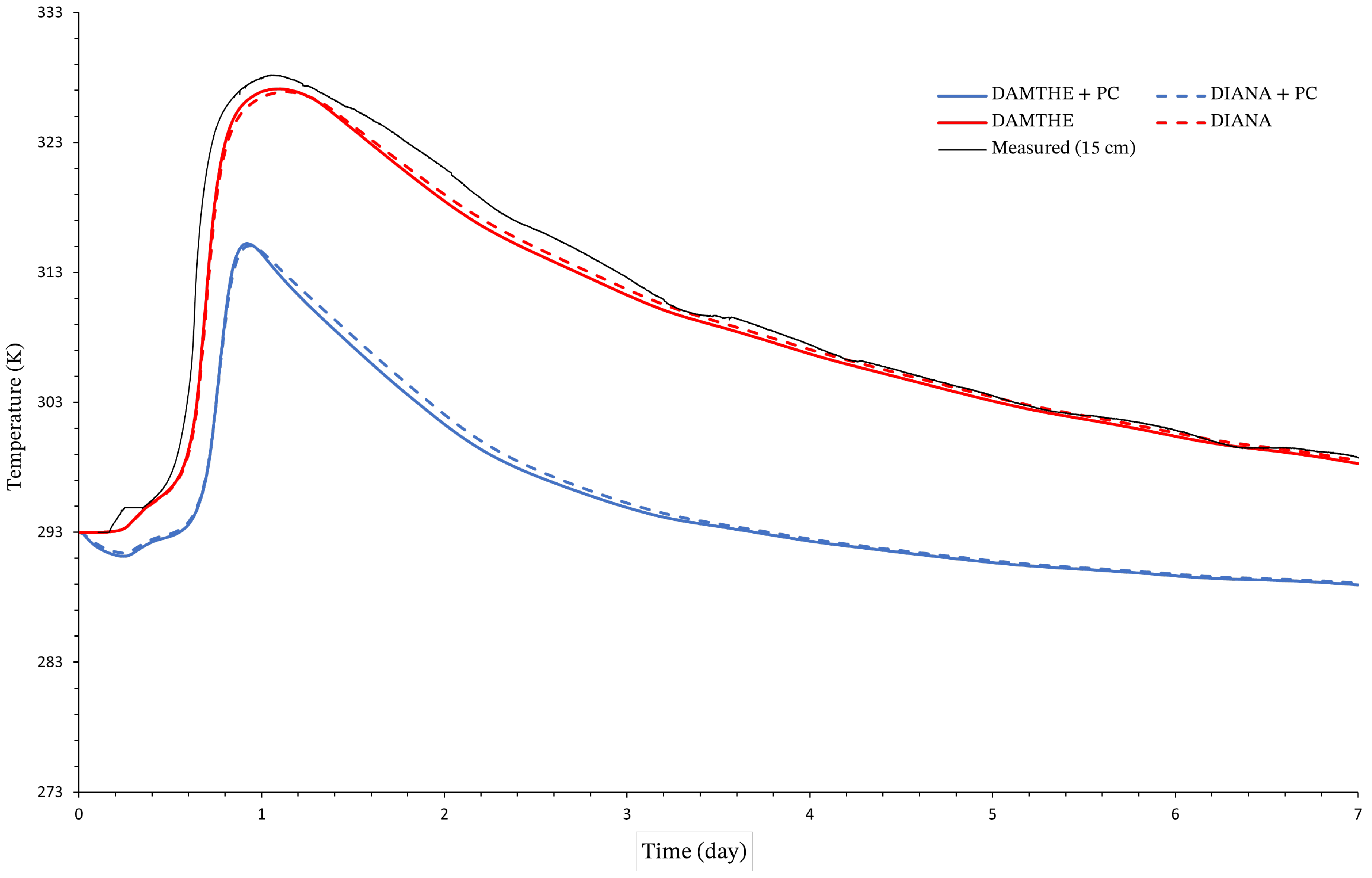
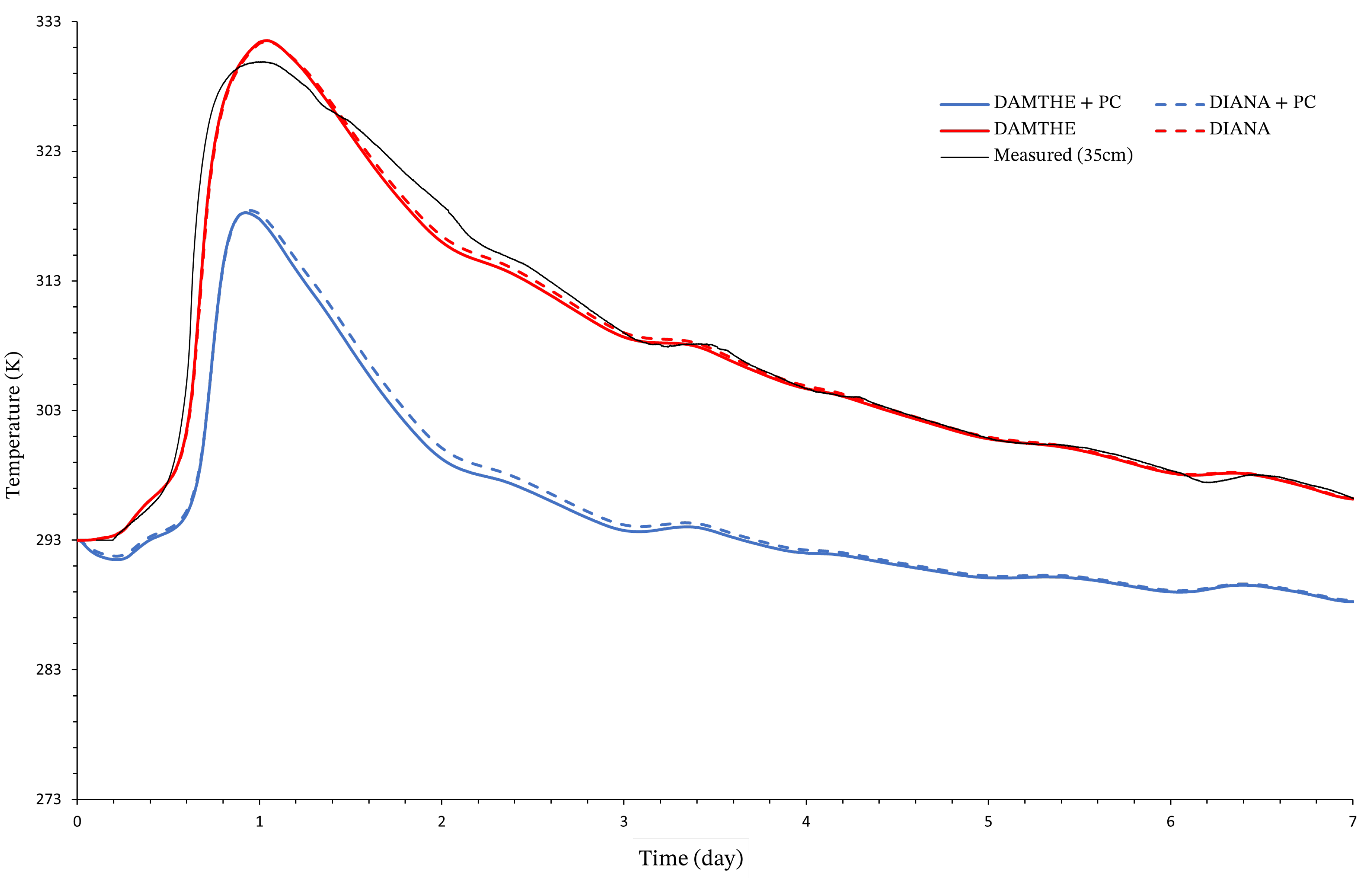
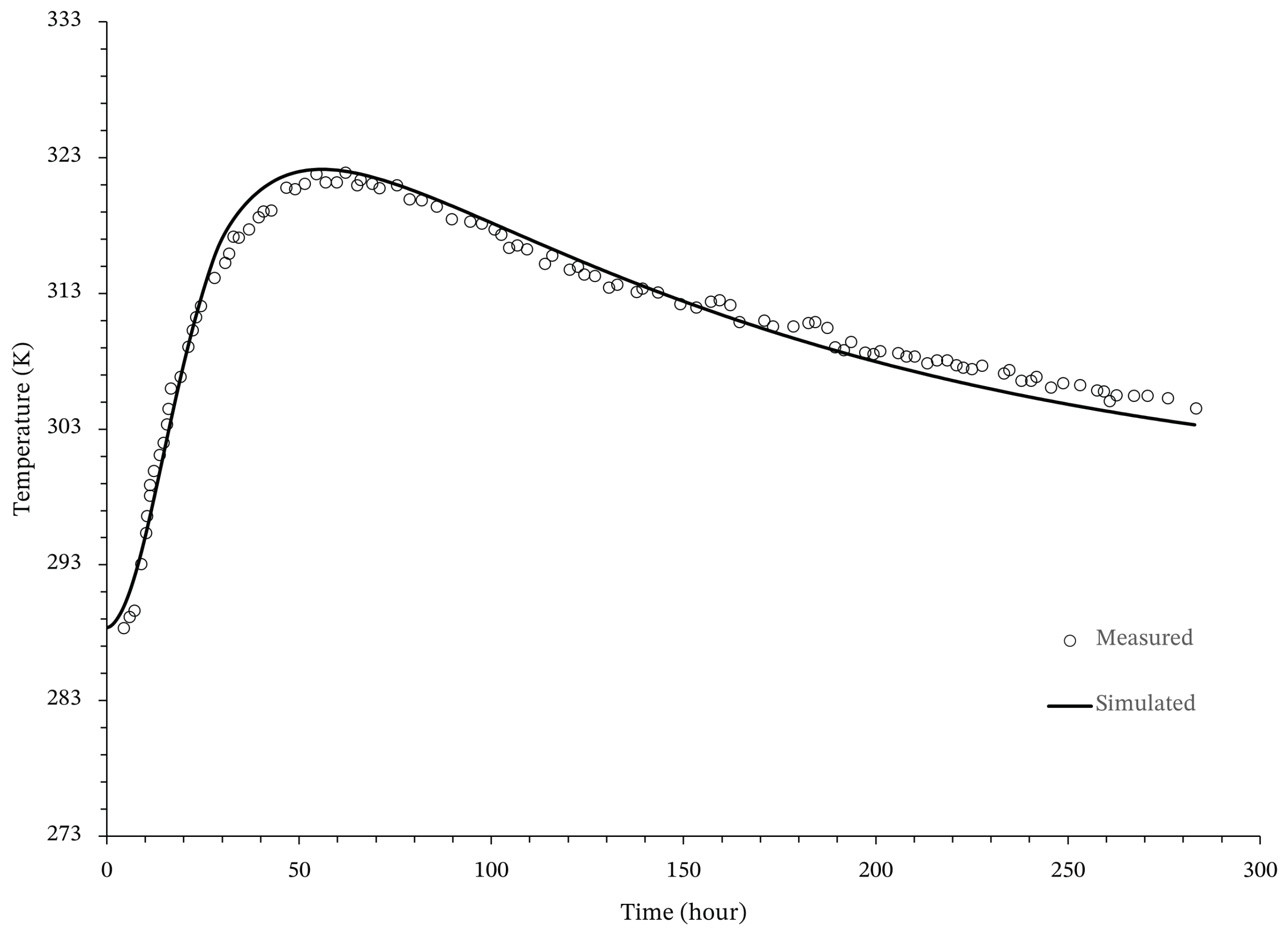
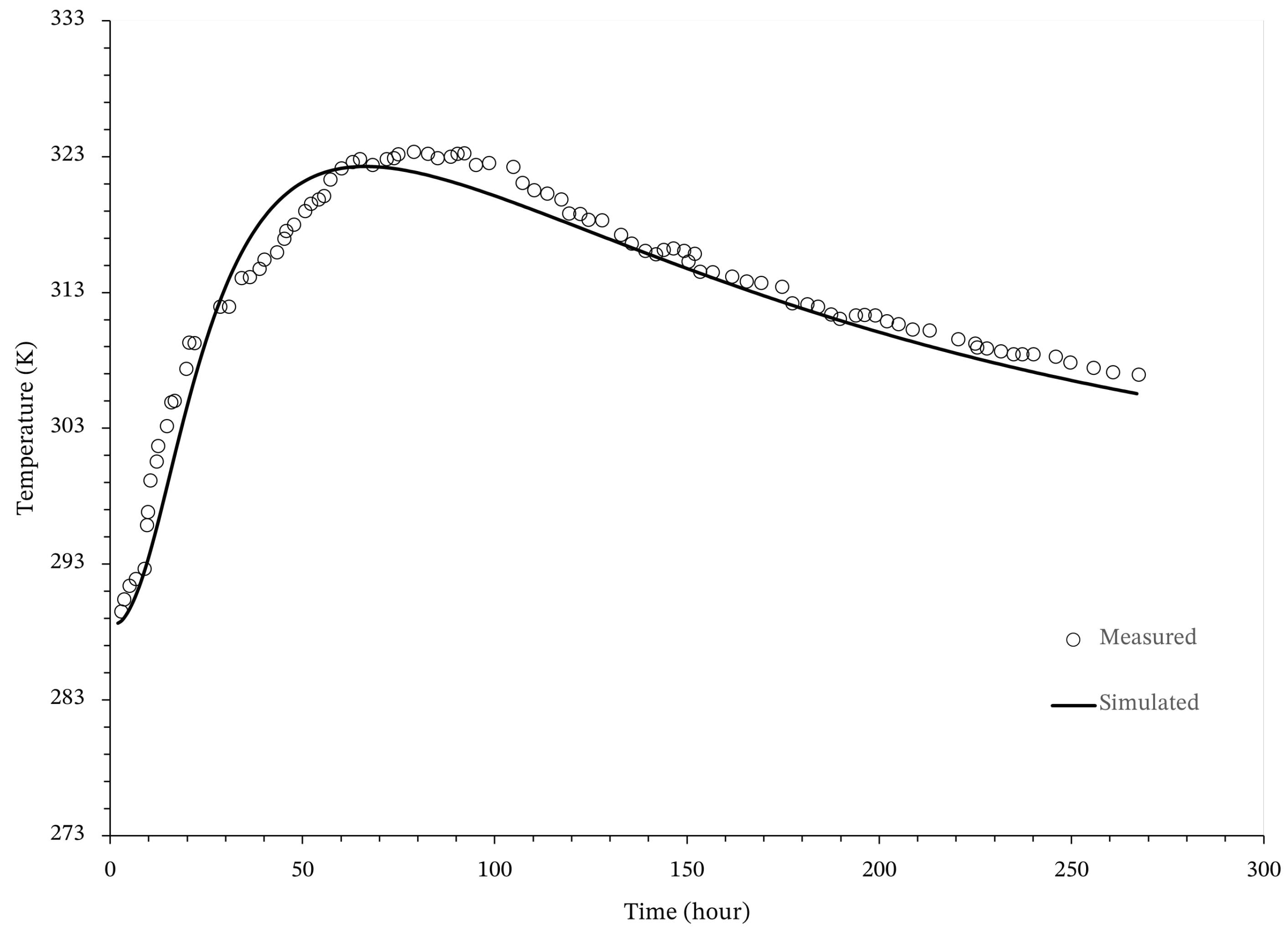
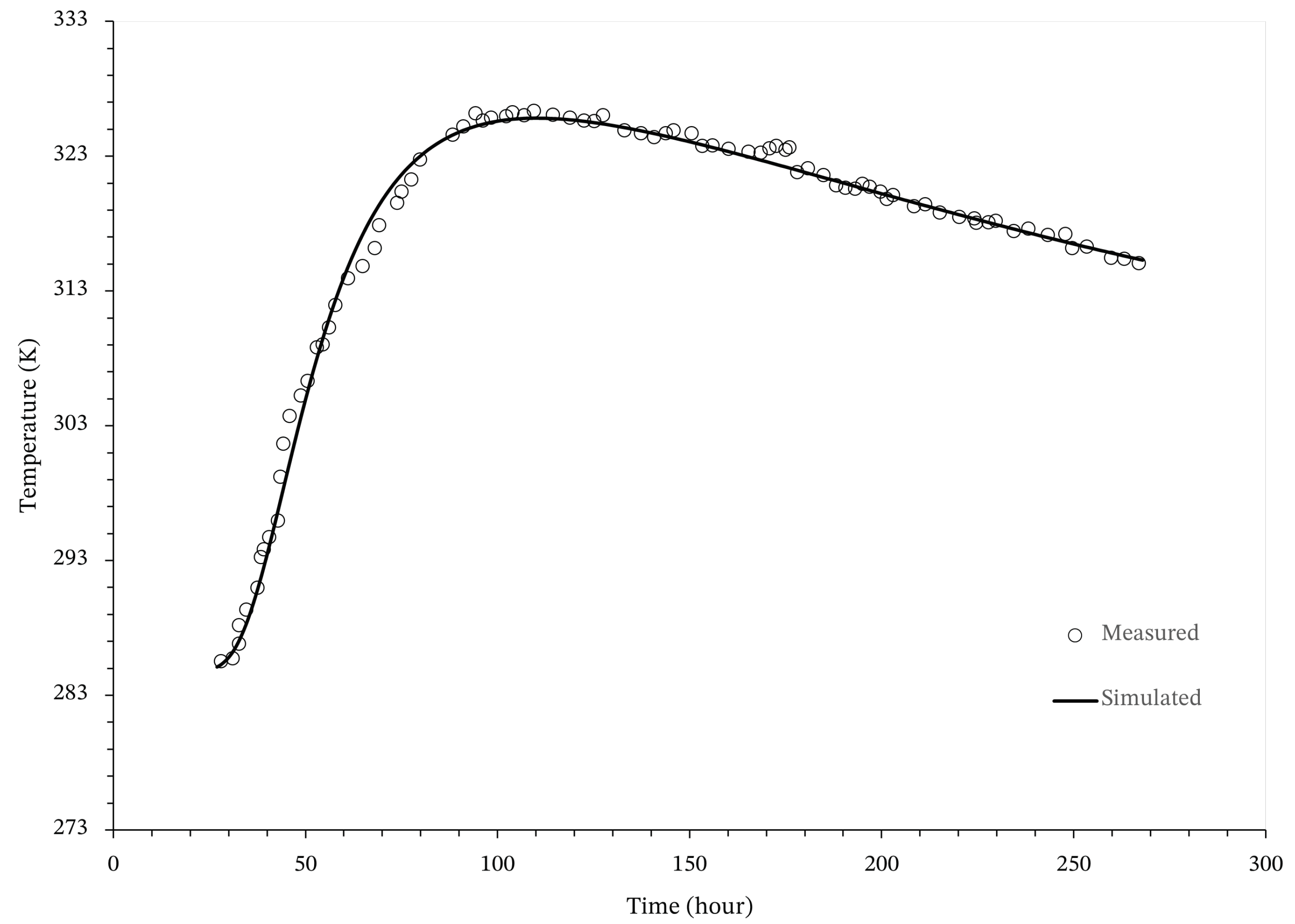
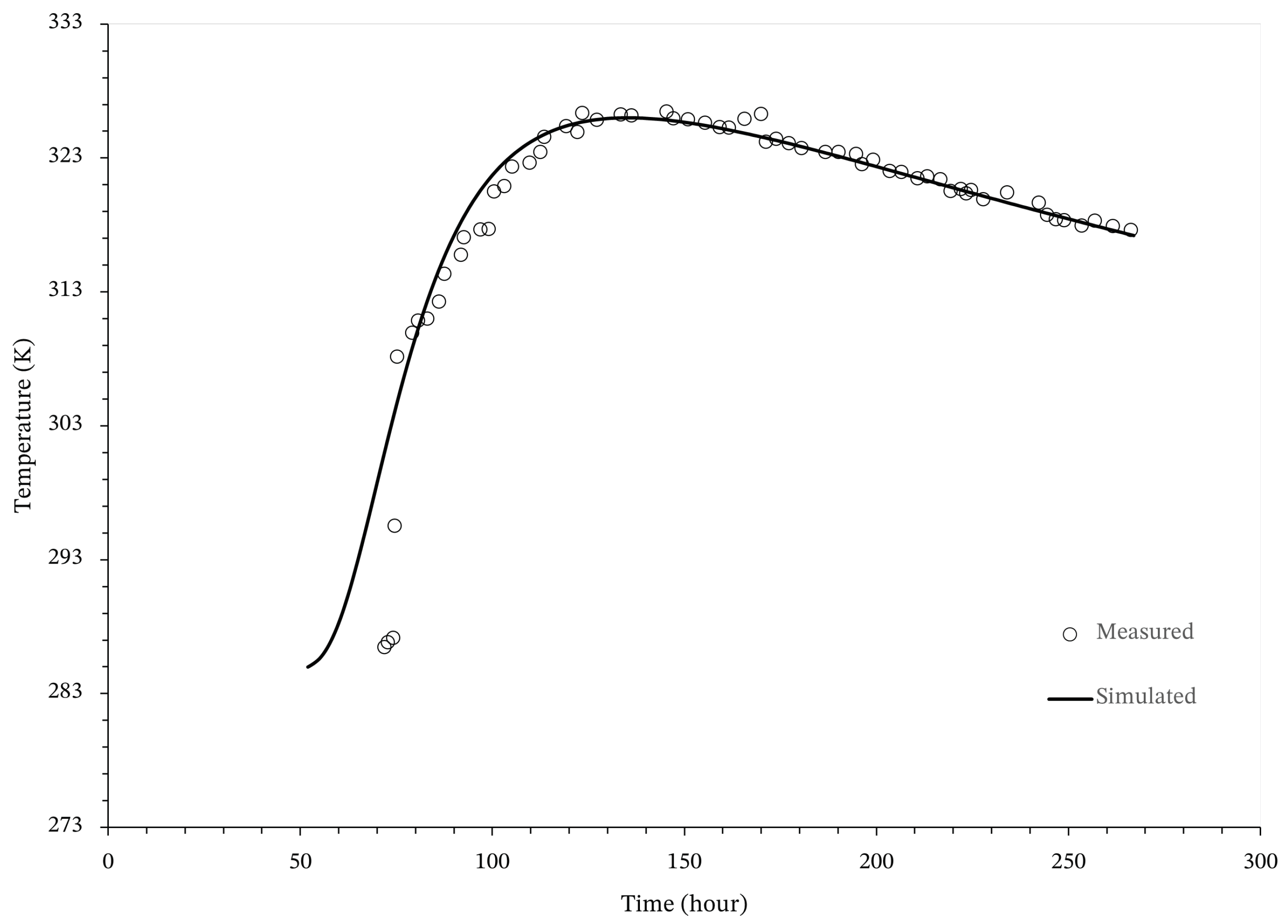
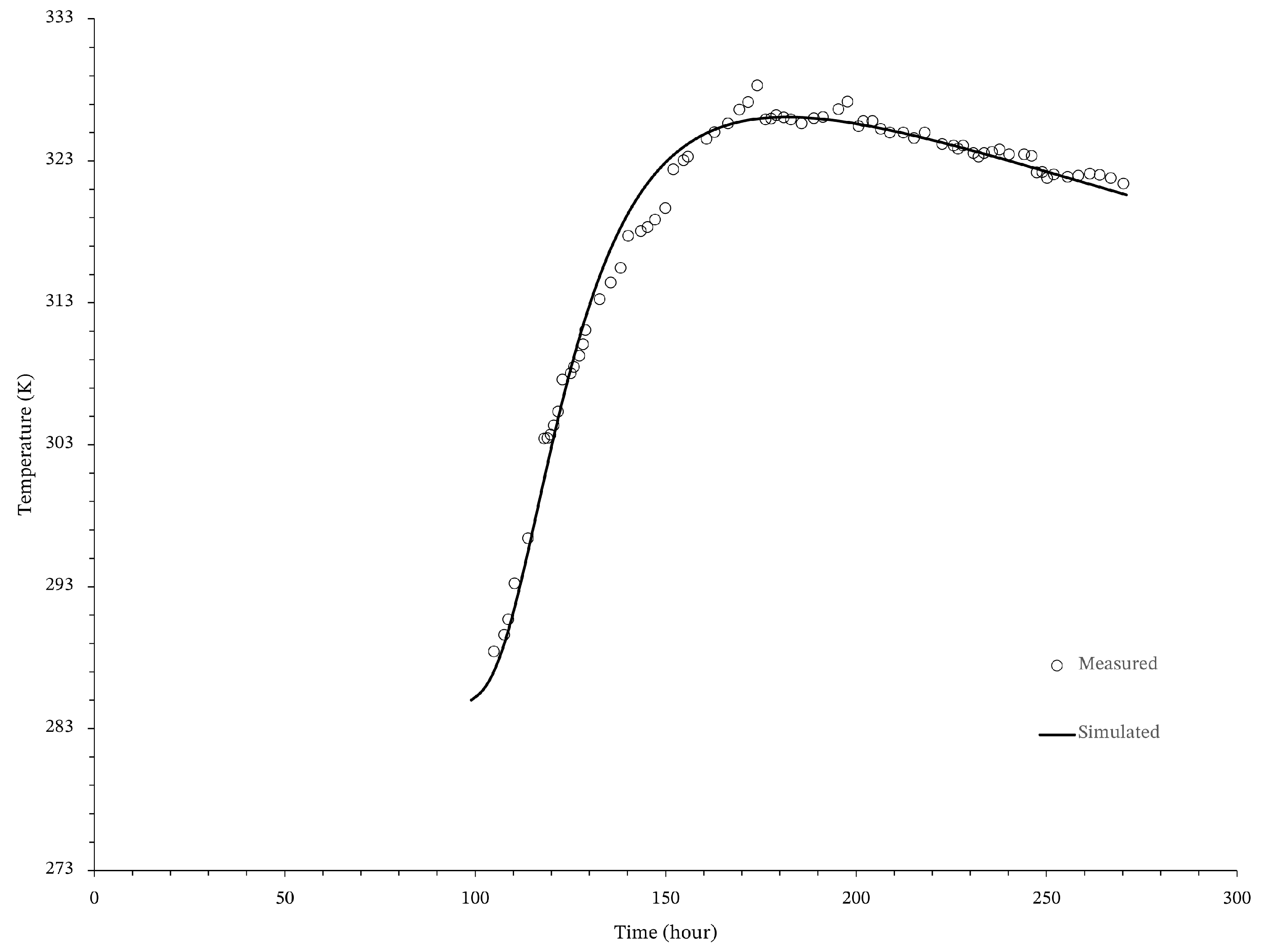
3. Validation
4. Sensitivity and Convergence Analysis
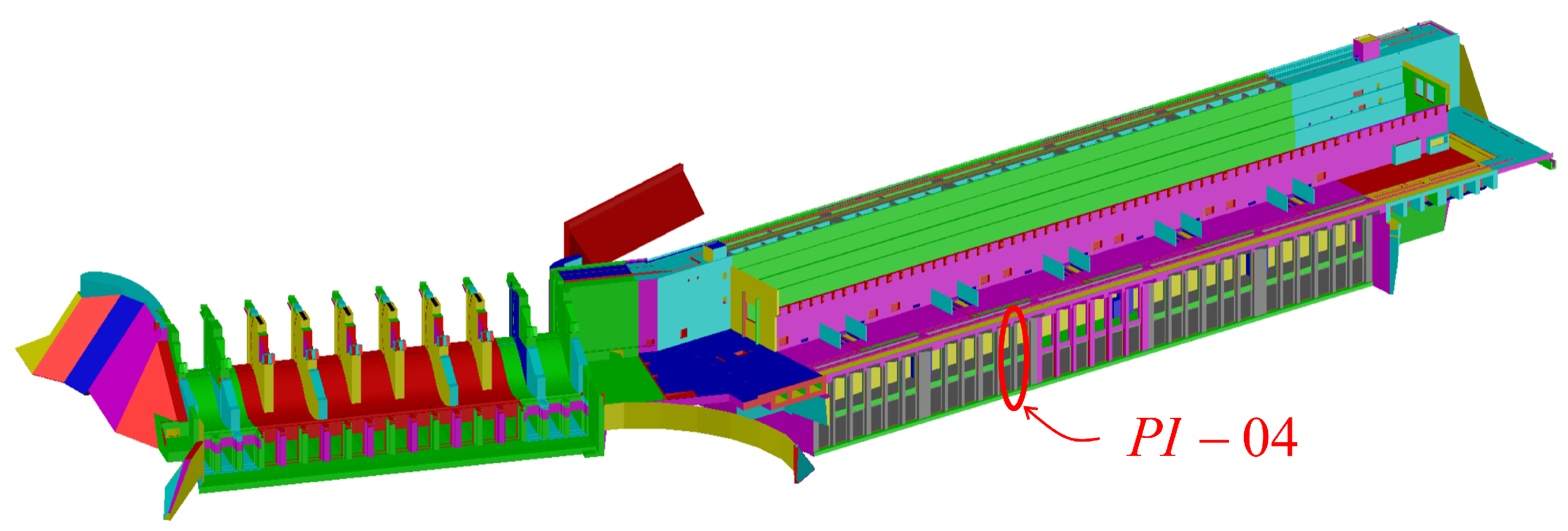
5. Case Study: Construction of Water Intake Structure Pillar of a Hydroelectric Power Plant
5.1. Layered Construction
5.2. Construction Parameters
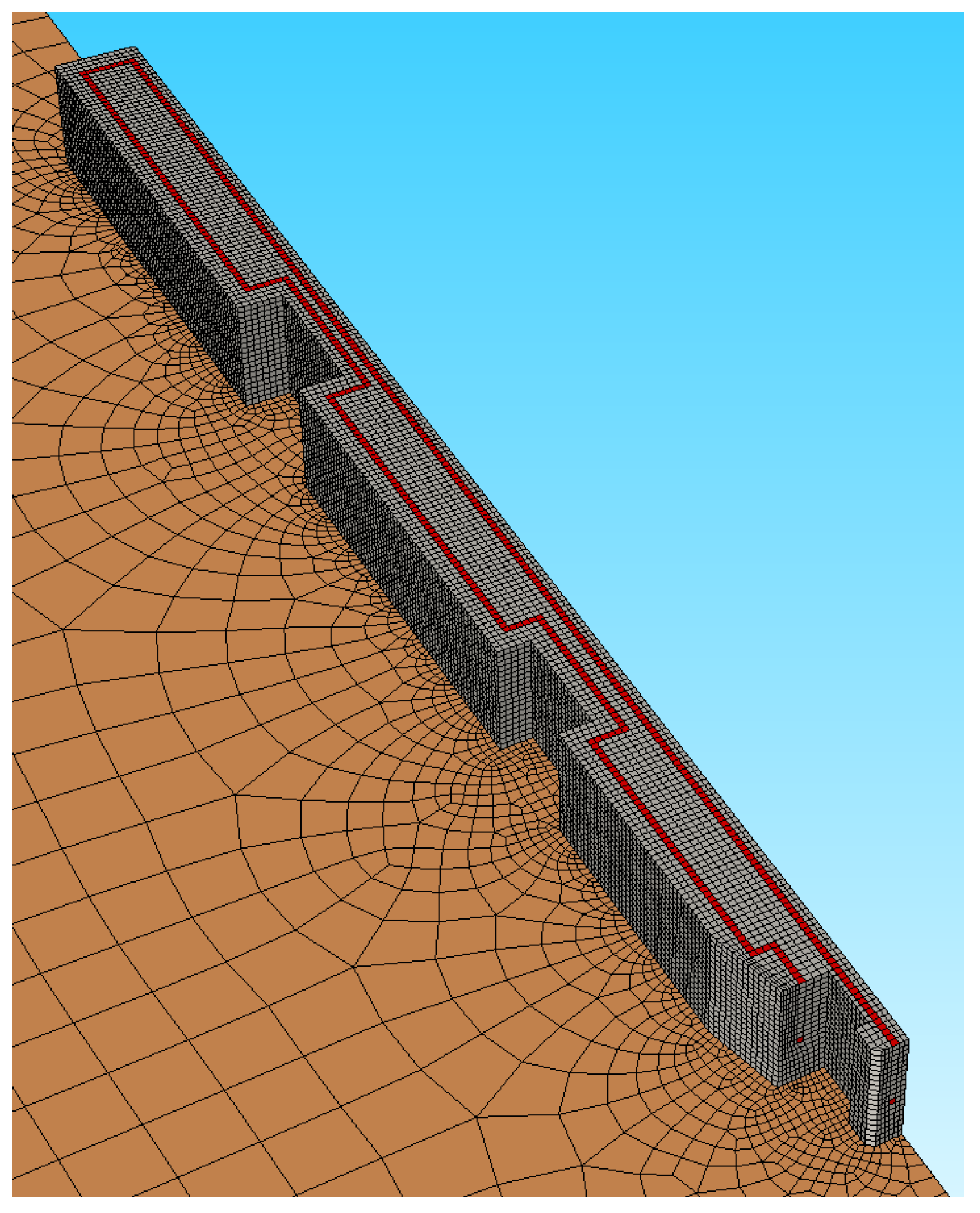
5.3. Geometry and Mesh
5.4. Material Properties
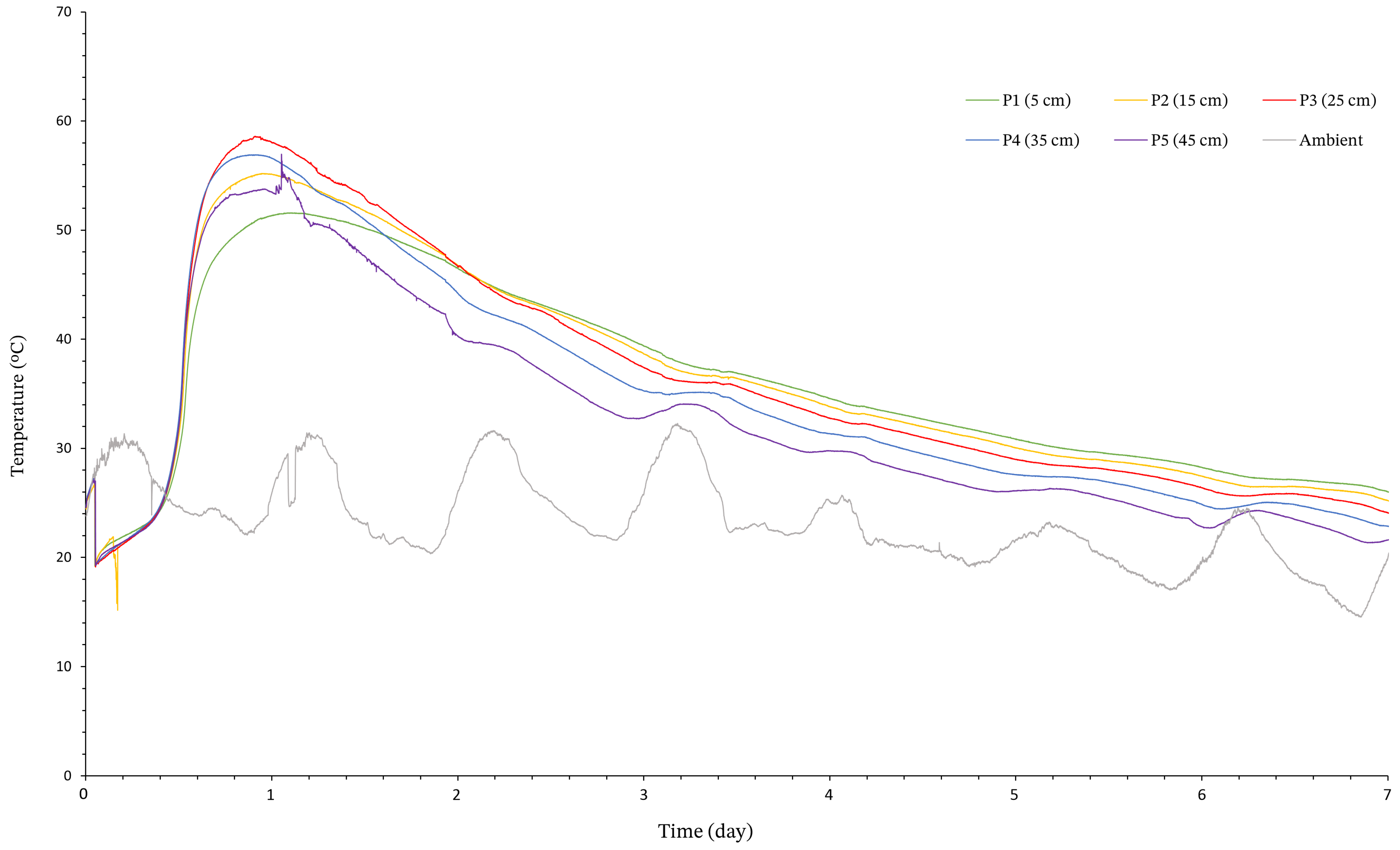
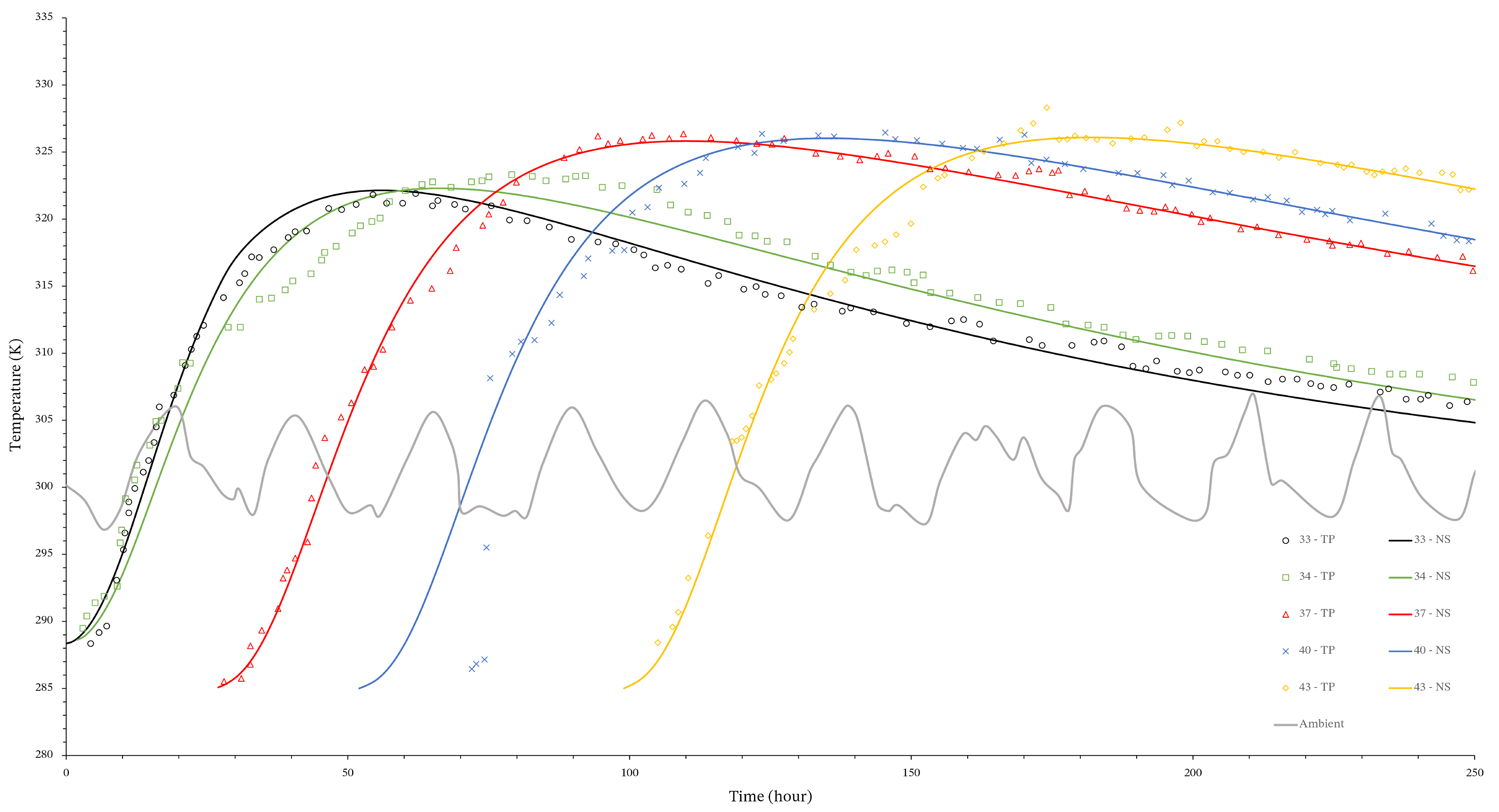
5.5. Results
6. Discussion and Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Fairbairn, E.; Azenha, M. Thermal Cracking of Massive Concrete Structures: State of the Art Report of the RILEM Technical Committee 254-CMS; Technical Report, RILEM; Springer: Cham, Switzerland, 2018. [Google Scholar] [CrossRef]
- Ulm, F.J.; Coussy, O. Modeling of thermochemomechanical couplings of croncrete at early ages. J. Eng. Mech. 1995, 121, 785–794. [Google Scholar] [CrossRef]
- Ulm, F.J.; Coussy, O. Strength Growth as Chemo-Plastic Hardening in Early Age Concrete. J. Eng. Mech. 1996, 122, 1123–1132. [Google Scholar] [CrossRef]
- Ulm, F.J.; Coussy, O. Couplings in early-age concrete: From material modeling to structural design. Int. J. Solids Struct. 1998, 35, 4295–4311. [Google Scholar] [CrossRef]
- Azenha, M. Numerical Simulation of the Structural Behaviour of Concrete Since Its Early Ages. Ph.D. Thesis, Faculdade de Engenharia da Universidade do Porto, Porto, Portugal, 2009. [Google Scholar]
- Xin, J.; Zhang, G.; Liu, Y.; Wang, Z.; Wu, Z. Effect of temperature history and restraint degree on cracking behavior of early-age concrete. Constr. Build. Mater. 2018, 192, 381–390. [Google Scholar] [CrossRef]
- Castilho, E.; Schclar, N.; Tiago, C.; Farinha, M.L.B. FEA model for the simulation of the hydration process and temperature evolution during the concreting of an arch dam. Eng. Struct. 2018, 174, 165–177. [Google Scholar] [CrossRef]
- Gimenes, M.; Cleto, P.R.; Rodrigues, E.A.; Lloberas-Valls, O.; Manzoli, O.L. Modeling the effect of material heterogeneity on the thermo-mechanical behavior of concrete using mesoscale and stochastic field approaches. Theor. Appl. Fract. Mech. 2024, 133, 104622. [Google Scholar] [CrossRef]
- Huang, Y.J.; Natarajan, S.; Zhang, H.; Guo, F.-Q.; Xu, S.-L.; Zeng, C.; Zheng, Z.-S. A CT image-driven computational framework for investigating complex 3D fracture in mesoscale concrete. Cem. Concr. Compos. 2023, 143, 105270. [Google Scholar] [CrossRef]
- Tu, W.; Zhang, M. Multiscale microstructure and micromechanical properties of alkali-activated concrete: A critical review. Cem. Concr. Compos. 2024, 152, 105664. [Google Scholar] [CrossRef]
- Zhang, Y.; Lei, Q.; Zhao, W.; Yang, Y.; Wang, Y.; Yan, Z.; Zhu, H.; Ju, J.W. An improved micromechanical model for the thermal conductivity of multi-scale fiber reinforced ultra-high performance concrete under high temperatures. Mater. Des. 2023, 236, 112503. [Google Scholar] [CrossRef]
- Li, X.; Zhang, Y.; Liu, J.; Zuo, X. Multi-scale numerical simulation on mechanical strength of concrete based on its microstructural evolution. Constr. Build. Mater. 2024, 443, 137672. [Google Scholar] [CrossRef]
- Li, X.N.; Zuo, X.B.; Li, L.; Liu, J.H. Multiscale modeling and simulation on mechanical behavior of fiber reinforced concrete. Int. J. Solids Struct. 2024, 286–287, 112569. [Google Scholar] [CrossRef]
- ACI. Guide to Mass Concrete; ACI Manual of Concrete Practice; American Concrete Institute: Farmington, MI, USA, 2005. [Google Scholar]
- Tasri, A.; Susilawati, A. Effect of cooling water temperature and space between cooling pipes of post-cooling system on temperature and thermal stress in mass concrete. J. Build. Eng. 2019, 24, 100731. [Google Scholar] [CrossRef]
- Kheradmand, M.; Azenha, M.; Vicente, R.; de Aguiar, J.L. An innovative approach for temperature control of massive concrete structures at early ages based on post-cooling: Proof of concept. J. Build. Eng. 2020, 32, 101832. [Google Scholar] [CrossRef]
- Kheradmand, M.; Vicente, R.; Azenha, M.; de Aguiar, J.L.B. A New Sustainable System for Piped Water Cooling of Mass Concrete Structures; Springer International Publishing: Berlin/Heidelberg, Germany, 2023; pp. 421–430. [Google Scholar]
- ICOLD. Cnventional Methods in Dam Construction; International Commission on Large Dams: Paris, France, 1990; Volume Bulletin 76. [Google Scholar]
- Baber, J.; Salet, T.A.M.; Lundberg, J.K. Øresund tunnel control of early age cracking. Proc. IABSE Stockh. Colloquium Tunn. Struct. 1998, 78, 175–180. [Google Scholar]
- Kim, J.K.; Kim, K.H.; Yang, J.K. Thermal analysis of hydration heat in concrete structures with pipe cooling system. Comput. Struct. 2001, 79, 163–171. [Google Scholar] [CrossRef]
- Lunniss, R.; Baber, J. Immersed Tunnels; CRC Press: Boca Raton, FL, USA; Taylor and Francis Group: Boca Raton, FL, USA, 2013. [Google Scholar]
- Sfikas, I.; Ingham, J.; MacDonald, J. Using finite element analysis to assess the thermal behaviour of concrete structures. Concrete 2017, 50–52. [Google Scholar]
- Fairbairn, E.; Silvoso, M.; Koenders, E.; Ribeiro, F.; Toledo, R.D. Thermo-chemo-mechanical cracking assessment for early-age mass concrete structures. Concr. Int. 2012, 34, 30–35. [Google Scholar]
- Myers, T.; Fowkes, N.; Ballim, Y. Modeling the cooling of concrete by piped water. J. Eng. Mech. 2009, 135, 1375–1383. [Google Scholar] [CrossRef]
- You, K.; Wang, F.; Wang, L.; Zhao, Z.; Liu, Y. A faster iterative method for solving temperature field of mass concrete with cooling pipes. AIP Conf. Proc. 2017, 1839, 020079. [Google Scholar] [CrossRef]
- Liu, X.; Zhang, C.; Chang, X.; Zhou, W.; Cheng, Y.; Duan, Y. Precise simulation analysis of the thermal field in mass concrete with a pipe water cooling system. Appl. Therm. Eng. 2015, 78, 449–459. [Google Scholar] [CrossRef]
- Zhong, R.; Hou, G.P.; Qiang, S. An improved composite element method for the simulation of temperature field in massive concrete with embedded cooling pipe. Appl. Therm. Eng. 2017, 124, 1409–1417. [Google Scholar] [CrossRef]
- Ding, J.; Chen, S. Simulation and feedback analysis of the temperature field in massive concrete structures containing cooling pipes. Appl. Therm. Eng. 2013, 61, 554–562. [Google Scholar] [CrossRef]
- Nguyen, T.C.; Nguyen, T.; Nguyen, V.; Do, T.M.D. Finite element analysis of temperature and stress fields in the concrete mass with pipe-cooling. Structutal Integr. Life 2020, 20, 131–135. [Google Scholar]
- Yang, J.K.; Lee, Y.; Kim, J.K. Heat transfer coefficient in flow convection of pipe-cooling system in massive concrete. J. Adv. Concr. Technol. 2011, 9, 103–114. [Google Scholar] [CrossRef]
- Yang, J.; Hu, Y.; Zuo, Z.; Jin, F.; Li, Q. Thermal analysis of mass concrete embedded with double-layer staggered heterogeneous cooling water pipes. Appl. Therm. Eng. 2012, 35, 145–156. [Google Scholar] [CrossRef]
- Zhu, B. Effect of cooling by water flowing in nonmetal pipes embedded in mass concrete. J. Constr. Eng. Manag. 2019, 125, 61–68. [Google Scholar] [CrossRef]
- Conceição, J.; Faria, R.; Azenha, M.; Miranda, M. A new method based on equivalent surfaces for simulation of the post-cooling in concrete arch dams during construction. Eng. Struct. 2020, 209, 109976. [Google Scholar] [CrossRef]
- Silva, A.; Laszczk, J.; Wrobel, L.; Ribeiro, F.; Nowak, A. A thermoregulation model for hypothermic treatment of neonates. Med. Eng. Phys. 2016, 38, 988–998. [Google Scholar] [CrossRef]
- Ferreira, D. (Ed.) DIANA Users Manual; DIANA FEA: Delft, The Netherlands, 2022. [Google Scholar]
- Rita, M. Otimização da Fase Construtiva de Estruturas de Concreto Massa em Ambiente Paralelo. Ph.D. Thesis, UFRJ, Rio de Janeiro, Brazil, 2015. [Google Scholar]
- De Faria, E. Predição da Exotermia da Reação de Hidratação do Concreto Através de Modelo Termo-quíMico e Modelo de Dados. Ph.D. Thesis, UFRJ, Rio de Janeiro, Brazil, 2004. [Google Scholar]
- Bejan, A. Heat Transfer; John Wiley and Sons, Inc.: Hoboken, NJ, USA, 1993. [Google Scholar]
- Bejan, A. Convection Heat Transfer; John Wiley and Sons, Inc.: Hoboken, NJ, USA, 2013. [Google Scholar]
- Cengel, Y. Heat Transfer: A Practical Approach; McGraw-Hill: New York, NY, USA, 2002. [Google Scholar]
- Arreaza, R. Utilizacion del sistema de postcooling para ejecutar vaciados masivos de granedes alturas. Premio Destaque Odebrecht 2011, 11, 1–35. [Google Scholar]
- Velasco, R.V. Concretos Auto-Adensáveis Reforçados com Elevadas Frações Volumétricas de Fibras de Aço: Propriedades ReolóGicas, fíSicas, mecâNicas e téRmicas. Ph.D. Thesis, UFRJ, Rio de Janeiro, Brazil, 2008. [Google Scholar]
- Hilaire, A. Etude des Déformations Différées des Bétons en Compression et en Traction, du Jeune au Long Terme: Application Aux Enceintes de Confinement. Ph.D. Thesis, École normale supérieure de Cachan—ENS Cachan, Cachan, France, 2014. [Google Scholar]



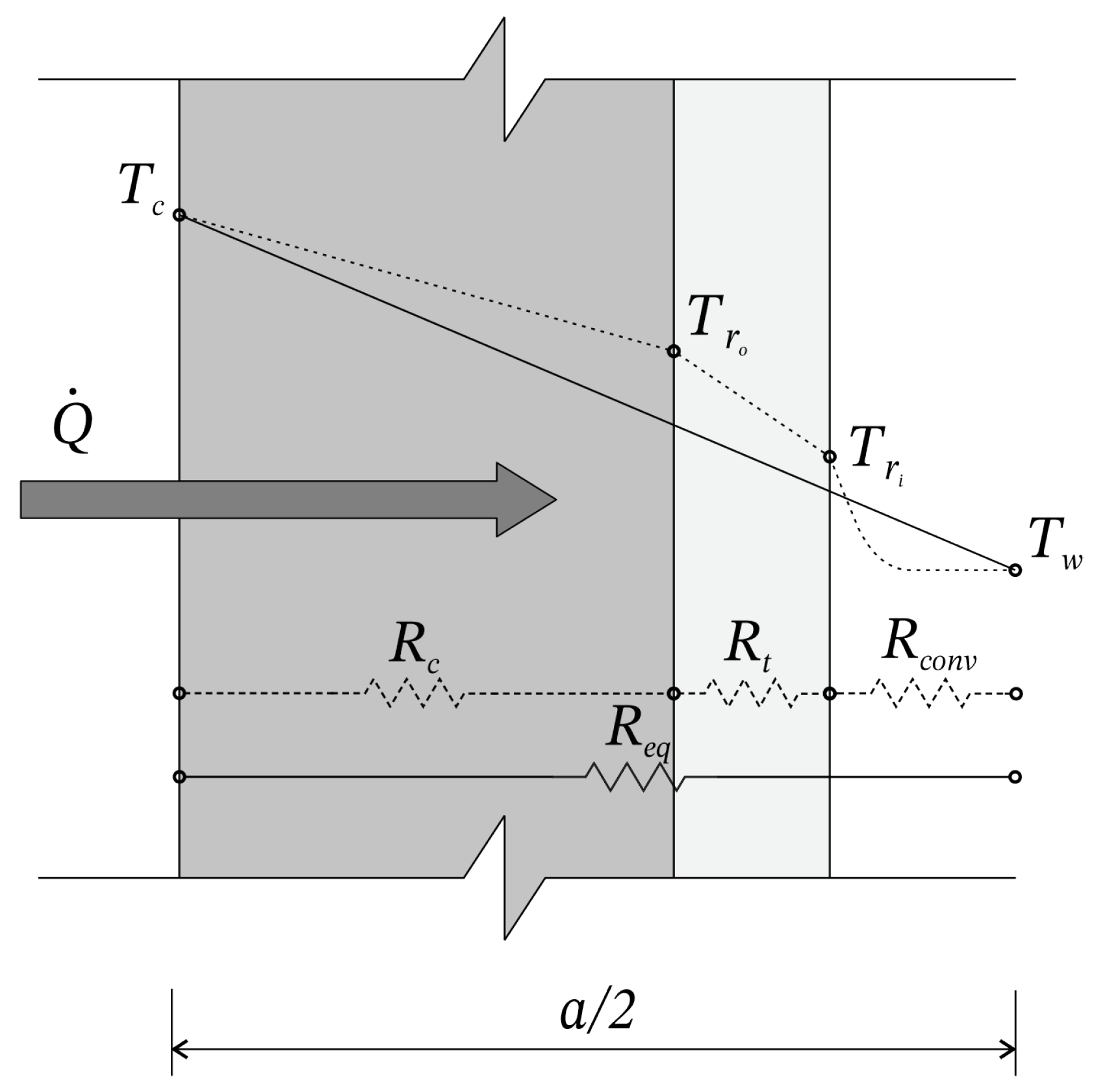
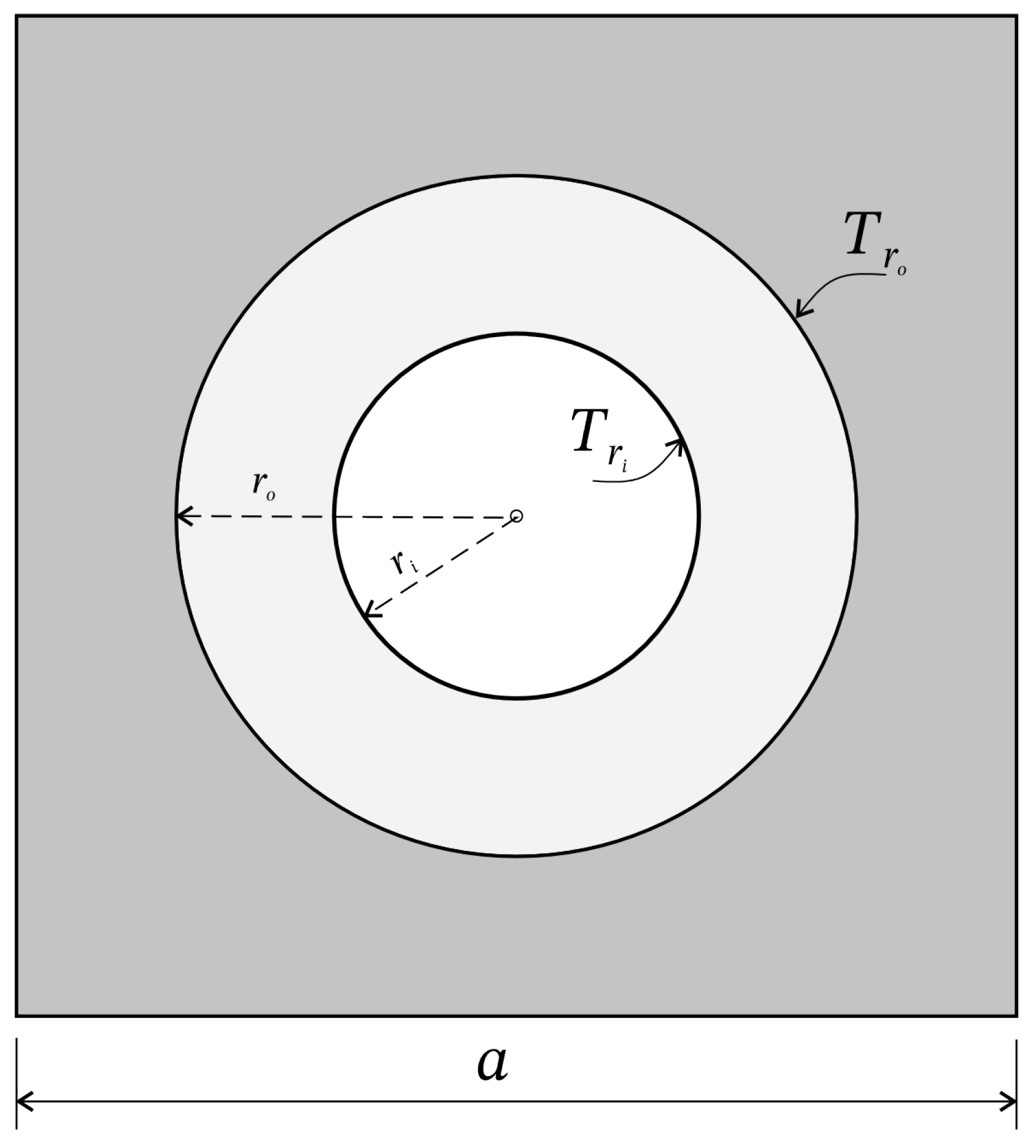
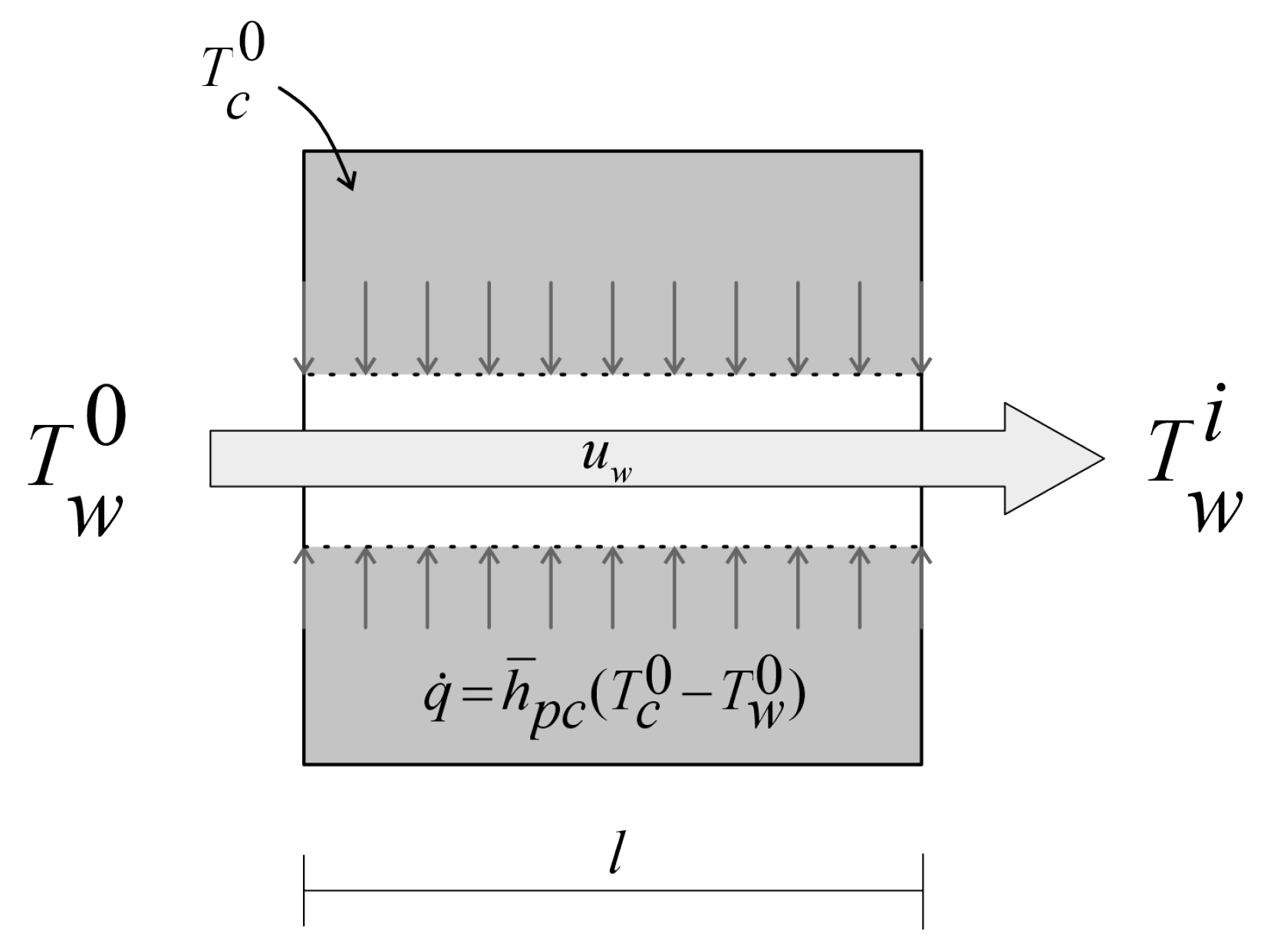





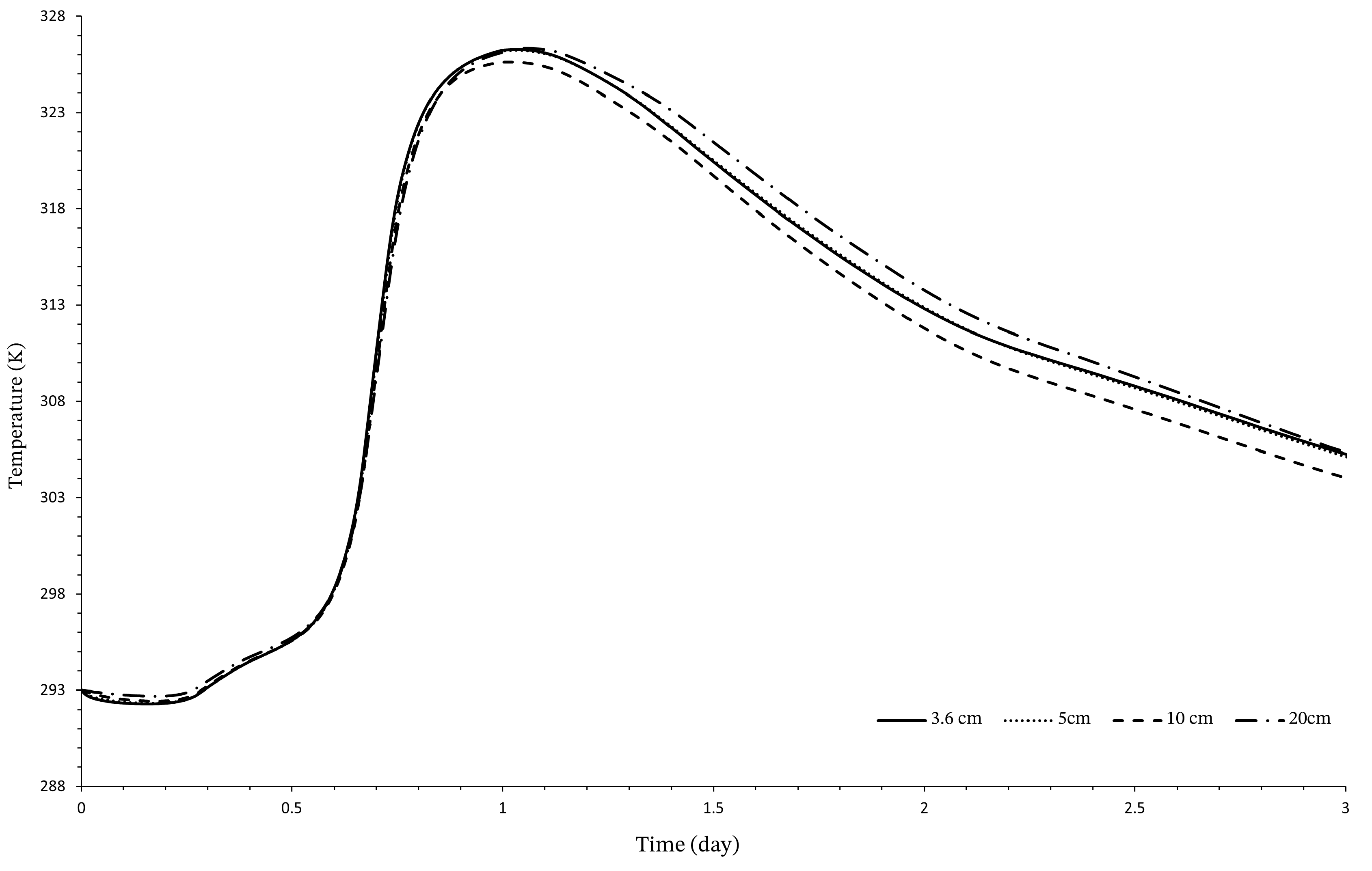




| Parameter | Value | Unit | Equations |
|---|---|---|---|
| l | 0.03600 | m | (28) and (32) |
| a | 0.03600 | m | (26) and (32) |
| b | 0.03600 | m | (26) and (32) |
| 0.07200 | s | (30) | |
| 1000.00 | kg/m3 | (32) | |
| 1086.00 | J/kg K | (2) | |
| 4184.00 | J/kg K | (32) | |
| 800.000 | J/kg K | (2) | |
| 1.56000 | W/m K | (2) and (26) | |
| 0.61000 | W/m K | (26) | |
| 2.50000 | W/m K | (2) | |
| 0.50000 | m/s | (26) | |
| 0.01270 | m | (26) | |
| 0.01535 | m | (26) | |
| 2000.00 | W/m2 K | (28) | |
| 4000.00 | K | (6) |
| l | a | Nodes | Elements | |||
|---|---|---|---|---|---|---|
| (m) | (m) | (m) | (m) | (W/m2 K) | No. | No. |
| 0.200 | 0.200 | 0.0127 | 0.01535 | 39.2562 | 4734 | 3955 |
| 0.100 | 0.100 | 0.0127 | 0.01535 | 50.4267 | 21,443 | 18,588 |
| 0.050 | 0.050 | 0.0127 | 0.01535 | 70.4829 | 97,787 | 87,300 |
| 0.036 | 0.036 | 0.0127 | 0.01535 | 86.8548 | 145,380 | 132,225 |
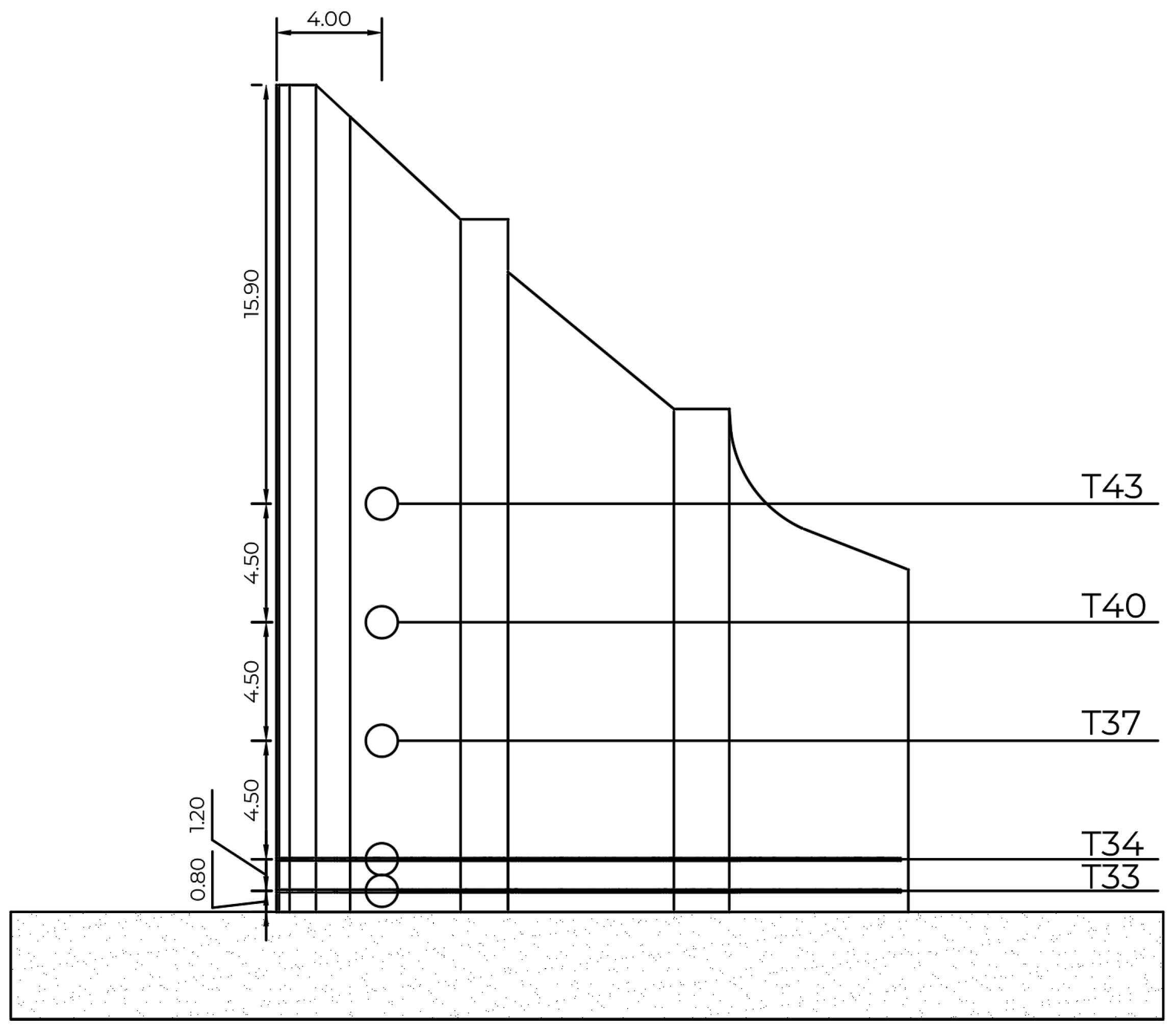
| Node | X-Axis | Y-Axis | Z-Axis | Thermocouple (TC) |
|---|---|---|---|---|
| 928,420 | 4.00 | 0.00 | 0.80 | 33 |
| 913,294 | 4.00 | 0.00 | 2.00 | 34 |
| 882,914 | 4.00 | 0.00 | 6.50 | 37 |
| 852,534 | 4.00 | 0.00 | 11.00 | 40 |
| 822,154 | 4.00 | 0.00 | 15.50 | 43 |
| Parameter | Value | Unit | Equations |
|---|---|---|---|
| l | 0.10000 | m | (28) and (32) |
| a | 0.10000 | m | (26) and (32) |
| b | 0.10000 | m | (26) and (32) |
| 0.20000 | s | (30) | |
| 1000.00 | kg/m3 | (32) | |
| 933.000 | J/kg K | (2) | |
| 4192.00 | J/kg K | (32) | |
| 870.000 | J/kg K | (2) | |
| 2.33000 | W/m K | (2) and (26) | |
| 0.58000 | W/m K | (26) | |
| 60.0000 | W/m K | (26) | |
| 2.50000 | W/m K | (2) | |
| 0.50000 | m/s | (26) | |
| 0.01270 | m | (26) | |
| 0.01535 | m | (26) | |
| 99.6500 | W/m2 K | (26) | |
| 59.6000 | W/m2 K | (28) | |
| 4000.00 | K | (6) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fraga, I.A.; Silva, A.B.C.G.; Fairbairn, E.M.R. A Mesoscopic Approach for the Numerical Simulation of a Mass Concrete Structure Construction Using Post-Cooling Systems. Buildings 2024, 14, 3232. https://doi.org/10.3390/buildings14103232
Fraga IA, Silva ABCG, Fairbairn EMR. A Mesoscopic Approach for the Numerical Simulation of a Mass Concrete Structure Construction Using Post-Cooling Systems. Buildings. 2024; 14(10):3232. https://doi.org/10.3390/buildings14103232
Chicago/Turabian StyleFraga, Igor A., Ana B. C. G. Silva, and Eduardo M. R. Fairbairn. 2024. "A Mesoscopic Approach for the Numerical Simulation of a Mass Concrete Structure Construction Using Post-Cooling Systems" Buildings 14, no. 10: 3232. https://doi.org/10.3390/buildings14103232
APA StyleFraga, I. A., Silva, A. B. C. G., & Fairbairn, E. M. R. (2024). A Mesoscopic Approach for the Numerical Simulation of a Mass Concrete Structure Construction Using Post-Cooling Systems. Buildings, 14(10), 3232. https://doi.org/10.3390/buildings14103232






