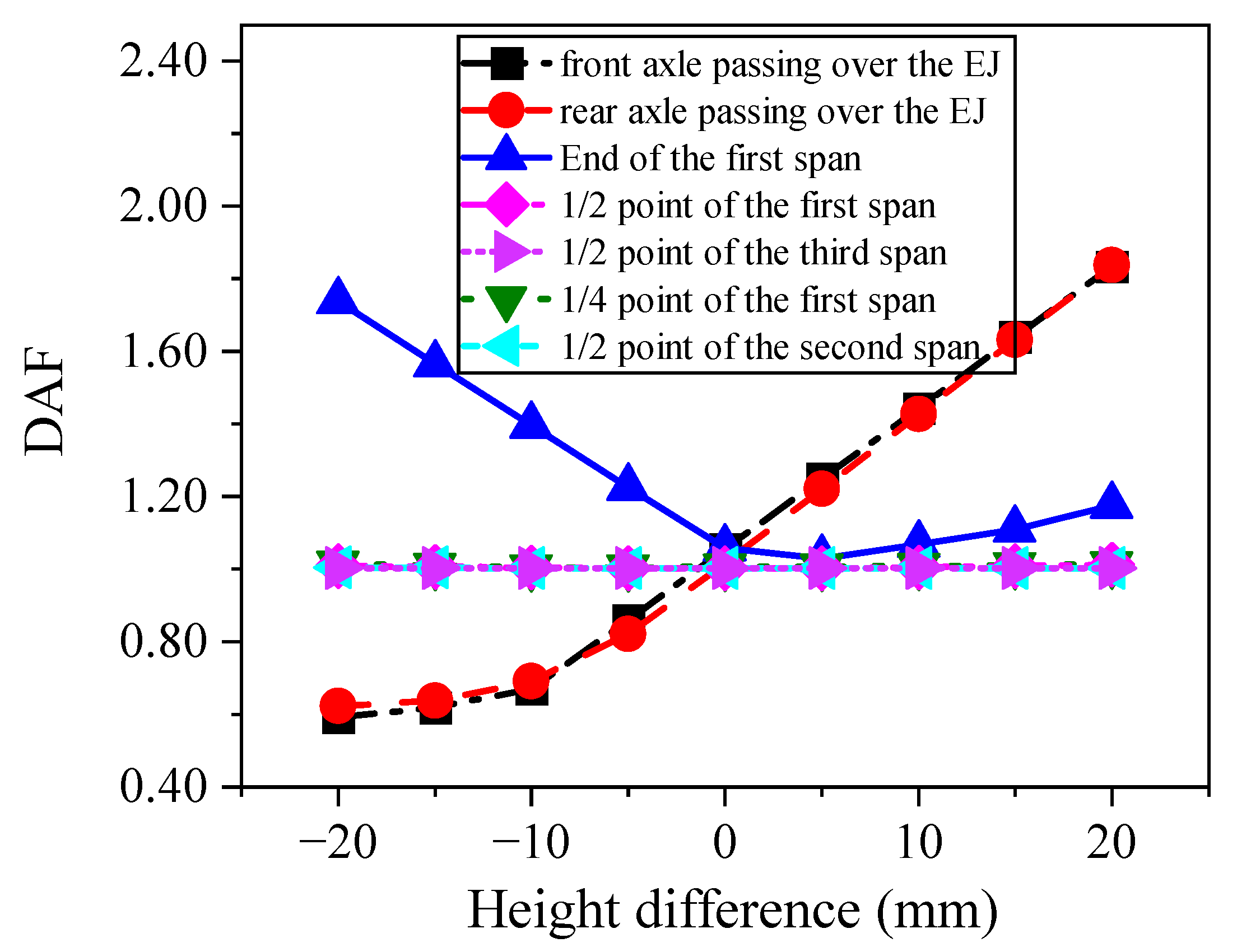
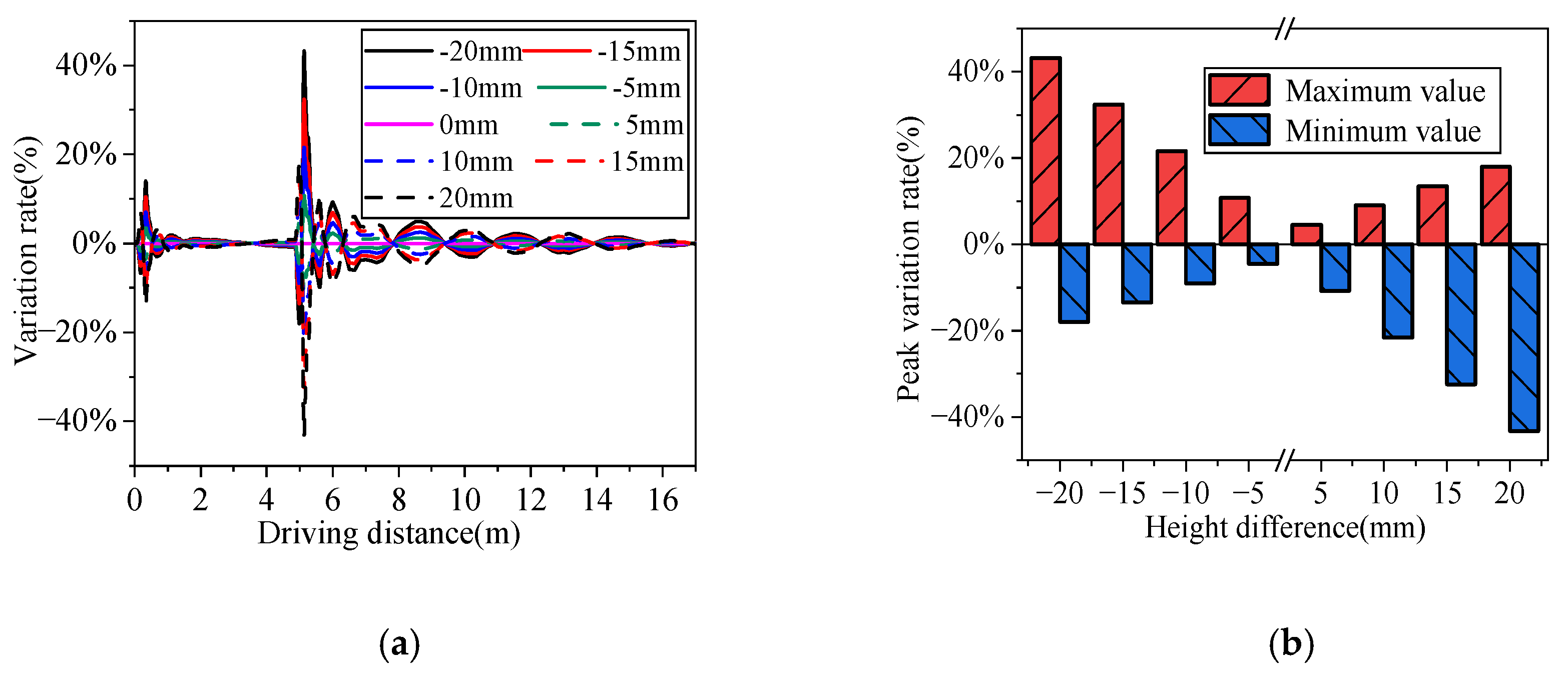
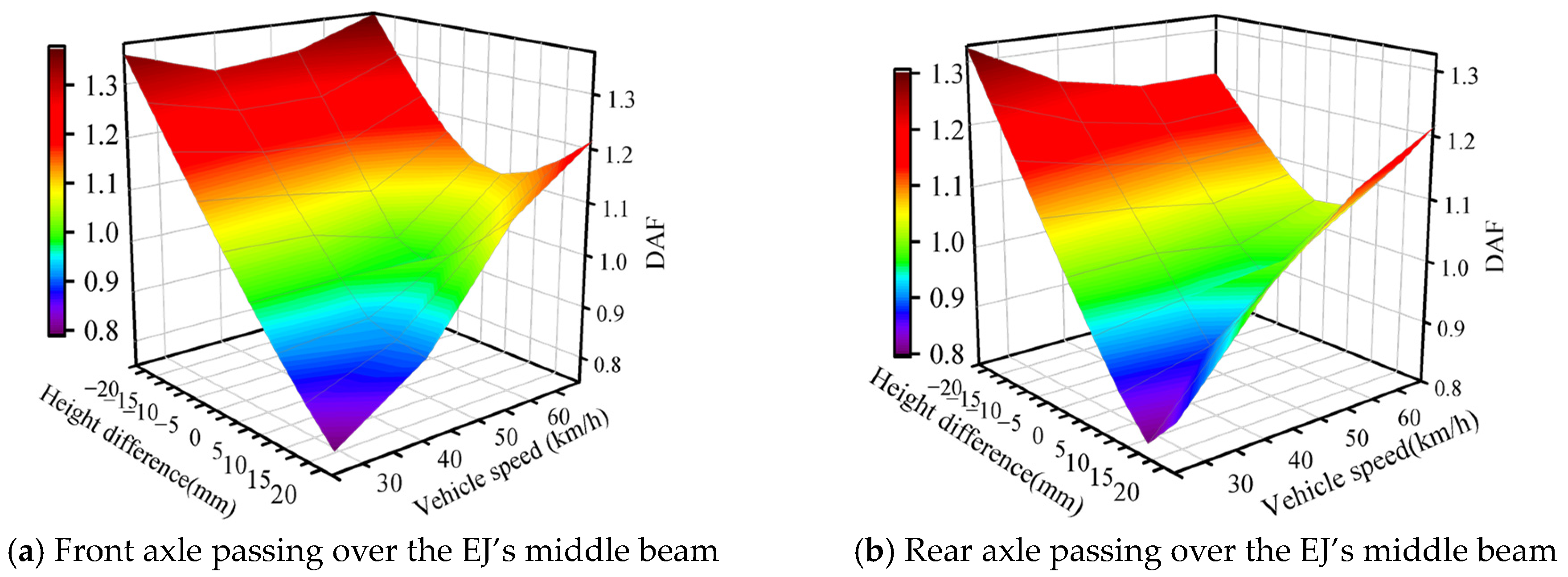
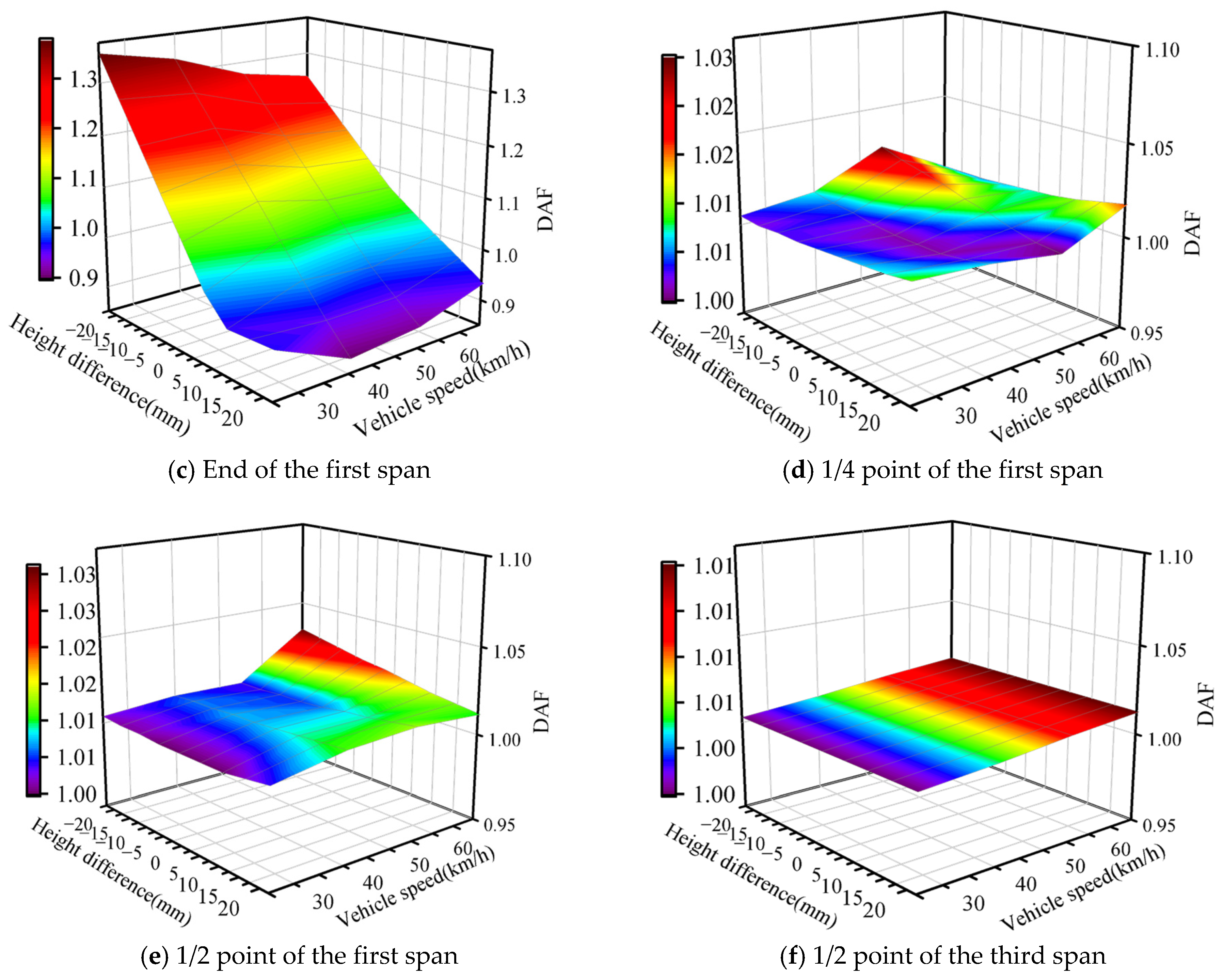
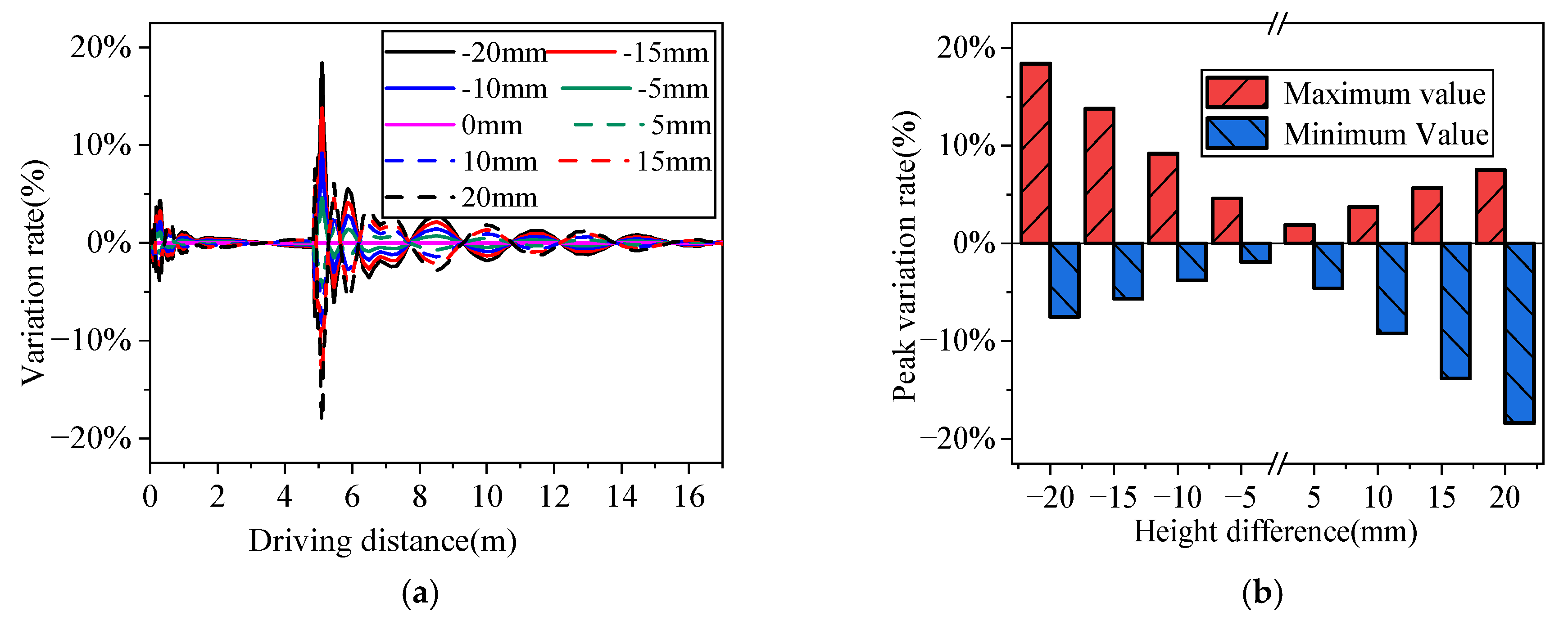
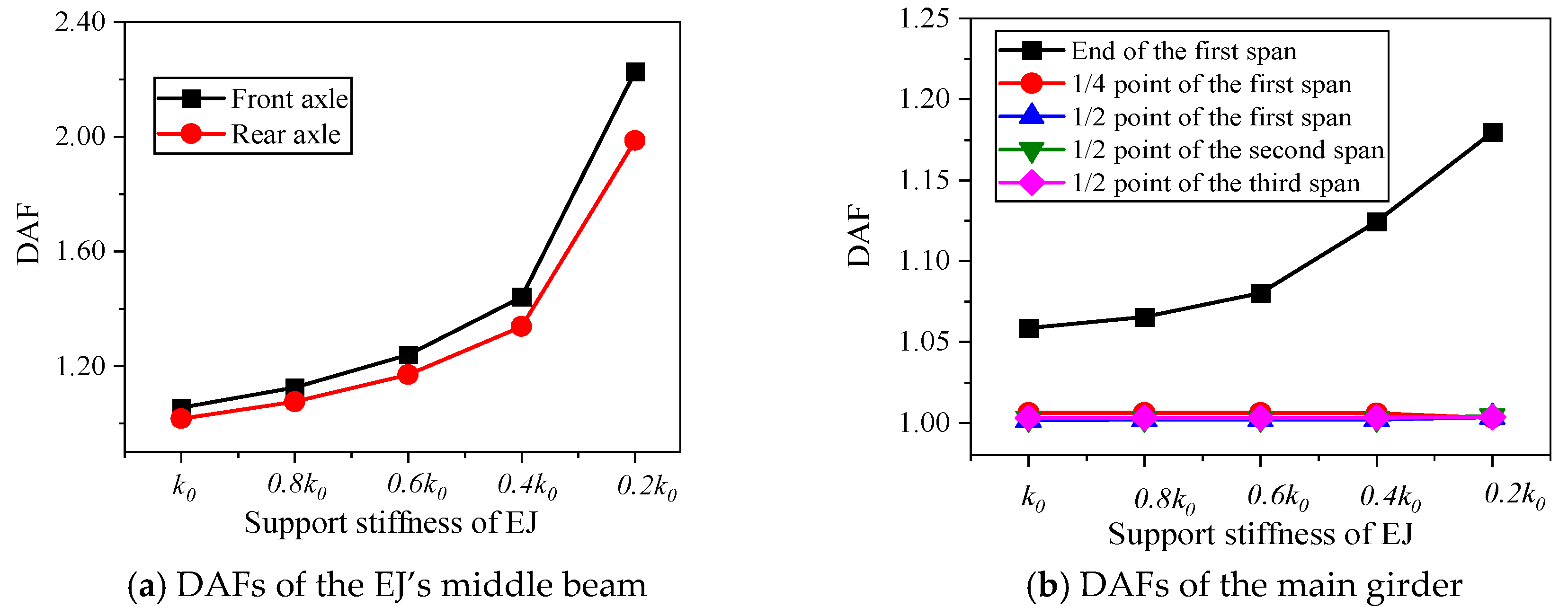
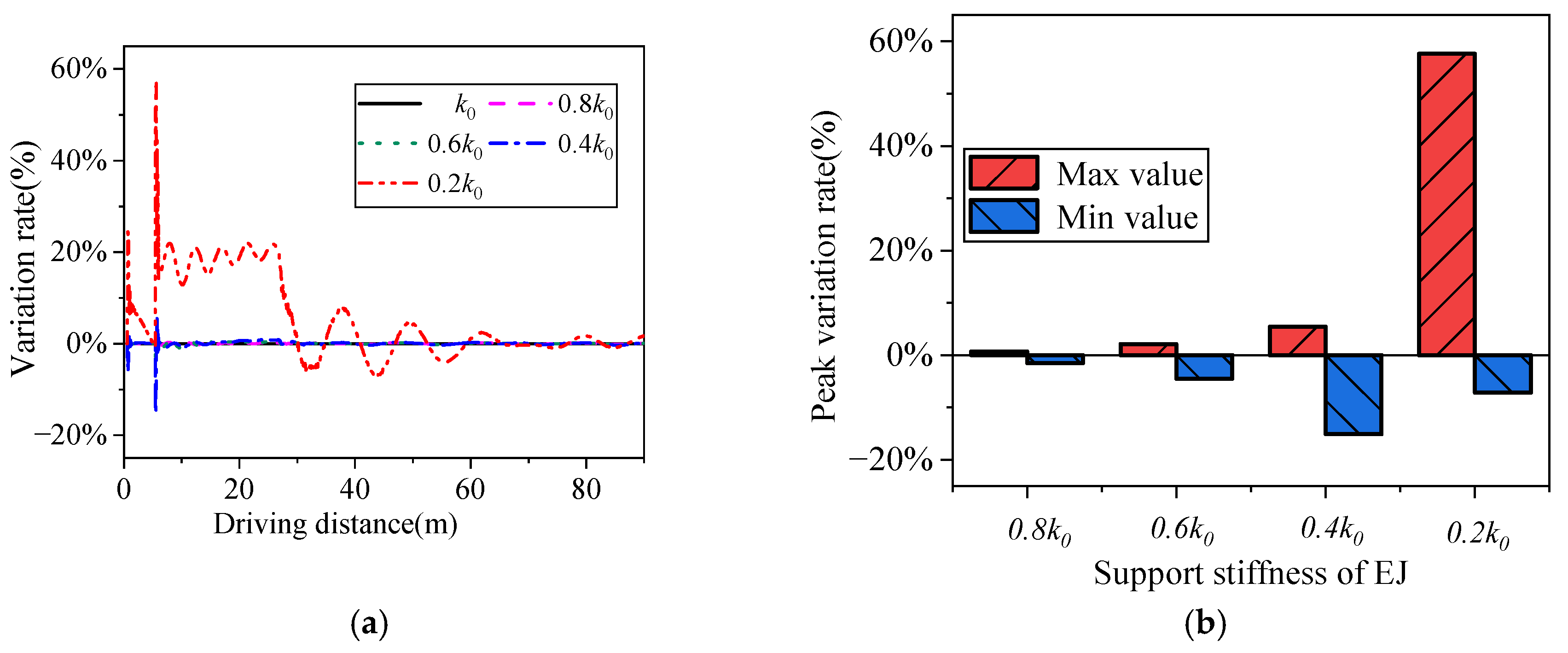
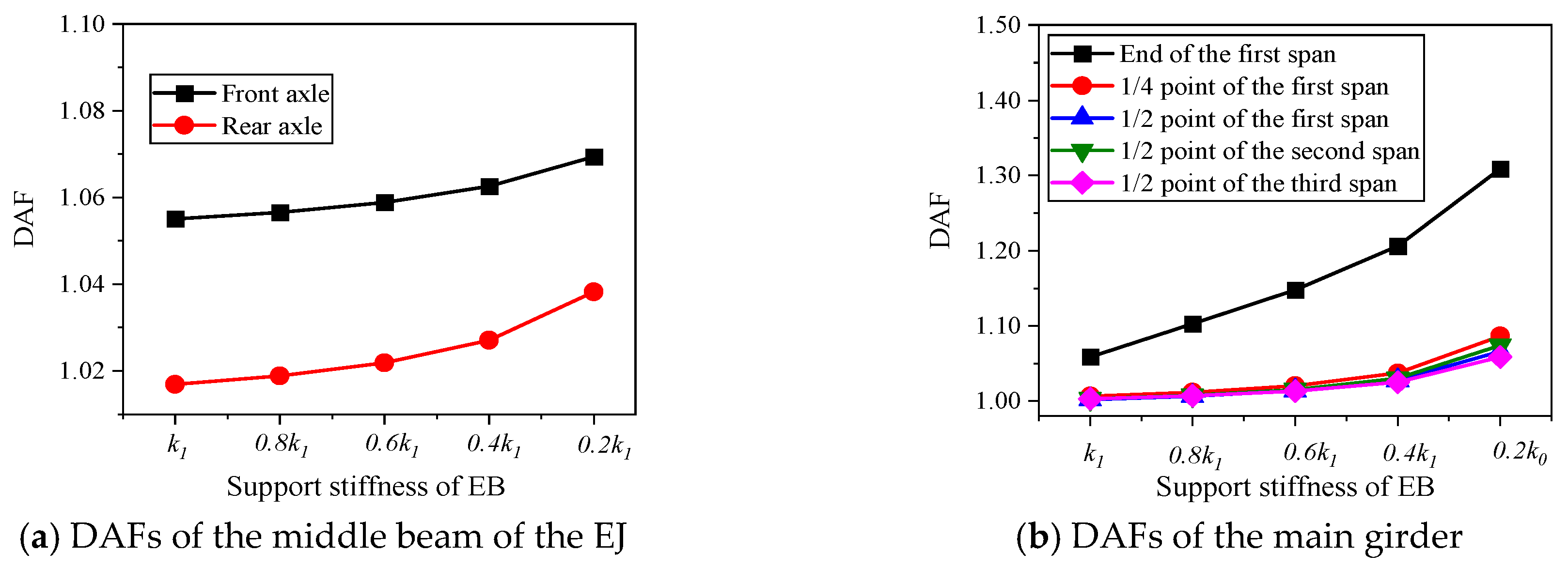
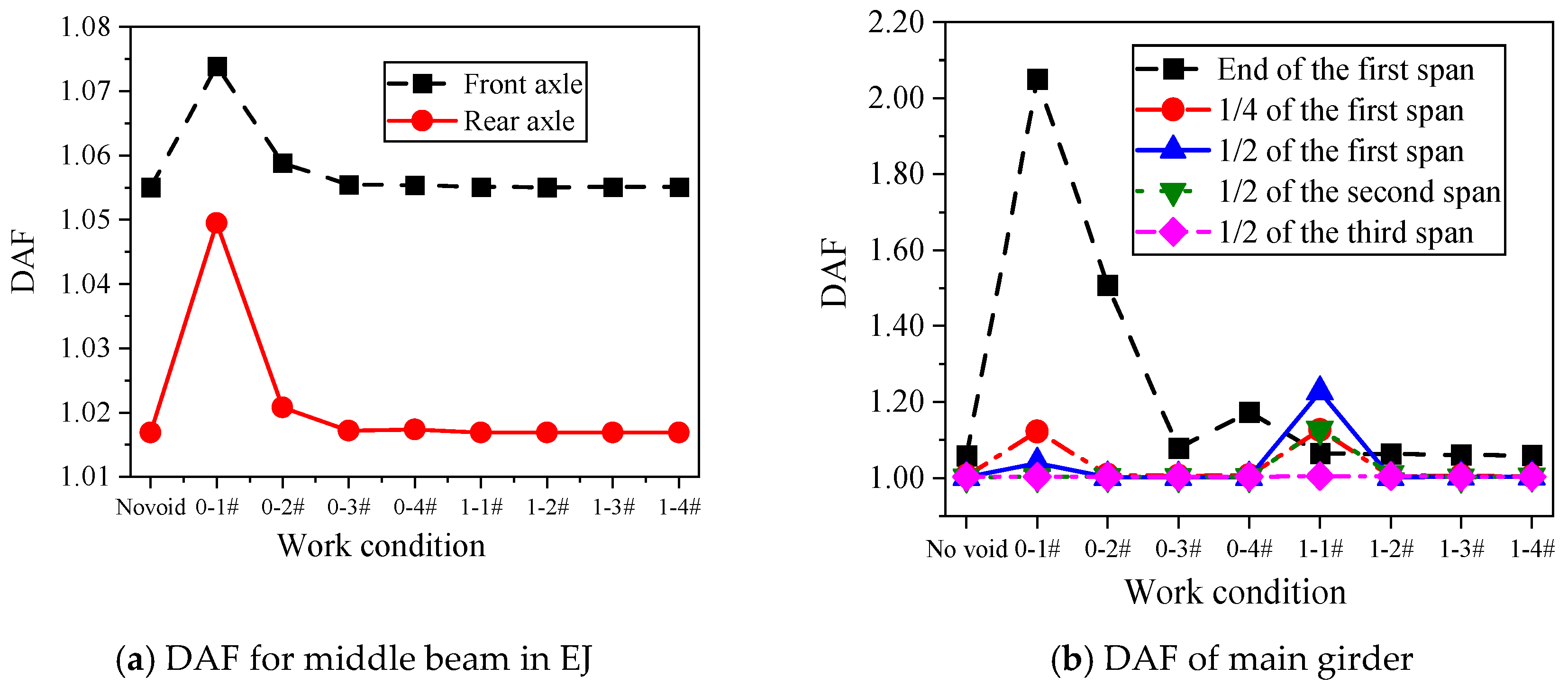
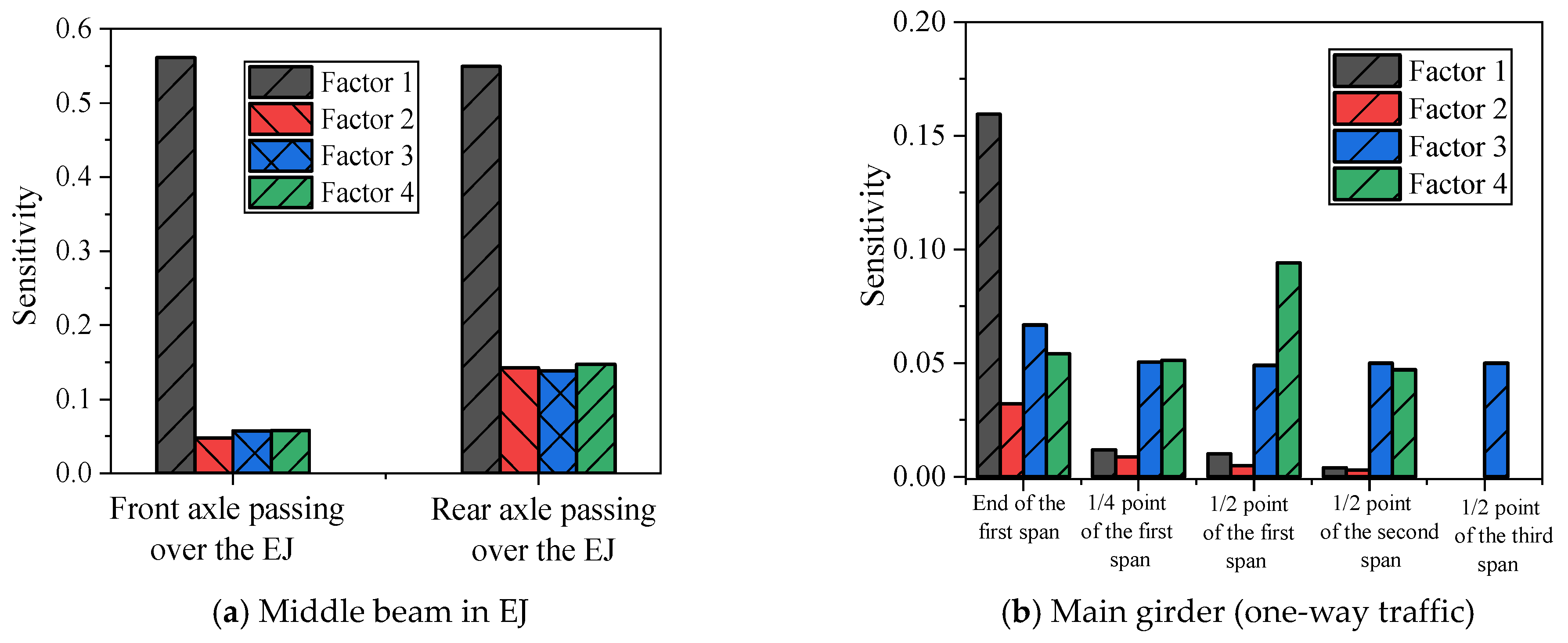
2.1. Without Considering E-B Parameters
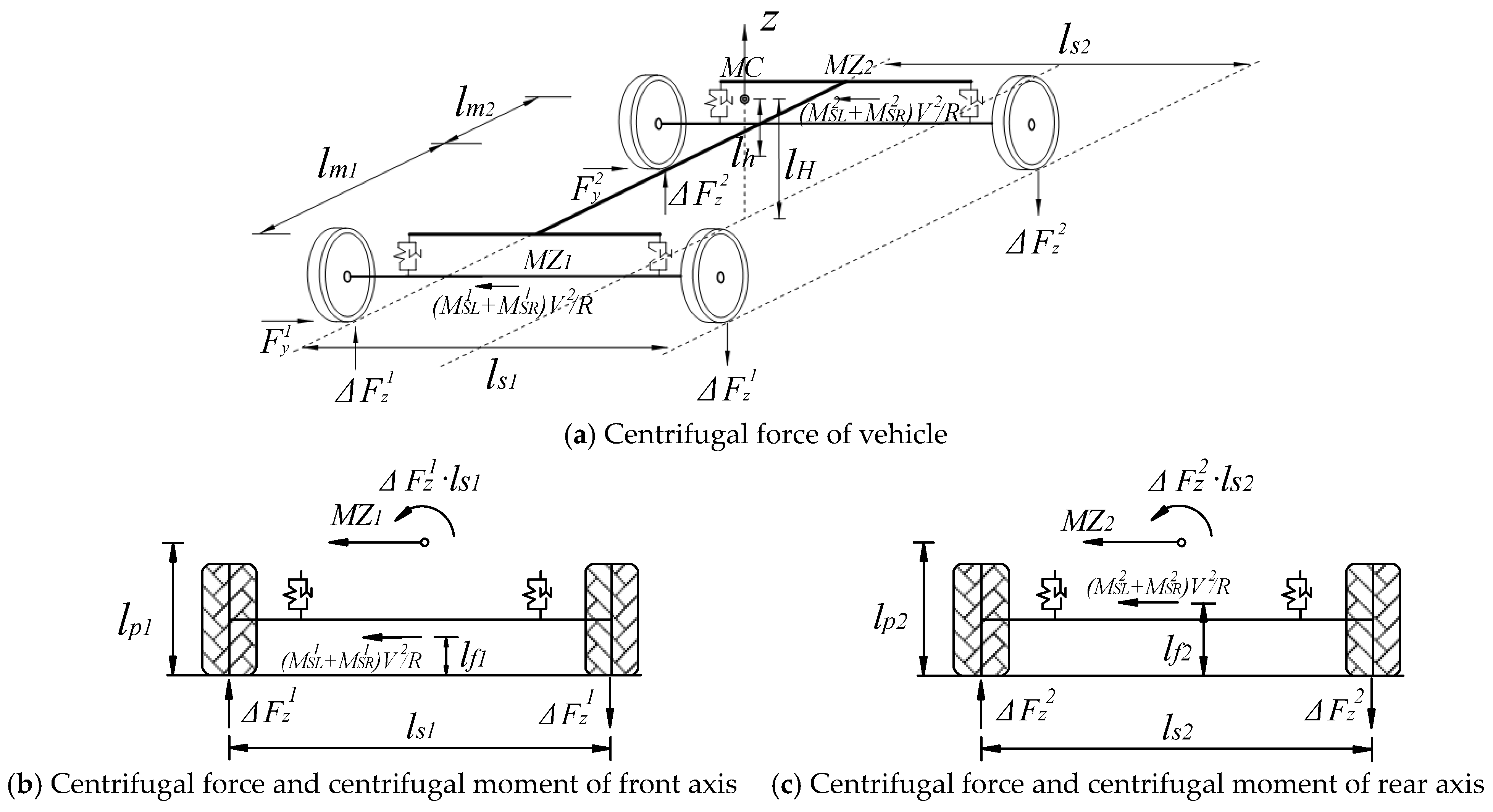
The vehicle body was equated to a rigid rod which was supported by the front
MZ1 and rear
MZ2 axle transient centers. The rigid rod was then supported by the vertical springs of the front and rear suspensions. The effect of centrifugal force on the wheel loads is shown in
Figure 1.
The vehicle model moves in a uniform circle motion with a constant speed
V. A centrifugal force
MvrV2/
R acts on the center of mass,
MC, of the vehicle body with mass
Mvr, where
R is the radius of curvature of the vehicle’s path under uniform circular motion. This centrifugal force produces a moment
MvrV2lh/
R around the instantaneous axis, where
lh is the distance from
MC to the instantaneous center. Since the body rotates around the instantaneous axis, its
MC experiences a lateral displacement
lhsin
χ that generates an additional moment
Mvrglhsin
χ ≈
Mvrglhχ. The total moment is given by Equation (1) as
where
χ is the roll angle of the vehicle body caused by the centrifugal moment. Alternatively, the moment
Tvrm is transmitted to the axle via the suspension spring. Given that
Kv1 and
Kv2 represent the roll angle stiffnesses of the front and rear axles, respectively, the moment
Tvrm can also be expressed by Equation (2) as
By combining Equation (1) with Equation (2), the roll angle of the vehicle body can be determined as shown in Equation (3).
Therefore, the spring moments of the front and rear axles can be determined, respectively as:
where
Tvrm1 and
Tvrm2 represent the spring moments of the front and rear axles, respectively. The centrifugal force is distributed to two instantaneous centers via the position of the center of mass. In other words, the front and rear axles distribute the centrifugal force as
MvrV2lm2/[
R(
lm1 +
lm2)],
MvrV2lm1/[
R(
lm1 +
lm2)], respectively.
The change in wheel load caused by centrifugal force is discussed using the front axle as an example. The wheel load difference
and the moment generated by the force arm
ls1 (the distance between the left and right wheel centers of the front axle) are balanced by the sum of the three moments: (a) the spring moment
Tvrm1 of the front axle; (b) the centrifugal force
MvrV2lm2/[
R(
lm1 +
lm2)] distributed to the front axle and its corresponding moment formed by its force arm
lp1 (the distance from the instantaneous center of the front axle
MZ1 to the bridge deck); (c) The moment formed by the centrifugal force acting on the front axle
and its corresponding force arm
lf1 (the distance from the center of mass of the front axle
MS1 to the bridge deck). Therefore, the aforementioned moment–balance relationship can be expressed as follows:
Similarly, by considering the rear axle as an isolated system and applying the moment–balance equation, the following relationship can be established:
By combining Equations (4)–(7), the difference between the actual wheel load and the static wheel load can be expressed as follows:
where
and
denote the differences in the vertical wheel loads generated by the front and rear axles relative to the static load, respectively;
and
represent the differences in the lateral wheel load generated by the front and rear axles relative to the static load, respectively; and the subscripts
L and
R refer to the left and right wheels, respectively. Additionally, as the vehicle travels along a curved path, the centrifugal forces generated by the front and rear axles of the vehicle are given as follows:
Assuming that the vehicle model is undergoing uniform circular motion on a curved girder bridge, with a constant traveling speed
V and curvature radius
R, it follows that the magnitudes of the vertical and lateral loads induced by centrifugal force do not vary with the position of the vehicle. Rather, only the direction of the force changes as the position of the vehicle changes, while remaining constant relative to the fixed coordinate system of the vehicle model. Consequently, taking into account the effects of centrifugal force, the force applied by the left wheel to the bridge can be represented as follows:
where the superscript
C indicates that the effect of centrifugal force has been considered. The
nth-order modal force
applied by the left wheel to the bridge considering the influence of centrifugal force can be represented as follows:
The equilibrium equation of vehicle–bridge coupling vibration, taking into account the effects of centrifugal force, can be presented as:
Within this equation, the load vector exerted by the vehicle on a curved bridge can be represented as follows:
In summary, the equilibrium equation for vehicle-bridge coupling vibration for a curved girder bridge and taking into account the effects of centrifugal force has been obtained. On this basis, further development can be undertaken to derive the equilibrium equation of vehicle-curved bridge coupling vibration considering E-B parameters.
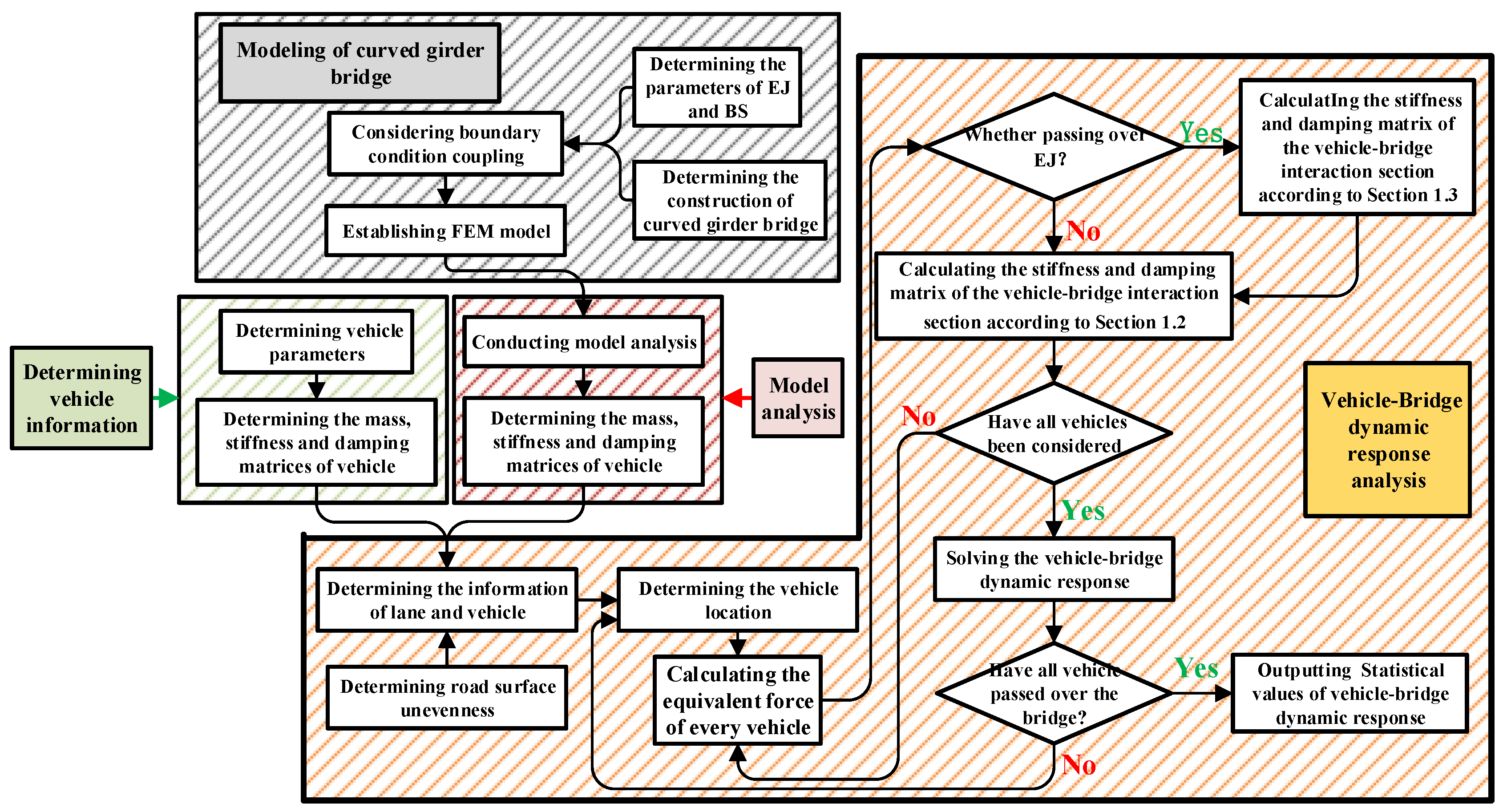
2.3. Flow Chart of the Analysis Method
The flow chart of the analysis method for vehicle–joint (bearing)–bridge coupling vibration considering centrifugal force is shown in
Figure 2. As shown in
Figure 2, the proposed analysis method for vehicle–joint–bridge coupling vibration that takes into account centrifugal force mainly involved three steps: Step (a), conducting numerical modeling of a curved girder bridge with EJs and EBs; Step (b), determining the modal information of a curved girder bridge with EJs and EBs, as well as vehicle parameters; and Step (c), calculating the coupled dynamic response of the vehicle–joint (bearing support)–bridge system. The detailed descriptions of the analysis method are as follows.
For Step (a), a numerical model of a bridge with EJ and EB was constructed in basis of a finite element analysis platform, and the material parameters (e.g., elastic modulus, density, and Poisson’s ratio), geometrical dimensions, and the basic design parameters of EJ, EB, and a main girder were considered in detail. On this basis, the boundary conditions of the numerical model need to be clarified through testing or design parameters. For Step (b), the modal information of a curved girder bridge with EJ and EB, as well as vehicles, was obtained on the basis of a refined finite element model and simplified vehicle model, respectively, including the mass, stiffness and the damping matrix of the EJ, EB, main girder, and vehicle. For Step (c), based on
Section 2.1 and 2.2, the equilibrium equation of vehicle–joint–bridge coupling vibration that takes into account centrifugal force was used to calculate the dynamic response of the system. This analysis method was of great significance for investigating vehicle-joint-bridge coupling vibration, taking into account centrifugal force.
2.4. Method Validation
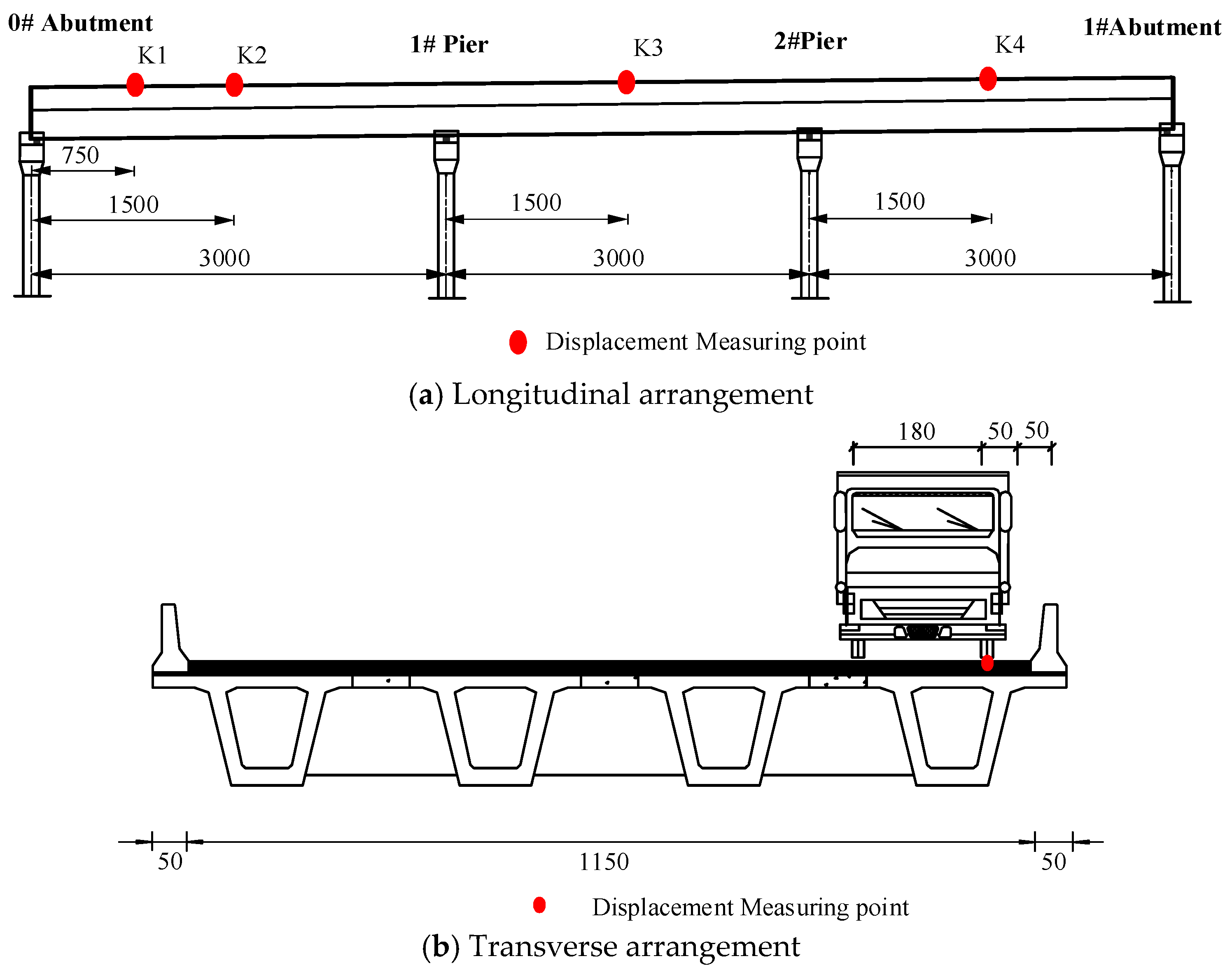
To validate the proposed method, the basic dynamic characteristics and vehicle-induced dynamic response of a curved continuous girder bridge were tested. The prototype bridge was a continuous curved prestressed concrete girder bridge, shown in
Figure 3. The main girder of the bridge was made of four prestressed concrete single-box girders. The span arrangement of the bridge was 3 × 30 m. The total width of the bridge deck was 12.5 m. The concrete grade of the main girder was C50. The GQF-MZL160 double-joint modular expansion joint was installed at the beam end of the main girder. The bearing support (BS) of the bridge was a basin rubber bearing with JPZ series. The materials of the side beam, middle beam and support beam of the EJ were 16 Mn steel. The longitudinal displacement measuring points were arranged at the 1/4 point (K1) and 1/2 point (K2) of the first span, the 1/2 point (K3) of the second span, and the 1/2 point (K4) of the third span. The transverse position of each measuring point was 1 m from the outside of the deck slab. The measuring points are shown in
Figure 4. Before the field testing, we inspected the technical condition of the EJ, EB, and main girder. The main detected parameters of the bridge are shown
Table 1.
As shown in
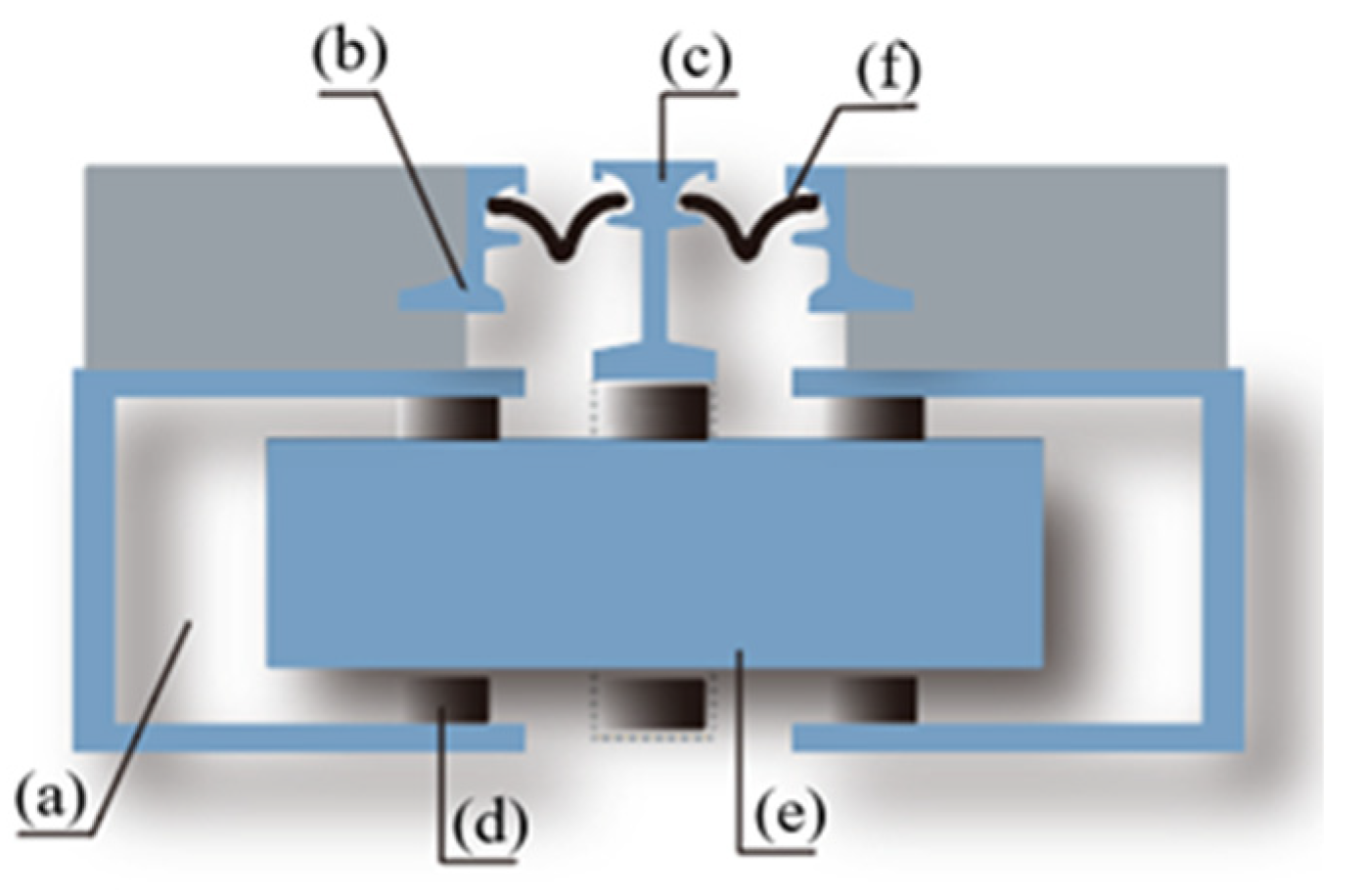
Table 1, in general, the technical state of the EJ, EB, and main girder was equivalent to the design state. Moreover, we can hardly adjust the actual parameters of EJ, EB, and main girder in a practical testing. In other words, during the field testing, the parameters of EJ, EB, and main girder were usually considered as constant values. Therefore, the parameters of the finite element model were selected as the same as the design parameters during verification of the analysis model. The ANSYS platform was used to establish a refined 3D analysis model of the curved girder bridge containing EJs and BSs. The concrete box girder of the main bridge was simulated by the Solid65 element, and the BSs were established by a Combin14 element with variable stiffnesses. The middle beam, side beam, and support beam of the EJ were all simulated by the Beam188 element. The elastic support connection between the middle beam and the support beam was also simulated by the Combin14 element. The support beam was coupled with the corresponding node of the main girder to simulate the actual boundary of the support beam. The prototype of the EJ model used in this paper was a double-seam modular expansion joint (GQF-MZL160), which has been widely used in various types of bridges. This type of expansion joint included a support box (a), a side beam (b), a central beam (c), a compression support (d), a support beam (e), waterproof sealing (f), and other auxiliary components, as shown in
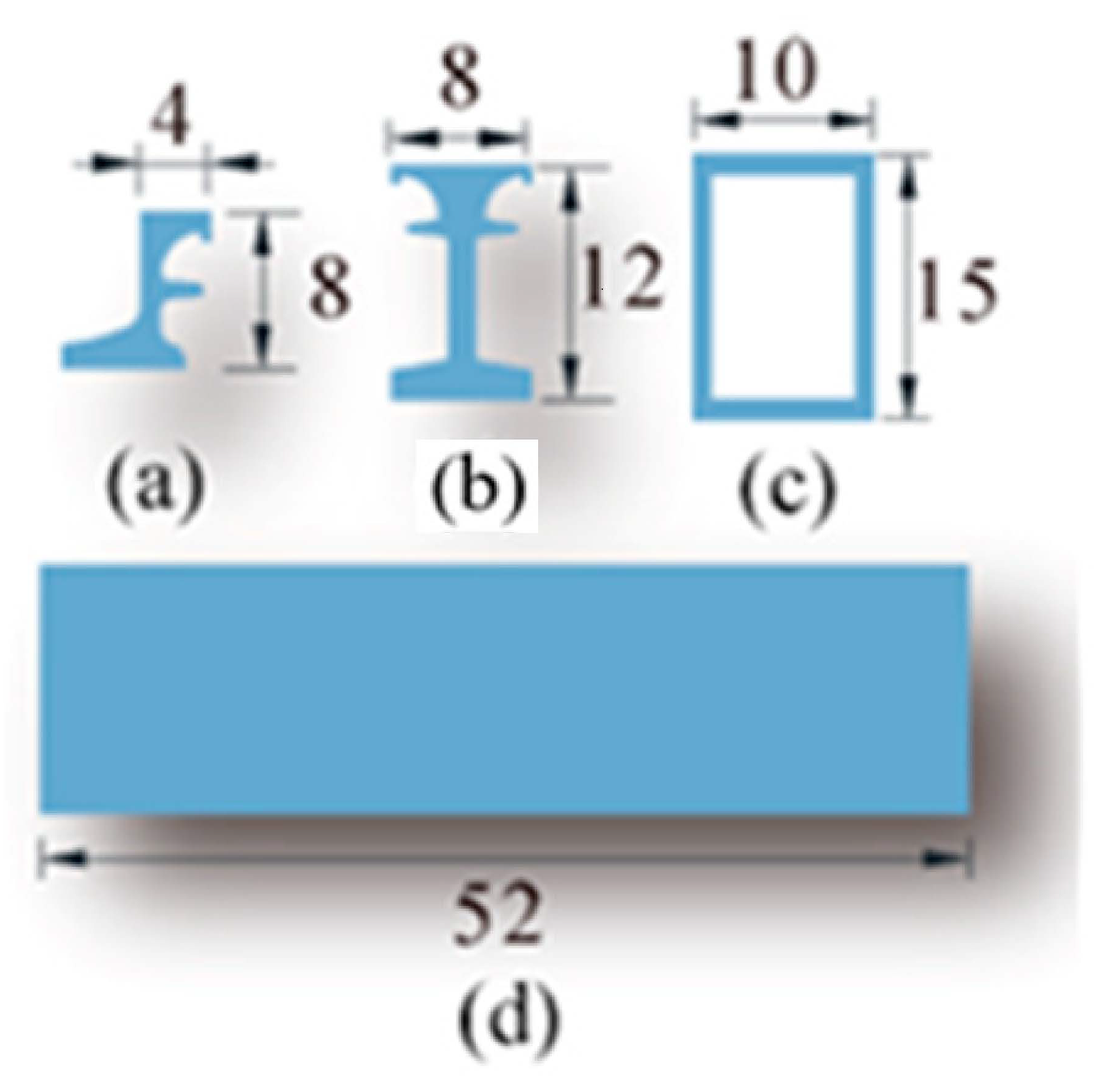
Figure 5. The main component parameters of this type of EJ are shown in
Figure 6, including a side beam (a), a central beam (b), and support beams (c and d). It should be noted that the parameters of the EJ model were strictly determined according to the actual design parameters of the prototype EJGQF-MZL160, including Young’s modulus, shear modulus, material density, Poisson’s ratio, and so forth. The detail parameters of GQF-MZL160 and basin rubber bearing are shown in
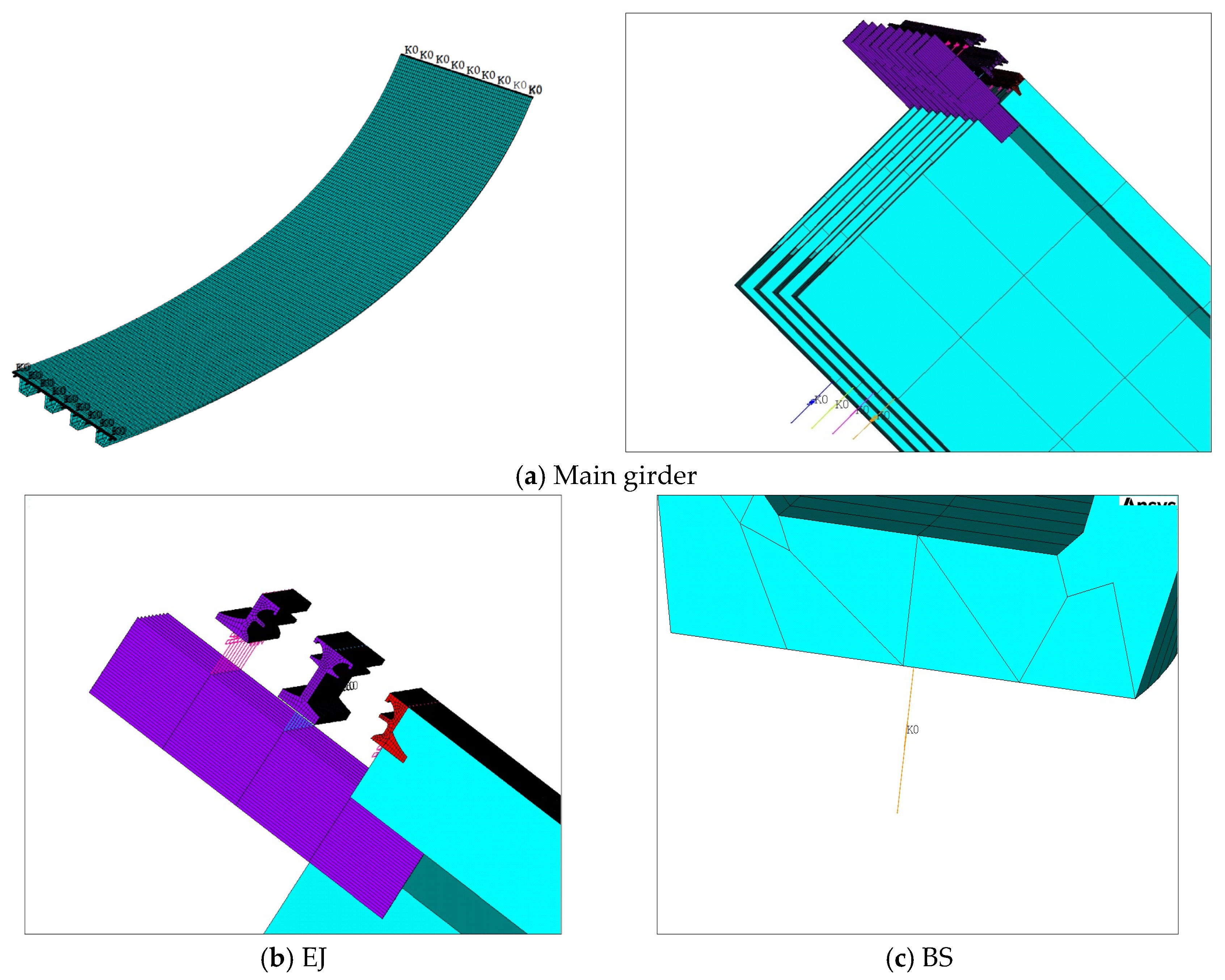
Table 2. The finite element model of the system is shown in
Figure 7.
The modal information of the finite element model was obtained through the subspace iterative method, given in
Table 3. As shown in
Table 3, the errors of the first three vibration frequencies between the calculated and tested results were in the range of 2.26~6.32%, which indicated that the refined finite element model can well reflect the dynamic characteristics of the prototype bridge. Meanwhile, the numerical model can be applied to the subsequent numerical analysis.
Through the trial calculations, the local vibration frequencies of the EJ were mainly in the range of 82 Hz~107 Hz. The first 20 vibration modals of the main girder and 50 vibration modals of the EJ were extracted for the subsequent analysis. A two-axle truck (total weight of about 283 kN) was selected as the loading vehicle. The truck was loaded at a speed of 30 km/h along the outer lane (the outside wheel was 0.5 m from the outside of the deck slab). The specific parameters of the vehicle model are described in the literature [
31].
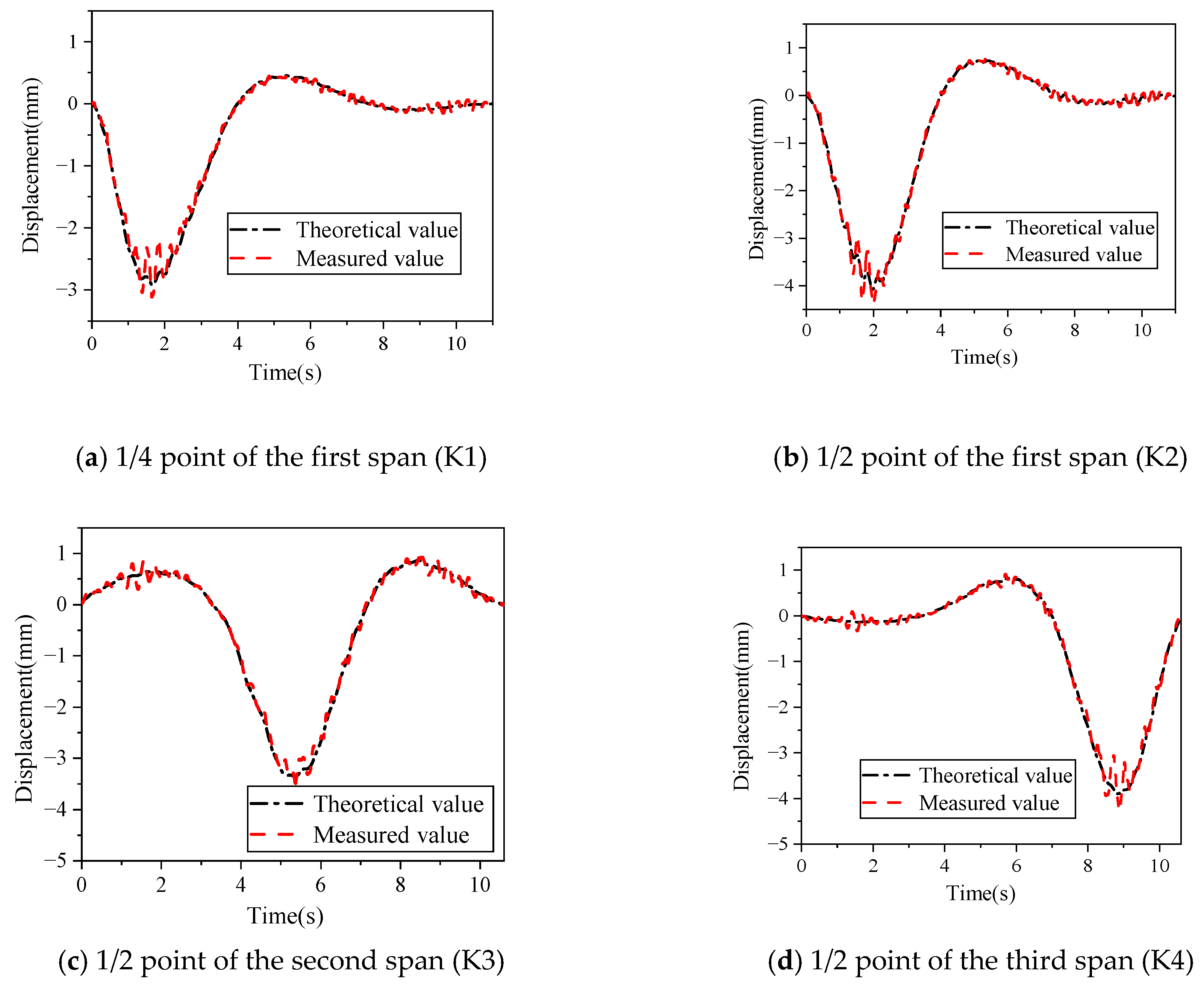
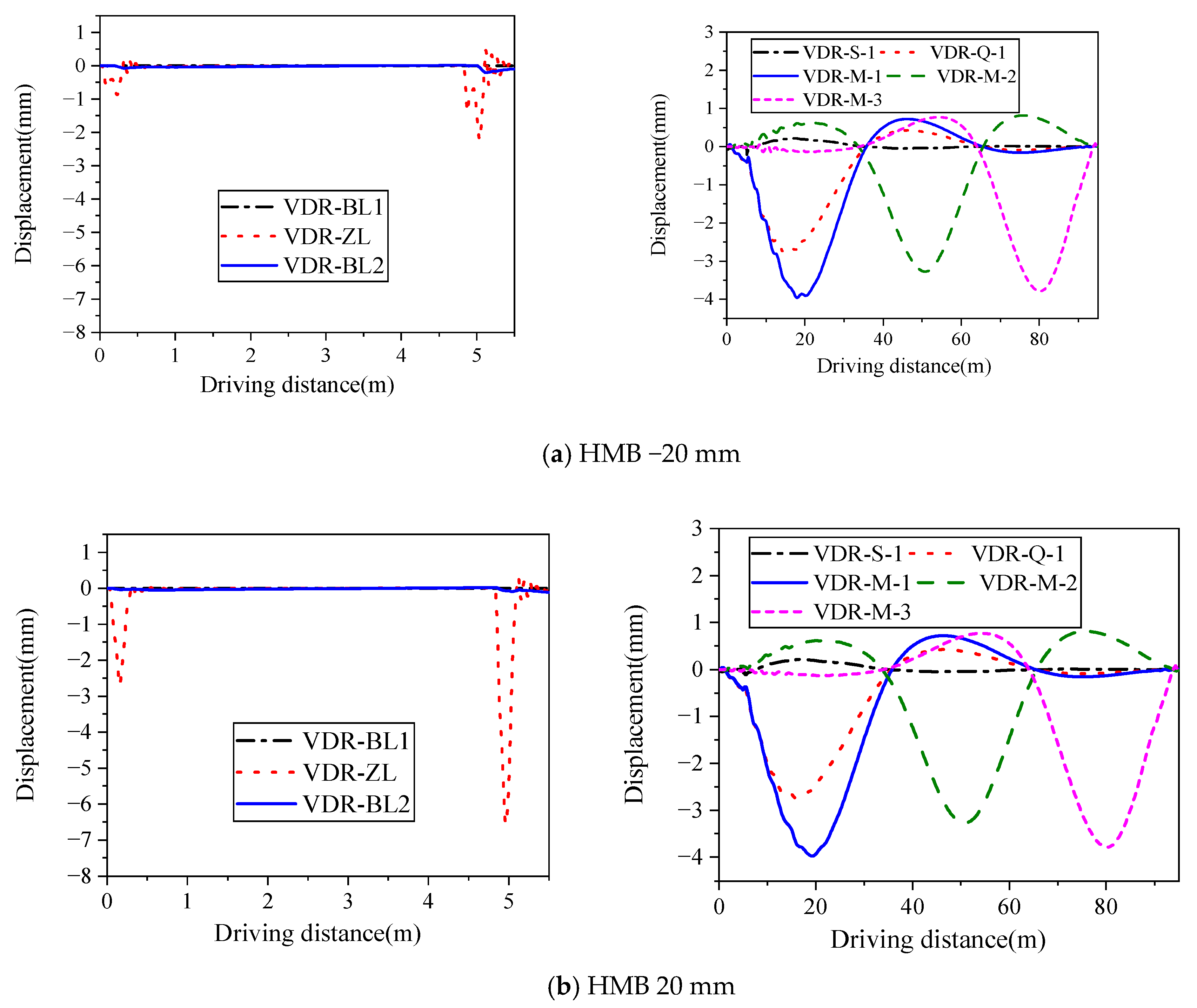
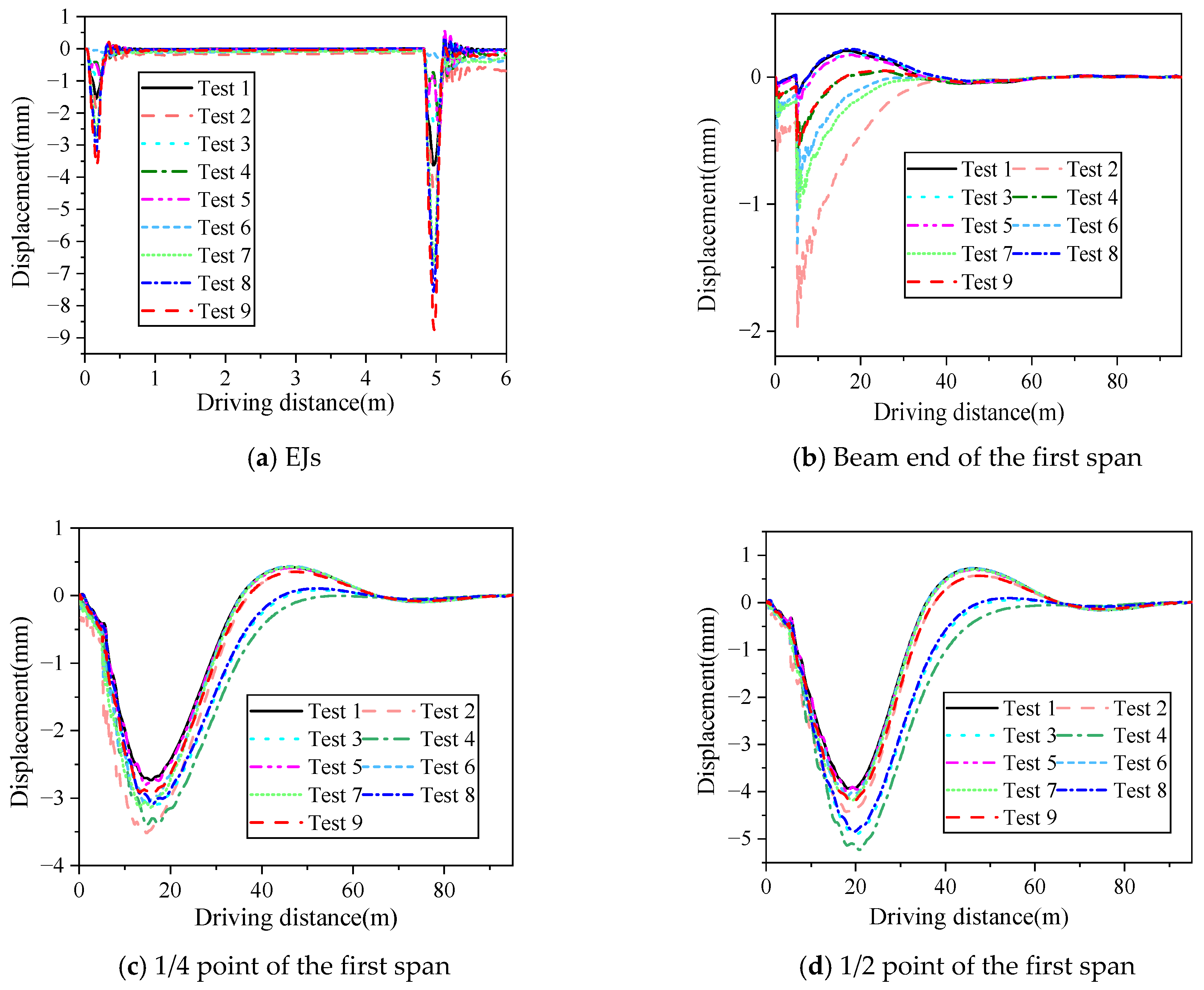
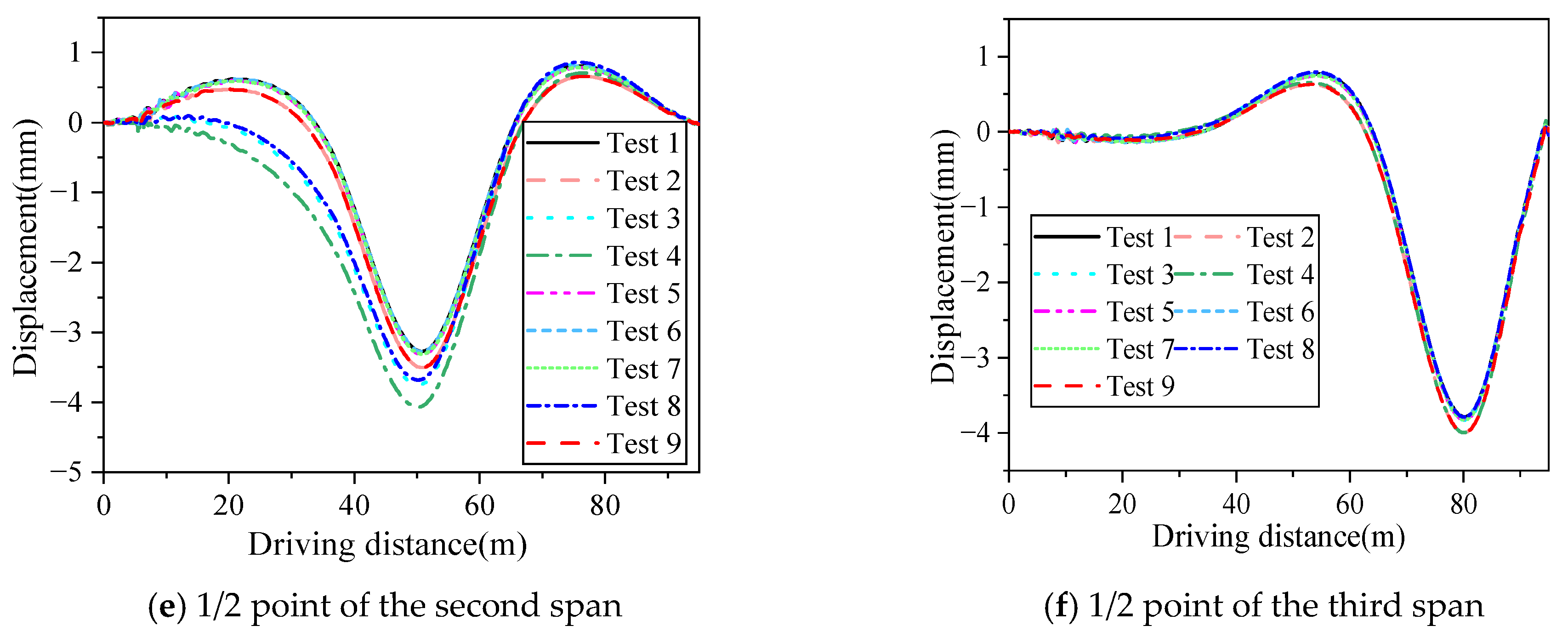
Figure 8 shows the comparison of the numerical and field-testing results of the displacement responses of the measuring points. The comparison of the peak vertical displacements of the typical measuring points is shown in
Table 4.
As shown in
Figure 8 and
Table 4, the calculated values fit well with the measured values, and the errors between the measured and calculated results were in the range of 4.01~8.24%. Because there were some differences between the actual parameters and the numerical parameters, including EJ, BS, and vehicle parameters. The numerical analysis results can be regarded as effective to some extent. Thus, the proposed method can be applied to analyze the vibration responses of the vehicle–joint (support)–bridge coupling taking into account the centrifugal force for curved girder bridges. It should be noted that the vehicle–bridge coupling vibration was characterized as nonlinear, random, and time-variable, and it was influenced by a variety of factors. The road (bridge deck) roughness was deemed as an extremely important influencing factor on the dynamic response of vehicle–bridge coupling vibration. The road (bridge deck) roughness always led to random variation in vehicle load (excitation of vehicle-induced vibration of the bridge), which in turn affected the dynamic response of the bridge. Therefore, the fluctuation of vehicle-induced vibration of the bridge increased with the deterioration of road (bridge deck) roughness, as shown in
Figure 8 [
41].