Application of Stochastic Finite Element Modeling to Reinforced Lightweight Concrete Beams Containing Expanded Polystyrene Beads

Abstract

Limited investigations have evaluated the effect of expanded polystyrene (EPS) beads on the structural lightweight concrete properties. EPS offers many features compared to natural or artificial lightweight aggregates including the elimination of aggregate saturation prior to concrete batching, ability to be fabricated on site, consistency in size and quality, and reduced cost. The main objective of this paper is to assess the suitability of finite element (FE) modeling based on deterministic and stochastic approaches to predict the shear strength behavior of reinforced concrete (RC) beams containing EPS additions. Test results showed that the experimental load-deflection properties recorded at failure can be well reproduced using both FE approaches. Nevertheless, the damaged-zone distribution and crack patterns that occur during the loading stages of RC beams cannot be approximated using the deterministic FE approach. In contrast, the stochastic method was quite suitable as it accounted for the concrete heterogeneity and altered spatial mechanical properties (such as compressive strength, splitting tensile strength, and Young’s modulus) due to EPS additions. Such data can be of interest to civil engineers seeking to predict the failure patterns and performance of structural lightweight members while reducing the time and resources needed to account for the concrete’s strength variability during experimental testing.

1. Introduction

Expanded polystyrene (EPS) is a plastic polymeric material having a closed cell structure that expands under the action of air pressure and/or expansive agents. It was discovered after some polymerization and vacuuming processes in a substance called styrol-styrene in 1839 [1]. EPS’ lightweight and hydrophobic properties are particularly suitable for insulation and packaging applications, as well as for prefabricated construction members such as sandwich panels [2,3,4,5].

Lightweight EPS-based concrete exhibits a high strength-to-weight ratio together with improved ductility, tensile strains, and thermal insulation [6,7,8,9,10]. ACI 213R-03 [11] states that the optimum compressive and splitting tensile strengths for lightweight concrete could lie within the ranges 21–35 and 2–4 MPa, respectively. Chen et al. [12] found that the 28-day compressive strength decreased from 59.2 MPa for EPS-free concrete to 22.1 and 10.6 MPa for mixtures containing 25% and 55% EPS, respectively. The corresponding density dropped from 2435 to 1820 and 875 kg/m³, respectively while the splitting tensile strength varied from 8.7 to 2.31 and 1.32 MPa, respectively [12]. Adeala et al. [1] reported that the size of EPS particles has a significant effect on concrete strength and ductility. The smaller the EPS grading size with lower percentages added is, the better are the mechanical properties [2,8,10]. EPS offers many benefits compared to natural or artificial lightweight aggregates (such as expanded clay, perlite, shale, or pumice), including its hydrophobic nature, which eliminates the need for aggregate saturation prior to concrete batching and minimizes the exchange of moisture with the cement paste during the hardening process [13,14,15]. Other EPS features include its spherical shape, which improves the workability of fresh concrete, consistency in size and quality, ability to be fabricated on site, and reduced cost.

Limited investigations have considered the use of EPS in structural lightweight concrete applications [1,3,16,17,18]. Nguyen et al. [17] showed that the ultimate load in reinforced concrete (RC) beams decreases as the EPS content increases, given the reduced density of the aggregate skeleton and weaker bond between the EPS and cement paste. The decrease in the beams’ cracking load and stiffness level can be overcome by a 20% increase in the longitudinal steel reinforcement ratio. Assaad et al. [3,14] reported that the bond to embedded steel bars and shear strength of RC beams without stirrups could drop by 40% and 25%, respectively, when 3 kg/m³ of EPS is added. The incorporation of 0.5% steel fibers was efficient to mitigate the detrimental effect of EPS additions and restore the previous properties because it improved the bridging effect of the RC beam properties.

Finite element (FE) modeling and mathematical regressions are often used to minimize the resources, energy, and hassle associated with the experimental testing of concrete structures [19,20,21,22]. Assaad et al. [2] modelled the behavior of sandwich EPS-based lightweight panels placed side by side and subjected to wind and seismic loading. The authors reported that the stability (i.e., bleeding and segregation) of produced EPS concrete is of paramount importance to reduce the material heterogeneity and avoid formation of weak zones, thus ensuring both the uniform distribution of stresses along the tongue-and-groove sandwich panel joints as well as good adherence along the embedded steel connectors. Nevertheless, it is to be noted that the FE modeling of concrete structures often considers a deterministic approach in which the material properties are considered constant throughout the investigated member [2]. This assumption, however, becomes unreliable especially in EPS-based concrete due to the higher number of voids and their effect on the variations of the overall mechanical and structural properties.

Stochastic FE approaches have been developed to model the behavior of heterogeneous materials, namely concrete. In fact, the heterogeneity of concrete emanates from numerous intrinsic (i.e., related to the mix design and eventual changes in material properties) and external factors (i.e., such as casting, vibration, and curing), which all variably affect the mechanical properties at the representative elementary volume [23,24,25]. The simplest approach to account for concrete variability consists of attributing to each material volume, using the Monte Carlo procedure, the mechanical properties following a given distribution and then performing the numerical simulation. Breysse et al. [26] proposed a modelization approach based on micro-structural geometry and topology using a discrete representation before performing an FE simulation. Rossi et al. [24] accounted for the initial material heterogeneity, including its splitting tensile strength and modulus of elasticity with respect to the size of the structure, in order to accurately represent crack propagation. This way, the fluctuations of the material parameters are modeled by means of discretized random fields, and the cracking process is represented using an FE discretization approach [27,28,29,30,31]. The choice of the mechanical property as a random field (i.e., tensile strength, Young’s modulus, or fracture energy), including its effect on the pre- and post-peak structural behavior, has been widely discussed [25,32,33].

This paper is the continuation of a comprehensive project undertaken to assess the performance of structural lightweight concrete beams containing EPS additions subjected to four-point bending [3]. Its main objective is to assess the suitability of two-dimensional FE modeling to predict the shear strength of RC beams without stirrups, which would complement the experimental programs while reducing the time and resources needed to account for the variability in concrete strength. The first part of this paper presents a summary of the experimental program executed, including the main findings related to the effect of EPS on the concrete mechanical properties and shear strength behavior of RC beams. Subsequently, the paper is divided into two phases, wherein the first one (i.e., deterministic FE method) considers the concrete mechanical properties as constant parameters in the modelling process. The second phase (i.e., stochastic FE method) accounts for the concrete heterogeneity due to EPS additions and the effect of spatial variability on the cracking patterns and performance of RC beams. The validity of FE models used to predict the behavior of real-scale 2.5 m length beams will be presented in a follow-up paper. Such data can be of interest to civil engineers and structural designers seeking to predict the variability of concrete properties in the strength and failure patterns of lightweight structural EPS-based members.

2. Summary of Experimental Program Executed for Shear Strength Testing of RC Beams Containing EPS Additions

Medium- and high-strength concrete mixtures prepared with 350 or 450 kg/m³ cement (w/c of 0.55 or 0.48, respectively) are considered in this work [2]. The EPS was introduced at a quantity of 2 or 3 kg/m³, while the natural sand and coarse aggregates adjusted to maintain a fixed sand-to-total aggregate ratio of 0.45. The spherical-shaped, white-colored EPS beads had a particle size of 2.5 to 3 mm (Figure 1); their density and specific gravity were 17 kg/m³ and 0.017, respectively.

At the age of 28 days, the concrete mechanical properties, including the hardened density, compressive strength (${\mathrm{f}}_{\mathrm{c}}^{\prime }$), splitting tensile strength (${\mathrm{f}}_{\mathrm{t}}$), and secant modulus of elasticity ($\mathrm{E}$), were determined as per ASTM C642, C39, C469, and C496, respectively. Averages of 3 to 5 values were considered for each property. The shear strength properties were determined using triplicate RC beams measuring 150 mm² in cross-section and 780 mm in length. The beams contained two 16 mm diameter longitudinal bars along with four stirrups positioned at the supports and loading points (Figure 1). The steel modulus of elasticity (${\mathrm{E}}_{\mathrm{s}})$ was 200 GPa while its yield stress (${\mathrm{f}}_{\mathrm{y}})$ and Poisson’s ratio (${\mathsf{\gamma }}_{\mathrm{s}})$ were equal to 420 MPa and 0.3, respectively. The RC beams were mounted on a simply supported set-up and subjected to vertical loading applied at constant rate of 4 kN/min to determine the load-deflection curves. A high-definition portable microscope was used to detect both the first diagonal and flexural cracking load during testing as well as the crack patterns for each beam.

Table 1 summarizes the density ($\mathsf{\rho }$) and mechanical concrete properties (i.e., ${\mathrm{f}}_{\mathrm{c}}^{\prime }$, ${\mathrm{f}}_{\mathrm{t}}$, $\mathrm{E}$) along with their coefficients of variation (COVs). The COV is computed as the ratio between the standard deviation of the various responses divided by the mean value and then multiplied by 100. Table 1 also summarizes the shear strength properties of RC beams, including both the load at which the first diagonal shear crack appeared as well as the ultimate load (P_max), deflection (δ_max), and maximum crack opening at failure. Clearly, the density of EPS-based concrete decreased due to the lightweight nature of such additions; this varied from 2375 kg/m³ for the 350-Control mix to 2205 and 1955 kg/m³ when 2 and 3 kg/m³ EPS was added, respectively. The corresponding ${\mathrm{f}}_{\mathrm{c}}^{\prime }$ dropped from 36.64 to 31.85 and 25.06 MPa, respectively, while $\mathrm{E}$ decreased from 29.8 to 24.2 and 19.8 GPa, respectively. The inferior mechanical properties of EPS concrete are normally associated with a weaker aggregate skeleton, especially along the interfacial transition zones between the EPS and cement mortar [3,13]. The expressions linking the various concrete properties are given as follows:

• ${\mathrm{f}}_{\mathrm{t}}$, MPa = 0.134 (${\mathrm{f}}_{\mathrm{c}}^{\prime }$, MPa) − 1.87    R² = 0.95
• E, GPa = 0.836 (${\mathrm{f}}_{\mathrm{c}}^{\prime }$, MPa) − 1.65     R² = 0.98
• $\mathsf{\rho }$, kg/m³ = 17.95 (${\mathrm{f}}_{\mathrm{c}}^{\prime }$, MPa) + 1527.1    R² = 0.45

Table 1. Density, ${\mathrm{f}}_{\mathrm{c}}^{\prime }$, ${\mathrm{f}}_{\mathrm{t}}$, $\mathrm{E}$, and RC shear strength properties, along with their COVs.

	Concrete Mechanical Properties				RC Beam Properties
	$\rho$, kg/m3	$f_c^{\prime }$, MPa	$f_t$, MPa	$E$, GPa	Load When First Crack Appeared, kN	Max. Crack Opening, mm	Pmax, kN	Deflection (δmax) at Pmax, mm
350-Control	2375 (1.9%)	36.64 (5.1%)	2.9 (6.8%)	29.8 (7.7%)	60.5 (11.4%)	0.7 (9.2%)	82.88 (8.8%)	3.9 (11.2%)
350-2 kg EPS	2205 (2.5%)	31.85 (8%)	2.11 (9.9%)	24.2 (11.5%)	51.3 (18.5%)	1.3 (16.1%)	58.62 (13.2%)	2.55 (16.4%)
350-3 kg EPS	1955 (2.3%)	25.06 (10.3%)	1.55 (11.2%)	19.8 (13%)	50.4 (18%)	1.52 (17%)	57.98 (18.6%)	2.37 (22.1%)
450-Control	2390 (2.7%)	48.2 (4.9%)	4.57 (7%)	38.76 (7.4%)	73.6 (9.6%)	0.86 (8%)	95.03 (9.6%)	3.57 (13%)
450-3 kg EPS	1895 (2.5%)	35.6 (10.6%)	3.3 (11%)	27.4 (13.2%)	44 (20.1%)	1.12 (12.3%)	50.52 (19.2%)	1.84 (22%)

Table 1. Density, ${\mathrm{f}}_{\mathrm{c}}^{\prime }$, ${\mathrm{f}}_{\mathrm{t}}$, $\mathrm{E}$, and RC shear strength properties, along with their COVs.

	Concrete Mechanical Properties				RC Beam Properties
	$\rho$, kg/m3	$f_c^{\prime }$, MPa	$f_t$, MPa	$E$, GPa	Load When First Crack Appeared, kN	Max. Crack Opening, mm	Pmax, kN	Deflection (δmax) at Pmax, mm
350-Control	2375 (1.9%)	36.64 (5.1%)	2.9 (6.8%)	29.8 (7.7%)	60.5 (11.4%)	0.7 (9.2%)	82.88 (8.8%)	3.9 (11.2%)
350-2 kg EPS	2205 (2.5%)	31.85 (8%)	2.11 (9.9%)	24.2 (11.5%)	51.3 (18.5%)	1.3 (16.1%)	58.62 (13.2%)	2.55 (16.4%)
350-3 kg EPS	1955 (2.3%)	25.06 (10.3%)	1.55 (11.2%)	19.8 (13%)	50.4 (18%)	1.52 (17%)	57.98 (18.6%)	2.37 (22.1%)
450-Control	2390 (2.7%)	48.2 (4.9%)	4.57 (7%)	38.76 (7.4%)	73.6 (9.6%)	0.86 (8%)	95.03 (9.6%)	3.57 (13%)
450-3 kg EPS	1895 (2.5%)	35.6 (10.6%)	3.3 (11%)	27.4 (13.2%)	44 (20.1%)	1.12 (12.3%)	50.52 (19.2%)	1.84 (22%)

As shown in Figure 2, all RC beams failed after the formation of a single major diagonal crack that started from the support and propagated diagonally at about 45° from the horizontal axis. The loads at which the crack appeared were 60.5 and 73.6 kN (i.e., about 73% and 77% of P_max, respectively) for the 350- and 450-Control beams, while the maximum crack opening varied within 0.7–0.86 mm. When EPS additions were used, the cracks appeared at higher relative loads (i.e., about 87% to 90% of P_max), with much larger openings varying between 1.12 and 1.52 mm. This can be associated with weaker interfacial transition zones within the aggregate skeleton, leading to rapid crack propagation and abrupt shear strength failure [16,17,18].

As expected, the ultimate load (P_max) that caused the beam’s failure decreased with EPS additions (Table 1). For example, this varied from 82.88 kN for the 350-Control beam to 58.62 and 57.98 kN for the 350-2 kg EPS and 350-3 kg EPS beams, respectively. The corresponding δ_max varied from 3.9 to 2.55 and 2.37 mm, respectively. Such results are in agreement with the drop in the concrete mechanical properties, reflecting the effect of density and aggregate skeleton on the shear strength of RC beams. Earlier studies showed that the aggregate interlock mechanism is particularly weakened with EPS additions, leading to inferior shear transfer along the developed cracks in RC beams produced without stirrups [3,17,18]. Assaad et al. [3] found that the fine and coarse aggregate volumes are reduced in EPS concrete, which reduces the internal friction within the aggregate skeleton, including the EPS/cement paste interfacial bonding. The COVs for P_max responses varied in the range 8–9.2% for the control beams and in the range 13.2–19.2% with EPS additions, reflecting the increased variability in the concrete properties.

3. Phase 1-Deterministic Finite Element (FE) Modeling

3.1. Description of the Model

The CAST3M processing software [34], developed by the French Atomic Energy Agency (CEA), is used here for the FE modeling. A quadrilateral 1 mm mesh size is used with bilinear finite elements (1170 elements) to model the non-linear beam behavior subjected to four-point bending under the hypothesis of plane stresses (Figure 3) [35,36]. Bar elements are adopted to model the stirrups and flexural steel reinforcement using the Von Mises plasticity approach with linear hardening; the steel modulus of elasticity, yield stress, and Poisson’s ratio are taken as 200 GPa, 420 MPa, and 0.3, respectively. The concrete–steel bond is considered perfect while the strains and stresses are computed following the steel elastic–plastic behavior with linear hardening.

The isotropic damage principle is used to model the concrete behavior [37,38]. It is characterized by a single damage scalar ($\mathrm{D}$) that is considered as a micro-cracking indicator following the combination of tensile damage (${\mathrm{D}}_{\mathrm{t}}$) and compression damage (${\mathrm{D}}_{\mathrm{c}}$), given as $\mathrm{D}={\mathsf{\alpha }}_{\mathrm{t}}{\mathrm{D}}_{\mathrm{t}}+{\mathsf{\alpha }}_{\mathrm{c}}{\mathrm{D}}_{\mathrm{c}}$. The load surface is controlled by a state variable $\left(\mathrm{U}\right)$ and an equivalent strain $\left({\mathsf{\epsilon }}_{\mathrm{eq}}\right)$, as shown in Equation (1):

$$\mathrm{f}\left({\mathsf{\epsilon }}_{\mathrm{eq}},\mathrm{U}\right)={\mathsf{\epsilon }}_{\mathrm{eq}}-\mathrm{U}$$

(1)

where ${\mathsf{\epsilon }}_{\mathrm{eq}}=\surd \sum _{\mathrm{i}=1}^3{\mathsf{\epsilon }}_{\mathrm{i}}^{+}$ and ${\mathsf{\epsilon }}_{\mathrm{i}}^{+}$ are the positive parts of the principal strains’ tensor (${\mathsf{\epsilon }}_1{ \mathsf{\epsilon }}_2{ \mathsf{\epsilon }}_3$). The variable $\mathrm{U}$ is initially taken to be equal to the strain threshold ${\mathsf{\epsilon }}_{\mathrm{D}0}$ (defined as ${\mathrm{f}}_{\mathrm{t}}/\mathrm{E}$ in the model). Then, during loading, it is equal to the maximum between the equivalent strain and the damage threshold.

To avoid pathological mesh dependency and limit the spreading of non-local damage, the Stress-Based Non-Local (SBNL) method is used. Giry et al. (2011) [39] developed this non-local regularization method to account for the stress state in the medium by averaging a mechanical quantity in its neighborhood using a weight function, as expressed in Equation (2):

$$\mathsf{\phi } \left(\mathrm{x} - \mathrm{s}\right)= \exp (-{\left(\frac{2 \left|\left|\mathrm{x} - \mathrm{s}\right|\right|}{{\mathrm{l}}_{\mathrm{c}} \mathsf{\rho }\left( \mathrm{x}, \mathsf{\sigma }\left(\mathrm{s}\right)\right)}\right)}^2)$$

(2)

where ρ (x, σ(s)) is the radial coordinate of the ellipsoid associated with the stress state of the point located at distance $\mathrm{s}$ in the direction (x − s). The characteristic length ${\mathrm{l}}_{\mathrm{c}}$ (intrinsic to the material, typically correlated to the aggregate size) multiplied by a single scalar ρ defines the evolution of interactions between the modeled points and internal length, which varies between 0 for unloaded material and ${\mathrm{l}}_{\mathrm{c}}$ when maximum tensile stress is reached [40]. ${\mathrm{l}}_{\mathrm{c}}$ is usually taken to be higher than three times the mesh density or the maximum aggregate diameter [27]. In this paper, the mesh density and characteristic length are taken as 10 and 20 mm, respectively, which are larger than the maximum EPS diameter to account for the connectivity and interfacial bonding with the cement paste [3,40,41]. The Mazars damage model, coupled with the SBNL approach, have been widely used to model RC structures, including beams subjected to four-point bending [38,39,40,41].

The loading at top of the modeled beam is applied on two small triangle-shaped areas to avoid stress concentration, while rectangular-shaped areas are considered at the bottom to avoid geometrical singularities [36]. The vertical displacement is blocked at each support while still keeping horizontal displacement free. The control and EPS-based concrete model parameters including, $\mathsf{\rho }$, ${\mathrm{f}}_{\mathrm{c}}^{\prime }$, ${\mathrm{f}}_{\mathrm{t}}$, and $\mathrm{E}$, are obtained from the experimental testing (Table 1). A monotonic 50 mm vertical displacement is applied to both loading points, and software is run to analyze and compare the crack patterns and load-deflection curves with the experimental results.

3.2. Damage Field Distribution

Figure 4, Figure 5 and Figure 6 plot the damage field distribution (0.98 < D < 1.00) determined at different loading levels (i.e., 25%, 50%, 75%, and 100% of P_max) for concrete mixtures prepared with 350 kg/m³ cement. The damaged area (D) is proven to physically represent the crack propagation and opening, allowing a better understanding of the crack distribution and propagation during the different loading stages until failure [36,42,43]. The blue areas indicate no damage (D = 0.98), while the red ones reveal the damaged area and crack position. Figure 4, Figure 5 and Figure 6 also plot the experimental vs. numerical load-deflection curves, which are discussed later in this text.

As shown, the first damaged cracks for the 350-Control beam occurred in the flexural span between the two loading supports, which then propagated in a vertical direction when the load was further increased. Such cracks were invisible during the experimental testing, reflecting the relevance of FE modeling for forecasting the initiation and distribution of damage during the different loading stages. The model showed no crack formations at 25% of P_max for the beams containing 2 or 3 kg/m³ EPS, unlike the damage observed at the same load level for the control concrete. This can be directly linked to the reduced modulus of elasticity of EPS-based concrete, leading to increased energy absorption and the redistribution of stresses with minimal crack formation [2,3,6]. As noted in Table 1, the E values decreased from 29.8 GPa for the 350-Control mix to 24.2 and 19.8 GPa for the 350-2 kg EPS and 350-3 kg EPS mixtures, respectively.

The inclined damaged cracks formed at a 45° angle from the horizontal axis became evident at about 50% of P_max for the control beam and at about 75% of P_max for the EPS-based concrete beams. Such results are in agreement with the experimental results (Table 1), whereby the relative load at which the first crack appeared visually in the control beams was lower than the one recorded for the beams containing EPS additions. The cracks propagated towards the shear span regions and become wider and deeper until failure occurred. As shown in Figure 5 and Figure 6, the damaged areas shown in red color appeared at 50% of P_max for the EPS-modified concrete beams, while this gradually occurred at between 50% and 75% of P_max for the control beam (Figure 4). This can be associated with weaker interfacial transition zones within the EPS aggregate skeleton, leading to rapid crack propagation and debonding along the diagonal cracks [2].

Regardless of the concrete type, the damage and crack pattern distributions at P_max have symmetrical shapes (Figure 4, Figure 5 and Figure 6), given the basic principle of the deterministic FE approach that considers the concrete mechanical properties as being homogeneous. However, this is not the case in the experimental testing (refer to Figure 2), where failure mainly occurred along one major diagonal crack. This highlights the need to consider concrete as a heterogenous material, as will be discussed later in the stochastic FE approach.

3.3. Equivalent Strain ε_eq Distribution

The ${\mathsf{\epsilon }}_{\mathrm{e}\mathrm{q}}$ is another tool in the Mazars model that is used to predict the crack position where damage is localized [37,38]. Figure 7 plots the ${\mathsf{\epsilon }}_{\mathrm{eq}}$ distribution throughout the RC beams at P_max for the 350 kg/m³ concrete mixtures. As earlier, there were two symmetrical cracks where higher strain concentrations appeared at failure. The maximum ${\mathsf{\epsilon }}_{\mathrm{eq}}$ decreased from 3.7 $\times {10}^{-2}$ for the control beam to 1.9 $\times {10}^{-2}$ and 1.2 $\times {10}^{-2}$ for the 350-2 kg EPS and 350-3 kg EPS mixtures, respectively, which can be related to the decrease in the Young’s modulus and tensile strength properties. The formation of larger green-colored zones in EPS-based beams reflects higher ${\mathsf{\epsilon }}_{\mathrm{eq}}$ along the longitudinal steel bars, which can be associated with poorer EPS/cement paste interfacial bonding that led to slippage around the embedded reinforcement [3,15,18].

It is worth noting that the Mazars model can also be used to predict the load at which the first diagonal crack appears during loading. In fact, the function expressed in Equation (1) depends on the equivalent strain (${\mathsf{\epsilon }}_{\mathrm{eq}}$) and the strain threshold $({\mathsf{\epsilon }}_{\mathrm{D}0}$) that delimits the elastic domain. When ${\mathsf{\epsilon }}_{\mathrm{eq}}>{\mathsf{\epsilon }}_{\mathrm{D}0}$, the damage scalar $\mathrm{D}$ rises rapidly, causing the formation of cracks [40]. The output of the deterministic FE model shows that the first crack appears at 77%, 84%, and 88% of P_max for the 350-Control, 350-2 kg EPS, and 350-3 kg EPS mixtures, respectively, which is in good agreement with the experimental test results shown in Table 1.

3.4. Maximum Load and Deflection at Failure

The experimental vs. numerical load-deflection curves are quite close to each other (Figure 4, Figure 5 and Figure 6). The load increased almost linearly at the first stages of loading until reaching the maximum value that represented the beam’s collapse. Hence, P_max, determined by numerical modeling varied from 80 kN for the 350-Control beam to 57.8 and 58.25 kN for the 350-2 kg EPS and 350-3 kg EPS beams, respectively, which represented a variation of 3.4%, 1.4%, and 0.5% from the experimental results. The corresponding variations between the numerical and experimental δ_max were 3%, 4%, and 6.7%, respectively.

The drop in P_max and δ_max responses, determined experimentally and numerically, can be directly linked to the reduced concrete density and strength due to EPS additions. For example, the density dropped from 2375 kg/m³ for the control concrete to 2205 and 1955 kg/m³ for those containing 2 or 3 kg/m³ EPS, respectively. The corresponding ${\mathrm{f}}_{\mathrm{c}}^{\prime }$ varied from 36.64 to 31.85 and 25.06 MPa, respectively. This could directly weaken the aggregate interlock mechanism, leading to reduced internal friction and the transfer of stresses along the developed shear cracks. Assaad et al. [3] reported that the poor EPS/cement paste interfacial bonding could further promote slippage around the flexural steel reinforcing bars and amplify the degradation of the beam properties. Nevertheless, such phenomena cannot be reproduced in the deterministic FE model since the concrete mechanical properties are considered homogenous with no weak zones created along the shear cracks [23,24,25]. These findings support the stochastic FE approach considered in Phase 2, which accounts for the concrete heterogeneity using discrete random fields associated with each property.

4. Phase 2-Stochastic FE Modeling for RC Beams

Concrete is a heterogeneous material whose mechanical properties, such as ${\mathrm{f}}_{\mathrm{c}}^{\prime }$, ${\mathrm{f}}_{\mathrm{t}}$, and $\mathrm{E}$, could remarkably differ from one location to another in a given structure [19,21,24]. The incorporation of EPS accentuates this heterogeneity due to its lightweight and soft nature, in addition to the altered cement paste/EPS interfacial transition zones that create weak zones with increased risks of debonding and the propagation of cracks [9,14,26,30]. Many researchers have highlighted the need to thoroughly control the EPS floating phenomenon using reduced w/c mixtures and/or the incorporation of viscosity-modifying agents that improve the concrete stability and risks of bleeding [10,16].

As previously discussed, in our experiments, the concrete and RC beam properties degraded with EPS additions due to the reduced material density and weaker aggregate skeleton phase. Yet, as shown in Table 1, it is important to note that such degradation was coupled with a remarkable increase in the COV (i.e., computed as Std/Mean) values, reflecting a higher spatial variability of the mechanical properties due to EPS additions. For example, the COV of E measurements increased from 7.7% for the 350-Control mix to 11.5% and 13% when 2 and 3 kg/m³ EPS was added, respectively. The corresponding COV for P_max almost doubled as it varied from 8.8% to 13.2% and 18.6%, respectively, while the COV for δ_max varied from 11.2% to 16.4% and 22.1%, respectively. This reflects the relevance of the random fields considered in the stochastic FE approach that offer the advantage of modeling the heterogeneous concrete nature and its effect on the RC beam properties.

4.1. Methodology

To model the spatial variability of concrete’s mechanical properties (${\mathrm{f}}_{\mathrm{c}}^{\prime }$, ${\mathrm{f}}_{\mathrm{t}}$, and $\mathrm{E}$), a Gaussian random field $\mathrm{V}\left(\mathrm{x}\right)$ associated with each variable is defined. The random field is defined by its mean $\mathsf{\mu }$, standard deviation $\mathrm{Std}$, covariance function ${\mathrm{C}}_{\mathrm{vv}} \left(\mathrm{x},{\mathrm{x}}^{\prime }\right)$ defining the spatial correlation (Equation (3)), and its Gaussian auto-correlation function $\mathsf{\rho }\left(\mathrm{x}\right)$(Equation (4)).

$${\mathrm{C}}_{\mathrm{vv}} \left(\mathrm{x},{\mathrm{x}}^{\prime }\right)= \mathrm{Std}\left(\mathrm{x}\right) \mathrm{Std}\left({\mathrm{x}}^{\prime }\right) \mathsf{\rho }\left(\mathrm{x},{\mathrm{x}}^{\prime }\right)$$

(3)

$$\mathsf{\rho }\left(\mathrm{x}\right)=\exp \left(-{\left( \frac{\mathrm{x}}{\mathrm{a}} \right)}^2\right)$$

(4)

Here, $\mathsf{\mu }$, $\mathrm{Std}$, and COV are derived from the experimental concrete testing, summarized in Table 1. The $\mathrm{a}$ value represents the auto-correlation length, which is a mesh or is aggregate-size dependent [32,33]; it is taken to be equal to the maximum aggregate size, 20 mm. The random field discretization consists of expressing the random field using a finite number of random variables gathered in a random vector. Hence, the random variables are defined on the considered FE mesh (Figure 3), which has a constant number of nodes ${\mathrm{n}}_{\mathrm{FE}}$:

$$\mathrm{V}\left(\mathrm{x}\right)\to {\tilde{\mathrm{V}}}_{\mathrm{FE}}\left(\mathrm{x}\right)=\left\{{\mathrm{V}}_{\mathrm{FE} \mathrm{k}}, \mathrm{k}=1\dots { \mathrm{n}}_{\mathrm{FE}}\right\}$$

The Cholesky decomposition method is used in various applications of random fields [26,27,28,32]. This method is applied to the covariance matrix ${\mathrm{C}}_{\mathrm{ij}}={\mathrm{Std}}^2 {\mathsf{\rho }}_{\mathrm{v}} \left(\mathrm{x},{\mathrm{x}}^{\prime }\right)$, which is an assembly of values of the covariance function ${\mathrm{C}}_{\mathrm{VV}}$ computed between two points $\mathrm{i}$ and $\mathrm{j}$ of the discretized random field. This decomposition approach consists of expressing the vector ${\tilde{\mathrm{V}}}_{\mathrm{FE}}\left(\mathrm{x}\right)$ as a sum of the mean value of the random field and a linear combination of standard Gaussian random variables $\mathrm{Y} \left(\mathrm{Y}=\left\{{\mathrm{Y}}_{\mathrm{k}}, \mathrm{k}=1\dots { \mathrm{n}}_{\mathrm{FE}}\right\}\right)$ having zero as the mean value and a standard deviation equal to 1, as expressed in Equation (5). B is a square matrix such that ${\mathrm{C}}_{\mathrm{ij}}={\mathrm{BB}}^{\mathrm{T}}$, where $\mathrm{T}$ is the transpose operator.

$${\tilde{\mathrm{V}}}_{\mathrm{FE}}\left(\mathrm{x}\right)=\mathsf{\mu }+\mathrm{BY}$$

(5)

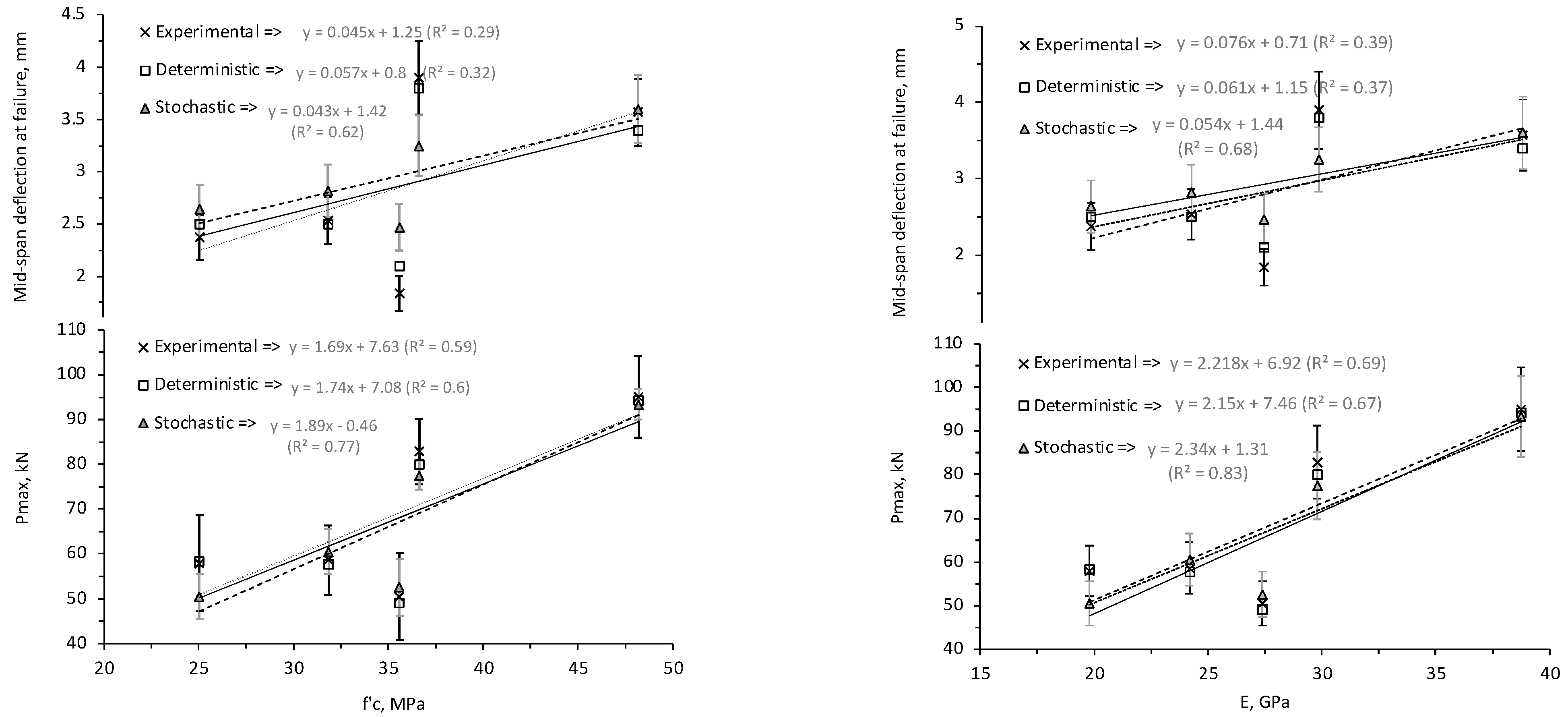
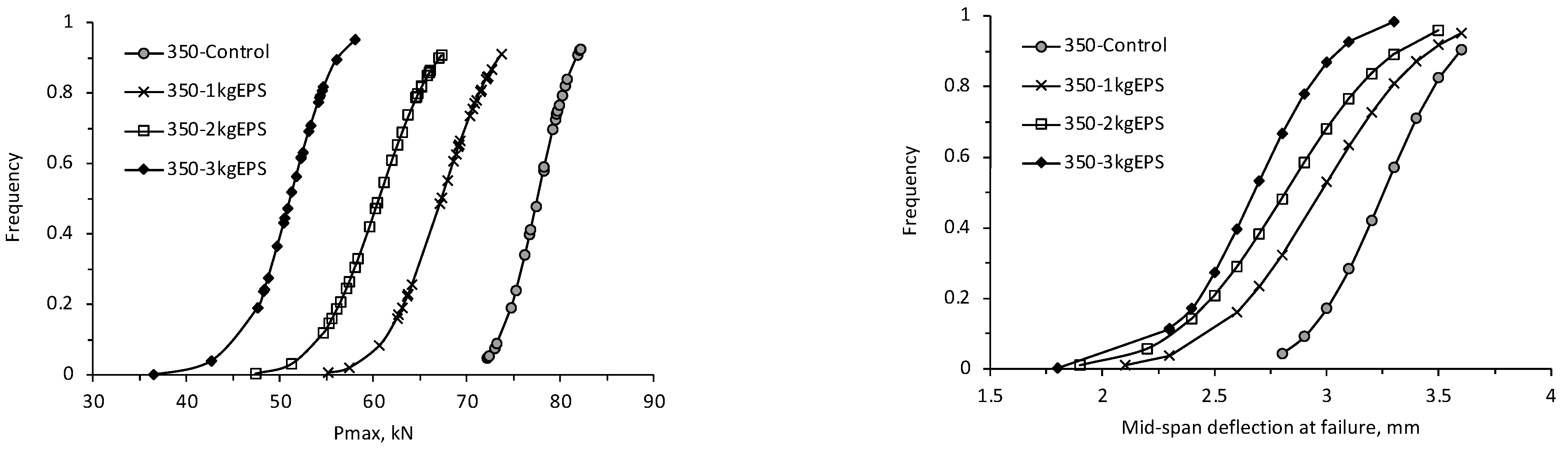
4.2. Application of Stochastic FE Method to RC Beams

Thirty (30) independent $\mathrm{E}$ and ${\mathrm{f}}_{\mathrm{t}}$ auto-correlated random field iterations are applied to each concrete mixture considered in this paper. This number of iterations is enough to cover the variability of the spatial concrete properties due to EPS additions and assess their effect on the altered performance of RC beams [35]. For each iteration, the crack patterns and load-deflection curves are determined to quantitatively estimate the uncertainty propagation of output results from those determined experimentally.

Figure 8 plots four (4) randomly selected field iterations related to E responses for the 350-2 kg EPS mix and their crack patterns at failure; the red and blue zones represent the highest and lowest E responses, respectively. Recall that the mean, Std, and COV values for this mixture were 24.2 GPa, 2.78 GPa, and 11.5%, respectively. Different crack patterns are obtained depending on the E distribution within the beam; however, a failure always occurs when major cracks are formed diagonally at about 45° from the horizontal axis. As shown in random field iteration no. 1 (RF1), a concentration of weak zones in the right region between the support and load application occurs, leading to a single 45° crack in this region. This crack pattern is similar to what was obtained experimentally for this mixture (refer to Figure 2). The weakest zone shifted to the left region in the second iteration (RF2), which also led to a single 45° crack. The altered location of the major cracks from one region to another reflects the concrete heterogeneity and scattering of mechanical properties within the beam. In the third and fourth iterations (RF3 and RF4), the scattering of Young’s modulus was not enough to localize the crack in one region, which resulted in two major cracks, just like in the output data obtained using the deterministic FE approach.

Figure 9 compares the experimental load-deflection curve to those obtained using the same four (4) randomly selected field iterations for the 350-2 kg EPS concrete beam; the iterations that led to the highest and lowest P_max values are also shown. Clearly, different curves are obtained for each iteration, which have altered both P_max and δ_max values. For these four iterations, P_max varies from 55.24 to 61.94 kN and δ_max from 2.4 to 2.9 mm. The value of P_max is affected by the scattering of both $\mathrm{E}$ and ${\mathrm{f}}_{\mathrm{t}}$. Recall that the mean and Std of ${\mathrm{f}}_{\mathrm{t}}$ responses for this mixture are equal to 2.11 and 0.21 MPa, respectively. Unlike in the deterministic approach, this reflects the relevance of the stochastic FE method, which accounts for the variability in concrete properties.

4.3. Comparison between Experimental vs. FE Modeling

Table 2. Comparison of P_max and δ_max values obtained experimentally vs. those determined using the deterministic or stochastic FE modeling methods.

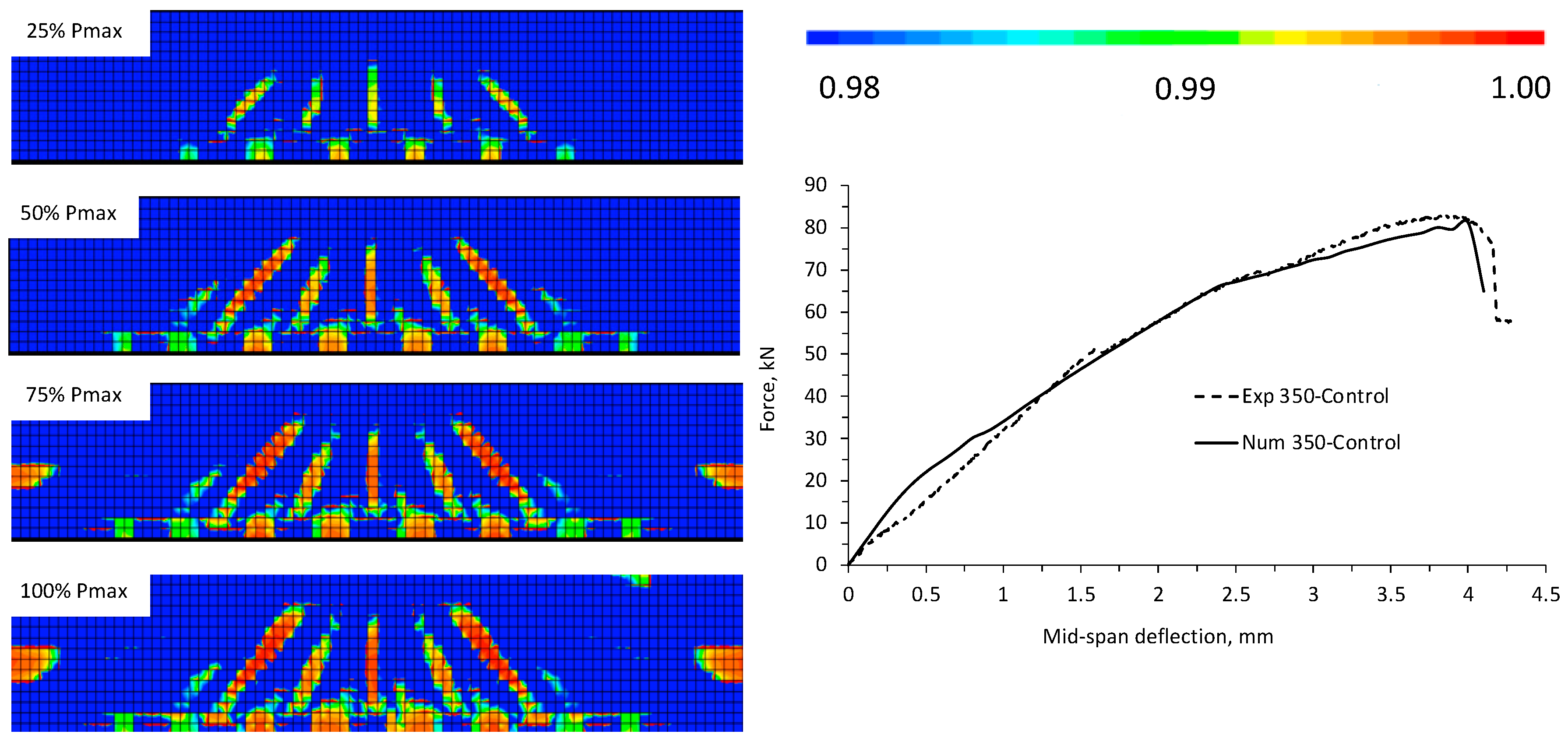
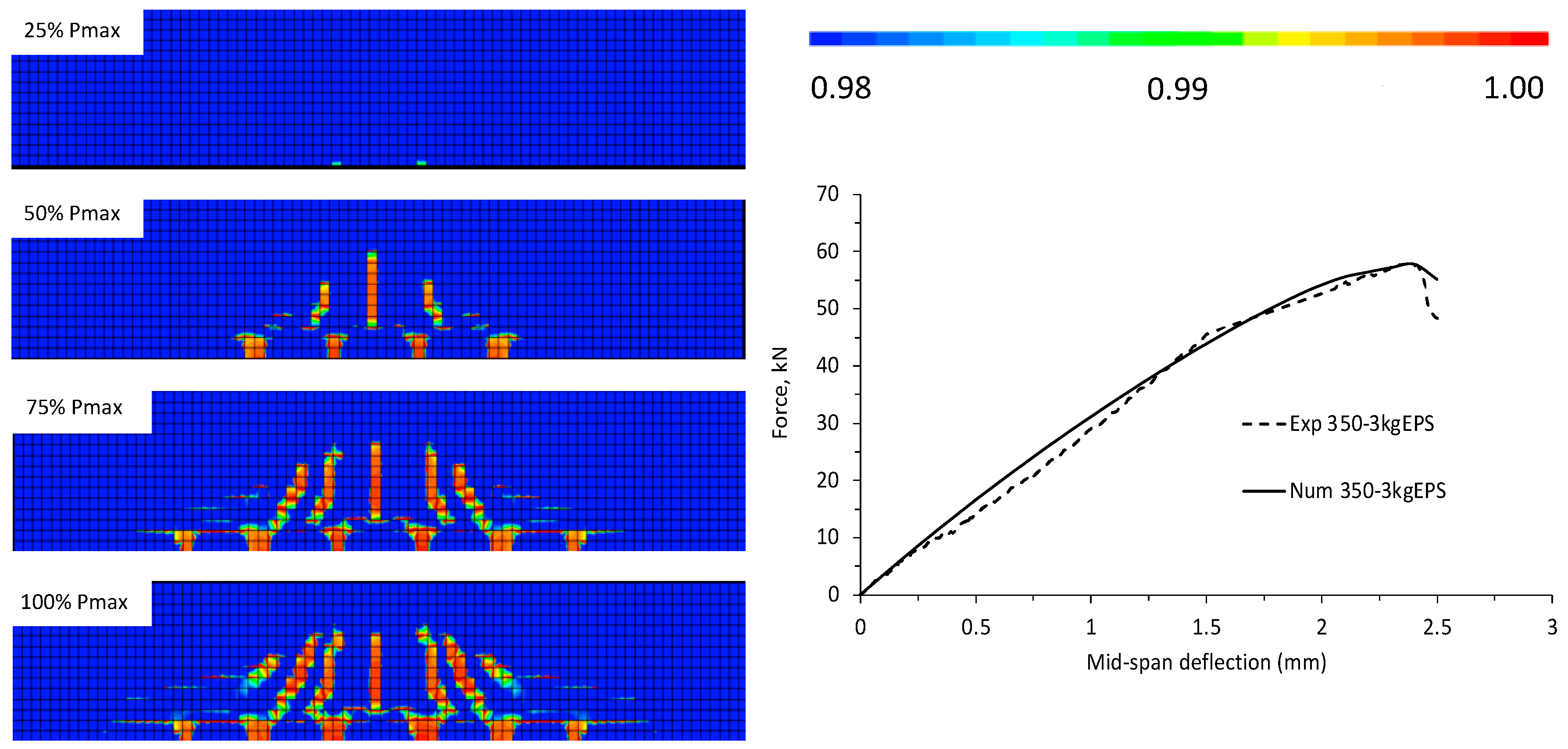
	Experimental Test		Deterministic FE		Stochastic FE
	Pmax, kN	δmax, mm	Pmax, kN	δmax, mm	Pmax, kN	δmax, mm
350-Control	82.88 Std = 7.3 COV = 8.8%	3.9 Std = 0.44 COV = 11.2%	80.04	3.78	77.53 Std = 3.21 COV = 4%	3.25 Std = 0.26 COV = 8.1%
350-2 kg EPS	58.62 Std = 7.73 COV = 13.2%	2.55 Std = 0.41 COV = 16.4%	57.8	2.45	60.54 Std = 5.03 COV = 8.3%	2.82 Std = 0.39 COV = 13.8%
350-3 kg EPS	57.98 Std = 10.78 COV = 18.6%	2.37 Std = 0.52 COV = 22.1%	58.25	2.53	50.5 Std = 5.1 COV = 10%	2.64 Std = 0.38 COV = 14.4%
450-Control	95.03 Std = 9.12 COV = 9.6%	3.57 Std = 0.46 COV = 13%	94.23	3.42	93.36 Std = 3.43 COV = 3.67%	3.6 Std = 0.14 COV = 3.9%
450-3 kg EPS	50.52 Std = 9.7 COV = 19.2%	1.84 Std = 0.4 COV = 22%	49.1	2.14	52.58 Std = 6.31 COV = 12%	2.47 Std = 0.404 COV = 16.3%

summarizes the P_max and δ_max values obtained experimentally and using the deterministic or stochastic FE models. Unlike in the deterministic approach, stochastic modeling offers the ability to provide a statistical analysis with Std and COV values for the output parameters. For example, a mean P_max of 77.53 kN is obtained for the 350-Control beam with Std and COV values of 3.21 kN and 4%, respectively. The P_max dropped to 60.54 kN for the 350-2 kg EPS beam, but with higher Std and COV values of 5.03 kN and 8.3%, respectively. Thus, the stochastic FE approach offers a relevant tool to complement experimental testing while reducing the hassle of time and resources required to assess the variability in concrete properties. Hence, instead of repeating the shear strength experiment using RC beams, the stochastic approach makes use of the mechanical properties (i.e., density, ${\mathrm{f}}_{\mathrm{c}}^{\prime }$, ${\mathrm{f}}_{\mathrm{t}}$, and E), which are easier to determine experimentally.

Figure 10 plots the relationships between ${\mathrm{f}}_{\mathrm{c}}^{\prime }$ (or E) values with respect to P_max and δ_max, determined experimentally and using the deterministic and stochastic FE models. The estimated standard deviations are shown to highlight the confidence intervals for P_max and δ_max (except for the deterministic approach, where only one value was obtained). Despite the presence of similar trends, it is clear that the stochastic approach yielded the highest coefficients of correlation (R²), reaching 0.77 and 0.62 when the ${\mathrm{f}}_{\mathrm{c}}^{\prime }$ responses were used to predict P_max and δ_max. This also applied for the E responses, where R² reached 0.83 and 0.68. This reflects the fact that the variability in the concrete mechanical properties within the same member plays a crucial role in appropriately predicting the shear strength performance of RC beams without stirrups. Recall that 30 iterations were used to determine the standard deviations for the stochastic FE model while only triplicate tests were used in the experimental program.

Cumulative density function (CDF) frequency curves for P_max and δ_max responses were derived from the 30 stochastic FE iterations and plotted in Figure 11 for the 350 kg/m³ cement concrete prepared with various EPS additions. These functions are useful to analyze the FE outputs with the frequency of occurrence for a given concrete composition [35]. As shown, mixtures containing higher EPS additions exhibited wider CDF curves, reflecting the increased scattering of output parameters. The output scattering occurred due to the heterogenous nature of EPS concrete and the random distribution of its properties (i.e., higher Std and COV), leading to increased variations in the RC beam properties.

5. Summary and Conclusions

This paper is part of a comprehensive project undertaken to assess the performance of structural lightweight concrete beams containing EPS additions. It mainly seeks to assess the suitability of deterministic and stochastic FE modeling to predict the failure patterns and shear strength of RC beams without stirrups. The validity of models using real-scale 2.5 m length RC beams will be presented in a follow-up paper.

Based on foregoing experiments, test results showed that the deterministic FE approach was capable of detecting both the loads at which the inclined cracks appeared on the RC beams as well as the damage field distribution that occurred during loading in the flexural and shear zones. The model showed no crack formations at 25% of P_max for beams containing EPS, unlike the damage observed at the same load level for the control concrete because of a different modulus of elasticity. Symmetrical damage and crack distributions were observed at all loading stages given the basic deterministic FE principle, which considers the concrete mechanical properties (${\mathrm{f}}_{\mathrm{c}}^{\prime }$, ${\mathrm{f}}_{\mathrm{t}}$, and $\mathrm{E}$) as being homogeneous. This, however, was not the case in the experimental testing, where failure occurred along one major crack developed on one side of the beam.

The random field iterations performed by stochastic FE modeling account for the concrete strength variability within the studied RC beam, which led to different scenarios of crack patterns and distributions at failure. Hence, while some iterations showed two symmetrical 45° diagonal cracks at failure, other iterations were shown to better reproduce the experimental tests, where a concentration of weak zones occurred next to the support reaction and led to one single 45° diagonal crack at failure. The COV values for P_max and δ_max increased for the EPS-based beams, reflecting the influence of such additions on the spatial variability of the mechanical and shear strength properties. The stochastic FE approach offers a relevant tool to complement experimental testing while reducing the hassle of time and resources required to assess the variability in concrete properties.