Abstract
The aim of this paper is to present a performance-based method to estimate uniform risk spectra (URS) for the seismic design and assessment of structures. These spectra, computed with the proposed methodology, provide the lateral capacity (in terms of spectral acceleration) that should be given to a structure, characterized by a reference single degree of freedom system, to achieve a predetermined exceedance rate of economic loss. This procedure involves the seismic hazard assessment necessary to define a seismic design level consistent with the accepted loss value, using a large enough number of synthetic seismic records of several magnitudes, which were obtained by means of an improved empirical Green function method. The statistics of the expected losses of a reference single degree of freedom system are obtained using Monte Carlo simulation, considering the seismic demand and the lateral strength of the structure as random variables. The method is divided into two main stages: (1) definition of the seismic hazard at the site of interest and (2) the probabilistic analysis of the seismic performance in terms of an economical loss ratio of nonlinear SDOF. To illustrate the proposed methodology and, subsequently, to validate it, a URS was computed for a site located in the Mexico City lake-bed zone, and its use in the design of three reinforced concrete frames is shown. The results show that the proposed spectra provide a sufficient approximation between the seismic risk level considered in the seismic design and that of the designed structure. It is concluded that the proposed procedure is a significant improvement over others considered in the literature and a useful research tool for the further development of risk-based earthquake engineering.
1. Introduction
A natural risk has several definitions, and from an economic point of view, it may be defined as the potential economic consequences derived from a natural phenomenon in a region, city, or country. Currently, seismic risk assessments have acquired importance because of the large losses presented due to recent earthquakes. The World Economic Forum [1] shows that even though the seismic codes are less permissive, earthquake-related losses keep increasing. This may be explained because, nowadays, there are more exposed assets (several new buildings are built) and most of the seismic building codes are oriented toward achieving only two main performance goals during the design process: (1) avoiding structural damage under frequent earthquakes and (2) avoiding building collapse under rare earthquakes, without considering the structural behavior and consequences of seismic events with intermediate intensities. This increases the uncertainty of damage occurrence and, consequently, the risk of uncontrolled losses, causing economic plans or emergency actions to lack a solid basis upon which to make decisions before and after a seismic event. Fortunately, there are very detailed methodologies [2,3,4,5] to assess structural performance, which employ different seismic response parameters, as well as to infer the corresponding time and reparation costs, such as that presented in FEMA P-58 [2]. However, these techniques are usually carried out for academic research activities or for critical structures; on the other hand, common structures are usually designed employing traditional approaches, which are easily handled by civil engineers in professional practice.
Currently, most building codes around the world use response spectral analysis (RSA) [6,7,8,9] to estimate the design seismic demands in low- and mid-rise structures; therefore, to upgrade the current basic seismic design methodologies, an improvement of the provided design spectra are necessary. Unfortunately, the current design methods that use uniform hazard design spectra, as well as elastic approximations, may not allow for the design of structures that will exhibit the expected structural performance under high-intensity seismic demands in which inelastic behavior may occur. This is evidenced by the damage patterns observed from recent earthquakes (Mexico 1985 [10,11], Loma Prieta 1989 [12], Northridge 1994 [13], Kobe 1995 [14], Ecuador 2016 [15], and Mexico 2017 [16]), where the expected safety levels provided by FEMA exhibited large uncertainties.
This paper proposes a new method to estimate the seismic demands to be employed in a risk-based design approach, the results of which may be easily implemented by civil engineers in practice, since RSA is still the predominant analysis method in many building codes. This approach would not require a subsequent seismic assessment once a structure is designed, as is required in other risk-based design methods. Such seismic demands are presented through uniform risk spectra (URS), which, through an RSA, define the lateral strength required by a structure so that it does not exceed an annual expected loss during each predefined time frame. The use of these type of spectra would allow the designer or building owner to decide on the acceptable risk level from the beginning of the design process. This could lead to, among other aspects, better financial protection plans for each designed building. The proposed URS represent inelastic spectra without reduction by overstrength for a given specific structural type.
The accuracy of the results obtained using these spectra was validated by computing the exceedance rate of the loss of three moment-resisting frames (MRFs), whose design demands were obtained using a URS. For this purpose, the methodology proposed by the Pacific Earthquake Engineering Institute Center (PEER) was used [4].
Different researchers have made efforts to improve the prediction of expected damage states, either from the design process through methodologies focused on reaching a given structural performance [17,18,19,20,21] or through seismic assessment methodologies, which are usually performed once a structure has already been designed or built [3,4,5,22,23]. However, most seismic design codes have not included these methodologies or, in the best case, they have been adopted only for a small part of the building catalogue, such as tall towers or essential buildings.
One way to guarantee an accepted damage pattern in low-rise and mid-rise structures designed using RSA is by considering the key structural characteristics in the development of the seismic design spectra, where these spectra provide the necessary lateral strength (in terms of spectral pseudo-acceleration, Say) so that a structure reaches a specific performance target. These spectra are obtained as a function of the dynamic characteristics of soil and the inelastic dynamic response of several single degree of freedom (SDOF) systems. One example are uniform ductility spectra, which are obtained by using reduction factors over elastic response or design spectra [24,25,26,27,28,29,30,31,32]; these factors are generally obtained from the statistical analysis and mathematical regressions of the response of instrumented buildings. These factors are easily implemented in building codes but, unfortunately, since only important buildings have been instrumented, only a few buildings are available to provide information.
Other types of spectra are oriented to achieve uniform rates of exceedance of engineering design parameters [33,34,35,36,37,38,39], such as damage indexes, damage states, or fragility approaches. These spectra are obtained from a statistical analysis of the SDOF response under seismic actions derived from seismic records, and they predict, with a good approximation level, the seismic performance in terms of physical damage. Recently, several studies concerning risk-targeted seismic design demands have been developed [34]. For instance, Kennedy and Short [40] and Cornell [41] developed a practical way to estimate the seismic risk of a structural system that, in addition, is also suitable for structural design, corresponding to a target reliability level where the limit states are defined in terms of the global ductility of the system.
Another important contribution is the approach proposed by Luco [42], where the main aim is to obtain the seismic hazard associated to a uniform collapse probability for structures located across the US. The approach using the means of inelastic GMPEs which, for instance, provides the distribution of an intensity measure associated with the capacity demand of SDOF systems, considers parameters as the yield strength [43,44,45]. On the other hand, several approaches in which the main aim is to obtain the seismic demands, in terms of the spectral acceleration associated to a defined limit state, are estimated using parametric models, which depend on several factors associated to the main characteristics of a structure [46]. However, they may not be suitable for the estimation of economic losses (i.e., risk), since they do not consider the reparation cost of the estimated damage.
2. Methodology
The proposed methodology is based on the total probability theorem, which, in this case, is used to quantify the annual exceedance rate of a pre-established loss value by considering both the seismic hazard and building vulnerability. Equation (1) shows the proposed model.
where is the annual exceedance rate of loss; is the seismic hazard represented as the occurrence probability of an earthquake with a defined magnitude from the i-th to the N-th seismic sources; and is the structural vulnerability represented by the exceedance probability of loss given the magnitude, M, epicentral distance, R, vibration period, T, post-yielding stiffness, , and lateral strength in terms of the yield spectral acceleration, . and are the minimum and maximum magnitudes of the seismic source.
To solve the proposed equation, the following steps are provided:
2.1. Stage 1
Definition of the seismic hazard accounting for the exceedance rate of the magnitudes of the sources considered and a set of seismic records (real or synthetics) representative of the seismic hazard of the site.
2.2. Stage 2
Computation of the nonlinear response in terms of loss for an SDOF whose vibration period and lateral strength values are predefined. The nonlinear response must be estimated for each seismic source and by using the corresponding seismic records obtained in the previous step. Loss associated to the nonlinear response is estimated by means of relating the expected damage patterns associated to a performance parameter (damage index) with the cost of their corresponding reparation actions.
For each seismic source, the exceedance probability of loss for a given magnitude, epicentral distance, vibration period, and lateral strength is obtained by analyzing statistically the results of the previous step.
The total exceedance rate of loss associated to the predefined dynamic and mechanical characteristics ( and ) of the SDOF is calculated using Equation (1).
If the previous steps are repeated for all magnitudes and considered values of lateral strengths, it is possible to obtain a 3D geometric surface that describes the relationship among the loss level, exceedance rate of loss, and lateral strength for a defined vibration period (Figure 1).

Figure 1.
3D surface of the relationship among loss (), exceedance rate of loss ( ()), and lateral strength () for a defined vibration period ().
By computing several 3D surfaces (Figure 1) associated to a range of vibration period values and, subsequently, by selecting the lateral strength corresponding to the same loss value and loss exceedance rate in all of the computed 3D surfaces, the URS will be obtained.
The aforementioned process is graphically represented as follows (Figure 2).
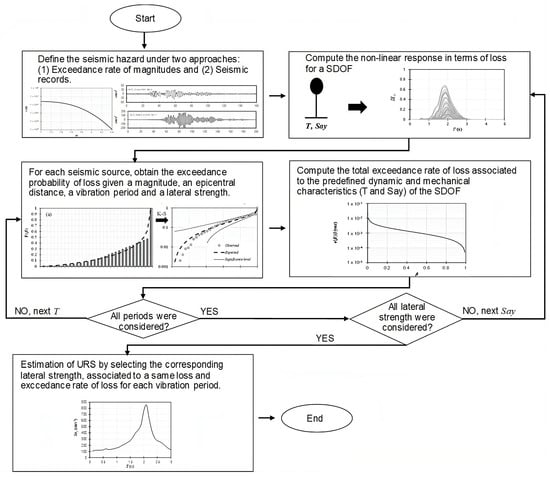
Figure 2.
Proposed flowchart for the estimation of URS.
3. Application Example
For illustrating the implementation of the proposed methodology and its results, an example application is presented. The example consisted of the development of a URS in terms of the normalized repair cost and, subsequently, the seismic assessment of three structures designed with such spectrum.
The selected site for the development of the URS was the SCT seismic station, one of the most iconic places in the seismic history of Mexico City. This site represents the wave amplification of strong ground motions, which is a unique characteristic of the soil of the city [47,48,49,50,51,52,53,54,55,56].
For the assessment of the results provided by the proposed spectra, three structures of one, fifteen, and twenty-five stories, whose lateral strengths were obtained from URS, were assessed in terms of their seismic risk [3,4,5,57]. It is expected that the risk level provided by the URS will be close enough to the risk calculated for such structures.
3.1. Defining the Seismic Hazard
In this example, for the sake of simplicity, only earthquakes generated from one seismic source were considered. Such seismic source is the Guerrero Gap, one of the most studied seismic zones by seismologist and civil engineers [58,59]. The earthquake generation model for the subduction zone of Guerrero is described using a characteristic earthquake model [60], whose parameters are T00 = 80 years, Mo = 7.0, Mu = 8.4, D = 7.5, F = 0, σM = 0.027, and To = 39.7 years [39,60]. Figure 3 shows the estimated exceedance rate of magnitudes curve for the Guerrero Gap.
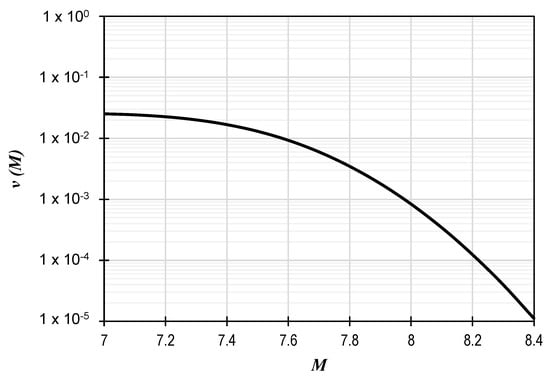
Figure 3.
Estimated exceedance rate of magnitudes for the Guerrero Gap.
To characterize the seismic hazard at the site, synthetic seismic ground motions were used because there are not enough real earthquake records for the selected magnitude threshold at the selected site; however, if it is desired to use real ground motions, they must be able to represent the seismic hazard of the analyzed seismic source. The synthetic records employed were computed by Niño et al. [59], who used an improved empirical Green function approach in which a source spectrum is defined by two corner frequencies and a summation scheme divided in two stages. In this approach, the epicentral distance, R, and the site effects are considered implicitly by means of the selected earthquake seed; the EW component of the 25 April 1989 earthquake (M 6.9) recorded at the SCT station was used. A total of 550 soft-soil seismic record, fifty records for each magnitude considered (M 7.2 to M 8.2), were employed to define the seismic hazard at the site. These 550 seismic records were extracted as a representative sample of the seismic hazard of the city [61] from the eleven thousand seismic records obtained by Niño et al. [59].
3.2. Computing the Nonlinear Response in Terms of Loss
The nonlinear seismic responses were estimated in terms of the Terán and Jirsa (DITJ) damage index [62] and, subsequently, classified by magnitude. The computed nonlinear response of several SDOF systems, with vibration periods between 0.01 and 5 s, which cover the typical period range of response spectra, for the record set considered was used to define the damage spectra considering pre-established combinations of stiffness and strength (T and ) for a damping ratio of 0.05 and a post-yielding rate of α = 0.05 [63].
The hysteretic model used was the Takeda model [64], which is representative of reinforced concrete (RC) structures. It should be noted that URS may be built for any hysteretic model. To define the post-yield stiffness ratio, it was necessary to consider the residual displacements [65,66,67], since high values of the post-yield stiffness ratio led to small residual displacements [24,68,69,70,71,72].
Figure 4 presents the estimated nonlinear responses as damage spectra using a post-yielding rate of α = 0.05 [63], where, for each spectrum, all SDOFs have the same lateral strength. It is observed that the damage indexes have a large variability, mainly because of each seismic record’s characteristics, such as intensities, frequency, and duration; this variability is considered in the computation of the probability of loss.
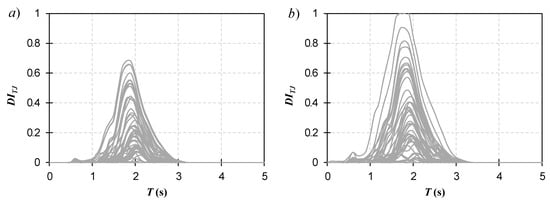
Figure 4.
Damage spectra for SDOF associated to Say = 100 gals and seismic records with magnitude of (a) 7.2 and (b) 7.3.
As it was mentioned previously, in this paper, the seismic risk was considered under economic terms so that the physical damage must be mapped to an economical value (repair cost ratio was considered). Specifically, some authors [73,74,75,76] have developed relationships between a damage index and the corresponding visible damage in the buildings; this allows for the definition of the necessary repair actions associated to each damage index limits and, subsequently, to estimate the economic cost. Table 1 shows the relationship proposed by Chacón and Paz [77] between the Park and Ang damage index (DIPA) [73] with the associated repair action and its repair cost ratio.

Table 1.
DIPA thresholds and their associated reparation cost [77] for RC structures.
To use the above relationship, the Park and Ang damage index values were mapped to the Teran and Jirsa [62] damage index by comparing the response of 50 inelastic SDOFs; the results are shown in Figure 5.
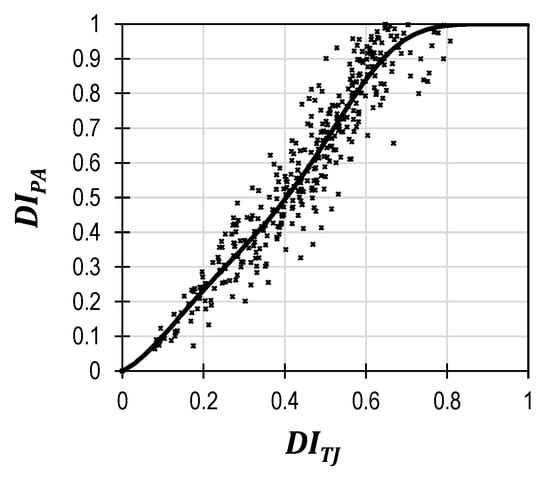
Figure 5.
The Park and Ang damage index and Teran and Jirsa damage index relationship. (Dots are the computed damage indexes, and the black line is the fitted curve).
By relating the data provided in Table 2, it is possible to fit a curve of the physical damage (DITJ)—structural loss ratio (β) for conventional RC structures. Figure 6 shows a fitted curve obtained through nonlinear regressions (Equation (2)); this curve was obtained by relating the midpoint of each DI interval and the corresponding loss ratio. In the same figure, it is possible to see that the physical characterization of damage does not have a linear relationship with the characterization of the economic loss. Reparation costs exhibit high variability; however, uncertainty between the repair cost and damage index was not considered in this study.
where β is the loss ratio, and DI is the selected damage index.

Table 2.
Relationship between the DIPA and DITJ.
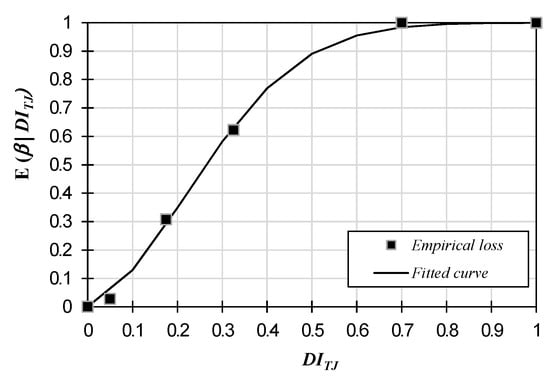
Figure 6.
Relationship between the damage index and expected loss.
By using Equation (2), the nonlinear responses given by the damage spectra (Figure 4) were mapped to economic losses.
3.3. Estimating the Exceedance Probability of Loss
For estimating the exceedance probability of loss, the nonlinear responses in terms of loss of the SDOFs were catalogued according to the M and R of the seismic records; subsequently, a statistical analysis was performed with the purpose of fitting a probability distribution function (PDF). Kolmogorov–Smirnov tests were performed to assess the goodness of fit of several probability distributions. Accordingly, beta PDF was deemed the most adequate. Furthermore, this PDF is delimited between zero and one, which is consistent with the loss ratio values. Figure 7 shows three examples of the performed Kolmogorov–Smirnov test, where it is possible to see a good fit of the beta PDF (i.e., expected) (dashed line) to the statistical data (i.e., observed) (bars graphic) for a 5% significance level.
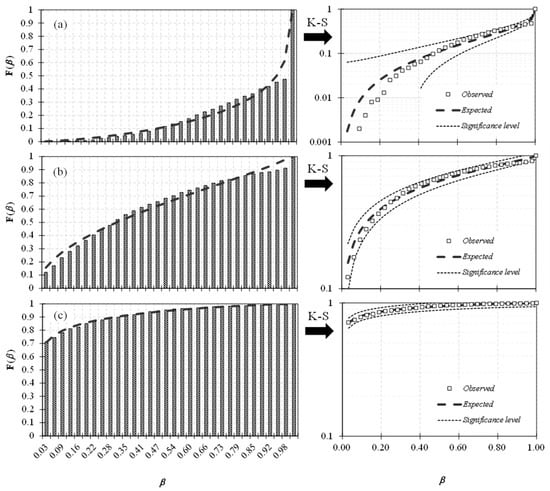
Figure 7.
Kolmogorov–Smirnov fitted test applied to the statistical data of the SDOF with T = 2.2 s and lateral strength of (a) 200, (b) 500, and (c) 1000 gals under the action of M 8.0 seismic records.
Thus, the loss PDF is defined as follows:
where BETA is the beta function, and a and b are shape parameters of the PDF. Such parameters are computed as follows:
where c[] is the variation coefficient of loss, and E[] is the expected value of loss, which were obtained from the aforementioned statistics analysis of the computed response in terms of loss for each family of inelastic SDOFs.
3.4. Computing the Exceedance Rate of Loss
Upon defining the exceedance rate of the magnitudes of the analyzed seismic source and the exceedance probability of loss, it is possible to solve Equation (1). Figure 8 shows an example of an exceedance rate of loss computed with Equation (1) for an SDOF with T = 2.2 s and = 300 gals.
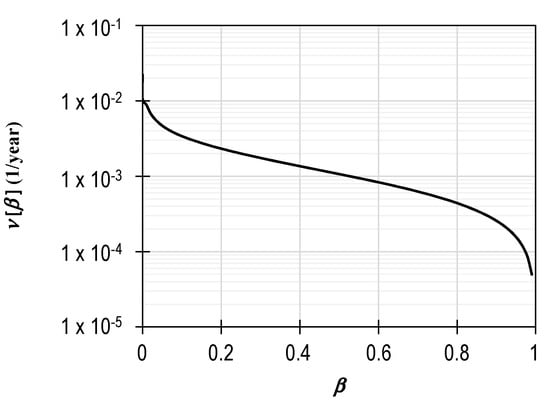
Figure 8.
Annual exceedance rate of the loss curve associated to Say = 300 gals and T = 2.2 s.
By repeating the previous steps for all of the considered lateral strengths, , but keeping constant the vibration period, T, it is possible to obtain a 3D surface that represents the relationship among loss, lateral strength, and exceedance rate of loss. Figure 9 shows an example of the 3D surface β-ν(β)- for a family of SDOF with T = 2.2 s.
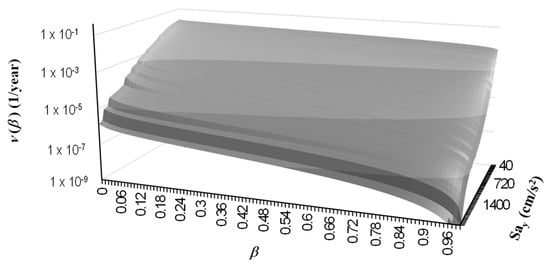
Figure 9.
β-ν(β)- surface of exceedance rate of loss curves associated to a T = 2.2 s.
To build a uniform risk spectrum, it is necessary to compute a 3D surface (β-ν(β)-) for each considered vibration period. Subsequently, a couple of loss and an exceedance rate of loss values must be selected. According to the selected loss and exceedance rate of loss values, the corresponding lateral strength in each 3D surface (i.e., each vibration period) must be obtained. The URS is the spectra built with all of the lateral strengths of the considered vibration periods associated to the same loss and exceedance rate of loss. Figure 10 shows a comparison between the uniform hazard spectra (UHS) and URS for the analyzed site in terms of the return period (RP), i.e., the inverse of the exceedance rate. It can be readily seen that differences in the spectral ordinates for different values of loss and return period exist. For instance, for a constant value of β, the spectral ordinates were higher as the RP increased; on the other hand, if the RP was constant and β increased, the seismic demands decreased, i.e., the accepted risk was higher, and the required strength of the structure was lower.
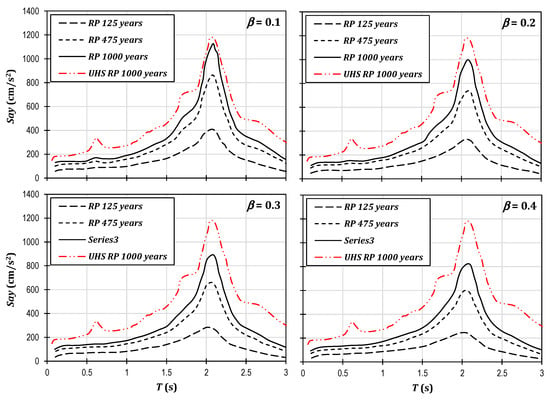
Figure 10.
Uniform risk spectra associated to several loss levels and return periods.
4. Accuracy of the Uniform Risk Spectra
In order to validate the URS’ accuracy, three reinforced concrete moment-resisting frames (MRFs) were analyzed. The basic mechanical characteristics of the materials were defined according to the Mexico City Building Code [78], and the lateral demands were obtained using RSA with the proposed uniform risk spectrum. It is expected that the risk level, β-ν(β), predicted using the URS is similar to that estimated via the Pacific Earthquake Engineering Research Institute (PEER) methodology [4,5].
4.1. Summary of Mechanical Characteristics
The concrete and steel reinforcement properties are Ec = 221,359 kg/cm2 (21,707 MPa); f’c =250 kg/cm2 (24.5 MPa); Es = 2,010,000 kg/cm2 (197,113 MPa); fy = 4200 kg/cm2 (412 MPa). Table 3 summarizes the main structural characteristics for the analysis, and Figure 11 shows the structural typology for each structure.

Table 3.
Mechanical and structural characteristics of the models.
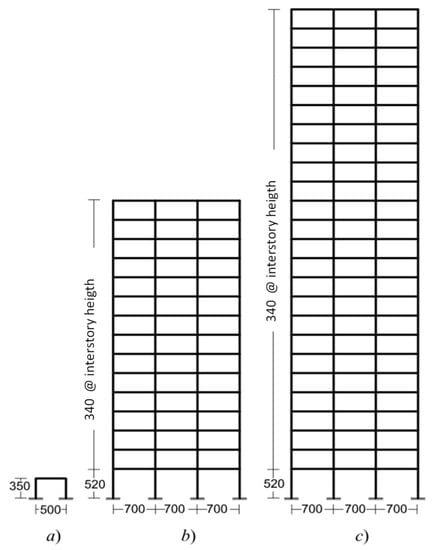
Figure 11.
MRF: (a) single bay, single story; (b) three bays, fifteen stories; (c) three bays, twenty-five stories, dimensions in cm.
The design seismic demands of each structure were calculated with RSA using the URS. Thus, all structures were designed for a 10% loss every 475 years; hence, the corresponding URS was employed (Figure 12).
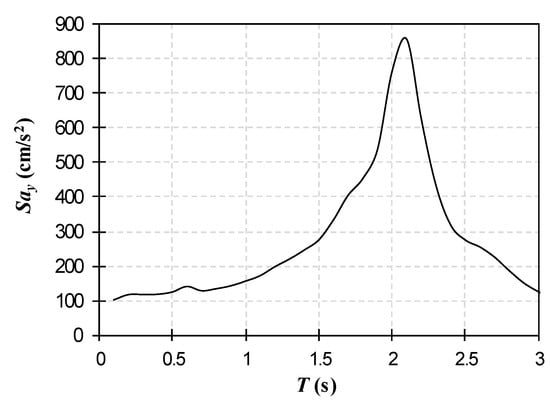
Figure 12.
Uniform risk spectrum associated to β = 0.1 and RP = 475 years.
For modeling the aforementioned MRFs, the DRAIN 2.0 [79] structural analysis program was used. To be in agreement with the used URS (Figure 11), the Takeda hysteretic model was adopted to represent their nonlinear behavior (beams and columns), considering a damping factor of 5% of the critical and a post-yielding stiffness ratio equal to 10%. For validation purposes, the strength of the structural elements was taken equal to the force demands of the structural elements obtained from the performed RSA.
It has been observed that overstrength is an important factor in the design process. To consider its effects, reduction factors [31,80] have been proposed; however, the use of these reduction factors was not included in the URS shown here.
4.2. Risk Assessment Process
The equation proposed to carry out the risk assessment (Equation (6)) is provided by the Pacific Earthquake Engineering Research Centre [4,57]:
where (DV|DM) is the probability of a decision vector exceeding a specific parameter measure; (DM|IM) is the damage exceedance probability given an intensity measure; and is the exceedance rate of the magnitudes.
Equation (6) considers both the seismic hazard and the building vulnerability under a probabilistic approach. It implies the expansion of the exceedance rate of the decision variables in terms of a loss measure and an intensity measure. Previous studies [3,4,5] have shown that this equation may be the best-known methodology for the seismic risk assessment of structures.
Since in this paper, the aim is to obtain the exceedance rate of loss, Equation (6) may be re-written as follows:
where G (DM|IM) is the seismic vulnerability (vulnerability curve), and is the seismic hazard (exceedance rate of intensities).
For estimating the seismic vulnerability of the analyzed structures, several incremental dynamic analyses (IDAs) [81] were carried out. For this purpose, the same 550 seismic records, as described previously, were used. Figure 13 shows the estimated IDA curves in terms of the maximum inter-story drift (γmax) for each structure; the gray lines represent the IDA curves for each seismic record, and the black line represents the average curve.
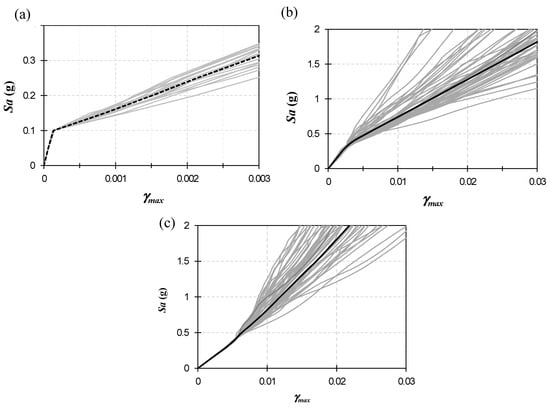
Figure 13.
IDA curves corresponding to (a) 1-story, (b) 15-story, and (c) 25-story structures.
On the other hand, to map the interstory drift obtained from the IDA curves to physical damage [82,83,84], the damage index vs. interstory drift curves were defined separately for three SDOF systems whose characteristics (T and Say) were consistent with those of the analyzed structures. For this purpose, the values for T of the SDOFs were taken equal to the fundamental periods of the MRF structures, and the Say values were defined as the spectral ordinates Sa of the design URS for the corresponding periods. Later, the damage index was mapped to loss using Equation (2). Figure 14 shows the obtained relationships for each structure.
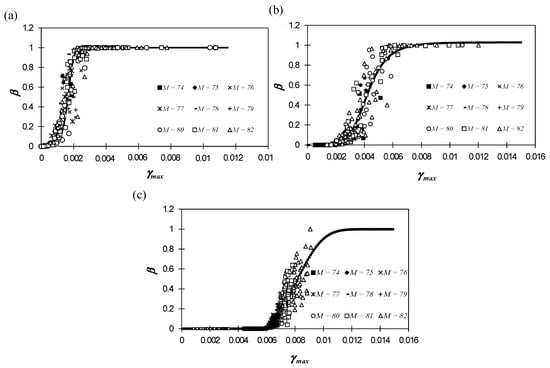
Figure 14.
Interstory drift vs. loss (markers) and fitted curve (continuous line) associated to (a) 1 story, (b) 15 stories, and (c) 25 stories for different magnitudes.
The two types of curves computed previously (IDA and interstory drift—loss curves) (Figure 13 and Figure 14) were related to estimate the corresponding vulnerability function for each structure; as a result, curves that relate the seismic intensity level and a loss value (Sa vs. β) were obtained. This process was performed for each computed IDA curve.
The vulnerability functions, VFs, are the result of the statistical analysis of the whole set of intensity measure vs. loss curves obtained for all of the considered seismic records; as a result, the expected value, E[β], and standard deviation, σ[β], associated to each intensity measure were obtained (Figure 15).
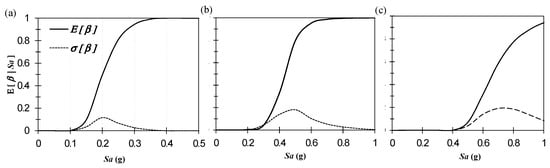
Figure 15.
Vulnerability function: (a) 1-story; (b) 15-story, and (c) 25-story structures.
Generally, the exceedance rate of intensities is obtained through a probabilistic seismic hazard assessment (PSHA). In this paper, the exceedance rate of intensities associated to each structural vibration period corresponding to the three analyzed structures were obtained with an inverse process, i.e., from the UHS obtained for the studied seismic source obtained by Niño et al. [59], where the exceedance rate of the magnitudes (Figure 3) was considered. The annual exceedance rate of intensity associated with each structural vibration period of the analyzed structures are presented in Figure 16.
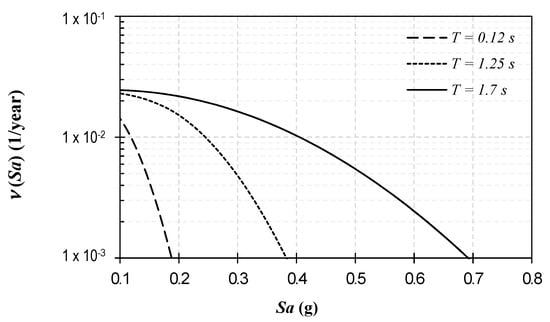
Figure 16.
Exceedance rate of intensities associated to the studied seismic source for structural vibration periods of 0.12, 1.25, and 1.80 s.
Equation (7) was solved for several levels of seismic intensity to obtain the corresponding exceedance rate of loss associated to the analyzed structures. These curves represent the mean number of times that a loss value is exceeded annually. The computed curves of the exceedance rate of loss of the three designed frames (continuous line) are shown in Figure 17 in addition to the design exceedance rate of loss of the URS (square marker).
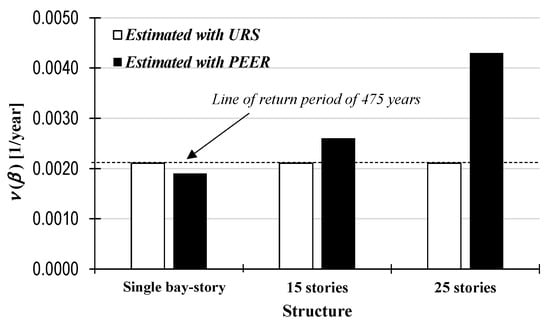
Figure 17.
Comparison between the estimated exceedance rate of loss from the design (URS) and the estimated exceedance rate of loss after the design using the PEER approach.
Keeping in mind that the presented structures were designed to exceed (on average) a 10% loss every 475 years, for the 1- and 15-story frames, the proposed URS allowed for the design of structures that developed a risk level close to the one desired, since the risk levels calculated for the designed structures were similar to that of the URS used (error less than 20%). On the other hand, for the case of 25-story frame, the URS would seem to underestimate the necessary seismic forces associated with the accepted risk level. The results for the 25-story frame might be attributable to simplifications in the estimation of the exceedance rate of loss curve. In this paper the correlation between damage and structural seismic response is based on the dynamic response of a reference SDOF system subjected to the action of several seismic ground motion records, without taking into account the effects that are present in complex structures, such as the local and global damage definition. This generated inconsistences in the estimation of the associated VFs, where, in the same way, high loss values were presented under relatively low demands. For this reason, the risk obtained from the seismic assessment was larger than expected.
To avoid these inconsistences, a very detailed damage analysis should be carried out for the whole structure during the seismic assessment process, such as the local (element) to global (structure) damage and its correlation with a performance parameter including interstory drift; this will allow for the better estimation of the VF and, subsequently, the corresponding exceedance rate of loss.
5. Conclusions
The proposed formulation to compute the uniform risk spectra offers a rational way to provide a predetermined seismic risk level for structures in an explicit manner from the beginning of the design process without the need for later assessment. This provides valuable information for civil engineers on the economic losses that a structure will have in its lifetime, contrary to the current design spectra of most seismic codes, which do not provide, at least in an explicit way, the consequences of choosing a reduction factor in the seismic demands. It is necessary to start considering seismic risk in the planning of new cities; therefore, URS may be useful as a first tool for the development of new structures.
The proposed formulation considers the main aspects that define the structural response of any building, the structural characteristics that define the seismic response of a structural type, and the seismic hazard of the site where a given structure will be built. Furthermore, to consider the possible economic loss associated with the structural damage, reparation cost was considered as the damage variable in this study. Nonetheless, it is important to highlight that the reparation costs present high variability with time compared to the structural characteristics or the seismic hazard This represents a great challenge for future studies where this variability may be introduced in the computation.
For the sake of simplicity, the proposed formulation was exemplified with the calculation of a URS associated to a specific site, considering a single seismic source. However, for the actual design of applications, it is necessary to consider all seismic sources that affect the site of interest.
Furthermore, a validation example of the seismic demands associated to a specific risk level was carried out through the seismic design of three different RC structures via RSA using one of the computed URS as the design spectra. The validation shows that the use of URS allows for the design of low- or medium-rise structures that approximate sufficiently the target seismic risk level. However, for the high-rise structures, the results were different to those expected, mainly due to simplifications in the calculation of the exceedance rate of loss curve using the PEER methodology.
It must be recognized that the main objective of the development of the URS shown herein is for them to be used in practical seismic design applications. Therefore, some simplifications that were considered in this work should be addressed in future studies, such as the effects of the overstrength or structural irregularities in the computation of the seismic demands using this type of spectra.
Author Contributions
Conceptualization, L.B. and M.N.; methodology, L.B. and M.N.; software, L.B. and M.N.; validation, M.N. and E.R.; formal analysis, C.G. and M.N.; investigation, L.B. and M.N.; resources, L.B. and M.N.; data curation, L.B. and C.G.; writing—original draft preparation, L.B., C.G. and M.N.; writing—review and editing, M.N. and E.R.; visualization, M.N. and E.R.; supervision, M.N. and E.R.; project administration, M.N.; funding acquisition, M.N. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Council of Humanities, Science, and Technology (CONAHCyT), project number: A1-S-35223, “Seismic Demands Definition for the Risk and Resilience-Based Design of Structures”.
Data Availability Statement
Data supporting reported results can be found in http://132.248.52.100:8080/xmlui/handle/132.248.52.100/10733.
Acknowledgments
The first and last authors thank CONAHCyT for the MSc and PhD scholarships awarded during the development of this work.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
References
- WEF. The Global Risk Report 2019. In Insight Report, 14th ed.; World Economic Forum: Geneva, Switzerland, 2019. [Google Scholar]
- Federal Emergency Management Agency (FEMA). Seismic Performance Assessment of Buildings-Methodology; Fema P-58-1; FEMA: Washington, DC, USA, 2012; Volume 1, p. 278.
- Moehle, J.; Stojadidinovic, B.; Kiureghian, A.; Yang, T. An Application of PEER Performance-Based Earthquake Engineering Methodology; Pacific Earthquake Engineering Research Centre: Berkeley, CA, USA, 2005; pp. 2–5. [Google Scholar]
- Günay, S.; Mosalam, K. PEER Performance-based earthquake engineering methodology, revised. J. Earthq. Eng. 2013, 17, 829–858. [Google Scholar] [CrossRef]
- Bazzurro, P.; Cornell, A.; Menun, C.; Motahari, M.; Luco, N. Advanced Seismic Assessment Guidelines; Pacific Earthquake Engineering Research Center: Berkeley, CA, USA, 2006. [Google Scholar]
- Esteva, L. Bases para la Formulacion de Decisiones de Diseno Sismico. Ph.D. Thesis, Universidad Autonoma Nacional de Mexico, Mexico City, Mexico, 1968. [Google Scholar]
- Esteva, L. Seismic risk and seismic design decisions. In Proceedings of the MIT Symposium, Seismic Design For Nuclear Power Plants, Cambrige, MA, USA, 15 March 1970. [Google Scholar]
- McGuire, R. Probabilistic seismic hazard analysis and design earthquakes. Bull. Seismol. Soc. Am. 1995, 85, 1275–1284. [Google Scholar] [CrossRef]
- McGuire, R. Probabilistic seismic hazard analysis: Early history. Earthq. Eng. Struct. Dyn. 2007, 37, 329–338. [Google Scholar] [CrossRef]
- Noreña, F.; Castañeda, C.; Iglesias, J. The Mexico Earthquake of September 19, 1985—Evaluation of the Seismic Capacity of Buildings in Mexico City. Earthq. Spectra 1989, 5, 19–25. [Google Scholar] [CrossRef]
- Hail, F.; Beck, J. Structural damage in Mexico City. Geophys. Res. Lett. 1986, 13, 589–592. [Google Scholar] [CrossRef]
- Bruneau, M. Preliminary report of structural damage from Loma Prieta (San Francisco) earthquake 1989 and pertinence to Canadian structural engineering practice. Can. J. Civ. Eng. 1990, 17, 198–208. [Google Scholar] [CrossRef]
- EERI. Northridge Earthquake, January 17, 1994. Preliminary Reconnaissance Report; 94-01; Earthquake Engineering Research Institute: Oakland, CA, USA, 1994. [Google Scholar]
- Muguruma, H.; Nishiyama, M.; Watanabe, F. Lessons learned from the Kobe earthquake—A Japanese perspective. PCI J. 1995, 40, 28–42. [Google Scholar] [CrossRef]
- Mera, W.; Vera, X.; La Tegola, A.; Ponce, G. April 2016 Ecuador Earthquake of Moment Magnitude Mw7.8: Overview and Damage Report. Key Eng. Mater. 2017, 747, 662–669. [Google Scholar] [CrossRef]
- Reinoso, E.; Quinde, P.; Buendía, L.; Ramos, S. Intensity and damage statistics of the September 19, 2017 Mexico earthquake: Influence of soft story and corner asymmetry on the damage reported during the earthquake. Earthq. Spectra 2021, 37, 1875–1899. [Google Scholar] [CrossRef]
- Park, R.; Paulay, T. Reinforced Concrete Structures; John Wiley and Sons: New York, NY, USA, 1976. [Google Scholar]
- Xiang, N.; Shahria, M. Displacement-based seismic design of bridge bents retrofitted with various bracing devices and their seismic fragility assessment under near-fault and far-field ground motions. Soil Dyn. Earthq. Eng. 2019, 119, 75–90. [Google Scholar] [CrossRef]
- Moehle, J. Displacement-based of RC structures subjected to earthquakes. Earthq. Spectra 1992, 8, 403–428. [Google Scholar] [CrossRef]
- Priestley, M.; Calvi, G. Concepts and procedures for direct displacement-based design and assessment. In Seismic Design Methodologies for the Next Generation of Codes; Fajfar, P., Krawinkler, H., Eds.; Routledge: Rotterdam, The Netherlands, 1997; pp. 171–182. [Google Scholar]
- López, S.; Ayala, G. Displacement-based seismic design method for RC frames. Rev. Mex. Ing. Sísmica 2013, 88, 91–111. (In Spanish) [Google Scholar]
- NZSEE; SESOC; NZGS. The Seismic Assessment of Existing Buildings; Technical Guidelines for Engineering Assessment: Wellington, New Zealand, 2017. [Google Scholar]
- PEER. Guidelines for Performance-Based Seismic Design of Tall Buildings; Report No. 2017/06; PEER & Charles Pankow Foundation: Berkeley, CA, USA, 2017. [Google Scholar]
- Riddell, R.; Newmark, N. Statistical Analysis of the Response of Nonlinear Systems Subjected to Earthquakes; Department of Civil Engineering University of Illinois at Urbana-Champaign: Urbana, IL, USA, 1979. [Google Scholar]
- Riddell, R.; Hidalgo, P.; Cruz, E. Response modification factors for earthquake resistant design of short period buildings. Earthq. Spectra 1989, 5, 571–590. [Google Scholar] [CrossRef]
- Hidalgo, P.; Arias, A. New Chilean code for earthquake resistant design of buildings. In Proceedings of the 4th U.S. National Conference Earthquake Engineering, Palms Spring, CA, USA, 20–24 May 1990. [Google Scholar]
- Nassar, A.; Krawinkler, H. Seismic Demands for SDOF and MDOF Systems; John Blume Earthquake Engineering Center; Department of Civil Engineering Report 95; Stanford University: Stanford, CA, USA, 1991. [Google Scholar]
- Miranda, E. Site-dependant strength-reduction factors. J. Struct. Eng. 1993, 115, 2166–2183. [Google Scholar]
- Anand, V.; Kumar, S. Sensitivity of strength reduction factor for structures considering soil-structure interaction. Structures 2022, 39, 593–606. [Google Scholar] [CrossRef]
- Miranda, E. Estimation of Maximum Inter-Storey Drift Demands in Displacement-Based Design. In Seismic Design Methodologies for the Next Generation of Codes; Fafjar, P., Krawinkler, H., Eds.; Routledge: Rotterdam, The Netherlands, 1997; pp. 253–264. [Google Scholar]
- Zerbin, M.; Aprile, A.; Spacone, E. New formulation of ductility reduction factor or RC frame-wall dual systems for design under earthquake loadings. Soil Dyn. Earthq. Eng. 2020, 138, 106279. [Google Scholar] [CrossRef]
- Chikh, B.; Mebarik, A.; Laouami, N.; Mehani, Y. Inelastic deformation ratio for seismic assessment of structures. Procedia Eng. 2017, 199, 558–563. [Google Scholar] [CrossRef]
- Mendoza, E.; Díaz, O.; Esteva, L. Consistent-reliability spectra for some nonlinear SDOF systems. In Proceedings of the ICCOSSAR 89 5th International Conference Structural Safety and Reliability, San Francisco, CA, USA, 10 August 1989. [Google Scholar]
- Gkimprixis, A.; Tubaldi, E.; Douglas, J. Comparison of methods to develop risk-targeted seismic design maps. Bull. Earthq. Eng. 2019, 17, 3727–3752. [Google Scholar] [CrossRef]
- Avelar, C.; Ayala, G.; de León, A. Design spectra determination for performance based seismic design. In Proceedings of the 9th International Conference Applications Statistics Probability Civil Engineering, Amsterdam, The Netherlands, 6–9 July 2003. [Google Scholar]
- Rivera, J. Design approach based on UAFR spectra for structures with displacement-dependent dissipating elements. Earthq. Spectra 2007, 23, 417–439. [Google Scholar] [CrossRef]
- Datta, D.; Ghosh, S. Estimating Park-Ang damage index using equivalent systems. In Proceedings of the 14th World Conference Earthquake Engineering, Beijing, China, 12–17 October 2008. [Google Scholar]
- Loth, C.; Baker, J. Rational design spectra for structural reliability assessment using the response spectrum method. Earthq. Spectra 2015, 31, 2007–2026. [Google Scholar] [CrossRef]
- Niño, M.; Ayala, G.; López, S. Uniform fragility spectra for the performance-based seismic design of structures considering variabilities in structural properties. Earthq. Eng. Struct. Dyn. 2018, 47, 1742–1754. [Google Scholar] [CrossRef]
- Kennedy, R.; Short, S.A. Basis for Seismic Provisions of DOE-STD-1020; Rep. No. UCRL-CR-111478; Lawrence Livermore National Laboratory, Livermore, Calif., and Rep. No. BNL52418; Brookhaven National Laboratory: Upton, NY, USA, 1994. [Google Scholar]
- Cornell, A. Calculating building seismic performance reliability: A basis for multi-level design norms. In Proceedings of the11th World Conference Earthquake Engineering, Acapulco, Mexico, 23–28 June 1996. [Google Scholar]
- Luco, N.; Ellingwood, B.; Hamburger, R.; Hooper, J.; Kimball, J.; Kircher, C. Risk-targeted versus current seismic design maps for the conterminous United States. In Proceedings of the SEAOC 2007 Convention, Squaw Creek, CA, USA, 26–29 September 2007. [Google Scholar]
- Sewell, R. Damage Effectiveness of Earthquake Ground Motion: Characterizations Based on the Performance of Structures and Equipment; Stanford University: Stanford, CA, USA, 1989. [Google Scholar]
- Borzognia, Y.; Hachem, M.; Campbell, K. Ground motion prediction equation (“attenuation relationship”) for inelastic response spectra. Earthq. Spectra 2010, 26, 1–23. [Google Scholar] [CrossRef]
- Douglas, J. Ground Motion Prediction Equations 1964–2021; Department of Civil and Environmental Engineering, University of Strathclyde: Glasgow, UK, 2022. [Google Scholar]
- Zizmond, J.; Dolsek, M. Formulation of risk-targeted seismic action for the force- based seismic design of structures. Earthq. Eng. Struct. Dyn. 2019, 48, 1406–1428. [Google Scholar] [CrossRef]
- Sanchez-Sesma, F.; Chávez-Pérez, S.; Suárez, M.; Bravo, M.; Pérez-Rocha, L.E. The Mexico Earthquake of September 19, 1985—On the Seismic Response of the Valley of Mexico. Earthq. Spectra 1988, 4, 569–589. [Google Scholar] [CrossRef]
- Bard, P.; Campillo, M.; Chavez-Garcia, F.; Sanchez-Sesma, F. The Mexico Earthquake of September 19, 1985—A theoretical investigation of large- and small-scale amplification effects in the Mexico City valley. Earthq. Spectra 1988, 4, 609–633. [Google Scholar] [CrossRef]
- Seed, H.; Romo, M.; Sun, J.; Jaime, A.; Lysmer, J. The Mexico earthquake of September 19, 1985—Relationships between soil conditions and earthquake ground motions. Earthq. Spectra 1988, 4, 687–729. [Google Scholar] [CrossRef]
- Kawase, H.; Aki, K. A study on the response of a soft basin for incident S, P, and Rayleigh waves with special reference to the long duration observed in Mexico City. Bull. Seismol. Soc. Am. 1989, 79, 1361–1382. [Google Scholar]
- Chavez-Garcia, F.; Bard, P. Site effects in Mexico City eight years after the September 1985 Michoacán earthquakes. Soil Dyn. Earthq. Eng. 1994, 13, 229–240. [Google Scholar] [CrossRef]
- Singh, S.K.; Quaas, R.; Ordaz, M.; Mooser, F.; Almora, D.; Torres, M.; Vasquez, R. Is there truly a “hard” rock site in the Valley of Mexico? Geophys. Res. Lett. 1995, 22, 481–484. [Google Scholar] [CrossRef]
- Reinoso, E.; Ordaz, M. Spectral ratios for Mexico City from free-field recordings. Earthq. Spectra 1999, 15, 273–295. [Google Scholar] [CrossRef]
- Jaimes, M.; Reinoso, E.; Ordaz, M. Comparison of methods to predict response spectra at instrumented sites given the magnitude and distance of an earthquake. J. Earthq. Eng. 2006, 10, 887–902. [Google Scholar] [CrossRef]
- Jaimes, M.; Gaytán, A.; Reinoso, E. Ground-motion prediction model from intermediate-depth intraslab earthquakes at the hill and lake-bed zones of Mexico City. J. Earthq. Eng. 2015, 19, 1260–1278. [Google Scholar] [CrossRef]
- Cruz-Atienza, V.; Tago, J.; Sanabria-Gomez, D.; Chaljub, E.; Etienne, V.; Vireux, J.; Quintanar, L. Long duration of ground motion in the paradigmatic valley of Mexico. Nat.-Sci. Rep. 2016, 6, 38807. [Google Scholar] [CrossRef] [PubMed]
- Cornell, A.; Krawinkler, H. Progress and challenges in seismic performance assessment. PEER Cent. News. 2000, 3, 1–4. [Google Scholar]
- Reinoso, E.; Jaimes, M. Criteria to obtain design accelerograms in sites affected by several seismic sources. Rev. Mex. Ing. Sísmica 2009, 81, 1–18. (In Spanish) [Google Scholar]
- Niño, M.; Ayala, G.; Ordaz, M. Ground-Motion Simulation by the Empirical Green’s Function Method with a Source Defined by Two Corner Frequencies and a Two-Stage Summation Scheme. Bull. Seismol. Soc. Am. 2018, 18, 901–912. [Google Scholar] [CrossRef]
- Ordaz, M.; Miranda, E.; Reinoso, E. Expert system for the seismic loss assessment in Mexico. In Proceedings of the 12th Mexico Conferernce Earthquake Engineering, Morelia, Mexico, 17–20 November 1999. (In Spanish). [Google Scholar]
- Benjamin, J.; Cornell, A. Probability, Statistics and Decision for Civil Engineers; Courier Corporation: Chelmsford, MA, USA, 1970. [Google Scholar]
- Terán, A.; Jirsa, J. A damage model for practical seismic design that accounts for low cycle fatigue. Earthq. Spectra 2005, 21, 803–832. [Google Scholar] [CrossRef]
- Borzognia, Y.; Bertero, V. Damage spectra: Characteristics and applications to seismic risk reduction. J. Struct. Div. 2003, 3, 411–438. [Google Scholar]
- Takeda, T.; Sozen, M.; Nielsen, N. Reinforced Concrete Response to Simulated Earthquakes. Struct. Div. ASCE 1970, 96, 2257–2573. [Google Scholar] [CrossRef]
- Nakashima, M.; Saburi, K.; Tsuji, B. Energy input and dissipation behaviour of structures with hysteretic dampers. Earthq. Eng. Struct. Dyn. 1996, 25, 483–496. [Google Scholar] [CrossRef]
- Connor, J.; Wasa, A.; Iwata, M.; Huang, Y. Damage-controlled structures I: Preliminary design methodology for seismically active regions. Bull. Seismol. Soc. Am. 1997, 12, 423–431. [Google Scholar] [CrossRef]
- Jing, J.; Ye, L.; Quian, J. Inelastic seismic response of lumped mass MDOF systems based on energy concept. Eng. Mech. 2003, 20, 31–37. [Google Scholar]
- Qiang, H.; Feng, P. Seismic responses of postyield hardening single-degree-of-freedom systems incorporating high-strength elastic material. Earthq. Eng. Struct. Dyn. 2019, 48, 611–633. [Google Scholar] [CrossRef]
- Borzi, B.; Calvi, G.; Elnashai, A.; Faccioli, E.; Boomer, J. Inelastic spectra for displacement-based seismic design. Soil Dyn. Earthq. Eng. 2001, 21, 47–61. [Google Scholar] [CrossRef]
- Farrow, K.; Kurama, Y. SDOF demand index relationships for performance-based design. Earthq. Spectra 2003, 19, 799–838. [Google Scholar] [CrossRef]
- Ruiz-García, J.; Miranda, E. Performance-Based Assessment of Existing Structures Accounting for Residual Displacements; Department of Civil and Environmental Engineering Report No. 153; Stanford University: Stanford, CA, USA, 2005. [Google Scholar]
- Fu, Q.; Menun, C. Residual displacement caused by fault-normal near-field ground motions. In Proceedings of the 8th U.S. National Conference Earthquake Engineering, San Francisco, CA, USA, 18–22 April 2006. [Google Scholar]
- Park, Y.; Ang, A.; Wen, Y. Seismic damage analysis of reinforced concrete buildings. J. Struct. Eng. 1985, 1, 740–757. [Google Scholar] [CrossRef]
- Kanno, R. Strength Deformation and Seismic Resistance of Joints between Steel Beams and Reinforced Concrete Columns; Cornell University: Ithaca, NY, USA, 1993. [Google Scholar]
- Stone, W.; Taylor, A. Seismic Performance of Circular Bridge Columns Designed in Accordance with AASHTO/CALTRANS Standards; NIST Building Sciences Series 170; Federal Highway Administration: McLean, VA, USA, 1993.
- EERI. Expected Seismic Performance of Buildings; Publication Number SP-10; EERI: Oakland, CA, USA, 1994. [Google Scholar]
- Chacón, R.; Paz, I. Seismic Performance Analysis of Typical School Building 780 post 97 on the Peruvian Coast. Master’s Thesis, Catholic University of Peru, San Miguel, Peru, 2016. (In Spanish). [Google Scholar]
- Mexico City Government. Normas Técnicas Complementarias para Diseño y Construcción de Estructuras de Concreto; Gaceta Oficial de la Ciudad de México: Mexico City, Mexico, 2017. (In Spanish)
- Prakash, V.; Powell, G.; Campbell, S. DRAIN, Base Program Description and User Guide; Department of Civil Engineering, University of California: Berkeley, CA, USA, 1993. [Google Scholar]
- Miranda, E. Strength reduction factors in performance-based design. In Proceedings of the Symposium to Honor Vitelmo Vertero, Berkeley, CA, USA, 31 January–1 February 1997. [Google Scholar]
- Vamvatzikos, D.; Cornell, A. Incremental dynamic analysis. Earthq. Eng. Struct. Dyn. 2001, 31, 491–514. [Google Scholar] [CrossRef]
- Kircher, C.; Nassar, A.; Kutsu, O.; Holmes, W. Development of building damage functions for earthquake loss estimation. Earthq. Spectra 1997, 13, 663–682. [Google Scholar] [CrossRef]
- Calvi, G. A displacement-based approach for vulnerability evaluation of classes of buildings. J. Earthq. Eng. 1999, 3, 411–438. [Google Scholar] [CrossRef]
- Panagiotakos, T.; Fardis, M. Deformations of reinforced concrete members at yielding and ultimate. ACI Struct. J. 2001, 98, 135–148. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).