Abstract
To maintain the life of building materials, it is critical to understand the hygrothermal transfer mechanisms (HTM) between the walls and the layers inside the walls. Due to the extreme instability of weather data, the actual data models of the HTM—the data being collected for actual buildings using modern sensor technologies—would appear to be a great difference from any theoretical models, in particular, for wood building materials. In this paper, we aim to consider a variety of data analysis tools for hygrothermal transfer features. A novel approach for peak and valley detection is proposed based on the discrete differentiation of the original data. Not to be limited to the measure of peak and valley delays for HTM, we propose a cross-correlation analysis to obtain the general delay between two daily time series, which seems to be representative of the delay in the daily time series. Furthermore, the seasonal pattern of the hygrothermal transfer combined with the correlation analysis reveals a reasonable relationship between the delays and the indoor and outdoor climates.
1. Introduction
Buildings are one of the largest energy consumers in the world, and improving their energy efficiency is crucial to mitigating climate change [1]. Buildings’ energy demand is predicted to continue growing worldwide in the coming decades [2]. Hygrothermal transfer of building exterior walls, which refers to the movement of heat and moisture through the wall assemblies, is an important aspect of building energy efficiency [3]. Moreover, the hygrothermal performance of exterior walls is a crucial issue in the design, assessment, and construction of energy-efficient buildings [4], which plays a vital role in building performance, including energy consumption [5], corrosion resistance of structural materials [6], occupant comfort and health [7], and material durability [8]. Research on the hygrothermal performance of exterior walls has been an important and active area of investigation since the mid-20th century. Two types of models are commonly used to study this topic: physical models and data-driven models [9]. Physical models are based on fundamental principles of heat and mass transfer and require detailed knowledge of the physical properties and behavior of the materials involved. On the other hand, data-driven models are based on machine learning methods or statistical analysis of measured data and do not necessarily require explicit knowledge of the underlying physical mechanisms.
Since the 1950s, extensive research has been conducted on physical models of heat and moisture transfer in porous media [9]. Various models have been developed, including the Philip and De Vries model, the Luikov model, the Whitaker model, the Künzel model, and the Mendes model. Simulation software, WUFI Pro, has been developed based on the physical models. Additionally, simulation platforms such as COMSOL Multiphysics, FLUENT, and MATLAB provide the possibility to develop simulation applications for studying HTM. These software tools are capable of accurately characterizing moisture diffusion and heat transfer within the layers of building walls, enabling a precise description of the exchange of water vapor between the room air and the outer walls. However, it relies heavily on simulations and mathematical models, which often do not accurately reflect the actual performance of buildings in real-world conditions. Moreover, physical models require heavy numerical computations and long calculation times and depend heavily on expert knowledge, with a large number of inputs needed to define the models. In addition, obtaining accurate parameters for the models can be difficult or impossible in certain cases.
With the rapid development of sensor and computer technology, there has been an increasing interest in using data-driven methods to analyze and understand hygrothermal transfer in building components. These methods rely on analyzing large datasets obtained from the sensors placed on and inside the building components. Tijskens et al. (2019) [10] trained different types of Deep Neural Networks, such as MLP, RNN (LSTM and GRU), or CNN, to predict different hygrothermal time series like temperature, relative humidity (RH), and moisture content at certain positions in a masonry wall and according to both outdoor and indoor climates. The results indicate that only RNN (Recurrent Neural Networks) and CNN (Convolutional Neural Networks) are able to capture the complex patterns of the hygrothermal response. Additionally, CNN performed significantly better and was 10 times faster than RNN. Tijskens et al. (2021) [11] fine-tuned the CNN model to predict the hygrothermal response for timber frame walls. It is shown that the network can accurately predict the hygrothermal time series and can be employed with confidence to estimate the moisture damage risks (mold growth, condensation run-off risk). Tzuc et al. (2021) [12] developed an Artificial Neural Network (ANN)-based model to study the hygrothermal behavior inside a concrete wall based on the temperature and RH of both the external environment and the microclimate. Furthermore, the study of Tzuc et al. (2021) was accompanied by a global sensitivity analysis that allowed us to identify the relevance and impact of the modeling variables on hygrothermal performance. However, while AI models can provide accurate predictions, their main and common drawback is that they lack the ability to provide a clear physical understanding of the underlying hygrothermal transfer processes (black box).
Identifying transfer patterns is a crucial step in calculating the dynamic changes of moisture within building materials under natural climatic conditions. However, understanding hygrothermal transfer quantitatively can be challenging due to the complexity of the transfer process, which is influenced by various factors such as regional climates and environments, wall construction materials, and configurations. To address this issue, advanced machine learning methods are required. In our previous study, we analyzed the hygrothermal transfer pattern from the outside of the wall (RHT12) to the interior bamboo and wood composite sheathing (RHT11) based on the peak delay of the daily hygrothermal time series [13]. The results revealed a dominant effect of RHT12 on RHT11, and an inherent time delay during hygrothermal transfer from RHT12 to RHT11. The transfer time ranged from 1 to 2 h for temperature and 1 to 4 h for RH Moreover, the study was also able to capture the seasonal patterns of hygrothermal transfer and revealed a linear relationship between temperature and moisture transfer. Specifically, the results showed that higher temperatures lead to faster moisture transfer from RHT12 to RHT11. In this study, we aim to further develop our understanding of hygrothermal transfer by expanding our analysis to include more datasets and proposing new approaches to improve accuracy. The main objective is to overcome the limitations of the physical models and AI models: (i) reduce the heavy requirement for input variables and computation time compared to physical models; and (ii) provide a physical understanding of the hygrothermal transfer patterns compared to AI models. The rest of the paper is organized as follows. The next section describes the experimental setup, including how and where the data were collected. Subsequently, Section 3 covers the methodology and framework of this study. Finally, in Section 4, the results are presented and discussed.
2. Experimental Setup
All data used in this study were collected from an experimental building located in the Huangshan Mountain district of Anhui Province, China, as depicted in Figure 1b. The building is a modern example of Hui-style residential architecture, constructed entirely of locally sourced bamboo and Chinese fir materials. The building was left in its natural state without heating or air conditioning to study its hygrothermal performance under regional climate conditions [13]. The use of the experimental building provides a unique opportunity to study the behaviors of building materials under natural conditions, without the confounding effects of heating and cooling systems. Moreover, the building’s construction using locally sourced materials highlights the potential for sustainable building practices that can benefit both the environment and local communities.
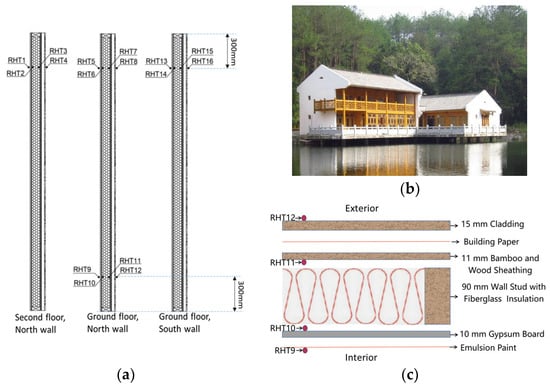
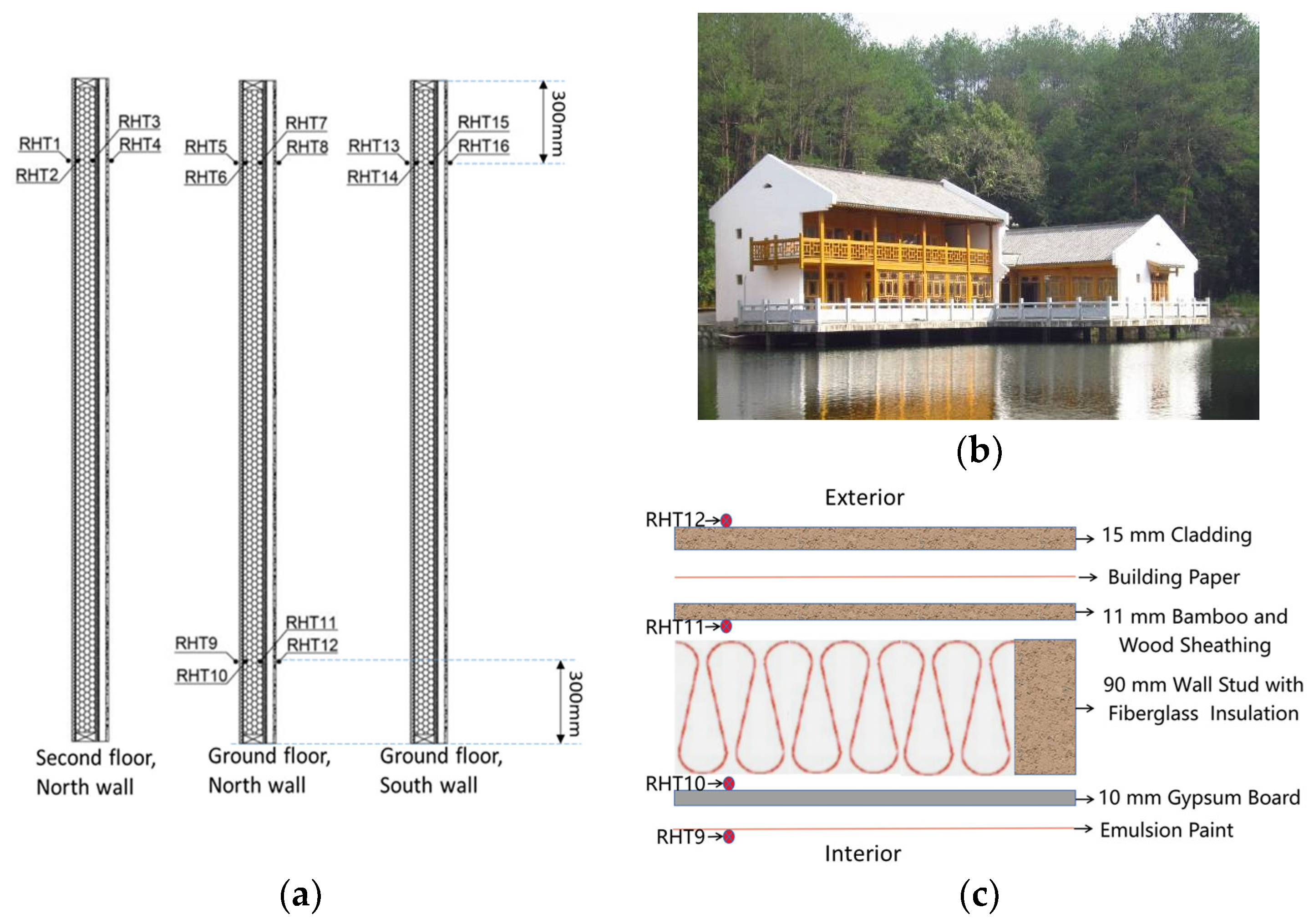
Figure 1.
(a) Sensor layout for a 2.8 m high wall section; (b) the experimental building; (c) the configuration and materials of the exterior wall (credited to [13]).
2.1. Exterior Wall Configuration and Sensor Installation
The exterior wall of the experimental building, depicted in Figure 1c, consisted of several layers, including manufactured cladding, sheathing membrane, bamboo and wood composite sheathing, studs, insulation, and gypsum. The structural panel sheathing on the exterior framing was 11 mm thick bamboo–wood composite, while the interior framing was finished with 10 mm thick gypsum board, which was painted with emulsion paint. The studs were filled with fiberglass insulation. In addition, the exterior bamboo–wood composite sheathing was covered with a vapor-permeable sheathing membrane to provide a water-resistive barrier. This configuration of materials and layers was designed to simulate a typical exterior wall construction for modern Chinese Hui-style residential buildings while also providing a controlled environment to study the hygrothermal performance of the wall under field conditions.
Figure 1a shows the sensor layout where 16 sensors were installed. These sensors were installed at different interfaces of the exterior wall to collect temperature and RH data. The sensors used were HygroClip S3 probes, capable of measuring temperature within a range of −40 °C to 60 °C and RH within a range of 0% to 100%. The sensors were connected to Campbell’s CR1000 data logger, which stored the collected data for further analysis. Continuing from our previous study [13], this study analyzed the data collected from the sensor set placed on the north wall of the building, positioned 300 mm above the ground, consisting of RHT9, RHT10, RHT11, and RHT12. The locations of these 4 sensors in the field are shown in Figure 1c.
2.2. Data Collection
The dataset was collected with the sensors RHT9–RHT12 from the year 2012 to 2017, while in this study only the dataset collected over the course of 2012 was used. The sensors measured temperature and RH values every 10 min, resulting in a total of 144 observations per day and 52,704 observations over the entire year. In this paper, T9, T10, T11, and T12 denote the temperature of sensors RHT9–RHT12, respectively, while RH9, RH10, RH11, and RH12 denote the RH of sensors RHT9–RHT12, respectively.
3. Methodology
3.1. Methodology Overviews
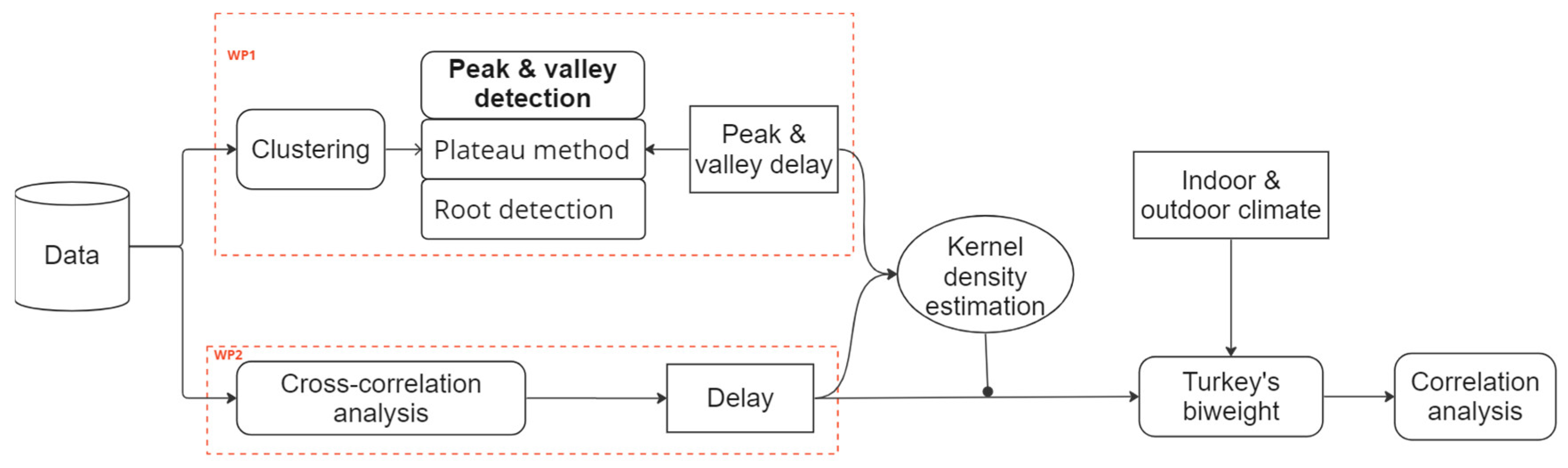
The research methodology is illustrated in Figure 2. Initially, the data analysis was conducted through two parallel work packages (WP1 and WP2). In WP1, a clustering analysis was performed (as detailed in Section 3.2.1) on the daily data segments to identify the most typical daily patterns. Subsequently, the peak and valley of the data segments were detected using two distinct methods proposed in this study, which are explained in detail in Section 3.2.2. The peak delay and valley delay were then used to represent the delay phenomena between adjacent sensors. The peak delay was determined by analyzing the difference between the peaks in the time domain, and similarly, the valley delay was determined. In WP2, the delay phenomenon between adjacent sensors was inferred through a correlation analysis, as explained in detail in Section 3.3.
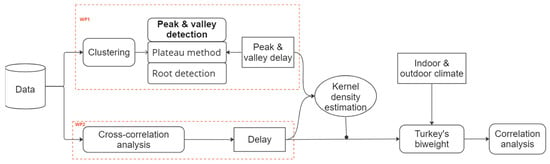
Figure 2.
An overview of the research workflow.
For a better visualization and quantitative comparison of the delay results obtained from WP1 and WP2, a kernel density estimation technique was utilized, as explained in Section 3.4. The results of the kernel density estimations indicated that the delay result of WP2 effectively represents the delay phenomenon across the entire dataset. As a result, this delay result, along with indoor and outdoor climate data, was fed into Turkey’s biweight algorithm to compute the monthly center of each variable, as detailed in Section 3.5. Finally, to explicitly reveal possible correlations between hygrothermal transfer properties and indoor/outdoor climates, a correlation analysis was applied to these monthly centers.
3.2. WP1
3.2.1. Clustering
To cluster the 366 days and identify the most typical daily patterns of RH, as studied in our previous paper [14], we found that utilizing hourly RH values as features and performing K-means clustering resulted in a highly concentrated pattern clustering outcome. Based on these findings, this study adopted the hourly RH values as features, with each hourly value calculated as the mean of the RH values recorded within the corresponding hour. This approach yielded a total of 366 samples (i.e., 366 days), each comprising 96 features (24 × 4, 24 stands for 24 h in a day, and 4 is the number of the channels of RH values that are RH9–12), which were subsequently used as the input for K-means clustering.
K-means clustering [15] is a popular unsupervised learning algorithm that partitions data points into k clusters based on their similarity. The algorithm works by iteratively assigning each data point to the cluster with the closest centroid, and then recalculating the centroids of each cluster based on the newly assigned data points. This process continues until the centroids converge and the clusters no longer change.
Firstly, we determined the optimal number of clusters for our dataset using the elbow method. The elbow method involves plotting the within-cluster sum of squares (WSS) for a range of cluster numbers and selecting the point at which the rate of decrease in WSS begins to level off, forming an “elbow” in the plot. This point represents the optimal number of clusters for the dataset. In addition, the silhouette coefficient for each data point is also calculated to assist in determining the optimal . This method measures the similarity of a data point to its assigned cluster relative to other clusters. The silhouette coefficient ranges from −1 to 1, with values closer to 1 indicating better clustering. Once we determined the optimal number of clusters, we then applied k-means clustering to the data using the scikit-learn library in Python. We ran the algorithm for 500 iterations with a random initialization to ensure convergence.
Overall, the k-means clustering approach allowed us to identify distinct daily patterns in the hygrothermal transfer of the building exterior wall and to group these patterns into clusters based on their similarity.
3.2.2. Peak and Valley Detection and Delay Calculation
First, the data is smoothed by an exponentially weighted (EW) moving average with a window size of 7. The EW function is calculated by Equation (1). In addition, the first seven observations in the dataset keep its original values.
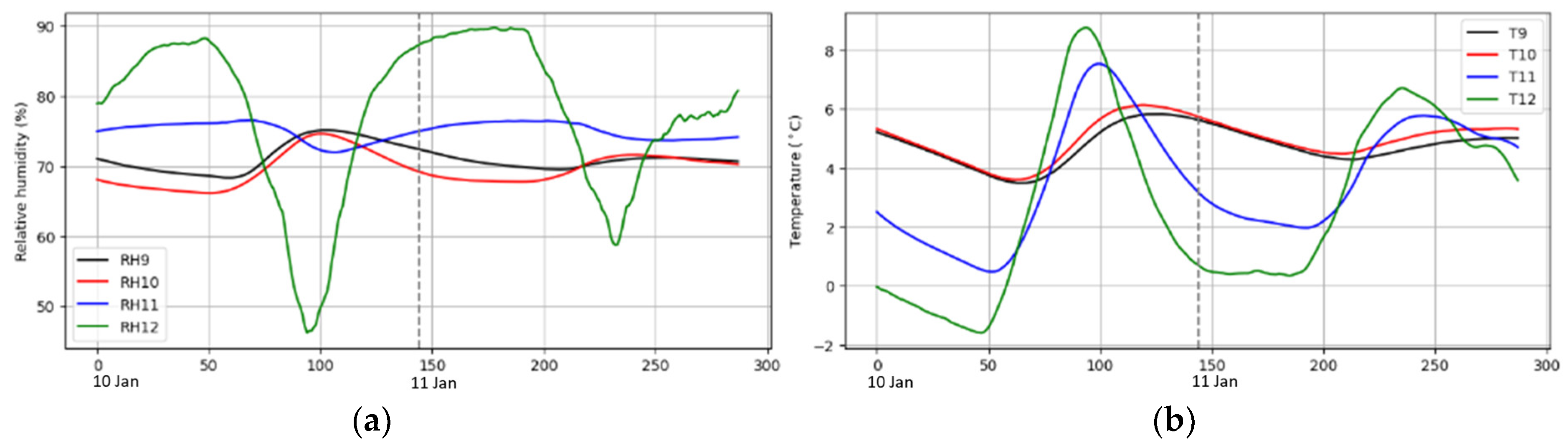
Figure 3 displays a two-day time series of smoothed RH and temperature data, which serves as an example in this study. The x-axis represents the index of the samples. Each increment of the index corresponds to a 10 min interval, as the data was collected with a logging time of 10 min. Consistent with our prior research findings in [13], outdoor RH (RH12) and temperature (T12) were found to exert a dominant influence on the inwall’s RH (RH10-11) and temperature (T10-11). That is, RHT12 has the largest amplitude and dominates the RH and temperature variations inside the wall. For example, as can be seen in Figure 3a, the increase/decrease trends happen in RH12 first until it reaches its peak/valley, followed by RH11 increasing/decreasing subsequently until its peak/valley which corresponds to the peak/valley of RH12. In a similar way, RH10 subsequently follows RH11. The same relationship appears among temperatures, as can also be observed in Figure 3b. In short, RHT12 was observed to be positively correlated with corresponding changes in the RH and temperature inside the wall.
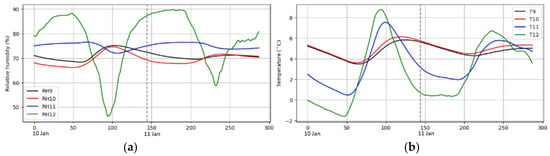
Figure 3.
An example of a two-day time series after smoothing: (a) relative humidity; (b) temperature.
To detect the daily peak and valley of each variable, two different methods were proposed as follows. As a result, the peak/valley delay between the adjacent sensors can then be calculated by the time difference between the peaks/valleys of the corresponding sensors. Specifically, the peak/valley delay between RHT12 and RHT11 is calculated by subtracting the timestamp of the peak/valley of RHT11 from the timestamp of the peak/valley of RHT12 on the same day. Likewise, the delay between RHT11 and RHT10 is calculated by subtracting the timestamp of the peak/valley of RHT10 from that of RHT11, and the delay between RHT10 and RHT9 is calculated by subtracting the timestamp of the peak/valley of RHT9 from that of RHT10.
- Plateau method
The peak detection, as referred to in our previous publication [13], records the indices and values of the peak point in the daily time series for each variable, i.e., RH12, RH11, RH10, RH9, T12, T11, T10, and T9. The method starts with finding the maximum and minimum values of the daily segment for each variable. It then creates a range of , where , and is the ratio parameter used to control the sensitivity of the peak detection algorithm. Then, the algorithm iterates backward through the data and identifies the first observation that has a value in the defined range . That identified observation is the peak . The mathematical expression is shown in Equation (2):
The peak delay time is calculated as the time difference between the peak of one sensor and the corresponding peak of its adjacent sensor. However, as explained in [13], RH12 and RH11 increase again in the afternoon, and sometimes they reach an even higher value than the peak that occurred earlier, which hinders us from correctly identifying the peak of RH12. We, therefore, limited the search range to overcome this issue, as illustrated in Equation (3).
Similarly, to identify the valley in the daily time series , the same algorithm can be adapted with adjustments. Firstly, the range is updated to , and then the valley can be defined as expressed by Equation (4).
However, Figure 3 reveals a potential issue with identifying the valleys of the RH10 and RH9 time series, as the following valley occurs on the next day, falling outside the daily segment. To address this issue, we have extended the search range for detecting the valleys of RH10 and RH9 using an expanded range, as described in Equation (5). In contrast, the temperature time series shows a distinct pattern, decreasing in the evening and presenting a risk of falling below the valley point earlier in the day. To tackle this issue, we have restricted the search range for identifying the valley of the daily temperature time series, as expressed in Equation (6). This approach allows us to identify the valley more accurately and avoid underestimating the temperature during the day. By adjusting the search range for each variable, we ensure that the valleys are accurately identified and captured, providing a robust basis for subsequent analysis.
- Root Detection
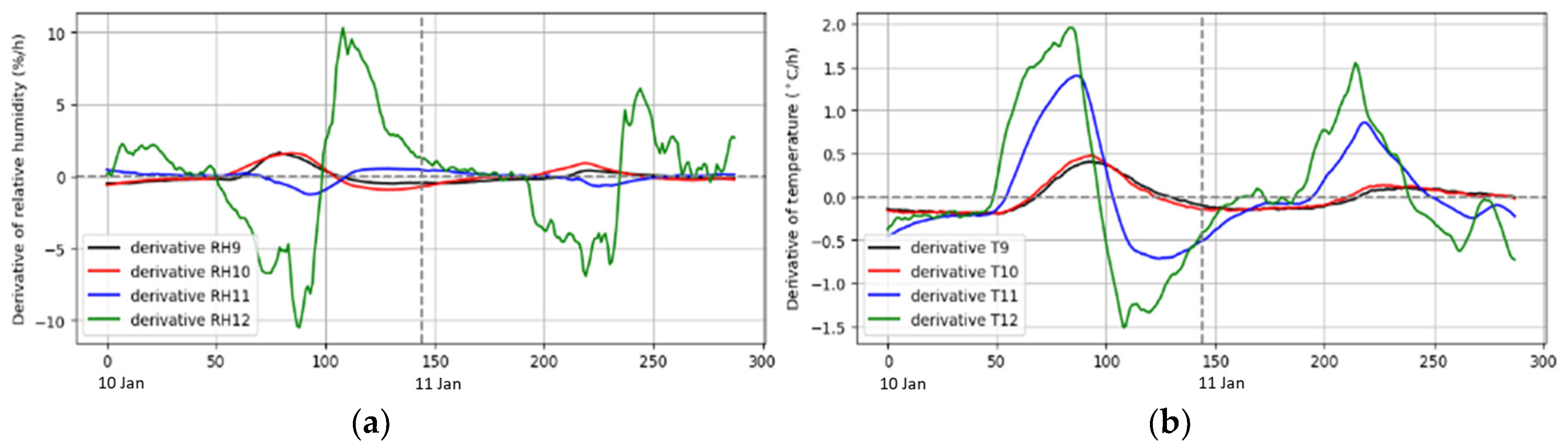
To identify the peak and valley of the daily time series from a fresh angle and potentially improve the identification of the peak point with greater accuracy and precision, as well as provide a more robust methodology for peak detection in noisy or irregularly spaced data, a two-step approach was employed. First, the discrete differentiation is calculated usingmin, to obtain the slope of the daily time series curve at each data point, which is subsequently smoothed by the EW moving average. Next, the data points were interpolated using the Python function “scipy.interpolate.interp1d” to obtain a continuous function that approximates the curve. Finally, the roots of the continuous function were found, which represent the peak and valley points in the original curve, respectively.
Figure 4 shows an example of the derivative of a two-day time series after being smoothed. However, multiple roots were detected around the corresponding peak and root in the original curve. To tackle this problem, similar to the plateau method, we first defined a search range that ensures that the peak falls within it, and then performed a backward search within this range to identify the first observation with ; is the derivative of at . The data point was identified as the one corresponding to the peak of the original data. Likewise, a search range is defined that ensures the valley falls within, and then a backward search is undertaken within this range to identify the first observation with ; is the derivative of at and is the data point that corresponds to the valley of the original data. The detailed calculation of the root detection can be found in Equations (7) and (8), as follows:
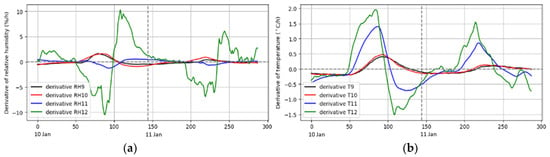
Figure 4.
An example of the derivative of a two-day time series after smoothing: (a) relative humidity; (b) temperature.
3.3. WP2
To obtain a general and systematic quantification of the delay between adjacent sensors on a daily basis, we proposed a cross-correlation analysis between the two-time series using the Spearman correlation coefficient. Cross-correlation [16] is originally a basic signal processing method that is used to analyze the similarity between two signals with different lags. Besides obtaining an idea of the precision of the matching between the two signals, the point of time (or index) of the maximum similarity can also be obtained.
To derive the delay between time series from two adjacent sensors on a daily basis, we first have one daily time series fixed, noted as {}. The length of the daily time series is 144 observations a day because of the 10 min interval sampling of the data collection. Then, the other time series has lags ranging from −144 to 144, noted as {. The choice of the range is to ensure the complete search for possible delays between any adjacent sensors, as well as to limit the search range for computational optimization. For each day , the Spearman correlation is calculated between time series and for each lag , noted as follows:
Then, the lag that corresponds to the maximum cross-correlation coefficient between and is selected, namely, . Consequently, the delay can be calculated using Equation (10) for each day .
3.4. Kernel Density Estimation
Kernel density estimation (KDE) is a non-parametric technique used for estimating the probability density function of a random variable based on a sample of data points [17]. The basic idea behind KDE is to estimate the density function as a weighted sum of kernel functions centered at each data point. The resulting density estimate is a smooth function that represents the underlying distribution of the data. One of the advantages of kernel density estimation is that it does not make any assumptions about the underlying distribution of the data, making it a flexible and powerful tool for data analysis.
KDE works by weighing each data point with a kernel function and computing a smoothed estimate of the PDF. The bandwidth parameter controls the smoothness of the KDE, and the resulting estimate can be used to evaluate the PDF at any point. The KDE algorithm used in this study is shown in the following.
For a sample , the KDE function is defined in the following way:
is the kernel; the Gaussian kernel is applied in this study, as expressed in Equation (12).
is the bandwidth; here, Scott’s rule-of-thumb [18] bandwidth estimator is used, and it is calculated using , where is the standard deviation of the sample and is the sample size.
3.5. Tukey’s Biweight
Tukey’s biweight is a robust estimator used in statistics to calculate the center and dispersion of a dataset, especially in the presence of outliers [19]. It is a popular alternative to mean and standard deviation as it is more resistant to the effects of extreme values. The biweight is defined as a weighted average of the observations, with the weights decreasing rapidly as the distance between an observation and the center of the dataset increases. The weight function used in the biweight is a cubic function, which makes it less sensitive to outliers than other robust estimators.
The algorithm starts by assuming an initial center, which could be the mean, median, or any other value. It then calculates a weight for each data point based on its distance from the center, as shown in Equations (13) and (14), with the weights decreasing rapidly as the distance increases. Any data point with its distance to the center greater than 3*IRQ is considered an outlier and is given a 0.00 weight. Using these weights, the algorithm computes a new center as a weighted average of the data points, as expressed in Equation (15). This new center is then used to compute a new set of weights, which, in turn, are used to update the center. This iterative process continues until the center converges to a stable estimate.
where and are the 75th and 25th percentiles of the input data, respectively. To normalize the weights ,
4. Results and Discussion
4.1. WP1
4.1.1. Clustering
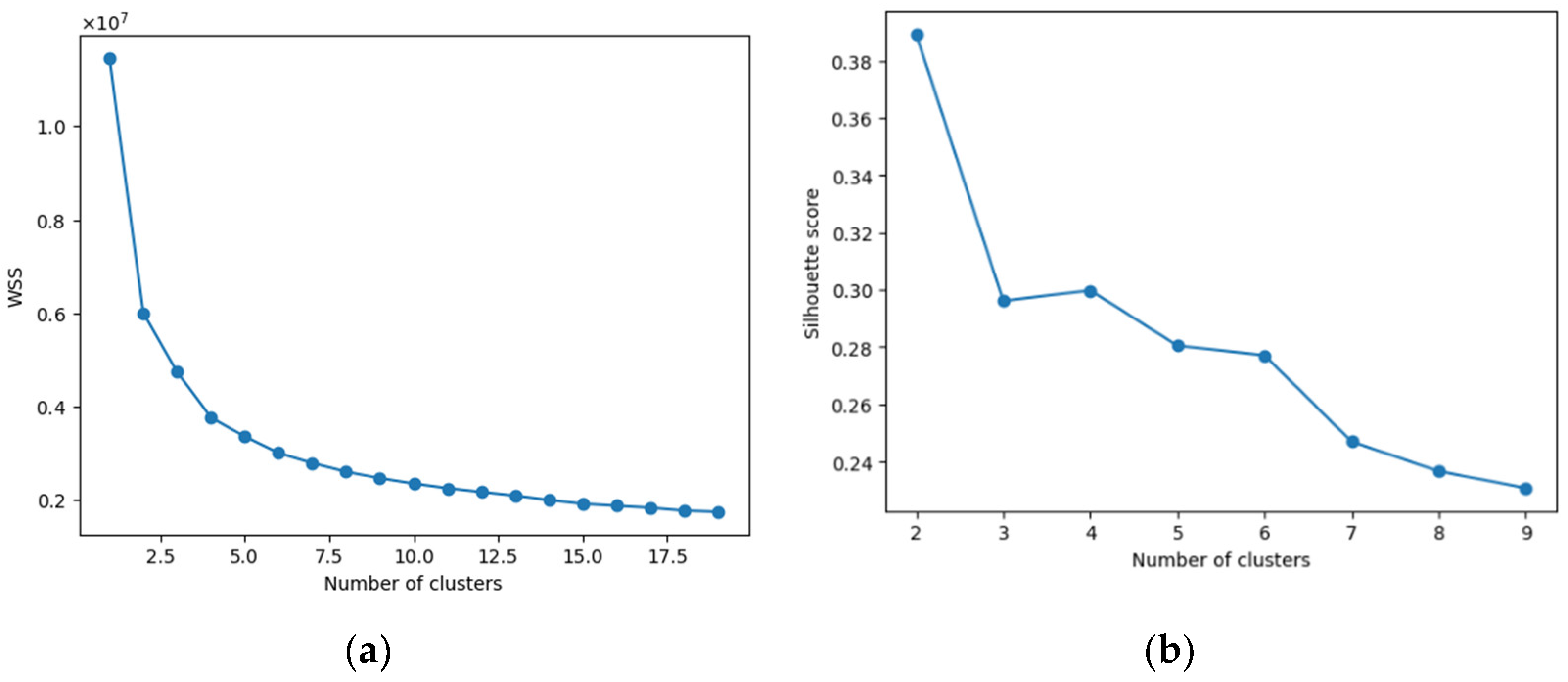
The purpose of clustering analysis is to aggregate the daily time series with similar patterns into the same cluster to identify the general patterns with better accuracy. Performing the k-means clustering on the preprocessed data with ranging from 1 to 19; the elbow plot is shown in Figure 5a.
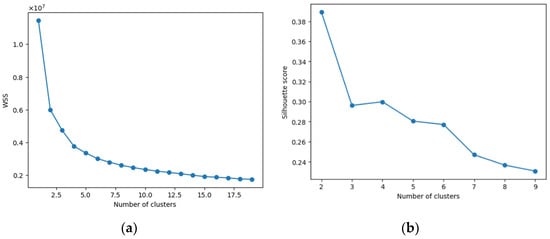
Figure 5.
(a) The elbow plot; (b) the silhouette plot.
Based on the analysis of the elbow plot, it was observed that the optimal number of clusters was either 2, 3, or 4. To further refine the optimal number, the silhouette scores for different cluster numbers were calculated, as shown in Figure 5b. Based on this evaluation, the optimal number of clusters was determined to be 2. Subsequently, the clustering algorithm was applied to the dataset, and the results indicated that out of the 366 daily time series, 178 fell into the cluster of interest.
4.1.2. Peak and Valley Delay
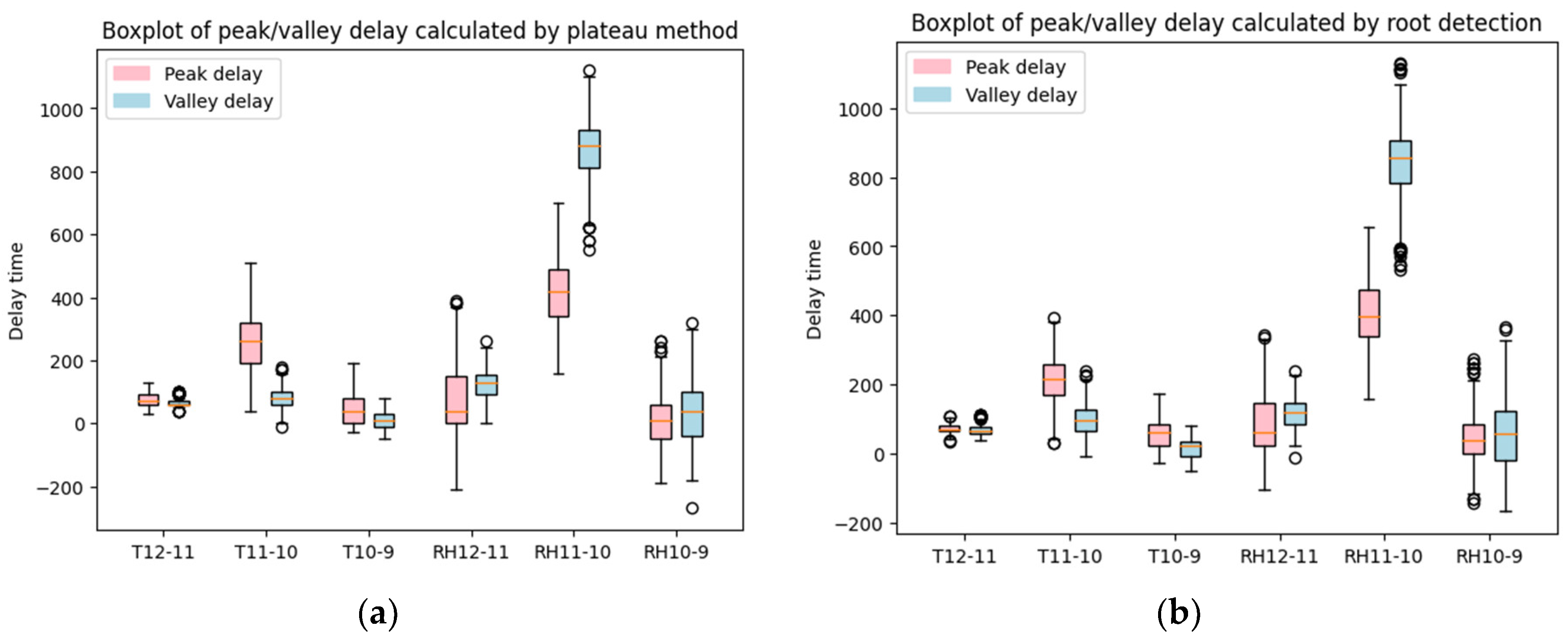
Based on the methodology described in Section 3.2.2, we were able to identify the peak and valley for each of the daily time series selected by the clustering analysis. Subsequently, the peak and valley delays between every pair of adjacent sensors were calculated. The distribution of these delays is presented in the form of a boxplot in Figure 6. Additionally, a more detailed histogram distribution of the delays can be found in Appendix A.
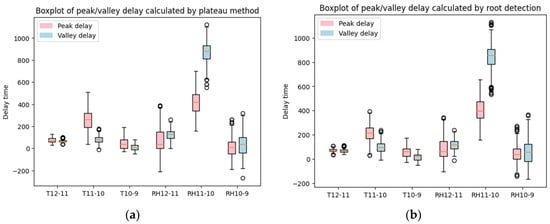
Figure 6.
Boxplot of peak/valley delay calculated by (a) the plateau method and (b) the root detection method.
First of all, Figure 6a shows that the peak and valley delays are mostly above 0, except for the delay between RHT10 and RHT9. This implies that RHT12 increases first until it reaches its peak, RHT11 subsequently increases until it reaches its peak, and RHT10 follows subsequently. Vice versa, RHT12 also decreases first until it reaches its valley, and RHT11 and RHT10 follow subsequently. Between RHT10 and RHT9, there is no consistent pattern that one always increases or decreases ahead of the other. It can then be concluded that the heat and moisture from the exterior of the building dominated the heat and moisture inside the wall layer where RHT11 is located, and subsequently, this dominance extended to the wall layer where RHT10 is located. The delay between RHT10 and RHT9 showed a distribution around 0, with delays both above and below 0, especially in the delay of RH. It can be inferred, unlike the relationship between RHT12–RHT11 or RHT11–RHT10, that there is no clear dominator between RHT10 and RHT9. At times, the heat and moisture of RHT10 may overpower RHT9, while at other times, the opposite may occur.
Furthermore, upon examining the boxplots in Figure 6a, the delay between RHT11 and RHT10 is the largest, which means it takes the longest time for heat and moisture to transfer between these two sensors. It is because the distance between RHT11 and RHT10 is the largest, as can be seen in Figure 1b. An intriguing observation is that the delay of T11–T10 has a significantly longer peak delay than valley delay, while for the delay of RH11–RH10, the valley delay is significantly longer than the peak delay. The peak transfer is slower than the valley transfer between T11 and T10 because the insulation material between them can prevent heat from rising, but it does not store heat. Therefore, the heat from T11 can slowly transfer to T10, while T10 quickly drops as T11 decreases. Regarding the peak transfer being faster than the valley transfer between RH11 and RH10, it can be explained by the rate of absorption being generally faster than the rate of desorption in porous materials in general [20]. This is because water has a high surface tension and can easily wet the surface of the porous material, allowing it to quickly enter the pores due to capillary action. Once inside the pores, water can be retained by the porous structure through hydrogen bonding and other attractive forces. In contrast, during desorption, the water has to overcome the attractive forces between the water molecules and the porous material to leave the pores. This can result in a slower rate of water release from the material. Furthermore, another interesting finding from the boxplots is that the delay of RH generally takes longer and has a higher variance compared to the delays of temperature. The longer transfer time for moisture compared to heat in building exterior walls can be attributed to the physical properties of building materials and different mechanisms of heat and moisture transfer. Moisture transfer involves the movement of water molecules through porous materials, which is a slower process compared to the transfer of heat energy [21]. Additionally, factors such as vapor pressure gradients, moisture barriers, and the hygroscopic properties of materials can further influence and slow down moisture transfer [22]. These factors contribute to a higher variance in transfer time for moisture compared to heat in building exterior walls.
Figure 6b illustrates the distribution of peak/valley delay calculated using the root detection method. As can be observed, there is no significant difference from the boxplots in Figure 6a. To further compare these two different peak/valley detection methods and their results, Section 4.3 offers a detailed and comprehensive comparison of the delays obtained from different methods.
4.2. WP2
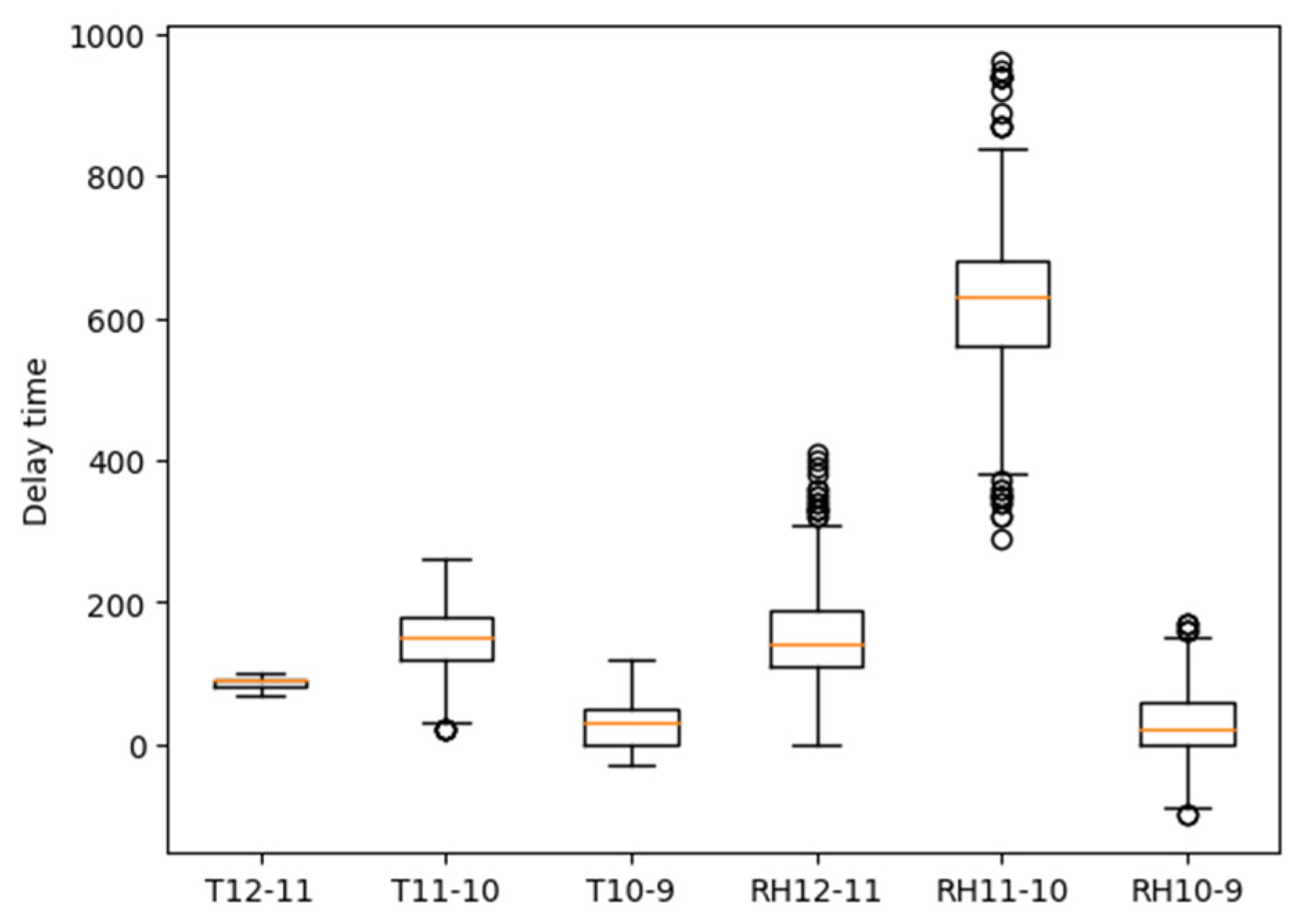
Based on the methodology described in Section 3.3, the delays between every pair of adjacent sensors were calculated for each day. The distribution of these delays is presented in the form of a boxplot in Figure 7. Additionally, a more detailed histogram distribution of the delays can be found in Appendix B.
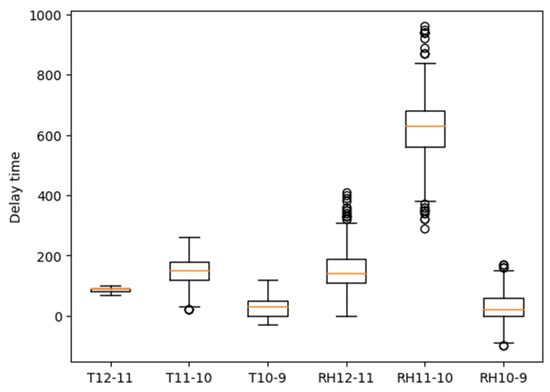
Figure 7.
Boxplot of delay calculated by cross-correlation analysis.
The results presented in Figure 7 are consistent with those described in Section 4.1.2. A similar conclusion can be drawn, namely that the hygrothermal conditions of RHT12 have a dominating effect on the variation in RHT11, and similarly, RHT11 has a dominant impact on RHT10. In addition, the delays between RHT11 and RHT10 are significantly longer than the delays of the other pairs of adjacent sensors. Last but not least, overall speaking, there is a higher variance in the delay of RH than the delay of temperature. To comprehensively and quantitatively compare the results obtained from WP1 and WP2, a KDE analysis was carried out, and the results are presented in Section 4.3.
4.3. Kernal Density Estimation
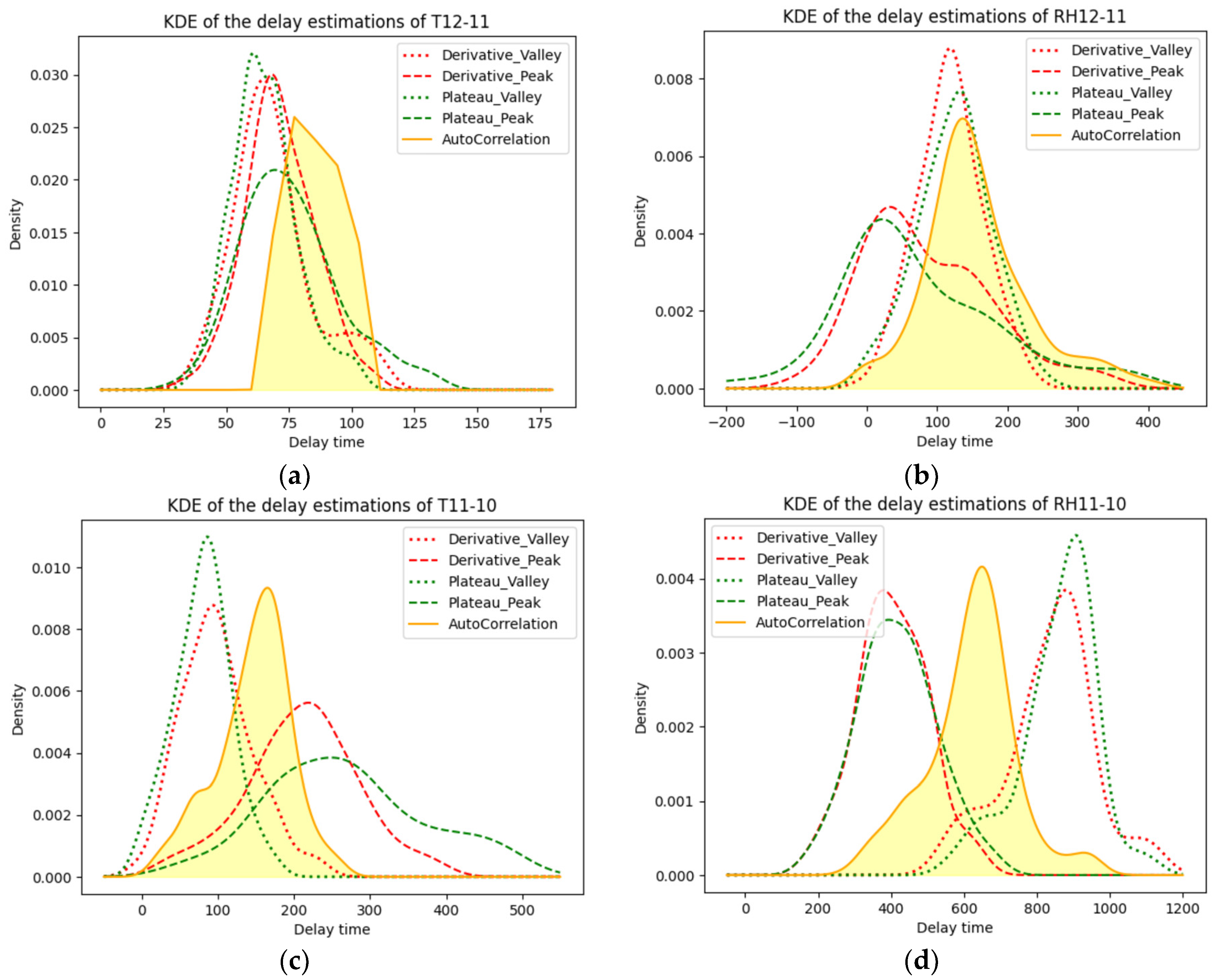
To visually and quantitatively compare the time delays obtained from the plateau method, root detection, and cross-correlation analysis, a KDE was performed on the delays of each pair of adjacent sensors. This allowed for explicit visualization and comparison of the delays generated by each method.
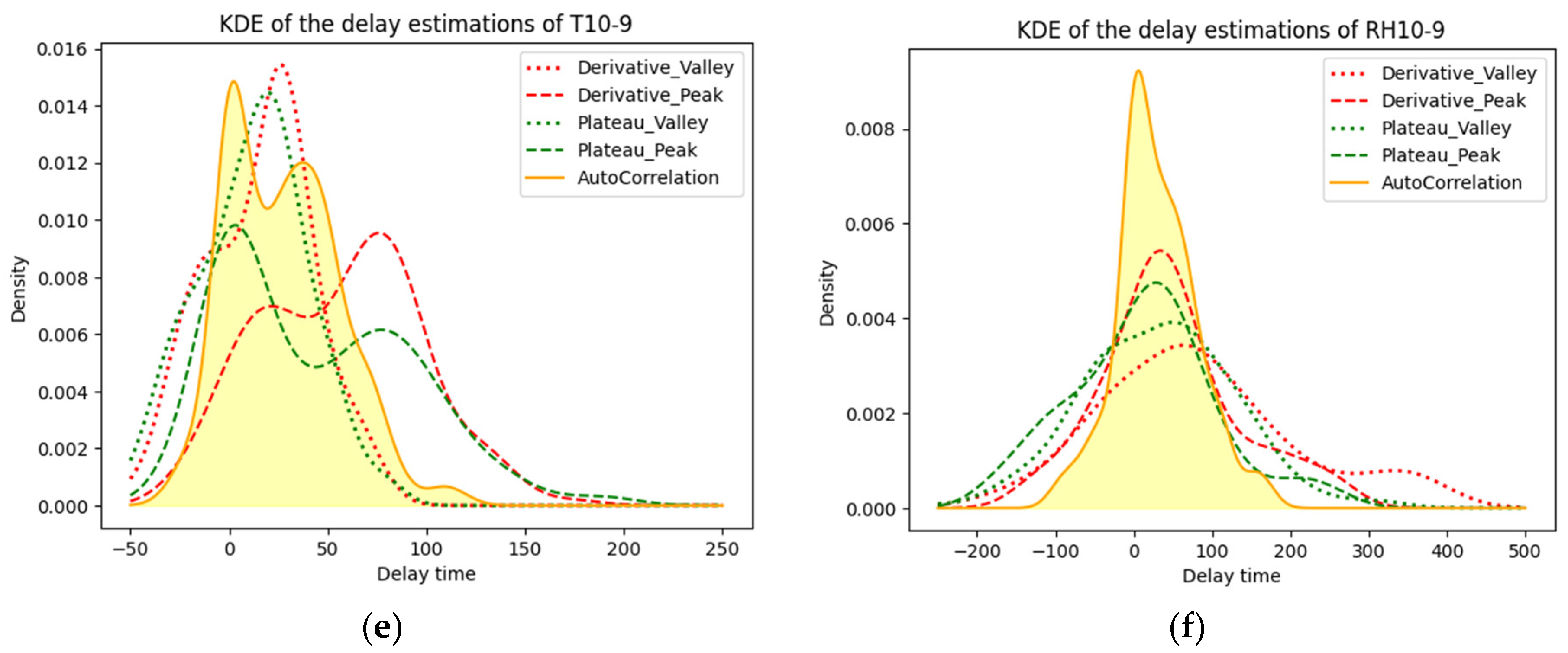
In Figure 8, note that the labels Derivative_Valley and Derivative_Peak refer to the delay of the valley and peak identified by the root detection method, respectively. The figure shows the KDE of the delays calculated by different methods. It can be observed that the results from the plateau method and the root detection method are similar, with no significant difference in their performance.
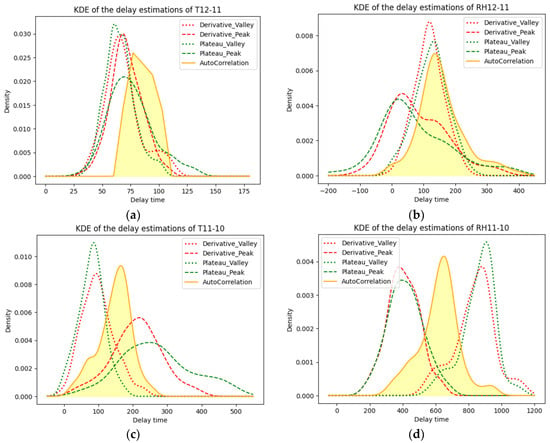
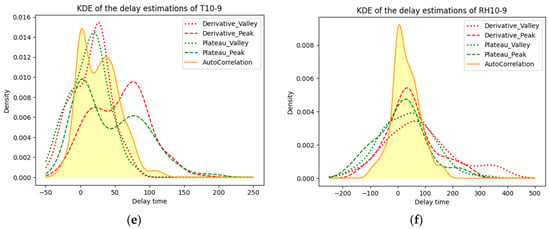
Figure 8.
KDE of the delay between (a) T12 and T11; (b) RH12 and RH11; (c) T11 and T10; (d) RH11 and RH10; (e) T10 and T9; and (f) RH10 and RH9.
As we can clearly see in Figure 8c,d, the peak delay of temperature is significantly longer than the valley delay, while the peak delay of RH is significantly shorter than the valley delay. The explanation behind this phenomenon is interpreted in Section 4.1.2. The delay calculated by the cross-correlation method is distributed between the peak and valley delays. This is expected since the delay was calculated based on the cross-correlation of the daily time series, which includes both peak and valley features over the course of the entire day. At the same time, as shown in Figure 8a,b, it slightly shows the pattern mentioned above, namely that the peak delay of temperature is longer than its valley delay and the peak delay of RH is shorter than its valley delay. It shows slightly because the distance between RHT12 and RHT11 is less than 1/3 of the distance between RHT11 and RHT10. The shorter the distance, the weaker such a pattern is. However, it is noteworthy that the delay calculated by cross-correlation is not distributed between the peak delay and valley delay, but rather skewed towards the right side. Furthermore, as shown in Figure 8e,f, the distribution of peak delay and valley delay does not show a clear pattern of one being longer than the other, which could be because the distance between RHT10 and RHT9 is too small for such a pattern to visually occur. The peak delay and valley delay are distributed in a similar range, and the delay calculated by cross-correlation also falls within that range.
Overall, these results show that the hygrothermal behavior of the wall is complex and dynamic, with different patterns of delay for temperature and RH, and different patterns between peak and valley delays. Besides, the cross-correlation method can provide a useful and overall representative measure of the delay in daily time series analysis.
4.4. Transfer Patterns at Monthly Scale
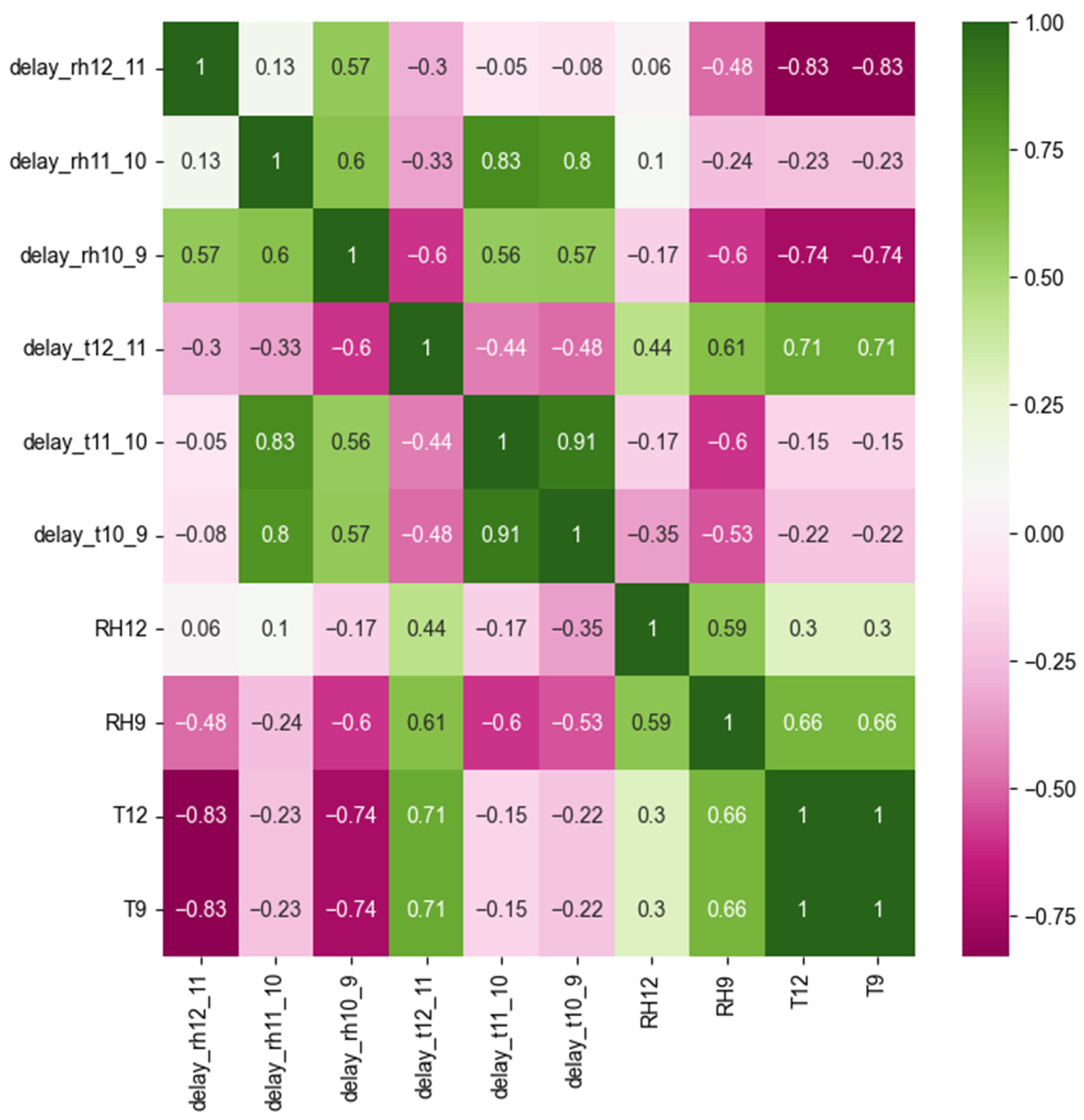
As discussed in [13], the monthly average RH peak delay time between RH11 and RH12 decreased as the outdoor monthly average temperature increased. In this study, we build upon this analysis by exploring the relationships between all adjacent sensor pairs and the indoor and outdoor climate variables. Specifically, we aggregated the daily delays, calculated using the cross-correlation method, to the monthly delays by computing the biweight center of the daily delays within each month. Similarly, we computed the monthly biweight center of the outdoor and indoor climate data series (RH12, T12, RH9, T9). We then calculated the Spearman correlation coefficients between the monthly biweight centers of the delays and the monthly biweight centers of the indoor and outdoor climate variables.
The results presented in Figure 9 indicate a strong negative monotonic correlation between the delay of RH11 and RH12 and both indoor and outdoor temperatures, as indicated by the Spearman correlation coefficients of -0.83. This finding is consistent with previous research [13]. Additionally, the delay between RH10 and RH9 is also negatively correlated with temperature to some extent, although it is less significant compared to the delay between RH11 and RH12. In contrast, the delay between RH11 and RH10 shows no correlation with indoor or outdoor RH or temperature; instead, it exhibits a strong positive monotonic correlation with the delay between T11 and T10. On the other hand, compared to the RH delay, the temperature delay is less correlated with indoor or outdoor temperature. The delay between T12 and T11 is only positively correlated with temperature to some degree, with a correlation coefficient of 0.71, whereas the delays between T11 and T10 and T10 and T9 show no clear correlations with temperature but are highly positively correlated with each other. This finding is intriguing as it demonstrates the potential of using the delay time of temperature and RH as key indicators for the quantitative characterization of hygrothermal transfer patterns. Such characterization provides a scientific foundation for analyzing the movement and storage of moisture within bamboo and wood composite walls.
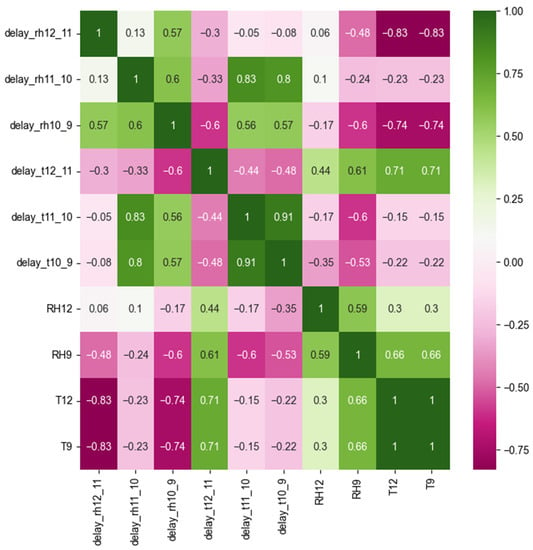
Figure 9.
Heatmap of the Spearman coefficients.
5. Conclusions
The literature review highlighted the limitations of data-driven models in explaining the physical behaviors of bio-based materials and the lack of moisture transfer time and accumulation estimation. In this research, we focused on modeling hygrothermal transfer patterns using data-driven methods for bio-based building exterior walls. We proposed a novel approach for peak and valley detection based on discrete differentiation, along with cross-correlation analysis for general delays between daily time series. The results showed no significant difference between the plateau method and root detection, and the delay calculated by cross-correlation was representative of the daily time series delay. Correlation analysis revealed a strong seasonal pattern in the delay between RH12 and RH11, indicating shorter transfer times with higher temperatures. The delay between RH11 and RH10 showed no clear seasonal pattern but was highly correlated with the delay between T11 and T10. For temperature delays, no strong seasonal patterns were evident, but the delays between T11 and T10 and T10 and T9 were strongly positively correlated. These findings will serve as a crucial foundation for our next investigation, which aims to model the movement and storage of moisture within the bio-based wall. Understanding the hygrothermal transfer mechanism is contingent upon accurately capturing the dynamics of moisture within the wall, making it an essential component of our research.
The future work includes analyzing the entire dataset collected from all 16 sensors over 5 years to validate whether the transfer patterns and seasonal patterns identified in the current data remain consistent. Besides, with a deep investigation and understanding of the hygrothermal transfer directions and time, we can further develop empirical models based on machine learning algorithms to predict the moisture dynamics inside building exterior walls.
Author Contributions
Conceptualization, W.S., X.W. and B.F.; methodology, W.S. and Y.Z.; software, Y.Z.; validation, X.W., R.G.N. and Y.R.; formal analysis, W.S.; investigation, Y.Z.; resources, X.W. and B.F.; writing—original draft preparation, W.S. and Y.Z.; writing—review and editing, Y.Z., Y.R., W.S. and R.G.N.; project administration, X.W., R.G.N., B.F. and W.S.; funding acquisition, B.F., X.W. and W.S.; supervision, Y.R., W.S. and B.F. All authors have read and agreed to the published version of the manuscript.
Funding
Part of the work represented in this paper was funded by the Fundamental Research Funds for the Central Non-profit Research Institution of CAF, Grant No. 31200433, and by the Provincial Academy of Forestry of Fujian Province of China, Grant No. 2022FKJ01.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
Appendix A.1
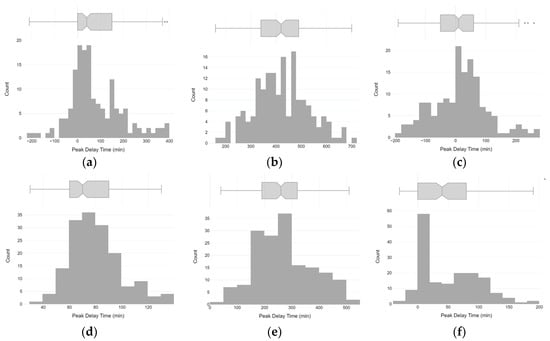
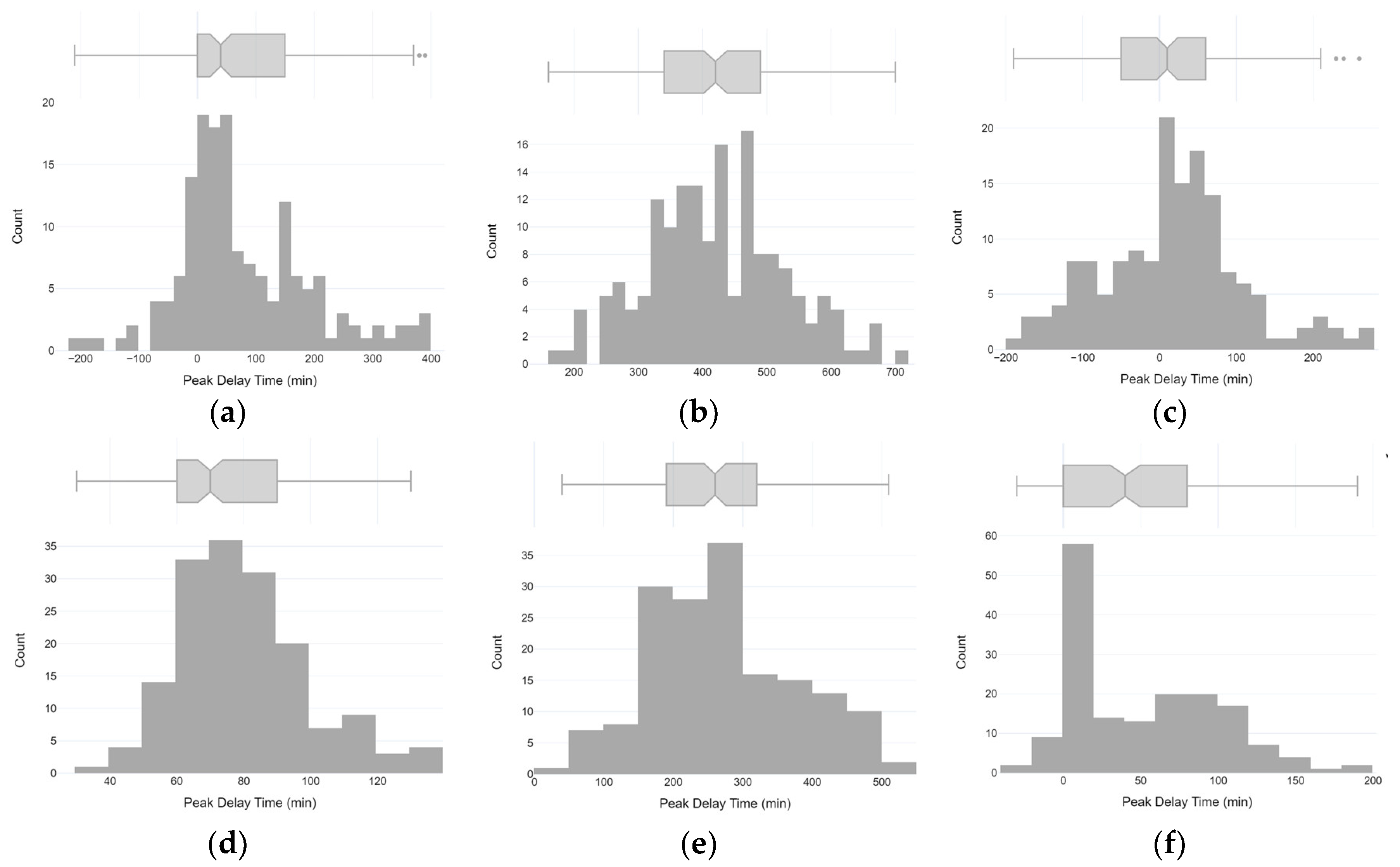
Figure A1.
Histograms of peak delays based on the plateau method between adjacent sensors: (a) RH12 and RH11; (b) RH11 and RH10; (c) RH10 and RH9; (d) T12 and T11; (e) T11 and T10; and (f) T10 and T9.
Figure A1.
Histograms of peak delays based on the plateau method between adjacent sensors: (a) RH12 and RH11; (b) RH11 and RH10; (c) RH10 and RH9; (d) T12 and T11; (e) T11 and T10; and (f) T10 and T9.
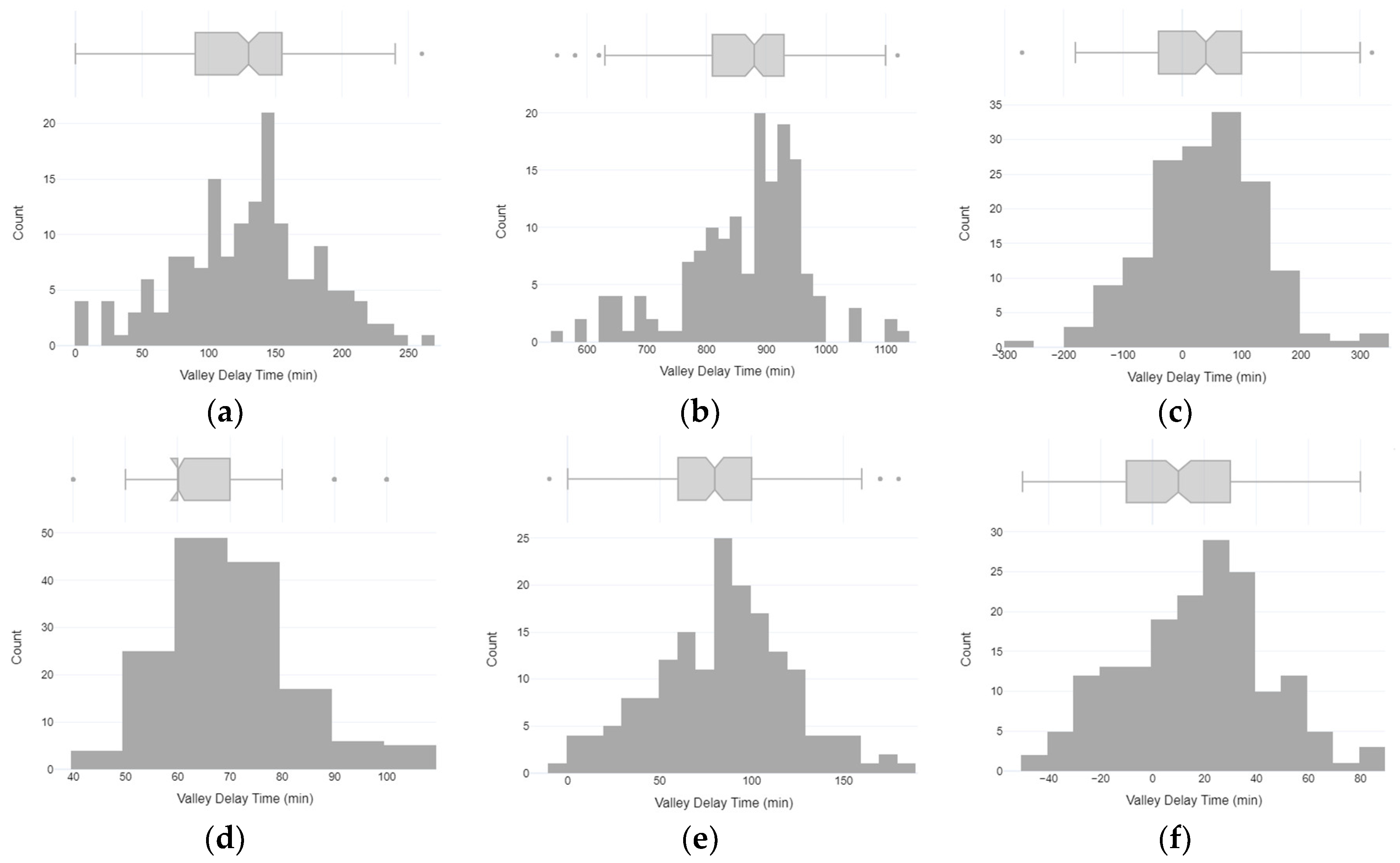
Appendix A.2
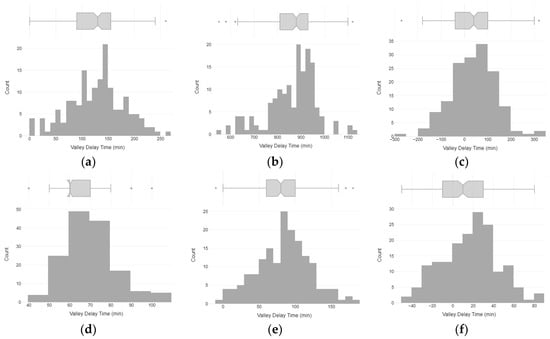
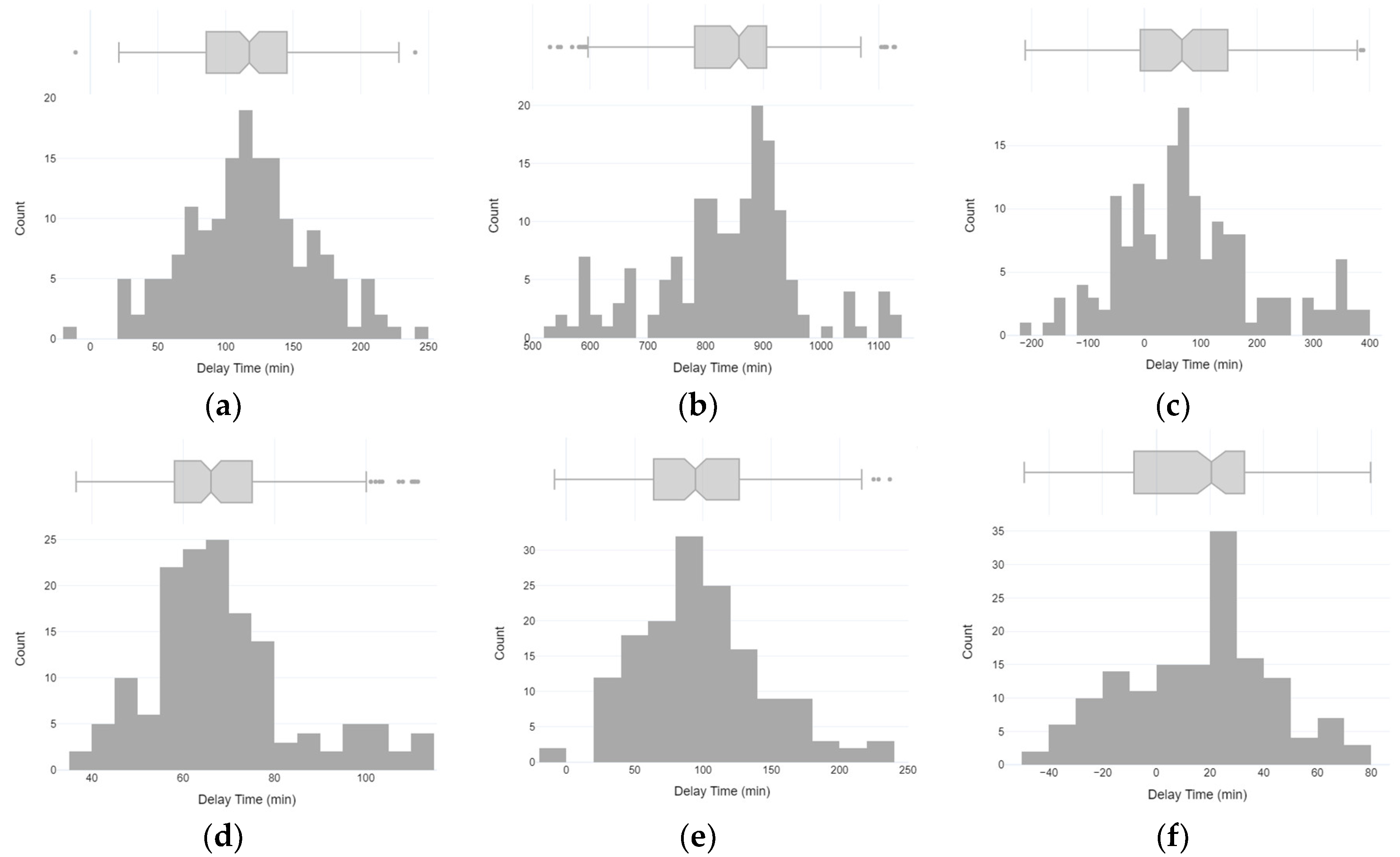
Figure A2.
Histograms of valley delays based on the plateau method between adjacent sensors: (a) RH12 and RH11; (b) RH11 and RH10; (c) RH10 and RH9; (d) T12 and T11; (e) T11 and T10; and (f) T10 and T9.
Figure A2.
Histograms of valley delays based on the plateau method between adjacent sensors: (a) RH12 and RH11; (b) RH11 and RH10; (c) RH10 and RH9; (d) T12 and T11; (e) T11 and T10; and (f) T10 and T9.
Appendix A.3
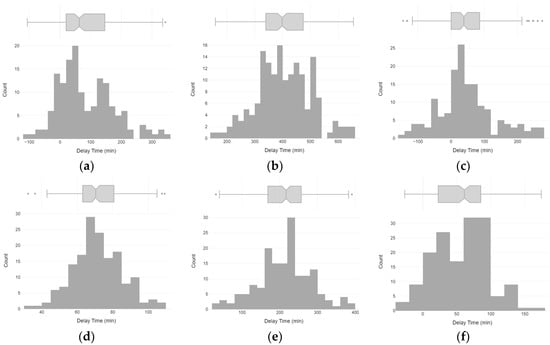
Figure A3.
Histograms of peak delays based on root detection between adjacent sensors: (a) RH12 and RH11; (b) RH11 and RH10; (c) RH10 and RH9; (d) T12 and T11; (e) T11 and T10; and (f) T10 and T9.
Figure A3.
Histograms of peak delays based on root detection between adjacent sensors: (a) RH12 and RH11; (b) RH11 and RH10; (c) RH10 and RH9; (d) T12 and T11; (e) T11 and T10; and (f) T10 and T9.
Appendix A.4
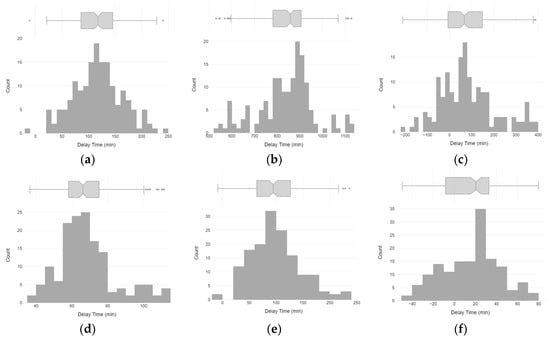
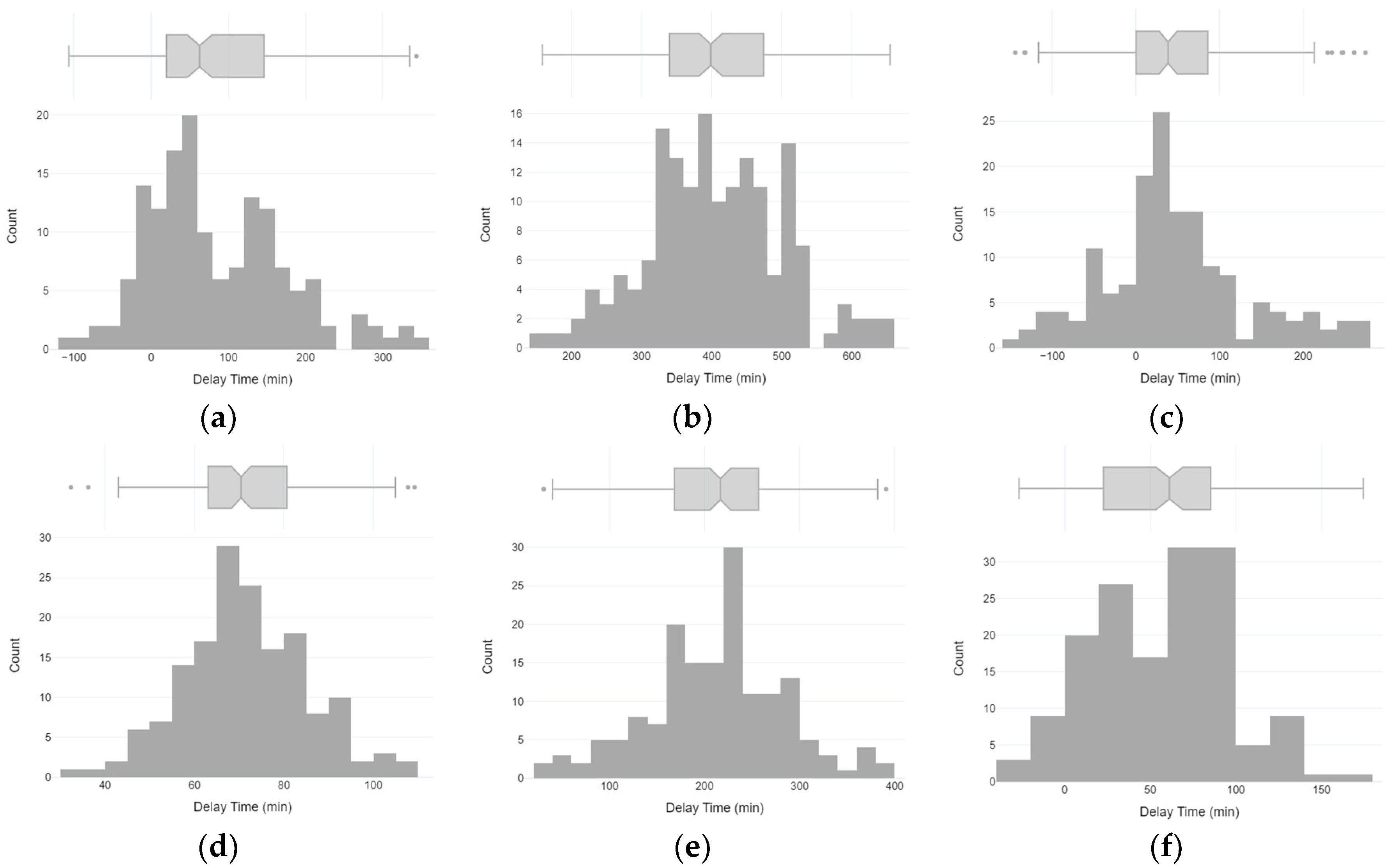
Figure A4.
Histograms of valley delays based on root detection between adjacent sensors: (a) RH12 and RH11; (b) RH11 and RH10; (c) RH10 and RH9; (d) T12 and T11; (e) T11 and T10; and (f) T10 and T9.
Figure A4.
Histograms of valley delays based on root detection between adjacent sensors: (a) RH12 and RH11; (b) RH11 and RH10; (c) RH10 and RH9; (d) T12 and T11; (e) T11 and T10; and (f) T10 and T9.
Appendix B
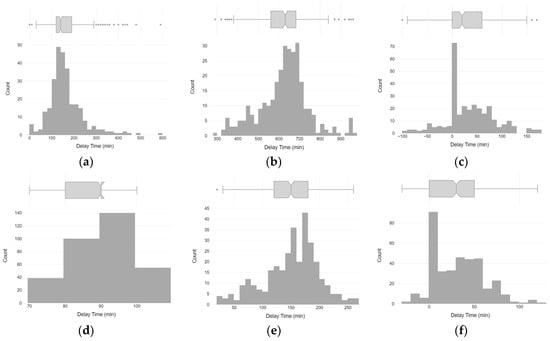
Figure A5.
Histograms of delays based on cross-correlation analysis between adjacent sensors: (a) RH12 and RH11; (b) RH11 and RH10; (c) RH10 and RH9; (d) T12 and T11; (e) T11 and T10; and (f) T10 and T9.
Figure A5.
Histograms of delays based on cross-correlation analysis between adjacent sensors: (a) RH12 and RH11; (b) RH11 and RH10; (c) RH10 and RH9; (d) T12 and T11; (e) T11 and T10; and (f) T10 and T9.
References
- Nejat, P.; Jomehzadeh, F.; Taheri, M.M.; Gohari, M.; Majid, M.Z.A. A global review of energy consumption, CO2 emissions and policy in the residential sector (with an overview of the top ten CO2 emitting countries). Renew. Sustain. Energy Rev. 2015, 43, 843–862. [Google Scholar] [CrossRef]
- Ibn-Mohammed, T.; Greenough, R.; Taylor, S.; Ozawa-Meida, L.; Acquaye, A. Operational vs. embodied emissions in buildings—A review of current trends. Energy Build. 2013, 66, 232–245. [Google Scholar] [CrossRef]
- Brambilla, A.; Sangiorgio, A. Moisture and Buildings: Durability Issues, Health Implications and Strategies to Mitigate the Risks; Woodhead Publishing: Sawston, UK, 2021. [Google Scholar]
- Pihelo, P.; Kalamees, T. The effect of thermal transmittance of building envelope and material selection of wind barrier on moisture safety of timber frame exterior wall. J. Build. Eng. 2016, 6, 29–38. [Google Scholar] [CrossRef]
- Antonyová, A.; Korjenic, A.; Antony, P.; Korjenic, S.; Pavlušová, E.; Pavluš, M.; Bednar, T. Hygrothermal properties of building envelopes: Reliability of the effectiveness of energy saving. Energy Build. 2013, 57, 187–192. [Google Scholar] [CrossRef]
- Taffese, W.Z.; Sistonen, E. Neural network based hygrothermal prediction for deterioration risk analysis of surface-protected concrete façade element. Constr. Build. Mater. 2016, 113, 34–48. [Google Scholar] [CrossRef]
- He, X.; Zhang, H.; Qiu, L.; Mao, Z.; Shi, C. Hygrothermal performance of temperature-humidity controlling materials with different compositions. Energy Build. 2021, 236, 110792. [Google Scholar] [CrossRef]
- Kukk, V.; Kaljula, L.; Kers, J.; Kalamees, T. Designing highly insulated cross-laminated timber external walls in terms of hygrothermal performance: Field measurements and simulations. Build. Environ. 2022, 212, 108805. [Google Scholar] [CrossRef]
- Hamdaoui, M.-A.; Benzaama, M.-H.; El Mendili, Y.; Chateigner, D. A review on physical and data-driven modeling of buildings hygrothermal behavior: Models, approaches and simulation tools. Energy Build. 2021, 251, 111343. [Google Scholar] [CrossRef]
- Tijskens, A.; Roels, S.; Janssen, H. Neural networks for metamodelling the hygrothermal behaviour of building components. Build. Environ. 2019, 162, 106282. [Google Scholar] [CrossRef]
- Tijskens, A.; Roels, S.; Janssen, H. Hygrothermal assessment of timber frame walls using a convolutional neural network. Build. Environ. 2021, 193, 107652. [Google Scholar] [CrossRef]
- Tzuc, O.M.; Gamboa, O.R.; Rosel, R.A.; Poot, M.C.; Edelman, H.; Torres, M.J.; Bassam, A. Modeling of hygrothermal behavior for green facade’s concrete wall exposed to nordic climate using artificial intelligence and global sensitivity analysis. J. Build. Eng. 2021, 33, 101625. [Google Scholar] [CrossRef]
- Wang, X.; Li, H.; Zhu, Y.; Peng, X.; Wan, Z.; Xu, H.; Nyberg, R.G.; Song, W.W.; Fei, B. Using Machine Learning Method to Discover Hygrothermal Transfer Patterns from the Outside of the Wall to Interior Bamboo and Wood Composite Sheathing. Buildings 2022, 12, 898. [Google Scholar] [CrossRef]
- Song, W.; Zhu, Y.; Wang, X.; Peng, X. An Investigation into Effective Data Analysis Methods for Sensor Datasets of a Sample Building. In Proceedings of the 5th International Conference on Big Data Technologies, Qingdao, China, 23–25 September 2022; pp. 125–130. [Google Scholar]
- Likas, A.; Vlassis, N.; Verbeek, J.J. The global k-means clustering algorithm. Pattern Recognit. 2003, 36, 451–461. [Google Scholar] [CrossRef]
- Campbell, J.Y.; Lo, A.W.; MacKinlay, A.C.; Whitelaw, R.F. The econometrics of financial markets. Macroecon. Dyn. 1998, 2, 559–562. [Google Scholar] [CrossRef]
- Wand, M.P.; Jones, M.C. Kernel Smoothing; CRC Press: Boca Raton, FL, USA, 1994. [Google Scholar]
- Scott, D.W. Multivariate Density Estimation: Theory, Practice, and Visualization; Wiley: New York, NY, USA, 1992. [Google Scholar]
- Flannery, B.P.; Press, W.H.; Teukolsky, S.A.; Vetterling, W. Numerical recipes in C; Press Syndicate of the University of Cambridge: New York, NY, USA, 1992; Volume 24, p. 36. [Google Scholar]
- Thybring, E.E.; Fredriksson, M.; Zelinka, S.L.; Glass, S.V. Water in wood: A review of current understanding and knowledge gaps. Forests 2022, 13, 2051. [Google Scholar] [CrossRef]
- Dinçer, İ.; Zamfirescu, C. Drying Phenomena: Theory and Applications; John Wiley & Sons: Hoboken, NJ, USA, 2016. [Google Scholar]
- Peuhkuri, R. Moisture Dynamics in Building Envelopes. Ph.D. Thesis, Technical University of Denmark, Lyngby, Denmark, 2003. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).