Passively Maintained Closed Cavity Façade—Experimental Validation of the Mathematical Thermal Model
Abstract
1. Introduction
2. Materials and Methods
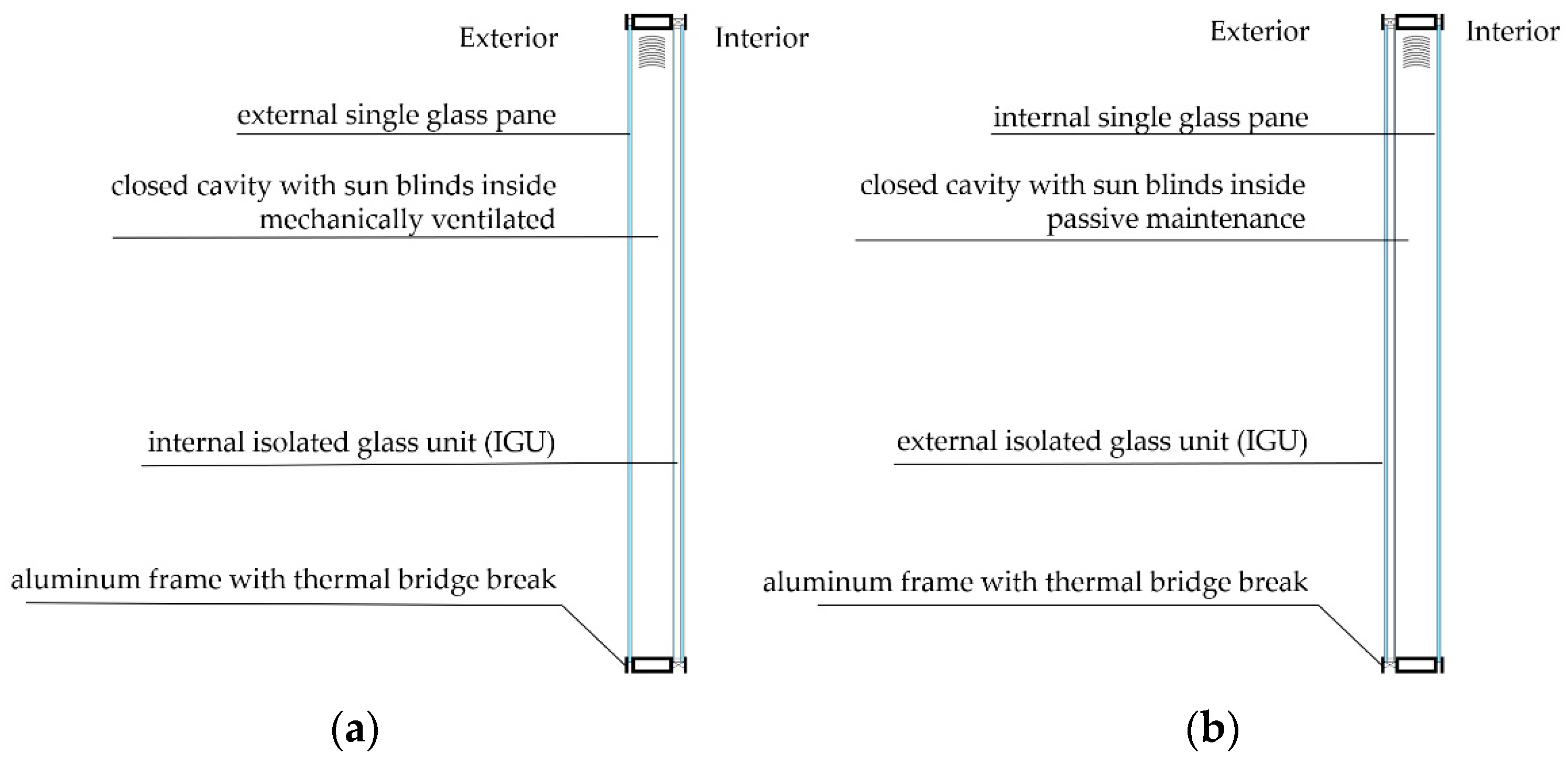
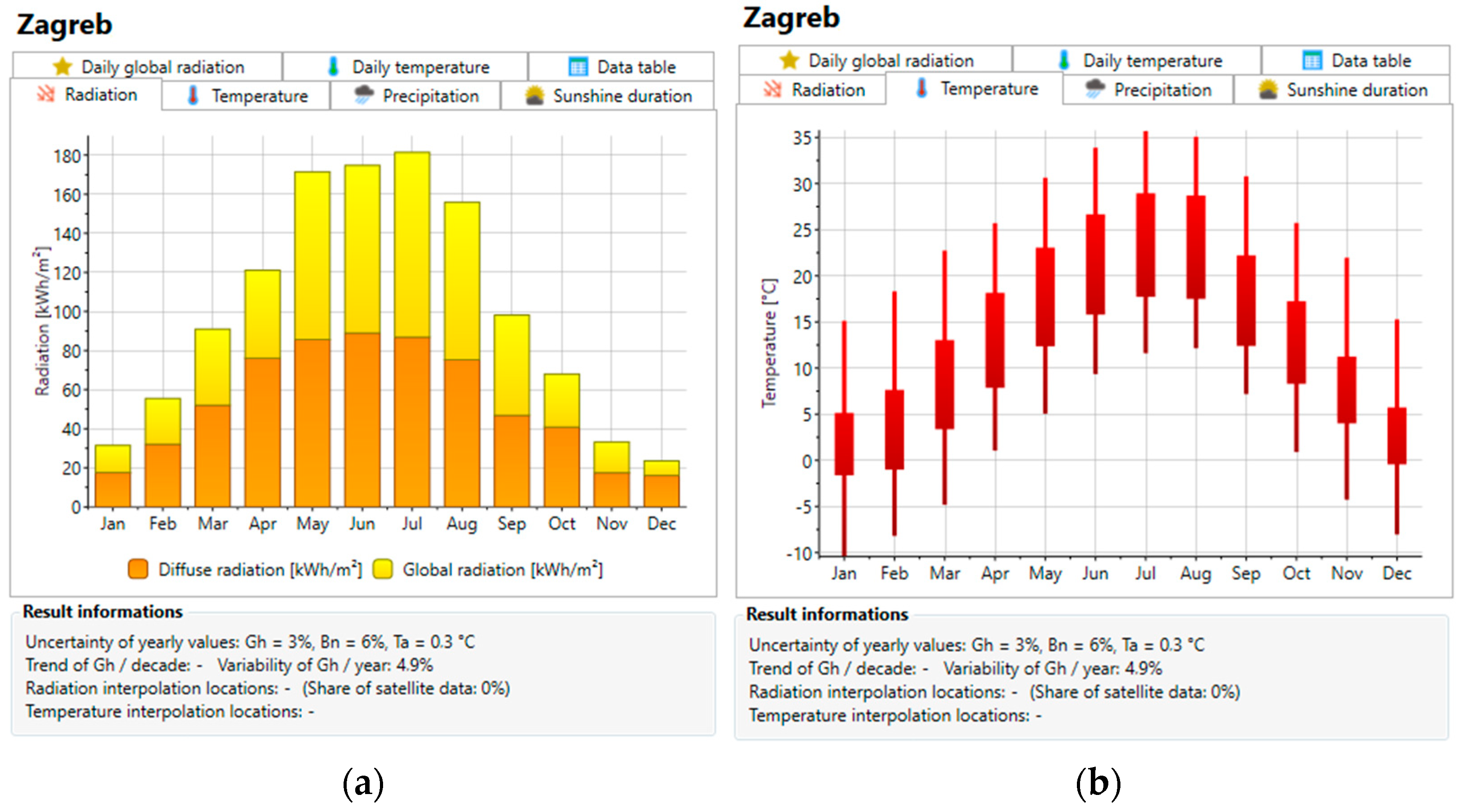
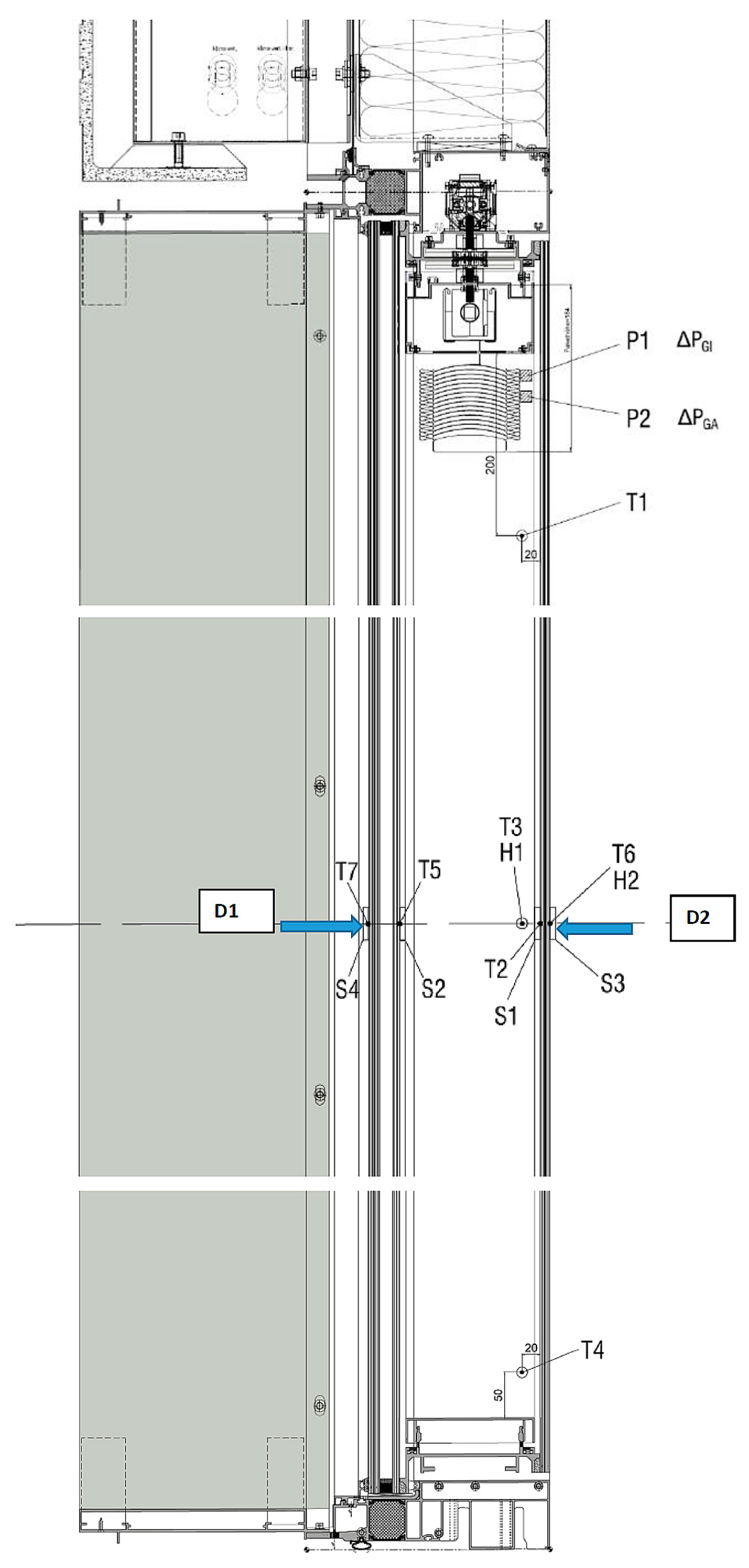
2.1. Experimental Model
2.2. Mathematical Model
2.3. Heat Transfer in CCF
| No. | Elements | Energy Transfer Type | |
|---|---|---|---|
| 1 | Interior | Inner glass | Convective, Radiative |
| 2 | Inner glass | Air gap | Convective |
| 3 | Inner glass | Sunshade | Radiative |
| 4 | Sunshade | Air gap | Convective |
| 5 | Sunshade | Inner glass | Radiative |
| 6 | Sunshade | Middle glass | Radiative |
| 7 | Inner glass | Middle glass | Conductive (by an air gap) |
| 8 | Middle glass | Outer glass | Radiative |
| 9 | Middle glass | Outer glass | Conductive (by argon layer) |
| 10 | Outer glass | Surrounding | Convective, Radiative |
| 11 | Interior | Façade frame | Convective, Radiative |
| 12 | Façade frame | Air gap | Convective, Radiative |
| 13 | Façade frame | Surrounding | Convective, Radiative, Conductive |
| 14 | Solar radiation | Outer glass | Solar gain |
| 15 | Solar radiation | Middle glass | Solar gain (transmitted) |
| 16 | Solar radiation | Sunshade | Solar gain (transmitted) |
| 17 | Solar radiation | Inner glass | Solar gain (transmitted) |
| 18 | Middle glass | Outer glass | Solar gain (reflected) |
| 19 | Sun blinds | Middle glass | Solar gain (reflected) |
| 20 | Solar radiation | Façade frame | Solar gain |

2.4. Radiative Heat Transfer
2.5. Convective Heat Transfer
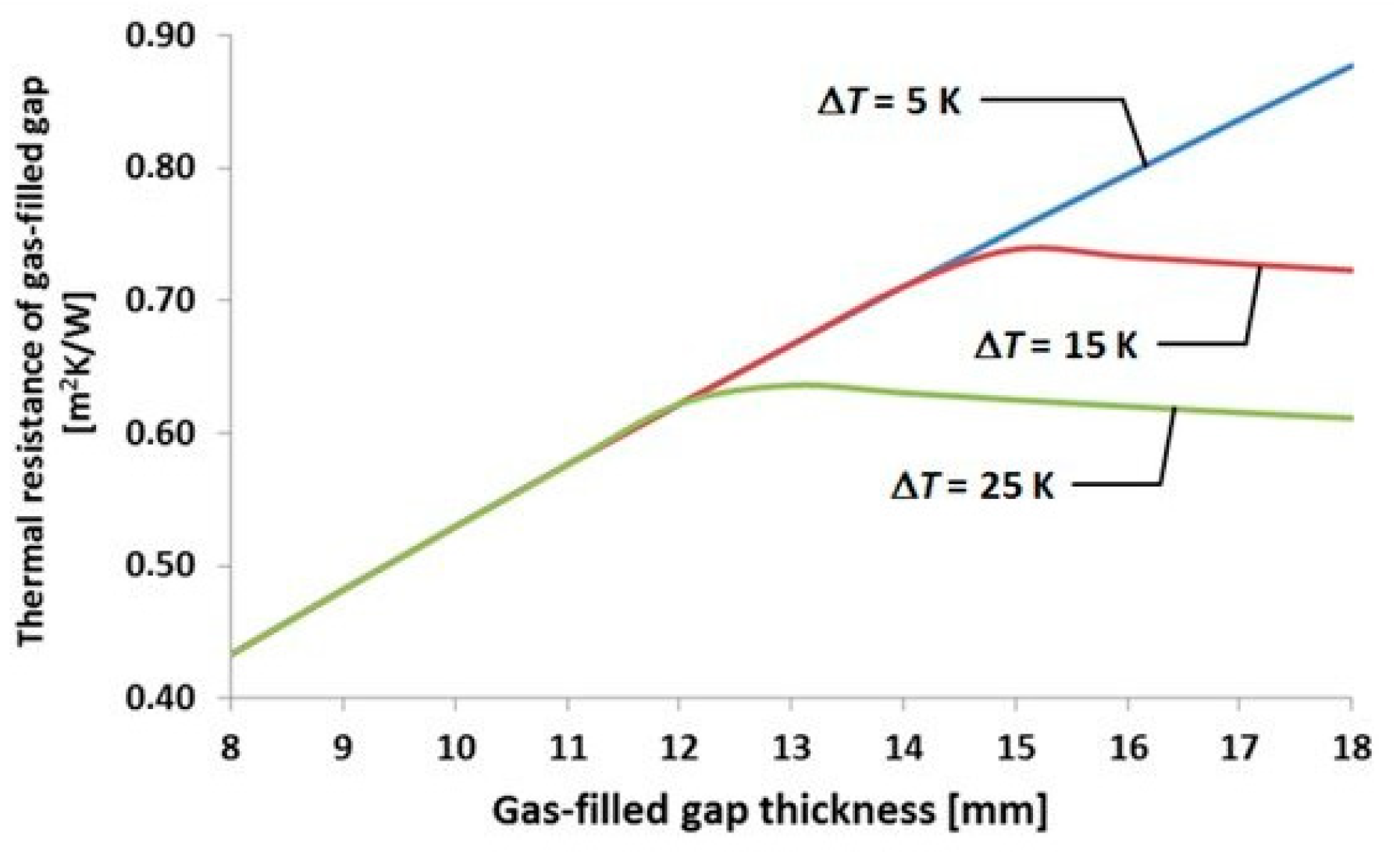
2.6. Conductive Heat Transfer
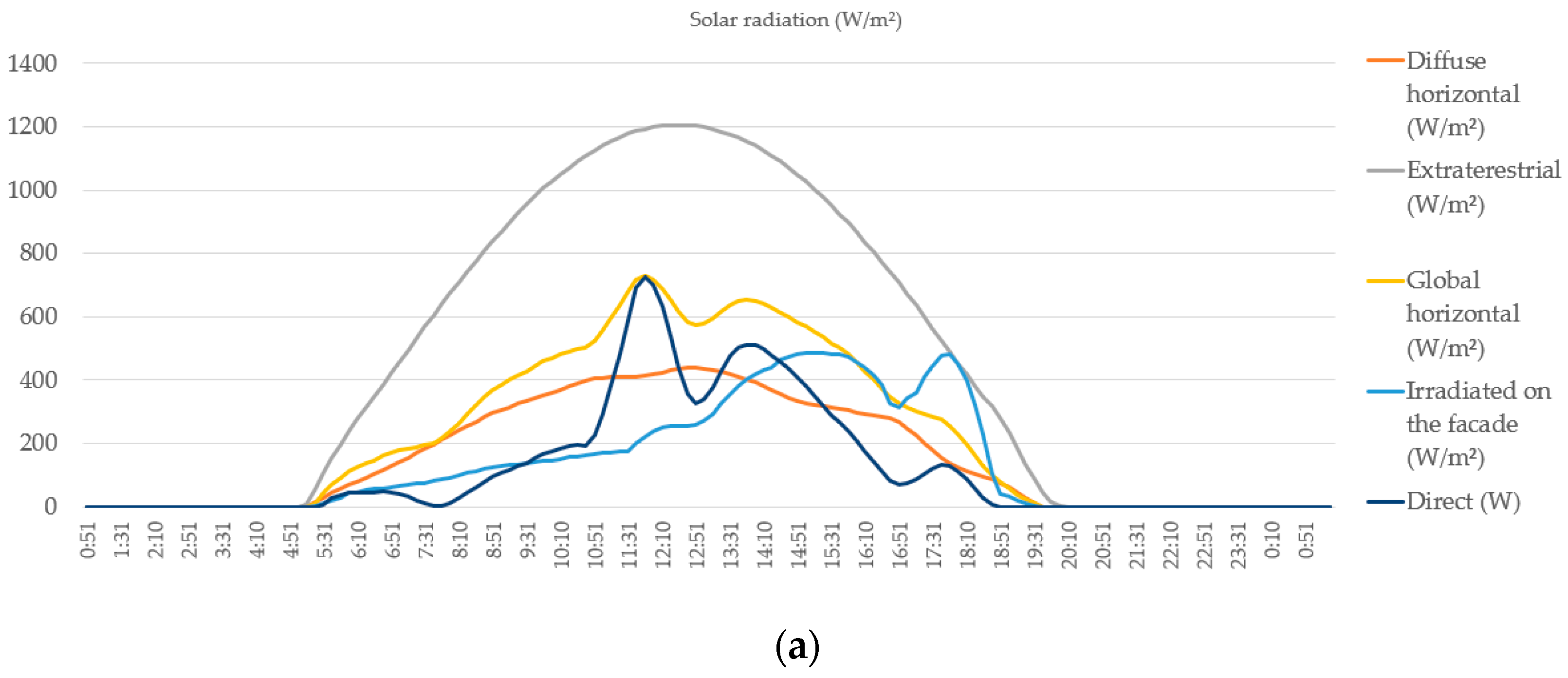
2.7. Solar Radiation
2.8. Glazing Properties
2.9. CCF Elements Temperature
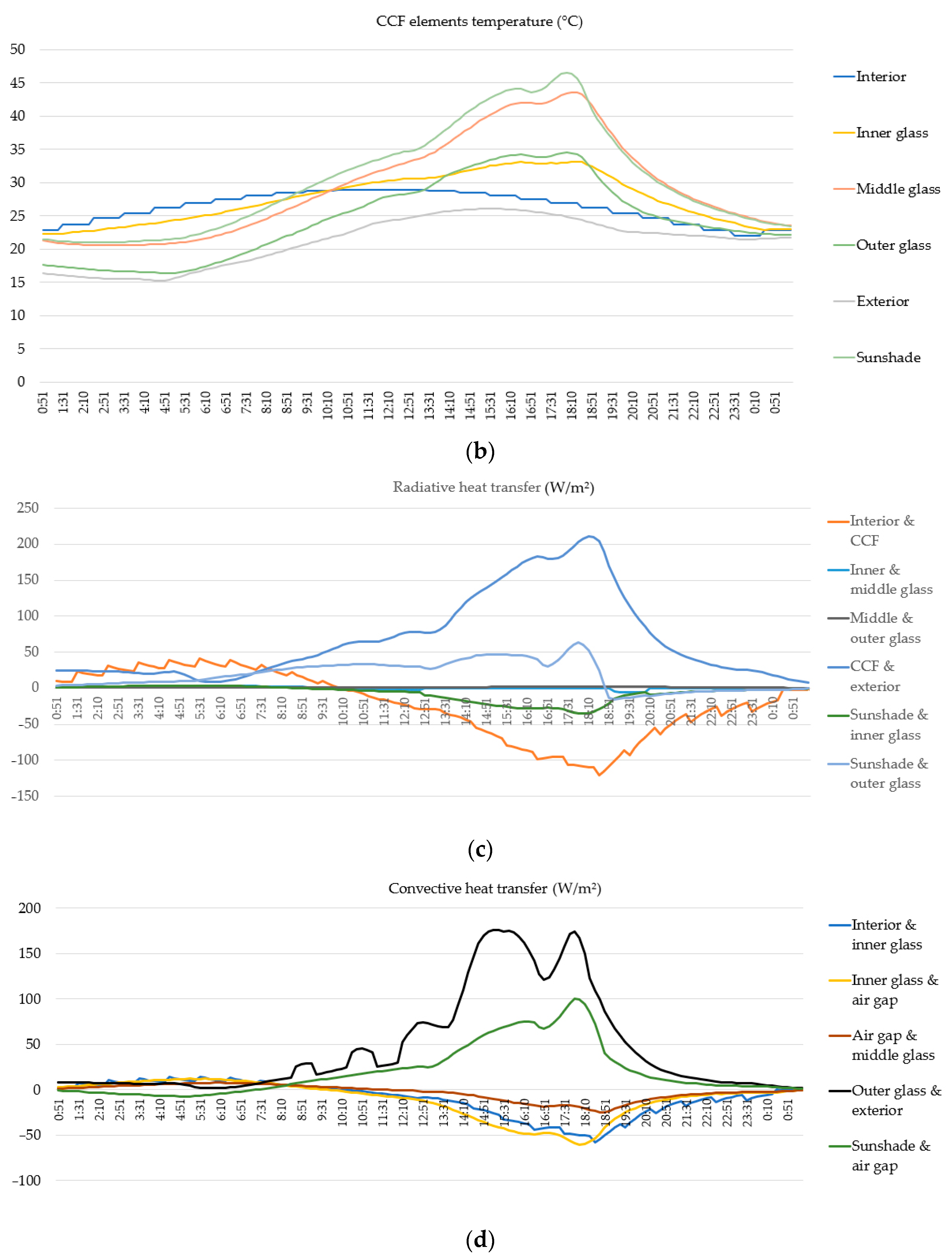
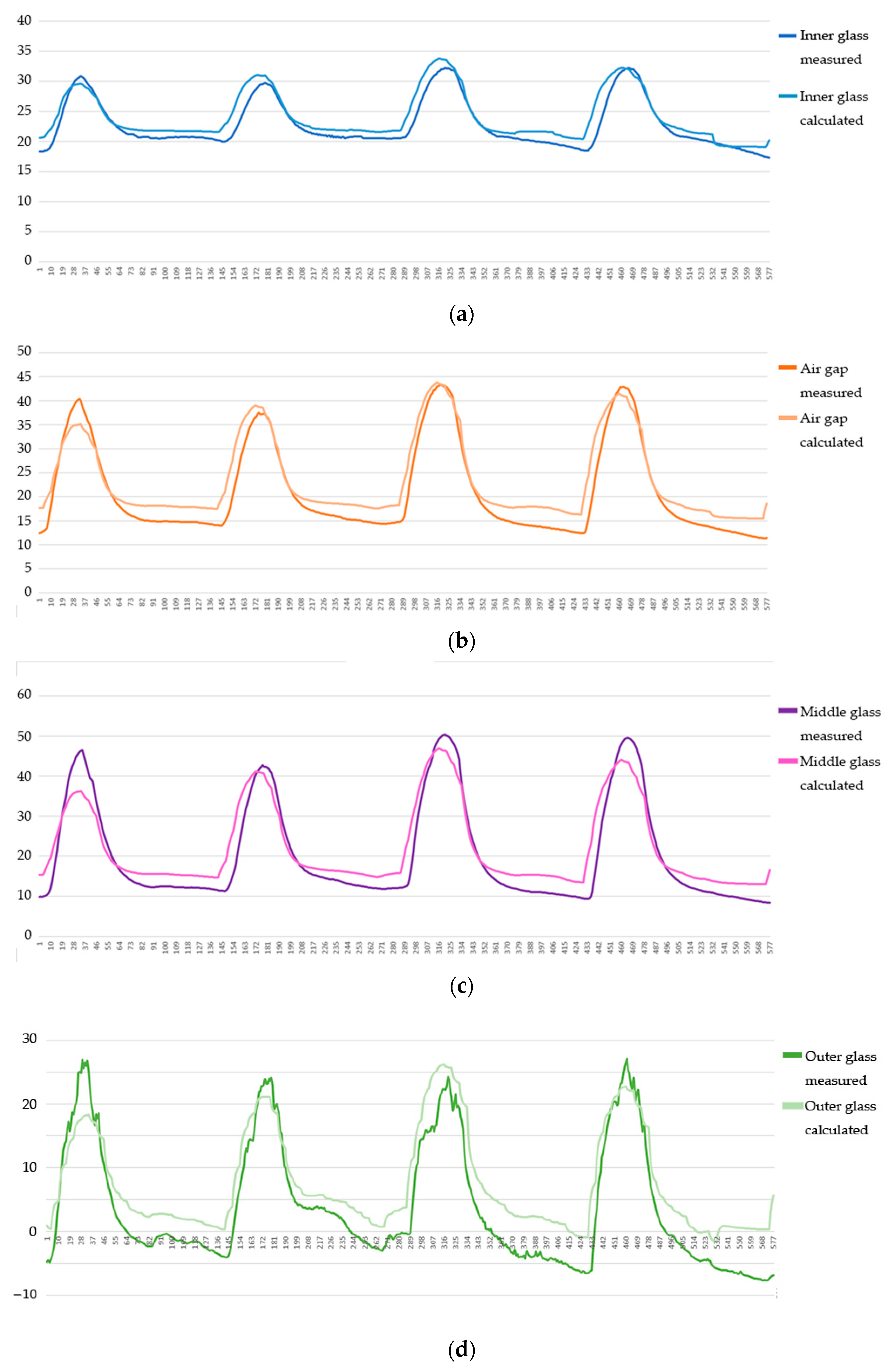
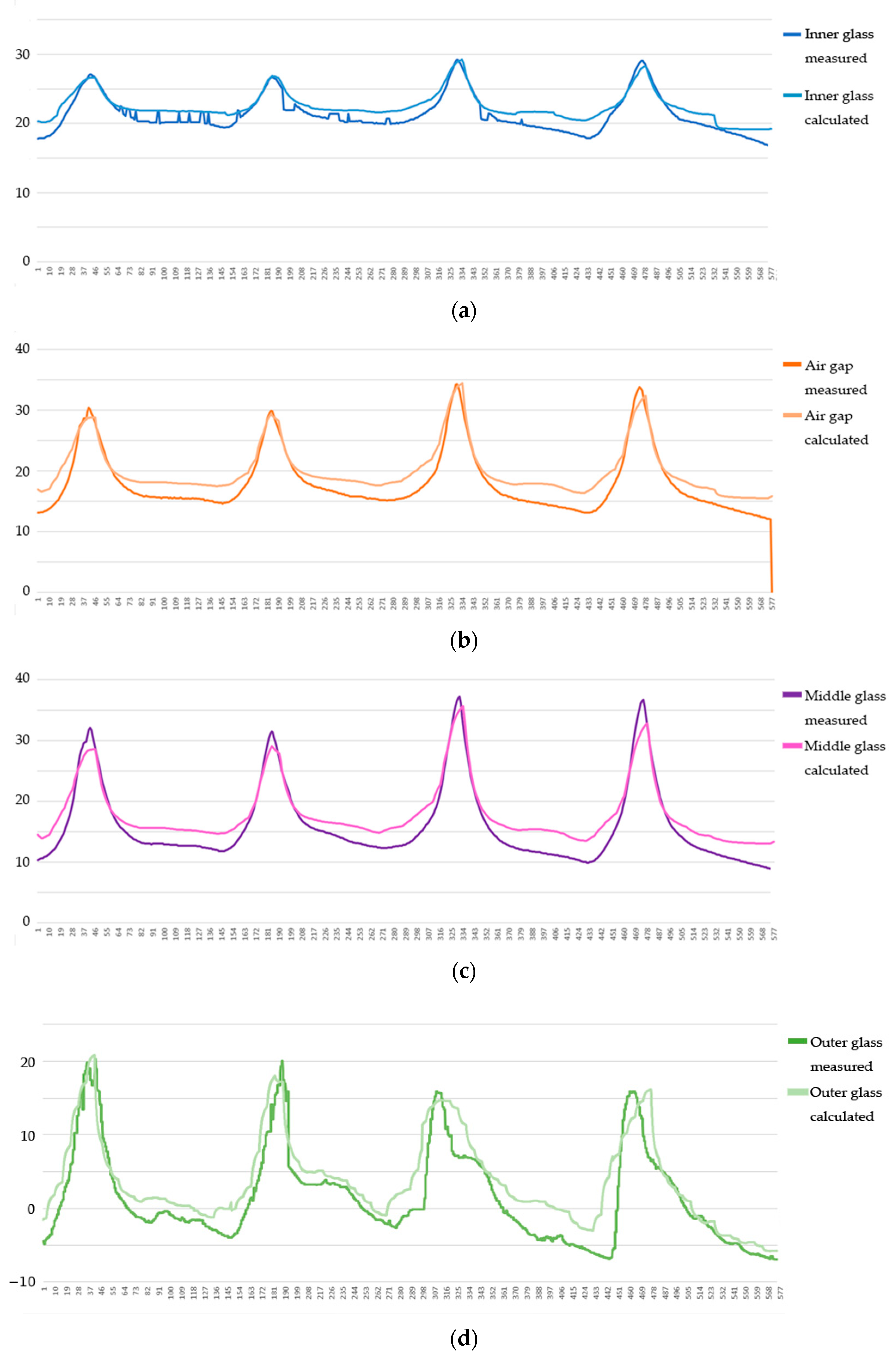
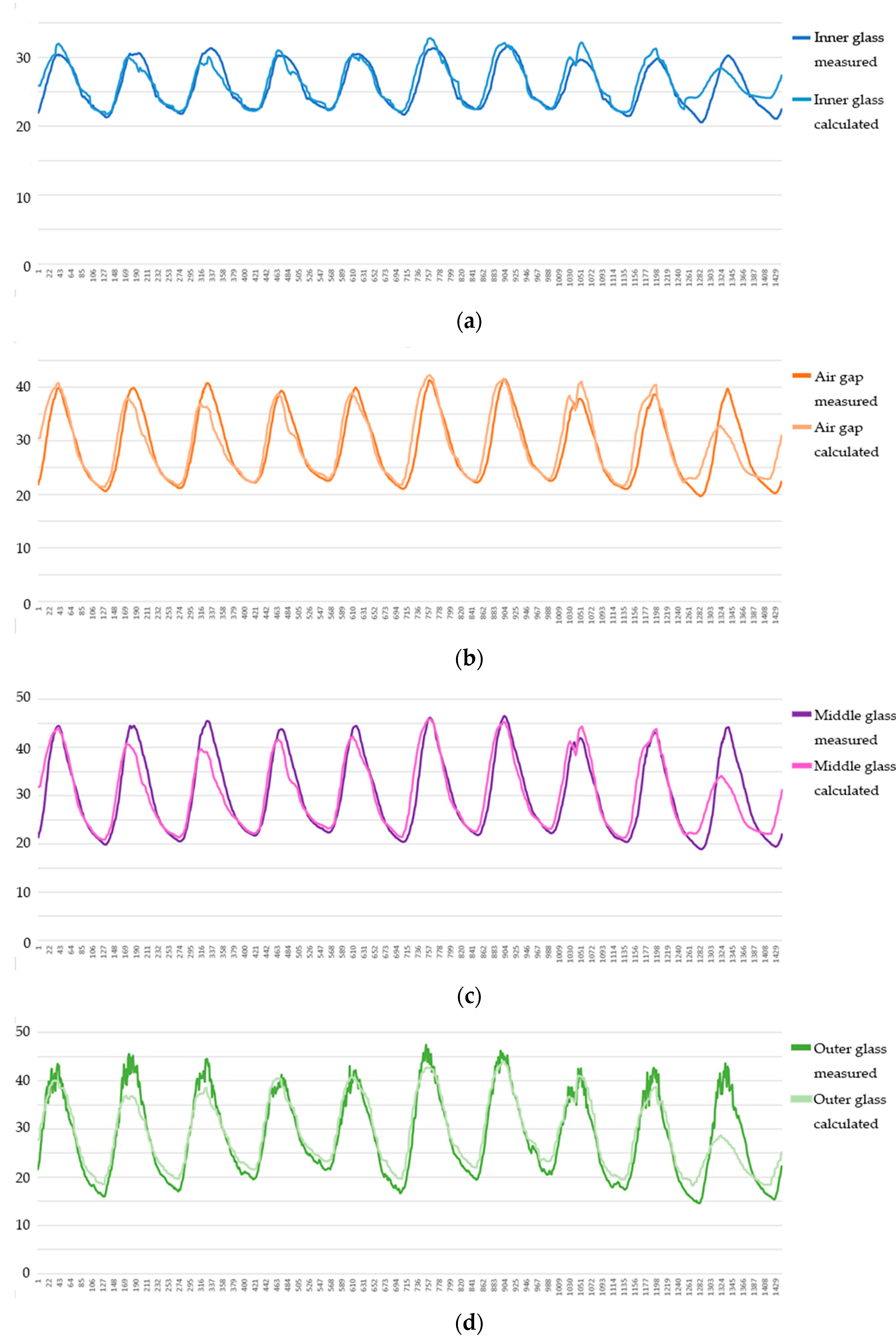
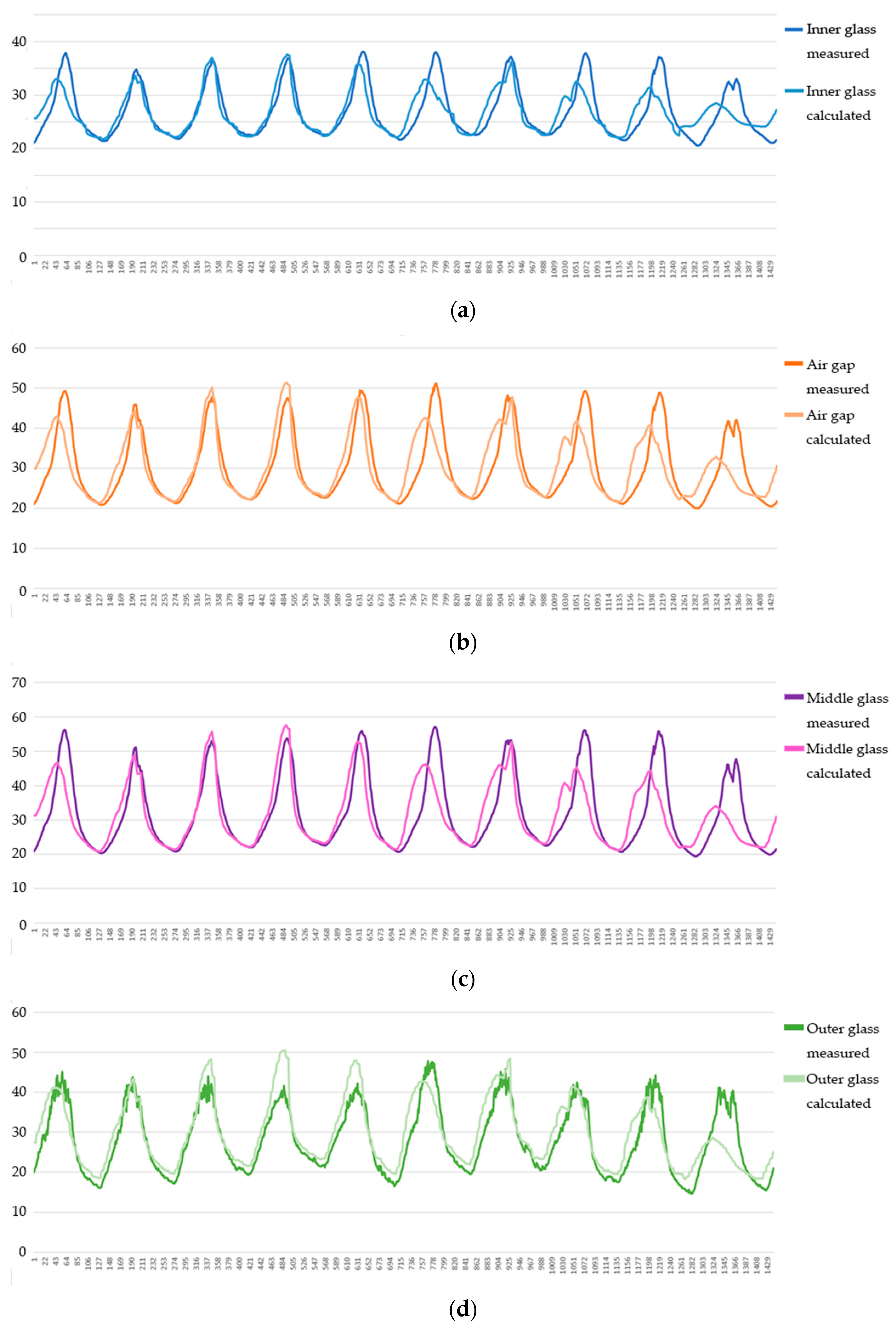
3. Results
4. Discussion
5. Conclusions and Future Work
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Symbol | Definition | Unit/ Constant Value |
| A | surface area of the body | [m2] |
| c | specific heat capacity | [J/(kg K)] |
| Cp | air-specific heat capacity | [J/(kg K)] |
| D | characteristic length | [-] |
| F1, F2 | Perez factor | [-] |
| g | gravitational constant | 9.81 [m/s2] |
| Gr | Grashof number | [-] |
| Gsol;dif | diffuse radiation onto the horizontal surface | [W/m2] |
| Gsol;dir | direct radiation onto the horizontal surface | [W/m2] |
| h | convective heat transfer coefficient | [W/(m2K)] |
| Icircum | Circumsolar irradiance | [W/m2] |
| Idif | diffuse radiation onto inclined surface | [W/m2] |
| Idif;tot | Total diffuse solar irradiance onto the inclined surface | [W/m2] |
| Idif;grnd | Diffuse solar irradiance on the inclined surface due to ground reflection | [W/m2] |
| Idir | direct radiation onto inclined surface | [W/m2] |
| Idir;tot | Total direct solar irradiance onto the inclined surface | [W/m2] |
| Itot | total solar irradiance | [W/m2] |
| k | air thermal conductivity | [W/(mK)] |
| m | mass of the component | [kg] |
| Nu | Nusselt number | [-] |
| P | radiative heat transfer rate | [W] |
| Pr | Prandtl number | [-] |
| Q | amount of energy in the component | [J] |
| Ra | Rayleigh number | [-] |
| Re | Reynolds number | [-] |
| T | absolute temperature of the body | [K] |
| T0 | ambient temperature | [K] |
| v | wind or airspeed | [m/s] |
| w | width | [m] |
| Greek symbols | ||
| µ | air dynamic viscosity | [kg/(m·s)] |
| βic | inclination of the façade element surface | [°] |
| γic | azimuth of the façade element surface | [°] |
| δ | Sun declination | [°] |
| ε | surface emissivity | [-] |
| θsol; ic | angle of incidence of the sun onto the façade element surface | [°] |
| ρ | air density | [kg/m3] |
| ρsol,grnd | albedo | [-] |
| σ | azimuth angle | 5.670374419...×10−8 [Wm−2K−4] |
| φw | geographic longitude | [°] |
| ω | angular incidence of the Sun from the local meridian | [°] |
References
- Laverge, J.; Schouwenaers, S.; Janssens, A. Overcoming condensation problems in a closed cavity double skin façade. In Proceedings of the Cold Climate HVAC 2009, Sisimiut, Greenland, 16–19 March 2009. [Google Scholar]
- GBD Magazine. Available online: https://gbdmagazine.com/closed-cavity-facades/ (accessed on 25 June 2023).
- Veršić, Z.; Nosil Mešić, M.; Binički, M.; Cvitković, I.; Petrac, D. A simulation of the physical characteristics of passively maintained closed cavity facades. Institue Technol. Res. 2023, 978, 11–14. [Google Scholar]
- Sdg 2. Transforming Our World: The 2030 Agenda for Sustainable Development. A/RES/70/1, 2015, United Nations. 2021. Available online: https://sdgs.un.org/publications/transforming-our-world-2030-agenda-sustainable-development-17981 (accessed on 15 July 2023).
- Huveners EM, P.; Van Herwijnen, F.; Soetens, F. Load sharing in insulated double glass units. Heron 2003, 48, 99–122. [Google Scholar]
- Laverge, J.; Schouwenaars, S.; Steeman, M.; Janssens, A.; Van Den Bossche, N. Condensation in a closed cavity double skin facade: A model for risk assessment. In Proceedings of the International Conference on Building Envelope Systems and Technologies (ICBEST 2010), Vancouver, BC, Canada, 27–30 June 2010. [Google Scholar]
- Van Den Bossche, N.; Van Den Brande, K.; De Bleecker, H.; Lori, G. Validation of a coupled pressure-equalization-thermal-mechanical model to study double-skin facades. E3S Web Conf. 2020, 172, 1–8. [Google Scholar] [CrossRef]
- Lori, G.; Van Den Brande, K.; Van Den Bossche, N.; De Bleecker, H. A simple numerical tool for superimposition of climatic load and wind load in Closed Cavity Facades: Importance of a coupled PE-thermal-mechanical model. Glas. Struct. Eng. 2022, 7, 487–506. [Google Scholar] [CrossRef]
- Lori, G.; Van Den Brande, K.; Van Den Bossche, N.; De Bleecker, H. Experimental validation of a numerical model for closed cavity façade glass structural calculation under dynamic cavity temperature, dry air flow and wind loads effects. Glas. Struct. Eng. 2022, 7, 523–545. [Google Scholar] [CrossRef]
- Lori, G.; Van Den Brande, K.; Van Den Bossche, N.; De Bleecker, H. Experimental and numerical assessment of permeability functions in closed cavity façades. Glas. Struct. Eng. 2022, 7, 507–521. [Google Scholar] [CrossRef]
- Wüest, T.; Luible, A. Thermal induced climatic loads of insulated glazed units in energy efficient facades. In Proceedings of the Challenging Glass 5 Conference on Architectural and Structural Applications of Glass, CGC 2016; Ghent University: Ghent, Belgium, 2016; pp. 261–270. [Google Scholar]
- Kozłowski, M.; Respondek, Z.; Wiśniowski, M.; Cornik, D.; Zemła, K. Experimental and Numerical Simulations of Climatic Loads in Insulating Glass Units by Controlled Change of Pressure in the Gap. Appl. Sci. 2023, 13, 1269. [Google Scholar] [CrossRef]
- Rashid, F.L.; Al-obaidi, M.A.; Dulaimi, A.; Mahmood, D.M.N. A Review of Recent Improvements, Developments, and Effects of Using Phase-Change Materials in Buildings to Store Thermal Energy. Designs 2023, 7, 90. [Google Scholar] [CrossRef]
- Rashid, F.L.; Al-gaheeshi, A.M.R.; Alhwayzee, M.; Ali, B.; Shah, N.A.; Chung, J.D. Mixed Convection in a Horizontal Channel—Cavity Arrangement with Different Heat Source Locations. Mathematics 2023, 11, 1428. [Google Scholar] [CrossRef]
- Rashid, F.L.; Hussein, A.K.; Malekshah, E.H.; Abderrahmane, A.; Guedri, K.; Younis, O. Review of Heat Transfer Analysis in Different Cavity Geometries with and without Nanofluids. Nanomaterials 2022, 12, 2481. [Google Scholar] [CrossRef]
- Gallo, P.; Romano, R. Adaptive Facades, Developed with Innovative Nanomaterials, for a Sustainable Architecture in the Mediterranean Area. Procedia Eng. 2017, 180, 1274–1283. [Google Scholar] [CrossRef]
- Pastori, S.; Mereu, R.; Mazzucchelli, E.S.; Passoni, S. Energy Performance Evaluation of a Ventilated Façade System through CFD Modeling and Comparison with International Standards. Energies 2021, 14, 193. [Google Scholar] [CrossRef]
- Jankovic, A.; Goia, F. Impact of double skin facade constructional features on heat transfer and fluid dynamic behaviour. Build. Environ. 2021, 196, 107796. [Google Scholar] [CrossRef]
- Jelle, B.P.; Kalnæs, S.E.; Gao, T. Low-Emissivity Materials for Building Applications: A State-of-the-Art Review and future research perspectives. Energy Build. 2015, 96, 329–356. [Google Scholar] [CrossRef]
- Maiorov, V.A. Heat transfer through a double-glazed window by radiation. IOP Conf. Ser. Mater. Sci. Eng. 2020, 939, 012048. [Google Scholar] [CrossRef]
- Iyi, D.; Hasan, R.; Penlington, R.; Underwood, C. Double skin façade: Modelling technique and influence of venetian blinds on the airflow and heat transfer. Appl. Therm. Eng. 2014, 71, 219–229. [Google Scholar] [CrossRef]
- Okada, T.; Ishige, R.; Ando, S. Analysis of thermal radiation properties of polyimide and polymeric materials based on ATR-IR spectroscopy. J. Photopolym. Sci. Technol. 2016, 29, 251–254. [Google Scholar] [CrossRef]
- Wellons, M. The Stefan-Boltzmann Law. In The Visual Dictionary of Photography; Bulb: Wooster, OH, USA, 2010. [Google Scholar]
- Hines, S. Greenhouse effect. In The Complete Guide to Climate Change; Routledge: London, UK, 2008. [Google Scholar] [CrossRef]
- Brown, F.E. Molecular and atomic weights. J. Chem. Educ. 1933, 10, 308–309. [Google Scholar] [CrossRef]
- Khalifa, A.J.N. Natural convective heat transfer coefficient—A review I. Isolated vertical and horizontal surfaces. Energy Convers. Manag. 2001, 42, 491–504. [Google Scholar] [CrossRef]
- O’Sullivan, C.T. Newton’s law of cooling—A critical assessment. Am. J. Phys. 1990, 58, 956–960. [Google Scholar] [CrossRef]
- Bright Hub Engineering. Available online: https://www.brighthubengineering.com/hvac/92660-natural-convection-heat-transfer-coefficient-estimation-calculations/?utm_content=cmp-true (accessed on 14 October 2022).
- Weir, G.; Muneer, T. Energy and environmental impact analysis of double-glazed windows. Energy Convers. Manag. 1998, 39, 243–256. [Google Scholar] [CrossRef]
- Respondek, Z. Influence of insulated glass units thickness and weight reduction on their functional properties. Open Eng. 2018, 8, 455–462. [Google Scholar] [CrossRef]
- Zoran, V.; Josip, G.; Marin, B.; Lucija, S. Factors in a Sustainability Assessment of a New Types of Closed Cavity Facades. MMM Int. J. Adv. Eng. Archit. Math. 2022, 16, 148–152. [Google Scholar]
- ISO 52016-1:2017; Energy Performance of Buildings—Energy Needs for Heating and Cooling; Internal Temperatures and Sensible and Latent Heat Loads—Part 1: Calculation Procedures. ISO: Geneva, Switzerland, 2017.
- ISO/TR 52010-2:2017; Energy performance of buildings—External climatic conditions—Part 2: Explanation and justification of ISO 52010-1. ISO: Geneva, Switzerland, 2017. Available online: https://www.iso.org/standard/67344.html (accessed on 15 July 2023).
- Focus on EPB standards. REHVA Eur. HVAC J. 2015, 52.
- Yang, D. Solar radiation on inclined surfaces: Corrections and benchmarks. Sol. Energy 2016, 136, 288–302. [Google Scholar] [CrossRef]
- Widén, J.; Munkhammar, J. Solar Radiation Theory, 1st ed.; Uppsala University: Uppsala, Sweden, 2019; ISBN 978-91-506-2760-2. [Google Scholar] [CrossRef]
- Perez, R.; Stewart, R.; Seals, R.; Guertin, T. The Development and Verification of the Perez Diffuse Radiation Model; Sandia National Laboratorie: Albuquerque, NM, USA; State University: Albany, NY, USA, 1988; p. 176.
- Thornsberry, C. Methicillin-resistant staphylococci. Clin. Lab. Med. 1989, 9, 255–267. [Google Scholar] [CrossRef] [PubMed]
- Pérez-Grande, I.; Meseguer, J.; Alonso, G. Influence of glass properties on the performance of double-glazed facades. Appl. Therm. Eng. 2005, 25, 3163–3175. [Google Scholar] [CrossRef]
- Walker, J.; Halliday, D.; Resnick, R. Fundamentals of Physics Halliday & Resnick, 10th ed.; Wiley: Hoboken, NJ, USA, 2014. [Google Scholar]



| Material | Dimensions Width (cm)/ Height (cm)/ Thickness (mm) | Specific Heat Capacity (J/kgK) | Solar Factor (-) | Emissivity (-) | Reflectivity (-) | Absorption (-) |
|---|---|---|---|---|---|---|
| Inner glass—inner pane | 133.3/235.9/5 | 840 | 0.71 | 0.89 | 0.45 | 0.19 |
| Inner glass—outer pane | 133.3/235.9/5 | 840 | 0.71 | 0.12 | 0.27 | 0.19 |
| Middle glass—inner side | 133.3/235.9/8 | 840 | 0.84 | 0.89 | 0.08 | 0.08 |
| Middle glass—outer side | 133.3/2 35.9/0 | 840 | 0.84 | 0.89 | 0.08 | 0.08 |
| Outer glass—inner pane | 149.7/258.7/6 | 840 | 0.36 | 0.01 | 0.11 | 0.18 |
| Outer glass—outer pane | 149.7/258.7/6 | 840 | 036 | 0.89 | 0.12 | 0.17 |
| Sun blinds | 133.3/235.9/1.5 | 880 | - | 0.94 | 0.59 | 0 |
| Argon | 149.7/258.7/14 | 520 | - | - | - | - |
| Air cavity | 133.3/235.9/155 | 1000 | - | - | - | - |
| Peripheral element—down | 133.3/12.8 | 880 | - | 0.94 | 0.59 | 0.41 |
| Peripheral element—left | 235.9/12.8 | 880 | - | 0.94 | 0.59 | 0.41 |
| Peripheral element—right | 235.9/12.8 | 880 | - | 0.94 | 0.59 | 0.41 |
| Peripheral element—up | 133.3/12.8 | 880 | - | 0.94 | 0.59 | 0.41 |
| Façade frame | 880 | - | 0.94 | 0.59 | 0.41 | |
| Frame cladding —overhang depth—down | 30.8 | 880 | - | 0.94 | 0.59 | 0.41 |
| Frame cladding —overhang depth—left | 18 | 880 | - | 0.94 | 0.59 | 0.41 |
| Frame cladding —overhang depth—right | 30.8 | 880 | - | 0.94 | 0.59 | 0.41 |
| Frame cladding —overhang depth—up | 30.8 | 880 | - | 0.94 | 0.59 | 0.41 |
| Material/ Component | Heat Transfer Coefficient, λ (W/mK) | Thickness, d (mm) | Heat Transfer Resistance, R (m2K/W) |
|---|---|---|---|
| Glass | 1 | 5 | 0.005 |
| PVB layer | 0.22 | 0.76 | 0.003 |
| Laminated glass * | - | 10.76 | 0.013 |
| 95% Argon, 5% Air | 0.025 | 16 | 0.640 |
| Air 130 mm (simplified) | 0.694 | 130 | 0.187 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Veršić, Z.; Binički, M.; Nosil Mešić, M.; Galić, J. Passively Maintained Closed Cavity Façade—Experimental Validation of the Mathematical Thermal Model. Buildings 2023, 13, 2031. https://doi.org/10.3390/buildings13082031
Veršić Z, Binički M, Nosil Mešić M, Galić J. Passively Maintained Closed Cavity Façade—Experimental Validation of the Mathematical Thermal Model. Buildings. 2023; 13(8):2031. https://doi.org/10.3390/buildings13082031
Chicago/Turabian StyleVeršić, Zoran, Marin Binički, Mateja Nosil Mešić, and Josip Galić. 2023. "Passively Maintained Closed Cavity Façade—Experimental Validation of the Mathematical Thermal Model" Buildings 13, no. 8: 2031. https://doi.org/10.3390/buildings13082031
APA StyleVeršić, Z., Binički, M., Nosil Mešić, M., & Galić, J. (2023). Passively Maintained Closed Cavity Façade—Experimental Validation of the Mathematical Thermal Model. Buildings, 13(8), 2031. https://doi.org/10.3390/buildings13082031







