Numerical Analysis on the Behavior of Floating Geogrid-Encased Stone Column Improved Foundation
Abstract
1. Introduction
2. Model Preparation and Validation
2.1. General
2.2. Soft Soil
2.3. Aggregates
2.4. Biaxial Geogrid
2.5. Interface
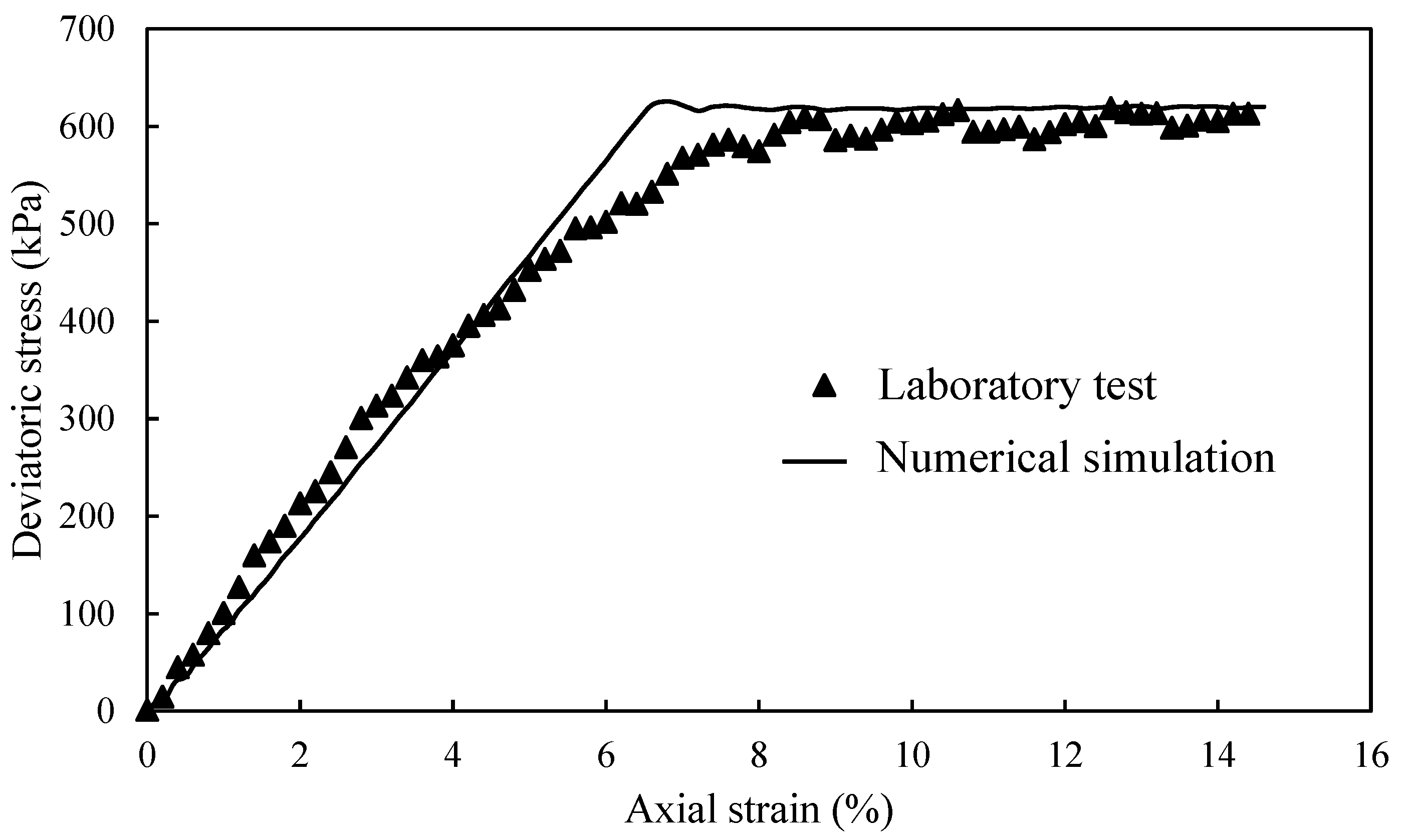
2.6. Model Validation
3. Results and Discussion
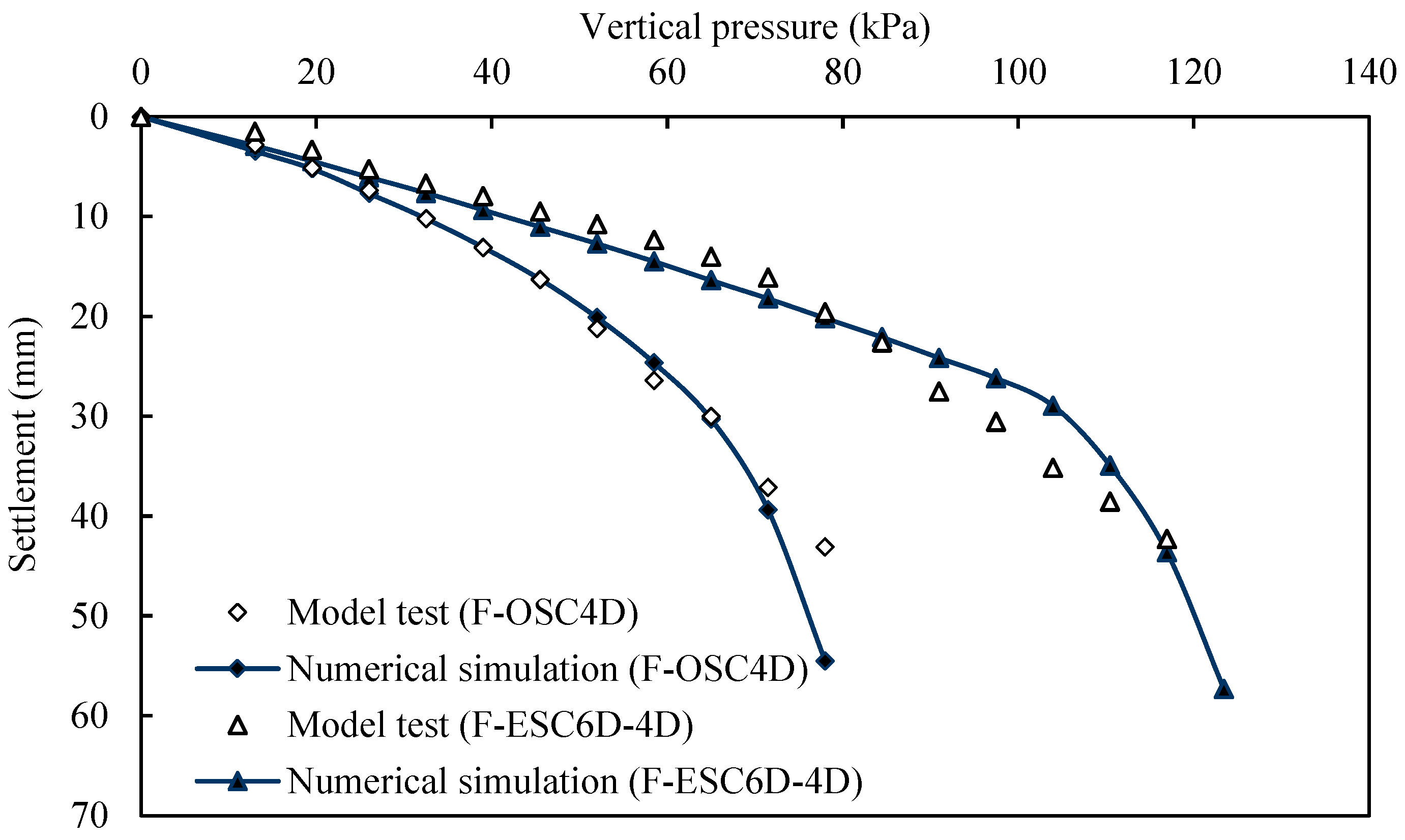
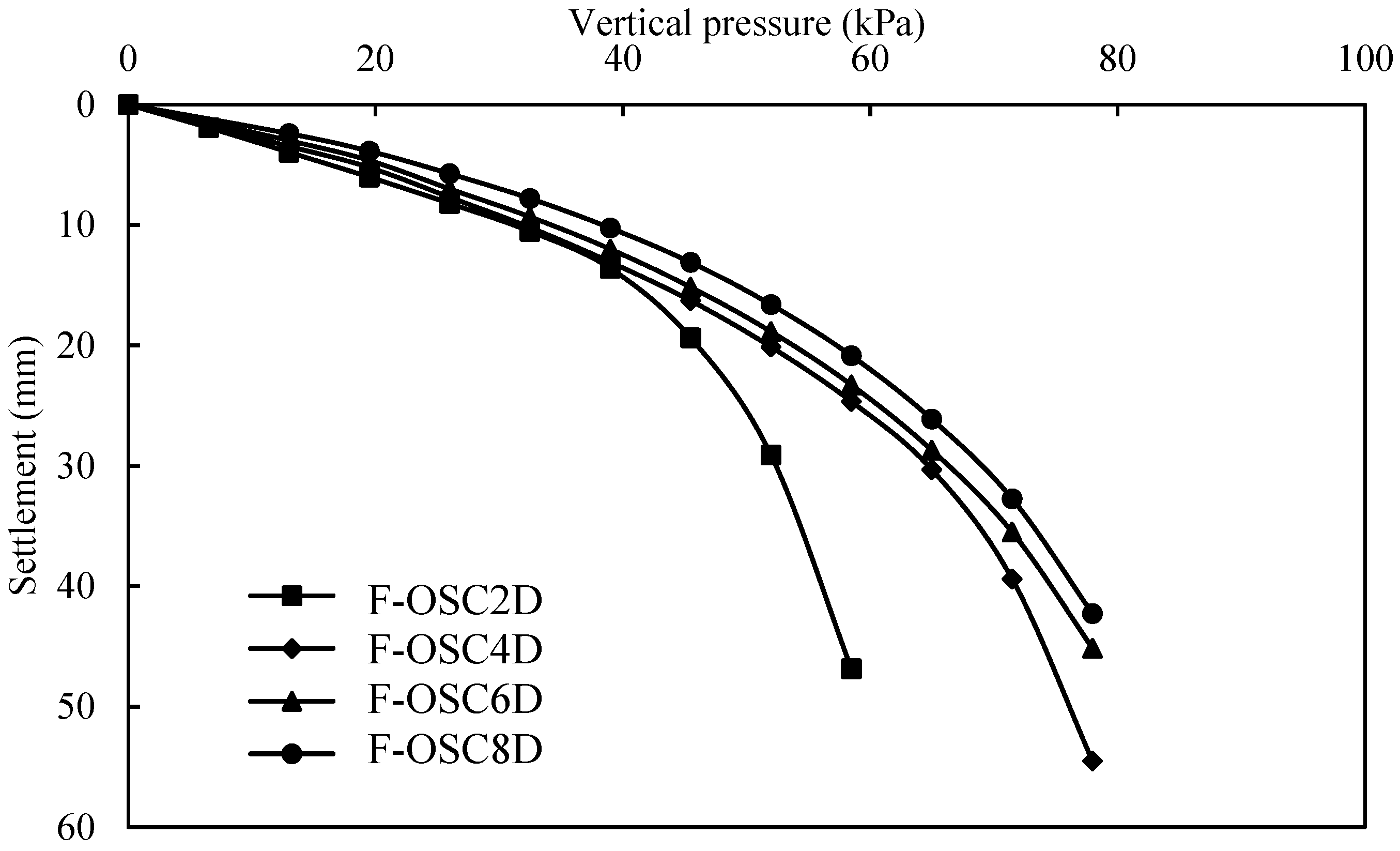
3.1. Load-Settlement Behavior
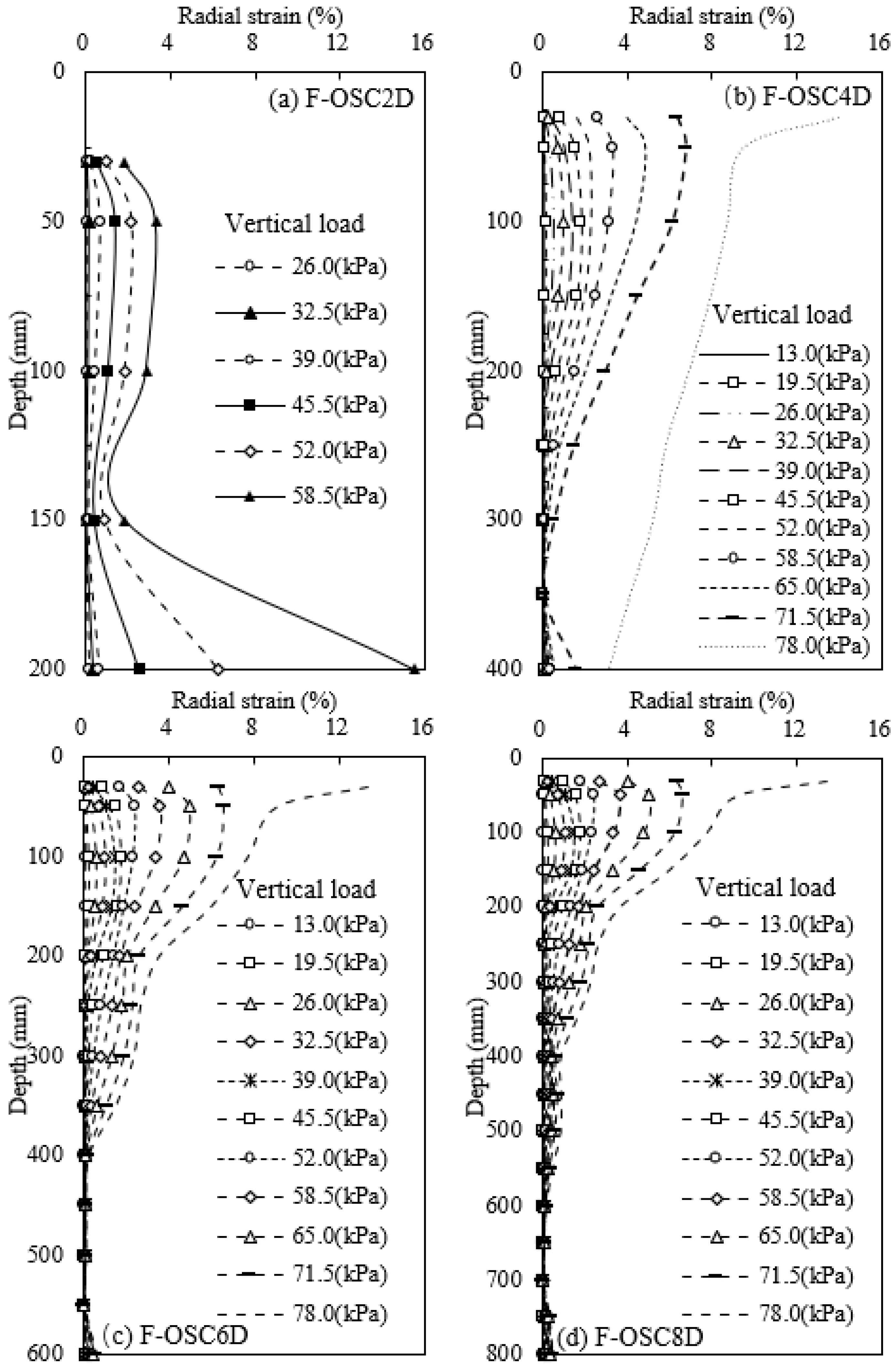
3.2. Bulging Deformation
3.3. Failure Mode
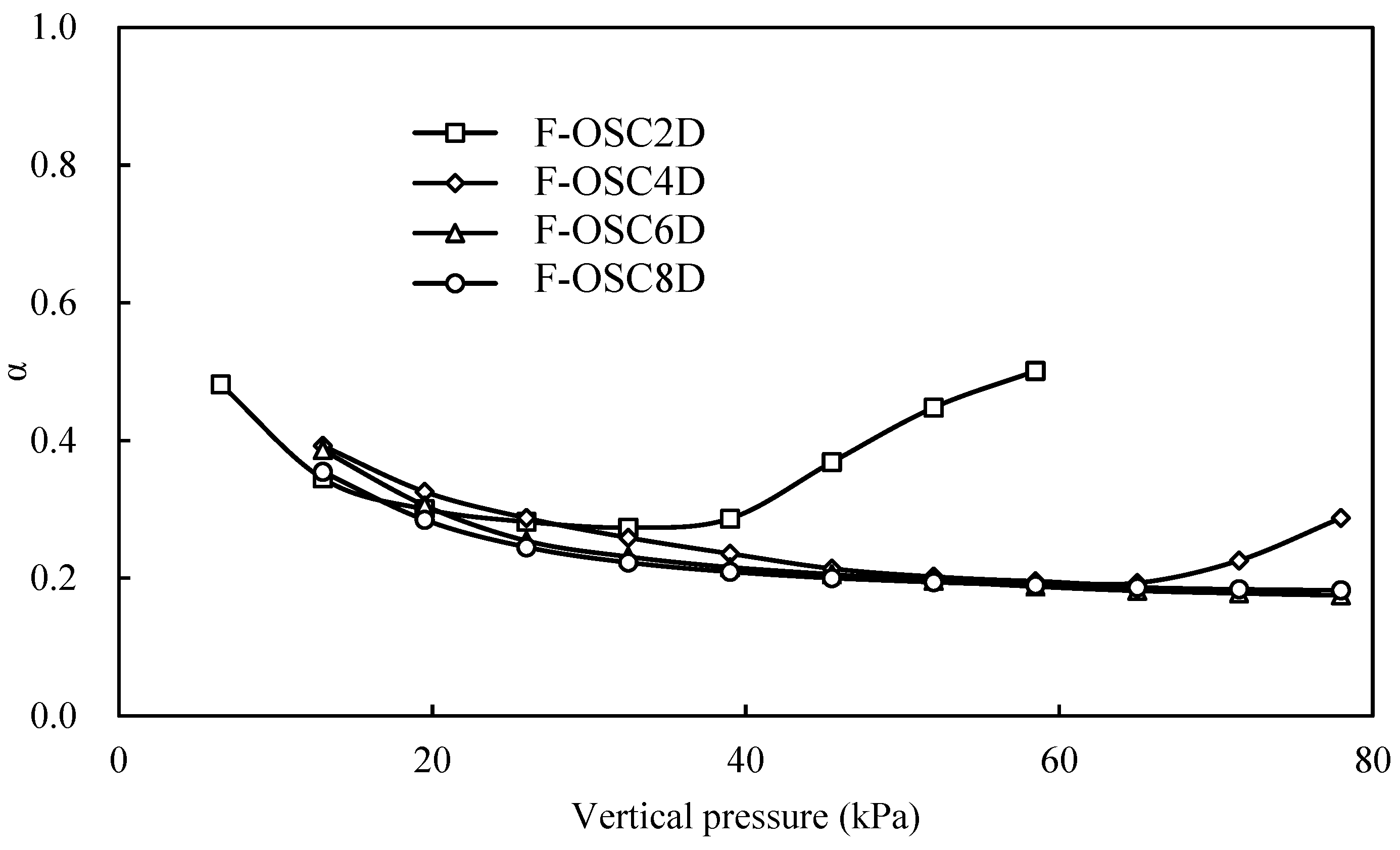
3.4. Load Transfer Coefficient
4. Conclusions
- (1)
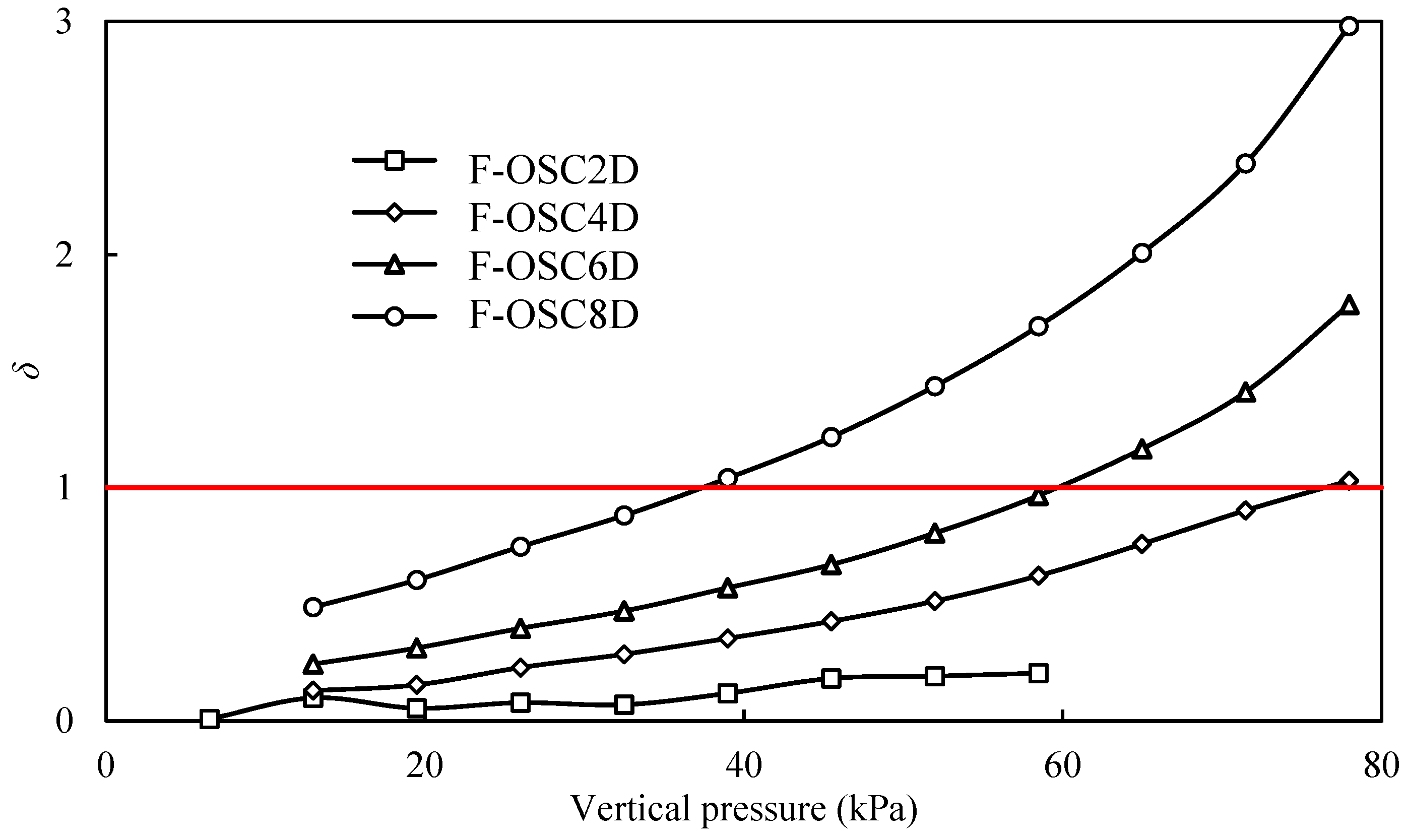
- The bearing capacity of F-OSCs increased with the increase in column and encasement length, and a critical length (i.e., 4D) was found in improving bearing capacity. The geogrid encasement could increase the bearing capacity of F-OSCs, and also had a critical length (i.e., 4D) in settlement improvement.
- (2)
- The bulging deformation was significant in F-OSCs and observed at the top of a long column and the full length of a short column. The geogrid encasement could constrain the OSC to decrease the bulging deformation due to excellent tensile strength. The short encasement length (e.g., 2D) could not effectively confine the column, and only the deformation transferred deeper.
- (3)
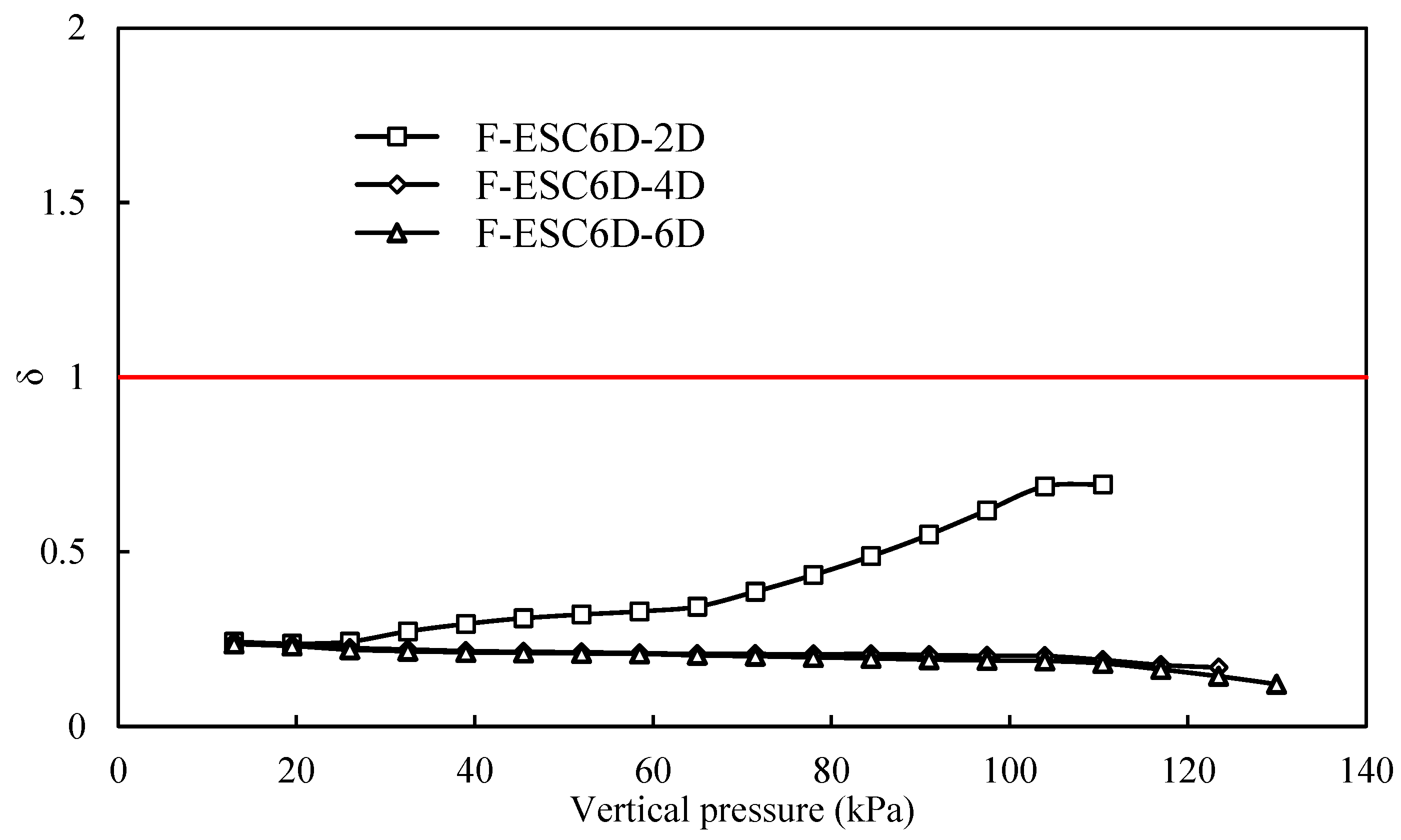
- The failure mode in F-OSCs was mainly a punching failure with bulging deformation for a short column (e.g., less than 4D), and was relative to the vertical pressure for a long column. The failure mode in F-ESCs was a punching failure with a slight bulging deformation due to a good integration improved by geogrid, and the punching degree increased with an increase in geogrid encasement length.
- (4)
- The load transfer coefficient in the short column would increase in a later stage due to a punching failure. The load transfer coefficient of F-OSCs or F-ESCs was relatively stable as the column length increased to a critical value (e.g., 4D) or the encasement length increased to a critical value (e.g., 4D).
5. Limitations
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhang, L.; Xu, Z.; Zhou, S. Vertical cyclic loading response of geosynthetic-encased stone column in soft clay. Geotext. Geomembr. 2020, 48, 897–911. [Google Scholar]
- Vijay Kumar, S.P.; Ganesh Kumar, S.; Datta Gupta, S. Performance assessment of composite skirted ground reinforcement system in liquefiable ground under repeated dynamic loading conditions. Bull. Earthq. Eng. 2022, 20, 1397–1429. [Google Scholar] [CrossRef]
- Rezaei, M.M.; Lajevardi, S.H.; Saba, H.; Ghalandarzadeh, A.; Zeighami, E. Laboratory study on single stone columns reinforced with steel bars and discs. Int. J. Geosynth. Ground Eng. 2019, 5, 2. [Google Scholar]
- Hasan, M.; Samadhiya, N.K. Performance of geosynthetic-reinforced granular piles in soft clays: Model tests and numerical analysis. Comput. Geotech. 2017, 87, 178–187. [Google Scholar] [CrossRef]
- Yoo, C.; Lee, D. Performance of geogrid-encased stone columns in soft ground: Full-scale load tests. Geosynth. Int. 2012, 19, 480–490. [Google Scholar]
- Ji, M.; Wang, J.; Zheng, J.-J.; Zheng, Y. Contribution of geosynthetic to the shear strength of geosynthetic encased stone columns. Geosynth. Int. 2023; ahead of print. [Google Scholar] [CrossRef]
- Ong, D.; Sim, Y.; Leung, C. Performance of field and numerical back-analysis of floating stone columns in soft clay considering the influence of dilatancy. Int. J. Geomech 2018, 18, 04018135. [Google Scholar]
- Almeida, M.; Lima, B.; Riccio, M.; Jud, H.; Cascão, M.; Roza, F. Stone columns field test: Monitoring data and numerical analyses. Geotech. Eng. J. SEAGS AGSSEA 2014, 45, 103–112. [Google Scholar]
- Gao, J.; Liu, L.; Zhang, Y.; Xie, X. Deformation mechanism and soil evolution analysis based on different types geogrid reinforced foundation. Constr. Build. Mater. 2022, 331, 127322. [Google Scholar] [CrossRef]
- Thakur, A.; Rawat, S.; Gupta, A.K. Experimental study of ground improvement by using encased stone columns. Innov. Infrastruct. Solut. 2021, 6, 1. [Google Scholar] [CrossRef]
- Thakur, A.; Rawat, S.; Gupta, A.K. Experimental and numerical modelling of group of geosynthetic-encased stone columns. Innov. Infrastruct. Solut. 2021, 6, 12. [Google Scholar] [CrossRef]
- Gu, M.; Mo, H.; Qiu, J.; Yuan, J.; Xia, Q. Behavior of floating stone columns reinforced with geogrid encasement in model tests. Front. Mater. 2022, 9, 980851. [Google Scholar] [CrossRef]
- Gu, M.; Cai, X.; Fu, Q.; Li, H.; Wang, X.; Mao, B. Numerical Analysis of Passive Piles under Surcharge Load in Extensively Deep Soft Soil. Buildings 2022, 12, 1988. [Google Scholar] [CrossRef]
- Gu, M.; Han, J.; Zhao, M. Three-Dimensional Discrete-Element Method Analysis of Stresses and Deformations of a Single Geogrid-Encased Stone Column. Int. J. Geomech. 2017, 17, 1–4. [Google Scholar] [CrossRef]
- Gu, M.; Cui, J.; Wu, Y.; Yuan, J.; Li, Y. Effects of Geogrid Encasement on Behavior of Stone Column-Improved Soft Clay. In Advances in Transportation Geotechnics IV; Springer: Cham, Switzerland, 2022; pp. 559–573. [Google Scholar]
- Gu, M.; Han, J.; Zhao, M. Three-dimensional DEM analysis of axially loaded geogrid-encased stone column in clay bed. Int. J. Geomech. 2020, 20, 04019180. [Google Scholar] [CrossRef]
- Hasan, M.; Samadhiya, N. Experimental and numerical analysis of geosynthetic-reinforced floating granular piles in soft clays. Int. J. Geosynth. Ground Eng. 2016, 2, 22. [Google Scholar] [CrossRef]
- Liu, F.; Guo, P.; Hu, H.; Zhu, C.; Gong, X. Loading Behavior and Soil-Structure Interaction for a Floating Stone Column under Rigid Foundation: A DEM Study. Geofluids 2021, 2021, 9508367. [Google Scholar] [CrossRef]
- Xu, Z.A.; Cy, B.; Jfc, A.; Zag, A. Numerical modeling of floating geosynthetic-encased stone column–supported embankments with basal reinforcement. Geotext. Geomembr. 2022, 50, 720–736. [Google Scholar]
- Yasser, F.; Altahrany, A.; Elmeligy, M. Numerical investigation of the settlement behavior of hybrid system of floating stone columns and granular mattress in soft clay soil. Int. J. Geo Eng. 2022, 13, 12. [Google Scholar] [CrossRef]
- Shahu, J.T.; Kumar, S.; Bhowmik, R. Ground Improvement for Transportation Infrastructure: Experimental Investigations on Cyclic Behavior of a Group of Granular Columns. Int. J. Geomech. 2023, 23, 04022309. [Google Scholar] [CrossRef]
- Sadaoui, O.; Bahar, R. Analyse numérique et expérimentale du comportement des ouvrages fondés sur un sol mou renforcé par des colonnes ballastées flottantes. Bull. Eng. Geol. Environ. 2020, 79, 2721–2745. [Google Scholar] [CrossRef]
- Bhatia, R.; Kumar, A. Load-Settlement Behavior of Concrete Debris Pile in Fly Ash Fill. J. Hazard. Toxic Radioact. Waste 2020, 24, 1–9. [Google Scholar] [CrossRef]
- Ehsaniyamchi, A.; Ghazavi, M. Short-term and long-term behavior of geosynthetic-reinforced stone columns. Soils Found. 2019, 59, 1579–1590. [Google Scholar] [CrossRef]
- Chen, J.-F.; Zhang, X.; Yoo, C.; Gu, Z.-A. Effect of basal reinforcement on performance of floating geosynthetic encased stone column-supported embankment. Geotext. Geomembr. 2022, 50, 566–580. [Google Scholar] [CrossRef]
- Fattah, M.Y.; Al-Neami, M.A.; Shamel Al-Suhaily, A. Estimation of bearing capacity of floating group of stone columns. Eng. Sci. Technol. Int. J. 2017, 20, 1166–1172. [Google Scholar] [CrossRef]
- Ng, K.S.; Tan, S.A. Design and analyses of floating stone columns. Soils Found. 2014, 54, 478–487. [Google Scholar] [CrossRef]
- Şahinkaya, F.; Vekli, M.; Çadır, C. Numerical analysis under seismic loads of soils improvement with floating stone columns. Nat. Hazards 2017, 88, 891–917. [Google Scholar] [CrossRef]
- Ali, M. Behavior of Ordinary and Encased Stone Columns End-Bearing and Floating in Soft Clay (Numerical Model). In Proceedings of the International Congress and Exhibition “Sustainable Civil Infrastructures: Innovative Infrastructure Geotechnology”, Cairo, Egypt, 24–28 November 2018. [Google Scholar]
- Debnath, P.; Dey, A.K. Bearing capacity of geogrid reinforced sand over encased stone columns in soft clay. Geotext. Geomembr. 2017, 45, 653–664. [Google Scholar] [CrossRef]
- Thakur, A.; Rawat, S.; Gupta, A.K. Experimental and Numerical Investigation of Load Carrying Capacity of Vertically and Horizontally Reinforced Floating Stone Column Group. Geotech. Geol. Eng. 2021, 39, 3003–3018. [Google Scholar] [CrossRef]
- Itasca. FLAC3D 6.0 Document; Itasca Consulting Group: Minneapolis, MN, USA, 2018. [Google Scholar]
- ASTM. Standard Practice for Classification of Soils for Engineering Purposes (Unified Soil Classification System); D2487-17; ASTM International: West Conshohocken, PA, USA, 2017. [Google Scholar]
- Potyondy, D.O.; Autio, J. Bonded-Particle Simulations of the In-Situ Failure Test At Olkiluoto. In Proceedings of the 38th U.S. Symposium on Rock Mechanics (USRMS), Washington, DC, USA, 7–10 July 2001. [Google Scholar]
- Gu, M.; Zhao, M.; Zhang, L.; Han, J. Effects of geogrid encasement on lateral and vertical deformations of stone columns in model tests. Geosynth. Int. 2016, 23, 100–112. [Google Scholar] [CrossRef]
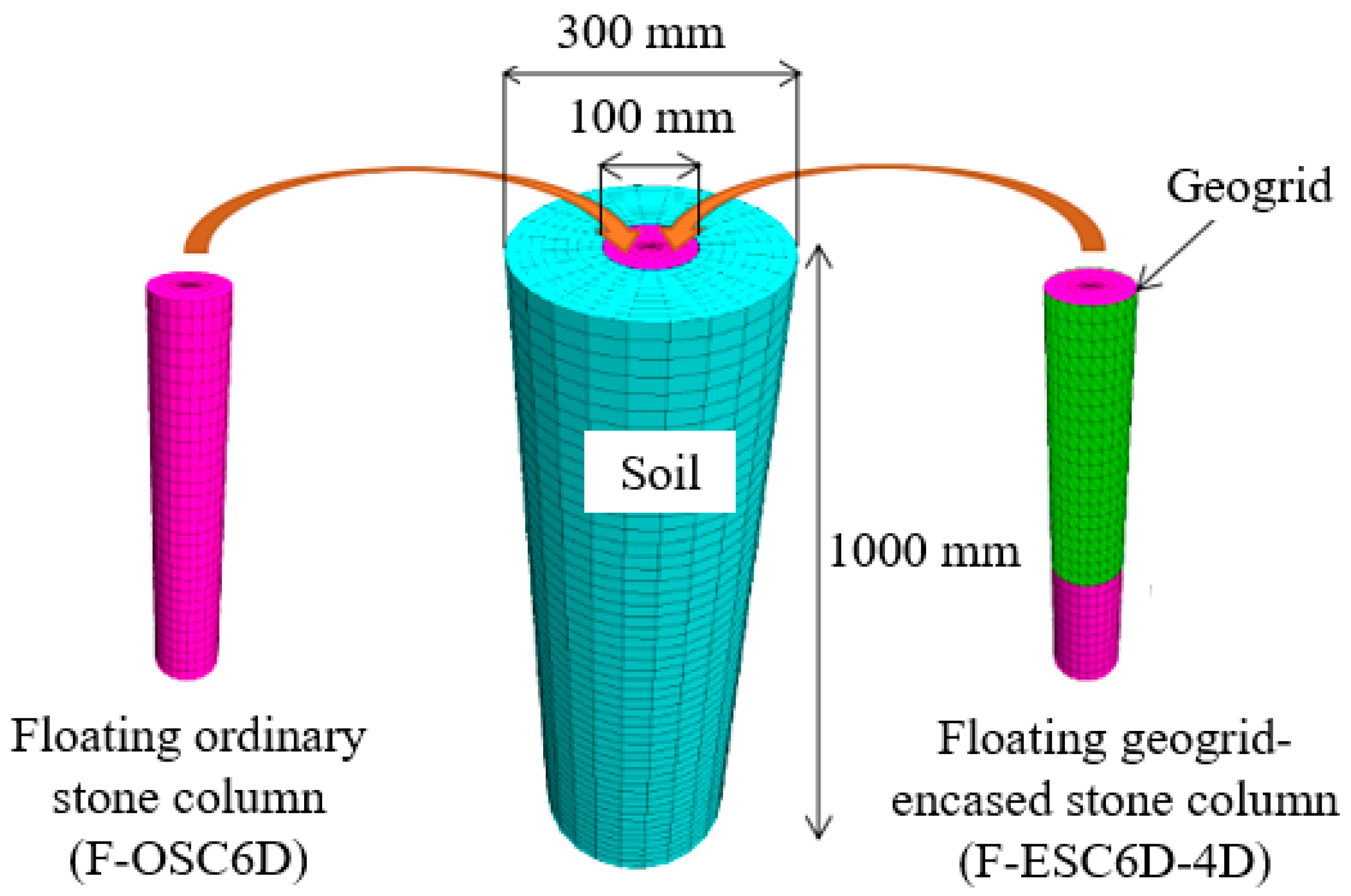





| Description | Stone Column | Geogrid | Model Box | ||
|---|---|---|---|---|---|
| Diameter (D) | Length (L) | Length (l) | Diameter (De) | Height (H) | |
| F-OSC2D | 100 mm | 200 mm | - | 300 mm | 1000 mm |
| F-OSC4D | 400 mm | ||||
| F-OSC6D | 600 mm | ||||
| F-OSC8D | 800 mm | ||||
| F-ESC6D-2D | 600 mm | 200 mm | |||
| F-ESC6D-4D | 600 mm | 400 mm | |||
| F-ESC6D-6D | 600 mm | 600 mm | |||
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Elastic modular | 0.3 MPa | Friction angle | 0° |
| Poisson’s ratio | 0.3 | Density | |
| Cohesion | 4.06 kPa |
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Elastic modular | 9.2 MPa | Friction angle | 42.9° |
| Poisson’s ratio | 0.27 | Density | |
| Cohesion | 0 kPa |
| Parameter | Value |
|---|---|
| Elastic modulus | 330 MPa |
| Passion’s ratio | 0.33 |
| Coupling spring cohesion (kPa) | 3.2 |
| Coupling spring friction angle (°) | 0 |
| Coupling spring shear stiffness (N/m3) | 3.2 × 104 |
| Thickness | 1 mm |
| Interface Position | Cohesion (kPa) | Friction (°) | Shear Stiffness (N/m) | Normal Stiffness (N/m) |
|---|---|---|---|---|
| Column side | 3.2 | 0 | 3.0 × 108 | 3.0 × 108 |
| Column bottom | 3.2 | 0 | 1.9 × 108 | 1.9 × 108 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cheng, Y.; Cai, X.; Mo, H.; Gu, M. Numerical Analysis on the Behavior of Floating Geogrid-Encased Stone Column Improved Foundation. Buildings 2023, 13, 1609. https://doi.org/10.3390/buildings13071609
Cheng Y, Cai X, Mo H, Gu M. Numerical Analysis on the Behavior of Floating Geogrid-Encased Stone Column Improved Foundation. Buildings. 2023; 13(7):1609. https://doi.org/10.3390/buildings13071609
Chicago/Turabian StyleCheng, Ye, Xiaocong Cai, Haizhao Mo, and Meixiang Gu. 2023. "Numerical Analysis on the Behavior of Floating Geogrid-Encased Stone Column Improved Foundation" Buildings 13, no. 7: 1609. https://doi.org/10.3390/buildings13071609
APA StyleCheng, Y., Cai, X., Mo, H., & Gu, M. (2023). Numerical Analysis on the Behavior of Floating Geogrid-Encased Stone Column Improved Foundation. Buildings, 13(7), 1609. https://doi.org/10.3390/buildings13071609






