Analyzing the Effect of Rotary Inertia and Elastic Constraints on a Beam Supported by a Wrinkle Elastic Foundation: A Numerical Investigation
Abstract
1. Introduction
2. Statement of the Problem
3. Determination of Natural Frequencies and Eigenmodes
3.1. Analytic Solution
3.2. Formulation of Finite Element Method
4. Results and Discussion
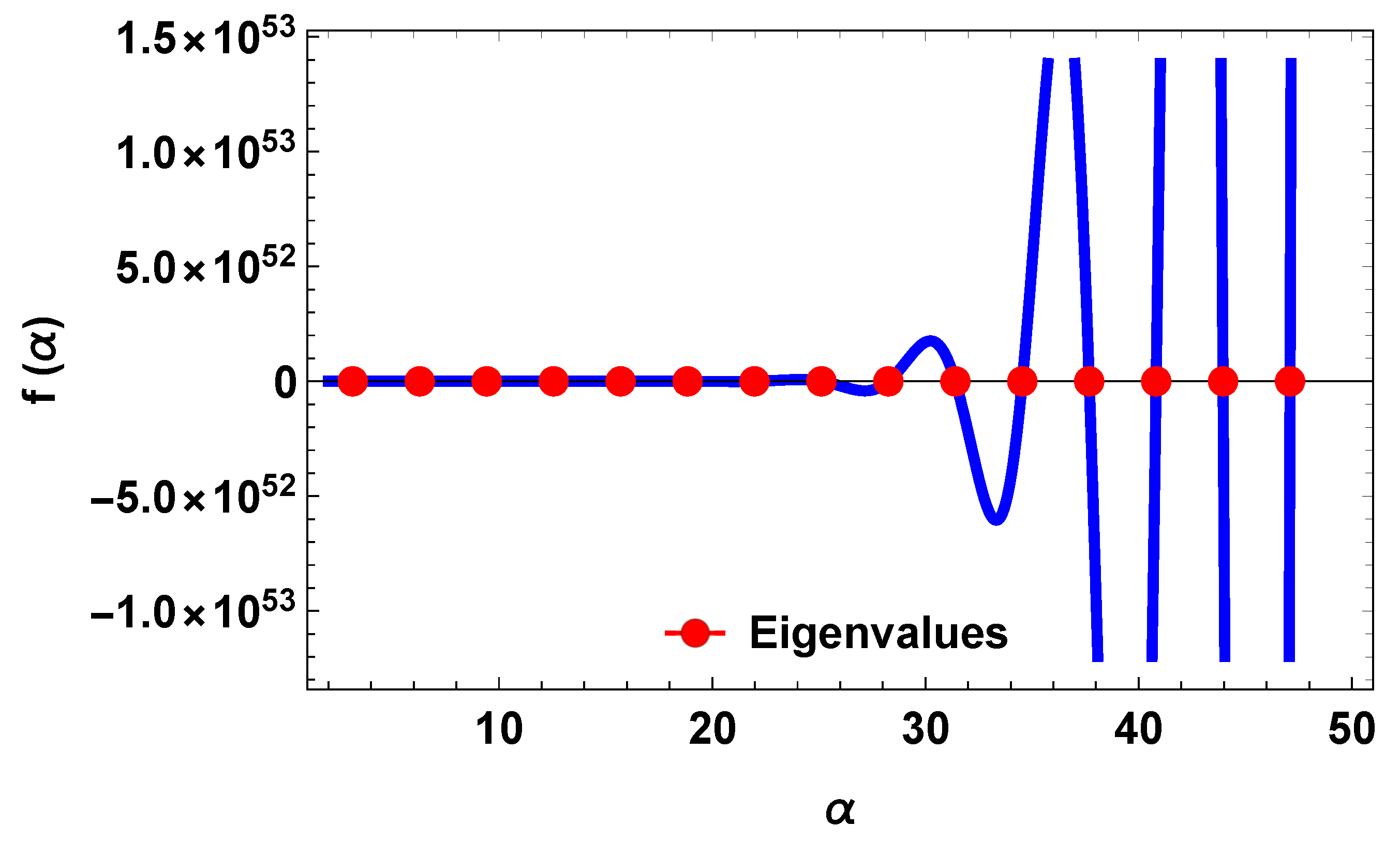
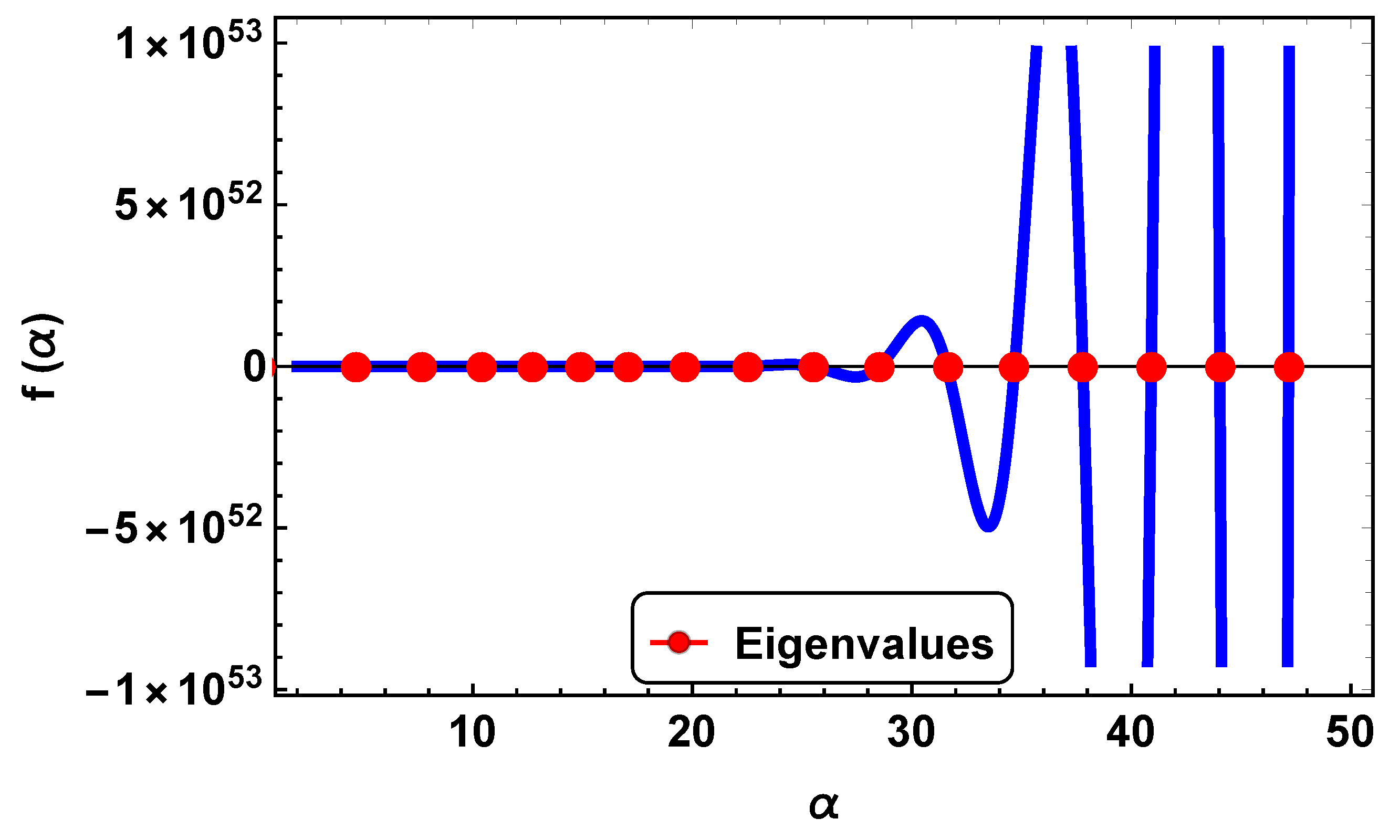
4.1. Graphical and Tabular Representations
4.2. Validation of the Results
5. Conclusions
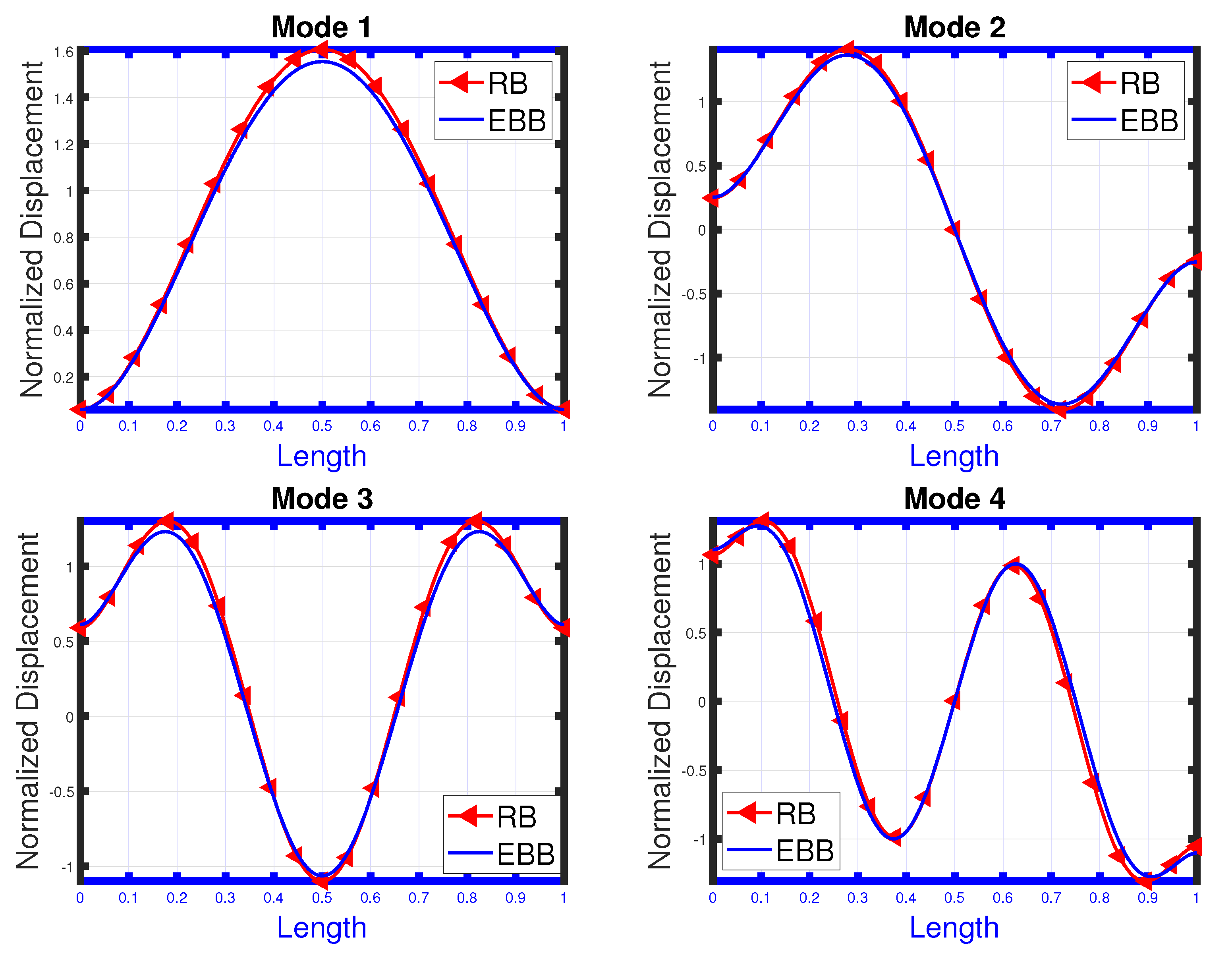
- The eigenvalues obtained in terms of the slenderness ratio for the RB depend on the geometry, unlike the EBB where eigenvalues do not depend on the slenderness ratio.
- The behavior of a beam under different conditions, such as the presence of rotatory inertia or placement on an elastic foundation, impacts its natural frequencies.
- For smaller stiffness parameters, the beam undergoes rigid body modes without significant internal deformation.
- The inclusion of rotational inertia had a minimal effect on the fundamental mode frequency, but it had a significant impact on the higher frequency modes.
- Placing the Winkler elastic foundation under the beam caused an increase in stiffness, leading to higher frequencies as the elastic foundation stiffness increased.
- A detailed tabular and graphical analysis proved that the vibration frequencies and mode shapes are more affected by the linear spring stiffness compared to rotary spring stiffness.
- Unlike independent beams, beams on an elastic foundation require higher frequencies to vibrate. Thus, by controlling the elastic foundation parameter, one can adjust the vibrating frequency to minimize collateral damage to the vibrating structure.
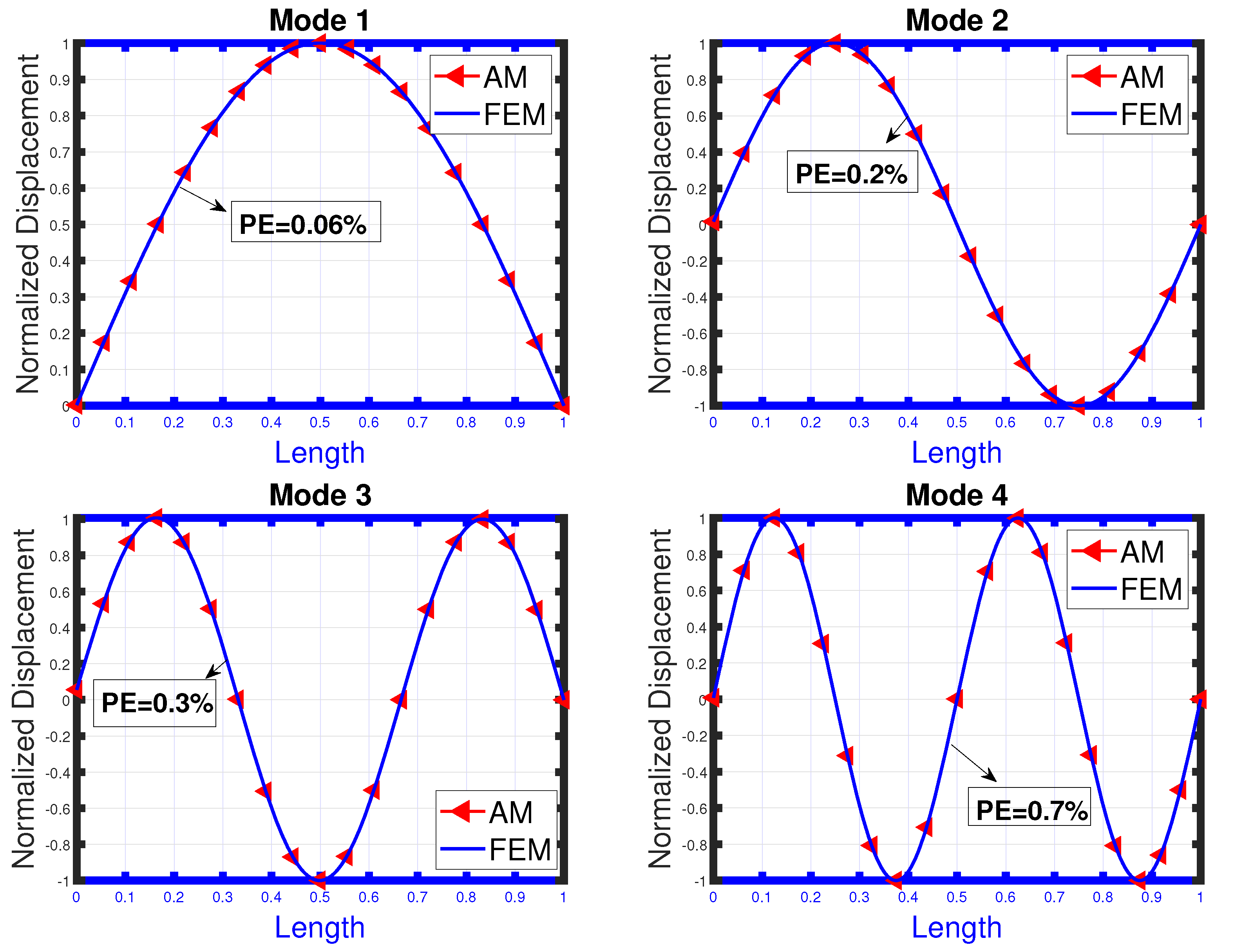
- While comparing results with the existing ones in the literature, it has been observed that the finite element scheme provided the best accuracy for obtaining the mode shapes of the beam structure.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chun, K.R. Free vibration of a beam with one end spring-hinged and the other free. J. Appl. Mech. 1972, 39, 1154–1155. [Google Scholar] [CrossRef]
- Lee, T.W. Vibration frequencies for a uniform beam with one end spring-hinged and carrying a mass at the other free end. J. Appl. Mech. 1973, 40, 813–815. [Google Scholar] [CrossRef]
- Lai, H.Y.; Hsu, J.C. An innovative eigenvalue problem solver for free vibration of Euler-Bernoulli beam by using the Adomian decomposition method. Comput. Math. Appl. 2008, 56, 3204–3220. [Google Scholar] [CrossRef]
- Smith, R.C.; Bowers, K.L.; Lund, J. A fully sinc-Galerkin method for Euler-Bernoulli beam models. Numer. Methods Partial. Differ. Equ. 1992, 8, 171–202. [Google Scholar] [CrossRef]
- Hess, M.S. Vibration frequencies for a uniform beam with central mass and elastic supports. J. Appl. Mech. 1964, 31, 556–557. [Google Scholar] [CrossRef]
- Grossi, R.O.; Arenas, B. A variational approach to the vibration of tapered beams with elastically restrained ends. J. Sound Vib. 1996, 195, 507–511. [Google Scholar] [CrossRef]
- Naguleswaran, S. Transverse vibration of a uniform Euler-Bernoulli beam under linearly varying axial force. J. Sound Vib. 2004, 275, 47–57. [Google Scholar] [CrossRef]
- Naguleswaran, S. Natural frequencies, sensitivity, and mode shape details of an Euler-Bernoulli beam with one-step change in cross-section and with ends on classical supports. J. Sound Vib. 2002, 252, 751–767. [Google Scholar] [CrossRef]
- Laura, P.A.A.; De Irassar, P.V.; Ficcadenti, G.M. A note on transverse vibrations of continuous beams subject to an axial force and carrying concentrated masses. J. Sound Vib. 1983, 86, 279–284. [Google Scholar] [CrossRef]
- Abbas, B.A.H. Vibrations of Timoshenko beams with elastically restrained ends. J. Sound Vib. 1984, 97, 541–548. [Google Scholar] [CrossRef]
- Rao, G.V.; Naidu, N.R. Free vibration and stability behavior of uniform beams and columns with non-linear elastic end rotational restraints. J. Sound Vib. 1994, 176, 130–135. [Google Scholar] [CrossRef]
- Civalek, Ö. Application of differential quadrature (DQ) and harmonic differential quadrature (HDQ) for buckling analysis of thin isotropic plates and elastic columns. Eng. Struct. 2004, 26, 171–186. [Google Scholar] [CrossRef]
- Kim, H.K.; Kim, M.S. Vibration of beams with generally restrained boundary conditions using Fourier series. J. Sound Vib. 2001, 245, 771–784. [Google Scholar] [CrossRef]
- Mahapatra, K.; Panigrahi, S.K. Dynamic Response of a Damped Euler–Bernoulli Beam Having Elastically Restrained Boundary Supports. J. Inst. Eng. (India) Ser. C 2019, 100, 891–905. [Google Scholar] [CrossRef]
- Villa-Morales, J.; Rodríguez-Esparza, L.J.; Ramírez-Aranda, M. Deflection of Beams Modeled by Fractional Differential Equations. Fractal Fract. 2022, 6, 626. [Google Scholar] [CrossRef]
- Zhao, X.; Chang, P. Free and forced vibration of a double beam with arbitrary end conditions connected with a viscoelastic layer and discrete points. Int. J. Mech. Sci. 2021, 209, 106707. [Google Scholar] [CrossRef]
- Wang, J.I. Vibration of stepped beams on elastic foundations. J. Sound Vib. 1991, 149, 315–322. [Google Scholar] [CrossRef]
- Lai, Y.C.; Ting, B.Y.; Lee, W.S.; Becker, B.R. Dynamic response of beams on elastic foundation. J. Struct. Eng. 1992, 118, 853–858. [Google Scholar] [CrossRef]
- Thambiratnam, D.; Zhuge, Y. Free vibration analysis of beams on elastic foundation. Compos. Struct. 1996, 60, 971–980. [Google Scholar] [CrossRef]
- Gülkan, P.; Alemdar, B.N. Two-parameter elastic foundation: A revisit. Struct. Eng. Mech. 1999, 7, 259–276. [Google Scholar] [CrossRef]
- Al-Hosani, K.; Fadhil, S.; El-Zafrany, A. Fundamental solution and boundary element analysis of thick plates on Winkler foundation. Comput. Struct. 1999, 70, 325–336. [Google Scholar] [CrossRef]
- Yayli, M.Ö.; Aras, M.; Aksoy, S. An efficient analytical method for vibration analysis of a beam on an elastic foundation with elastically restrained ends. Shock Vib. 2014, 2014, 159213. [Google Scholar] [CrossRef]
- Nawaz, R.; Nuruddeen, R.I.; Zia, Q.M. An asymptotic investigation of the dynamic and dispersion of an elastic five-layered plate for anti-plane shear vibration. J. Eng. Math. 2021, 128, 1–12. [Google Scholar] [CrossRef]
- Asif, M.; Nawaz, R.; Nuruddeen, R.I. Dispersion of elastic waves in an inhomogeneous multilayered plate over a Winkler elastic foundation with imperfect interfacial conditions. Phys. Scr. 2021, 96, 125026. [Google Scholar] [CrossRef]
- Doeva, O.; Masjedi, P.K.; Weaver, P.M. Static analysis of composite beams on variable stiffness elastic foundations by the Homotopy Analysis Method. Acta Mech. 2021, 232, 4169–4188. [Google Scholar] [CrossRef]
- Zhiyuan, L.; Yepeng, X.; Dan, H. Analytical solution for vibration of functionally graded beams with variable cross-sections resting on Pasternak elastic foundations. Int. J. Mech. Sci. 2021, 191, 106084. [Google Scholar]
- Mirzabeigy, A.; Madoliat, R.; Vahabi, M. Free vibration analysis of two parallel beams connected together through variable stiffness elastic layer with elastically restrained ends. Adv. Struct. Eng. 2017, 20, 275–287. [Google Scholar] [CrossRef]
- Njim, E.K.; Muhannad, A.W.; Sadeq, H.B. A Critical Review of Recent Research of Free Vibration and Stability of Functionally Graded Materials of Sandwich Plate. IOP Conf. Ser. Mater. Sci. Eng. 2021, 1094, 012081. [Google Scholar] [CrossRef]
- Sheng, G.G.; Wang, X. The dynamic stability and nonlinear vibration analysis of stiffened functionally graded cylindrical shells. Appl. Math. Model. 2018, 56, 389–403. [Google Scholar] [CrossRef]
- Valipour, P.; Ghasemi, S.E.; Khosravani, M.R.; Ganji, D.D. Theoretical analysis on nonlinear vibration of fluid flow in single-walled carbon nanotube. J. Theor. Appl. Phys. 2016, 10, 211–218. [Google Scholar] [CrossRef]
- Rao, S.S. Vibration of Continuous Systems; John Wiley and Sons: Hoboken, NJ, USA, 2007; ISBN 978-0-471-77171-5. [Google Scholar]
- Han, S.M.; Benaroya, H.; Wei, T. Dynamics of transversely vibrating beams using four engineering theories. J. Sound Vib. 1999, 225, 935–988. [Google Scholar] [CrossRef]
- Ferreira, A.J.M. MATLAB Codes for Finite Element Analysis: Solids and Structures; Solid Mechanics and Its Applications 157; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Kreyszig, E. Advanced Engineering Mathematics, 10th ed.; John Wiley and Sons: Hoboken, NJ, USA, 2009. [Google Scholar]
- Meirovitch, L. Fundamentals of Vibrations (Long Grove); McGraw-Hill Education: New York, NY, USA, 2001. [Google Scholar]
- Leissa, A.W.; Qatu, M.S. Vibrations of Continuous Systems; McGraw-Hill Education: New York, NY, USA, 2011. [Google Scholar]
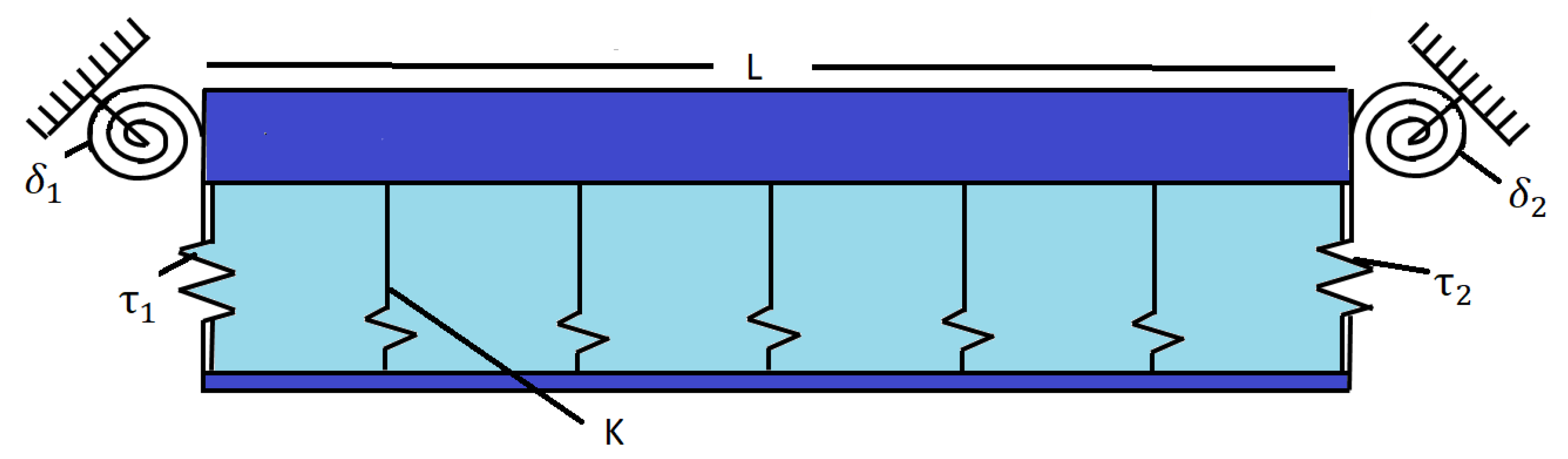

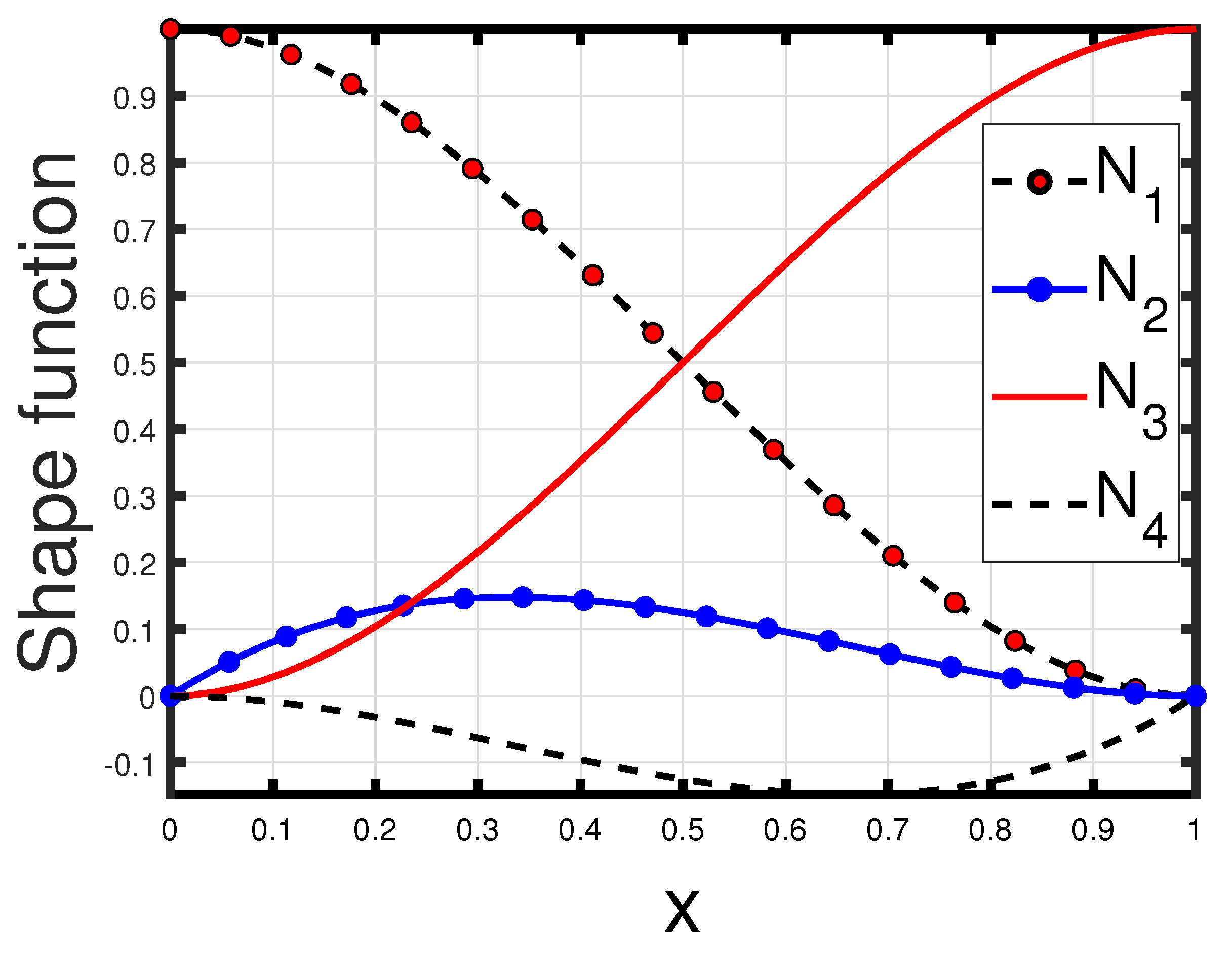
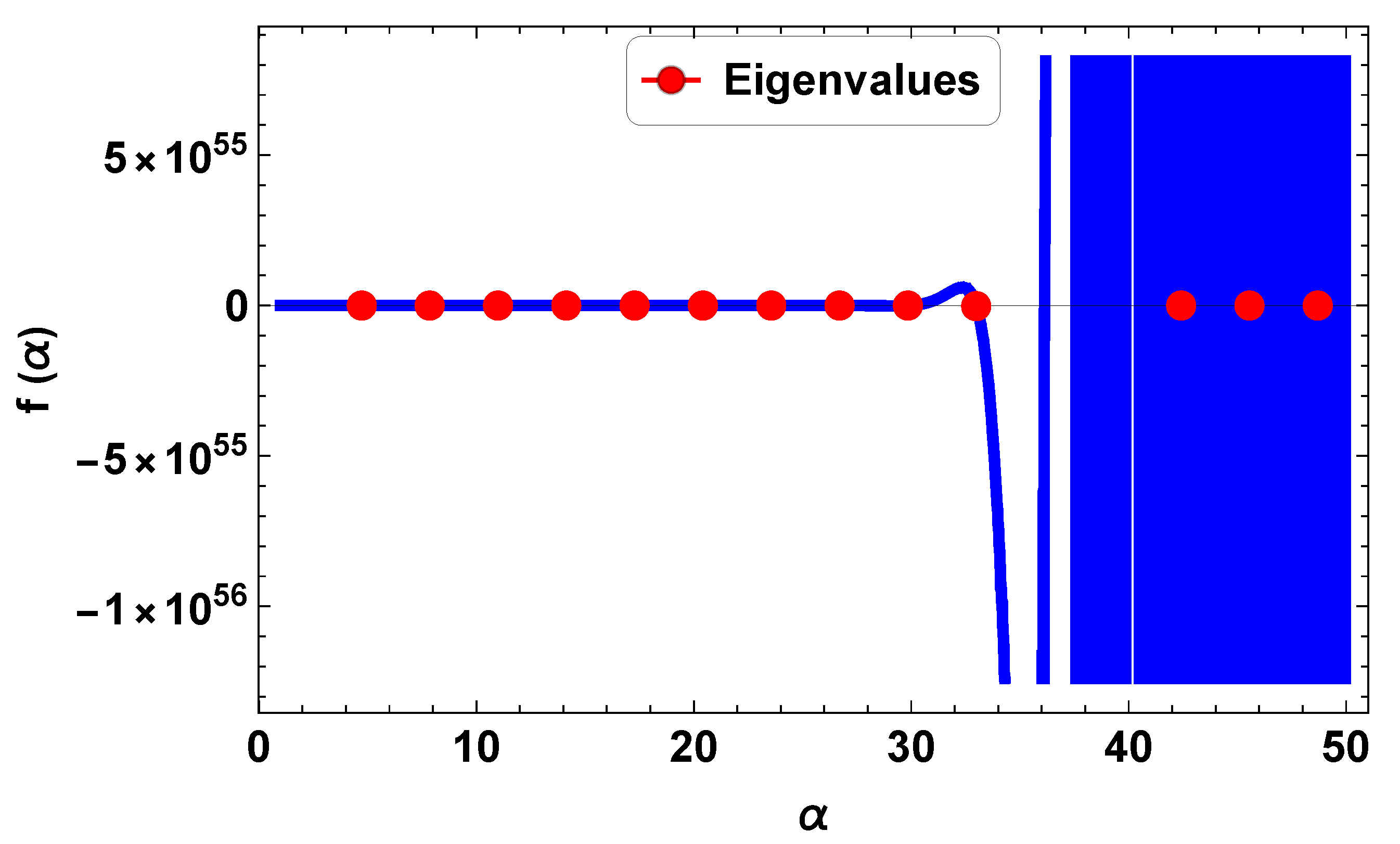
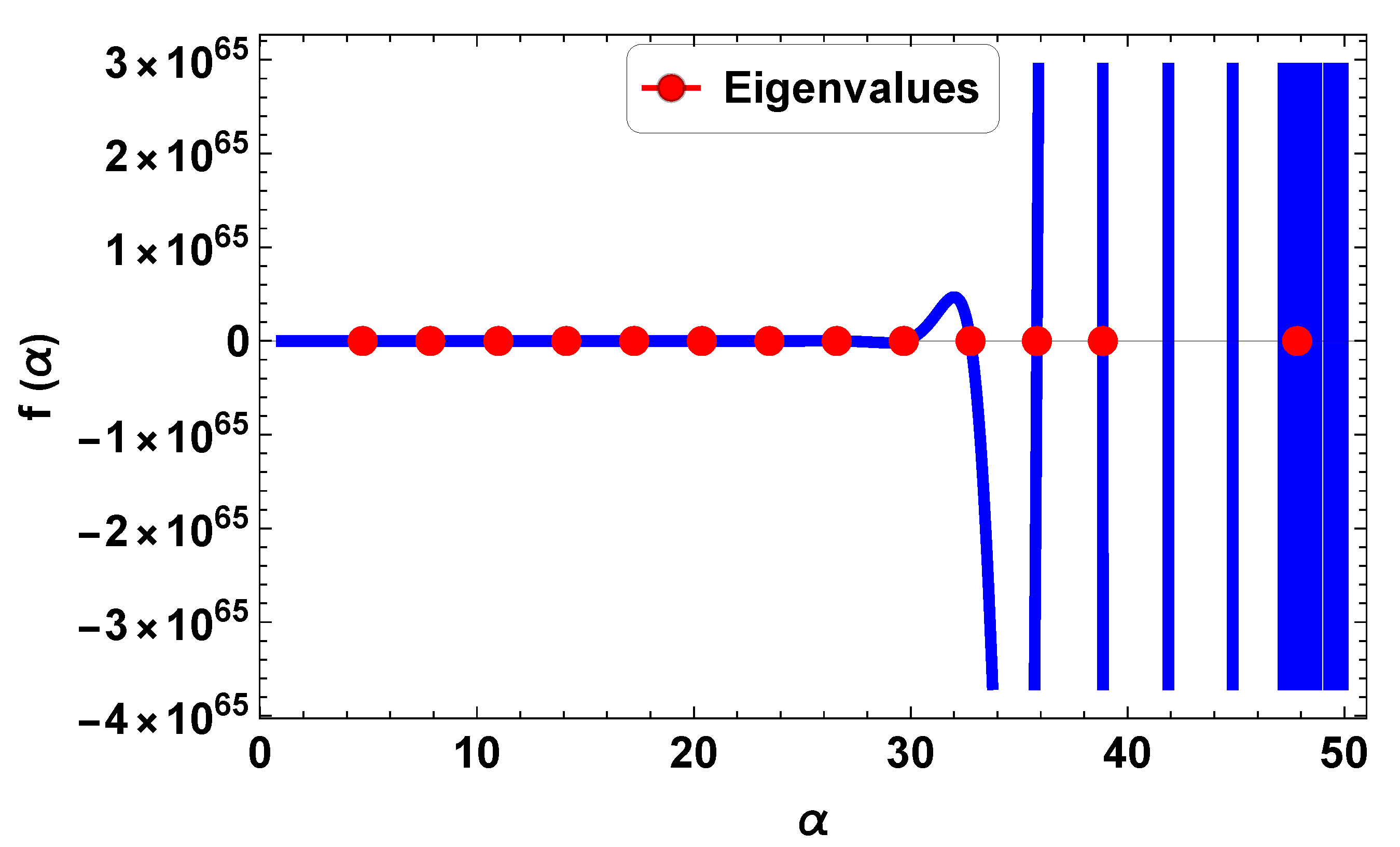


| BC | (Clamped-Clamped Beam) | |||
| RB-AM | 250.696553 | 670.332080 | 1257.418531 | 1957.632175 |
| RB-FEM | 250.508697 | 668.569075 | 1250.974018 | 1952.105425 |
| PE | 0.07 | 0.2 | 0.5 | 0.2 |
| EBB-FEM | 253.570332 | 698.649266 | 1368.685838 | 2260.407107 |
| BC | ||||
| RB-AM | 244.547215 | 627.425812 | 1108.8354005 | 11,607.889441 |
| RB-FEM | 244.381088 | 626.097545 | 1105.006215 | 1600.50013598 |
| PE | 0.06 | 0.2 | 0.3 | 0.4 |
| EBB-FEM | 247.081229 | 648.3165172 | 1170.690514 | 1732.887219 |
| BC | ||||
| RB-AM | 0.939639 | 3.597750 | 242.763465 | 637.058042 |
| RB-FEM | 0.939654 | 3.595103 | 242.07727 | 633.471148 |
| PE | 0.01 | 0.07 | 0.2 | 0.5 |
| EBB-FEM | 0.9401511 | 3.63815 | 253.7942605 | 699.31880034 |
| BC | ||||
| RB-AM | 0 | 0.359903 | 242.612375 | 636.908474 |
| RB-FEM | 0.094067 | 0.359129 | 241.926479 | 633.3220740 |
| PE | 0 | 0.2 | 0.2 | 0.5 |
| EBB-FEM | 0.09731147 | 0.364811 | 253.638632 | 699.161921 |
| BC | (Free-Free Beam) | |||
| RB-AM | 0 | 0 | 242.6108484 | 636.906962 |
| RB-FEM | 0 | 0 | 241.924691 | 633.315889 |
| PE | 0 | 0 | 0.2 | 0.5 |
| EBB-FEM | 0 | 0 | 253.637057 | 699.1906165 |
| K | |||||
|---|---|---|---|---|---|
| RB-AM | 244.635620 | 627.458744 | 1108.853233 | 1607.90124959 | |
| RB-FEM | 244.469433 | 626.1304062 | 1105.023973 | 1600.51188801 | |
| PE | 0.06 | 0.2 | 0.3 | 0.4 | |
| EBB-FEM | 247.1705 | 648.350565 | 1170.709371 | 1732.899957 | |
| 245.429833 | 627.755057 | 1109.013621 | 1608.0075189 | ||
| 245.263102 | 626.426070 | 1105.1837765 | 1600.617654 | ||
| 0.06 | 0.2 | 0.3 | 0.4 | ||
| 247.973024 | 648.656915 | 1170.879057 | 1733.01459964 | ||
| 254.75624506 | 631.803299 | 1111.738550003 | 1610.2197737 | ||
| 253.0629107 | 629.375057 | 1106.7805309 | 1601.674927 | ||
| 0.6 | 0.3 | 0.4 | 0.5 | ||
| 255.859337 | 651.712493 | 1172.574581 | 1734.160598 | ||
| 321.011724 | 659.535432 | 1226.516780 | 1619.654366 | ||
| 320.793113 | 658.136708 | 1222.621996 | 1612.209306 | ||
| 0.06 | 0.2 | 0.3 | 0.4 | ||
| 324.34210031 | 681.515201 | 1189.396883 | 1745.579210 | ||
| 696.079274 | 890.563168 | 1264.837768 | 1711.141649 | ||
| 701.049992 | 896.218158 | 1270.112079 | 1713.973989 | ||
| 0.7 | 0.6 | 0.4 | 0.1 | ||
| 708.897576 | 928.332346 | 1346.106578 | 1855.905373 |
| BC | ||||
| RB-AM | 247.876023 | 663.070974 | 1244.440889 | 1948.406590 |
| RB-FEM | 247.692291 | 661.344524 | 1238.119361 | 1933.149164 |
| PE | 0.07 | 0.2 | 0.5 | 0.7 |
| EBB-FEM | 250.685988 | 690.7803537 | 1353.424206 | 1933.149164 |
| BC | ||||
| RB-AM | 118.095539 | 439.042478 | 939.30890 | 1578.319082 |
| RB-FEM | 118.024116 | 438.040036 | 934.620135 | 1566.555535 |
| PE | 0.06 | 0.2 | 0.4 | 0.7 |
| EBB-FEM | 119.183343 | 454.989152 | 1014.407906 | 1796.176890 |
| BC | ||||
| RB-AM | 110.868207 | 431.774070 | 931.988756 | 1571.619022 |
| RB-FEM | 110.801167 | 430.788243 | 927.610823 | 1559.904574 |
| PE | 0.06 | 0.2 | 0.4 | 0.7 |
| EBB-FEM | 111.889149 | 447.456074 | 1006.476980 | 1788.564665 |
| BC | (Supported-Supported beam) | |||
| RB-AM | 110.860491 | 431.766562 | 931.981563 | 1571.612216 |
| RB-FEM | 110.793383 | 430.779004 | 927.586263 | 1559.814971 |
| [31] | 110.867126 | 431.85454 | 932.340065 | —– |
| PE | 0.06 | 0.2 | 0.3 | 0.7 |
| EBB-FEM | 111.881330 | 447.448294 | 1006.469162 | 1788.556629 |
| [31] | 111.888296 | 447.553217 | 1006.994779 | —– |
| K | |||||
|---|---|---|---|---|---|
| RB-AM | 111.073523 | 431.8216718 | 932.009064 | 1571.629866 | |
| RB-FEM | 110.996365 | 430.835737 | 927.631036 | 1559.915337 | |
| PE | 0.06 | 0.2 | 0.4 | 0.7 | |
| EBB-FEM | 112.086260 | 447.505404 | 1006.498912 | 1788.577007 | |
| 112.562480 | 432.249847 | 932.191820 | 1571.727457 | ||
| 112.737932 | 431.262934 | 927.812933 | 1560.012200 | ||
| 0.1 | 0.2 | 0.2 | 0.7 | ||
| 113.844930 | 447.794913 | 1006.696279 | 1778.688080 | ||
| 128.943498 | 436.508501 | 934.017415 | 1572.703052 | ||
| 128.865529 | 435.512864 | 929.629948 | 1560.980497 | ||
| 0.06 | 0.2 | 0.4 | 0.7 | ||
| 130.120866 | 452.362476 | 1008.667823 | 1789.798432 | ||
| 235.877972 | 477.008461 | 952.080831 | 1582.425719 | ||
| 235.735339 | 475.919341 | 947.608469 | 1570.630622 | ||
| 0.06 | 0.2 | 0.4 | 0.7 | ||
| 238.735339 | 494.333492 | 1028.175362 | 1800.864299 | ||
| 667.650974 | 772.987265 | 1116.758071 | 1676.553113 | ||
| 667.247203 | 771.222161 | 1111.511651 | 1664.055472 | ||
| 0.06 | 0.2 | 0.4 | 0.7 | ||
| 673.799540 | 801.064028 | 1206.019299 | 1907.996384 |
| BC | ||||
| RB-AM | 0.939662 | 110.809968 | 431.603421 | 931.7944980 |
| RB-FEM | 0.939663 | 110.742948 | 430.617197 | 927.411308 |
| PE | 0.001 | 0.6 | 0.2 | 0.4 |
| EBB-FEM | 0.939852 | 111.8306027 | 447.292920 | 100.640580 |
| BC | ||||
| RB-AM | 0.297149 | 110.802923 | 431.601704 | 931.794248 |
| RB-FEM | 0.297230 | 110.735907 | 430.615483 | 927.410579 |
| PE | 0.02 | 0.06 | 0.2 | 0.4 |
| EBB-FEM | 0.297394 | 111.823493 | 447.2291140 | 100.640501 |
| BC | ||||
| RB-AM | 0.0939667 | 110.802218 | 431.601533 | 931.794167 |
| RB-FEM | 0.093957 | 110.735202 | 430.615312 | 927.410506 |
| PE | 0.01 | 0.06 | 0.2 | 0.4 |
| EBB-FEM | 0.098001 | 111.822788 | 447.290962 | 100.640493 |
| BC | ||||
| RB-AM | 0.0297149 | 110.802148 | 431.601515 | 931.794167 |
| RB-FEM | 0.029710 | 110.735133 | 430.615295 | 927.410498 |
| PE | 0.01 | 0.06 | 0.2 | 0.4 |
| EBB-FEM | 0.033645 | 111.822711 | 447.290944 | 100.640493 |
| BC | ||||
| RB-AM | 0 | 110.802140 | 431.601513 | 931.794166 |
| RB-FEM | 0.001565 | 110.735124 | 430.615293 | 927.410498 |
| PE | 0 | 0.06 | 0.2 | 0.4 |
| EBB-FEM | 0.033058 | 111.8227109 | 447.290943 | 100.640493 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kanwal, G.; Nawaz, R.; Ahmed, N. Analyzing the Effect of Rotary Inertia and Elastic Constraints on a Beam Supported by a Wrinkle Elastic Foundation: A Numerical Investigation. Buildings 2023, 13, 1457. https://doi.org/10.3390/buildings13061457
Kanwal G, Nawaz R, Ahmed N. Analyzing the Effect of Rotary Inertia and Elastic Constraints on a Beam Supported by a Wrinkle Elastic Foundation: A Numerical Investigation. Buildings. 2023; 13(6):1457. https://doi.org/10.3390/buildings13061457
Chicago/Turabian StyleKanwal, Gulnaz, Rab Nawaz, and Naveed Ahmed. 2023. "Analyzing the Effect of Rotary Inertia and Elastic Constraints on a Beam Supported by a Wrinkle Elastic Foundation: A Numerical Investigation" Buildings 13, no. 6: 1457. https://doi.org/10.3390/buildings13061457
APA StyleKanwal, G., Nawaz, R., & Ahmed, N. (2023). Analyzing the Effect of Rotary Inertia and Elastic Constraints on a Beam Supported by a Wrinkle Elastic Foundation: A Numerical Investigation. Buildings, 13(6), 1457. https://doi.org/10.3390/buildings13061457






