Natural Ventilation in Low-Cost Housing: An Evaluation by CFD
Abstract
1. Introduction
2. Materials and Methods
- (a)
- Poor urban insertion: the building is located in a peripheral and expanding area of the city, far from the center and urban mobility;
- (b)
- Built area: this type of building has a reduced area;
- (c)
- Constructive standardization: the building follows the same floor plan as the others in the housing complex;
- (d)
- The building presents thermal comfort problems due to the standardization of the construction project;
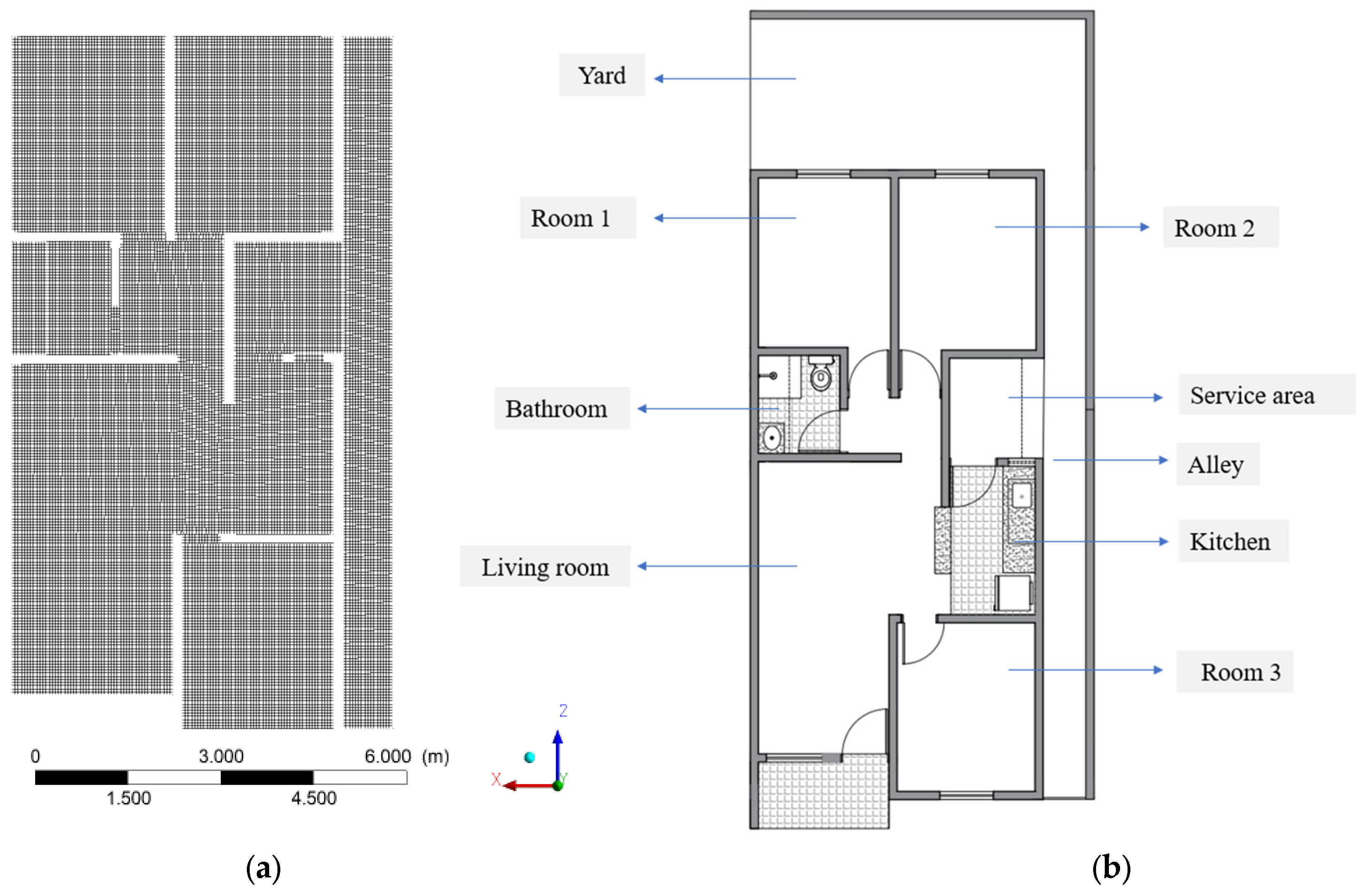
2.1. Experimental Procedures
- (a)
- In the integrated room (living and dining room): measurement of the initial condition of temperature and relative humidity of the air in the window opening of the room, using the digital thermohygrometer equipment. The data were confronted with information from the official meteorological data of temperature and relative humidity for the city of Campina Grande, Brazil, presenting results very close to the information collected on site.
- (b)
- Room 01: measurement of the initial conditions of temperature and relative humidity. The infrared thermometer equipment was directed to all the walls of the room, obtaining approximate values.
- (c)
- Room 02: a digital thermohygrometer was used to measure the air inlet and outlet conditions (temperature and relative humidity). The infrared thermometer was positioned on all the walls of the room, presenting results with small variations.
- (d)
- Room 03: Temperature and relative humidity were measured. It was verified that the air temperature was higher in the window opening than inside the room.
- (e)
- Living room: In this space, as described in the other rooms of the residence, a digital thermohygrometer was used to verify the initial temperature and relative humidity conditions.
- (a)
- Bathroom: environment with a single air outlet, via an opening skylight.
- (b)
- Alley (side setback): with the anemometer equipment, positioned close to the entrance (approximately 2 cm), the air velocity was measured, and the values obtained at that point were averaged. As it is an area without coverage, the temperature presented a value higher than that found inside the building.
- (c)
- Services Area: the air inlet and outlet conditions (temperature, velocity, and relative humidity) were verified.
- (d)
- Leisure area (rear yard setback): as it is an open environment, the air velocity was measured in the bedroom windows, pointing the anemometer from the outside towards the inside of the environment. With the infrared thermometer, the temperature of the walls was verified, which showed a high value due to the time of day (12:22 p.m.) and for receiving direct incidence of solar radiation.
2.2. Theoretical Procedures
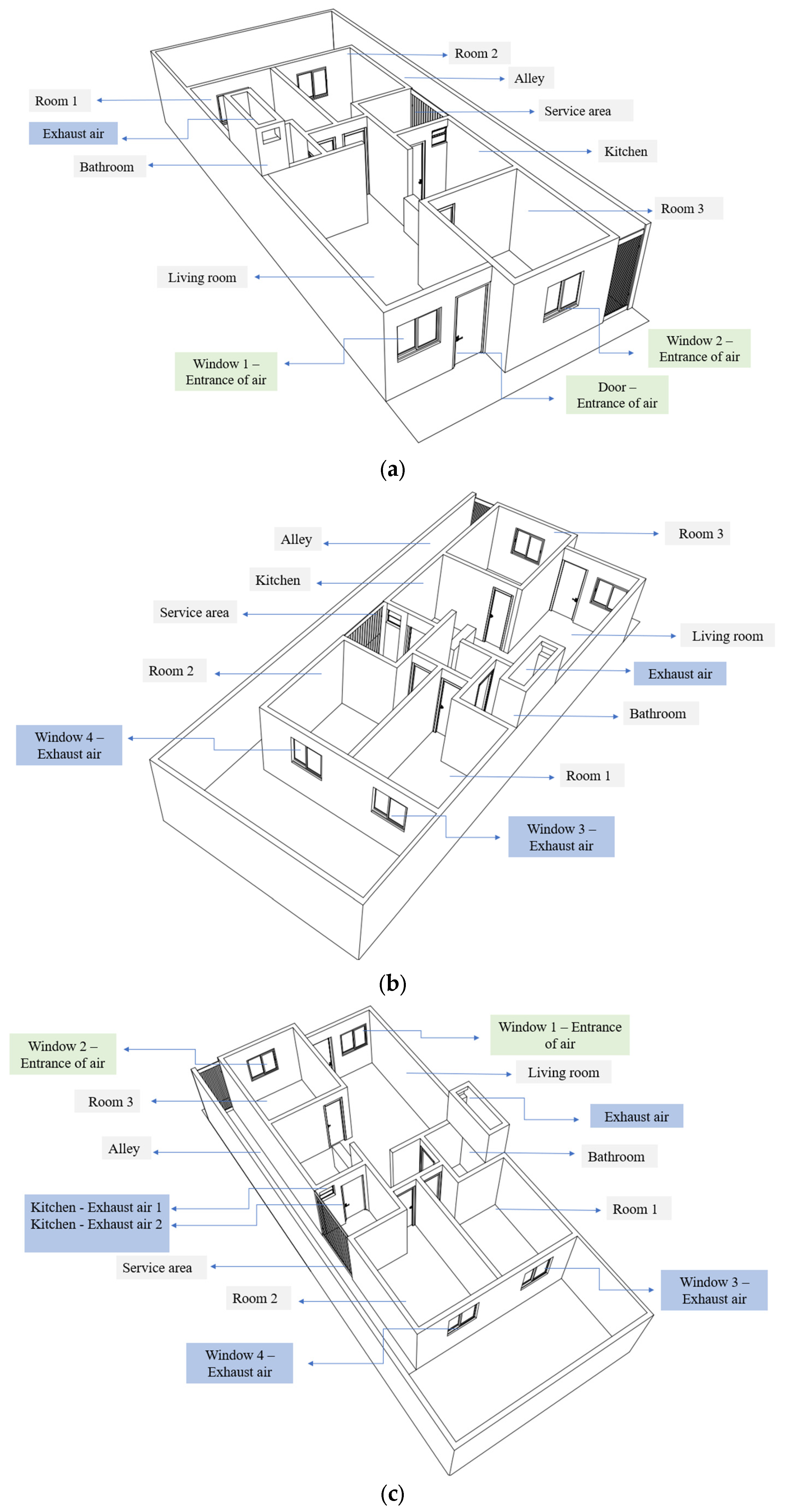
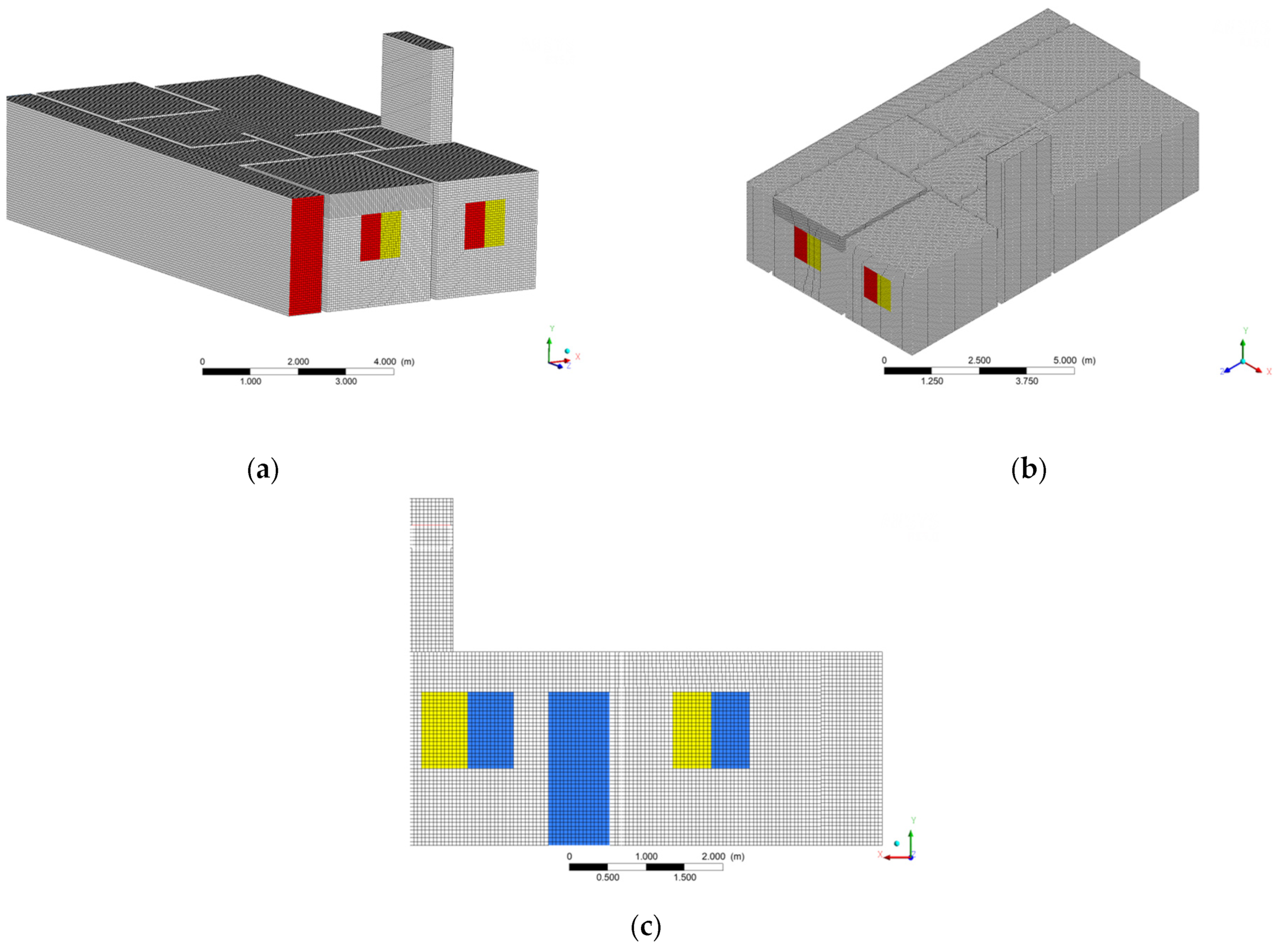
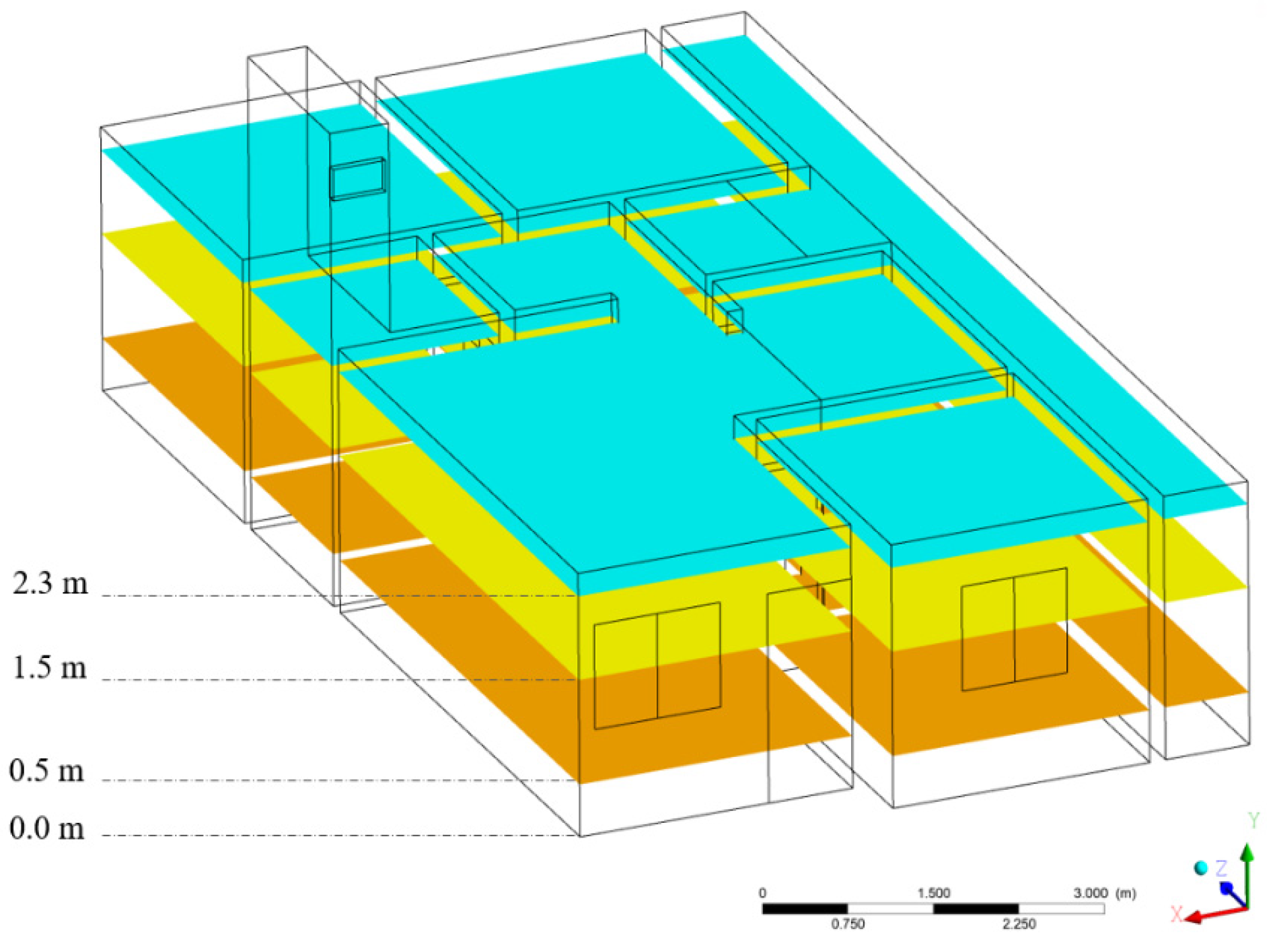
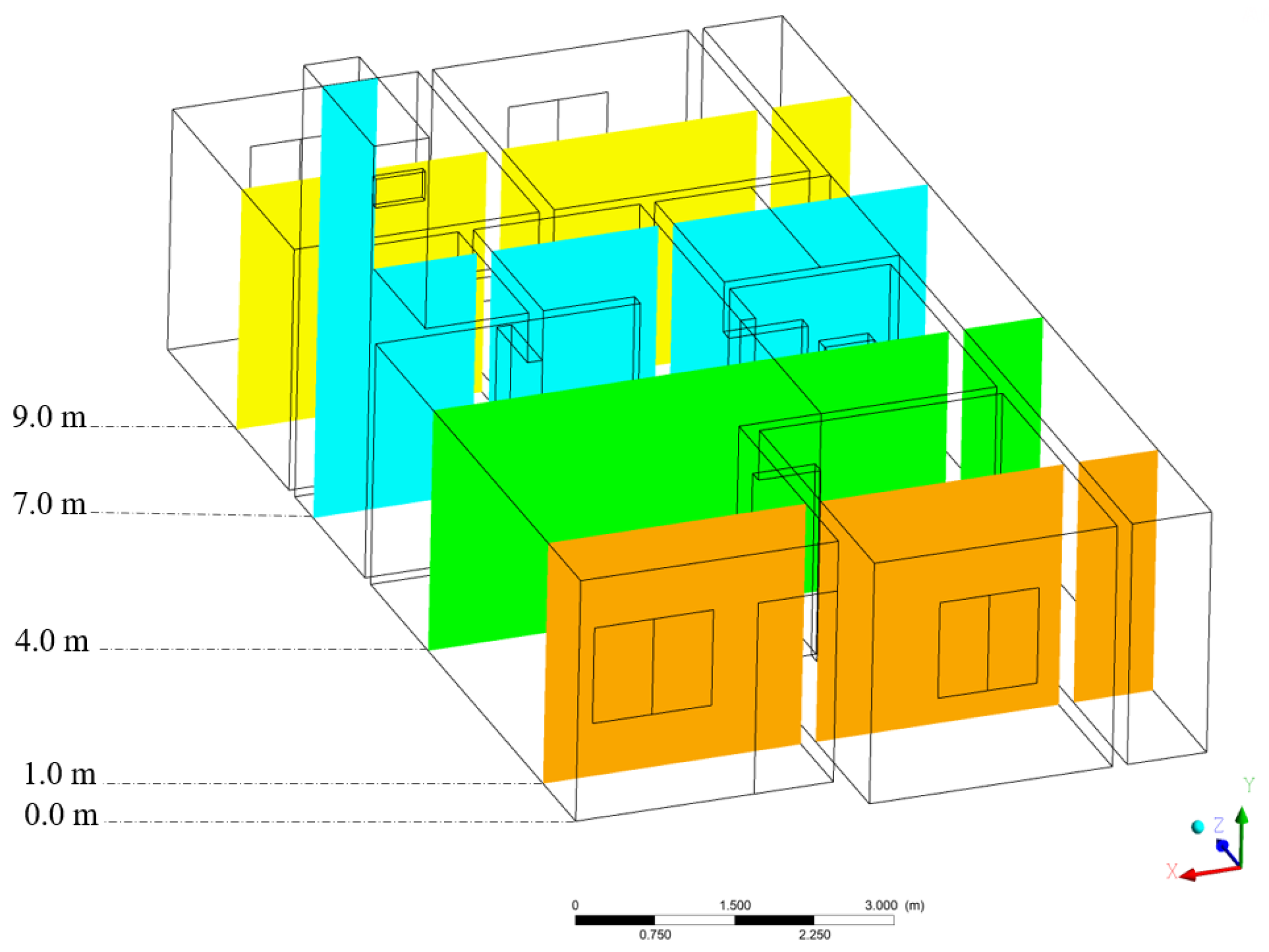
2.2.1. Geometry and the Physical and Computational Domains
2.2.2. Mathematical Formulation
- (a)
- Continuity
- (b)
- Momentum
- (c)
- Turbulence
- (d)
- Energy
- (e)
- Species Transfer
- (a)
- Thermophysical properties of the air are variables with the temperature.
- (b)
- Simulation was carried out without the presence of furniture and others components and physical interference of residents inside the house.
2.2.3. Boundary Conditions
- (a)
- Inlet
- -
- Prescribed Velocity (Inlet Velocity)
- (b)
- Outlet
- -
- Prescribed mass flow
- -
- Prescribed pressure
- (c)
- Walls
2.2.4. Numerical Solution Techniques
- (a)
- Pressure-velocity coupling COUPLED
- (b)
- Spatial interpolation
- (c)
- Relaxation factors
- (d)
- Convergence criteria
2.2.5. Studied Cases
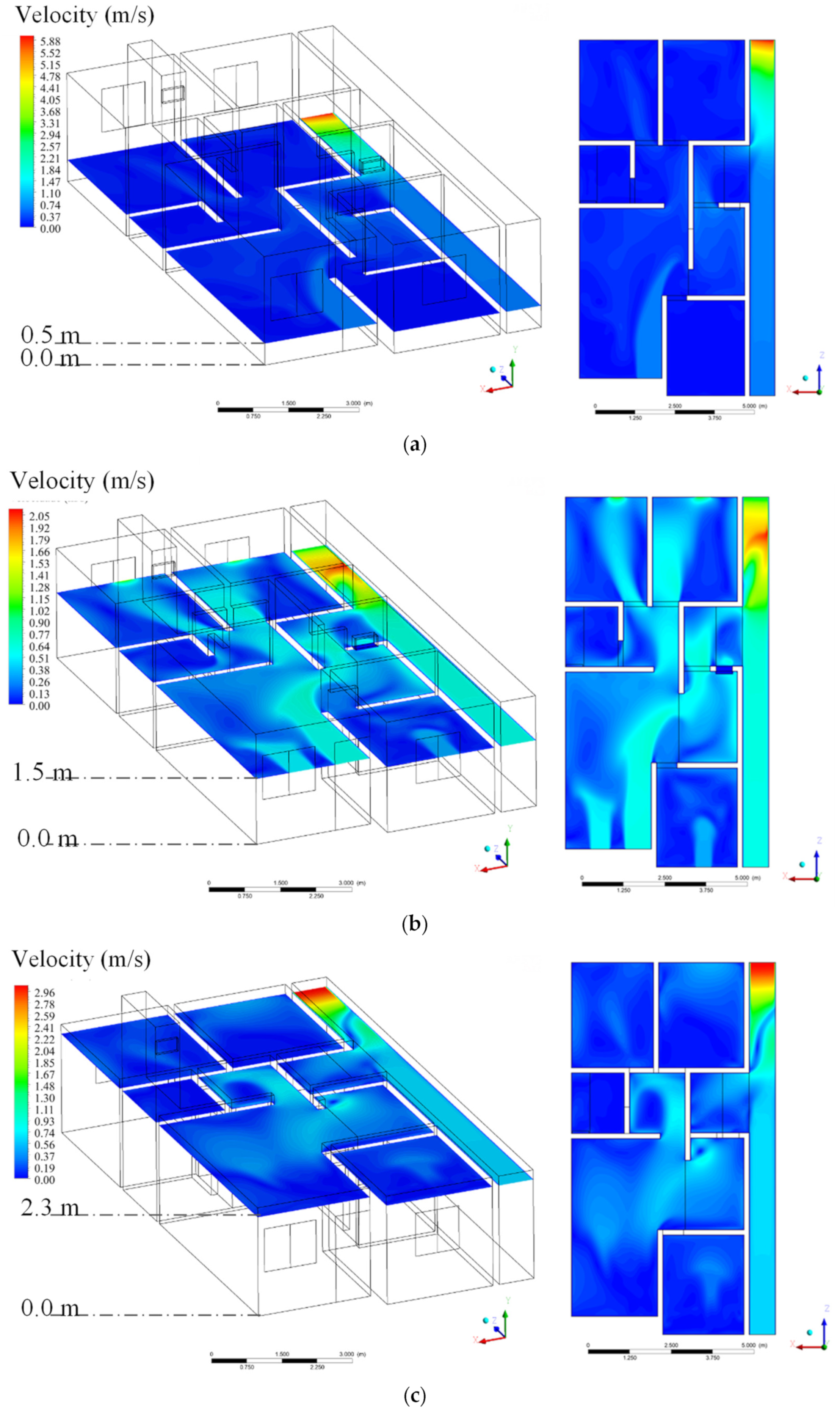
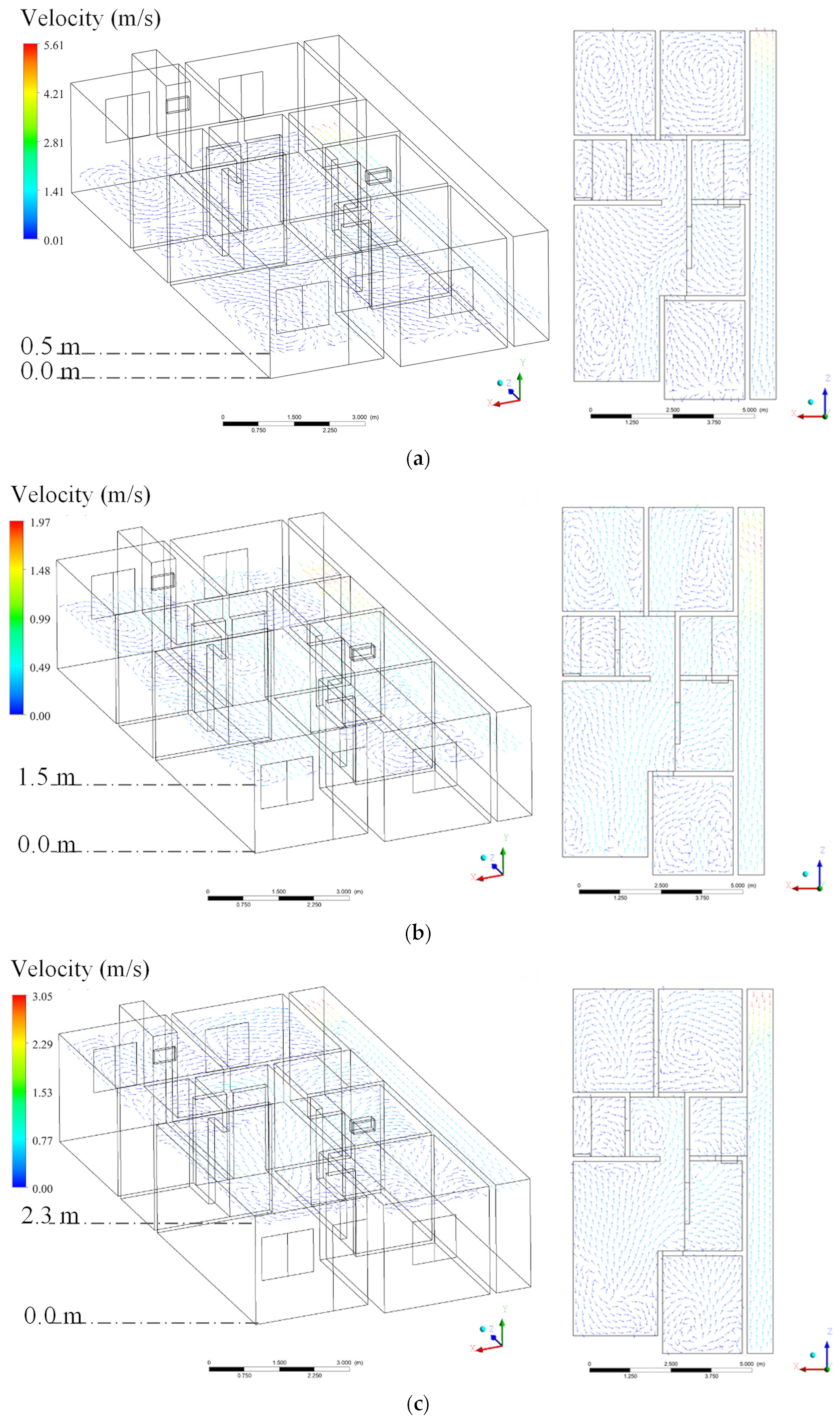
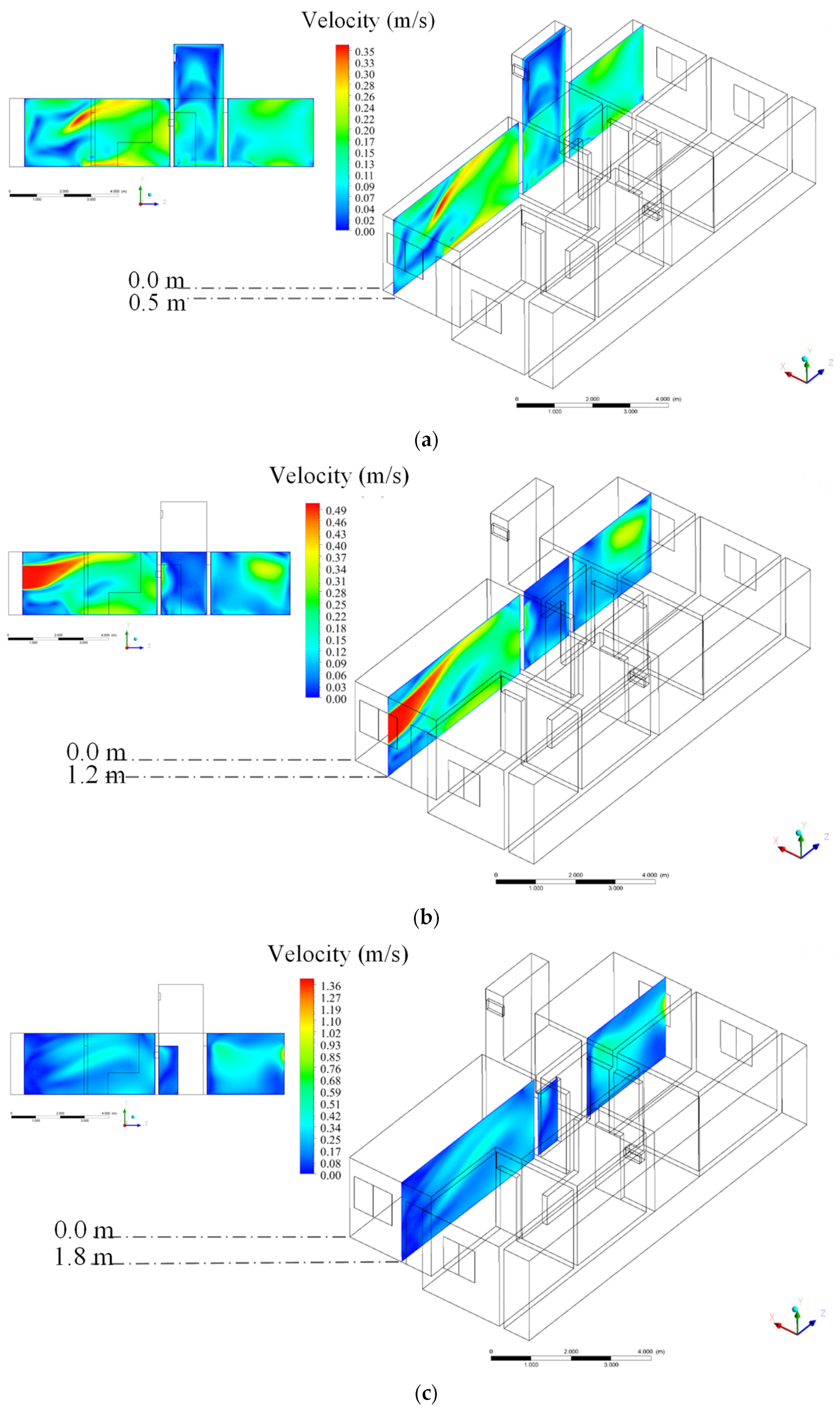
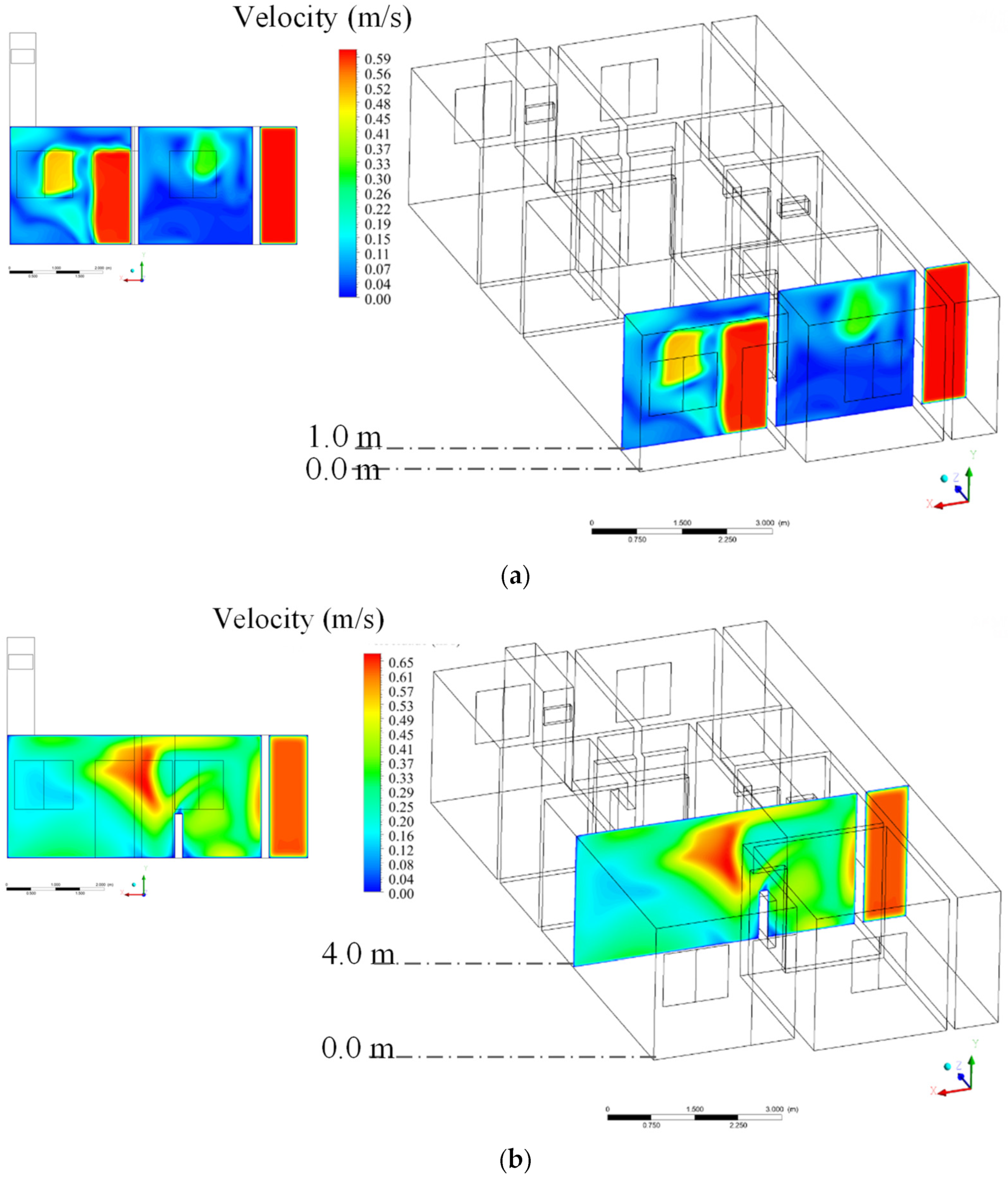
3. Results and Discussion
3.1. Experimental
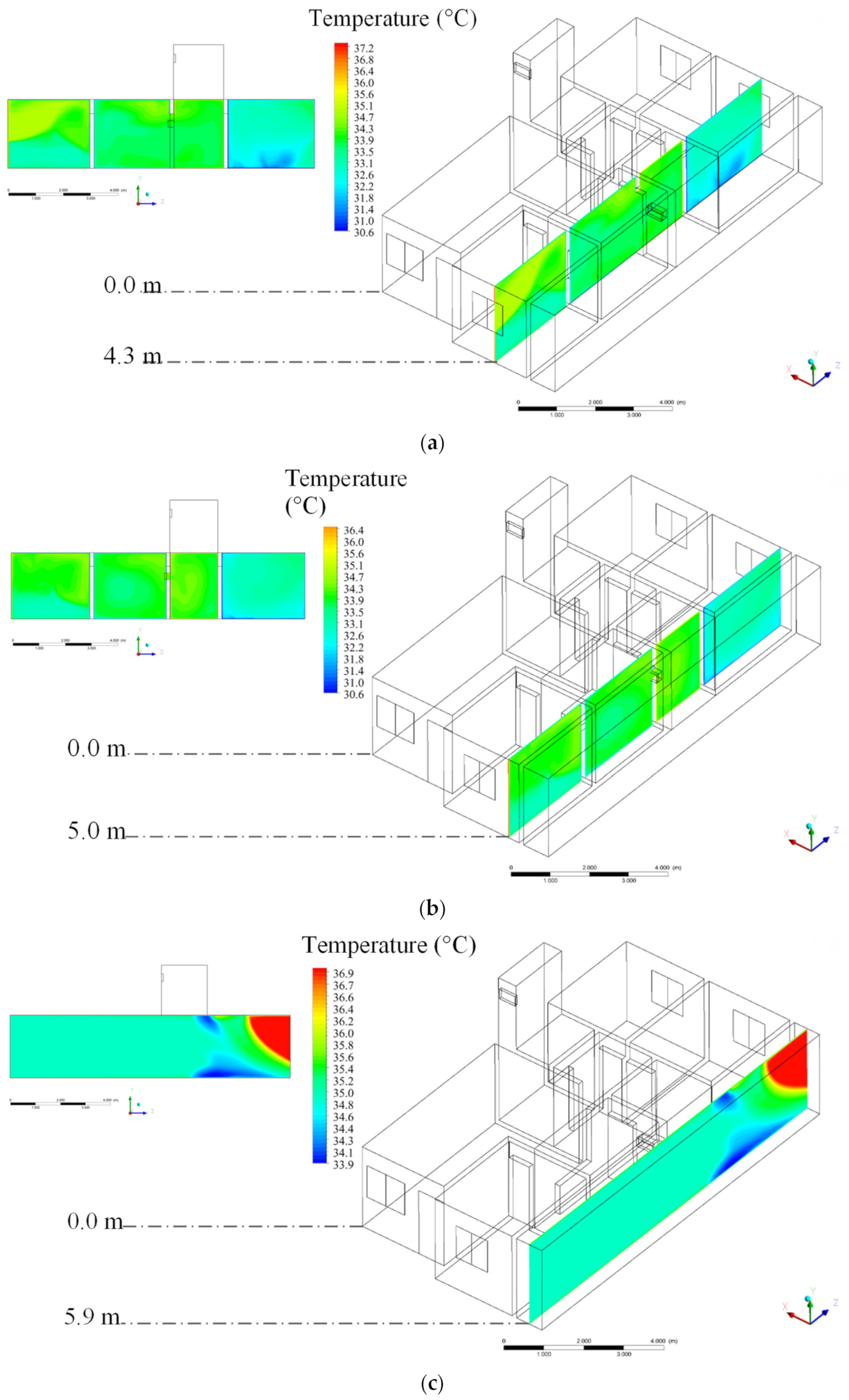
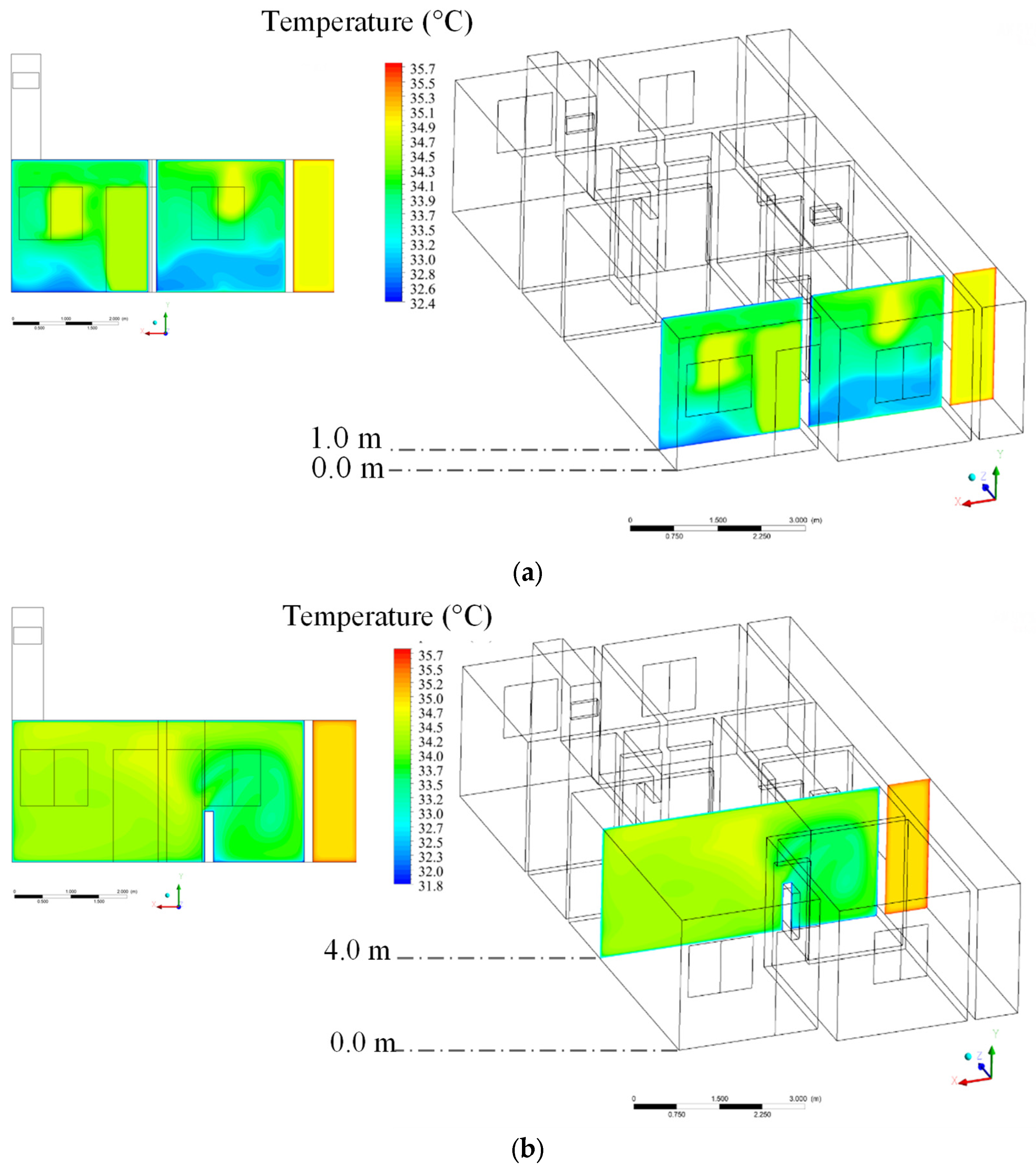
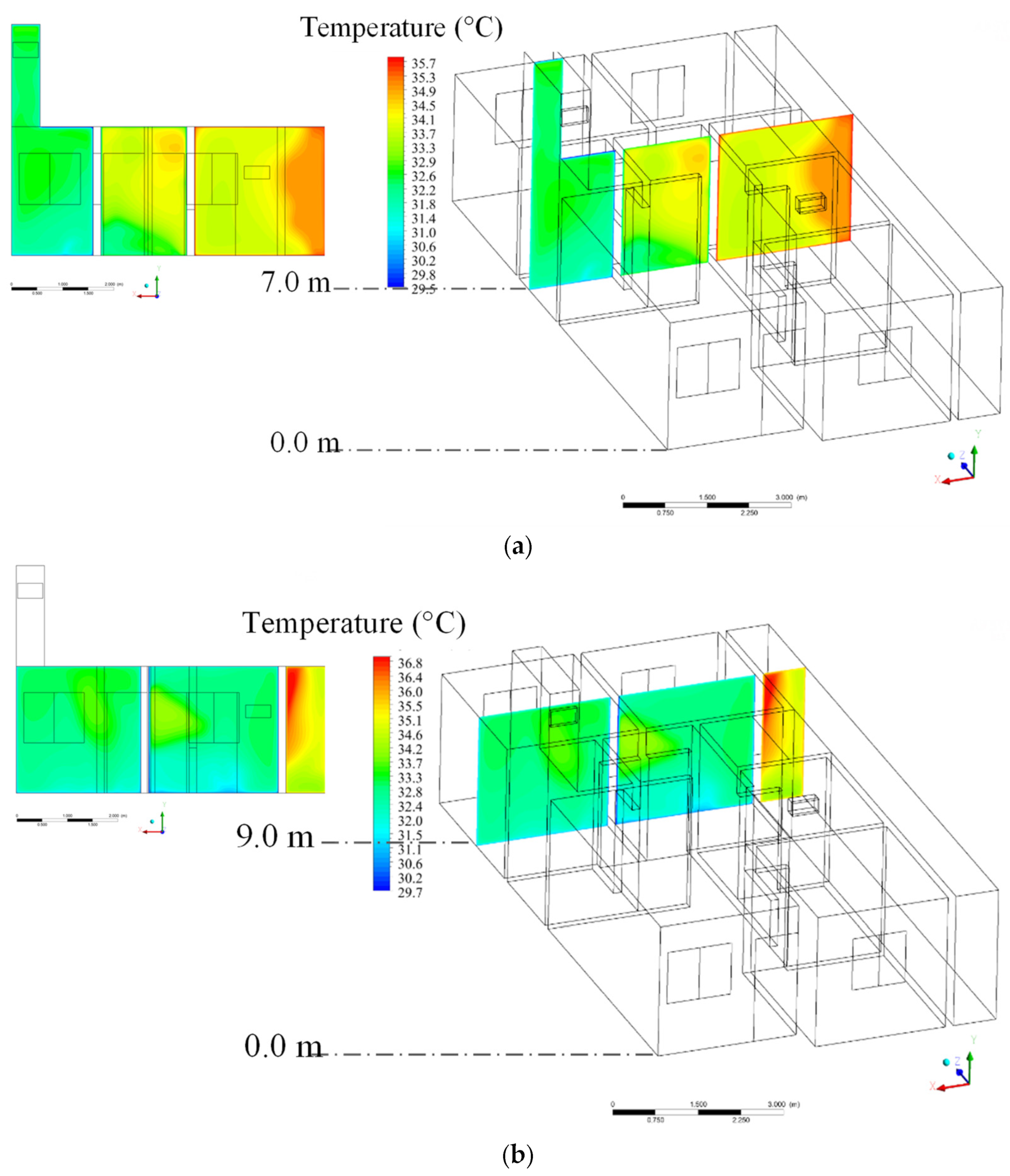
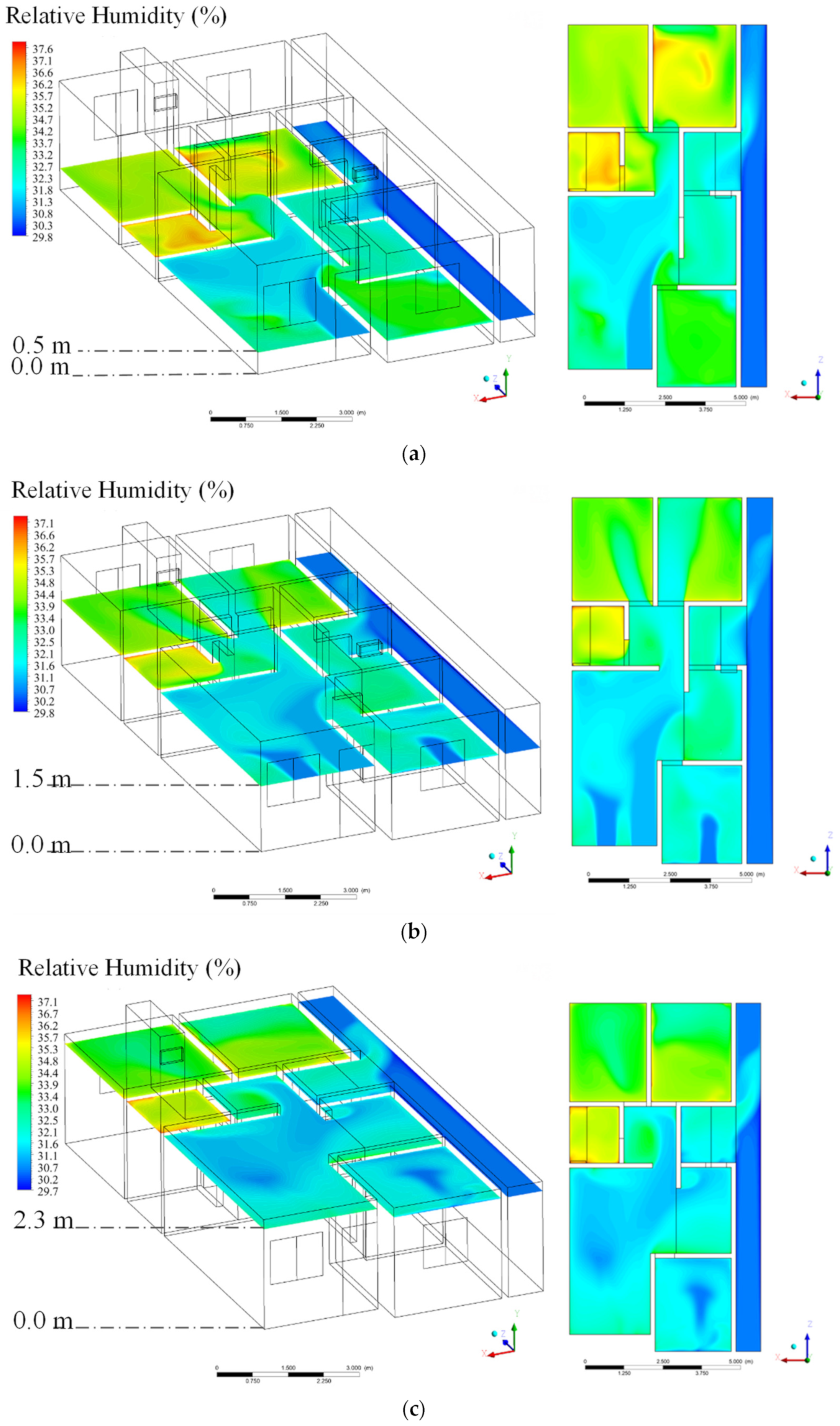
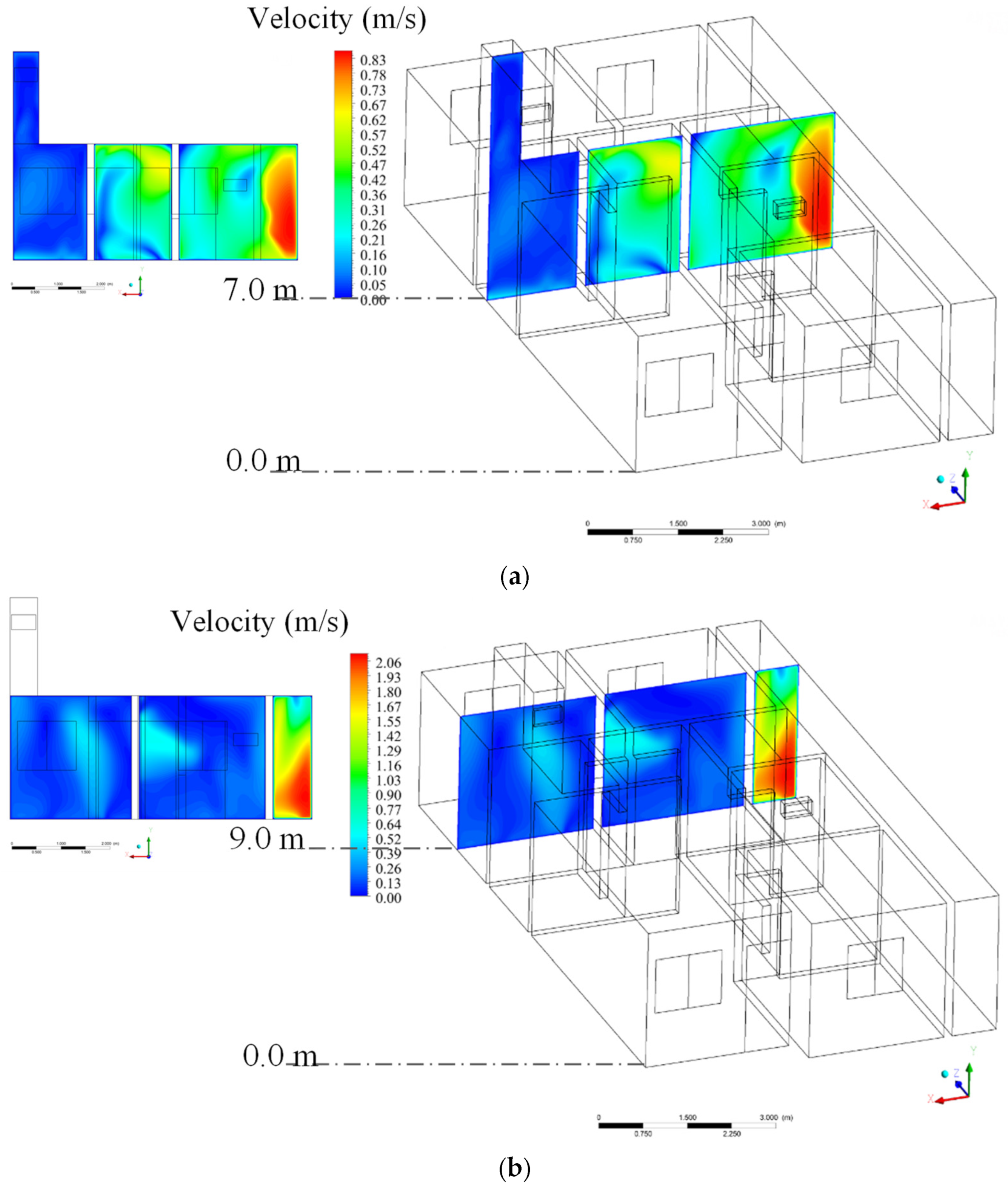
3.2. Theoretical (Simulated)
4. Conclusions
- (a)
- Natural ventilation inside the building was inefficient, culminating in an increase in the internal temperature and leading to the need to use a mechanical ventilation system to improve thermal comfort.
- (b)
- The position of the door and window openings in the building arrangements had a direct influence on the decrease in temperature.
- (c)
- Lower temperature values in environments with greater airflow recirculation, via cross ventilation, prove that the relevant parameter is not only the velocity of the air passing through the system but also the architecture of the building.
- (d)
- The low values of relative humidity are nonetheless within the range considered pleasant, which helps to minimize the common discomfort in hot and dry climates.
- (e)
- Variations in air velocity verified inside the house do not cause thermal discomfort to residents.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Abiko, A.K. Introduction to Housing Management; EPUSP Editora: São Paulo, Brazil, 2004; Available online: http://publicacoes.pcc.usp.br/PDF/ttcap12.pdf (accessed on 9 September 2020). (In Portuguese)
- Santos, C.H.M. Federal Housing Policies in Brazil: 1964–1998; Ministry of Finance, Secretary of State for Planning and Evaluation: Brasília, Brazil, 1999; p. 32. Available online: http://periciajudicial.adm.br/pdfs/Politica_%20Federal_%20Habita%C3%A7%C3%A3o%20_Brasil%20_IPEA_1964_1998.pdf (accessed on 9 September 2020). (In Portuguese)
- ONU-Habitat-United Nations Organization. The Right to Adequate Housing. Informative File nº 21/rev. 1. 2010. Available online: http://www.ohchr.org/Documents/Publications/FS21_rev_1_Housing_sp.pdf (accessed on 10 November 2020). (In Spanish).
- Frota, A.B.; Schiffer, S.R. Thermal Comfort Manual, 5th ed.; Studio Nobel: São Paulo, Brazil, 2001. (In Portuguese) [Google Scholar]
- Romero, M.; Ornstein, S. Post-Occupancy Evaluation: Methods and Techniques Applied to Social Housing, 1st ed.; ANTAC Editora: Porto Alegre, Brazil, 2003. (In Portuguese) [Google Scholar]
- Diligenti, M.P. Sustainability and Social Interest Housing: Social Movements and the (Re)Signification of the Place. In Proceedings of the 1st National Meeting of the National Association for Research and Graduate Studies in Architecture and Urbanism (ENANPARQ), Rio de Janeiro, Brazil, 29 November–3 December 2010; Available online: https://www.anparq.org.br/dvd-enanparq/simposios/51/51-655-1-SP.pdf (accessed on 10 November 2020). (In Portuguese).
- Silva, E.F. Searching for Habitability: Adjustments Inserted in the Boa Sorte Housing Complex in Coimbra. MG. Master’s Thesis, Civil Engineering, Federal University of Viçosa, Viçosa, Brazil, 2011. Available online: https://www.locus.ufv.br/handle/123456789/3759 (accessed on 20 October 2020). (In Portuguese).
- Imai, C. User Participation in Evaluation Processes: Methodologies and Results. In Environmental Quality in Housing Post-Occupancy Assessment; Villa, S.B., Ornstein, S.W., Eds.; Editora Oficina de Textos: São Paulo, Brazil, 2013; Chapter 4; pp. 75–88. (In Portuguese) [Google Scholar]
- ABNT Stardard-NBR 15575; Residential Buildings-Performance. Associação Brasileira de Normas Técnicas: Rio de Janeiro, Brazil, 2013. (In Portuguese)
- ABNT Standard-NBR 15220-3; Thermal Performance of Buildings Part 3: Brazilian Bioclimatic Zoning and Construction Guidelines for Single-Family Housing of Social Interest. Associação Brasileira de Normas Técnicas: Rio de Janeiro, Brazil, 2005. (In Portuguese)
- Frota, A.B.; Schiffer, S.R. Thermal Comfort Manual, 6th ed.; Studio Nobel: São Paulo, Brazil, 2003. (In Portuguese) [Google Scholar]
- Mistriotis, A.; De Jong, T. Computational Fluid Dynamics (CFD) as a tool for the analysis of ventilation and indoor microclimate in agricultural buildings. Neth. J. Agri. Sci. 1997, 45, 81–96. [Google Scholar] [CrossRef]
- Norton, T.; Sun, D.W.; Grant, J.; Fallon, R.; Dodd, V. Applications of computational fluid dynamics (CFD) in the modelling and design of ventilation systems in the agricultural industry: A review. Bioresour. Technol. 2007, 98, 2386–2414. [Google Scholar] [CrossRef] [PubMed]
- Saraz, J.A.O.; Tinôco, I.F.F.; Rocha, K.S.O.; Mendes, L.B.; Norton, T. A CFD based approach for determination of ammonia concentration profile and flux from poultry houses with natural ventilation. Rev. Fac. Nac. Agron. Medellin 2016, 69, 7825–7834. [Google Scholar] [CrossRef]
- Naboni, E.; Lee, D.S.H.; Fabbri, K. Thermal Comfort-CFD maps for Architectural Interior Design. Procedia Eng. 2017, 180, 110–117. [Google Scholar] [CrossRef]
- Aghniaey, S.; Lawrence, T.M.; Sharpton, T.N.; Douglass, S.P.; Oliver, T.; Sutter, M. Thermal comfort evaluation in campus classrooms during room temperature adjustment corresponding to demand response. Build. Environ. 2019, 148, 488–497. [Google Scholar] [CrossRef]
- Alizadeh, M.; Sadrameli, S.M. Numerical modeling and optimization of thermal comfort in building: Central composite design and CFD simulation. Energy Build. 2018, 164, 187–202. [Google Scholar] [CrossRef]
- Usman, F.; Bakar, A.R.A. Thermal Comfort Study Using CFD Analysis in Residential House with Mechanical Ventilation System. In Proceedings of the AICCE’19: Transforming the Nation for a Sustainable Tomorrow 4, Penang, Malaysia, 21–22 August 2019; Springer: Cham, Switzerland, 2020; Volume 53, pp. 1613–1628. [Google Scholar] [CrossRef]
- Chen, L.; Fabian-Wheeler, E.E.; Cimbala, J.M.; Hofstetter, D.; Patterson, P. Computational Fluid Dynamics Modeling of Ventilation and Hen Environment in Cage-Free Egg Facility. Animals 2020, 10, 1067. [Google Scholar] [CrossRef] [PubMed]
- ANSYS Inc. ANSYS FLUENT Theory Guide; Release 15.0; ANSYS Inc.: Canonsburg, PA, USA, 2013; 814p. [Google Scholar]
- Anderson, W.K.; Bonhaus, D.L. An implicit upwind algorithm for computing turbulent flows on unstructured grids. Comput. Fluids 1994, 23, 1–21. [Google Scholar] [CrossRef]
- Leonard, B.P.; Mokhtari, S. ULTRA-SHARP Non-Oscillatory Convection Schemes for High-Speed Steady Multidimensional Flow, NASA TM 1-2568 (ICOMP-90-12); NASA Lewis Research Centre: Sandusky, OH, USA, 1990.
- Barth, T.; Jespersen, D. The design and application of upwind schemes on unstructured meshes. In Proceedings of the 27th Aerospace Sciences Meeting, Reno, NV, USA, 9–12 January 1989; p. 366. [Google Scholar]
- Alaman, A. Hygrothermal comfort conditions in buildings. In Board of Scientific and Technical Research “Juan de la Cierva” of the Higher Council for Scientific Research; Enero: Madrid, Spain, 1968. (In Spanish) [Google Scholar]
- WHO. WHO Official Records n°2, 2012. Available online: http://www.who.int/library/collections/historical/es (accessed on 11 October 2021).
- ASHRAE. Ashrae Epidemic Task Force: Schools & Universities. 2021. Available online: https://www.ashrae.org/file%20library/technical%20resources/covid-19/ashrae-reopening-schools-and-universities-c19-guidance.pdf (accessed on 12 December 2021).
- Givoni, B. Basic Study of Ventilation Problems in Houses in Hot Countries; Building Research Station of the Institute of Technology: Haifa, Israel, 1962. [Google Scholar]




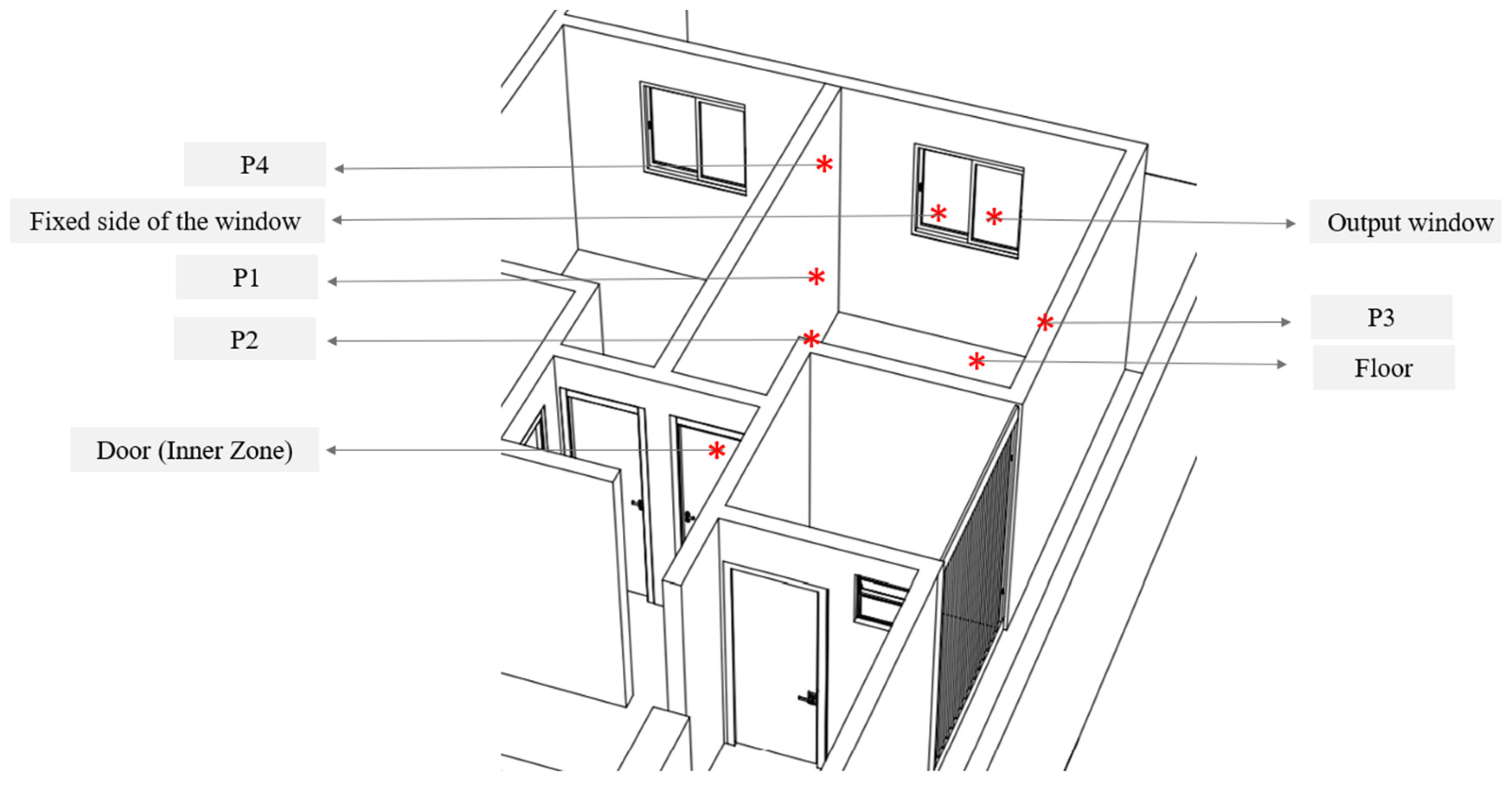

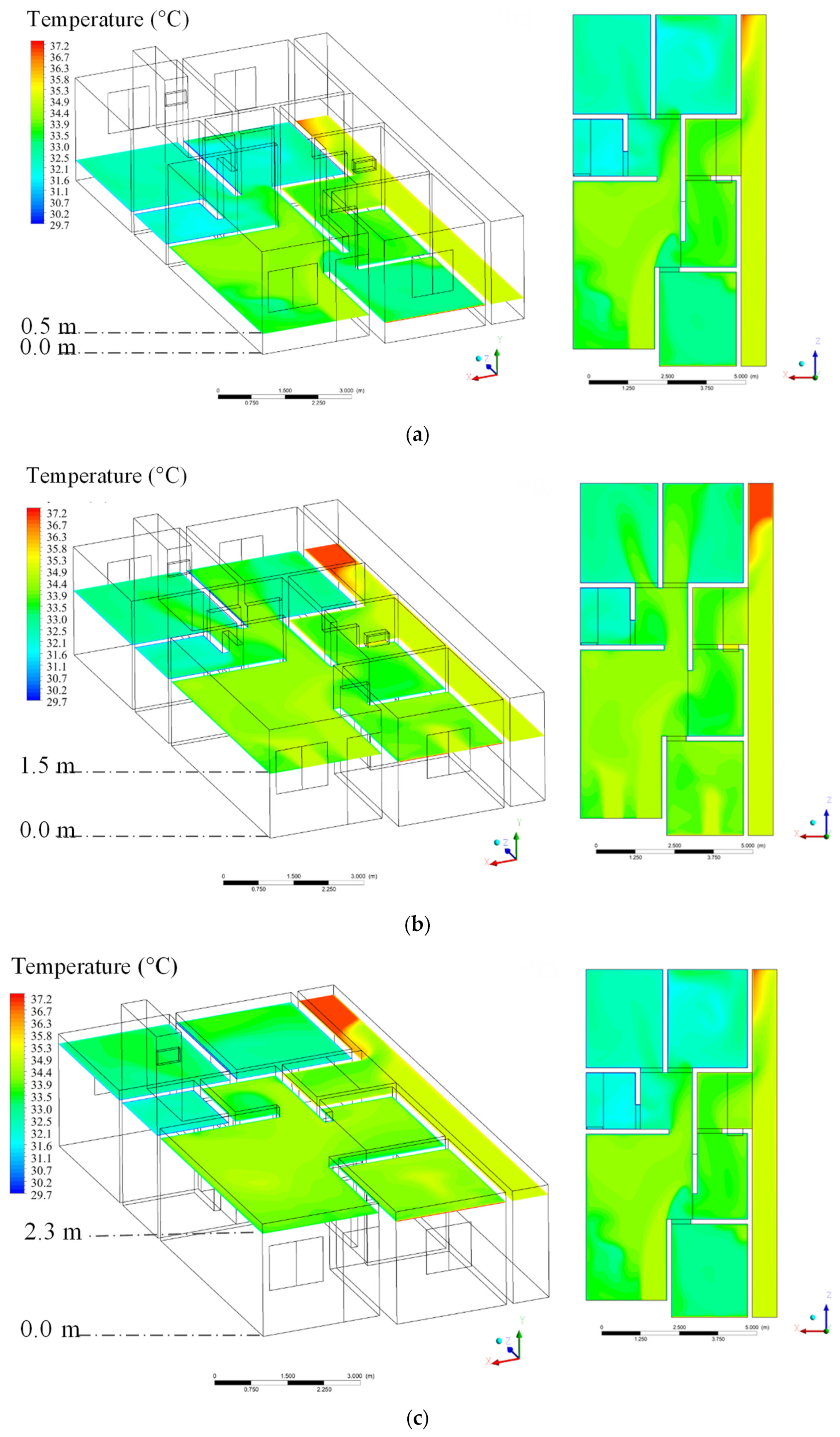
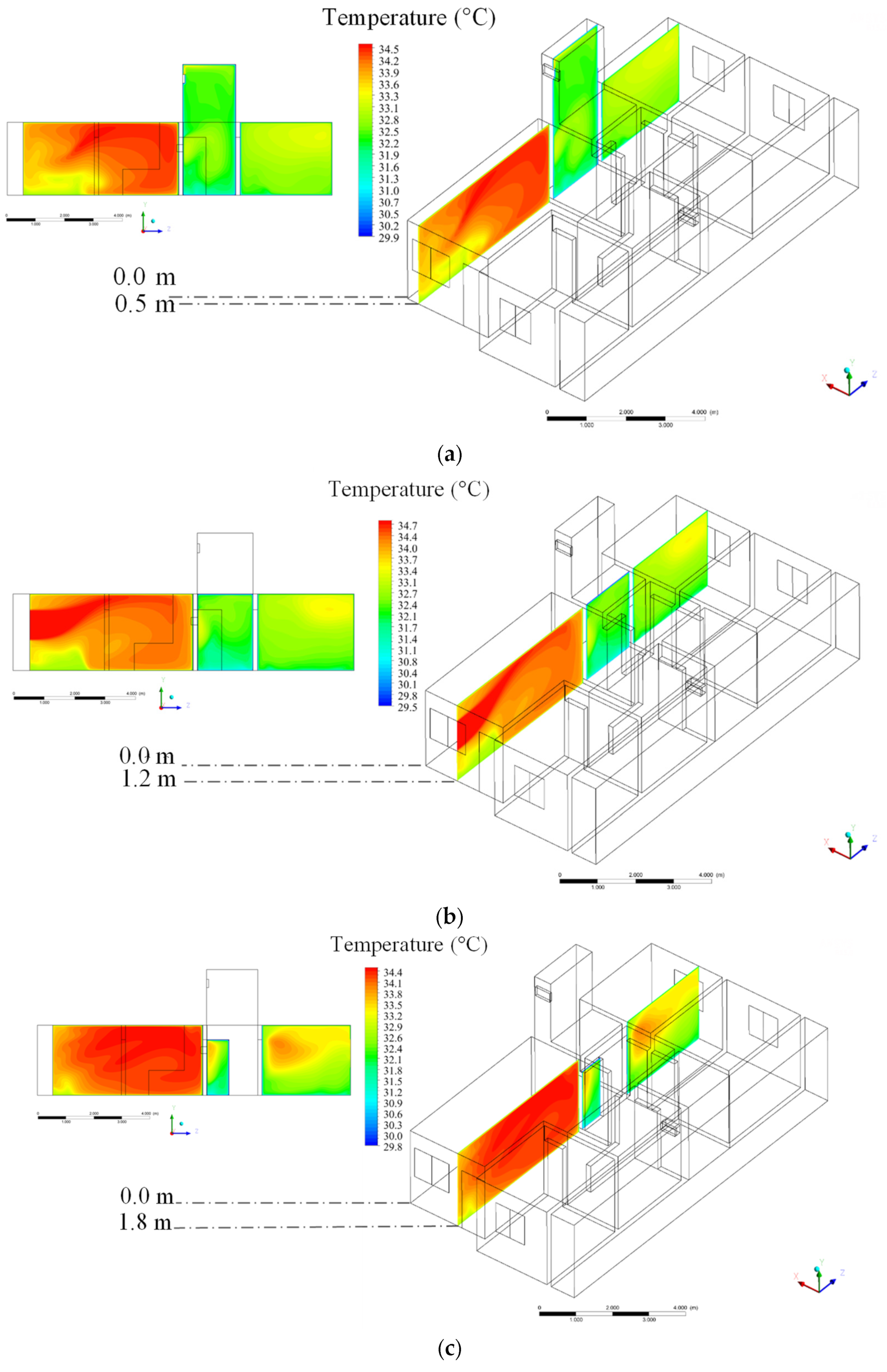
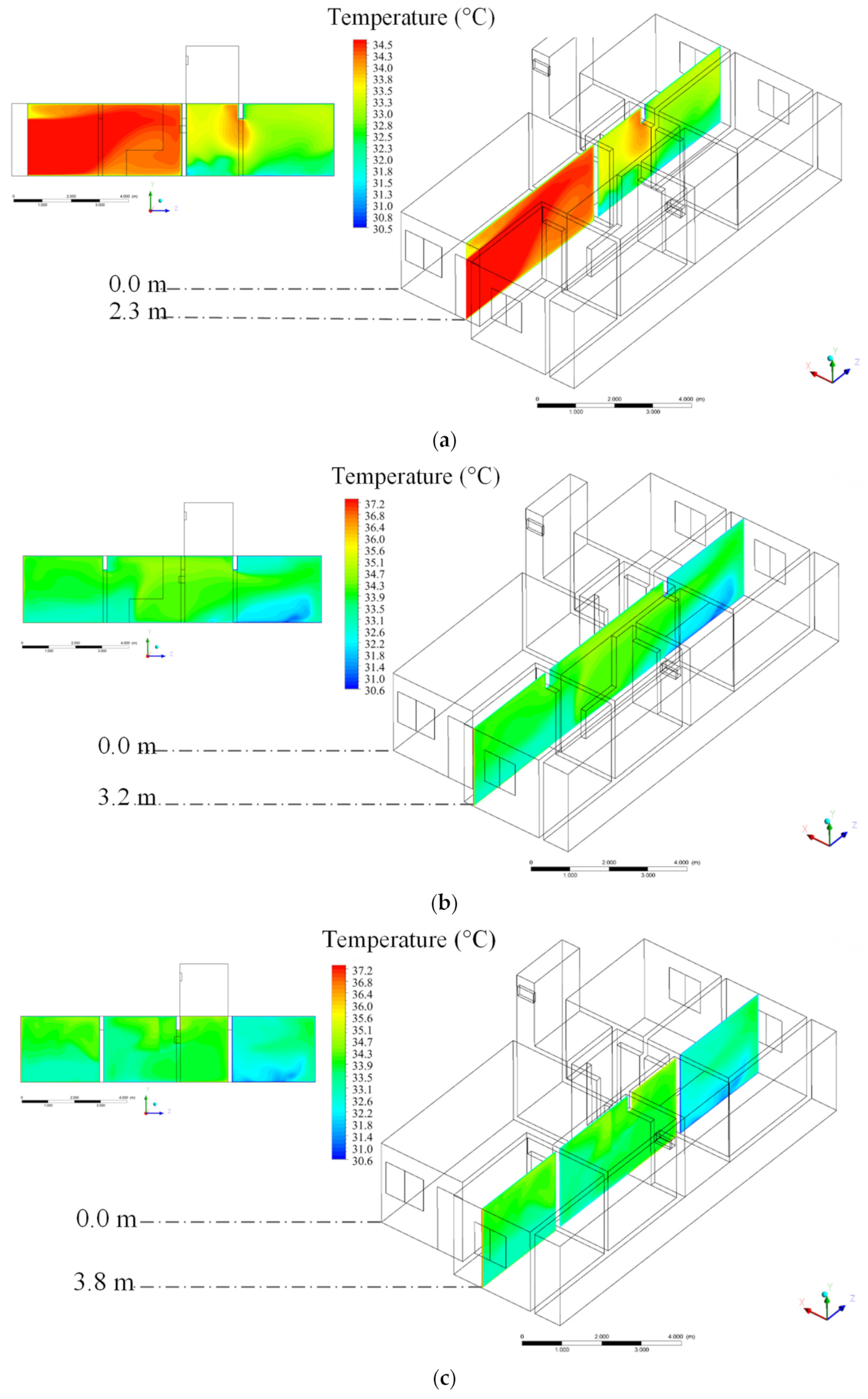
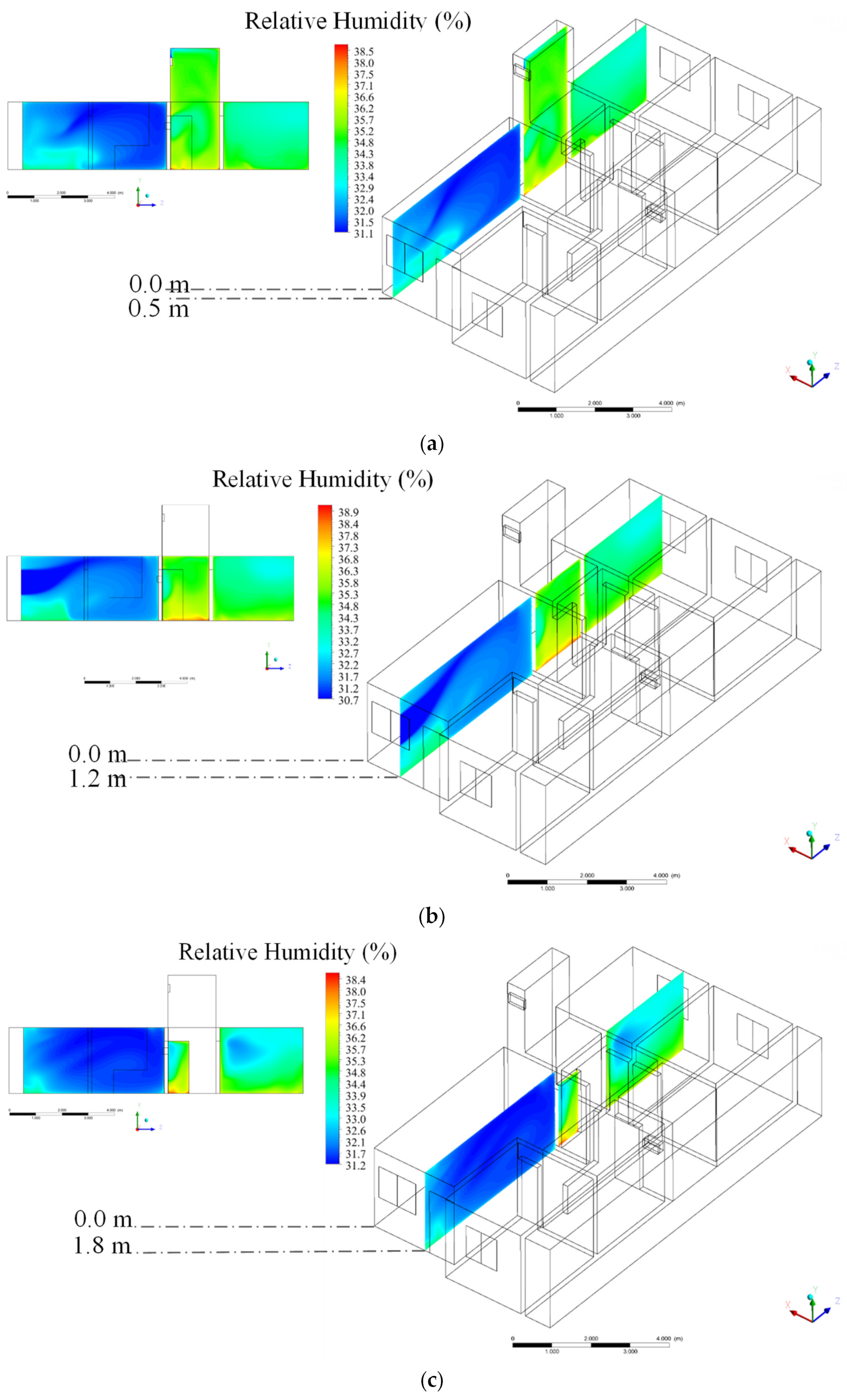
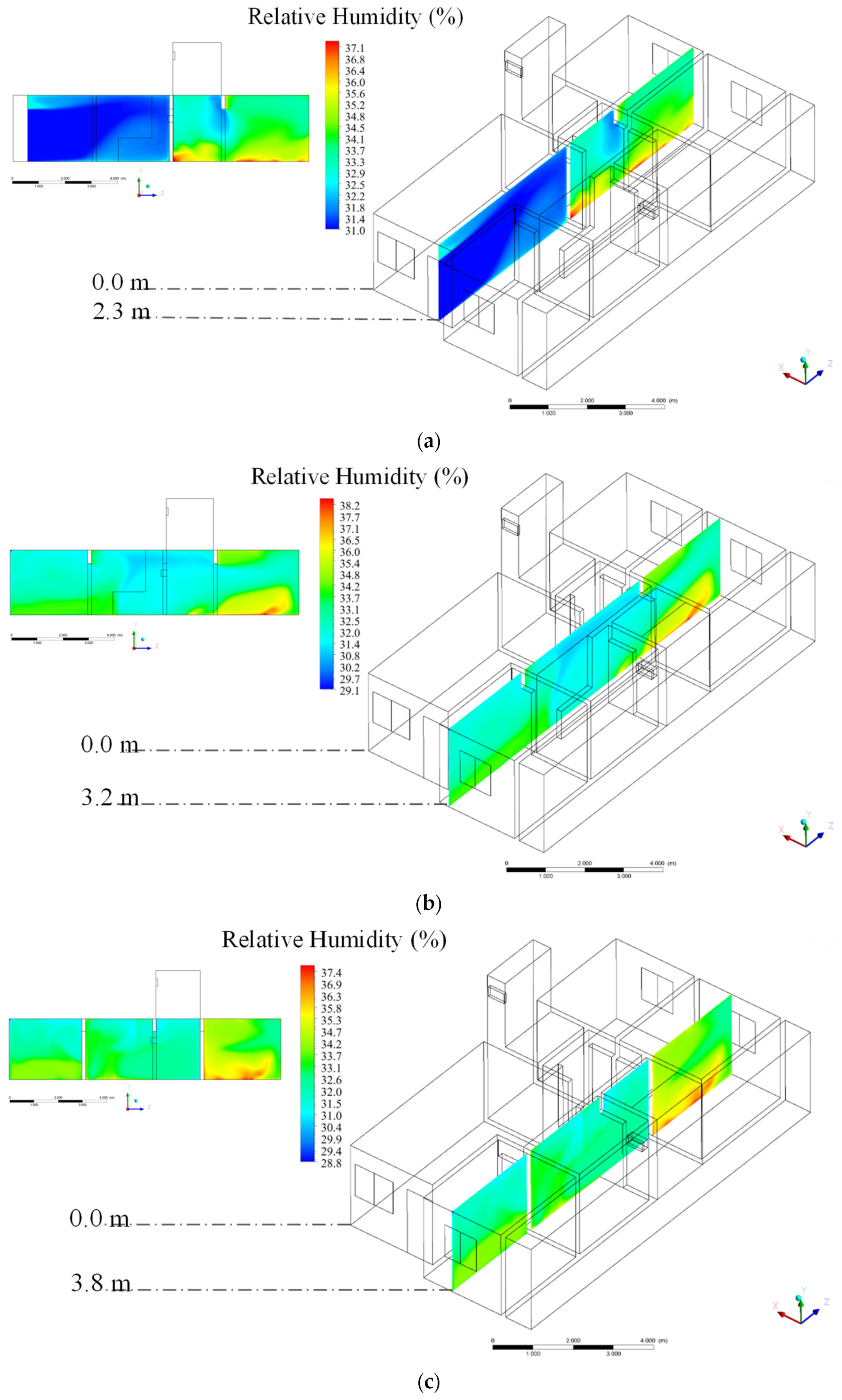
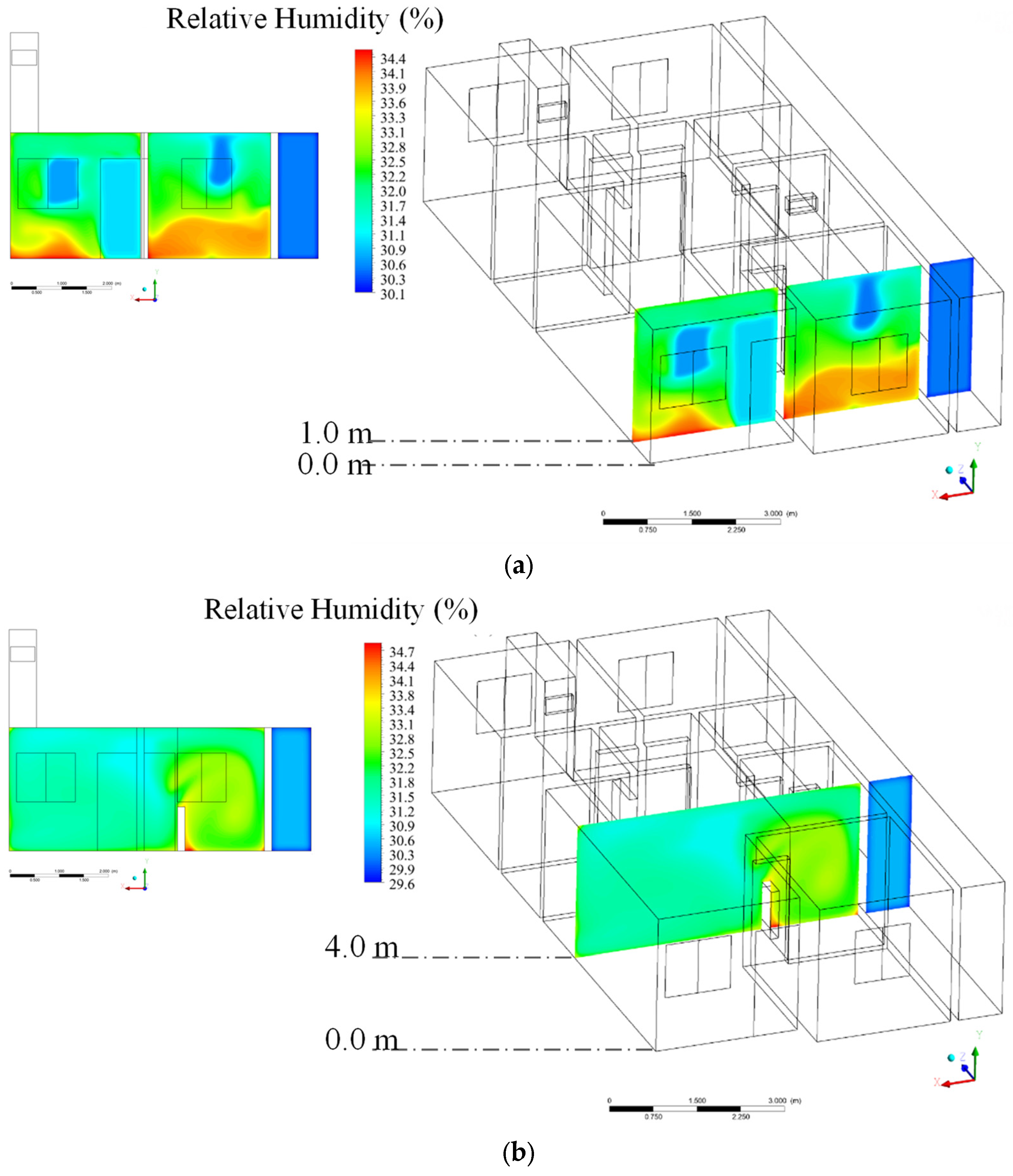
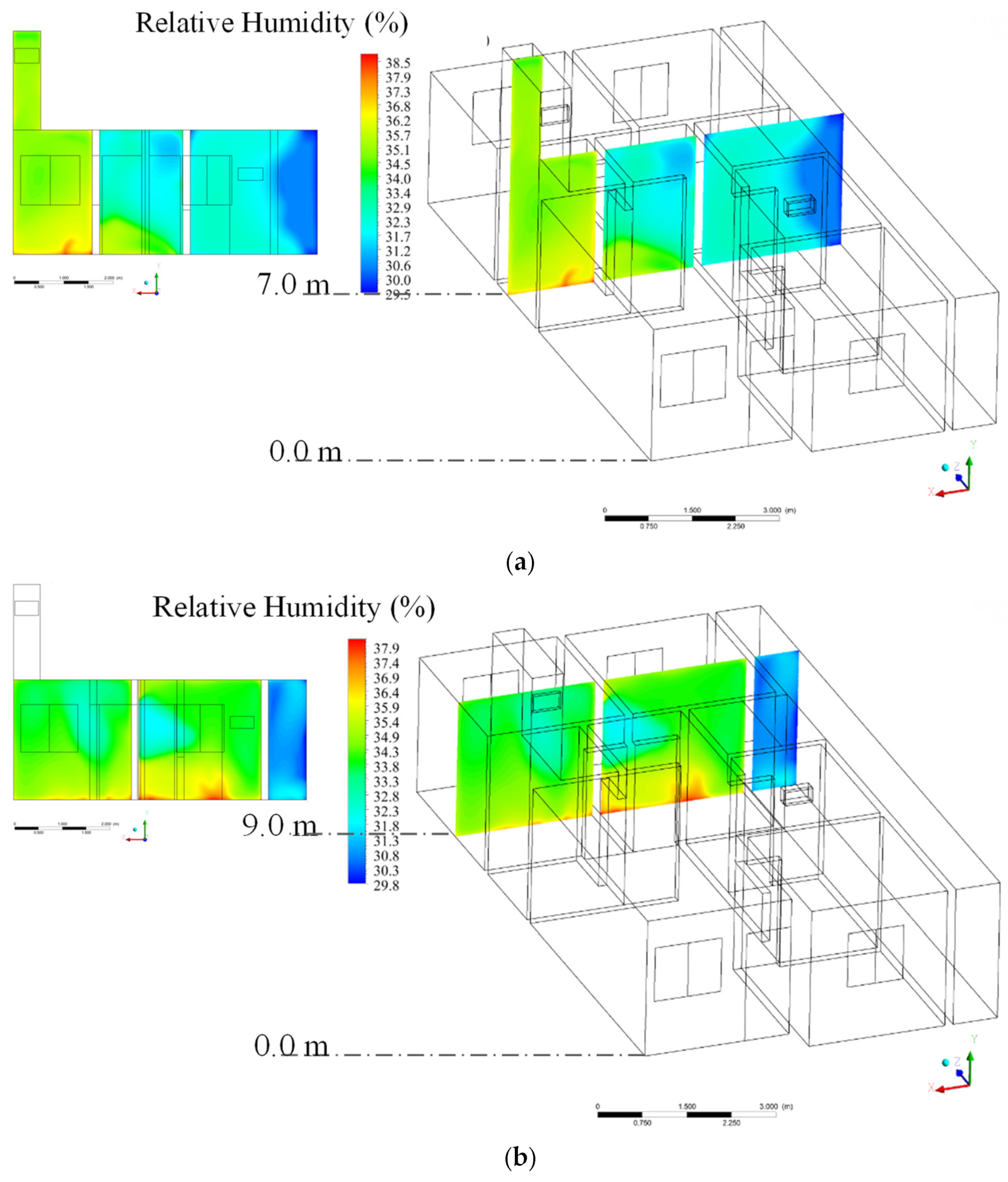


| Mesh | Number of Elements |
|---|---|
| 1 | 504,237 |
| 2 | 1,360,049 |
| 3 | 2,661,152 |
| 4 | 3,923,659 |
| Relaxation Factors | Value |
|---|---|
| Pressure | 0.5 |
| Momentum | 0.5 |
| Density | 1 |
| Boundary Force | 1 |
| Turbulent kinetic energy | 0.75 |
| Turbulence dissipation rate | 0.75 |
| Turbulent viscosity | 1 |
| Mass fraction of water | 0.75 |
| Mass fraction of oxygen | 0.75 |
| Energy | 0.75 |
| Conservation Equations | Convergence Criteria |
|---|---|
| Velocity in the x, y, and z directions | 0.001 |
| Continuity | 0.001 |
| k | 0.001 |
| ε | 0.002 |
| Energy | 0.00001 |
| Mass fraction of water | 0.001 |
| Mass fraction of oxygen | 0.001 |
| Component | Air Inlet | |||||||
|---|---|---|---|---|---|---|---|---|
| Window | Door | Angulation | Temperature | Relative Humidity | ||||
| 1 | 2 | 3 | 4 | 1 | 2 | |||
| Open | Open | Open | Open | Open | Open | 90° | Measured | Measured |
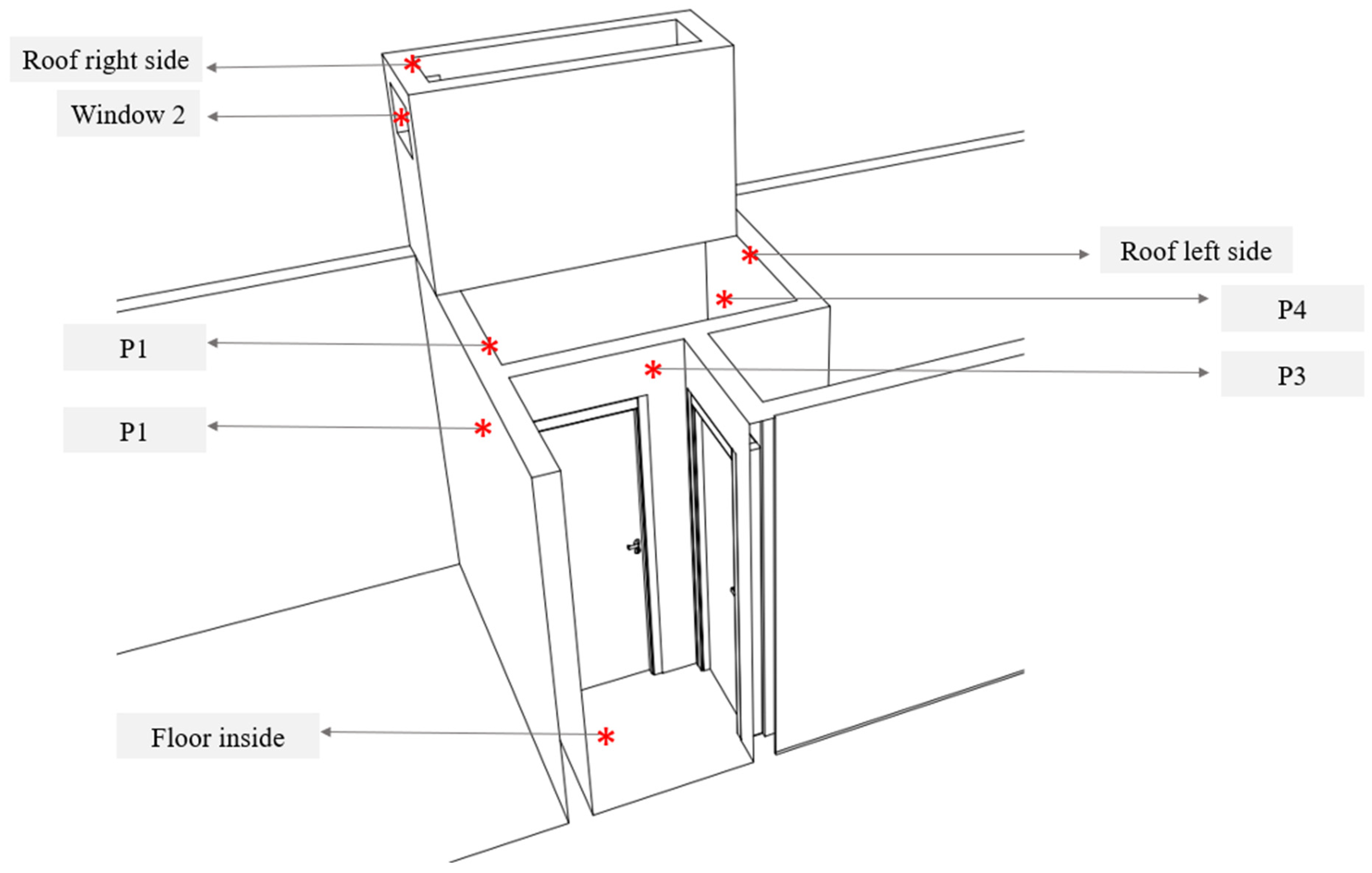
| Locations | Boundary Conditions | Value |
|---|---|---|
| P1 | Stationary wall with uniform and constant temperature | 32.7 °C |
| P2 | 32.7 °C | |
| P3 | 33 °C | |
| P4 | 31 °C | |
| P5 | 31.7 °C | |
| P6 | 31.6 °C | |
| P7 | 31.6 °C | |
| P8 | 31.6 °C | |
| Ceiling | 32.6 °C | |
| Floor | 32.5 °C | |
| Fixed part of the window | 33.2 °C | |
| Outlet window | Velocity inlet with prescribed temperature and relative humidity | 0.5 m/s 34.8 °C 31.76% |
| Door | Velocity inlet with prescribed temperature and relative humidity | 0.6 m/s 34.6 °C 41% |
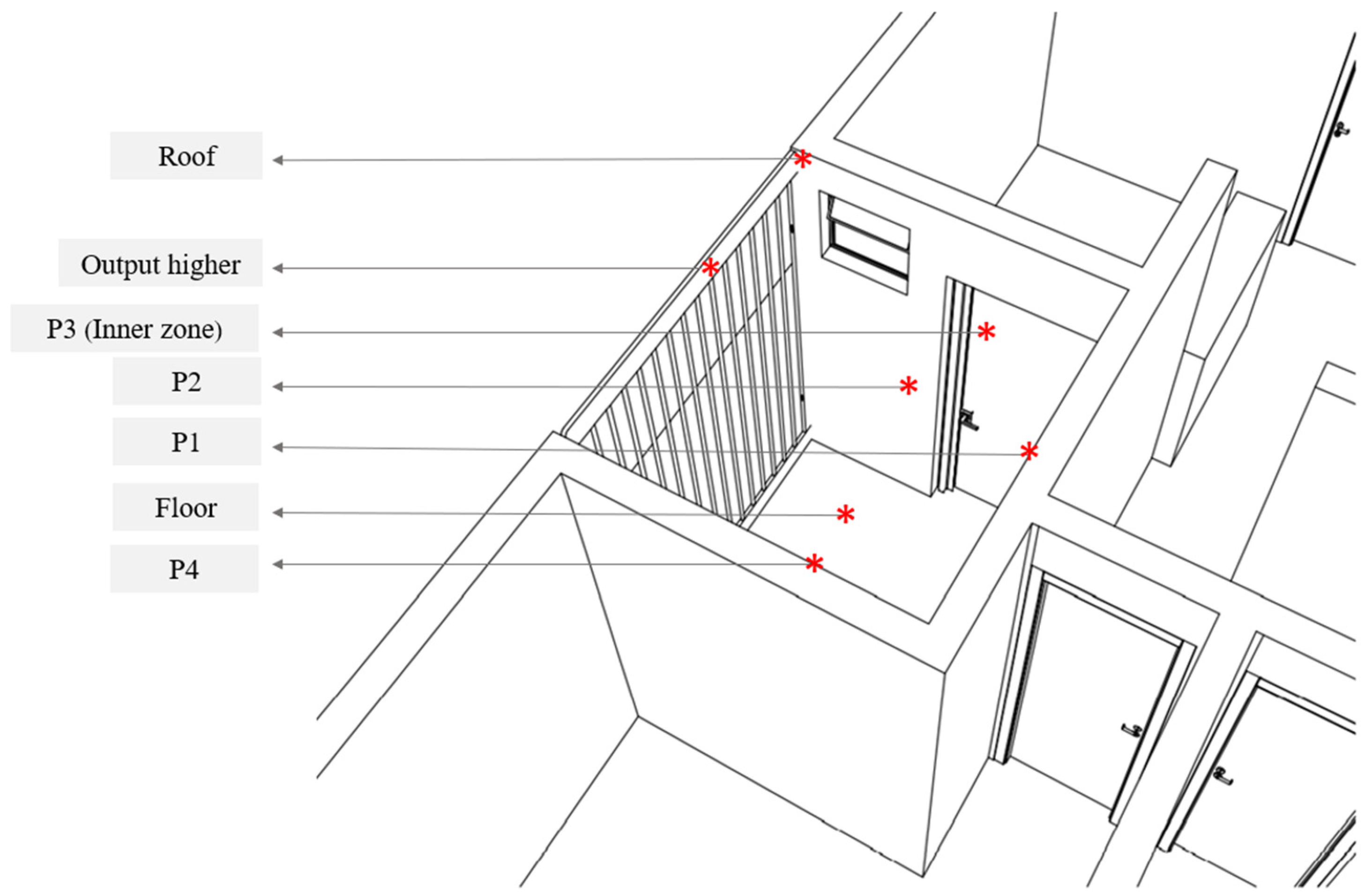
| Locations | Boundary Conditions | Value |
|---|---|---|
| P1 | Stationary wall with uniform and constant temperature. | 31.2 °C |
| P2 | 30.3 °C | |
| P3 | 29.7 °C | |
| P4 | 29.8 °C | |
| Right ceiling | 30.5 °C | |
| Left ceiling | 29.4 °C | |
| Floor | 30.3 °C | |
| Door | Interior zone | - |
| Locations | Boundary Conditions | Value |
|---|---|---|
| P1 | Stationary wall with uniform and constant temperature. | 35.7 °C |
| P2 | 30.3 °C | |
| P3 | Interior zone | - |
| P4 | Stationary wall with uniform and constant temperature. | 35 °C |
| Ceiling | 35.5 °C | |
| Floor | 35.3 °C | |
| Door | Interior zone | - |
| Locations | Boundary Conditions | Value |
|---|---|---|
| P1 | Stationary wall with uniform and constant temperature. | 32 °C |
| P2 | 31.8 °C | |
| P3 | 31.9 °C | |
| P4 | 32 °C | |
| Ceiling | 32.6 °C | |
| Floor | 31.9 °C | |
| Door | Interior zone | - |
| Little window | Interior zone | - |
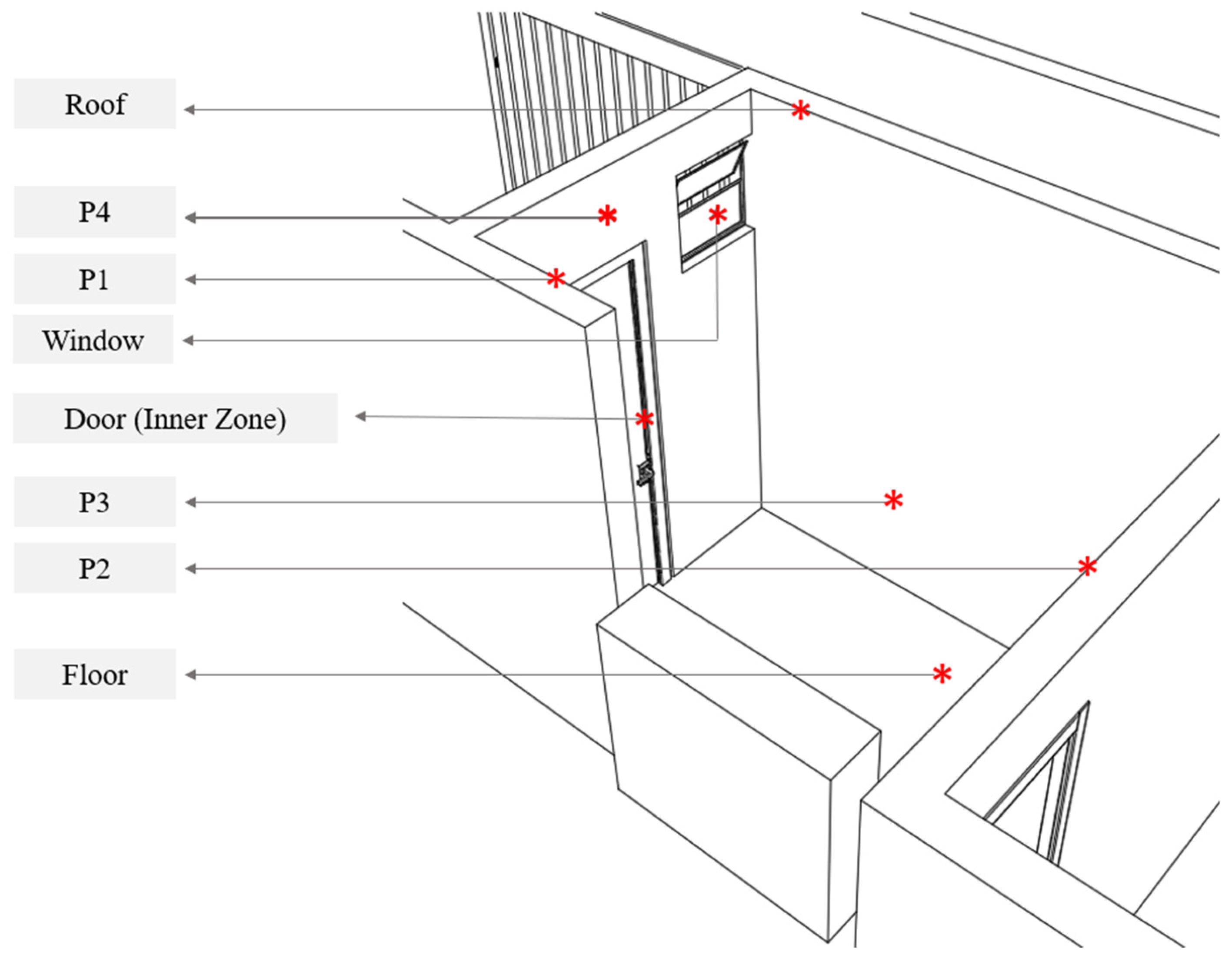
| Locations | Boundary Conditions | Value |
|---|---|---|
| P1 | Stationary wall with uniform and constant temperature | 31.1 °C |
| P2 | 30.5 °C | |
| P3 | 30.6 °C | |
| P4 | 31.6 °C | |
| Ceiling | 32 °C | |
| Floor | 30.9 °C | |
| Fixed part of the window | 31.6 °C | |
| Outlet window | Mass flow with prescribed temperature and relative humidity | 0.395643 kg/s 40.6 °C 41% |
| Door | Interior zone | - |
| Locations | Boundary Conditions | Value |
|---|---|---|
| P1 | Stationary wall with uniform and constant temperature. | 29.7 °C |
| P2 | 30.6 °C | |
| P3 | 30.4 °C | |
| P4 | 31.6 °C | |
| Ceiling | 31.6 °C | |
| Floor | 30.5 °C | |
| Fixed part of the window | 31.6 °C | |
| Outlet window | Mass flow with prescribed temperature and relative humidity | 0.395038 kg/s 41 °C 40% |
| Door | Interior zone | - |
| Locations | Boundary Conditions | Value |
|---|---|---|
| P1 | Stationary wall with uniform and constant temperature. | 32.4 °C |
| P2 | 37.3 °C | |
| P3 | 33.5 °C | |
| P4 | 32.9 °C | |
| Ceiling | 32.9 °C | |
| Floor | 34 °C | |
| Fixed part of the window | 37.7 °C | |
| Inlet window | Inlet velocity with prescribed temperature and relative humidity | 0.3 m/s 34.9 °C 31% |
| Door | Interior zone | - |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rocha, L.A.; Gomez, R.S.; Delgado, J.M.P.Q.; Vieira, A.N.O.; Santos, I.B.; Luiz, M.R.; Oliveira, V.A.B.; Oliveira Neto, G.L.; Vasconcelos, D.B.T.; Silva, M.J.V.; et al. Natural Ventilation in Low-Cost Housing: An Evaluation by CFD. Buildings 2023, 13, 1408. https://doi.org/10.3390/buildings13061408
Rocha LA, Gomez RS, Delgado JMPQ, Vieira ANO, Santos IB, Luiz MR, Oliveira VAB, Oliveira Neto GL, Vasconcelos DBT, Silva MJV, et al. Natural Ventilation in Low-Cost Housing: An Evaluation by CFD. Buildings. 2023; 13(6):1408. https://doi.org/10.3390/buildings13061408
Chicago/Turabian StyleRocha, Lívia A., Ricardo S. Gomez, João M. P. Q. Delgado, Antônio N. O. Vieira, Ivonete B. Santos, Márcia R. Luiz, Vital A. B. Oliveira, Guilherme L. Oliveira Neto, Danielle B. T. Vasconcelos, Márcio J. V. Silva, and et al. 2023. "Natural Ventilation in Low-Cost Housing: An Evaluation by CFD" Buildings 13, no. 6: 1408. https://doi.org/10.3390/buildings13061408
APA StyleRocha, L. A., Gomez, R. S., Delgado, J. M. P. Q., Vieira, A. N. O., Santos, I. B., Luiz, M. R., Oliveira, V. A. B., Oliveira Neto, G. L., Vasconcelos, D. B. T., Silva, M. J. V., Cabral, A. S., & Lima, A. G. B. (2023). Natural Ventilation in Low-Cost Housing: An Evaluation by CFD. Buildings, 13(6), 1408. https://doi.org/10.3390/buildings13061408











