Compatible Truss-Arch Model for Predicting the Shear Strength of Steel Shape-Reinforced Concrete (SRC) Beams

Abstract

A steel shape-reinforced concrete (SRC) beam, in which a steel profile is encased in an R.C. section, is an essential configuration of steel-concrete composite members. Nevertheless, the precise estimation of shear strength for SRC elements is currently being explored due to the challenges associated with incorporating steel-concrete interaction. This paper establishes a compatible truss-arch model to simulate the shear behavior of SRC beams and predict their maximum shear strength. In the established model, the shear contribution of the R.C. encasement is evaluated using the traditional truss-arch model, and a stress decomposition based on von Mises yielding criterion and strain compatibility is conducted within the steel shape to decouple its shear contribution. Finally, the validity of the proposed model is confirmed using a comprehensive database. The comparison between the experimental and calculated results demonstrates that the established model can effectively and reliably calculate the SRC beams’ shear strength.

1. Introduction

As shown in Figure 1a, steel shape-reinforced concrete (SRC), in which a steel profile (e.g., H-shaped steel, steel plate, or steel box) is encased in an R.C. section, is widely applied as transfer elements or columns in high-rise buildings. As an essential configuration of steel-concrete composite members, the local buckling of bare steel can be eliminated by introducing outer concrete encasement; meanwhile, compared with traditional R.C. members, the energy dissipation capacity can be enhanced due to the existence of an inner steel profile [1,2,3]. Until now, many countries have launched design guidelines for SRC members/structures [4,5,6], and in the ultimate state design, predicting the load-carrying capacities (bending, shear, and torsion) is essential to preventing structural elements from failure.

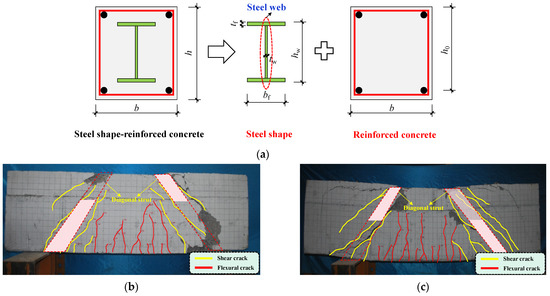
Figure 1. (a) Steel shape-reinforced concrete beams; (b) Shear failure mode of R.C. beam; (c) Shear failure mode of SRC beam.

Unlike the flexural strength predictions based on simple plane section assumptions, the shear strength evaluation of steel-concrete composite members (including SRC) is more complex due to the so-called “composite action” between the steel profile and adjacent concrete. Under flexural action, the composite action exists on the plane section, namely that the normal strains of concrete, rebar, and steel shape along the sectional height must follow a linear distribution, and the strain field and the constitutive law can easily obtain the corresponding stress distribution. In this case, the steel and concrete can be merged into a composite cross-section, and both the steel and concrete are in compression above the neutral axis and in tension below the neutral axis. However, under shear action, the composite action should exist on the vertical section (following the shear stress flow), and in this case, the R.C. part and the steel profile behave in parallel, and the stress among these two parts cannot be unified due to the different failure modes. Under applied shear, the behavior of R.C. is governed by the diagonal cracking due to the diagonal directions of the principal stresses and the weaker tensile strength, whereas the stress within the steel profile follows the yielding criterion. Therefore, the R.C. and steel profiles of SRC members can be regarded as two nonlinear shear springs in parallel, and the shear contributions are related to their stiffness [7].

The strength predictions for SRC members in current design codes follow the same principles as the aforementioned mechanical behavior, namely, the plane section assumption in flexural strength predictions and the strength superposition in shear strength predictions. Nevertheless, the traditional strength superposition was challenged by the experimental results of Chen et al. [8]. In their experiments, twelve specimens, including two concrete beams and ten SRC beams, were designed to explore the effect of steel shape on static behavior. Among these SRC specimens, the geometric dimensions (width and height of the cross-section) and material properties were all the same, and the cross-sectional depth of the steel shape was different under the condition of the same cross-sectional area (the web thickness varied), namely that the nominal shear strengths of these steel shapes were almost the same. According to the traditional strength superposition, the overall shear resistance of SRC beams is the sum of the contributions of R.C. and steel profile, which can be calculated following the shear equations of R.C. and bare steel. If so, the peak load of the SRC beams in Ref. [8] should be comparable; nevertheless, the maximum load difference between these specimens was up to 50%, indicating that the simple strength superposition is questionable and there is interaction between R.C. and steel shape during the loading process. As shown in Figure 1b,c, the explicit failure patterns of traditional R.C. and SRC are almost the same, namely, the crushing of the inclined concrete strut; meanwhile, the stress state and deflection of the encased steel cannot be observed and determined directly, making the shear resistance calculation of the steel profile complex. Therefore, the load-sharing mechanism is essential for SRC members.

With the aim of investigating the load-sharing mechanism, many researchers have established mechanics-based models. On the basis of the softened strut-and-tie (SST) model adopted for R.C. members [9], Lu [10] and Chen et al. [8] extended the SST model to SRC beams, and the steel shape was simplified as longitudinal or diagonal reinforcement. However, there was no direct experimental evidence to reveal the steel shape’s role, whereas F.E. results show that the steel web’s stress at both principal directions was striking, indicating that the steel web behaved in bi-directional rather than one-way reinforcement [11]. Deng et al. [12] put forward a modified direct strut-and-tie model (DSTM) for predicting the shear resistance of SRC beams. In their model, the steel web is simplified as stirrups or longitudinal rebar; however, unlike stirrups in R.C. members that contribute strength after concrete cracking, the continuous steel web can improve the rigidity and strength of the entire member from the beginning of the loading process. Zeng et al. [13] and Ke et al. [14] adopted the modified compression field theory (MCFT) in SRC members [15], in which the shear contribution of the steel profile is obtained by multiplying the shear strain by the shear modulus. However, its rationality is doubtful because the steel profile is not in pure shear during the loading process. To conclude, current shear models for SRC beams are deduced from those of R.C. members, and the encased steel shape is basically simplified as discrete one-way steel reinforcement. It seems reasonable because the explicit failure patterns between SRC and R.C. members are similar, namely, the development of inclined concrete cracks; however, the effect of the encased steel shape on the overall shear strength needs further investigation because of the two-way property and the coupled stress distribution.

To further explore the shear mechanism of SRC members, an innovative approach is proposed to evaluate the shear resistance mechanism of SRC girders in this paper. The R.C. part is simulated using a simplified composite truss analogy, while the steel profile’s shear contribution is obtained based on the yielding criterion with strain compatibility. Finally, the accuracy of the established model is validated by comparing it with previously published models and available experimental test data in the literature.

2. Proposed Model

2.1. Model Description

As illustrated in Figure 2, the proposed model is composed of two major parts: (1) The composite truss consists of longitudinal and transverse reinforcements, concrete, and two steel flanges; (2) the vertical steel web. The total shear strength V_u is the sum of the shear capacities of these two mechanisms: the composite truss V_c and the vertical web V_ss. As mentioned before, the crack and failure patterns of SRC beams are similar to those of R.C. beams, indicating that the composite truss can reach the corresponding shear strength at the maximum load. In contrast, the shear contribution of the vertical steel web can be determined following deformation compatibility to show the steel-concrete interaction.

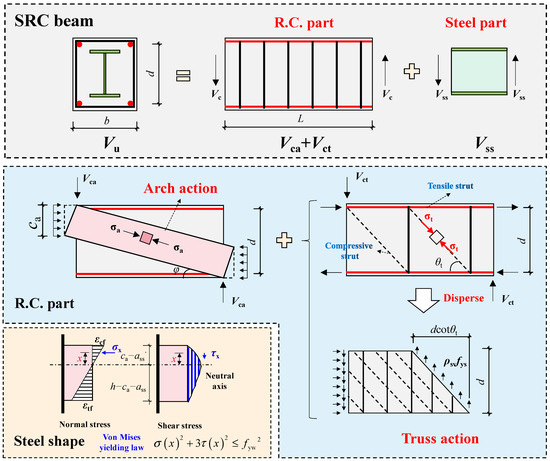
Figure 2. Model configuration (V_ct and V_ca are the shear resistance of the truss arch and arch action).

In addition, in the proposed model, the top and bottom flanges and the vertical web of H-shaped steel work through different anti-shear mechanisms. The steel flanges play roles in the composite truss to reinforce the diagonal strut, and the steel web directly carries the vertical shear according to available test results [8,11]. However, these components operate integrally in terms of strain compatibility. In this case, strain compatibility can be employed to ensure coherence between the vertical web and two flanges and to assess their contact.

2.2. Truss-Arch Modeling of Composite Truss

The shear behavior of the composite truss is modeled using the truss-arch model, which was proposed by Ichinose [16] and has been applied in the Architectural Institute of Japan (AIJ) Design Guidelines. According to existing knowledge, the shear behavior of R.C. members is strongly affected by the shear span-to-depth ratio λ [17]. λ can be obtained by dividing the shear span length by the cross-sectional height, and the shear span is the distance between the loading point and the adjacent support. When λ is low, the arch action, which follows the path connecting the loading point and the support, governs the shear behavior. When λ is high, the truss action is dominant. The truss-arch model can capture the characteristics mentioned above; therefore, it has been widely applied in the shear strength/stiffness predictions of R.C. members. The shear resistance of the truss-arch model is the sum of the truss action V_ct and the arch action V_ca. As indicated in Figure 2, V_ct can be expressed as:

$$V_{\mathrm{ct}}=bd{\rho }_{\mathrm{sv}}{f}_{\mathrm{ys}}\cot {\theta }_{\mathrm{t}}$$

(1)

$${\rho }_{\mathrm{sv}}=\frac{A_{\mathrm{sv}}}{bs}$$

(2)

where V_ct is the truss action’s shear contribution; b is the cross-sectional width; d is the distance from the center of the compressive rebar to that of the tensile rebar; ρ_sv is the ratio of the transverse reinforcements; f_ys is the yield strength of the transverse reinforcements; θ_t is the angle between the horizontal axis and the compressive strut; A_sv is the cross-sectional area of the stirrup ribs; s is the stirrup spacing.

θ_t can be obtained following the constant angle truss model (CATM) proposed by Kim and Mander [18]. As a mechanics-based model, CATM is deduced based on the principle of minimum potential energy, as follows:

$${\theta }_{\mathrm{t}}={\tan }^{-1}{\left(\frac{\frac{{\rho }_{\mathrm{sv}}}{{\rho }_{\mathrm{sl}}}\cdot \frac{A_{\mathrm{v}}}{A_{\mathrm{g}}}}{0.61}\right)}^{0.25}$$

(3)

where ρ_sl is the ratio of the tensile reinforcement, including longitudinal rebar and steel flange at the tensile section; A_v is the shear area, A_v = bd; A_g is the gross area of the entire cross-section.

As indicated in Figure 2, in the truss-arch model, the arch action can be simulated as a direct strut connecting the loading point and the adjacent support. It appears that the diagonal concrete serves as a compressive strut in truss and arch actions, and the compressive stresses of the diagonal concrete in truss and arch actions can be σ_t and σ_a, respectively. If the value σ_t + σ_a exceeds the effective strength of the diagonal concrete, the composite truss fails. In fact, the σ_t and σ_a are not in the same direction, and the shear contributions of the truss and arch models should follow the corresponding stiffness. Nevertheless, most existing research assumed that σ_t and σ_a worked in the same direction and applied plastic analysis for simplification, which has been proven acceptable for engineering purposes [19]. In this case, the shear contribution of the arch action V_ca can be expressed as follows:

$${\sigma }_{\mathrm{t}}=\frac{{\rho }_{\mathrm{sv}}{f}_{\mathrm{ys}}}{{\sin }^2{\theta }_{\mathrm{t}}}$$

(4)

$$V_{\mathrm{ca}}=b{c}_{\mathrm{a}}\left(0.85\beta f_{\mathrm{c}}-{\sigma }_{\mathrm{t}}\right)\tan \phi$$

(5)

where σ_t is the compressive stress of the diagonal concrete in the truss action, which can be obtained by the free-body diagram of the applied truss; c_a is the cross-sectional depth of the arch, which equals the cross-sectional depth of the neutral axis at the loading section; β is the softened factor of the cracked concrete; φ is the inclination of the arch, φ = (h − c_a)/L; L is the length of the shear span; h is the height of the cross-section.

According to existing knowledge, when concrete experiences shear force, the effective compressive strength of concrete f_ce varies according to the transverse tensile strain ε_t. In this case, the compressive strength of concrete will be “softened” with the increase in the loading process [15]. Theoretically, the concrete softened should be evaluated using softening equations; nevertheless, obtaining ε_t at a certain load level is complex, and iterative analysis must be included to obtain ε_t accurately. In the proposed model, the concrete softening is evaluated by the equations in ACI 318 [17], in which the effect on concrete strength can be expressed as 0.85βf_c and the softened factor β can be determined as:

$$\{\begin{array}{l}\beta =0.75,\mathrm{if}{\displaystyle \sum \frac{A_{si}}{b{s}_{\mathrm{i}}}}\sin {\alpha }_{\mathrm{i}}\ge 0.003\\ \beta =0.60,\mathrm{if}{\displaystyle \sum \frac{A_{si}}{b{s}_{\mathrm{i}}}}\sin {\alpha }_{\mathrm{i}}<0.003\end{array}$$

(6)

where A_si is the total area of distributed reinforcement at spacing s_i in the i-th direction of reinforcements crossing a strut at an angle α_i to the axis of a strut, whose detailed meaning can be found in provision R23.5.3 in ACI 318 [17].

The cross-sectional depth of the arch c_a can be obtained based on the elastic analysis [9]:

$$c_{\mathrm{a}}=\sqrt{{\left[n{\rho }_{\mathrm{sl}}+\left(n-1\right){\rho }^{\prime }{}_{{}_{\mathrm{sl}}}\right]}^2+2\left[n{\rho }_{\mathrm{sl}}+\left(n-1\right){\rho }^{\prime }{}_{{}_{\mathrm{sl}}}d/h\right]}-\left[n{\rho }_{\mathrm{sl}}+\left(n-1\right){\rho }^{\prime }{}_{{}_{\mathrm{sl}}}\right]$$

(7)

where n = E_s/E_c; E_s and E_c are the moduli of elasticity of steel and concrete, respectively; ρ_sl′ is the ratio of the compressive reinforcement, including the steel flange and longitudinal rebar at the compressive section.

2.3. Stress Decomposition of Steel Shape

As mentioned before, under applied shear force, the encased steel of SRC beams works through two shear mechanisms. For example, the two flanges of H-shaped steel can be regarded as longitudinal reinforcement in the composite truss, and the vertical web is directly subjected to the applied shear force. In the vertical steel web, the normal and shear stresses exist simultaneously; therefore, it is essential to decouple the shear stress along the web section to determine its shear contribution.

According to existing experimental results, the steel web could be fully yielded; in this case, the normal and shear stresses at web elements must obey the yielding law [11]. As shown in Figure 2, the yielding criterion proposed by von Mises is applied here, as expressed in Equation (8).

$$\sigma {\left(x\right)}^2+3\tau {\left(x\right)}^2\le f_{\mathrm{yw}}{}^2$$

(8)

where f_yw is the steel web’s yield strength.

It is essential to mention that the concrete encasement transmitted the applied load to the encased steel, unlike bare steel members. However, there is currently a lack of available test results and reliable finite element evidence regarding the mechanisms of load sharing. As a result, determining the stress distribution only according to the shear force and bending moment at a specific section does not have a definitive solution. Therefore, it is necessary to conduct stress decomposition of the steel web while making reasonable assumptions [20]. Available test results showed a strong bond between the concrete encasement and the steel profile when sufficient concrete cover was present [11]. Existing test results indicated that the R.C. section and the steel web displayed compatible behavior according to the strain monitor, conforming to the assumption of the plane section [11].

Therefore, the normal stress of the vertical web can be easily determined by σ_x = E_sε_x, and the corresponding shear stress τ_x can be deduced by the yielding criterion (Equation (8)). The steel web’s shear contribution V_ss can be obtained by integrating τ_x along the cross-section, as follows:

$$V_{\mathrm{ss}}=V_{\mathrm{sa}}+V_{\mathrm{sb}}$$

(9)

$$V_{\mathrm{sa}}=t_{\mathrm{w}}{\displaystyle {\int }_0^{c_{\mathrm{a}}-a_{\mathrm{ss}}{}^{\prime }}\tau \left(x\right)dx}=t_{\mathrm{w}}{\displaystyle {\int }_0^{c_{\mathrm{a}}-a_{\mathrm{ss}}{}^{\prime }}\sqrt{\frac{f_{\mathrm{yw}}^2-{\sigma }_{\mathrm{x}}^2}{3}}dx=t_{\mathrm{w}}}{\displaystyle {\int }_0^{c_{\mathrm{a}}-a_{\mathrm{ss}}{}^{\prime }}\sqrt{\frac{f_{\mathrm{yw}}^2-{\left(E_{\mathrm{s}}\frac{{\epsilon }_{\mathrm{cf}}x}{c_{\mathrm{a}}-a_{\mathrm{ss}}{}^{\prime }}\right)}^2}{3}}dx}$$

(10)

$$V_{\mathrm{sb}}=t_{\mathrm{w}}{\displaystyle {\int }_0^{h-c_{\mathrm{a}}-a_{\mathrm{ss}}}\tau \left(x\right)dx}=t_{\mathrm{w}}{\displaystyle {\int }_0^{h-c_{\mathrm{a}}-a_{\mathrm{ss}}}\sqrt{\frac{f_{\mathrm{yw}}^2-{\sigma }_{\mathrm{x}}^2}{3}}dx=}{t}_{\mathrm{w}}{\displaystyle {\int }_0^{h-c_{\mathrm{a}}-a_{\mathrm{ss}}}\sqrt{\frac{f_{\mathrm{yw}}^2-{\left(E_{\mathrm{s}}\frac{{\epsilon }_{\mathrm{tf}}x}{h-c_{\mathrm{a}}-a_{\mathrm{ss}}}\right)}^2}{3}}dx}$$

(11)

$${\epsilon }_{\mathrm{cf}}=\frac{c_{\mathrm{a}}-a_{\mathrm{ss}}{}^{\prime }}{c_{\mathrm{a}}}{\epsilon }_{\mathrm{c}}$$

(12)

$${\epsilon }_{\mathrm{tf}}=\frac{h-c_{\mathrm{a}}-a_{\mathrm{ss}}}{c_{\mathrm{a}}}{\epsilon }_{\mathrm{c}}$$

(13)

where V_sa is the shear contribution above the neutral axis; V_sb is the shear contribution below the neutral axis; c_a is the sectional depth of the compression area at the loading section, which can be obtained following Equation (7); a_ss′ and a_ss are the thickness of the concrete cover of the steel flanges in compression and tension; t_w is the steel web’s thickness; ε_cf is the strain of the steel flange in compression; ε_tf is the strain of the steel flange in compression; ε_c is the strain at the extremely compressive fiber at the loading section, ε_c = (1 − 0.44λ)ε_c0 [21,22]; ε_c0 is the peak compressive strain of concrete.

It is difficult to find accurate solutions for V_sa and V_sb; therefore, using a suitable numerical integration method is advisable. In this case, the two-point Gauss truss model is utilized, and Equations (10) and (11) can be rewritten as follows:

$$V_{\mathrm{sa}}=t_{\mathrm{w}}{\displaystyle \sum _{i=1}^2\frac{c_{\mathrm{a}}-a_{\mathrm{ss}}{}^{\prime }}{2}{\omega }_{\mathrm{i}}\sqrt{\frac{f_{\mathrm{yw}}^2-{\left[\frac{E_{\mathrm{s}}{\epsilon }_{\mathrm{cf}}}{c_{\mathrm{a}}-a_{\mathrm{ss}}{}^{\prime }}\left(\frac{c_{\mathrm{a}}-a_{\mathrm{ss}}{}^{\prime }}{2}+\frac{c_{\mathrm{a}}-a_{\mathrm{ss}}{}^{\prime }}{2}{t}_{\mathrm{i}}\right)\right]}^2}{3}}}$$

(14)

$$V_{\mathrm{sb}}=t_{\mathrm{w}}{\displaystyle \sum _{i=1}^2\frac{h-c_{\mathrm{a}}-a_{\mathrm{ss}}}{2}{\omega }_{\mathrm{i}}\sqrt{\frac{f_{\mathrm{yw}}^2-{\left\{\frac{E_{\mathrm{s}}{\epsilon }_{\mathrm{tf}}}{h-c_{\mathrm{a}}-a_{\mathrm{ss}}}\left[\left(\frac{h-c_{\mathrm{a}}-a_{\mathrm{ss}}}{2}\right)+\left(\frac{h-c_{\mathrm{a}}-a_{\mathrm{ss}}}{2}\right)t_{\mathrm{i}}\right]\right\}}^2}{3}}}$$

(15)

where ω_i and t_i are the numerical weight factor and the normalized coordinate of the ith numerical point. In the two-point Gauss truss model, t₁ = −0.55735 and t₂ = 0.55735; ω₁ = ω₂ = 1.0.

2.4. Calculation Process

The calculation process can be found below:

(1)

Input the geometric dimensions, reinforcement details, and the properties of concrete and steel;

(2)

Calculate the shear resistance of the truss and arch actions V_ct + V_ca by Equations (1)–(7);

(3)

Calculate the shear resistance of the vertical steel web V_ss by Equations (9)–(15);

(4)

Calculate the overall shear strength of SRC beams by V_ct + V_ca + V_ss.

3. Results and Discussions

3.1. Test Database

In this section, a database consisting of 50 SRC beams is established to verify the proposed model, and all these specimens were reported to fail in typical shear [8,10,12,13,23]. The test samples in the database exhibit a range of properties, as follows:

(1)

The compressive strength of concrete varies from 23.3 MPa to 46.6 MPa;

(2)

The yield strength of steel web varies from 265 MPa to 332 MPa;

(3)

The steel shape ratio varies from 2.16% to 6.62%;

(4)

The shear span-to-depth ratio varies from 0.84 to 2.00;

(5)

The width of the cross-section varies from 150 mm to 450 mm;

(6)

The height of the cross-section varies from 240 mm to 650 mm;

(7)

The stirrup ratio varies from 0.00% to 0.52%.

Table 1 presents a summary of the references utilized for conducting the comparison.

Table 1. Test database.

Ref.	Specimen ID	Steel Shape	fyw/MPa	ρss /%	L/mm	b/mm	h/mm	ρsv /%	ρsl /%	fc/MPa	fys/MPa	fyw/MPa	Ve/kN	Vu/kN
[8]	BH1	H450 × 200 × 9 × 14	312	3.80	460	450	550	/	1.32	40.10	/	312	2423	2364
	BH2	H390 × 200 × 10 × 16	330	4.03	460	450	550	/	1.32	40.10	/	330	2399	2353
	BH3	H300 × 200 × 13 × 15	313	3.84	460	450	550	/	1.32	40.10	/	313	2109	2216
	BH4	H200 × 200 × 20 × 12	280	3.36	460	450	550	/	1.32	40.10	/	280	1766	1999
	BWH2	H390 × 200 × 10 × 16	330	4.03	460	450	550	/	1.32	40.10	/	330	2399	2353
	BWH2A	H390 × 200 × 15 × 16	312	4.76	460	450	550	/	1.32	40.10	/	312	2281	2578
	BWH2B	H390 × 200 × 20 × 16	303	5.48	460	450	550	/	1.32	40.10	/	303	2605	2802
[10]	SRC1-00	H300 × 150 × 6.5 × 9	332	2.16	975	350	600	/	1.45	28.90	/	332	772	686
	SRC1-00-T	H300 × 150 × 6.5 × 9	332	2.16	975	350	600	/	1.45	28.90	/	332	751	686
	SRC1-00-E	H300 × 150 × 6.5 × 9	332	2.16	975	350	600	/	1.45	28.90	/	332	799	686
	SRC1-00-D	H300 × 150 × 6.5 × 9	332	2.16	975	350	600	/	1.45	28.90	/	332	695	686
	SRC1-50	H300 × 150 × 6.5 × 9	332	2.16	975	350	600	0.09	1.45	27.70	380	332	861	798
	SRC1-25	H300 × 150 × 6.5 × 9	332	2.16	975	350	600	0.18	1.45	32.20	380	332	877	885
	SRC1-17	H300 × 150 × 6.5 × 9	332	2.16	975	350	600	0.26	1.45	28.90	380	332	923	835
	D1-N	H198 × 99 × 4.5 × 7	325	3.16	338	200	350	0.52	0.36	24.50	407	325	408	373
	D2-FS	H198 × 99 × 4.5 × 7	325	3.16	338	200	350	0.52	0.36	23.90	407	325	415	366
	D3-WS	H198 × 99 × 4.5 × 7	325	3.16	338	200	350	0.52	0.36	23.90	407	325	395	366
	DB1-15-NS	H198 × 99 × 4.5 × 7	325	3.16	338	200	350	0.52	0.36	23.30	407	325	391	359
	DB2-15-NS	H198 × 99 × 4.5 × 7	325	3.16	338	200	350	0.52	0.36	24.50	407	325	409	373
	DB3-NTNS	H198 × 99 × 4.5 × 7	325	3.16	338	200	350	/	0.36	23.70	/	325	396	316
	DB4-15-FS	H198 × 99 × 4.5 × 7	325	3.16	338	200	350	0.52	0.36	23.90	407	325	414	366
	DB5-15-WS	H198 × 99 × 4.5 × 7	325	3.16	338	200	350	0.52	0.36	23.90	407	325	398	366
[11]	PPSRC1	H500 × 200 × 9 × 14	317	3.37	650	450	650	0.16	0.84	24.30	393	317	2170	1898
	PPSRC2	H500 × 200 × 9 × 14	317	3.37	975	450	650	0.16	0.84	24.30	393	317	1600	1388
[12]	B1-1.5	I16	312	4.97	390	200	260	0.28	1.21	27.09	298	312	304	287
	B1-1.5p	I16	312	4.97	390	200	260	0.28	1.21	39.47	298	312	367	341
	B2-1.0	I16	312	4.97	260	200	260	0.28	1.21	34.23	298	312	495	437
	B2-1.5	I16	312	4.97	390	200	260	0.28	1.21	34.23	298	312	342	315
	B2-2.0	I16	312	4.97	520	200	260	0.28	1.21	34.23	298	312	255	261
	B3-1.0	I16	312	5.13	260	200	260	0.28	1.21	44.98	298	312	467	533
	B3-1.5	I16	312	5.13	390	200	260	0.28	1.21	44.98	298	312	373	383
	B3-2.0	I16	312	5.13	520	200	260	0.28	1.21	44.98	298	312	322	300
[13]	SRRAC-1	I16	265	6.62	342	150	300	0.05	1.13	30.00	393	265	379	400
	SRRAC-2	I16	265	6.62	342	150	300	0.05	1.13	26.40	393	265	366	382
	SRRAC-3	I16	265	6.62	228	150	300	0.05	1.13	27.60	393	265	499	510
	SRRAC-4	I16	265	6.62	342	150	300	0.05	1.13	27.60	393	265	371	388
	SRRAC-5	I14	265	6.62	456	150	300	0.05	1.13	27.60	393	265	280	338
	SRRAC-6	I16	283	5.78	342	150	300	0.05	1.13	27.60	393	283	339	378
[23]	SRRC1	I14	327	4.92	240	180	240	0.31	1.18	34.31	339	327	319	305
	SRRC2	I14	327	4.92	336	180	240	0.31	1.18	34.31	339	327	239	239
	SRRC3	I14	327	4.92	432	180	240	0.31	1.18	34.31	339	327	184	207
	SRRC4	I14	327	4.92	240	180	240	0.31	1.18	35.26	339	327	343	309
	SRRC5	I14	327	4.92	336	180	240	0.31	1.18	35.26	339	327	245	242
	SRRC6	I14	327	4.92	432	180	240	0.31	1.18	35.26	339	327	172	207
	SRRC7	I14	327	4.92	240	180	240	0.31	1.18	36.03	339	327	325	313
	SRRC8	I14	327	4.92	336	180	240	0.31	1.18	36.03	339	327	245	245
	SRRC9	I14	327	4.92	432	180	240	0.31	1.18	36.03	339	327	178	208
	SRRC10	I14	327	4.92	240	180	240	0.31	1.18	44.20	339	327	368	359
	SRRC11	I14	327	4.92	240	180	240	0.31	1.18	46.61	393	327	368	373
	SRRC12	I14	327	4.92	240	180	240	0.31	1.18	33.20	393	327	343	299

b is the width of the cross-section; h is the depth of the cross-section; f_c is the concrete strength in compression; f_ys is the yield strength of stirrups; f_yw is the steel web’s yield strength; L is the shear span length; V_e is the experimental shear strength; V_u is the shear strength calculated using the proposed model; ρ_sl is the rebar ratio; ρ_ss is the steel shape ratio; ρ_sv is the stirrup ratio.

3.2. Comparison between Tested and Calculated Results

A comparison was made between the test results and the shear strengths calculated using the proposed model, as shown in Table 1 and Figure 3. The results demonstrate that the established model can predict the shear strength of SRC girders accurately. The average ratio of calculated to tested shear strength (AVG) is 0.98, and its coefficient of variation (CoV) is 0.10. In order to verify the proposed steel-concrete interaction, this section compares the predicted results using the proposed model and the traditional strength superposition. The strength superposition, which is basically applied in code-based shear equations, means V_u = V_ct + V_ca + V_ss,p, in which V_ct + V_ca can be determined by the proposed truss-arch analogy and V_ss,p is the steel web’s shear resistance using plastic analysis (V_ss,p = 0.6f_ywt_wh_w, where h_w is the steel web’s cross-sectional height). Based on strength superposition, the average ratio of predicted results to tested results was found to be 1.44 with a coefficient of variation of 0.12, indicating that the proposed model can achieve higher precision. This comparison highlights the questionable validity of the strength superposition assumption, specifically when considering the steel web as plastic under pure shear. Moreover, the overestimated shear strengths indicate that the resistance along the vertical direction of the steel web is reduced due to the normal stress induced by bending. Therefore, the proposed steel-concrete interaction model, which incorporates strain compatibility, accurately predicts V_ss (the shear strength of the steel web).

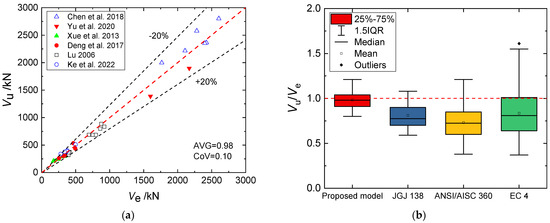
Figure 3. (a) Comparison between tested and calculated results [8,10,11,12,13,23]; (b) Comparison between different shear formulas.

As depicted in Figure 3, a comparative analysis was conducted between the test results and the shear formulas specified in the design guidelines (without coefficients), and the corresponding shear equations can be referred to in Table 2. The calculation results show that the JGJ 138 equation [4] had an AVG of 0.81 and a CoV of 0.18, the ANSI/AISC 360 equation [5] had values of 0.73 and 0.27, and the Eurocode 4 equation [6] had values of 0.74 and 0.31. The comparison indicates that the shear equations based on design codes exhibit a significant level of strength underestimation and a wide scattering of results. While prioritizing higher reliability in the shear strength prediction of SRC members may appear rational due to the brittle failure property, it is crucial to address the issue of excessively underestimated strength predictions. This discrepancy not only results in a significant waste of construction materials but also contradicts the goals of a sustainable environment. Therefore, there is an urgent need to conduct a comprehensive investigation into the shear mechanisms of the SRC beam. As mentioned above, shear equations/models of traditional R.C. members can be employed to evaluate the shear contribution of the concrete encasement; some emerging tool, e.g., deep learning, needs to be involved in the future to predict the shear strength of SRC members [24].

Table 2. Shear formulas in current design codes.

Code	Vu = Vc + Vss
	Vc	Vss
JGJ 138 [4]	$\frac{1.05}{\lambda +1}{f}_{\mathrm{t}}b{h}_0+f_{\mathrm{ys}}\frac{A_{\mathrm{sv}}}{s}{h}_0$	$\frac{0.58}{\lambda }{f}_{\mathrm{yw}}{t}_{\mathrm{w}}{h}_{\mathrm{w}}$
ANSI/AISC-360 [5]	$0.17\sqrt{f_{\mathrm{c}}}b{h}_0+f_{\mathrm{ys}}\frac{A_{\mathrm{sv}}}{s}{h}_0$	$0.60f_{\mathrm{yw}}{t}_{\mathrm{w}}{h}_{\mathrm{w}}$
BS EN 1994-1-1 [6]	$\left[0.18\left(1+\sqrt{2000/9h_0}\right){\left(100{\rho }_{\mathrm{sl}}{f}_{\mathrm{c}}\right)}^{\frac{1}{3}}\right]b{h}_0+0.9f_{\mathrm{ys}}\frac{A_{\mathrm{sv}}}{s}{h}_0\cot \theta$	$0.58f_{\mathrm{yw}}{t}_{\mathrm{w}}{h}_{\mathrm{w}}$

h₀ is the distance from the centroid of the tensile reinforcements to the extreme compression fiber of concrete; f_t is the concrete tensile strength.

In addition, there is another shear model proposed by the authors for predicting the shear strength of SRC models [25]; however, these two models focus on different aspects of shear behavior; this model aims to decouple the shear contributions of the R.C. and encased steel profile, while the other model aims to address the relationship between the shear stiffness of these two parts, which can be better applied in CES beams with high-strength steel. Theoretically, the proposed model should be further refined to adapt to high-strength steel profiles, namely that the steel profile is not yielded at the maximum load; however, the proposed shear model is feasible for current engineering practices. A combination of the two aforementioned models will be established in the future.

4. Conclusions

An innovative shear strength model for SRC girders is put forward in this paper. The principal attributes of the proposed model can be summarized as follows:

(1)

Multiple shear mechanisms, which consist of a vertical steel web and a composite truss, exist to resist the applied shear load. In the proposed model, the shear strength of the composite truss is evaluated using the traditional truss-arch model, and a stress decomposition based on von Mises yielding criterion is conducted within the steel shape to decouple its shear contribution. Finally, the total shear strength can be determined by superimposing the shear contributions of these two mechanisms;

(2)

Through verification with 50 available test results for SRC beams, the proposed model demonstrated its superiority. The predictions generated by the proposed model (with an AVG of 0.98 and a CoV of 0.10) exhibited significantly better agreement with the test results when compared with existing shear equations. For instance, the JGJ 138 equation had an AVG of 0.81 and a CoV of 0.18, the ANSI/AISC 360 equation had values of 0.73 and 0.27, and the Eurocode 4 equation had values of 0.74 and 0.31, indicating that the established model can effectively and reliably predict the shear strength of SRC beams.