Experimental, Theoretical and Numerical Research Progress on Dynamic Behaviors of RC Structural Members
Abstract
1. Introduction
2. Experimental Studies on Dynamic Behaviors of RC Structural Members
2.1. Overview of Dynamic Loading Tests on Structural Members
2.2. Measurement Methods for Dynamic Loading Test
2.3. Summary of Experimental Findings
2.4. Discussion on Dynamic Loading Tests
3. Theoretical Studies on Dynamic Behaviors of RC Structural Members
3.1. Dynamic Modified Model at Material Level
3.2. Dynamic Modified Model at Member Level
3.3. Discussion on Dynamic Modified Models
4. Numerical Studies on Dynamic Behaviors of RC Structural Members
4.1. Overview of Numerical Studies Considering Dynamic Effect
4.2. Numerical Model for Simulating Structural Dynamic Behaviors
4.2.1. Finite Element Model Considering Dynamic Effect
4.2.2. Hysteretic Model Considering Dynamic Effect
4.3. Discussion on Numerical Simulation Works
5. Concluding Remarks
- (1)
- According to the statistical results of available experiments on RC structural members under dynamic loading rates and seismic load, many tests have been performed on RC beams and column members under uniaxial loading schemes and static and dynamic loading rates. As compared with high loading rate tests, the experiments under median loading rates have been inadequate.
- (2)
- In several experimental studies, structural parameters were designed to be different in order to facilitate investigation of their influences on the dynamic behaviors of RC structural members. Most dynamic loading tests measured bearing capacity, displacement, strain, crack development and failure patterns. In addition, seismic damage and energy dissipation were indirectly acquired in a number of experiments.
- (3)
- Based on the results of available dynamic loading tests, the following conclusion was reached: with increased loading rates, the bearing capacity, stiffness and energy dissipation capacity of members were enhanced, while ductility might be reduced, and the degradation of stiffness and bearing capacity aggravated. As for failure mode, research findings have not led to consistency or consensus.
- (4)
- To reflect the influences of loading rates on the mechanical properties of RC materials, the DIF models established on the dynamic loading tests have been the most widely used. By summarizing the DIF models for concrete and reinforcing steel, it was determined that the mechanical behavior parameters for general dynamic modification included compressive strength, tensile strength, elastic modulus of concrete and the yielding strength and ultimate strength of reinforcing steel.
- (5)
- The mechanism of dynamic effects on RC structural members under seismic load could be explained by the strain rate-sensitivity of materials, the inertial effects of members and evolutions of micro-cracks. However, few research works have focused on this issue. Dynamic modified models for mechanical behavior parameters of RC structural members have been developed using finite element (FE) simulation or experimental results. These models considered the influences of loading rates and different structural parameters, and could be directly applied to estimate the dynamic behaviors of RC structural members.
- (6)
- Base on available FE software and self-compiled programs, various numerical methods have been undertaken by researchers to establish FE models to simulate the dynamic behaviors of RC structural members under different loading rates. Moreover, the dynamic hysteretic model established on the dynamic loading test data provided an effective approach to reasonably consider the influences of dynamic effects.
- (7)
- Through comparison with the test data, it was noted that more accurate results could be obtained using numerical models and methods that considered dynamic effects. In a few studies, cracking patterns, damage and failure modes of RC structural members were accurately captured through numerical simulations. Moreover, numerical studies could be applied to a broader range of structural parameters and loading rates, facilitating parametric analyses of the dynamic behaviors of RC structural members.
- (1)
- For dynamic loading tests, more research on RC structural members subjected to multidimensional dynamic loads should be carried out. Moreover, more tests should focus on the influence of dynamic effects on the deformation and damage mechanisms of structural members. Furthermore, in-depth studies are required to elucidate the influence of dynamic effects on structural members with different parameters and failure modes.
- (2)
- Among dynamic modified models, DIF models are the most commonly used to consider the impact of dynamic effects on RC structural members. Due to randomness in structural members and external dynamic loads, the capability of dynamic modification, at the material level, to reliably reflect dynamic effects at the member level should be verified. In addition, the suitability and accuracy of the models proposed at the member level need to be improved based on supplementary data test data and advanced theoretical methodologies.
- (3)
- For numerical simulation analysis, researchers should refine the available FE numerical models of RC structural members by incorporating shear and bond-slip behaviors with their consideration of dynamic effects. Moreover, more effort should be applied to improving model applicability and computational efficiency. Furthermore, the seismic damage evolution and failure mechanisms of RC structural members and structures must be deeply investigated, utilizing refined models and methods for numerical simulation.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Cao, X.-Y.; Feng, D.-C.; Li, Y. Assessment of various seismic fragility analysis approaches for structures excited by non-stationary stochastic ground motions. Mech. Syst. Signal Process. 2023, 186, 109838. [Google Scholar] [CrossRef]
- Fu, H.C.; Erki, M.A.; Seckin, M. Review of Effects of Loading Rate on Concrete in Compression. J. Struct. Eng. 1991, 117, 3645–3659. [Google Scholar] [CrossRef]
- Li, H.; Huo, L. Multiaxial Seismic Dynamic Effect of RC Structure; Science Press: Beijing, China, 2021. [Google Scholar]
- Wang, D.B.; Fan, G.X.; Zhang, H. Dynamic behaviors of reinforced concrete columns under multi-dimensional dynamic loadings. J. Vib. Shock. 2016, 35, 35–41. [Google Scholar]
- Song, Y.; Wang, J.; Han, Q. Dynamic performance of flexure-failure-type rectangular RC columns under low-velocity lateral impact. Int. J. Impact Eng. 2023, 175, 104541. [Google Scholar] [CrossRef]
- Witarto, W.; Lu, L.; Roberts, R.H.; Mo, Y.L.; Lu, X. Shear-critical reinforced concrete columns under various loading rates. Front. Struct. Civ. Eng. 2014, 8, 362–372. [Google Scholar] [CrossRef]
- Reinschmidt, K.F.; Hansen, R.J.; Yang, C.Y. Dynamic tests of reinforced concrete columns. J. Proc. 1964, 61, 317–334. [Google Scholar]
- Adhikary, S.D.; Li, B.; Fujikake, K. Dynamic behavior of reinforced concrete beams under varying rates of concentrated loading. Int. J. Impact Eng. 2012, 47, 24–38. [Google Scholar] [CrossRef]
- Hongnan, L.; Li, M. Dynamic test and numerical simulation of reinforced concrete beams. J. Vib. Shock. 2015, 34, 110–115. [Google Scholar]
- Adhikary, S.D.; Li, B.; Fujikake, K. Effects of high loading rate on reinforced concrete beams. Aci Struct. J. 2014, 111, 651–660. [Google Scholar] [CrossRef]
- Li, M.; Li, H.N. Effects of Loading Rate on Reinforced Concrete Beams. In Proceedings of the 15th World Conference on Earthquake Engineering, Lisboa, Portugal, 24–28 September 2011. [Google Scholar]
- Xiao, S.; Zhang, H. Effects of Loading Rate on the Shear Behaviors of RC Beams. J. Water Resour. Archit. Eng. 2018, 16, 7–13+19. [Google Scholar]
- Marder, K.J.; Motter, C.J.; Elwood, K.J.; Clifton, G.C. Effects of variation in loading protocol on the strength and deformation capacity of ductile reinforced concrete beams. Earthq. Eng. Struct. Dyn. 2018, 47, 2195–2213. [Google Scholar] [CrossRef]
- Fujikake, K.; Li, B.; Soeun, S. Impact response of reinforced concrete beam and its analytical evaluation. J. Struct. Eng. 2009, 135, 938–950. [Google Scholar] [CrossRef]
- Adhikary, S.D.; Li, B.; Fujikake, K. Strength and behavior in shear of reinforced concrete deep beams under dynamic loading conditions. Nucl. Eng. Des. 2013, 259, 14–28. [Google Scholar] [CrossRef]
- Xu, B.; Chen, J.M.; Xu, N. Test on strain rate effects and its simulation with dynamic damaded plasticity model for RC shear walls. Eng. Mech. 2012, 29, 39–287. [Google Scholar]
- Zhang, X. Effects of Loading Rates on Seismic Behavior of Reinforced Concrete High Shear Walls. Master’s Thesis, Dalian University of Technology, Dalian, China, 2012. [Google Scholar]
- Yupu, S.; Xiaoli, Z. Influence of Strain Rate on Earthquake Resistance Effect of Reinforced Concrete Shear Wall. Ind. Constr. 2012, 42, 7–11. [Google Scholar]
- Xu, N. Study on the Performance Test and Numerical Simulation of Reinforced Concrete Shear Wall under Rapid Loading. Ph.D. Thesis, Hunan University, Changsha, China, 2012. [Google Scholar]
- Chung, L.; Shah, S.P. Effect of loading rate on anchorage bond and beam-column joints. Struct. J. 1989, 86, 132–142. [Google Scholar]
- Wang, L.; Fan, G.; Qin, Q.; Song, Y. Experimental study on seismic behavior of reinforced concrete frame joints with consideration of strain rate effect. J. Build. Struct. 2014, 35, 38. [Google Scholar]
- Guoxi, F.; Yupu, S.; Licheng, W. Study on the Seismic Performance of Reinforced Concrete Beam-Coulumn Joints under Different Strain Rates. Ind. Constr. 2014, 44, 1. [Google Scholar]
- Pan, H. Effects of Strain Rate Sensitivity on Dynamic Properties of Reinforced Concrete Materials and Beam-Column Joints. Master’s Thesis, Dalian University of Technology, Dalian, China, 2012. [Google Scholar]
- Qin, Q. Study on Seismic Behavior of Reinforced Concrete Frame Joints with the Consideration of Strain Rate Effect. Master’s Thesis, Dalian University of Technology, Dalian, China, 2013. [Google Scholar]
- Asprone, D.; Frascadore, R.; Ludovico, M.D.; Prota, A.; Manfredi, G. Influence of strain rate on the seismic response of RC structures. Eng. Struct. 2012, 35, 29–36. [Google Scholar] [CrossRef]
- Wang, W. Study on the Seismic Analysis Method of Structure Considering Strain Rate Effect. Ph.D. Thesis, Dalian University of Technology, Dalian, China, 2013. [Google Scholar]
- Liu, H.; Li, H. Seismic-Collapse Analysis of Reinforced Concrete Frame Structure Considering Cumulative Damage and Strain Rate Effect. Eng. Mech. 2018, 35, 87. [Google Scholar] [CrossRef]
- Li, H.N.; Li, R.H.; Li, C.; Wang, D.B. Development of hysteretic model with dynamic effect and deterioration for seismic-performance analysis of reinforced concrete structures. J. Struct. Eng. 2020, 146, 04020215. [Google Scholar] [CrossRef]
- CEB. CEB-FIP Model Code 1990, First Draft; CEB Bull. Committee Euro-International du Beton: Lausanne, Switzerland, 1990; p. 195. [Google Scholar]
- Lin, F.; Gu, X.; Kuang, X.; Yin, X. Constitutive Models for Reinforcing Steel Barsunder High Strain Rates. J. Build. Mater. 2008, 11, 14–20. [Google Scholar]
- Li, M. Effects of Rate-Dependent Properties of Material on Dynamic Properties of Reinforced Concrete Structural. Ph.D. Thesis, Dalian University of Technology, Dalian, China, 2011. [Google Scholar]
- Ross, C.A.; Tedesco, J.W.; Kuennen, S.T. Effects of Strain-Rate on Concrete Strength. Aci. Mater. J. 1995, 92, 37–47. [Google Scholar]
- Li, R. Study on Seismic Performance of Reinforced Concrete Structure Considering Dynamic Effects. Ph.D. Thesis, Dalian University of Technology, Dalian, China, 2020. [Google Scholar]
- Rouchette, A.; Zhang, W.P.; Chen, H. Simulation of Flexural Behavior of Reinforced Concrete Beams under Impact Loading. Appl. Mech. Mater. 2013, 351–352, 1018–1023. [Google Scholar] [CrossRef]
- Ghannoum, W.; Saouma, V.; Haussmann, G.; Polkinghorne, K.; Eck, M.; Kang, D.H. Experimental investigations of loading rate effects in reinforced concrete columns. J. Struct. Eng. 2012, 138, 1032–1041. [Google Scholar] [CrossRef]
- Thomas, R.J.; Sorensen, A.D. Review of strain rate effects for UHPC in tension. Constr. Build. Mater. 2017, 153, 846–856. [Google Scholar] [CrossRef]
- Gholipour, G.; Zhang, C.; Mousavi, A.A. State-of-the-Art Review on Responses of RC Structures Subjected to Lateral Impact Loads. Arch. Comput. Methods Eng. 2020, 28, 2477–2507. [Google Scholar]
- Hao, H.; Hao, Y.; Li, J.; Chen, W. Review of the current practices in blast-resistant analysis and design of concrete structures. Adv. Struct. Eng. 2016, 19, 1193–1223. [Google Scholar] [CrossRef]
- Ullah, A.; Ahmad, F.; Jang, H.W.; Kim, S.W.; Hong, J.W. Review of analytical and empirical estimations for incident blast pressure. KSCE J. Civ. Eng. 2017, 21, 2211–2225. [Google Scholar] [CrossRef]
- Das, N.; Nanthagopalan, P. State-of-the-art review on ultra high performance concrete—Ballistic and blast perspective. Cem. Concr. Compos. 2022, 127, 104383. [Google Scholar] [CrossRef]
- Bertero, V.; Rea, D.; Mahin, S.; Atalay, M. Rate of loading effects on uncracked and repaired reinforced concrete members. In Proceedings of the Fifth World Conference on Earthquake Engineering, Rome, Italy, 25–29 June 1973; pp. 1461–1470. [Google Scholar]
- Kulkarni, S.M.; Shah, S.P. Response of reinforced concrete beams at high strain rates. ACI Struct. J. 1998, 95, 705–715. [Google Scholar]
- White, T.W.; Soudki, K.A.; Erki, M.A. Response of RC Beams Strengthened with CFRP Laminates and Subjected to a High Rate of Loading. J. Compos. Constr. 2001, 5, 153–162. [Google Scholar] [CrossRef]
- Zhang, X.X.; Ruiz, G.; Yu, R.C. Experimental study of combined size and strain rate effects on the fracture of reinforced concrete. J. Mater. Civ. Eng. 2008, 20, 544–551. [Google Scholar] [CrossRef]
- GuiLan, Y. The Research on Strain Rate Effect of Dynamic Behaviors of Reinforced Concrete Remembers. Master’s Thesis, Harbin Institute of Technology, Harbin, China, 2010. [Google Scholar]
- Shiyun, X.; Wenbo, C.; Haohao, P. Experimental study on mechanical behavior of reinforced concrete beams at different loading rates. J. Build. Struct. 2012, 33, 142–146. [Google Scholar]
- Zhou, H.; Xing, X.; Xie, Y.; Yuan, H. Experimental Study on Dynamic Loading Size Effect of RC Beam-Column. J. Basic Sci. Eng. 2020, 28, 1187–1196. [Google Scholar]
- Otani, S.; Kaneko, T.; Shiohara, H. Strain Rate Effect on Performance of Reinforced Concrete Members; Kajima Technical Research Institute, Kajima Corporation: Tokyo, Japan, 2003. [Google Scholar]
- Guo, J.; Cai, J.; Chen, Q.; Liu, X.; Wang, Y.; Zuo, Z. Dynamic behaviour and energy dissipation of reinforced recycled aggregate concrete beams under impact. Constr. Build. Mater. 2019, 214, 143–157. [Google Scholar] [CrossRef]
- Wu, X.-Q.; Zhong, B.; Lv, Y.; Li, Z.-X.; Chouw, N. Experimental Study on Dynamic Amplification Factor of Simple-Supported Reinforced Concrete Beams Under Impact Loading Generated by an Impulse Hammer. Int. J. Struct. Stab. Dyn. 2020, 21, 2150036. [Google Scholar] [CrossRef]
- Adhikary, S.D.; Li, B.; Fujikake, K. Residual resistance of impact damaged reinforced concrete beams. Mag. Concr. Res. 2015, 67, 364–378. [Google Scholar] [CrossRef]
- Zeng, X. Experimental and Numerical Study of Behaviors of RC Beams and Columns under Impact Loadings and Rapid Loadings. Ph.D. Thesis, Hunan University, Changsha, China, 2014. [Google Scholar]
- Feng, Z.; Wang, X.; Zhang, S.; Chu, Y. Experimental investigation on cantilever square CFST columns under lateral continuous impact loads. J. Constr. Steel Res. 2022, 196, 107416. [Google Scholar] [CrossRef]
- Mutsuyoshi, H.; Machida, A. Dynamic properties of reinforced concrete piers. In Proceedings of the 8th World Conference on Earthquake Engineering, San Francisco, CA, USA, 21–28 July 1984. [Google Scholar]
- Fukuda, T.; Sanuki, S.; Miyakawa, M.; Fujikake, K. Influence of loading rate on shear failure resistance of RC beams. Appl. Mech. Mater. 2011, 82, 229–234. [Google Scholar] [CrossRef]
- Yuan, J.; Weijian, Y.I. Tests for effects of loading rate on shear behaviors of RC beams. J. Vib. Shock. 2019, 38, 119–127. [Google Scholar]
- Ye, J.-B.; Cai, J.; Chen, Q.-J.; Liu, X.; Tang, X.-L.; Zuo, Z.-L. Experimental investigation of slender RC columns under horizontal static and impact loads. Structures 2020, 24, 499–513. [Google Scholar] [CrossRef]
- Xiang, S.; Zeng, L.; Liu, Y.; Mo, J.; Ma, L.; Zhang, J.; Chen, J. Experimental study on the dynamic behavior of T-shaped steel reinforced concrete columns under impact loading. Eng. Struct. 2020, 208, 110307. [Google Scholar] [CrossRef]
- Gutierrez, E.; Magonette, G.; Verzeletti, G. Experimental studies of loading rate effects on reinforced concrete columns. J. Eng. Mech. 1993, 119, 887–904. [Google Scholar] [CrossRef]
- Bousias, S.N.; Verzeletti, G.; Fardis, M.N.; Gutierrez, E. Load-Path Effects in Column Biaxial Bending with Axial Force. J. Eng. Mech. 1995, 121, 596–605. [Google Scholar] [CrossRef]
- Li, B.; Park, R.; Tanaka, H. Constitutive behaviour of high strength concrete under dynamic loading. ACI Struct. J. 2000, 97, 619–629. [Google Scholar]
- Perry, S.H.; Alshaikh, A.H.; Cheong, H.K. Influence of strain rate on laterally confined concrete columns subjected to cyclic loading. J. Mater. Res. 1986, 1, 382–389. [Google Scholar] [CrossRef]
- Zou, D.J.; Liu, T.J.; Teng, J.; Yan, G.L. Strain rate effect on uniaxial compressive behaviour of concrete columns. J. Vib. Shock. 2012, 31, 145–150. [Google Scholar]
- Wang, D.B. Dynamic Effects on Seismic Behavior of Reinforced Concrete Column. Ph.D. Thesis, Dalian University of Technology, Dalian, China, 2013. [Google Scholar]
- Jiang, Z. Dynamic Loading Experiment and Numerical Simulation Study on Reinforced Concrete Columns. Master’s Thesis, Hunan University, Changsha, China, 2012. (In Chinese). [Google Scholar]
- Liu, B.; Fan, W.; Guo, W.; Chen, B.S.; Liu, R. Experimental investigation and improved FE modeling of axially-loaded circular RC columns under lateral impact loading. Eng. Struct. 2017, 152, 619–642. [Google Scholar] [CrossRef]
- Liu, L.; Zong, Z.; Ma, Z.J.; Qian, H.; Gan, L. Experimental Study on Behavior and Failure Mode of PSRC Bridge Pier under Close-In Blast Loading. J. Bridge Eng. 2021, 26, 04020124. [Google Scholar] [CrossRef]
- Lee, T.-H.; Choi, S.-J.; Yang, D.-H.; Kim, J.-H.J. Experimental Seismic Structural Performance Evaluations of RC Columns Strengthened by Stiff-Type Polyurea. Int. J. Concr. Struct. Mater. 2022, 16, 65. [Google Scholar] [CrossRef]
- Wei, J.; Li, J.; Wu, C. An experimental and numerical study of reinforced conventional concrete and ultra-high performance concrete columns under lateral impact loads. Eng. Struct. 2019, 201, 109822. [Google Scholar] [CrossRef]
- Fan, W.; Shen, D.; Yang, T.; Shao, X. Experimental and numerical study on low-velocity lateral impact behaviors of RC, UHPFRC and UHPFRC-strengthened columns. Eng. Struct. 2019, 191, 509–525. [Google Scholar] [CrossRef]
- Orozco, G.; Ashford, S. Effects of Large Velocity Pulses on Reinforced Concrete Bridge Columns; PEER Report 2002/23; Pacific Earthquake Engineering Research Center, University of California: Berkeley, CA, USA, 2002. [Google Scholar]
- Shah, S.P.; Wang, M.L.; Lan, C. Model concrete beam-column joints subjected to cyclic loading at two rates. Mater. Struct. 1987, 20, 85–95. [Google Scholar] [CrossRef]
- Gibson, N. Performance of Beam to Column Bridge Joints Subjected to a Large Velocity Pulse; PEER Report 2002/24; Pacific Earthquake Engineering Research Center, University of California: Berkeley, CA, USA, 2002. [Google Scholar]
- Fan, G.X. Study on the Dynamic Mechanical Properties of Reinforced Concrete Beam-Column Joints. Ph.D. Thesis, Dalian University of Technology, Dalian, China, 2015. [Google Scholar]
- Wang, L.; Qin, Q.; Fan, G.; Song, Y. Finite element analysis on mechanical behavior of reinforced concrete beam-column joint considering strain rate effect. J. Build. Struct. 2014, 35, 131. [Google Scholar]
- Chiu, C.K.; Sung, H.F.; Chiou, T.C. Experimental quantification of seismic damage for RC infill walls using static and dynamic loading test. J. Build. Eng. 2022, 50, 104177. [Google Scholar] [CrossRef]
- Yılmaz, T.; Kıraç, N.; Anil, Ö.; Erdem, R.T.; Kaçaran, G. Experimental Investigation of Impact Behaviour of RC Slab with Different Reinforcement Ratios. KSCE J. Civ. Eng. 2019, 24, 241–254. [Google Scholar] [CrossRef]
- Wang, D.B.; Li, H.N.; Li, G. Experimental study on dynamic mechanical properties of reinforced concrete column. J. Reinf. Plast. Compos. 2013, 32, 1793–1806. [Google Scholar] [CrossRef]
- Long, Y. Study on Fast Loading Test and Dynamic Hysteresis Law of Reinforced Concrete Column. Master’s Thesis, Hunan University, Changsha, China, 2010. [Google Scholar]
- Zhang, H. Strain Rate Effect of Materials on Seismic Response of Reinforced Concrete Frame-Wall Structure. Master’s Thesis, Dalian University of Technology, Dalian, China, 2012. [Google Scholar]
- Liu, L. Study on Seismic Behavior of RC Columns in Flexural-Shear Failure. Ph.D. Thesis, Hunan University, Changsha, China, 2018. [Google Scholar]
- Wang, D.B.; Li, H.N.; Li, G. Experimental tests on reinforced concrete columns under multi-dimensional dynamic loadings. Constr. Build. Mater. 2013, 47, 1167–1181. [Google Scholar] [CrossRef]
- Wang, D.; Li, H. Effects of strain rate on dynamic behavior of reinforced concrete column. J. Earthq. Eng. Eng. Vib. 2011, 31, 67–72. [Google Scholar]
- Zielinski, A.J.; Reinhardt, H.W.; Körmeling, H.A. Experiments on concrete under uniaxial impact tensile loading. Matériaux Constr. 1981, 14, 103–112. [Google Scholar] [CrossRef]
- Yon, J.H.; Hawkins, N.M.; Kobayashi, A.S. Strain-rate sensitivity of concrete mechanical properties. ACI Mater. J. 1992, 89, 146–153. [Google Scholar]
- Cadoni, E.; Labibes, K.; Berra, M. High-strain-rate tensile behaviour of concrete. Mag. Concr. Res. 2000, 52, 365–370. [Google Scholar] [CrossRef]
- Lin, G.; Yan, D.; Yuan, Y. Response of concrete to dynamic elevated-amplitude cyclic tension. ACI Mater. J. 2007, 104, 561. [Google Scholar]
- Chen, X.; Bu, J.; Xu, L. Effect of strain rate on post-peak cyclic behavior of concrete in direct tension. Constr. Build. Mater. 2016, 124, 746–754. [Google Scholar] [CrossRef]
- Yan, D.; Lin, G.; Wang, Z.; Zhang, Y. A Study on Direct Tensile Properties of Concrete at Different Strain Rates. China Civ. Eng. J. 2005, 38, 97–103. [Google Scholar]
- Xiao, S.; Tian, Z. Experimental study on the uniaxial dynamic tensile damage of concrete. China Civ. Eng. J. 2008, 41, 14–20. [Google Scholar]
- Chen, Y.; Wang, Y.; Chen, X. Experimental research on effects of strain rate on tensile stress-strain curve of concrete in axial tension condition. Build. Struct. 2015, 45, 4. [Google Scholar]
- Yan, D.M.; Lin, G. Experimental Study on the Uniaxial Dynamic Compression Properties of Concrete. Water Sci. Eng. Technol. 2005, 6, 8–10. [Google Scholar]
- Goldsmith, W. Dynamic behavior of concrete. Exp. Mech. 1966, 6, 65–79. [Google Scholar] [CrossRef]
- Watson, A.J.; Hughes, B.P. Compressive strength and ultimate strain of concrete under impact loading. Mag. Concr. Res. 1978, 30, 189–199. [Google Scholar]
- Grote, D.L.; Park, S.W.; Zhou, M. Dynamic behavior of concrete at high strain rates and pressures: I. experimental characterization. Int. J. Impact Eng. 2001, 25, 869–886. [Google Scholar] [CrossRef]
- Sun, J.S.; Ma, L.J.; Dou, Y.M.; Zhou, J. Effect of strain rate on the compressive mechanical properties of concrete. Adv. Mater. Res. 2012, 450–451, 244–247. [Google Scholar] [CrossRef]
- Guo, Y.B.; Gao, G.F.; Jing, L.; Shim, V.P.W. Response of high-strength concrete to dynamic compressive loading. Int. J. Impact Eng. 2017, 108, 114–135. [Google Scholar] [CrossRef]
- Dong, Y.; Xie, H.; Zhao, P. Experimental study and constitutive model of the whole process of concrete compression under different strain rates. J. Hydraul. Eng. 1997, 7, 72–77. [Google Scholar]
- Chang, K.C.; Lee, G.C. Strain rate effect on structural steel under cyclic loading. J. Eng. Mech. 1987, 113, 1292–1301. [Google Scholar] [CrossRef]
- Restrepo-Posada, J.I.; Dodd, L.L.; Park, R.; Cooke, N. Variables affecting cyclic behavior of reinforcing steel. J. Struct. Eng. 1994, 120, 3178–3196. [Google Scholar] [CrossRef]
- Soroushian, P.; Choi, K.B. Steel mechanical properties at different strain rates. J. Struct. Eng. 1987, 113, 663–672. [Google Scholar] [CrossRef]
- Cadoni, E.; Fenu, L.; Forni, D. Strain rate behaviour in tension of austenitic stainless steel used for reinforcing bars. Constr. Build. Mater. 2012, 35, 399–407. [Google Scholar] [CrossRef]
- Li, M.; Li, H. Dynamic test and constitutive model for reinforcing steel. China Civ. Eng. J. 2010, 43, 70–75. [Google Scholar]
- Reinhardt, H.W.; Rossi, P.; Mier, J.G.M.V. Joint investigation of concrete at high rates of loading. Mater. Struct. 1990, 23, 213–216. [Google Scholar] [CrossRef]
- Ross, C.A.; Jerome, D.M.; Tedesco, J.W.; Hughes, M.L. Moisture and strain rate effects on concrete strength. ACI Mater. J. 1996, 93, 293–300. [Google Scholar]
- Cadoni, E.; Labibes, K.; Albertini, C.; Berra, M.; Giangrasso, M. Strain-rate effect on the tensile behaviour of concrete at different relative humidity levels. Mater. Struct. 2001, 34, 21. [Google Scholar] [CrossRef]
- Ranjith, P.G.; Jasinge, D.; Song, J.Y.; Choi, S.K. A study of the effect of displacement rate and moisture content on the mechanical properties of concrete: Use of acoustic emission. Mech. Mater. 2008, 40, 453–469. [Google Scholar] [CrossRef]
- Filiatrault, A.; Holleran, M. Stress-strain behavior of reinforcing steel and concrete under seismic strain rates and low temperatures. Mater. Struct. 2001, 34, 235–239. [Google Scholar] [CrossRef]
- Yan, D.M.; Xu, W. Strain-rate sensitivity of concrete: Influence of temperature. Adv. Mater. Res. 2011, 243–249, 453–456. [Google Scholar] [CrossRef]
- Pajak, M. The influence of the strain rate on the strength of concrete taking into account the experimental techniques. Laval Théologique Philos. 2011, 39, 423–428. [Google Scholar]
- Chen, X.; Wu, S.; Zhou, J.; Chen, Y.; Qin, A. Effect of testing method and strain rate on stress-strain behavior of concrete. J. Mater. Civ. Eng. 2013, 25, 1752–1761. [Google Scholar] [CrossRef]
- Bischoff, P.H.; Perry, S.H. Compressive behaviour of concrete at high strain rates. Mater. Struct. 1991, 24, 425–450. [Google Scholar] [CrossRef]
- Barpi, F. Impact behaviour of concrete: A computational approach. Eng. Fract. Mech. 2004, 71, 2197–2213. [Google Scholar] [CrossRef]
- Georgin, J.F.; Reynouard, J.M. Modeling of structures subjected to impact: Concrete behavior under high strain rate. Cem. Concr. Compos. 2003, 25, 131–143. [Google Scholar] [CrossRef]
- Lorefice, R.; Etse, G.; Carol, I. Viscoplastic approach for rate-dependent failure analysis of concrete joints and interfaces. Int. J. Solids Struct. 2008, 45, 2686–2705. [Google Scholar] [CrossRef]
- Pedersen, R.R.; Simone, A.; Sluys, L.J. An analysis of dynamic fracture in concrete with a continuum visco-elastic visco-plastic damage model. Eng. Fract. Mech. 2008, 75, 3782–3805. [Google Scholar] [CrossRef]
- Eibl, J.; Schmidt-Hurtienne, B. Strain-rate-sensitive constitutive law for concrete. J. Eng. Mech. 1999, 125, 1411–1420. [Google Scholar] [CrossRef]
- Ragueneau, F.; Gatuingt, F. Inelastic behavior modelling of concrete in low and high strain rate dynamics. Comput. Struct. 2003, 81, 1287–1299. [Google Scholar] [CrossRef]
- Ren, X.D.; Li, J. Stochastic damage constitutive model for concrete considering strain rate effect. Key Eng. Mater. 2009, 400–402, 251–256. [Google Scholar] [CrossRef]
- Hao, Y.; Hao, H. Influence of the concrete DIF model on the numerical predictions of RC wall responses to blast loadings. Eng. Struct. 2014, 73, 24–38. [Google Scholar] [CrossRef]
- Lee, S.; Kim, K.M.; Cho, J.Y. Investigation into pure rate effect on dynamic increase factor for concrete compressive strength. Proc. Eng. 2017, 210, 11–17. [Google Scholar] [CrossRef]
- Malvar, L.J. Review of Static and Dynamic Properties of Steel Reinforcing Bars. ACI Mater. J. 1998, 95, 609–616. [Google Scholar]
- Tedesco, J.W.; Ross, C.A. Strain-rate-dependent constitutive equations for concrete. J. Press. Vessel. Technol. 1998, 120, 398–405. [Google Scholar] [CrossRef]
- Xiao, S.; Zhang, J. Experimental study on dynamic compression of concrete under load history. J. Dalian Univ. Technol. 2011, 51, 6. [Google Scholar]
- Johnson, G.R.; Cook, W.H. A Constitutive Model and Data for Metals Subjected to Large Strains, High Strain Rates and High Temperatures. In Proceedings of the 7th International Symposium on Ballistics, Hague, The Netherlands, 19–21 April 1983; pp. 541–547. [Google Scholar]
- Morquio, A.; Riera, J.D. Size and strain rate effects in steel structures. Eng. Struct. 2004, 26, 669–679. [Google Scholar] [CrossRef]
- Rodríguez-Martínez, J.A.; Rusinek, A.; Klepaczko, J.R. Constitutive relation for steels approximating quasi-static and intermediate strain rates at large deformations. Mech. Res. Commun. 2009, 36, 419–427. [Google Scholar] [CrossRef]
- Cotsovos, D.M.; Stathopoulos, N.D.; Zeris, C.A. Behavior of RC beams subjected to high rates of concentrated loading. J. Struct. Eng. 2008, 134, 1839–1851. [Google Scholar] [CrossRef]
- Xiao, S.; Xu, D. Influence of strain rate effect on reinforced concrete column. J. Disaster Prev. Mitig. Eng. 2009, 29, 668–675. [Google Scholar]
- Zhan, T.; Wang, Z.; Ning, J. Failure behaviors of reinforced concrete beams subjected to high impact loading. Eng. Fail. Anal. 2015, 56, 233–243. [Google Scholar] [CrossRef]
- Valipour, H.R.; Luan, H.; Foster, S.J. Analysis of RC beams subjected to shock loading using a modified fibre element formulation. Comput. Concr. 2009, 6, 377–390. [Google Scholar] [CrossRef]
- Xu, B.; Liang, T.; Long, Y. Strain rate effects on dynamic behavior of reinforcement concrete columns with various reinforcement ratio. J. Civ. Archit. Environ. Eng. 2012, 47, 24–38. [Google Scholar]
- Sharma, A.; Ožbolt, J. Influence of high loading rates on behavior of reinforced concrete beams with different aspect ratios—A numerical study. Eng. Struct. 2014, 79, 297–308. [Google Scholar] [CrossRef]
- Xiao, S.Y. Numerical study of dynamic behaviour of RC beams under cyclic loading with different loading rates. Mag. Concr. Res. 2015, 67, 325–334. [Google Scholar] [CrossRef]
- Li, R.H.; Li, H.N.; Li, C. Seismic performance assessment of RC frame structures subjected to far-field and near-field ground motions considering strain rate effect. Int. J. Struct. Stab. Dyn. 2018, 18, 1850127. [Google Scholar] [CrossRef]
- Zhang, H.; Li, H.N.; Li, C.; Cao, G.W. Experimental and numerical investigations on seismic responses of reinforced concrete structures considering strain rate effect. Constr. Build. Mater. 2018, 173, 672–686. [Google Scholar] [CrossRef]
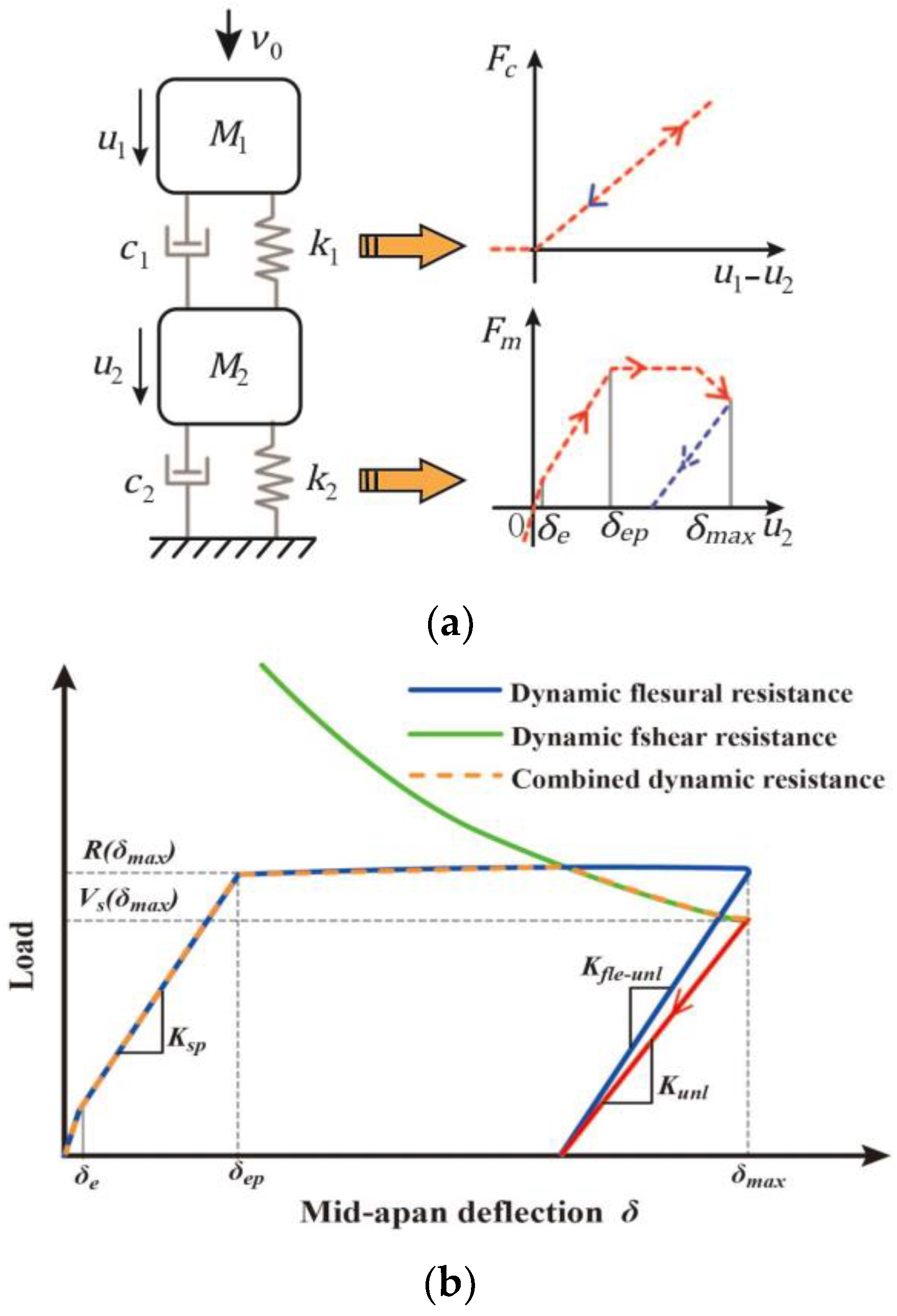
- Jia, P.C.; Wu, H.; Fang, Q. An improved 2DOF model for dynamic behaviors of RC members under lateral low-velocity impact. Int. J. Impact Eng. 2023, 173, 104460. [Google Scholar] [CrossRef]
- Yang, Z. Numerical Simulation Study on the Dynamic Mechanical Behaviors of Reinforced Concrete Shear Walls. Master’s Thesis, Dalian University of Technology, Dalian, China, 2019. [Google Scholar]
- Zhao, D.B.; Yi, W.J.; Kunnath, S.K. Numerical simulation and shear resistance of reinforced concrete beams under impact. Eng. Struct. 2018, 166, 387–401. [Google Scholar] [CrossRef]
- Li, R.H.; Li, C.; Li, H.N.; Yang, G.; Zhang, P. Improved estimation on seismic behavior of RC column members: A probabilistic method considering dynamic effect and structural parameter uncertainties. Struct. Saf. 2023, 101, 102308. [Google Scholar] [CrossRef]
- Stochino, F.; Carta, G. SDOF models for reinforced concrete beams under impulsive loads accounting for strain rate effects. Nucl. Eng. Des. 2014, 276, 74–86. [Google Scholar] [CrossRef]
- Krauthammer, T.; Shanaa, H.M.; Assadi, A. Response of structural concrete elements to severe impulsive loads. Comput. Struct. 1994, 53, 119–130. [Google Scholar] [CrossRef]
- Shi, Y.; Li, Z.X.; Hao, H. Bond slip modelling and its effect on numerical analysis of blast-induced responses of RC columns. Struct. Eng. Mech. 2009, 32, 251–267. [Google Scholar] [CrossRef]
- Guner, S.; Vecchio, F.J. Analysis of shear-critical reinforced concrete plane frame elements under cyclic loading. J. Struct. Eng. 2011, 137, 834–843. [Google Scholar] [CrossRef]
- Li, H.; Chen, W.; Hao, H. Dynamic response of precast concrete beam with wet connection subjected to impact loads. Eng. Struct. 2019, 191, 247–263. [Google Scholar] [CrossRef]
- Jin, L.; Lan, Y.; Zhang, R.; Du, X. Impact resistance of RC beams under different combinations of mass and velocity: Mesoscale numerical analysis. Arch. Civ. Mech. Eng. 2020, 20, 119. [Google Scholar] [CrossRef]
- Clough, R.W. Effect of Stiffness Degradation on Earthquake Ductility Requirements. In Proceedings of Japan Earthquake Engineering Symposium; Macuze Company: Macuse, Mozambique, 1966. [Google Scholar]
- Takeda, T. Reinforced Concrete Response to Simulated Earthquakes. J. Struct. Div. Proc. Am. Soc. Civ. Eng. 1970, 96, 2557–2573. [Google Scholar] [CrossRef]
- Ozcebe, G.; Saatcioglu, M. Hysteretic shear model for reinforced concrete members. J. Struct. Eng. 1989, 115, 132–148. [Google Scholar] [CrossRef]
- Park, Y.J.; Ang, A.H.S. Mechanistic seismic damage model for reinforced concrete. J. Struct. Eng. 1985, 111, 722–739. [Google Scholar] [CrossRef]
- Wen, Y.K. Method for Random Vibration of Hysteretic Systems. J. Eng. Mech. Div. 1976, 102, 249–263. [Google Scholar] [CrossRef]
- Takayanagi, T.; Schnobrich, W.C. Non-linear analysis of coupled wall systems. Earthq. Eng. Struct. Dyn. 2010, 7, 1–22. [Google Scholar] [CrossRef]
- Saatcioglu, M.; Alsiwat, J.M.; Ozcebe, G. Hysteretic Behavior of Anchorage Slip in R/C Members. J. Struct. Eng. 1992, 118, 2439–2458. [Google Scholar] [CrossRef]
- Xu, S.Y. Modeling Axial-Shear-Flexure Interaction of RC Columns for Seismic Response Assessment of Bridges. Ph.D. Thesis, University of California, Los Angeles, CA, USA, 2010. [Google Scholar]
- Qu, Z.; Ye, L. Strength Deterioration Model Based on Effective Hysteretic Energy Dissipation for RC members under Cyclic Loading. Eng. Mech. 2011, 28, 45–051. [Google Scholar]
- D’Ambrisi, A.; Filippou, F.C. Modeling of cyclic shear behavior in RC members. J. Struct. Eng. 1999, 125, 1143–1150. [Google Scholar] [CrossRef]
- Gu, X.; Huang, Q.; Wu, Z. Analysis of load-displacement relationship for RC columns under reversed load considering accumulative damage. Earthq. Eng. Eng. Vib. 2006, 24, 7. [Google Scholar]
- Zheng, H.; Zheng, S.; He, J.; Zhang, Y.; Shang, Z. Research on restoring force model of reinforced concrete rectangular beams considering reinforcement corrosion. J. Cent. South Univ. Sci. Technol. 2020, 51, 10. [Google Scholar]
- Zheng, S.; Rong, X.; Zhang, Y.; Dong, L. Restoring force model of freeze-thaw injury reinforced concrete shear walls. Huazhong Univ. Sci. Technol. Nat. Sci. Ed. 2019, 47, 6. [Google Scholar]
- Erberik, M.A. Importance of Degrading Behavior for Seismic Performance Evaluation of Simple Structural Systems. J. Earthq. Eng. 2011, 15, 32–49. [Google Scholar] [CrossRef]
- Wang, B.; Zheng, S.; Guo, X.; Li, L. Study on restoring force model of SRHSHPC frame columns considering damage effects. J. Build. Struct. 2012, 33, 69–76. [Google Scholar]
- Dowell, R.K.; Seible, F.; Wilson, E.L. Pivot Hysteresis Model for Reinforced Concrete Members. Aci Struct. J. 1998, 95, 607–617. [Google Scholar]
- Mostaghel, N.; Byrd, R.A. Analytical Description of Multidegree Bilinear Hysteretic System. J. Eng. Mech. 2000, 126, 588–598. [Google Scholar] [CrossRef]
- Yan, C.; Yang, D.; Ma, Z.J.; Jia, J. Hysteretic model of SRUHSC column and SRC beam joints considering damage effects. Mater. Struct. 2017, 50, 88. [Google Scholar] [CrossRef]
- Wang, P.H.; Ou, Y.C.; Chang, K.C. A new smooth hysteretic model for ductile flexural-dominated reinforced concrete bridge columns. Earthq. Eng. Struct. Dyn. 2017, 46, 2237–2259. [Google Scholar] [CrossRef]
- Yu, B.; Ning, C.L.; Li, B. Hysteretic Model for Shear-Critical Reinforced Concrete Columns. J. Struct. Eng. 2016, 142, 04016056. [Google Scholar] [CrossRef]
- Sezen, H.; Chowdhury, T. Hysteretic Model for Reinforced Concrete Columns Including the Effect of Shear and Axial Load Failure. J. Struct. Eng. Asce 2009, 135, 139–146. [Google Scholar] [CrossRef]
- Leborgne, M.R.; Ghannoum, W.M. Calibrated analytical element for lateral-strength degradation of reinforced concrete columns. Eng. Struct. 2014, 81, 35–48. [Google Scholar] [CrossRef]
- Chao, S.H.; Loh, C.H. A biaxial hysteretic model for a structural system incorporating strength deterioration and pinching phenomena. Int. J. Non Linear Mech. 2009, 44, 745–756. [Google Scholar] [CrossRef]
- Guo, Z.; Yang, Y. State-of-the-art of restoring force models for RC structures. World Earthq. Eng. 2004, 20, 47–51. [Google Scholar]
- Yu, J.; Li, Y.; Xia, H. Hysteretic shear model for RC columns with construction joint. J. Build. Struct. 2011, 32, 84–91. [Google Scholar]
- Cai, M.; Gu, X.; Hua, J.; Lin, F. Seismic response analysis of reinforced concrete columns considering shear effects. J. Build. Struct. 2011, 32, 97–108. [Google Scholar]
- Zhao, J.; Dun, H. A restoring force model for steel fiber reinforced concrete shear walls. Eng. Struct. 2014, 75, 469–476. [Google Scholar] [CrossRef]
- Huang, C.; Li, Y.; Gu, Q.; Liu, J. Machine learning–based hysteretic lateral force-displacement models of reinforced concrete columns. J. Struct. Eng. 2022, 148, 04021291. [Google Scholar] [CrossRef]
- Song, J.; Pincheira, J. Spectral Displacement Demands of Stiffness and Strength-Degrading Systems. Earthq. Spectra 2000, 16, 817–851. [Google Scholar] [CrossRef]
- Ibarra, L.F.; Medina, R.A.; Krawinkler, H. Hysteretic models that incorporate strength and stiffness deterioration. Earthq. Eng. Struct. Dyn. 2010, 34, 1489–1511. [Google Scholar] [CrossRef]
- Guo, Y.; Long, M. Parameter Identification and Application of Reinforced Concrete Column Based on Modified Ibarra-Medina-Krawinkler Hysteretic Model. J. Hunan Univ. Nat. Sci. 2021, 48, 126–134. [Google Scholar]
- Galal, E.M.; Ghobarah, A. Flexural and shear hysteretic behaviour of reinforced concrete columns with variable axial load. Eng. Struct. 2003, 25, 1353–1367. [Google Scholar] [CrossRef]
- Zhang, Y.; Han, S. Hysteretic Model for Flexure-shear Critical Reinforced Concrete Columns. J. Earthq. Eng. 2018, 22, 1639–1661. [Google Scholar] [CrossRef]
- Zhang, H.; Li, H.N.; Wang, Z. Study on Strain Rate Effect in High-Rise Reinforced Concrete Shear Wall Structure. Adv. Mater. Res. 2011, 243–249, 5854–5857. [Google Scholar] [CrossRef]
- Wang, C.Q.; Xiao, J.Z.; Sun, Z.P. Seismic analysis on recycled aggregate concrete frame considering strain rate effect. Int. J. Concr. Struct. Mater. 2016, 10, 307–323. [Google Scholar] [CrossRef]
- Pankaj, P.; Lin, E. Material modelling in the seismic response analysis for the design of RC framed structures. Eng. Struct. 2005, 27, 1014–1023. [Google Scholar] [CrossRef]
- Iribarren, B.S.; Berke, P.; Bouillard, P.; Vantomme, J.; Massart, T.J. Investigation of the influence of design and material parameters in the progressive collapse analysis of RC structures. Eng. Struct. 2011, 33, 2805–2820. [Google Scholar] [CrossRef]
- Zhang, H.; Li, H.N. Dynamic analysis of reinforced concrete structure with strain rate effect. Mater. Res. Innov. 2011, 15, s213–s216. [Google Scholar] [CrossRef]
- Cao, X.-Y.; Feng, D.-C.; Beer, M. Consistent seismic hazard and fragility analysis considering combined capacity-demand uncertainties via probability density evolution method. Struct. Saf. 2023, 103, 102330. [Google Scholar] [CrossRef]




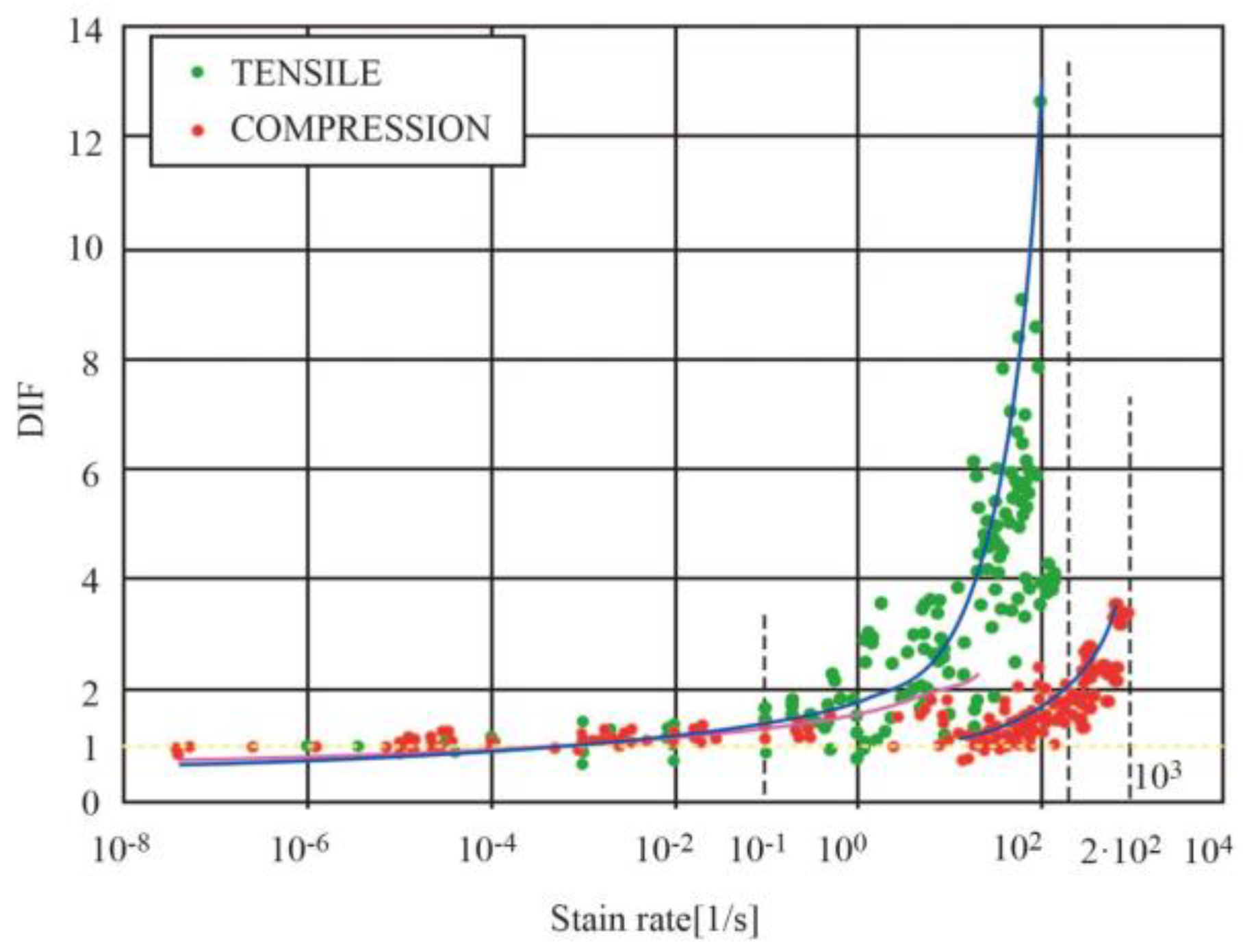
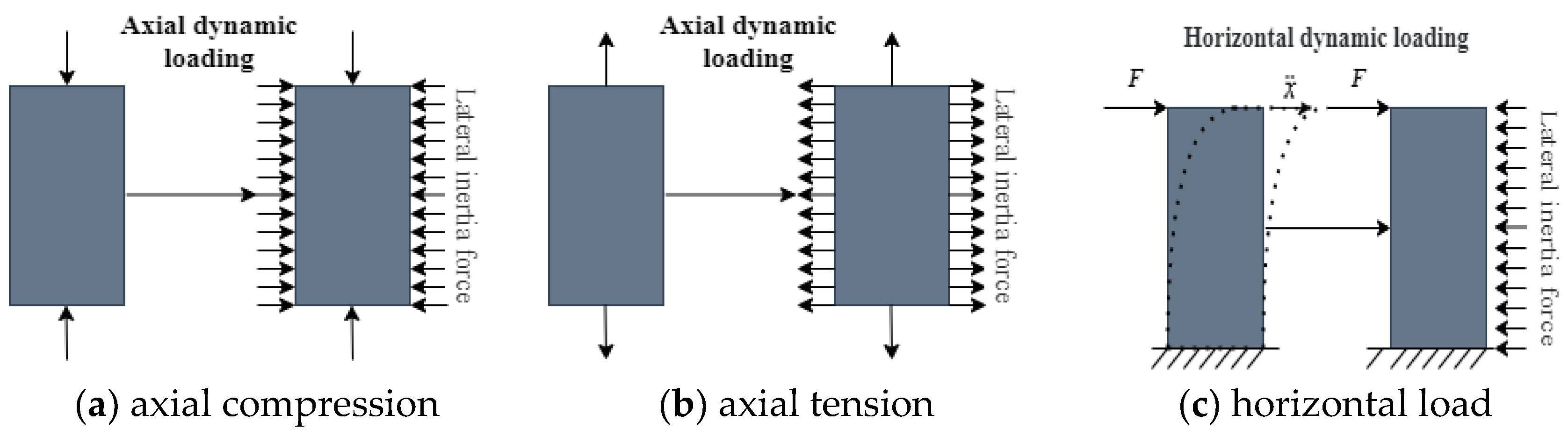
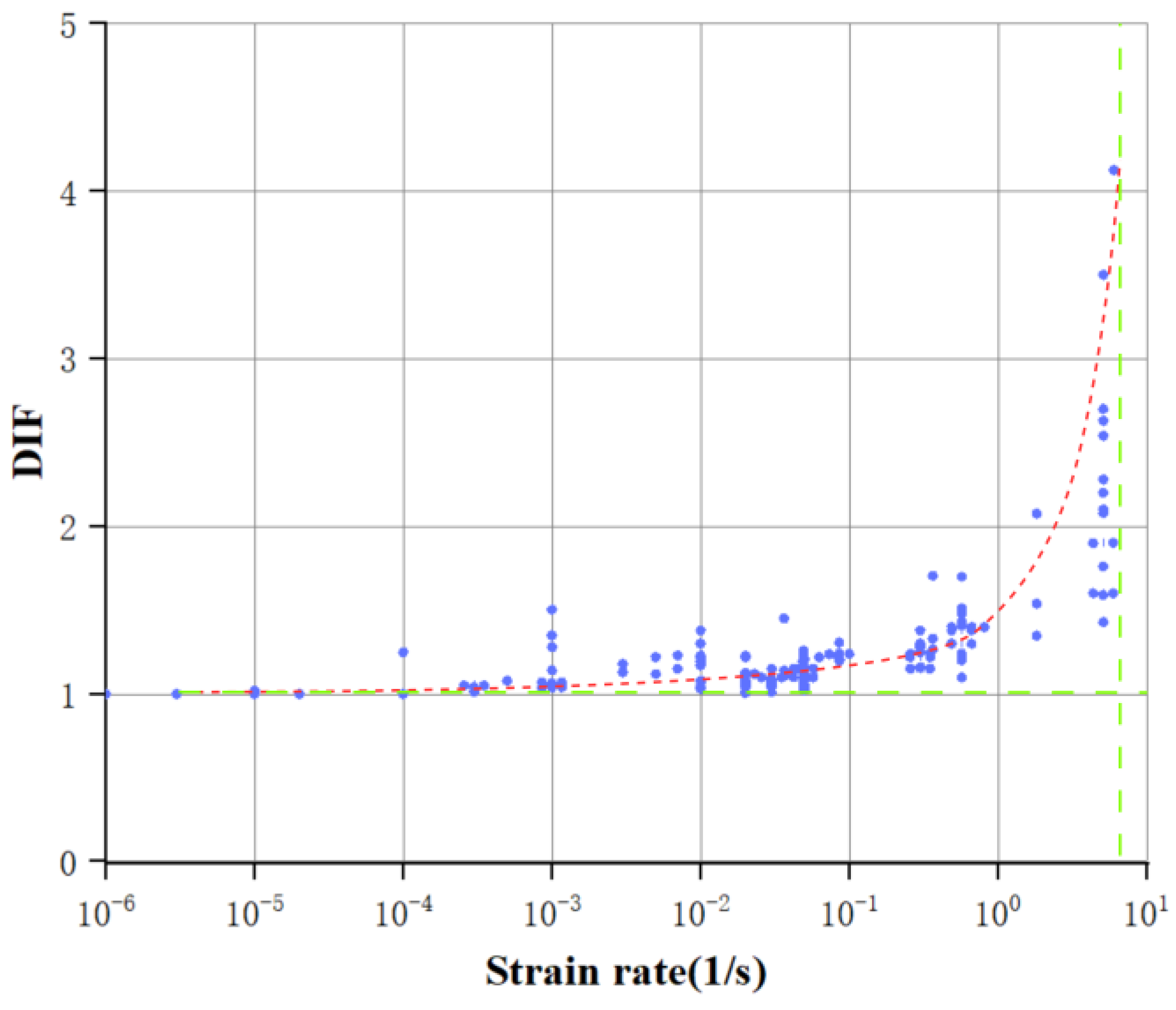
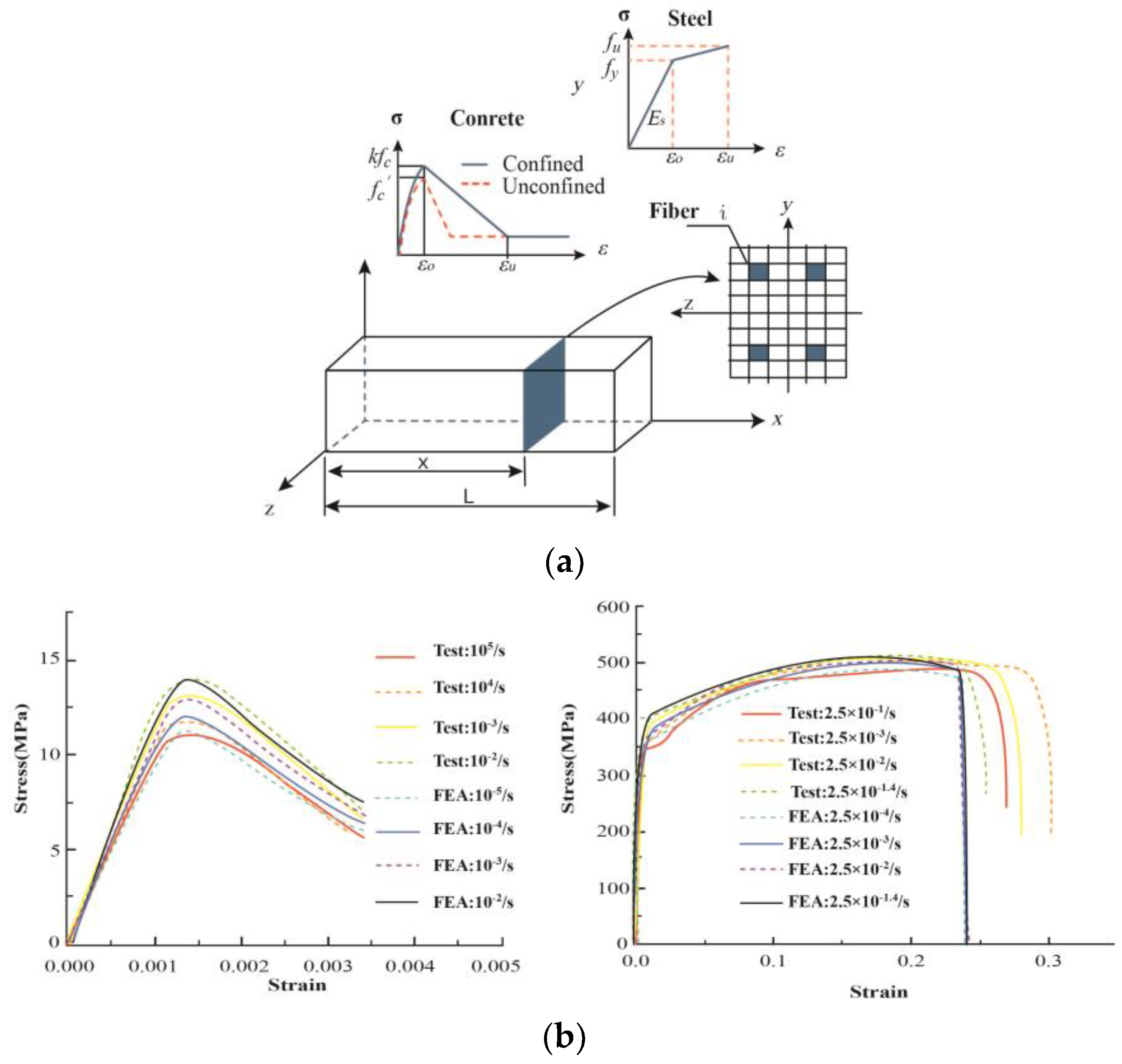

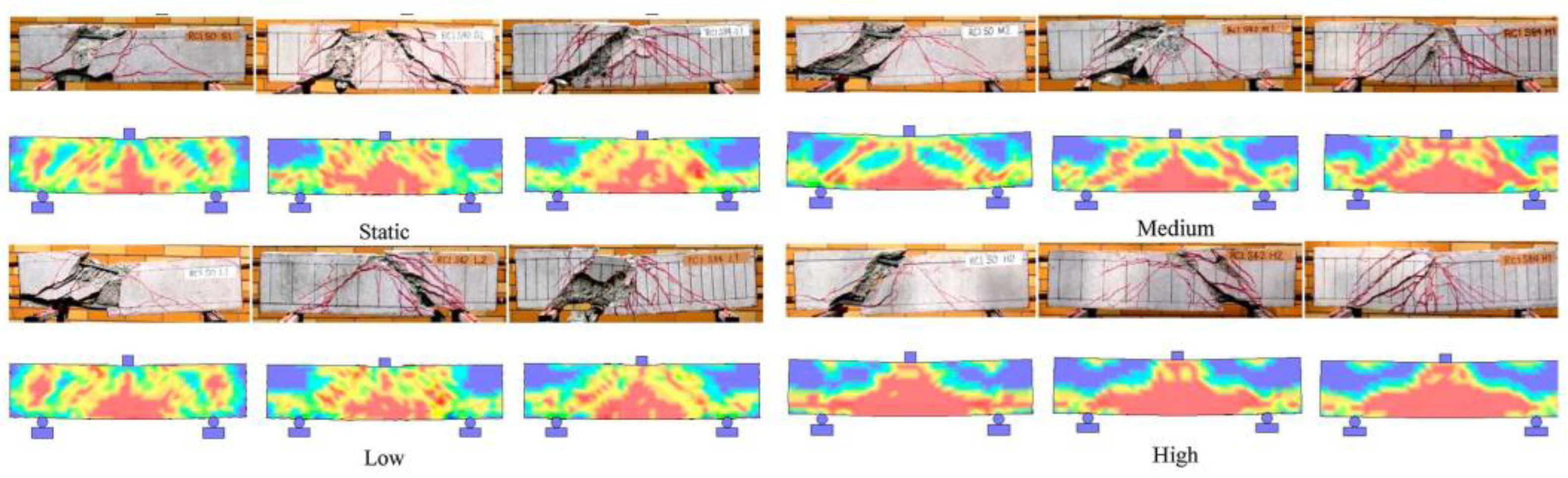
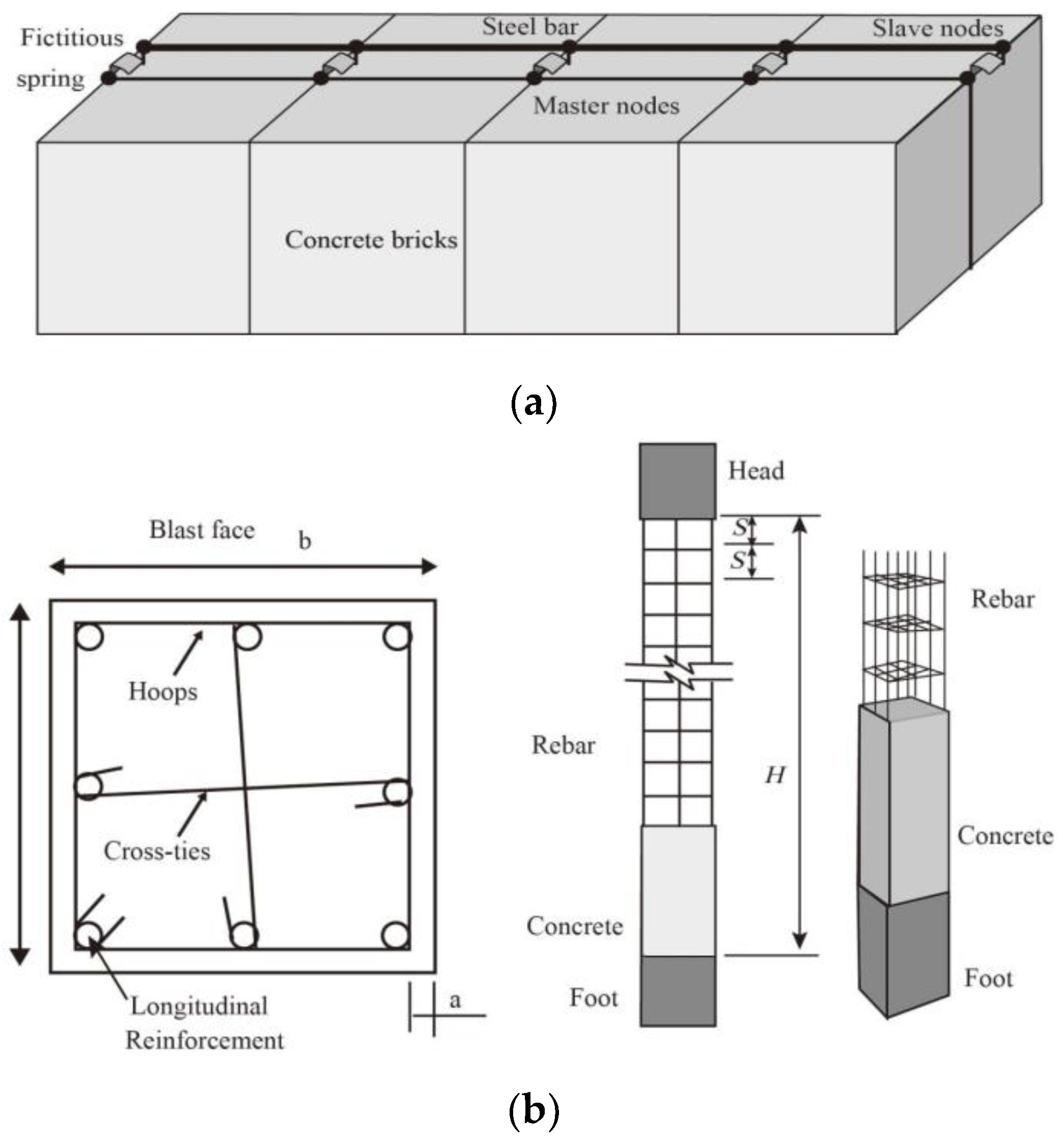
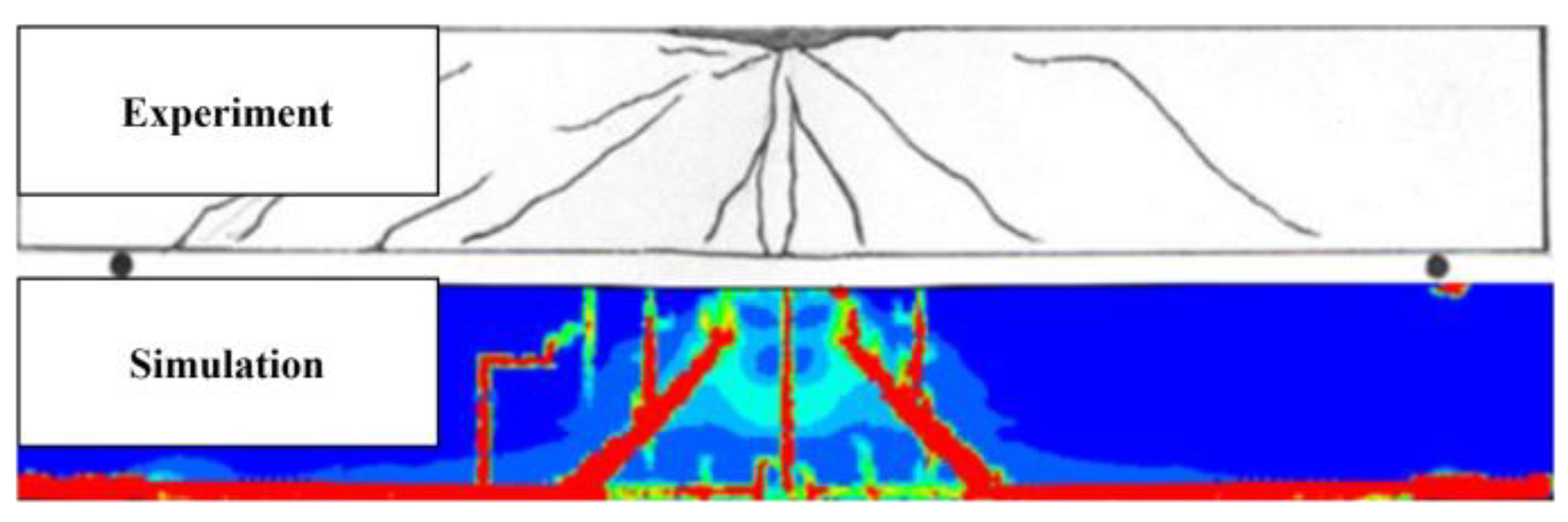
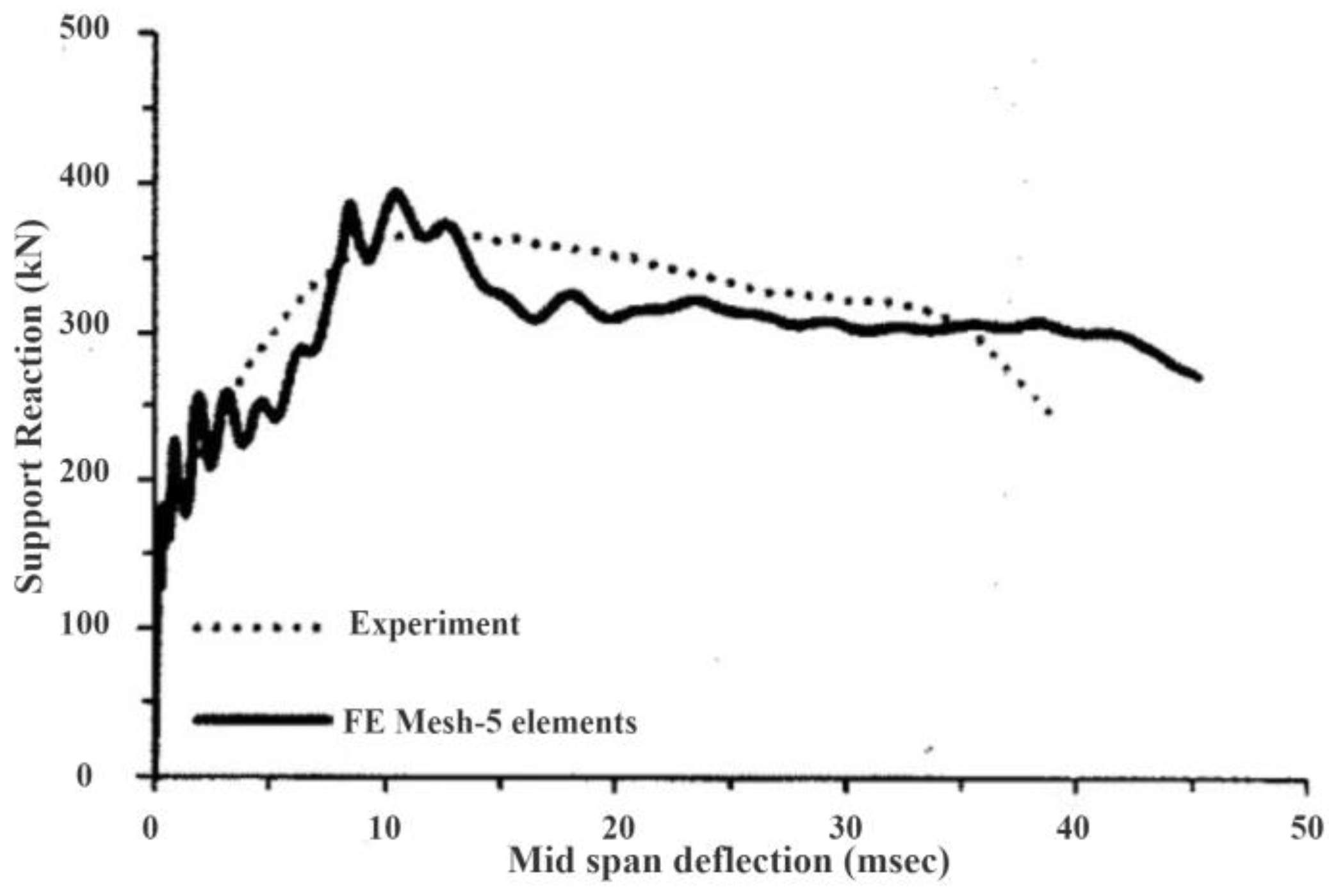

| No. | Reference | Type | Number | Loading Rate | Loading Scheme |
|---|---|---|---|---|---|
| 1 | Bertero et al. [41] | Beam | 6 | 0.1, 10/s | Mono, cycl |
| 2 | Kulkarni and Shah [42] | Beam | 14 | 0.0071–380 mm/s | Mono |
| 3 | White et al. [43] | Beam | 4 | 0.0167–36 mm/s | Mono, Cycl |
| 4 | Zhang et al. [44] | Beam | 36 | 1.05 × 10−5, 1.25 × 10−3/s | Mono |
| 5 | Marder et al. [13] | Beam | 17 | 100 Hz | Mono, Cycl |
| 6 | Yan [45] | Beam | / | 1 × 10−5–1 × 10−3/s | Cycl |
| 7 | Xiao et al. [46] | Beam | 5 | 0.1–10 mm/s | Mono |
| 8 | Li and Li [11] | Beam | 16 | 0.05–30 mm/s | Mono, Cycl |
| 9 | Zhou et al. [47] | Beam | 7 | 0.06 mm–66 mm/s | Mono |
| 10 | Otani et al. [48] | Beam | 8 | 0.1, 100 mm/s | Cycl |
| 11 | Guo [49] | Beam | 12 | 0, 2, 6 m/s | Mono |
| 12 | Wu et al. [50] | Beam | 3 | 87.89–135.8 Hz | Mono |
| 13 | Song et al. [5] | Beam | 5 | 3.5–6 m/s | Mono |
| 14 | Adhikary et al. [8,10,15] | Beam | 24 | 4 × 10−4–2 m/s | Mono |
| 15 | Adhikary et al. [51] | Beam | 30 | 0–5.6 m/s | Mono |
| 16 | Zeng [52] | Beam | 6 | 10−2/s–8.85 m/s | Mono |
| 17 | Feng et al. [53] | Beam | 10 | 3–7.7 m/s | Mono |
| 18 | Mutsuyoushi and Machida [54] | Beam | 14 | 0.1, 10, 100 cm/s | Mono, Cycl |
| 19 | Fukuda et al. [55] | Beam | 48 | 4 × 10−4–2 m/s | Mono |
| 20 | Yuan and Yi [56] | Beam | 18 | 3.5 × 10−4–1 m/s | Mono |
| 21 | Ye et al. [57] | Beam | 14 | 0.8 m/s | Mono |
| 22 | Fujikake [14] | Beam | 6 | 5 × 10−4 m/s, 2 m/s | Mono |
| 23 | Xiang et al. [58] | Column | 7 | / | Mono |
| 24 | Gutierrez et al. [59] | Column | 3 | 0.02–1 Hz | Cycl |
| 25 | Bousias et al. [60] | Column | 12 | / | Cycl, Biax |
| 26 | Li et al. [61] | Column | 30 | 0.000011–0.0167/s | Mono |
| 27 | Witarto et al. [6] | Column | 4 | 0.05–5 Hz | Cycl |
| 28 | Perry et al. [62] | Column | 4 | 0.7 × 10−4–0.7 × 10−3/s | Mono, Cycl |
| 29 | Yan [45] | Column | / | 10−5–10−2/s | Mono |
| 30 | Zou et al. [63] | Column | / | 10−5–10−2/s | Mono |
| 31 | Wang et al. [64] | Column | 30 | 0.1–50 mm/s | Mono, Cycl, Biax |
| 32 | Jiang [65] | Column | 12 | 0.1–20 mm/s | Mono, Cycl, Biax |
| 33 | Ghannoum et al. [35] | Column | 10 | 0.25–1061 mm/s | Cycl |
| 34 | Liu et al. [66] | Column | 10 | 0, 4.85, 6.86 m/s | Mono |
| 35 | Liu et al. [67] | Column | 13 | / | Mono |
| 36 | Lee et al. [68] | Column | 6 | / | Cycl |
| 37 | Wei et al. [69] | Column | 6 | 4.95–5.42 m/s | Mono |
| 38 | Fan et al. [70] | Column | 8 | 6.86, 5.42 m/s | Mono |
| 39 | Orozco and Ashford [71] | Column | 3 | 0.22–1 m/s | Cycl |
| 40 | Shah et al. [72] | Joint | 3 | 2.5 × 10−3–1.0 Hz | Cycl |
| 41 | Chung and Shah [20] | Joint | 12 | 0.0025–2.0 Hz | Cycl |
| 42 | Gibson et al. [73] | Joint | 4 | 0–405 mm/s | Cycl |
| 43 | Pan [23] | Joint | 10 | 0.1–10 mm/s | Cycl |
| 44 | Fan et al. [74] | Joint | 3 | 0.4–40 mm/s | Cycl |
| 45 | Wang et al. [75] | Joint | 8 | 0.4–40 mm/s | Cycl |
| 46 | Zhang [17] | Shear wall | 7 | 10−5–10−3/s | Cycl |
| 47 | Xu et al. [16] | Shear wall | 2 | 1–10 mm/s | Cycl |
| 48 | Chiu et al. [76] | Infill wall | 6 | 0–0.4 g | Cycl |
| 49 | Yilmaz et al. [77] | Slab | 9 | 4.43, 4.95, 5.42 m/s | Mono |
| Model | Range of Dynamic Strain Rate | Quasi-Static Strain Rate | Type of Formula | Modified Parameters |
|---|---|---|---|---|
| CEB model [29] | Exponential | |||
| Malvar model [122] | Exponential | |||
| Tedesco and Ross model [123] | Linear logarithmic | |||
| Yan model [89] | Linear logarithmic | . | ||
| Xiao and Zhang model [124] | Linear logarithmic | |||
| Li model [31] | Linear logarithmic |
| Model | Range of Dynamic Strain Rate | Quasi-Static Strain Rate | Type of Formula | Modified Parameters |
|---|---|---|---|---|
| CEB model [29] | Linear logarithmic | . | ||
| Malvar model [122] | Exponential | |||
| Lin Feng model [30] | Linear logarithmic | |||
| Li and Li model [103] | Linear logarithmic |
| Reference | Equations of Dynamic Modified Model | Model Type |
|---|---|---|
| Adhikary et al. [8] | Maximum resistance of RC regular beams (1) With transverse reinforcements (2) Without transverse reinforcements | FE simulation results-based (Deterministic) |
| Adhikary et al. [15] | Maximum resistance of RC deep beams (1) With transverse reinforcements (2) without transverse reinforcements | FE simulation results-based (Deterministic) |
| Wang [64] | Ultimate bearing capacity of RC columns (1) Different axial load ratio | FE simulation results-based (Deterministic) |
| (2) Different concrete strength conditions | ||
| (3) Different longitudinal reinforcement ratios | ||
| Li et al. [33] | Mechanical behavior parameters of RC columns (including yielding and ultimate bearing capacity, effective stiffness and ductility coefficient) | Experimental date-based (Probabilistic) |
| Fan [74] | Shear bearing capacity of RC joints | Experimental date-based (Deterministic) |
| Yan [45] | Elasticity modulus of RC beams (1) With transverse reinforcements (2) Without transverse reinforcements | Experimental date-based (Deterministic) |
| Song [5] | Dynamic increase factor in flexural strength of RC column | FE simulation results-based (Deterministic) |
| Rouchette et al. [34] | Simplified formula for mid-span deflection of RC beams under impact loading | FE simulation results-based (Deterministic) |
| Reference | Type | Elements | Parameter | Effectiveness |
|---|---|---|---|---|
| Wang [64] | Column | Solid element and truss element | Strain rates | Correlation between strain and strength under unidirectional dynamic loading test. |
| Wang [26] | Column | Three-dimensional fiber beam and birth–death element | Loading scheme Strain rate | User material subroutine for RC structural members considering the strain rate effect of materials. |
| Liu and Li [27] | Column | Three-dimensional fiber beam and birth–death element | Strain rates Damage | The dynamic behaviors of RC beams and column members. |
| Adhikary et al. [10] | Beam | Solid and beam element | Strain rates Inertia Longitudinal reinforcing ratio Stirrup ratio Shear span ratio Dynamic shear resistance | The dynamic shear resistance of RC deep beams was found to increase as the loading rates were increased. |
| Zhao et al. [139] | Beam | Solid and Hughes–Liu beam elements | Strain rates Beam span Shear Impact mass Reinforcement ratio Sectional dimension | The resistance characteristics of localized shear failure of RC beam members subjected to varying loading rates. |
| Wang [64] | Column | Fiber beam-column element with plastic hinges | Strain rates Shear Bond-slip Axial compression ratio Longitudinal reinforcement ratio Shear span ratio Concrete strength | Reflected the bearing capacity and stiffness degradation of structural members under different loading rates. |
| Shi et al. [143] | Column | One-dimensional slide line model | Strain rates Shear Slip Damage | The blast-induced dynamic responses of RC column members considering the bond shear modulus, maximum elastic slip strain and damage curve exponential coefficient. |
| Rouchette et al. [34] | Beam | 3-D spar element, solid element, bond-link element | Strain rates Corroded steel bar Flexural Bond-slip Impact mass Beam geometry Concrete strength Reinforcement ratio The solicitation force | Simulated the flexural behavior of reinforced concrete beams considering the bond between concrete and steel bar under impact loading. The accuracy of the FE numerical model could be improved, as compared with the no-bond-slip model. |
| Valipour et al. [131] | Beam | Fiber element | Strain rates Shear Impact mass | Dynamic analysis of reinforced concrete beams subjected to high strain rate loads considering the possible failure of shear. |
| Guner and Vecchio [144] | Shear wall | Secant-stiffness-based finite-element algorithm | Strain rates Shear | A simplified method for the dynamic analyses of shear-critical RC frame members under impact and seismic load. The influences of dynamic effects and the shear effect were incorporated based on the DIF models and the rotating smeared crack approach. |
| Jia et al. [137] | Beam | 2DOF model | Strain rates Flexural Shear Impact mass Reinforcement ratio Concrete strength | Predicted the possible failure modes (i.e., the punching shear, shear, flexure, flexure-shear and instability) of RC structural members subjected to low-velocity impact load. |
| Adhikary et al. [15] | Beam | Hughes–Liu beam element and solid element | Strain rates Shear Bond-slip Impact mass | The relationship between failure mode and impact mass of RC beam members under impact load. |
| Li et al. [145] | Beam | Hughes–Liu beam element with 2 × 2 Gauss quadrature | Strain rates Impact energy Inclination angle of drop weight Concrete strength | Investigated the dynamic behavior of beams subjected to impact loading rates. The influences of dynamic effects and excessive distortion due to large deformations under impact loads were incorporated, based on the DIF models and a method to automatically remove the distorted elements, based on predefined criteria. |
| Yang [138] | Shear wall | Solid and truss element | Strain rates Shear span ratio Reinforcement ratio Failure mode | Mechanical property and failure mode subjected to dynamic loading rates. |
| Song and Zhang [18] | Shear wall | Solid and truss element | Strain rates Shear span ratio Axial compression ratio | The response of RC shear wall with different shear span ratios and axial compression ratios under quasi-static load and dynamic load with high strain rate. |
| Degradation Effect Factors | Relevant Studies | |
|---|---|---|
| Single factor |
| Clough [147], Takeda [148], Wen [151], Takayanagi and Schnobrich [152], Saatcioglu et al. [153], Xu [154], Qu and Ye [155], |
| Ambrisi and Filippou [156] | |
| Multiple factor |
| Gu et al. [157], Zheng et al. [158], Zheng et al. [159], Erberik [160], Wang et al. [161] |
| Park and Ang [150], Ozcebeand Saatcioglu [149], Dowell et al. [162], Mostaghel and Byrd [163], Yan et al. [164], Wang et al. [165], Yu et al. [166], Sezen and Chowdhury [167], Leborgne and Ghannoum [168], Chao and Loh [169], Guo and Yang [170], Yu et al. [171], Cai et al. [172], Zhao and Dun [173], Huang et al. [174] | |
| Song and Pincheira [175], Ibarra et al. [176], Guo and Long [177], Li [33] | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, R.; Gao, M.; Li, H.; Li, C.; Wang, D. Experimental, Theoretical and Numerical Research Progress on Dynamic Behaviors of RC Structural Members. Buildings 2023, 13, 1359. https://doi.org/10.3390/buildings13051359
Li R, Gao M, Li H, Li C, Wang D. Experimental, Theoretical and Numerical Research Progress on Dynamic Behaviors of RC Structural Members. Buildings. 2023; 13(5):1359. https://doi.org/10.3390/buildings13051359
Chicago/Turabian StyleLi, Rouhan, Mao Gao, Hongnan Li, Chao Li, and Debin Wang. 2023. "Experimental, Theoretical and Numerical Research Progress on Dynamic Behaviors of RC Structural Members" Buildings 13, no. 5: 1359. https://doi.org/10.3390/buildings13051359
APA StyleLi, R., Gao, M., Li, H., Li, C., & Wang, D. (2023). Experimental, Theoretical and Numerical Research Progress on Dynamic Behaviors of RC Structural Members. Buildings, 13(5), 1359. https://doi.org/10.3390/buildings13051359








