Performance-Based Assessment of RC Building with Short Columns Due to the Different Design Principles
Abstract
1. Introduction
2. Short Column in RC Structures
3. Performance-Based Assessment and Design Principles
4. Structural Models and Analysis Results
4.1. Description of the Numerical Model
4.2. Investigation of Short Column Effect by the Strength-Based Design Approach
4.2.1. Investigation of the Change in Relative Storey Drifts
4.2.2. Investigation of Soft-Storey Formation
4.2.3. Investigation of Column Shear Force Variation
4.3. Investigation of the Short Column Effect by the Deformation-Based Design Approach
5. Conclusions
- (a)
- Earthquake codes in Türkiye have been updated over time, and the last earthquake code came into force in 2019. In this code, designs can be made according to strength and deformation. In this study, short column effects were tried to be revealed for four different structural models using both methods. The structural models were created for three different situations: the hill slope effect, band-type window and mezzanine floor, which may cause short column formation. The results obtained from the structural analyses using SAP2000 were compared with the reference building model with no short columns. The findings obtained from the study are summarised below;
- (b)
- According to the Strength-based Design Approach:
- (1)
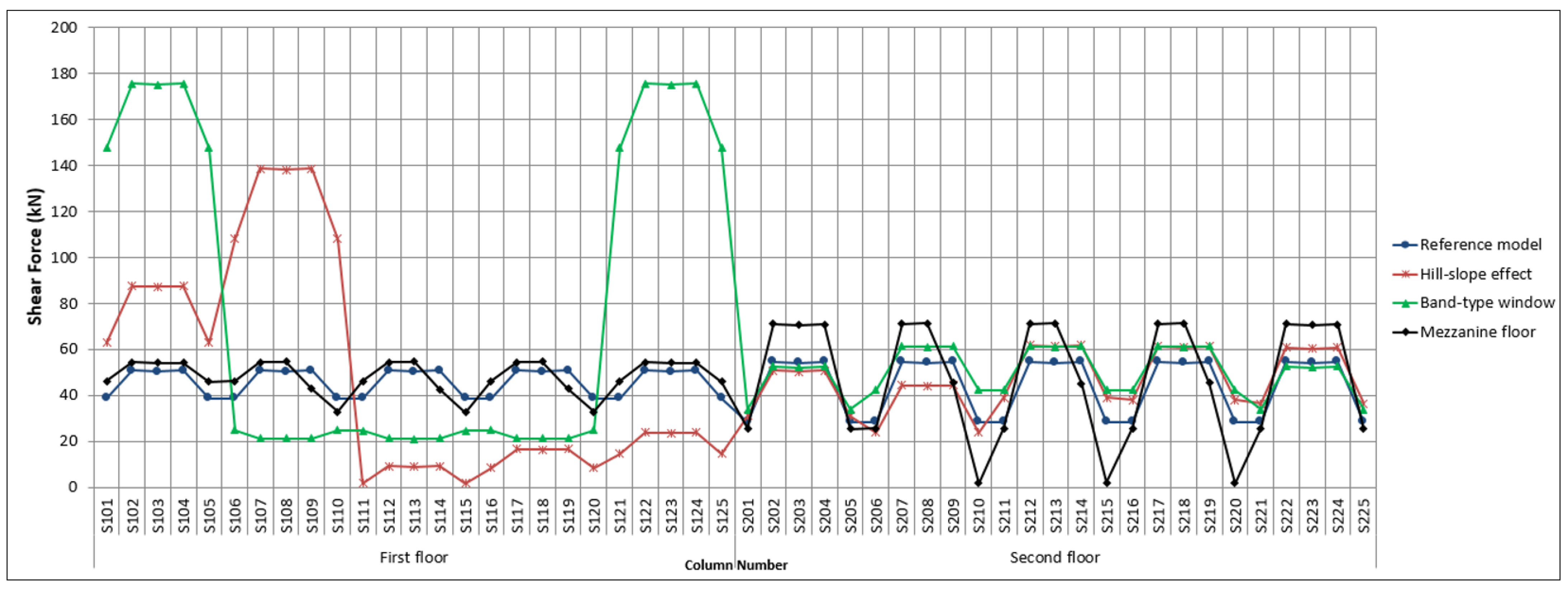
- Short columns formed due to the band-type window formation reduced the relative drifts of the ground storey by 88% compared to the reference model. The mentioned ratio decreased to 31% in buildings with a hill-slope effect. However, the mezzanine floor reduced the second-floor relative drifts by 43% compared to the reference model. It is clear that these effects are related to the increase in rigidity with the decrease in column lengths. In addition to these, the maximum relative drifts of all floors and the highest relative drifts occurred in the band-type window. The displacements are inversely proportional to the column’s stiffness (especially the length of the column). However, while the stiffness increases in short columns, the shear forces obtained by dividing the moments occurring at the column ends by the column length increase significantly;
- (2)
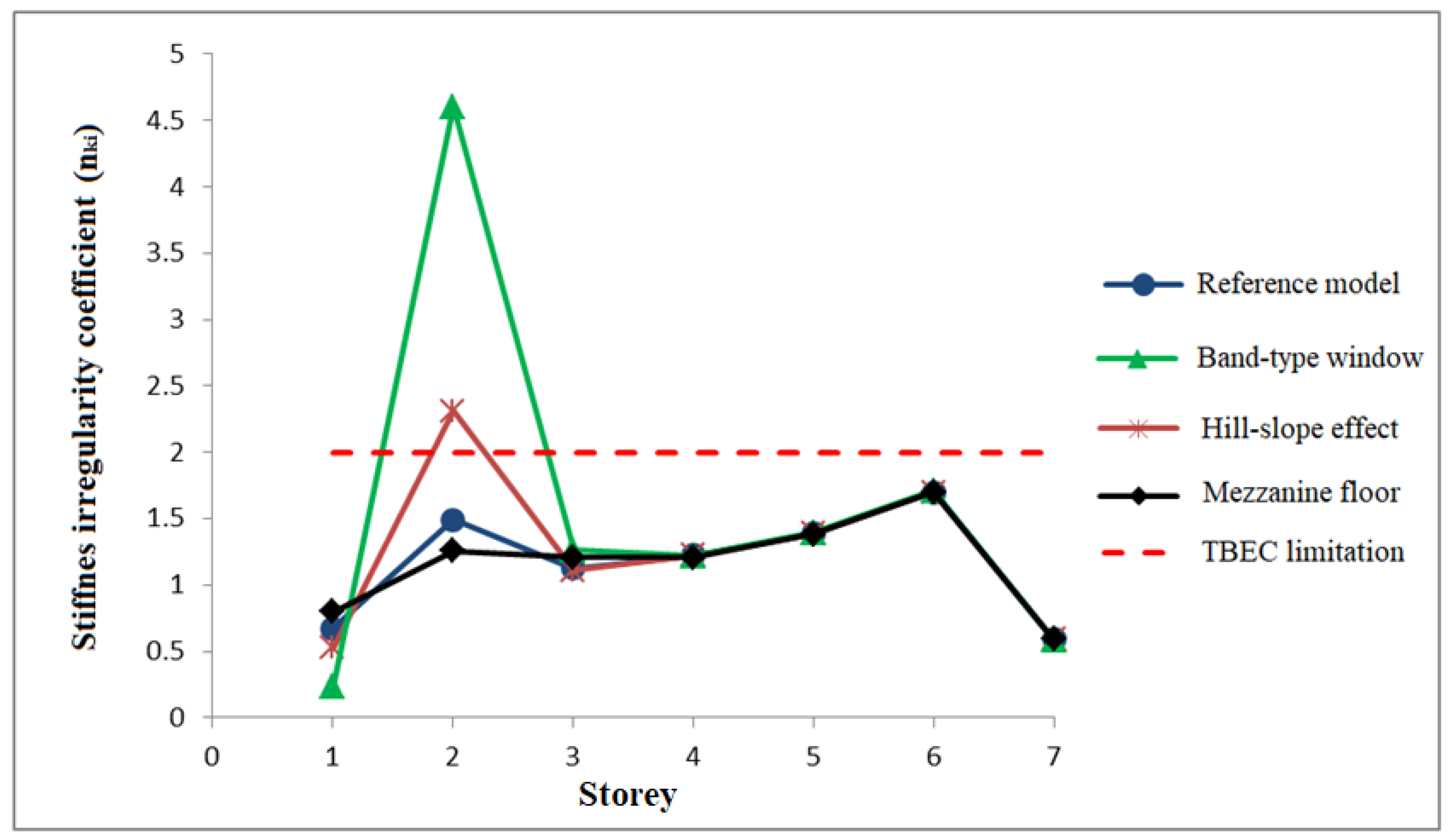
- It was determined that the relative drifts from the first floor of the building decreased significantly due to the band-type window and slope effect, which caused the second floor to fall into the soft-storey status. The soft storey phenomenon is related to the average relative storey drifts of the floors. If the stiffness irregularity coefficient, which is found by dividing the average storey drift ratio in the floor in the direction of the earthquake direction, by the average relative storey drift ratio of one upper or lower storey, is greater than 2.0, soft storey irregularity is observed;
- (3)
- According to TBEC-2018, the stiffness irregularity coefficient (nki) can be more than 2, especially in buildings with band-type windows. This indicates that the irregularity referred to as B2 may be critical for these buildings. A similar situation exists in models with a hill-slope effect, albeit limited. In the case of this irregularity, some limitations have been introduced for the application of the Equivalent Seismic Load Method;
- (4)
- When the changes in the shear forces in the columns are examined, it is seen that the highest increase occurs in the first and fifth axes of the Band-Type buildings and in the first and second axes of the buildings having the hill-slope effect. However, these increases were not at a level that could cause shear damage to the columns. Considering the frequency of stirrups and crossties used, concrete compressive strength and column sections, it is seen that the shear demand does not exceed the shear capacity of the columns.
- (c)
- According to the Deformation-based Design Approach;
- (1)
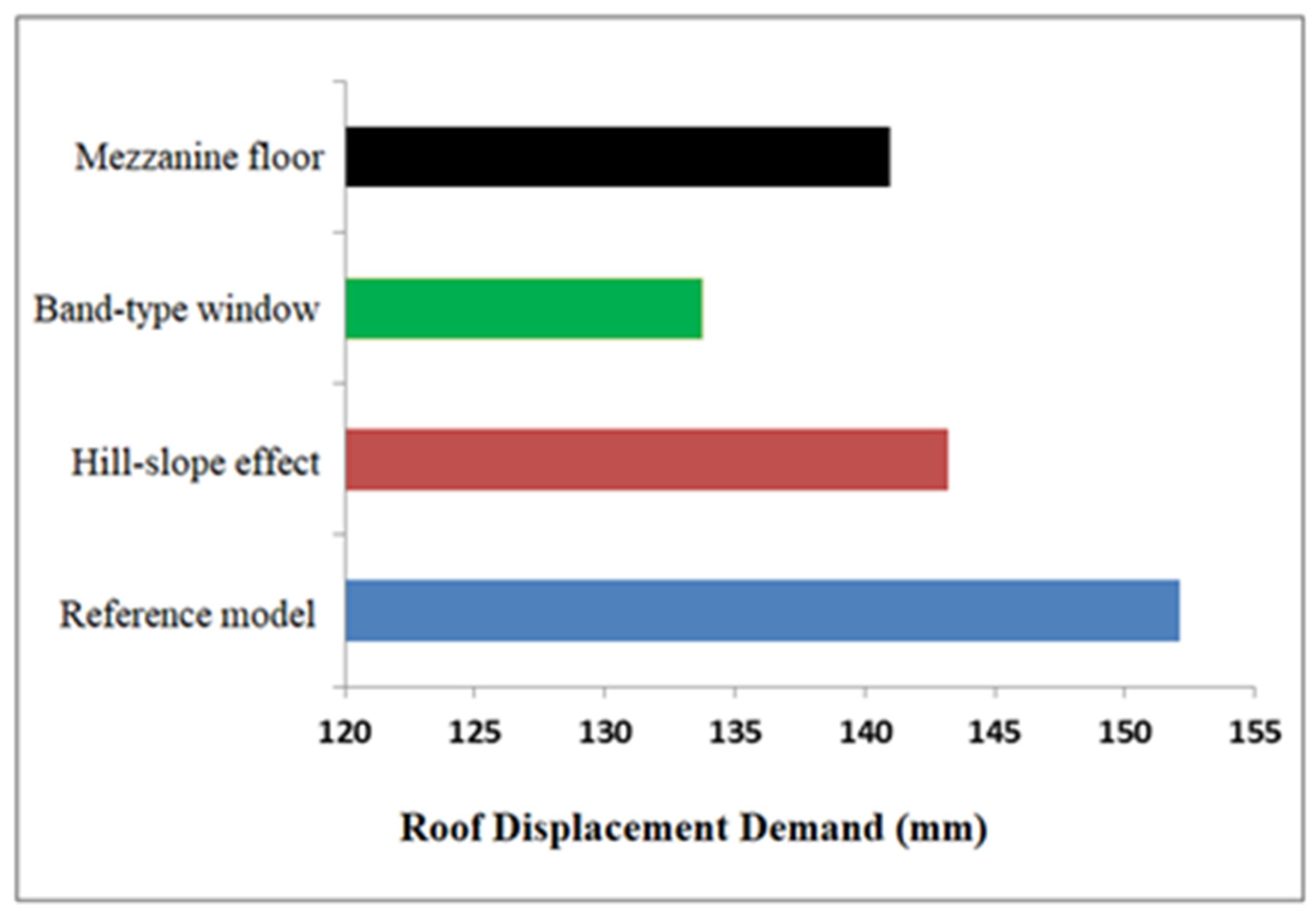
- Changing stiffness has also changed the period of the buildings and the displacement demand. Here, it is seen that the building with the least ductility requirement is the buildings with Band-Type type short columns. However, it should not be forgotten that the demand for shear force increases in this model inversely proportional to the displacement;
- (2)
- Especially in buildings with the hill slope effect, the increase in plastic rotation demands 4–5 times compared to the reference building has significantly increased the bending damage of the columns in this building. Similarly, in buildings with band-type windows, the plastic rotation demands increase 2–3 times in the relevant axes compared to the reference building. The increase in plastic rotation demands, especially on critical floors, may cause increased column damage and insufficient global performance of the building;
- (3)
- Since the period decreases with the increase in stiffness in short-column models, the roof displacement demands of these models are lower than the reference model. In this situation, it is incorrect to think that the short column models’ performance is better than the reference model. Because of the short column formation, the plastic rotation of the short columns increases considerably, even with low roof demands. In the short-column models created within the scope of the study, the plastic rotations occurring in the short columns increased significantly, but since these values did not exceed the controlled damage limit, the performance status of the models did not change. However, in different buildings with different storey numbers, blueprints and material properties, the plastic rotations increasing in this size in short columns can change the performance status of the buildings.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Yel, N.S.; Arslan, M.H.; Aksoylu, C.; Erkan, İ.H.; Arslan, H.D.; Işık, E. Investigation of the Earthquake Performance Adequacy of Low-Rise RC Structures Designed According to the Simplified Design Rules in TBEC-2019. Buildings 2022, 12, 1722. [Google Scholar] [CrossRef]
- Ademović, N.; Kalman Šipoš, T.; Hadzima-Nyarko, M. Rapid assessment of earthquake risk for Bosnia and Herzegovina. Bull. Earthq. Eng. 2020, 18, 1835–1863. [Google Scholar] [CrossRef]
- Bilgin, H.; Shkodrani, N.; Hysenlliu, M.; Ozmen, H.B.; Isik, E.; Harirchian, E. Damage and performance evaluation of masonry buildings constructed in 1970s during the 2019 Albania earthquakes. Eng. Fail. Anal. 2022, 131, 105824. [Google Scholar] [CrossRef]
- Kaminosono, T. Evaluation method for seismic capacity of existing reinforced concrete buildings in Japan. In Memoria; Centro Nacional de Prevención de Desastes (CENAPRED): Mexico City, México; Agencia de Cooperación Internacional (JICA): Tokyo, Japan; Centro para el Desarrollo Regional (UNCRD): Nagoya, Japan, 1992; pp. 44–53. [Google Scholar]
- National Research Council of Canada (NRCC). Manual for Screening of Buildings for Seismic Investigation; Canadian Standard; National Research Council of Canada: Ottowa, ON, Canada, 1993.
- Okada, T. Needs to Evaluate Real Seismic Performance of Buildings-Lessons from the 1995 Hyogoken-Nambu Earthquake. INCEDE Rep. 1999, 15, 225–231. [Google Scholar]
- Gulay, F.G.; Kaptan, K.; Bal, E.I.; Tezcan, S.S. P25-scoring method for the collapse vulnerability assessment of R/C buildings. Procedia Eng. 2011, 14, 1219–1228. [Google Scholar] [CrossRef]
- Bülbül, M.A.; Harirchian, E.; Işık, M.F.; Aghakouchaki Hosseini, S.E.; Işık, E. A hybrid ANN-GA model for an automated rapid vulnerability assessment of existing RC buildings. Appl. Sci. 2022, 12, 5138. [Google Scholar] [CrossRef]
- Dogan, G.; Ecemis, A.S.; Korkmaz, S.Z.; Arslan, M.H.; Korkmaz, H.H. Buildings damages after Elazığ, Turkey earthquake on 24 January 2020. Nat. Hazards 2021, 109, 161–200. [Google Scholar] [CrossRef]
- Bektaş, N.; Kegyes-Brassai, O. Development in fuzzy logic-based rapid visual screening method for seismic vulnerability assessment of buildings. Geosciences 2023, 13, 6. [Google Scholar] [CrossRef]
- Ghobarah, A.; Galal, K.E. Seismic rehabilitation of short rectangular RC columns. J. Earthq. Eng. 2004, 8, 45–68. [Google Scholar] [CrossRef]
- Moretti, M.; Tassios, T.P. Behaviour of short columns subjected to cyclic shear displacements: Experimental results. Eng. Struct. 2007, 29, 2018–2029. [Google Scholar] [CrossRef]
- ASCE. Seismic Evaluation and Retrofit of Existing Buildings; ASCE/SEI, 41-17; ASCE: Reston, VA, USA, 2017. [Google Scholar]
- Arslan, M.H.; Korkmaz, H.H. What is to be learned from damage and failure of reinforced concrete structures during recent earthquakes in Turkey? Eng. Fail. Anal. 2007, 14, 1–22. [Google Scholar] [CrossRef]
- Tsantilis, A.V.; Triantafillou, T.C. Innovative seismic isolation of masonry infills using cellular materials at the interface with the surrounding RC frames. Eng. Struct. 2018, 155, 279–297. [Google Scholar] [CrossRef]
- Moehle, J.P.; Mahin, S.A. Observations on the behavior of reinforced concrete buildings during earthquakes. ACI Spec. Publ. 1991, 127, 67–90. [Google Scholar]
- Wang, Y.Y. Lessons learned from the “5.12” Wenchuan earthquake: Evaluation of earthquake performance objectives and the importance of seismic conceptual design principles. Earthq. Eng. Eng. Vib. 2008, 7, 255–262. [Google Scholar] [CrossRef]
- Yen, W.P.; Chen, G.; Buckle, I.; Allen, T.; Alzamora, D.; Ger, J.; Arias, J.G. Post-Earthquake Reconnaissance Report on Transportation Infrastructure: Impact of the 27 February 2010, Offshore Maule Earthquake in Chile; FHWA-HRT-11-030; Federal Highway Administration: Richmond, VA, USA, 2011.
- Meral, E. Investigation of short column effects in reinforcement concrete buildings. Int. J. Eng. Res. Dev. 2019, 11, 515–527. [Google Scholar]
- Şeker, M.; Bedirhanoglu, İ. Investigation of shear behaviour of reinforced concrete captive column with low strength concrete. Dicle Univ. J. Eng. (DUJE) 2019, 10, 385–395. [Google Scholar]
- Balik, F.S.; Bahadir, F. Investigation of short column behaviors at 1/5 scaled reinforced concrete frames using different strengthening methods. J. Inst. Sci. Technol. 2019, 9, 433–445. [Google Scholar] [CrossRef]
- Işık, E.; Karasin, İ.B.; Ulu, A.E. Investigation of earthquake behavior of reinforced-concrete buildings built on soil slope. Eur. J. Sci. Eng. 2020, 20, 162–170. [Google Scholar]
- Haji, M.; Naderpour, H.; Kheyroddin, A. Experimental study on influence of proposed FRP-strengthening techniques on RC circular short columns considering different types of damage index. Compos. Struct. 2019, 209, 112–128. [Google Scholar] [CrossRef]
- Chen, C.Y.; Liu, K.C.; Liu, Y.W.; Huang, W.J. A case study of reinforced concrete short column under earthquake using experimental and theoretical investigations. Struct. Eng. Mech. 2010, 36, 197–206. [Google Scholar] [CrossRef]
- Moretti, M.; Tassios, T.P. Behavior and ductility of reinforced concrete short columns using global truss model. ACI Struct. J. 2006, 103, 319–327. [Google Scholar]
- Çelebi, E.; Aktas, M.; Çağlar, N.; Özocak, A.; Kutanis, M.; Mert, N.; Özcan, Z. 23 October 2011 Turkey/Van–Ercis earthquake: Structural damages in the residential buildings. Nat. Hazards 2013, 65, 2287–2310. [Google Scholar] [CrossRef]
- Alih, S.C.; Vafaei, M. Performance of reinforced concrete buildings and wooden structures during the 2015 Mw 6.0 Sabah earthquake in Malaysia. Eng. Fail. Anal. 2019, 102, 351–368. [Google Scholar] [CrossRef]
- Pozos-Estrada, A.; Chávez, M.M.; Jaimes, M.Á.; Arnau, O.; Guerrero, H. Damages observed in locations of Oaxaca due to the Tehuantepec Mw8. 2 earthquake, Mexico. Nat. Hazards 2019, 97, 623–641. [Google Scholar] [CrossRef]
- Liu, C.; Fang, D.; Zhao, L. Reflection on earthquake damage of buildings in 2015 Nepal earthquake and seismic measures for post-earthquake reconstruction. Structures 2021, 30, 647–658. [Google Scholar] [CrossRef]
- Arslan, M.H. An evaluation of effective design parameters on earthquake performance of RC buildings using neural networks. Eng. Struct. 2010, 32, 1888–1898. [Google Scholar] [CrossRef]
- Işik, E.; Ulu, A.E.; Aydin, M.C. A case study on the updates of Turkish rapid visual screening methods for reinforced-concrete buildings. Bitlis Eren Univ. J. Sci. Technol. 2021, 11, 97–103. [Google Scholar]
- Bektaş, N.; Kegyes-Brassai, O. Conventional RVS methods for seismic risk assessment for estimating the current situation of existing buildings: A state-of-the-art review. Sustainability 2022, 14, 2583. [Google Scholar] [CrossRef]
- Ay, B.Ö.; Erberik, M.A. Seismic risk assessment of low-rise and mid-rise reinforced concrete structures in Turkey. In Proceedings of the Sixth National Conference on Earthquake Engineering, Istanbul, Turkey, 16–20 October 2007; pp. 37–48. [Google Scholar]
- Doğangün, A. Betonarme Yapıların Hesap ve Tasarımı; Birsen Yayınevi: Istanbul, Turkey, 2013. [Google Scholar]
- Işık, E. Size effects of columns on buckling. In Proceedings of the 5th International Science Technology and Engineering Conference, St. Petersburg, Russia, 6–8 April 2015. [Google Scholar]
- Yamada, M.; Furui, S. Shear resistance and explosive cleavage failure of reinforced concrete members subjected to axial load. In Proceedings of the 8th International Congress IABSE, New York, NY, USA, 9–14 September 1968; pp. 1091–1102. [Google Scholar]
- Moretti, M.L.; Tassios, T.P. Design in shear of reinforced concrete short columns. Earthq. Struct. 2013, 4, 265–283. [Google Scholar] [CrossRef]
- Bal, İ.E.; Tezcan, S.S.; Gülay, G.F. P25 rapid screening method to determine the collapse vulnerability of r/c buildings. In Proceedings of the Sixth National Conference on Earthquake Engineering, Istanbul, Turkey, 16–20 October 2007; pp. 661–674. [Google Scholar]
- Doğan, T.P.; Kızılkula, T.; Mohammadi, M.; Erkan, İ.H.; Kabaş, H.T.; Arslan, M.H. A comparative study on the rapid seismic evaluation methods of reinforced concrete buildings. Int. J. Dis. Risk Reduct. 2021, 56, 102143. [Google Scholar] [CrossRef]
- Çağatay, İ.H. Investigation of parameters affecting short column of buildings. In Proceedings of the Sixth National Conference on Earthquake Engineering, Istanbul, Turkey, 16–20 October 2007; pp. 29–236. [Google Scholar]
- İnan, T.; Korkmaz, K. Investigation of vertical structural irregularities. Erciyes Üniversitesi Fen Bilim. Enstitüsü Derg. 2012, 28, 240–248. [Google Scholar]
- Guevara, L.T.; Garcia, L.E. The captive-and short-column effects. Earthq. Spectra 2005, 21, 141–160. [Google Scholar] [CrossRef]
- Dowrick, D.J. Earthquake Resistant Design for Engineers and Architects; John Wiley & Sons: Chichester, NH, USA, 1987. [Google Scholar]
- Colomb, F.; Tobbi, H.; Ferrier, E.; Hamelin, P. Seismic retrofit of reinforced concrete short columns by CFRP materials. Compos. Struct. 2008, 82, 475–487. [Google Scholar] [CrossRef]
- Işık, E. The effects of 23 October 2011 Van earthquake on near-field and damaged on structures. Int. Anatolia Acad. Online J. Sci. Sci. 2014, 2, 10–25. [Google Scholar]
- Karakostas, C.; Lekidis, V.; Makarios, T.; Salonikios, T.; Sous, I.; Demosthenous, M. Seismic response of structures and infrastructure facilities during the Lefkada, Greece earthquake of 14 August 2003. Eng. Struct. 2005, 27, 213–227. [Google Scholar] [CrossRef]
- Aliaari, M.; Memari, A.M. Analysis of masonry infilled steel frames with seismic isolator subframes. Eng. Struct. 2005, 27, 487–500. [Google Scholar] [CrossRef]
- Caglar, N.; Vural, I.; Kirtel, O.; Saribiyik, A.; Sumer, Y. Structural damages observed in buildings after the 24 January 2020 Elazığ-Sivrice earthquake in Türkiye. Case Stud. Constr. Mater. 2023, 18, e01886. [Google Scholar] [CrossRef]
- Education and Job. Available online: http://educationandjob1.blogspot.com.tr/2014_05_01_archive.html (accessed on 6 May 2022).
- Jayaguru, C.; Subramanian, K. Seismic behaviour of partially infilled RC frames retrofitted using GFRP laminates. Exp. Tech. 2012, 36, 82–91. [Google Scholar] [CrossRef]
- Eleftheriadou, A.K.; Karabinis, A.I. Seismic vulnerability assessment of buildings based on damage data after a near field earthquake (7 September 1999 Athens-Greece). Earthq. Struct. 2012, 3, 117–140. [Google Scholar] [CrossRef]
- Aydınoğlu, M.N. A response spectrum-based nonlinear assessment tool for practice: Incremental response spectrum analysis (IRSA), ISET. J. Earthq. Technol. 2007, 44, 169–192. [Google Scholar]
- Kutanis, M.; Boru, O.E. The need for upgrading the seismic performance objectives. Earthq. Struct. 2014, 7, 401–414. [Google Scholar]
- İlki, A.; Celep, Z. Betonarme yapıların deprem güvenliği. In Proceedings of the 1. Türkiye Deprem Mühendisliği ve Sismoloji Konferansı, Ankara, Turkey, 1–14 October 2011. [Google Scholar]
- Fajfar, P. Capacity spectrum method based on inelastic demand spectra. Earthq. Eng. Struct. Dyn. 1999, 28, 979–993. [Google Scholar] [CrossRef]
- Gholizadeh, S. Performance-based optimum seismic design of steel structures by a modified firefly algorithm and a new neural network. Adv. Eng. Softw. 2015, 81, 50–65. [Google Scholar] [CrossRef]
- Işık, E.; Kutanis, M. Performance based assessment for existing residential buildings in Lake Van basin and seismicity of the region. Earthq. Struct. 2015, 9, 893–910. [Google Scholar] [CrossRef]
- Chopra, A.K.; Goel, R.K. A modal pushover analysis procedure for estimating seismic demands for buildings. Earthq. Eng. Struct. Dyn. 2002, 31, 561–582. [Google Scholar] [CrossRef]
- Foti, D. A new experimental approach to the pushover analysis of masonry buildings. Comput. Struct. 2015, 147, 165–171. [Google Scholar] [CrossRef]
- Hsiao, F.P.; Oktavianus, Y.; Ou, Y.C. A pushover seismic analysis method for asymmetric and tall buildings. J. Chin. Inst. Eng. 2015, 38, 991–1001. [Google Scholar] [CrossRef]
- Casapulla, C.; Argiento, L.U. The comparative role of friction in local out-of-plane mechanisms of masonry buildings. Pushover analysis and experimental investigation. Eng. Struct. 2016, 126, 158–173. [Google Scholar] [CrossRef]
- Gholipour, M.; Alinia, M.M. Considerations on the pushover analysis of multi-story steel plate shear wall structures. Period. Polytech. Civ. Eng. 2016, 60, 113–126. [Google Scholar] [CrossRef]
- Wang, C.; Xiao, J.; Liu, W.; Ma, Z. Unloading and reloading stress-strain relationship of recycled aggregate concrete reinforced with steel/polypropylene fibers under uniaxial low-cycle loadings. Cem. Concr. Compos. 2022, 131, 104597. [Google Scholar] [CrossRef]
- TBEC-2018; Turkish Building Earthquake Code. T.C. Resmi Gazete: Ankara, Turkey, 2018.
- Available online: https://tdth.afad.gov.tr (accessed on 2 February 2022).
- SAP2000; Integrated Software for Structural Analysis & Design. Computers & Structures, Inc.: Berkeley, CA, USA, 2011.




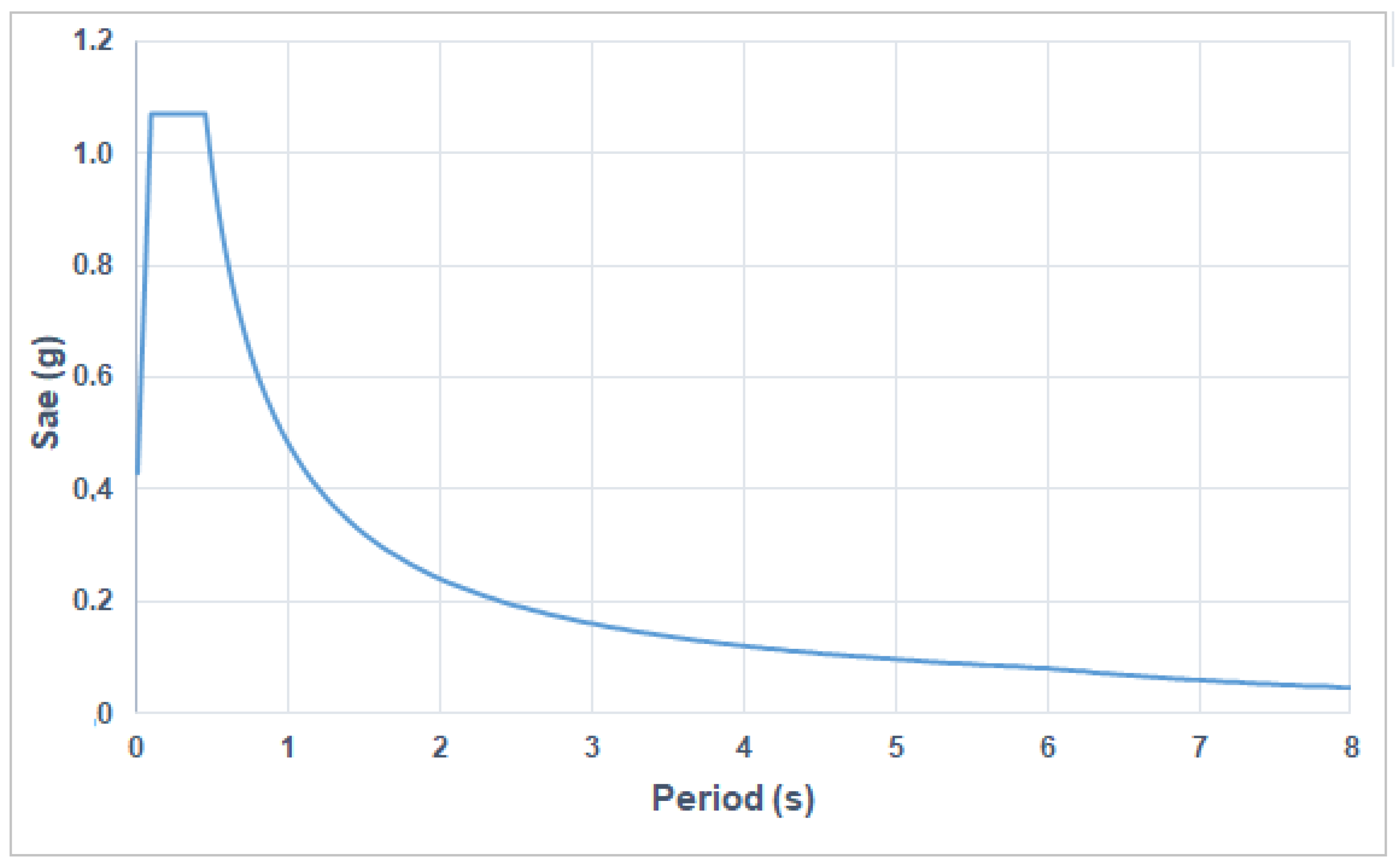









| Number of storeys | 7 |
| Storey height | 3 m |
| Concrete grade | C25 |
| Reinforcement grade | B420C |
| Dead load (g) | 4.5 kN/m2 |
| Live load (q) | 2 kN/m2 |
| Location of the structure (Latitude-Longitude) | 37.73534–30.305906 |
| Infill wall load (g) | 4 kN/m |
| Column stirrup reinforcement * | Φ8/100 (mm) |
| Beam stirrup reinforcement * | Φ8/100 (mm) |
| Local soil class | ZD |
| SDS | 1.0721 |
| SD1 | 0.4786 |
| Live load reduction coefficient (n) | 0.3 |
| Hill Slope Effect | Band-Type Window | Mezzanine Floor | |
|---|---|---|---|
| Axes with a short column | All columns on the 4th and 5th axes of the 1st storey | All columns on the 1st and 5th axes of the 1st storey | All axes of the 2nd storey |
| Short column length | 1.5 m | 0.7 m | 2 m |
| Number of short columns/total columns (%) | 5.71% (10/175) | 5.71% (10/175) | 14.29% (25/175) |
| Model | Reference Model | Band-Type Window | Hill-Slope Effect | Mezzanine Floor |
|---|---|---|---|---|
| Period (s) | 0.989 | 0.868 | 0.928 | 0.903 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Işık, E.; Ulutaş, H.; Harirchian, E.; Avcil, F.; Aksoylu, C.; Arslan, M.H. Performance-Based Assessment of RC Building with Short Columns Due to the Different Design Principles. Buildings 2023, 13, 750. https://doi.org/10.3390/buildings13030750
Işık E, Ulutaş H, Harirchian E, Avcil F, Aksoylu C, Arslan MH. Performance-Based Assessment of RC Building with Short Columns Due to the Different Design Principles. Buildings. 2023; 13(3):750. https://doi.org/10.3390/buildings13030750
Chicago/Turabian StyleIşık, Ercan, Hakan Ulutaş, Ehsan Harirchian, Fatih Avcil, Ceyhun Aksoylu, and Musa Hakan Arslan. 2023. "Performance-Based Assessment of RC Building with Short Columns Due to the Different Design Principles" Buildings 13, no. 3: 750. https://doi.org/10.3390/buildings13030750
APA StyleIşık, E., Ulutaş, H., Harirchian, E., Avcil, F., Aksoylu, C., & Arslan, M. H. (2023). Performance-Based Assessment of RC Building with Short Columns Due to the Different Design Principles. Buildings, 13(3), 750. https://doi.org/10.3390/buildings13030750










