Abstract
Conceptual cost estimation is an important step in project feasibility decisions when there is not enough information on detailed design and project requirements. Methods that enable quick and reasonably accurate conceptual cost estimates are crucial for achieving successful decisions in the early stages of construction projects. For this reason, numerous machine learning methods proposed in the literature that use different learning mechanisms. In recent years, the case-based reasoning (CBR) method has received particular attention in the literature for conceptual cost estimation of construction projects that use similarity-based learning principles. Despite the fact that CBR provides a powerful and practical alternative for conceptual cost estimation, one of the main criticisms about CBR is its low prediction performance when there is not a sufficient number of cases. This paper presents a bootstrap aggregated CBR method for achieving advancement in CBR research, particularly for conceptual cost estimation of construction projects when a limited number of training cases are available. The proposed learning method is designed so that CBR can learn from a diverse set of training data even when there are not a sufficient number of cases. The performance of the proposed bootstrap aggregated CBR method is evaluated using three data sets. The results revealed that the prediction performance of the new bootstrap aggregated CBR method is better than the prediction performance of the existing CBR method. Since the majority of conceptual cost estimates are made with a limited number of cases, the proposed method provides a contribution to CBR research and practice by improving the existing methods for conceptual cost estimating.
1. Introduction
Conceptual cost estimates are usually needed at the very early stages of construction projects for feasibility and budgeting decisions. As detailed design is performed after the feasibility decisions, the design drawings and specifications are not available during these early stages and conceptual cost estimates have to performed with very limited information. Hence, conceptual cost estimates are not expected to be as precise as the detailed cost estimates. On the other hand, since key project decisions are based on the conceptual cost estimates, inaccurate estimates may lead to lost opportunities and lower than expected returns []. Therefore, methods that enable quick and reasonably accurate conceptual cost estimates are crucial for achieving successful decisions in the early stages of construction projects.
Numerous statistical and machine learning methods have been presented in the literature for conceptual estimation of construction costs. The majority of proposed methods use historical data of project costs and the information of parameters impacting costs. In recent years, the case-based reasoning (CBR) method has received particular attention as it does not require the development of an explicit domain model unlike the majority of the statistical and machine learning methods. A review of CBR methods revealed that cost estimation has been the top CBR application area in construction management [].
In the CBR method, previous cases are adapted to determine a solution to a new problem or to make a prediction for a new case. One of the main advantages of CBR is that it does not require development of an explicit domain model []. CBR could also be used when the data of cases are incomplete or limited []. However, in cost estimation, as previous projects are not exactly the same as the new project, CBR may not achieve successful predictions when there are not a sufficient number of cases [].
Since the majority of conceptual cost estimates are based on predictions developed with limited small data sets, a few studies suggested compensating attributes deviations between the new case and the retrieved case for improving the accuracy of the CBR methods. Ji et al. (2010) [], Jin et al. (2012) [], and Jin et al. (2014) [] presented revision models for improving accuracy of the CBR methods for conceptual cost estimation. Ji et al. (2018) [] proposed a learning method for knowledge retention based on a data-mining approach to manage missing data set values.
In recent years, ensemble learning methods have received increasing attention within the machine learning community as they are very effective in a broad spectrum of problem domains and real-world applications [,,]. Numerous ensemble learning methods have been proposed to promote diversity among different models to reduce variance and improve accuracy. One of the ensemble learning methods is bootstrap aggregation. In the bootstrap aggregating (bagging) method, multiple versions of a predictor are generated by making bootstrap replicates of the learning set and these multiple versions are used to obtain an aggregated predictor for improving accuracy []. Bagging is very well suited for problems with small training data sets such as conceptual cost estimation []. Tests on real and simulated data sets have shown that the bagging method can improve the accuracy significantly for classification and regression problems [].
Despite the fact that little research is focused on revisions models and learning methods, ensemble learning methods such as bagging have not been considered in the literature for improving the accuracy of CBR methods. Within this context, the main objective of this paper is to narrow these gaps in the literature and present a bootstrap aggregated CBR method for improving the accuracy of conceptual cost estimates.
2. CBR Method for Conceptual Cost Estimation
CBR has received increasing attention in the construction management literature in recent years, particularly for estimation of construction costs []. In an early study, Yau and Yang (1998) [] showed the potential use of CBR for cost estimating using hypothetically generated cost data. Kim et al. (2005) [] compared performances of regression, ANN, and CBR methods based on the historical data of building projects and concluded that NN and CBR models were appropriate for estimating construction costs. Ji et al. (2011) [] developed a military facility cost estimation system using CBR.
Numerous techniques were proposed to improve the accuracy of CBR methods for conceptual cost estimation. One of the most common techniques is to use genetic algorithms (GA) for optimal determination of the attribute weights. Ji et al. (2011) [] developed an attribute weight assignment technique in which GA optimization was performed along with a similarity scoring method based on the Euclidean distance concept. Choi et al. (2013) [] combined rough set theory, CBR, and GA techniques to predict the costs of public road construction projects. Ji et al. (2018) [] presented a learning method for knowledge retention in CBR cost models that updated the attribute weight using a GA. Ji et al. (2011) [], Jin et al. (2012) [], and Jin et al. (2014) [] focused on revision algorithms and Ahn et al. (2014) adopted the impulse–momentum theorem of physics for improving the accuracy of the CBR methods. Ahn et al. (2020) [] examined the impact of normalization techniques on the performance of CBR for conceptual cost estimation.
The majority of the CBR techniques that have been proposed for improving the accuracy of the CBR cost models focus on the optimization of attribute weights or revision algorithms. However, CBR may not provide adequate accuracy when limited data are available for cost estimation. The literature includes very limited alternatives for improving the accuracy of CBR methods when there is not a sufficient number of cases. Ensemble learning methods, particularly bagging, may provide a high potential for improving the accuracy of conceptual cost estimates especially when limited data are available. Few researchers have used bagging to improve the accuracy of regression trees and subset selection in linear regression [] and support vector machines []; however, to the best knowledge of the authors, the bagging method has not been used to improve the accuracy of CBR methods. Hence, the main objective of this research is to present a new bootstrap aggregated CBR method to improve the accuracy of existing CBR methods for conceptual cost estimation.
3. CBR Method with Bagging
In the proposed bootstrap aggregated CBR method (CBR-BSR), several training sets are produced using the original training set with the bootstrap sampling method as summarized in Figure 1. A CBR model is developed for each training data set using a GA- integrated framework and each CBR model is used to predict the test sample. Finally, the predictions are combined to determine an aggregate point estimate for each project in the test sample. In the following sections, the proposed CBR method with bagging is explained.
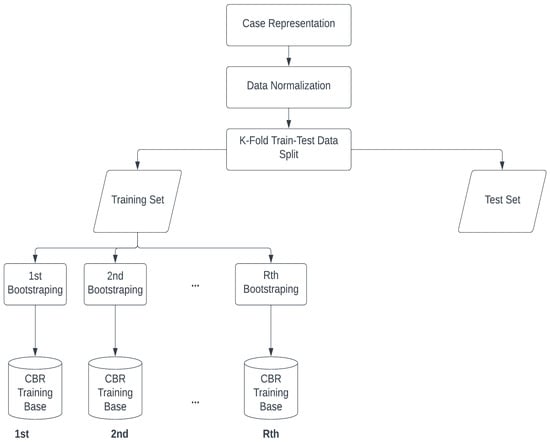
Figure 1.
CBR-BSR Train-Test Split.
3.1. Bootstrap Method
The bootstrap method involves re-sampling of the existing data in which new R samples, each the same size as the observed data, are randomly drawn with a replacement from the observed data. The main idea of bootstrap is to mimic the process of sampling observations from the population by resampling data from the observed sample []. Sonmez (2008) [] integrated regression and probabilistic cost estimation techniques with bootstrap for range estimation of construction costs. In a similar study, bootstrap is used to quantify the prediction variability of neural network models for cost estimation []. Gardner et al. (2017) [] used bootstrap-enabled stochastic conceptual cost estimating of highway projects with neural networks without requiring any assumptions regarding the probability distributions. The bootstrap method is utilized in a quantity range estimation framework using support vector regression []. Tsai and Li (2008) [] emphasized the potential of bootstrap to generate virtual samples for filling the information gaps of sparse data, and applied the bootstrap method for the modeling of manufacturing systems with neural networks. However, to the best knowledge of the authors, the bootstrap method has not been used in the literature for improving the accuracy of CBR methods, particularly for conceptual cost estimation, which is the main focus of the proposed method.
3.2. Data Normalization and Resampling
In the CBR-BSR, first bootstrap resampling is performed. Hence, the proposed method enables R samples instead of a single case sample for training. The data are normalized before bootstrap resampling is executed. Ji et al. (2010b) [] and Ahn et al. (2020) [] emphasized the positive effect of data preprocessing on the accuracy of CBR cost models. In a study of performance evaluation of normalization-based CBR models, Ahn et al. (2020) [] concluded that interval and ratio normalization are appropriate methods. In this study, all data are normalized first using a min-max normalization with a scale of 0–1, and the normalized data are split into training and testing sets. Then, the training case sample c = (c1, c2, …, cn), which includes the data of project1, project2, …, projectn, is resampled with the bootstrap method in which R bootstrap case samples c1* = (c11*, c12*, …, c1n*), c2* = (c21*, c22*, …, c2n*), …, cr* = (cr1*, cr2*, …, crn*) of a random sample with size n are drawn with a replacement from the population of n projects (c1, c2, …, cn) that are in the test set. The star notation indicates that c* is not the actual data set, c, but rather a resampled version of c. The bootstrap data set (c1*, c2*, …, cr*) consists of members of the original data set (c1, c2, …, cn), some appearing zero times, some appearing once, and some appearing twice or more. The proposed CBR-BSR method uses all of the resampled case data c1* = (c11*, c12*, …, c1n*), c2* = (c21*, c22*, …, c2n*), …, cr* = (cr1*, cr2*, …, crn*) in the CBR training database instead of the single case sample c = (c1, c2, …, cn) as shown in Figure 1.
3.3. Case Retrieval and Case Reuse
The second step in the proposed method is case retrieval and case reuse. To retrieve similar cases from the database of training cases, a total similarity score is calculated for each test case using Equation (1):
where denotes the similarity score between the training set, T, and test set variables, and t and wi denote the attribute weight of each independent variable, i. Similarity scores of each independent variable in total, I, and number of attributes are measured with modified Euclidian distance [] using Equation (2):
where t is the case that is being tested to find the most similar training cases in the CBR database. Modified Euclidian distance shows the similarity index of a variable where 0 denotes lowest similarity and 1 denotes highest similarity. Attribute weights, wi, measure how much an independent variable contributes to the total similarity score.
The total similarity score shows how much a test case is similar to a training case sample. The similar cases are determined according to the kth nearest neighborhood algorithm [] using the total similarity score; the most similar k training cases that have the highest similarity score are then reused to generate the prediction of the current test case in a query. The value of parameter k needs to be determined for the CBR model to make a prediction. If k = 1, then the most similar case is accepted as the predicted value. If k = 3, then the most similar 3 cases are averaged for the predicted value. Finding the optimal parameter k can be obtained by cross validation or a grid search procedure. Once the parameter k is determined, the average of dependent variable values of the similar k training cases are used to predict the dependent variable value of the new case.
3.4. GA Attribute Weight Optimization Framework
Attribute weights of independent variables are used to calculate the total similarity score. The effect of each independent variable’s similarity score on the total similarity score is proportional to the attribute weights. Attribute weights can be optimized to improve the accuracy of the CBR models. GAs that originated from the evolutionary computing principles [] are commonly used to optimize the attribute weights of the CBR models [,,].
A GA framework is integrated into the proposed CBR-BSR method for optimization of the attribute weights. The GA weight optimization framework is applied while creating an initial population with size P as shown in Figure 2. Since I is the total number of independent variables, and each independent variable is denoted as i, each chromosome consists of I number of genes. The initial population is generated randomly; however, it is scaled such that the summation of the attribute weights satisfies Equation (3). An example chromosome is shown in Figure 3.
A fitness evaluation function is used to determine the chromosomes that will survive in the next generation. The selection mechanism is based on fitness evaluation. In this regard, a fitness evaluation function that measures the closeness of fit of the predictions is defined as in Equation (4), where Mean Absolute Percent Error (MAPE) measures the closeness of fit values of the actual and predicted values of the independent variables according to each chromosome’s attribute weights. The proposed fitness evaluation function enables a larger chance of survival for the solutions with lower MAPE, where MAPE is a measure for the fit of the CBR model to the test cases for the attribute weights determined by a particular chromosome, and is calculated by Equations (4) and (5):
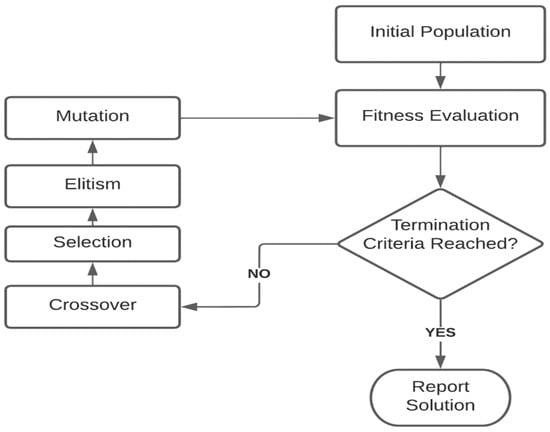
Figure 2.
GA Attribute Weight Optimization Framework.
New solutions are obtained though crossover and mutation operations. A one-point crossover methodology is applied in order to create new candidate solutions. A random number, m, is generated between 1 and I, where I is the total number of independent variables. Genes from 1 to m and m + 1 to I between father and mother chromosomes are exchanged. The amount of crossover is determined according to the crossover ratio. Mutation is applied in order to overcome premature convergence to a local optimum. In mutation, a chromosome is selected randomly and only one gene of the selected chromosome is randomly changed with a random number between 0 and 1. The number of mutations is determined by the mutation ratio. For each crossover and mutation, the operation genotype of the chromosomes is normalized so that Equation (3) is satisfied.

Figure 3.
GA Chromosome Representation.
The chromosomes that will survive in the next generation are determined by an elitist selection method, where a predetermined ratio of the best chromosomes is directly copied to the next generation. The elitist selection method guarantees survival of the best chromosomes in the next generation. The idea of evolutionary computing generates higher changes to those chromosomes that have higher fitness values. Therefore, as the population evolves, better chromosomes should have a higher chance to be selected. The roulette wheel selection method is used to determine the chromosomes that will survive in the next generation in addition to the best chromosomes selected by the elitist selection. A probability of selection, P(s), is assigned to each chromosome, s, based on their fitness value ratio according to Equation (6), in which S is the total population size:
GA parameter selection is an important step in order to achieve high quality solutions. DeJong (1975) [] and Bramlette (1991) [] suggested that the optimal range values for population size should be in the range of [50–100], crossover ratio between 50% to 70%, and mutation ratio around 0.01. Different combinations of GA parameters were tested for adequate selection of the parameters. Finally, a crossover ratio of 60%, a population size of 50, and a mutation rate of 0.01 were selected as the GA final parameters.
In CBR-BSR calculations, as the number of generations increases, the total computation time increases significantly due to the computational load. Since a fast convergence is needed, the number of generations is selected as 100 and 1000. The results of the 100 generation and 1000 generation are compared with each other, and due to the lower computation load and fast convergence, 100 generation is selected.
3.5. Aggregation
Ensemble learning heavily relies on the combining strategy of multiple predictions into one prediction. In the proposed CBR-BSR method, bagging [] is selected as the ensemble learning method. Bagging combines each bootstrapped data set’s prediction and uses the average of the predictions as the final prediction, as shown in Figure 4. The advantages of bagging are two-fold. First, CBR can learn from a diverse set of training sets that were created using bootstrapping. Second, bagging as an ensemble learner reduces the overfitting of the model [].
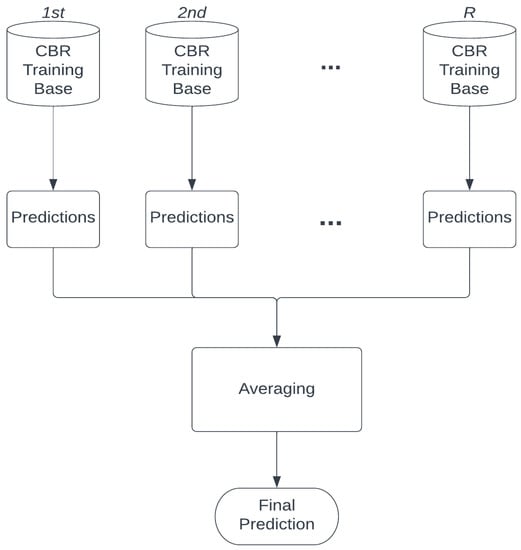
Figure 4.
Bagging Overview.
4. Model Comparison
4.1. Data Sets
In order to compare the prediction performance of the proposed CBR-BSR method with the existing CBR methods, and to highlight its domain independence, three data sets are used. Data sets are taken from previous cost estimating studies and are summarized in Table 1. Data set 1 consists of 24 office building costs that were published in Karshenas (1984) []. Data reported in this study consists of location, time of construction, number of floors, building height, floor area, and total cost data of office buildings. Total cost data were adjusted for location and the year of construction. Data set 2 consists of the field canal improvement project compiled from Elmousalami et al. (2018a) [] and Elmousalami et al. (2018b) []. Area served, pipeline length, number of irrigation valves, and construction year of field canal improvement project data for the years 2010 to 2015 are included in the data set. Data set 3 consists of 30 continuing care retirement community projects (CCRC) in the USA used in the research conducted by Sonmez (2004) []. Sonmez (2004) [] used seven independent variables and these variables were eliminated through a backward elimination strategy. Finally, time index, total building area, location index, percent health center and common area, and area per unit are the independent variables used to build the models in the study.

Table 1.
Test Cases.
4.2. Test Results
The performance of the proposed CBR-BSR method is compared with the existing CBR method with a GA (CBR-GA) prediction attribute weight optimization to reveal the advancement achieved with the new method CBR-BSR. In order to ensure fair evaluation of the CBR-BSR method performance, random selection of test data sets is crucial. A five-fold cross-validation technique is used to make the comparisons using the aforementioned three data sets. Five-fold cross-validation requires random splitting of each data set into a train and test split. For each and every fold, 20% of the total data set is used for testing purposes and the remaining 80% is used for training purposes. Averaging five- fold results provide a reasonable and fair comparison of the overall results since all data sets are used for testing purposes.
In the first data set, for each fold, the CBR-BSR method improved the prediction performances of the CBR-GA method except for Fold 5, as shown in Table 2. The overall performance of the CBR-BSR method was improved from 32.75% to 25.88%. The reason for low performance in Fold 5 is due to the random selection mechanism of the test cases. However, the five-fold cross validation technique uses an average of all folds’ MAPE% values, which outperformed the existing CBR-GA method for all three data sets. For the second data set, the MAPE values of CBR-BSR (11.32%) were less than the MAPE values of CBR-GA (15.29%), as shown in Table 3. The proposed CBR-BSR method with a MAPE value of 15.59% also performed better than CBR-GA for Data set 3, which had a MAPE value of 16.38%, as shown in Table 4.

Table 2.
MAPE % Performances of Data set 1.

Table 3.
MAPE % Performances of Data set 2.

Table 4.
Prediction Performances of Data set 3.
To test the significance of the improvements achieved with the new method, a paired t-test with α = 0.05 is conducted using all of the absolute percent error values that are obtained from the three data sets. The t value for the conducted test was calculated as 2.19 and the critical t value (tc) for α = 0.05 with degrees of freedom (df) = 221 is 1.97. Thus, the results revealed that CBR-BSR predictions are statistically improved compared to the CBR-GA for the three data sets used in this study, which underlines the contribution of the new method.
5. Conclusions
In this paper, a bootstrap aggregated CBR method was presented for conceptual cost estimation of construction projects. The ensemble learner uses the bagging method to generate multiple versions of the predictor by making bootstrap replicates of the learning set. These multiple versions are used to obtain an aggregated predictor for improving accuracy. Three data sets were used to evaluate the prediction performance of the new ensemble learner-integrated CBR method and to highlight the method’s domain independence. The results reveal that bootstrap aggregated CBR improves the prediction performance of the existing CBR method. Hence, the proposed method presents an advancement to the research in CBR and to the practice, in particular when a limited number of cases are available for conceptual cost estimation.
The focus of this paper was the CBR method, as conceptual cost estimation is usually performed with limited data sets and CBR may not achieve successful predictions when there is not a sufficient number of cases. However, the bootstrap aggregated CBR method can be integrated into other machine learning methods, such as neural networks, or support vector regression for improving conceptual cost estimates when limited data are available. Integration of alternative ensemble learning methods, such as random forest trees or AdaBoost, could be areas for future research on conceptual cost estimation. Moreover, results can also be validated with more data sets from different research areas. The results of this paper indicate the potential of bootstrap aggregation for improving the prediction accuracy of CBR in conceptual cost estimation with limited data availability.
Author Contributions
Conceptualization, F.U. and R.S.; methodology, F.U. and R.S.; software, F.U.; validation, F.U. and R.S; formal analysis, F.U.; investigation, F.U. and R.S.; resources, F.U. and R.S.; data curation, R.S.; writing—original draft preparation, F.U. and R.S.; writing—review and editing, F.U. and R.S.; visualization, F.U.; supervision, R.S.; project administration, R.S.; funding acquisition, F.U and R.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data sets used in this study can be found from reference papers.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| N | Training Case Sample Size |
| n | Training Case Sample Index Starting From 1 to N |
| T | Test Case Sample Size |
| t | Test Case Sample Index Starting From 1 to T |
| I | Independent Variable Size |
| i | Independent Variable Starting From 1 to I |
| R | Bootstrapped Training Sample |
| r | Bootstrapped Training Sample Index Starting From 1 to R |
| V | Predicted Sample Size |
| v | Predicted Values Starting From 1 to V |
| m | Random Number Between 1 to I |
References
- Oberlender, G.D.; Trost, S.M. Predicting accuracy of early cost estimates based on estimate quality. J. Constr. Eng. Manag. 2021, 127, 173–182. [Google Scholar] [CrossRef]
- Hu, X.; Xia, B.; Skitmore, M.; Chen, Q. The application of case-based reasoning in construction management research: An overview. Autom. Constr. 2016, 72, 65–74. [Google Scholar] [CrossRef]
- Watson, I.; Marir, F. Case-based reasoning: A review. Knowl. Eng. Rev. 1994, 9, 327–354. [Google Scholar] [CrossRef]
- Kolodner, J.L. An introduction to case-based reasoning. Artif. Intell. Rev. 1992, 6, 3–34. [Google Scholar] [CrossRef]
- Jin, R.; Cho, K.; Hyun, C.; Son, M. MRA-based revised CBR model for cost prediction in the early stage of construction projects. Expert Syst. Appl. 2012, 39, 5214–5222. [Google Scholar] [CrossRef]
- Ji, S.H.; Park, M.; Lee, H.S. Data preprocessing–based parametric cost model for building projects: Case studies of Korean construction projects. J. Constr. Eng. Manag. 2010, 136, 844–853. [Google Scholar] [CrossRef]
- Jin, R.; Han, S.; Hyun, C.; Kim, J. Improving accuracy of early stage cost estimation by revising categorical variables in a case-based reasoning model. J. Constr. Eng. Manag. 2014, 140, 04014025. [Google Scholar] [CrossRef]
- Ji, S.H.; Ahn, J.; Lee, E.B.; Kim, Y. Learning method for knowledge retention in CBR cost models. Autom. Constr. 2018, 96, 65–74. [Google Scholar] [CrossRef]
- Polikar, R. Ensemble learning. In Ensemble Machine Learning; Springer: Boston, MA, USA, 2012; pp. 1–34. [Google Scholar]
- Sagi, O.; Rokach, L. Ensemble learning: A survey. Wiley Interdiscip. Rev. Data Min. Knowl. Discov. 2018, 8, e1249. [Google Scholar] [CrossRef]
- Campagner, A.; Ciucci, D.; Cabitza, F. Aggregation models in ensemble learning: A large-scale comparison. Inf. Fusion 2023, 90, 241–252. [Google Scholar] [CrossRef]
- Ferreira, A.J.; Figueiredo, M.A. Boosting algorithms: A review of methods, theory, and applications. Ensemble Mach. Learn. Methods Appl. 2012, 35–85. [Google Scholar] [CrossRef]
- Breiman, L. Bagging predictors. Mach. Learn. 1996, 24, 123–140. [Google Scholar] [CrossRef]
- Yau, N.J.; Yang, J.B. Case-based reasoning in construction management. Comput. Aided Civ. Infrastruct. Eng. 1998, 13, 143–150. [Google Scholar] [CrossRef]
- Kim, S.Y.; Choi, J.W.; Kim, G.H.; Kang, K.I. Comparing cost prediction methods for apartment housing projects: CBR versus ANN. J. Asian Archit. Build. Eng. 2005, 4, 113–120. [Google Scholar] [CrossRef]
- Ji, S.H.; Park, M.; Lee, H.S.; Ahn, J.; Kim, N.; Son, B. Military facility cost estimation system using case-based reasoning in Korea. J. Comput. Civ. Eng. 2011, 25, 218–231. [Google Scholar] [CrossRef]
- Choi, S.; Kim, D.Y.; Han, S.H.; Kwak, Y.H. Conceptual cost-prediction model for public road planning via rough set theory and case-based reasoning. J. Constr. Eng. Manag. 2014, 140, 04013026. [Google Scholar] [CrossRef]
- Ahn, J.; Ji, S.-H.; Ahn, S.-J.; Park, M.; Lee, H.-S.; Kwon, N.; Lee, E.B.; Kim, Y. Performance evaluation of normalization-based CBR models for improving construction cost estimation. Autom. Constr. 2020, 119, 103329. [Google Scholar] [CrossRef]
- Croux, C.; Joossens, K.; Lemmens, A. Trimmed bagging. Comput. Stat. Data Anal. 2007, 52, 362–368. [Google Scholar] [CrossRef]
- Efron, B.; Tibshirani, R.J. An Introduction to the Bootstrap; Chapman and Hall: New York, NY, USA, 1993. [Google Scholar]
- Sonmez, R. Parametric range estimating of building costs using regression models and bootstrap. J. Constr. Eng. Manag. 2008, 134, 1011–1016. [Google Scholar] [CrossRef]
- Sonmez, R. Range estimation of construction costs using neural networks with bootstrap prediction intervals. Expert Syst. Appl. 2011, 38, 9913–9917. [Google Scholar] [CrossRef]
- Gardner, B.J.; Gransberg, D.D.; Rueda, J.A. Stochastic conceptual cost estimating of highway projects to communicate uncertainty using bootstrap sampling. ASCE-ASME J. Risk Uncertain. Eng. Syst. Part A Civ. Eng. 2017, 3, 05016002. [Google Scholar] [CrossRef]
- Idowu, O.S.; Lam, K.C. Conceptual Quantities Estimation Using Bootstrapped Support Vector Regression Models. J. Constr. Eng. Manag. 2020, 146, 04020018. [Google Scholar] [CrossRef]
- Tsai, T.I.; Li, D.C. Utilize bootstrap in small data set learning for pilot run modeling of manufacturing systems. Expert Syst. Appl. 2008, 35, 1293–1300. [Google Scholar] [CrossRef]
- Ji, C.; Hong, T.; Hyun, C. CBR revision model for improving cost prediction accuracy in multifamily housing projects. J. Manag. Eng. 2010, 26, 229–236. [Google Scholar] [CrossRef]
- Hyung, W.-G.; Kim, S.; Jo, J.-K. Improved similarity measure in case-based reasoning: A case study of construction cost estimation. Eng. Constr. Archit. Manag. 2020, 27, 561–578. [Google Scholar] [CrossRef]
- Altman, N.S. An Introduction to Kernel and Nearest-Neighbor Nonparametric Regression. Am. Stat. 1992, 46, 3. [Google Scholar]
- Holland, J.H. Adaptation in Natural and Artificial Systems; University of Michigan Press: Ann Arbor, MI, USA, 1975. [Google Scholar]
- DeJong, K. Analysis of the Behavior of a Class of Genetic Adaptive. Ph.D. Thesis, University of Michigan, Ann Arbor, MI, USA, 1975. [Google Scholar]
- Bramlette, M.F. Initialization, mutation and selection methods in genetic algorithms for function optimization. In Proceedings of the Fourth International Conference on Genetic Algorithms, San Diego, CA, USA, 13–16 July 1991; pp. 100–107. [Google Scholar]
- Fitzgerald, J.; Azad, R.M.A.; Ryan., C. A bootstrapping approach to reduce over-fitting in genetic programming. In Proceedings of the 15th Annual Conference Companion on Genetic and Evolutionary Computation, Amsterdam, The Netherlands, 6–10 July 2013; pp. 1113–1120. [Google Scholar]
- Karshenas, S. Predesign cost estimating method for multistory buildings. J. Constr. Eng. Manag. 1984, 110, 79–86. [Google Scholar] [CrossRef]
- ElMousalami, H.H.; Elyamany, A.H.; Ibrahim, A.H. Predicting conceptual cost for field canal improvement projects. J. Constr. Eng. Manag. 2018, 144, 04018102. [Google Scholar] [CrossRef]
- Elmousalami, H.H.; Elyamany, A.H.; Ibrahim, A.H. Evaluation of cost drivers for field canals improvement projects. Water Resour. Manag. 2018, 32, 53–65. [Google Scholar] [CrossRef]
- Sonmez, R. Conceptual cost estimation of building projects with regression analysis and neural networks. Can. J. Civ. Eng. 2004, 31, 677–683. [Google Scholar] [CrossRef]
- Elmousalami, H.H. Artificial intelligence and parametric construction cost estimate modeling: State-of-the-art review. J. Constr. Eng. Manag. 2020, 146, 03119008. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).