Abstract
To build the equivalent relationship of the mechanical behavior of ring nets under static punching and dynamic impact conditions, a series of tests with different parameters were conducted. The equivalent coefficients of breaking force, breaking displacement, and net energy dissipation were defined to describe the potential relationship. Besides, sensitivity analyses were made. The results showed that, with the increase of impact velocity, the equivalent coefficients of breaking force decreased as a power function, and the equivalent coefficients of breaking displacement and net energy dissipation both decreased linearly. As the ring diameter increased, the equivalent coefficients of breaking force increased linearly, but the equivalent coefficients of breaking displacement and net energy dissipation both decreased linearly. With the increase of the aspect ratio of ring net, the equivalent coefficients of breaking force and breaking displacement decreased linearly and exponentially, respectively, and the equivalent coefficients of net energy dissipation decreased as a power function. With the increase of the ratio of loading head area to ring net area, the equivalent coefficients of breaking force increased as a power function, and the equivalent coefficients of breaking displacement and net energy dissipation decreased and increased linearly, respectively. The influence degrees of these parameters are as follows: impact velocity > ring diameter > aspect ratio of ring net > ratio of loading area to ring net area. Based on these four parameters, the equivalent coefficient formulas of static punching and dynamic impact were established.
1. Introduction
A steel wire ring net with the characteristic of flexibility and high strength is an important intercept component of flexible protection systems for rockfall mitigation (Figure 1). The net is formed by multiple rings loosely connected [1]. A single ring is usually made of steel wire with a diameter of 3 mm and a tensile strength of 1770 Mpa, which is wound with different numbers of turns and fixed with buckles.

Figure 1.
Ring net applications: (a) active flexible protection structure; (b) passive flexible protection structure; (c) flexible rock-shed; (d) guided flexible protection structure.
Ring nets may be subject to different load patterns, depending on the type of protection structure. For example, in a flexible active protective structure, as shown in Figure 2a, the net is anchored to the slope by rock bolts. When potentially dangerous rocks become loose and fall due to external factors, the movement space of rocks is limited by the net, and the net is subjected to an approximate static load. Castro-Fresno et al. [2] designed a static load test frame and studied the behavior of ring nets under concentrated and distributed loads. Compared to a concentrated load, the ultimate deformation of the net under distributed load decreased, but the ultimate bearing capacity increased by two times. Bertrand et al. [3,4] conducted static punching tests of a 2 m × 2 m ring net to reveal the relationship between punching bearing capacity and contact area. Albrecht et al. [5] conducted in-plane tension tests of ring nets and built a simulation model based on the discrete element method. Xu et al. [6] proposed a method for calculating the energy dissipation of a ring net based on static punching tests. Nicot et al. [7] carried out the static tensile test of a single ring and found that the deformation process of the ring has the characteristics of three stages, and they built a mechanical model to simulate the constitutive relationship curve of the ring net. Paola et al. [8] studied the influence of different connection nodes on the mechanical properties of wire rope net and carried out an in situ test of the active net system. Antonio et al. [9] studied the influence of boundary conditions, punching element size, action position, anchor plate size, and other factors on the bearing capacity of the net through tests and numerical simulation analysis.
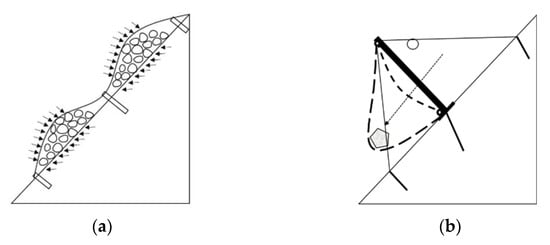
Figure 2.
Different load patterns: (a) quasi-static load; (b) dynamic load.
In passive flexible protection systems and flexible rock sheds (Figure 2b), the net is subjected to typical dynamic impact loads during arresting rockfalls. The deformation ability of the net basically determines its buffering capacity. Peila et al. [10] designed and carried out the full scale impact test of the passive protective net and studied the impact mechanical response of the protective net system under different impact energy. Gerber et al. [11] carried out an impact test of a 250 kJ–3000 kJ passive protective net and found that, with the increase of impact energy, the maximum impact deformation and residual deformation of the mesh increased in a logarithmic function, and the increase was not obvious after the impact energy reached 2000 kJ. Tan et al. [12] compared the deformation and impact force of flexible and rigid structures under the same impact condition and found that the impact duration of flexible structures increased to 4–8 times that of rigid structures, and the impact force of flexible structures decreased more than 50% compared to rigid structures. Buzzi et al. [13,14] carried out impact tests in a self-designed vertical rockfall impact test frame and analyzed the failure types of the net under rock impact with different sizes and shapes, and then they revealed the influence of rock size on the energy dissipation capacity of the net. Yu et al. [15] found that the number of steel wire strands and boundary constraints influenced the impact deformation of the net, but the deformation remained relatively stable at about 30–40% of the system deformation. Koo et al. [16] compared the dynamic impact response of a flexible net subjected to the impact of sphere-shaped blocks and flat plate blocks and found that the deformation was significantly reduced under flat plate block impact. Qi et al. [17] expanded and analyzed the impact of the falling rock rotation on a passive protection system through numerical simulation. It was found that, as the ratio of rotational kinetic energy to translational kinetic energy increases, the net deformation decreases.
Thus far, most research on ring nets has focused on the behavior under static or dynamic impact conditions individually. According to the European Assessment Document [18], static tensile and quasi-static punching tests on the net should be conducted before they can be adopted in a flexible protective structure. However, a dynamic impact test is not required. It is unknown whether the results of static punching tests are directly applicable to dynamic loads, as few studies have compared the mechanical behavior of ring nets under static and dynamic loads. To fill this research gap, a series of static punching tests and dynamic impact tests were conducted, combined with numerical analysis, to shed light on the equivalent relationship of the mechanical behavior of ring nets under these test conditions. The findings hope to provide a reference for ring net designs and applications.
2. Static Punching Test
2.1. Test Equipment
The test equipment adopted in the static punching test comprised a punching test frame, spherical crown punching head, connecting shackle, displacement sensor, tension sensor, and hydraulic actuator (Figure 3). Positioning holes were located around the base beam and were used to connect the net to the punching test frame by shackles. The size of the ring net was 3 m × 3 m. The diameter of the bottom surface of the spherical crown punching head was 1 m, which was placed directly below the center of the fixed flexible ring net and connected with a plate hinge pin. A tension sensor and a displacement sensor were used to collect the force and deformation synchronously.
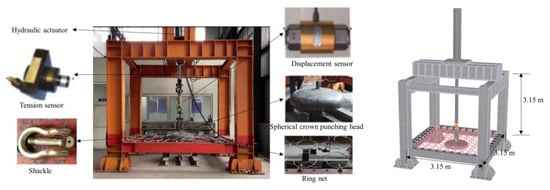
Figure 3.
Test equipment.
2.2. Test Conditions and Loading Methods
The deformation and force characteristics of ring nets with different numbers of windings were investigated by static punching tests. To ensure the reliability of the test, three sets of tests were carried out for each ring net specification. Table 1 shows the test conditions. In the preparation stage of the test, the spherical crown punching head was slowly lifted by the hydraulic actuator until the bottom surface of the punching head was parallel to the initial ring net surface to offset the initial ring net relaxation. During the test, the ring net deformed in conjunction with the lifting of the punching head until the breakage of the ring net. The whole punching process was recorded by a high-speed camera with 500 fps. As shown in Figure 3, the punching force and displacement were recorded by a tension sensor and a displacement sensor, respectively.

Table 1.
Test conditions.
2.3. Static Test Process and Results
After the test started, the ring net began to tighten as the punching head was lifted, leading to the relative sliding between the rings and tension development. With further loading, the ring net began to deform. Bending deformation progressed to tensile deformation until the ring net reached the limit state. The central rings that had direct contact with the loading head changed from a perfect circle to an ellipse and finally a trapezoid. The rings, which were directly connected to the boundary shackles, converted the perfect circle into an ellipse and finally a triangle. The middle rings were transformed from a perfect circle to an ellipse and finally a rectangle (Figure 4). The overall ring net was in the shape of an inverted “V.” Loading continued until the ring net broke. The shape of the net after breaking is presented in Figure 4c. The failure position was located at the edge of the punching head. Figure 5 shows the force-displacement curves of ring nets with diverse specifications obtained in the test, with the position of 85% of total deformation approximated as the boundary state of net breakage.

Figure 4.
Test process: (a) ring net tightening; (b) ring deformation before breakage; (c) ring net after broken.
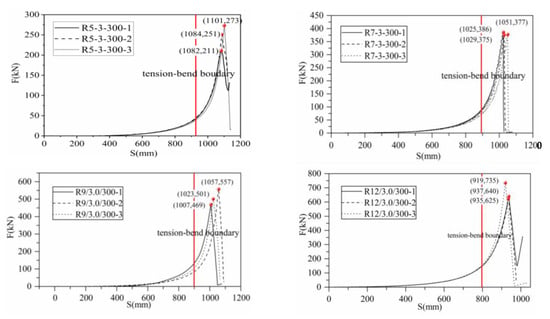
Figure 5.
Force displacement curves of the ring net with different specifications.
The breaking forces and breaking displacements of ring nets with different specifications are shown in Table 2. The force-displacement curve was integrated to obtain the energy absorbed by the ring net. As the ring net winding number was increased from 5 to 12, the punching displacement of the ring net decreased by 14.6%, the punching force increased by 170.5%, and the energy dissipation increased by 174.7%.

Table 2.
Breaking force and breaking displacement of ring nets with different specifications under a static punching condition.
3. Dynamic Impact Test
3.1. Test Equipment
The dynamic impact test frame was a rigid frame composed of steel columns and steel beams placed on concrete columns. The main part of the frame was composed of four steel columns and four steel beams. The drop weight was 0.76 t and 0.8 m in diameter. The size of the ring net was 3.9 × 3.9 m. The ring net was attached to the steel beams by surrounding shackle connectors (Figure 6).
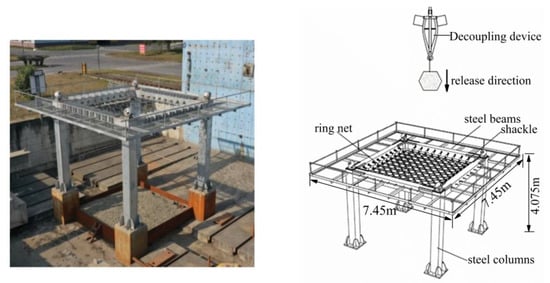
Figure 6.
Dynamic impact test device.
3.2. Test Conditions and Loading Methods
During the test, the drop weight was lifted to a predetermined height and then released to fall freely to impact the ring net. The entire impact process was recorded by a high-speed camera with 500 fps, and an accelerometer was placed inside the drop weight to record the impact-related data. The test cases are shown in Table 3.

Table 3.
Test cases.
3.3. Dynamic Test Process and Results
Before the drop weight touched the ring net, the ring net was in a natural state of relaxation. After the drop weight touched the net, the ring net began to tighten and finally break. Before the block penetrated the net, the ring net was in a “V” shape (Figure 7), the shape of the rings at the impact area was approximately rectangular, and the shape of the rings connected with the shackle changed to a triangle shape. The force-displacement curves of the drop weight are illustrated in Figure 8. When time t = 0 s, the drop weight contacted the net. The residual kinetic energy of the drop weight at the moment of mesh breakage was subtracted from the total impact energy to obtain the maximum impact energy that the net could withstand. The ring net breaking force and breaking displacement under different specifications are shown in Table 4. With the increase in the ring net winding number from 5 to 12, the ring net breaking displacement decreased by 9.72%, the ring net breaking force increased by 131.08%, and the ring net energy dissipation increased by 183.98%.

Figure 7.
Test process: (a) test rock falls freely; (b) test rock impacts the ring net; (c) failure point.
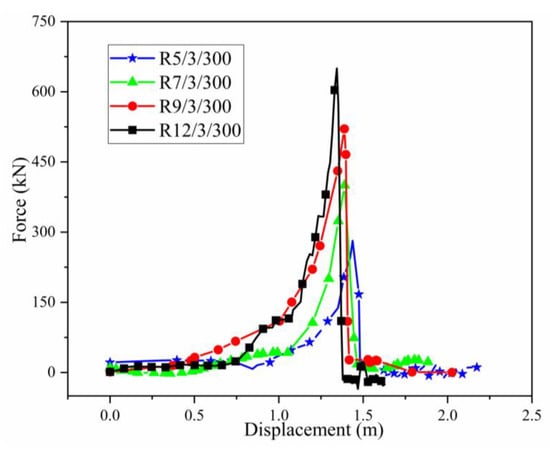
Figure 8.
Force displacement curves of the ring net with different specifications.

Table 4.
Breaking force and breaking displacement of ring nets with different specifications under a dynamic impact condition.
4. Comparative Analysis of Static and Dynamic Test Results
To facilitate a comparison of the mechanical properties of the ring net under the aforementioned test conditions, the equivalent coefficients of breaking force (kF), breaking displacement (kD), and net energy dissipation (kE) are defined below (Equation (1)):
where FD and FS are the ring net breaking force, SD and SS are the ring net breaking displacement, and ED and ES are the ring net energy dissipation under the dynamic impact test and static punching test, respectively.
As the size of the net used in the static test and the dynamic test was not the same, the equivalent mechanical behaviors of the ring net in static tests the size of 3.9 m × 3.9 m and a loading punching head with the diameter of 0.8 m were calculated according to the analytical method of Guo et al. [19]. The calculation data are shown in Table 5.

Table 5.
Equivalence breaking force and breaking displacement of ring nets with different specifications under a static punching condition.
The static and dynamic test data (Table 2 and Table 5) were substituted in Equation (1) to generate the distribution of each generation coefficient, as shown in Figure 9.
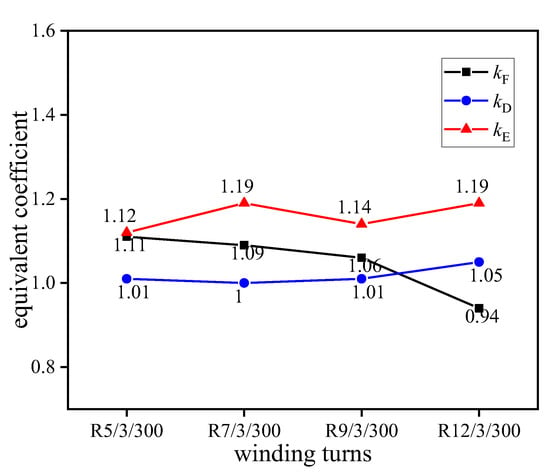
Figure 9.
Correlation coefficient curves under different winding turns.
It can be seen in Figure 9 that kF decreased slightly with the increase of the number of windings of the net ring, with an average value of 1.05, indicating that under the dynamic impact, the breaking force of the net was slightly larger than the static punching force. In addition, kD increased slightly with the increase of the number of winding turns of the net ring, with a mean of 1.01. This shows that breaking displacement caused by dynamic shock was slightly larger than that caused by static punching. With the increase of the number of winding turns, kE showed an overall increasing trend, with an average value of 1.16, indicating that under dynamic shock, the impact energy absorbed by the net was greater than that under static conditions. This finding is attributed to the absolute energy of the ring net, which is composed of internal energy and work conducted by external forces. The internal energy is generated mainly by the plastic and elastic strain of the ring net. Under static force breaking, when the rock hits the net, the kinetic energy is zero. When any one of the rings in the net was broken, the loading was stopped immediately. Under static punching, one or two rings at the edge of the loading place were damaged, and the ultimate energy dissipation capacity of the ring net was only a single ring. The moment the falling rock contacted the net, the initial kinetic energy was generated, and then the impact position was damaged, with the breakage of multiple rings at the same time. As a result, the ultimate energy dissipation capacity of the net increased significantly. The capacity of the net energy dissipation mechanism under the static punch test was lower than that under the dynamic impact test. Therefore, the energy consumed by the ring net under the dynamic impact was substantially greater than that under static punching.
5. Parametric Analysis
LS-DYNA [20,21] was used to numerically analyze the mechanical behavior of the ring net under the dynamic impact and static punching test conditions. The numerical model of the static punching test was simplified into three parts: a ring net, loading side (punching head), and fixed side (shackle). The net and shackle were simulated by beam elements with the characteristic size of 0.25 m, and the loading side was simulated by solid elements with the characteristic size of 0.25 m. The boundary conditions were as follows: one end of the shackle was fixed, displacement was restricted in three directions of XYZ, rotation was not limited in any direction, and displacement was applied to the loading end. The lifting speed of the loading end was 5 mm/s. The material parameters in the model are shown in Table 6.

Table 6.
Model parameters in the static punching test.
The dynamic impact test model was simplified into five parts: a ring net, steel column, beam, drop weight, and shackle. The beam and shackle were simulated by beam elements with the characteristic size of 0.25 m, and the drop weight was simulated by solid elements with the characteristic size of 0.25 m. The boundary constraints were the steel columns, and the hinged constraints were the shackles. The material parameter in the model is shown in Table 7.

Table 7.
Model parameters in the dynamic impact test.
Plastic deformation and ring net failure can be expected during the test process. Thus, segmented nonlinear material was used to describe the ring material in the finite element simulation. The stress–strain curve is illustrated in Figure 10 [22], and the criterion for failure was 1770 Mpa of tensile stress [23]. For the numerical model of the main components, please refer to papers about the flexible rockfall barrier by Zhao et al. [24], Xu et al. [6], and Qi et al. [25]. In order to guarantee the correct stiffness and mass of the net, an equivalent cross-section radius was employed, as given by [26]:
where n are the numbers of windings, and r are the diameter of the steel wire.
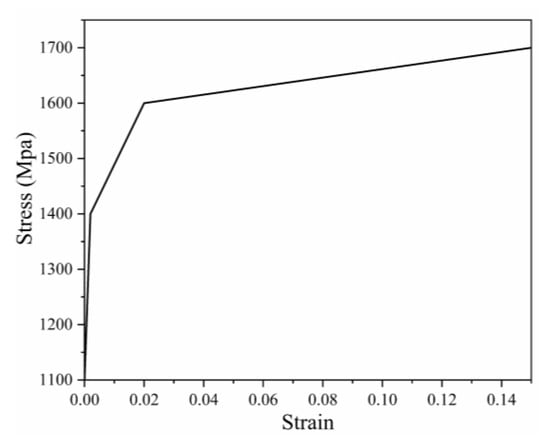
Figure 10.
Stress–strain curve.
5.1. Comparative Analysis of Finite Element Simulation and Test
Figure 11 and Figure 12 show the deformation process of the ring net under static punching and dynamic impact simulated by finite element methods. Both the ring net deformation and ring net breakage site obtained from the simulations were consistent with the experimental results. The force-displacement curve of the ring net under the simulation was compared with the test results, as shown in Figure 13 and Figure 14. The peak error was below 5%.
Figure 11.
Ring net deformation process in the static punching test: (a) ring net relaxation state; (b) ring net deformation; (c) ring net breakage.
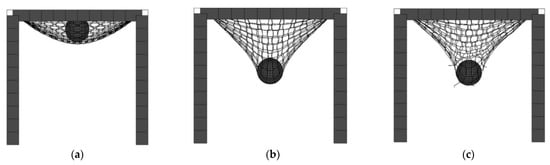
Figure 12.
Ring net deformation process in the dynamic impact test: (a) ring net relaxation state; (b) ring net deformation; (c) ring net breakage.
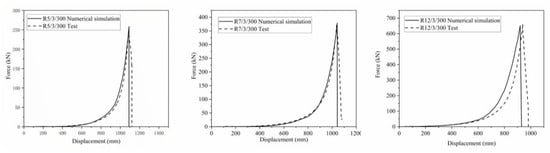
Figure 13.
Comparison of experimental and numerical simulation results in the static punching test.
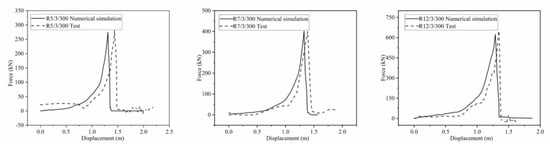
Figure 14.
Comparison of experimental and numerical simulation results in the dynamic shock test.
5.2. Analysis of Rockfall Impact Velocity
The parameters in the static punching and dynamic impact models were as follows: net size: 3.9 × 3.9 m, net specification: R7/3/300, diameter of the punching head: 0.8 m, and diameter of the falling rock: 0.8 m. The rockfall impact velocities were 17 m/s, 20 m/s, 25 m/s, and 35 m/s. The breaking force, breaking displacement, and net energy consumption of the ring net under different impact velocities are shown in Figure 15.
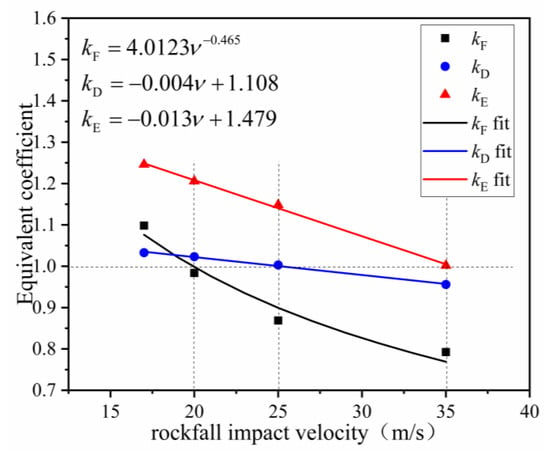
Figure 15.
Equivalent coefficients at different rockfall impact velocities.
As shown in Figure 15, with an increase in the impact velocity, kF decreased linearly from 1.082 to 0.792, a decrease of 26.8%, kD decreased from 1.024 to 0.948, a decrease of 26.8%, and kE decreased linearly from 1.246 to 1.002, a decrease of 19.6%. As the contact time between the tested rock and ring net was shorter at higher rather than lower velocity speeds, the energy dissipation effects of the ring net were insufficient to prevent ring net deformation and failure. The equivalent coefficient of the breaking force of the ring net under static punching and dynamic impact decreased as a power function, and the equivalent coefficient of breaking displacement and net energy consumption decreased linearly. When the speed was greater than 20 m/s, kF was less than 1, indicating that the dynamic breaking force was lower than the static breaking force. Conversely, when the speed exceeded 25 m/s, kD was less than 1. The findings also indicated that dynamic breaking displacement was smaller than static breaking displacement. At rockfall impact velocity speeds greater than 35 m/s, kE was less than 1, demonstrating that the dynamic energy consumption was less than the static energy consumption. Consequently, when the impact velocity is bigger than 35 m/s, the breaking force, the breaking displacement, and the energy consumption of the mesh under static tests will be greater than those of dynamic tests.
5.3. Analysis of the Influence of Ring Diameter
Keeping the net size, net specification, punching head diameter, and rockfall diameter the same as the parameters in the analysis of rockfall impact velocity, we established models with ring diameters of 250 mm, 300 mm, 350 mm, 400 mm, and 450 mm. The distribution of the equivalent coefficients is shown in Figure 16.
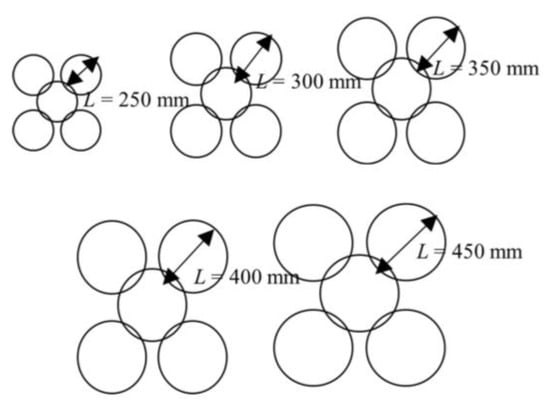
Figure 16.
Ring net model with different ring diameters.
As shown in Figure 17, with an increase in ring diameter, kF increased from 1.055 to 1.136, an increase of 7.68%, kD decreased from 1.110 to 0.832, a decrease of 25.04%, and kE decreased from 1.295 to 1.165, an increase of 10.03%. These findings demonstrate that, with an increase in ring diameter under static punching, kF increased linearly and that kD and kE decreased linearly. In addition, under static punching, as the ring diameter increased, net deformation increased, and net breaking force decreased. In contrast, under dynamic impact conditions, an increase in ring diameter led to a decrease in ring number and an increase in the impact force of falling rock on the mesh, which shortened the time for the falling rock to impact the net and weakened the net’s ability to dissipate the energy of the falling rock. kF and kE were always greater than 1.0 under static tests and dynamic tests. However, when the ring diameter was larger than 350 mm, kD was less than 1.0, indicating that the breaking displacement in static tests can be expected to be greater than that in dynamic tests.
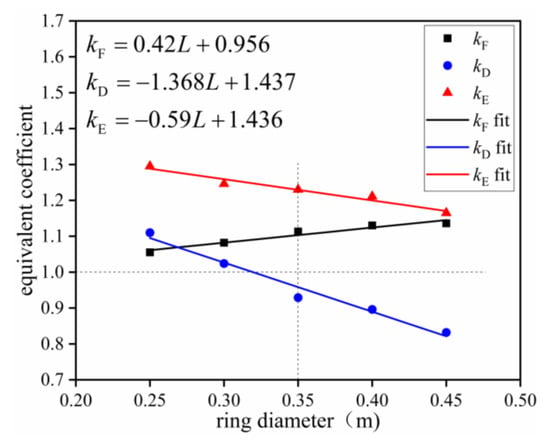
Figure 17.
Equivalent coefficients at different ring diameters.
5.4. Analysis of the Influence of Ring Net Aspect Ratio
In this analysis, the net size, net specifications, punching head diameter, and rockfall diameter were the same as in the analysis of rockfall impact velocity. The aspect ratios in the ring net models were 1:1, 1.2:1, 2:1, and 3:1 (Figure 18).
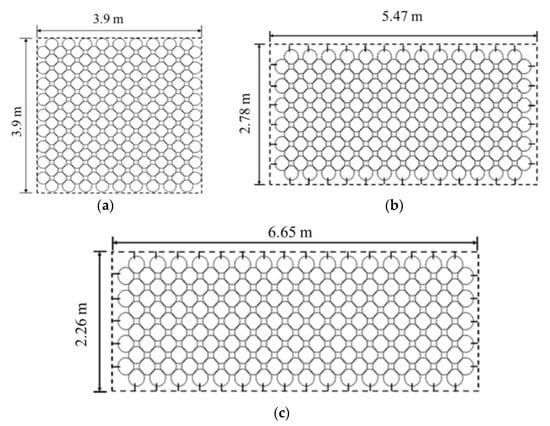
Figure 18.
Ring net models with different ring network aspect ratios: (a) ring net aspect ratio of 1:1; (b) ring net aspect ratio of 2:1; (c) ring net aspect ratio of 3:1.
As shown in Figure 19, with the increase in the ring net aspect ratio, kF, kD, and kE all showed a decreasing trend. Specifically, kF decreased from 1.082 to 0.769, a reduction of 28.9%, kD decreased from 1.024 to 0.952, a reduction of 7.0%, and kE decreased from 1.25 to 0.958, a reduction of 23%. When the ring net aspect ratio was increased, the number of rings in the uncontacted area of the loading end increased. As a result, excessive ring deformation in the local area in contact with the puncture head led to net damage first. In contrast, a low level of ring deformation in uncontacted areas of the net resulted in an uneven force and ring net failure. This phenomenon was more obvious under dynamic impact than static punching due to the dynamic effect of rockfall. In the dynamic impact situation, ring net breakage occurred, thereby reducing the overall energy consumption performance of the ring net. When the aspect ratio was greater than 1.5, kF was less than 1.0. This clearly shows that the breaking force obtained in a static test will be greater than that obtained in a dynamic test. When the aspect ratio was more than 2, kD and kE were less than 1.0. This finding demonstrates that breaking displacement and net energy consumption obtained in static tests will be greater than those found in dynamic tests at ring net aspect ratios greater than 2.0. This finding points out the need to consider the difference when using the static punching result in these conditions, which should be paid attention to in practical applications of ring nets in the field.
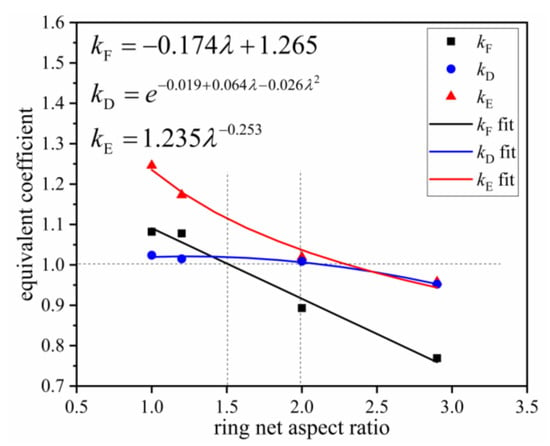
Figure 19.
Equivalent coefficients at different ring net aspect ratios.
5.5. Analysis of the Influence of the Loading Head Area to Ring Net Area Ratio
Keeping the net size and net specification the same as in the analysis of rockfall impact velocity, models with 14, 15, 16, and 17 of 0.033, 0.042, 0.052, and 0.062, respectively, with corresponding head diameters of 0.8 m, 0.9 m, 1.0 m, and 1.1 m, respectively, were established as shown in Figure 20.
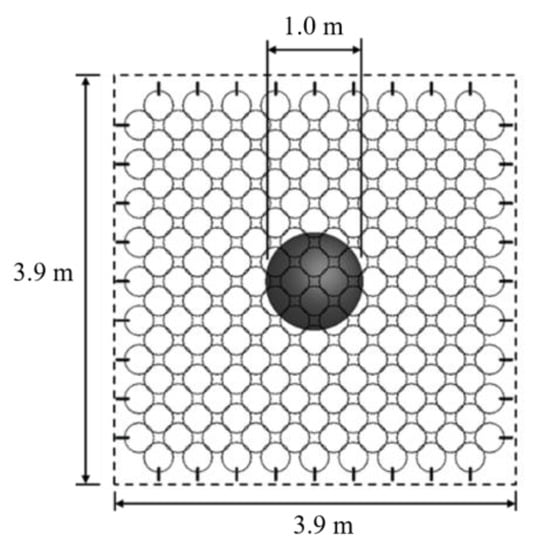
Figure 20.
The ratio of loading head area to ring net area.
Figure 21 indicates the equivalent coefficient curves of different ratios of loading head area to ring net area. With an increase in the loading head area to ring net area ratio, kF increased from 1.082 to 1.270 (an increase of 17.4%), kD decreased from 1.024 to 1.006, (a reduction of 1.7%), and kE gradually increased from 1.246 to 1.412 (an increase of 13.3%). These findings were attributed to the decrease in the diameter of the falling rock and the “bullet effect” produced by the dynamic impact of the falling rock. At the same kinetic energy, the impact force on the ring net closest to the impact center point of the falling rock increased. The impact force then decreased as the distance from the center point increased. Falling rocks with small diameters impact at a higher speed than falling rocks with larger diameters, causing rings in the local area of impact to be broken first. At the same time, rings outside this area fail to function in energy dissipation, thus affecting the overall energy dissipation performance of the ring net. In contrast, the larger the diameter of the falling rock, the larger the contact area with the surface of the ring net. Under these conditions, the axial force on the rings at the center of the impact of the rockfall is reduced, which delays the failure time to a ring net failure. The impact force on the ring net increased following an increase in the diameter of the falling rock. These findings indicate that, when both kF and kE are greater than 1, breaking force and net energy consumption values obtained in static tests will be less than those found in dynamic tests. In addition, the breaking displacement obtained in force tests will be greater than that in dynamic tests.
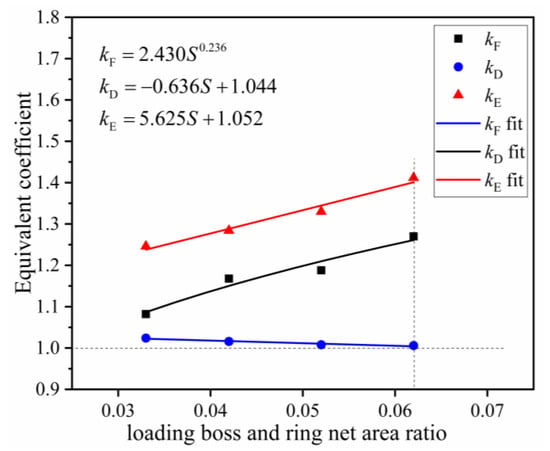
Figure 21.
Equivalent coefficients at different loading head areas to ring net area ratios.
5.6. Analysis of Equivalence Coefficient Sensitivity
To clarify the degree of influence of parameters, such as rockfall impact velocity (v), ring diameter (L), ring net aspect ratio (λ), and the loading head area to ring net area ratio (S), on the mechanical behavior of ring nets under static punching and dynamic impact, a sensitivity analysis was conducted. The curve of each parameter with the equivalent factor of breaking force, breaking displacement, and net energy consumption was fitted. The following relational formulas were obtained:
According to the sensitivity calculation formula:
where is the sensitivity, is the sensitivity function of the sensitive parameter, is the fitting function, is the reference value of the sensitive parameter, and is the value of the system function at .
The sensitivity value of the equivalent coefficient of breaking force (kF) is as follows.
The sensitivity value of the equivalent coefficient of breaking displacement (kD) is as follows:
The sensitivity value of the equivalent coefficient of energy dissipation (kE) is as follows:
Taking as the benchmark model parameters, the corresponding equivalent factors were kF = 1.082, kD = 1.024, and kE = 1.246. Using Equations (3)–(9), the sensitivity values of each performance parameter were calculated, as displayed in Figure 22.
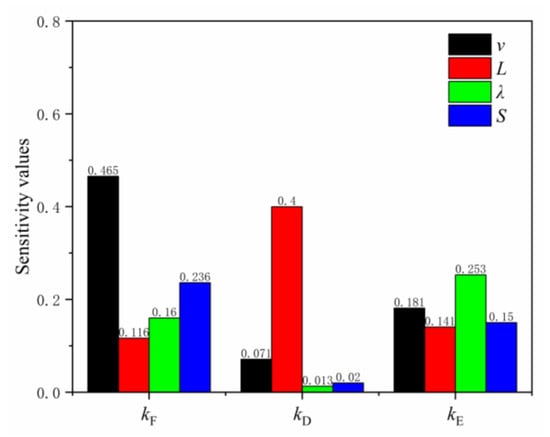
Figure 22.
Sensitivity values of various performance parameters.
From Figure 22, it can be seen that rockfall impact velocity is the main factor affecting kF, followed by the ratio of the loading head area to ring net area (sensitivity value: 0.236) and ring net aspect ratio (sensitivity value: 0.160). As the sensitivity value of the ring diameter was small (0.116), this factor exerted little influence on kF. In contrast, ring diameter was the main factor affecting kD, with a sensitivity value of 0.400, and the second factor was rockfall impact velocity (sensitivity value: 0.0709), followed by the ratio of loading area to ring net area (sensitivity value: 0.0205). The sensitivity value of the ring net aspect ratio was 0.013, pointing to an insignificant impact. In terms of kE, the main sensitive factor was the ring net aspect ratio, with a sensitivity value of 0.253, followed by the impact velocity of the drop weight (sensitivity value: 0.181) and the ratio of the loading head area to the ring net area (sensitivity value: 0.150). The effect of the ring diameter on kE, with a sensitivity value of 0.141, was small.
Given the sensitivity values for rockfall velocity (v), ring diameter (L), ring net aspect ratio (λ), and the ratio of the loading area to ring net area (S) (0.717, 0.656 0.580, and 0.406, respectively), the degree of influence of these parameters was as follows: ᴠ > L > λ > S.
6. Equivalence of Static Punching and Dynamic Impact Results
To further explore the mechanical behavior of the ring net under static punching and dynamic impact, 17 models with different parameters were included in a parametric analysis, and ring net breaking force, breaking displacement, and energy consumption were analyzed (Table 8).

Table 8.
Corresponding kF, kD, and kE values under different rockfall impact velocities, ring diameters, ring net aspect areas, and loading head area to ring net areas.
First-order polynomial function and multivariable and multiparameter fitting were performed to determine the functional relationship between kF, kD, and kE and rockfall impact velocity (ᴠ), ring diameter (L), ring net length-width ratio (λ), and loading area to ring net area (S) values under the test conditions in the present study. The fitting formula below can provide a reference for ring net design.
Using the normalization formula, the equivalent coefficients of breaking force, breaking displacement, and net energy consumption can also be quickly clarified. For example, ring net size = 3.9 m × 3.0 m, ring net specification = R7/3/250, rockfall impact velocity = 22 m/s, and rockfall diameter = 1.2 m. By substitute these data into Equation (10), you can obtain: kF = 1.341, kD = 1.084, and kE = 1.498. This shows that the breaking force under dynamic impact is 1.341 times that under static conditions. Therefore, the breaking force results under static conditions are suitable and safe for dynamic conditions. However, the breaking displacement of dynamic impact is 1.084 times that of static condition. Therefore, during the actual design, sufficient deformation space should be reserved, especially on both sides of the road, to ensure that the dynamic impact will not enter the boundary.
When the ring net size = 5.68 m × 2.63 m, ring net specification = R7/3/300, rockfall impact velocity = 36 m/s, and rockfall diameter = 0.6 m, these data can be substituted into Equation (10) to obtain, kF = 0.452, kD = 0.897, kE = 0.722. Due to the high speed and the large slenderness ratio of the ring net, the bullet effect is formed, and the breaking force and energy consumption are significantly reduced, which are only 0.452 and 0.722 under the static condition. Therefore, under the actual dynamic impact, it is no longer appropriate to directly use the static results to guide the dynamic condition design. The static results should be multiplied by the corresponding equivalent coefficient to select the model. According to CECS 827-2021 [27], under the premise that other conditions remain unchanged, it is necessary to increase the ring net size to R12/3/300.
7. Conclusions
In this paper, the results of static punching tests and dynamic impact tests of ring nets were compared, and numerical simulations and equivalent analyses of the mechanical properties of the ring nets under these test conditions were conducted. The following conclusions can be drawn:
- With an increase in the impact velocity, the equivalent coefficient of the breaking force of the ring net decreased as a power function, and the equivalent coefficients of tensile displacement and energy consumption decreased linearly. When the impact velocity was greater than 35 m/s, the breaking force, the breaking displacement, and the energy consumption of the ring net under static punching test were larger than those under dynamic impact test.
- With an increase in ring diameter, the equivalent coefficient of the ring net breaking force increased linearly, and the equivalent coefficients of ring net tensile displacement and energy consumption decreased linearly. When the ring diameter is greater than 350 mm, the rupture displacement predicted by the static punching test will be larger than that predicted by the dynamic impact test.
- With an increase in ring net aspect ratio, the equivalent coefficient of ring net breaking force decreased linearly. The exponential function of the equivalent coefficient of tensile displacement also decreased, and the equivalent coefficient of ring net energy consumption decreased as a power function. When the aspect ratio is higher than 2, the breaking force, the breaking displacement, and the energy consumption of the mesh under static punching test will be larger than those under the dynamic impact test.
- With an increase in the ratio of the loading head area to the ring net area, the power function of the equivalent coefficient of the ultimate breaking force increased, the equivalent coefficient of ring net tensile displacement decreased linearly, and the equivalent coefficient of ring net energy consumption increased linearly.
- The degree of influence of the parameters was as follows: impact velocity (v) > ring diameter (L) > ring net length to width ratio (λ) > ratio of loading head area to ring net area (S).
- Models considering the effect of impact velocity, ring diameter, ring net aspect ratio, and ratio of the loading head area to the ring net area were built to reveal ring net performance under static punching and dynamic impact conditions.
It should be clarified that the findings from this study are based on specific types of ring nets. Further studies on additional factors that could influence the performance of ring nets are recommended. For example, the impact angle of rockfall, multiple rockfall impacts, and a flexible boundary may be taken into account.
Author Contributions
Conceptualization, X.Q., Q.D., S.Y. and X.W.; methodology, X.Q. and Q.D.; software, X.Q. and Q.D.; validation, X.Q., Q.D. and Z.Y.; formal analysis, X.Q. and Q.D.; investigation, L.Z.; resources, X.Q.; data curation, X.Q. and Q.D.; writing-original draft preparation, X.Q. and Q.D.; writing-review and editing, L.Z. and Z.Y.; visualization, Q.D., L.Z. and Z.L.; supervision, L.Z., S.Y. and X.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Transportation Science and Technology project of Sichuan Province (Grant No. 2020-B-01), the Key Science and Technology Projects in the Transportation Industry in 2020 (Grant No. 2020-MS3-101), the Department of Science and Technology of Sichuan Province (Grant No. 2018JY0029), and the Key Research and Development Program of Sichuan Province (Grant No. 2019YFG0001).
Data Availability Statement
Data will be made available on request.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Escallon, J.P.; Boetticher, V.; Wendeler, C.; Chatzi, E.; Bartelt, P. Mechanics of chain-link wire nets with loose connections. Eng. Struct. 2015, 101, 68–87. [Google Scholar] [CrossRef]
- Castro-Fresno, D.; Luis, L.Q.; Bianco-Fernandez, E.; Zamora-Barraza, D. Design and evaluation of two laboratory tests for the nets of a flexible anchored slope stabilization system. Geotech. Test. J. 2014, 32, 315–324. [Google Scholar] [CrossRef]
- Bertrand, D.; Trad, A.; Chauvel, R.; Limam, A. Discrete element simulation of an innovative metallic net dedicated to rockfall protection: A multi-scale approach. In Third Euro Mediterranean Symposium on Advances in Geomaterials and Structures; LGC-ENIT: Djerba, Tunisie, 2010. [Google Scholar]
- Bertrand, D.; Trad, A.; Limam, A.; Silvani, C. Full-scale dynamic analysis of an innovative rockfall fence under impact using the discrete element method: From the local scale to the structure scale. Rock Mech. Rock Eng. 2012, 45, 885–900. [Google Scholar] [CrossRef]
- Albrecht, V.B.; Axel, V. Numerical modelling of chain-link steel wire nets with discrete elements. Can. Geotech. J. 2019, 56, 398–419. [Google Scholar] [CrossRef]
- Xu, H.; Gentilini, C.; Yu, Z.; Qi, X.; Zhao, S. An energy allocation based design approach for flexible rockfall protection barriers. Eng. Struct. 2018, 173, 831–852. [Google Scholar] [CrossRef]
- Nicot, F.; Cambou, B.; Mazzoleni, G. From a constitutive modelling of metallic rings to the design of rockfall restraining nets. Int. J. Numer. Anal. Methods Geomech. 2015, 25, 49–70. [Google Scholar] [CrossRef]
- Paola, B.; Claudio, O.; Daniele, P. Full-scale testing of draped nets for rock fall protection. Can. Geotech. J. 2009, 46, 306–317. [Google Scholar] [CrossRef]
- Antonio, P.; Fabio, G.; Lorenzo, B. Discrete element analysis of the punching behaviour of a secured drapery system: From laboratory characterization to idealized in situ conditions. Acta Geotech. 2021, 16, 2553–2573. [Google Scholar] [CrossRef]
- Peila, D.; Pelizza, S.; Sassudelli, F. Evaluation of Behaviour of Rockfall Restraining Nets by Full Scale Tests. Rock Mech. Rock Eng. 1998, 31, 1–24. [Google Scholar] [CrossRef]
- Gerber, W.; Boell, A. Type-Testing of Rockfall Barriers-Comparative Results: International Proceedings of the Interpraevent Congress; Universal Academy Press, Inc.: Nigata, Japan, 2006. [Google Scholar]
- Tan, D.; Yin, J.; Qin, J.; Zhu, Z. New thoughts for impact force estimation on flexible barriers. In Advancing Culture of Living with Landslides; Springer International Publishing: Ljubljana, Slovenia, 2017; pp. 457–463. [Google Scholar] [CrossRef]
- Buzzi, O.; Spadari, M.; Giacomini, A.; Fityus, S.; Sloan, S.W. Experimental testing of rockfall barriers designed for the low range of impact energy. Rock Mech. Rock Eng. 2013, 46, 701–712. [Google Scholar] [CrossRef]
- Buzzi, O.; Leonarduzzi, E.; Krummenacher, B.; Volkwein, A.; Giacomini, A. Performance of high strength rock fall meshes: Effect of block size and mesh geometry. Rock Mech. Rock Eng. 2015, 48, 1221–1231. [Google Scholar] [CrossRef]
- Yu, Z.X.; Qiao, Y.K.; Zhao, L.; Xu, H.; Zhao, S.C.; Liu, Y.P. A simple analytical method for evaluation of flexible rockfall barrier part 1: Working mechanism and analytical solution. Adv. Steel Constr. 2018, 14, 115–141. [Google Scholar] [CrossRef]
- Koo, R.C.H.; Kwan, J.S.H.; Lam, C.; Ng, C.W.W.; Yiu, J.; Choi, C.E.; Ng, A.K.L.; Ho, K.K.S.; Pun, W.K. Dynamic response of flexible rockfall barriers under different loading geometries. Landslides. 2017, 14, 905–916. [Google Scholar] [CrossRef]
- Qi, X.; Pei, X.; Han, R.; Yang, Y.; Meng, Q.; Yu, Z. Analysis of the effects of a rotating rock on rockfall protection barriers. Geotech. Geol. Eng. 2018, 36, 3255–3267. [Google Scholar] [CrossRef]
- EOTA. Falling Rock Protection Kits. EAD 340059–00–0106, 2018/C417/07. European Organisation for Technical Assessment, Avenue des Arts 40 Kunstlaan, B—1040 Brussels. 2018. Available online: https://www.eota.eu/eads (accessed on 5 February 2023).
- Guo, L.; Yu, Z.; Luo, L.; Qi, X.; Zhao, S. An analytical method of puncture mechanical behavior of ring nets based on the load path equivalence. Eng. Mech. 2020, 37, 129–139. (In Chinese) [Google Scholar] [CrossRef]
- Livermore Software Technology Corporation. LSTC LS-DYNA R7.1 Keyword User’s Manual Vol I; Livermore Software Technology Corporation: Troy, MI, USA, 2005. [Google Scholar]
- Livermore Software Technology Corporation. LSTC LS-DYNA R7.1 Keyword User’s Manual Vol II; Livermore Software Technology Corporation: Troy, MI, USA, 2005. [Google Scholar]
- Zhang, L.Y. Study on Damage Mechanical Behavior of Wire-Ring Net under Repeated Impacts. Bachelor’s Thesis, Southwest Jiaotong University, Chengdu, China, 2019. [Google Scholar]
- Li, Z.M. Study on the Mechanical Behavior of the Flexible Intercepting Net. Bachelor’s Thesis, Southwest Jiaotong University, Chengdu, China, 2016. [Google Scholar]
- Zhao, S.C.; Yu, Z.X.; Wei, T.; Qi, X. Test study of force mechanism and numerical calculation of safety netting system. China Civ. Eng. J. 2013, 46, 122–128. (In Chinese) [Google Scholar] [CrossRef]
- Qi, X.; Yu, Z.X.; Zhao, L.; Xu, H.; Zhao, S.C. A new numerical modelling approach for flexible rock fall protection barriers based on failure mode. Adv. Steel Construction 2018, 14, 479–495. [Google Scholar]
- Yu, Z.; Liu, C.; Guo, L.; Zhao, L.; Zhao, S. Nonlinear Numerical Modeling of the Wire-Ring Net for Flexible Barriers. Shock Vib. 2019, 2019, 3040213. [Google Scholar] [CrossRef]
- T/CECS 824-2021; Technical Specification for Passive Flexible Protection Barrier Structure Engineering. China Association for Engineering Construction Standardization: Beijing, China, 2021.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).