Experimental Study on the Mechanical Properties of Composite Damped Hinge Bearings
Abstract
1. Introduction
2. Configuration and Working Principle of the CDHB
2.1. Configuration
2.2. Working Principle
3. Test Design
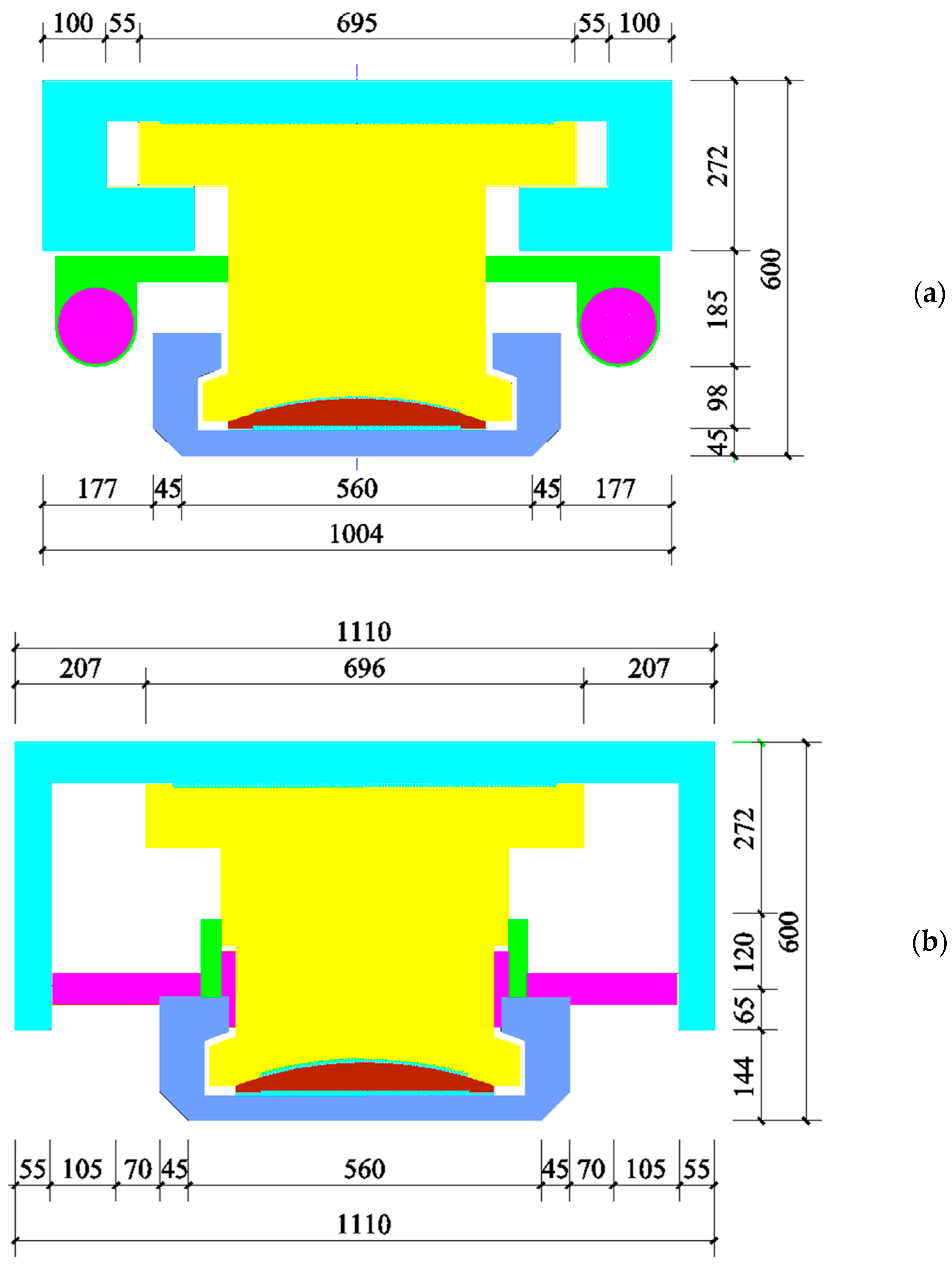
3.1. Specimen Design
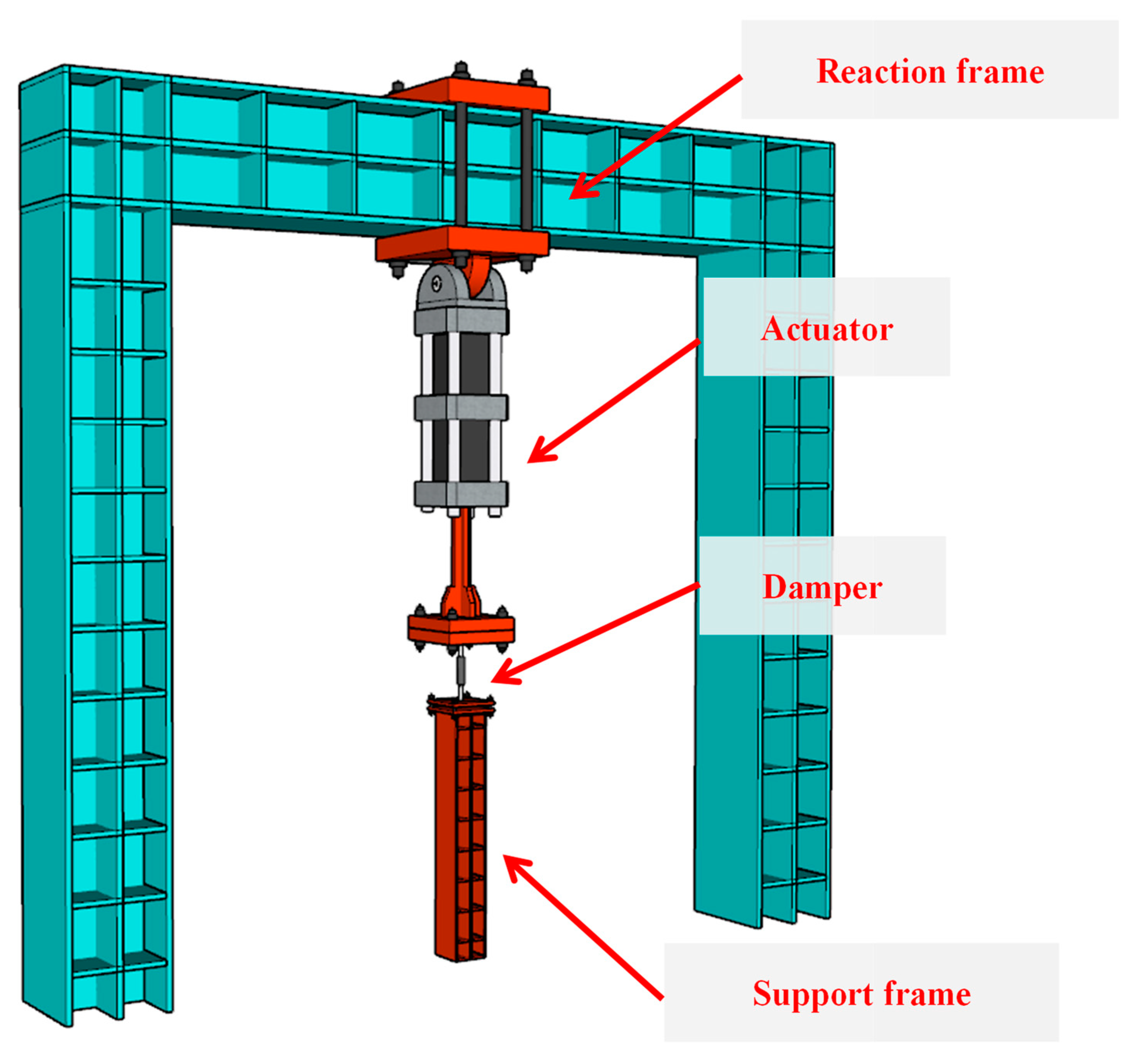
3.2. Loading Device and Loading Scheme
3.2.1. Loading Device
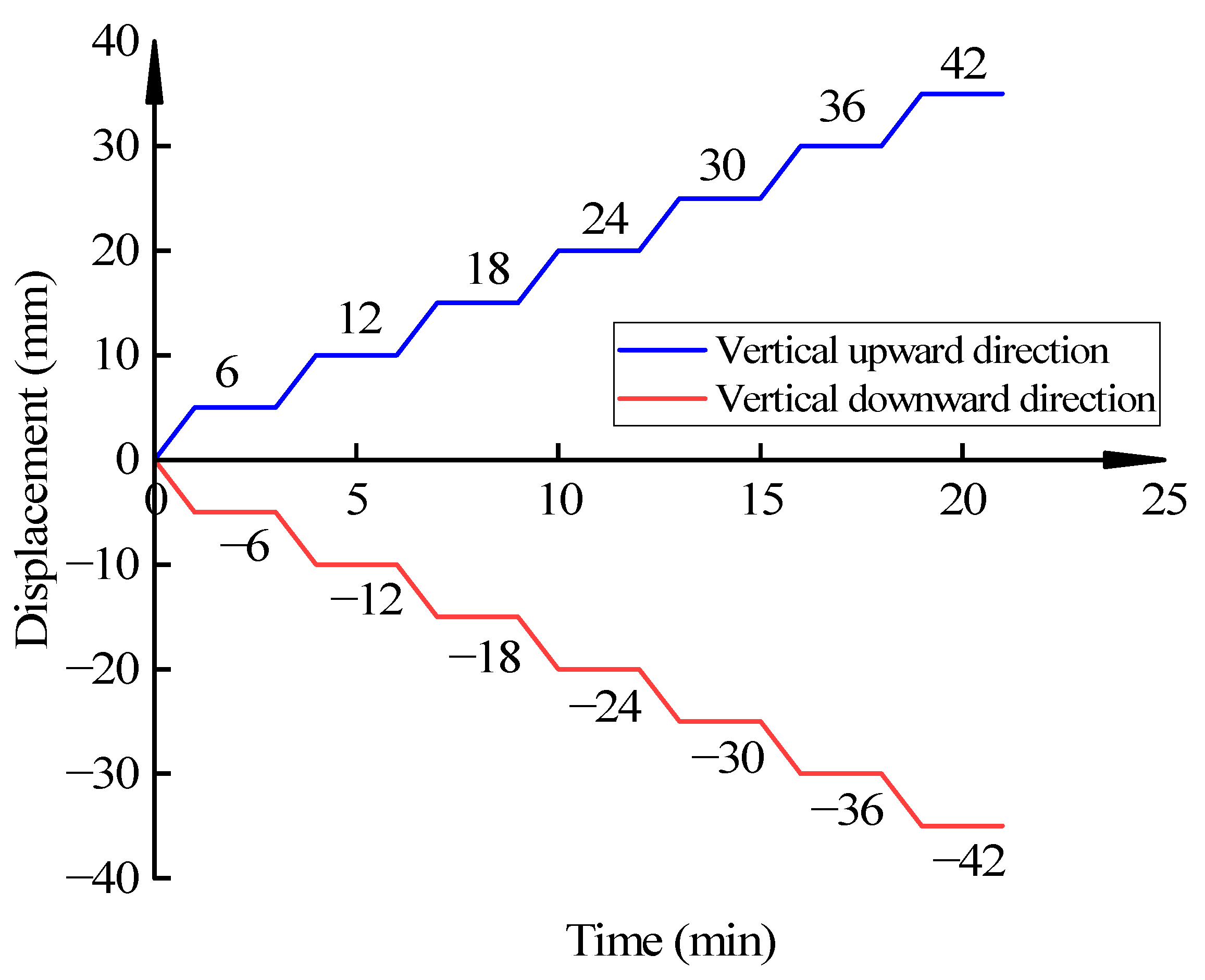
3.2.2. Loading Scheme
4. Test Results
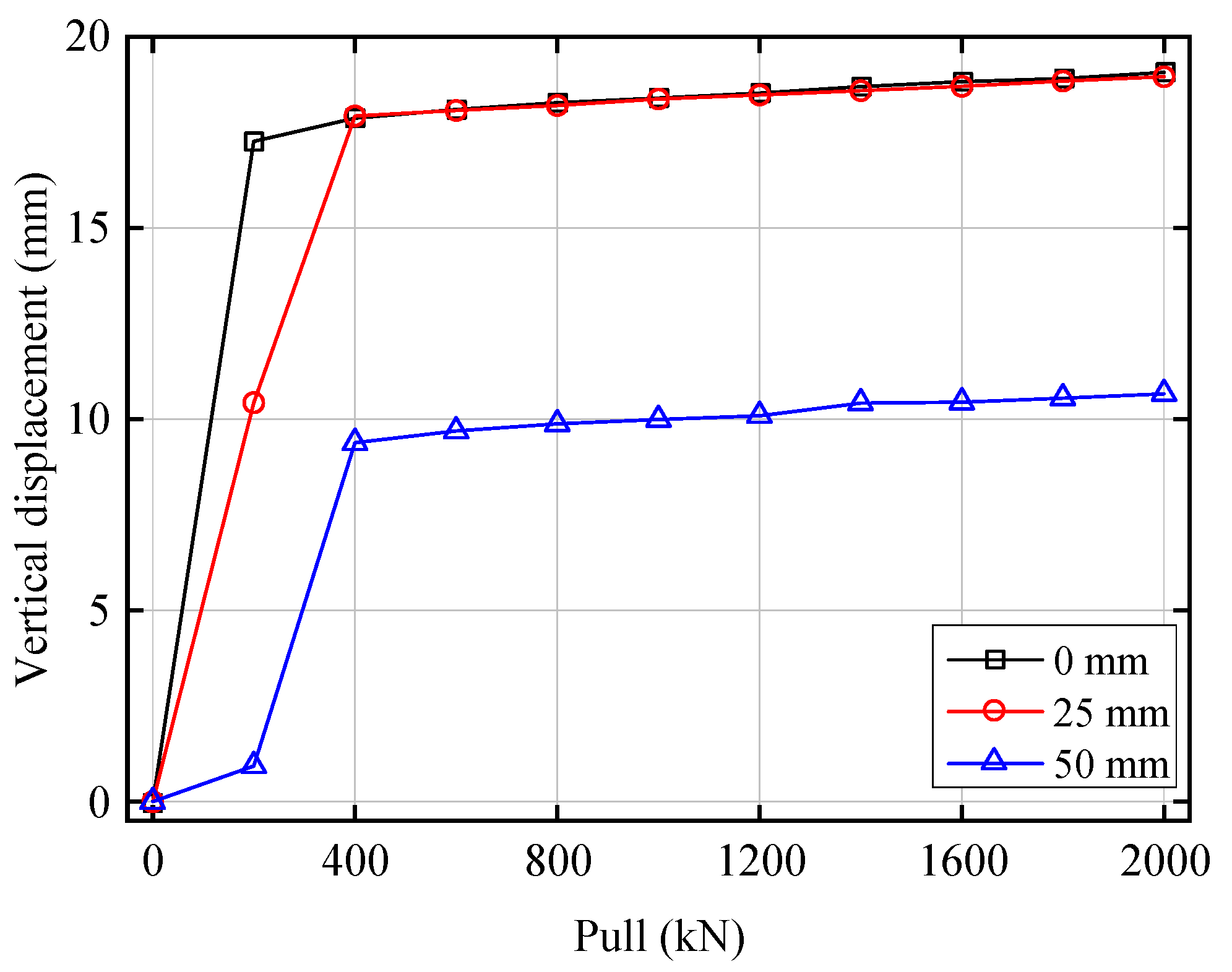
4.1. Vertical Bearing Capacity Performance
4.2. Rotation Performance
4.3. Mechanical Properties of the Built-In Dampers
5. Conclusions
- (1)
- The CDHB is always in an elastic state within the design ranges of the vertical pressure and tension. The CDHB’s vertical deformation increases linearly with the increasing of pressure and tension and decreases with the increasing of the initial horizontal displacement;
- (2)
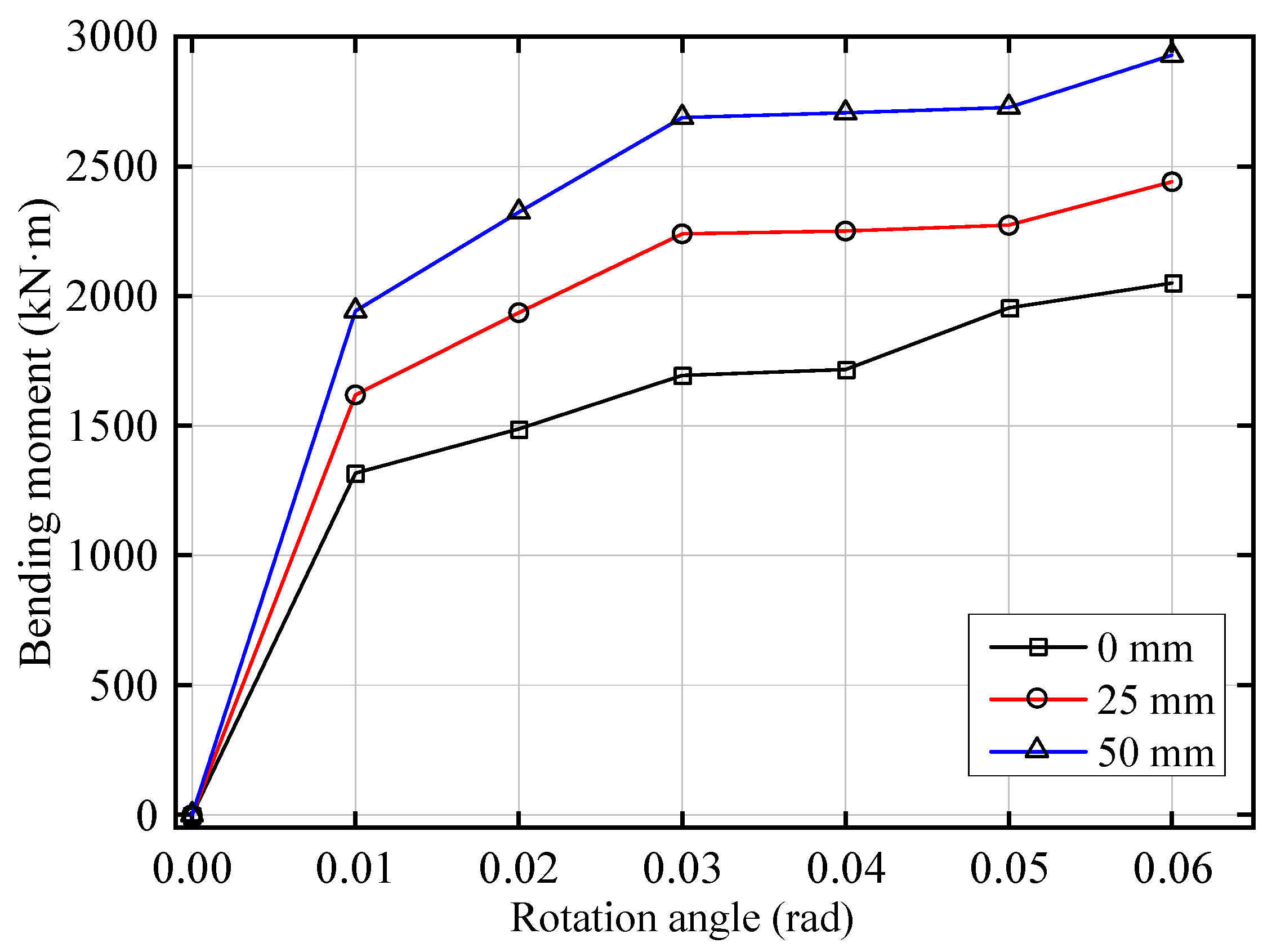
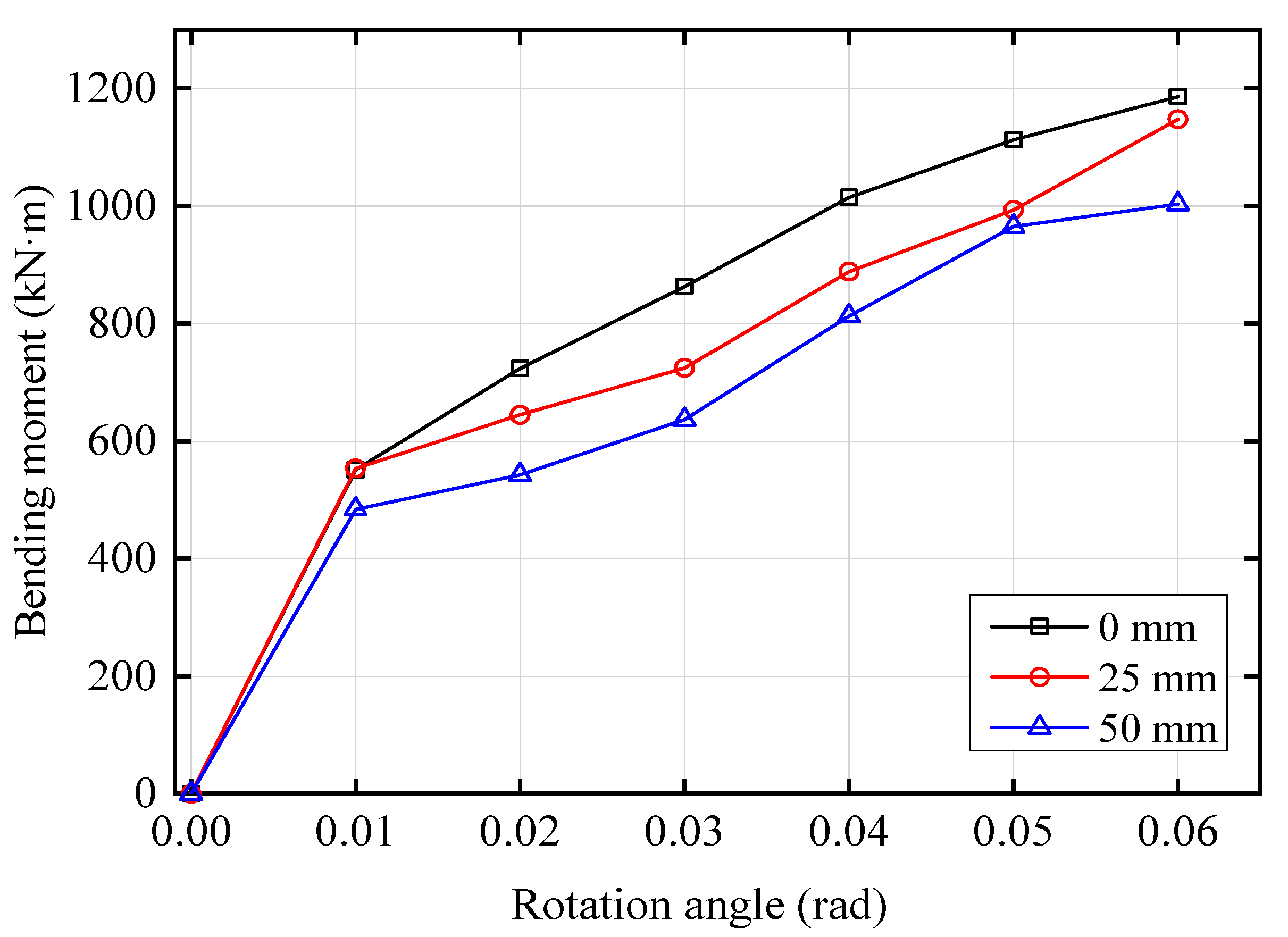
- Under vertical loading, the CDHB can always meet the requirement of reaching a rotation angle of 0.6 rad. Under the initial displacement of 0 mm, 25 mm, and 50 mm, the CDHB’s maximum pressure bending moment is 2850 kN·m, 2450 kN·m, and 2100 kN·m, respectively, and its maximum tension bending moment is 1190 kN·m, 1150 kN·m, and 975 kN·m, respectively. With the increase of the initial horizontal displacement, the CDHB tends to rotate more easily;
- (3)
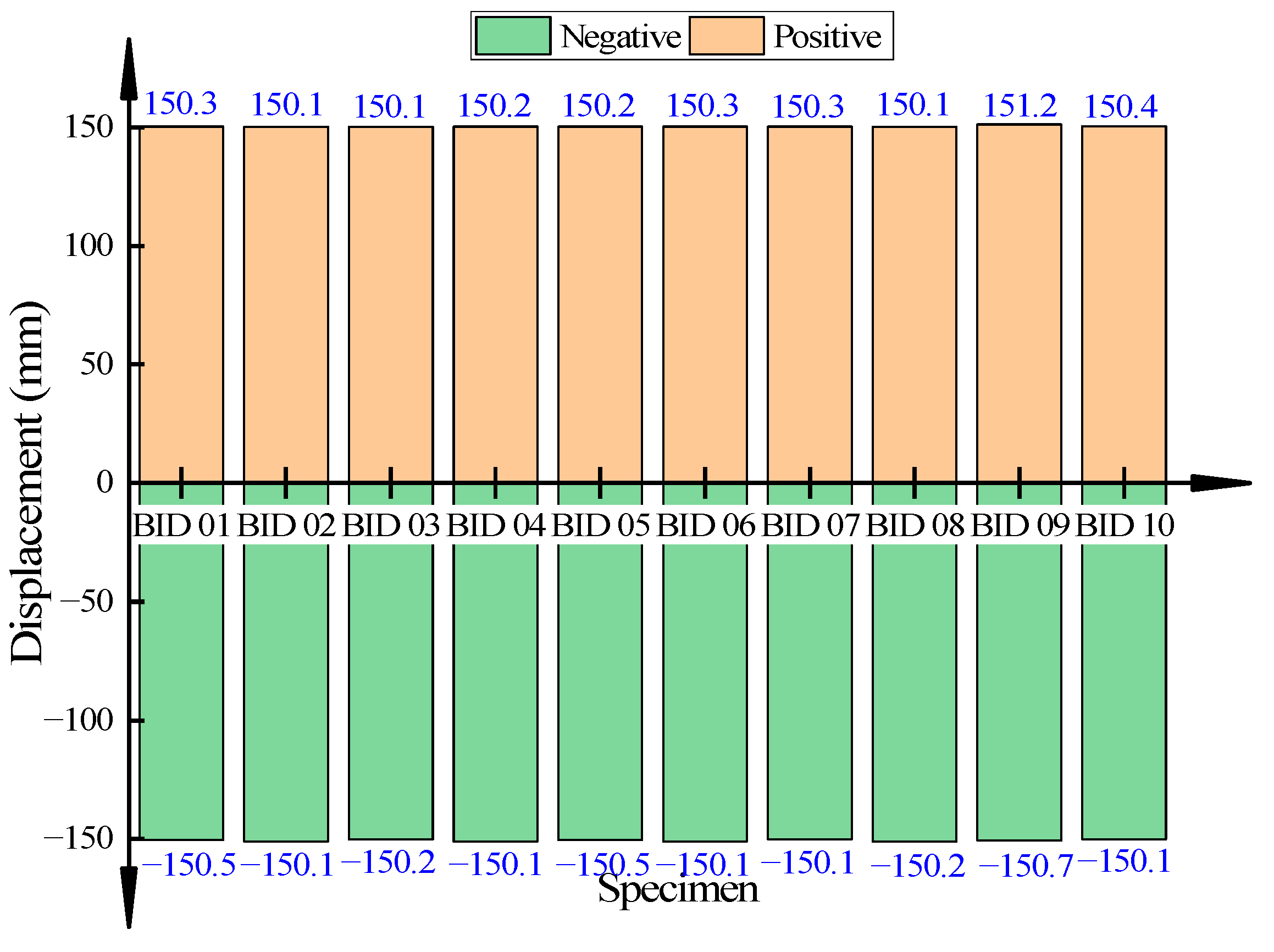
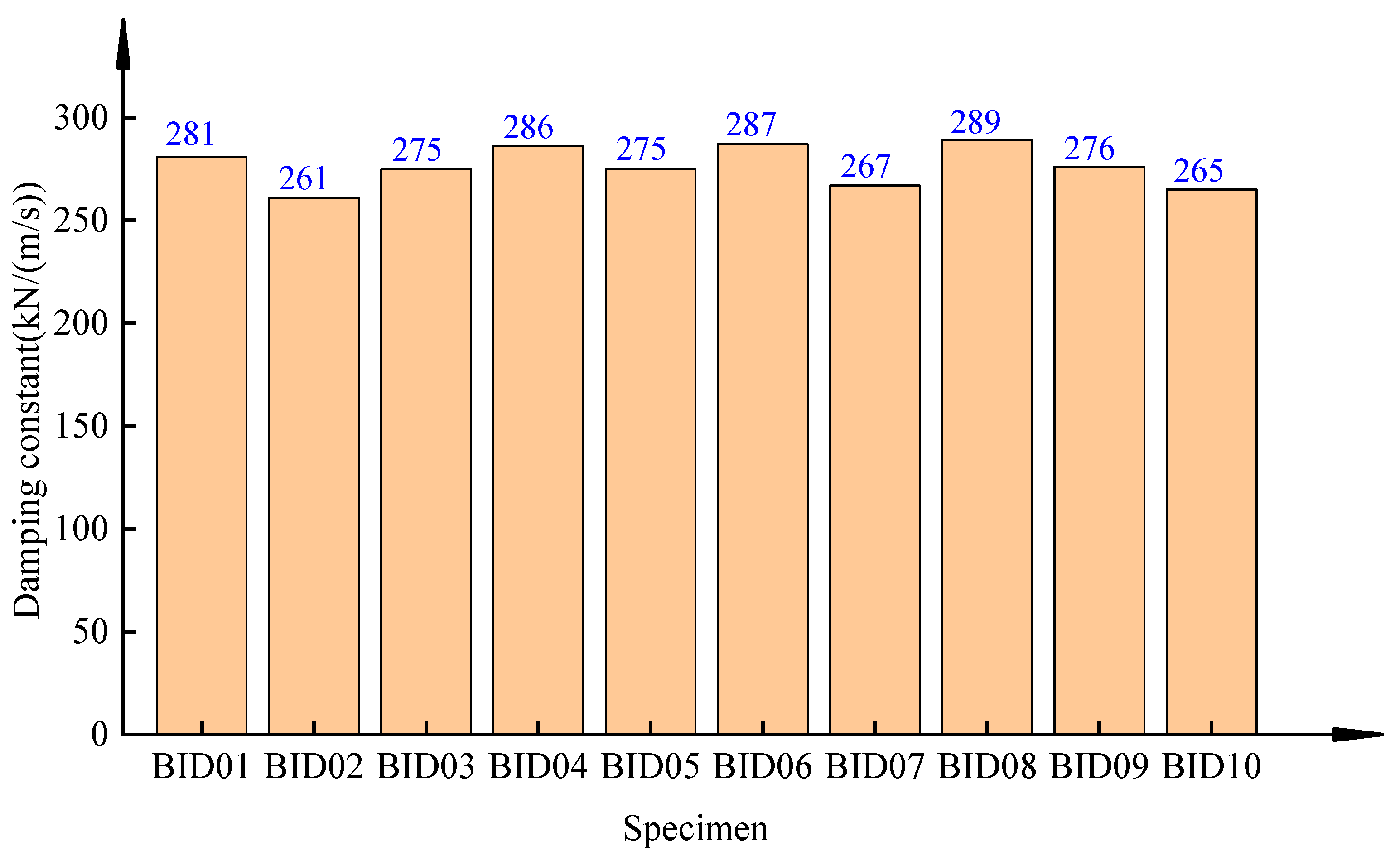
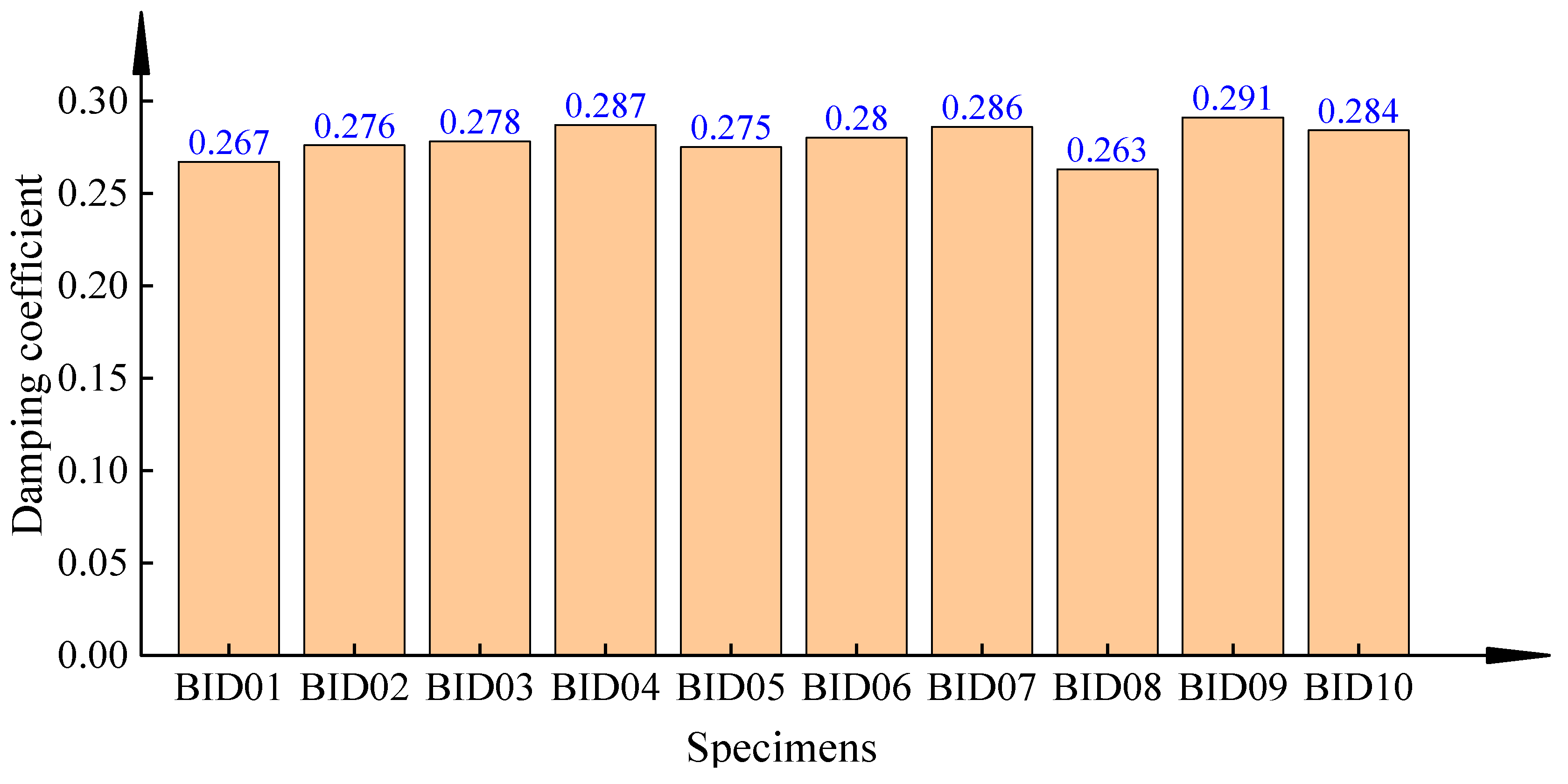
- When the built-in damper is scaled down by a large proportion, its ultimate displacement, maximum damping force, damping constant, and damping coefficient are all stable. The built-in dampers can meet the bearing’s requirement of 100 mm displacement and provide a damping force of about 180 kN along the direction of the dampers.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Aydin, E.; Dutkiewicz, M.; Öztürk, B.; Sonmez, M. Optimization of elastic spring supports for cantilever beams. Struct. Multidiscip. Optim. 2020, 62, 55–81. [Google Scholar] [CrossRef]
- Gu, Z.Y.; Sun, Z.; Xu, Y.K.; Wang, Y. Vertical Seismic Response Analysis of Large Span Isolated Structures under Multi-Dimensional and Multi-Support Excitations. In IOP Conference Series: Earth and Environmental Science; Qingdao, China, 2019. [Google Scholar]
- Zhang, H.; Liang, X.; Gao, Z.; Zhu, X. Seismic performance analysis of a large-scale single-layer lattice dome with a hybrid three-directional seismic isolation system. Eng. Struct. 2020, 214, 110627. [Google Scholar] [CrossRef]
- Xu, Z.-D.; Wang, S.-A.; Xu, C. Experimental and numerical study on long-span reticulate structure with multidimensional high-damping earthquake isolation devices. J. Sound Vib. 2014, 333, 3044–3057. [Google Scholar] [CrossRef]
- Warn, G.; Ryan, K.L. A review of seismic isolation for buildings: Historical development and research needs. Buildings 2012, 2, 300–325. [Google Scholar] [CrossRef]
- Zhai, Y.; Fu, X.; Chen, Y.; Hu, W. Study on column-top seismic isolation of single-layer latticed domes. Sustainability 2019, 11, 936. [Google Scholar] [CrossRef]
- Li, X.; Xue, S.; Cai, Y. Three-dimensional seismic isolation bearing and its application in long span hangars. Earthq. Eng. Eng. Vib. 2013, 12, 55–65. [Google Scholar] [CrossRef]
- Shi, K.; Pan, W.; Jiang, Z.; Lv, J. Investigation of rotation and shear behaviours of complex steel spherical hinged bearings subject to axial tensile load. Struct. Eng. Mech. Int’l J. 2020, 73, 123–132. [Google Scholar]
- Karbakhsh, R.A.; Bin, O.I.; Binti, I.Z.; Ab-Malek, K. P-Δ and end rotation effects on the influence of mechanical properties of elastomeric isolation bearings. J. Struct. Eng. 2012, 138, 669–675. [Google Scholar] [CrossRef]
- Inaba, Y.; Terazawa, Y.; Matsui, R.; Kumagai, T.; Takeuchi, T. Cyclic loading tests on steel roof bearings and effects on roof responses. J. Struct. Constr. Eng. 2018, 83, 1129–1137. [Google Scholar] [CrossRef]
- Kim, B.C.; Park, D.C.; Kim, H.S. Development of composite spherical bearing. Compos. Struct. 2006, 75, 231–240. [Google Scholar] [CrossRef]
- Kim, B.C. Endurance and performance of a composite spherical bearing. Compos. Struct. 2009, 87, 71–79. [Google Scholar] [CrossRef]
- Fenz, D.M.; Constantinou, M.C. Spherical sliding isolation bearings with adaptive behavior: Experimental verification. Earthq. Eng. Struct. Dyn. 2008, 37, 185–205. [Google Scholar] [CrossRef]
- Cui, Y.; Gao, X.; Liu, H.; Yamada, S. Experimental study on seismic behavior of roof joint. Int. J. Steel Struct. 2018, 18, 1373–1383. [Google Scholar] [CrossRef]
- Chen, Z.; Ding, Y.; Shi, Y.; Li, Z. A vertical isolation device with variable stiffness for long-span spatial structures. Soil Dyn. Earthq. Eng. 2019, 123, 543–558. [Google Scholar] [CrossRef]
- Li, S.; Dezfuli, F.H.; Wang, J.Q.; Alam, M.S. Longitudinal seismic response control of long-span cable-stayed bridges using shape memory alloy wire-based lead rubber bearings under near-fault records. J. Intell. Mater. Syst. Struct. 2018, 29, 703–728. [Google Scholar] [CrossRef]
- Landi, L.; Grazi, G.; Diotallevi, P. Comparison of different models for friction pendulum isolators in structures subjected to horizontal and vertical ground motions. Soil Dyn. Earthq. Eng. 2016, 81, 75–83. [Google Scholar] [CrossRef]
- Ponzo, F.C.; Di Cesare, A.; Leccese, G.; Nigro, D. Shake table testing on restoring capability of double concave friction pendulum seismic isolation systems. Earthq. Eng. Struct. Dyn. 2017, 46, 2337–2353. [Google Scholar] [CrossRef]
- Calvi, P.M.; Calvi, G.M. Historical development of friction-based seismic isolation systems. Soil Dyn. Earthq. Eng. 2018, 106, 14–30. [Google Scholar] [CrossRef]
- Zhou, Y.; Chen, P. Shaking table tests and numerical studies on the effect of viscous dampers on an isolated RC building by friction pendulum bearings. Soil Dyn. Earthq. Eng. 2017, 100, 330–344. [Google Scholar] [CrossRef]
- Shang, J.; Tan, P.; Zhang, Y.; Han, J.; Mi, P. Seismic isolation design of structure using variable friction pendulum bearings. Soil Dyn. Earthq. Eng. 2021, 148, 106855. [Google Scholar] [CrossRef]
- Constantinou, M.; Mokha, A.; Reinhorn, A. Study of sliding bearing and helical-steel-spring isolation system. J. Struct. Eng. 1991, 117, 1257–1275. [Google Scholar] [CrossRef]
- Rezaei, A.; Van Paepegem, W.; De Baets, P.; Ost, W.; Degrieck, J. Adaptive finite element simulation of wear evolution in radial sliding bearings. Wear 2012, 296, 660–671. [Google Scholar] [CrossRef]
- Shrimali, M.; Jangid, R. Seismic response of liquid storage tanks isolated by sliding bearings. Eng. Struct. 2002, 24, 909–921. [Google Scholar] [CrossRef]
- Ozsarac, U.; Findik, F.; Durman, M. The wear behaviour investigation of sliding bearings with a designed testing machine. Mater. Des. 2007, 28, 345–350. [Google Scholar] [CrossRef]
- Whittaker, A.S.; Bertero, V.V.; Thompson, C.L.; Alonso, L.J. Seismic testing of steel plate energy dissipation devices. Earthq. Spectra 1991, 7, 563–604. [Google Scholar] [CrossRef]
- Tsai, K.C.; Chen, H.W.; Hong, C.P.; Su, Y.F. Design of steel triangular plate energy absorbers for seismic-resistant construction. Earthq. Spectra 1993, 9, 505–528. [Google Scholar] [CrossRef]
- Kaynia, A.M.; Veneziano, D.; Biggs, J.M. Seismic effectiveness of tuned mass dampers. J. Struct. Div. 1981, 107, 1465–1484. [Google Scholar] [CrossRef]
- Ministry of Housing and Urban-Rural Development of the People’s Republic of China. Spherical Bearing for Steel Building; GB/T32836-2016; Standards Press of China: Beijing, China, 2017.
- Ministry of Housing and Urban-Rural Development of the People’s Republic of China. Technical Specification for Seismic Energy Dissipation of Buildings; JGJ297-2013; China Architecture and Building Press: Beijing, China, 2013.
- Ministry of Housing and Urban-Rural Development of the People’s Republic of China. Dampers for Vibration Energy Dissipation of Buildings; JG/T209-2012; China Architecture and Building Press: Beijing, China, 2012.














| No. | Parameter Type | Numerical Value |
|---|---|---|
| 1 | Vertical compression property | 5000 kN |
| 2 | Vertical tension property | 2000 kN |
| 3 | Horizontal load-bearing capacity | 200 kN |
| 4 | Allowable rotation angle | 0.06 rad |
| 5 | Unidirectional sliding displacement | 100 mm |
| No. | Parameter Type | Numerical Value |
|---|---|---|
| 1 | Damping constant C kN/(m/s) | 300 |
| 2 | Design stroke(mm) | ±125 |
| 3 | Design damping force (kN) | 100 |
| Working Condition | Working Condition Description | Initial Displacement |
|---|---|---|
| 1 | Pure compression | 0 mm |
| 2 | 25 mm | |
| 3 | 50 mm | |
| 4 | Pure tension | 0 mm |
| 5 | 25 mm | |
| 6 | 50 mm | |
| 7 | Compression rotation | 0 mm |
| 8 | 25 mm | |
| 9 | 50 mm | |
| 10 | Tension rotation | 0 mm |
| 11 | 25 mm | |
| 12 | 50 mm |
| Force Direction | F1.3f1/Ff1 | F1.6f1/Ff1 | F1.9f1/Ff1 | F2.1f1/Ff1 | |
|---|---|---|---|---|---|
| BID 01 | + | 0.98 | 0.97 | 0.95 | 0.96 |
| − | 0.99 | 1.02 | 0.89 | 0.9 | |
| BID 02 | + | 0.96 | 0.97 | 0.94 | 0.96 |
| − | 0.89 | 1 | 0.9 | 0.92 | |
| BID 03 | + | 0.97 | 0.97 | 0.95 | 0.97 |
| − | 0.99 | 0.95 | 0.9 | 0.92 | |
| BID 04 | + | 0.98 | 0.95 | 0.95 | 0.94 |
| − | 1.01 | 1.01 | 0.9 | 0.92 | |
| BID 05 | + | 0.98 | 0.97 | 0.95 | 0.95 |
| − | 0.99 | 1.02 | 0.89 | 0.9 | |
| BID 06 | + | 0.98 | 0.95 | 0.95 | 0.96 |
| − | 1.01 | 1 | 0.9 | 0.92 | |
| BID 07 | + | 0.98 | 0.97 | 0.94 | 0.94 |
| − | 1 | 1 | 0.9 | 0.91 | |
| BID 08 | + | 0.98 | 0.95 | 0.95 | 0.96 |
| − | 1 | 1.02 | 0.9 | 0.92 | |
| BID 09 | + | 0.98 | 0.96 | 0.95 | 0.93 |
| − | 0.99 | 1.02 | 0.9 | 0.92 | |
| BID 10 | + | 0.97 | 0.96 | 0.95 | 0.96 |
| − | 1.01 | 1.02 | 0.89 | 0.9 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, S.; He, Z.; Ou, T.; Zhou, Y. Experimental Study on the Mechanical Properties of Composite Damped Hinge Bearings. Buildings 2023, 13, 383. https://doi.org/10.3390/buildings13020383
Lin S, He Z, Ou T, Zhou Y. Experimental Study on the Mechanical Properties of Composite Damped Hinge Bearings. Buildings. 2023; 13(2):383. https://doi.org/10.3390/buildings13020383
Chicago/Turabian StyleLin, Songwei, Zhiming He, Tong Ou, and Yun Zhou. 2023. "Experimental Study on the Mechanical Properties of Composite Damped Hinge Bearings" Buildings 13, no. 2: 383. https://doi.org/10.3390/buildings13020383
APA StyleLin, S., He, Z., Ou, T., & Zhou, Y. (2023). Experimental Study on the Mechanical Properties of Composite Damped Hinge Bearings. Buildings, 13(2), 383. https://doi.org/10.3390/buildings13020383





