Abstract
The dynamic response of curved steel beams has long been a research focus in curved bridges. The formula for the dynamic response under a moving load was derived according to the basic principles of the precise integration method. Combined with the necessary conditions of this method, the stiffness matrix of a variable-curvature beam was obtained using matrix inversion, and the mass matrix of the structure was obtained using the concentrated mass method. The dynamic response of the structure was obtained by applying moving loads and masses at different speeds to the curved beam. Finite element simulation and laboratory curved-beam models of the variable-curvature steel beam were established. By comparing the laboratory measurement results against the theoretical data obtained in this study, we propose that our theory has practical engineering significance. It can be used as a theoretical basis for the study of variable curvature steel beam structures and for guiding the construction of curved beams.
1. Introduction
Curved beams are important constituents of many engineering and aerospace structures, and they have been applied in various components, such as high-speed machinery, vehicle shells, and lightweight bridges. The curved bridge has a unique streamlined structure, with smooth and bright lines, designed so that the structure and the surrounding environment are in harmony, in line with the public’s aesthetic needs. Such bridges are more suitable than straight beams in mountainous areas [1] (Yao Lingsen,1989). Curved girders play an important role in urban bridges and highways [2] (Zhao, Y.Y. et al., 2006), and curved girder bridges can be a good solution to problems such as topography and constraints imposed by tall buildings. However, when constrained by factors such as small spaces in urban construction, bridges with different radii of curvature must be arranged together, usually with a bridge of variable curvature as a transition between them. These bridges can be similarly used between curved and straight segments [3] (Zhang Yuanhai, 2005). As shown in Figure 1 and Figure 2, curved bridges are used in a wide range of applications, either as viaducts between cities or across mountains, valleys, and seas.

Figure 1.
Curved crossing bridge.

Figure 2.
Curve-type approach bridge across the sea.
When a vehicle moves on a variable-curvature girder bridge, unlike a straight girder segment, in addition to the vertical moving load, a torsional moment related to the radius of curvature is generated on the girder, which means the dynamic response is more complex [4]. Therefore, studying the dynamic response of variable curvature girders can prevent lateral overturning and fatigue damage to the girders. As shown in Figure 3, when considering the dynamic response of a bridge affected by vehicle loads, the steel box beam is generally taken as the main bearing member. Hence, it is necessary to study elliptical curved steel beams. The mechanical model designed in this study is a simplified form of an actual bridge.

Figure 3.
Curved beam structure with steel box beam as cross section.
Theoretical and experimental studies on curved girder bridges have been conducted since the early 1980s, with fruitful results. Vlasov et al. [5] studied the curved-beam structure with a circular cross-section and proposed the statics theory of elastic thin-walled members. Morri D.L. et al. [6] used the finite element method to study curved-beam structures. Based on the basic equation of a curved beam, Ni Guorong, Wang Yong, and Xiong Guoxiang [7] used differential equations and numerical integration involving parabolic, hyperbolic, elliptical, and variable-curvature beams to find engineering solutions for beams with variable cross-sections and curvatures. In recent years, many research institutes have also achieved success in the field of variable curvature beams. C. Yu et al. [8] conducted a dynamic sensitivity analysis based on a variable-curvature beam model with functionally graded porous FGP under general boundary conditions. Qingshan Wang et al. [9] studied the convergence and numerical verification of laminated composite beams with variable curvature under different boundary conditions. Jie Yu [10] derived an analytical solution to the static force of a beam with variable curvature. Mingdong Chen derived the stiffness matrix of a beam of constant curvature [11].
The calculation of the dynamic response of a bridge under a moving load is the basic problem of vehicle–bridge coupling, which was solved in terms of mechanics principles [12]. At present, the dynamics of curved beams is still a multi-scale and diversified research direction. Jun Luo et al. [13] proposed a semi-analytical solution for the free vibration of curvilinear rails with a vehicle–bridge coupling. Abdoos H. et al. [14] achieved the out-of-plane dynamic response of a curved beam under the action of a moving mass underlying an elastic foundation. S. H. Li et al. [15] obtained analytical solutions for the vertical, torsional, radial, and axial responses of a curved beam under a three-way moving load. Poojary Jatin et al. [16] developed a cracked bending beam element to investigate the effects of moving load velocity, depth, and crack location on the dynamic response of the beam in combination with the presence of cracks in the structure. Fei Han et al. [17] explored the coupling effect of vehicle speed on vehicle driving dynamic response under a random vehicle load. Xia Zhang et al. [18] integrated the influences of various factors on the dynamic response of a curved deck.
The precise integration method pioneered by Wanxie Zhong [19] can still obtain a highly accurate numerical solution to the problem where the applied point of the external dynamic load is fixed, i.e., using a sizable integral time step. Y.B. Yang and C.M. Wu [20] derived analytical solutions for horizontal curved beams under vertical and horizontal moving loads, providing clear physical insights into various vehicle-induced phenomena on curved beams. Jong-Shyong Wu and Lieh-Kwang Chiang [21] obtained the stiffness and mass matrices of a curved-beam element from the force–displacement relationship and kinetic energy equation by considering the effects of out-of-plane shear deformation of the curved beam and the effects of rotational inertia due to bending and torsional vibrations. They obtained the dynamic response under moving loads at different radii of curvature. Yahui Zhang [22] constructed the right-end term of the dynamic equation that can simulate the continuous movement of loads. A precise integral 2N algorithm was used to solve the dynamic equation. The dynamic response of a uniform, simply supported straight beam under a moving load was solved. Typical numerical calculations showed that the obtained numerical solution was almost identical to the analytical solution, even when using a sparse mesh division. In the case of the external load acting on the structure being strictly linear within the integral step, the high-precision structural-response time history could be obtained, even when the integral step was more extensive. Hence, the algorithm has been widely used in the dynamic structural analysis of straight girder bridges, optimal control, precise solutions of partial differential equations, and unsteady stochastic dynamics. Junping Pu et al. [23] applied the precise integration method to simulate the dynamic response processes of isotropic and variable-section simply supported girder bridge models under moving simple harmonic loads. Q. Gao et al. [24] proposed a fast and accurate integration method for solving structural dynamics problems. Yuefeng Shao et al. [25] proposed an algorithm for vehicle–bridge coupling and sensitivity analysis based on the step-by-step solution technique of the exact time integral method. The dynamic response of a discrete-supported curved track under moving loads with different curvatures, speeds, and other influencing factors was analyzed by Chen-Chen Zheng and Qiang Huang et al. [26]. The effects of uncertain parameters and random ground shaking on the seismic response and dynamic damage probability of slopes were analyzed and discussed by Rui Pang et al. [27]. Tomasz Maleska and Damian Beben [28] presented the results of a numerical study of earth-steel bridges with different overburden depths under seismic excitation and analyzed the results of different boundary conditions for earth-steel bridges with the same soil overburden depth. Xiaofei Li and Haosen Zhai et al. [29] constructed the stiffness matrices of curved beams using a semi-analytical method of structural mechanics.
The finite element method has been one of the most common methods recently used to study the subject of curved beams, but much work has been involved when building different models. For example, finite element modeling is limited by the variation of curvature when studying curved beams with variable curvature, and it is impractical to use the sparse cell division method for curved beams with large curvature; otherwise, it will cause large errors. In this study, we propose a model based on structural mechanics, which can obtain efficient and accurate numerical calculation results using the precise integration method. In this study, the dynamic theory of structural out-of-plane variable curvature beams is analyzed based on existing studies. We take the dynamic response of a variable-curvature beam under a vehicle load as the research object; this can contribute to the subsequent engineering analysis of dangerous sections under vehicle loads and the prevention of bridge damage. In addition to moving loads, when considering the influence of external dynamic loads on steel structures with variable curvature, the precise integration method can be applied to simulate the steel structure, which can obtain more accurate dynamic time-course results more efficiently, to prevent damage to the steel beam with variable curvature, control the beam vibration, etc.
2. Basic Principles of Precise Integration
The method of fine integration is essentially a high-precision method for calculating partial differential equations, which uses the basic principle of multi-scale wavelet transform to construct a multi-scale wavelet interpolation operator. It then uses the operator to discretize the partial differential equation into a system of ordinary differential equations. Finally, the system of equations is solved by the fine integration method.
The multi-degree-of-freedom dynamic balance equation in structural dynamics is
where M, C, and K are the mass, damping, and stiffness matrices, respectively; , , and are the displacement, velocity, and acceleration vectors, respectively, of the structure; and F(t) is the external force vector.
If the initial displacement and initial velocity are known, the intermediate variable p can be set so that , i.e., , and we can obtain
For convenience, let
where , , , and .
In practical problems, the mass, damping, and stiffness of the structure are all known parameters, so the matrix H is also a constant moment. Substituting Equations (3)–(5) into Equation (2), we can write the inhomogeneous equation,
i.e., the structural dynamics response equation, for which the general solution is
We introduce the exponential matrix
for which the precise solution is obtained by reducing it to
where m can be chosen as ; since , which itself is not a large time interval, will be a much smaller time interval. For the time interval , we apply a Taylor expansion to obtain
where I is the unit matrix and , where L denotes the truncated phase of the Taylor expansion. Substituting Equation (10) into Equation (9), we obtain
By the recurrence law of 2N, , where the middle term in the recurrence relation is .
Thus, Equation (11) can be written as
Generally, the calculation of is sufficiently accurate and satisfies the requirements if we take L = 4 and N = 20.
For the homogeneous equation, the integral term of the general solution of the dynamic response equation is zero. For the time-invariant system, H is a constant matrix. The general solution of the equation takes the following form:
Let the time step delta equal τ. Then,
After the matrix T is calculated by the above method, the time integration becomes
For non-homogeneous equations, if the non-homogeneous term r is linear in the time step , i.e., the equation is
then we can formulate
3. Variable-Curvature Beam Analysis
Based on the precise integration method, a known matrix H is a prerequisite for the analysis of the dynamic response of a curved beam with variable curvature under moving loads. This means that the discrete method is used to divide the beam into segments and find the stiffness matrix K, mass matrix M, and damping matrix C under the parameters of the model.
The definition of a variable-curvature beam is that the curvature of each point on the beam is different, which means that the solution of the geometric relationship of the linear term is the premise of analyzing the subsequent dynamics problems. There are various types of lines with variable curvatures, such as sinusoids, catenaries, ellipses, and so on. In addition, the line shape also needs to consider whether the curvature changes quickly or slowly; i.e., different bending beam models can be obtained by changing different line shape parameters and can be compared against the constant curvature model. In summary, elliptic curve beams that meet all the above requirements are the main objects of this study.
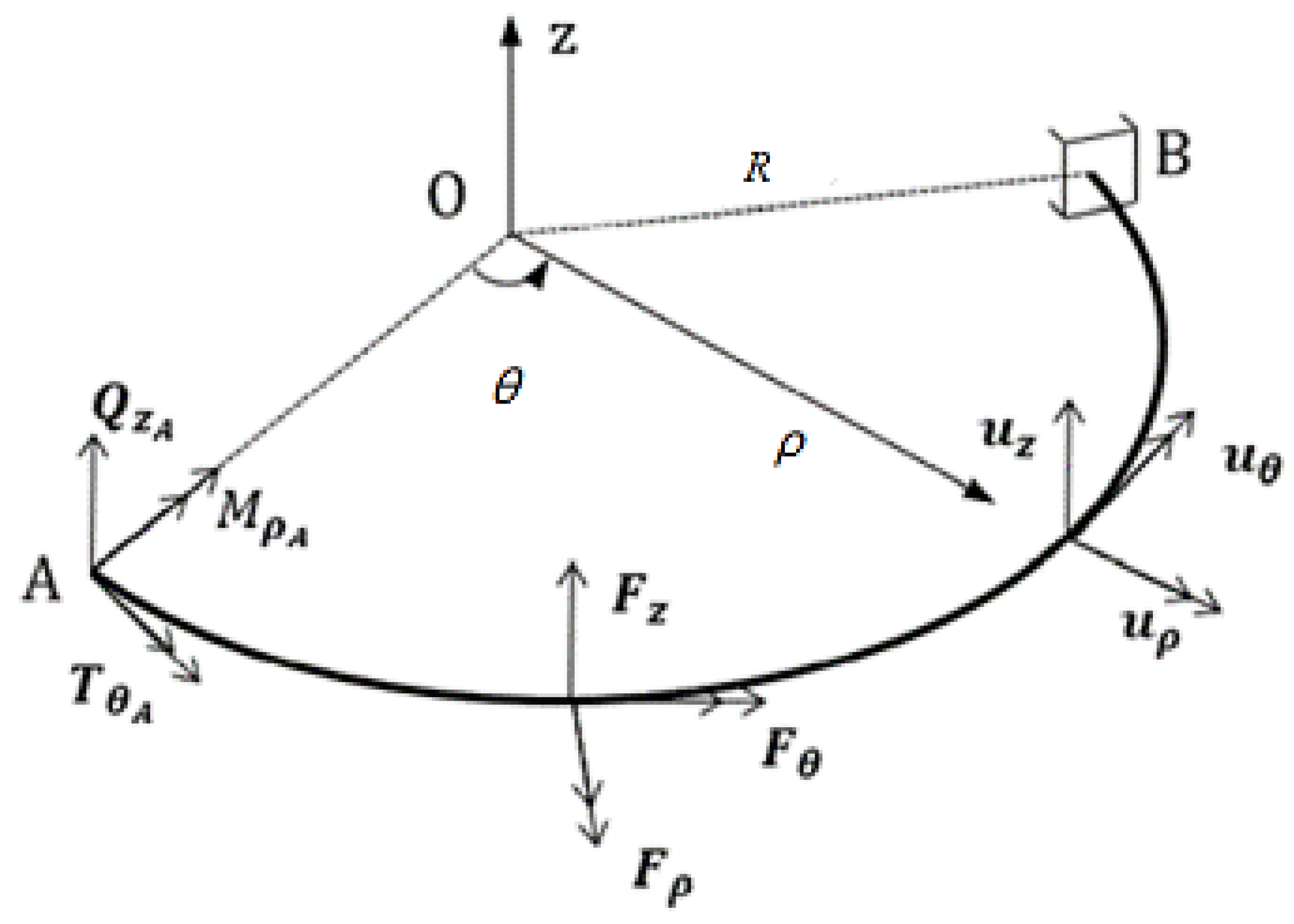
Owing to the structural form of a space-curved beam, it is appropriate to use a column coordinate system to analyze the problem. The out-of-plane curved beam is divided into N segments. Hence, there are N + 1 nodes, each with three degrees of freedom, i.e., vertical, radial around the plane, and tangential rotation around the plane, corresponding to three forms of out-of-plane generalized loads, i.e., vertical force , radial force couple , and circumferential torque , as shown in Figure 4.
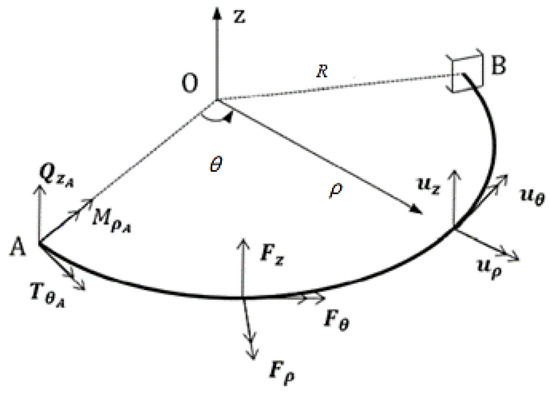
Figure 4.
Statics analysis model of curved beam.
Only three internal forces are generated in any section of the full beam: shear force perpendicular to the plane of the curved beam, bending moment around the radial axis, and torque around the circumferential axis. The restraint at the end section of the beam requires that these three reaction forces be provided to the extent that no rigid body displacement occurs in the full beam. Therefore, the three forms of reaction forces provided by the constraint at boundary A are vertical force , force dipole moment , and torque . As a result, in this study, the variable curvature beam is set as a cubic super-stationary structure.
Excluding the fixed ends of the beam, the number of nodes is N − 1, and each node has three degrees of freedom: vertical, rotational, and torsional. Therefore, the dimension of the stiffness matrix is 3(N − 1) 3(N − 1), and similarly for the flexibility matrix. The stiffness matrix can be obtained by inverting the flexibility matrix. The elements in any column of the flexibility matrix D represent the displacements of the remaining nodes under a unit load. In this way, the entire flexibility matrix can be decomposed into a superposition of nine flexibility matrices: vertical uncoupled, rotational uncoupled, torsional uncoupled, vertical-torsional coupled, vertical-torsional coupled, rotational-vertical coupled, rotational-torsional coupled, torsional-vertical coupled, and torsional-torsional coupled. These reflect the mutual coupling between the three forms of generalized displacements within the curved beam.
Superposition of the nine matrices yields a flexibility matrix D of 3(N − 1) × 3(N − 1) order, which can be inverted to obtain the final discretized stiffness matrix,
Based on the concentrated mass method, the masses in the out-of-plane direction of freedom on the curved beam are concentrated at discrete nodes, i.e., the translational mass in the vertical direction, the rotational inertia in the bending direction, and the rotational inertia in the twisting direction. The masses assigned to each node are statically determined. This produces the concentrated mass matrix in the out-of-plane direction of the elliptical beam.
The mass coefficients associated with rotation are given in the form of the inertia of rotation about each axis. The bending inertia of a section about a radial axis is given by , and the torsional inertia of a section about a tangential axis is given by . Hence, the rotational inertia matrices are
The three sub-matrices are expanded and superimposed separately to obtain the concentrated mass matrix of the curved-beam structure containing the rotational inertia terms.
The dynamical model of a curved-beam structure can be simplified to a mass-discrete structural system, as shown in Figure 5, where the cross-section of the beam form is a non-opening thin-walled section and the effect of section warpage is not considered.
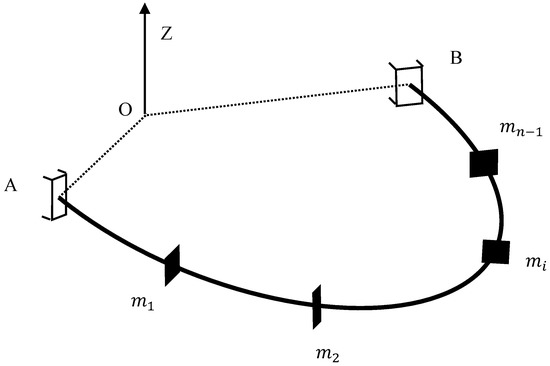
Figure 5.
Dynamic model of beam structure with variable curvature.
4. Numerical Example
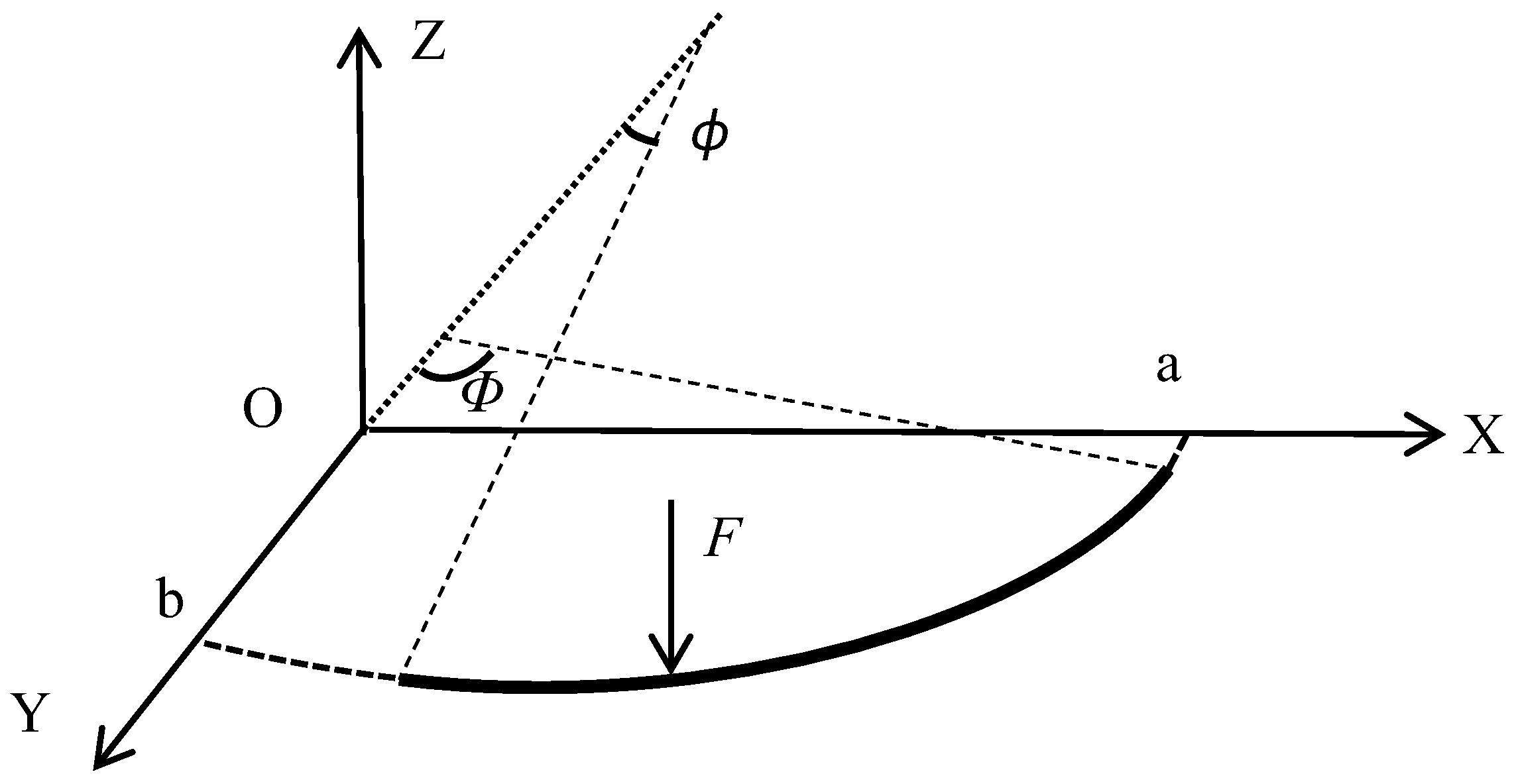
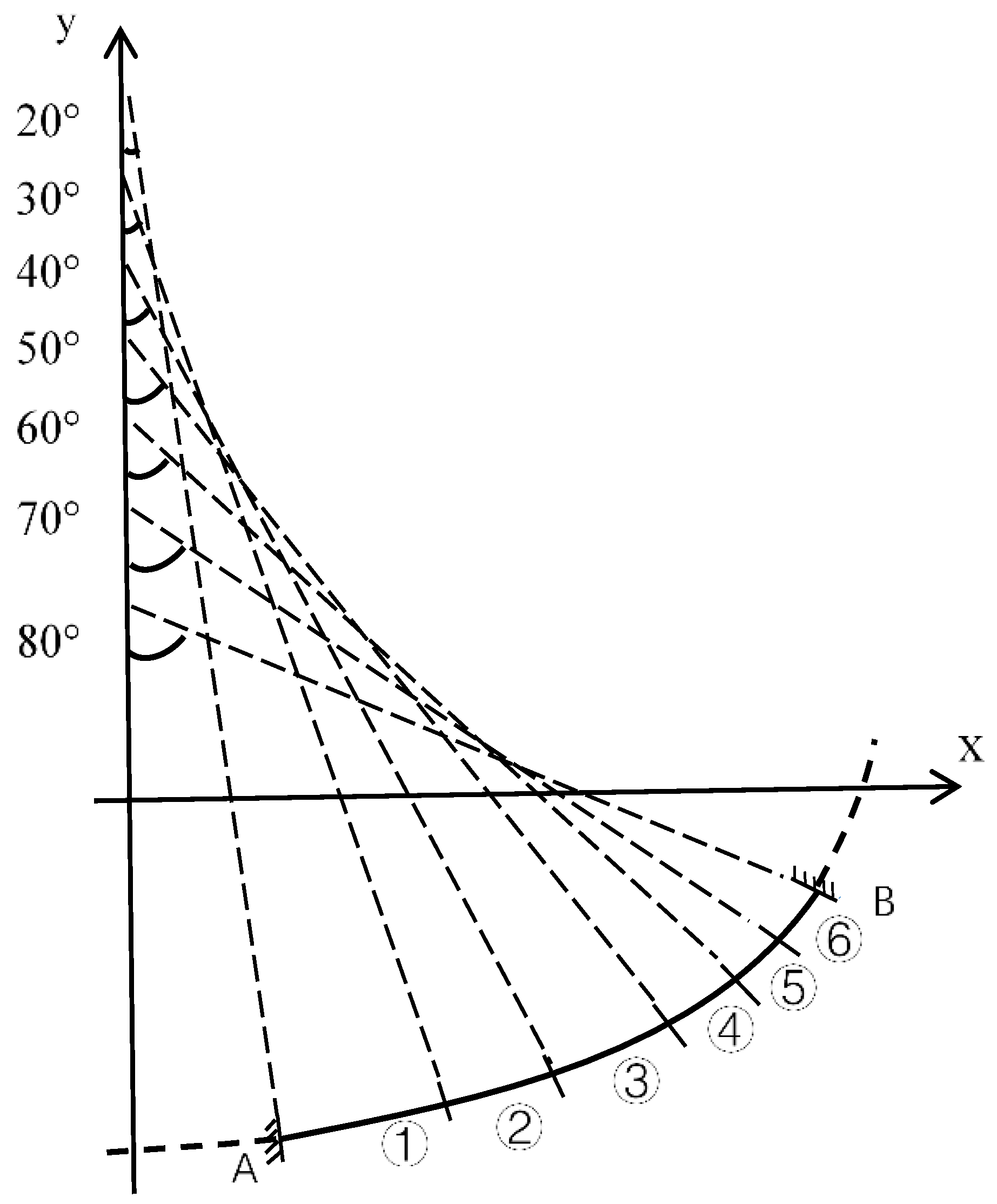
An elliptical curved girder bridge section conforming to the elliptical linear variable curvature was selected for study, and the elliptical curved girder model was simplified based on the assumption that the central axis of shear of a curved girder bridge coincides with the shaped centroid axis of the section. The simplified model was chosen in a right-angle coordinate system. An elliptical arc was taken from an ellipse with a semi-long axis length a and a semi-short axis length b. The ellipse is a symmetric figure, and in order to make the intercepted arc segment general, we chose one-fourth of the structure for the interception, as shown in Figure 6, by selecting the part of the plane in any quadrant of the Cartesian coordinate system and choosing the points on the ellipse whose angles between the normal and negative directions of the Y-axis are φ and Φ, respectively, as the endpoints of the intercepted arc segment.
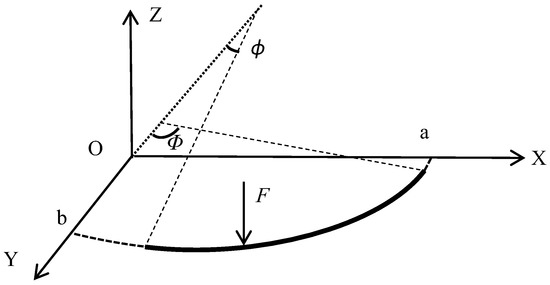
Figure 6.
Dimensions of beam with variable curvature.
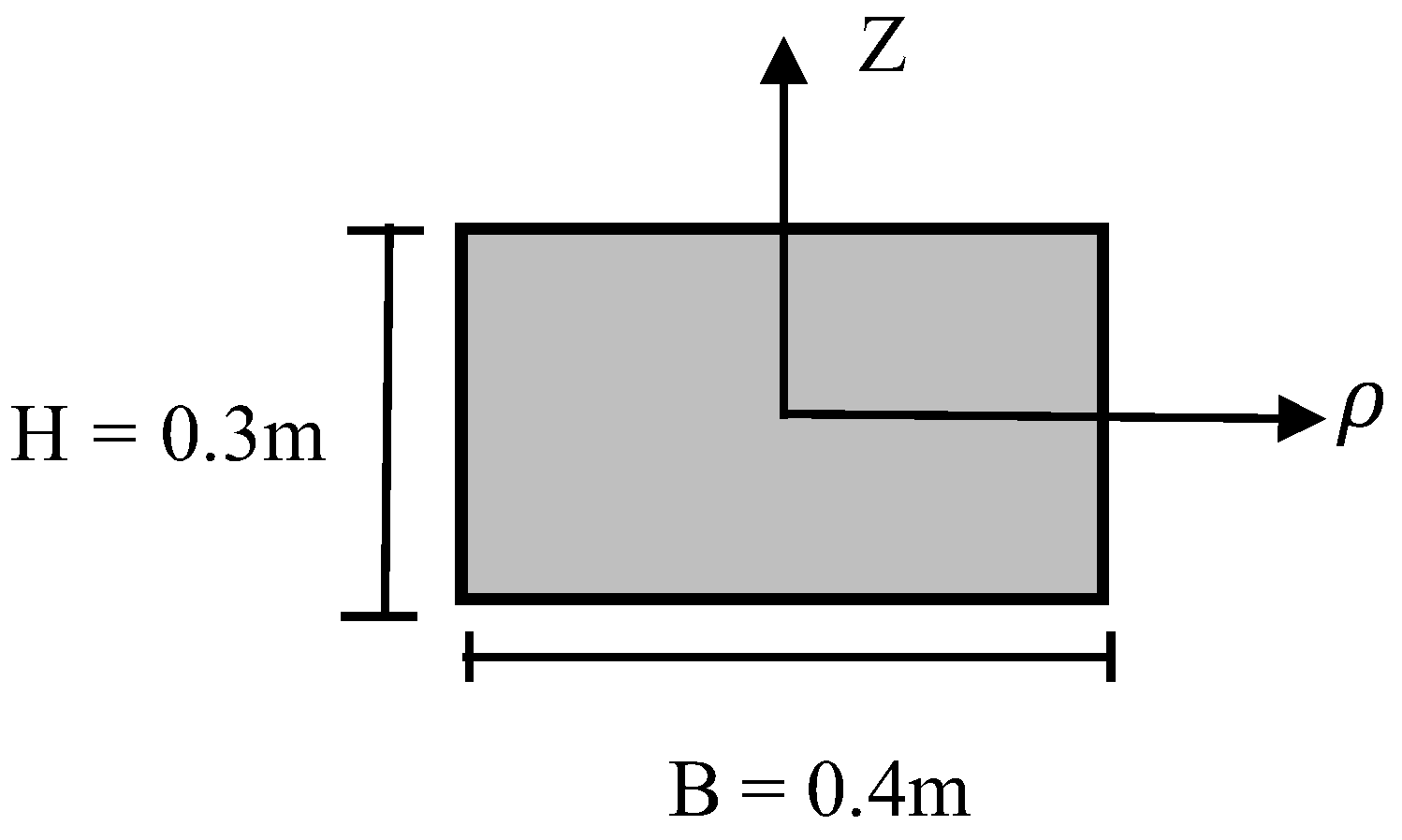
To facilitate the study of the overall dynamic response of the beam, a rectangular section was used in this study, while other sections could also be converted or equated to rectangular sections. The example used a rectangular section with a variable curvature steel beam, with section height H = 0.3 m, width B = 0.4 m, cross-sectional area A = 0.12 m2, angle φ of the left end with respect to the Y-axis of 20°, angle Φ of the right end with respect to the Y-axis of 80°, long elliptical axis length a = 60 m, and short axis length b = 30 m. The rectangular cross-sectional dimensions are shown in Figure 7.
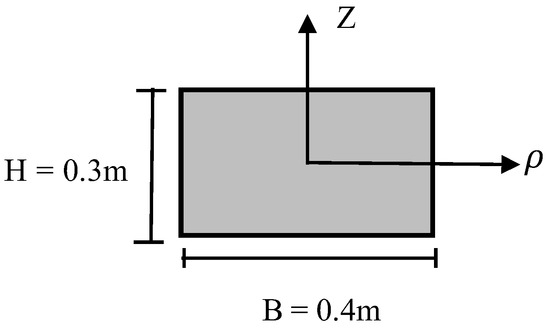
Figure 7.
Cross-section of beam with variable curvature.
The physical and geometric parameters of the bridge are shown in Table 1.

Table 1.
Basic parameters of the elliptical curved beam.
The variable-curvature beam was divided into six elements, following the method of dividing one element for every 10° change of curvature on the beam. The division of the entire beam unit is shown in Figure 8, with element numbers ① to ⑥ from left to right. Therefore, the flexibility of the structure could be solved according to the structural mechanics force method and the principle of virtual work, and it could be integrated to obtain a flexibility matrix of dimensions 15 × 15.
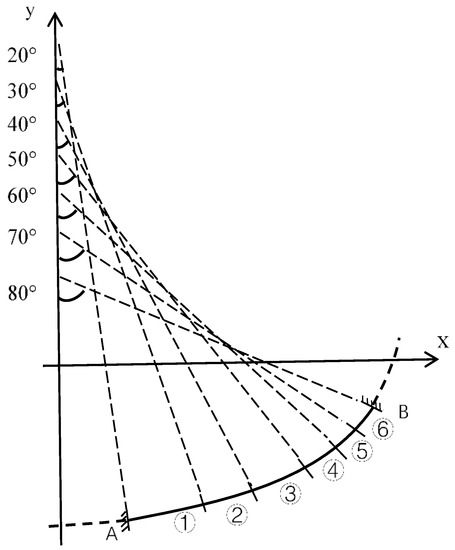
Figure 8.
Element division of variable-curvature beam.
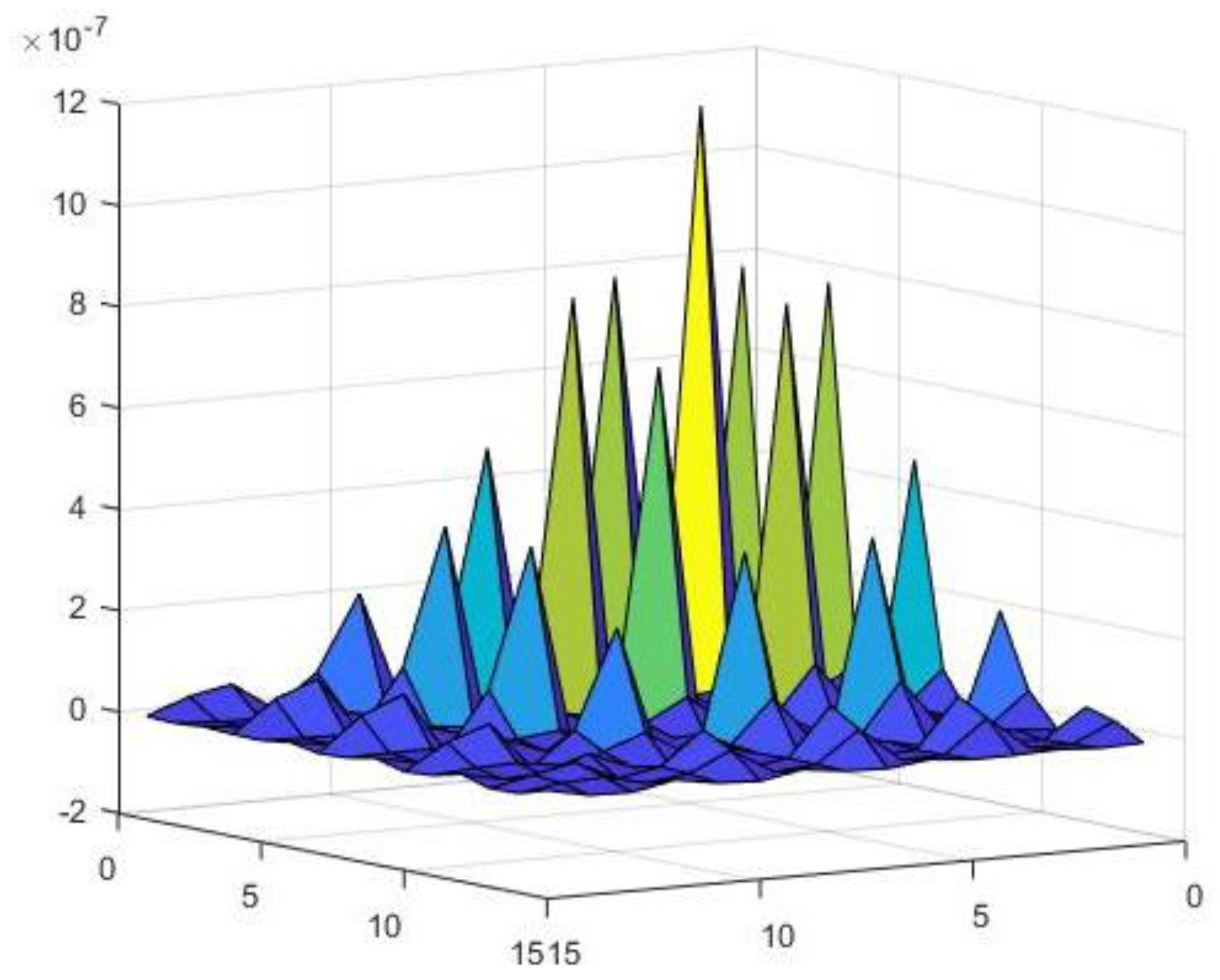
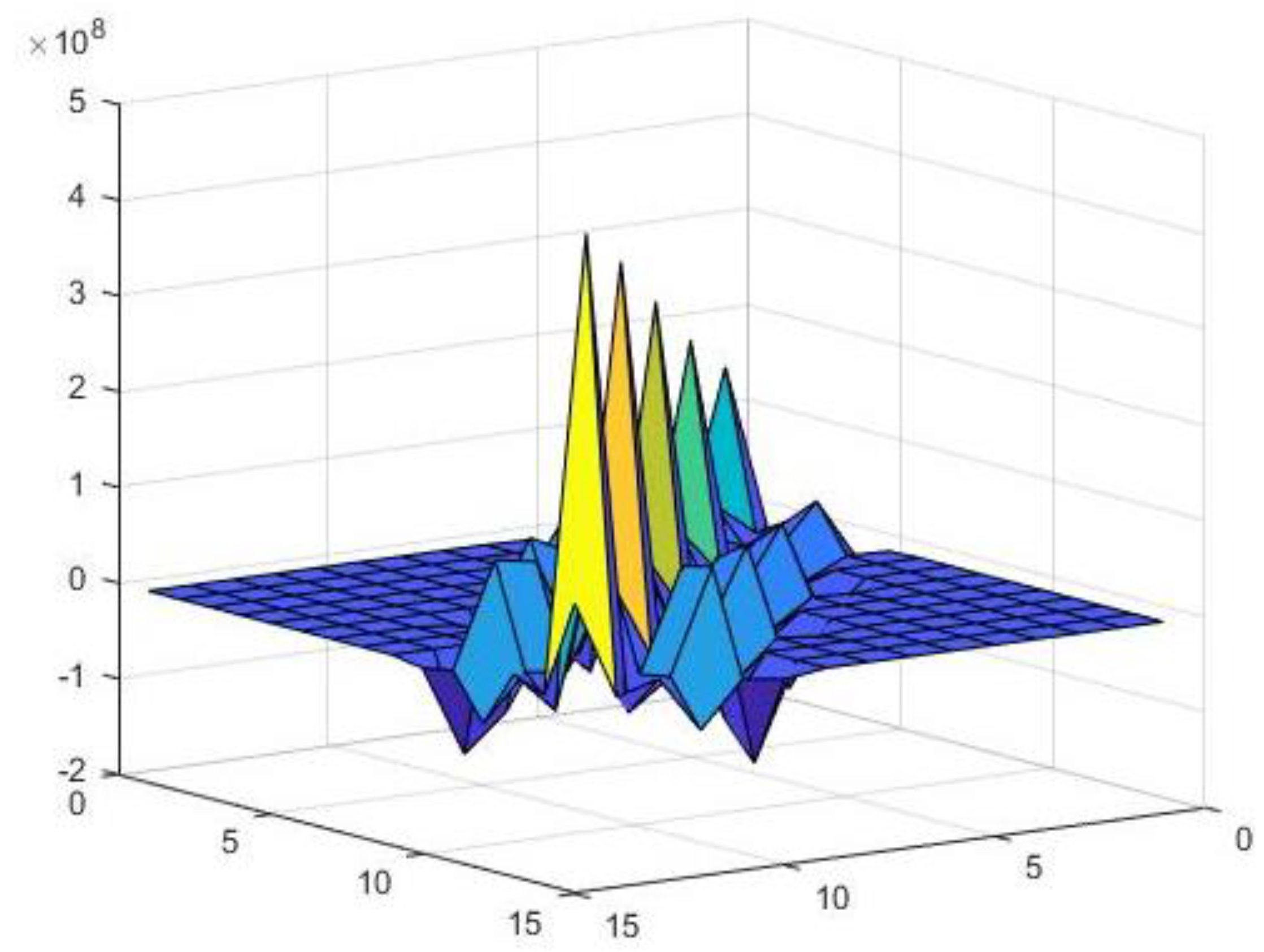
Figure 9 shows the flexibility matrix of the numerical model. From Equation (18), the inverse of the flexibility matrix yields a stiffness matrix θ with a dimension of 15 × 15, as shown in Figure 10.
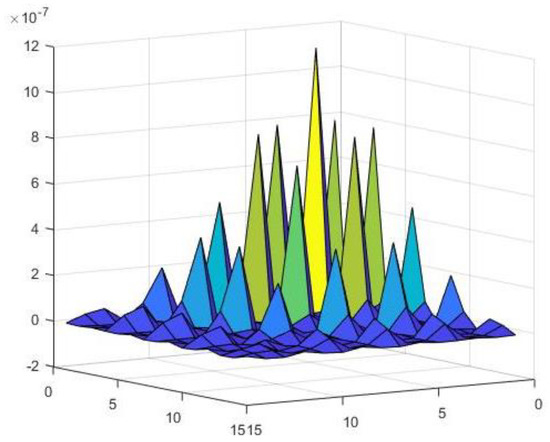
Figure 9.
Numerical distribution of flexibility matrix (type one).
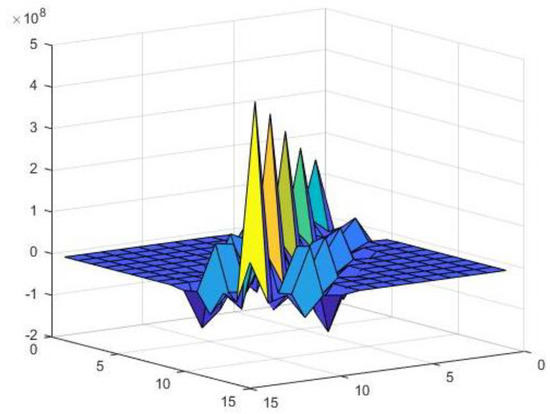
Figure 10.
Numerical distribution of flexibility matrix (type two).
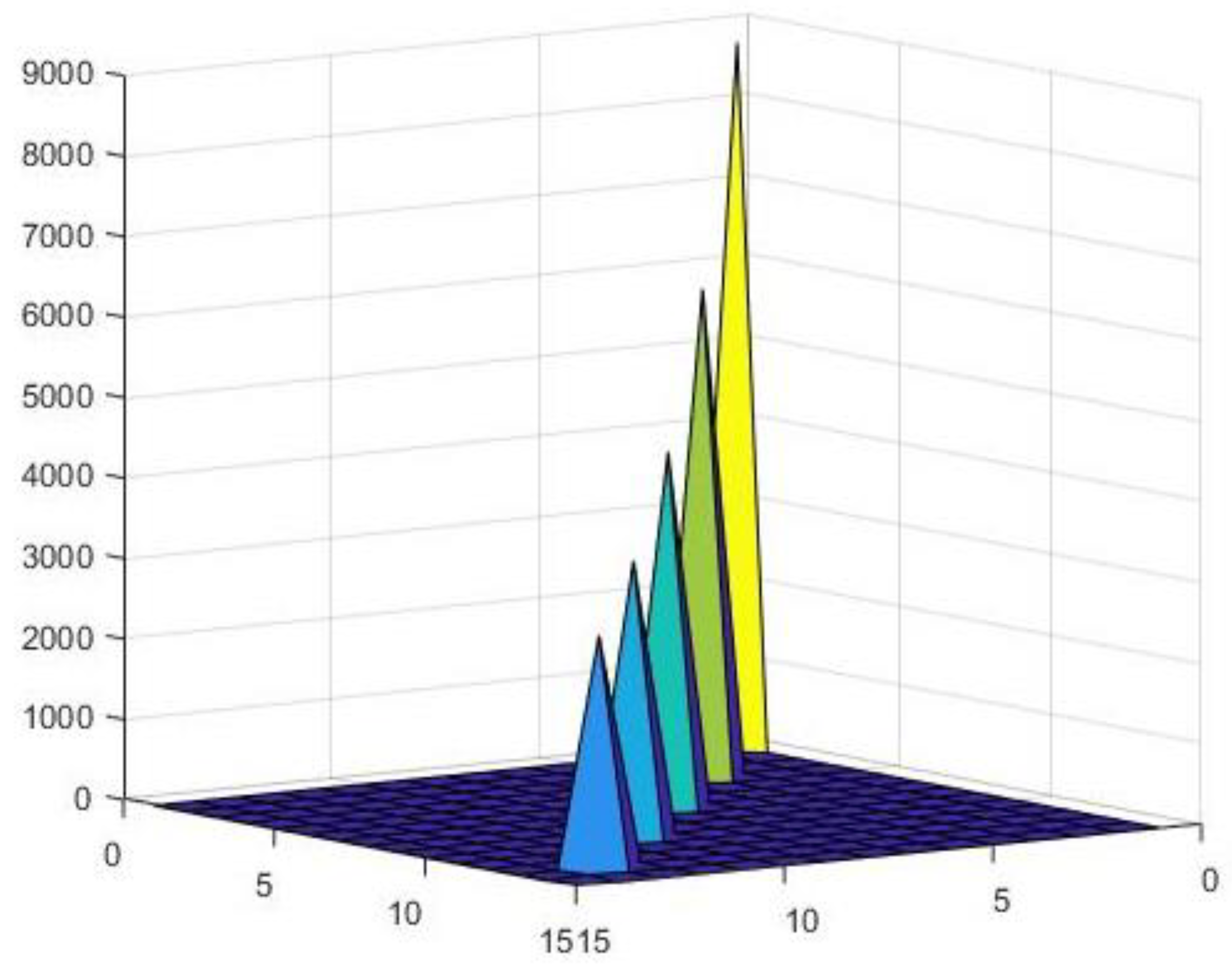
The variable-curvature beam structure is divided into six segments, with knots as connection points. The mass of each arc segment can be assumed to be gathered into a point mass determined by statics at each of the junction points. The concentrated mass matrix is shown in Figure 11.
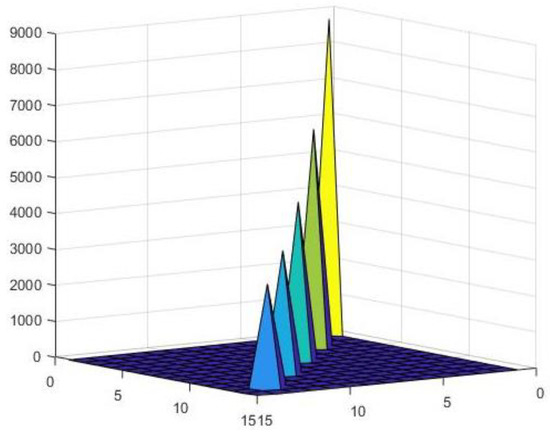
Figure 11.
Numerical distribution of mass matrix.
4.1. Uniform Action of Moving Loads with Negligible Mass
The purpose of dynamic analysis of variable-curvature beam structures is to guide the design of curved bridges, where moving loads differ by many orders of magnitude compared with the self-weight of the curved beam, and the mass of the moving loads can be ignored and considered as concentrated forces. In addition to the self-weight load of the structure and the magnitude of the vehicle load, the effect of the moving speed on the dynamic response of a curved bridge is critical.
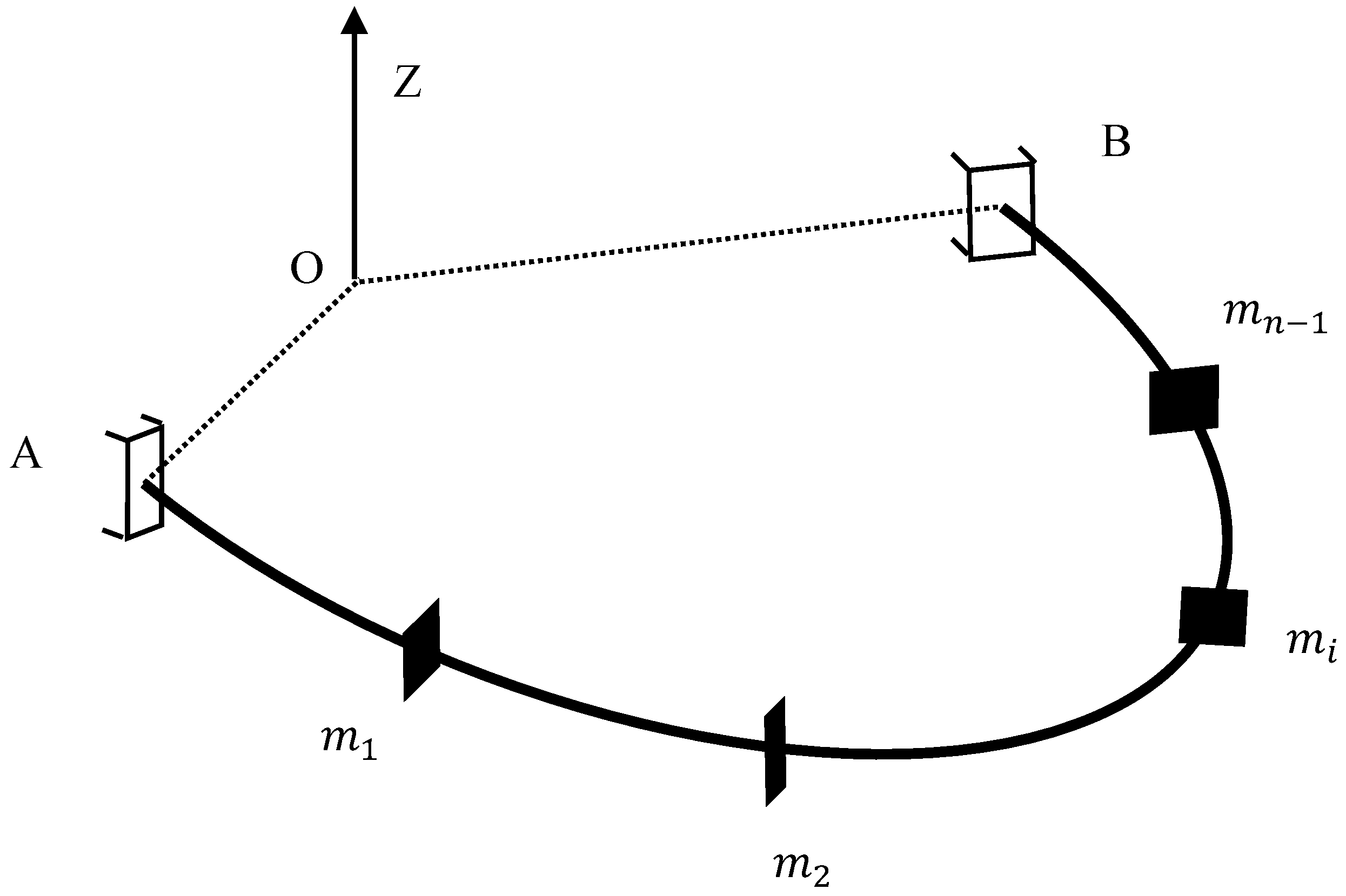
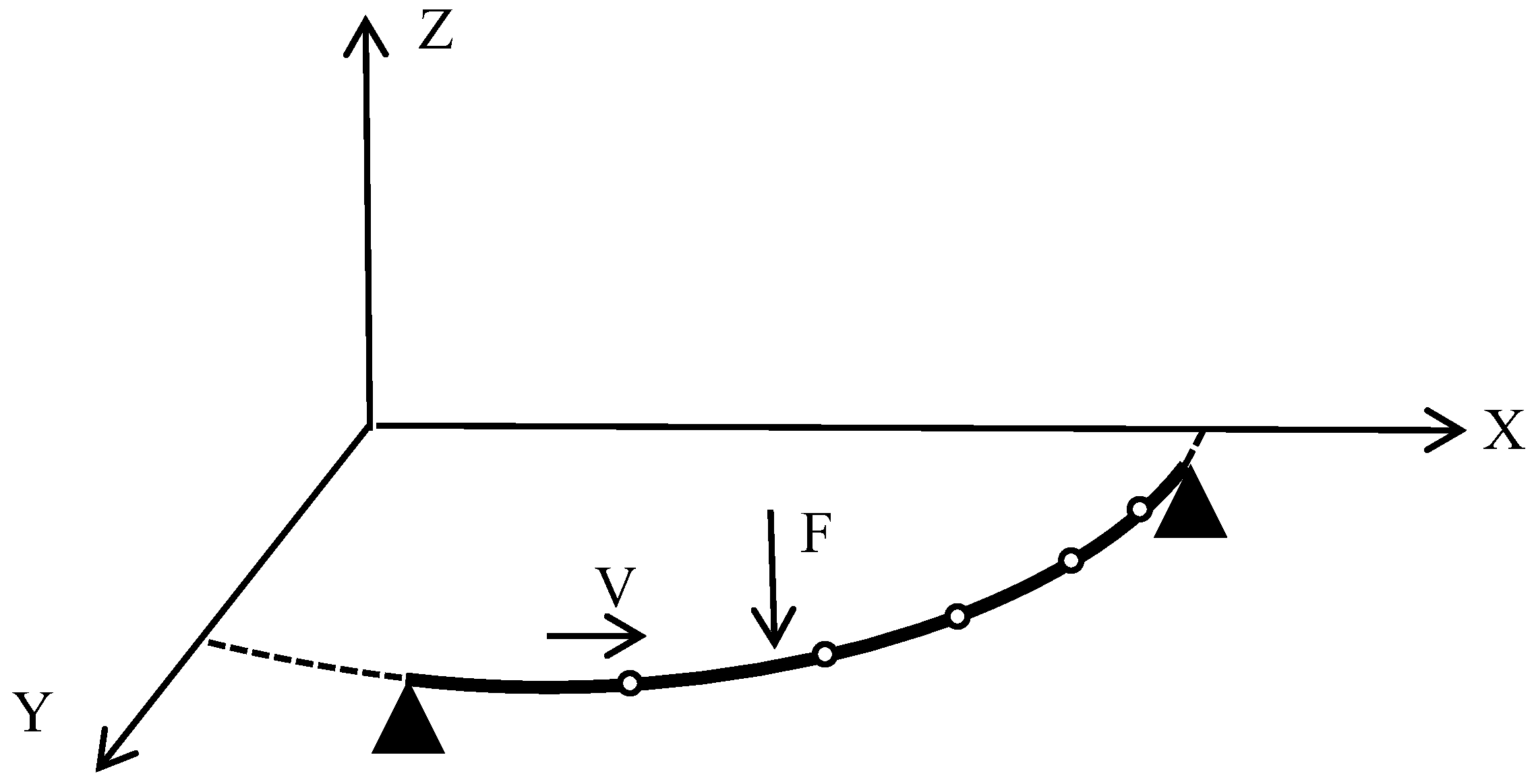
The response of an undamped variable-curvature beam with fixed restraint under a uniform-velocity moving load was calculated by moving a concentrated load of constant size from A to B. The beam cells were angularly varied equally by adjusting the time step so that the load moved exactly by one cell distance in each time step, as shown in Figure 12.
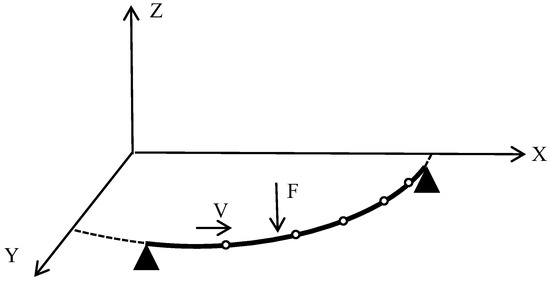
Figure 12.
Variable-curvature beam subjected to moving load F with uniform speed.
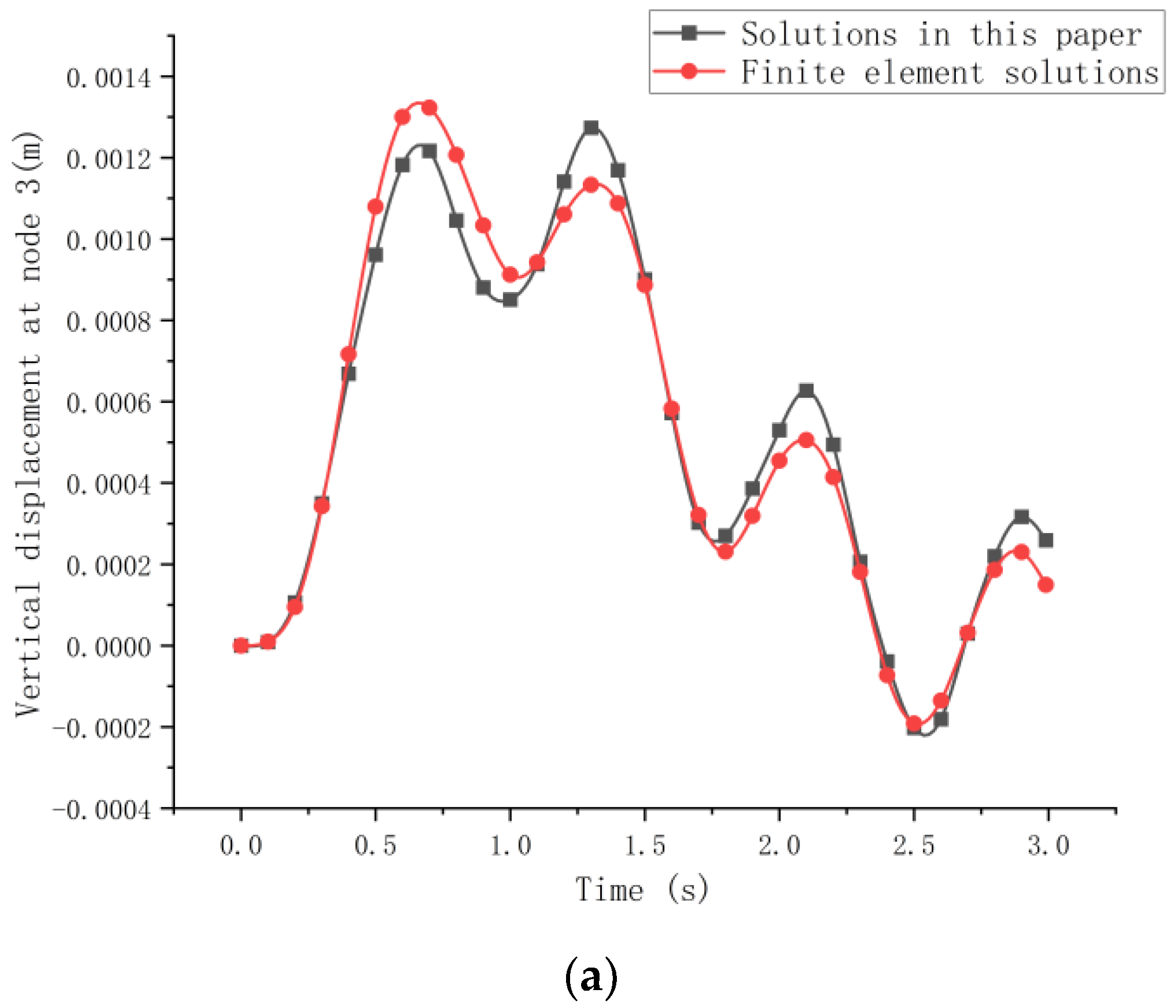
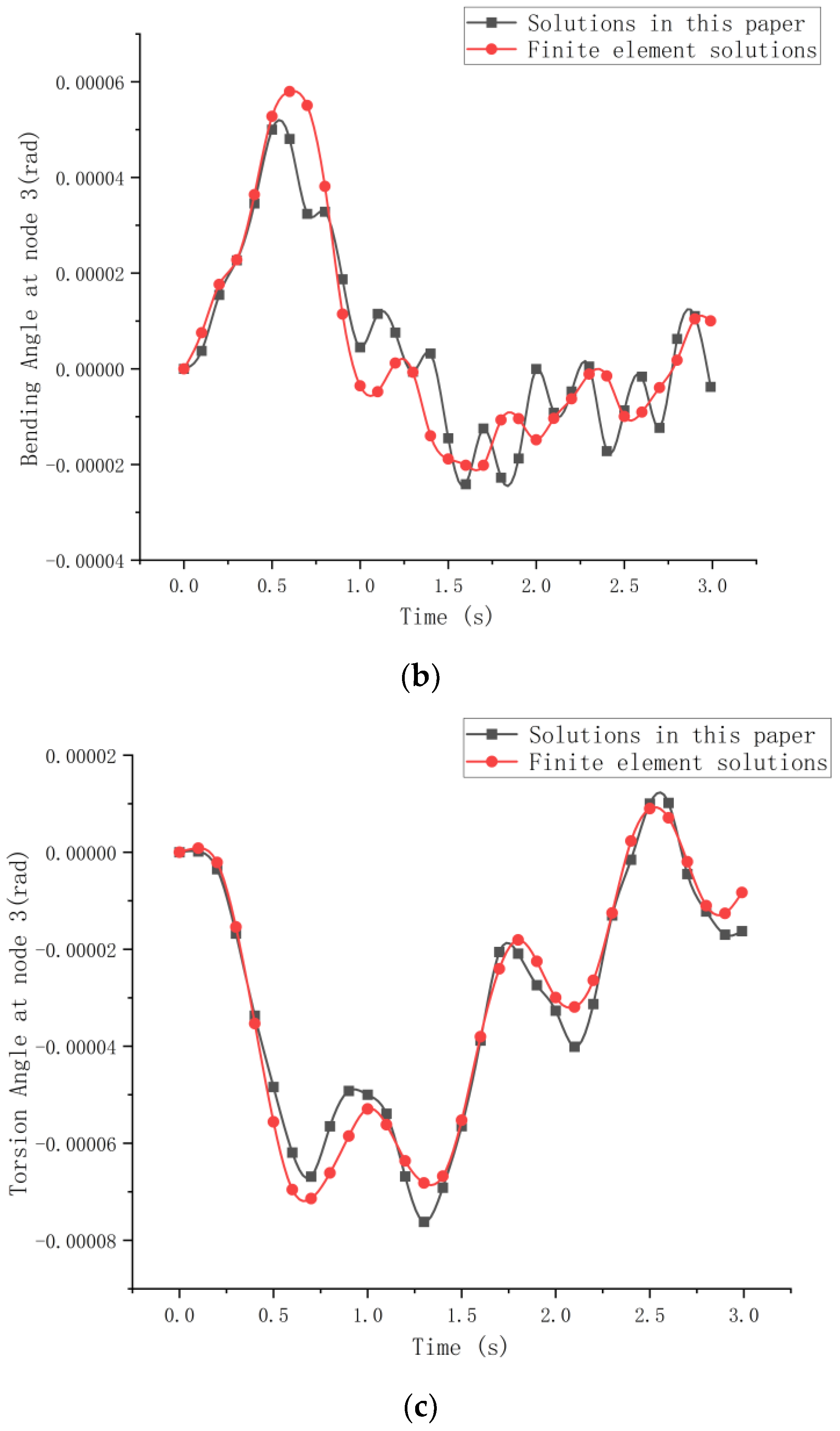
The black triangles in the figure represent the constraints at both ends of the curved beam, and the out-of-plane part is generally considered as a fixed constraint. The white dots indicate the nodes between the units after dividing the units on the beam. To verify the proposed method, finite element software was applied to simulate the moving load acting on the variable-curvature beam, and the derived dynamic response was compared to the precise integration method of this study. A finite element model with the same line type and the same properties was also created in Ansys and divided into six-cell structures. Using the precise integration method, the speed of the moving concentrated force was set to 11 m/s, and the magnitude of the force was set to 1000 N. Moving from left to right on the beam, taking node as an example, the time course curve was studied, and the displacement response comparison in Figure 13 was obtained.
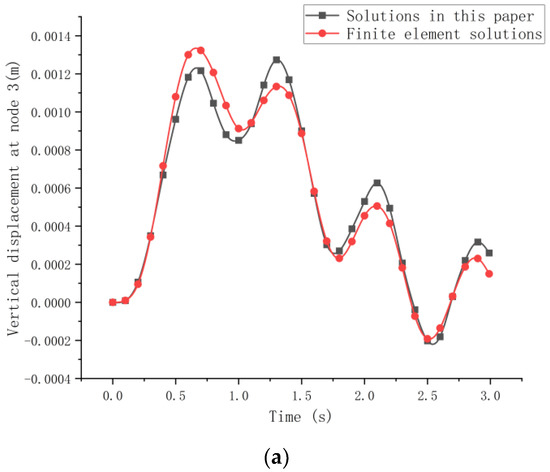
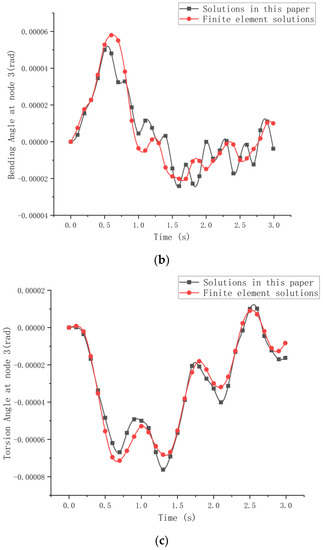
Figure 13.
Displacement response diagram of node 3 under uniform moving load F. (a) Vertical displacement response. (b) Bending angle response. (c) Torsion angle response.
The calculation steps and calculation times of the two methods are compared to obtain the data in Table 2.

Table 2.
Calculation time comparison.
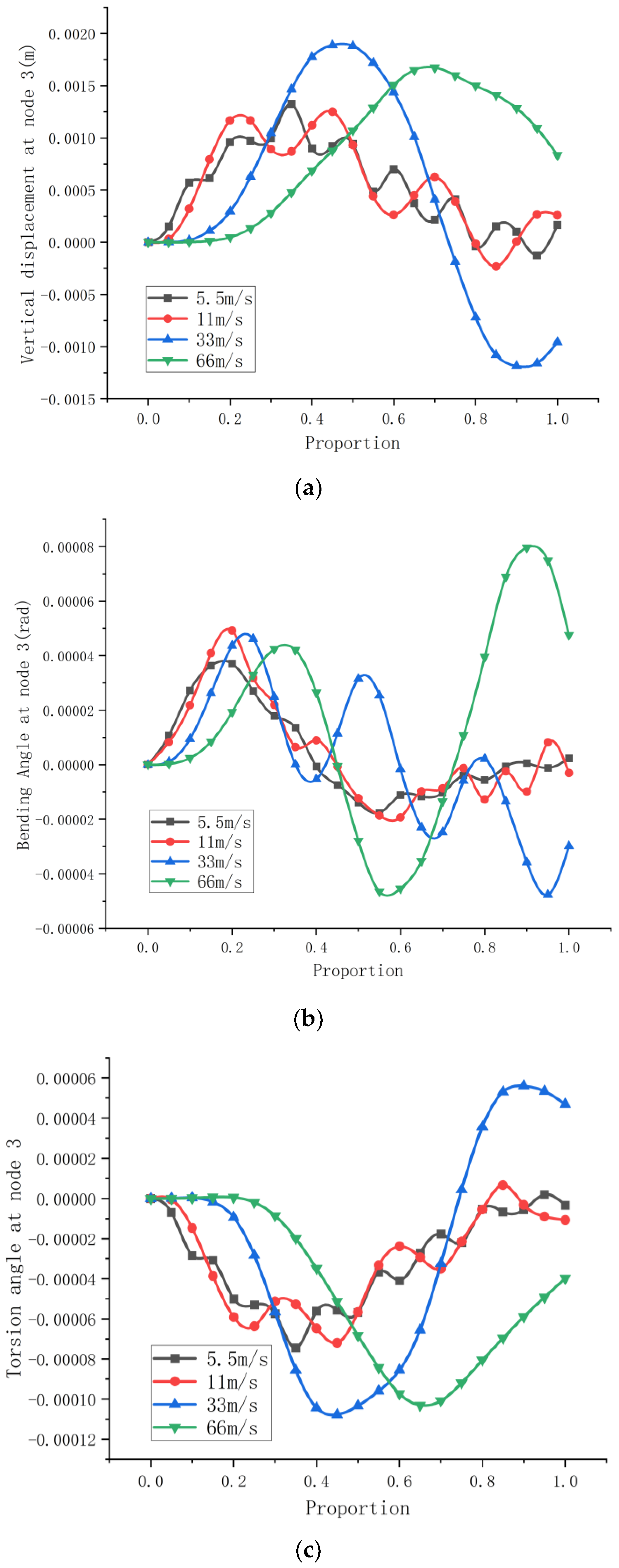
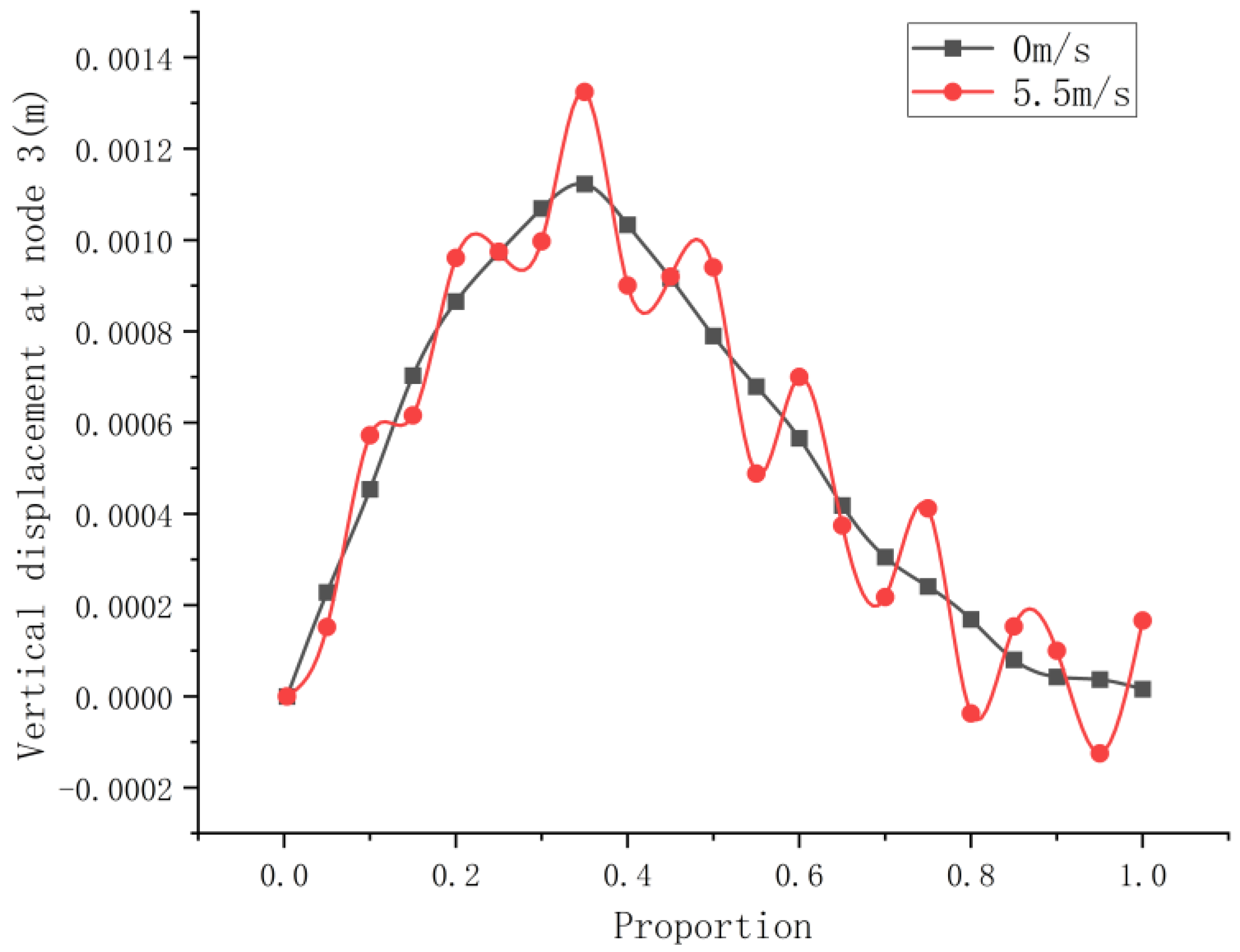
The dynamic response curves of beam node with three degrees of freedom are shown in Figure 14 for the cases when the external force F of uniform velocity passes through the variable-curvature beam at 5.5 m/s, 11 m/s, 33 m/s, and 66 m/s. The x-coordinate in the figure is the ratio of the arc length moved by the dynamic load to the total length of the curved beam arc. Figure 15 shows the vibration curves of the influence line in the static state and the vertical displacement of the beam in the small velocity case.
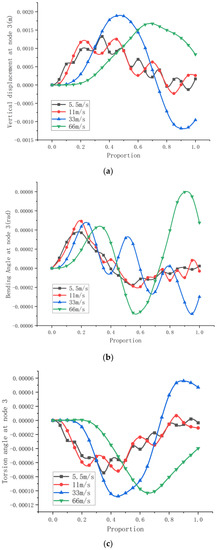
Figure 14.
Response of load F at different moving speeds. (a). Vertical displacement response at different moving speeds. (b). Bending angle response at different moving speeds. (c) Torsion angle response at different moving speeds.
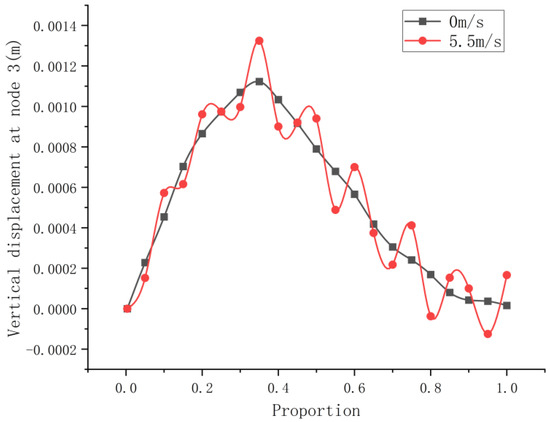
Figure 15.
Static and dynamic contrast diagram of the beam with variable curvature.
4.2. Dynamic Response under Moving Mass
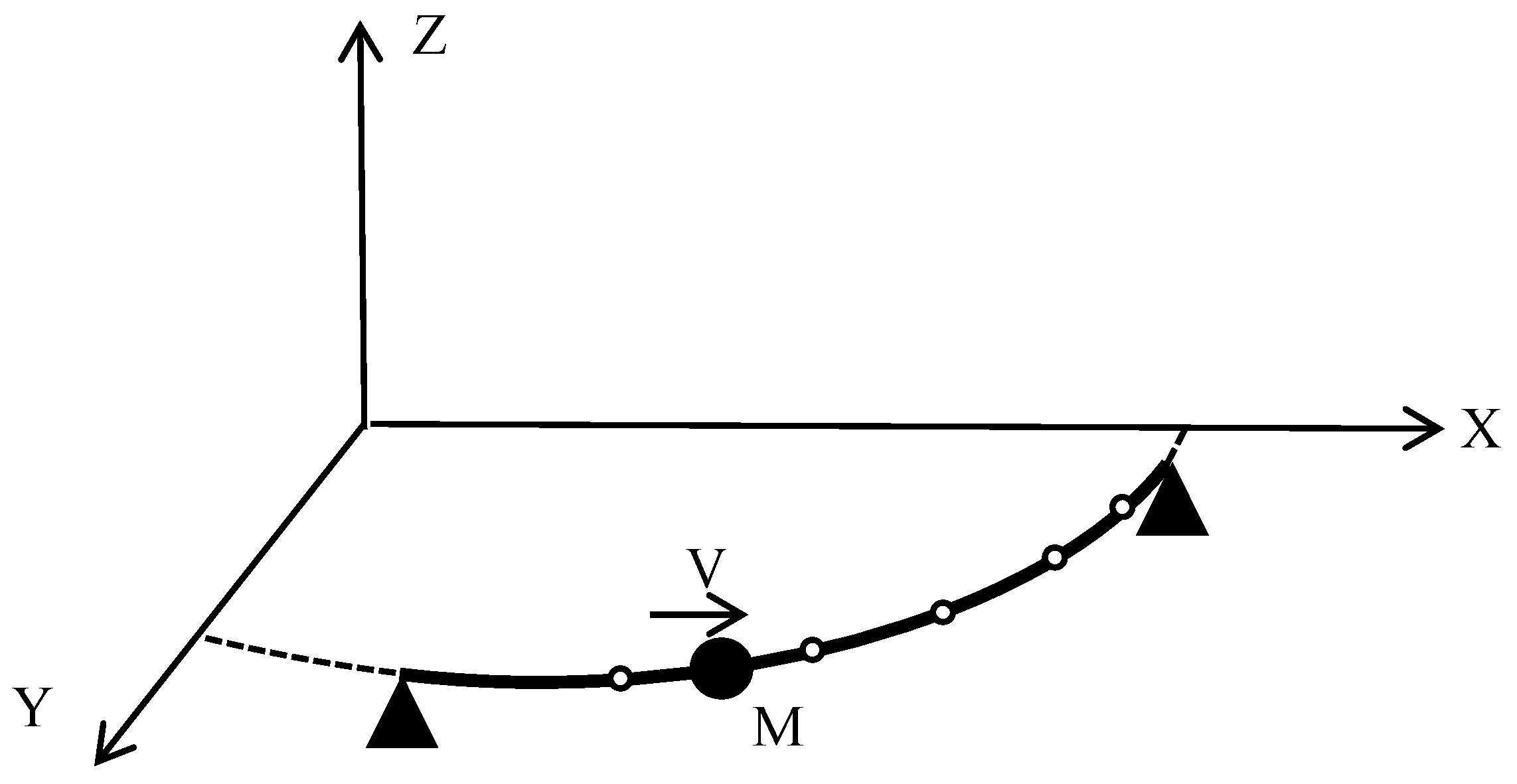
The previous section provides a solution to the dynamic response under moving loads that neglects masses but affects the vertical displacement timescale of the curved beam when large-mass loads are applied to the beam. In practical engineering, moving objects coupling the mass of the moving load to the mass matrix of the bridge are more accurate in modeling the vibration response of a bridge under vehicle loads. Therefore, solving the dynamic time responses of the three directions of freedom of the curved beam under the action of a large-mass load is of great importance in analyzing the vibration response generated by a heavy vehicle passing along the curved beam. The structural analysis of a uniform mass m with different velocities of vertical forces acting on a variable-curvature beam is shown in Figure 16.
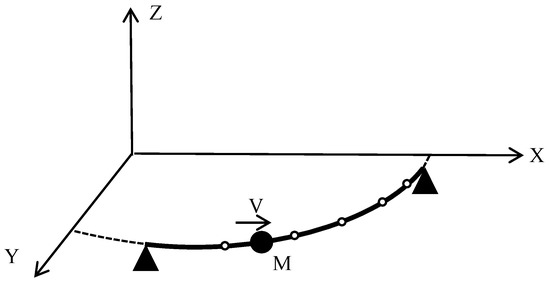
Figure 16.
Variable-curvature beam subjected to a moving mass M with uniform speed.
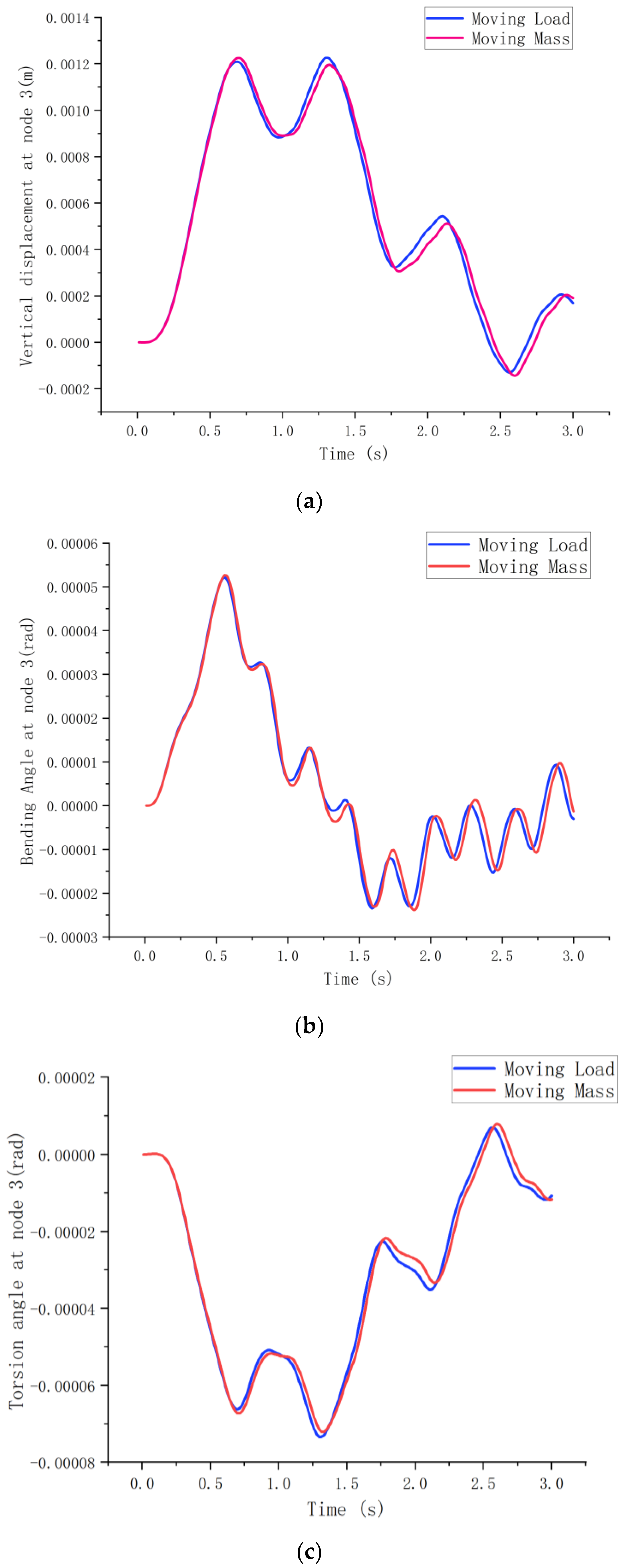
The mass matrix of the curved beam changed with time as the large-mass load moved across the beam. The speed of movement of the large mass was set to 11 m/s, and the movement was from left to right. Taking node 3, , as an example, a time-course curve was determined, which provided a comparison of the displacement response of the moving load and the moving mass in Figure 17.
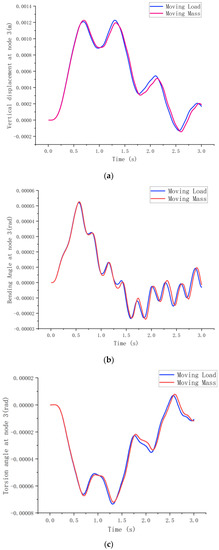
Figure 17.
Displacement response of node 3 under uniform moving mass. (a). Vertical displacement response. (b). Bending angle response. (c). Torsion angle response.
As seen in Figure 17, the displacement–time courses of forced vibrations of the variable-curvature beam with the time-dependent mass matrix taken into account were broadly consistent with the displacement vibration trends compared to the moving load alone. However, owing to the effect of the mass matrix, the vibration of the moving mass was relatively lagged, and the displacement amplitudes were small in all three directions of freedom.
5. Experimental Model
In addition to verification by the finite element method, the theoretical correctness of the study and the accuracy of its computational solutions could be verified through experimental data from an actual model built using a steel structure of variable curvature in the laboratory and subjecting the model to loading tests with moving loads.
A curved steel beam of elliptical linear shape with a long half-axis of 60 cm and a short half-axis of 30 cm was designed under the conditions available in the laboratory. The beam had a constant rectangular cross-section with a width of 5 cm and thickness of 0.5 cm. Considering that the spatially curved beam would be subjected to vertical forces, moments around the radial direction, and torques around the tangential direction at each section, the spatially curved beam had to be a three-time super-stationary structure. One in-plane rotatable support was provided at the beam’s 40° and 140° positions. The arrangement of the laboratory curved-beam model is shown in Figure 18.

Figure 18.
Laboratory model of the elliptical linear curved beam.
The parameters of the bridge are shown in Table 3.

Table 3.
Material parameters of model.
As shown in Figure 19 and Figure 20, a sliding ramp was placed at the left end of the beam, and two lubricated wire ropes were fixed at the same spacing on the upper surface of the beam as a track for the sphere to slide. Next, 0.75 kg balls were released at the left end at different speeds. Lubricant was applied to the balls and track to minimize the effect of friction on the sliding track. Vertical displacement sensors were placed at the span and 80° positions of the curved beam, and the length of time the ball traveled the full length of the curved beam and the change in vertical displacement at the sensor placement were recorded. The velocity of the ball was changed, and the vertical displacement data were then measured again.

Figure 19.
Erection of track on the curved beam.

Figure 20.
Sensors were placed on the beam for the experiment.
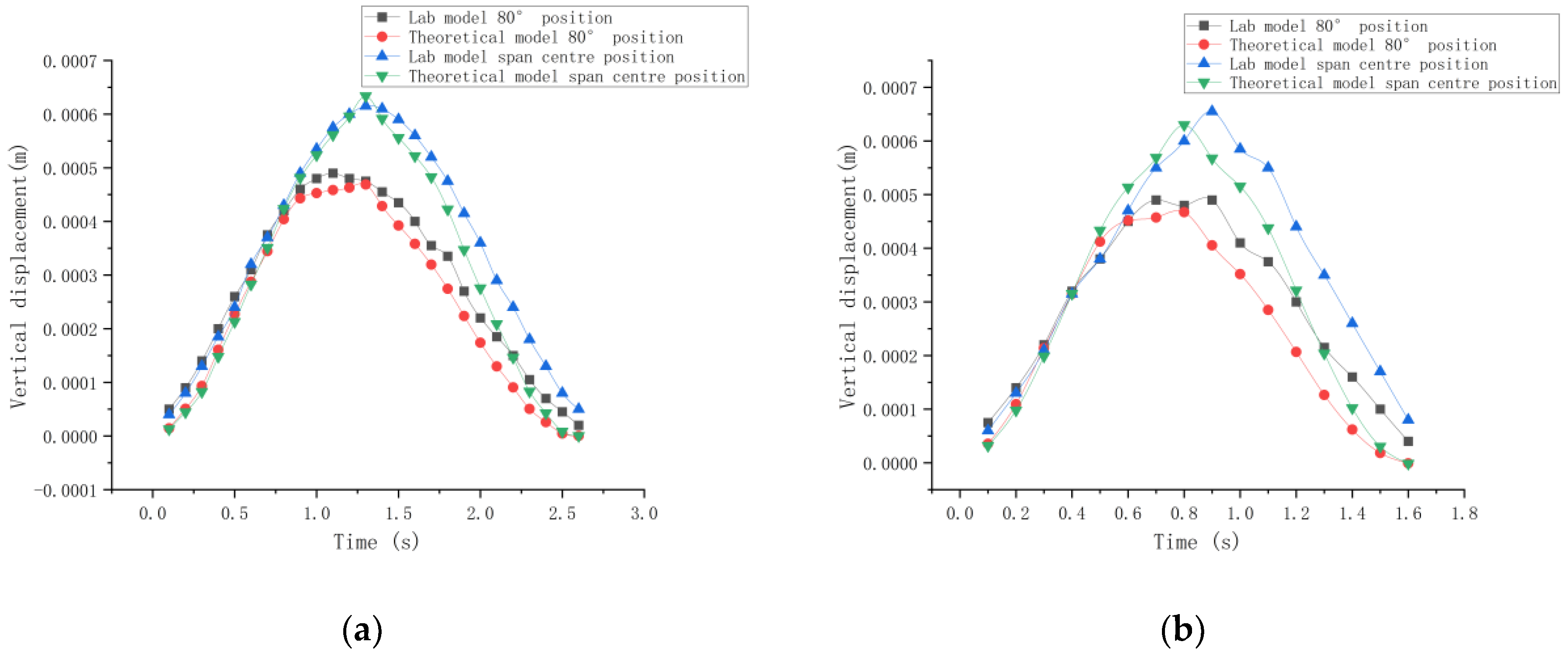
Theoretical calculation results according to the theory in this study were based on the model dimensions, weight of the ball, and length of movement. The experimental data were compared to the theory, as shown in Figure 21. From the comparison, as the speed of the moving ball increased, the vertical displacement–time curve showed small oscillations, which was consistent with the theoretical results in the previous study.
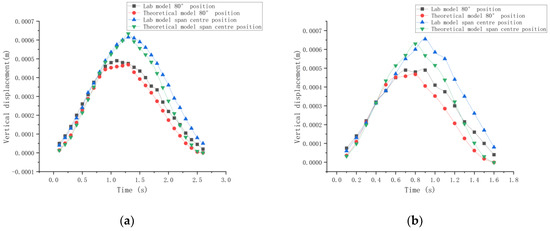
Figure 21.
Comparison of dynamic response of laboratory model with theoretical model. (a) The ball moving at a speed of 1.2 m/s. (b) The ball moving at a speed of 2 m/s.
6. Conclusions
Based on the existing precise integration method, the stiffness matrix of a variable-curvature steel beam was obtained through matrix inversion, and the mass matrix was obtained by the concentrated mass method to solve the dynamic response of a variable-curvature beam under moving loads. The theoretical results were compared to the finite element calculation results and experimental data to obtain the following conclusions.
- (1)
- The finite element model was compared with the theoretical calculations in this paper, and the displacement–time curves agree well. Therefore, the precise integration method can be applied to analyze the vibration response of the variable-curvature beam under various operating conditions.
- (2)
- Although the direction of the action of the moving load was vertical, unlike a straight beam, the application of the load in one direction produced displacements in three directions of freedom. In addition, during the movement of the load, the vertical displacement and the torsional angle of rotation displayed the same trends in time and opposite directions.
- (3)
- The static diagram shows the influence line under an external load. In the case of small velocities, the time-course curve oscillates in the vicinity of the influence line. However, as the velocity increases, the displacement in the direction of the three degrees of freedom tends to oscillate irregularly up and down. The line shape of the curve changes, the slope of the points on the curve decreases, the curve trends more gently, and the amplitude of the oscillations increases.
- (4)
- When a moving load is applied to a variable-curvature beam, the displacement–time curve line shape of its forced vibration is influenced by the velocity, and the time curve vibration lags more under a large-mass load compared to a moving load.
- (5)
- Numerical results show that the exact integration method can achieve equally accurate numerical calculations and is more efficient when dividing the same number of elements and using the same calculation steps than the currently widely used finite element method.
- (6)
- The correctness of the theory in this paper was verified through experiments. Since the mass of the small ball set in this study was large, the damping effect was not considered in the theoretical analysis. Consequently, the time-course curve results obtained from the experiments lagged more compared with the theoretical calculation. Considering the influence of experimental error, the curve fits better, so our theory has a more efficient engineering application value for guiding the actual bridge alignment design, setting the maximum load capacity of the bridge, disease analysis, preventing bridge damage, etc.
Author Contributions
Conceptualization, X.L.; investigation, D.Z.; data curation, H.Z.; writing—original draft preparation, H.Z.; writing—review and editing, X.L., H.Z. and D.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Data presented in this research are available upon request from the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Yao, L.S. Curved Beam; People’s Communications Press: Beijing, China, 1989. [Google Scholar]
- Zhao, Y.Y.; Kang, H.J.; Feng, R. Research Progress of Curved Beams. Adv. Mech. 2006, 2, 170–186. [Google Scholar]
- Zhang, Y.H. Theoretical Analysis of Bridge Structure; Science Press: Beijing, China, 2005. [Google Scholar]
- Luo, H.Y. Analysis and Research on Mechanical Properties of Curved Girder Bridges. Master’s Thesis, Chang‘an University, Xi‘an, China, 2014. (In Chinese). [Google Scholar]
- Vlasov, V.Z. Thin-Walled Elastic Beams, 2nd ed.; Israel Program for Scientific Translation: Jerusalem, Israel, 1961. [Google Scholar]
- Morris, D.L. Curved Beamed Stiffness Coefficients. J. Struct. Div. 1968, 94. [Google Scholar] [CrossRef]
- Ni, G.R.; Wang, Y.; Xiong, G.X. Engineering Solution of Variable Section and Curvature Beam. J. Chang. Railw. Inst. 1991, 9, 40–50. (In Chinese) [Google Scholar]
- Yu, C.; Lu, J.; Li, S.; Xu, W.; Chiu, C. Dynamics Sensitivity Analyses of Functionally Graded Porous (FGP) Curved Beams with Variable Curvatures and General Boundary Conditions. Int. J. Struct. Stab. Dyn. 2021, 21, 2150151. [Google Scholar] [CrossRef]
- Wang, Q.S.; Choe, K.; Tang, J.Y.; Shuai, C.J.; Wang, A.L. Vibration analyses of general thin and moderately thick laminated composite curved beams with variable curvatures and general boundary conditions. Mech. Adv. Mater. Struct. 2020, 27, 991–1005. [Google Scholar] [CrossRef]
- Yu, J. Static Analytical Solution of Plane Beam with Variable Curvature under Variable Temperature. Master’s Thesis, Dalian Maritime University, Dalian, China, 2019. (In Chinese). [Google Scholar]
- Chen, M.D. Dynamic Characteristics Analysis and Experiment of Curved Structures Based on Exact Algorithm of Structural Mechanics. Master’s Thesis, Dalian Maritime University, Dalian, China, 2021. (In Chinese). [Google Scholar]
- Henchi, R.; Fafard, M.; Dhatt, G.; Talbot, M. Dynamic Behavior of Multi-span Beams under Moving Loads. J. Sound Vib. 1997, 199, 33–50. [Google Scholar] [CrossRef]
- Luo, J.; Zhu, S.Y.; Zhai, W.M. Formulation of curved beam vibrations and its extended application to train-track spatial interactions. Mech. Syst. Signal Process. 2022, 165, 108393. [Google Scholar] [CrossRef]
- Abdoos, H.; Khaloo, A.R.; Foyouzat, M.A. On the out-of-plane dynamic response of horizontally curved beams resting on elastic foundation traversed by a moving mass. J. Sound Vib. 2020, 479, 115397. [Google Scholar] [CrossRef]
- Li, S.H.; Ren, J.Y. Analytical study on dynamic responses of a curved beam subjected to three-directional moving loads. Appl. Math. Model. 2018, 58, 365–387. [Google Scholar] [CrossRef]
- Poojary, J.; Roy, S.K. In Plane Radial Vibration of Uncracked and Cracked Circular Curved Beams Subjected to Moving Loads. Int. J. Struct. Stab. Dyn. 2021, 21, 2150146. [Google Scholar] [CrossRef]
- Han, F.; Wang, D.H.; Dan, D.H. Dynamic response of a bridge deck pavement. Proc. Inst. Civ. Eng. Transp. 2019, 172, 221–232. [Google Scholar] [CrossRef]
- Zhang, X.; Chen, E.; Li, L.Y.; Si, C.D. Development of the Dynamic Response of Curved Bridge Deck Pavement Under Vehicle–Bridge Interactions. Int. J. Struct. Stab. Dyn. 2022, 22, 2241003. [Google Scholar] [CrossRef]
- Zhong, W.X.; Williams, F.W. A Precise Time Step Integration Method. Proc. Inst. Mech. Eng. Part C 1994, 208, 427–430. [Google Scholar] [CrossRef]
- Yang, Y.B.; Wu, C.M. Dynamic Response of a Horizontally Curved Beam Subjected to Vertical and Horizontal Moving Loads. J. Sound Vib. 2001, 242, 519–537. [Google Scholar] [CrossRef]
- Wu, J.S.; Chiang, L.K. Out-of-plane responses of a circular curved Timoshenko beam due to a moving load. Int. J. Solids Struct. 2003, 40, 7425–7448. [Google Scholar] [CrossRef]
- Zhang, Y.H.; Zhang, S.Y.; Zhao, Y.; Song, G.; Lin, J.H. A Precise Integration Method for Bridges Subjected to Moving Loads. Chin. J. Comput. Mech. 2006, 23, 290–294. [Google Scholar]
- Pu, J.P.; Liu, P.; Zhou, K.; Wang, Q. Fine time integral calculation of dynamic response of bridge under moving load. Bull. Sci. Technol. 2009, 25, 83–88. [Google Scholar]
- Gao, Q.; Wu, F.; Zhang, H.W.; Zhong, W.X.; Howson, W.P. A fast precise integration method for structural dynamics problems. Struct. Eng. Mech. 2012, 43, 1–13. [Google Scholar] [CrossRef]
- Shao, Y.F.; Brownjohn, J.M.W.; Miao, C.Q.; Wang, M.M. A precise time-integration linear vehicle-bridge interaction method and dynamic sensitivity analysis. Structures 2021, 33, 4596–4603. [Google Scholar] [CrossRef]
- Zheng, C.C.; Huang, Q.; Liu, G.B. Vibration Characteristics of Track with Discrete Support Curve under Moving Load. J. Ningbo Univ. NSEE 2021, 34, 74–80. [Google Scholar]
- Pang, R.; Xu, B.; Zhou, Y.; Song, L.F. Seismic time-history response and system reliability analysis of slopes considering uncertainty of multi-parameters and earthquake excitations. Comput. Geotech. 2021, 136, 104245. [Google Scholar] [CrossRef]
- Maleska, T.; Beben, D. Behaviour of soil-steel composite bridge with various cover depths under seismic excitation. Steel Compos. Struct. 2022, 42, 747–764. [Google Scholar]
- Li, X.F.; Zhai, H.S.; Pan, Z.Y. Free Vibration Analysis of Curved Beam with Variable Curvature (Elliptic Line) Based on Semi-analytical Method of Structural Mechanics. J. Vib. Eng. Technol. 2022, in press. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).