Load–Displacement Behaviour and a Parametric Study of Hybrid Rubberised Concrete Double-Skin Tubular Columns
Abstract
:1. Introduction
2. Experimental Investigation
3. Finite Element Modelling
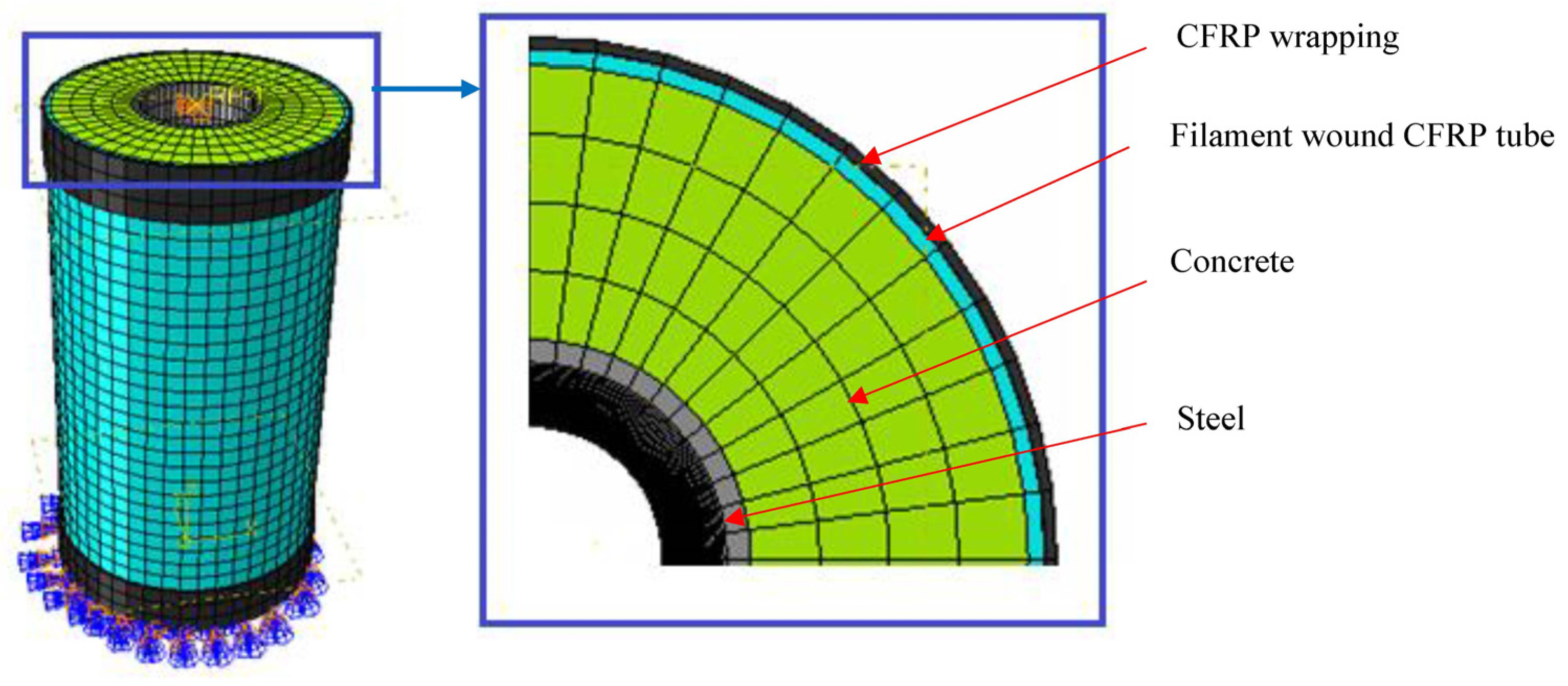
3.1. Element Type and Meshing
3.2. Material Model
3.2.1. Filament-Wound CFRP Tube
3.2.2. Rubberised Concrete
3.2.3. Steel
3.2.4. CFRP Wrapped at the Top and Bottom
3.3. Surface Interaction and Boundary Conditions
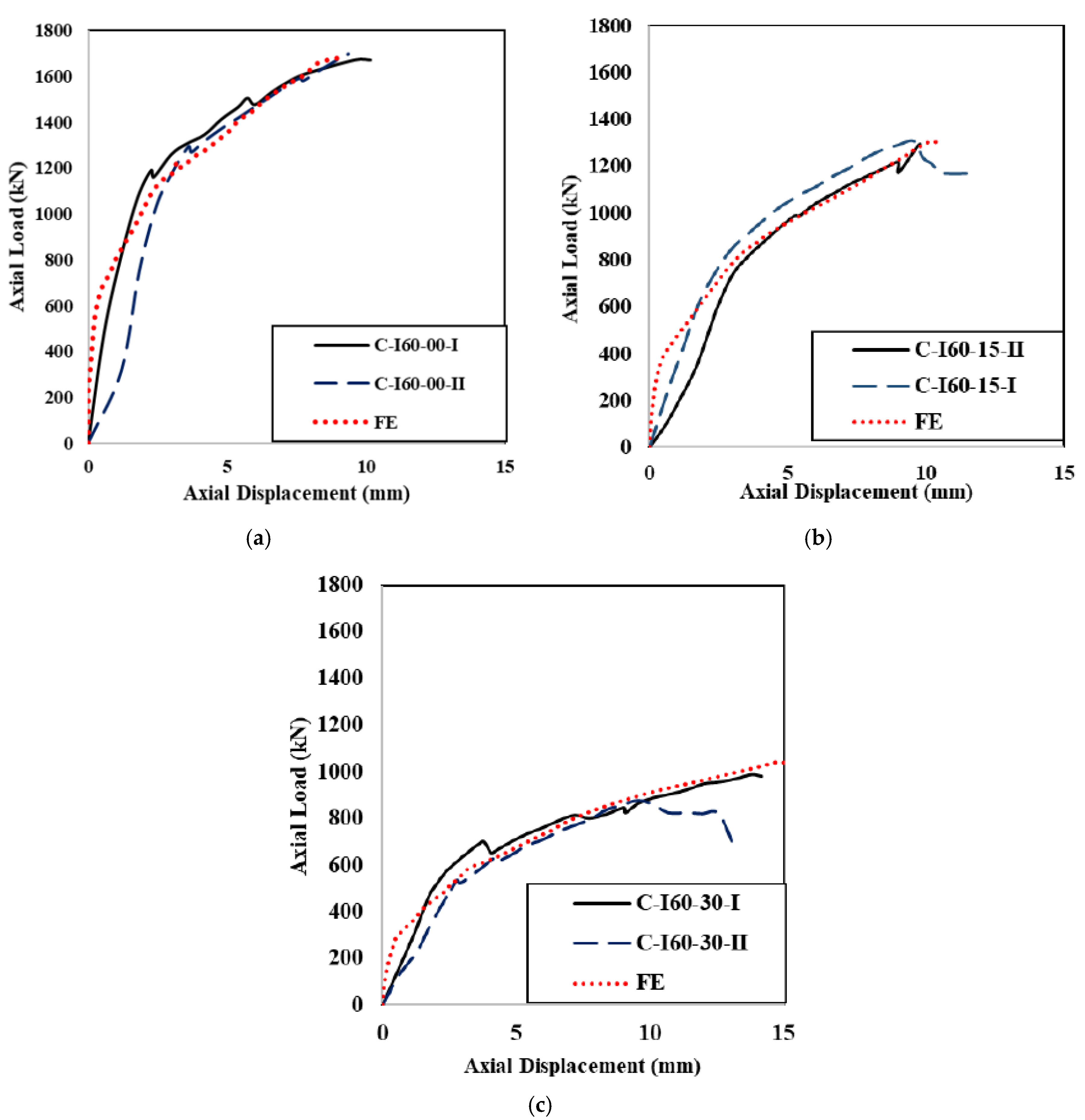
4. Validation of the Numerical Model
5. Parametric Study
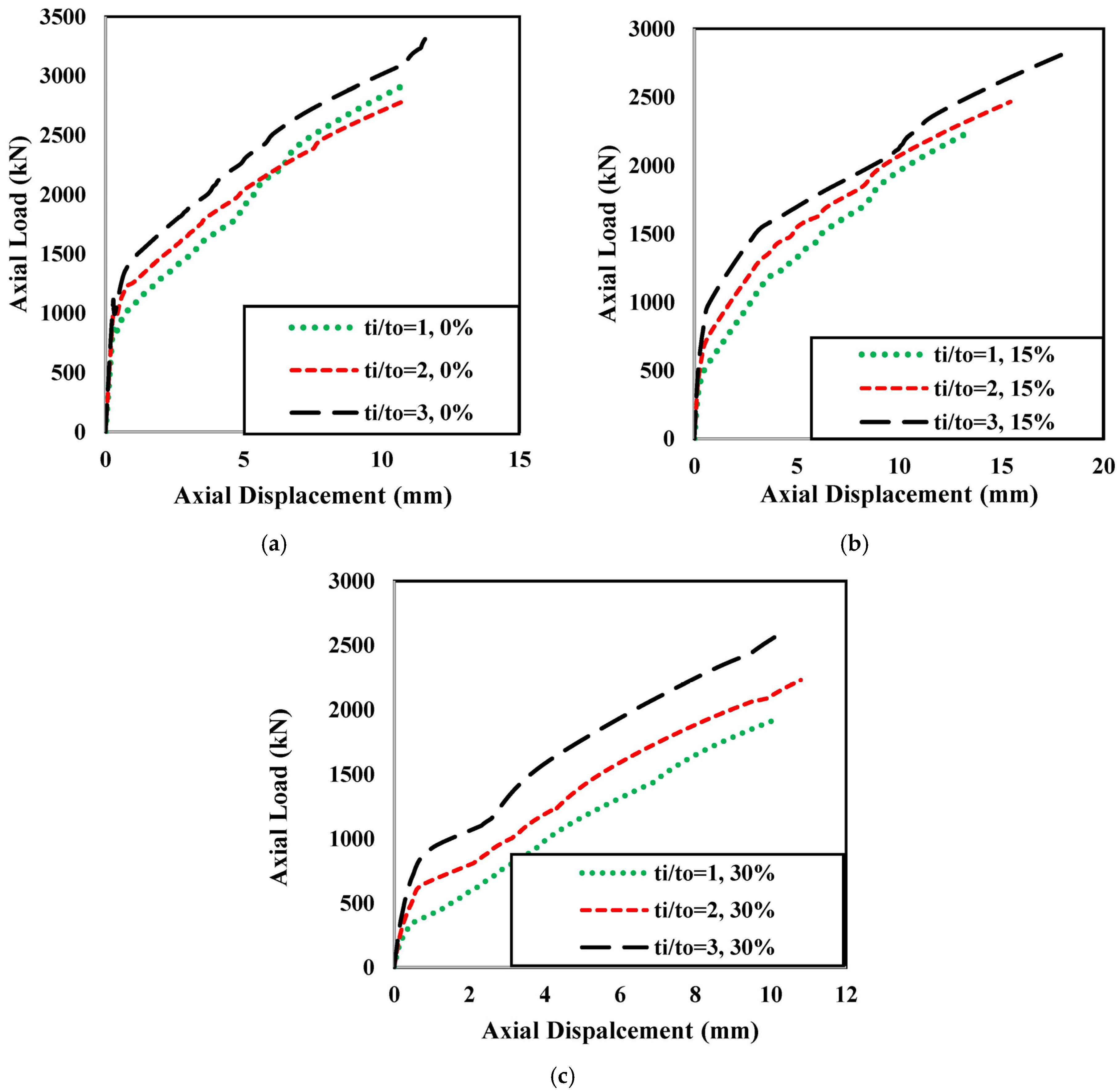
5.1. Effect of the Thickness Ratio
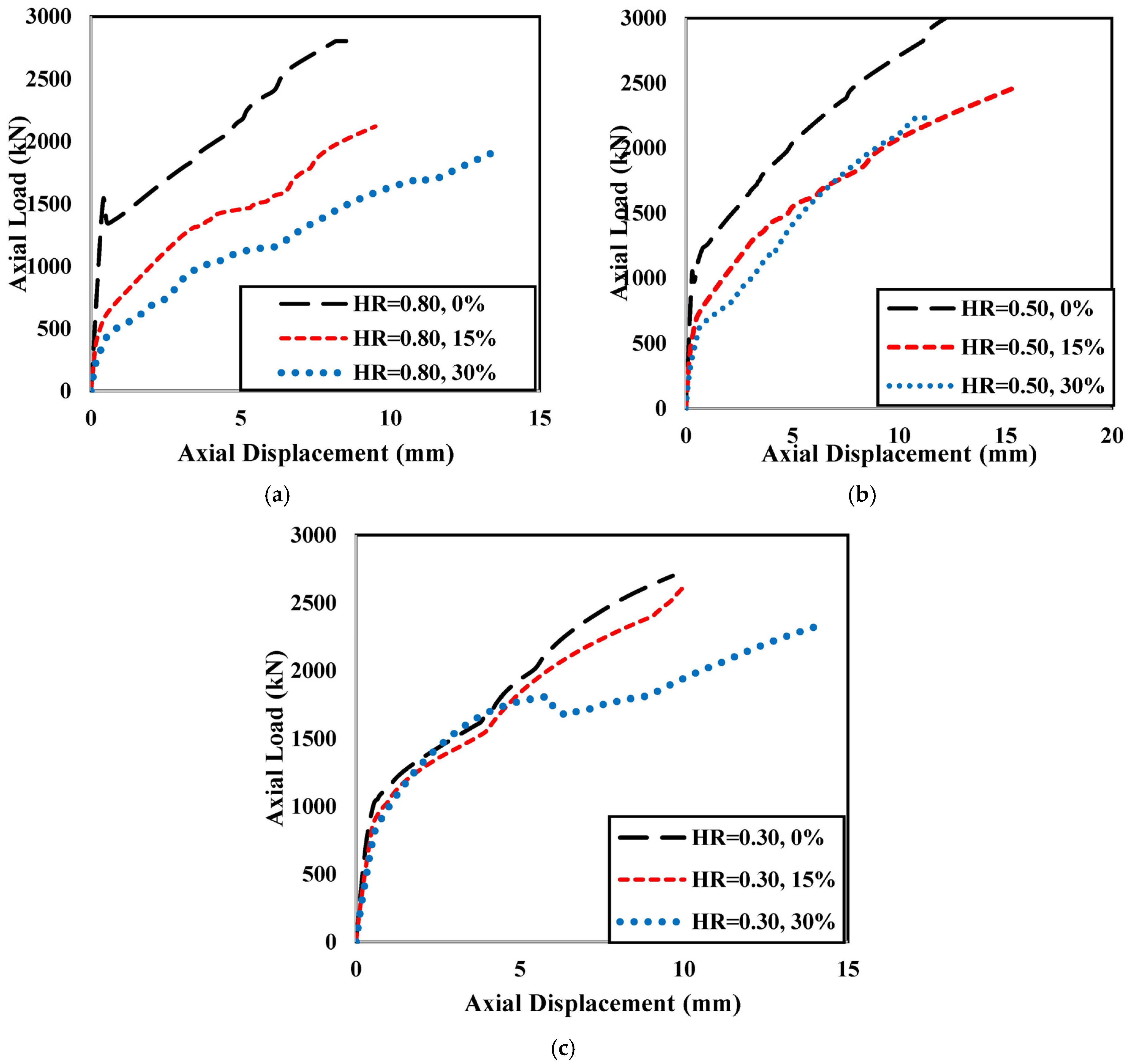
5.2. Effect of the Hollow Ratio
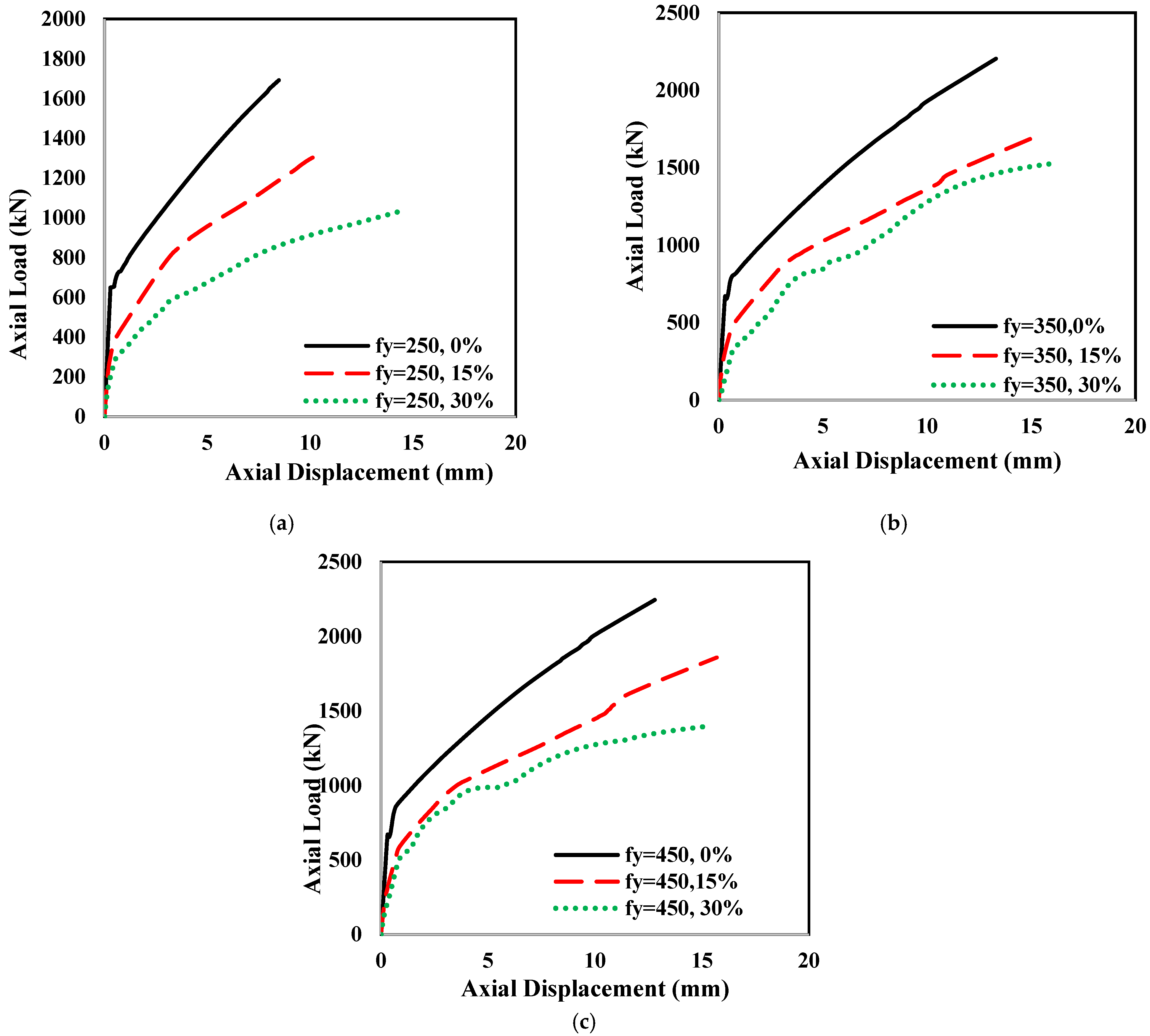
5.3. Effect of Steel Tube Yield Strength
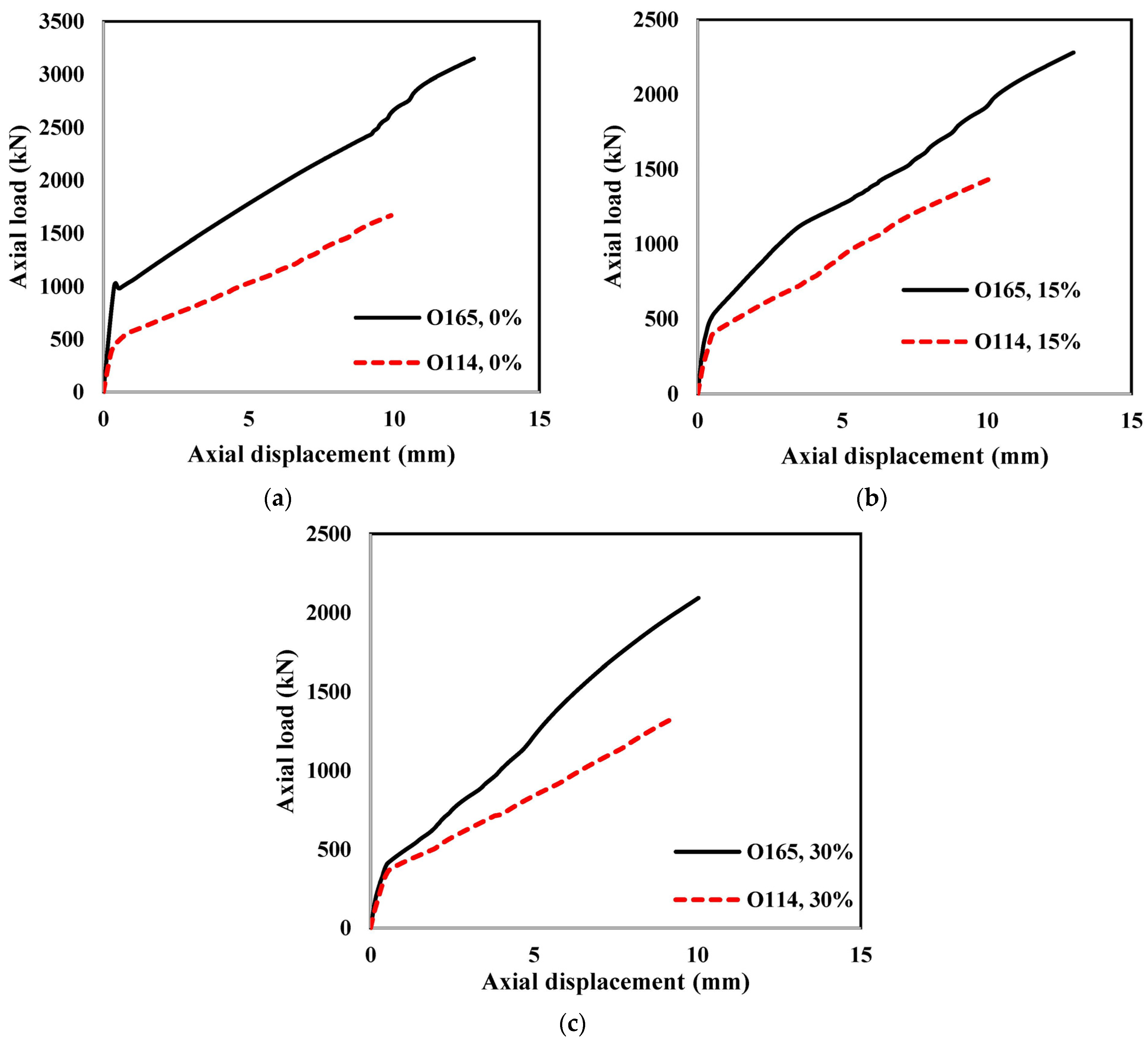
5.4. Effect of the Diameter of the CFRP Tube
6. Comparison with Existing Design Guideline
7. Conclusions
- i.
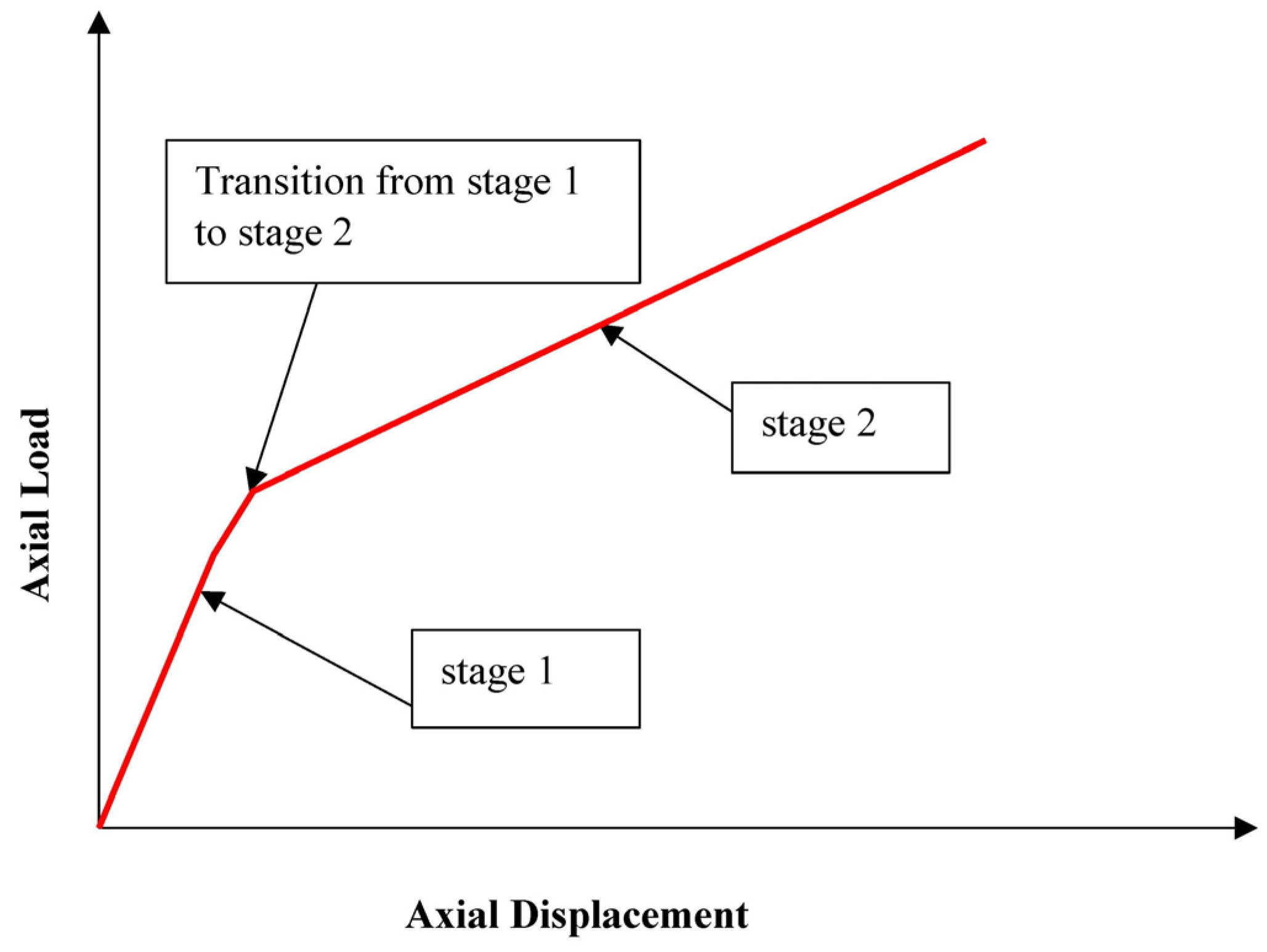
- The axial load capacity of the hybrid RuDSTCs is enhanced with an increase in the tube thickness, yield strength of steel, and inner steel tube diameter and a decrease in the hollow ratio. Increasing the rubber content results in a flatter second stage of the load–displacement curve, indicating ductile behaviour compared with the non-rubberised columns.
- ii.
- For the same thickness ratio, the axial capacity of the column decreases with the increase in the rubber content. Again, for the same strength of the inner tube steel, increasing the percentage of rubber resulted in a smoother transition from the first stage to the second stage of the load–displacement curve. A higher grade of steel also showed a greater stiffness of the hybrid column.
- iii.
- A larger outer diameter of the CFRP tube resulted in a stiffer second stage of the column. The yielding of steel tubes occurred at a similar displacement, but the axial load value varied significantly for the non-rubberised columns.
- iv.
- The strength and stiffness of the hybrid columns decreased with the increasing rubber content. A gradual and smooth transition of the load–displacement curve was observed for the 30% rubberised concrete compared with the 15% non-rubberised concrete.
- v.
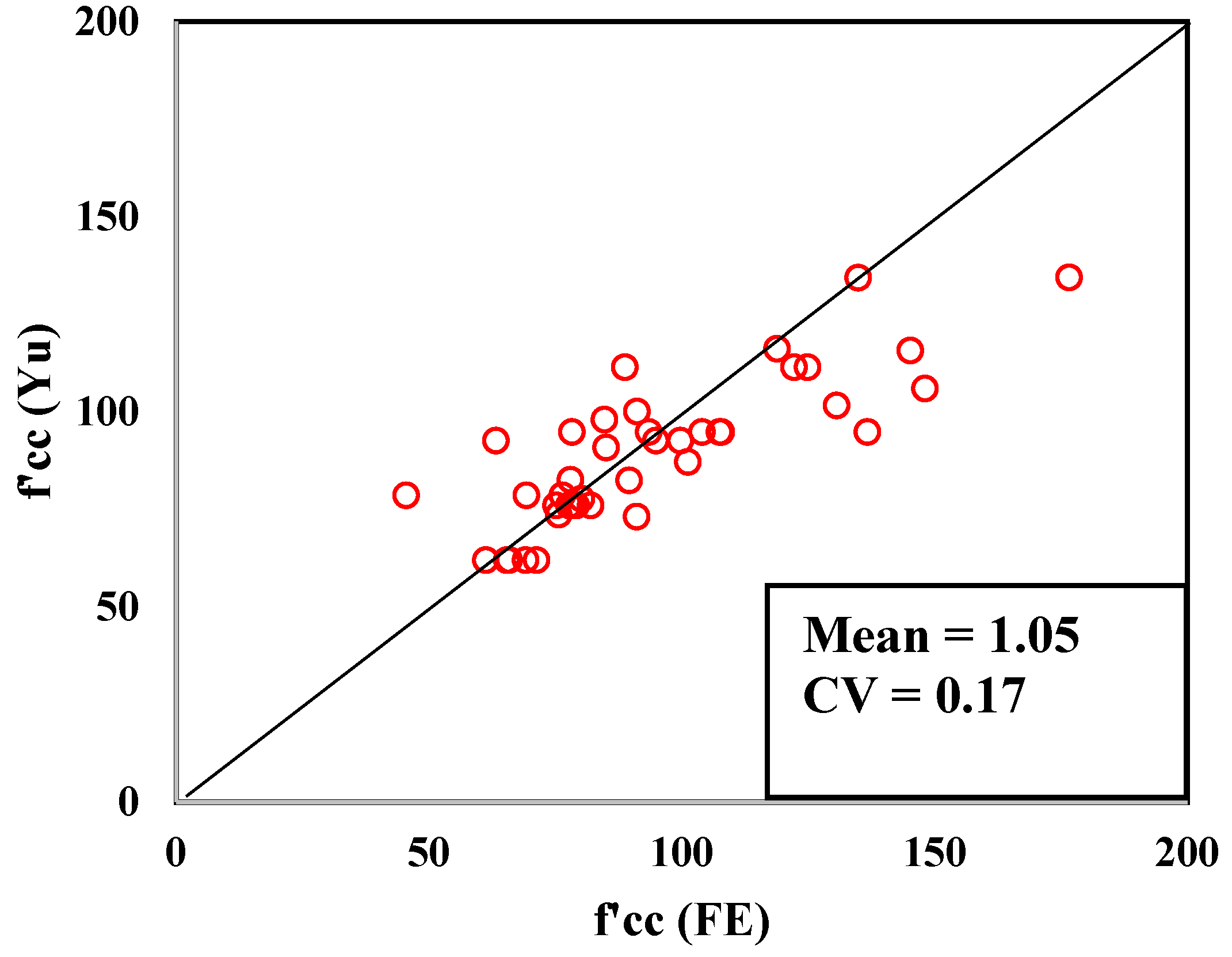
- The confined concrete strength of the hybrid RuDSTCs obtained from the parametric study was compared with the results obtained from the modified Yu et al. model using rubberised concrete properties. A good correlation was achieved, which indicated that the modified Yu et al.’s model can be used to predict the capacity of hybrid RuDSTCs.
- vi.
- Further exploration of hybrid columns under varying loading conditions, including long-term cyclic loading, environmental influences, and impact loading, will present an opportunity to deepen our understanding of their structural behaviour and accommodation for practical use.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bompa, D.; Elghazouli, A.; Xu, B.; Stafford, P.; Ruiz-Teran, A. Experimental assessment and constitutive modelling of rubberised concrete materials. Constr. Build. Mater. 2017, 137, 246–260. [Google Scholar] [CrossRef]
- Najim, K.; Hall, M. A review of the fresh/hardened properties and applications for plain-(PRC) and self-compacting rubberised concrete (SCRC). Constr. Build. Mater. 2010, 24, 2043–2051. [Google Scholar] [CrossRef]
- Raffoul, S.; Garcia, R.; Pilakoutas, K.; Guadagnini, M.; Medina, N.F. Optimisation of rubberised concrete with high rubber content: An experimental investigation. Constr. Build. Mater. 2016, 124, 391–404. [Google Scholar] [CrossRef]
- Rezaifar, O.; Hasanzadeh, M.; Gholhaki, M. Concrete made with hybrid blends of crumb rubber and metakaolin: Optimization using Response Surface Method. Constr. Build. Mater. 2016, 123, 59–68. [Google Scholar] [CrossRef]
- Fawzia, S.; Zhao, X.; Al-Mahaidi, R.; Rizkalla, S. Investigation into the bond between CFRP and steel tubes. In FRP Composites in Civil Engineering-CICE 2004, Proceedings of the 2nd International Conference on FRP Composites in Civil Engineering, Adelaide, Australia, 8–10 December 2004; Taylor and Francis: Oxford, UK, 2004. [Google Scholar]
- Tafsirojjaman, T.; Fawzia, S.; Thambiratnam, D.; Zhao, X. Seismic strengthening of rigid steel frame with CFRP. Arch. Civ. Mech. Eng. 2019, 19, 334–347. [Google Scholar] [CrossRef]
- Colombi, P.; Poggi, C. An experimental, analytical and numerical study of the static behavior of steel beams reinforced by pultruded CFRP strips. Compos. Part B Eng. 2006, 37, 64–73. [Google Scholar] [CrossRef]
- George, J.M.; Kimiaei, M.; Elchalakani, M.; Fawzia, S. Experimental and numerical investigation of underwater composite repair with fibre reinforced polymers in corroded tubular offshore structural members under concentric and and ecentric axial loads. Eng. Struct. 2021, 227, 111402. [Google Scholar] [CrossRef]
- Zeng, J.; Guo, Y.; Li, L.; Chen, W. Behavior and Three-Dimensional Finite Element Modeling of Circular Concrete Columns Partially Wrapped with FRP Strips. Polymers 2018, 10, 253. [Google Scholar] [CrossRef]
- Nasrin, S.; Ibrahim, A. Numerical study on the low-velocity impact response of ultra-high-performance fiber reinforced concrete beams. Structures 2019, 20, 570–580. [Google Scholar] [CrossRef]
- Zhang, B.; Teng, J.G.; Yu, T. Compressive Behavior of Double-Skin Tubular Columns with High-Strength Concrete and a Filament-Wound FRP Tube. J. Compos. Constr. 2017, 21, 04017029. [Google Scholar] [CrossRef]
- Duarte, A.; Silva, B.; Silvestre, N.; de Brito, J.; Júlio, E.; Castro, J. Finite element modelling of short steel tubes filled with rubberized concrete. Compos. Struct. 2016, 150, 28–40. [Google Scholar] [CrossRef]
- Duarte, A.; Silva, B.; Silvestre, N.; de Brito, J.; Júlio, E.; Castro, J. Tests and design of short steel tubes filled with rubberised concrete. Eng. Struct. 2016, 112, 274–286. [Google Scholar] [CrossRef]
- Silva, A.; Jiang, Y.; Castro, J.; Silvestre, N.; Monteiro, R. Monotonic and cyclic flexural behaviour of square/rectangular rubberized concrete-filled steel tubes. J. Constr. Steel Res. 2017, 139, 385–396. [Google Scholar] [CrossRef]
- Youssf, O.; ElGawady, M.A.; Mills, J.E.; Ma, X. An experimental investigation of crumb rubber concrete confined by fibre reinforced polymer tubes. Constr. Build. Mater. 2014, 53, 522–532. [Google Scholar] [CrossRef]
- Khusru, S.; Fawzia, S.; Thambiratnam, D.P.; Elchalakani, M. A parametric study: High performance double skin tubular column using rubberised concrete. Compos. Struct. 2020, 235, 111741. [Google Scholar] [CrossRef]
- Ayough, P.; Ibrahim, Z.; Sulong, N.R.; Hsiao, P.-C.; Elchalakani, M. Numerical analysis of square concrete-filled double skin steel tubular columns with rubberized concrete. Structures 2021, 32, 1026–1047. [Google Scholar] [CrossRef]
- Youssf, O.; Hassanli, R.; Mills, J.E.; Zhuge, Y. Axial compression behaviour of hybrid double-skin tubular columns filled with rubcrete. J. Compos. Sci. 2019, 3, 62. [Google Scholar] [CrossRef]
- Khusru, S.; Thambiratnam, D.P.; Elchalakani, M.; Fawzia, S. Experimental testing of novel hybrid rubberised concrete double skin tubular columns with filament wound CFRP tube under axial compressive loading. Compos. Struct. 2021, 276, 114568. [Google Scholar] [CrossRef]
- Mander, J.B.; Priestley, M.J.N.; Park, R. Theoretical stress-strain model for confined concrete. J. Struct. Eng. 1988, 114, 1804–1826. [Google Scholar] [CrossRef]
- De Maio, U.; Gaetano, D.; Greco, F.; Lonetti, P.; Pranno, A. The damage effect on the dynamic characteristics of FRP-strengthened reinforced concrete structures. Compos. Struct. 2023, 309, 116731. [Google Scholar] [CrossRef]
- De Maio, U.; Gaetano, D.; Greco, F.; Lonetti, P.; Blasi, P.N.; Pranno, A. The Reinforcing Effect of Nano-Modified Epoxy Resin on the Failure Behavior of FRP-Plated RC Structures. Buildings 2023, 13, 1139. [Google Scholar] [CrossRef]
- Chen, J.; Zhao, C.; Ding, F.; Xiang, P. Experimental study on the seismic behavior of precast concrete column with grouted corrugated sleeves and debonded longitudinal reinforcements. Adv. Struct. Eng. 2019, 22, 3277–3289. [Google Scholar] [CrossRef]
- Li, Y.; Zhao, X.; Raman, R.S. Mechanical properties of seawater and sea sand concrete-filled FRP tubes in artificial seawater. Constr. Build. Mater. 2018, 191, 977–993. [Google Scholar] [CrossRef]
- Manual ASUs. The Abaqus Software Is a Product of Dassault Systèmes Simulia Corp, Version 6; Dassault Systèmes: Providence, RI, USA, 2014.
- Tao, Z.; Han, L.-H.; Zhao, X.-L. Behaviour of concrete-filled double skin (CHS inner and CHS outer) steel tubular stub columns and beam-columns. J. Constr. Steel Res. 2004, 60, 1129–1158. [Google Scholar] [CrossRef]
- Hashin, Z.; Rotem, A. A fatigue failure criterion for fiber reinforced materials. J. Compos. Mater. 1973, 7, 448–464. [Google Scholar] [CrossRef]
- Toh, W.; Bin Tan, L.; Tse, K.M.; Giam, A.; Raju, K.; Lee, H.P.; Tan, V.B.C. Material characterization of filament-wound composite pipes. Compos. Struct. 2018, 206, 474–483. [Google Scholar] [CrossRef]
- Yu, T.; Teng, J.; Wong, Y.; Dong, S. Finite element modeling of confined concrete-II: Plastic-damage model. Eng. Struct. 2010, 32, 680–691. [Google Scholar] [CrossRef]
- Lubliner, J.; Oliver, J.; Oller, S.; Onate, E. A plastic-damage model for concrete. Int. J. Solids Struct. 1989, 25, 299–326. [Google Scholar] [CrossRef]
- Hibbitt, H.; Karlsson, B.; Sorensen, P. Abaqus Analysis User’s Manual Version 6; Dassault Systèmes Simulia Corp: Providence, RI, USA, 2011. [Google Scholar]
- Hany, N.F.; Hantouche, E.G.; Harajli, M.H. Finite element modeling of FRP-confined concrete using modified concrete damaged plasticity. Eng. Struct. 2016, 125, 1–14. [Google Scholar] [CrossRef]
- Papanikolaou, V.K.; Kappos, A.J. Confinement-sensitive plasticity constitutive model for concrete in triaxial compression. Int. J. Solids Struct. 2007, 44, 7021–7048. [Google Scholar] [CrossRef]
- Bompa, D.; Elghazouli, A. Stress–strain response and practical design expressions for FRP-confined recycled tyre rubber concrete. Constr. Build. Mater. 2020, 237, 117633. [Google Scholar] [CrossRef]
- Han, L.-H.; Li, Y.-J.; Liao, F.-Y. Concrete-filled double skin steel tubular (CFDST) columns subjected to long-term sustained loading. Thin-Walled Struct. 2011, 49, 1534–1543. [Google Scholar] [CrossRef]
- Pagoulatou, M.; Sheehan, T.; Dai, X.; Lam, D. Finite element analysis on the capacity of circular concrete-filled double-skin steel tubular (CFDST) stub columns. Eng. Struct. 2014, 72, 102–112. [Google Scholar] [CrossRef]
- Lam, L.; Teng, J.G. Design-Oriented Stress-Strain Model for FRP-Confined Concrete in Rectangular Columns. J. Reinf. Plast. Compos. 2003, 22, 1149–1186. [Google Scholar] [CrossRef]
- Li, Y.; Zhao, X.; Singh, R.R.; Al-Saadi, S. Experimental study on seawater and sea sand concrete filled GFRP and stainless steel tubular stub columns. Thin-Walled Struct. 2016, 106, 390–406. [Google Scholar] [CrossRef]
- Teng, J.G.; Jiang, T.; Lam, L.; Luo, Y.Z. Refinement of a Design-Oriented Stress–Strain Model for FRP-Confined Concrete. J. Compos. Constr. 2009, 13, 269–278. [Google Scholar] [CrossRef]
- Yu, T.; Wong, Y.; Teng, J. Behavior of hybrid FRP-concrete-steel double-skin tubular columns subjected to eccentric Compression. Adv. Struct. Eng. 2010, 13, 961–974. [Google Scholar] [CrossRef]

| Specimen | PFE | PEXP | PEXP/PFE |
|---|---|---|---|
| kN | kN | ||
| C-I60-00-I | 1792 | 1671 | 0.93 |
| C-I60-00-II | 1792 | 1692 | 0.94 |
| C-I60-15-I | 1329 | 1314 | 0.98 |
| C-I60-15-II | 1329 | 1286 | 0.97 |
| C-I60-30-I | 1034 | 987 | 0.95 |
| C-I60-30-II | 1034 | 888 | 0.86 |
| Specimen ID | % Rubber | FRP Tube | Steel Tube | Control Concrete Strength | |||
|---|---|---|---|---|---|---|---|
| Do (mm) | to (mm) | Di (mm) | ti (mm) | fy (mm) | f′c (MPa) | ||
| Group 1, thickness ratio | |||||||
| ti/to = 1, 0% | 0% | 200 | 2.5 | 101.6 | 2.5 | 250 | 50 |
| ti/to = 1, 15% | 15% | 200 | 2.5 | 101.6 | 2.5 | 250 | |
| ti/to = 1, 30% | 30% | 200 | 2.5 | 101.6 | 2.5 | 250 | |
| ti/to = 2, 0% | 0% | 200 | 2.5 | 101.6 | 5.0 | 250 | 50 |
| ti/to = 2, 15% | 15% | 200 | 2.5 | 101.6 | 5.0 | 250 | |
| ti/to = 2, 30% | 30% | 200 | 2.5 | 101.6 | 5.0 | 250 | |
| ti/to = 3, 0% | 0% | 200 | 2.5 | 101.6 | 7.5 | 250 | 50 |
| ti/to = 3, 15% | 15% | 200 | 2.5 | 101.6 | 7.5 | 250 | |
| ti/to = 3, 30% | 30% | 200 | 2.5 | 101.6 | 7.5 | 250 | |
| Group 2, hollow ratio | |||||||
| HR = 0.30, 0% | 0% | 200 | 2.5 | 60.3 | 5.0 | 250 | 50 |
| HR = 0.30, 15% | 15% | 200 | 2.5 | 60.3 | 5.0 | 250 | |
| HR = 0.30, 30% | 30% | 200 | 2.5 | 60.3 | 5.0 | 250 | |
| HR = 0.50, 0% | 0% | 200 | 2.5 | 101.6 | 5.0 | 250 | 50 |
| HR = 0.50, 15% | 15% | 200 | 2.5 | 101.6 | 5.0 | 250 | |
| HR = 0.50, 30% | 30% | 200 | 2.5 | 101.6 | 5.0 | 250 | |
| HR = 0.80, 0% | 0% | 200 | 2.5 | 159 | 5.0 | 250 | 50 |
| HR = 0.80, 15% | 15% | 200 | 2.5 | 159 | 5.0 | 250 | |
| HR = 0.80, 30% | 30% | 200 | 2.5 | 159 | 5.0 | 250 | |
| Group 3, steel tube yield strength | |||||||
| fy = 250, 0% | 0% | 152 | 2.5 | 60.3 | 3.6 | 250 | 50 |
| fy = 250, 15% | 15% | 152 | 2.5 | 60.3 | 3.6 | 250 | |
| fy = 250, 30% | 30% | 152 | 2.5 | 60.3 | 3.6 | 250 | |
| fy = 350, 0% | 0% | 152 | 2.5 | 60.3 | 3.6 | 350 | 50 |
| fy = 350, 15% | 15% | 152 | 2.5 | 60.3 | 3.6 | 350 | |
| fy = 350, 30% | 30% | 152 | 2.5 | 60.3 | 3.6 | 350 | |
| fy = 450, 0% | 0% | 152 | 2.5 | 60.3 | 3.6 | 450 | 50 |
| fy = 450, 15% | 15% | 152 | 2.5 | 60.3 | 3.6 | 450 | |
| fy = 450, 30% | 30% | 152 | 2.5 | 60.3 | 3.6 | 450 | |
| Group 4, diameter of CFRP tube | |||||||
| O114, 0% | 0% | 114 | 3.0 | 60.3 | 3.6 | 250 | 50 |
| O114, 15% | 15% | 114 | 3.0 | 60.3 | 3.6 | 250 | |
| O114, 30% | 30% | 114 | 3.0 | 60.3 | 3.6 | 250 | |
| O165, 0% | 0% | 165 | 3.0 | 60.3 | 3.6 | 250 | 50 |
| O165, 15% | 15% | 165 | 3.0 | 60.3 | 3.6 | 250 | |
| O165, 30% | 30% | 165 | 3.0 | 60.3 | 3.6 | 250 | |
| Specimen ID | fcc′(FE) MPa | fcc′(Yu) MPa | Ratio of fcc′(FE) fcc′(Yu) |
|---|---|---|---|
| ti/to = 1, 0% | 107.46 | 94.78 | 1.13 |
| ti/to = 1, 15% | 78.33 | 76.01 | 1.03 |
| ti/to = 1, 30% | 65.90 | 61.97 | 1.06 |
| ti/to = 2, 0% | 93.47 | 94.78 | 0.99 |
| ti/to = 2, 15% | 76.90 | 76.01 | 1.01 |
| ti/to = 2, 30% | 60.90 | 61.97 | 0.98 |
| ti/to = 3, 0% | 118.32 | 94.78 | 1.25 |
| ti/to = 3, 15% | 92.34 | 76.01 | 1.21 |
| ti/to = 3, 30% | 79.20 | 61.97 | 1.28 |
| HR = 0.30, 0% | 78.29 | 94.78 | 0.83 |
| HR = 0.30, 15% | 75.15 | 76.01 | 0.99 |
| HR = 0.30, 30% | 65.40 | 61.97 | 1.06 |
| HR = 0.50, 0% | 107.85 | 94.78 | 1.14 |
| HR = 0.50, 15% | 79.12 | 76.01 | 1.04 |
| HR = 0.50, 30% | 69.12 | 61.97 | 1.12 |
| HR = 0.80, 0% | 136.73 | 94.78 | 1.44 |
| HR = 0.80, 15% | 77.73 | 76.01 | 1.02 |
| HR = 0.80, 30% | 61.26 | 61.97 | 0.99 |
| fy = 250, 0% | 117.69 | 111.36 | 1.06 |
| fy = 250, 15% | 92.38 | 92.60 | 1.00 |
| fy = 250, 30% | 47.81 | 78.56 | 0.61 |
| fy = 350, 0% | 122.21 | 111.36 | 1.10 |
| fy = 350, 15% | 94.88 | 92.60 | 1.02 |
| fy = 350, 30% | 89.52 | 78.56 | 1.14 |
| fy = 450, 0% | 124.90 | 111.36 | 1.12 |
| fy = 450, 15% | 99.72 | 92.60 | 1.08 |
| fy = 450, 30% | 69.32 | 78.56 | 0.88 |
| O114, 0% | 176.65 | 134.40 | 1.31 |
| O114, 15% | 145.20 | 115.64 | 1.26 |
| O114, 30% | 130.66 | 101.59 | 1.29 |
| O165, 0% | 148.10 | 105.92 | 1.40 |
| O165, 15% | 101.21 | 87.15 | 1.16 |
| O165, 30% | 91.12 | 73.11 | 1.25 |
| Mean | 1.09 | ||
| CV | 0.12 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khusru, S.; Thambiratnam, D.P.; Elchalakani, M.; Fawzia, S. Load–Displacement Behaviour and a Parametric Study of Hybrid Rubberised Concrete Double-Skin Tubular Columns. Buildings 2023, 13, 3131. https://doi.org/10.3390/buildings13123131
Khusru S, Thambiratnam DP, Elchalakani M, Fawzia S. Load–Displacement Behaviour and a Parametric Study of Hybrid Rubberised Concrete Double-Skin Tubular Columns. Buildings. 2023; 13(12):3131. https://doi.org/10.3390/buildings13123131
Chicago/Turabian StyleKhusru, Shovona, David P. Thambiratnam, Mohamed Elchalakani, and Sabrina Fawzia. 2023. "Load–Displacement Behaviour and a Parametric Study of Hybrid Rubberised Concrete Double-Skin Tubular Columns" Buildings 13, no. 12: 3131. https://doi.org/10.3390/buildings13123131
APA StyleKhusru, S., Thambiratnam, D. P., Elchalakani, M., & Fawzia, S. (2023). Load–Displacement Behaviour and a Parametric Study of Hybrid Rubberised Concrete Double-Skin Tubular Columns. Buildings, 13(12), 3131. https://doi.org/10.3390/buildings13123131








