Evaluating Earthquake Stability of Solar Module Soundproofing Structure by 3D Numerical Analysis
Abstract
:1. Introduction
2. Analysis Model Development for Examining Dynamic Behavior of the Sound Barrier Wall Structure
2.1. Structural Analysis for the Existing and Target Sound Barrier Wall Structures
2.2. Analysis Model Development
2.3. Input Seismic Load Determination
2.4. Determination of Analysis Case
3. Seismic Safety Evaluation for Sound Barrier Wall Structures
3.1. Seismic Safety Evaluation for Sound Barrier Wall Structures
3.2. Evaluation of the Dynamic Safety of Solar Modules in the Target Structure
4. Conclusions
- The structure under examination incorporates bifacial solar modules as replacements for some of the acoustic insulation and reflective panels present in the conventional sound barrier setup. Utilizing FLAC3D—a commercial three-dimensional (3D) finite-difference analysis software—the dynamic behavior of this modified structure was rigorously assessed under seismic conditions. Before this analysis, property adjustments were made for the key components of the target structure—the sound barrier columns, acoustic insulation panels, and solar modules. These adjustments ensured that the mass and lateral stiffness, critical parameters affecting dynamic behavior during seismic events, closely mirrored those of the actual structure.
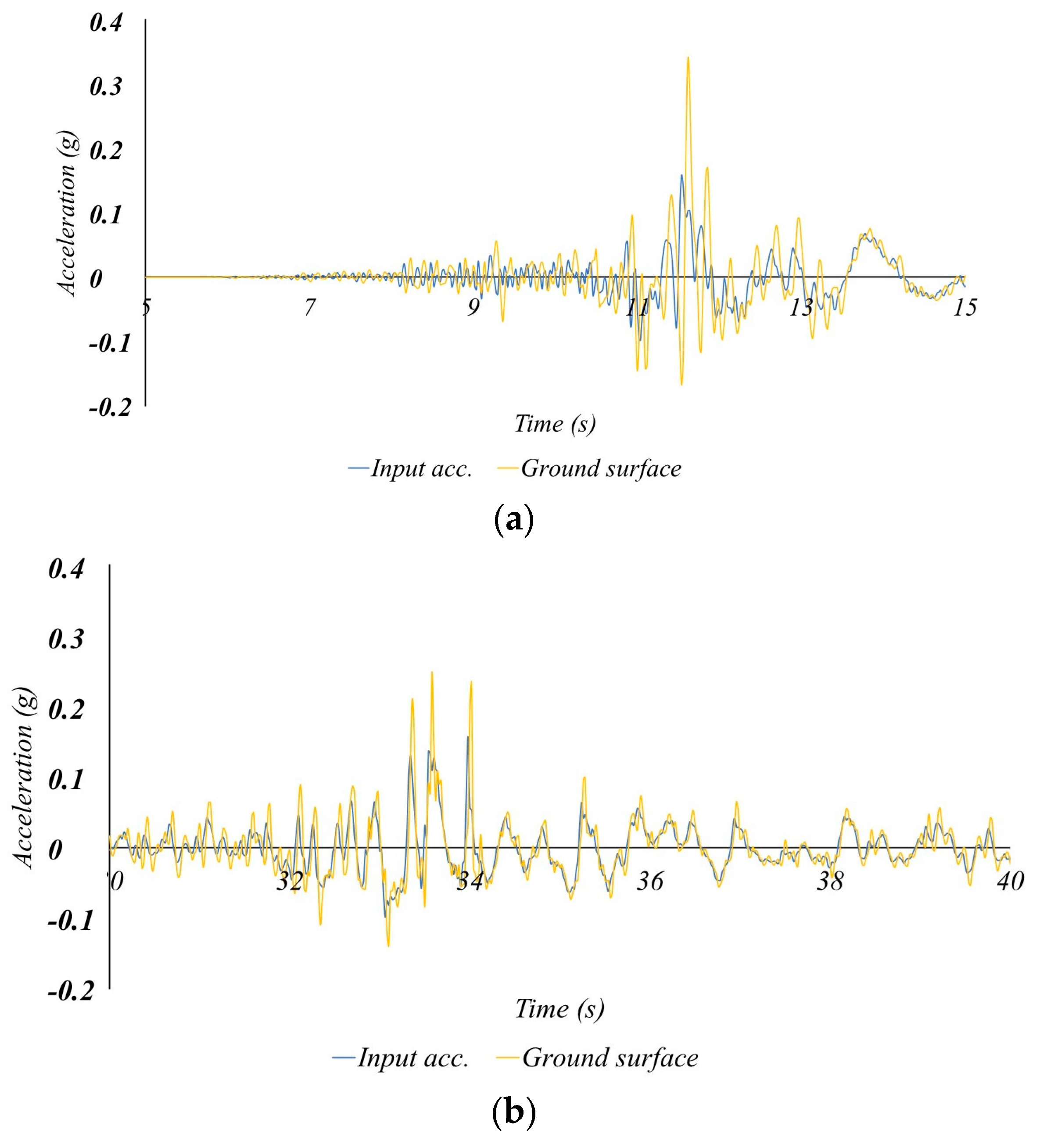
- For the designated demonstration site of the structure under scrutiny, ground conditions were meticulously analyzed, and a subsequent ground response analysis was conducted. This was executed to procure the input earthquake time history essential for assessing the structure’s dynamic behavior during seismic events. For the site response analysis, two distinct types of seismic waves were employed: the Hachinohe seismic wave, characterized as a long-period wave, and the Pohang seismic wave, a domestic short-period wave. These selections were made to consider varying characteristics of input seismic waves. Earthquakes with return periods of 500 years, 1000 years, and 2400 years were incorporated as input ground accelerations, aligning with the collapse-prevention thresholds defined in domestic seismic design standards.
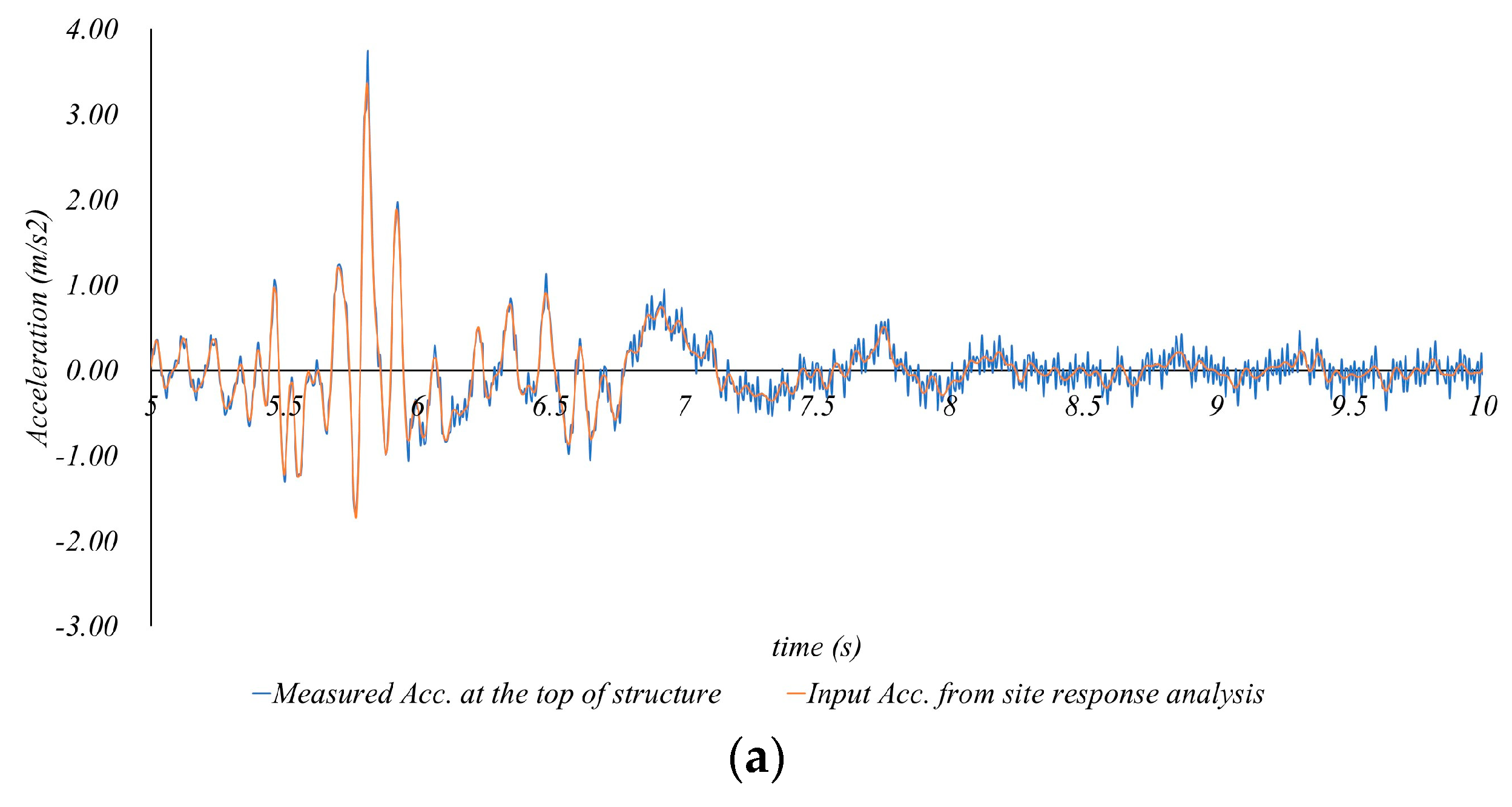
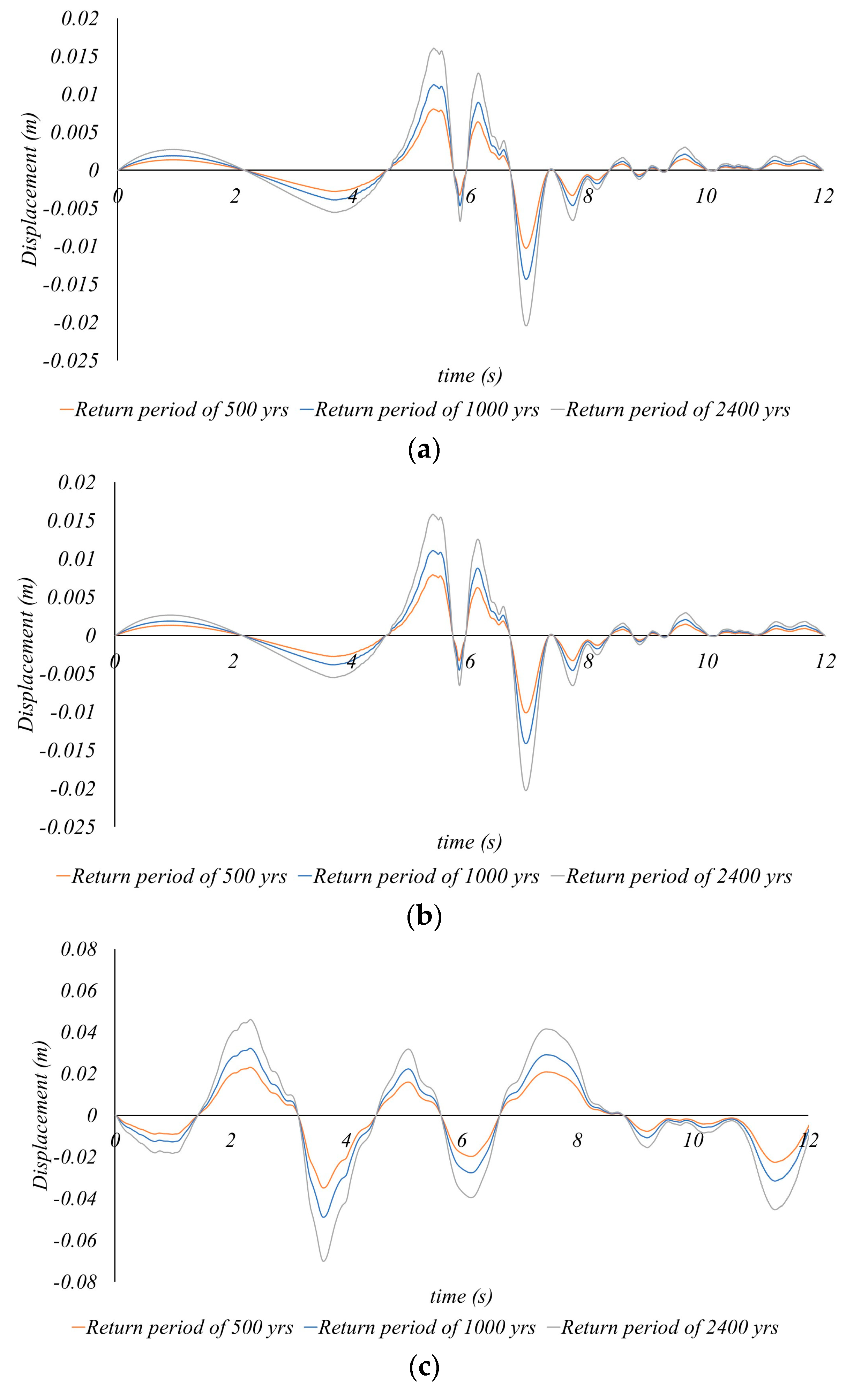
- In seismic scenarios, the peak displacement and stress experienced by the structure under consideration were 70 mm and 140 MPa, respectively, or lower. These levels are well within the supportive capabilities of the structure’s columns, which are constructed from H-beams known for their relatively high stiffness. Additionally, the inertial forces—critical factors in seismic behavior—are minimized due to the lightweight nature of the acoustic insulation panels and bifacial solar modules. Based on these analytical outcomes, the structure is adjudged to possess adequate seismic resilience, capable of withstanding both the 2400-year and 1000-year return period earthquakes. The latter aligns with the first-grade collapse prevention criteria in domestic seismic design standards.
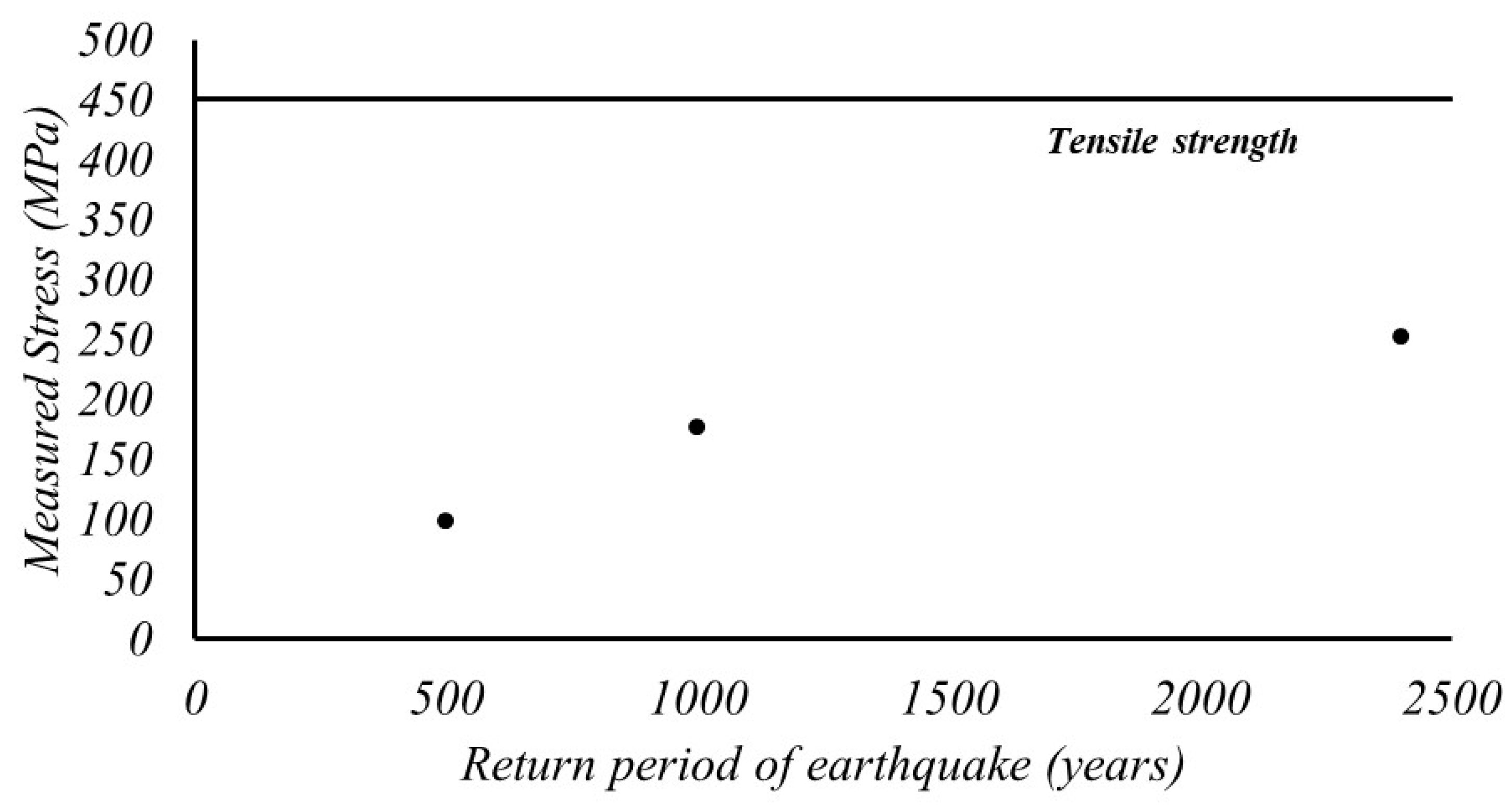
- Although the overall structure showed adequate seismic resilience, the bifacial solar modules emerged as potential weak points, vulnerable to damage from seismic-induced displacement and stress. Subsequent specialized seismic safety evaluations for these solar modules revealed that stress levels exceeding their compressive strength were observed at the apex of the structure, which is the locus of maximal displacement. Consequently, these findings imply that the solar modules within the target structure are at risk of damage during earthquakes that meet or exceed the first-grade collapse prevention criteria, consistent with the seismic design standards for high-speed railways in Korea.
- The solar modules’ vulnerability stems from their intrinsically low tensile strength, attributable to their construction from tempered glass. Given the anticipated damage arising from seismic-induced displacements, remedial engineering measures are warranted. These could encompass strategies such as reducing the distance to the neutral axis or enhancing the overall structural stiffness to mitigate the risk of damage.
- In the case of the newly developed double-sided solar sound barrier structure, the power required by the railway structure is generated in the immediate vicinity of the railway facility, which is an economically and environmentally efficient structure with high energy saving efficiency. It also has the advantage of utilizing the existing sound barrier site and not requiring additional space. If complementary measures are taken to ensure seismic safety, it is judged that it will be highly utilized as an eco-friendly and economical structure.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Directorate—General for Energy. Technical Assistance in Realisation of the 4th Report on Progress of Renewable Energy in the EU; ECOFYS: Utrecht, The Netherlands, 2019. [Google Scholar]
- Kang, M. Green New Deal: Korea; BOOKK: Seoul, Republic of Korea, 2020. [Google Scholar]
- Choi, J. Proposal on future domestic use of solar roads. J. Korean Asph. Inst. 2021, 11, 323–330. [Google Scholar]
- Japan for Sustainability. Japanese Railway Company to Build a Mega Solar Power Plant in Rail Yard; Japan for Sustainability: Tokyo, Japan, 2013. [Google Scholar]
- Lim, H. Demonstration of solar power suitable for railway for noise reduction and carbon neutrality. J. Korean Soc. Urban Adm. 2022, 1, 20–25. [Google Scholar]
- MOLIT. Planning and Research on Establishing a System to Advance Earthquake-Resistant Technology for Railway Infrastructure; Ministry of Land, Infrastructure and Transport: Sejong, Republic of Korea, 2012.
- KR C-02060; Mainline Units and Safety Facilities. Korea Rail Network Authority: Daejeon, Republic of Korea, 2017.
- Jin, J.; Zhu, C.; Wu, R.; Liu, Y.; Li, M. Comparative noise reduction effect of sound barrier based on statistical energy analysis. J. Comput. Methods Sci. Eng. 2021, 21, 737–745. [Google Scholar] [CrossRef]
- Liu, G.; Wang, R.; Liu, X.; Li, S.; Tong, C. Simulation Analysis on Noise Reduction Effect of Sound Barriers with Different Geometric Shapes for High-Speed Train. IOP Conf. Ser. Mater. Sci. Eng. 2019, 612, 052038. [Google Scholar] [CrossRef]
- Liu, Y.; Yang, B.; Zhang, X.P.; Zhong, Z.F.; Dong, H.X.; Sun, H.Y. Test and Analysis of Noise Reduction Effect for Different Heights and Distances of Sound Barrier. Adv. Mater. Res. 2011, 243–249, 4447–4450. [Google Scholar] [CrossRef]
- Reiter, P.; Wehr, R.; Ziegelwanger, H. Simulation and measurement of noise barrier sound-reflection properties. Appl. Acoust. 2017, 123, 133–142. [Google Scholar] [CrossRef]
- Sousa, L.; Pereira, L.; Montes-González, D.; Ramos, D.; Amado-Mendes, P.; Barrigón-Morillas, J.M.; Godinho, L. Experimental Analysis and Simulation of a Porous Absorbing Layer for Noise Barriers. Appl. Sci. 2023, 13, 2638. [Google Scholar] [CrossRef]
- Zhang, X.; Liu, R.; Cao, Z.; Wang, X.; Li, X. Acoustic performance of a semi-closed noise barrier installed on a high-speed railway bridge: Measurement and analysis considering actual service conditions. Measurement 2019, 138, 386–399. [Google Scholar] [CrossRef]
- Nusairat, J.; Liang, R.Y.; Engel, R.; Hanneman, D.; Abu-Hejleh, N.; Yang, K. Drilled Shaft Design for Sound Barrier Walls, Signs, and Signals; Report. No. CDOT-DTD-R-2004; Colorado Department of Transportation: Denver, CO, USA, 2004; Volume 8.
- Do Kim, S.; Jung, W.Y. Wind Fragility for Soundproof Wall with the Variation of Section Shape of Frame. Int. J. Civ. Environ. Eng. 2017, 11, 1551–1557. [Google Scholar] [CrossRef]
- Ali, T.; Lee, J.; Kim, R.E. Machine learning tool to assess the earthquake structural safety of systems designed for wind: In application of noise barriers. Earthq. Struct. 2022, 23, 315–328. [Google Scholar]
- Tursunkululy, T.; Zhangabay, N.; Avramov, K.; Chernobryvko, M.; Kambarov, M.; Abildabekov, A.; Narikov, K.; Azatkulov, O. Oscillation frequencies of the reinforced wall of a steel vertical cylindrical tank for petroleum products depending on winding pretension. East.-Eur. J. Enterp. Technol. 2023, 3, 14–25. [Google Scholar] [CrossRef]
- Tursunkululy, T.; Zhangabay, N.; Suleimenov, U.; Abshenov, K.; Utelbayeva, A.; Moldagaliyev, A.; Kolesnikov, A.; Turashova, Z.; Karshyga, G.; Kozlov, P. Analysis of strength and eigenfrequencies of a steel vertical cylindrical tank without liquid, reinforced by a plain composite thread. Case Stud. Constr. Mater. 2023, 18, e02019. [Google Scholar] [CrossRef]
- Kwon, S.Y.; Yoo, M.; Hong, S. Earthquake Risk Assessment of Underground Railway Station by Fragility Analysis Based on Numerical Simulation. Geomech. Eng. 2020, 21, 143–152. [Google Scholar] [CrossRef]
- Yoo, M.; Kwon, S.Y.; Hong, S. Dynamic Response Evaluation of Deep Underground Structures Based on Numerical Simulation. Geomech. Eng. 2022, 29, 269–279. [Google Scholar] [CrossRef]
- Kwon, S.Y.; Yoo, M. A Study on the Dynamic Behavior of a Vertical Tunnel Shaft Embedded in Liquefiable Ground during Earthquakes. Appl. Sci. 2021, 11, 1560. [Google Scholar] [CrossRef]
- Ji, Y.; Kim, B.; Kim, K. Evaluation of liquefaction potentials based on shear wave velocities in Pohang City, South Korea. Int. J. Geo-Eng. 2021, 12, 1–10. [Google Scholar] [CrossRef]
- Yun, J.-W.; Han, J.-T. Dynamic behavior of pile-supported wharves by slope failure during earthquake via centrifuge tests. Int. J. Geo-Eng. 2021, 12, 1–11. [Google Scholar] [CrossRef]
- Nguyen, A.-D.; Nguyen, V.-T.; Kim, Y.-S. Finite element analysis on dynamic behavior of sheet pile quay wall dredged and improved seaside subsoil using cement deep mixing. Int. J. Geo-Eng. 2023, 14, 1–18. [Google Scholar] [CrossRef]
- MOLIT. Korea Seismic Design, General; KDS 17 00 00:2018; Ministry of Land, Infrastructure and Transport: Sejong, Republic of Korea, 2018.
- Itasca Consulting Group. FLAC3D (Fast Lagrangian Analysis of Continua in 3Dimensions) User’s Guide; Itasca Consulting Group: Minnesota, MN, USA, 2006. [Google Scholar]
- Sun, C.-G.; Cho, C.-S.; Son, M.; Shin, J.S. Correlations Between Shear Wave Velocity and In-Situ Penetration Test Results for Korean Soil Deposits. Pure Appl. Geophys. 2013, 170, 271–281. [Google Scholar] [CrossRef]
- Bowles, E.B. Foundation Analysis and Design, 2nd ed.; McGraw-Hill Book Company: New York, NY, USA, 1977. [Google Scholar]
- Seed, H.B.; Idriss, I.M. Soil Moduli and Damping Factors for Dynamic Response Analysis; Report No. EERC 70-10; Earthquake Engineering Research Center, University of California: Berkeley, CA, USA, 1970. [Google Scholar]
- Schnabel, P.B.; Lysmer, J.; Seed, H.B. SHAKE: A Computer Program for Earthquake Response Analysis of Horizontally Layered Sites; Report No. EERC 72-12; Earthquake Engineering Research Center, University of California: Berkeley, CA, USA, 1972. [Google Scholar]
- Qiao, Q.; Li, J.; Mou, B. Compressive behavior of bolted built-up H-section column using high-strength steel. Thin-Walled Struct. 2022, 171, 108818. [Google Scholar] [CrossRef]
- Ministry of Land, Infrastructure and Transport. Soundproof Wall; KCS 44 80 05; Ministry of Land, Infrastructure and Transport: Sejong, Republic of Korea, 2023.
- ASTM C1048-12; Standard Specification for Heat-Strengthened and Fully Tempered Flat Glass. ASTM International: West Conshohocken, PA, USA, 2012.
- Japan Road Association. Specifications for Highway Bridges, V Seismic Design; Japan Road Association: Tokyo, Japan, 2012. [Google Scholar]
- European Commision. Eurocode 8: Design for Structures for Earthquake Resistance; European Commission: Brussels, Belgium, 1998. [Google Scholar]
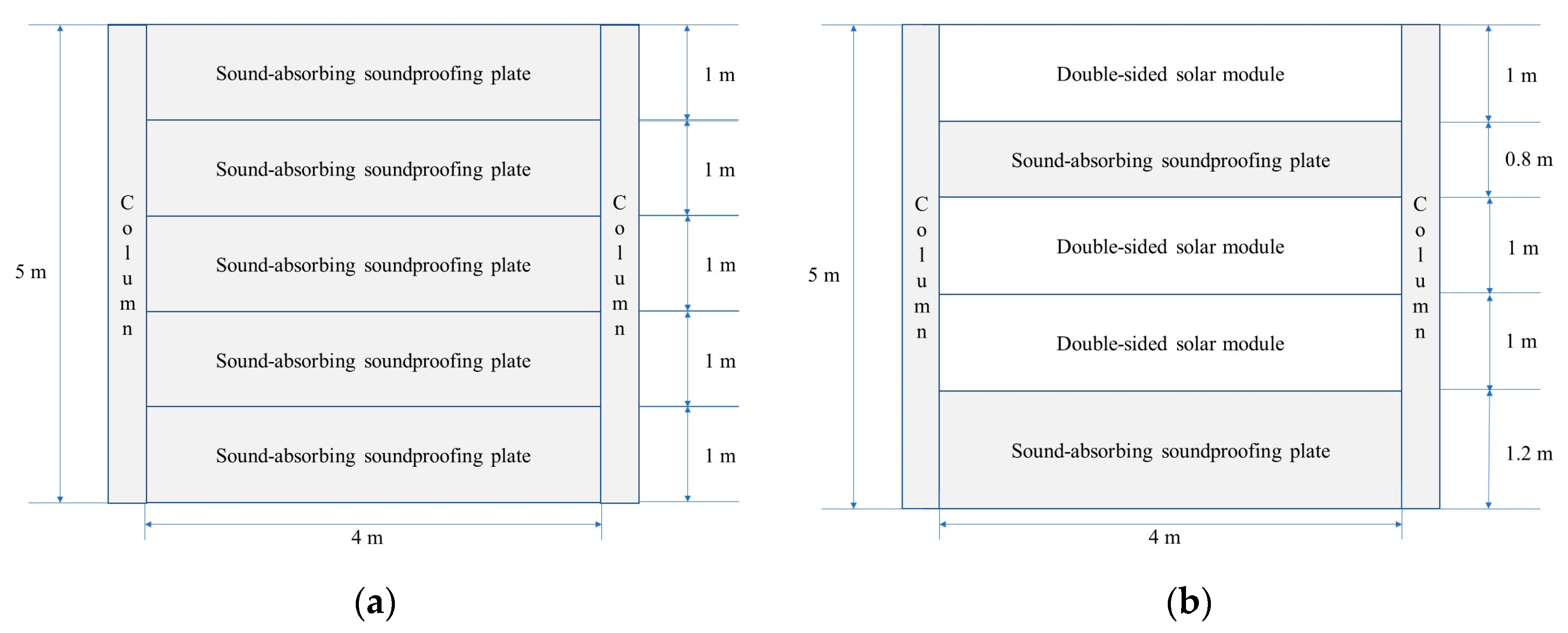
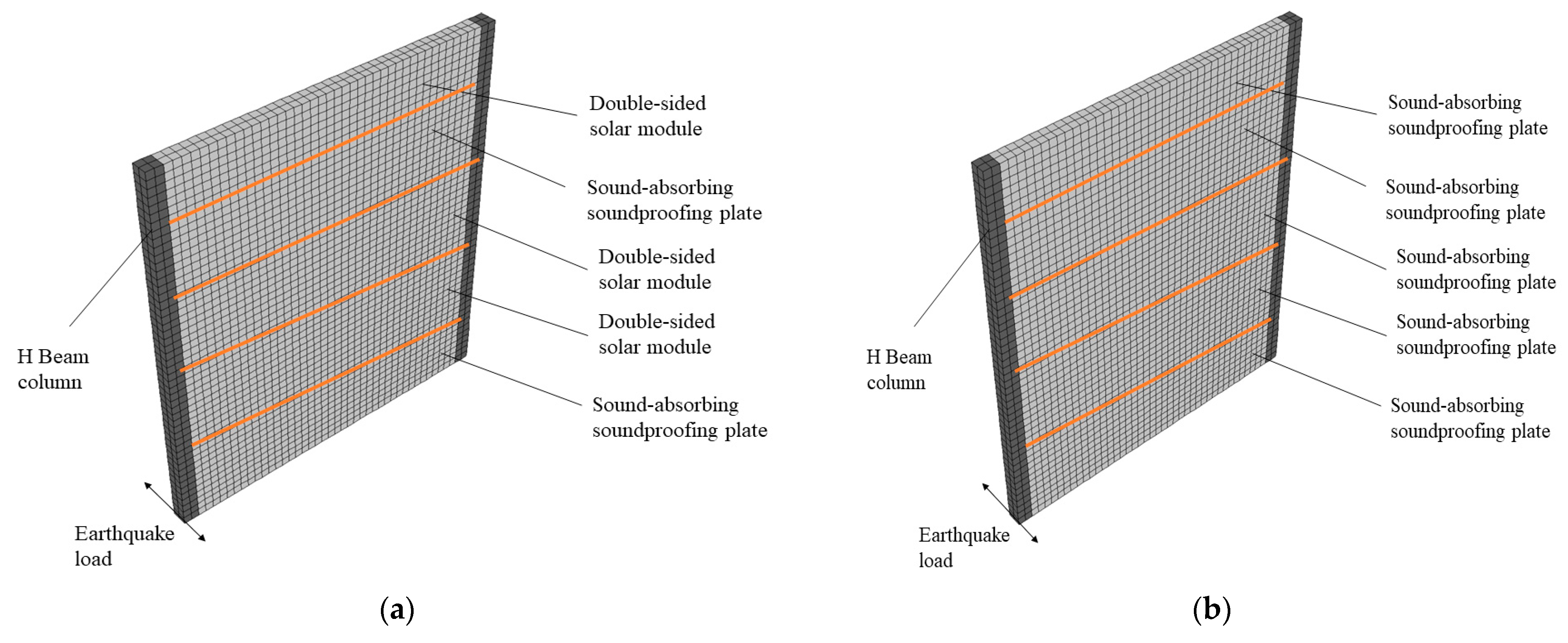


| H Beam Column | Sound-Absorbing Soundproofing Plate | Double-Sided Solar Module | ||||
|---|---|---|---|---|---|---|
| Actual Properties | Modeling Properties | Actual Properties | Modeling Properties | Actual Properties | Modeling Properties | |
| I (mm4) | 4.6 × 107 | 1.3 × 108 | 3.2 × 107 | 2.7 × 109 | 6.8 × 105 | 2.7 × 109 |
| E (kPa) | 210,000,000 | 72,615,218 | 200,000,000 | 2,419,825 | 70,000,000 | 17,885 |
| Density (kg/m3) | 7850 | 595 | 150 | 130 | ||
| Depth (m) | SPT-N | Unit Weight (kN/m3) | Vs (m/s) |
|---|---|---|---|
| 0.50 | 12.00 | 16.2 | 181.2 |
| 1.00 | 8.00 | 14.7 | 159.2 |
| 1.50 | 6.00 | 14.0 | 145.2 |
| 2.00 | 8.00 | 14.7 | 159.2 |
| 2.50 | 36.00 | 19.0 | 257.2 |
| 3.00 | 40.00 | 19.4 | 266.0 |
| Seismic Zone Factor I (Z) | hazard Factor (I) for Each Return Period | ||
|---|---|---|---|
| 500 Years | 1000 Years | 2400 Years | |
| 0.11 | 1 | 1.4 | 2.0 |
| Return Period of Earthquake (Year) | Input Acc. (g) | Site Response Analysis Results | |
|---|---|---|---|
| Pohang Earthquake (1) | Hachinohe Earthquake (2) | ||
| 500 | 0.11 | 0.253 | 0.185 |
| 1000 | 0.154 | 0.336 | 0.242 |
| 2400 | 0.22 | 0.435 | 0.356 |
| Case No. | Structure | Input Earthquake | Input Acceleration |
|---|---|---|---|
| 1 | Existing sound barrier structure | Pohang Earthquake (1) | 0.253 g, 0.336 g, 0.435 g |
| 2 | Double-sided solar-module-integrated sound barrier wall structure | Pohang Earthquake (1) | 0.253 g, 0.336 g, 0.435 g |
| 3 | Double-sided solar-module-integrated sound barrier wall structure | Hachinohe earthquake (2) | 0.185 g, 0.242 g, 0.356 g |
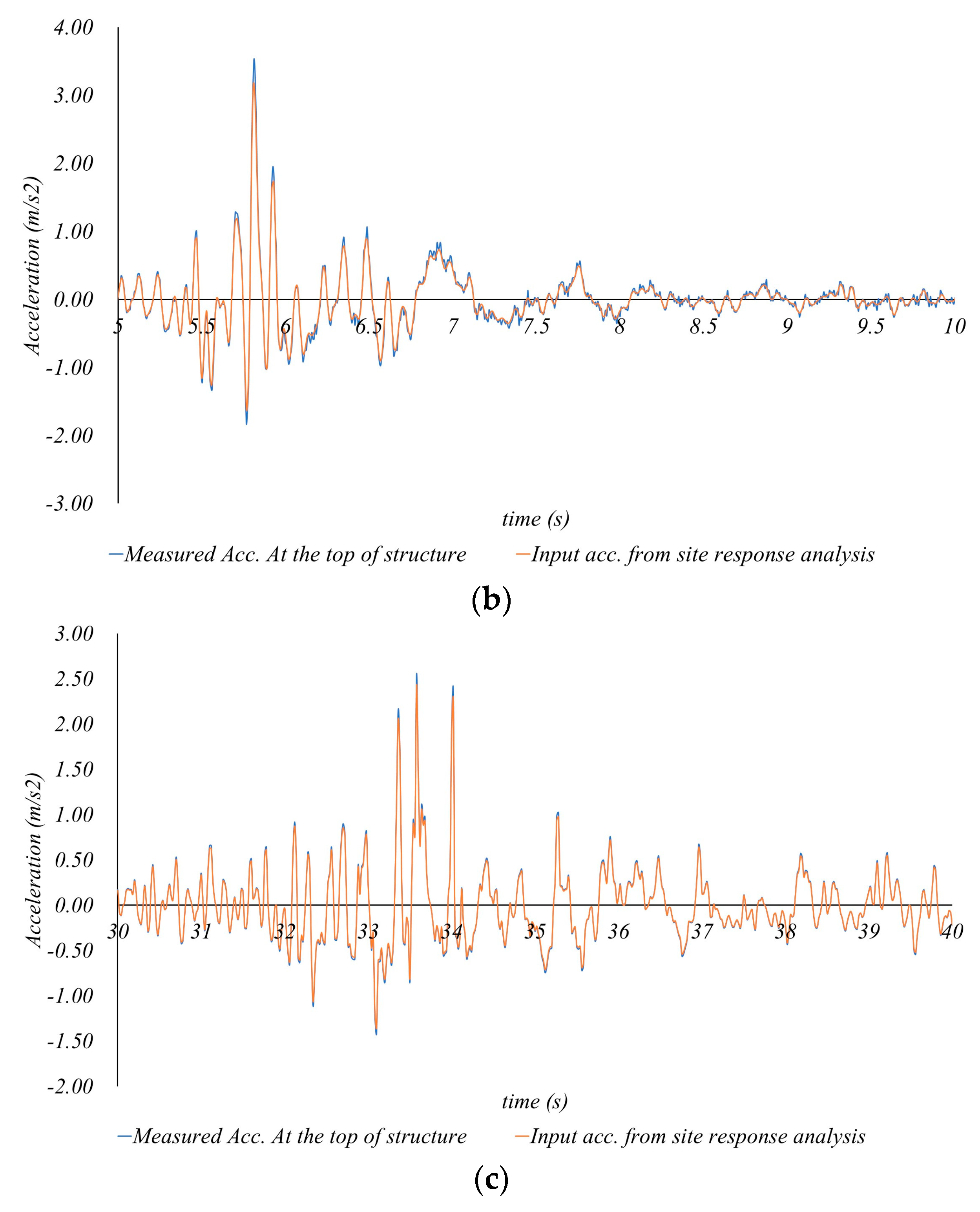
| Case No. | Return Period of Earthquake (Year) | Input Acc. from Site Response Analysis (g) | Measured Acc. at the Top of Sound Barrier Structure (g) | Amplification Ratio |
|---|---|---|---|---|
| 1 | 500 | 0.253 | 0.279 | 1.102 |
| 1000 | 0.340 | 0.370 | 1.088 | |
| 2400 | 0.435 | 0.470 | 1.080 | |
| 2 | 500 | 0.253 | 0.275 | 1.087 |
| 1000 | 0.340 | 0.367 | 1.079 | |
| 2400 | 0.435 | 0.465 | 1.069 | |
| 3 | 500 | 0.185 | 0.198 | 1.070 |
| 1000 | 0.242 | 0.257 | 1.062 | |
| 2400 | 0.356 | 0.371 | 1.042 |
| Case No. | Return Period of Earthquake (Year) | Maximum Displacement (mm) | Maximum Stress (MPa) | Yield Stress of H-beam (MPa) [31] |
|---|---|---|---|---|
| Case 1 | 500 | 10.26 | 20.68 | 773 |
| 1000 | 14.33 | 28.89 | ||
| 2400 | 20.46 | 41.25 | ||
| Case 2 | 500 | 10.08 | 20.32 | |
| 1000 | 14.13 | 28.49 | ||
| 2400 | 20.02 | 40.80 | ||
| Case 3 | 500 | 34.93 | 70.42 | |
| 1000 | 48.98 | 98.74 | ||
| 2400 | 70.17 | 141.46 |
| Area | Wind Speed (m/s) | Design Load (kPa) | Test Load (kPa) | Load Capacity Rating |
|---|---|---|---|---|
| Inland | 30 | 1.2 | 1.6 | No. 5 |
| West Coast | 35 | 1.7 | 2.2 | No. 4 |
| West-South coast South Coast East-South coast | 40 | 2.2 | 2.9 | No. 3 |
| East coast Jeju Area Special Area | 45 | 2.8 | 3.6 | No. 2 |
| Other areas | 50 | 3.4 | 4.4 | No. 1 |
| Case No. | Return Period of Earthquake (Year) | Maximum Displacement (mm) | Maximum Stress (MPa) | Tensile Strength of Double-Sided Solar Module (MPa) [33] |
|---|---|---|---|---|
| Case 1 | 500 | 10.26 | 98.496 | 450 |
| 1000 | 14.33 | 137.568 | ||
| 2400 | 20.46 | 196.416 | ||
| Case 2 | 500 | 10.08 | 33.87 | 45 |
| 1000 | 14.13 | 47.48 | ||
| 2400 | 20.02 | 68.01 | ||
| Case 3 | 500 | 34.93 | 117.3648 | |
| 1000 | 48.98 | 164.5728 | ||
| 2400 | 70.17 | 235.7712 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kwon, S.Y.; Kim, J.; Yoo, M. Evaluating Earthquake Stability of Solar Module Soundproofing Structure by 3D Numerical Analysis. Buildings 2023, 13, 3075. https://doi.org/10.3390/buildings13123075
Kwon SY, Kim J, Yoo M. Evaluating Earthquake Stability of Solar Module Soundproofing Structure by 3D Numerical Analysis. Buildings. 2023; 13(12):3075. https://doi.org/10.3390/buildings13123075
Chicago/Turabian StyleKwon, Sun Yong, Jongkwan Kim, and Mintaek Yoo. 2023. "Evaluating Earthquake Stability of Solar Module Soundproofing Structure by 3D Numerical Analysis" Buildings 13, no. 12: 3075. https://doi.org/10.3390/buildings13123075
APA StyleKwon, S. Y., Kim, J., & Yoo, M. (2023). Evaluating Earthquake Stability of Solar Module Soundproofing Structure by 3D Numerical Analysis. Buildings, 13(12), 3075. https://doi.org/10.3390/buildings13123075






