Definition of Compliance Criterion Weights for Bridge Construction Method Selection and Their Application in Real Projects ^†

Abstract

The main research purpose of the present paper is the establishment of certain compliance criteria, applied for the selection of the most appropriate, per case, bridge construction method, as well as the definition of the weights of these criteria. The five basic concrete bridge construction methods considered in this study are: Cast-in-place, Precast I-Girder, Incremental Launching, Advanced Shoring, and Balanced Cantilever. In this context, the choice of construction method in a concrete road bridge project is proposed based on seven compliance criteria which are: safety, economy, durability, construction speed, serviceability, aesthetics, and environmental harmonization. The inclusion of all these criteria is achieved via the decision-making tool of multi-criteria analysis. A notable innovation of the current study is that road bridges are divided into three categories (bridges for highways, national roads, and provincial roads), in accordance with the importance of the road that contains them. Thus, three different sets of weights of criteria are calculated, corresponding to each bridge category. The research method used for this purpose was a structured questionnaire that was distributed to a large number of selected experts in the field of bridges, who come either from academia or the construction industry. The research results showed that the criteria of safety and economy are the most significant according to the experts, while aspects such as the correlations between experts’ profile and their weights were also considered. Finally, the derived criterion weights were applied to two case studies of real bridge projects in Greece.

1. Introduction

Road bridges are structures that provide passage over a barrier or gap. Bridges also constitute one of the three categories of construction projects, the other two being buildings and special structures. Compared to the other two types of construction projects, bridges are ranked second in terms of investment volumes, but first in terms of construction difficulty. As road bridges can be categorized according to the materials used to build the structure, the focus of the current study is on concrete road bridges.

The subject of the construction or the maintenance of road bridges has been addressed extensively in the international literature. This becomes evident from a plethora of studies that examine various issues such as the most economical design of certain structural members of the bridge as well as the improvement of the bridge design in relation to their earthquake resistance or their capacity under traffic loading. In fact, most of these studies concern technical issues of the design of bridge structures. Conversely, the current study deals with decision-making regarding concrete road bridges and specifically with the selection of the most suitable bridge construction method in cases where there is a need for the construction of a concrete road bridge. In the specific paper, this is achieved with the aid of the decision-making tool of multi-criteria analysis.

1.1. Relevant Research on Multi-Criteria Analysis Applications in Bridges

Multi-criteria analysis methods have been widely used at an international level for various decision-making issues related to road bridges. Some indicative studies on this topic are described below. Initially, according to Patel et al. [1], the resilience of infrastructure considers four attributes, which include rapidity, resourcefulness, resilience robustness, and finally redundancy (4Rs), which are related to technical, organizational, social, and economic (TOSE) dimensions. Current practice evaluates bridge resilience using the factors associated only with the 4Rs, but the current research additionally considers the TOSE dimensions. This paper proposes a Bridge Resilience Index, thus facilitating a roadmap for managing, maintaining, and enhancing the resilience of bridges. To accomplish this, certain multi-criteria decision-making techniques are used, such as the Analytical Hierarchy Process (AHP), to obtain relative weights of the 4Rs and their associated TOSE factors; the TOPSIS method to determine the 4Rs; and the Weighted Sum Method (WSM) to assess the Bridge Resilience Index.

Descamps et al. in 2011 [2] investigated an improvement method based on multiple criteria for lightweight bridges. The approach encompasses a constrained force density method. The latter was developed in order to enforce geometric restrictions. Then, the approach was extended to investigate identification of optimized forms via simultaneous consideration of the force density method and multi-objective genetic algorithms. It was proposed that the approach be implemented in larger scale applications.

Balali et al. in 2014 [3] presented the use of the multi-criteria method PROMETHEE for the selection of appropriate materials and appropriate construction methods, as well as the structural system of a bridge, with the aid of a case study. Furthermore, in 2013 Chaphalkar and Shirke [4] proposed the fuzzy AHP multi-criteria method in conjunction with a second multicriteria method, fuzzy TOPSIS, for selecting the type of structural system of a bridge, afterwards comparing the results of the two multi-criteria methods.

Stefanidou and Kappos [5] proposed in 2021 a methodology for bridge fragility curves of actual bridges, which was extended to bridges with various retrofit schemes. The approach for the choice of bridge retrofit scheme is based on a number of identified performance criteria.

According to Zeng et al. [6], bridge structures across active faults are vulnerable to large surface deformation and velocity pulses. The specific research proposes the adoption of a multi-criteria optimizing methodology and examines the damping effect of the optimized damper system on a cable-stayed bridge across a strike–slip fault. Within this research initiative, the mainstream multiple-criteria decision analysis theory is optimized by incorporating new function forms and a control parameter to evaluate the optimum fault-crossing angles of the case bridge. The optimum multi-criteria approach is accompanied by the beetle antennae search algorithm to improve the damper system of the case bridge.

Zhu et al. [7] presented in 2023 a multi-criteria optimization approach regarding reliable adaptation strategies of coastal bridges. The introduced methodology could produce adaptation strategies focusing on the main superstructure unseating failure. This can be accomplished by implementing a pragmatic bridge vulnerability analysis, applying multi-criteria optimization towards the performance of different adaptations and finally investigating strategy reliability against the unknown occurrence of imminent climate futures. A number of exogenous uncertainties are also examined. These include future economics and climate scenarios, which are also evaluated via sensitivity analysis.

Tegos and Aretoulis in 2019 [8] focused on the pre-selection of the most suitable bridge type. The approach considered not only cost-effectiveness but also the satisfaction of a number of conflicting compliance criteria. The development of a reliable decision support system regarding that kind of selection is a significant research objective. Moreover, certain evaluation criteria governing bridge design are established. The specific criteria are then weighted and incorporated within two multi-criteria analysis methods. The application of these methods can lead to the respective optimal selection of the bridge type, among a number of potentially appropriate alternatives [8].

Bana e Costa et al. [9] introduced in 2008 a multiple criteria approach which evaluates and hierarchizes bridges and tunnels based on specific parameters and criteria. These include their structural vulnerability and strategic significance towards the creation and application of civil protection strategies. The latter involve both retrofitting and emergency response, in the case of seismic occurrences.

Pan [10] also in 2008 emphasized that the identification of an appropriate bridge construction method is critical for the success of bridge construction projects. The AHP methodology has been broadly applied for providing solutions in multiple criteria decision analysis problems. However, it has been reported that the standard AHP approach is not capable of managing unknown parameters associated with the consideration of one’s preference to an exact number or ratio. The current research introduces a fuzzy AHP model to overcome this difficulty. The suggested methodological method incorporates fuzzy numbers and the α-cut concept to respond to the imprecision inherent to the process of subjective judgment. Finally, a case study that assesses bridge construction methods is shown in order to highlight the application of the model.

The following research paper by Jaafaru and Agbelie [11] combines machine learning, multi-criteria analysis and evolutionary optimization models for bridge maintenance planning. This paper provides a bridge maintenance planning framework considering financial and performance parameters. The specific study managed to analyze 95 bridges in a network with an 84% accuracy machine learning model prediction. The decision-makers’ preferences were utilized to hierarchize all bridges via multi-attribute utility theory.

Bakhtin [12] in 2022 introduced the results of the creation of a complex algorithm for multi-criteria optimization of biocrossings (landscape bridges) on high speed roads. The research focus is on accidents with wildlife. The emphasis was based on the issue of multi-criteria optimization of landscape bridges, with a very large number of criteria and parameters, and indeed in two directions. These directions considered a classical road overpass over migration routes and a landscape bridge over a motorway.

Antoniou et al. [13] in 2016 introduced an approach for cost pre-estimation and material quantity formulation for overpass bridges. This model is based on data from fifty-seven existing bridges. The aim is to assist stakeholders in the bridge construction industry when selecting the most cost-effective design solution, towards the reduction of the risk of failure and the loss of funding [13].

Pouraminian and Pourbakhshian [14] in 2019 dealt with the study of the shape of a concrete arched bridge, involving a particle swarm optimization algorithm. According to the results appearing in this study, the Pareto front is generated, which enables the decision-maker or designer to pick the compromise solution. This is achieved within twenty optimum designs. Furthermore, in order to facilitate the tasks of the decision-maker, two multiple objective decision-making methods were applied to identify the optimum solution.

Božanić et al. [15] in 2019 focused their research effort on the introduction of a model for the allocation of a single-span bailey bridge. To that end, the authors applied multi-criteria decision analysis. Based on relevant studies, the seven key criteria which have the greatest influence on the selection were identified in earlier work by Kočić: (1) access roads, (2) scope of work on site arrangement, (3) properties of banks, (4) width of water barrier, (5) masking conditions, (6) scope of works on joining access roads with the crossing point, (7) protection of units.

In 2021 Upadhya et al. [16] focused their research interest on a very critical topic. Their emphasis is placed on a multi-criteria decision-making approach for the choice of a bridge superstructure construction method. Based on AHP and questionnaire surveys, they managed to come up with a decision support system. The AHP method identified the most appropriate method of bridge superstructure construction.

Finally, the study by Keshavarz-Ghorabaee et al. [17] aims at the bridge design and mainly at the multi-criteria problem, applying the TOPSIS method to clarify and assess the conceptual design process under uncertainty. In the presentation of the proposed approach, an example of multi-criteria assessment of bridge design, with quantitative and qualitative criteria, is applied. Summarizing most of the research papers focus on bridge design issues. A limited number of papers deal with decision-making specifically on selecting the construction method.

1.2. Introduction to the Proposed Approach

Currently, five dominant bridge construction methods exist: Cast-in-place, Precast I-Girder, Incremental Launching, Advanced Shoring, and Balanced Cantilever. When a road bridge project is to be constructed, the choice of the corresponding method is not an easy one, since the methods present significant differences in terms of their principles, technical characteristics and requirements. At the same time, there are a number of parameters that must be considered, namely: the topographic features of the area, as well as the requirements for safety, economy, durability, aesthetics of the project, etc. As a result, the construction method should be aligned with these parameters, which are usually antagonistic. Therefore, a compromise is required in order to satisfy all the above parameters or criteria.

Despite the existence of the aforementioned factors in bridge design, in practice, until recently the choice of construction method was based almost exclusively on the economic criterion, or in other cases, the decision relied on the subjective opinion of the involved engineers, based only on their own bridge design experience. In contrast, the present study attempts to contribute to the development of an approach for a justified selection of the best ranking bridge construction method on a case-by-case basis among the five dominant ones. The main novelty of this research is that the selection will be based on the performance of the alternative construction methods against seven criteria that are established within the present study, which are: safety, economy, durability, construction speed, serviceability, aesthetics, and environmental harmonization. The inclusion of the set of criteria and the management of such a complex problem are achieved in the current research via the use of multi-criteria analysis.

The overarching goal of the present paper is the definition of the weights of the compliance criteria, which is crucial for the application of multi-criteria analysis. The research approach that was chosen for the evaluation of the criterion weights is the questionnaire survey. Thus, a structured questionnaire was distributed to a substantial number of Greek bridge experts. One of the challenges of this research was the appropriate selection of a representative sample of experts. More specifically, the 19 experts to whom the survey was addressed come from academia and the construction industry. A number of these selected experts belong to the private sector, and a corresponding number belong to the public sector.

Moreover, a noteworthy novelty of the current study is that the concrete road bridges have been categorized into three classes, namely bridges for highways, national roads, and provincial roads, taking into consideration that each bridge category has different importance and requirements. Consequently, the questionnaire survey does not produce universal criterion weights applicable to all road bridges. Instead, the survey succeeds in defining three specialized sets of criterion weights, assigned to each road bridge category.

Additionally, an important objective of this paper was to investigate if the evaluated weights of the experts are affected by their field of activity and experience, and to draw useful conclusions. Furthermore, the research investigated any possible correlations among the criterion weights themselves.

As far as the structure of the paper is concerned, in Section 2 the proposed compliance criteria for the selection of bridge construction method are presented analytically. In the Section 3, the methods that were used in this study are described. In particular, the decision-making tool of multi-criteria analysis is presented in Section 3.1, while the questionnaire survey is analyzed in Section 3.2. Subsequently, the Section 4 contains the findings of the questionnaire survey, namely the exported sets of the criterion weights, as well as the description of the participating experts. Section 5 includes the application of correlation analysis among the criterion weights, as well as the examined correlation between the experts’ field of activity and the proposed weights. Section 6 contains the discussion of the results. Section 7 includes the two case studies of the research, where the set of weights, corresponding to the bridge categories of highways and national roads, are applied in two real bridge projects in Greece, aiming at the selection of the most suitable construction method per case. Finally, Section 8 includes the conclusions and future research.

2. Compliance Criteria for the Selection of Bridge Construction Method

The choice of the most appropriate per-case construction method in a road bridge project, as already mentioned, must be aligned with a pool of defined criteria. However, for years the selection of bridge construction method in practice was mostly based on the criterion of economy. In the current research in contrast, a more integrated approach is considered.

In particular, seven compliance criteria are introduced to this end, which include: safety, economy, durability, construction speed, serviceability, aesthetics, and environmental harmonization. A brief definition of the concept of each compliance criterion, according to a previous study of Tegos and Markogiannaki [18] in 2019, is presented below:

• Safety

This criterion corresponds not only to the level of safety according to current codes (Eurocodes) for bridges, but moreover to the additional level of safety resulting from the response of statically indeterminate structures. In countries with high seismicity, the term safety mainly corresponds to seismic safety.

• Economy

The criterion is related to the intended reduction of the cost of the project, yet without devaluation of the rest of criteria. In the context of this study, the criterion of Economy is related only to the construction cost of the project, while the maintenance cost is taken into account in the criterion of Durability. It is noted that in recent years, there have been continuous research efforts regarding the limitation of bridge construction cost.

• Durability

The term Durability refers to the minimization of maintenance needs during the lifetime of the project. In the case of bridges, maintenance needs are associated with the use of bearings, joints, and seismic dampers. As mentioned above, the maintenance cost of a bridge is reflected in the performance of the criterion of Durability, and not in Economy. It is noteworthy that sometimes maintenance cost could even reach the construction cost level.

• Construction Speed

The criterion of Construction Speed is directly related to the expected completion time of the project, which is intended to be minimized. The (average) construction speed is defined here as the ratio of the length of the bridge deck to the total construction time of the bridge (namely the deck, the abutments, the piers, and their foundations). The aforementioned total construction time includes also the assembling, disassembling and transfer times of the necessary mechanical equipment used in the construction.

• Serviceability

The usual concept of serviceability is linked to the quality of traffic service; however, in this study, the term “Serviceability” means the development of an adequate structural response to the imposed deformations (namely the expansion and contraction of the deck) during the operation phase of the bridge. It is notable that the use of bearings is the best solution to the problem of serviceability.

• Aesthetics

The concept of Aesthetics in the field of bridges includes certain established rules related to the choice of geometric dimensions, which attempt to reconcile safety and geometric proportions that contribute to an aesthetic effect. Some indicative aesthetic rules are the following: all piers should have the same width; the variability of height of the deck cross-sections (arc shape) is positively evaluated; etc.

• Environmental Harmonization

The criterion of Environmental Harmonization is related to the existing architectural tradition of the area, as well as to the surrounding landscape of the bridge. The selection of the deck type and the geometric dimensions of the bridge should be affected by these two factors and be in harmony with them. In addition, the concept of this criterion includes the desirable minimization of landscape alteration and environmental impact in the area affected by the bridge project.

3. Methods

The methods that were used in this study mainly consist of the questionnaire survey, as well as the use of multi-criteria analysis (MCA), in order to build on the results of the questionnaire.

More specifically, two MCA methods were used. Initially the Analytic Hierarchy Process (AHP) was used for the core of the research, namely the calculation of the compliance criterion weights, and secondly, the PROMETHEE method was used specifically to calculate the performance of the bridge construction methods in the two case studies. The algorithm of the AHP method was applied manually with the aid of Microsoft Excel, whereas the PROMETHEE method was applied using the relevant software Visual PROMETHEE (Version 1.4.0.0.). Moreover, the program IBM SPSS Statistics was used for a more thorough analysis of the research results, namely for the implementation of correlation analysis.

In the following section, first, the multi-criteria analysis methods are presented, followed by the analytical presentation of the content of the questionnaire.

3.1. Multi-Criteria Analysis Methods of AHP and PROMETHEE

3.1.1. Definition

The tool of multi-criteria analysis (MCA) is a dominant application of operations research in the field of decision-making. The method constitutes a systematic and mathematically standardized procedure, suitable for dealing with complex decision-making problems, in which many competing alternatives (projects, actions, or scenarios) exist and a number of conflicting compliance criteria are taken into account. In the case of the present study, the competing alternatives include the five aforementioned bridge construction methods. The ultimate goal of the method of multi-criteria analysis is to achieve a rational compromise among the considered criteria, and thus to lead to the optimal choice [18]. In the current study, two specific multi-criteria methods are used, and they are presented below.

3.1.2. The AHP Multi-Criteria Method

The method of multi-criteria analysis that is used primarily in this paper (for the computation of weights of the compliance criteria) is the Analytic Hierarchy Process (AHP). The AHP method was developed by T.L. Saaty in the USA in 1977 and is one of the most widespread MCA approaches. AHP aims to quantify relative priorities for a given set of alternatives on a ratio scale, based on the judgment of the decision-maker [19]. The alternatives are evaluated against several quantitative and/or qualitative criteria, depending on how they contribute in achieving the overall goal that has been set.

More specifically, in the first step of the analytic hierarchy process, the decision-making problem is structured according to a hierarchy, where the top element is the overall goal of the decision. The second level of the hierarchy represents the criteria, while the lowest level represents the alternatives [20].

The second step of the method includes the calculation of the priorities (scores), which is performed based on the pairwise comparisons provided by the decision-makers. Each lower level of the hierarchy is prioritized according to its immediate upper level [20]. These pairwise comparisons are carried out using Saaty’s fundamental 1–9 scale [19]. This scale enables the decision-maker to integrate his knowledge and experience in an intuitive way, in order to express the intensity of his preference between two elements of the same level.

Thus, the criteria are prioritized in terms of their importance with respect to the overall goal via the performance of successive pairwise comparisons among them. The result of this procedure is the definition of the priorities (relative weights) of the criteria. Subsequently, the alternatives are prioritized, via pairwise comparisons among them, in terms of their importance with respect to each specific criterion. This procedure leads to the determination of the local priorities of the alternatives. Ultimately, the two aforementioned types of priorities lead to the calculation of the global priorities of the alternatives and, by extension, to their final ranking. However, the current study focuses only on the initial stage of this process, namely on the definition of the criterion weights, which is achieved with the aid of the questionnaire survey.

In general, the strength of AHP is that it provides a structured yet relatively simple solution to the decision-making problem, as it organizes tangible and intangible factors in a systematic way [21]. In the context of the present study, this property of the method is very important, as the research contains certain quantitative criteria, such as Economy and Construction Speed, but also many qualitative ones such as Serviceability, Aesthetics or Environmental Harmonization.

3.1.3. The PROMETHEE Multi-Criteria Method

The second multi-criteria analysis method used in the study (for the evaluation of the construction methods in the two case studies) is PROMETHEE. The acronym stands for “Preference Ranking Organization METHod for Enrichment Evaluations”. PROMETHEE is a widely known and used outranking method that was developed by J.P. Brans in 1982 and further extended by Brans and Vincke in 1985 [22], Brans et al. in 1986 [23]. Its characterization as an outranking method means that the method is based on pairwise comparisons of the alternatives, while the ultimate goal of PROMETHEE is to provide the decision-maker with a ranking of the existing alternatives.

Before the application of the method, the decision-maker needs at first to define the criteria taken into account for the decision. Then, all the alternatives to be ranked need to be evaluated according to those criteria [20]. The implementation of PROMETHEE requires two additional types of information, which are: (1) the weights of the criteria under study, and (2) the preference function used by the decision-maker when comparing the contribution of the alternatives in terms of each separate criterion. Therefore, the PROMETHEE method is based on the computation of preference degrees. A preference degree is a score which expresses how an alternative is preferred over another alternative, based on the criterion considered, from the decision-maker’s point of view. A preference degree of 1 thus means a total preference for one of the alternatives and a preference degree of 0 means that there is no preference at all, while if there is some preference, but it is not total, then the intensity will be between 0 and 1 [20].

More specifically, according to Ishizaka and Nemery [20], the method includes three main steps:

• Computation of preference degrees for every ordered pair of actions (alternatives) on each criterion;
• Computation of uni-criterion flows (which are an aggregation of the criterion preference degrees, globally for an action);
• Computation of global flows (which are an aggregation of the uni-criterion flows, by taking into account the weights of the criteria).

Thus, the global positive, negative, and net flows are computed. Eventually, PROMETHEE II (the most basic version of the method), which is used in the current paper, provides a complete ranking of the alternatives from the best to the worst one based on their global net flows [24].

3.2. Presentation of the Questionnaire

The questionnaire developed in this research had a title quite similar to the title of the current paper, namely: “Determination of compliance criterion weights for the selection of bridge construction method”. The number of experts, to whom the questionnaire was addressed, is nineteen, and they come from either the construction industry or the academic/research field, and they are among the most experienced engineers in the field of bridges in Greece. The content of the questionnaire is analytically presented below and divided into discrete subsections, which are, specifically: the questions about the profile of the participants, the necessary information for the experts, the explanation for the three versions of the questionnaire, and finally a presentation of the main part of the questionnaire [25].

3.2.1. Profile of the Participants

In the initial part of the questionnaire, there are three questions about the profile of the experts (engineers) that participate in the survey: In the first one, the experts are asked about their main field of activity in relation to bridges. Four possible answers are provided, namely: Private Sector, Public Sector, Academia, Research Field. In the second one, they are asked about the type of their employment in relation to bridges, where the possible answers include: Project Manager, Designer, Job in Construction Company, Supervising Engineer, Bridge Design Reviewer, Academic, Researcher. Finally, the third question concerns the years of their experience in the field of Bridges (up to 5 years, 5–10 years, 10–20 years, or more than 20 years).

3.2.2. Necessary Information Provided to the Experts

Afterwards, the experts are provided with some necessary information or explanations for completing the questionnaire, such as: the subject of the doctoral research, part of which is the current survey, as well as the goal of the questionnaire, a concise definition of multi-criteria analysis, the names of the alternative construction methods, and the compliance criteria that are used in the research. Subsequently, the participants are provided with a brief definition of the concept of each compliance criterion, which is similar to the corresponding part of Section 2.

3.2.3. The Three Versions of the Questionnaire

In the current study, concrete road bridges are divided into three categories, depending on their importance, namely: bridges of highways, of national roads, and of provincial roads. Consequently, three different sets of weights of the compliance criteria need to be calculated, one for each different bridge category. That means that the experts are asked to complete the questionnaire in its three versions; specifically, they have to complete three similar sub-questionnaires, essentially with the same questions each, but from a different point of view.

The above-mentioned categorization is essential, as it is obvious that the priority (weight) of many criteria varies depending on the importance of the road containing the bridge in question. It is reasonable that regarding the bridges for provincial roads, the criterion of Economy is usually predominant, while regarding the bridges for highways in particular, other criteria, such as durability or aesthetics, could have a significant weight. An additional noteworthy difference is that the highways are usually built in a new environment, while the national and provincial roads are built near residential areas or existing road networks, presenting more legislative restrictions on construction. All the above explanations are also provided to the experts in the questionnaire.

3.2.4. The Main Part of the Questionnaire

What follows is the main part of the questionnaire. This includes the three similar sub-questionnaires, of which one is dedicated to questions about bridges for highways, one to questions about bridges of national roads and one to questions about bridges for provincial roads. As already mentioned, the questions in each sub-questionnaire are exactly the same; however, the experts are asked to respond to each sub-questionnaire from a different perspective each time, keeping in mind the different needs of each bridge category.

Each sub-questionnaire contains 22 questions, in which:

• The first one asks the experts to make a preliminary prioritization of the seven compliance criteria, depending on their importance in the process of selecting a bridge construction method. The goal of this question is for the experts to form an initial opinion on the subject, before the main questions.
• The questions 2–22 contain the successive pairwise comparisons of all the compliance criteria. This means that each criterion is compared to every other criterion. These questions have all the same pattern and consist of 2 parts:

  (1)

  In the first sub-question, the experts are asked which criterion of the two of the respective pair (e.g., safety or durability) is more important, while they also have the choice of answering that the two criteria are equivalent in importance.

  (2)

  In the second sub-question, they are asked to rate the degree of predominance of the criterion they have chosen over the other. Here, the possible answers are 5 adverbs that express a gradual increase, stating that the criterion predominates: imperceptibly/slightly/appreciably/significantly/catalytically. Each adverb corresponds to a value on a scale from 1 to 5, which is used afterwards for the application of the multi-criteria analysis method of AHP.

4. Findings of the Questionnaire Survey

4.1. Presentation of the Calculated Weights of the Criteria

The responses of the nineteen experts to the questionnaire were converted into suitable values for the algorithm of the multi-criteria analysis method of AHP, which was applied successively 19 times, for each one of the three bridge categories (i.e., 57 times in total). This process led to the calculation of the criterion weights of each expert, and eventually, to the final weights of compliance criteria (the averages of the 19 experts’ weights per criterion), concerning the bridges of highways (

Table 1. Experts’ weights of compliance criteria for bridges for highways (part 1).

	Experts	1	2	3	4	5	6	7	8	9	10
Criteria
Safety		0.248	0.266	0.290	0.279	0.269	0.260	0.246	0.279	0.288	0.302
Durability		0.212	0.253	0.258	0.186	0.265	0.175	0.151	0.219	0.192	0.168
Economy		0.171	0.136	0.136	0.186	0.164	0.192	0.302	0.153	0.184	0.133
Aesthetics		0.107	0.099	0.073	0.100	0.049	0.116	0.041	0.052	0.082	0.043
Constr. Speed		0.100	0.096	0.106	0.099	0.112	0.127	0.096	0.104	0.114	0.092
Serviceability		0.092	0.075	0.075	0.088	0.089	0.065	0.125	0.143	0.087	0.216
Environ. Harmon.		0.070	0.075	0.062	0.062	0.052	0.065	0.039	0.050	0.053	0.046

Main field of activity of experts: Exp. 1: Academic, Exp. 2: Research, Exp. 3: Research, Exp. 4: Private Sector, Exp. 5: Private Sector, Exp. 6: Private Sector, Exp. 7: Public Sector, Exp. 8: Private Sector, Exp. 9: Public Sector, Exp. 10: Public Sector.

and

Table 2. Experts’ weights of compliance criteria for bridges for highways (part 2).

	Experts	11	12	13	14	15	16	17	18	19	Average
Criteria
Safety		0.255	0.274	0.339	0.263	0.225	0.254	0.253	0.069	0.299	0.261
Durability		0.193	0.219	0.171	0.207	0.209	0.216	0.228	0.106	0.229	0.203
Economy		0.126	0.154	0.108	0.161	0.159	0.082	0.157	0.369	0.148	0.169
Aesthetics		0.083	0.064	0.060	0.120	0.056	0.126	0.105	0.049	0.051	0.078
Constr. Speed		0.121	0.093	0.069	0.090	0.085	0.051	0.110	0.240	0.087	0.105
Serviceability		0.129	0.128	0.206	0.091	0.216	0.158	0.084	0.133	0.140	0.123
Environ. Harmon.		0.092	0.067	0.046	0.068	0.050	0.114	0.062	0.033	0.046	0.061

Main field of activity of experts: Exp. 11: Private Sector, Exp. 12: Public Sector, Exp. 13: Private Sector, Exp. 14: Public Sector, Exp. 15: Academic, Exp. 16: Private Sector, Exp. 17: Private Sector, Exp. 18: Academic, Exp. 19: Private Sector.

), the bridges for national roads (

Table 3. Experts’ weights of compliance criteria for bridges for national roads (part 1).

	Experts	1	2	3	4	5	6	7	8	9	10
Criteria
Safety		0.203	0.228	0.226	0.224	0.308	0.234	0.278	0.254	0.253	0.253
Durability		0.130	0.144	0.123	0.135	0.200	0.117	0.178	0.173	0.117	0.151
Economy		0.222	0.207	0.245	0.220	0.173	0.234	0.098	0.191	0.214	0.218
Aesthetics		0.071	0.073	0.057	0.070	0.066	0.070	0.057	0.045	0.064	0.057
Constr. Speed		0.195	0.159	0.199	0.177	0.145	0.159	0.229	0.143	0.180	0.151
Serviceability		0.116	0.119	0.095	0.115	0.044	0.117	0.109	0.131	0.119	0.113
Environ. Harmon.		0.063	0.070	0.055	0.059	0.064	0.069	0.051	0.063	0.053	0.057

and

Table 4. Experts’ weights of compliance criteria for bridges for national roads (part 2).

	Experts	11	12	13	14	15	16	17	18	19	Average
Criteria
Safety		0.250	0.250	0.322	0.223	0.259	0.300	0.221	0.069	0.307	0.245
Durability		0.206	0.150	0.161	0.158	0.225	0.203	0.160	0.106	0.169	0.158
Economy		0.132	0.191	0.110	0.195	0.127	0.067	0.200	0.369	0.219	0.191
Aesthetics		0.101	0.065	0.076	0.075	0.051	0.115	0.066	0.049	0.052	0.067
Constr. Speed		0.095	0.174	0.046	0.163	0.092	0.062	0.182	0.240	0.124	0.153
Serviceability		0.140	0.109	0.224	0.120	0.198	0.138	0.115	0.133	0.093	0.124
Environ. Harmon.		0.076	0.061	0.059	0.066	0.048	0.115	0.056	0.033	0.037	0.061

) and the bridges for provincial roads (

Table 5. Experts’ weights of compliance criteria for bridges for provincial roads (part 1).

	Experts	1	2	3	4	5	6	7	8	9	10
Criteria
Safety		0.174	0.144	0.138	0.191	0.154	0.176	0.241	0.217	0.208	0.278
Durability		0.114	0.160	0.114	0.113	0.128	0.115	0.160	0.184	0.113	0.231
Economy		0.237	0.236	0.261	0.226	0.284	0.232	0.228	0.225	0.233	0.135
Aesthetics		0.062	0.067	0.074	0.059	0.040	0.065	0.052	0.041	0.057	0.045
Constr. Speed		0.211	0.196	0.241	0.208	0.210	0.232	0.115	0.188	0.208	0.178
Serviceability		0.136	0.130	0.111	0.131	0.117	0.115	0.151	0.094	0.120	0.088
Environ. Harmon.		0.066	0.067	0.061	0.072	0.067	0.065	0.053	0.051	0.061	0.045

and

Table 6. Experts’ weights of compliance criteria for bridges for provincial roads (part 2).

	Experts	11	12	13	14	15	16	17	18	19	Average
Criteria
Safety		0.272	0.238	0.321	0.176	0.203	0.284	0.159	0.069	0.324	0.209
Durability		0.187	0.166	0.159	0.119	0.130	0.198	0.117	0.106	0.150	0.146
Economy		0.147	0.193	0.080	0.205	0.222	0.116	0.234	0.369	0.210	0.214
Aesthetics		0.072	0.062	0.060	0.067	0.070	0.096	0.069	0.049	0.040	0.060
Constr. Speed		0.153	0.166	0.044	0.195	0.195	0.061	0.234	0.240	0.142	0.180
Serviceability		0.103	0.106	0.233	0.170	0.116	0.162	0.117	0.133	0.081	0.127
Environ. Harmon.		0.066	0.069	0.102	0.068	0.063	0.084	0.069	0.033	0.053	0.064

).

4.2. Description of the Participating Experts

Concerning the profile of the 19 experts that participated in the survey, there is a variety regarding the main field of activity related to bridges that was stated by the experts, as shown in the footnotes under Table 1 and Table 2. Thus, there are 5 experts from the public sector (and, more specifically, from the state-owned company Egnatia Odos S.A.), 9 experts from the private sector, 3 experts from academia and 2 experts from the research field. Moreover, in

Table 7. Experts’ experience and types of their employment in relation to bridges.

Expert	Years of Experience	Project Manager	Designer	Construction Company	Supervising Engineer	Bridge Design Reviewer	Academic	Researcher
1	>20		√		√	√	√	√
2	10–20		√			√		√
3	5–10							√
4	10–20			√	√			√
5	up to 5		√			√
6	up to 5	√	√			√
7	>20	√
8	>20		√
9	>20		√		√	√
10	>20		√		√	√
11	10–20		√
12	>20		√		√	√
13	>20		√			√
14	>20	√	√	√	√	√		√
15	10–20	√		√			√	√
16	>20		√			√
17	5–10		√	√				√
18	>20					√	√
19	10–20		√			√

, the additional characteristics of the experts are presented.

5. Correlation Analysis

To achieve a further analysis of the results of the criterion weights, the tool of correlation analysis was also applied, with the aid of IBM SPSS Statistics, in two ways: (1) among the variables regarding the profile of the experts and the weights assigned to the compliance criteria by the experts, and (2) among the derived criterion weights themselves. In the software platform IBM SPSS Statistics, concerning the first application, no correlations were identified, but on the other hand, significant correlations were identified regarding the second application among the criterion weights.

5.1. Implementation of Correlation Analysis among the Criterion Weights

It is noteworthy that, according to Field [26], the Pearson’s correlation coefficient and the significance value are the indicating factors for the assessment of the correlation analysis’ results. More specifically, the Pearson’s correlation coefficient is a measure of the linear relationship between two variables. It takes on values close to 1 for strong relationships and −1 for adverse strong relationships. Moreover, significance values less than 0.05 reveal strong correlation, while those values that range between 0.05 and 0.06 demonstrate the tendency to correlate.

In this study, the values of the calculated criterion weights from the 19 experts were used to identify the correlations among the criterion weights. That means that the weights of each criterion were associated with the weights of each one of the rest of criteria, in order to identify the degree of correlation among them. This correlation analysis was conducted separately for all 3 bridge categories (bridges for highways, for national roads, and for provincial roads), for which individual criterion weights were calculated.

The specific part of the study can reveal interesting aspects about the way the criteria are weighted by the most of the experts. For instance, it can reveal if there is any pattern according to which some criteria usually receive directly proportional weight or some others receive inversely proportional weight.

Table 8. Results from correlation analysis for highways.

Criteria	Safety	Durability	Economy	Aesthetics	Constr. Speed	Serviceability	Environ. Harmoniz.
Safety	1	0.491 *	−0.758 ***		−0.815 ***
Durability		1	−0.660 **		−0.510 *
Economy			1		0.781 ***		−0.584 **
Aesthetics				1		−0.513 *	0.741 ***
Constr. speed					1
Serviceability						1
Environ. harmoniz.							1

Note: N = 19, blank cells: not significant (p > 0.05), * p < 0.05, ** p < 0.01, *** p < 0.001, two-tailed significance.

,

Table 9. Results from correlation analysis for national roads.

Criteria	Safety	Durability	Economy	Aesthetics	Constr. Speed	Serviceability	Environ. Harmoniz.
Safety	1	0.599 **	−0.795 ***		−0.664 **
Durability		1	−0.775 ***		−0.642 **
Economy			1	−0.527 *	0.662 **		−0.573 *
Aesthetics				1	−0.517 *		0.859 ***
Constr. speed					1	−0.547 *	−0.497 *
Serviceability						1
Environ. harmoniz.							1

Note: N = 19, blank cells: not significant (p > 0.05), * p < 0.05, ** p < 0.01, *** p < 0.001, two-tailed significance.

and

Table 10. Results from correlation analysis for provincial roads.

Criteria	Safety	Durability	Economy	Aesthetics	Constr. Speed	Serviceability	Environ. Harmoniz.
Safety	1	0.670 **	−0.855 ***		−0.815 ***
Durability		1	−0.675 **		−0.600 **
Economy			1		0.776 ***		−0.639 **
Aesthetics				1			0.530 *
Constr. speed					1	−0.545 *	−0.546 *
Serviceability						1	0.670 **
Environ. harmoniz.							1

Note: N = 19, blank cells: not significant (p > 0.05), * p < 0.05, ** p < 0.01, *** p < 0.001, two-tailed significance.

present the results of the correlation analysis regarding the criterion weights for highway bridges, national road bridges and provincial road bridges, respectively. In particular, each one of these three tables depicts the results with the values of Pearson’s correlation coefficient, but only for the cases where the two-tailed significance was below 0.05, i.e., where there was strong correlation between two criterion weights. It is also notable that in the three tables, certain symbols have been used to represent the different levels of significance of the correlations. Specifically, beyond the cases with significance (p) below 0.05, there is a special interest for those ones where the significance value is less than 0.01, and even more for the cases where it is less than 0.001 (presenting the strongest possible correlation).

An examination of the results of correlation analyses conducted for the three bridge categories, and specifically of the values of Pearson’s correlation coefficient (r), led to the following conclusions:

Concerning the criterion weights for the highway bridges, the most significant positive correlations were those between Economy and Construction Speed (where the value of the correlation coefficient r is equal to 0.781), and between Aesthetics and Environmental Harmonization (where r is equal to 0.741). On the other hand, the most significant negative correlations were those between Safety and Construction Speed (r = –0.815) and those between Safety and Economy (r = –0.758). As is shown in Table 8, in all these cases, the significance (p) value is less than 0.001; that is, the correlation is of the highest possible degree. It should be noted that a strong positive correlation of two variables means that, as one variable increases, the other increases by a proportionate amount. Conversely, in a negative correlation, if one variable increases, the other decreases by a proportionate amount [26].

Regarding the criterion weights for the bridges of national roads (Table 9), the most significant correlations, with a value of p below 0.001, were the positive one between Aesthetics and Environmental Harmonization (r = 0.859) and the negative correlations between Safety and Economy (r = −0.795), and between Durability and Economy (r = −0.775). Moreover, it is noteworthy that Construction Speed was significantly correlated, on the one hand negatively with Safety (r = −0.664) and Durability (r = −0.642), and on the other hand positively with Economy (r = 0.662), with p < 0.01 in all cases.

Finally, as far as the bridges for provincial roads are concerned (Table 10), the strongest correlations (with p < 0.001) were the following: Economy was significantly and positively correlated with Construction Speed (r = 0.776), and it was negatively correlated with Safety (r = −0.855), while Safety was also negatively correlated with Construction Speed (r = −0.815). Also noteworthy (but with p < 0.01) are the significant correlations between Durability and Safety, positively (r = 0.670), and between Durability and Economy, negatively (r = −0.675).

5.2. Correlations between Experts’ Field of Activity and Their Weights

In the present study, an attempt was also made to investigate any possible correlation of the experts’ field of activity with their weights, in order to draw useful conclusions concerning the priorities of each field that deals with bridges in Greece. Despite the fact that initially the use of the platform IBM SPSS Statistics did not show significant correlations regarding this kind of variable, the specific issue was examined in this study via a different methodology, with the aid of Microsoft Excel.

More specifically, the experts who come from the Academic and the Research fields, namely the experts No. 1, 2, 3, 15 and 18, were grouped together, considered “theoreticians”. On the other side are the experts who come from the “field of applications” (the rest of the experts), who are divided into two separate sub-categories: the experts from the public sector and the experts from the private sector. Consequently, there are a total of three subgroups of experts that were examined in this section.

Afterwards, for each bridge category and for each criterion separately, the data from Table 1, Table 2, Table 3, Table 4, Table 5 and Table 6 were used via the following procedure: the weights of the experts belonging to each one of the above subgroups were separated from the rest of the weights, and the average of them was calculated. The averages calculated in this way constitute the special weights of criteria that correspond to each one of the above three subgroups of experts and are presented in the below three

Table 11. Weights per subgroup of experts for the bridges for highways.

	Criteria	Safety	Durability	Economy	Aesthetics	Constr. Speed	Serviceability	Environ. Harmoniz.
Subgroups
“Theoreticians”		0.220	0.208	0.194	0.077	0.125	0.118	0.058
Experts from Public Sector		0.275	0.187	0.187	0.070	0.097	0.129	0.055
Experts from Private Sector		0.276	0.209	0.146	0.082	0.098	0.123	0.066

,

Table 12. Weights per subgroup of experts for the bridges for national roads.

	Criteria	Safety	Durability	Economy	Aesthetics	Constr. Speed	Serviceability	Environ. Harmoniz.
Subgroups
“Theoreticians”		0.197	0.145	0.234	0.060	0.177	0.132	0.054
Experts from Public Sector		0.251	0.151	0.183	0.064	0.179	0.114	0.058
Experts from Private Sector		0.269	0.169	0.172	0.073	0.126	0.124	0.066

and

Table 13. Weights per subgroup of experts for the bridges for provincial roads.

	Criteria	Safety	Durability	Economy	Aesthetics	Constr. Speed	Serviceability	Environ. Harmoniz.
Subgroups
“Theoreticians”		0.146	0.125	0.265	0.065	0.217	0.125	0.058
Experts from Public Sector		0.228	0.158	0.199	0.057	0.172	0.127	0.059
Experts from Private Sector		0.233	0.150	0.195	0.060	0.164	0.128	0.070

, per bridge category.

6. Discussion

In the current section, the main findings of the questionnaire survey regarding the weights of the compliance criteria are discussed. Moreover, the findings from the application of correlation analysis among the criterion weights, as well as the ones regarding the correlations between experts’ profile and their weights, are discussed too.

6.1. Discussion of the Findings of the Questionnaire Survey

The results regarding the final weights of compliance criteria per bridge category, namely the averages of the 19 experts, presented in Table 2, Table 4, and Table 6, provide the following rankings among the criteria:

Bridges of Highways:

(1) Safety, (2) Durability, (3) Economy, (4) Serviceability, (5) Construction Speed, (6) Aesthetics, (7) Environmental Harmonization

Bridges of National Roads:

(1) Safety, (2) Economy, (3) Durability, (4) Construction Speed, (5) Serviceability, (6) Aesthetics, (7) Environmental Harmonization

Bridges of Provincial Roads:

(1) Economy, (2) Safety, (3) Construction Speed, (4) Durability, (5) Serviceability, (6) Environmental Harmonization, (7) Aesthetics

In general, the results show clear differences among the three final groups of weights of the criteria, which correspond to the three bridge categories. These differences include substantial increases or decreases in the weight of some criteria, by around 5–6%, or even over 7% in the case of Construction Speed, as well as significant changes in the final ranking for certain criteria, among the three bridge categories.

It is interesting to note that the criterion of Economy is ranked third in the bridges for highways, then second in the bridges for national roads, and finally first in the bridges for provincial roads. Also notable are the changes in the weight and the ranking of Durability, but presenting an opposite trend, as it is ranked second in the case of highways, then third in national roads, while it is ranked fourth in the provincial roads.

Moreover, in all three bridge categories, the criteria of Safety and Economy are always in the first three places in the final rankings, and one of them always occupies first place. On the other hand, the criteria of Aesthetics and Environmental Harmonization in all bridge categories are ranked in the last two places, while especially in the cases of national and provincial roads, there is a significant difference between their weights and the weights of the rest of criteria.

6.2. Discussion of the Correlation Analysis among the Criterion Weights

Regarding the results of correlation analysis applied among the criterion weights, it is worth mentioning that there are certain criteria which, in all three bridge categories, appear significantly and positively correlated with each other, as regards their weighting by the 19 experts. This means that, as one criterion weight increases, the other increases by a proportionate amount. These pairs of criteria are in particular:

(1)

Economy with Construction Speed,

(2)

Aesthetics with Environmental Harmonization,

(3)

Safety with Durability (mainly in national road and provincial road bridges)

On the other hand, there are more pairs of criteria which always appear significantly and negatively correlated with each other. As mentioned above, in a significant negative correlation, if one criterion weight increases, the other decreases by a proportionate amount. The most notable among these pairs of criteria with negative correlations are the following:

(1)

Safety with Economy (probably the most significant correlation of all, with a value of p always below 0.001),

(2)

Safety with Construction Speed,

(3)

Durability with Economy,

(4)

Durability with Construction Speed (mainly in national road and provincial road bridges)

6.3. Discussion of the Correlations between Experts’ Profile and Their Weights

An initial finding that emerges from the correlation of the experts’ field of activity with their weights, and more specifically from Table 11, Table 12 and Table 13 above, is that the experts from the public sector show great similarities with those from the private sector, both in their weight rankings and in the weight values themselves. The only exceptions are: (1) their weights for the criterion of Economy in the highway bridges, which is evaluated as much more important by the experts of the public sector, as they rank it second (along with Durability) with a weight of 0.187, while those of the private sector rank it third, with a significant difference behind Durability, and (2) the criterion of Construction Speed in national road bridges, which is valued much more by public sector experts (who rank it third, with a very high weight of 0.179, while the private sector experts rank it fourth, with a not so great weight of 0.126. In general, the experts who come from the field of applications seem to evaluate the criterion of Safety as the most important in any case, since they rank it first by far in all three bridge categories.

On the other hand, the experts whose weights differ greatly from the other two categories are the “theoreticians”, namely these from the Academic and the Research fields. These experts tend to rate Economy very high in all bridge categories, and always higher than the other two subgroups, ranking it third but very close to Durability and Safety in highway bridges, first in national road bridges, and first by an overwhelming margin of almost 12% in provincial road bridges. Moreover, they tend to rate Construction Speed higher than the other groups of experts, giving to the criterion in all bridge categories a higher ranking compared to the total of 19 experts of the survey (fourth instead of fifth in Highway bridges, third instead of fourth in national road bridges and second instead of third in provincial road bridges).

7. Case Studies

The problem of selecting the most suitable construction method is examined for two case studies, namely two real bridge projects in Greece, by using multi-criteria analysis and, by extension, the relative weights of the compliance criteria that were calculated in the present study. The use of two case studies that belong to different bridge categories was deemed necessary, so that there would be an opportunity to apply two of the three different sets of weights of the criteria that were calculated in the present study, corresponding to the three bridge categories.

The two selected bridge projects are very similar, both in their length and their height from the ground, but as mentioned above, the first one belongs to the national road network, while the second one to the highway network of Greece. For each case study, detailed information on its data, as well as figures, are presented below, while in each one of them multi-criteria analysis is applied in order to select the most suitable bridge construction method per case.

7.1. Case Study 1

The project that was examined in the first case study is the G1 River Bridge of the Sminthi—Echinos Section (70.1.5) of the Vertical Axis 70 of Egnatia Motorway, located near Xanthi, in the Eastern Macedonia Prefecture of Greece. The final study was submitted and approved in 2017, but the bridge is not yet constructed. In practice, it is designed to be constructed with the Cast-in-place method, span by span, and has the following data.

It is a river bridge located very close to Sminthi Village; it is part of a national road and has a total length of 336 m. This, according to the design of the bridge, is distributed in 10 spans as follows: 24.00 m + 8 × 36.00 m + 24.00 m. The bridge has a maximum height of 18 m above ground, while its longitudinal slope ranges from 1.9 to 7.0%. The deck of the bridge has a width of 10.20 m, which, together with the sidewalks, is 14.20 m. The bridge is in seismic zone I and is shown in Figure 1. Based on the geometric data (total bridge length and maximum height of bridge above ground), it can be easily understood that, among the five existing construction methods, only the four of them are feasible, namely Cast-in-place, Precast I-Girder, Incremental Launching, and the Advanced Shoring method. Apparently, the method that was rejected is the Balanced Cantilever, due to the low height of the bridge above ground.

7.1.1. Additional Technical Data of the Real Bridge

The one branched river bridge is configured by a continuous superstructure with ten spans (total length 336.0 m on the bridge axis) made of prestressed concrete, which was cast in situ. The bridge is to be constructed in nine stages, starting from the southern abutment (A1) with construction joints at 20% of every span. In plan, the bridge horizontal alignment is on three successive circular arcs with radii of 150, 300, and 160 m, respectively, as well as the corresponding transition curves, located very close to Sminthi Village and at a great length within the river bed, close to the banks of two streams (Miroi and Magdi). The red line is also on a vertical concave arc with a radius of 6000 m, at a height ranging between 3.0 and 18.0 m from the natural terrain.

The piers, which have clear heights ranging between 7.3 and 17.5 m, have a single-column configuration and a rectangular cross-section (1.5 × 3.0 m) with semicircular edges (r = 0.75 m) and are founded on pile caps. The superstructure is monolithically connected to the seven central piers P2 to P8, resting on bearings at the outermost piers P1 and P9, as well as at the abutments, forming a case of semi-integral bridge with satisfactory behavior for both vertical as well as horizontal loads, with expansion joints only at the abutments and with reasonable displacements.

The cross-section of the girder is voided slab beam with a height of 1.8 m, a total width of 14.20 m (upper flange including 10.2 m deck and 2.0 m sidewalks at both edges) with a variable transverse inclination (max = 7%), carrying two-way traffic. Safety barriers, street lighting poles, insulation of the deck with a special membrane, and drainage of the deck with longitudinal and vertical drainage pipes are also provided.

7.1.2. Application of Multi-Criteria Analysis for the Selection

The multi-criteria analysis method of PROMETHEE II is applied, using the four feasible construction methods which were mentioned above, as alternatives. For the needs of its application, the software Visual PROMETHEE was used.

The seven compliance criteria were applied with a nine-point scale, while all criteria need to be maximized. The weights of the criteria were derived from the weights of compliance criteria from the 19 experts for the bridges for national roads (please see Table 4: last column). In addition, the Preference function selected was the V-shape, with a preference threshold (P) equal to 3, as it was considered the most appropriate function for the needs of this selection problem.

The performance of each construction method against each criterion is presented in

Table 14. Evaluations of the construction methods for case study 1.

	Criteria	Safety	Durability	Economy	Aesthetics	Constr. Speed	Serviceability	Environ. Harmoniz.
C. Methods
Cast-in-place		7	8	6	7	5	6	7
Precast I-Girder		5	5	8	5	9	9	5
Incremental Launching		6	6	4	8	4	5	8
Advanced Shoring method		6	6	3	7	5	5	7

as follows. It is noted that the evaluations of the four alternatives were obtained via a special questionnaire addressed to an expert in bridge design (one of the 19 who participated in the main survey), who brings together the qualities of a bridge designer, a bridge design reviewer, and a researcher in this field. However, the most important fact is that he was directly involved in the real design of the specific bridge (as well as in the design of the bridge of the second case study).

As follows in

Table 15. Flows (scores) of the four alternatives for case study 1.

Constr. Methods/Flows	Phi+	Phi−	Phi
Cast-in-place	0.4113	0.1491	0.2622
Precast I-Girder	0.4472	0.2965	0.1507
Incremental Launching	0.1372	0.3089	−0.1716
Advanced Shoring	0.0903	0.3316	−0.2412

, the resulting positive, negative, and net preference flows of the alternatives are presented, as they emerged from Visual PROMETHEE:

Therefore, based on the net preference flows (the last column “Phi”), the ranking of the four feasible construction methods, from best to worst is the following:

• Cast-in-place
• Precast I-Girder
• Incremental Launching
• Advanced Shoring

Eventually, according to the application of multi-criteria analysis, the chosen bridge construction method in the first case study is Cast-in-place, verifying the actual design of the bridge. Precast I-Girder was ranked second, not by a very large margin.

7.2. Case Study 2

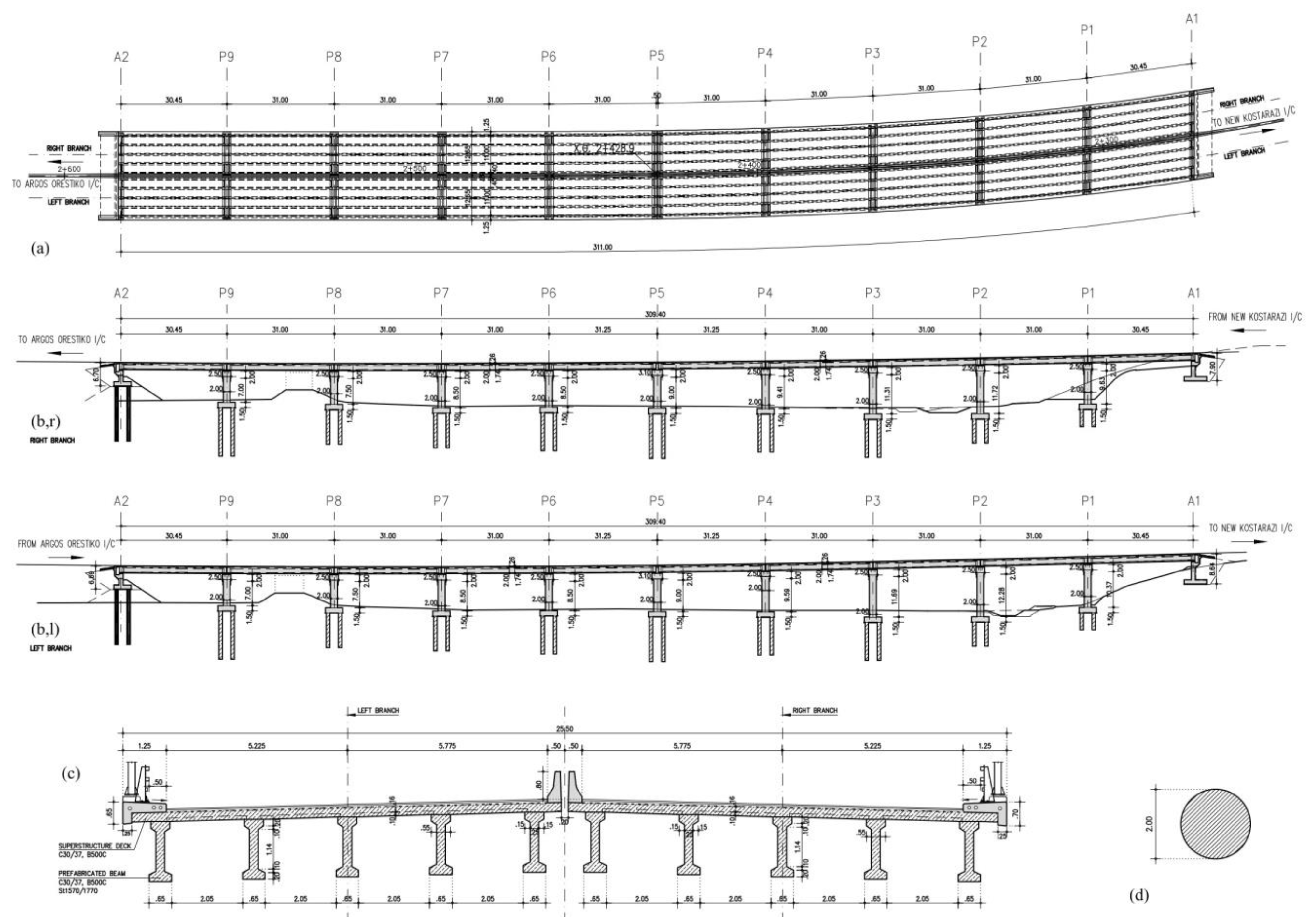
The project that is examined in the second case study is the T4 Valley Bridge of the New Kostarazi—Argos Orestiko Section (45.1.4) of the Vertical Axis 45 of Egnatia Motorway, located between Siatista and Krystallopigi in the Western Macedonia Prefecture of Greece. The final study was submitted and approved in 2003; the bridge was then constructed and was opened to traffic in 2005. In practice, it was designed and constructed with the Precast I-Girder method and possesses the following data.

It is a valley bridge with two independent branches, one for each traffic direction; it is part of the Egnatia vertical motorway network, so it is considered part of the highway network, and it has a total length of 309.4 m. This, according to the design of the bridge, is distributed in 10 spans as follows: 30.45 m + 6 × 31.00 + 2 × 31.25 m + 30.45 m. The bridge has a maximum height of 15 m above ground, while its longitudinal slope ranges from −2.0 to 2.5%. Each branch of the bridge carries one-way traffic, with two traffic and one emergency lane, a sidewalk on the external edge, and a safety barrier on the internal edge between the branches, which are 20 cm apart. Each branch has a deck with a width of 11.00 m, which together with the sidewalk and the safety barrier is 12.65 m. Thus, the total width of the bridge is 25.50 m.

The bridge is in seismic zone I and is shown in Figure 2. Based on the geometric data (total bridge length and maximum height of bridge above ground), it can be easily understood that, among the five existing construction methods, only the four of them are feasible, as in case study 1, namely Cast-in-place, Precast I-Girder, Incremental Launching, and Advanced Shoring. Apparently, the method that was rejected is the Balanced Cantilever, due to the low height of the bridge above ground.

7.2.1. Additional Technical Data of the Real Bridge

The two-branched valley bridge is configured by a series of simply supported prestressed precast girders (total length 309.45 m on the bridge axis) forming a 10 span T-beam grid superstructure. Each branch span consists of five double T precast beams, with a height of 1.74 m at an axial distance of 2.70 m. A 10 cm-thick precast slab is placed between the beams to support the additional 16 cm-thick slab, which was cast in situ during construction. The total thickness of the deck slab (flange) is thus 26 cm, and the total height of the slab beam is 2.0 m. The five beams are laterally connected with the flange and two cross girders at the pier supports (no intermediate connection). In order to avoid the expense of installing and maintaining/replacing joints, a continuous slab arrangement is provided in the longitudinal direction. Thus, the deck slab is continuous over five spans and only three expansion/contraction joints are needed (abutments A1, A2, and pier P5).

The beams rest on circular elastometallic bearings above the pier cap beams, forming a floating seismic isolation system with low damping. The piers of each branch are independent, stithy-shaped, and founded on pile caps. The piers, which have clear heights ranging between 7.0 and 12.3 m, have a single-column configuration and a circular cross-section with a 2.0 m diameter. The cap beam has a width of 2.5 m (except M5 where b = 3.1 m) and a height which varies from 0.8 to 2.0 m. Antiseismic stoppers are provided at an appropriate distance so as to remain inactive during the seismic design action.

In plan, the bridge horizontal alignment is on the transition to a curve with 800 m radius for almost half of the length and on a straight line for the rest of the length. The red line is also on a vertical concave arc with a radius of 9000 m, at a height ranging between 8.0 and 15.0 m from the natural terrain.

The transverse inclination of each branch is variable (max = 7%), carrying one-way traffic. Safety barriers, street lighting poles, insulation of the deck with a special membrane and drainage of the deck with longitudinal and vertical drainage pipes are also provided.

7.2.2. Application of Multi-Criteria Analysis for the Selection

The multi-criteria method of PROMETHEE II is applied also in case study 2, using the four feasible construction methods as Alternatives, again with the aid of the software Visual PROMETHEE.

The exact same settings as in case study 1 are used in the program, concerning the scale of the criteria and the Preference function, but here the criterion weights used are different, as they were derived from the weights of compliance criteria extracted by the 19 experts for the bridges of highways (please see Table 2: last column).

As follows in

Table 16. Evaluations of the construction methods for case study 2.

	Criteria	Safety	Durability	Economy	Aesthetics	Constr. Speed	Serviceability	Environ. Harmoniz.
C. Methods
Cast-in-place		7	7	6	6	5	5	6
Precast I-Girder		5	5	9	5	9	9	5
Incremental Launching		6	6	5	7	4	5	7
Advanced Shoring method		6	6	5	6	5	5	6

, the performance of the construction methods against each criterion is presented. The evaluations of the four alternatives were obtained from the same expert as in case study 1, via the same special questionnaire.

In

Table 17. Flows (scores) of the four Alternatives for case study 2.

Constr. Methods/Flows	Phi+	Phi−	Phi
Cast-in-place	0.2709	0.1478	0.1231
Precast I-Girder	0.3970	0.2680	0.1290
Incremental Launching	0.1133	0.2260	−0.1127
Advanced Shoring method	0.0787	0.2181	−0.1394

below, the positive, negative, and net preference flows of the alternatives, which were derived from the program of Visual PROMETHEE, are presented:

Consequently, based on the above net preference flows, the final ranking of the four participating construction methods, from best to worst, is the following:

• Precast I-Girder
• Cast-in-place
• Incremental Launching
• Advanced Shoring

In conclusion, the application of multi-criteria analysis indicated that the selectable construction method in the second case study is the Precast I-Girder, thus verifying the selection of the construction method that was made in practice. It is noteworthy that the Cast-in-place method was ranked second by only a very marginal difference from Precast I-Girder, indicating that in fact it could also be a suitable construction method for the current bridge project.

7.3. Discussion of Results of the Two Case Studies

According to the results extracted from the multi-criteria analysis, in two bridge projects in Greece that are quite similar in terms of their geometric data, but differ regarding their bridge category, two different distributions of weights of the compliance criteria were applied and ultimately, different results were obtained in terms of the selected construction method.

Moreover, it is notable that the methods of Incremental Launching and Advanced Shoring, which were ranked third and fourth in both final rankings, had particularly low scores with a very large distance from the first two methods in the bridge of case study 1, which is part of a national road. However, in the bridge of case study 2, which is part of a highway, the distances of the two aforementioned methods from the others have been noticeably reduced. This could be explained by the fact that the specific two methods are usually not particularly suitable for national (or provincial) roads due to their technical requirements.

8. Conclusions

The main research purpose of the present study was the proposal of seven compliance criteria for the selection of the most appropriate per-case bridge construction method, as well as the definition of the weights of these criteria, in order for them to be used in the decision-making tool of multi-criteria analysis. An important novelty of this research is exactly the use of these seven compliance criteria, instead of the use of only the criterion of economy, which was dominant in practice for years regarding the selection of bridge construction method. Another remarkable innovation of the study is that three different sets of criterion weights are calculated, corresponding to the three different categories of road bridges that are defined in the study, namely the bridges of highways, of national roads and of provincial roads. Thus, the proposed weights of compliance criteria are adjusted to the different importance of each bridge project.

The practical significance of the research lies in the fact that the compliance criteria and their weights extracted from the present study could be possibly utilized by awarding authorities for the evaluation and the assignment of the optimal design approach for bridge projects. In this way, the essential matter of the selection of bridge construction method could be addressed in a rational and systematized way, via multi-criteria analysis, instead of a possibly subjective choice of the method by individual designers, based only on their own experience from previous bridge projects. In addition, there will be no need to calculate new weights of criteria for each individual bridge project, since the three proposed sets of criterion weights can cover all the range of the usual concrete road bridges, in terms of their importance and requirements.

Regarding the weights of compliance criteria extracted from the research, it is worth mentioning that the criteria of Safety and Economy appear to be the two most popular criteria among the 19 bridge experts who participated in the present survey, considering all three categories of bridges. In fact, in all of the categories, these two criteria always occupy the first two or three places. In addition, the criterion of Durability is also evaluated as particularly important, as it maintains generally high positions in the experts’ rankings, and especially in the most important category, namely highway bridges, it occupies second place. Conversely, it is notable that the criteria of Aesthetics and Environmental Harmonization are clearly underestimated in the preferences of experts, having been ranked in the last two places in all bridge categories.

The general preference of the experts towards the criterion of Safety could be possibly explained by the fact that this term mainly corresponds to seismic safety, and Greece is the most seismically active region in Europe, due to some unique geological characteristics that it presents. On the other hand, their preference towards the criterion of Economy most probably indicates the limited budgeting of public works, such as bridges in Greece, which could sometimes present constraints that are taken into account by the decision-makers in selecting the bridge construction method.

In addition, an important finding of the research is that there are obvious differences among the three final sets of weights of the compliance criteria, corresponding to the three bridge categories, of highways, national roads and provincial roads. These differences concern both the final ranking and the weight values of certain criteria, and thus, they justify the choice made in the research to treat the three bridge categories separately, depending on their importance.

Concerning the profile of the bridge experts that participated in the survey, it is noteworthy that the opinions of the experts coming from the public sector, regarding the relative importance of the compliance criteria, generally resemble to a large extent the opinions of the experts from the private sector. Compared to these groups of experts who come from the field of applications, the views of the experts from the Academic and the Research fields differ greatly, especially regarding the criteria of Economy and Construction Speed, which they tend to rate much higher in any bridge category. Moreover, the fact that the 19 experts participating in the research come from all fields related to bridges, namely from both academia and construction industry (that is represented from the private and public sector), is considered that has led to certain weights of compliance criteria that present a significant degree of mutual acceptance by all parties who expertise in bridge design.

Regarding the results of the correlation analysis among the criterion weights, it is noteworthy that in all three bridge categories, the pair of the criteria Economy—Construction Speed, as well as the pair of Safety—Durability present strong positive correlation. On the other hand, the pairs of the criteria Safety—Economy, Safety—Construction Speed, and Durability—Economy present strong negative correlation.

Finally, it is worth mentioning that, when applying multi-criteria analysis for the selection of the most suitable construction method in a bridge project, the weights of the compliance criteria that are used can play a very important role in the final decision, but not always the decisive one, as the choice is also based on other essential factors such as the geometric data of the bridge or the data of the project area, which may affect the performance of the methods against the criteria. The current research considered seven compliance criteria and implemented two multi-criteria analysis methods. As part of the future research, it is proposed that more criteria could be considered and additional methods of multi-criteria analysis could be implemented in the context of the selection of bridge construction method.