Estimating Optimal Cost, Insulation Layer Thickness, and Structural Layer Thickness of Different Composite Insulation External Walls Using Computational Methods
Abstract
:1. Introduction
2. Methodology
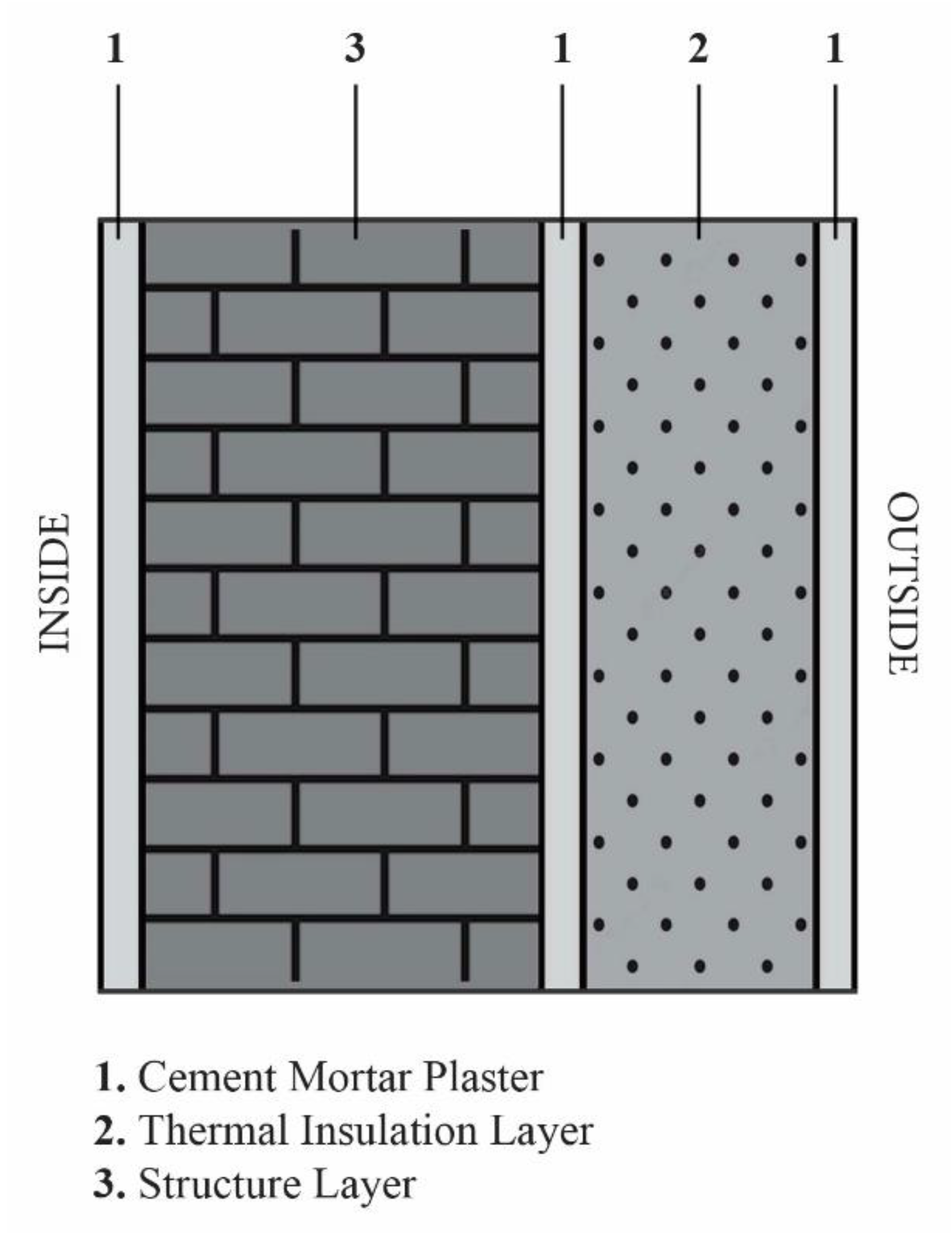
2.1. Case Study of a Masonry Wall Construction in Beijing
2.2. Mathematical Model
2.2.1. Initial Investment Cost of a CIEW
2.2.2. Heating and Cooling Loss through CIEW
2.2.3. Energy Consumption Cost
2.2.4. Life Cycle Cost
2.2.5. Payback Period
2.2.6. Economic Insulation Layer Thickness and Overall U Value
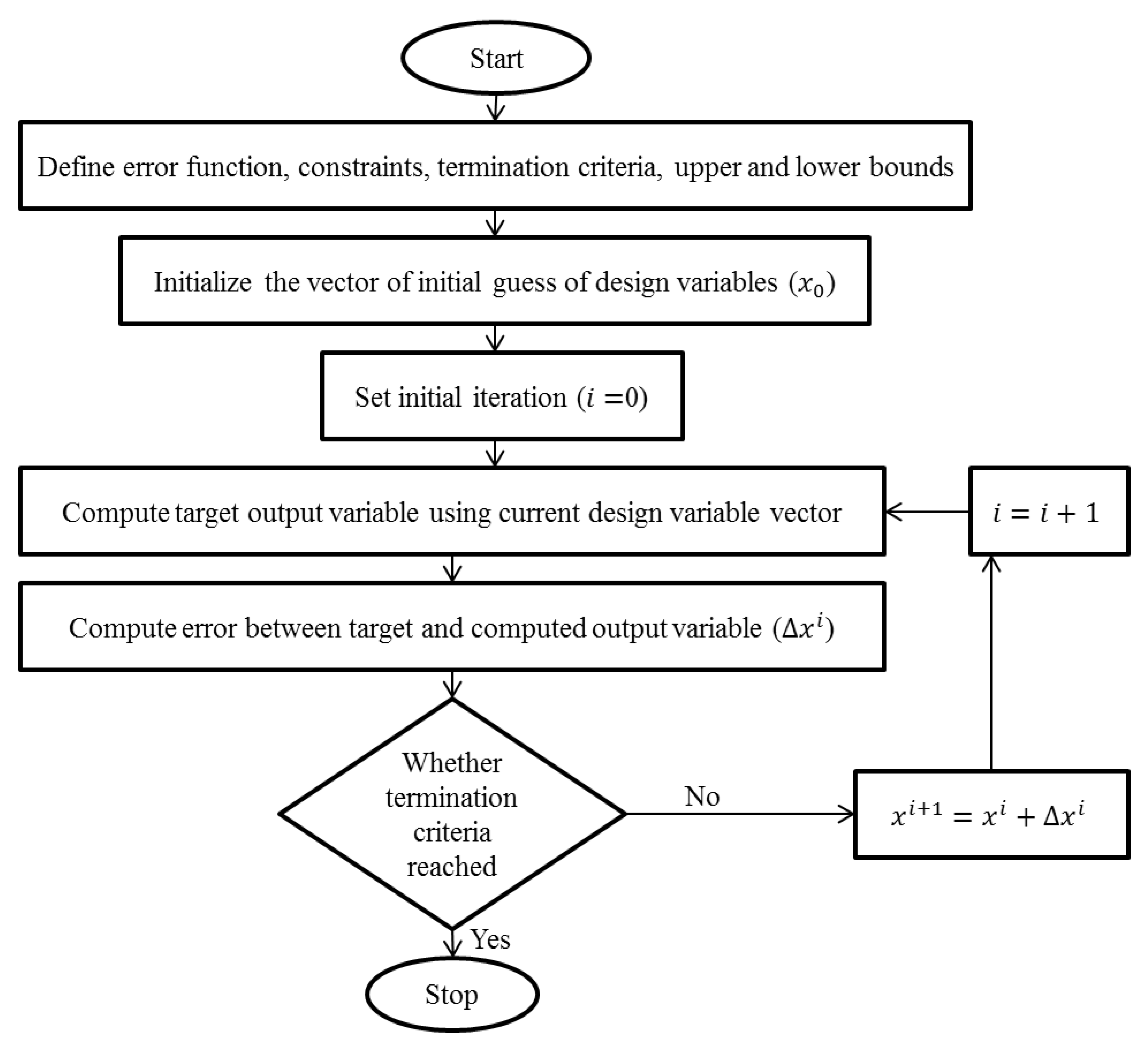
2.3. Optimization Technique: Nonlinear Least Squares Error Method (LSE)
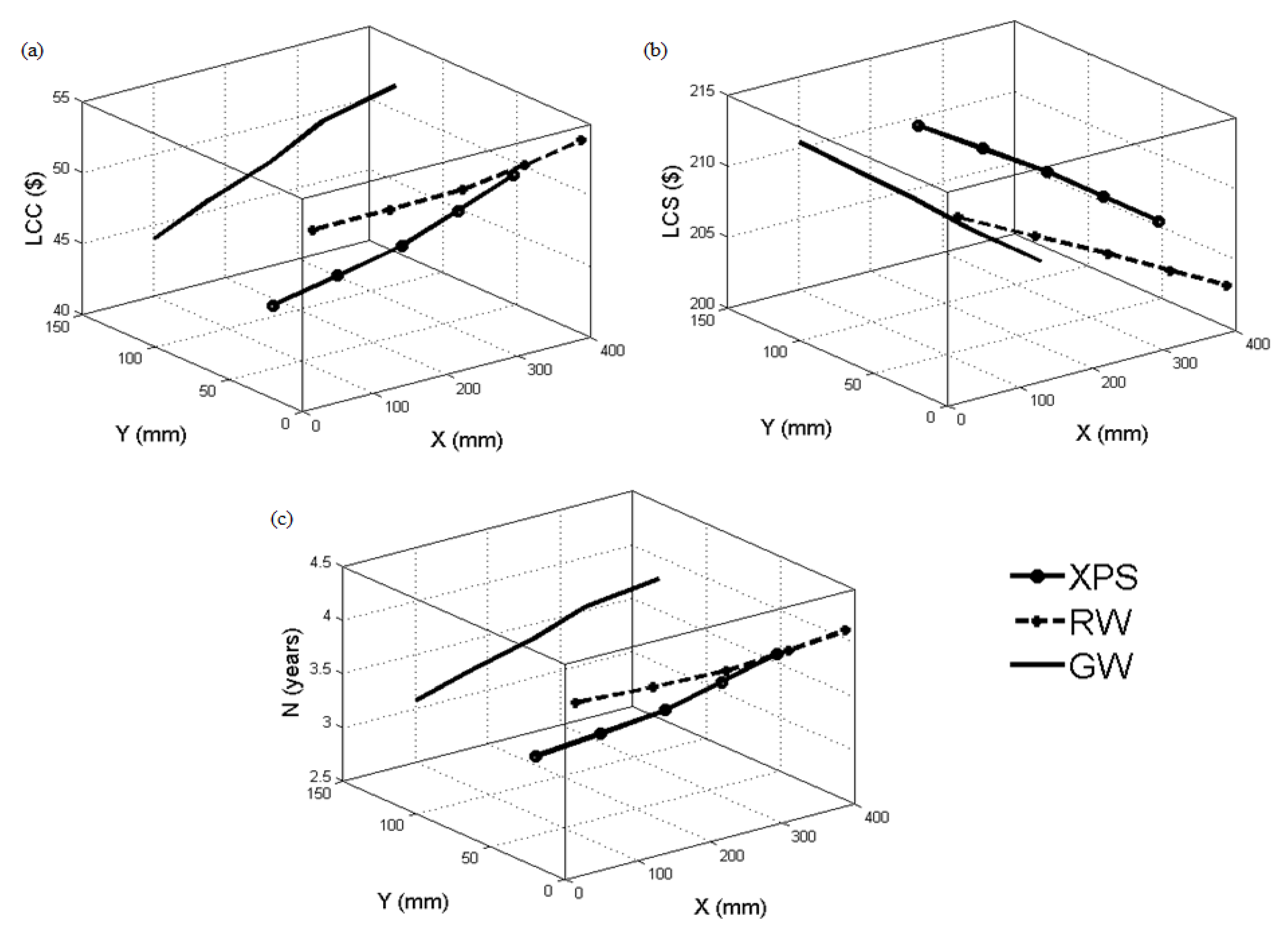
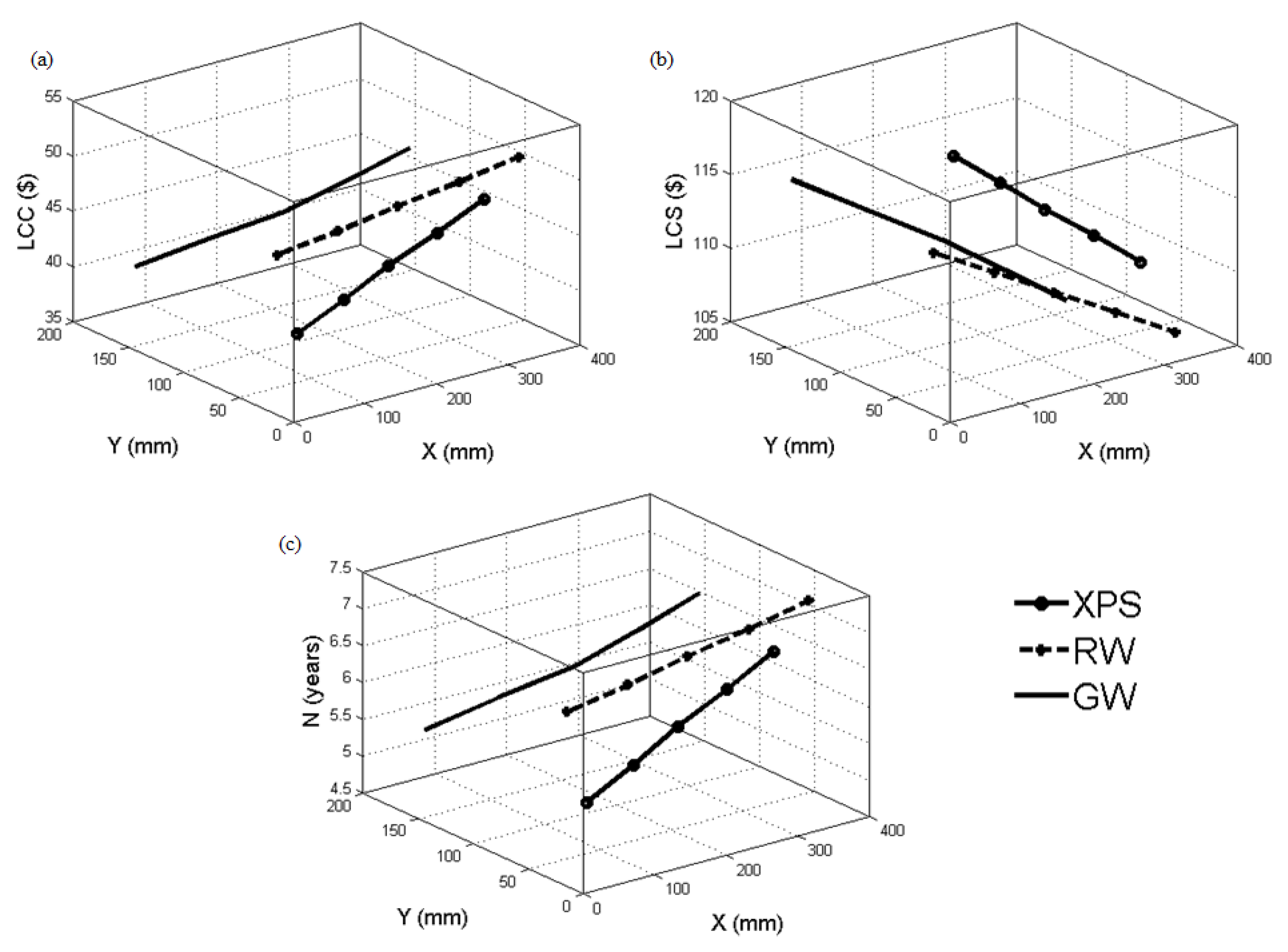
3. Results
4. Discussion
4.1. Comparison between LSE and LCCA
4.1.1. Percentage Value Comparison
4.1.2. Comparative Analysis of Optimal Thickness
4.1.3. Payback Period
4.1.4. U-Value Comparison
4.1.5. Structural and Insulation Layer Thickness Comparison for Different Heating Systems
4.2. Traditional Methodologies vs. New Insights
5. Conclusions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Abbreviations | |
| ASHP | Air-Source Heat Pump |
| CIEW | Composite Insulation External Walls |
| CFB | Circulating Fluidized Bed |
| GFB | Grate-Fired Boiler |
| GW | Glass Wool |
| HVAC | Heating, Ventilating, and Air Conditioning |
| LCCA | Life Cycle Cost Analysis |
| LSE | Least Squares Error |
| LCC | Life Cycle Cost (USD) |
| LCS | Life Cycle Savings (USD) |
| N | Payback period (years) |
| RW | Rock Wool |
| XPS | Extruded Polystyrene |
| X | Optimal structural layer thickness (mm) |
| Y | Optimal insulation layer thickness (mm) |
| Symbols | |
| Lower heating value of energy consumed per unit of heating (kJ/kg, kJ/m3, or kJ/kWh) | |
| Efficiency of the heating source | |
| Efficiency of the network | |
| Fuel cost for heating per unit kilogram, volume, or kilowatt hour (USD/m·t, USD/km3, or USD/MWh) | |
| Coefficient of performance of the cooling system | |
| Price of the insulation material per unit volume (USD/m3) | |
| Labour and insulation installation cost per unit area (USD/m2) | |
| Material and labour costs associated with mortar plaster on a unit surface area (USD/m2) | |
| Thermal conductivity of the structure material layer (W/m.K) | |
| Thermal conductivity of the insulation material layer (W/m.K) | |
| Heating degree days based on 18 °C (°C·d) | |
| Cooling degree days based on 26 °C (°C·d) | |
| Overall thermal resistance of walls, excluding that offered by structural and insulation layers (m2k/W) | |
| Price of electricity per unit kilowatt hour (USD/kW) | |
| Service life of the insulating material (years) | |
| Initial investment cost of the wall per unit area (USD/m2) | |
| Overall heat transfer coefficient offered by the external wall with mortar, structural, and insulation layer (W/m2K) | |
| Overall heat transfer coefficient of the CIEW, without considering the insulation and structural layer (W/m2K) | |
| Overall heat transfer coefficient offered by the structural and insulation layer (W/m2K) | |
| Heating losses through the wall, considering structure and insulation layers (kJ/kg, kJ/m3, or kJ/kWh) | |
| Cooling losses through the wall, considering structure and insulation layers (kJ/kg, kJ/m3, or kJ/kWh) | |
| Difference in heating losses through the wall, without considering structure and insulation layers (kJ/kg, kJ/m3, or kJ/kWh) | |
| Difference in cooling losses through the wall, without considering Structure and insulation layers (kJ/kg, kJ/m3, or kJ/kWh) | |
| Annual energy consumption cost through CIEW (USD/kW) | |
| Difference between heating and cooling energy costs saved with and without considering structure and insulation layers (USD/kW) | |
| Present worth factor | |
| Inflation discount rates (%) | |
| Market discount rates (%) | |
| A given structural layer thickness (mm) | |
| Economic insulation layer thickness (Equation (16)) (mm) | |
| Overall U value at (Equation (15)) (W/m2K) |
References
- Mousavi, S.; Rismanchi, B.; Brey, S.; Aye, L. Lessons Learned from PCM Embedded Radiant Chilled Ceiling Experiments in Melbourne. Energy Rep. 2022, 8, 54–61. [Google Scholar] [CrossRef]
- Aggarwal, V.; Meena, C.S.; Kumar, A.; Alam, T.; Kumar, A.; Ghosh, A.; Ghosh, A. Potential and Future Prospects of Geothermal Energy in Space Conditioning of Buildings: India and Worldwide Review. Sustainability 2020, 12, 8428. [Google Scholar] [CrossRef]
- Ali, A. Determination of Optimum Thickness of Nano and Traditional Insulation Materials for Building External Walls by Using Degree-Day Approach for Different Climatic Regions in Egypt. MSA Eng. J. 2022, 1, 39–58. [Google Scholar] [CrossRef]
- Malka, L.; Kuriqi, A.; Haxhimusa, A. Optimum Insulation Thickness Design of Exterior Walls and Overhauling Cost to Enhance the Energy Efficiency of Albanian’s Buildings Stock. J. Clean. Prod. 2022, 381, 135160. [Google Scholar] [CrossRef]
- Balo, F.; Ulutaş, A. Energy-Performance Evaluation with Revit Analysis of Mathematical-Model-Based Optimal Insulation Thickness. Buildings 2023, 13, 408. [Google Scholar] [CrossRef]
- Dong, Y.; Kong, J.; Mousavi, S.; Rismanchi, B.; Yap, P.-S. Wall Insulation Materials in Different Climate Zones: A Review on Challenges and Opportunities of Available Alternatives. Thermo 2023, 3, 38–65. [Google Scholar] [CrossRef]
- Li, X.; Densley Tingley, D. A Whole Life, National Approach to Optimize the Thickness of Wall Insulation. Renew. Sustain. Energy Rev. 2023, 174, 113137. [Google Scholar] [CrossRef]
- Espejel-Blanco, D.F.; Hoyo-Montaño, J.A.; Arau, J.; Valencia-Palomo, G.; García-Barrientos, A.; Hernández-De-León, H.R.; Camas-Anzueto, J.L. HVAC Control System Using Predicted Mean Vote Index for Energy Savings in Buildings. Buildings 2022, 12, 38. [Google Scholar] [CrossRef]
- Ramin, H.; Hanafizadeh, P.; Akhavan-Behabadi, M.A. Determination of Optimum Insulation Thickness in Different Wall Orientations and Locations in Iran. Adv. Build. Energy Res. 2016, 10, 149–171. [Google Scholar] [CrossRef]
- Rosti, B.; Omidvar, A.; Monghasemi, N. Optimal Insulation Thickness of Common Classic and Modern Exterior Walls in Different Climate Zones of Iran. J. Build. Eng. 2020, 27, 100954. [Google Scholar] [CrossRef]
- Hou, J.; Zhang, T.; Liu, Z.; Hou, C.; Fukuda, H. A Study on Influencing Factors of Optimum Insulation Thickness of Exterior Walls for Rural Traditional Dwellings in Northeast of Sichuan Hills, China. Case Stud. Constr. Mater. 2022, 16, e01033. [Google Scholar] [CrossRef]
- Ziapour, B.M.; Rahimi, M.; Yousefi Gendeshmin, M. Thermoeconomic Analysis for Determining Optimal Insulation Thickness for New Composite Prefabricated Wall Block as an External Wall Member in Buildings. J. Build. Eng. 2020, 31, 101354. [Google Scholar] [CrossRef]
- Huang, J.; Feng, W.; Huang, Z.; Wang, S. Optimum Construction Form and Overall U-Value of Composite Insulation External Wall. Energy Sources Part A Recovery Util. Environ. Eff. 2023, 45, 5806–5822. [Google Scholar] [CrossRef]
- Tian, Y.; Wu, J.; Xu, Z.; Yang, J.; Guan, X. Optimal Analysis of Multi-Energy System towards Low-Carbon Building. In Proceedings of the 2022 China Automation Congress (CAC), Xiamen, China, 25–27 November 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 6323–6328. [Google Scholar]
- Dai, B.; Zhao, R.; Liu, S.; Xu, T.; Qian, J.; Wang, X.; Yang, P.; Wang, D. CO2 System Integrated with Ejector and Mechanical Subcooling: A Comprehensive Assessment. Appl. Therm. Eng. 2023, 234, 121269. [Google Scholar] [CrossRef]
- Zhu, Y.; Zhang, T.; Ma, Q.; Fukuda, H. Thermal Performance and Optimizing of Composite Trombe Wall with Temperature-Controlled DC Fan in Winter. Sustainability 2022, 14, 3080. [Google Scholar] [CrossRef]
- Simpeh, E.K.; Pillay, J.-P.G.; Ndihokubwayo, R.; Nalumu, D.J. Improving Energy Efficiency of HVAC Systems in Buildings: A Review of Best Practices. IJBPA 2022, 40, 165–182. [Google Scholar] [CrossRef]
- Evins, R. A Review of Computational Optimisation Methods Applied to Sustainable Building Design. Renew. Sustain. Energy Rev. 2013, 22, 230–245. [Google Scholar] [CrossRef]

| CFB | |||||
|---|---|---|---|---|---|
| XPS | |||||
| (mm) | (mm) | (mm) | (USD) | (USD) | (Years) |
| 200 | 127 | 73 | 36.95 | 115.83 | 4.97 |
| 250 | 187 | 63 | 39.00 | 113.77 | 5.33 |
| 300 | 259 | 41 | 40.22 | 112.54 | 5.54 |
| 350 | 321 | 29 | 42.13 | 110.62 | 5.88 |
| 400 | 383 | 17 | 44.05 | 108.70 | 6.22 |
| RW | |||||
| (mm) | (mm) | (mm) | (USD) | (USD) | (Years) |
| 200 | 123 | 77 | 43.21 | 109.54 | 6.07 |
| 250 | 191 | 59 | 44.59 | 108.16 | 6.32 |
| 300 | 259 | 41 | 45.97 | 106.77 | 6.57 |
| 350 | 326 | 24 | 47.42 | 105.31 | 6.83 |
| 400 | 394 | 6 | 48.80 | 103.92 | 7.08 |
| GW | |||||
| (mm) | (mm) | (mm) | (USD) | (USD) | (Years) |
| 200 | 53 | 147 | 40.31 | 112.48 | 5.56 |
| 250 | 119 | 131 | 42.68 | 110.11 | 5.98 |
| 300 | 185 | 115 | 45.05 | 107.74 | 6.40 |
| 350 | 251 | 99 | 47.41 | 105.37 | 6.83 |
| 400 | 313 | 87 | 49.88 | 102.91 | 7.27 |
| GFB | |||||
|---|---|---|---|---|---|
| XPS | |||||
| (mm) | (mm) | (mm) | (USD) | (USD) | (Years) |
| 200 | 121 | 79 | 42.32 | 214.52 | 2.95 |
| 250 | 184 | 66 | 44.17 | 212.67 | 3.13 |
| 300 | 247 | 53 | 46.02 | 210.82 | 3.32 |
| 350 | 306 | 44 | 48.14 | 208.69 | 3.53 |
| 400 | 365 | 35 | 50.27 | 206.57 | 3.75 |
| RW | |||||
| (mm) | (mm) | (mm) | (USD) | (USD) | (Years) |
| 200 | 139 | 61 | 48.17 | 208.65 | 3.53 |
| 250 | 208 | 42 | 49.55 | 207.27 | 3.67 |
| 300 | 275 | 25 | 50.93 | 205.88 | 3.81 |
| 350 | 337 | 13 | 52.38 | 204.42 | 3.96 |
| 400 | 396 | 4 | 53.76 | 203.03 | 4.10 |
| GW | |||||
| (mm) | (mm) | (mm) | (USD) | (USD) | (Years) |
| 200 | 67 | 133 | 45.27 | 211.60 | 3.24 |
| 250 | 126 | 124 | 47.64 | 209.23 | 3.48 |
| 300 | 187 | 113 | 50.00 | 206.86 | 3.72 |
| 350 | 244 | 106 | 52.37 | 204.49 | 3.96 |
| 400 | 311 | 89 | 54.84 | 202.02 | 4.21 |
| ASHP | |||||
|---|---|---|---|---|---|
| XPS | |||||
| (mm) | (mm) | (mm) | (USD) | (USD) | (Years) |
| 200 | 123 | 77 | 37.40 | 118.89 | 4.90 |
| 250 | 179 | 71 | 39.73 | 116.55 | 5.30 |
| 300 | 234 | 66 | 42.14 | 114.15 | 5.71 |
| 350 | 291 | 59 | 44.41 | 111.88 | 6.11 |
| 400 | 347 | 53 | 46.75 | 109.54 | 6.52 |
| RW | |||||
| (mm) | (mm) | (mm) | (USD) | (USD) | (Years) |
| 200 | 112 | 88 | 44.23 | 112.05 | 6.08 |
| 250 | 176 | 74 | 45.91 | 110.36 | 6.37 |
| 300 | 239 | 61 | 47.67 | 108.60 | 6.68 |
| 350 | 303 | 47 | 49.36 | 106.91 | 6.98 |
| 400 | 366 | 34 | 51.12 | 105.15 | 7.29 |
| GW | |||||
| (mm) | (mm) | (mm) | (USD) | (USD) | (Years) |
| 200 | 34 | 166 | 40.95 | 115.37 | 5.51 |
| 250 | 105 | 145 | 43.19 | 113.12 | 5.90 |
| 300 | 177 | 123 | 45.41 | 110.89 | 6.28 |
| 350 | 242 | 108 | 47.80 | 108.50 | 6.70 |
| 400 | 306 | 94 | 50.22 | 106.08 | 7.13 |
| CFB-XPS | CFB-RW | CFB-GW | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| (USD) | (USD) | (years) | (USD) | (USD) | (years) | (USD) | (USD) | (years) | |||
| 0.995 | −0.995 | 0.995 | 1.000 | −1.000 | 1.000 | 1.000 | −1.000 | 1.000 | |||
| −0.981 | 0.982 | −0.981 | −1.000 | 1.000 | −1.000 | −0.998 | 0.998 | −0.998 | |||
| GFB-XPS | GFB-RW | GFB-GW | |||||||||
| (USD) | (USD) | (years) | (USD) | (USD) | (years) | (USD) | (USD) | (years) | |||
| 0.998 | −0.999 | 0.998 | 0.999 | −0.999 | 0.999 | 1.000 | −1.000 | 1.000 | |||
| −0.991 | 0.991 | −0.991 | −0.988 | 0.988 | −0.988 | −0.991 | 0.991 | −0.991 | |||
| ASHP-XPS | ASHP-RW | ASHP-GW | |||||||||
| (USD) | (USD) | (years) | (USD) | (USD) | (years) | (USD) | (USD) | (years) | |||
| 1.000 | −1.000 | 1.000 | 1.000 | −1.000 | 1.000 | 0.999 | −0.999 | 0.999 | |||
| −0.998 | 0.998 | −0.999 | −1.000 | 1.000 | −1.000 | −0.993 | 0.993 | −0.992 | |||
| XPS | RW | GW | ||||
|---|---|---|---|---|---|---|
| Heating System | LCC (%) | LCS (%) | LCC (%) | LCS (%) | LCC (%) | LCS (%) |
| CFB | −5.03 | 7.04 | −7.41 | 9.12 | 1.51 | 4.50 |
| GFB | −2.15 | 5.60 | −8.16 | 7.66 | 4.89 | 3.94 |
| ASHP | −0.28 | 3.29 | −4.41 | 7.56 | 2.02 | 4.28 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alrasheed, M.R.A. Estimating Optimal Cost, Insulation Layer Thickness, and Structural Layer Thickness of Different Composite Insulation External Walls Using Computational Methods. Buildings 2023, 13, 2774. https://doi.org/10.3390/buildings13112774
Alrasheed MRA. Estimating Optimal Cost, Insulation Layer Thickness, and Structural Layer Thickness of Different Composite Insulation External Walls Using Computational Methods. Buildings. 2023; 13(11):2774. https://doi.org/10.3390/buildings13112774
Chicago/Turabian StyleAlrasheed, Mohammed R. A. 2023. "Estimating Optimal Cost, Insulation Layer Thickness, and Structural Layer Thickness of Different Composite Insulation External Walls Using Computational Methods" Buildings 13, no. 11: 2774. https://doi.org/10.3390/buildings13112774
APA StyleAlrasheed, M. R. A. (2023). Estimating Optimal Cost, Insulation Layer Thickness, and Structural Layer Thickness of Different Composite Insulation External Walls Using Computational Methods. Buildings, 13(11), 2774. https://doi.org/10.3390/buildings13112774






