Abstract
In the article, the semi-permanent aluminum alloy portal frame is used as the research background, beam-column joints are used as the research object, and experimental and numerical analyses are carried out. The influence of different bolt diameters and arch angles on the mechanical properties of beam-column joints under vertical load was analyzed using five sets of experiments. The experimental results show that the load–displacement curves of different bolt diameters in the elastic stage are basically consistent. After entering the plastic stage, the ultimate load first increases and then decreases, and the ultimate displacement is basically consistent. According to the experiment, there is no significant difference in the load–displacement curve when the arch angle increases from 90 degrees to 108 degrees. When the arch angle increases to 126 degrees, the stiffness and ultimate bearing capacity of the node under vertical load significantly increase. Then, a numerical analysis model was established to analyze the mechanical performance of beam-column joints under horizontal loads. The numerical analysis results indicate that under horizontal load, as the diameter of the bolt increases, the yield load, yield displacement, ultimate load, and ultimate displacement of the beam-column node exhibit no significant changes, and the change amplitude is minimal. When the beam-column node is subjected to horizontal loads, as the arch angle increases, the yield and ultimate displacement increase by 2.14 times and 2.78 times, respectively, and the yield and ultimate load decrease by 58% and 48%, respectively. Finally, a simplified design method for beam-column joints was proposed based on experiments and numerical analysis.
1. Introduction
The commonly used types of joints in aluminum alloy spatial structures include gusset joints, bolt ball joints, cast aluminum joints, and hub joints, as shown in Figure 1. So far, some researchers have conducted a series of studies on these aluminum alloy joints and achieved excellent results.

Figure 1.
Diagram of aluminum alloy joints.
Guo et al. [1,2,3] conducted an experimental study on the out-of-plane bearing capacity of plate joints and obtained the failure modes of the joints under different plate thicknesses. They found that as the plate thickness increased, the stiffness of the joints increased. They proposed a four-line model of semi-rigid out-of-plane plate joints. Then, through theoretical analysis, the bending stiffness and corresponding critical bending moment values of the joints in each stage of the four-line model were derived. Finally, a numerical model was established to simulate the stiffness of the bolt fixation stage and the hole wall pressure bearing stage, and based on the numerical analysis results, a formula for the out-of-plane bending stiffness of the joint was obtained. Then, based on out-of-plane research, a semi-rigid four-line model of in-plane aluminum alloy plate joints was obtained with numerical simulation. Guo et al. [4] conducted experimental research on the out-of-plane hysteresis performance of aluminum alloy plate joints. The experimental results showed that due to the gap between the bolt hole and the bolt rod, the hysteresis curve was not quite complete, and the torque relative rotation hysteresis curve showed that the joint had good energy dissipation capacity. Moreover, as the thickness of the joint plate increased, the command performance of the joint gradually improved. Ma et al. [5] proposed a new type of column plate joint based on the traditional aluminum alloy plate joint and obtained the bending moment angle curves of the column plate joint around the strong axis, weak axis, and torsion directions. Then, they were introduced into the grid shell beam element model. The analysis results showed that the column plate stage is still in the elastic stage when the grid shell is unstable. Chen et al. [6] conducted experimental research on the out-of-plane hysteresis performance of plate joints and obtained the hysteresis curve, ductility ratio, and energy dissipation rate of plate joints. In addition, they were compared with numerical simulation results and were found to be consistent. Liu et al. [7] conducted experimental research on the low cycle fatigue performance of plate joints, obtained the low cycle fatigue failure mechanism and fatigue life of plate joints, and then conducted numerical simulation. The numerical simulation results were significantly consistent with the experimental results. Finally, a local feature based low cycle fatigue life prediction method was proposed. Zhao et al. [8,9] improved the plate joint and proposed two new types of aluminum alloy joints. Through experimental research, it was found that both types of joints have good mechanical properties and can be used for single-layer aluminum alloy lattice shell structures.
Hiyama et al. [10] proposed a formula for calculating the stiffness of aluminum alloy bolted ball joints through experimental and numerical simulation analysis. Liu et al. [11,12] studied a new type of aluminum alloy bolt spherical joint and evaluated it through tensile tests and numerical simulations. The tensile performance and failure mechanism of aluminum alloy bolt spherical joints was explored, and ultimately, a calculation formula for the tensile capacity of aluminum alloy bolt spherical joints was proposed. Shi et al. [13] conducted full-scale tests on three forms of cast aluminum joints in conjunction with the Chenshan Botanical Garden Greenhouse Exhibition Hall project. The test results showed that the cast aluminum joints had a greater flexural stiffness outside the plane and a smaller stiffness in the plane, making them typical semi-rigid joints. Their failure mode was brittle fracture failure. Subsequently, numerical simulations were conducted, and a simplified calculation formula for their bearing capacity was proposed. Cast aluminum joints can be widely used in aluminum alloy spatial structures. Sugizaki, K et al. [14,15] conducted experimental research on the basic mechanical properties of the cast aluminum joint, and the research results showed that adjusting the material properties of the component can ensure that the ultimate tensile bearing capacity of the joint is approximately the product of the tensile strength of the pipe and the cross-sectional area, which also indicates that this joint has an obvious semi-rigidity. Yonemaru et al. [16] conducted bending tests on aluminum alloy and carbon fiber-reinforced composite hub joint trusses, and the results showed that the overall truss buckling occurred due to the failure of the upper components.
The lightweight portal frame itself has the advantages of large building space, simple structural stress, and clear transmission path. The aluminum alloy portal frame structure combines many advantages brought by materials [17,18], such as lightweight, high strength, corrosion resistance, and high assembly rate. Therefore, aluminum alloy portal frame structures can be used not only in traditional permanent buildings such as workshops and warehouses, but also in temporary or semi-permanent buildings such as healthcare camps, exhibitions, sports events, and logistics warehousing. At present, there are relatively few research results on aluminum alloy portal frame joints. In this article, a new type of beam-column joint for aluminum alloy portal steel frames is proposed. Then, experimental research and numerical simulation analysis were conducted on this new type of beam-column joint. Finally, based on experiments and numerical simulations, a simplified design method for this type of joint was proposed.
2. Test Scheme
2.1. Specimens Design
To explore the mechanical properties of aluminum alloy portal frame beam-column joints, in this section, beam-column joint specimens are designed as shown in Figure 2. The beam-column joint specimens are made of H-shaped aluminum alloy members and double C-shaped double groove connectors tightly connected by bolts. Among them, the cross-sectional size of the aluminum alloy I-beam is H203 × 106 × 11 × 11 mm, and the channel steel connection is C181 × 47.5 × 5 × 10 mm. Six and four bolt holes are, respectively, set on the upper and lower flanges of the H-shaped aluminum alloy I-beam, and six bolt holes are set on the web of the I-beam. At the same time, bolt holes are set at the corresponding positions of the flange and web of the double groove connector. The diameter of the bolt holes is determined based on the corresponding bolt diameter (greater than 0.2 mm of the bolt diameter). The lengths of aluminum alloy I-beams are 1240 mm and 990 mm, respectively, and the lengths of channel steel connectors are 470 mm. The distribution spacing of bolts on the flange and web is 148 mm. The structural dimensions of the specimens are shown in Figure 2a. The aluminum alloy I-beams are cut and drilled in the factory, and the double groove connectors are welded from steel plates. The two are then transported to the laboratory for assembly and connection, as shown in Figure 2b.
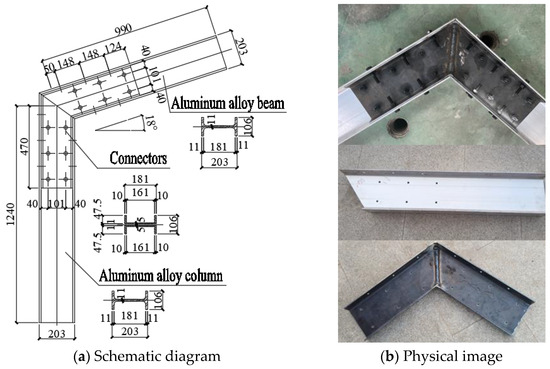
Figure 2.
Test specimen.
For portal frames, the bolt diameter and arch angle of beam-column joints have a significant impact on the mechanical performance of their beam-column joints. Therefore, a total of 5 beam-column joint specimens were designed in this chapter, and the parameters of each specimen are detailed in Table 1. From this table, it can be seen that this experiment mainly designed beam-column joint specimens with different bolt diameters (8 mm, 14 mm, and 20 mm) and different arch angles (90°, 108°, and 126°) to explore the impact of different bolt diameters and arch angles on the mechanical properties of aluminum alloy portal frame beam-column joints. It should be noted that when studying the influence of bolt diameter or arch angle, other structural parameters of beam-column joints remain consistent.

Table 1.
Detailed information of joints.
2.2. Testing System
The loading site of this experiment is shown in Figure 3a. The experimental system mainly includes reaction frame (composed of reaction beam and column), jack, consolidation support, loading control instrument, and data acquisition instrument. During the experiment, the lower end of the specimen is first tightly connected to the consolidation support, and then, a vertical concentrated force is applied to the specimen through a jack, as shown in Figure 3b. Four bolts and end plates are used to securely connect the jack to the reaction beam, ensuring that the position of the loading point does not shift during the loading process, as shown in Figure 3c. The consolidation support is tightly connected to the foundation through vertically arranged threaded steel bars, while the bottom of the specimen is tightly connected to the consolidation support through three drainage flat bolts, ensuring the formation of consolidation constraint boundary conditions at the bottom of the specimen, as shown in Figure 3d. By using the above loading methods and support forms, the boundary conditions of aluminum alloy portal frame beam-column joints under vertical load can be simulated, thereby ensuring the effectiveness of the test results. During the experiment, the loading control instrument was used to control the loading speed. In this experiment, the loading speed was 1 mm/min, and the data collection instrument was used to record the test data at each moment.
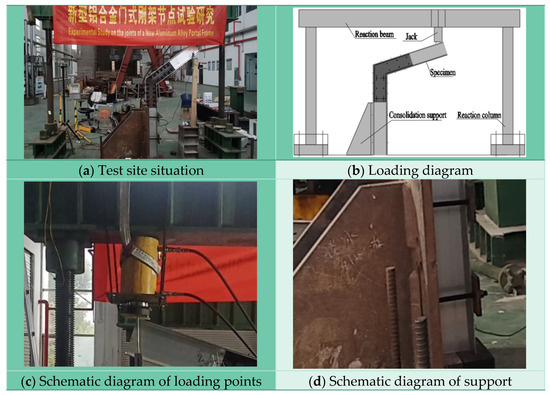
Figure 3.
Schematic diagram of test.
During the experiment, the strain and displacement data of the specimen at each moment are recorded using a data acquisition instrument, and the positions of each measuring point are shown in Figure 4. To obtain the strain variation pattern of H-type aluminum alloy beams and C-type channel steel connections under vertical load, a total of 10 sets of strain gauges were set at different parts of the cross-section, as shown in Figure 4a. Among them, strain gauges 1–5 are arranged on the cross-section of aluminum alloy beams, and gauges 6–10 are arranged on channel steel connectors. The No.1 strain gauge is arranged on the upper flange of the aluminum alloy beam, the 2nd, 3rd, and 4th are, respectively, arranged on the beam web from top to bottom, and the 5th is arranged on the lower flange of the aluminum alloy beam. Strain gauges 6 and 10 are, respectively, arranged on the upper and lower flanges on the left side of the channel steel connection, while gauges 7, 8, and 9 are evenly arranged on the web plate of the channel steel connection. The full cross-section strain changes in aluminum alloy beams and channel steel connections are monitored and recorded during the loading cycle using 10 strain gauges.
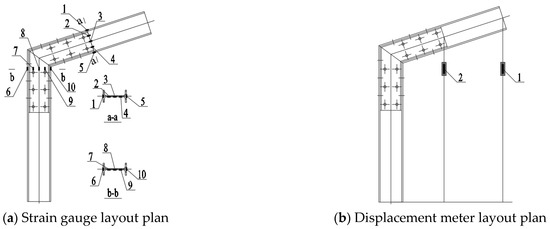
Figure 4.
Schematic diagram of measurement point layout.
Two displacement meters are, respectively, arranged at the time loading point and the end of the channel steel connection, as shown in Figure 4b. The No. 1 displacement meter is set on the end side of the aluminum alloy beam flange to record the displacement changes at the end points of the aluminum alloy beam. The No. 2 displacement meter is set on the end side of the channel steel connector to record the displacement changes at the end of the channel steel connector.
2.3. Material Property Test
The H-shaped I-beam of the test piece is made of 6061-T6 [19,20] aluminum alloy profile, and the double groove connector is made of Q235 steel. Samples from the same batch of aluminum and steel used in the test components are obtained and processed into standard specimens for material properties testing [21], as shown in Figure 5a. The main length of the material test piece is 250 mm, with both ends being 55 mm and 25 mm in length and width, and the middle section being 90 mm and 15 mm in length and width, respectively. The two ends and middle section are transitioned through a circular arc with a radius of 36 mm. The dimensions of the test piece are shown in Figure 5b. The material testing tensile machine tightly clamps the two ends of the material test piece, and then begins to apply axial tension, as shown in Figure 5c. The failure mode of the specimens is shown in Figure 5d, and all of them show tensile failure of the middle section. The results of the material properties test are summarized in Table 2.
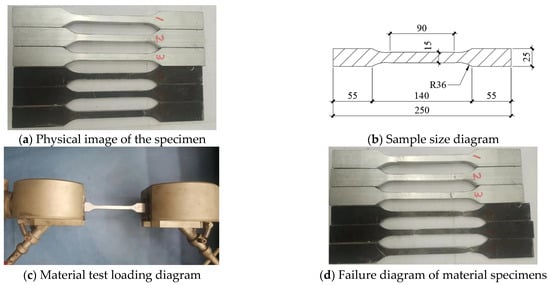
Figure 5.
Schematic diagram of material properties test.

Table 2.
Material test results.
3. Analysis of Test Results
3.1. Failure Characteristics
For beam-column joints with different bolt diameters, the failure state of the bolt hole wall needs to be focused on. Therefore, the bolts were removed after the specimen failed, and the state of the bolt hole wall is shown in Figure 6. When the bolt diameter is 8 mm, there is a significant extrusion deformation on the hole wall. When the bolt diameter is 14 mm, some bolt hole walls show slight compression deformation, while some hole walls show no significant compression. The bolt diameter increased to 20 mm, and the bolt hole walls remained intact without obvious signs of compression. From the above analysis, it can be seen that as the diameter of the bolt increases, the extrusion area of the bolt hole wall increases, and the extrusion deformation of the hole wall gradually decreases.

Figure 6.
Failure modes of different bolt diameters.
The failure modes of beam-column joint specimens with different arch angles are summarized in Figure 7. From this figure, it can be seen that the failure modes of the beam-column joint specimens are basically consistent at different arch angles. As the vertical load increases, the bending moment at the corner of the aluminum alloy portal frame beam-column joint gradually increases, causing buckling failure of the outer flange corner of the double groove connection, and is accompanied by an increase in the gap between the aluminum alloy beam flanges.

Figure 7.
Failure modes from different angles.
3.2. Strain Curve
In order to investigate the variation law of the full section strain of aluminum alloy beams and double groove connectors during vertical load loading, the loading cycle was divided into five specimen joints, and the strain distribution status of each joint section was extracted, as shown in Figure 8. Observing the strain graph curves at various time points, the observations made are as follows:
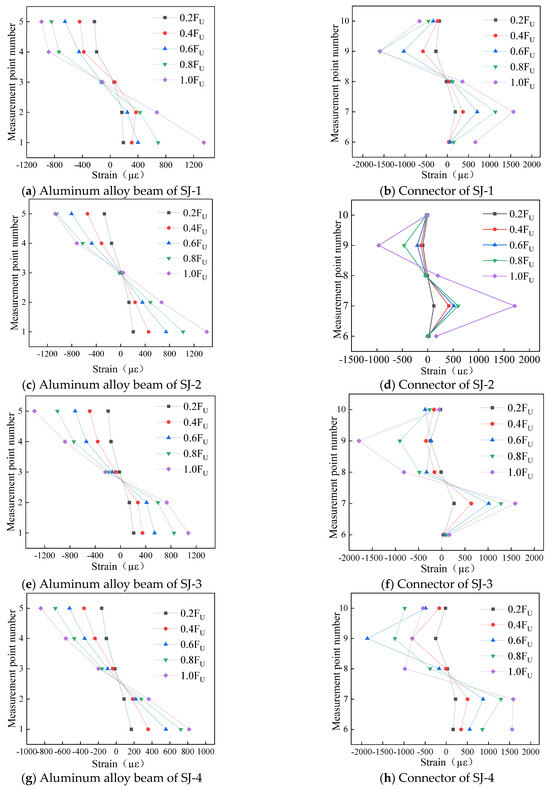
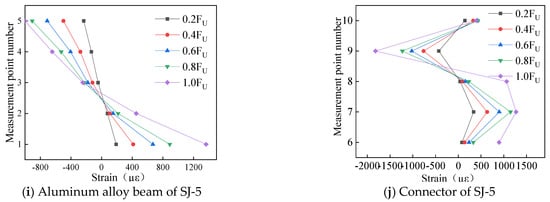
Figure 8.
Schematic diagram of strain distribution.
- (1)
- The cross-sectional strain distribution of aluminum alloy beams and channel steel connectors of each specimen is basically consistent, which is due to the similar structural forms and consistent loading methods of each joint specimen;
- (2)
- The strain distribution of aluminum alloy beams is similar to that of composite I-shaped sections under bending moment, showing a general pattern of larger strain on the upper and lower flanges and smaller strain on the web;
- (3)
- The maximum strain of the channel steel connection occurs at the junction of the web and the upper and lower flanges, with the strain values of the upper and lower flanges in the middle and the strain in the middle of the web being the smallest.
The strain distribution of aluminum alloy beams basically indicates that the specimen mainly bears the action of bending moment under vertical load, and the position of strain 0 is not far below the center point of the section, indicating that the component simultaneously bears the action of shear force, but the shear force is relatively small. By analyzing the strain distribution pattern of double groove connectors, it can be concluded that the web of the double groove connector is responsible for transmitting most of the bending moment, while the flange transmits a small portion of the bending moment. Therefore, in joint design, the thickness of the web plate of the double groove connection should be appropriately increased.
3.3. Load–Displacement Curve
Based on the analysis factors of different bolt diameters and arch angles, the load−displacement curves of the specimens were summarized and compared, as shown in Figure 9. The load−displacement curve of aluminum alloy portal frame beam-column joints under vertical load mainly includes three stages: elastic stage, yield stage, and degradation stage. A detailed analysis of the load−displacement curves for different bolt diameters and arch angles based on three stages is conducted.
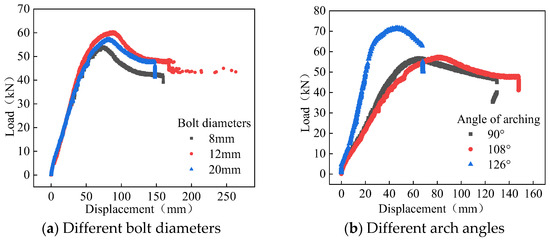
Figure 9.
Load−displacement curve.
The load−displacement curves of different diameters are shown in Figure 9a. In the elastic stage, the load–displacement curves of different bolt diameters are basically consistent, and the yield load is close to 50 kN. After entering the plastic stage, the load–displacement curves of different diameters begin to show differences, meaning that the ultimate load first increases and then decreases, and the ultimate displacement is basically the same. Among them, the ultimate load is 52 kN for a diameter of 8 mm, 63 kN for a diameter of 12 mm, and 58 kN for a diameter of 20 mm. This is because as the diameter of the bolt increases, the shear-bearing capacity of the bolt group increases, resulting in an increase in the bearing capacity of the specimen. But, when the bearing capacity of the bolt group is greater than the bearing capacity of the net section of the rod, increasing the bolt diameter will not cause an increase in the bearing capacity of the specimen, but will instead cause a decrease in the net section area, leading to a downward trend in the bearing capacity of the specimen. In the degradation stage, the downward trend observed in load–displacement curves with different diameters is basically consistent, and the differences between the three curves are the same as those in the plastic stage, so we will not elaborate on them here.
The load−displacement curves for different arch angles are summarized in Figure 9b. When the arch angle increases from 90 degrees to 108 degrees, the load–displacement curve basically matches in the elastic stage, and there is a slight difference between the plastic stage and the degradation stage. When the arch angle increases to 126 degrees, there are significant differences in the load–displacement curve in the elastic stage, yield joint, and degradation stage, that is, the stiffness and ultimate bearing capacity of the specimen under vertical load significantly increase, with an increase of 30% in ultimate bearing capacity and a decrease of 35% in ultimate displacement. The reason for the above phenomenon is that when the arch angle increases to a certain extent, the force on the beam under vertical load changes from mainly bending to compression bending. Axial pressure can improve the bending performance of the beam to a certain extent, thereby reducing the vertical displacement caused by bending moment.
4. Establishment of Numerical Models
4.1. Numerical Model
Based on the geometric symmetry of aluminum alloy portal frame beam-column joints, a 1/2 joint model was established in ABAQUS with the cross-section of the center line of the aluminum alloy I-beam web as the symmetry plane, as shown in Figure 10a. The geometric dimensions of the numerical model are strictly consistent with the experimental components, in order to verify the effectiveness of the model compared with the experimental results. Each component adopts an eight-joint six-sided linear reduced integral element (C3D8R element). The grid size of aluminum alloy beams and connectors is 5 mm, the grid size of bolts is 2 mm, and the total number of grids in the node model is 65,000. During the modeling process, aluminum alloy beams, double groove connectors, and bolts will be divided into different component groups to facilitate model calculation and query of later calculation results.
Figure 10.
Joint numerical model.
The division of finite element mesh directly determines the accuracy and speed of calculation. The mesh division of this model is shown in Figure 10b. According to the structural and stress characteristics of the beam-column joints, the grid density should be appropriately increased at the corners and bolt connections of the model, and relatively small grid densities can be used for grid division at other positions, but it should be ensured that no less than two segments of grid are divided along the thickness direction.
When conducting numerical simulations, the selection of material models will directly determine the effectiveness of the calculation results. In the numerical model of beams and columns, there are mainly two types of materials, namely, aluminum alloy and steel. Based on the results of material properties tests, the Ramberg–Osgood model was used for aluminum alloy [22,23], and the double-line model was used for steel, as shown in Figure 11.
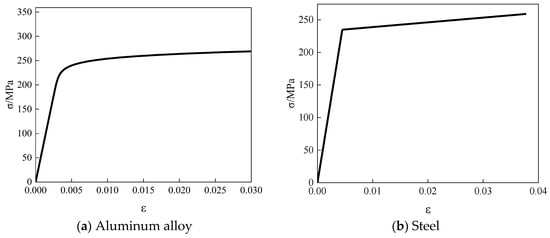
Figure 11.
Material models.
According to the loading scheme and constraint conditions of the test specimen, the boundary conditions of this model mainly include three aspects, namely, fixed end constraints, symmetric constraints, and contact settings [24]. The fixed end constraint is consistent with the experiment, that is, a consolidation constraint is set at the bottom of the column component of the beam-column joint specimen to constrain the displacement and rotation of the column bottom, as shown in Figure 12a. According to the geometric symmetry of the joint specimen, symmetric constraints are set on the central section of the web, as shown in Figure 12b. Relative sliding occurs between different components of the specimen, so it is necessary to set up a “limited slip” contact. The bolt rod and bolt hole wall only need to be set up with a normal “hard contact”, while other contacts need to consider friction, that is, set a tangential “Coulomb friction” with a friction coefficient of 0.3. The coupling point is set at the center of the section at the loading end, which is used to apply the load, as shown in Figure 12c.
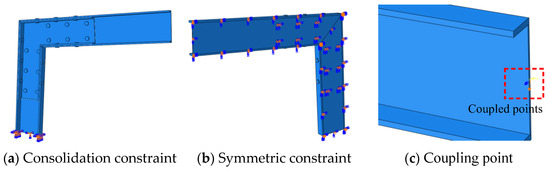
Figure 12.
Boundary conditions.
4.2. Model Validation
To verify the effectiveness of the numerical model, test specimens SJ-1 and SJ-5 were simulated, and the comparison of load–displacement curves is shown in Figure 13. From this figure, it can be seen that the load–displacement curves of the experiment and numerical simulation are relatively consistent, especially the variation law of the second type curve is basically consistent. The ultimate loads and displacements for experiments and numerical simulations are listed in Table 3. The comparison results show that the ultimate load error between the experiment and numerical simulation is only 4.77%, and the ultimate displacement error is only 4.01%. Obviously, this type of numerical model can be used for parameter analysis of aluminum alloy portal frame beam-column joints.
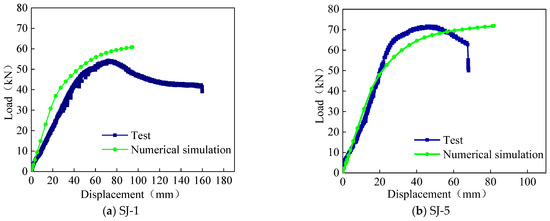
Figure 13.
Comparison of load–displacement curves.

Table 3.
Comparison of test and numerical simulation results.
5. Parameterized Analysis of Numerical Simulation
5.1. Basic Model Parameters
Before conducting numerical simulation parameter analysis, the basic model information will be introduced, and subsequent models will adjust the response parameters based on the different analysis parameters of the basic model. The cross-sectional dimensions of the H-type aluminum alloy rod in the basic model are H200 × 100 × 8 × 10, the cross-sectional dimensions of the groove type connector are 2C180 × 46 × 5 × 10, the arch angle is 96 degrees, the bolt grade is 10.9, and the bolt diameter is 20 mm. The H-type aluminum alloy rod is made of 6061-T6 aluminum alloy (from China) profile, and the channel steel connector is made of Q235 steel (from China). On the basis of the basic model, a numerical analysis model is established for different bolt diameters, arch angles, and thickness of groove connectors, in order to analyze the influence of these factors on the mechanical properties of aluminum alloy portal frame beam-column joints. In the basic model, the load forms are divided into three types, namely, vertical concentrated force and horizontal concentrated force, which are used to analyze the force characteristics and deformation mechanism of this type of joint under the action of out-of-plane vertical load and in-plane horizontal load.
5.2. Mechanical Properties under Vertical Loads
The mechanical performance of aluminum alloy portal frame beam-column joints under vertical load was studied through experiments with different bolt diameters and arch angles. Here, numerical simulation was used to supplement and analyze the influence of arch angle and channel steel wall thickness on the vertical performance of this type of joint. The vertical load–displacement curves for different arch angles and channel steel wall thicknesses are summarized in Figure 14 and Table 4 and Table 5:
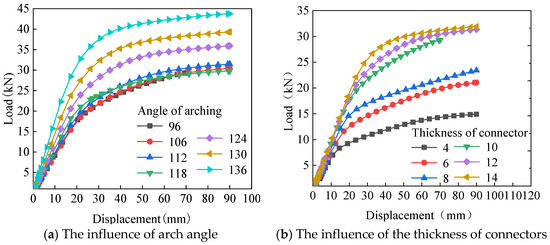
Figure 14.
Vertical load–displacement curve.

Table 4.
Key results of different arch angles under vertical loads.

Table 5.
Key results of wall thickness of different connections under vertical load.
- (1)
- As the arch angle increases (from 96 degrees to 136 degrees), there is no obvious change in yield displacement and ultimate displacement, and the change amplitude is small. The yield load and ultimate load gradually increase (2.04 times and 1.90 times, respectively), and the failure characteristics gradually change from groove type connection failure to H-type aluminum alloy rod failure;
- (2)
- As the wall thickness of the groove type connector increases from 4 mm to 14 mm, the yield displacement and yield load increase by 2.44 and 3.96 times, respectively, and the ultimate displacement and ultimate load increase by 1.8 and 2.46 times, respectively. The failure characteristic changes from the groove type connector failure to the H-type aluminum alloy rod failure;
- (3)
- As the arch angle increases, there is a gradual increase in vertical bearing capacity of beam-column joints. As the wall thickness of groove connectors increases, the increase in vertical bearing capacity of beam-column joints is gradually reduced.
The yield stress state and ultimate stress state of aluminum alloy portal frame beam-column joints under vertical load at different arch angles are shown in Figure 15. When the beam-column joint begins to yield, as the arch angle increases, the stress of the H-type aluminum alloy rod gradually increases, and the stress of the bolt changes without obvious regularity. The stress of the groove type connection remains basically unchanged. When the beam-column joint reaches the limit state, with an increase in the arch angle, the stress of the H-type aluminum alloy beam and the groove connection remains basically unchanged, and the stress change in the bolts shows no obvious pattern.
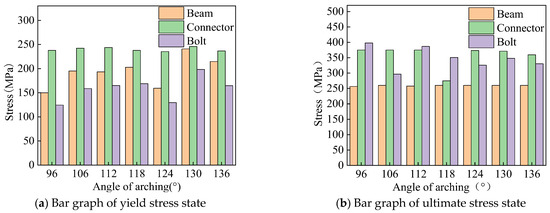
Figure 15.
Stress bar chart of different arch angles under vertical load.
The yield stress state and ultimate stress state of aluminum alloy portal frame beam-column joints under vertical load are shown in Figure 16, when the wall thickness of different groove connectors is different. As the wall thickness of the groove type connector increases, the stress of the H-type aluminum alloy rod gradually increases when the aluminum alloy portal frame beam-column joint yields. The stress of the groove type connector remains unchanged, and the stress of the bolt significantly increases. As the wall thickness of the groove type connector increases, when the beam-column joint reaches the limit state, the stress of the H-type aluminum alloy rod remains unchanged. The stress of the groove type connector has no obvious change pattern, and the change amplitude is small, and the stress of the bolt shows a trend of increasing first and then decreasing.
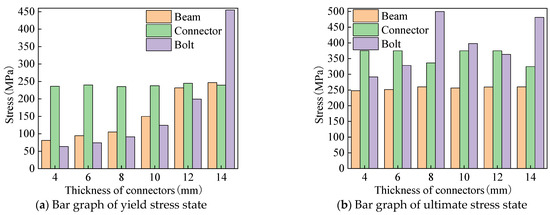
Figure 16.
Stress bar chart of different thicknesses of connectors under vertical load.
5.3. Mechanical Properties under Horizontal Loads
In aluminum alloy portal frames, beam-column joints mainly bear vertical and horizontal loads. The mechanical performance of this type of joint under vertical load has been previously explored, and now, we are conducting research on its mechanical performance under horizontal load. The influence of different bolt diameters, arch angles, and wall thicknesses of groove connectors on the load-bearing performance of aluminum alloy portal frame beam-column joints under horizontal load are summarized in Figure 17 and Table 6, Table 7 and Table 8. Through analysis, the conclusions drawn are as follows:
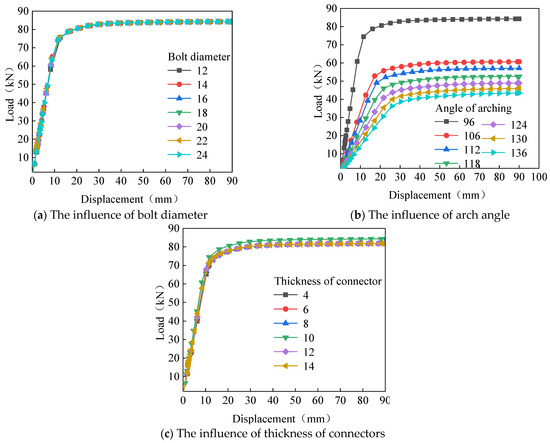
Figure 17.
Horizontal load–displacement curve.

Table 6.
Key results of different bolt diameters under horizontal load.

Table 7.
Key results of different arch angles under horizontal loads.

Table 8.
Key results of wall thickness of different connections under horizontal load.
- (1)
- Under horizontal load, as the bolt diameter increases, there is no significant change in the yield load, yield displacement, ultimate load, and ultimate displacement of the beam-column joint, and the change amplitude is minimal. This is because when the bearing capacity of the bolt group is greater than the bearing capacity of the member section, increasing the bolt diameter does not enhance the horizontal bearing performance.
- (2)
- When the beam-column joint is subjected to horizontal load, as the arch angle increases, the yield and ultimate displacement gradually increase (2.14 times and 2.78 times, respectively), and the yield and ultimate load gradually decrease (58% and 48%, respectively). This is because as the arch angle increases, the axial force generated by the horizontal load gradually decreases and the bending moment gradually increases.
- (3)
- The wall thickness of different groove connectors has little effect on the horizontal load-bearing performance of aluminum alloy portal frame beam-column joints. For instance, as the wall thickness changes, the load–displacement curves basically overlap, and the changes in yield displacement, yield load, ultimate displacement, and ultimate load are minimal.
- (4)
- Under horizontal loads, the failure mode of joints mainly manifests as beam failure and connector failure under different bolt diameters, arch angles, and connection wall thicknesses.
The yield and ultimate stress states of aluminum alloy portal frame beam-column joints under horizontal load with different bolt diameters are shown in Figure 18. There is no significant difference in the stress of H-type aluminum alloy rods at joint yield and ultimate state, while the stress of bolts at joint yield and ultimate state decreases with an increase in diameter. This is because an increase in bolt diameter will increase the stress area of the bolt, thereby significantly reducing its stress.
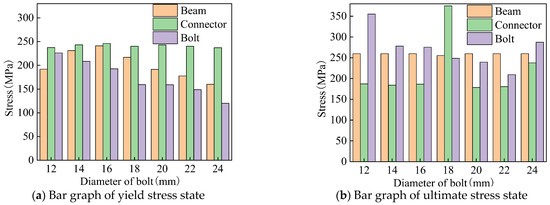
Figure 18.
Stress bar chart of different bolt diameters under horizontal load.
The yield and ultimate stress states of aluminum alloy portal frame beam-column joints under horizontal load at different arch angles are shown in Figure 19. As the arch angle increases, the stress of the H-shaped aluminum alloy beam remains unchanged during joint yielding and failure, the stress of the groove type connector increases first and then remains unchanged, and the stress of the bolts shows a trend of increasing first and then decreasing.
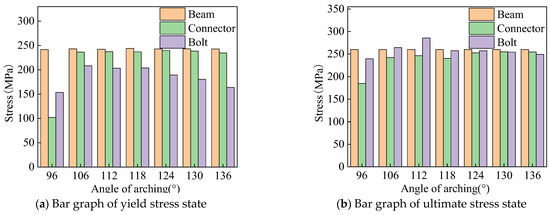
Figure 19.
Stress bar chart of different arch angles under horizontal load.
When the wall thickness of the groove type connector changes, the yield and ultimate stress state changes in the aluminum alloy portal frame beam-column joints under horizontal load are shown in Figure 20. As the wall thickness of the groove connection increases, the stress of the H-type aluminum alloy beam at joint yield gradually increases, but the increase is relatively small. The stress of the groove type connector has no obvious change pattern, and the change amplitude is relatively large when the joint yields, while the change amplitude is relatively small when the joint fails. When the joint yields and fails, the stress of the bolt increases with an increase in the wall thickness of the groove connection, and its variation is significant.
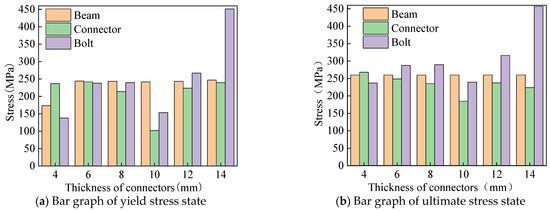
Figure 20.
Stress bar chart of different thicknesses of connectors under horizontal load.
6. Joint Construction Design
6.1. Joint Construction Improvement
Through experiments and numerical analysis of aluminum alloy portal frame beam-column joints, it can be concluded that the main failure feature of the joints is the failure of the web plate at the intersection of the beam-column joints with the groove connectors, as shown in Figure 21. For structures, the connection joints should not be damaged before the components, so it is necessary to take strengthening measures for these types of joints.

Figure 21.
Characteristics of joint structure failure.
According to the characteristics of the damage, structural strengthening measures such as adding partitions can be adopted, as shown in Figure 22. This partition can effectively improve the buckling resistance of the groove type connector’s web plate (out-of-plane), while providing effective support for the flange of the groove type connector, thereby comprehensively improving the load-bearing performance of aluminum alloy portal frame beam-column joints.
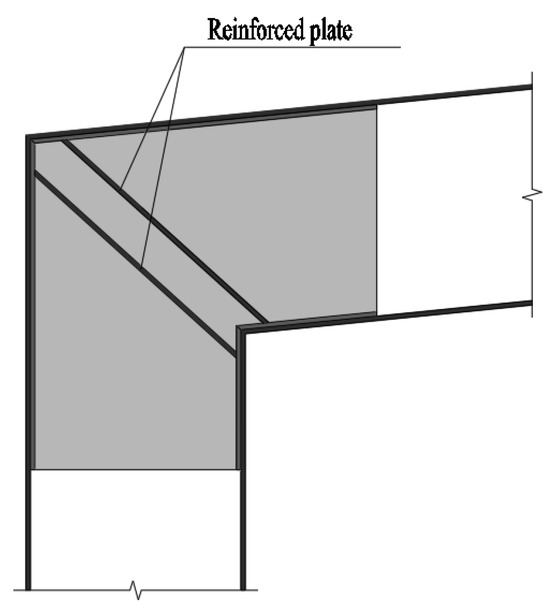
Figure 22.
Strengthening measures for joint.
6.2. Joint Design Method
In order to meet the structural design principle of “strong joints and weak members”, the joint design should meet the principle of not damaging the joint before the component. By analyzing the influence of different bolt diameters on the bearing performance of beam-column joints under vertical and horizontal loads, it can be concluded that when the bearing capacity of the bolt group is greater than that of aluminum alloy members, increasing the bolt diameter has no effect on the bearing performance of the joint [25,26]. Therefore, the bearing capacity of the bolt group only needs to be greater than that of the aluminum alloy rod:
In the formula, n is the number of bolts, d is the diameter of the bolt, t is the thickness of the H-type aluminum alloy rod, fc is the compressive strength of the aluminum alloy bolt connection, fv is the shear strength of the bolt, f is the design strength of the aluminum alloy, and An is the net cross-sectional area of the H-type aluminum alloy rod.
The numerical simulation parameter analysis results for different wall thicknesses of groove connectors indicate that their thickness has a significant impact on the vertical bearing performance of beam-column joints, while their impact on the horizontal bearing performance is relatively small. The bearing capacity of the groove type connector should be greater than that of the H-type aluminum alloy rod. Therefore, the steel model of the groove type connector should ensure that its design strength is greater than the corresponding aluminum alloy rod, and the thicknesses of its web and flange should be greater than those of the aluminum alloy rod [26,27].
7. Conclusions
The aluminum alloy portal frame beam-column joint was considered as the research object, and experiments and numerical analysis were conducted to fully explore the mechanical performance of the joint under vertical and horizontal loads. The main conclusions are as follows:
- (1)
- The experimental results indicate that as the diameter of the bolt increases, the damage situation at the bolt hole diameter of the specimen continues to improve, and the degree of compression at the bolt hole wall gradually decreases. The failure mode of beam-column joints does not change significantly with the change in arch angle, that is, the change in arch angle has no effect on the failure form and location of the specimen.
- (2)
- The experimental results show that the load–displacement curve mainly consists of three stages, namely, the elastic stage, yield stage, and degradation stage. In the elastic stage, the load–displacement curves of different bolt diameters are basically consistent. After entering the plastic stage, the ultimate load first increases and then decreases, and the ultimate displacement is basically consistent.
- (3)
- According to the experiment, there is no significant difference in the load–displacement curve when the arch angle increases from 90 degrees to 108 degrees. When the arch angle increases to 126 degrees, the stiffness and ultimate bearing capacity of the joint under vertical load significantly increase.
- (4)
- As the wall thickness of the groove type connector increases from 4 mm to 14 mm, the vertical yield displacement and yield load increase by 2.44 and 3.96 times, respectively, and the ultimate displacement and ultimate load increase by 1.8 and 2.46 times, respectively.
- (5)
- Under horizontal load, as the diameter of the bolt increases, the yield load, yield displacement, ultimate load, and ultimate displacement of the beam-column joint show no significant changes, and the amplitude of changes is minimal.
- (6)
- When the beam-column joint is subjected to horizontal loads, as the arch angle increases, the yield and ultimate displacement increase by 2.14 times and 2.78 times, respectively, and the yield and ultimate load decrease by 58% and 48%, respectively.
- (7)
- The research results of this article can be used for the design of aluminum alloy portal frames, and a series of studies on the mechanical performance of the overall portal frame structure should be carried out in the future.
Author Contributions
Conceptualization, G.W. and X.L.; methodology, Z.X.; software, Z.X.; validation, G.W., J.P. and C.Z.; formal analysis, Q.C.; investigation, G.W.; resources, X.L.; data curation, Z.X.; writing—original draft preparation, Z.X.; writing—review and editing, Z.X.; visualization, G.W.; supervision, X.L.; project administration, G.W.; funding acquisition, X.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by [Research on a new type of aluminum alloy portal frame structure] grant number [YH2023001] And The APC was funded by [Guangzhou Yuehong Membrane Structure Engineering Co., Ltd.].
Data Availability Statement
Not applicable.
Acknowledgments
This research was financially supported by Guangzhou Yuehong Membrane Structure Engineering Co., Ltd., Guangzhou, China.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Guo, X.; Xiong, Z.; Luo, Y.; Xu, H.; Liang, S. Block tearing and local buckling of aluminum alloy gusset joint plates. KSCE J. Civ. Eng. 2016, 20, 820–831. [Google Scholar] [CrossRef]
- Guo, X.; Xiong, Z.; Luo, Y.; Qiu, L.; Liu, J. Experimental investigation on the semi-rigid behaviour of aluminium alloy gusset joints. Thin-Walled Struct. 2015, 87, 30–40. [Google Scholar] [CrossRef]
- Xiong, Z.; Guo, X.; Luo, Y.; Xu, H. Numerical analysis of aluminium alloy gusset joints subjected to bending moment and axial force. Eng. Struct. 2017, 152, 1–13. [Google Scholar] [CrossRef]
- Guo, X.; Zhu, S.; Liu, X.; Liu, L. Experimental study on hysteretic behavior of aluminum alloy gusset joints. Thin-Walled Struct. 2018, 131, 883–901. [Google Scholar] [CrossRef]
- Ma, H.; Yu, L.; Fan, F.; Yu, Z. Mechanical performance of an improved semi-rigid joint system under bending and axial forces for aluminum single-layer reticulated shells. Thin-Walled Struct. 2019, 142, 322–339. [Google Scholar] [CrossRef]
- Xu, S.; Chen, Z.; Wang, X.; Mazzolani, F.M. Hysteretic out-of-plane behavior of the temcor joint. Thin-Walled Struct. 2015, 94, 585–592. [Google Scholar] [CrossRef]
- Wu, Y.; Liu, H.; Chen, Z.; Liu, Y. Study on low-cycle fatigue performance of aluminum alloy temcor joints. KSCE J. Civ. Eng. 2020, 24, 195–207. [Google Scholar] [CrossRef]
- Wang, G.; Zhao, C.Q.; Ma, J. Experimental and numerical study on the bending performance of an aluminium alloy flower-gusset composite joint. Structures 2021, 33, 2475–2486. [Google Scholar]
- Wang, G.; Zhao, C.Q. Experimental and theoretical study on the bearing capacity of FGC joints for single-layer aluminium alloy lattice shell structures. Structures 2021, 33, 2445–2458. [Google Scholar]
- Hiyama, Y.; Ishikawa, K.; Kato, S. Buckling behaviour of aluminum alloy double layer truss grid using ball joint system. In Proceedings of the IASS-LAS98 Conference; International Association for Shell and Spatial Structure (IASS): Madrid, Spain, 1998; Volume 9. [Google Scholar]
- Liu, H.; Gu, A.; Chen, Z. Mechanical properties and design method of aluminum alloy bolt-sphere Joints. Struct. Eng. Int. 2019, 31, 30–39. [Google Scholar] [CrossRef]
- Liu, H.; Gu, A.; Chen, Z. Tensile properties of aluminum alloy bolt-sphere joints under elevated temperatures. KSCE J. Civ. Eng. 2020, 24, 525–536. [Google Scholar] [CrossRef]
- Shi, G.; Ban, H.; Bai, Y.; Wang, Y.; Luo, C.; Shi, Y. A novel cast aluminum joint for reticulated shell structures: Experimental study and modeling. Adv. Struct. Eng. 2013, 16, 1047–1059. [Google Scholar] [CrossRef]
- Sugizaki, K.; Kohmura, S. Experimental study on buckling behaviour of a triodetic aluminum space frame. In Proceedings of the International Association for Shell and Space Structure, Tokyo, Japan, 19–22 October 1993; Volume 10, pp. 205–212. [Google Scholar]
- Sugizaki, K.; Kohmura, S. Experimental study on buckling behaviour of a triodetic aluminum space frame: No.2 ultimate bearing strength of a single-layer space frame. In Proceedings of the IASS-ASCE International Symposium, Atlanta, GA, USA, 24–28 April 1994; Volume 4, pp. 478–484. [Google Scholar]
- Yonemaru, K.; Fujisaki, T.; Nakatsuji, T. Development of space truss structure with CFRP. Mater. Struct. 1997, 8, 81–87. [Google Scholar]
- Mazzolani, F.M. 3D aluminium structures. Thin-Walled Struct. 2012, 61, 258–266. [Google Scholar] [CrossRef]
- Wang, Y.; Fan, F.; Lin, S. Experimental investigation on the stability of aluminium alloy 6082 circular tubes in axial compression. Thin-Walled Struct. 2015, 89, 54–66. [Google Scholar] [CrossRef]
- GB/T 50429-2007; Code for Design of Aluminium Structures. General Administration of Quality Supervision, Inspection and Quarantine of the People’s Republic of China: Beijing, China, 2007.
- GB/T 228.1-2010; Metallic Materials—Tensile Testing—Part 1: Method of Test at Room Temperature. General Administration of Quality Supervision, Inspection and Quarantine of the People’s Republic of China: Beijing, China, 2011.
- Sun, Y.; Zhang, K.; Gong, G. Material properties of structural aluminium alloys after exposure to fire. Structures 2023, 55, 2105–2111. [Google Scholar] [CrossRef]
- Ramberg, W.; Osgood, W.R. Description of Stress-Strain Curves by Three Parameters; NACA TN-902; National Advisory Committee for Aeronautics: Washington, DC, USA, 1943. [Google Scholar]
- Sun, Y.; Fu, Z.; Song, Y.; Xia, J. Cross-Sectional Behavior of Aluminum Alloy Channel Section Stub Columns after Exposure to Fire. J. Struct. Eng. 2023, 149, 04023085. [Google Scholar] [CrossRef]
- Zhou, W.; Ai, S.; Chen, M.; Zhang, R.; He, R.; Pei, Y.; Fang, D. Preparation and thermodynamic analysis of the porous ZrO2/(ZrO2 + Ni) functionally graded bolted joint. Compos. Part B Eng. 2015, 82, 13–22. [Google Scholar] [CrossRef]
- Zhou, W.; Zhang, R.; Fang, D. Design and analysis of the porous ZrO2/(ZrO2+Ni) ceramic joint with load bearing-heat insulation integration. Ceram. Int. 2015, 42, 1416–1424. [Google Scholar] [CrossRef]
- Tian, L.; Li, M.; Li, L.; Li, D.; Bai, C. Novel joint for improving the collapse resistance of steel frame structures in column-loss scenarios. Thin-Walled Struct. 2023, 182, 110219. [Google Scholar] [CrossRef]
- Yang, Y.; Lin, B.; Zhang, W. Experimental and numerical investigation of an arch–beam joint for an arch bridge. Arch. Civ. Mech. Eng. 2023, 23, 101. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).