The Generation of the Target Aftershock Spectrum Based on the Conditional Mean Spectrum of Aftershocks
Abstract
:1. Introduction
2. The Target Aftershock Spectrum
3. Determination of Aftershock Seismic Parameters
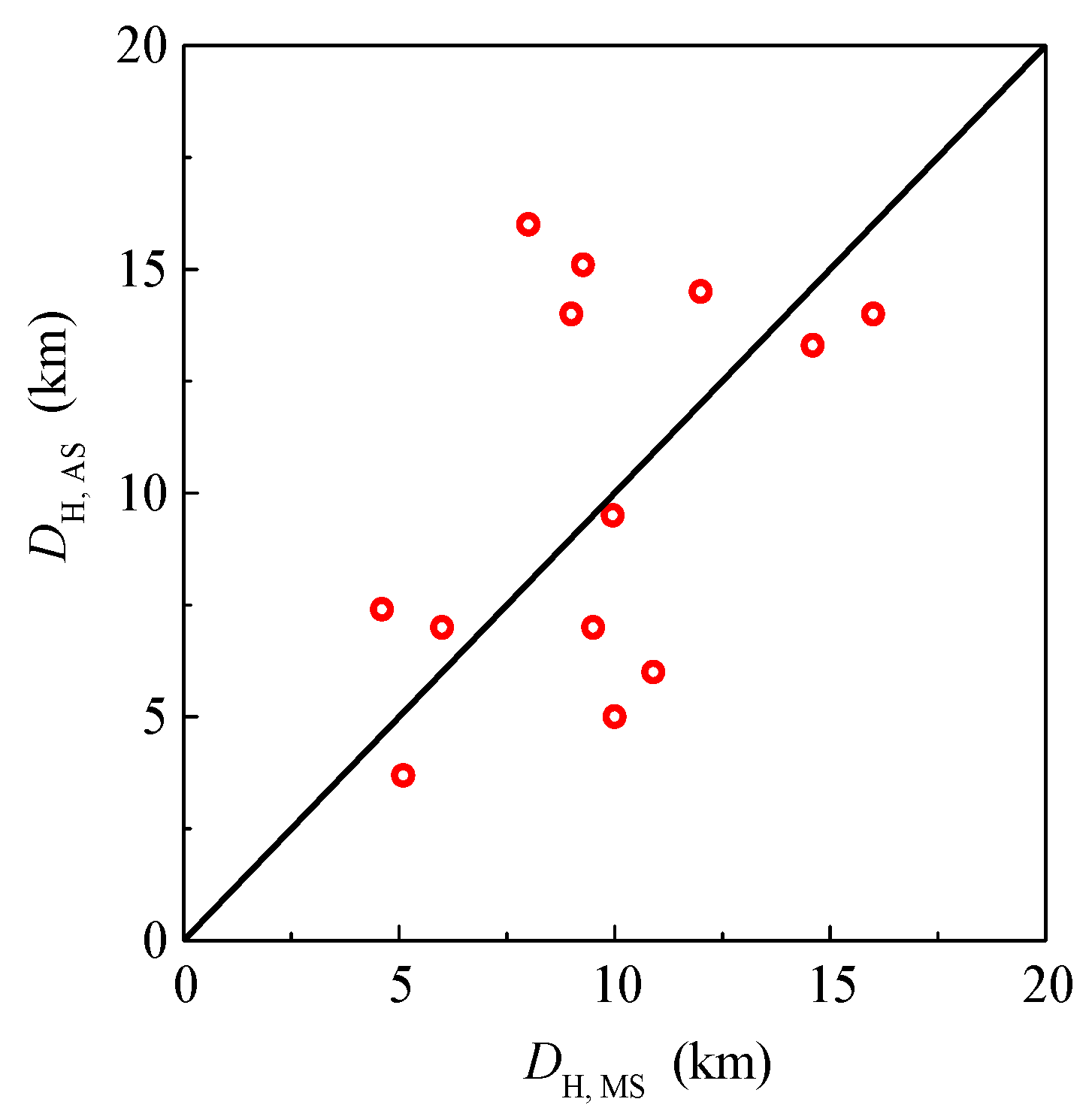
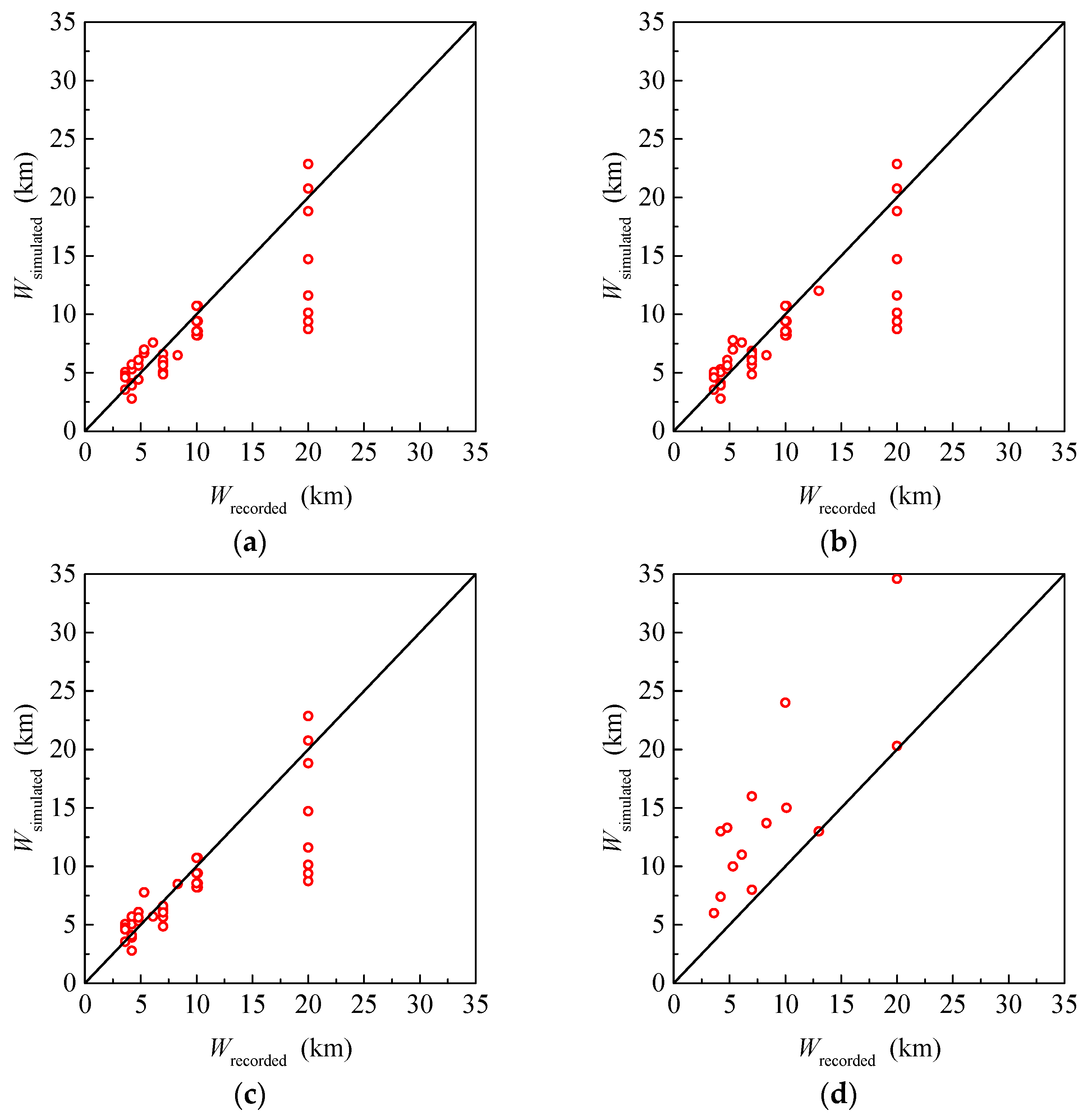
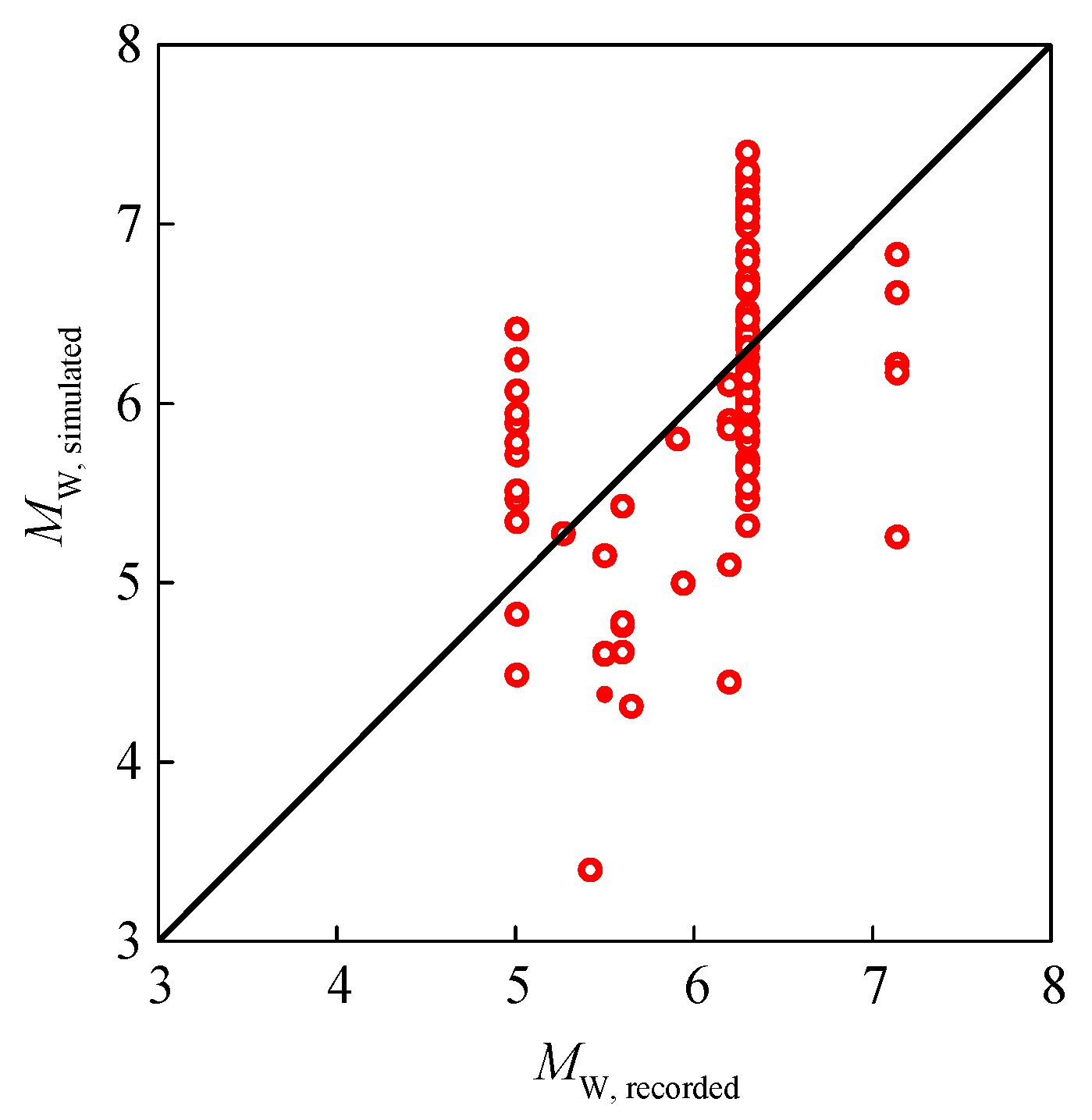
3.1. The Parameters Related to the Source
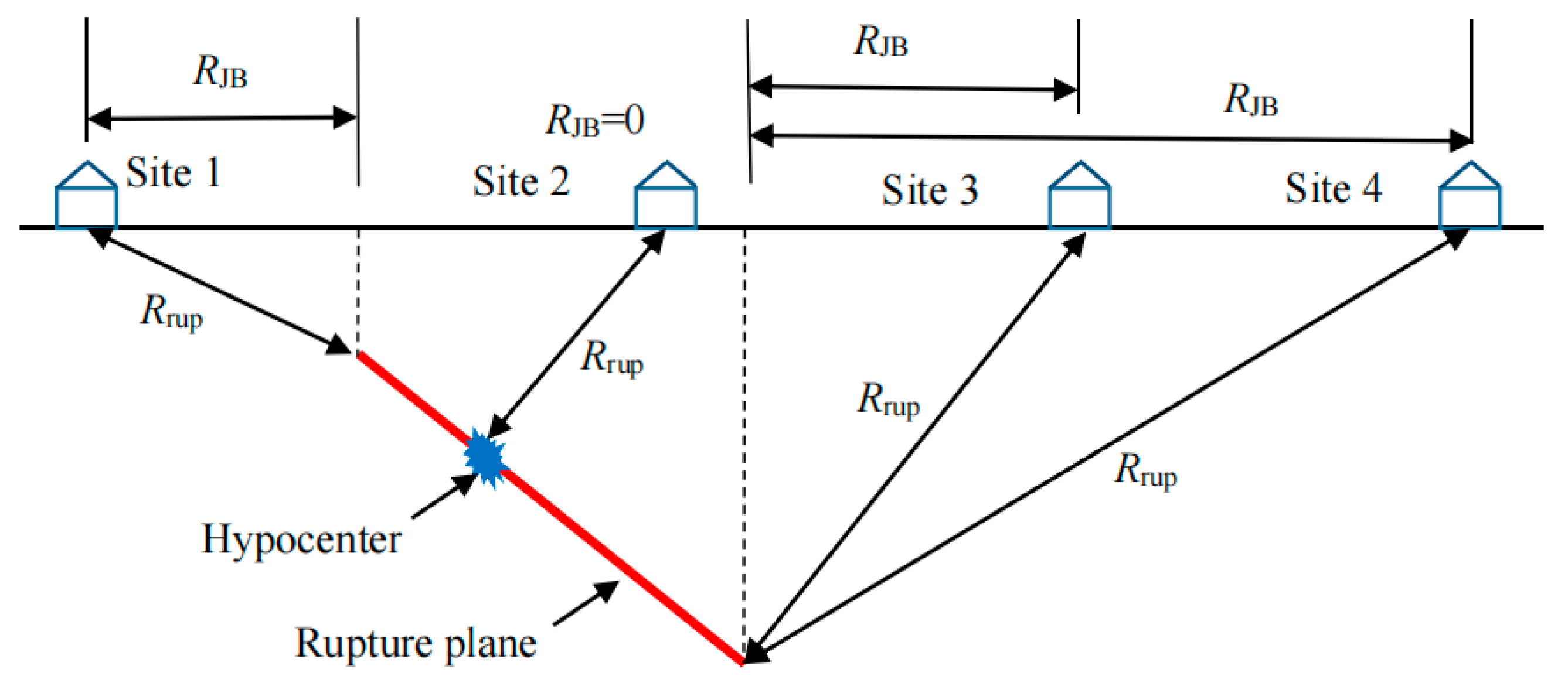
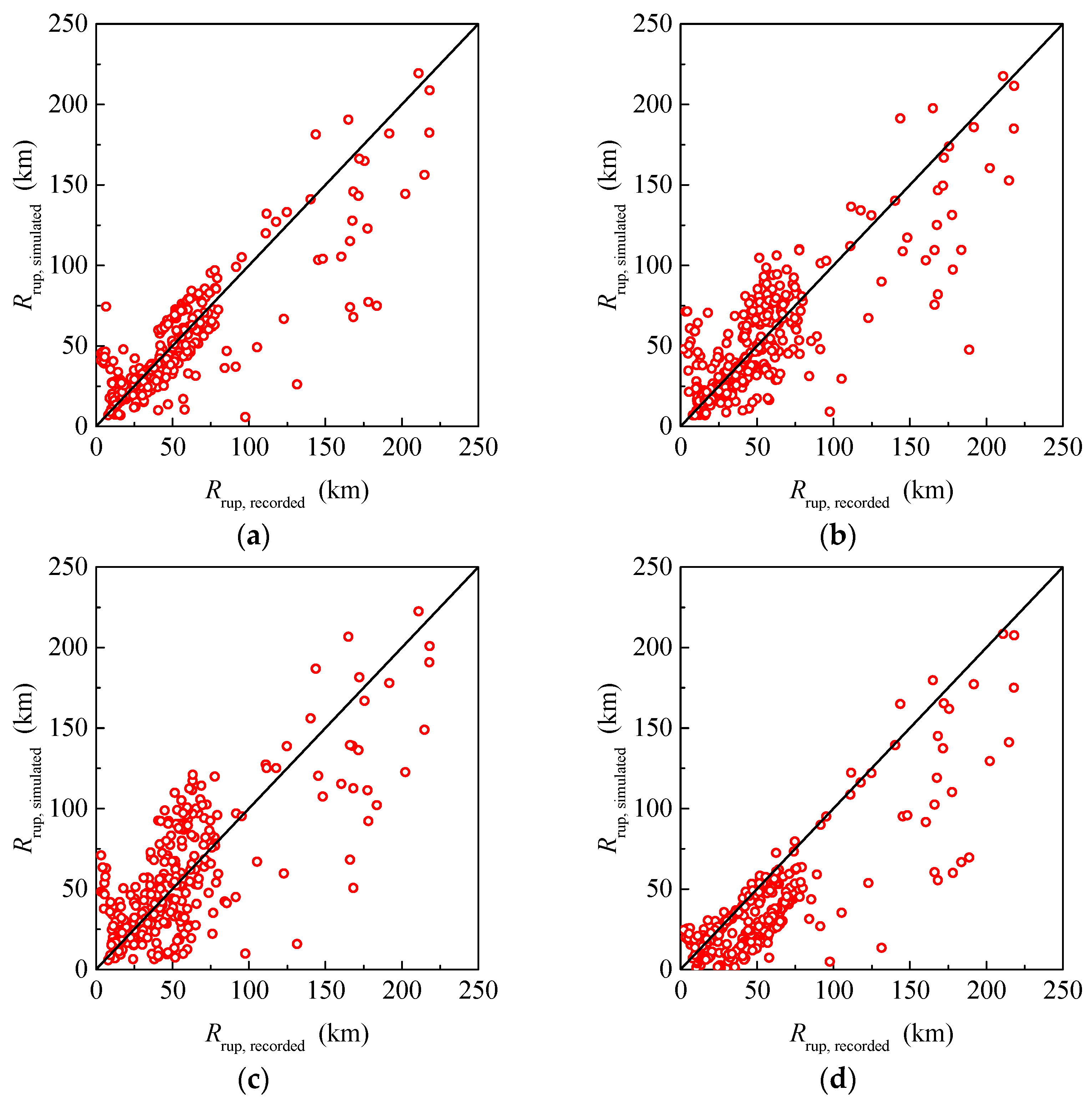
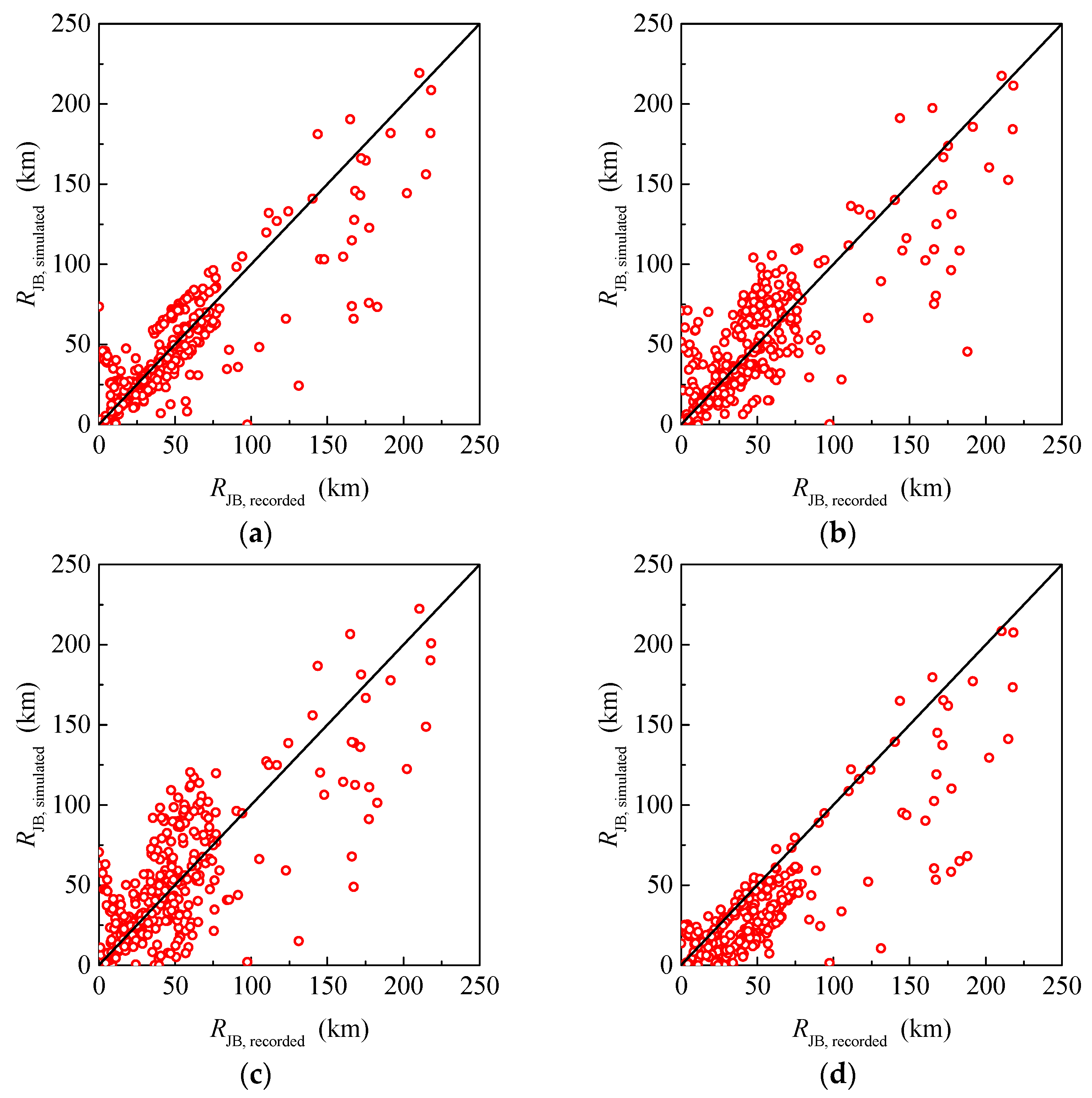
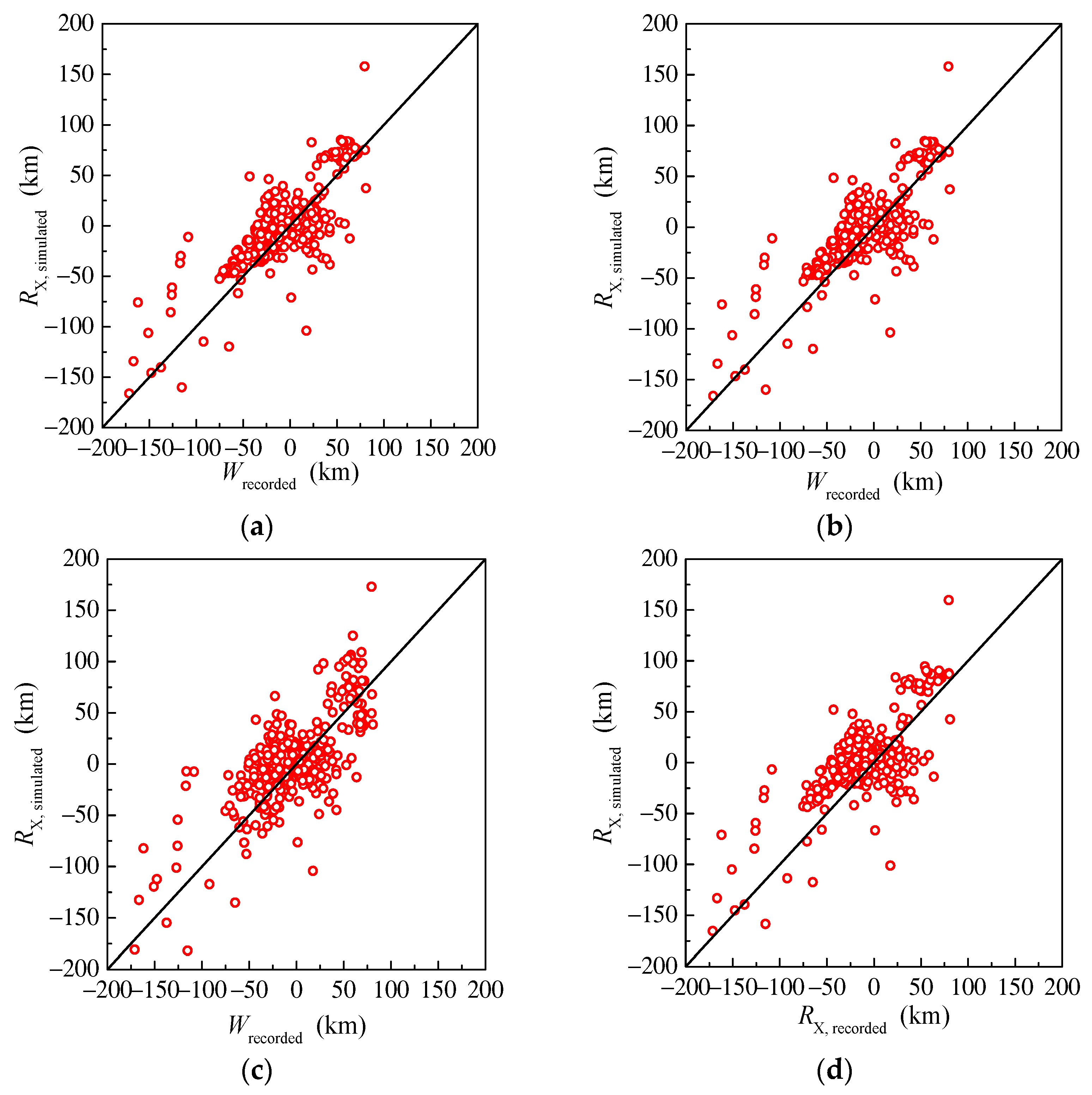
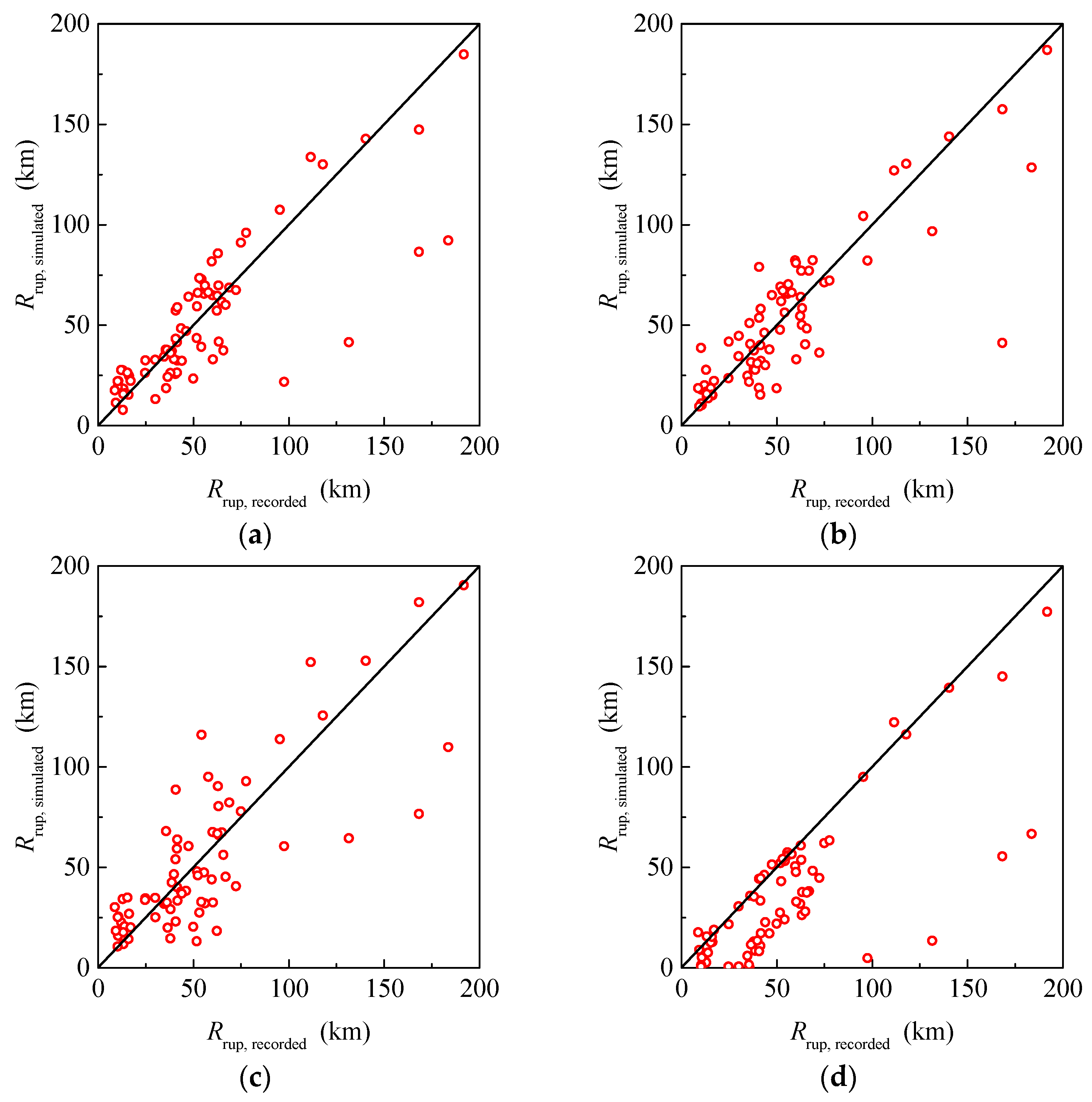
3.2. The Parameters Related to the Distance
3.3. Other Parameters
4. Conditional Mean Spectrum of the Aftershocks
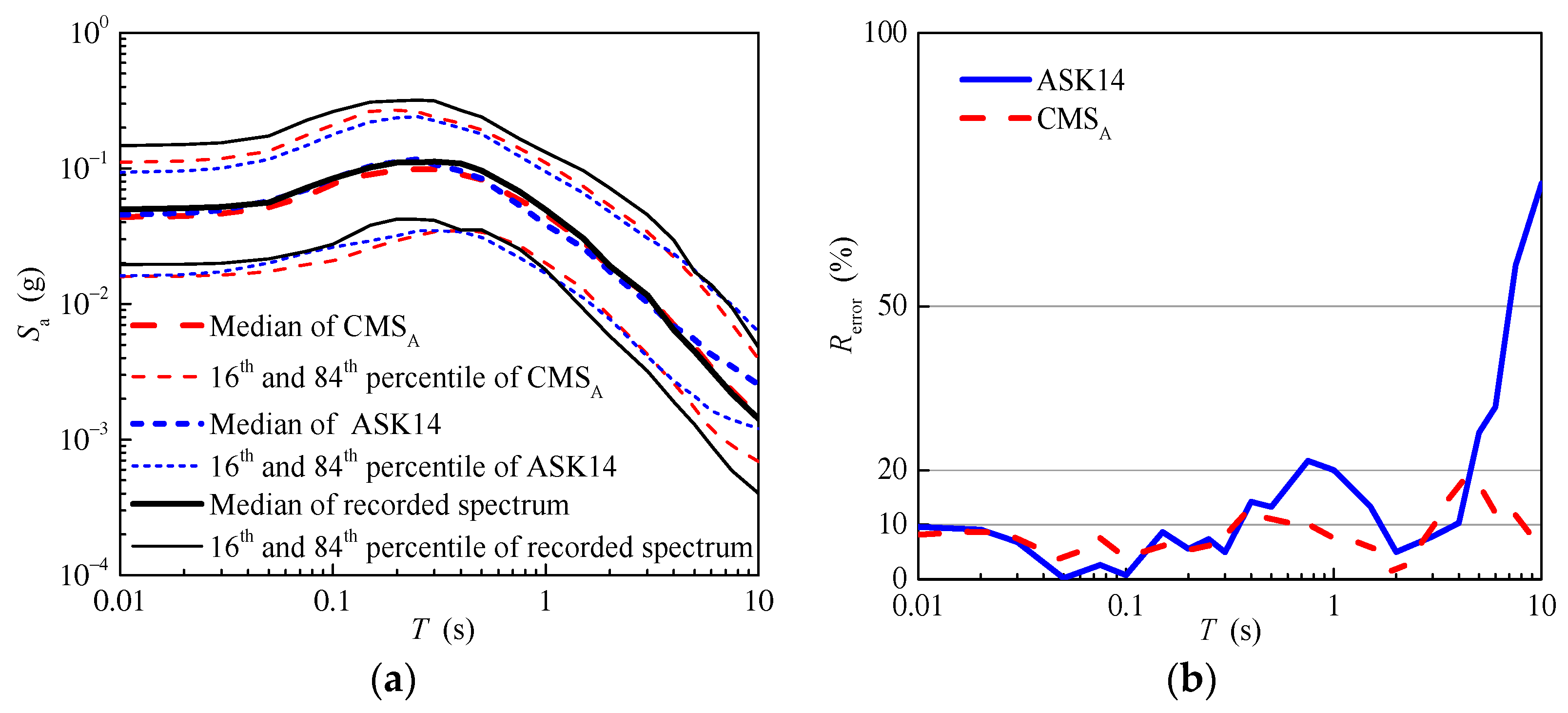
4.1. The Aftershock Magnitude Is Known
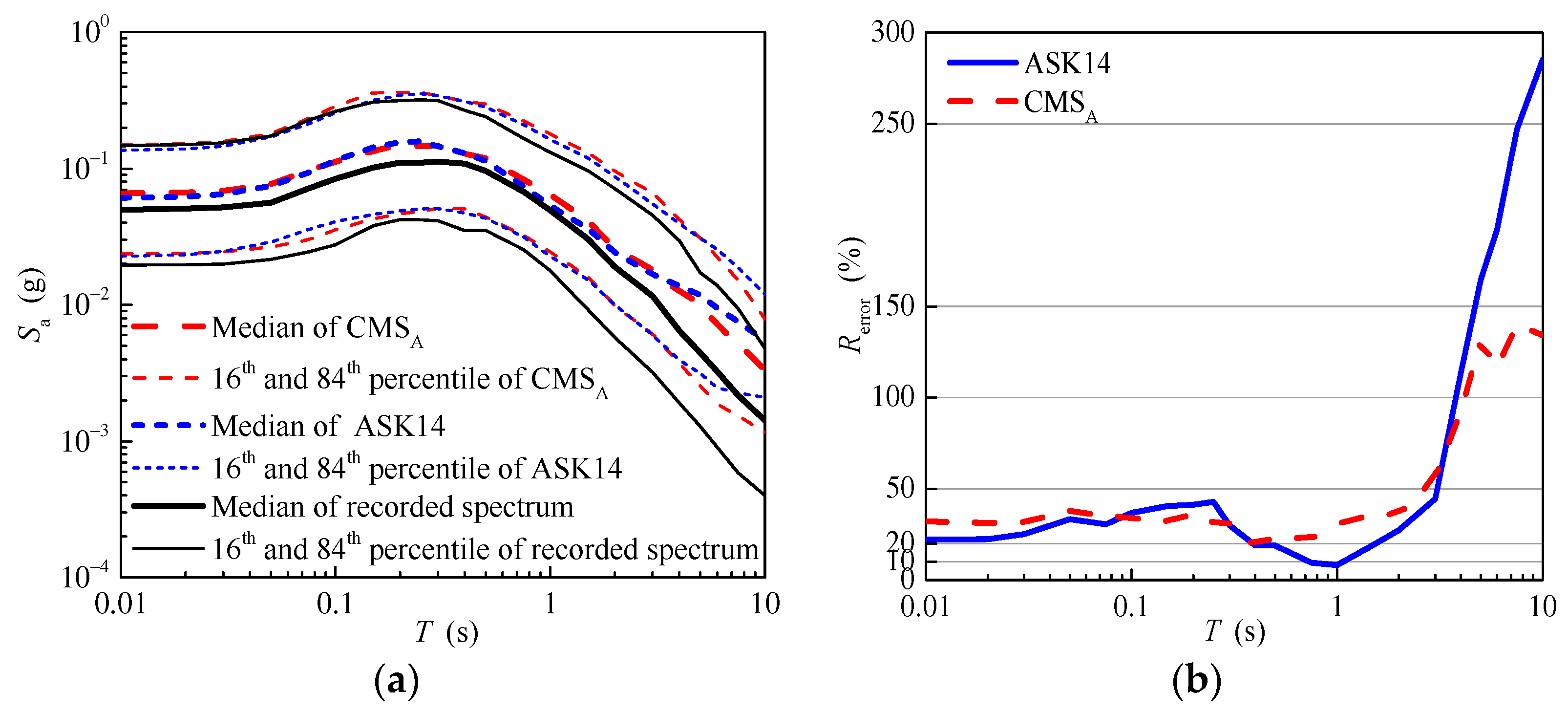
4.1.1. The Simulated Seismic Parameters for the Aftershock Ground Motions
4.1.2. The Response Spectrum of the Aftershock Ground Motions
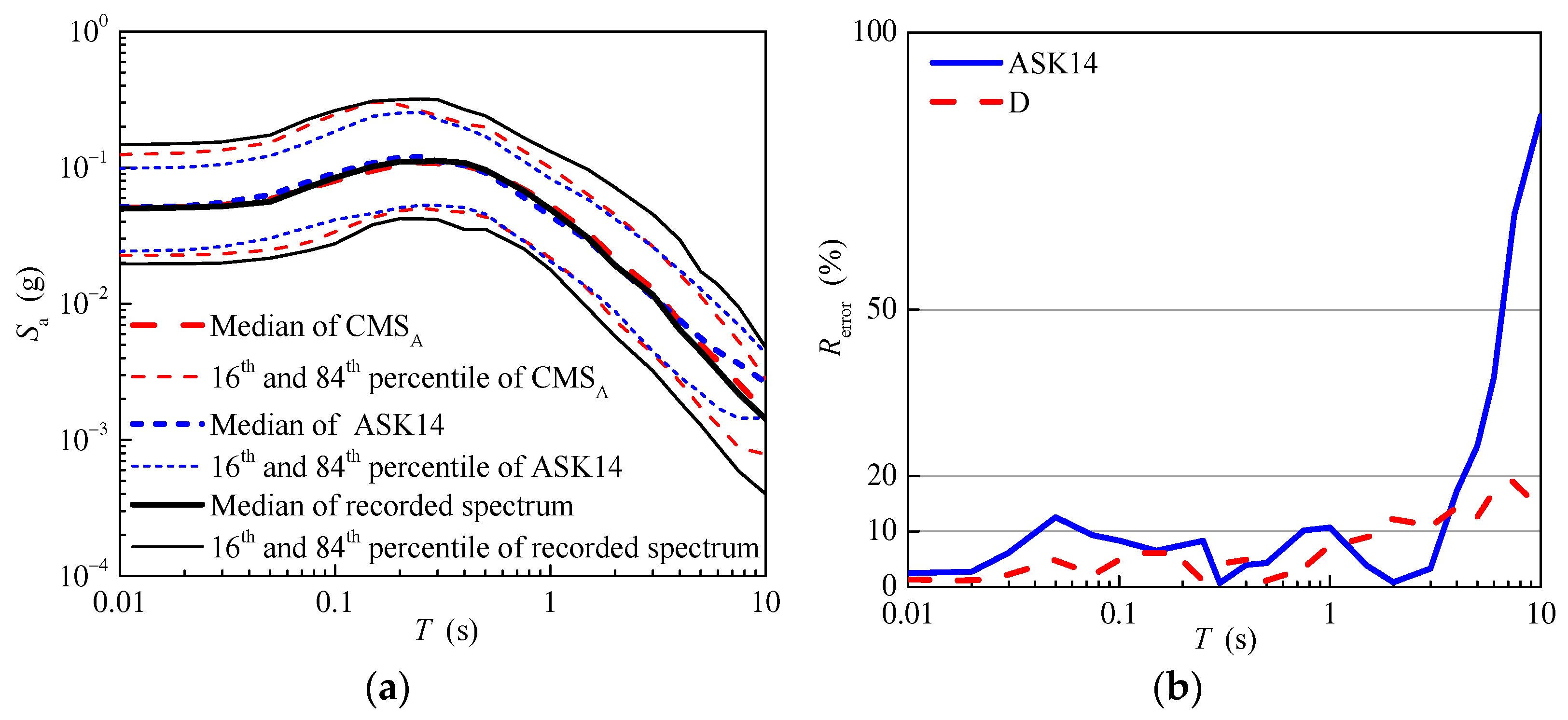
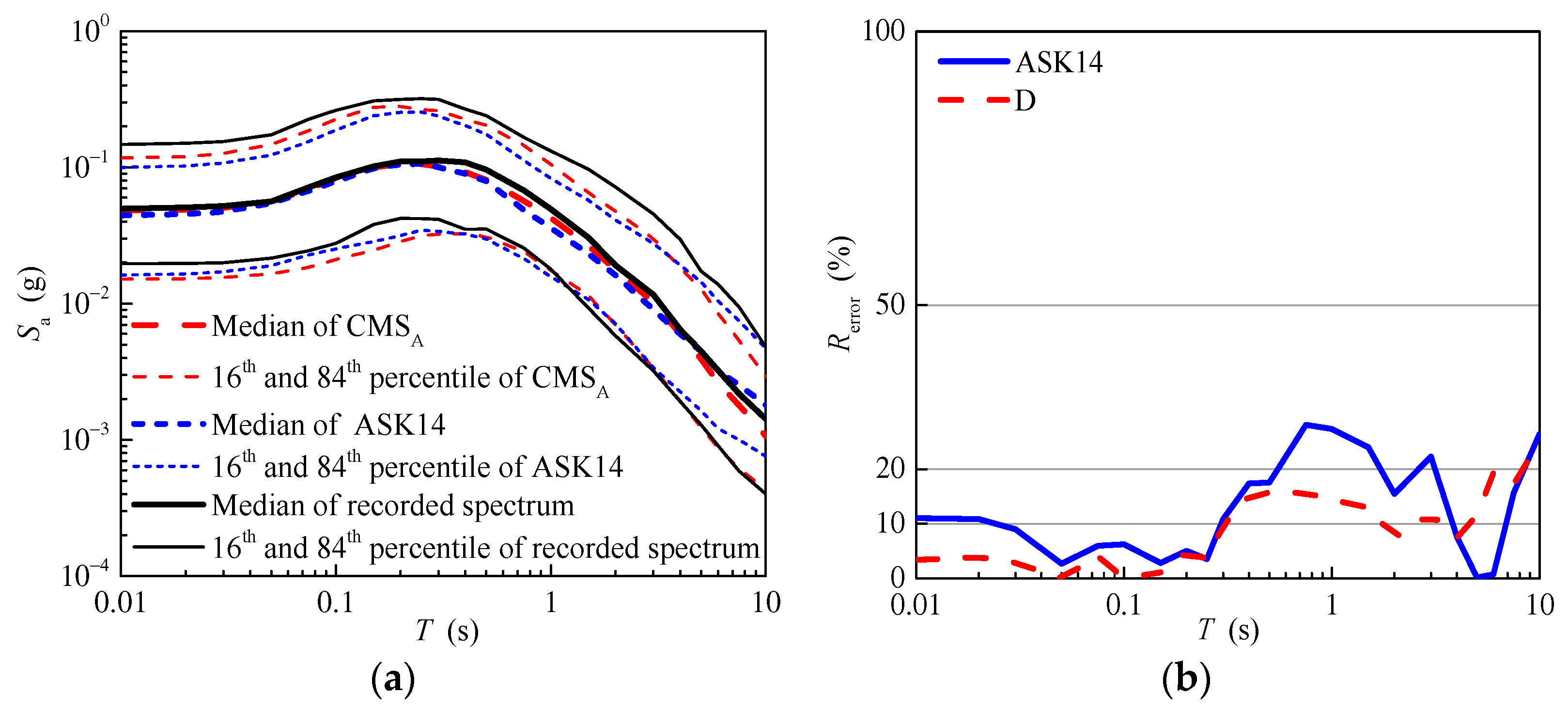
4.2. The Aftershock Magnitude Is Unknown
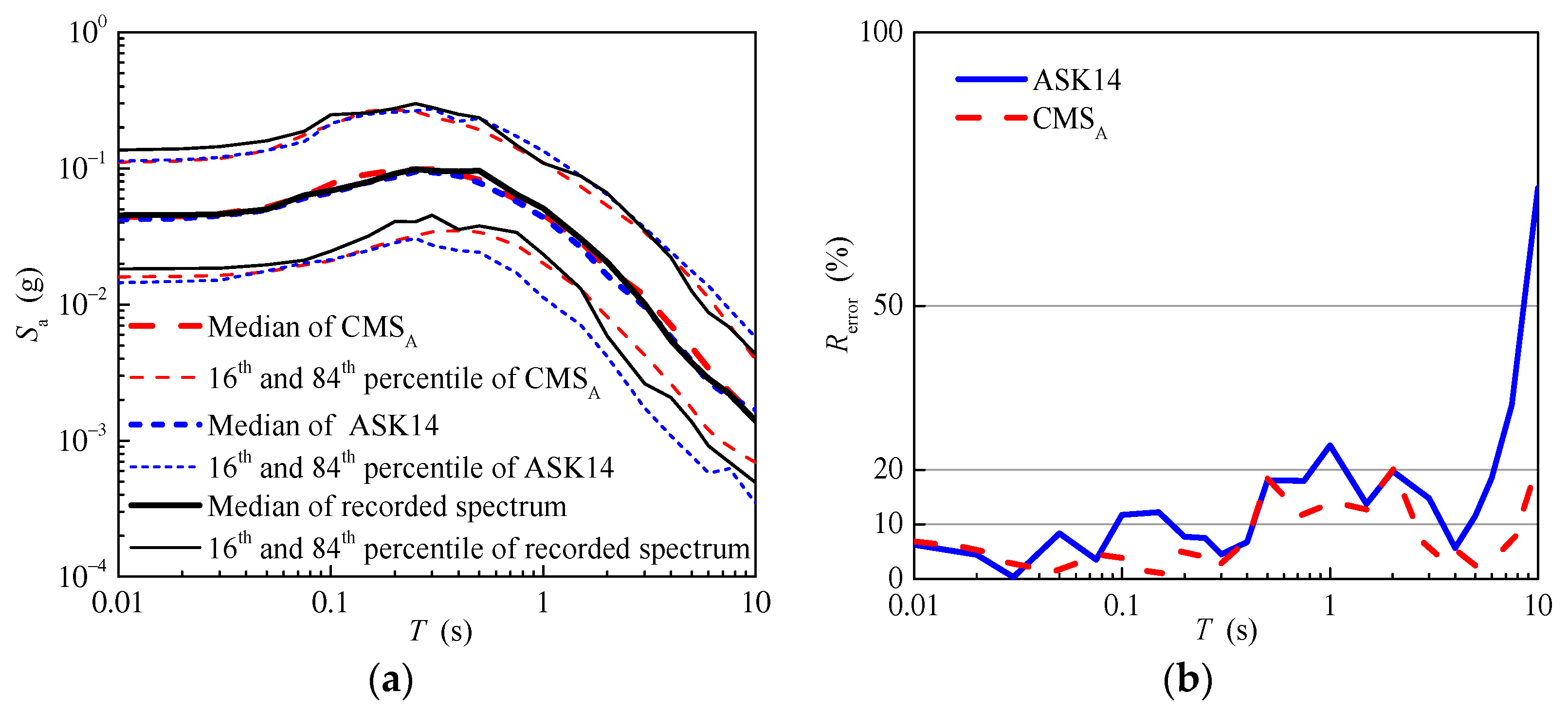
4.2.1. The Simulated Seismic Parameters for the Aftershock Ground Motions
4.2.2. The Response Spectrum of the Aftershock Ground Motions
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
List of Abbreviations and Symbols
| Abbreviations: | (Alphabetically!!) |
| AS | Aftershock |
| ASK14 | GMPE proposed by Abrahamson et al. in 2014 [31] |
| CMSA | Conditional mean spectrum of aftershocks |
| ETAS | Epidemic-type aftershock sequence |
| GMPE | Ground motion prediction equation |
| MS | Main shock |
| Probability density function | |
| Symbols: | (Alphabetically!!) |
| A | Area of the circular region (km2) |
| a, b | Regression coefficients of the rupture length and rupture width |
| Beta function for the corresponding elements 2.2 and 2.3 | |
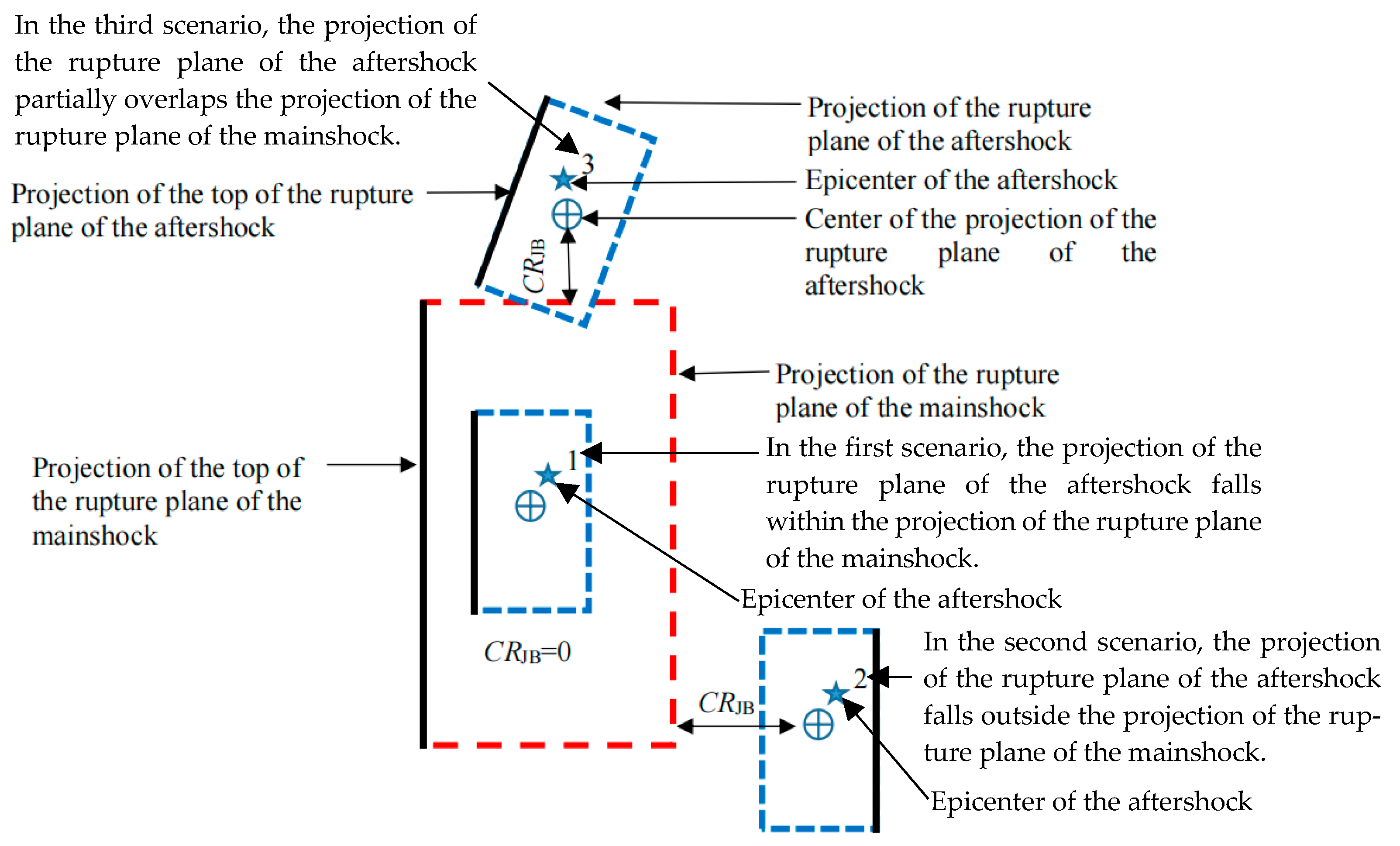
| CRJB | Centroid Joyner–Boore distance |
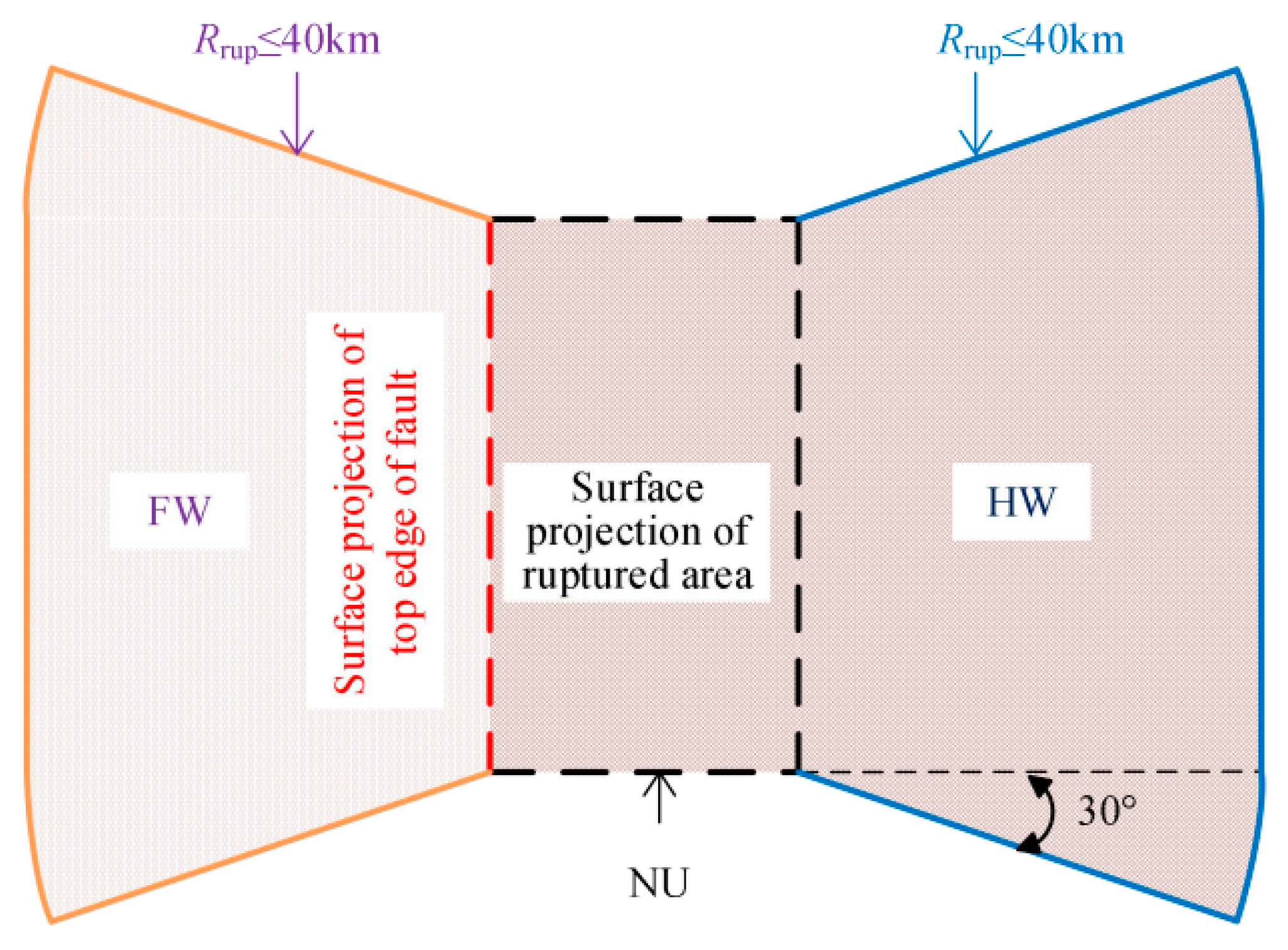
| FW | Site within the footwall region |
| HW | Site within the hanging wall region |
| L | Rupture length |
| LA | Rupture length of the aftershock |
| LM | Rupture length of the main shock |
| MA | Magnitude of the aftershock |
| MM | Magnitude of the main shock |
| NU | Site within the neutral region |
| PDF of the selected beta distribution | |
| RA | Source-to-site distance of an aftershock |
| Rerror | Relative error |
| Rrup, A | Rupture distance of the aftershock |
| Rrup, M | Rupture distance of the main shock |
| RX | Distance measured perpendicular to the fault strike from the surface projection of the up-dip edge of the fault plane |
| Sa,A | Spectral accelerations of the aftershock |
| Sa,M | Spectral accelerations of the mainshock |
| Ti | The ith period of the response spectrum |
| W | Rupture width |
| WA | Rupture width of the aftershock |
| WM | Rupture width of the main shock |
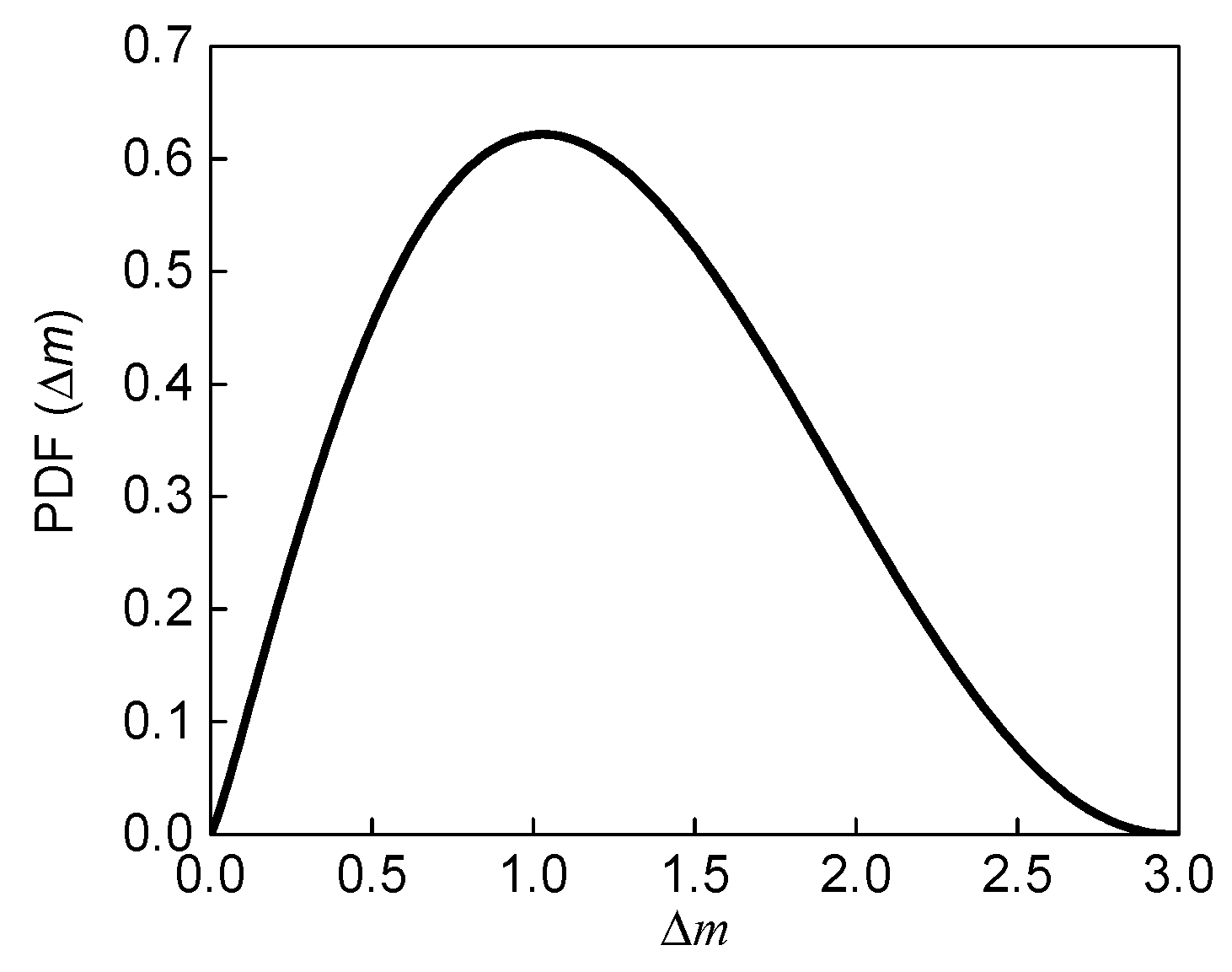
| Δm | Magnitude difference between the mainshock and its largest aftershock |
| Epsilon values of the aftershock | |
| Epsilon values of the mainshock | |
| Mean of lnSa,A predicted using the GMPE | |
| Conditional mean of the lnSa,A conditioned on the lnSa,M at the period Ti | |
| Mean of the logarithm of the recorded response spectrum for the aftershock ground motions | |
| Mean of the logarithm of the predicted response spectrum | |
| at the period | |
| at the period Ti | |
| at the period | |
| Correlation coefficient between and at the period | |
| Standard deviation of lnSa,A predicted using the GMPE | |
| at the period | |
| at the period |
References
- Kam, W.Y.; Pampanin, S.; Elwood, K. Seismic performance of reinforced concrete buildings in the 22 February Christchurch (Lyttleton) earthquake. Bull. N. Z. Soc. Earthq. Eng. 2011, 44, 239–278. [Google Scholar] [CrossRef]
- Torfehnejad, M.; Sensoy, S. Aftershock collapse capacity assessment of special steel moment frame structures. Structures 2023, 56, 105046. [Google Scholar] [CrossRef]
- Saed, G.; Balomenos, G.P. Fragility framework for corroded steel moment-resisting frame buildings subjected to mainshock-aftershock sequences. Soil Dyn. Earthq. Eng. 2023, 171, 107975. [Google Scholar] [CrossRef]
- Rajabi, E.; Golestani, Y. Study of steel buildings with LCF system under critical mainshock-aftershock sequence: Evaluation of fragility curves and estimation of the response modification factor by artificial intelligence. Structures 2023, 56, 105044. [Google Scholar] [CrossRef]
- Huang, X.; Liu, J.; Wang, N.; Xu, S. Pseudo-dynamic experimental study on seismically isolated prefabricated RC structure with roller-bearing subjected to mainshock-aftershock sequences. J. Build. Eng. 2023, 65, 105775. [Google Scholar] [CrossRef]
- Tesfamariam, S.; Goda, K. Risk assessment of CLT-RC hybrid building: Consideration of earthquake types and aftershocks for Vancouver, British Columbia. Soil Dyn. Earthq. Eng. 2022, 156, 107240. [Google Scholar] [CrossRef]
- Pang, R.; Zai, D.; Xu, B.; Liu, J.; Zhao, C.; Fan, Q.; Chen, Y. Stochastic dynamic and reliability analysis of AP1000 nuclear power plants via DPIM subjected to mainshock-aftershock sequences. Reliab. Eng. Syst. Saf. 2023, 235, 109217. [Google Scholar] [CrossRef]
- Fang, C.; Ping, B.; Zheng, Y.; Ping, Y.; Ling, H. Seismic fragility and loss estimation of self-centering steel braced frames under mainshock-aftershock sequences. J. Build. Eng. 2023, 73, 106433. [Google Scholar] [CrossRef]
- Du, M.; Zhang, S.; Wang, C.; She, L.; Li, J.; Lu, T. Seismic fragility assessment of aqueduct bent structures subjected to mainshock-aftershock sequences. Eng. Struct. 2023, 292, 116505. [Google Scholar] [CrossRef]
- Pang, R.; Xu, B.; Zhou, Y.; Zhang, X.; Wang, X. Fragility analysis of high CFRDs subjected to mainshock-aftershock sequences based on plastic failure. Eng. Struct. 2020, 206, 110152. [Google Scholar] [CrossRef]
- Hatzigeorgiou, G.D.; Beskos, D.E. Inelastic displacement ratios for SDOF structures subjected to repeated earthquakes. Eng. Struct. 2009, 31, 2744–2755. [Google Scholar] [CrossRef]
- Li, Y.; Song, R.; Van De Lindt, J.W. Collapse fragility of steel structures subjected to earthquake mainshock-aftershock sequences. J. Struct. Eng. 2014, 140, 04014095. [Google Scholar] [CrossRef]
- Torres, J.R.; Bojórquez, E.; Bojórquez, J.; Leyva, H.; Ruiz, S.E.; Reyes-Salazar, A.; Palemón-Arcos, L.; Rivera, J.L.; Carvajal, J.; Reyes, H.E. Improving the seismic performance of steel frames under mainshock–aftershock using post-tensioned connections. Buildings 2023, 13, 1676. [Google Scholar] [CrossRef]
- Furinghetti, M.; Lanese, I.; Pavese, A. Experimental hybrid simulation of severe aftershocks chains on buildings equipped with curved surface slider devices. Buildings 2022, 12, 1255. [Google Scholar] [CrossRef]
- Wei, J.; Ying, H.; Yang, Y.; Zhang, W.; Yuan, H.; Zhou, J. Seismic performance of concrete-filled steel tubular composite columns with ultra high performance concrete plates. Eng. Struct. 2023, 278, 115500. [Google Scholar] [CrossRef]
- Zheng, X.; Shen, Y.; Zong, X.; Su, H.; Zhao, X. Vulnerability analysis of main aftershock sequence of aqueduct based on incremental dynamic analysis method. Buildings 2023, 13, 1490. [Google Scholar] [CrossRef]
- Ruiz-García, J.; Ramos-Cruz, J.M. Collapse strength ratios for structures under mainshock-aftershock subduction seismic sequences. Structures 2023, 56, 104864. [Google Scholar] [CrossRef]
- Nugroho, L.Z.; Chiu, C.-K. Damage-controlling seismic design of low- and mid-rise RC buildings considering mainshock-aftershock sequences. Structures 2023, 57, 105099. [Google Scholar] [CrossRef]
- Yakhchalian, M.; Yakhchalian, M. An advanced intensity measure for aftershock collapse fragility assessment of structures. Structures 2022, 44, 933–946. [Google Scholar] [CrossRef]
- Goda, K.; Taylor, C.A. Effects of aftershocks on peak ductility demand due to strong ground motion records from shallow crustal earthquakes. Earthq. Eng. Struct. Dyn. 2012, 41, 2311–2330. [Google Scholar] [CrossRef]
- Kim, B.; Shin, M. A model for estimating horizontal aftershock ground motions for active crustal regions. Soil Dyn. Earthq. Eng. 2017, 92, 165–175. [Google Scholar] [CrossRef]
- Hu, S.; Gardoni, P.; Xu, L. Stochastic procedure for the simulation of synthetic main shock-aftershock ground motion sequences. Earthq. Eng. Struct. Dyn. 2018, 47, 2275–2296. [Google Scholar] [CrossRef]
- Wang, G.; Pang, R.; Yu, X.; Xu, B. Permanent displacement reliability analysis of soil slopes subjected to mainshock-aftershock sequences. Comput. Geotech. 2023, 153, 105069. [Google Scholar] [CrossRef]
- Pu, W.; Li, Y. Evaluating structural failure probability during aftershocks based on spatiotemporal simulation of the regional earthquake sequence. Eng. Struct. 2023, 275, 115267. [Google Scholar] [CrossRef]
- Khalil, C.; Lopez-Caballero, F. Lifetime response of a liquefiable soil foundation-embankment system subjected to sequences of mainshocks and aftershocks. Soil Dyn. Earthq. Eng. 2023, 173, 108107. [Google Scholar] [CrossRef]
- Ghotbi, A.R.; Taciroglu, E. Conditioning criteria based on multiple intensity measures for selecting hazard-consistent aftershock ground motion records. Soil Dyn. Earthq. Eng. 2020, 139, 106345. [Google Scholar] [CrossRef]
- Ding, Y.; Chen, J.; Shen, J. Prediction of spectral accelerations of aftershock ground motion with deep learning method. Soil Dyn. Earthq. Eng. 2021, 150, 106951. [Google Scholar] [CrossRef]
- Chaiyasarn, K.; Buatik, A.; Mohamad, H.; Zhou, M.; Kongsilp, S.; Poovarodom, N. Integrated pixel-level CNN-FCN crack detection via photogrammetric 3D texture mapping of concrete structures. Autom. Constr. 2022, 140, 104388. [Google Scholar] [CrossRef]
- Abadel, A.A. Physical, mechanical, and microstructure characteristics of ultra-high-performance concrete containing lightweight aggregates. Materials 2023, 16, 4883. [Google Scholar] [CrossRef]
- Zhu, R.G.; Lu, D.G.; Yu, X.H.; Wang, G.Y. Conditional mean spectrum of aftershocks. Bull. Seismol. Soc. Am. 2017, 107, 1940–1953. [Google Scholar] [CrossRef]
- Abrahamson, N.A.; Silva, W.J.; Kamai, R. Summary of the ASK14 ground motion relation for active crustal regions. Earthq. Spectra 2014, 30, 1025–1055. [Google Scholar] [CrossRef]
- Han, R.; Li, Y.; van de Lindt, J. Assessment of seismic performance of buildings with incorporation of aftershocks. J. Perform. Constr. Facil. 2015, 29, 04014088. [Google Scholar] [CrossRef]
- Yeo, G.L.; Cornell, C.A.A. probabilistic framework for quantification of aftershock ground-motion hazard in California: Methodology and parametric study. Earthq. Eng. Struct. Dyn. 2009, 38, 45–60. [Google Scholar] [CrossRef]
- Kumitani, S.; Takada, T. Probabilistic assessment of buildings damage considering aftershocks of earthquakes. J. Struct. Constr. Eng. 2009, 74, 459–465. [Google Scholar] [CrossRef]
- Wells, D.L.; Coppersmith, K.J. New empirical relationships among magnitude, rupture length, rupture width, rupture area, and surface displacement. Bull. Seismol. Soc. Am. 1994, 84, 974–1002. [Google Scholar]
- Ancheta, T.D.; Darragh, R.B.; Stewart, J.P.; Seyhan, E.; Silva, W.J.; Chiou, B.S.-J.; Wooddell, K.E.; Graves, R.W.; Kottke, A.R.; Boore, D.M. NGA-West2 database. Earthq. Spectra 2014, 30, 989–1005. [Google Scholar] [CrossRef]
- Han, R.; Li, Y.; van de Lindt, J. Seismic risk of base isolated non-ductile reinforced concrete buildings considering uncertainties and mainshock–aftershock sequences. Struct. Saf. 2014, 50, 39–56. [Google Scholar] [CrossRef]
- Abrahamson, N.; Silva, W.J. Empirical response spectral attenuation relations for shallow crustal earthquakes. Seismol. Res. Lett. 1997, 68, 94–127. [Google Scholar] [CrossRef]




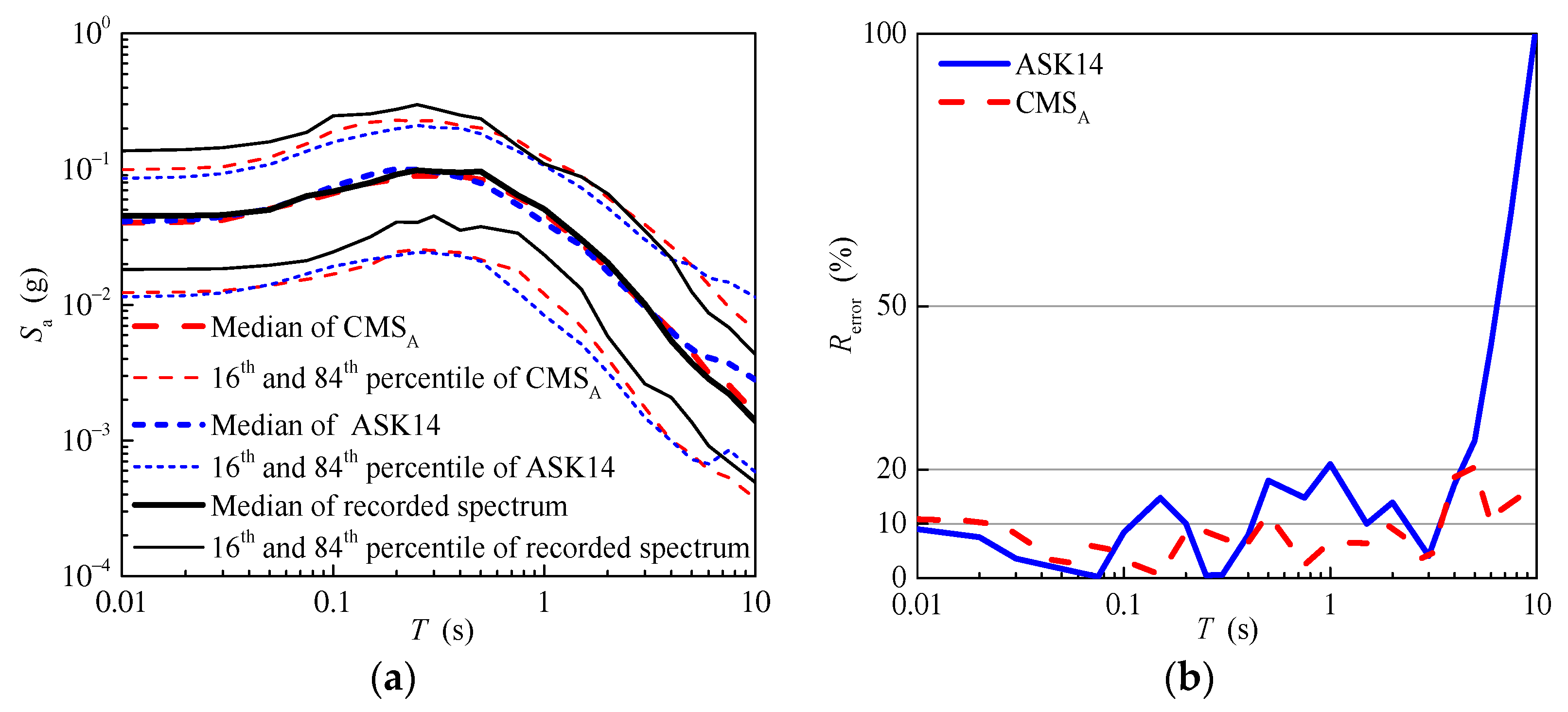
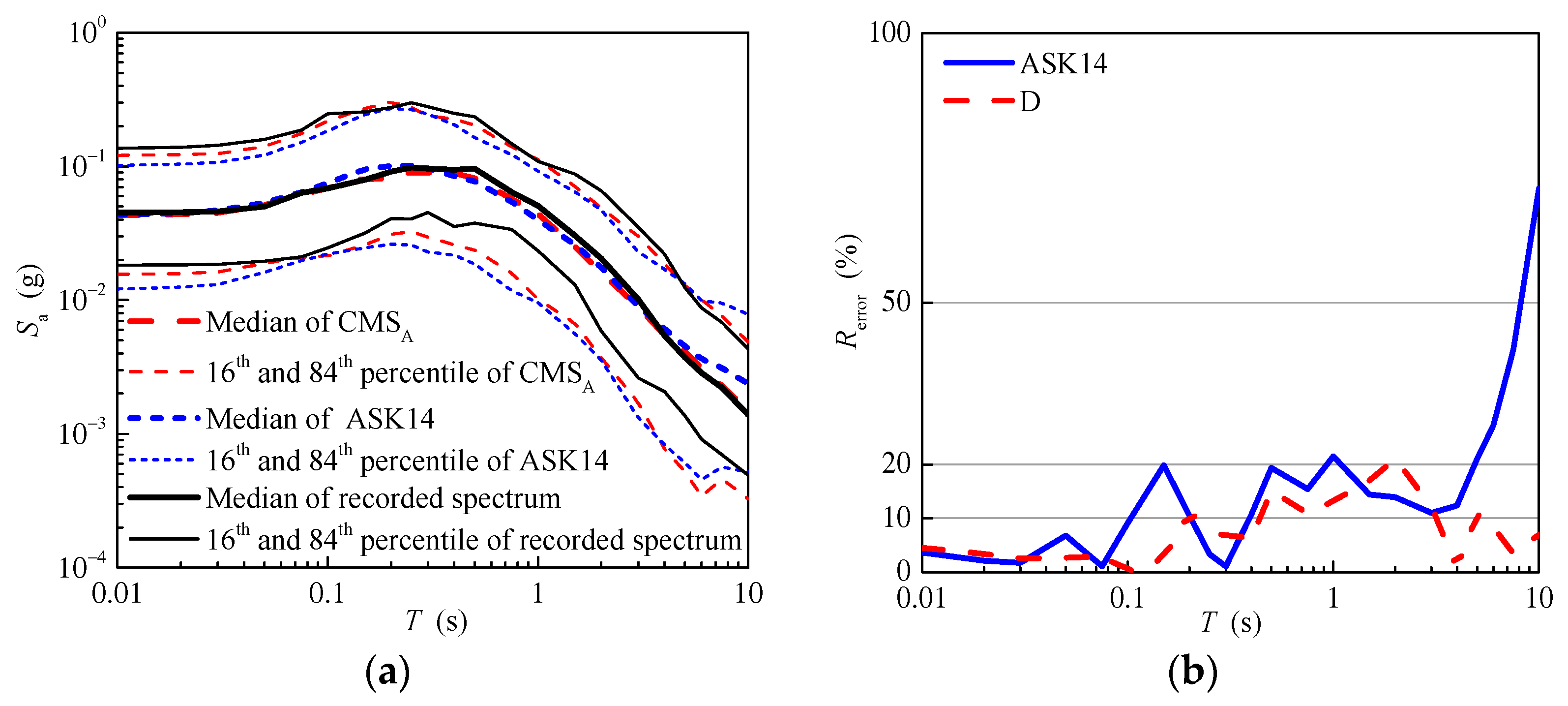
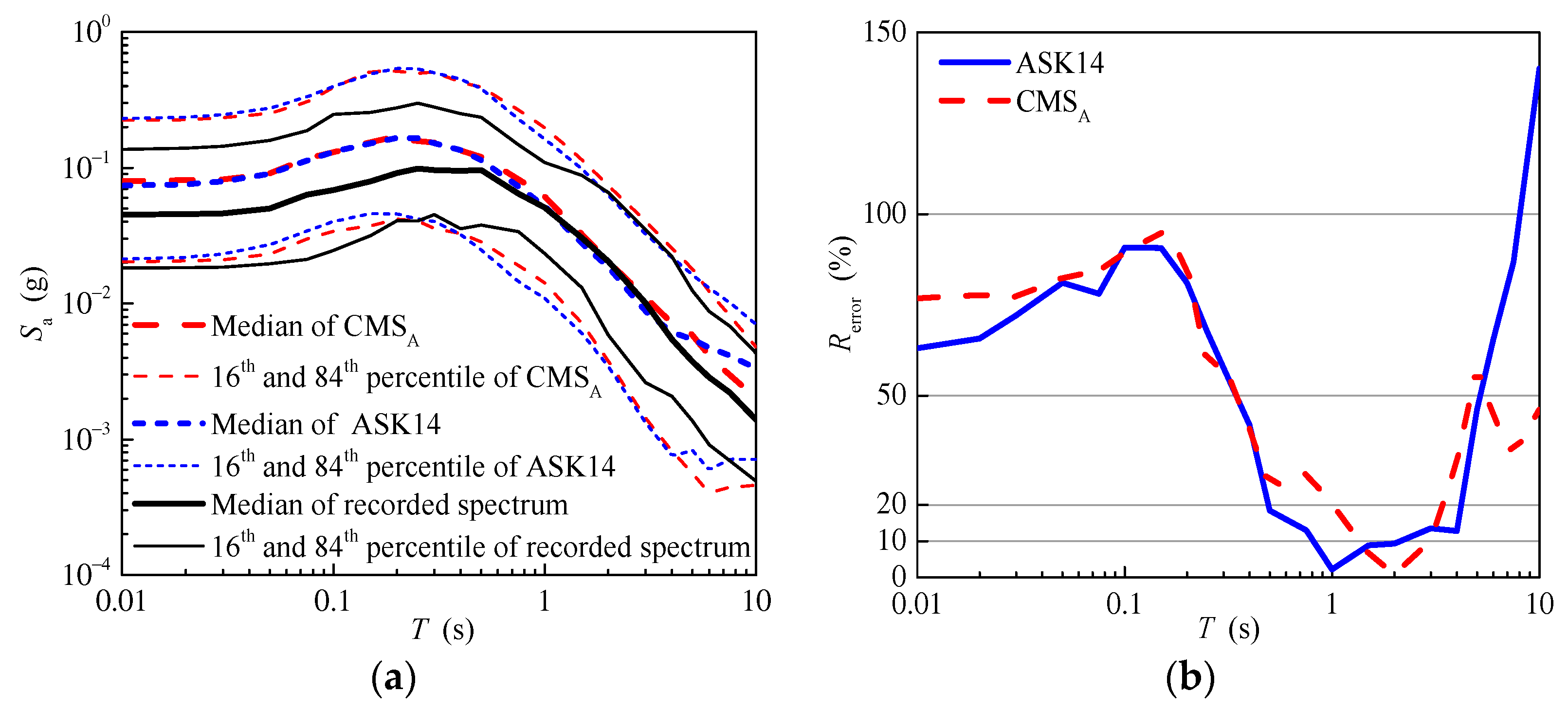
| L (km) | W (km) | ||||
|---|---|---|---|---|---|
| Type of the Rupture | a | b | Type of the Rupture | a | b |
| Strike slip | −2.57 | 0.62 | Strike slip | −0.76 | 0.27 |
| Reverse | −2.42 | 0.58 | Reverse | −1.61 | 0.41 |
| Normal | −1.88 | 0.50 | Normal | −1.14 | 0.35 |
| All | −2.44 | 0.59 | All | −1.01 | 0.32 |
| EQID | Earthquake Name | Number of Stations | MW | Class | CRJB (km) |
|---|---|---|---|---|---|
| 40 | Friuli, Italy-01 | 0.5 | 6.5 | C1 | 0 |
| 43 | Friuli, Italy-02 | 0.5 | 5.91 | C2-0040 | 8.79 |
| 50 | Imperial Valley-06 | 12 | 6.53 | C1 | 0 |
| 51 | Imperial Valley-07 | 12 | 5.01 | C2-0050 | 0 |
| 53 | Livermore-01 | 1 | 5.8 | C1 | 0 |
| 54 | Livermore-02 | 1 | 5.42 | C2-0053 | 10.75 |
| 56 | Mammoth Lakes-01 | 1 | 6.06 | C1 | 0 |
| 61 | Mammoth Lakes-06 | 1 | 5.94 | C2-0056 | 5.24 |
| 68 | Irpinia, Italy-01 | 2 | 6.9 | C1 | 0 |
| 69 | Irpinia, Italy-02 | 2 | 6.2 | C2-0068 | 2.41 |
| 76 | Coalinga-01 | 0.5 | 6.36 | C1 | 0 |
| 80 | Coalinga-05 | 0.5 | 5.77 | C2-0076 | 0 |
| 103 | Chalfant Valley-02 | 1 | 6.19 | C1 | 0 |
| 104 | Chalfant Valley-03 | 1 | 5.65 | C2-0103 | 4.01 |
| 113 | Whittier Narrows-01 | 1 | 5.99 | C1 | 0 |
| 114 | Whittier Narrows-02 | 1 | 5.27 | C2-0113 | 0 |
| 136 | Kocaeli, Turkey | 5 | 7.51 | C1 | 0 |
| 138 | Duzce, Turkey | 5 | 7.14 | C2-0136 | 15.68 |
| 137 | Chi-Chi, Taiwan | 40 | 7.62 | C1 | 0 |
| 175 | Chi-Chi, Taiwan-06 | 40 | 6.3 | C2-0137 | 0 |
| 234 | Umbria Marche, Italy | 4 | 6 | C1 | 0 |
| 237 | Umbria Marche (aftershock 1), Italy | 4 | 5.5 | C2-0234 | 0 |
| 274 | L’Aquila, Italy | 4 | 6.3 | C1 | 0 |
| 275 | L’Aquila (aftershock 1), Italy | 4 | 5.6 | C2-0274 | 0 |
| 281 | Darfield, New Zealand | 3 | 7 | C1 | 0 |
| 346 | Christchurch, New Zealand | 3 | 6.2 | C2-0281 | 23.68 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, R.; Du, B.; Yang, Y.; Lu, D. The Generation of the Target Aftershock Spectrum Based on the Conditional Mean Spectrum of Aftershocks. Buildings 2023, 13, 2660. https://doi.org/10.3390/buildings13102660
Zhu R, Du B, Yang Y, Lu D. The Generation of the Target Aftershock Spectrum Based on the Conditional Mean Spectrum of Aftershocks. Buildings. 2023; 13(10):2660. https://doi.org/10.3390/buildings13102660
Chicago/Turabian StyleZhu, Ruiguang, Bohan Du, Yekai Yang, and Dagang Lu. 2023. "The Generation of the Target Aftershock Spectrum Based on the Conditional Mean Spectrum of Aftershocks" Buildings 13, no. 10: 2660. https://doi.org/10.3390/buildings13102660
APA StyleZhu, R., Du, B., Yang, Y., & Lu, D. (2023). The Generation of the Target Aftershock Spectrum Based on the Conditional Mean Spectrum of Aftershocks. Buildings, 13(10), 2660. https://doi.org/10.3390/buildings13102660








