Abstract
Mathematical optimization can be a useful strategy for minimizing energy usage while designing low-energy buildings. To handle building energy optimization challenges, this study provides an effective hybrid technique based on the pelican optimization algorithm (POA) and the single candidate optimizer (SCO). The suggested hybrid algorithm (POSCO) benefits from both the robust local search power of the single candidate method and the efficient global search capabilities of the pelican optimization. To conduct the building optimization task, the optimization method was developed and integrated with the EnergyPlus codes. The effectiveness of the proposed POSCO method was verified using mathematical test functions, and the outcomes were contrasted with those of conventional POA and other effective optimization techniques. Application of POSCO for global function optimization reveals that, among the thirteen considered functions, the proposed method was best at finding the global solution for seven functions, while providing superior results for the other functions when compared with competitive techniques. The suggested POSCO is applied for reducing an office buildings’ annual energy use. Comparing POSCO to POA procedures, the building energy usage is reduced. Furthermore, POSCO is compared to simple POA and other algorithms, with the results showing that, at specific temperatures and lighting conditions, the POSCO approach outperforms selected state-of-the-art methods and reduces building energy usage. As a result, all data suggests that POSCO is a very promising, dependable, and feasible optimization strategy for dealing with building energy optimization models. Finally, the building energy optimization findings for various climatic conditions demonstrate that the changes to the weather dataset had limited effect on the efficiency of the optimization procedure.
1. Introduction
The process of selecting the optimal design from a wide range of options is known as building energy optimization, which complies with energy performance standards. Building energy optimization creates an automated approach by combining traditional design techniques with simulation-aided design techniques [1]. The energy simulation system and the optimization engine are the two crucial engines that power the process and direct the design flow. Thermostatic comfort, cost, and energy performance are examples of optimization objective functions [1].
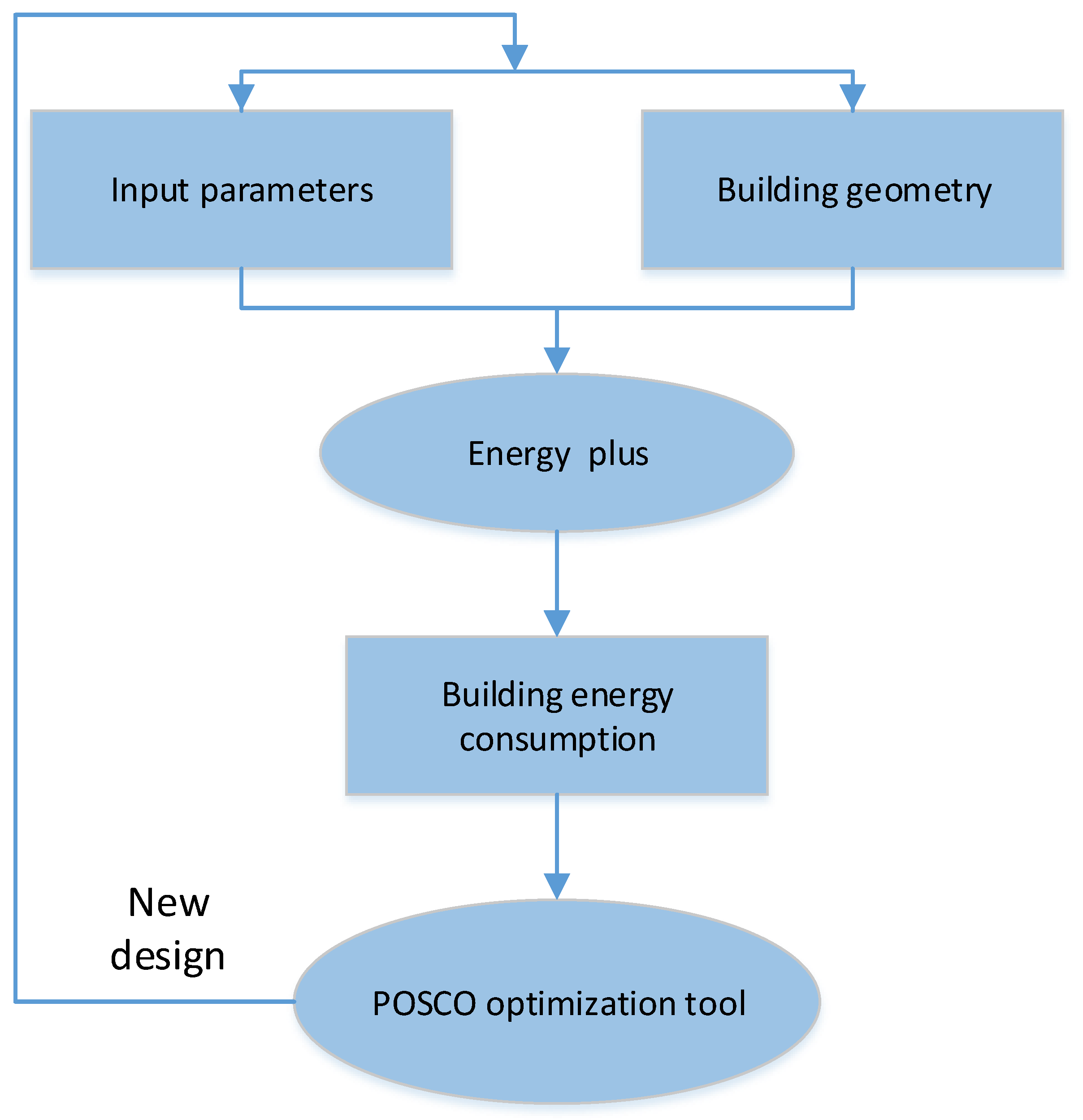
As demonstrated in various significant review works [2], building energy optimization (BEO), a new technology, has developed into an extremely active research field. Its benefits have been demonstrated to possibly reduce building energy usage by up to 30% when compared to a benchmark design [3]. According to Figure 1, the BEO technique uses optimization algorithms to produce new designs depending on the outcomes of energy simulations and predetermined design goals [4]. The use of this technique has benefited the optimization of building envelopes, including construction, form, and double-skin facades, building systems, including HVAC and lighting, and renewable energy generation, including combined heat and power (CHP), solar technologies, ground energy, and storage systems. The BEO workflow relies heavily on optimization methods, as seen in Figure 1. Therefore, the efficacy and efficiency of the BEO approach depends significantly on the performance of optimization algorithms.
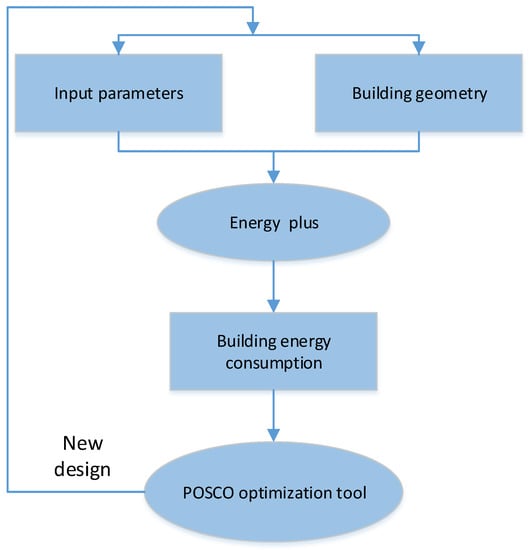
Figure 1.
Ideal building energy optimization tool framework.
Several approaches for building energy optimization have been presented. They can be grouped into three categories: analytical techniques, iterative algorithms, and metaheuristic algorithms. Analytical approaches extract these factors via a sequence of difficult mathematical equations [5]. They are simple to apply, but they have several drawbacks, including the need for particular mathematical qualities and assumptions. In some circumstances, these assumptions may result in large inaccuracies or a loss of solution accuracy [6]. Newton–Raphson and Lambert W-functions are iterative techniques that are extremely sensitive to the initial guess and gradient information [7]. Furthermore, because these approaches are multimodal, nonlinear, and limited, they need a convex optimum function and produce unsatisfactory solutions for BEO situations [8]. Due to their great performance on nonlinear and complicated optimizations, metaheuristic algorithms have gained a lot of attention for BEO to overcome the disadvantages of the first two techniques [9]. Metaheuristic algorithms have the benefit of not being confined to continuous, differentiable, or convex situations. Furthermore, they are simple conceptually and computationally, execute a relatively efficient search, and offer flexibility in handling difficult issues [10,11,12,13,14,15,16].
To address the constraints of numerical approaches, metaheuristic optimization procedures have recently been widely employed BEO problems. Metaheuristic optimization approaches have several advantages, including enhanced conjunction, protection from initial guess, lack of singularity condition, and consideration of all data points rather than key locations [17]. To achieve the best BEO design, the literature has made extensive use of metaheuristic optimization techniques. According to previous research [18], The majority of the primary literature on BEO, or around 64%, makes use of these optimization strategies. The GA and its modified forms dominate among intelligent optimization algorithms, making up about 41% of the core literature. The PSO algorithm comes in second, making up about 13% of the core literature. For instance, Lorestani and Ardehali [19] created a simulation model for the optimization of an autonomous CHP system that used renewable energy sources using a newly designed evolutionary particle swarm optimization (PSO) method. In order to increase the performance of a thermal-phase change material (T-PCM) of an office building, Pereira and Aeleneia [20] utilized a genetic algorithm (GA).
When picking these optimization algorithms, the pace of convergence, accuracy, and implementation complexity are all crucial things to consider [21]. Despite the fact that all of these approaches have been shown to be perfect for parameter estimation, they each have their own set of boundaries, such as the number of important parameters that must be established, the difficulty of the operation, and the computational time required to complete the estimation. In the pursuit of simple and speedier solutions, researchers are working on developing efficient optimization algorithms for BEO problems under various environmental situations.
Even while metaheuristic algorithms can produce satisfactory results, no algorithm can solve all optimization problems better than others. As a consequence, a number of research has been carried out in order to improve the performance and efficiency of the original metaheuristic algorithms and adapt them to a specific application. The literature study shows that providing fresh optimization algorithms to address real-world problems is highly desired. Some of these studies are as follows: application of genetic algorithms for the identification of structural damage location [22] and damping controller design for power system oscillations [23]; developing moth-flame optimization (MFO) for damage identification of bridge structures [24]; solving engineering design optimization problems using artificial bee colony algorithm [25]; optimization of shallow foundation based on tunicate swarm optimization algorithm [26]; adaptive version of particle swarm optimization for Bayesian damage identification [27]; application of firefly optimization algorithm for slope stability evaluation [28]; and identification of structural damage using a new version of the whale optimization algorithm [29].
A recently developed bioinspired metaheuristic optimization technique called the pelican optimization algorithm (POA) is motivated by the search and hunting behavior of pelicans. The POA was first suggested by Seyyedabbasi & Kiani [30] and search agents in this approach are pelicans that search for food sources. When it comes to finding the best solutions, POA performs better than other competing techniques and is well suited to problems in practical optimization.
To use any optimization approach at its best, a balance between exploitation and exploration must be kept throughout the search procedure. POA searches a wide region because it is a global search approach; thus, when utilized alone, it might not produce the greatest results. Search engine approaches, such as pattern search and single candidate optimizer, utilize the local search but can also benefit from the global search [31]. Due to these approaches’ unique qualities, there is an opportunity for hybridization. In light of the foregoing, a combination of the pelican optimization and single candidate optimizer, known as POSCO, is developed and is utilized in the current task. The suggested POSCO approach’s performance is evaluated by comparing its results in a literature-based benchmark problem to those of existing strategies. The results of the proposed technique are compared with six well-established methods for BEO to illustrate the better performance of POSCO. The numerical experiments show that the new algorithm is capable of producing better optimum solutions and outperforms previous approaches in the literature. The simulation results show that the novel optimization approach may achieve the lowest root mean square error and reach superior optima in diverse photovoltaic cells than prior methods.
Therefore, the key contributions of this study can be summed up as follows:
- The development of POSCO, a powerful hybrid metaheuristic method based on single candidate and pelican optimization, has been made.
- Thirteen popular benchmarking functions are used to evaluate POSCO’s performance for numerical function optimization, and the findings are contrasted with those of other widely used optimization techniques.
- To show how well the suggested method works when used on real-life issues, the new method is used to build the energy optimization problem.
- The efficiency of the proposed POSCO for BEO is investigated and the results acquired are contrasted with those previously assessed by the other procedures.
2. Pelican Optimization Algorithm
The pelican optimization algorithm is a swarm-based technique in which pelicans are participants (i.e., candidate solution) [32]. According to their position in the search space, each population member recommends solutions for the problem. In the first step of the POA, the population members are initialized at random using the problem’s lower and upper boundaries based on Equation (1).
A matrix entitled the population matrix (X) in Equation (2) and is used to identify pelican population members in the POA. The columns of this matrix indicate the proposed values for the problem variables, while the rows represent candidate solutions.
Based on each of the potential solutions, the objective function of the given problem can be assessed using the POA. Using a vector known as the objective function vector in Equation (3), the values obtained for the objective function are calculated. Each of the possible solutions can be used to assess the objective function value of the assumed problem. In Equation (3), the values for the objective function are calculated using a vector known as the objective function vector:
where F denotes the objective function vector and represents the ith candidate solution’s objective function value.
To update possible solutions, the POA replicates pelican behavior when attacking and hunting prey. Moving approaching prey and winging on the water surface are the two stages of this hunting method.
- a.
- Moving Approaching the Prey or Exploration Phase:
The pelicans recognize the prey’s location in the first phase and then fly toward it. The exploration capability of the POA in identifying diverse areas of search space is achieved by simulating this pelican’s behavior. POA’s exploration capacity in the specific investigation of the problem-solving domain is increased as a result of this. The aforementioned ideas, as well as the pelican’s strategy for approaching the prey, are mathematically modelled in Equation (4):
where represents the updated state of the ith pelican in the jth dimension based on phase 1, I is a number that can be either 1 or 2 at random, pj is the prey’s position in the jth dimension, and Fp is the value of its objective function.
The parameter I is chosen at random for each iteration and each participant and has an impact on the POA’s exploration ability to accurately scan the search space.
In the POA, a new pelican position is accepted if the objective function value enhances in that location. The algorithm is prohibited from expanding to non-optimal locations in this kind of updating process. Equation (5) is used to model this mechanism:
where denotes the recent condition of the ith pelican and is the value of its objective function according to phase 1.
- b.
- Exploitation Phase or Water Surface Winging:
In the exploitation phase, the pelicans expand their wings to lift the fish higher after reaching the water’s surface, then collect the victim in their throat pouch. To converge to a better result, the algorithm must investigate the points in the neighborhood of the pelican’s location mathematically. Equation (6) mathematically simulates pelican behavior during hunting:
After all individuals have been adjusted according to the mentioned first and second phases, the best candidate solution will be updated according to the new population status and the values of the objective function. The POA moves on to the next iteration, and the process based on Equations (4)–(7) is repeated until the entire computation is completed. Eventually, as an optimal solution to the given problem, the best candidate solution obtained during the algorithm iterations is presented.
The various steps of the POA are presented as a pseudo-code in Algorithm 1.
| Algorithm 1: Pseudo-code of the pelican optimization algorithm |
| Determine the POA population size (N) and the number of iterations (T) Initialization of the position of pelicans randomly based on Equation (1) Calculate the objective function of the population For t = 1:T Generate the position of the prey at random For I = 1:N Phase 1: Moving towards prey (exploration phase) For j = 1:m Calculate new status of the jth dimension using Equation (4) End Update the ith population member using Equation (5) Phase 2: Winging on the water surface (exploitation phase) For j = 1:m. Calculate new status of the jth dimension using Equation (6) End Update the ith population member using Equation (7) End Update best candidate solution End Output best solution obtained by POA |
As mentioned in this section, the POA has three parameters to be adjusted for solving any optimization problems: population size (N), the maximum number of iterations (T), and the R factor. To select the appropriate values for these parameters, a series of sensitivity analyses have been conducted in the original paper [32]. According to the obtained results presented by Trojovský and Dehghani [32], as the number of population members (N) increases, the value of the objective function decreases. However, the computation time will be increased. Similarly, increasing the algorithm’s maximum number of iterations (T) from 100 to 1000 improves the algorithm’s exploitation power, allowing it to produce better solutions. Finally, the results of the sensitivity analysis show that the POA has a very low sensitivity to changes in the parameter R and, in most cases, provides the same solution. In the general analysis and comparison of the results [32], it was found that POA has the best performance for the value of R equal to 0.2.
3. Single Candidate Optimizer
In contrast to the majority of the currently used searching algorithms, which rely on a swarm of particles for the duration of the whole optimization process, single candidate optimizer (SCO) only considers one candidate solution in its search for better alternatives. In the suggested scheme, the Tmax function evaluations or iterations that make up the overall optimization process are split into two phases, with the candidate solution updating its position in each phase in a different way. In order to create a single, robust algorithm, the SCO approach combines the single candidate technique and the two-phase strategy. The algorithm, most importantly, uses a special set of equations to update the candidate solution’s position exclusively on the basis of its information, i.e., its location at the time. When T1 function evaluations are completed, the first phase of SCO comes to an end, and T2 function evaluations are undertaken in the second phase, where T1 + T2 = Tmax. The candidate solution adjusts its places as follows throughout the first stage of SCO:
where rand1 is a random number in interval [0, 1]. Here is how w is defined mathematically:
where t denotes the current function evaluation or iteration, b the constant value, and Tmax the maximum number of function evaluations, respectively. After thoroughly examining the area surrounding the best spot found in the first phase, the second phase of SCO conducts a deep search. Phase Two’s last stages assist to narrow the search area and concentrate primarily on potential areas. As the second phase progresses, the candidate solution changes its position as seen below:
where is a different random variable with a [0, 1] range, and are the borders’ upper and lower limits, respectively. The most crucial parameter in SCO is w, which is in charge of striking a balance between exploration and exploitation. From Equation (9), the number of function evaluations causes w to fall off exponentially. This behavior is essential because a relatively high value of w at the start of the search process aids in effectively exploring the search space, while at the completion of the optimization procedure, a small value of w improves the exploitation capabilities. Being stuck in local optima, especially in the later stages of the search process, is one of the key drawbacks of metaheuristic strategies. If no fitness improvement is made in m successive function evaluations, SCO addresses this problem by updating the location of the candidate solution in a different way in the second phase. The number of function evaluations m that cannot successively enhance fitness is counted using a counter c. The updated candidate’s ability to obtain successful fitness is assessed using the binary parameter p, where p = 1 signals a successful fitness improvement and p = 0 indicates a failed fitness improvement. A candidate solution updates its position according to Equation (10) in the second stage of SCO; however, if completing m successive function evaluations does not increase the fitness value, the candidate solution changes its location as follows:
The candidate solution is able to switch from exploitation to exploration in Equation (11) and this helps it escape from the local minimum. When certain variables’ placements are changed, it is occasionally possible for their values to deviate from the expected range or bounds. If a variable’s value is greater than either its upper bound or lower bound, the updated locations are set as follows to prevent it from crossing those boundaries:
In Equation (12), if the updated location is outside of boundaries, the updated dimension of a candidate solution is given the same value as the overall best value. In SCO, a single candidate solution x is produced at random and then updated repeatedly to look for a better one. The following is the generation of the initial potential solution:
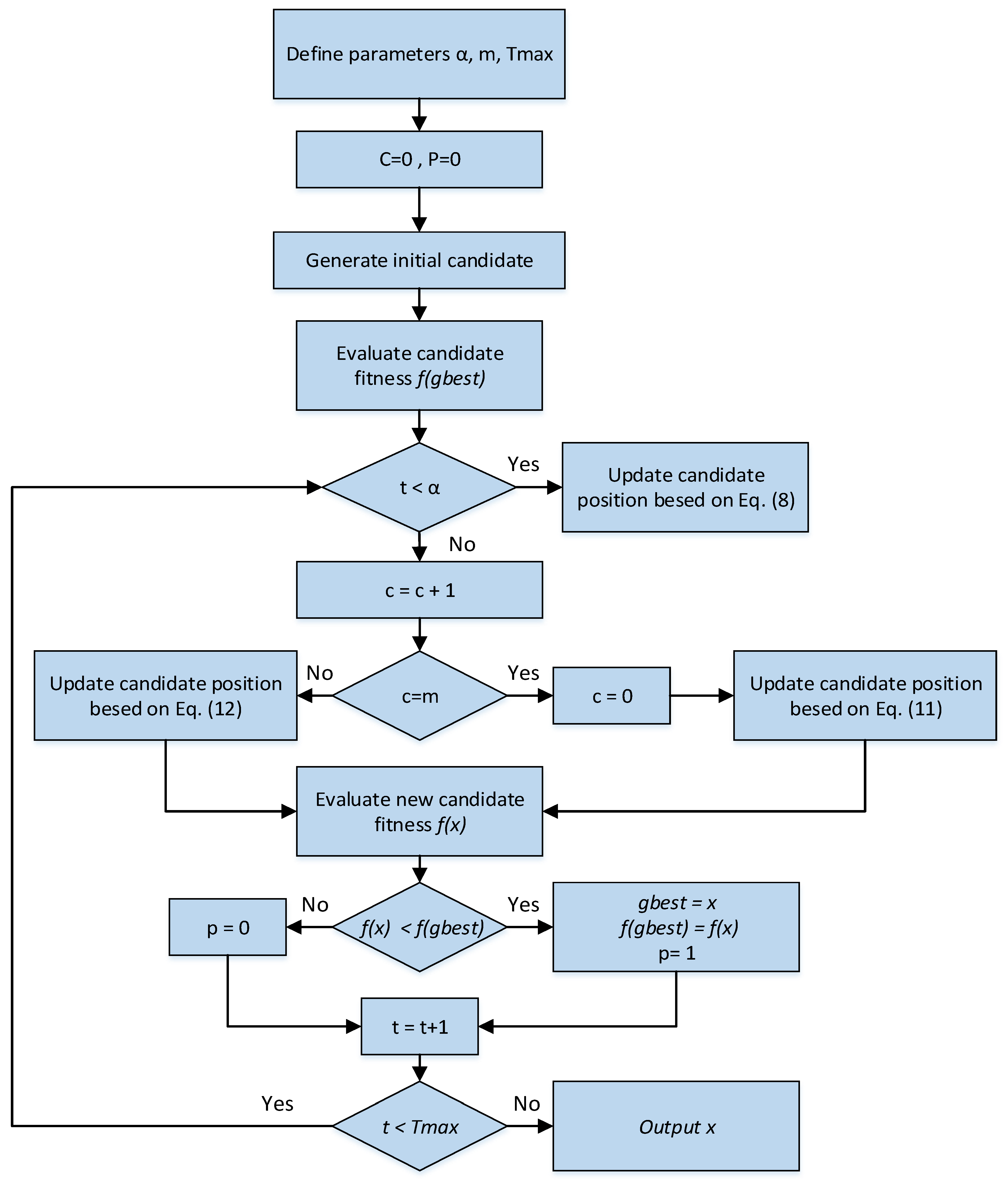
The flowchart of the single candidate optimizer (SCO) is presented in Figure 2.
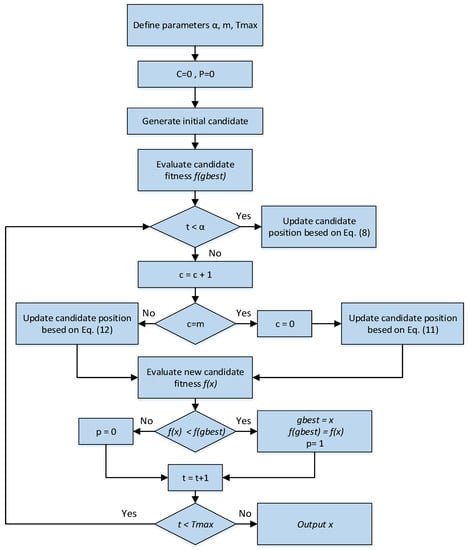
Figure 2.
Flowchart of SCO algorithm.
4. Hybrid Pelican and Single Candidate Optimizer
By integrating two or more methodologies, a hybrid strategy can tackle the same problem. The objective of hybridization is to mix the benefits of each approach to increase the accuracy of the outcome [33].
In the present work, the POSCO approach, which combines pelican optimization algorithm (POA) and single candidate optimizer (SCO) methods, has been developed. A global optimization strategy known as the pelican algorithm successfully explores the solution area and is likely to produce an optimal or nearly optimum answer. It may, therefore, be used in combination with techniques for local optimization like SCO.
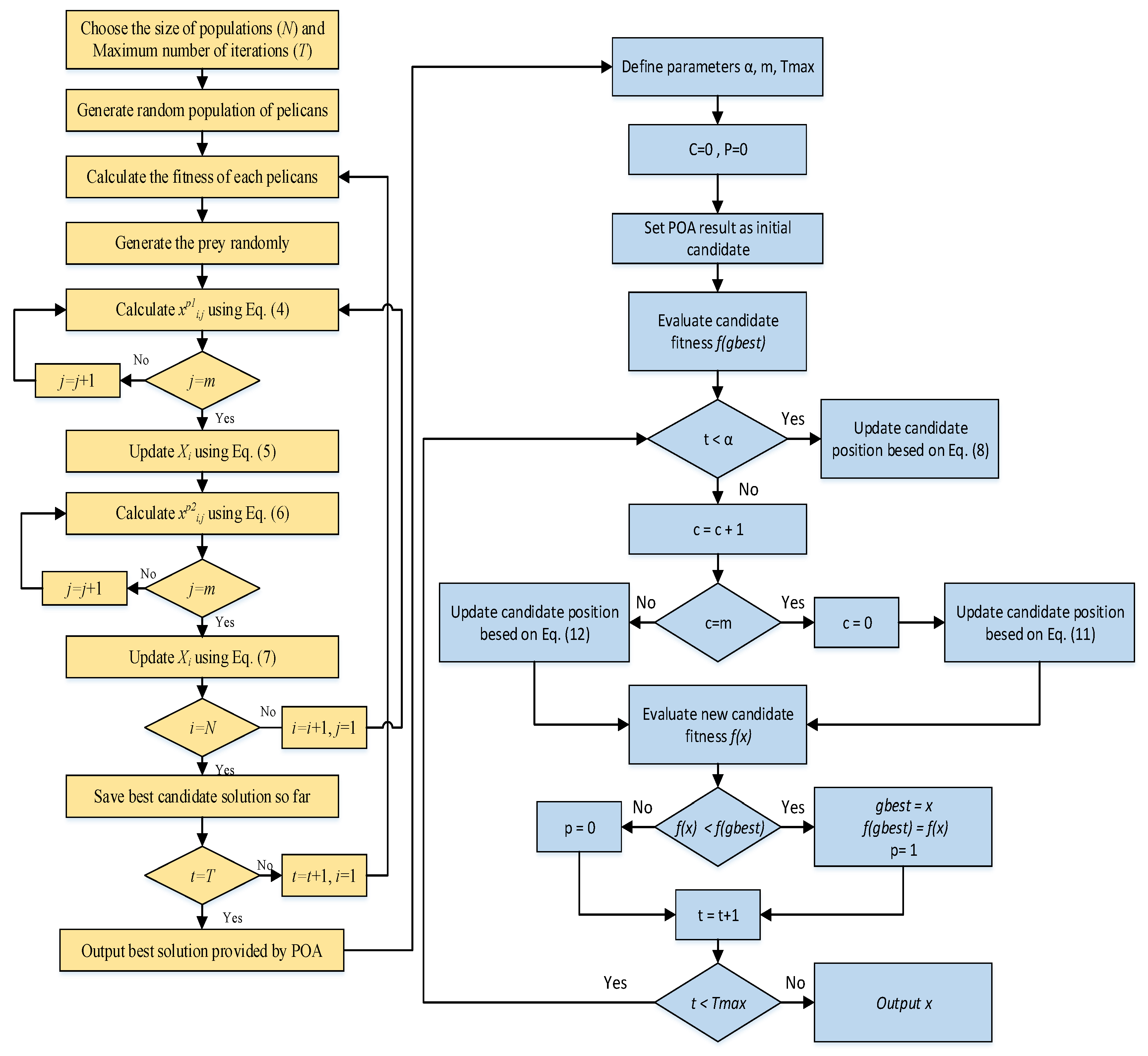
The SCO is helpful for investigating a small region, but it is seldom helpful for bigger areas. The tremendous global and local searching powers of the SCO algorithm, as well as those of the POA, may be combined in the suggested hybrid strategy. Pelican optimization’s (POA) global performance is outstanding, and it is simple to escape local minima. By increasing the number of iterations, the POA can enhance the findings’ accuracy. However, POA is unable to improve the findings’ accuracy when the number of generations is sufficiently high. Because of this, POA’s local search functionality is still subpar. The single candidate optimizer is a local optimization approach, and the starting point has a considerable influence on the algorithm’s output. However, SCO will be a straightforward and useful tactic if a superb beginning point is selected. To find the optimum solution in this research, we effectively combined the advantages of SCO as a local optimization and POA as a global optimization. The hybrid approach that has been suggested begins with the POA, since the SCO depends on the first solution. The POA is employed to continue looking after a predetermined number of repetitions. The SCO is then permitted to perform a local search, starting with the POA’s best option. It is worth mentioning that, in addition to improving the accuracy of the results, choosing the right starting point will also make the method more stable. Without any information, the SCO considers a random solution as the starting point. If this random solution is very far from the best solution, the algorithm will be unable to find the optimal global solution, and the stability of the algorithm will decrease. The proposed hybrid algorithm’s process flow is depicted in Figure 3.
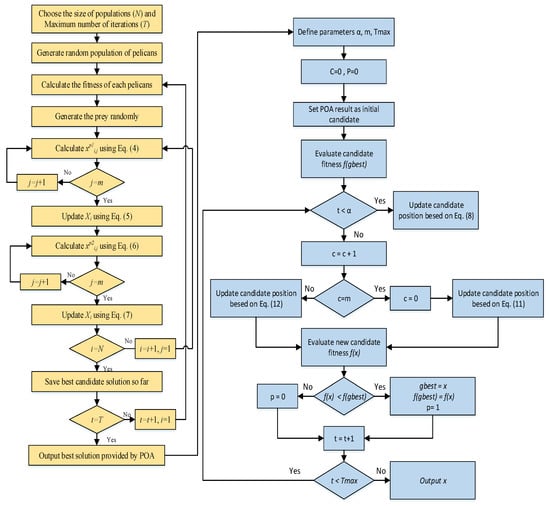
Figure 3.
Hybrid POSCO.
5. Building Energy Optimization Problems
The purpose of the current study is to analyze POSCO’s efficiency in building energy optimization. As a result, two benchmark structures with a weather profile for Houston, Chicago, and Seattle were chosen as the benchmark instances. The building’s energy consumption was then optimized using the POSCO algorithm. There are three components to the building energy optimization (BEO) challenge. Building energy modeling, which simulates a building’s energy model and calculates energy consumption, makes up the first section. The optimization method, which is the second component, uses the simulation data to modify the building factors and arrive at an ideal outcome. The integration of the optimization algorithm and simulations is the third component. We will talk about these three components later in this section.
5.1. Simple Office Building
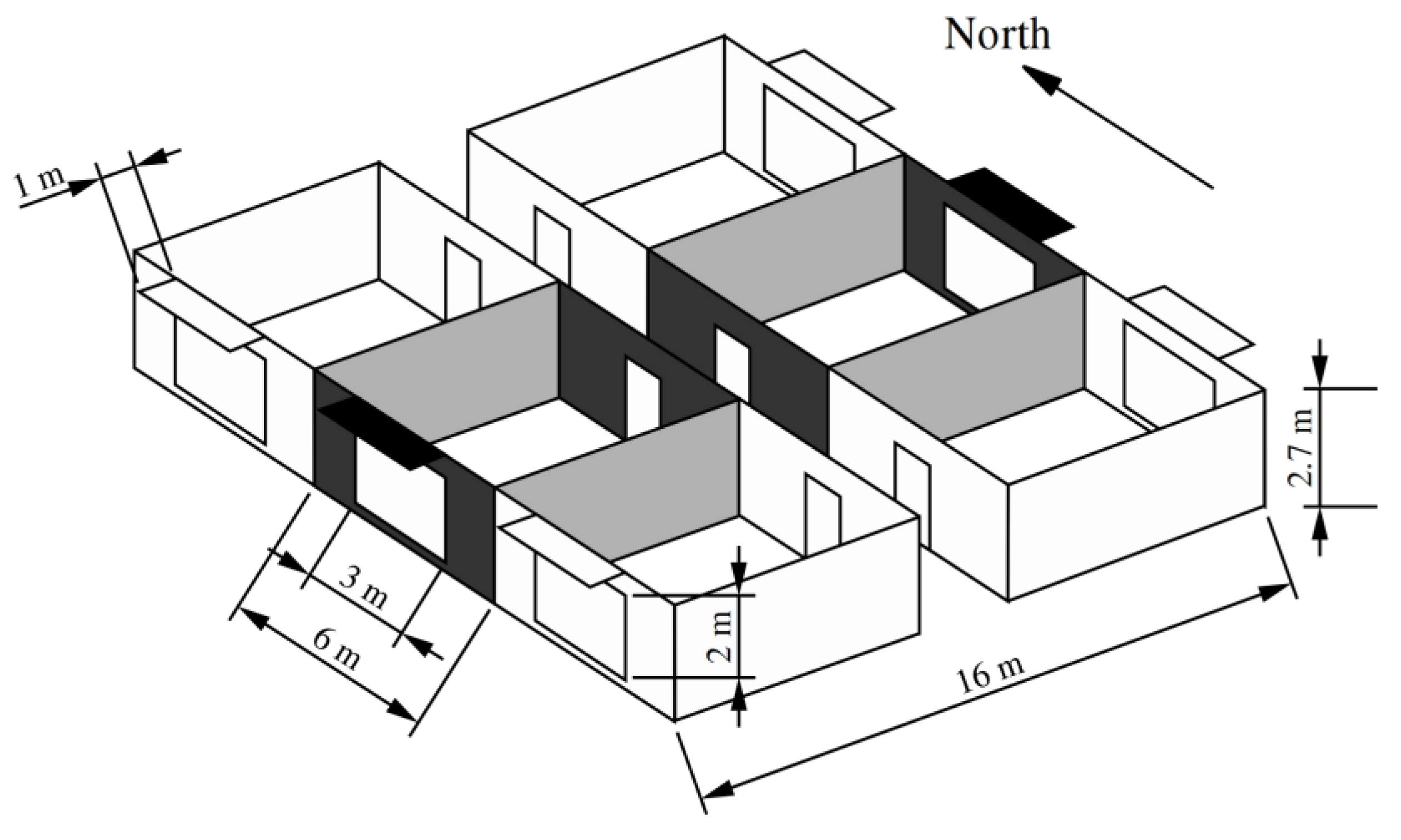
A benchmark office building with four choice factors was used to conduct a case study. The structure has already been covered in a variety of literary works, including [34,35]. The building model is depicted schematically in Figure 4. The decision factors X1–X4 are shown in Table 1.
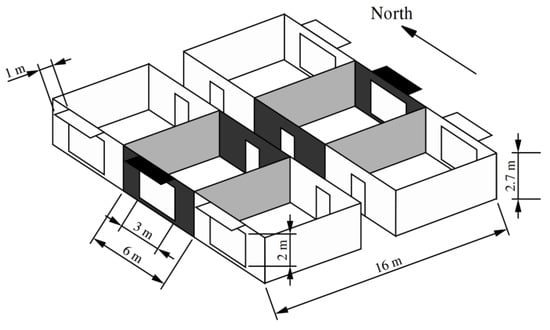
Figure 4.
Building model of BEO problem for a simple office building [34].

Table 1.
The modest office building’s decision factors.
These factors include building orientation, window sizes for the East and West facades, and shading transmittance. The external walls are built of wood siding (1 cm thick), insulation (10 cm thick), and concrete (20 cm thick), and have a U-value of 0.25 W/(m2 K). Carpet, 5 cm of concrete, padding, and concrete (18 cm) make up the floor and ceiling. Bricks used for the internal walls have a 12 cm thickness. There is an outside shading mechanism, and the double-panel windows are Krypton gas-filled and low-emissivity. The objective function is the sum of the energy consumption of a chiller, a boiler, and lighting as presented in the following equation:
The energy consumption of chillers and boilers is related to cooling and heating loads. Therefore, heating and cooling loads related to energy consumption can be defined by the following equations:
where Qh(.), Qc(.), and E(.) stand for the yearly energy usage for heating, cooling, and zone lighting electricity consumption in kWh/a, respectively.
According to Waibel et al. [35], the plant’s heating and cooling efficiencies of ηh = 0.44 and ηc = 0.77 were utilized, respectively. In addition, the primary energy factor (PEF) for electricity is set to 3.0 to convert site electricity to source fuel energy consumption.
Finally, the following equation illustrates the goal of minimizing the building’s energy consumption:
where A represents the building’s conditioned surface area. The annual energy consumption is divided by the floor area A; hence, the objective of these problems is to minimize the primary annual energy consumption in kWh/m2a.
In general, load and weather conditions affect performance coefficients, which may be altered. In order to consider the effect of external climate conditions on energy consumption, three different types of weather data are utilized in the analysis [34]. In the first case, typical meteorological year (TMY2) weather data for Houston Intercontinental (TX), in the second case, TMY2 weather data for Chicago O’Hare (IL), and for the third case, TMY2 weather data for Seattle Tacoma (WA) are considered [34].
5.2. Detailed Office Building
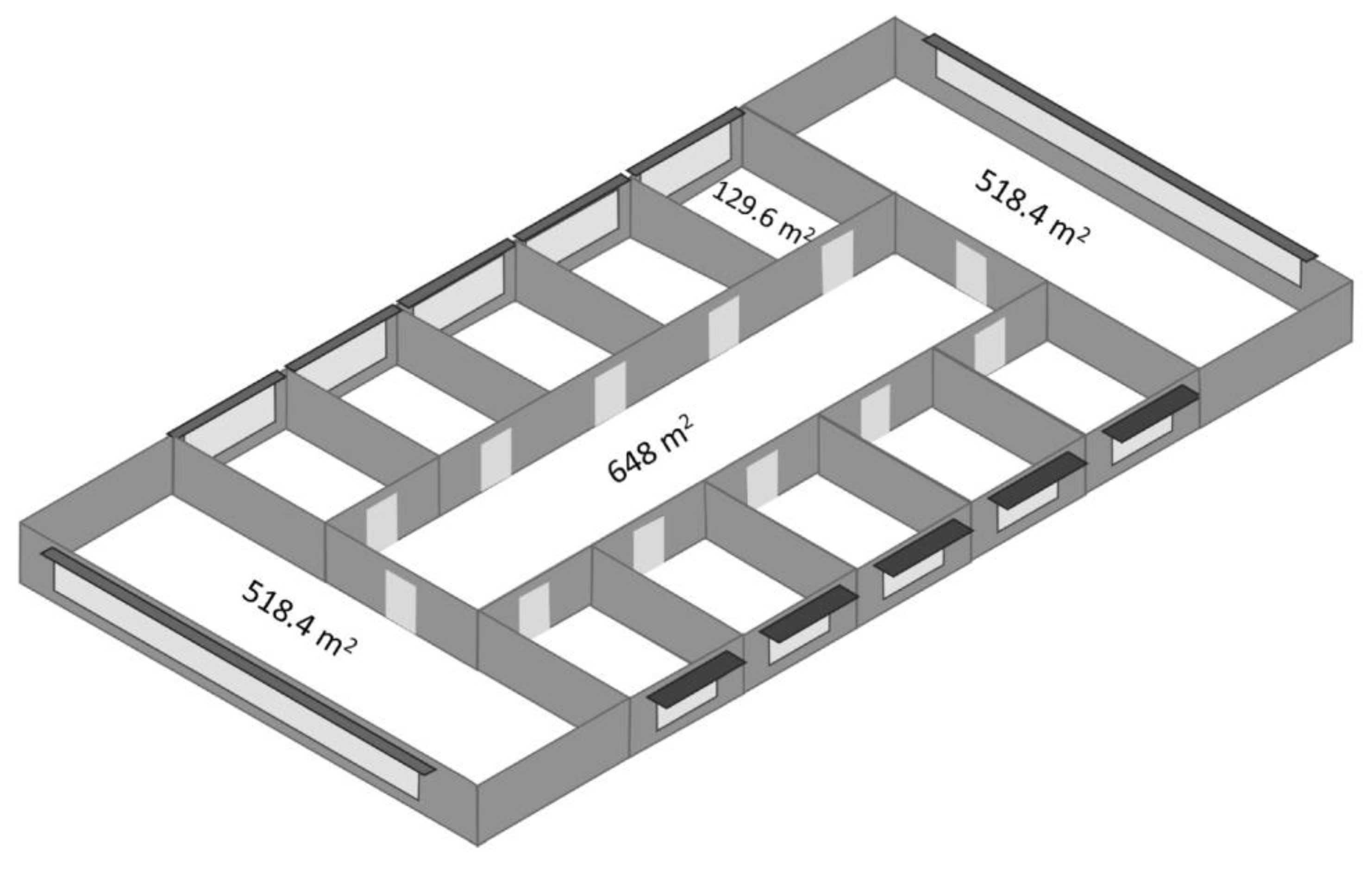
A more identical version of the first building can be found in the second structure. Wetter and Wright also conducted research on this structure [34]. A huge zone in the west and east of the structure is encircled by five smaller zones on either side that are facing north and south, with well-insulated floors and ceilings (adiabatic). Figure 5 shows a view of the building model.
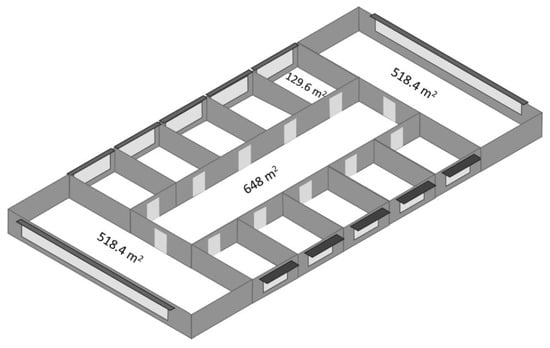
Figure 5.
Building model of BEO problem for detailed office building [34].
As listed in Table 2, this structure has 13 decision variables. The goal is to reduce the office’s annual primary energy consumption per square meter of area (kWh/m2 a). Energy use for cooling coils, fans, heating, and zone lighting is included in the energy consumption. The BOP can be written as follows:
where the heating coil (Eh), cooling coil (Ec), fans and zone lighting energy consumption (Eel) were considered. Here, the primary energy factors for electricity (PEFel = 3) and gas (PEFgas = 1) are also taken into consideration.

Table 2.
The detailed office building’s decision factors.
Similar to the last instance, three different weather files are taken into account in this problem. Weather data from the typical meteorological year (TMY2) for Seattle Tacoma (WA), Chicago O’Hare (IL), and Houston Intercontinental (TX) are considered.
5.3. Simulation Software for Building Energy Consumption
An EnergyPlus (EP) simulation tool is utilized in the current work to model the building’s thermal action and calculate the relevant energy usage. EnergyPlus, one of the US Department of Energy’s software programs, can simulate an energy analysis of an entire building [36]. There is no graphical user interface for the EP; instead, it calculates energy usage by reading input data from a text file. The results are then reported in an output text file. During the building simulations, EP determines a building’s fundamental heating and cooling demands based on the supplied thermal control set points. The primary plant’s energy consumption, secondary HVAC system conditions, and coil loads are all included in the loading conditions. Due to the fact that EP’s calculations are based on the venerable DOE-2 and BLAST algorithms, they are precise and quick [36]. In order to start the transient calculations, the starting situations were evaluated during warm-up until the structure achieves a stable state. Using the meteorological data, convection and radiation were combined to provide the exterior walls’ and roof’s boundary conditions. The transient energy equation was solved using a 15-min time step and the conduction transfer function. Each month, more shading-related information was added. The calculations were run over the course of a full year.
5.4. Combining the POSCO Algorithm with EP
The EP was coupled with the POSCO optimization algorithm using a coupling subroutine. As previously noted, EP’s input and output files serve as the primary means of communication. To simulate and estimate the building’s yearly energy consumption, a subroutine was created that defined the building model, changed the building control settings, and executed the EP in conjunction with a climate profile. The subroutine will then hold off on writing the outcomes to the output file until the EP has finished computing. The subroutine will then read the building’s predicted energy consumptions. The control parameters (also known as optimization variables) are modified by the optimization code before being sent via the subroutine into the EP’s input file. The EP is then excited, the energy consumptions are read (objective), and the results are passed to the POSCO algorithm. The POSCO selects a fresh set of ideal design parameters and inputs them into EP’s input file through the function.
6. Verification of the POSCO
The accomplishment and efficacy of the proposed POSCO have been compared and confirmed in this part using a set of numerical reference test functions. These functions are frequently utilized in the literature on empirical data to assess the effectiveness of optimizers [37,38].
Table 3 and Table 4 illustrate the mathematical model and properties of these test functions. This standard set is broken down into two groups: unimodal functions, with a single global best for testing the speed and enslavement power of algorithms, and multi-modal functions, with multiple local minimums and a global ideal for testing the ability of algorithms to avoid local optima and conduct exploratory analysis. The recommended algorithms were developed in MATLAB R2020b. It is best to minimize each of these functions. Additionally, the dimension of all functions is 30.

Table 3.
Unimodal benchmark functions.

Table 4.
Multimodal benchmark functions.
The original POA and some famous and efficient optimization techniques, such as particle swarm optimization (PSO) introduced by [39], firefly algorithm (FA) proposed by [40], Multi-Verse Optimizer (MVO) introduced by [41], Tunicate Swarm Algorithm (TSA) developed by [38], and Salp Swarm Algorithm (SSA) [42], are contrasted with the suggested POSCO. To preserve consistency in the evaluation of competitive techniques, the population size is set at 30, and the maximum number of function evaluations (FE) is chosen to be 30,000 for all metaheuristics. As a result, each algorithm’s maximum number of iterations is changed depending on the maximum number of FE that was chosen.
The outcomes of a single metaheuristic technique run are unpredictable and may not be accurate. In order to offer a fair comparison and assess the effectiveness of the algorithms, statistical analysis should be carried out. The results of 30 runs for each of the aforementioned approaches are reported in Table 5 and Table 6 in order to solve this issue.

Table 5.
Results of unimodal test functions comparison.

Table 6.
Results of multimodal test functions comparison.
Table 5 and Table 6 demonstrate that, for all functions, POSCO may offer superior solutions than traditional POA and other optimization approaches, according to the average value of the goal functions. The outcomes also demonstrate that the POSCO algorithm’s mean and standard deviation are substantially lower than those of the other techniques, demonstrating the algorithm’s stability. According to the results, POSCO beats both the conventional method and additional optimization techniques.
7. Results and Comparison
The POSCO was used in this part to decrease the energy usage of the buildings mentioned in Section 5. This structure, as previously indicated, was also optimized in [35]. In [35], To ensure a fair comparison of different optimization strategies, the number of evaluations for the function was set to 100 (dim + 1). The number of choice variables in this situation is dim, which is 4 and 13 in the considered cases. Moreover, the problem is solved 20 times, and the findings were presented as a box plot.
7.1. Simple Office Building Results
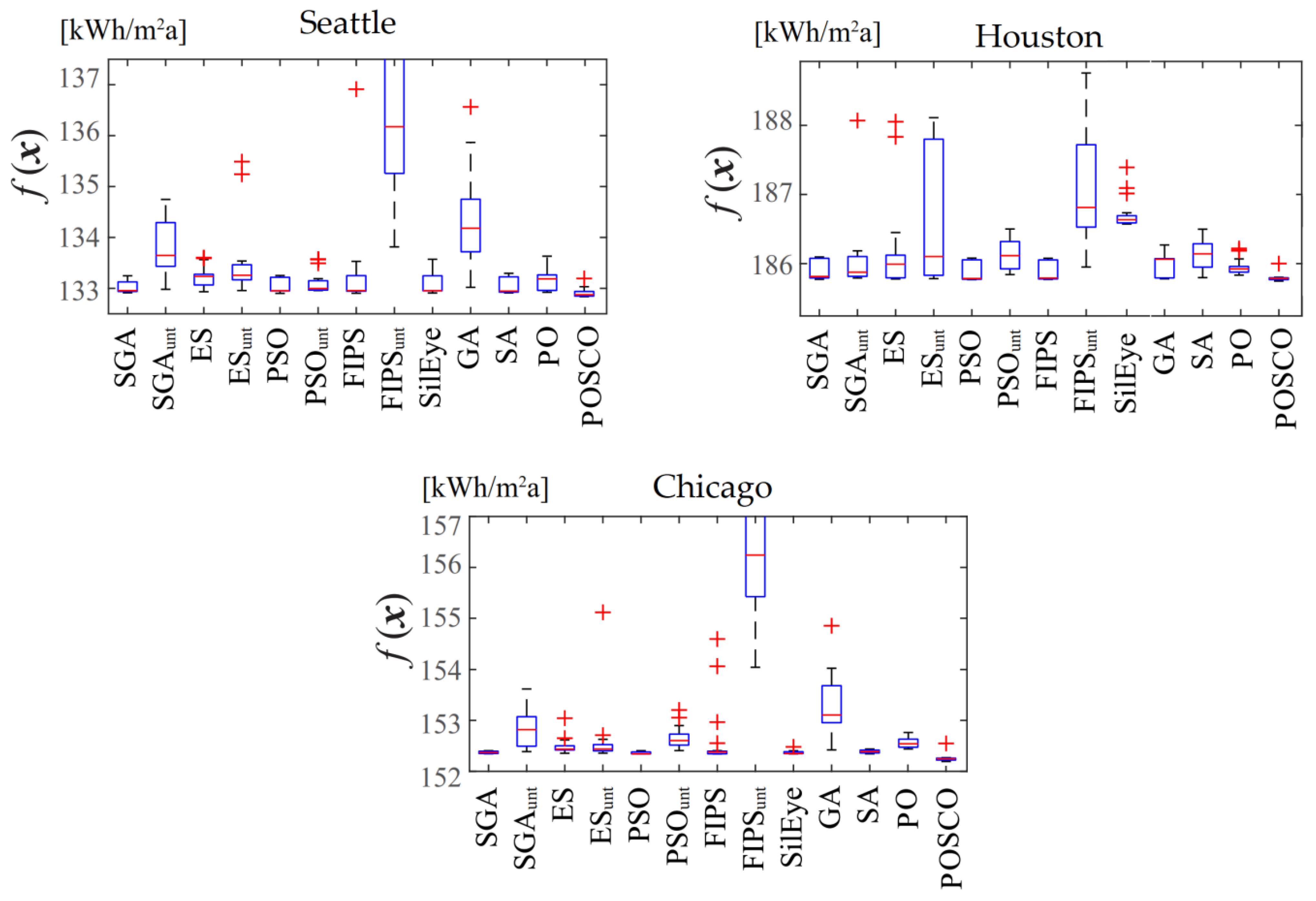
Figure 6 compares the findings of the current investigation by POSCO with those found in the literature for various optimization techniques described by Waibel et al. [35]. Figure 6 shows the POSCO box plot findings for the best and worst instances relevant for each weather condition. FIPSunt and GA perform the poorest in this task in terms of median and spread, but other algorithms regularly outperform them with low median and spread. As can be observed, when compared to the algorithms used in the literature, the POSCO worst case might still produce usable results. Additionally, POSCO’s best-case scenario might deliver exceptional performance in locating the optimal solution. The PSO technique, which provides the best solution for the basic office in Seattle in the range of 132.9–133.5, is one of the finest approaches. The POSCO offers the best option, which falls between 132.6 and 133, with a few points outside of that range. As a result, the worst possible outcome for PSO may be calculated as 133.5, while POSCO results in 133. For the other area, the results are almost the same. The best values of the annual energy usage for Chicago and Houston are 152.2 and 185.5, respectively, which are lower than those evaluated by PO and other techniques. The algorithm was run 20 times, as indicated. The optimum control settings attained for the straightforward office are shown in Table 7.
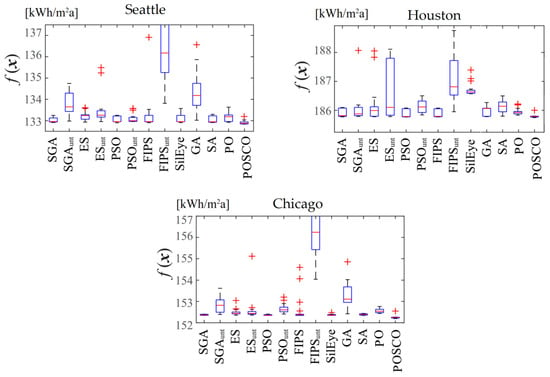
Figure 6.
Box-Whisker plots of the results comparison for a simple office.

Table 7.
Optimized decision variables of the simple office building.
7.2. Detailed Office Building Results
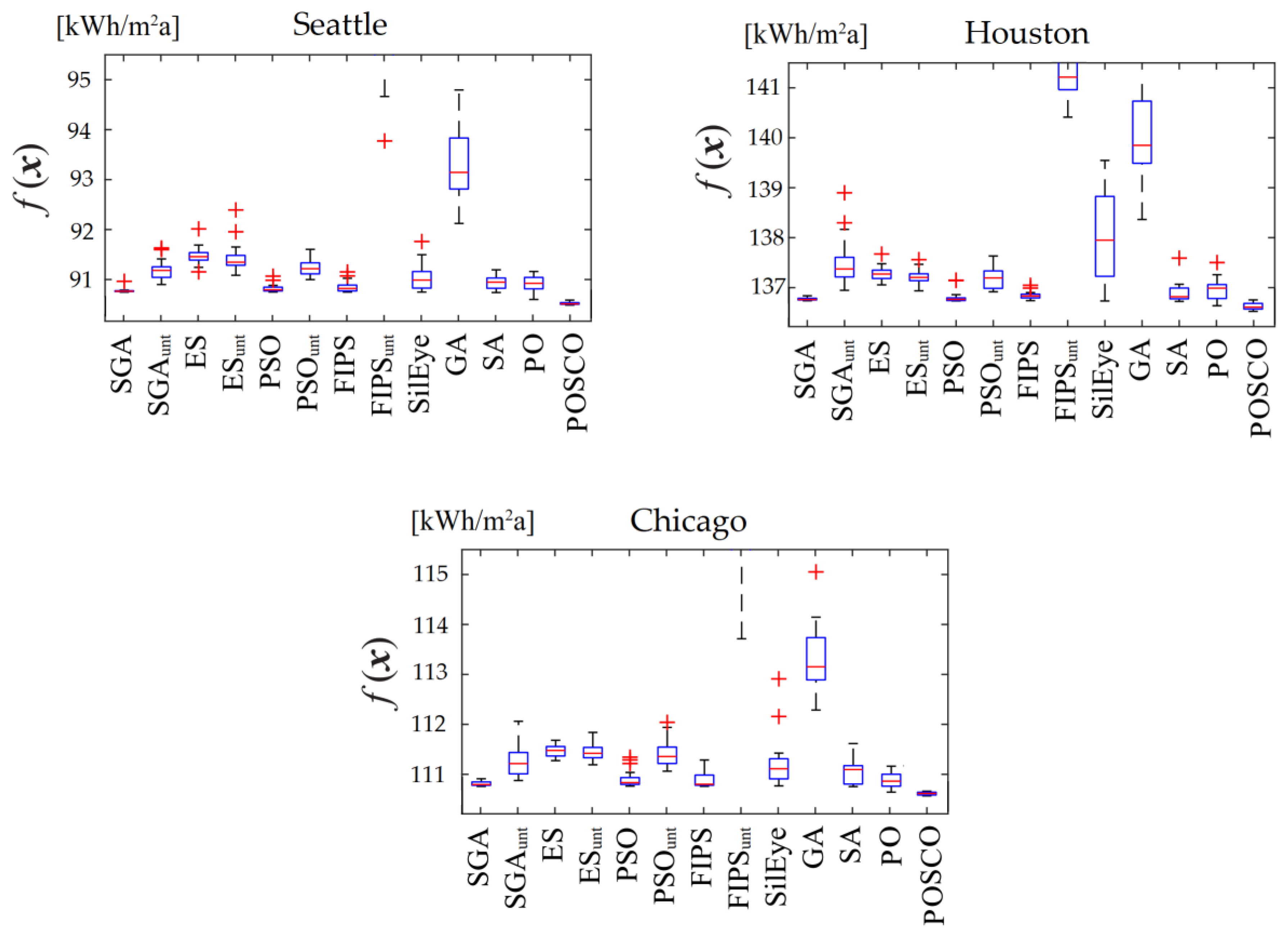
For each weather situation, the final cost values determined by the chosen algorithms are box plotted in Figure 7. Even though the boxes of the weakest, non-competitive optimizers will be cropped, the Y-axes have been resized such that the better optimizers’ boxes can still be identified. As can be observed, FIPSunt and GA have the worst median and spread values.
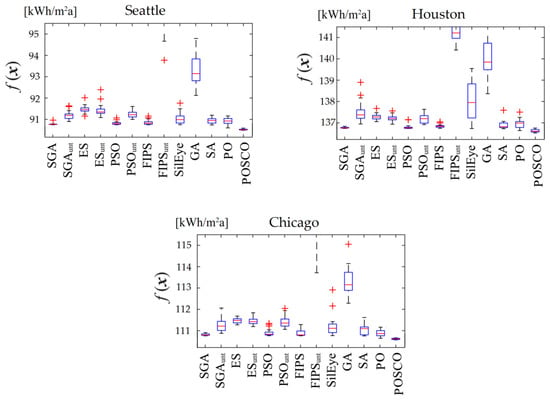
Figure 7.
Box-Whisker plots of the results comparison for the detailed office.
The outcomes appear to be similar to the first issue. PO, SGA, PSO, FIPS, and SA could find acceptable results with low medians and spreads. Surprisingly, the proposed POSCO outperforms other methods in all cases, and the annual energy consumption calculated by POSCO is lower than that achieved by the competitive approaches. According to the results of Figure 7, the most accurate yearly energy usage values for Seattle, Houston, and Chicago are 90.3, 136.4, and 110.5, respectively. These values are almost 0.5 percent lower than the best values obtained in the literature. Aside from this, it appears that the performance of individual optimizers has not been impacted by the change in the weather file.
8. Conclusions
This study presented a hybrid optimization strategy built on the pelican optimization, as well as single candidate optimizer (POSCO), for evaluation of the minimum energy consumption of buildings. The proposed methodology takes advantage of the pelican optimization’s powerful exploratory ability, as well as the single candidate technique’s efficient local search capacity. Several unimodal and multimodal benchmark functions are used to evaluate how well the suggested approach performs. In light of the findings, POSCO surpasses basic POA and other techniques in terms of determining the global solution. When compared to competing methodologies, the proposed method could determine the global best for seven of the thirteen functions that were taken into consideration, and it also produced better results for the remaining functions. The suggested POSCO is then applied to reduce an office building’s yearly energy consumption. Based on the findings of the experiment, the solutions generated by the proposed POSCO are superior to the comparative algorithms for optimizing building energy consumption. The best annual energy usage values for Seattle, Houston, and Chicago, per the results, are almost 0.5 percent less than the best records found in the literature. Additionally, the change to the weather file does not seem to have influenced how well each optimizer is performing individually. The competition simulation results suggest that POSCO may be regarded as a promising candidate approach for BEO models and can estimate the best design effectively and reliably.
Author Contributions
X.Y.: methodology, software, data curation. M.A.K.: conceptualization, investigation. R.B.Y.S.: writing—review & editing, formal analysis. M.K.: writing—original draft preparation, methodology. S.K.: writing—original draft preparation, resources. M.L.N.: supervision, project administration, validation, funding acquisition, writing—review & editing. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Thailand Science Research and Innovation Fundamental Fund fiscal year 2023.
Data Availability Statement
The data that support the findings of this study are available from the corresponding author upon request.
Conflicts of Interest
This research work abides by the highest standards of ethics, professionalism, and collegiality. All authors have no explicit or implicit conflict of interest of any kind related to this manuscript.
References
- Tian, Z.; Chen, W.; Tang, P.; Wang, J.; Shi, X. Building energy optimization tools and their applicability in architectural conceptual design stage. Energy Procedia 2015, 78, 2572–2577. [Google Scholar] [CrossRef]
- Si, B.; Tian, Z.; Jin, X.; Zhou, X.; Shi, X. Ineffectiveness of optimization algorithms in building energy optimization and possible causes. Renew. Energy 2019, 134, 1295–1306. [Google Scholar] [CrossRef]
- Wetter, M.; Wright, J. Comparison of a generalized pattern search and a genetic algorithm optimization method. In Proceedings of the 8th IBPSA Conference, Eindhoven, The Netherlands, 11–14 August 2003; pp. 1401–1408. [Google Scholar]
- Si, B.; Tian, Z.; Jin, X.; Zhou, X.; Tang, P.; Shi, X. Performance indices and evaluation of algorithms in building energy efficient design optimization. Energy 2016, 114, 100–112. [Google Scholar] [CrossRef]
- Gu, M.; Cai, X.; Fu, Q.; Li, H.; Wang, X.; Mao, B. Numerical Analysis of Passive Piles under Surcharge Load in Extensively Deep Soft Soil. Buildings 2022, 12, 1988. [Google Scholar] [CrossRef]
- Zhang, C.; Ali, A.; Sun, L. Investigation on low-cost friction-based isolation systems for masonry building structures: Experimental and numerical studies. Eng. Struct. 2021, 243, 112645. [Google Scholar] [CrossRef]
- Fu, Q.; Gu, M.; Yuan, J.; Lin, Y. Experimental Study on Vibration Velocity of Piled Raft Supported Embankment and Foundation for Ballastless High Speed Railway. Buildings 2022, 12, 1982. [Google Scholar] [CrossRef]
- Li, X.; Wang, H.; Yang, C. Driving mechanism of digital economy based on regulation algorithm for development of low-carbon industries. Sustain. Energy Technol. Assess. 2022, 102909. [Google Scholar] [CrossRef]
- Zheng, W.; Zhou, Y.; Liu, S.; Tian, J.; Yang, B.; Yin, L. A deep fusion matching network semantic reasoning model. Appl. Sci. 2022, 12, 3416. [Google Scholar] [CrossRef]
- Noori, A.; Shahbazadeh, M.J.; Eslami, M. Designing of wide-area damping controller for stability improvement in a large-scale power system in presence of wind farms and SMES compensator. Int. J. Electr. Power Energy Syst. 2020, 119, 105936. [Google Scholar] [CrossRef]
- Eslami, M.; Neshat, M.; Khalid, S.A. A novel hybrid sine cosine algorithm and pattern search for optimal coordination of power system damping controllers. Sustainability 2022, 14, 541. [Google Scholar] [CrossRef]
- Noroozi, M.; Mohammadi, H.; Efatinasab, E.; Lashgari, A.; Eslami, M.; Khan, B. Golden Search Optimization Algorithm. IEEE Access 2022, 10, 37515–37532. [Google Scholar] [CrossRef]
- Eslami, M.; Shareef, H.; Mohamed, A.; Khajehzadeh, M. Optimal location of PSS using improved PSO with chaotic sequence. In Proceedings of the International Conference on Electrical, Control and Computer Engineering 2011 (InECCE), Kuantan, Malaysia, 21–22 June 2011; pp. 253–258. [Google Scholar]
- Eslami, M.; Shareef, H.; Mohamed, A.; Khajehzadeh, M. Coordinated design of PSS and SVC damping controller using CPSO. In Proceedings of the 2011 5th International Power Engineering and Optimization Conference, Shah Alam, Malaysia, 6–7 June 2011; pp. 11–16. [Google Scholar]
- Khajehzadeh, M.; Keawsawasvong, S.; Nehdi, M.L. Effective hybrid soft computing approach for optimum design of shallow foundations. Sustainability 2022, 14, 1847. [Google Scholar] [CrossRef]
- Rad, M.M.; Ibrahim, S.K. Optimal plastic analysis and design of pile foundations under reliable conditions. Period. Polytech. Civ. Eng. 2021, 65, 761–767. [Google Scholar]
- Chin, V.J.; Salam, Z.; Ishaque, K. Cell modelling and model parameters estimation techniques for photovoltaic simulator application: A review. Appl. Energy 2015, 154, 500–519. [Google Scholar] [CrossRef]
- Shi, X.; Tian, Z.; Chen, W.; Si, B.; Jin, X. A review on building energy efficient design optimization rom the perspective of architects. Renew. Sustain. Energy Rev. 2016, 65, 872–884. [Google Scholar] [CrossRef]
- Lorestani, A.; Ardehali, M. Optimization of autonomous combined heat and power system including PVT, WT, storages, and electric heat utilizing novel evolutionary particle swarm optimization algorithm. Renew. Energy 2018, 119, 490–503. [Google Scholar] [CrossRef]
- Pereira, R.; Aelenei, L. Optimization assessment of the energy performance of a BIPV/T-PCM system using Genetic Algorithms. Renew. Energy 2019, 137, 157–166. [Google Scholar] [CrossRef]
- Zheng, W.; Yin, L.; Chen, X.; Ma, Z.; Liu, S.; Yang, B. Knowledge base graph embedding module design for Visual question answering model. Pattern Recognit. 2021, 120, 108153. [Google Scholar] [CrossRef]
- Huang, M.-S.; Gül, M.; Zhu, H.-P. Vibration-based structural damage identification under varying temperature effects. J. Aerosp. Eng. 2018, 31, 04018014. [Google Scholar] [CrossRef]
- Eslami, M.; Shareef, H.; Mohamed, A.; Khajehzadeh, M. Damping Controller Design for Power System Oscillations Using Hybrid GA-SQP. Int. Rev. Electr. Eng.-IREE 2011, 6, 888–896. [Google Scholar]
- Huang, M.; Lei, Y.; Li, X.; Gu, J. Damage identification of bridge structures considering temperature variations-based SVM and MFO. J. Aerosp. Eng. 2021, 34, 04020113. [Google Scholar] [CrossRef]
- Akay, B.; Karaboga, D. Artificial bee colony algorithm for large-scale problems and engineering design optimization. J. Intell. Manuf. 2012, 23, 1001–1014. [Google Scholar] [CrossRef]
- Arabali, A.; Khajehzadeh, M.; Keawsawasvong, S.; Mohammed, A.H.; Khan, B. An Adaptive Tunicate Swarm Algorithm for Optimization of Shallow Foundation. IEEE Access 2022, 10, 39204–39219. [Google Scholar] [CrossRef]
- Luo, J.; Huang, M.; Xiang, C.; Lei, Y. Bayesian damage identification based on autoregressive model and MH-PSO hybrid MCMC sampling method. J. Civ. Struct. Health Monit. 2022, 12, 361–390. [Google Scholar] [CrossRef]
- Khajehzadeh, M.; Taha, M.R.; Eslami, M. Opposition-based firefly algorithm for earth slope stability evaluation. China Ocean. Eng. 2014, 28, 713–724. [Google Scholar] [CrossRef]
- Huang, M.; Cheng, X.; Lei, Y. Structural damage identification based on substructure method and improved whale optimization algorithm. J. Civ. Struct. Health Monit. 2021, 11, 351–380. [Google Scholar] [CrossRef]
- Seyyedabbasi, A.; Kiani, F. Sand Cat swarm optimization: A nature-inspired algorithm to solve global optimization problems. Eng. Comput. 2022, 1–25. [Google Scholar] [CrossRef]
- Shami, T.M.; Grace, D.; Burr, A.; Mitchell, P.D. Single candidate optimizer: A novel optimization algorithm. Evol. Intell. 2022, 1–25. [Google Scholar] [CrossRef]
- Trojovský, P.; Dehghani, M. Pelican optimization algorithm: A novel nature-inspired algorithm for engineering applications. Sensors 2022, 22, 855. [Google Scholar] [CrossRef]
- Cherki, I.; Chaker, A.; Djidar, Z.; Khalfallah, N.; Benzergua, F. A Sequential Hybridization of Genetic Algorithm and Particle Swarm Optimization for the Optimal Reactive Power Flow. Sustainability 2019, 11, 3862. [Google Scholar] [CrossRef]
- Wetter, M.; Wright, J. A comparison of deterministic and probabilistic optimization algorithms for nonsmooth simulation-based optimization. Build. Environ. 2004, 39, 989–999. [Google Scholar] [CrossRef]
- Waibel, C.; Wortmann, T.; Evins, R.; Carmeliet, J. Building energy optimization: An extensive benchmark of global search algorithms. Energy Build. 2019, 187, 218–240. [Google Scholar] [CrossRef]
- Crawley, D.B.; Lawrie, L.K.; Pedersen, C.O.; Winkelmann, F.C. Energy plus: Energy simulation program. ASHRAE J. 2000, 42, 49–56. [Google Scholar]
- Zervoudakis, K.; Tsafarakis, S. A mayfly optimization algorithm. Comput. Ind. Eng. 2020, 145, 106559. [Google Scholar] [CrossRef]
- Kaur, S.; Awasthi, L.K.; Sangal, A.; Dhiman, G. Tunicate swarm algorithm: A new bio-inspired based metaheuristic paradigm for global optimization. Eng. Appl. Artif. Intell. 2020, 90, 103541. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95-International Conference on Neural Networks, Perth, WA, Australia, 27 November—1 December 1995; pp. 1942–1948. [Google Scholar]
- Yang, X.S. Firefly algorithms for multimodal optimization. Lect. Notes Comput. Sci. 2009, 5792, 169–178. [Google Scholar]
- Mirjalili, S.; Mirjalili, S.M.; Hatamlou, A. Multi-verse optimizer: A nature-inspired algorithm for global optimization. Neural Comput. Appl. 2016, 27, 495–513. [Google Scholar] [CrossRef]
- Mirjalili, S.; Gandomi, A.H.; Mirjalili, S.Z.; Saremi, S.; Faris, H.; Mirjalili, S.M. Salp Swarm Algorithm: A bio-inspired optimizer for engineering design problems. Adv. Eng. Softw. 2017, 114, 163–191. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).