BIM-Based Resource Tradeoff in Project Scheduling Using Fire Hawk Optimizer (FHO)
Abstract
1. Introduction
2. Literature Review
2.1. Studies of Resource Trade-Offs
2.2. Applications of Building Information Modelling
| Authors | Time | Cost | Quality | Risk | CO2 | Other Parameters | BIM |
|---|---|---|---|---|---|---|---|
| Hajiagha et al. [59] | |||||||
| Tran and Long [3] | |||||||
| Zheng [60] | |||||||
| Al Haj and El-Sayegh [61] | |||||||
| Khalili-Damghani et al. [62] | |||||||
| Moghadam et al. [63] | |||||||
| Zahraie and Tavakolan [64] | |||||||
| Huynh et al. [65] | |||||||
| Banihashemi and Khalilzadeh [66] | |||||||
| Ghoddousi et al. [67] | |||||||
| Mahmoudi and Feylizadeh [68] | |||||||
| Ebrahimnezhad et al. [69] | |||||||
| Mungle et al. [70] | |||||||
| Koo et al. [71] | |||||||
| Heravi and Moridi [72] | |||||||
| Mohammadipour and Sadjadi [40] | |||||||
| Jeunet and Bou Orm [73] | |||||||
| Hamta et al. [74] | |||||||
| Kosztyán and Szalkai [75] | |||||||
| Current Study |
3. Framework for Resource Tradeoff
3.1. Initialization and Decision Variables
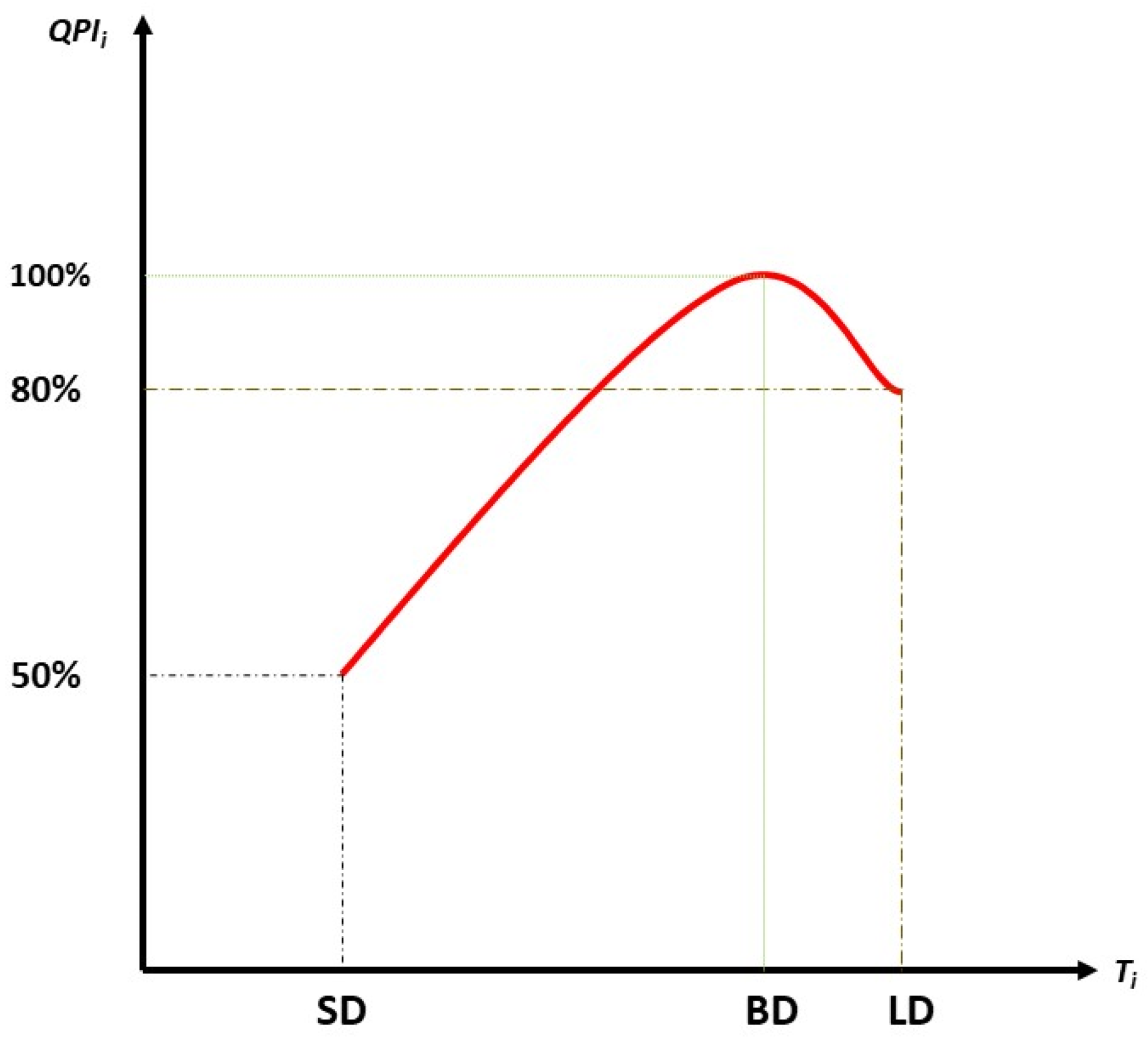
3.2. BIM Module
3.3. Fire Hawk Optimizer (FHO)
3.3.1. Inspiration
3.3.2. Mathematical Model
4. Optimization Results
5. Discussion
6. Conclusions
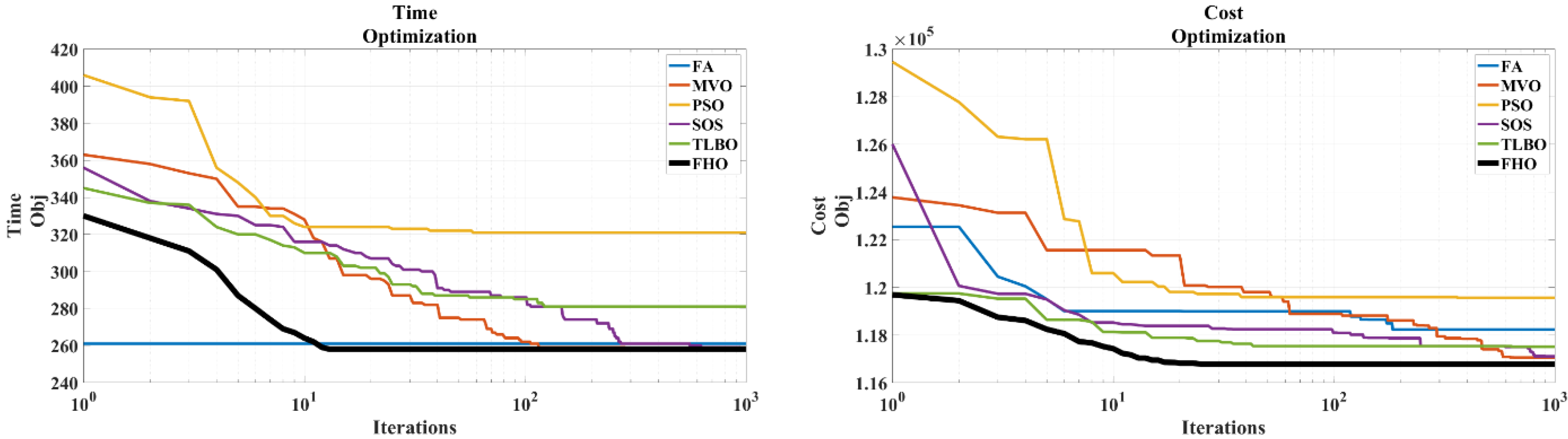
- Based on the outcomes of best optimization runs conducted by different methods in dealing with time optimization, the FHO algorithm could reach the lowest time for the case study, accounting for 258 days.
- The FHO can provide 116,783 ($) for the cost of the case study, which is the best among all approaches.
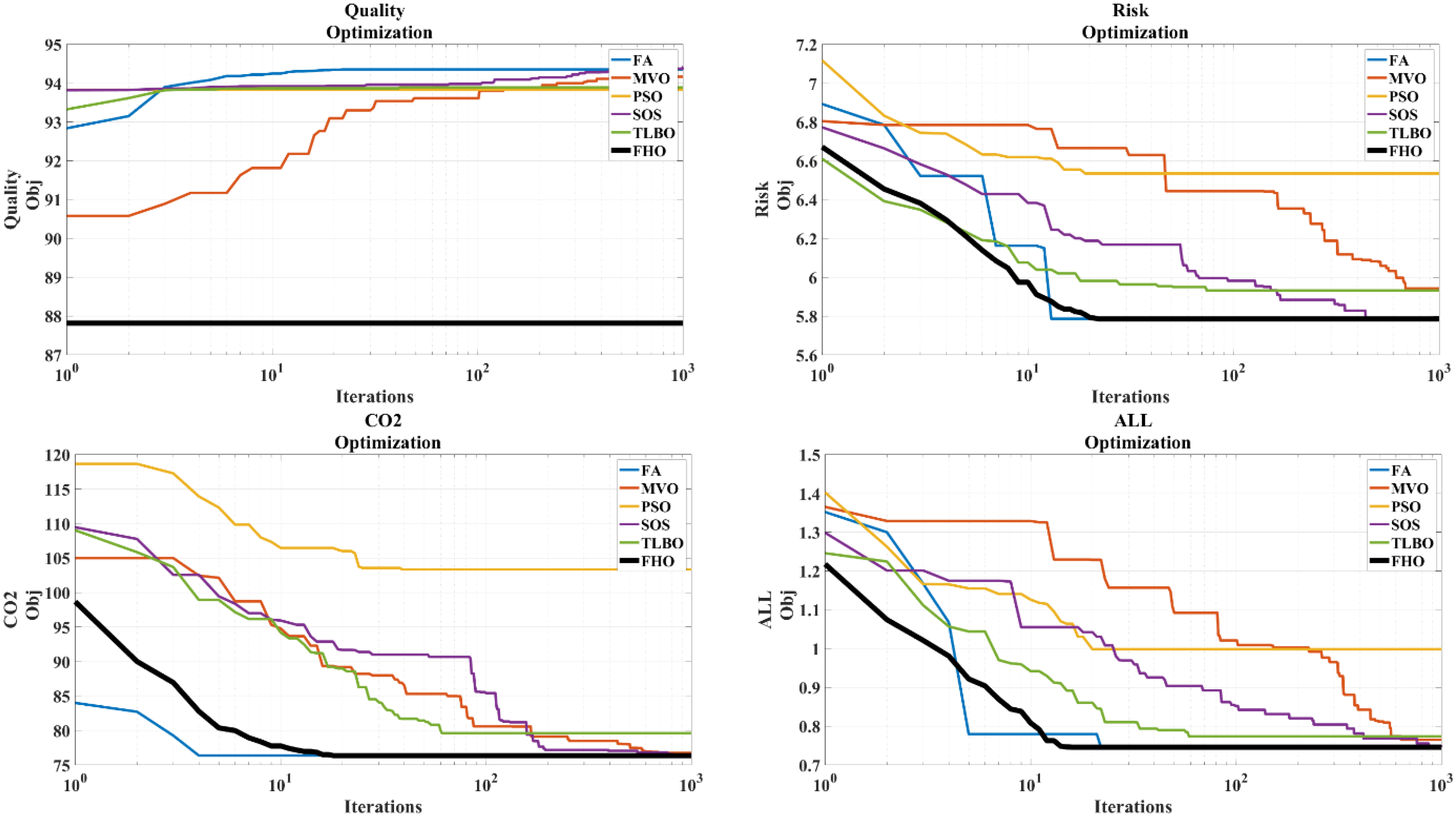
- Regarding quality optimization, the FHO is capable of providing reasonable quality value, but the SOS algorithm gave the best results.
- The FHO algorithm is able to provide the best results for both risk and CO2 optimization in the case study, compared to other alternative algorithms.
- Based on the best results of the TCQRCT problem, the FHO algorithm can provide a score of 0.74, which is much better than the other algorithms.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| NO | Activity | Logical | Mode 1 | Mode 2 | Mode 3 | Mode 4 | Mode 5 | ||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Time | Cost $ | Quality % | Risk | CO2 | Time | Cost $ | Quality % | Risk | CO2 | Time | Cost $ | Quality % | Risk | CO2 | Time | Cost $ | Quality % | Risk | CO2 | Time | Cost $ | Quality % | Risk | CO2 | |||
| 1 | Foundation | - | 26 | 8100 | 90.65 | 14.96667 | 225.3313 | 24 | 7850 | 89.2 | 12 | 198.45 | 20 | 8120 | 92.1 | 12.5 | 187.52 | 15 | 8400 | 78.9 | 12.9 | 98.32 | 13 | 9408 | 74.955 | 16.31367 | 108.152 |
| 2 | Retaining wall | 1FS + 1 | 15 | 2252 | 94.905 | 13.21667 | 137.9707 | 13 | 2150 | 94.51 | 10.5 | 125.08 | 11 | 2220 | 95.3 | 11.3 | 111.04 | 9 | 2410 | 87.1 | 11.54 | 54.25 | 8 | 2699.2 | 82.745 | 14.40617 | 59.675 |
| 3 | Columns of ground | 2FS | 13 | 2015 | 91.155 | 10.33333 | 116.3133 | 10 | 1980 | 90.21 | 8 | 101.3 | 7 | 2042 | 92.1 | 9.4 | 98 | 6 | 2100 | 85.45 | 9.5 | 36.32 | 5 | 2352 | 81.1775 | 11.26333 | 39.952 |
| 4 | Beam and roof of ground | 3FS + 1 | 10 | 4325 | 91.98 | 11.95167 | 188.2833 | 8 | 3652 | 91.4 | 9.65 | 169.91 | 6 | 3920 | 92.56 | 9.8 | 152.36 | 4 | 4150 | 86.41 | 10.3 | 111.25 | 3 | 4648 | 82.0895 | 13.02732 | 122.375 |
| 5 | Columns of 1st floor | 4FS + 2 | 13 | 1550 | 93.605 | 5.58 | 190.8767 | 10 | 1200 | 92.65 | 4.2 | 178.35 | 7 | 1356 | 94.56 | 5.4 | 148 | 6 | 1420 | 89.36 | 6 | 128.6 | 5 | 1590.4 | 84.892 | 6.0822 | 141.46 |
| 6 | Beam and roof of 1st floor | 5FS + 1 | 10 | 3600 | 95.625 | 12.82 | 177.7653 | 8 | 3200 | 94.8 | 10.3 | 177.88 | 6 | 3410 | 96.45 | 10.65 | 125.36 | 4 | 3540 | 85.45 | 11.02 | 45.25 | 3 | 3964.8 | 81.1775 | 13.9738 | 49.775 |
| 7 | Columns of 2nd floor | 6FS + 2 | 13 | 1550 | 92.04 | 8.038 | 158.5137 | 10 | 1200 | 91.3 | 6.32 | 143.65 | 7 | 1356 | 92.78 | 7.05 | 127.63 | 6 | 1420 | 84.12 | 7.8 | 35.98 | 5 | 1590.4 | 79.914 | 8.76142 | 39.578 |
| 8 | Beam and roof of 2nd floor | 7FS + 1 | 10 | 3600 | 97.575 | 9.275 | 183.8583 | 8 | 3200 | 96.5 | 7.25 | 169.25 | 6 | 3410 | 98.65 | 8.25 | 145.25 | 4 | 3540 | 88.89 | 8.5 | 89.54 | 3 | 3964.8 | 84.4455 | 10.10975 | 98.494 |
| 9 | Columns of 3rd floor | 8FS + 2 | 13 | 1550 | 93.99 | 6.903333 | 150.1917 | 10 | 1200 | 93.4 | 5.3 | 145.25 | 7 | 1356 | 94.58 | 6.4 | 111.25 | 6 | 1420 | 78.45 | 6.45 | 74.63 | 5 | 1590.4 | 74.5275 | 7.524633 | 82.093 |
| 10 | Beam and roof of 3rd floor | 9FS + 1 | 10 | 3600 | 91.475 | 3.541667 | 167.4697 | 8 | 3200 | 90.5 | 2.65 | 151.72 | 6 | 3410 | 92.45 | 3.47 | 134.89 | 4 | 3540 | 82.1 | 3.9 | 125.25 | 3 | 3964.8 | 77.995 | 3.860417 | 137.775 |
| 11 | Columns of 4th floor | 10FS + 2 | 13 | 1550 | 92.825 | 6.316667 | 114.523 | 10 | 1200 | 91.4 | 4.5 | 106.58 | 7 | 1356 | 94.25 | 6.8 | 89.25 | 6 | 1420 | 86.45 | 7 | 65.32 | 5 | 1590.4 | 82.1275 | 6.885167 | 71.852 |
| 12 | Beam and roof of 4th floor | 11FS + 1 | 10 | 3600 | 96.375 | 15.29833 | 156.7313 | 8 | 3200 | 95.3 | 11.85 | 143.56 | 6 | 3410 | 97.45 | 13.9 | 124.58 | 4 | 3540 | 91.2 | 14.2 | 43.56 | 3 | 3964.8 | 86.64 | 16.67518 | 47.916 |
| 13 | Columns of 5th floor | 12FS + 2 | 13 | 1550 | 95.315 | 11.845 | 163.6473 | 10 | 1200 | 94.62 | 9.45 | 144.32 | 7 | 1356 | 96.01 | 10.02 | 135.98 | 6 | 1420 | 86.41 | 11.3 | 97.2 | 5 | 1590.4 | 82.0895 | 12.91105 | 106.92 |
| 14 | Beam and roof of 5th floor | 13FS + 1 | 10 | 3600 | 98.57 | 4.689 | 139.1107 | 8 | 3200 | 97.4 | 3.21 | 126.98 | 6 | 3410 | 99.74 | 5.4 | 111.04 | 4 | 3540 | 91.02 | 5.52 | 56.98 | 3 | 3964.8 | 86.469 | 5.11101 | 62.678 |
| 15 | Columns of ridge roof | 14FS + 1 | 5 | 420 | 91.815 | 5.851667 | 124.31 | 3 | 356 | 91.6 | 4.25 | 114.25 | 2 | 411 | 92.03 | 6.08 | 98.4 | 1 | 580 | 83.25 | 6.85 | 75.98 | 1 | 649.6 | 79.0875 | 6.378317 | 83.578 |
| 16 | Beam and roof of ridge floor | 15FS + 1 | 6 | 1110 | 92.96 | 3.342333 | 168.6317 | 4 | 980 | 92.45 | 2.51 | 156.32 | 3 | 995 | 93.47 | 3.25 | 132.07 | 2 | 1020 | 87.98 | 3.65 | 100.36 | 2 | 1142.4 | 83.581 | 3.643143 | 110.396 |
| 17 | Brickworks of ground | 4FS + 1 | 14 | 1620 | 94.035 | 1.658333 | 166.89 | 11 | 1480 | 93 | 1.05 | 157.45 | 9 | 1620 | 95.07 | 2.14 | 127.8 | 8 | 1740 | 79.99 | 2.45 | 98.65 | 7 | 1948.8 | 75.9905 | 1.807583 | 108.515 |
| 18 | Mechanical installations of ground | 17FS + 2 | 10 | 1300 | 95.355 | 8.316667 | 109.0827 | 8 | 1220 | 94.5 | 6.5 | 101.98 | 6 | 1352 | 96.21 | 7.4 | 84.52 | 4 | 1480 | 82.14 | 7.65 | 24.65 | 3 | 1657.6 | 78.033 | 9.065167 | 27.115 |
| 19 | Electrical installations of ground | 17FS + 2 | 15 | 1250 | 95.54 | 6.08 | 128.7647 | 13 | 1100 | 95.3 | 4.9 | 121.07 | 9 | 1260 | 95.78 | 5.01 | 99.04 | 6 | 1350 | 89.65 | 5.63 | 68.42 | 5 | 1512 | 85.1675 | 6.6272 | 75.262 |
| 20 | Brickworks of 1st floor | 6FS + 1 | 14 | 1800 | 92.21 | 5.149333 | 125.9527 | 11 | 1620 | 90.7 | 3.54 | 114.06 | 9 | 1870 | 93.72 | 5.89 | 101.5 | 8 | 1942 | 80.45 | 6 | 45.65 | 7 | 2175.04 | 76.4275 | 5.612773 | 50.215 |
| 21 | Mechanical installations of 1st floor | 20FS + 2 | 10 | 1600 | 97.525 | 5.934667 | 130.917 | 8 | 1520 | 97 | 4.22 | 125.97 | 6 | 1710 | 98.05 | 6.41 | 97.65 | 4 | 1780 | 91.45 | 6.54 | 82.63 | 3 | 1993.6 | 86.8775 | 6.468787 | 90.893 |
| 22 | Electrical installations of 1st floor | 20FS + 2 | 9 | 1420 | 97.65 | 3.786333 | 167.2277 | 7 | 1350 | 96.4 | 2.87 | 151.26 | 5 | 1420 | 98.9 | 3.61 | 134.95 | 4 | 1500 | 87.26 | 3.75 | 111.52 | 3 | 1680 | 82.897 | 4.127103 | 122.672 |
| 23 | Brickworks of 2nd floor | 8FS + 1 | 14 | 1800 | 93.495 | 5.546667 | 193.3917 | 11 | 1620 | 92.3 | 4.2 | 178.32 | 9 | 1870 | 94.69 | 5.3 | 152.47 | 8 | 1942 | 83.45 | 5.5 | 97.52 | 7 | 2175.04 | 79.2775 | 6.045867 | 107.272 |
| 24 | Mechanical installations of 2nd floor | 23FS + 2 | 10 | 1680 | 94.93 | 12.066 | 138.6687 | 8 | 1532 | 94.15 | 9.34 | 126.47 | 6 | 1750 | 95.71 | 10.98 | 110.8 | 4 | 1780 | 88.98 | 11.36 | 64.52 | 3 | 1993.6 | 84.531 | 13.15194 | 70.972 |
| 25 | Electrical installations of 2nd floor | 23FS + 2 | 9 | 1420 | 92.55 | 10.74167 | 181.7427 | 7 | 1350 | 90.47 | 8.45 | 175.65 | 5 | 1420 | 94.63 | 9.41 | 134.74 | 4 | 1500 | 78.32 | 9.5 | 86.52 | 3 | 1680 | 74.404 | 11.70842 | 95.172 |
| 26 | Brickworks of 3rd floor | 10FS + 1 | 14 | 1800 | 94.16 | 2.455 | 165.5457 | 11 | 1620 | 93.32 | 1.65 | 149.08 | 9 | 1870 | 95 | 2.91 | 134.29 | 8 | 1942 | 85.65 | 3.2 | 98.42 | 7 | 2175.04 | 81.3675 | 2.67595 | 108.262 |
| 27 | Mechanical installations of 3rd floor | 26FS + 2 | 10 | 1680 | 91.82 | 2.866 | 178.6877 | 8 | 1530 | 91.24 | 2.04 | 170.36 | 6 | 1740 | 92.4 | 3.09 | 134.95 | 4 | 1780 | 86.97 | 5.2 | 74.77 | 3 | 1993.6 | 82.6215 | 3.12394 | 82.247 |
| 28 | Electrical installations of 3rd floor | 26FS + 2 | 9 | 1420 | 90.435 | 8.185 | 159.032 | 7 | 1350 | 90 | 6.45 | 156.65 | 1420 | 90.87 | 7.14 | 114.78 | 4 | 1500 | 82.42 | 7.65 | 64.52 | 3 | 1680 | 78.299 | 8.92165 | 70.972 | |
| 29 | Brickworks of 4th floor | 12FS + 1 | 14 | 1800 | 96.155 | 12.95467 | 159.094 | 11 | 1620 | 94.98 | 10.32 | 142.36 | 9 | 1870 | 97.33 | 11 | 130.02 | 8 | 1942 | 86.41 | 11.4 | 111.78 | 7 | 2175.04 | 82.0895 | 14.12059 | 122.958 |
| 30 | Mechanical installations of 4th floor | 29FS + 2 | 10 | 1695 | 93.375 | 8.26 | 163.8757 | 8 | 1570 | 92.63 | 6.4 | 153.21 | 6 | 1760 | 94.12 | 7.5 | 126.97 | 4 | 1780 | 86.35 | 7.7 | 42.63 | 3 | 1993.6 | 82.0325 | 9.0034 | 46.893 |
| 31 | Electrical installations of 4th floor | 29FS + 2 | 9 | 1420 | 94.63 | 6.648667 | 158.8867 | 7 | 1350 | 94.17 | 4.98 | 147.36 | 5 | 1420 | 95.09 | 6.5 | 124.36 | 4 | 1500 | 87.42 | 6.52 | 35.59 | 3 | 1680 | 83.049 | 7.247047 | 39.149 |
| 32 | Brickworks of 5th floor | 14FS + 1 | 14 | 1800 | 93.02 | 4.885 | 128.853 | 11 | 1620 | 92.83 | 3.45 | 120.32 | 9 | 1870 | 93.21 | 5.34 | 99.99 | 8 | 1942 | 88.2 | 5.98 | 65.42 | 7 | 2175.04 | 83.79 | 5.32465 | 71.962 |
| 33 | Mechanical installations of 5th floor | 32FS + 2 | 10 | 1680 | 94.025 | 3.137667 | 124.2857 | 8 | 1530 | 93.4 | 2.09 | 111.14 | 6 | 1740 | 94.65 | 3.77 | 101.65 | 4 | 1780 | 85.72 | 3.89 | 85.41 | 3 | 1993.6 | 81.434 | 3.420057 | 93.951 |
| 34 | Electrical installations of 5th floor | 32FS + 2 | 9 | 1420 | 95.065 | 2.351333 | 213.33 | 7 | 1350 | 94.42 | 1.52 | 199.32 | 5 | 1420 | 95.71 | 2.95 | 165.42 | 4 | 1500 | 90.45 | 3.02 | 123.65 | 3 | 1680 | 85.9275 | 2.562953 | 136.015 |
| 35 | Rooftop | 34FS | 15 | 935 | 93.62 | 8.639667 | 188.6087 | 10 | 870 | 92.41 | 6.47 | 178.65 | 7 | 890 | 94.83 | 8.45 | 143.68 | 5 | 920 | 80.65 | 9.2 | 99.98 | 4 | 1030.4 | 76.6175 | 9.417237 | 109.978 |
| 36 | Elevator | 34FS + 2 | 17 | 2400 | 90.805 | 7.126 | 105.351 | 15 | 2150 | 90.56 | 5.24 | 100.36 | 11 | 2350 | 91.05 | 7.23 | 79.65 | 8 | 2680 | 82.42 | 7.77 | 24.63 | 7 | 3001.6 | 78.299 | 7.76734 | 27.093 |
| 37 | Facade | 34FS + 5 | 55 | 5320 | 91.575 | 4.351333 | 194.41 | 52 | 4580 | 91.15 | 3.12 | 189.32 | 37 | 5120 | 92 | 4.63 | 142.62 | 29 | 5980 | 79 | 4.97 | 75.63 | 25 | 6697.6 | 75.05 | 4.742953 | 83.193 |
| 38 | Outdoors | 35FS + 1 | 37 | 2420 | 92.63 | 11.958 | 143.945 | 32 | 2100 | 91.78 | 9.12 | 134.65 | 25 | 2850 | 93.48 | 11.25 | 111.45 | 19 | 3412 | 84.53 | 11.32 | 80.25 | 16 | 3821.44 | 80.3035 | 13.03422 | 88.275 |
References
- Feng, C.-W.; Liu, L.; Burns, S.A. Using Genetic Algorithms to Solve Construction Time-Cost Trade-Off Problems. J. Comput. Civ. Eng. 1997, 11, 184–189. [Google Scholar] [CrossRef]
- Chen, P.-H.; Weng, H. A two-phase GA model for resource-constrained project scheduling. Autom. Constr. 2009, 18, 485–498. [Google Scholar] [CrossRef]
- Tran, D.H.; Long, L.D. Project scheduling with time, cost and risk trade-off using adaptive multiple objective differential evolution. Eng. Constr. Archit. Manag. 2018, 25, 623–638. [Google Scholar] [CrossRef]
- Orm, M.B.; Jeunet, J. Time cost quality trade-off problems: A survey exploring the assessment of quality. Comput. Ind. Eng. 2018, 118, 319–328. [Google Scholar] [CrossRef]
- Shankar, N.R.; Raju, M.; Srikanth, G.; Bindu, P.H. Time, cost and quality trade-off analysis in construction of projects. Contemp. Eng. Sci. 2011, 4, 289–299. [Google Scholar]
- Lotfi, R.; Yadegari, Z.; Hosseini, S.; Khameneh, A.; Tirkolaee, E.; Weber, G. A robust time-cost-quality-energy-environment trade-off with resource-constrained in project management: A case study for a bridge construction project. J. Ind. Manag. Optim. 2022, 18, 375–396. [Google Scholar] [CrossRef]
- Monghasemi, S.; Nikoo, M.R.; Fasaee, M.A.K.; Adamowski, J. A novel multi criteria decision making model for optimizing time–cost–quality trade-off problems in construction projects. Expert Syst. Appl. 2015, 42, 3089–3104. [Google Scholar] [CrossRef]
- Abbasi, S.; Noorzai, E. The BIM-Based multi-optimization approach in order to determine the trade-off between embodied and operation energy focused on renewable energy use. J. Clean. Prod. 2021, 281, 125359. [Google Scholar] [CrossRef]
- Nguyen, D.-T.; Chou, J.-S.; Tran, D.-H. Integrating a novel multiple-objective FBI with BIM to determine tradeoff among resources in project scheduling. Knowl.-Based Syst. 2022, 235, 107640. [Google Scholar] [CrossRef]
- Dhiman, G.; Garg, M.; Nagar, A.; Kumar, V.; Dehghani, M. A novel algorithm for global optimization: Rat Swarm Optimizer. J. Ambient Intell. Humaniz. Comput. 2021, 12, 8457–8482. [Google Scholar] [CrossRef]
- Yampolskiy, R.V.; Ashby, L.; Hassan, L. Wisdom of Artificial Crowds—A Metaheuristic Algorithm for Optimization. J. Intell. Learn. Syst. Appl. 2012, 4, 98–107. [Google Scholar] [CrossRef]
- Xie, L.; Han, T.; Zhou, H.; Zhang, Z.-R.; Han, B.; Tang, A. Tuna Swarm Optimization: A Novel Swarm-Based Metaheuristic Algorithm for Global Optimization. Comput. Intell. Neurosci. 2021, 2021, 9210050. [Google Scholar] [CrossRef] [PubMed]
- Karaboga, D.; Basturk, B. Artificial bee colony (ABC) optimization algorithm for solving constrained optimization problems. In Proceedings of the Foundations of Fuzzy Logic and Soft Computing, Berlin/Heidelberg, Germany, 18–21 June 2007; pp. 789–798. [Google Scholar]
- Talatahari, S.; Azizi, M.; Gandomi, A.H. Material Generation Algorithm: A Novel Metaheuristic Algorithm for Optimization of Engineering Problems. Processes 2021, 9, 859. [Google Scholar] [CrossRef]
- Azizi, M.; Shishehgarkhaneh, M.B.; Basiri, M. Optimum design of truss structures by Material Generation Algorithm with discrete variables. Decis. Anal. J. 2022, 3, 100043. [Google Scholar] [CrossRef]
- Azizi, M. Atomic orbital search: A novel metaheuristic algorithm. Appl. Math. Model. 2021, 93, 657–683. [Google Scholar] [CrossRef]
- Azizi, M.; Talatahari, S.; Giaralis, A. Optimization of Engineering Design Problems Using Atomic Orbital Search Algorithm. IEEE Access 2021, 9, 102497–102519. [Google Scholar] [CrossRef]
- Azizi, M.; Mohamed, A.W.; Shishehgarkhaneh, M.B. Optimum design of truss structures with atomic orbital search considering discrete design variables. In Handbook of Nature-Inspired Optimization Algorithms: The State of the Art; Springer: Cham, Switzerland, 2022; pp. 189–214. [Google Scholar]
- Cunz, D.; Larson, D. Building information modeling. Under Constr. Am. Bar Assoc. 2006, 1–3. Available online: http://www.imageserve.com/naples2013/eunder_construction_12_06.pdf (accessed on 12 September 2022).
- Borrmann, A.; König, M.; Koch, C.; Beetz, J. Building Information Modeling: Technologische Grundlagen und Industrielle Praxis; Springer: Wiesbaden, Germany, 2015. [Google Scholar]
- Khondoker, M.T.H. Automated reinforcement trim waste optimization in RC frame structures using building information modeling and mixed-integer linear programming. Autom. Constr. 2021, 124, 103599. [Google Scholar] [CrossRef]
- Baghalzadeh Shishehgarkhaneh, M.; Fard Moradinia, S. The role of Building Information Modeling (BIM) in reducing the number of project dispute resolution sessions. In Proceedings of the 8th National Conference on Civil Engineering, Architecture and Sustainable Urban Development of Iran, Mashhad, Iran, 5 November 2020. [Google Scholar]
- Farzaneh, A.; Monfet, D.; Forgues, D. Review of using Building Information Modeling for building energy modeling during the design process. J. Build. Eng. 2019, 23, 127–135. [Google Scholar] [CrossRef]
- Charef, R.; Alaka, H.; Emmitt, S. Beyond the third dimension of BIM: A systematic review of literature and assessment of professional views. J. Build. Eng. 2018, 19, 242–257. [Google Scholar] [CrossRef]
- Charef, R.; Emmitt, S.; Alaka, H.; Fouchal, F. Building Information Modelling adoption in the European Union: An overview. J. Build. Eng. 2019, 25, 100777. [Google Scholar] [CrossRef]
- Seyis, S. Mixed method review for integrating building information modeling and life-cycle assessments. Build. Environ. 2020, 173, 106703. [Google Scholar] [CrossRef]
- Daqiqnia, A.H.; Fard Moradinia, S.; Baghalzadeh Shishehgarkhaneh, M. Toward Nearly Zero Energy Building Designs: A Comparative Study of Various Techniques. AUT J. Civ. Eng. 2021, 5, 12. [Google Scholar]
- Nadeem, A.; Wong, A.K.D.; Wong, F.K.W. Bill of Quantities with 3D Views Using Building Information Modeling. Arab. J. Sci. Eng. 2015, 40, 2465–2477. [Google Scholar] [CrossRef]
- Van Eynde, R.; Vanhoucke, M. A reduction tree approach for the Discrete Time/Cost Trade-Off Problem. Comput. Oper. Res. 2022, 143, 105750. [Google Scholar] [CrossRef]
- Sonmez, R.; Bettemir, Ö.H. A hybrid genetic algorithm for the discrete time–cost trade-off problem. Expert Syst. Appl. 2012, 39, 11428–11434. [Google Scholar] [CrossRef]
- Babu, A.J.G.; Suresh, N. Project management with time, cost, and quality considerations. Eur. J. Oper. Res. 1996, 88, 320–327. [Google Scholar] [CrossRef]
- Khang, D.B.; Myint, Y.M. Time, cost and quality trade-off in project management: A case study. Int. J. Proj. Manag. 1999, 17, 249–256. [Google Scholar] [CrossRef]
- Ndamlabin Mboula, J.E.; Kamla, V.C.; Tayou Djamegni, C. Cost-time trade-off efficient workflow scheduling in cloud. Simul. Model. Pract. Theory 2020, 103, 102107. [Google Scholar] [CrossRef]
- Hu, W.; He, X. An Innovative Time-Cost-Quality Tradeoff Modeling of Building Construction Project Based on Resource Allocation. Sci. World J. 2014, 2014, 673248. [Google Scholar] [CrossRef]
- Afruzi, E.N.; Najafi, A.A.; Roghanian, E.; Mazinani, M. A multi-objective imperialist competitive algorithm for solving discrete time, cost and quality trade-off problems with mode-identity and resource-constrained situations. Comput. Oper. Res. 2014, 50, 80–96. [Google Scholar] [CrossRef]
- Sharma, K.; Trivedi, M.K. AHP and NSGA-II-Based time–cost–quality trade-off optimization model for construction projects. In Artificial Intelligence and Sustainable Computing, Proceedings of the 4th International Conference on Sustainable and Innovative Solutions for Current Challenges in Engineering & Technology, ICSISCET 2022, Gwalior, India, 18–19 December 2022; Springer: Singapore, 2022; pp. 45–63. [Google Scholar]
- Ozcan-Deniz, G.; Zhu, Y.; Ceron, V. Time, cost, and environmental impact analysis on construction operation optimization using genetic algorithms. J. Manag. Eng. 2012, 28, 265–272. [Google Scholar] [CrossRef]
- Tran, D.-H.; Luong-Duc, L.; Duong, M.-T.; Le, T.-N.; Pham, A.-D. Opposition multiple objective symbiotic organisms search (OMOSOS) for time, cost, quality and work continuity tradeoff in repetitive projects. J. Comput. Des. Eng. 2018, 5, 160–172. [Google Scholar] [CrossRef]
- Luong, D.-L.; Tran, D.-H.; Nguyen, P.T. Optimizing multi-mode time-cost-quality trade-off of construction project using opposition multiple objective difference evolution. Int. J. Constr. Manag. 2021, 21, 271–283. [Google Scholar] [CrossRef]
- Mohammadipour, F.; Sadjadi, S.J. Project cost–quality–risk tradeoff analysis in a time-constrained problem. Comput. Ind. Eng. 2016, 95, 111–121. [Google Scholar] [CrossRef]
- Amoozad Mahdiraji, H.; Sedigh, M.; Razavi Hajiagha, S.H.; Garza-Reyes, J.A.; Jafari-Sadeghi, V.; Dana, L.-P. A novel time, cost, quality and risk tradeoff model with a knowledge-based hesitant fuzzy information: An R&D project application. Technol. Forecast. Soc. Chang. 2021, 172, 121068. [Google Scholar] [CrossRef]
- Sharma, K.; Trivedi, M.K. Latin hypercube sampling-based NSGA-III optimization model for multimode resource constrained time–cost–quality–safety trade-off in construction projects. Int. J. Constr. Manag. 2020, 1–11. [Google Scholar] [CrossRef]
- Keshavarz, E.; Shoul, A. Project Time-Cost-Quality Trade-off Problem: A Novel Approach Based on Fuzzy Decision Making. Int. J. Uncertain. Fuzziness Knowl.-Based Syst. 2020, 28, 545–567. [Google Scholar] [CrossRef]
- He, W.; Shi, Y.; Kong, D. Construction of a 5D duration and cost optimisation model based on genetic algorithm and BIM. J. Eng. Des. Technol. 2019, 17, 929–942. [Google Scholar] [CrossRef]
- Rahmani Asl, M.; Zarrinmehr, S.; Bergin, M.; Yan, W. BPOpt: A framework for BIM-based performance optimization. Energy Build. 2015, 108, 401–412. [Google Scholar] [CrossRef]
- Sekhar, A.; Maheswari, J.U. BIM integration and value engineering: Design for assembly, optimization, and real time cost visualization in off-site construction. In Proceedings of the Construction Research Congress 2022, Arlington, VA, USA, 9–12 March 2022; pp. 791–801. [Google Scholar]
- Kim, S.; Chin, S.; Kwon, S. A Discrepancy Analysis of BIM-Based Quantity Take-Off for Building Interior Components. J. Manag. Eng. 2019, 35, 05019001. [Google Scholar] [CrossRef]
- ElMenshawy, M.; Marzouk, M. Automated BIM schedule generation approach for solving time–cost trade-off problems. Eng. Constr. Archit. Manag. 2021, 28, 3346–3367. [Google Scholar] [CrossRef]
- Mashayekhi, A.; Heravi, G. A decision-making framework opted for smart building’s equipment based on energy consumption and cost trade-off using BIM and MIS. J. Build. Eng. 2020, 32, 101653. [Google Scholar] [CrossRef]
- Yongge, X.; Ya, W. Study on trade-off of time-cost-quality in construction project based on BIM. In Proceedings of the 2015 International Conference on Economics, Social Science, Arts, Education and Management Engineering, Xi’an, China, 12–13 December 2015; pp. 864–870. [Google Scholar]
- Yu, J.; Wang, J.; Hua, Z.; Wang, X. BIM-based time-cost optimization of a large-span spatial steel structure in an airport terminal building. J. Facil. Manag. 2021, 20, 469–484. [Google Scholar] [CrossRef]
- Gelisen, G.; Griffis, F.H. Automated Productivity-Based Schedule Animation: Simulation-Based Approach to Time-Cost Trade-Off Analysis. J. Constr. Eng. Manag. 2014, 140, B4013007. [Google Scholar] [CrossRef]
- Khosakitchalert, C.; Yabuki, N.; Fukuda, T. Improving the accuracy of BIM-based quantity takeoff for compound elements. Autom. Constr. 2019, 106, 102891. [Google Scholar] [CrossRef]
- Ma, G.; Zhang, L. Exact Overlap Rate Analysis and the Combination with 4D BIM of Time-Cost Tradeoff Problem in Project Scheduling. Adv. Civ. Eng. 2019, 2019, 9120795. [Google Scholar] [CrossRef]
- Shadram, F.; Mukkavaara, J. An integrated BIM-based framework for the optimization of the trade-off between embodied and operational energy. Energy Build. 2018, 158, 1189–1205. [Google Scholar] [CrossRef]
- Sandberg, M.; Mukkavaara, J.; Shadram, F.; Olofsson, T. Multidisciplinary Optimization of Life-Cycle Energy and Cost Using a BIM-Based Master Model. Sustainability 2019, 11, 286. [Google Scholar] [CrossRef]
- Baghalzadeh Shishehgarkhaneh, M.; Fard Moradinia, S.; Keivani, A. Time and cost management of dam construction projects based on Building Information Modeling (BIM) (A Case Study in Kurdistan Province). In Proceedings of the 7th International Congress on Civil Engineering, Architecture and Urban Development, Tehran, Iran, 7–9 December 2021. [Google Scholar]
- Azizi, M.; Talatahari, S.; Gandomi, A.H. Fire Hawk Optimizer: A novel metaheuristic algorithm. Artif. Intell. Rev. 2022. [Google Scholar] [CrossRef]
- Hajiagha, S.H.R.; Akrami, H.; Hashemi, S.S.; Mahdiraji, H.A. An integer grey goal programming for project time, cost and quality trade-off. Eng. Econ. 2015, 26, 93–100. [Google Scholar]
- Zheng, H. The bi-level optimization research for time-cost-quality-environment trade-off scheduling problem and its application to a construction project. In Proceedings of the Tenth International Conference on Management Science and Engineering Management, Baku, Azerbaijan, 30 August–2 September 2016; pp. 745–753. [Google Scholar]
- Al Haj, R.A.; El-Sayegh, S.M. Time–cost optimization model considering float-consumption impact. J. Constr. Eng. Manag. 2015, 141, 04015001. [Google Scholar] [CrossRef]
- Khalili-Damghani, K.; Tavana, M.; Abtahi, A.-R.; Santos Arteaga, F.J. Solving multi-mode time–cost–quality trade-off problems under generalized precedence relations. Optim. Methods Softw. 2015, 30, 965–1001. [Google Scholar] [CrossRef]
- Moghadam, E.K.; Sharifi, M.; Rafiee, S.; Chang, Y.K. Time–Cost–Quality Trade-Off in a Broiler Production Project Using Meta-Heuristic Algorithms: A Case Study. Agriculture 2019, 10, 3. [Google Scholar] [CrossRef]
- Zahraie, B.; Tavakolan, M. Stochastic time-cost-resource utilization optimization using nondominated sorting genetic algorithm and discrete fuzzy sets. J. Constr. Eng. Manag. 2009, 135, 1162–1171. [Google Scholar] [CrossRef]
- Huynh, V.-H.; Nguyen, T.-H.; Pham, H.C.; Huynh, T.-M.-D.; Nguyen, T.-C.; Tran, D.-H. Multiple Objective Social Group Optimization for Time–Cost–Quality–Carbon Dioxide in Generalized Construction Projects. Int. J. Civ. Eng. 2021, 19, 805–822. [Google Scholar] [CrossRef]
- Banihashemi, S.A.; Khalilzadeh, M. Time-cost-quality-environmental impact trade-off resource-constrained project scheduling problem with DEA approach. Eng. Constr. Archit. Manag. 2020, 28, 1979–2004. [Google Scholar] [CrossRef]
- Ghoddousi, P.; Eshtehardian, E.; Jooybanpour, S.; Javanmardi, A. Multi-mode resource-constrained discrete time–cost-resource optimization in project scheduling using non-dominated sorting genetic algorithm. Autom. Constr. 2013, 30, 216–227. [Google Scholar] [CrossRef]
- Mahmoudi, A.; Feylizadeh, M.R. A grey mathematical model for crashing of projects by considering time, cost, quality, risk and law of diminishing returns. Grey Syst. Theory Appl. 2018, 8, 272–294. [Google Scholar] [CrossRef]
- Ebrahimnezhad, S.; Ahmadi, V.; Javanshir, H. Time-cost-quality trade-off in a CPM1 network using fuzzy logic and genetic algorithm. Int. J. Ind. Eng. Prod. Manag. 2013, 24, 361–376. [Google Scholar]
- Mungle, S.; Benyoucef, L.; Son, Y.-J.; Tiwari, M. A fuzzy clustering-based genetic algorithm approach for time–cost–quality trade-off problems: A case study of highway construction project. Eng. Appl. Artif. Intell. 2013, 26, 1953–1966. [Google Scholar] [CrossRef]
- Koo, C.; Hong, T.; Kim, S. An integrated multi-objective optimization model for solving the construction time-cost trade-off problem. J. Civ. Eng. Manag. 2015, 21, 323–333. [Google Scholar] [CrossRef]
- Heravi, G.; Moridi, S. Resource-constrained time-cost tradeoff for repetitive construction projects. KSCE J. Civ. Eng. 2019, 23, 3265–3274. [Google Scholar] [CrossRef]
- Jeunet, J.; Bou Orm, M. Optimizing temporary work and overtime in the Time Cost Quality Trade-off Problem. Eur. J. Oper. Res. 2020, 284, 743–761. [Google Scholar] [CrossRef]
- Hamta, N.; Ehsanifar, M.; Sarikhani, J. Presenting a goal programming model in the time-cost-quality trade-off. Int. J. Constr. Manag. 2021, 21, 1–11. [Google Scholar] [CrossRef]
- Kosztyán, Z.T.; Szalkai, I. Hybrid time-quality-cost trade-off problems. Oper. Res. Perspect. 2018, 5, 306–318. [Google Scholar] [CrossRef]
- Azizi, M.; Mousavi, A.; Ejlali, R.; Talatahari, S. Optimum design of fuzzy controller using hybrid ant lion optimizer and Jaya algorithm. Artif. Intell. Rev. 2020, 53, 1553–1584. [Google Scholar] [CrossRef]
- Panwar, A.; Jha, K.N. Integrating Quality and Safety in Construction Scheduling Time-Cost Trade-Off Model. J. Constr. Eng. Manag. 2021, 147, 04020160. [Google Scholar] [CrossRef]
- Zhang, L.; Du, J.; Zhang, S. Solution to the time-cost-quality trade-off problem in construction projects based on immune genetic particle swarm optimization. J. Manag. Eng. 2014, 30, 163–172. [Google Scholar] [CrossRef]
- Al-Gahtani, K.S. Float Allocation Using the Total Risk Approach. J. Constr. Eng. Manag. 2009, 135, 88–95. [Google Scholar] [CrossRef]
- Garza, J.M.d.l.; Prateapusanond, A.; Ambani, N. Preallocation of Total Float in the Application of a Critical Path Method Based Construction Contract. J. Constr. Eng. Manag. 2007, 133, 836–845. [Google Scholar] [CrossRef]
- Long, L.D.; Tran, D.-H.; Nguyen, P.T. Hybrid multiple objective evolutionary algorithms for optimising multi-mode time, cost and risk trade-off problem. Int. J. Comput. Appl. Technol. 2019, 60, 203–214. [Google Scholar] [CrossRef]
- Yang, X.-S. Firefly algorithm, stochastic test functions and design optimisation. arXiv 2010, arXiv:1003.1409. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.; Hatamlou, A. Multi-Verse Optimizer: A nature-inspired algorithm for global optimization. Neural Comput. Appl. 2015, 27, 495–513. [Google Scholar] [CrossRef]
- Eberhart, R.; Kennedy, J. Particle swarm optimization. In Proceedings of the IEEE International Conference on Neural Networks, Perth, Australia, 27 November–1 December 1995; pp. 1942–1948. [Google Scholar]
- Tejani, G.G.; Savsani, V.J.; Patel, V.K. Adaptive symbiotic organisms search (SOS) algorithm for structural design optimization. J. Comput. Des. Eng. 2016, 3, 226–249. [Google Scholar] [CrossRef]
- Rao, R.V. Teaching-learning-based optimization algorithm. In Teaching Learning Based Optimization Algorithm; Springer: Cham, Switzerland, 2016; pp. 9–39. [Google Scholar]
- Gutierrez, G.; Gardella, R.; Ryan, B. New Colorado VA Hospital Is State of the Art, and More than $1 Billion Over Budget. Available online: https://www.nbcnews.com/storyline/va-hospital-scandal/new-colorado-va-hospital-state-art-more-1-billion-over-n898091 (accessed on 18 August 2020).


| FA | MVO | PSO | SOS | TLBO | FHO (Current Study) | |
|---|---|---|---|---|---|---|
| Time | 261 | 258 | 321 | 258 | 281 | 258 |
| Cost | 118,230 | 117,056 | 119,564.8 | 117,104.6 | 117,512 | 116,783 |
| Quality | 94.35 | 94.16 | 93.82 | 94.41 | 93.89 | 87.81 |
| Risk | 5.78 | 5.94 | 6.53 | 5.78 | 5.93 | 5.78 |
| CO2 | 76.35 | 76.74 | 103.35 | 76.35 | 79.60 | 76.35 |
| All | 0.74 | 0.76 | 0.99 | 0.74 | 0.77 | 0.74 |
| FA | MVO | PSO | SOS | TLBO | FHO (Current Study) | |
|---|---|---|---|---|---|---|
| Time | ||||||
| Best | 261 | 258 | 321 | 258 | 281 | 258 |
| Mean | 261 | 258.9 | 392.7 | 260.76 | 300.6 | 258.03 |
| Worst | 261 | 261 | 453 | 266 | 316 | 259 |
| Std | 0 | 1.21 | 35.07 | 1.71 | 9.04 | 0.18 |
| Computational time (s) | 2.19 | 1.61 | 2.35 | 1.40 | 1.44 | 8.66 |
| Cost | ||||||
| Best | 118,230 | 117,056 | 119,564.8 | 117,104.6 | 117,512 | 116,783 |
| Mean | 118,558.6 | 117,511.9 | 135,480.6 | 117,498.3 | 118,322.9 | 116,839.7 |
| Worst | 118,780 | 118,284.6 | 155,151.7 | 117,920 | 119,070 | 117,011 |
| Std | 148.09 | 271.58 | 9952.33 | 222.75 | 397.19 | 59.57 |
| Computational time (s) | 2.16 | 1.57 | 2.13 | 1.39 | 1.44 | 9.66 |
| Quality | ||||||
| Best | 94.35 | 94.16 | 93.82 | 94.41 | 93.89 | 87.81 |
| Mean | 94.46 | 94.24 | 93.89 | 94.54 | 94.01 | 89.63 |
| Worst | 94.56 | 94.40 | 94.12 | 94.62 | 94.27 | 91.46 |
| Std | 0.04 | 0.05 | 0.06 | 0.04 | 0.08 | 0.78 |
| Computational time (s) | 9.05 | 1.44 | 2.11 | 1.40 | 1.44 | 2.03 |
| Risk | ||||||
| Best | 5.78 | 5.94 | 6.53 | 5.78 | 5.93 | 5.78 |
| Mean | 5.78 | 6.07 | 7.13 | 5.79 | 6.03 | 5.78 |
| Worst | 5.78 | 6.28 | 7.46 | 5.82 | 6.20 | 5.78 |
| Std | 9.03 × 10−16 | 8.45 × 10−02 | 2.47 × 10−1 | 0.01 | 6.99 × 10−2 | 9.03 × 10−16 |
| Computational time (s) | 2.27 | 1.56 | 2.05 | 1.39 | 1.43 | 8.67 |
| CO2 | ||||||
| Best | 76.35 | 76.44 | 103.35 | 76.35 | 79.60 | 76.35 |
| Mean | 76.35 | 77.87 | 116.23 | 76.68 | 88.24 | 76.40 |
| Worst | 76.35 | 80.41 | 129.54 | 77.20 | 94.47 | 76.59 |
| Std | 1.45 × 10−14 | 0.92 | 6.20 | 0.24 | 4.19 | 0.06 |
| Computational time (s) | 1.93 | 1.59 | 2.29 | 1.38 | 1.42 | 12.52 |
| All | ||||||
| Best | 0.74 | 0.76 | 0.99 | 0.74 | 0.77 | 0.74 |
| Mean | 0.74 | 0.84 | 1.42 | 0.75 | 0.86 | 0.74 |
| Worst | 0.74 | 0.95 | 1.67 | 0.78 | 0.94 | 0.74 |
| Std | 2.26 × 10−16 | 0.04 | 0.21 | 0.01 | 0.04 | 2.26 × 10−16 |
| Computational time (s) | 1.98 | 1.70 | 2.42 | 1.38 | 1.43 | 10.96 |
| Number | Objective | Mode of Activities |
|---|---|---|
| 1 | Time | FA:55555555555555555555555555555555555555 |
| MVO:55555555555555555555555555535555555555 | ||
| PSO:54435325555255525554445513453113245445 | ||
| SOS:55555555555555555555555555535555555555 | ||
| TLBO:55555555451455444555452455535554533555 | ||
| FHO:55555555555555555555555555535555555555 | ||
| 2 | Cost | FA:43334343343242333433343332332343434342 |
| MVO:44423244423333243443442432432432444332 | ||
| PSO:23323225253434543344542434433424342234 | ||
| SOS:43423432334442343442432533432432434332 | ||
| TLBO:43444442424243244342432443234444244332 | ||
| FHO:43424442444242343442432442432442434332 | ||
| 3 | Quality | FA:33331133333111131131333333331331133311 |
| MVO:13331131311313331331131111333133113311 | ||
| PSO:11111111111111111111111111111111111111 | ||
| SOS:13113333131333313313113333313313313133 | ||
| TLBO:11311111111111111111111113311111111111 | ||
| FHO:15344214411545354222554535254442254422 | ||
| 4 | Risk | FA:22222222222222222222222222222222222222 |
| MVO:22222222222225525232222222222222252222 | ||
| PSO:22334322222225253225425431323232412424 | ||
| SOS:22222222222222222222222222222222222222 | ||
| TLBO:23222322322222222232231222222322222222 | ||
| FHO:22222222222222222222222222222222222222 | ||
| 5 | CO2 | FA:44444444444444444444444444444444444444 |
| MVO:15544232142225444342331444434454444444 | ||
| PSO:15544232142225444342331444434454444444 | ||
| SOS:44444444444444444444444444444444444444 | ||
| TLBO:54443454444543444544444445445444544444 | ||
| FHO:44444444444444444444444444444444444444 | ||
| 6 | All | FA:33333333333333333333333333333333333333 |
| MVO:33333333333333323333333333333333333353 | ||
| PSO:33323343223244133333535234333222333333 | ||
| SOS:33333333333333333333333333333333333333 | ||
| TLBO:33333333333333333333333332333333332333 | ||
| FHO:33333333333333333333333333333333333333 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shishehgarkhaneh, M.B.; Azizi, M.; Basiri, M.; Moehler, R.C. BIM-Based Resource Tradeoff in Project Scheduling Using Fire Hawk Optimizer (FHO). Buildings 2022, 12, 1472. https://doi.org/10.3390/buildings12091472
Shishehgarkhaneh MB, Azizi M, Basiri M, Moehler RC. BIM-Based Resource Tradeoff in Project Scheduling Using Fire Hawk Optimizer (FHO). Buildings. 2022; 12(9):1472. https://doi.org/10.3390/buildings12091472
Chicago/Turabian StyleShishehgarkhaneh, Milad Baghalzadeh, Mahdi Azizi, Mahla Basiri, and Robert C. Moehler. 2022. "BIM-Based Resource Tradeoff in Project Scheduling Using Fire Hawk Optimizer (FHO)" Buildings 12, no. 9: 1472. https://doi.org/10.3390/buildings12091472
APA StyleShishehgarkhaneh, M. B., Azizi, M., Basiri, M., & Moehler, R. C. (2022). BIM-Based Resource Tradeoff in Project Scheduling Using Fire Hawk Optimizer (FHO). Buildings, 12(9), 1472. https://doi.org/10.3390/buildings12091472










