Abstract
Recently, the light-type pier can be easily observed in urban elevated roads and bridge structures. This type of pier is broadly used in the field of structural engineering. The Thin-Walled Steel-Reinforced Concrete Pier (TSRCP), as the typical pier of the light-type piers, shows a better mechanical performance than the conventional reinforced concrete pier due to the enhancement of the H-shape steel. In terms of the TSRCP, the designed parameters, including the depth–width ratio (DWR) and axial compression ratio (ACR), have been determined in this study as the concerned variables. Then, a low cyclic loading experiment is conducted based on the three test specimens to investigate the effects of the concerned variables on the failure of the specimens. Meanwhile, some comparative studies are carried out based on the failure processes and modes, critical loading values (cracking, yielding and ultimate state), strain and ductility. The obtained experimental results demonstrate that all specimens illustrate a bending failure mode under the vertical and horizontal low cyclic loadings. Furthermore, for the concerned variables, the increasing DWR will reduce the ultimate bearing capacity of the TSRCP but enhance the plastic deformation. For the ACR, the decrease positively affects the cracking load, further improving the ultimate bearing capacity; however, the deformation capacity will be restrained. Finally, Abaqus is adopted to model the failure processes of three specimens; the comparative study has been conducted based on the simulated and experimental results. After that, the effects of the concerned variables on the failure performances are discussed. Meanwhile, the horizontal ultimate bearing capacity calculated equation for the TSRCP was deduced and validated based on the experimental and simulated data; the verification proves that the proposed equation can obtain a good result. In this study, the complex calculated process of the original equation can be simplified, which not only provides a convenient and useful way to design and manufacture this type of component but can serve as a guideline for validating the practical engineering applications.
1. Introduction
As the light-type pier shows several benefits, including its light weight, less required material and lower construction cost, it has been widely used in the last several decades in the structural design of urban viaducts, railway bridges and high-speed road bridges, which shows an excellent development trend and good application value [] Among the different categories of light-type piers, the classic is the thin-walled pier with a slender shape with a larger depth–width ratio (DWR). Thus, the horizontal force will cause a larger displacement on the top of this type of pier. Meanwhile, regarding the wide utilization of this type of pier in actual bridge engineering, it is necessary to evaluate the seismic performance to ensure the safety and operation of the bridge. In this regard, Pinto et al. [] conducted a study based on the existing models of the bridges in Austria; the findings show that these models not only cannot satisfy the current seismic code but also illustrate the adverse failure modes. Lehman et al. [] carried out an experimental evaluation of the reinforced concrete column; the results demonstrated that the failure of the column is closely related to the buckling of longitudinal bars. Zhang et al. [] focused on the concrete columns strengthened with carbon textile-reinforced concrete taking a uniaxial load; the corresponding confinement behavior and stress–strain responses were studied. Afterward, the team of Zhang et al. [,] also considered the mechanical performance of the reinforced concrete with corroded reinforcement.
Other studies [,,,,] firstly established the analytical models based on practical bridge engineering. The seismic performance of reinforced concrete piers were investigated, and ductility coefficients were also studied through the experiments. In studies [,,], aiming at the rectangular reinforced concrete piers, the experiments were conducted under cyclic loading; the results indicated that this shape of the column has significant ductility and seismic performance. Furthermore, Zhao et al. [] and Cassese et al. [] investigated the seismic performance of the rectangular hollow piers; the outcomes showed that the bending failure mode occurred in the pier with the larger DWR. Moreover, Su et al. [] studied the effects of yield strength of longitudinal reinforcement and the compressive strength of concrete on the seismic performance of reinforced concrete piers; the results showed that all test specimens illustrate a classical bending failure mode, and regarding the different shapes of cross-sections, the compressive strength of concrete has more serious effects on the pier with rectangular cross-section than a circular one. However, the above-mentioned statements only consider the conventional reinforced concrete pier. Some new types of piers, such as the thin-walled steel-reinforced concrete pier (TSRCP), were not mentioned, which could be a potential research topic of interest.
TSRCP can simultaneously adopt the merits of concrete and steel structures, namely, their reasonable force transmission, large bearing capacity and good stability [,], and the application of this type of pier can ensure the requirements for seismic performance and wind resistance. Therefore, Johansson et al. [] reported that the bearing capacity of the steel-concrete short column is determined based on the yielding strength of the steel. Both reported that the increase in the axial compression ratio can enhance the shearing strength of the steel-reinforced concrete column [,]. Then, Chang et al. [] and Nie et al. [] reported that a tubed, steel-reinforced concrete column also shows good ductility and seismic performance under combined loading conditions. Meanwhile, Naito et al. [] implemented the cyclic lateral loading test based on the steel-reinforced-concrete specimens; the ultimate state was defined as the spalling of concrete cover and buckling of the flange in H-shape steel, then the ductility of the steel-reinforced-concrete column was analyzed. Zhang et al. [] and Zhu et al. [] pointed out that the hoop reinforcements and the section steel constraint on the concrete were two key factors to the seismic performance. Yin et al. [] also reported that the seismic performance of the pier is mainly determined by the adopted cross-section of the section steel and the steel ratio, and Cao et al. [] verified the effects of the steel ratio on the ductility through the Abaqus finite element simulation. Furthermore, Yang and Song [] emphasized that not only does the axial load coefficient but also the reinforcement form of the steel section has a significant influence on the seismic performance of the high-strength concrete column. Moreover, Fang et al. [] and Wang et al. [] found good ductility and anti-seismic behavior in the cross-shaped steel-reinforced concrete column. Other studies [,] aimed at the partially prefabricated steel-reinforced concrete composite column; the corresponding seismic performance was evaluated, and the results showed that the specimen with a small DWR showed a shear failure, and the one with a large DWR showed a bending shear failure.
According to the above-mentioned studies, it can be seen that reinforced concrete columns are mainly adopted in the piers of the existing bridges; the corresponding cross-sections are the most rectangular of the sections, and the application of a steel-reinforced concrete pier and the thin-walled section are rare. Thus, in order to fill this research gap, this study uses a conventional reinforced concrete column combined with a steel–concrete composite structure to construct a TSRCP. Then, the axial compression ratio and DWR are determined as concerned variables; the experiment under low cyclic loading is conducted based on the designed test specimens to investigate the failure performance of the TSRCP. Furthermore, the failure processes have been modelled based on the Abaqus to conduct a comparative study. We also discuss the effects of the concerned variables. Moreover, the horizontal ultimate bearing capacity equation for TSRCP has been proposed for the engineering application.
The remaining sections are organized as follows: Section 2 introduces the design of specimens and experimental procedure; Section 3 discusses the obtained experimental results. Section 4 conducts the finite element analysis to make a comparison. Furthermore, we further discuss the effects of the concerned variables on the failure performances of the specimens in Section 5. After that, the horizontal ultimate bearing capacity equation for the TSRCP is proposed in Section 6. Finally, several conclusions and perspectives are presented in Section 7.
2. Experimental Procedure
2.1. Design of Specimens
To analyze the effects of the concerned variables on the failure performance, three test specimens were designed and listed in Table 1. It should be pointed out that SRCZ-2 was designed as a standard specimen, and SRCZ-1 and SRCZ-3 were manufactured to study the axial compression ratio (ACR) and depth–width ratio (DWR), respectively. The corresponding equations can be shown as follows:
where denotes the axial compression designed value of the column; stands for the cross-sectional area; is the design value of axial compressive strength of concrete; is the length of the column and is the shorter dimension of the section. For each test specimen, the cross-sectional size is 250 mm × 800 mm, and it was manufactured based on C30 concrete and Q235B H-shape steel (Height × Width × Web Thickness × Flange Thickness is 100 mm × 120 mm × 10 mm × 10 mm). Then, between the different types of steel, the connection was formed through the batten plate, which has a thickness and width of 6 mm and 30 mm, respectively. Furthermore, a steel plate was adopted to fix the bottom of the H-shape steel and the foundation. Meanwhile, the longitudinal(vertical, number 10, diameter 16 mm) and hooped reinforcements (diameter 8 mm, the space is 150 mm) are both HRB335 steel. The related parameters and the reinforcement arrangements are shown in Table 1 and Figure 1.

Table 1.
The Design Parameters for the Test Specimens.
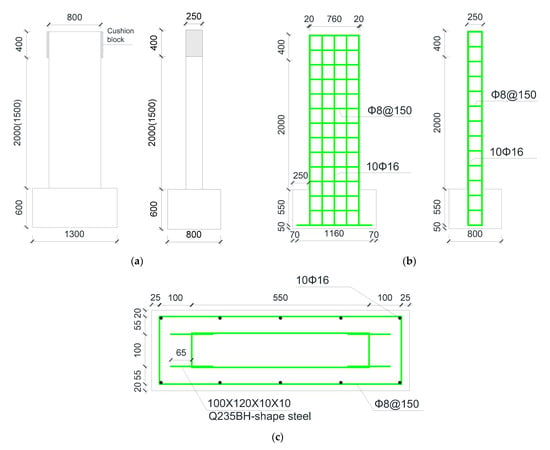
Figure 1.
The Dimension and Steel Arrangement of the Test Specimens. (a) The dimensions of the test specimens. (b) Reinforcement arrangement. (c) H-shape steel arrangement.
Based on the above-mentioned design parameters and drawings, the three specimens were manufactured in the laboratory; the reinforcement skeleton was constructed based on the longitudinal and hooped reinforcements. Then, the batten plate was welded on the wing of the adjacent H-shape steel. Afterward, the reinforcement skeleton and H-shape steel were assembled for the subsequent pouring of concrete. The process is illustrated in Figure 2.

Figure 2.
The Manufacturing Process of the Test Specimens. (a) Reinforcement skeleton. (b) H-shape steel. (c) Pouring of concrete.
2.2. The Mechanical Performance of the Used Materials
In order to measure the actual strength of the used materials, according to the Chinese Specification and Code <GB/T 2975-2018>, the adopted reinforcement and H-shape steel (including web and flange) were handled to obtain three groups of steel specimens for the standard tensile test. In addition, three concrete cubes of 150 mm × 150 mm × 150 mm were utilized to measure the strength of the adopted concrete. The test results of the two materials are illustrated in Table 2.

Table 2.
The Measured Strength of the Two Materials.
2.3. The Monitored Indicators and Layout of Sensors
2.3.1. Cracks Monitoring
The appearance of cracks on the surface of the concrete is always a good indicator to conduct an analysis of the failure of the test specimen. For the purposes of the clear and obvious observation of cracks, it must be ensured that the surface of the concrete is clean before the test. Then, a series of square grids (10 cm × 10 cm) were plotted on the surfaces of the front and back of the test specimen. Meanwhile, during the loading process, the location and development of the emerged cracks should be carefully observed. After every load level has been achieved, the emerged cracks should be painted black, accompanied by the corresponding load and displacement written near the cracks. Next, the maximum width of the current cracks must be recorded. Finally, after the experiment finishes, the entire distribution of the cracks should be photographed.
2.3.2. Strain Measurement
Regarding the requirement of strain measurement, several strain gauges were fixed on the reinforcement and the surface of the concrete in this study. As shown in Figure 3a, a total of four strain rosettes were placed on the H-shape steel and some strain gauges for the reinforcement skeleton (Figure 3b). The locations were 50 mm and 1/4 of a column length away from the foundation. For the concrete, there were five strain gauges in the front, and three gauges on each side (Figure 3c).
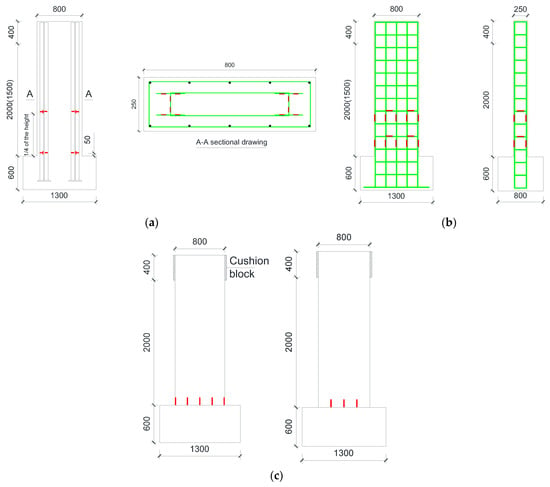
Figure 3.
The Layout of the Strain Gauges. (a) H-shape steel. (b) Reinforcement. (c) Concrete.
2.3.3. Displacement Measurement
Then, a total of four displacement gauges were installed on the column. As shown in Figure 4, there was one for the top, two for the middle, and one for the top surface of the foundation.
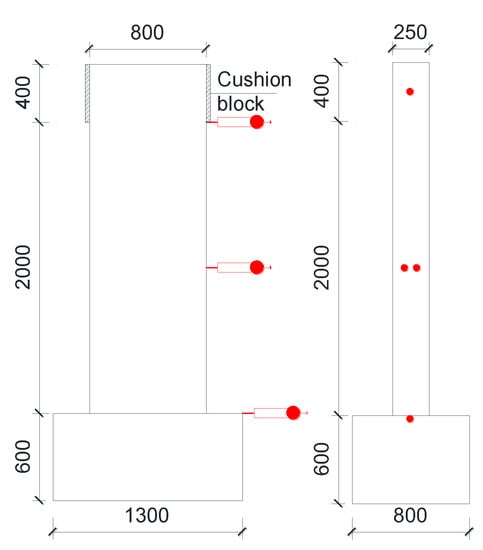
Figure 4.
The Layout of Displacement Gauges.
2.4. Test Setup
The load test was conducted in accordance with the Chinese Specification and Code <JGJ 101-2015>; the load and displacement were both adopted to control the test []. An electro-hydraulic servo loading system was utilized to apply the external load; firstly, the required axial compressive load was provided through the vertical jack []. Regarding the different ACRs, different loads were adopted for each specimen, such as 400 kN for SRCZ-3, and 200 kN for the other specimens. After that, the vertical load should be kept constant as a precondition for the subsequent horizontal load.
Before the specimen yielding, the experiment process was controlled based on the applied load. Meanwhile, the applied external load followed the mechanism of incremental step loading; the initial load should achieve 20% of the max load; Then, the incremental load step is 10%, and each step of the external load must be repeated once. Then, when the yielding has emerged in the specimen, the corresponding relative displacement on the top of the column , should be recorded for the next controlling mechanism; namely, the subsequent load should refer to multiples of , for each step, it should be repeated three times. Based on the mechanism mentioned above, the horizontal load should be monitored; when the corresponding load value has decreased to 85% of the peak value, or the specimen cannot bear the preset axial compressive load, the applied external load will be stopped. The schematic diagram and loading protocol of the test are illustrated in Figure 5.
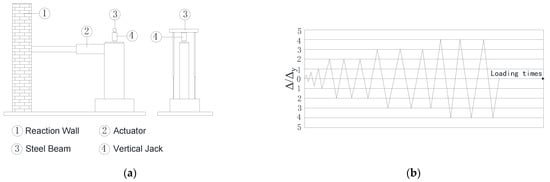
Figure 5.
The Test Setup. (a) The schematic diagram. (b) The loading protocol.
3. Analysis and Discussion of Experimental Results
3.1. The Measured Load and Failure Mode
After the test has been completed, the measured load data and the corresponding displacement values are listed in Table 3, as well as the failure mode. Overall, the measured data of SRCZ-2 was taken as the benchmark and the DWR and ACR as the concerned variables. For the DWR, the increase of the DWR will reduce the yielding and ultimate loads by 25.32% and 14.40%, respectively. Still, it will enhance the corresponding displacements by the percentages of 23.56% and 23.42%, respectively. Meanwhile, regarding the ACR, this parameter shows a positive correlation with the yielding and ultimate loads, but it has negative effects on the corresponding displacements. In addition, the increasing rates of the yielding and ultimate loads are 8.32% and 7.76%, respectively, and for the corresponding displacements, the declining ratios are 19.46% and 7.25%, respectively.

Table 3.
The Experimental Loads, Corresponding Displacements and Failure Modes.
Regarding the failure mode, all specimens have shown a bending failure, which can be described as follows: (1) in the initial stage, no cracks emerged in the column under a small horizontal load. When the external load achieved the value of the cracking load, some micro horizontal cracks were observed on the two sides of the middle and bottom of the column; (2) The micro horizontal cracks gradually increased and became more obvious with the increasing external load; meanwhile, some shearing diagonal cracks emerged in the same location, which continued to extend to the longitudinal center or bottom of the column. (3) Afterward, the diagonal cracks converge to form multiple X-shaped oblique cracks. (4) Finally, due to the enhancement of external load, the diagonal cracks gradually widened, and the concrete at the bottom of the column was crushed, and the ultimate load was achieved. Furthermore, it can be observed that a similar failure process occurred in SRCZ-1 and SRCZ-2—the diagonal cracks showed a form of dense distribution. However, the diagonal cracks in SRCZ-3 were sparser than in the other specimens and occurred later in the experiment. The final failure form and distribution of the cracks of each specimen are shown in Figure 6.
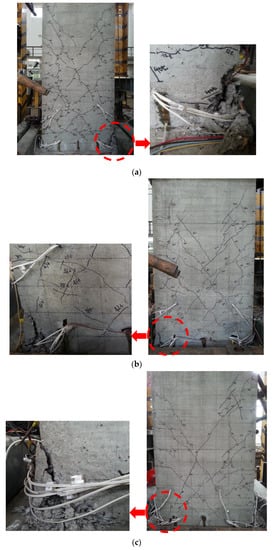
Figure 6.
The Distribution of Cracks and the Failure Modes. (a) SRCZ-1 and its zoomed figure. (b) SRCZ-2 and its zoomed figure. (c) SRCZ-3 and its zoomed figure.
3.2. Load–Displacement Curves
The hysteresis loops and skeleton curves of the three specimens are extracted based on the measured data plotted in Figure 7 and Figure 8, respectively.
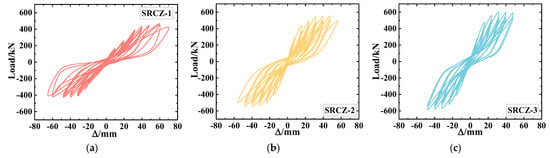
Figure 7.
The Hysteresis Loops. (a) SRCZ-1. (b) SRCZ-2. (c) SRCZ-3.
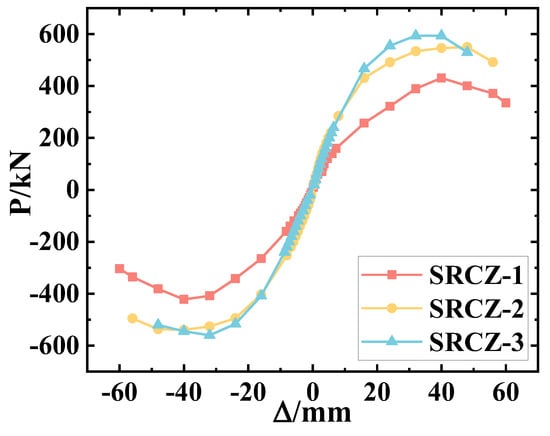
Figure 8.
The Skeleton Curves.
From Figure 7, it can be seen that: (1) all hysteresis loops show a form of bow, which means that the three specimens have good energy dissipation capacities, and there are some effects of shear force in the bending failure mode; (2) Compared with the others, the loop of the SRCZ-1 is fuller, which indicates that the hysteretic performance of the concrete columns benefits from the increase in the DWR; (3) from the loop of the SRCZ-3, it can be found that the larger ACR, the thinner the loop; thus, increasing the ACR will cause negative effects on the energy dissipation capacity of the column.
Figure 8 illustrates a similar trend for the three specimens from the perspective of the skeleton curves. Combining the curves in Figure 8 and the data in Table 3, it can be found that SRCZ-1 shows a minimum ultimate bearing capacity, but for the maximum ultimate displacement, a contrary situation can be observed in SRCZ-3. Furthermore, the slope of the curve of SRCZ-1 is more complanate than SRCZ-2 and SRCZ-3, which means a slow increase in the bearing capacity. After achieving the ultimate state, SRCZ-3 shows the most serious degeneration in its mechanical performance, followed by SRCZ-2, then SRCZ-1.
In conclusion, the specimen with a larger SR has a better plastic deformation performance, and the larger ACR can reduce the plastic deformation performance.
3.3. Load–Strain Curves
Figure 9 illustrates the measured load–strain data of the H-shape steel; it can be observed that the maximum principal tensile and compressive strains both achieve the yielding values. The angle of the principal strain direction is around 45°, and the increasing rate of principal compressive strain is higher than the tensile one. Therefore, for the condition of low cyclic loading, the compressive load has a stronger effect on this type of column, which can further validate the final failure form at the bottom of the column.
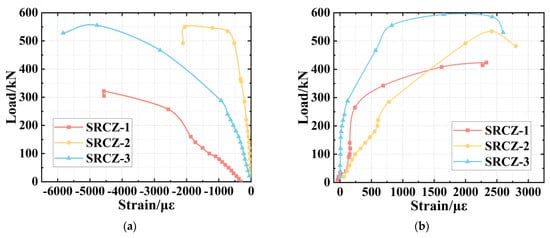
Figure 9.
Load–Strain Curve of the H-shape Steel. (a) Compressive strain. (b) Tensile strain.
The experimental results show that the longitudinal reinforcement on the outside of the column bottom has yielded, but the inner reinforcement has not. This situation is due to the bending force that will cause the peak bending positive stress on the outside of the bottom and the small stress on the inside. Regarding the above-mentioned situation, at the outer corner of the column bottom, the steel bar under the longitudinal stress of which the load–strain curve is plotted in Figure 10. The figure shows that the reinforcements achieved the yielding strain, and before the concrete was crushed, the load and strain showed a linear correlation. Then, the longitudinal strains showed an obvious increase until the yielding. Furthermore, when the specimens achieved the ultimate load, inaccurate measurements occurred in some strain gauges.
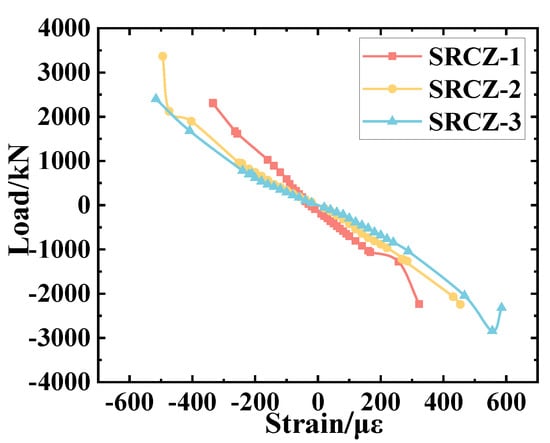
Figure 10.
Load–Strain Curve of the Longitudinal Reinforcement.
Figure 11 illustrates the load–strain curves of the hoop reinforcement of each specimen. It can be observed that the smaller strain values emerged in SRCZ-1 and SRCZ-2, which means the hoop reinforcements of the two specimens did not achieve yielding, and the mechanical performances were not fully used; this situation further proves the failure modes of the two specimens are both bending failures. However, from the perspective of SRCZ-3, the corresponding strain is larger than the others, and the value is close to the yielding value. Therefore, a stronger shearing force occurred in the hooped reinforcement in the specimen with a high ACR.
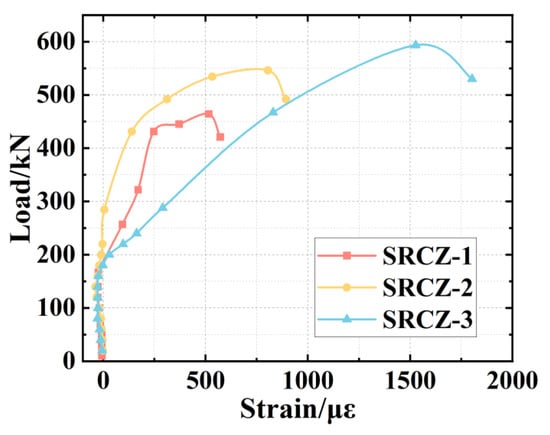
Figure 11.
Load–Strain Curve of the Hooped Reinforcement.
3.4. Ductility Results
Based on the measured data, for each specimen, the displacement ductility coefficient (DDC), yielding displacement drift ratio (YDDR), and ultimate displacement drift ratio (UDDR) are calculated and listed in Table 4; the corresponding equations of the above indicators are respectively shown as follows:
where is the ductility; and are the YDDR and UDDR, respectively; is the displacement corresponding to the ultimate load, and stands for the yielding displacement. For YDDR is the height of the column.

Table 4.
The Ductility Results of the Test Specimens.
For the data of SRCZ-2, compared with SRCZ-1 and SRCZ-3, the results show its DDC increased by 14.6% and 1.8%, respectively; the corresponding YDDR raised by 7.9% and 19.3%. For the UDDR, the values of SRCZ-1 and SRCZ-3 are the same; thus, the UDDR of SRCZ-2 increased by 21%. Because the SRCZ-1 is of maximum DWR but minimum DDC among the three specimens, it means that the larger the DWR, the further enhanced flexibility of the column. However, the useful displacement in the final stage is limited. Moreover, the increased ACR showed a negative effect on the ductility of the column. For a comprehensive analysis, the SR equalled 6 and can be determined as the best value among the adopted test specimens.
4. Nonlinear Finite Element Analysis
4.1. Finite Element Model of the Test Specimen
4.1.1. Material Parameter and Element Type
For the purpose of accurate analytical results, the material properties of the steel and concrete are both referred to as the measured data in Section 2.2, and the constitutive model of each material is adopted according to Ref. [], namely, the damage plastic constitutive model for the concrete, and the steel ideal elastoplastic model for the steel. Furthermore, the solid element C3D8R in Abaqus is used to model the concrete and H-shape steel, and for the internal reinforcement skeleton, T3D2 is adopted.
4.1.2. Geometric Model, Contact and Boundary Conditions
Regarding the actual test and the research content, taking SRCZ-1 as an example, the finite element model (FEM) is obtained based on Abaqus and shown in Figure 12. For the boundary conditions, different constraint methods in Abaqus were adopted in different locations. Firstly, ties were established between the cushion blocks and column body, the loading point and the cushion blocks are fixed by coupling constraints, the reinforcement skeleton is embedded into the column body, and the batten plates and H-shape steel are also linked based on ties. Furthermore, the surface-to-surface contact relationship should be defined between the surfaces of the H-shape steel and concrete. Meanwhile, considering the contact relationship is nonlinear, it needs to adopt the mechanism of a limited slide.
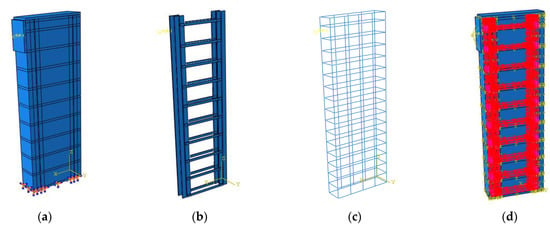
Figure 12.
The Abaqus Finite Element Model. (a) Overall Model. (b) H-shape Steel. (c) Reinforcement Skeleton. (d) Contact Condition.
4.1.3. Meshing
Figure 13 demonstrates the meshing situation of the FEM; considering the complexity of the model, it should be cut into multiple regular hexahedrons, then the mesh operation can be conducted. To balance the accuracy and computational efficiency, the concrete was meshed by the sweep method with a size of 0.05. The H-shape steel and reinforcement skeleton were meshed using automatic meshing with a size of 0.04.
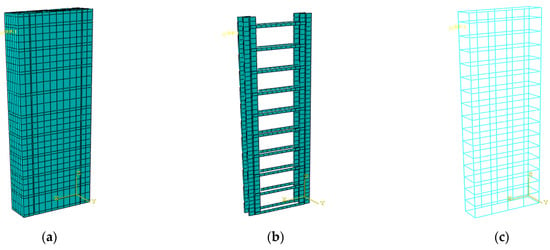
Figure 13.
The Meshing of the Finite Element Model. (a) Concrete. (b) H-shape Steel. (c) Reinforcement Skeleton.
4.2. The Comparative Study of Experimental and Analytical Results
4.2.1. The Ultimate Load
Table 5 lists the measured and analytical loads of the specimens in the ultimate state. The table shows that the analytical results showed good consistency with the experimental results; namely, SRCZ-1 (with the largest DWR) had a minimum load and maximum displacement. Meanwhile, SRCZ-3 (with the largest ACR) showed maximum load and minimum displacement. Furthermore, the results of FEM demonstrated that some errors, for the ultimate load, the analytical data were around 1.13–1.14 times for the experimental data of the three specimens. Meanwhile, for the ultimate displacement, they were also larger than the experimental specimens. The ratios between the analytical and experimental data are 1.12, 1.20 and 1.15 for SRCZ-1, SRCZ-2 and SRCZ-3, respectively.

Table 5.
The Comparison of the Analytical and Experimental Results.
Moreover, the errors between the simulated and experimental results are possibly due to the following aspects: (1) The boundary constraints of the bottom of the FEM are not totally consistent with the actual test, and the effects of the foundation on the column were considered; however, horizontal displacement will emerge in the foundation; (2) The adopted constitutive model in Abaqus only roughly models the elastic and plastic stage, which cannot totally reflect the stress distribution in a cross-section of the concrete before and after cracking; meanwhile, the concrete damage was conducted through the simple and single damage factor to change the elastic modulus rather than using the birth–death element method to consider the failed concrete. In sum, all of these factors contributed to the modeling errors.
4.2.2. The Load–Displacement Curve
Figure 14 illustrates the analytical and experimental load–displacement curves; it can be found that (1) overall, all curves show processes of the gradual transition from the elastic to the plastic stage. Then, to be destroyed and before cracking, all the curves change trends are linear. Furthermore, good consistency can be observed between the experimental and analytical specimens; (2) Among all of the specimens, the increasing trend of bearing capacity of SRCZ-1 is slower: however, after the ultimate state, a faster decrease can be observed in the curves of SRCZ-2 and SRCZ-3. Thus, the enhancement of DWR can improve the plastic deformation performance in the later stage, which is also consistent with the measured results.
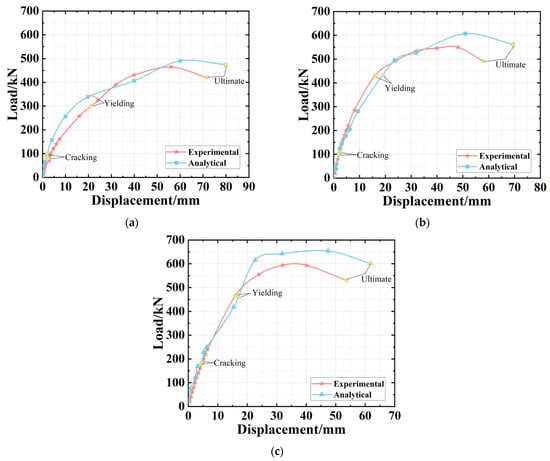
Figure 14.
The Comparative Results of Experimental and Analytical Load–Displacement Curves. (a) SRCZ-1. (b) SRCZ-2. (c) SRCZ-3.
In the comprehensive analysis, the simulated results can reflect a good consistency with the experiment results, which also proved that the determinations of the related material parameters, meshing, contact and boundary conditions are reasonable, and the finite element analysis is reliable and feasible.
4.2.3. The Failure Mode and Crack Development
Because the crack development of the specimen cannot be directly observed in Abaqus, it can only be roughly evaluated based on the equivalent plastic strain diagram. Thus, taking SRCZ-1 as the example, the corresponding diagram is shown in Figure 15. From the data, it can be deduced that the cracks in the FEM are located at the bottom of the column, mostly showing the form of horizontal bending cracks and shearing diagonal cracks in the body of the column. In addition, the strain diagram also illustrates that the cracks develop rapidly in the lower third of the body; the slim and wide cracks occur at the upper and lower part, respectively, and the cracks converge into the main diagonal tensile crack. Furthermore, the cracks at the bottom of the column converged together, which is consistent with the experimental phenomena; namely, the concrete at the bottom is gradually crushed with the increasing loading. In conclusion, the distribution of simulated cracks is approximately consistent with the experimental results; however, in the upper part of the column, the horizontal cracks at the edge are not obvious, contrary to the practical situation. This is likely because the adopted constitutive model is not very accurate.
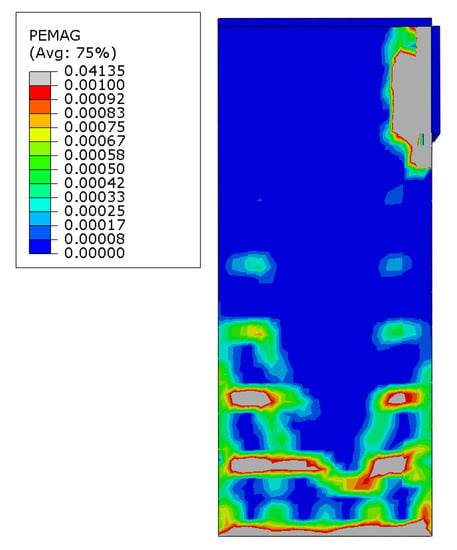
Figure 15.
Equivalent Plastic Strain Diagram of SRCZ-1.
4.2.4. Extended Numerical Analysis on the Designed Parameters of a Thin-Walled Steel-Reinforced Concrete Pier
To further investigate the failure performance of the pier herein, except for the originally designed parameters, the analysis has been extended based on the FEM. For the concrete strength, C25 and C35 were studied, then for the DWR and ACR, the ratios of 4 and 20 were investigated, respectively. The simulated results will be compared with the experimental data; thus, the effects of the changes in these parameters on the failure performance can be studied.
- (1)
- The Concrete Strength
The C25 and C35 concrete were adopted to simulate the numerical specimens, then the test process was conducted on the specimens. Then, the load–displacement curves were plotted in Figure 16a, and the changing trend between the ultimate load and the concrete strength is shown in Figure 16b. As shown in Figure 16b, the stronger the concrete, the higher the ultimate bearing capacity. However, Figure 16a illustrates that the enhanced strength of the concrete will cause an increase in the slope of the declining stage in the load–displacement curve, which means that the higher strength of the concrete will lead to a fast declination of the bearing capacity in the later stage of the test.
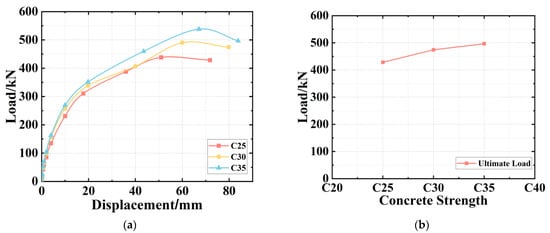
Figure 16.
The Simulated Results of Different Concrete Strength. (a) Load–Displacement Curves. (b) The Ultimate Load.
- (2)
- The DWR
The simulated specimen with the DWR of 4 was used to carry out the extended study. The obtained load–displacement curve and the changing relationship between the ultimate load and the DWR were extracted and plotted in Figure 17. From the figure, it can be observed that when the DWR rises to 6 from 4, the corresponding ultimate load will be enhanced. However, when the ratio increases to 8, the ultimate load will be somewhat reduced. Furthermore, the higher DWR will slow down the declining trend of the bearing capacity in the later stage of the test. Therefore, the best DWR can be determined as 6 among the adopted test specimens.
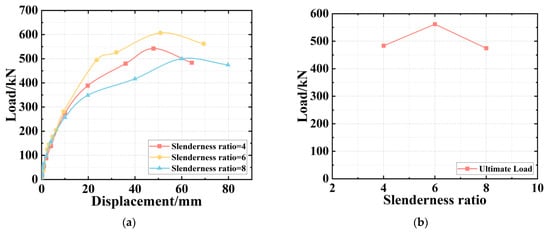
Figure 17.
The Simulated Results of Different DWR. (a) Load–Displacement Curves. (b) The Ultimate Load.
- (3)
- The ACR
Herein, the simulated specimen with the ACR of 20 is adopted. Figure 18 illustrates the load–displacement curves under the different ACR and the changing relationship between the ultimate load and ACR. The figure shows that the enhancement of the ACR can improve the ultimate bearing capacity and accelerate the decrease rate of the bearing capacity. In sum, the increasing ACR can enhance the ultimate bearing capacity, but the plastic deformation performance will be reduced.
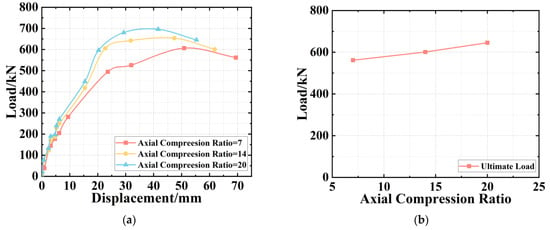
Figure 18.
The Simulated Results of Different ACR. (a) Load–Displacement Curves. (b) The Ultimate Load.
5. Discussion on the Effects of ACR and DWR on the Failure Performance
According to the above-mentioned experimental results, analytical findings and comparative outcomes, it can be seen that for the same material properties and loading mode, the mechanical performance of the specimen was seriously influenced by the ACR and DWR. Thus, in this section, the details will be further discussed.
5.1. The Effects of ACR
The specimen with a higher ACR has a better bearing capacity under the preset compressive force. Meanwhile, although the same failure mode can be observed in the three specimens, the specimens with larger ACRs show fewer cracks than those with smaller ACR, and the corresponding horizontal bearing capacities have obvious improvements.
Figure 11 illustrates that the specimen with a higher ACR is larger than the others for the strains with hooped reinforcement. Regarding the situation and the preset compressive force, the hooper reinforcements can apply stronger constraints to the internal concrete, enhancing the bearing capacity. The above-mentioned statements can also be validated in the FEM simulation.
Furthermore, the FEM simulation also demonstrates that when the failure has occurred in the specimen as well as then the failure of the internal concrete because of the fixed steel ratio in the section, the area that can bear load is also kept constant. This situation can be reflected in Figure 18, namely causing the ends of the load–displacement curves to be gradually approached.
5.2. The Effects of DWR
Due to the action of the horizontal cyclic loading, the H-shape steel and reinforcement skeleton is used to resist the bending tensile stress. Regarding this situation, the diverse specimens with different DWRs show a similar deformation behavior in the elastic stage; the starting point of each specimen is also consistent. Then, when the concrete at the bottom of the specimen is cracked, and the axial tensile stress has mainly emerged in the longitudinal reinforcement and steel skeleton, the specimen will start to enter the plastic energy dissipation stage (Figure 8 and Figure 17).
For the skeleton curves, the peak point has a negative correlation with the DWR; namely, the larger DWR, the smaller the peak point. It can also be observed that the hysteresis loop of the specimen with the higher DWR is fuller. Meanwhile, Figure 6 illustrates the larger crack area that occurred in the specimen with the higher DWR. The stress area has a positive correlation with the increased DWR, which means such a specimen can rely on the good plastic deformation of the steel and the brittle fracture of the concrete to absorb the external energy to enhance the seismic performance. However, Table 3 depicts that the increasing DWR means a decrease in the bearing capacity of the specimen; thus, DWR shows a negative effect on the bearing capacity. In this regard, the suitable DWR can be determined to be six based on the experimental results.
6. Horizontal Ultimate Bearing Capacity Equation for Thin-Walled Steel-Reinforced Concrete Pier
According to Ref. [], when the bending failure has occurred, the horizontal ultimate bearing capacity of TSRCP can be obtained by the equation as follows:
where is the bending bearing capacity in the normal section of the column; and denote the height of the column body and the height of the cross-section, respectively; and stands for the influence coefficient of the foundation to the constraint in the end of the column. In this study, because the specimens all show a form of bending failure, and on the compression side of the column, the tensile reinforcement on the skeleton and the H-shape steel all have achieved yielding, it can be stated that the specimens like small, eccentric compression. Therefore, referring to the calculated model of Ref. [] (Figure 19), regarding the force condition of small eccentric compression, the normal section-bearing capacity of TSRCP can be obtained as follows:
where is the axial compressive force; can be determined as 1, which is the equivalent rectangular stress coefficient of the concrete; denotes the designed concrete strength; stands for the width of the cross-section; indicates the height of compressive area; and are the working and total height of the cross-section, respectively; and are the tensile and compressive strengths of the longitudinal reinforcement, respectively; and are the tensile and compressive strengths of the H-shape steel; and are the sectional areas of the longitudinal tensile reinforcement and compression reinforcement, respectively, due to the symmetrical reinforcement, ; and are the areas of H-shaped steel under the tensile and compression conditions, respectively; and mean the distance from the edge of the section to the joint force points of the longitudinal tension and compression reinforcements on the outside, respectively; and are the distance from the centroids of tensile and compression H-shape steels to the edge of the section, respectively; denotes the horizontal spacing between each longitudinal stressed reinforcement; stands for the eccentricity of axial force to the center of cross center; and is the additional eccentricity; it can be defined as the lager one of 20 mm and 1/30 of section size in the eccentric direction.
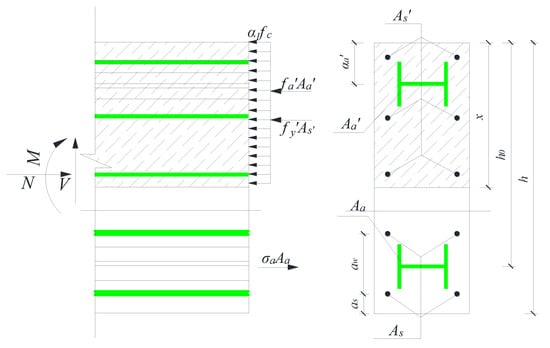
Figure 19.
The Calculated Model of the Horizontal Ultimate Bearing Capacity.
Then, to substitute the obtained to the Equation (6), the horizontal ultimate bearing capacity of TSRCP can be obtained. However, the above-mentioned statement will lead to a complex calculated equation; therefore, in this study, the analyses of the failure process and the experimental results are conducted to simplify the complex equation, then the simplified and practical equation is proposed as follows:
where and are the height and width of the cross-section; is the working height of the cross-section, ; is the designed compressive strength; is the yielding strength of the hooped reinforcement is the yielding strength of the H-shape steel web; and stand for the height and thickness of the H-shape steel web; means the total area of the hooped reinforcements in the same cross-section; is the spacing between each hoop reinforcement, and is the axial compression force of the column.
The experimental results of Ref. [] are used to validate the proposed equation’s feasibility. The related data of the three specimens are substituted into the proposed equation, and the obtained results are listed in Table 6. It can be seen that the average ratio of experimental and calculated values is 1.13; the corresponding mean square error is 0.021, which proves that the proposed method is feasible.

Table 6.
The Calculated Results Based on Ref. [].
To further validate the applicability and feasibility of the proposed equation, based on the obtained results of the test, the horizontal ultimate bearing capacity of the three specimens can be calculated and listed as shown in Table 7. In addition, the measured data and simulated results of FEM are adopted to conduct a comparative analysis. From Table 7, it can be seen that the average ratio between the experimental and calculated values is 1.03, the average mean square error (MSE) is 0.062, and for the simulated and calculated values, the average ratio is 1.17, and the average MSE is 0.076. Therefore, the comparative results illustrate good consistency between the experimental, calculated and simulated data, further validating the proposed equation’s feasibility.

Table 7.
The Experimental, Calculated and Simulated Results.
Moreover, the comparative results in Table 6 and Table 7 illustrate that when the proposed equation is adopted, the calculated horizontal ultimate bearing capacities are conservative and cautious, which not only can reduce the complexity of design calculation, but also satisfy the safety requirements in engineering applications.
7. Conclusions and Outlooks
In this study, a low cyclic loading mechanical test was conducted based on three test specimens to assess the effects of DWR and ACR on the failure performance of a thin-walled steel-reinforced concrete pier. According to the test results, finite element analysis was used to model the test process through Abaqus. Finally, a simplified and useful equation was proposed to calculate the horizontal ultimate bearing capacity of the column. Based on the experimental research and theoretical analysis, several conclusions can be drawn:
(1) For the low cyclic loading condition, TSRCP will show a form of bending failure. It can be observed that the specimen’s failure is accompanied by the concrete at the bottom of the foundation having been crushed. Meanwhile, the enhancement of DWR will reduce the ultimate bearing capacity of the pier but improve the plastic deformation performance. Regarding the comparative results, the change in the DWR cannot enhance the deformation capacity of the specimen; thus, based on the comprehensive analysis of the displacement ductility coefficient (DDC), yielding displacement drift ratio (YDDR) and ultimate displacement drift ratio (UDDR), the DWR equalling 6 can be determined as the best value among the adopted test specimens.
(2) The increased ACR enhanced the upper bounds of the cracking load and restrained the occurrence and development of the cracks to further improve the ultimate bearing capacity but limit the deformation capacity. Furthermore, from the perspective of the H-shape steel of the three specimens, the principal compressive strains along the vertical direction all reached yielding. For the reinforcement skeleton, the longitudinal reinforcements on the outside of the bottom of the column all yielded, but the reinforcements on the inner side did not. Moreover, the hooped reinforcements did not yield.
(3) The FEM based on Abaqus can reflect the whole process of the mechanical test well; the comparative studies show that the simulated and experimental data are with good consistency. Meanwhile, based on the extended numerical analysis, it can be found that the concrete strength shows the most serious effect on the ultimate bearing capacity of the TSRCP under the vertical load and low cyclic load; the stronger the concrete, the higher the ultimate bearing capacity. However, the ultimate bearing capacity will show a fast-declining trend in the later stage of the test.
(4) Considering the complexity of the existing calculated equation for the horizontal ultimate bearing capacity of the thin-walled steel-reinforced concrete pier in this study, analyses of the failure process and the experimental results were used to simplify the complex equation. Then, simplified and practical data were proposed. Based on the experimental, simulated, and referred data, the accuracy and feasibility of the proposed equation have been validated. Therefore, the proposed formula can simplify the complex calculation process of the horizontal ultimate bearing capacity, which not only provides a convenient and useful way to design and manufacture this type of component but can be used as a guideline for validating its applications in practical engineering.
Author Contributions
Conceptualization, H.C.; methodology, H.C. and B.X.; software, Q.L.; validation, H.C., B.X. and J.G.; formal analysis, B.X.; investigation, J.G.; resources, H.C.; data curation, Q.L.; writing—original draft preparation, H.C.; writing—review and editing, J.G.; visualization, Q.L.; supervision, B.X.; project administration, H.C.; funding acquisition, H.C. and B.X. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by the Research Project of Basic Science (NATURAL SCIENCE) of Colleges and Universities in Jiangsu Province, China (No. 22KJD560007) and the Fundamental Research Funds for the Central Universities, CHD (NO. 300102212525).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Yuan, X.J.; Liu, F. Comparing Hysteretic Behavior of Flexible Piers with Different Stirrup Ratio and Slenderness Ratio. Adv. Mater. Res. 2011, 261–263, 576–580. [Google Scholar] [CrossRef]
- Pinto, A.V.; Molina, J.; Tsionis, G. Cyclic tests on large-scale models of existing bridge piers with rectangular hollow cross-section. Earthq. Eng. Struct. Dyn. 2003, 32, 1995–2012. [Google Scholar] [CrossRef]
- Lehman, D.; Moehle, J.; Mahin, S.; Calderone, A.; Henry, L. Experimental Evaluation of the Seismic Performance of Reinforced Concrete Bridge Columns. J. Struct. Eng. 2004, 130, 869–879. [Google Scholar] [CrossRef]
- Zhang, Q.; Wei, Z.Y.; Gu, X.L. Confinement behavior and stress–strain response of square concrete columns strengthened with carbon textile reinforced concrete (CTRC) composites. Eng. Struct. 2022, 266, 114592. [Google Scholar] [CrossRef]
- Zhang, Q.; Zheng, N.H.; Gu, X.L. Study of the confinement performance and stress-strain response of RC columns with corroded stirrups. Eng. Struct. 2022, 266, 114476. [Google Scholar] [CrossRef]
- Yeh, Y.K.; Mo, Y.L.; Yang, C.Y. Seismic performance of hollow circular bridge piers. Struct. J. 2001, 98, 862–871. [Google Scholar]
- Yeh, Y.-K.; Mo, Y.L.; Yang, C.Y. Seismic Performance of Rectangular Hollow Bridge Columns. J. Struct. Eng. 2002, 128, 60–68. [Google Scholar] [CrossRef]
- Mo, Y.L.; Nien, I.C. Seismic Performance of Hollow High-Strength Concrete Bridge Columns. J. Bridge Eng. 2002, 7, 338–349. [Google Scholar] [CrossRef]
- Mo, Y.L.; Yeh, Y.-K.; Hsieh, D.M. Seismic Retrofit of Hollow Rectangular Bridge Columns. J. Compos. Constr. 2004, 8, 43–51. [Google Scholar] [CrossRef]
- Mo, Y.L.; Wong, D.C.; Maekawa, K. Seismic performance of hollow bridge columns. Struct. J. 2003, 100, 337–348. [Google Scholar]
- Tirasit, P.; Kawashima, K. Seismic Performance of Square Reinforced Concrete Columns under Combined Cyclic Flexural and Torsional Loadings. J. Earthq. Eng. 2007, 11, 425–452. [Google Scholar] [CrossRef]
- Chang, S.-Y. Experimental Studies of Reinforced Concrete Bridge Columns under Axial Load Plus Biaxial Bending. J. Struct. Eng. 2010, 136, 12–25. [Google Scholar] [CrossRef]
- Zhang, Q.; Gong, J.-X.; Zhang, Y.-Q. Lateral-Load Behavior Prediction and Pushover Analysis of Reinforced Concrete Columns Including Shear Effects. Adv. Struct. Eng. 2013, 16, 741–758. [Google Scholar] [CrossRef]
- Zhao, Y.; Jiang, H.Y.; Gu, J.; Wang, R.Q. Seismic Performance of Reinforced Concrete Rectangular Hollow Bridge Piers. Adv. Mater. Res. 2013, 859, 95–99. [Google Scholar] [CrossRef]
- Cassese, P.; Ricci, P.; Verderame, G.M. Experimental study on the seismic performance of existing reinforced concrete bridge piers with hollow rectangular section. Eng. Struct. 2017, 144, 88–106. [Google Scholar] [CrossRef]
- Su, J.; Wang, J.; Li, Z.; Liang, X. Effect of reinforcement grade and concrete strength on seismic performance of reinforced concrete bridge piers. Eng. Struct. 2019, 198, 109512. [Google Scholar] [CrossRef]
- Roderick, J.W.; Rogers, D.F. Load Carrying Capacity of Simple Composite Columns. J. Strl. Div. 1969, 95, 209–228. [Google Scholar] [CrossRef]
- Bridge, R.Q. Design Of Composite Columns–Steel, Concrete or Composite Approach? Compos. Construct. Steel Concr. 2011, 6, 276–290. [Google Scholar]
- Johansson, M.; Gylltoft, K. Mechanical Behavior of Circular Steel–Concrete Composite Stub Columns. J. Struct. Eng. 2002, 128, 1073–1081. [Google Scholar] [CrossRef]
- Zhou, X.; Liu, J. Seismic behavior and strength of tubed steel reinforced concrete (SRC) short columns. J. Constr. Steel Res. 2010, 66, 885–896. [Google Scholar] [CrossRef]
- Gan, D.; Guo, L.; Liu, J.; Zhou, X. Seismic behavior and moment strength of tubed steel reinforced-concrete (SRC) beam-columns. J. Constr. Steel Res. 2011, 67, 1516–1524. [Google Scholar] [CrossRef]
- Chang, X.; Wei, Y.-Y.; Yun, Y.-C. Analysis of steel-reinforced concrete-filled-steel tubular (SRCFST) columns under cyclic loading. Constr. Build. Mater. 2012, 28, 88–95. [Google Scholar] [CrossRef]
- Nie, J.-G.; Wang, Y.-H.; Fan, J.-S. Experimental research on concrete filled steel tube columns under combined compression-bending-torsion cyclic load. Thin. Wall. Struct. 2013, 67, 1–14. [Google Scholar] [CrossRef]
- Naito, H.; Akiyama, M.; Suzuki, M. Ductility Evaluation of Concrete-Encased Steel Bridge Piers Subjected to Lateral Cyclic Loading. J. Bridge. Eng. 2011, 16, 72–81. [Google Scholar] [CrossRef]
- Zhang, S.A.; Zhao, Z.Z.; He, X.G. Flexural Behavior of SRC Columns under Axial and Bilateral Loading. Appl. Mech. Mater. 2012, 166, 3383–3390. [Google Scholar] [CrossRef]
- Zhu, W.; Jia, J.; Gao, J.; Zhang, F. Experimental study on steel reinforced high-strength concrete columns under cyclic lateral force and constant axial load. Eng. Struct. 2016, 125, 191–204. [Google Scholar] [CrossRef]
- Yin, F.; Wang, R.-W.; Cao, W.-L.; Zhao, Y.; Song, Y. Experimental and analytical research on steel reinforced high-strength concrete columns with different steel sections. Structures 2021, 34, 4350–4363. [Google Scholar] [CrossRef]
- Cao, X.; Wu, L.; Li, Z. Behaviour of steel-reinforced concrete columns under combined torsion based on ABAQUS FEA. Eng. Struct. 2020, 209, 109980. [Google Scholar] [CrossRef]
- Yang, B.S.; Song, S.H. Study on the Factors Affecting the Anti-Seismic Performance of Steel Reinforced High-Strengh Concrete Columns. Adv. Mater. Res. 2012, 535–537, 1842–1846. [Google Scholar] [CrossRef]
- Fang, L.; Zhang, B.; Jin, G.-F.; Li, K.-W.; Wang, Z.-L. Seismic behavior of concrete-encased steel cross-shaped columns. J. Constr. Steel Res. 2015, 109, 24–33. [Google Scholar] [CrossRef]
- Wang, Q.; Shi, Q.; Tao, Y. Experimental and numerical studies on the seismic behavior of steel reinforced concrete compression-bending members with new-type section steel. Adv. Struct. Eng. 2016, 19, 255–269. [Google Scholar] [CrossRef]
- Yang, Y.; Xue, Y.; Yu, Y.; Gao, F. Experimental study on seismic performance of partially precast steel reinforced concrete columns. Eng. Struct. 2018, 175, 63–75. [Google Scholar] [CrossRef]
- Yang, Y.; Wang, C.; Chang, H.; Xue, Y. Experimental study on seismic performance of steel reinforced high-strength concrete composite columns. IOP Conf. Ser. Earth Environ. Sci. 2021, 676, 012065. [Google Scholar] [CrossRef]
- Xu, W.; Ma, B.; Duan, X.; Li, J. Experimental investigation of seismic behavior of UHPC connection between precast columns and footings in bridges. Eng. Struct. 2021, 239, 112344. [Google Scholar] [CrossRef]
- Wang, J.; Shen, Y.; Li, G.; Chen, M.; Fan, C. Quasi-Full-Scale Experimental Study on Bridge Precast Concrete Columns under Static Loading. J. Bridge Eng. 2021, 26, 04021031. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).