5.1. Frontal Model
In the numerical tests that are presented, a free rotational upper plate boundary condition was considered, similar to the experimental tests taken as reference [
1]. Nevertheless, it is important to mention that the adopted boundary condition at the upper plate (free or non-rotating) have a meaningless effect in the predicted peak strength value and failure mode.
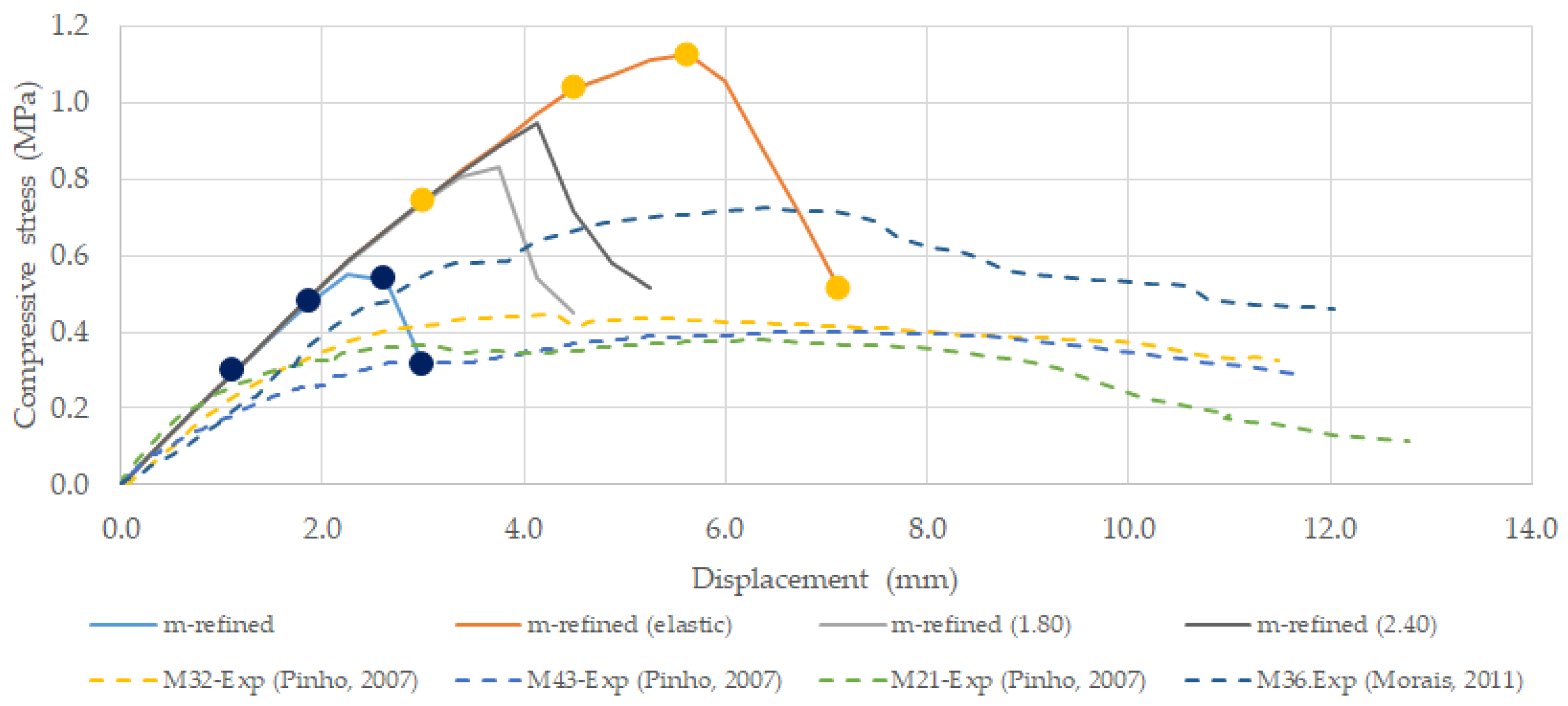
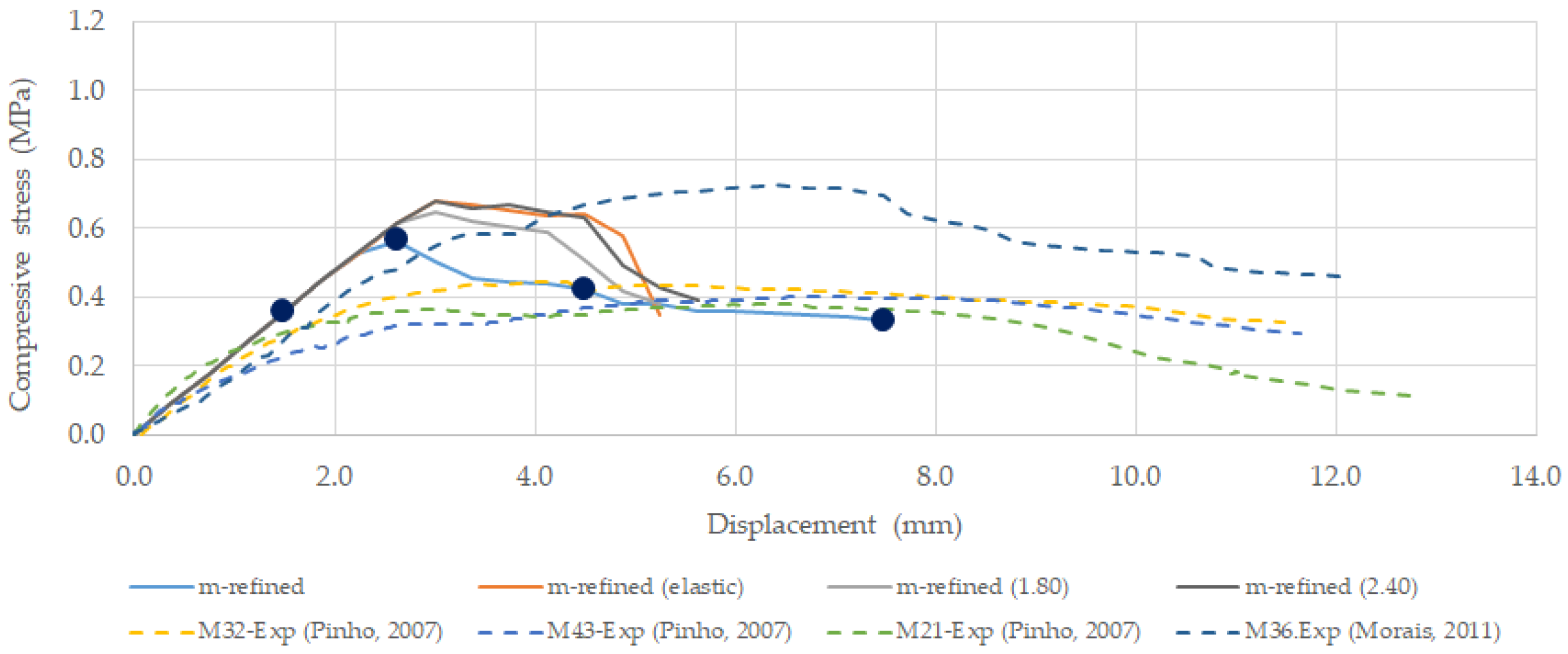
Figure 10 presents the numerical stress-displacement response predictions obtained for the 2D-PM numerical refined particle assembly model (m-refined) that was developed based on the frontal side of specimen M43, with a % of mortar of around 25%. In
Figure 10 it is shown the numerical prediction with the calibrated contact constitutive model adopting a yield plateau under uniaxial compression with a maximum value of 0.80 MPa (m-refined), the numerical prediction adopting the traditional elastic behaviour under compression (m-refined (elastic)) [
13] and two additional numerical simulations adopting higher uniaxial compression yield values of 1.80 MPa (m-refined (1.40)) and 2.40 MPa (m-refined (2.80)). As pointed out in the calibration section, the mortar adopted in the experimental tests had a maximum uniaxial compression stress of 0.65 MPa. The experimental stress-displacement curves for four wall specimens [
2] are also presented in
Figure 10.
It can be observed,
Figure 10, that it is possible to numerically predict a masonry wall response under uniaxial testing closer to the obtained experimentally, if a parameter calibration is carried out in order to mimic the known experimental behaviour of each wall component, mortar and stone, under uniaxial and bending tests. The m-refined 2D-PM numerical model give a good prediction in terms of initial elastic response and peak strength. Regarding the ductility the m-refined 2D-PM predictions are less ductile that the observed experimental response. It can also be observed that with an elastic contact model under compression, the 2D-PM numerical model predicts a higher peak strength and a less brittle response. This indicates that the mortar response under compression is one of the mechanisms that contribute to a more ductile response under uniaxial compression. The presented numerical results point out that it is important to assess the mortar response under biaxial confinement.
In
Table 5 are shown the numerically obtained elastic modulus, peak strength and maximum displacement at peak strength, as well as the average experimental values obtained in [
1,
30]. The m-refined 2D-PM numerical model is able to predict values closer to the obtained experimentally, namely the peak stress. As mentioned, the ductility measure as the maximum displacement at peak stress is lower. The numerical model with an elastic behaviour under compression predicts a higher peak strength and wall ductility.
In
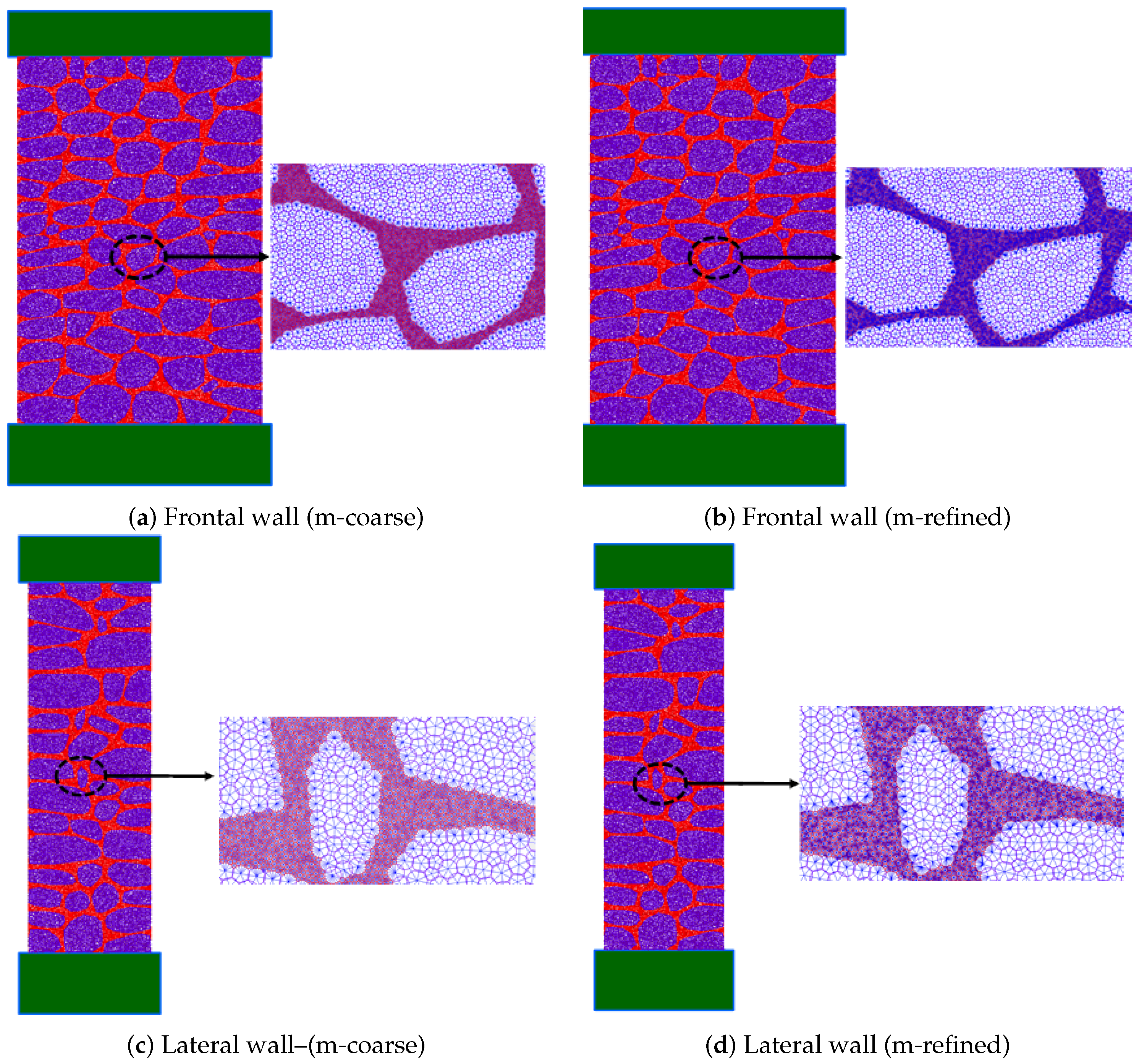
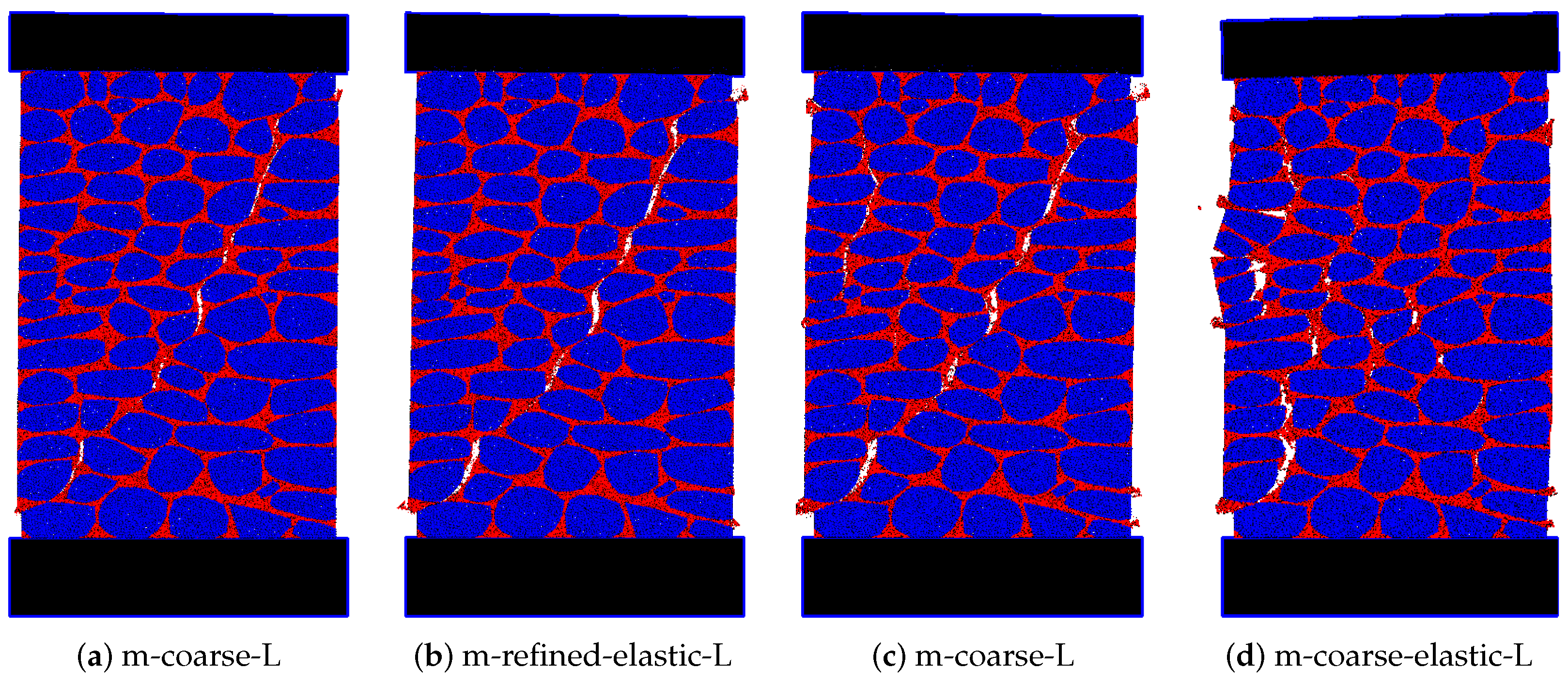
Figure 11 are shown the final failure models for the frontal numerical 2D-PM models adopting a refined and a coarse mortar particle assembly. It is shown that the numerical models with a maximum yield compressive stress of 0.80 MPa predict a final diagonal cracking for both mortar discretization (m-refined and m-coarse). If an elastic model is adopted under compression a more complex failure mode is obtained for both mortar discretizations: a final crack is formed due to the bending of the wall lateral stone column. As shown in
Section 3.3 both numerical predictions are in good agreement with the failure models recorded experimentally [
2].
Figure 12 shows the damage evolution throughout the uniaxial compression test for the 2D-PM m-refined model and for the m-refined (elastic) model. Cracking occurs for a load of around 85% of the peak strength in the m-refined model and for around 50% for the m-refined (elastic) model. The cracked contacts are mostly tensile cracks, under tensile/shear loading condition, but a relevant number of cracks under shear/compression also occur in both numerical models. In concrete or rock specimens compression tests [
13] crack occur mainly under tensile/shear conditions. The fact that shear cracks occur in the wall numerical models is due to the larger difference in stiffness and strength that occur in the components of masonry wall, when compared to normal concrete (aggregate, cement paste).
As shown in
Figure 12, there is a significant number of contacts that cracked under tensile forces, that are found to be under compression at later loading stages. This clearly shows that even if crack occurs, forces can still be transmitted due to the fact that the contacts are later under compression. For example, in a 2D-PM model of a more homogeneous material under uniaxial compression this phenomenon does not occur, see calibration section and [
13]. The ductility of the masonry walls is clearly associated to these contacts that work under compression in pure friction. These results also reinforce the relevance of further understanding mortar behaviour under biaxial compression. When an elastic behaviour is adopted under compression, for the m-m and m-s contacts, the 2D-PM model predicts an increase in the ductility and peak strength.
Table 6 presents the maximum compression stress at contacts for the m-refined (elastic) model at different loading stages.
As shown in
Table 6, high contact compressive stress values are predicted clearly indicating that for this type of walls, more complex behaviour under compression need to be taken into account for the mortar. The contact constitutive model should not only consider yielding as adopted in this work but also softening and stiffening under uniaxial compression/shear [
31].
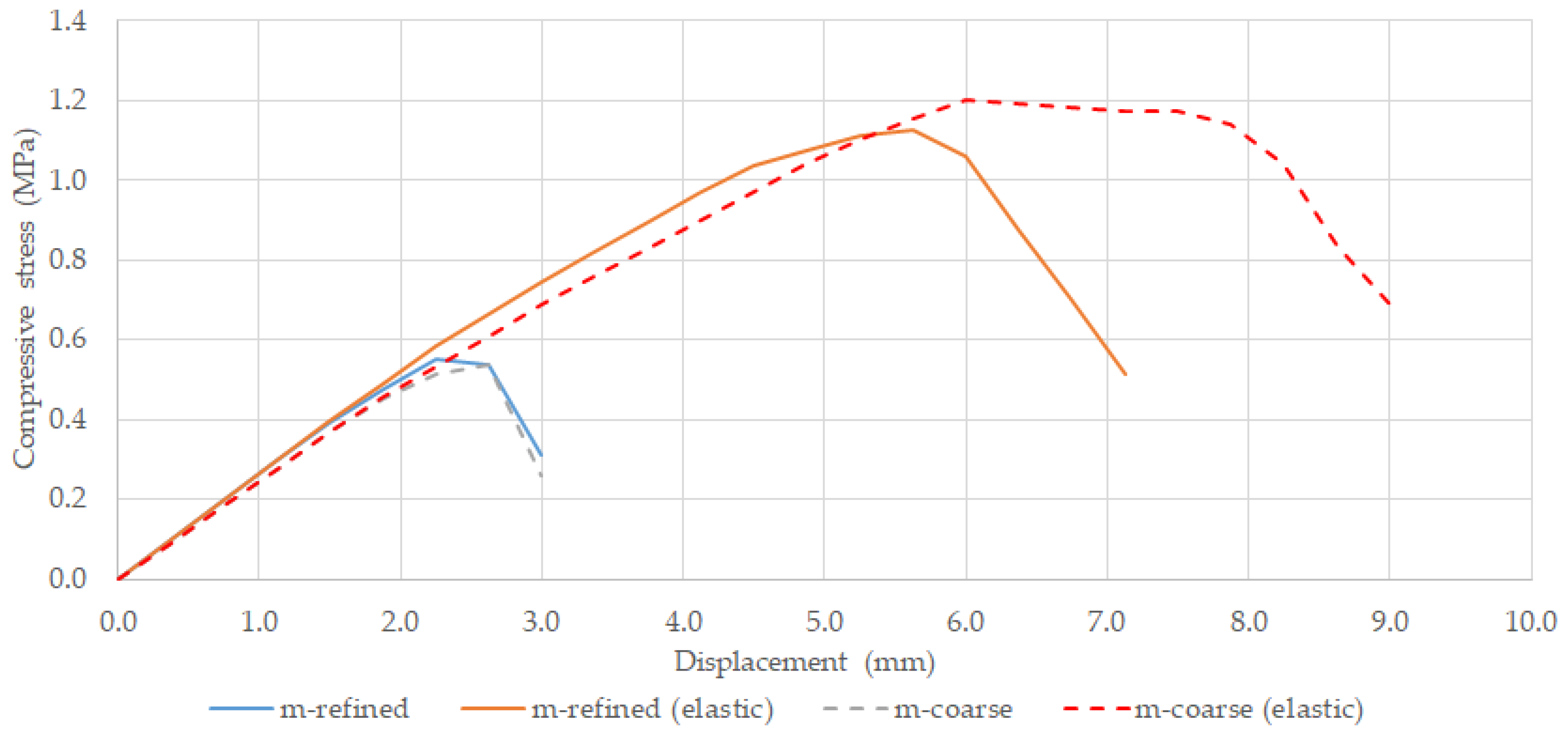
Figure 13 presents the numerical stress-displacement response predictions for the coarser 2D-PM model (m-coarse) and for the refined 2D-PM model (m-refined) mortar discretizations.
As shown, a coarser mortar discretization predicts a behaviour similar to the predicted with a finer particle discretization for a contact constitutive model with a yield plateau and for an elastic contact model under compression.
As pointed out in the calibration section, only with a finer particle discretization it is possible to predict a mortar maximum flexure stress closer to the experimental values. The presented numerical studies indicate that the mortar flexure response does not have a meaningful influence in the wall compressive strength. The 2D-PM m-refined model has a total simulation time of around 53 h, with around 2.20 h of simulation per 10,000 steps and the m-coarse model has a total simulation time of 27 h, with around 1.25 h of simulation per 10,000 steps, significantly less. The presented results clearly point out that with the coarser mortar discretization (m-coarse) it is possible to greatly reduce the simulation times without compromising the quality of the numerical predictions.
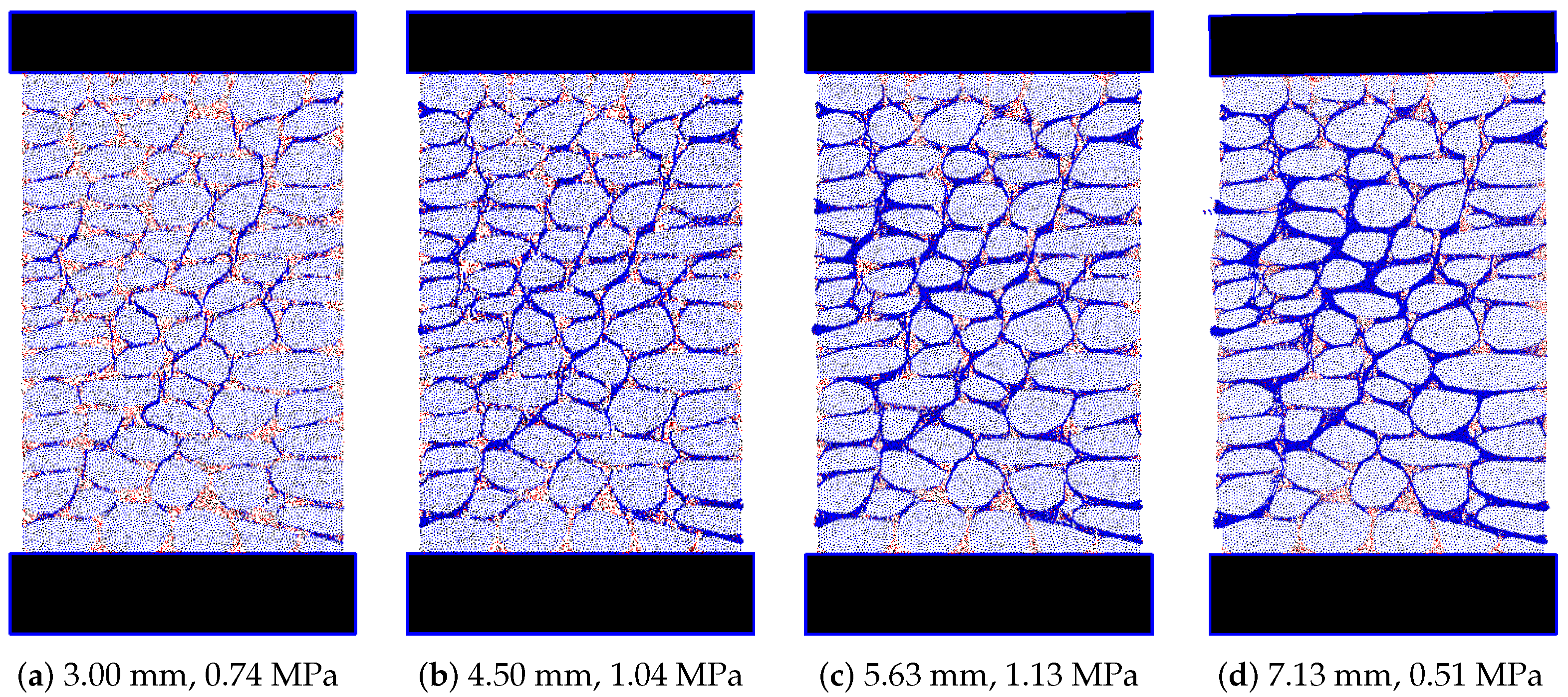
In
Figure 14 it is shown the contact damage evolution for the points defined in the stress-displacement curve presented in
Figure 10, for the numerical model m-refined.
It can be observed that, when a yield plateau of 0.80 MPa is adopted in compression, the damage starts to occur in very localized areas, throughout the wall inside the mortar,
Figure 14a,b. Closer to the peak load, damage starts to concentrate at a diagonal surface which will correspond to the final failure mode. With an elastic contact model under compression,
Figure 15, the numerical model predicts a less localized damage distribution when compared with the m-refined model.
By including a high shear strength capacity, the 2D-PM model, m-refined (elastic), is able to restrain the formation of the diagonal macroscopic crack that occurs in the 2D-PM m-refined model. In the 2D-PM numerical model with an elastic behaviour, the failure mode is due to the bending of the wall at the lateral stone stacks. As before, the results presented in
Figure 14 and
Figure 15 clearly show the relevance of the mortar behaviour under a biaxial state of stress, which in our view is due to the high heterogeneity of the wall components.
5.2. Lateral Model
The numerical model of the lateral sides was also developed in order to assess if the lateral side can also be a valid analysis option, regarding the peak strength and the wall overall behaviour. This study was carried out, given that the computational requirements for a lateral model are much lower when compared with the frontal 2D-PM model computational costs.
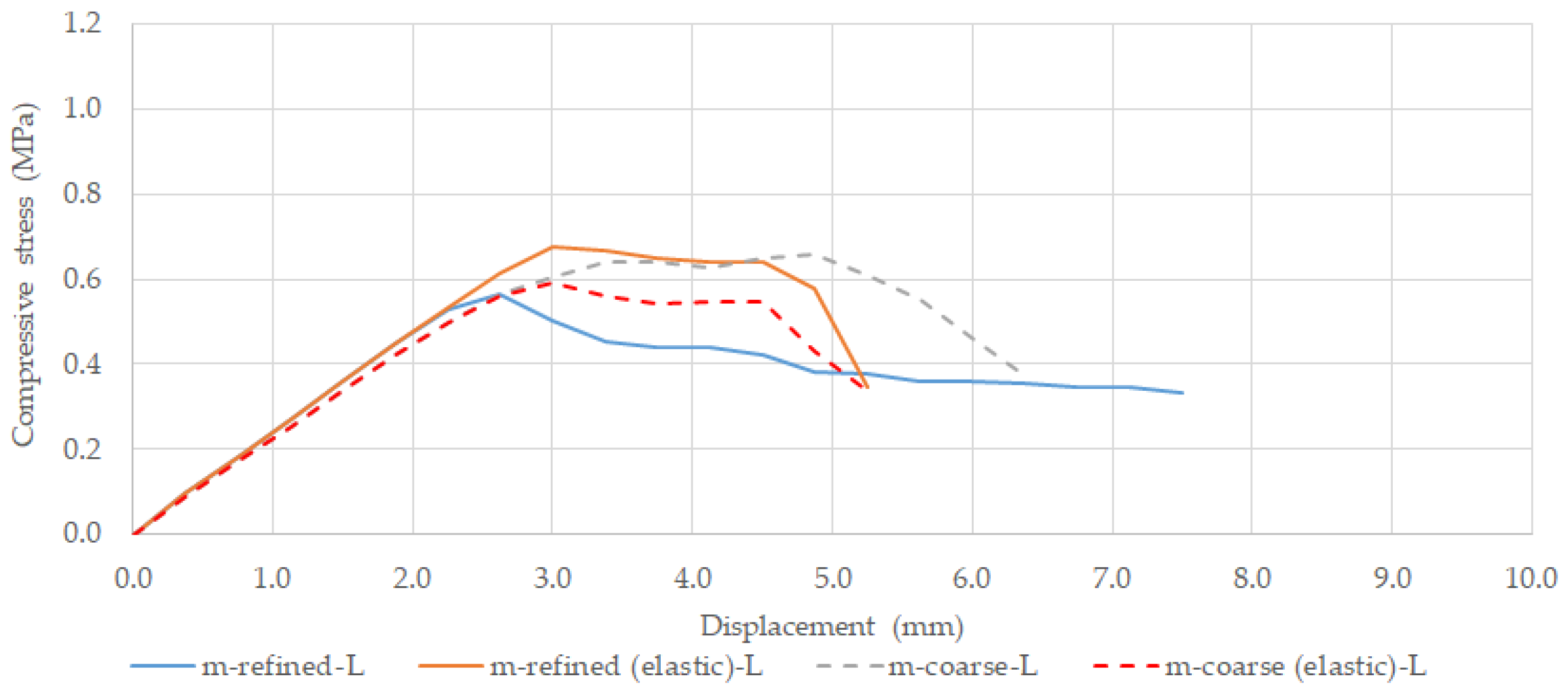
Figure 16 presents the numerical stress-displacement response predictions obtained with the lateral models and the 2D-PM numerical predictions obtained with the frontal models.
As shown in
Figure 16, the numerical predictions with the calibrated contact constitutive models adopting a yield plateau under uniaxial compression with a maximum value of 0.80 MPa (m-refined) and the numerical predictions with the traditional elastic behaviour under compression (m-refined (elastic)) are very similar.
Figure 16 shows that it is possible to numerically predict a masonry wall response under uniaxial testing with the lateral models. The 2D-PM model results obtained with the lateral and with the frontal models, point out that the adopted experimental lateral width mostly influences the wall ductility, which is higher in the lateral models with a reduced width.
Figure 16 also shows that in the lateral models, with a wall width of 0.40 m, the adopted contact constitutive model under compression has a lower influence in the predicted numerical results, when compared with the frontal model. A similar result is obtained with the coarser mortar discretization.
In
Table 7 are shown the numerically obtained elastic modulus, peak strength and maximum displacement at peak strength, as well as the average experimental values obtained [
1,
30].
Table 7.
Elastic properties and peak-strength—numerical and experimental values [
1].
Table 7.
Elastic properties and peak-strength—numerical and experimental values [
1].
| Model | [kN] | E [GPa] | [MPa] | [mm] |
|---|
| m-refined | 270 | 0.254 | 0.56 | 3.38 |
| m-refined-elastic | 325 | 0.254 | 0.68 | 4.50 |
| [1] | 168 (238) | - | 0.49 (0.73) | 5.97 (6.39) |
It can be seen that the 2D-PM lateral m-refined numerical model is able to predict values closer to the obtained experimentally, namely the peak stress. The similar response of the frontal and lateral numerical models is related to the fact that the walls have similar stone arrangements. Nevertheless, it is shown that a lateral wall model when compared with the frontal model has a higher ductility.
In
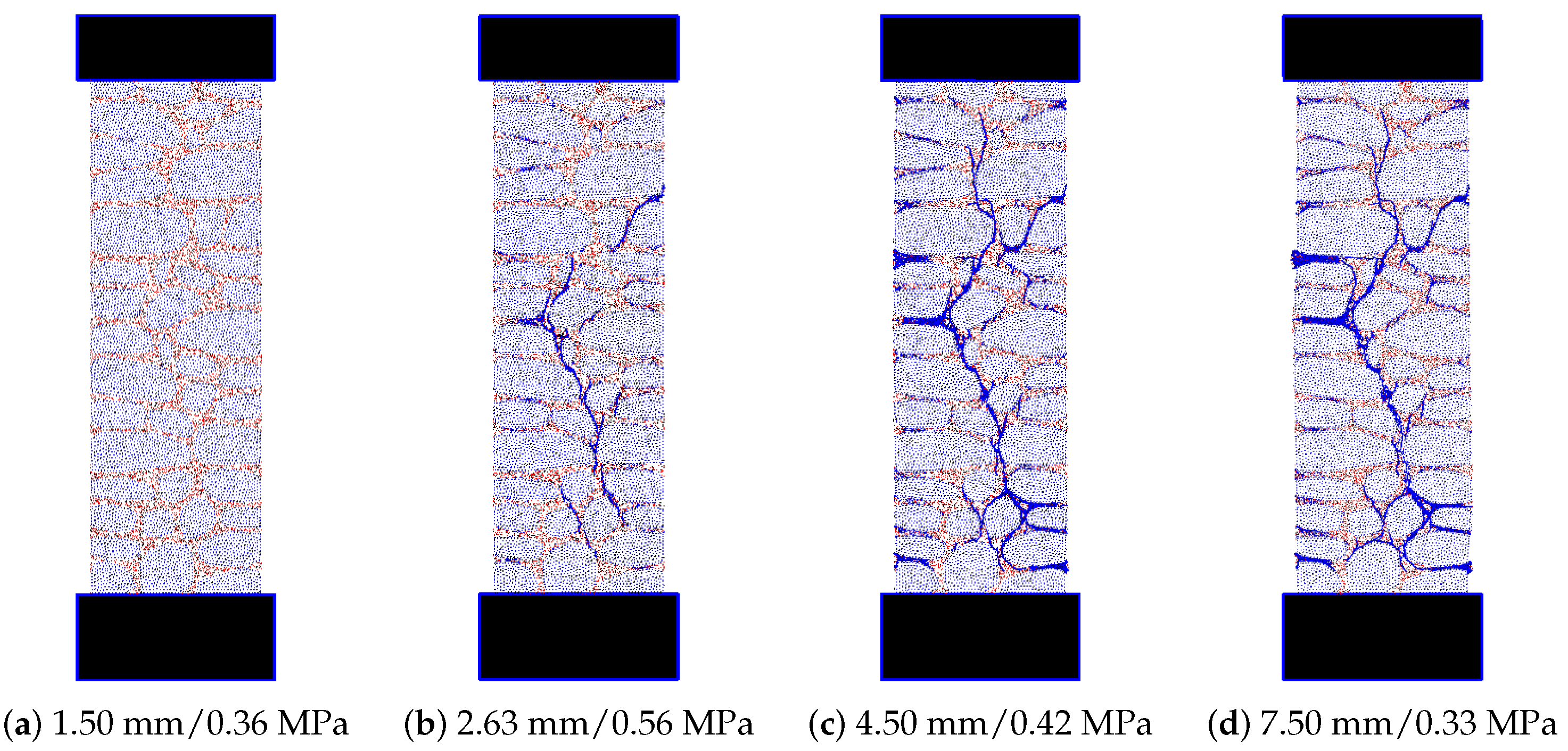
Figure 17 are shown the final failure models for the lateral numerical models adopting a refined and a coarse mortar particle assembly.
In the lateral numerical models, the failure predicted with a maximum yield compressive stress of 0.80 MPa is closer to the failure mode predicted with an elastic model under compression, for both mortar discretizations. In both models a final macroscopic crack is formed due to the bending of the wall lateral stone column, which occurs due to a loss of stiffness in the mortar vertical alignments.
Figure 18 shows the damage evolution for the lateral model with a refined mortar discretization. Like in the frontal model the crack occurs initially at the mortar due to tensile loading and then evolves throughout the wall within the mortar and finally it localizes leading to the final failure mode.
Figure 19 presents the 2D-PM numerical stress-displacement response predictions for the coarse (m-coarse) and for the refined (m-refined) mortar discretizations. Like in the frontal model, the coarse mortar discretization predicts a behaviour similar to the predicted with a finer particle discretization, for both adopted constitutive models.
The m-refined model has a total simulation time of around 60 h, with around 1.00 h of simulation per 10,000 steps and the m-coarse model has a total simulation time of 20 h with around 0.61 h of simulation per 10,000 steps.
The presented numerical results point out that with a lateral wall model adopting a coarser mortar discretization (m-coarse), it is possible to greatly reduce the simulation times without compromising the quality of the numerical predictions, namely the peak strength. The results also show that a numerical model of the lateral wall section can be adopted, not only to predict the peak strength but also to numerically assess reinforcement solutions.