A Quantitative Analysis on Key Factors Affecting the Thermal Performance of the Hybrid Air-Based BIPV/T System
Abstract
:1. Introduction
- Comprehensive quantitative examination of the impact of system parameters, including uncertainty propagation and sensitivity ranking: the documented volume of the analysis of the role of performance-related factors is grossly insufficient, and the conclusions are difficult to generalize due to the reality of incomplete, weakly correlated and highly limited parameters. Although global sensitivity analysis (GSA) is a preferable alternative, there are very few systematic assessment efforts based on this method due to the characteristics of various indicators and the high processing cost.
- A systematic design approach for the HAB-BIPV/T system: the HAB-BIPV/T system has few documented design cases, making it difficult to penetrate a massive market. A comprehensive thermal performance assessment considering the uncertainties from various perspectives and ranking for influential factors are still not systematically addressed. Among the existing relevant studies, deterministic experimental situations frequently struggle to establish universal mapping due to configurable aspects such as system design and operating conditions, which severely limit the reference value.
2. Model Description and Indicators
3. Finite Element Method
3.1. Governing Equations
3.2. Boundary Conditions
3.3. Control Variables
4. Uncertainty Quantification
- 1.
- Uncertainty propagation analysis (UPA): the probability density function (PDF), cumulative distribution function (CDF), probability plot (PP) and cumulative distribution function (CHF) were calculated to understand in detail how the uncertainties of inputs propagate to quantities of interest.
- 2.
- Global sensitivity analysis (GSA): the perturbation effects of uncertain inputs were ranked according to their significance and were quantified to determine how uncertainties in the quantities of interest were apportioned to the various inputs.
4.1. Probabilistic-Based UPA Method
4.2. Sequential GSA Method
4.2.1. Morris Screening
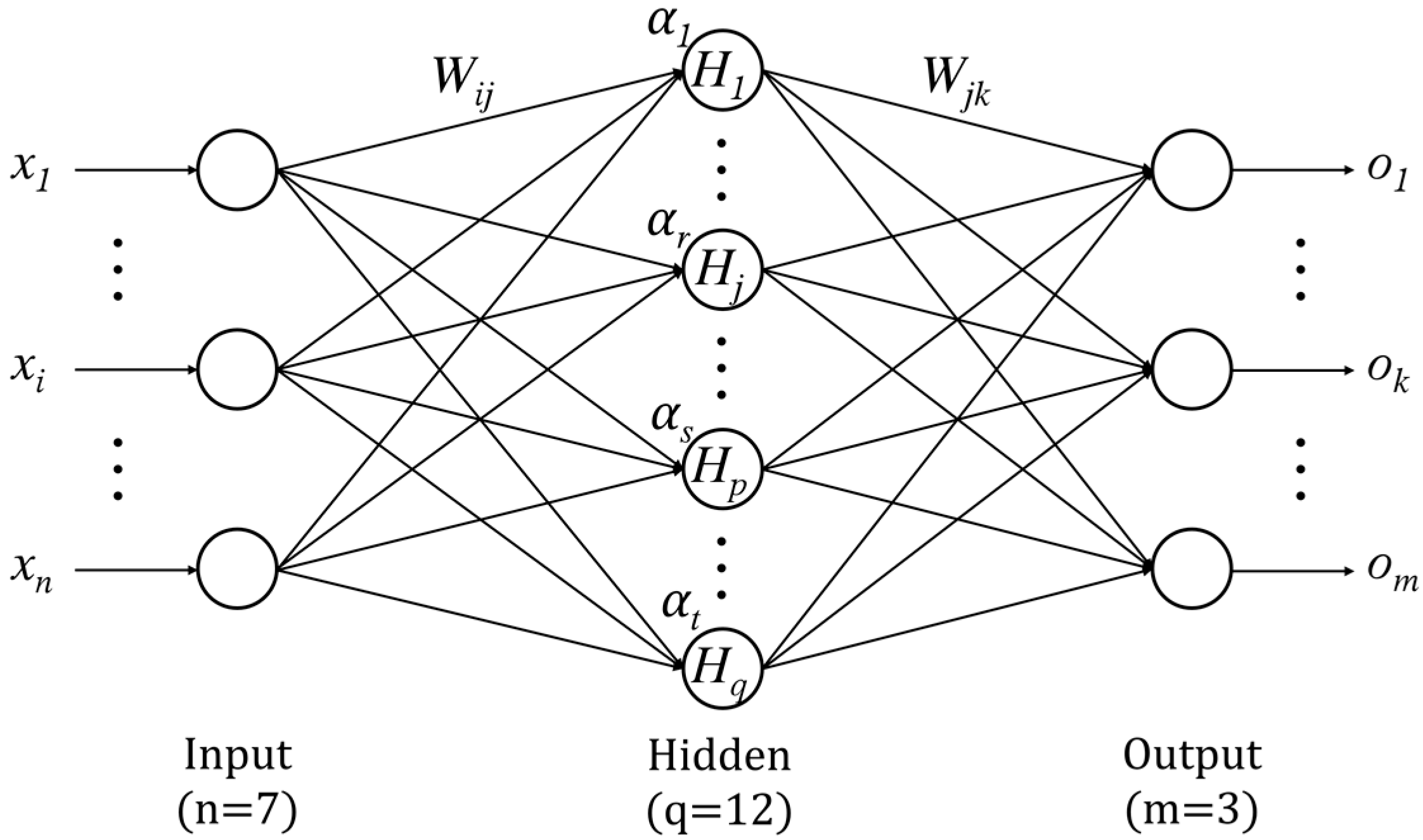
4.2.2. BPNN-Based Sobol’ Method
4.3. Implementation of Uncertainty Quantification in FEM Program
5. Result and Discussion
5.1. Uncertainty Propagation
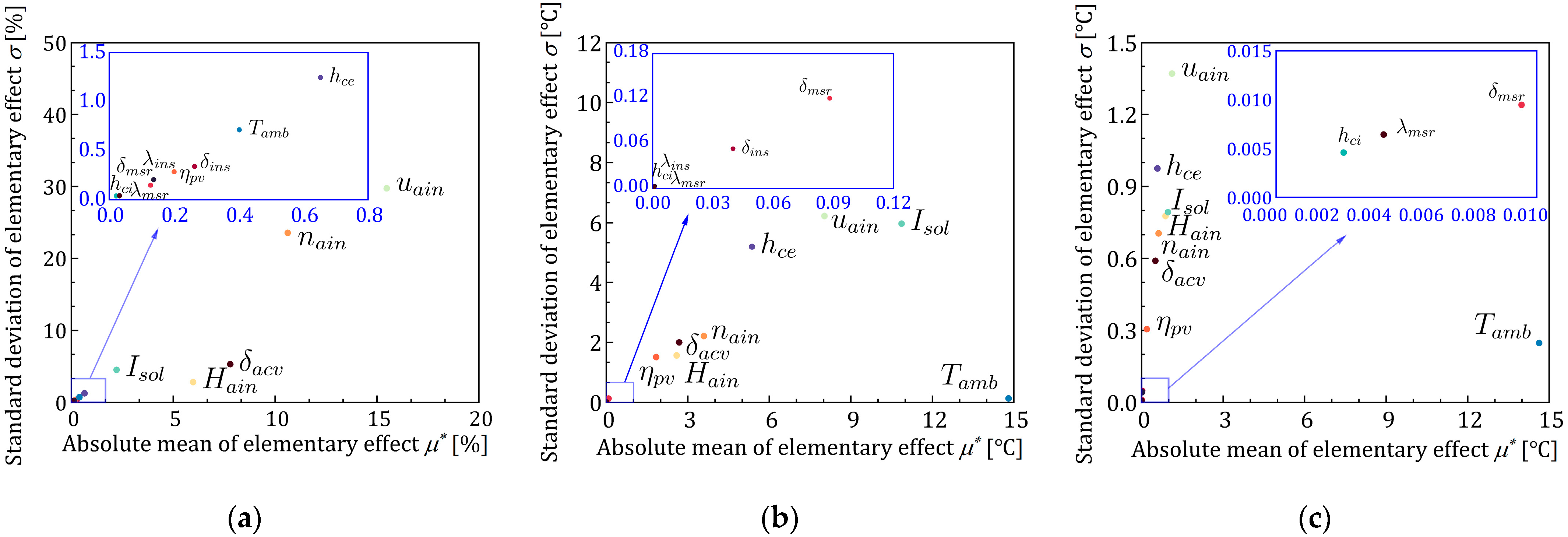
5.2. Parameter Screening by Morris
5.3. Sobol’ Indices Based on BPNN Model
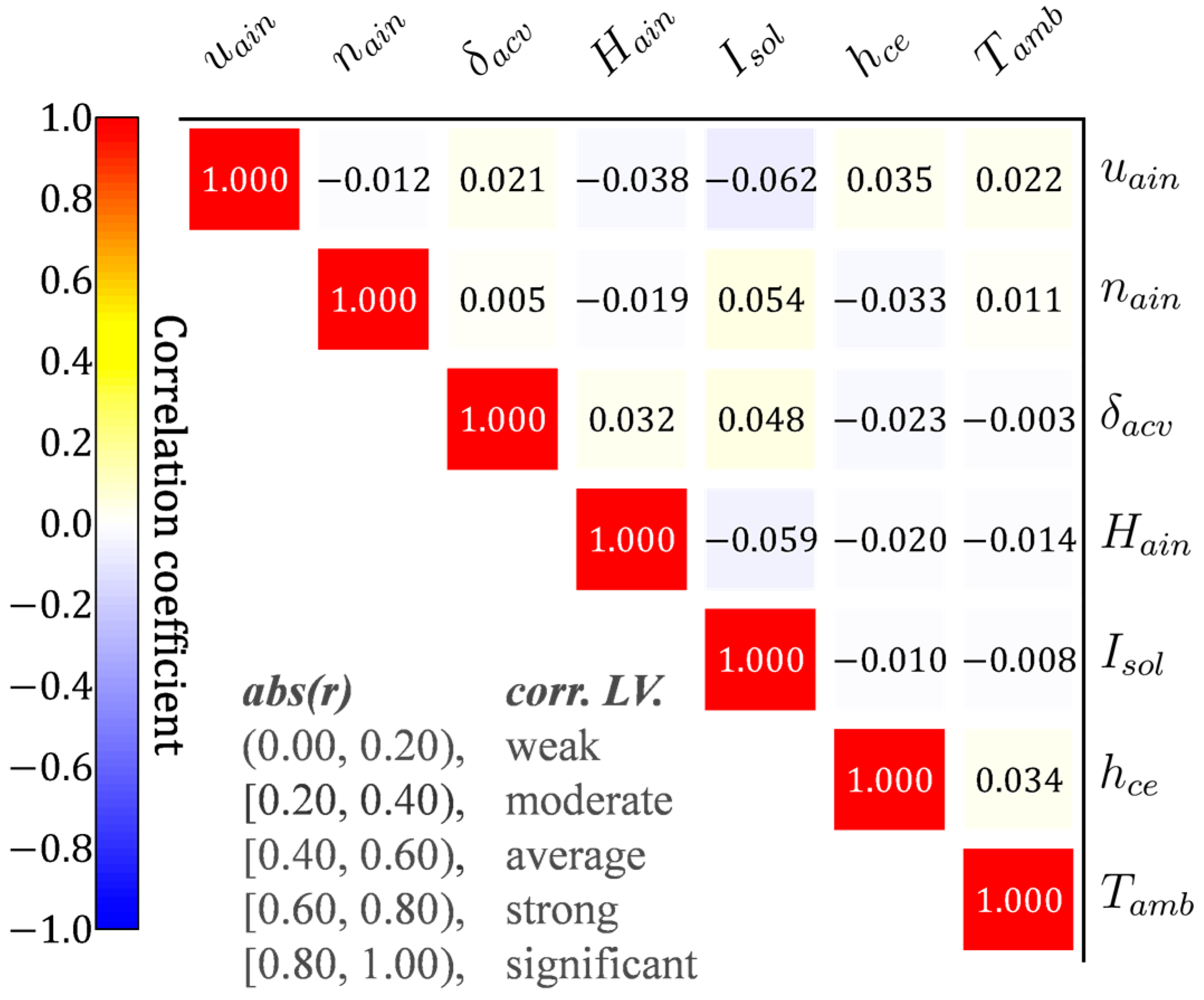
5.3.1. Parameter Correlation Analysis
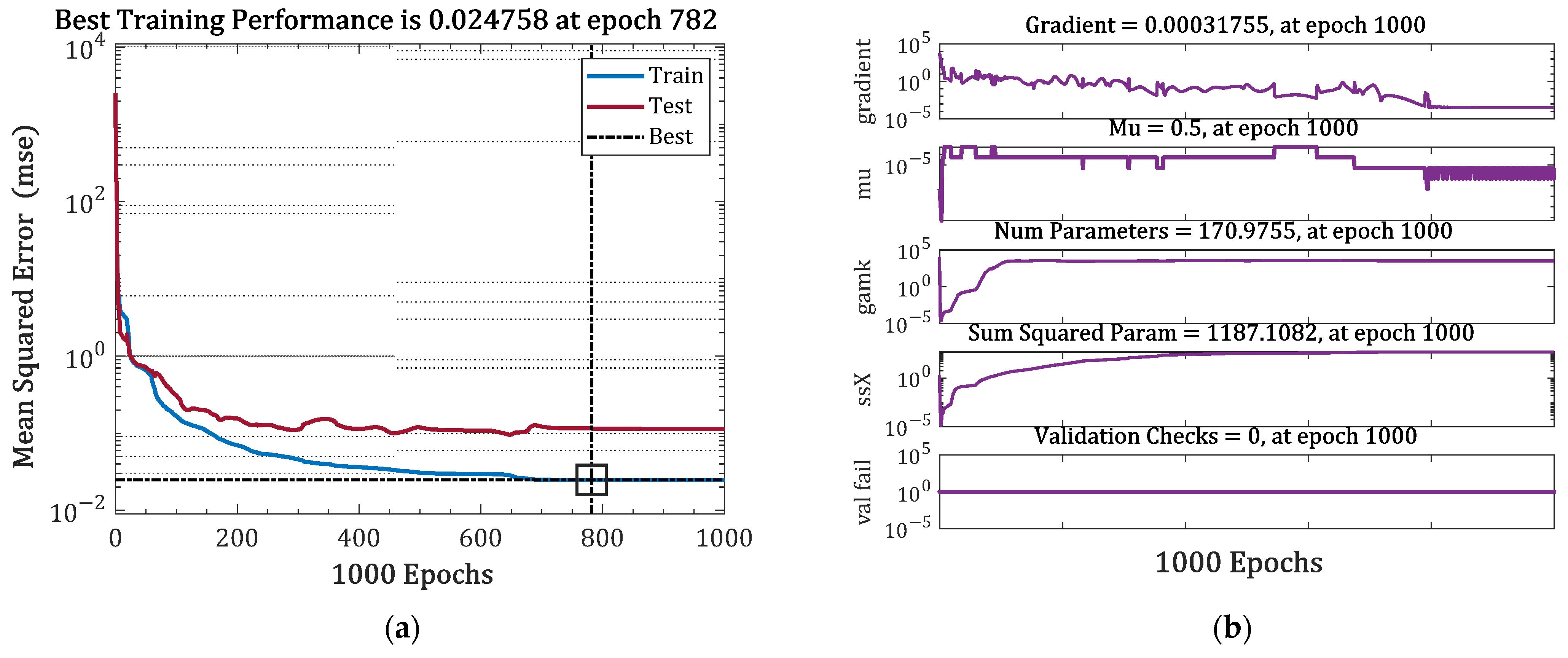
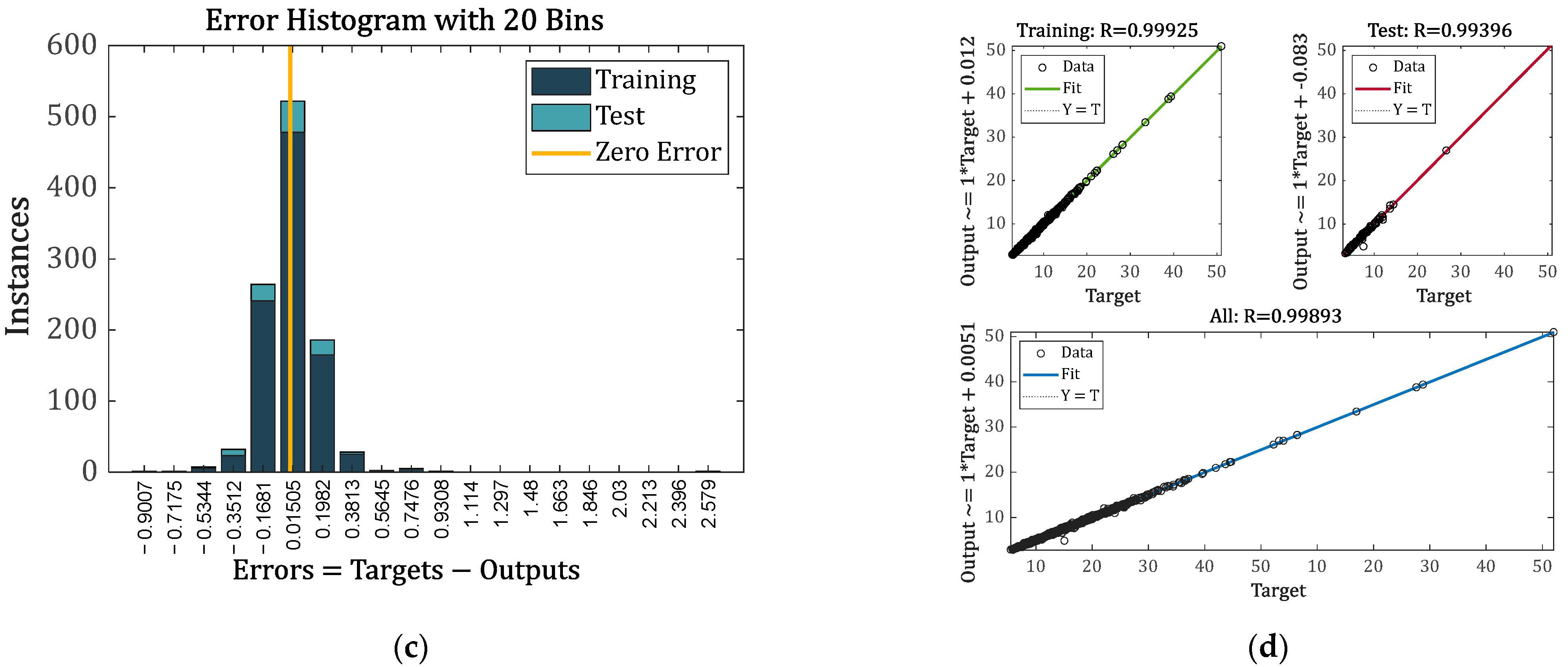
5.3.2. BPNN-Based Surrogate Model
5.3.3. Sensitivity Quantification
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
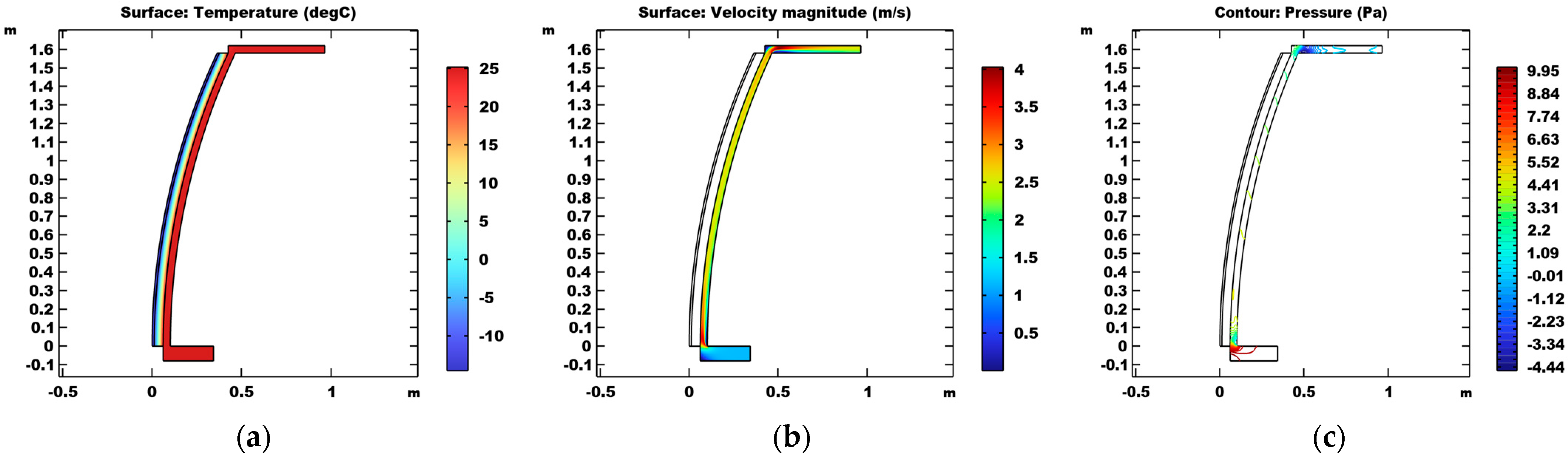
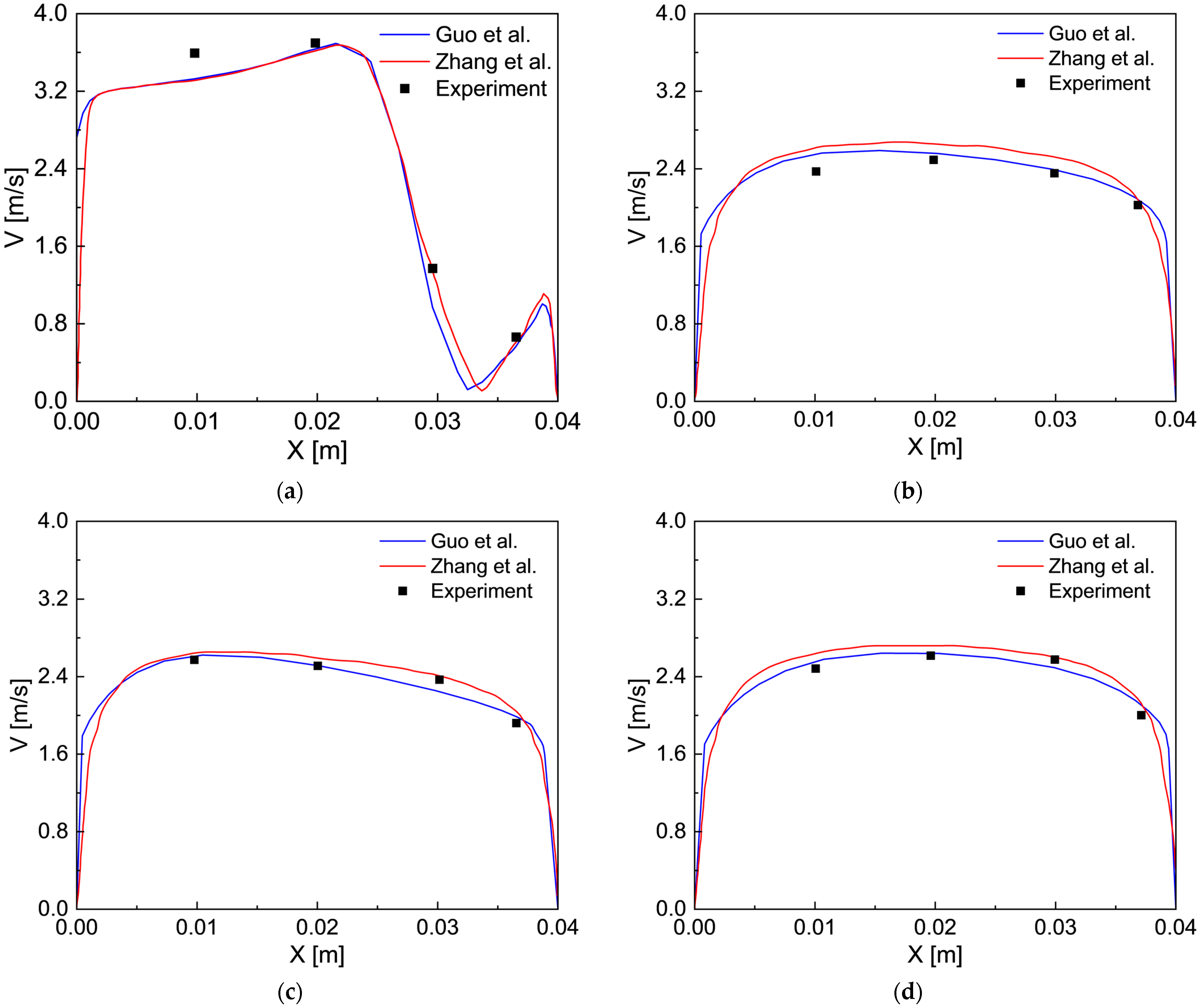
References
- IEA. Net Zero by 2050 A Roadmap for the Global Energy Sector; IEA: Pairs, France, 2021. [Google Scholar]
- IEA. Roadmap for Energy-Efficient Buildings and Construction in the Association of Southeast Asian Nations; IEA: Paris, France, 2022. [Google Scholar]
- IEA. Tracking Buildings 2021; IEA: Pairs, France, 2021. [Google Scholar]
- IEA. Solar PV; IEA: Pairs, France, 2021. [Google Scholar]
- Rounis, E.D.; Athienitis, A.; Stathopoulos, T. Review of Air-Based PV/T and BIPV/T Systems-Performance and Modelling. Renew. Energy 2021, 163, 1729–1753. [Google Scholar] [CrossRef]
- Yang, T.; Athienitis, A.K. A Study of Design Options for a Building Integrated Photovoltaic/Thermal (BIPV/T) System with Glazed Air Collector and Multiple inlets. Sol. Energy 2014, 104, 82–92. [Google Scholar] [CrossRef]
- Tripanagnostopoulos, Y.; Nousia, T.; Souliotis, M.; Yianoulis, P. Hybrid Photovoltaic/Thermal Solar systems. Sol. Energy 2002, 72, 217–234. [Google Scholar] [CrossRef]
- Brahim, T.; Jemni, A. Economical Assessment and Applications of Photovoltaic/Thermal Hybrid Solar Technology: A Review. Sol. Energy 2017, 153, 540–561. [Google Scholar] [CrossRef]
- Sultan, S.M.; Ervina Efzan, M.N. Review on Recent Photovoltaic/Thermal (PV/T) Technology Advances and Applications. Sol. Energy 2018, 173, 939–954. [Google Scholar] [CrossRef]
- Al-Waeli, A.H.A.; Sopian, K.; Kazem, H.A.; Chaichan, M.T. Photovoltaic/Thermal (PV/T) Systems: Status and Future prospects. Renew. Sustain. Energy Rev. 2017, 77, 109–130. [Google Scholar] [CrossRef]
- Maghrabie, H.M.; Abdelkareem, M.A.; Al-Alami, A.H.; Ramadan, M.; Mushtaha, E.; Wilberforce, T.; Olabi, A.G. State-of-the-Art Technologies for Building-Integrated Photovoltaic Systems. Buildings 2021, 11, 383. [Google Scholar] [CrossRef]
- Chaibi, Y.; El Rhafiki, T.; Simón-Allué, R.; Guedea, I.; Luaces, S.C.; Gajate, O.C.; Kousksou, T.; Zeraouli, Y. Air-Based Hybrid Photovoltaic/Thermal Systems: A Review. J. Clean. Prod. 2021, 295, 126211. [Google Scholar] [CrossRef]
- Agrawal, S.; Tiwari, G.N. Overall Energy, Exergy and Carbon Credit Analysis by Different Type of Hybrid Photovoltaic Thermal Air Collectors. Energy Convers. Manag. 2013, 65, 628–636. [Google Scholar] [CrossRef]
- Hussain, F.; Othman, M.Y.H.; Sopian, K.; Yatim, B.; Ruslan, H.; Othman, H. Design Development and Performance Evaluation of Photovoltaic/Thermal (PV/T) Air Base Solar Collector. Renew. Sustain. Energy Rev. 2013, 25, 431–441. [Google Scholar] [CrossRef]
- Yazdanifard, F.; Ameri, M. Exergetic Advancement of Photovoltaic/Thermal Systems (PV/T): A Review. Renew. Sustain. Energy Rev. 2018, 97, 529–553. [Google Scholar] [CrossRef]
- Das, D.; Kalita, P.; Roy, O. Flat Plate Hybrid Photovoltaic-Thermal (PV/T) System: A Review on Design and Development. Renew. Sustain. Energy Rev. 2018, 84, 111–130. [Google Scholar] [CrossRef]
- Liu, K.; Zhu, B.; Chen, J.; Liu, K.; Zhu, B.; Chen, J. Low-Carbon Design Path of Building Integrated Photovoltaics: A Comparative Study Based on Green Building Rating Systems. Buildings 2021, 11, 469. [Google Scholar] [CrossRef]
- Zondag, H.A. Flat-Plate PV-Thermal Collectors and Systems: A Review. Renew. Sustain. Energy Rev. 2008, 12, 891–959. [Google Scholar] [CrossRef] [Green Version]
- Kern, E.C., Jr.; Russell, M.C. Combined Photovoltaic and Thermal Hybrid Collector Systems. In Proceedings of the Combined Photovoltaic and Thermal Hybrid Collector Systems, Washington, DC, USA, 5 June 1978. [Google Scholar]
- Florschuetz, L.W. Extension of the Hottel-Whillier Model to the Analysis of Combined Photovoltaic/Thermal Flat Plate Collectors. Sol. Energy 1979, 22, 361–366. [Google Scholar] [CrossRef]
- Hegazy, A.A. Comparative Study of the Performances of Four Photovoltaic/Thermal Solar Air Collectors. Energy Convers. Manag. 2000, 41, 861–881. [Google Scholar] [CrossRef]
- Rounis, E.D.; Athienitis, A.K.; Stathopoulos, T. BIPV/T Curtain Wall Systems: Design, Development and Testing. J. Build. Eng. 2021, 42, 103019. [Google Scholar] [CrossRef]
- Yang, T.; Athienitis, A.K. Experimental Investigation of a Two-Inlet Air-Based Building Integrated Photovoltaic/Thermal (BIPV/T) System. Appl. Energy 2015, 159, 70–79. [Google Scholar] [CrossRef]
- Qureshi, U.; Baredar, P.; Kumar, A. Effect of Weather Conditions on the Hybrid Solar PV/T Collector in Variation of Voltage and Current. Int. J. Res. 2014, 1, 872–879. [Google Scholar]
- Li, G.; Pei, G.; Ji, J.; Yang, M.; Su, Y.; Xu, N. Numerical and Experimental Study on A PV/T System with Static Miniature Solar Concentrator. Sol. Energy 2015, 120, 565–574. [Google Scholar] [CrossRef]
- Athienitis, A.K.; Barone, G.; Buonomano, A.; Palombo, A. Assessing Active and Passive Effects of Façade Building Integrated Photovoltaics/Thermal Systems: Dynamic Modelling and Simulation. Appl. Energy 2018, 209, 355–382. [Google Scholar] [CrossRef]
- Rounis, E.D.; Athienitis, A.K.; Stathopoulos, T. Multiple-Inlet Building Integrated Photovoltaic/Thermal System Modelling Under Varying Wind and Temperature Conditions. Sol. Energy 2016, 139, 157–170. [Google Scholar] [CrossRef] [Green Version]
- Chen, L.; Yang, J.; Li, P. Modelling the Effect of BIPV Window in the Built Environment: Uncertainty and Sensitivity. Build. Environ. 2022, 208, 108605. [Google Scholar] [CrossRef]
- Gonçalves, J.E.; van Hooff, T.; Saelens, D. Understanding the Behaviour of Naturally-Ventilated BIPV Modules: A Sensitivity Analysis. Renew. Energy 2020, 161, 133–148. [Google Scholar] [CrossRef]
- Liu, X.; Wu, Y.; Hou, X.; Liu, H. Investigation of the Optical Performance of a Novel Planar Static PV Concentrator with Lambertian Rear Reflectors. Buildings 2017, 7, 88. [Google Scholar] [CrossRef] [Green Version]
- Mirsadeghi, M.; Cóstola, D.; Blocken, B.; Hensen, J.L.M. Review of External Convective Heat Transfer Coefficient Models in Building Energy Simulation Programs: Implementation and Uncertainty. Appl. Therm. Eng. 2013, 56, 134–151. [Google Scholar] [CrossRef]
- Montazeri, H.; Blocken, B. New Generalized Expressions for Forced Convective Heat Transfer Coefficients at Building Facades and Roofs. Build. Environ. 2017, 119, 153–168. [Google Scholar] [CrossRef] [Green Version]
- Agrawal, B.; Tiwari, G.N. Life Cycle Cost Assessment of Building Integrated Photovoltaic Thermal (BIPVT) Systems. Energy Build. 2010, 42, 1472–1481. [Google Scholar] [CrossRef]
- Delisle, V.; Kummert, M. Cost-Benefit Analysis of Integrating BIPV-T Air Systems Into Energy-Efficient Homes. Sol. Energy 2016, 136, 385–400. [Google Scholar] [CrossRef]
- Debbarma, M.; Sudhakar, K.; Baredar, P. Comparison of BIPV and BIPVT: A Review. Resour.-Effic. Technol. 2017, 3, 263–271. [Google Scholar] [CrossRef]
- Yang, S.; Fiorito, F.; Prasad, D.; Sproul, A.; Cannavale, A. A Sensitivity Analysis of Design Parameters of BIPV/T-DSF in Relation to Building Energy and Thermal comfort Performances. J. Build. Eng. 2021, 41, 102426. [Google Scholar] [CrossRef]
- Yang, S.; Cannavale, A.; Di Carlo, A.; Prasad, D.; Sproul, A.; Fiorito, F. Performance Assessment of BIPV/T Double-Skin Façade for Various Climate Zones in Australia: Effects on Energy Consumption. Sol. Energy 2020, 199, 377–399. [Google Scholar] [CrossRef]
- Assoa, Y.B.; Sauzedde, F.; Boillot, B. Numerical Parametric Study of the Thermal and Electrical Performance of A BIPV/T Hybrid Collector for Drying Applications. Renew. Energy 2018, 129, 121–131. [Google Scholar] [CrossRef]
- Bambara, J.; Athienitis, A.K.; O’Neill, B. Design and Performance of a Photovoltaic/Thermal System Integrated with Transpired Collector. Ashrae Trans. 2011, 117, 403–410. [Google Scholar]
- Rounis, E.; Kruglov, O.; Ioannidis, Z.; Athienitis, A.; Stathopoulos, T. Experimental Investigation of BIPV/T Envelope System with Thermal Enhancements for Roof and Curtain Wall Applications. In Proceedings of the 34th European PV Solar Energy Conference (EU PVSEC), Amsterdam, The Netherlands, 25–29 September 2017. [Google Scholar]
- Wan, T.; Bai, Y.; Wu, L.; He, Y. Multi-criteria decision making of integrating thermal comfort with energy utilization coefficient under different air supply conditions based on human factors and 13-value thermal comfort scale. J. Build. Eng. 2021, 39, 102249. [Google Scholar] [CrossRef]
- Zhang, S.; Lin, Z.; Ai, Z.; Wang, F.; Cheng, Y.; Huan, C. Effects of operation parameters on performances of stratum ventilation for heating mode. Build. Environ. 2019, 148, 55–66. [Google Scholar] [CrossRef]
- Pepper, D.W.; Heinrich, J.C. The Finite Element Method: Basic Concepts and Applications with MATLAB®, MAPLE, and COMSOL; CRC Press: Boca Raton, FA, USA, 2017. [Google Scholar]
- Zhang, T.; Tian, L.; Lin, C.-H.; Wang, S. Insulation of commercial aircraft with an air stream barrier along fuselage. Build. Environ. 2012, 57, 97–109. [Google Scholar] [CrossRef]
- GB 50176-2016; Code for Thermal Design of Civil Building. Ministry of Housing and Urban-Rural Development of the People’s Republic of China: Beijing, China, 2017.
- Martín-Chivelet, N.; Kapsis, K.; Wilson, H.R.; Delisle, V.; Yang, R.; Olivieri, L.; Polo, J.; Eisenlohr, J.; Roy, B.; Maturi, L.; et al. Building-Integrated Photovoltaic (BIPV) Products and Systems: A Review of Energy-Related Behavior. Energy Build. 2022, 262, 111998. [Google Scholar] [CrossRef]
- Duffie, J.A.; Beckman, W.A.; Blair, N. Solar Engineering of Thermal Processes, Photovoltaics and Wind; John Wiley & Sons: Hoboken, NJ, USA, 2020. [Google Scholar]
- Chen, Y.; Athienitis, A.K.; Galal, K. Modeling, Design and Thermal Performance of a BIPV/T System Thermally Coupled with a Ventilated Concrete Slab in a Low Energy Solar House: Part 1, BIPV/T System and House Energy Concept. Sol. Energy 2010, 84, 1892–1907. [Google Scholar] [CrossRef]
- Wei, T. A Review of Sensitivity Analysis Methods in Building Energy Analysis. Renew. Sustain. Energy Rev. 2013, 20, 411–419. [Google Scholar] [CrossRef]
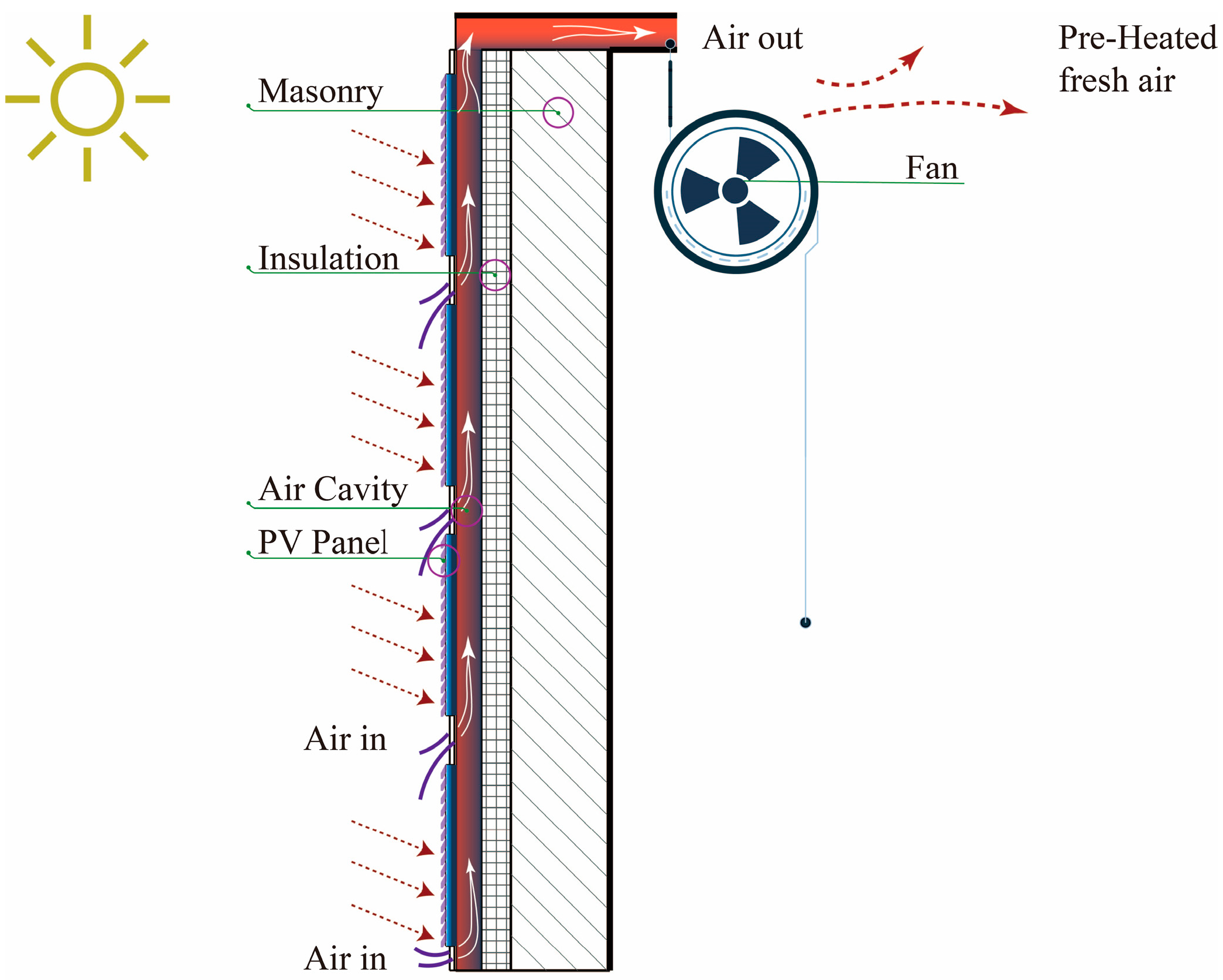
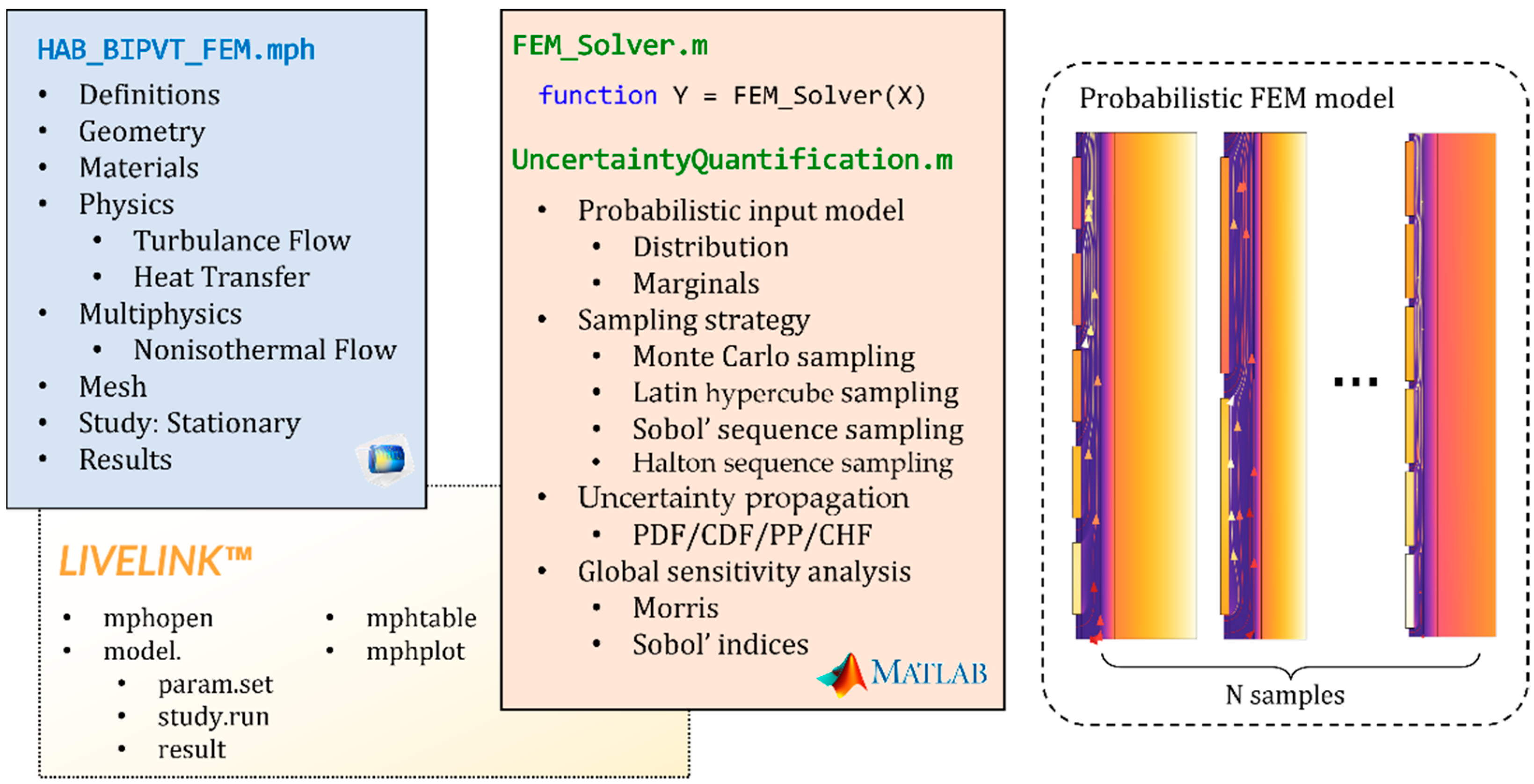


| # | Control Variables | Abbr. | Unit | Distribution | Marginals | Ref. |
|---|---|---|---|---|---|---|
| 1 | Air cavity thickness | cm | U (5.0, 15.0) | [5, 15] | [5,23,39,40,46,47,48] | |
| 2 | Insulation thickness | cm | U (4.0, 10.0) | [4, 10] | [5,23,39,40,46,47,48] | |
| 3 | Insulation thermal conductivity | W/(m·K) | U (0.5, 2.0) | [0.5, 2] | [5,23,39,40,46,47,48] | |
| 4 | Masonry thickness | cm | U (11.5, 49.0) | [11.5, 49] | [5,23,39,40,46,47,48] | |
| 5 | Masonry thermal conductivity | W/(m·K) | U (0.025, 0.050) | [0.025, 0.05] | [5,23,39,40,46,47,48] | |
| 6 | PV conversion efficiency | — | U (0.10, 0.25) | [0.1, 0.25] | [5,23,39,40,46,47,48] | |
| 7 | Number of air inlets | — | U (3, 8) | [3, 8] | [5,23,39,40,46,47,48] | |
| 8 | Air inlet height | cm | U (5.0, 20.0) | [5, 20] | [5,23,39,40,46,47,48] | |
| 9 | Air inlet velocity | m/s | U (0.01, 5.00) | [0.01, 5] | [5,23,39,40,46,47,48] | |
| 10 | Solar radiation intensity | W/m2 | N (600, 1352) | [200, 1000] | [5,23,39,40,46,47,48] | |
| 11 | Outer ambient temperature | degC | N (0.55, 2.452) | [−6.8, 7.9] | [5,23,39,40,46,47,48] | |
| 12 | Outer combined heat transfer coef. | W/(m2·K) | N (19, 1.352) | [12, 26] | [5,23,39,40,46,47,48] | |
| 13 | Inner combined heat transfer coef. | W/(m2·K) | N (8, 0.772) | [4, 12] | [5,23,39,40,46,47,48] |
| Control Variables | Indicators | ||
|---|---|---|---|
| AUI | TPV | TAO | |
| ●● | ●●● | ● | |
| ●● | ●●● | ● | |
| ●●● | ○○ | ● | |
| ●●● | ●● | ● | |
| ● | ○○○ | ○○ | |
| ○ | ●●● | ○○ | |
| ● | ○○○ | ○○ | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, J.; Jin, Y.; Li, Z.; Li, M. A Quantitative Analysis on Key Factors Affecting the Thermal Performance of the Hybrid Air-Based BIPV/T System. Buildings 2022, 12, 1135. https://doi.org/10.3390/buildings12081135
Guo J, Jin Y, Li Z, Li M. A Quantitative Analysis on Key Factors Affecting the Thermal Performance of the Hybrid Air-Based BIPV/T System. Buildings. 2022; 12(8):1135. https://doi.org/10.3390/buildings12081135
Chicago/Turabian StyleGuo, Juanli, Yongyun Jin, Zhenyu Li, and Meiling Li. 2022. "A Quantitative Analysis on Key Factors Affecting the Thermal Performance of the Hybrid Air-Based BIPV/T System" Buildings 12, no. 8: 1135. https://doi.org/10.3390/buildings12081135
APA StyleGuo, J., Jin, Y., Li, Z., & Li, M. (2022). A Quantitative Analysis on Key Factors Affecting the Thermal Performance of the Hybrid Air-Based BIPV/T System. Buildings, 12(8), 1135. https://doi.org/10.3390/buildings12081135







