1. Introduction
First safety and then economy are the two key requirements of a structure. An engineer can design, analyze, and erect structures in a variety of ways but that cannot guarantee the most economical solution. In the conventional design practice, multiple manual iterations must be executed to attain a design that is safe as well as the most economical, but it is a hectic and time taking process. Thus, the design problem should be expressed as an optimization problem that minimizes the cost while keeping in view all the safety requirements. Most of the optimization-related work in civil engineering, consulting Adeli and Sarma [
1], has focused on minimizing the weight of structures, benefitting the steel construction, as it comprises of a single material only. Hence, the critical goal of the reinforced concrete (RC) optimization is to minimize the material cost while following all the limitations as described by the design codes.
The extraordinary progress in technology and computational competencies in the past few decades has sparked an interest in the optimization of structural design [
2,
3,
4]. Optimization is the technique of finding the best solution among the set of all feasible solutions. In the field of structural engineering, it provides an opportunity to find objective-based designs for complex real-world problems in an efficient manner [
5]. However, before the application of optimization, the design problem must be mathematically modeled into an optimization problem by defining variables, constraints, and bounds. After the problem formulation, numerous existing techniques each with unique characteristics can be applied for achieving optimality in design [
6]. Metaheuristic techniques are considered as the most appropriate for solving non-linear and non-convex problems, such as those of RC structures [
3,
4,
5,
6,
7]. Design optimization has been used on every type of RC member and has been proven to be a fast and efficient tool for drastic improvement of design [
8,
9,
10,
11,
12,
13,
14,
15]. According to the critical review on RC optimization by Afzal et al. [
3], the dominating factor in the current era of RC optimization is the minimization of cost. The review also reveals that most of the work has been done on frames and beams, while isolated footings are the least investigated structure in this field.
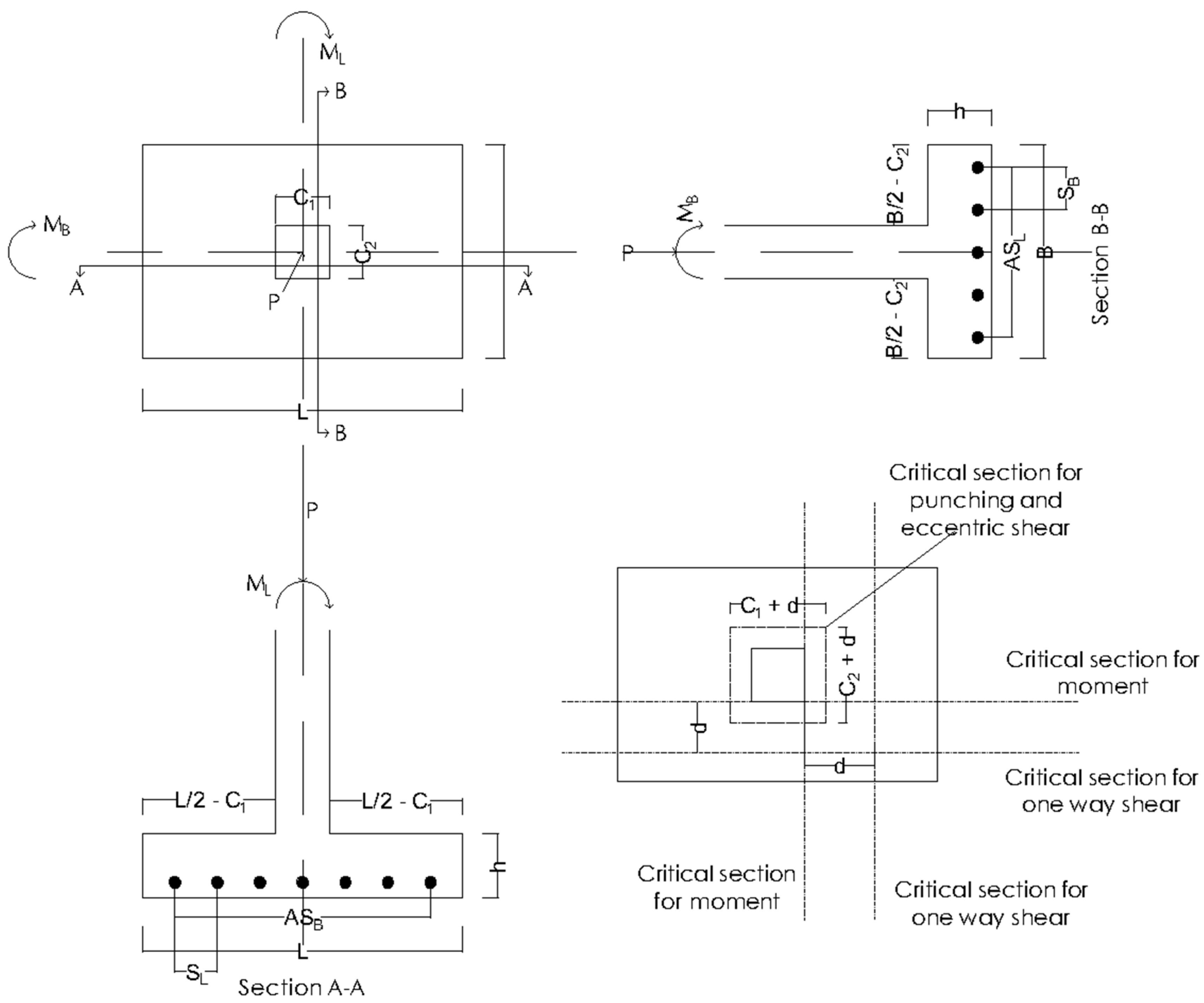
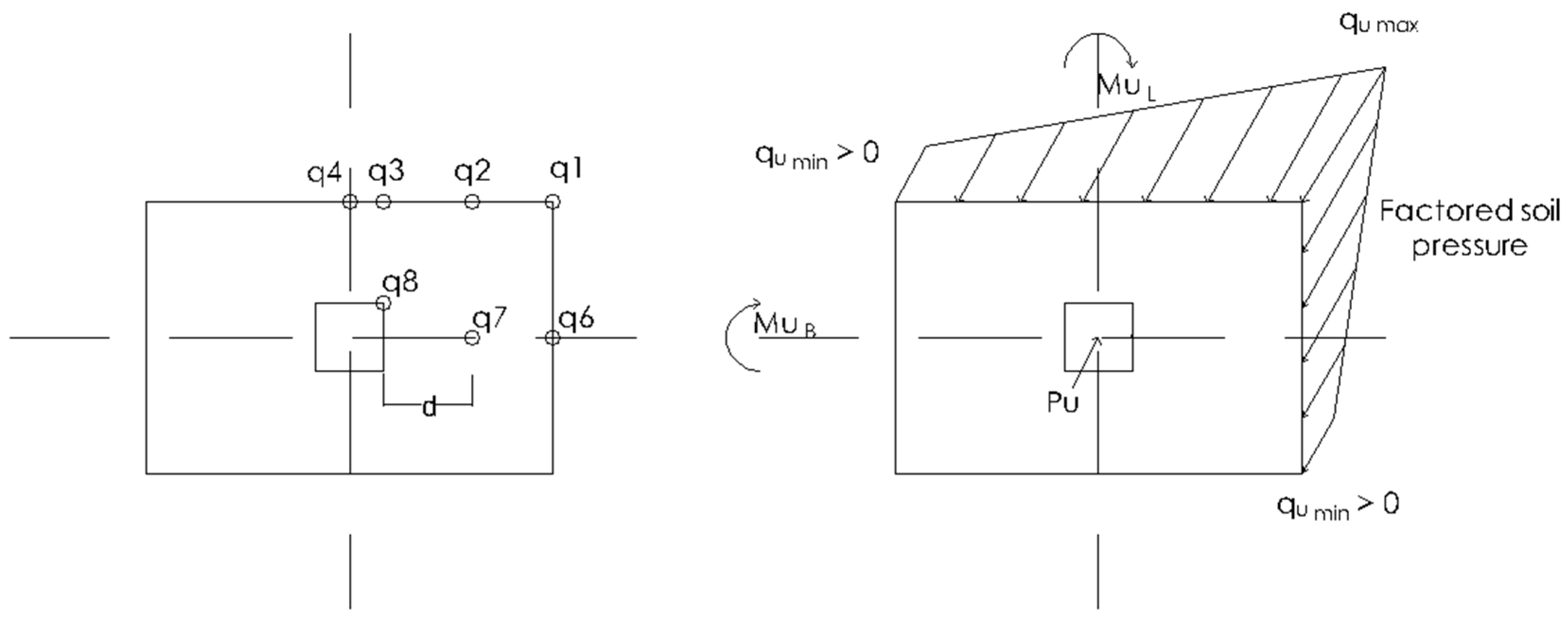
Footings are among the most important and commonly designed structural members. The types of shallow foundations are Combined and Isolated footings. The Isolated footing is the most common footing type selected by a design engineer for small to medium level design projects. Footings must satisfy the serviceability and ultimate limit state conditions and must be designed to withstand three types of failures, structural failure, geotechnical failure, and loss of equilibrium. Structural failure includes shear failure, bending failure, and the failure of the bond between steel and concrete. Geotechnical failure includes sliding, settlement, and bearing failure, while the loss of equilibrium includes eccentricity problems that result in the overturning and combined failure in the structure and ground.
The majority of works on the optimization of isolated footings that have been published in the literature have focused mainly on the problem formulation and the utilization of various linear and nonlinear techniques. In 1972, Bhavikatti and Hedge [
16] presented an optimization model that resulted in a 8–10% cost reduction. However, the proposed model was based on linear optimization, which affects the accuracy of the results. In 1985, Namq and Al-Ani [
17] presented the cost optimization of spread footings subjected to eccentricities in both directions by using the graphical Rosenbrocks method. The research showed that the optimum ratio of footing length to width (
/
) is directly proportional to the ratio of the difference between the eccentricities in both directions to the eccentricity in the short direction and there is no such effect of steel to concrete unit cost ratio in this optimum L/B ratio. Basudhar et al. [
18] used nonlinear programming (NLP) to perform an optimum cost analysis of a rigid foundation and found that the variation in the cost was due to variation in area ratios. The used technique, however, does not guarantee a global optimum, as the solution is likely to get trapped in local minima. Wang and Kulhawy [
19] presented a design method that considered construction economics in the design of isolated footings with the objective to achieve minimum cost. Al-Douri [
20] presented research on the optimization of trapezoidal combined footing by using Hookes and Jeeves’ model, but this study ignores the reinforcement as a design variable. Rizwan et al. [
21] presented a combined footing optimization using a modified complex method. This model was only limited to a property line, and the reinforcement area and the cost function calculations were not comprehensive. Luevanos-Rojas et al. [
22] and Lopez-Chavarria et al. [
23] presented the numerical modeling for optimization of RC isolated footings and corner combined footings, respectively, considering real soil pressure. But the model was based on optimizing the contact area with the soil and does not necessarily reflect cost optimization. Santillán et al. [
24] presented numerical experimentation on the optimization of eccentrically loaded footings based on real soil pressures and under varying loading conditions. The model was limited in capacity to the property line and foundation type, where one of the columns lies on the property line. The constraints did not account for the spacing limitations for steel reinforcement, and the cost function was only limited to concrete and steel reinforcement costs. Solorzano and Plevris [
25] utilized the Genetic Algorithm (GA) to optimize the material cost and reduce the design time. They did not consider the eccentric shear in the design of the RC isolated footings. The cost of formwork and the effect of material strength on the optimized cost was also ignored. Chaudhuri and Maity [
26] used Unified Particle Swarm Optimization (UPSO) and a binary coded GA and concluded that UPSO shows faster convergence than binary coded GA but that the GA was much more suitable to fulfill both the conservative and economic design of the footings. Single objectives, such as least cost, carbon emissions and weight have been successfully implemented using the algorithms mentioned so far. However, a Pareto front must be established to deal with many objectives at once and only particular algorithms can achieve this. Using the Hybrid Big Bang-Big Crunch Algorithm (BB-BC), Camp and Assadollahi [
27] investigated the minimum cost and minimum carbon emission by using weighted cost and carbon emissions as objective functions. Using Multi-Integer Non-Linear Programming (MINLP) and Discrete Continuous Optimizer (DICOPT), Jelušič and Žlender [
28] studied the least production cost including the cost of each material and activity. All the works mentioned above have developed a particular framework and articulated metaheuristics as a superior technique for non-linear and non-convex design optimization problems.
Even though these previous studies have shown the efficiency of optimization techniques, still their use in the construction industry is rare. This is because these techniques can only be used if the designer has a thorough understanding of problem formulation, optimization techniques and the ability to computer code the design problems in complex programming languages, such as C++, MATLAB, and Fortran. To solve this problem, Rawat and Mittal [
29] developed a spreadsheet tool based on the “Generalized Reduced Gradient” (GRG) algorithm. However, just like any other non-linear programming technique, their proposed tool only provides the local minimum at best. Hence, the primary goal of this research was to develop a spreadsheet-based tool for optimizing the design of isolated footings for the lowest cost using advanced metaheuristic techniques. This has been achieved by using the Evolutionary Algorithm (EA) and the Genetic Algorithm (GA). A spreadsheet program is used as an interface. It accepts the original design as input and calculates the important data for optimizing the design in compliance with ACI 318-14 [
30]. After this process, the algorithm of choice can be applied for optimization. The obtained results from this research using the EA and the GA are then compared with the findings of Rawat and Mittal [
29]. Further, as a novel objective, this study also proposes a unique solution for easier and practical application of optimization by developing ranges for economical proportioning of RC isolated pad footings. This was achieved by doing an in-depth parametric investigation for cost optimization using GA. The parametric analysis was divided into three sections namely, the effects of geometric parameters (Length
, Width
and Thickness
of footing), structural parameters (Area of steel along length
and width
of the footing), and the effects of material strength parameters (concrete compressive strength
and steel yield strength
with varying cost) on isolated footings. The results yielded optimized ranges for different variables for cost-effective designs. To establish the variables, constraints, and feasible ranges, the research paper first presents the optimization problem modeling and formation of spreadsheet-based tool based on a comprehensive review of the literature in methodology. Then case studies are discussed, followed by the results and discussion sections, which evaluate the developed tool’s efficiency, ease of use, and effectiveness. Lastly, the parametric investigation is presented in detail.
3. Case Studies
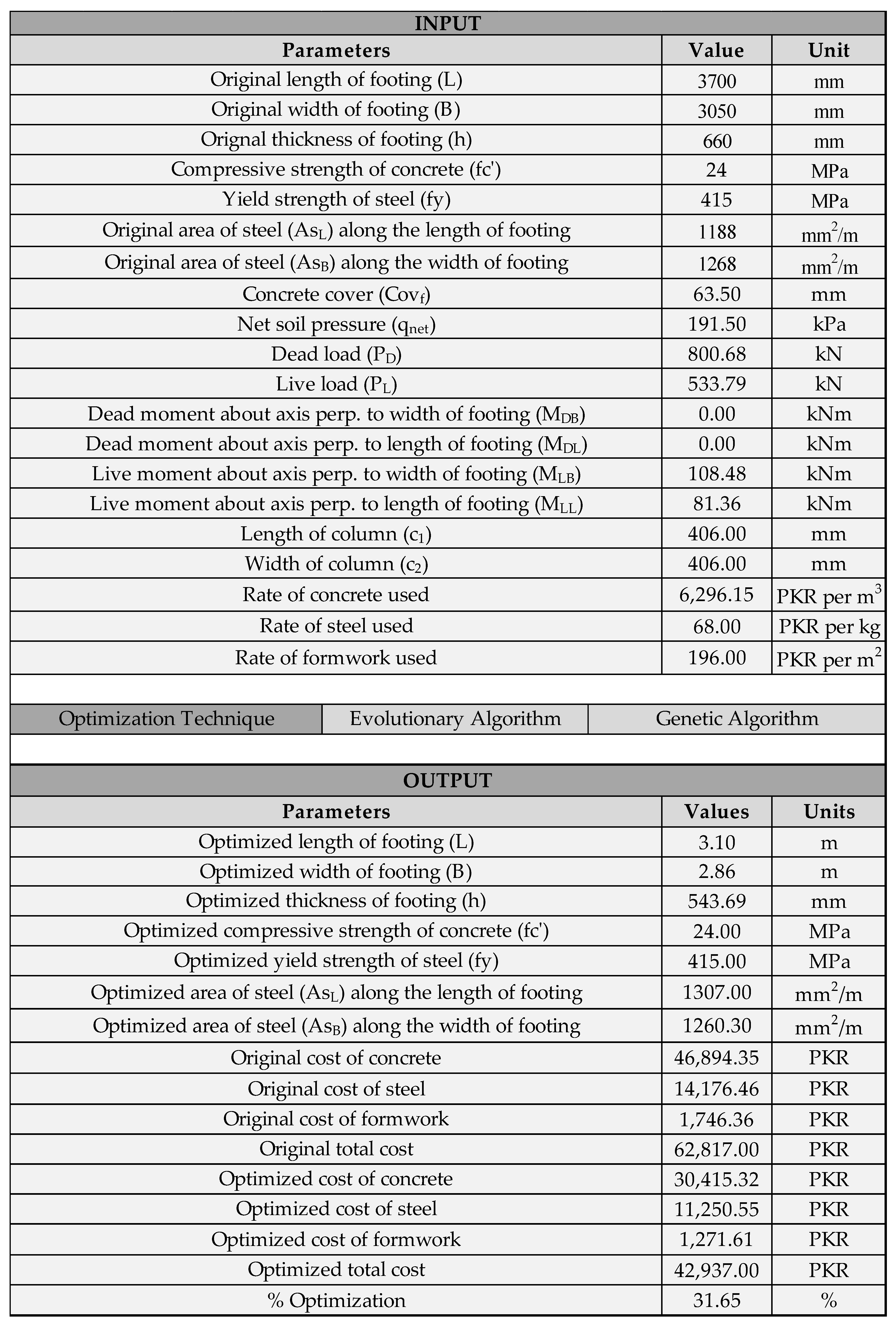
Four design examples from the publication titled “Optimization of Eccentrically Loaded RC Isolated Footings” by Rawat and Mittal [
29] were taken to be designed and optimized in the developed spreadsheet. These examples incorporated both the concentric and eccentric loading conditions. The input parameters for the four examples are shown in
Table 3.
Example 1 [
39] and example 2 [
40] are eccentrically loaded footing cases incorporating moments while example 3 [
41] and example 4 [
42] design concentrically loaded footings. The total costs were calculated based on the same unit rates as used in the reference [
29] for accurate comparison and to show the effectiveness of the developed tool and its superiority in terms of percentage optimization over the approach used in the reference study [
29]. The rates are repeated here as Rs. 6296.15 per cubic meter for concrete (
, Rs. 68 per kg for reinforcing bars (
, and Rs. 196 per square meter for formwork
. The conventional calculations mentioned in the source texts of the four examples were then compared with their optimized counterparts obtained from spreadsheet tool using the EA and the GA algorithms and with the results of Rawat and Mittal [
29] who used the GRG algorithm, to measure the tool’s effectiveness and for cost comparison. Lengths and widths for examples 1, 3 and 4 were obtained from service loads and moments, whereas in example 2, the factored load and moments were used as was done by Shah and Jain [
40] in the published conventional design. This convention was not changed here so that the results can be compared more accurately. Further, in example 1, a difference in the total cost obtained by Rawat and Mittal [
29] appears from the cost mentioned here. This is possibly due to the reason that no steel was provided in the transverse direction by Rawat and Mittal [
29], whereas in order to meet the requirements prescribed by the code, the minimum steel in this direction was provided in the current study.
4. Results and Discussion
The geometric parameters (
,
and
) and the reinforcement parameters (
and
) were obtained as results from the developed tool by the run of algorithms. The results for the four examples considered are presented in
Table 4,
Table 5,
Table 6 and
Table 7. Material strength parameters
,
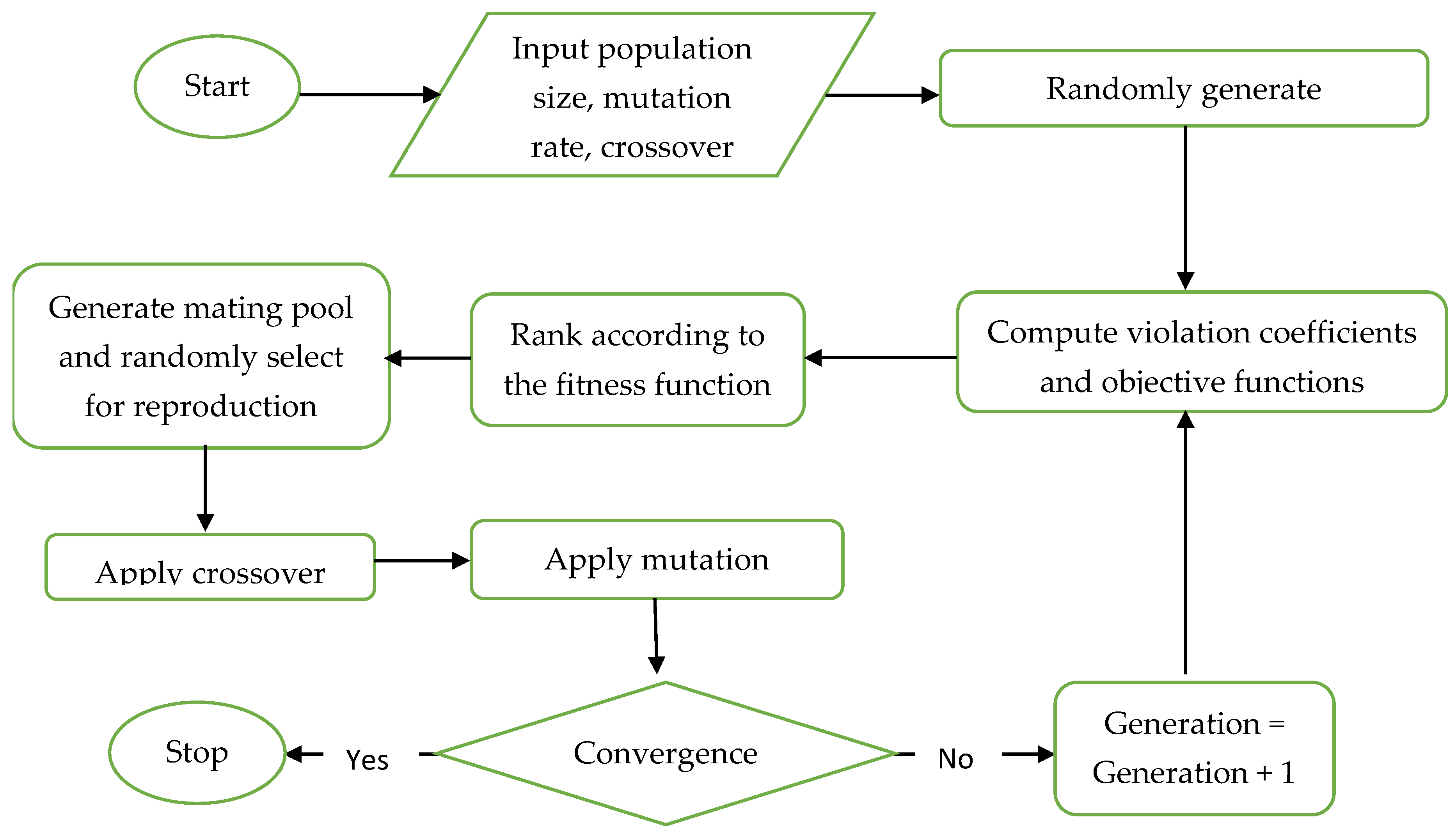
) were kept the same as used in the conventional design. The setting used in the solver includes a mutation rate of 0.075 and a population size of 50. Variables were bounded and the stopping criterion was “30 s without improvement”. Because of the random seed, different results can be attained for each run, so numerous runs were made to get the utmost optimized results. Here, the random seed value was set to zero, which means that the obtained solution can either be worse or better than the earlier solution. Other settings include convergence rate, which can further improve the degree of optimization, but it will increase the computational time. The EA is highly dependent on starting input values, so at first conventionally designed values were taken as input values. The stopping criterion used for this study was 30 s without improvement at a convergence rate of 0.000001.
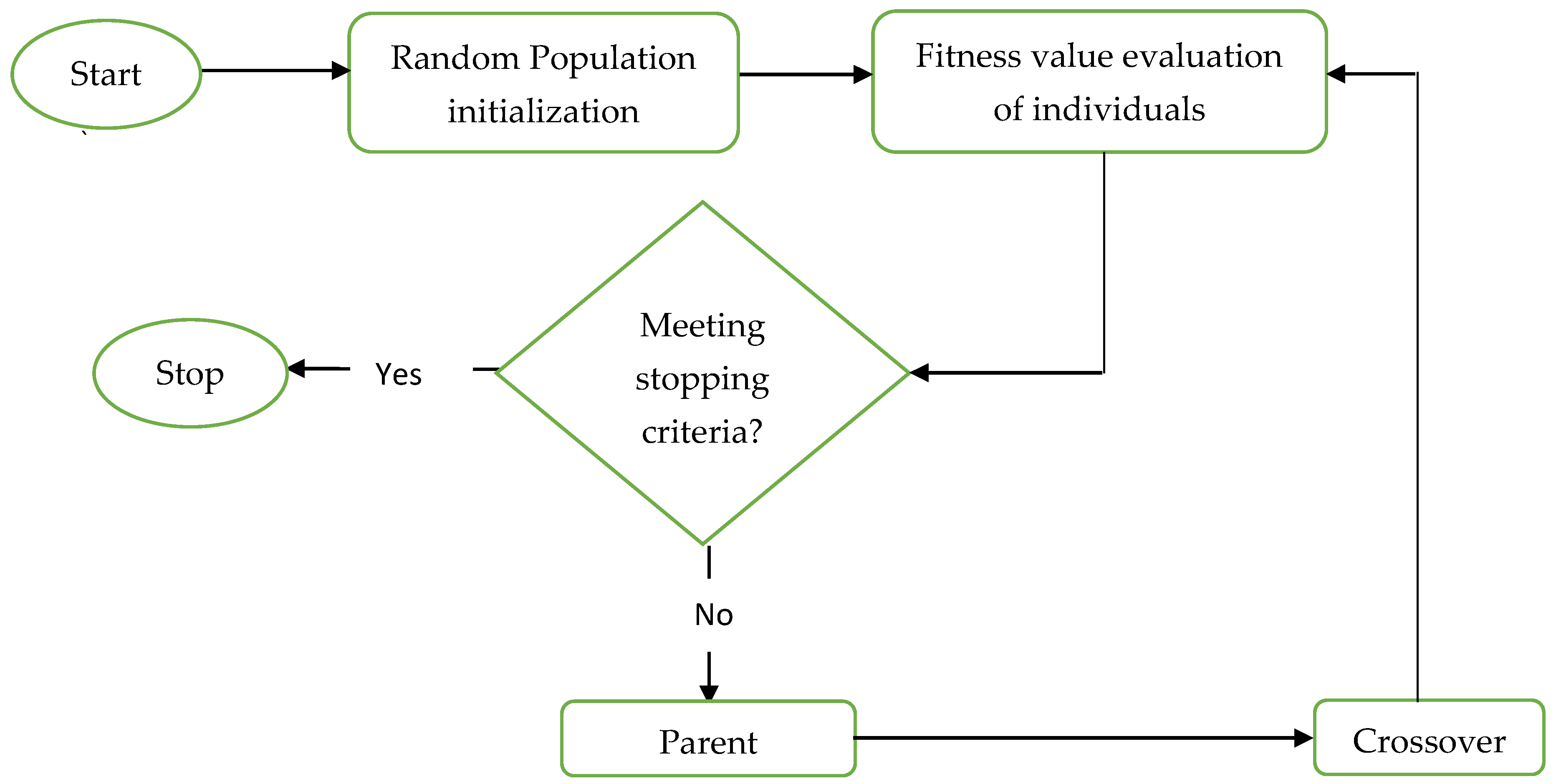
The GA is implemented by using the spreadsheet tool by simply inputting the variables and parameters of an isolated footings and using the Evolver add-in tool. The GA must be run separately from the Evolver Table. The setting used for the GA in the spreadsheet includes a population size of 50, mutation rate of 0.075, and a cross over rate of 0.5. The maximum rate of change of 0.01% in 20,000 trails was set as the stopping criteria for optimization in the settings. The “Recipe method” was used in the adjustable group setting. In this method, all adjustable variables are varied independently of each other keeping them in their specified bounds to obtain the best mixed solution space.
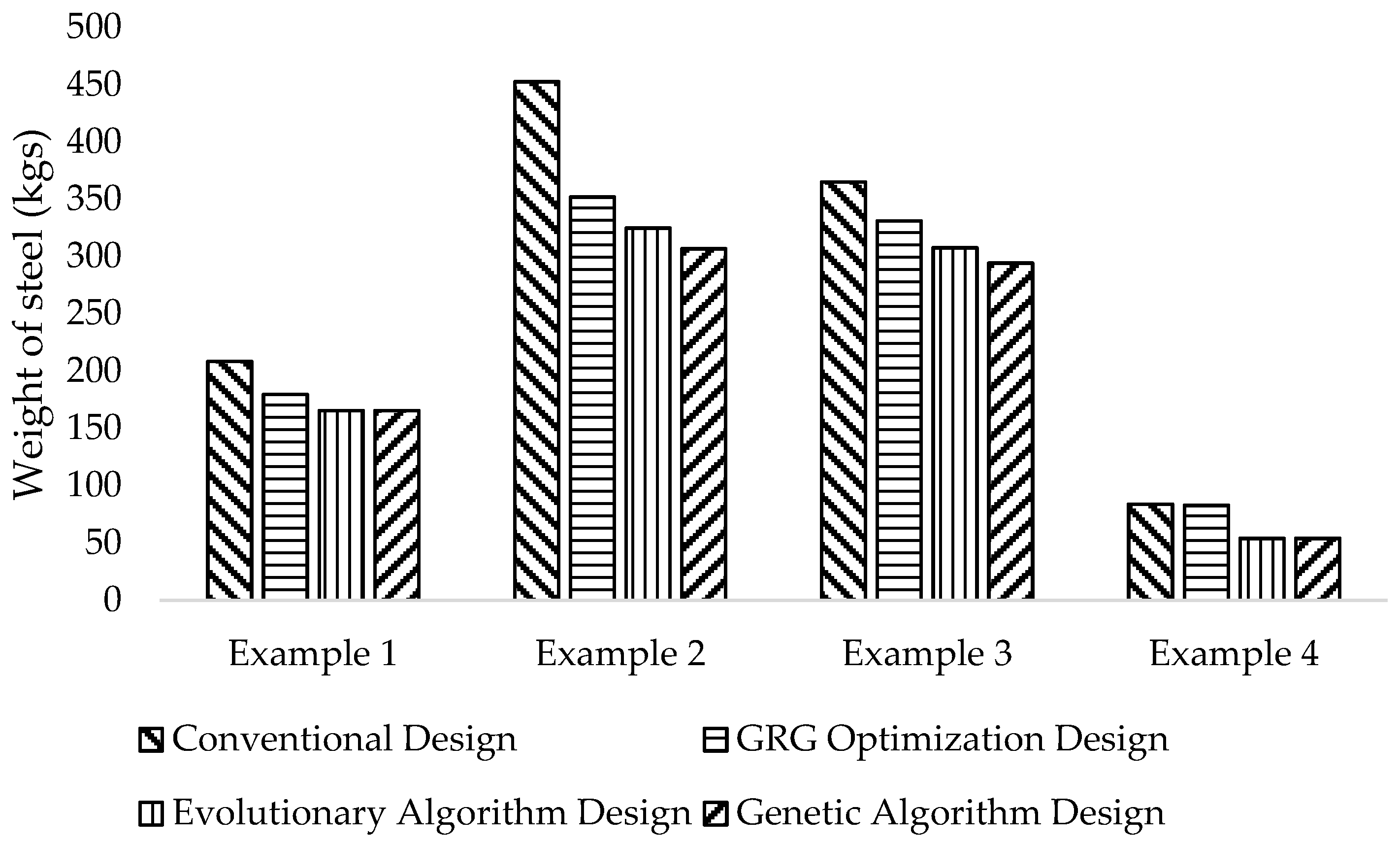
Figure 7 graphically compares the cost obtained using the EA and the GA algorithms in the developed spreadsheet tool with the cost obtained from the conventional design and the optimized design using GRG as obtained by Rawat and Mittal [
29].
Table 4,
Table 5,
Table 6 and
Table 7 represent the values of the variables obtained for examples 1–4 along with the percentage optimization achieved from the conventional design cost.
In example 1, by using the EA, two successive runs were made. Run one of 31.953 s with 1188 sub-problems and run two of 32.046 s with 1119 sub-problems. The original volume of concrete was 7.45 m3, while the optimized quantity was 4.83 m3. The original quantity of steel was 208.48 kg while the optimized quantity was 165.47 kg. This resulted in the optimization of overall cost by 31.63%. By using the GA, one run of 54 s with total of 20,095 trials was made. This further reduced steel weight to 165.45 kg but without a change in concrete volume. This resulted in an optimization of overall cost by 31.65%.
In example 2, by using the EA, the original volume of concrete of 15.7 m3 was optimized to 8.22 m3 and the total quantity of steel of 452.59 kg was optimized to 316.87 kg. This resulted in an optimization of overall cost by 43.01% by the two succeeding runs; run one of 31.797 s with 1160 sub-problems and run two of 32.434 s with 1292 sub-problems. By using the GA, one run of 56 s with total of 20,387 trials was made. This further reduced the concrete volume to 8.2 m3 and steel weight to 306.8 kg. This resulted in an optimization of overall cost by 44.04%
In example 3, by using the EA, two consecutive runs were made. Run one of 32.047 s with 1212 sub-problems and run two of 88.25 s with 3125 sub-problems. The original volume of concrete of 10.18 m3 was optimized to 8.19 m3 and the original quantity of steel of 364.95 kg was optimized to 307.65 kg. This resulted in an optimization of overall cost by 18.4%. By using the GA, one run of 53 s with total of 20,001 trials was made which further reduced steel weight to 294.19 kg without a change in concrete volume resulting in an optimization of overall cost by 19.41%.
In example 4, the EA reduced the original volume of concrete of 2.54 m3 to 1.8 m3 and the quantity of steel from 83.92 kg to 66.42 kg, which resulted in an optimization of overall cost by 26.45% by the two consecutive runs; run one of 57.157 s with 2874 sub-problems and run two of 31.625 s with 994 sub-problems. By using the GA, one run of 99 s with total of 32,222 trials was made. This further reduced steel weight to 53.91 kg but without a change in concrete volume. This resulted in an optimization of overall cost by 28.14%.
The results showed that the optimization algorithms have tried to reduce both steel and concrete quantity. The reduction of steel has played a vital role in cost reduction. as it is more expensive material.
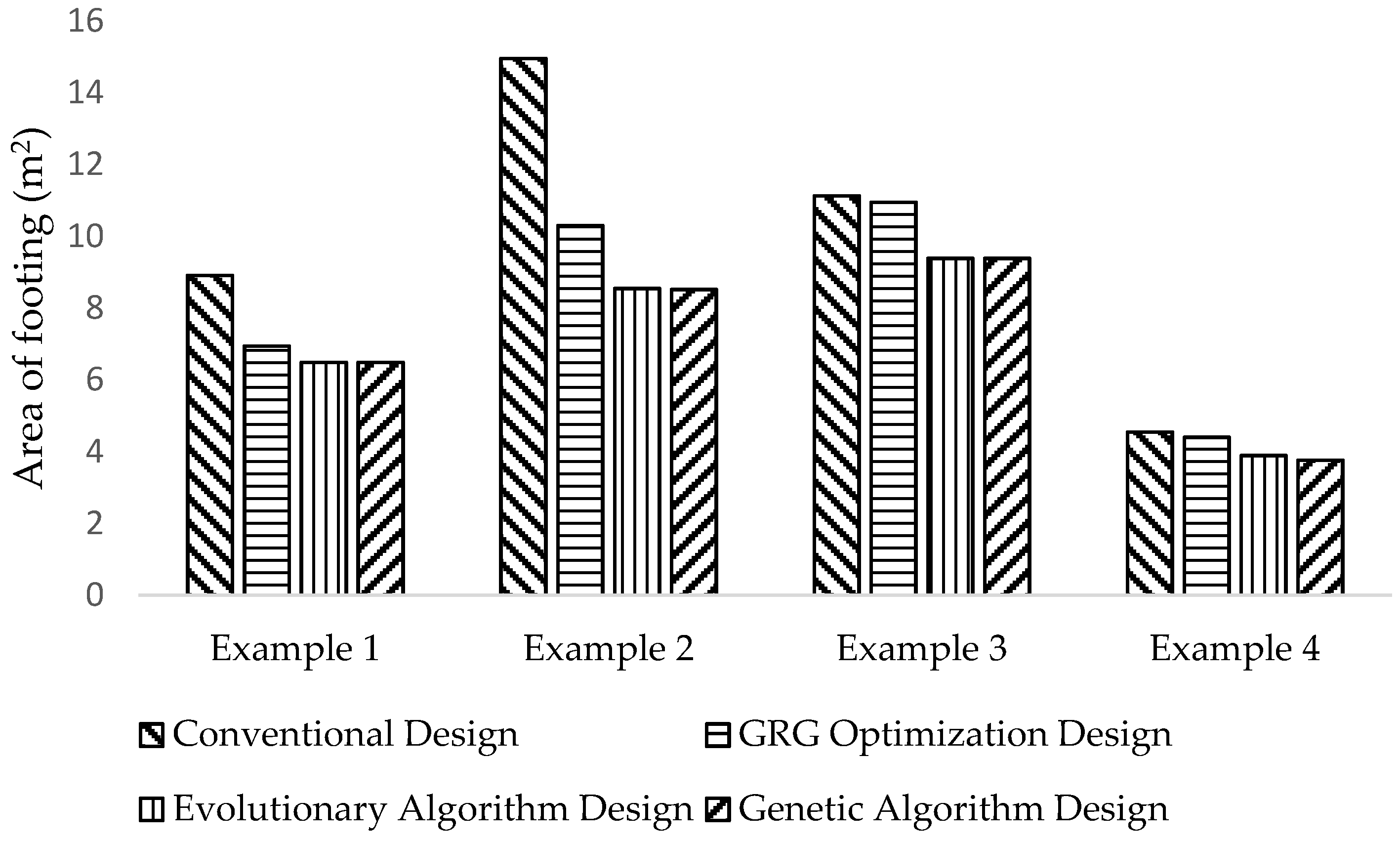
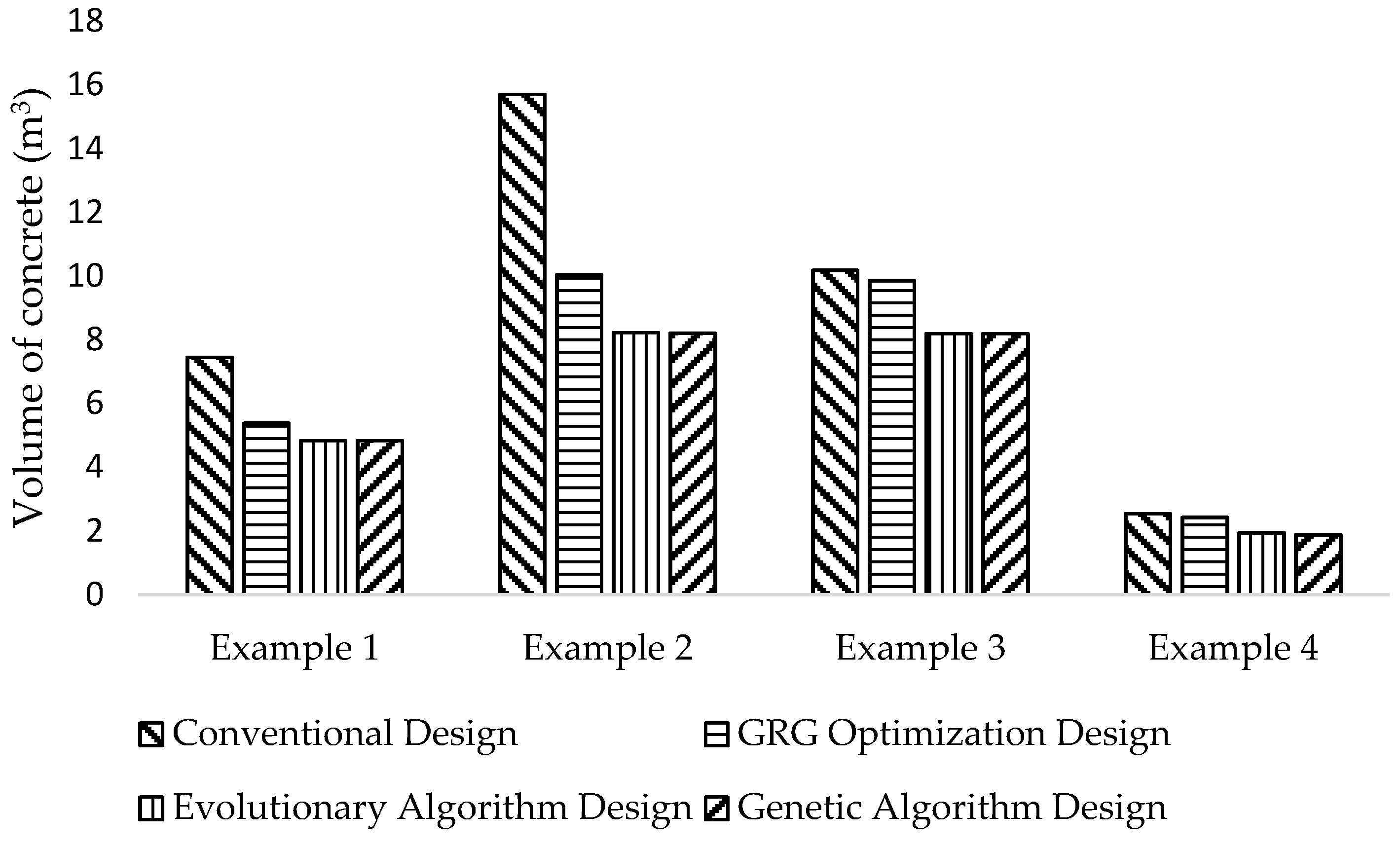
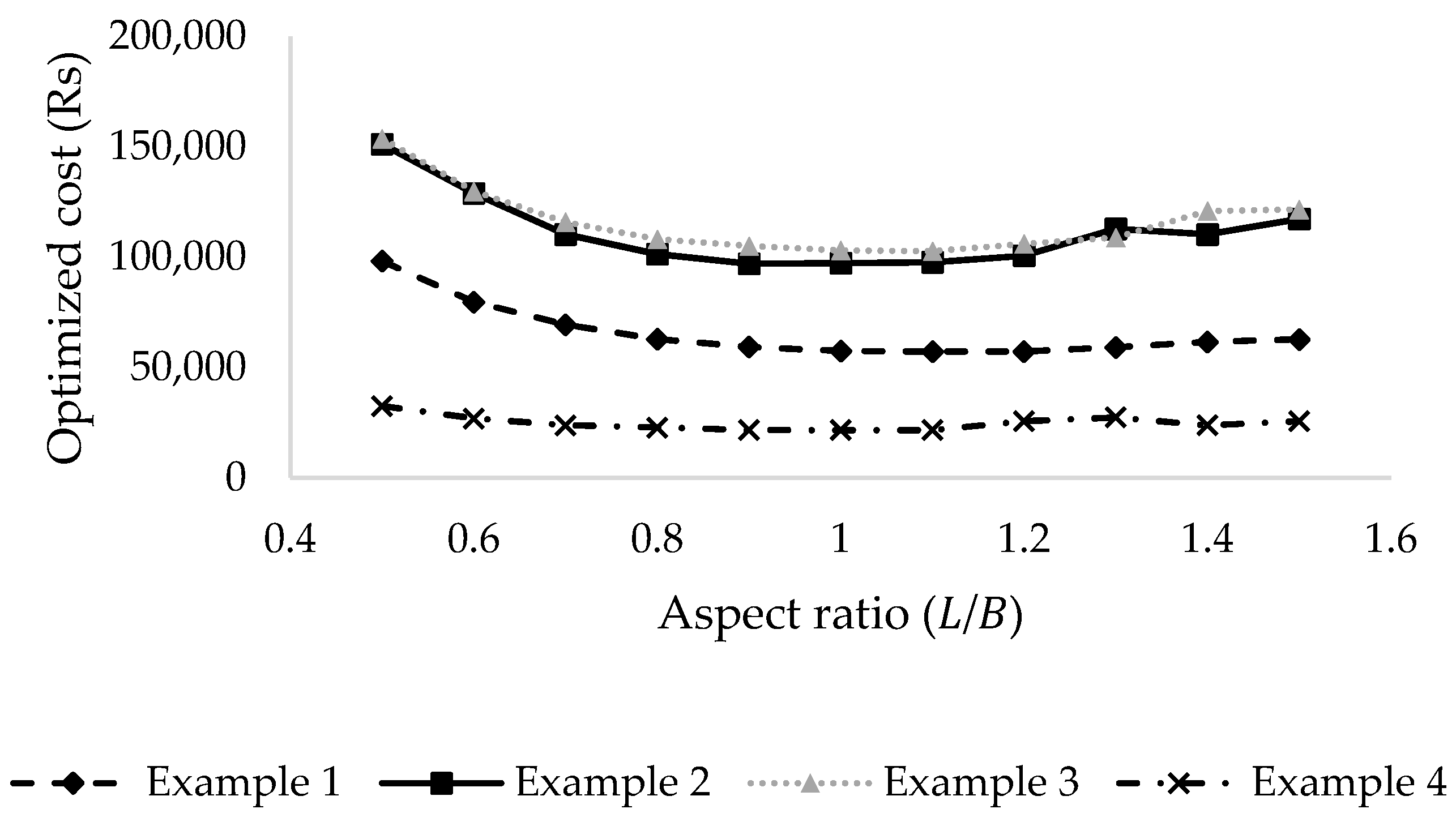
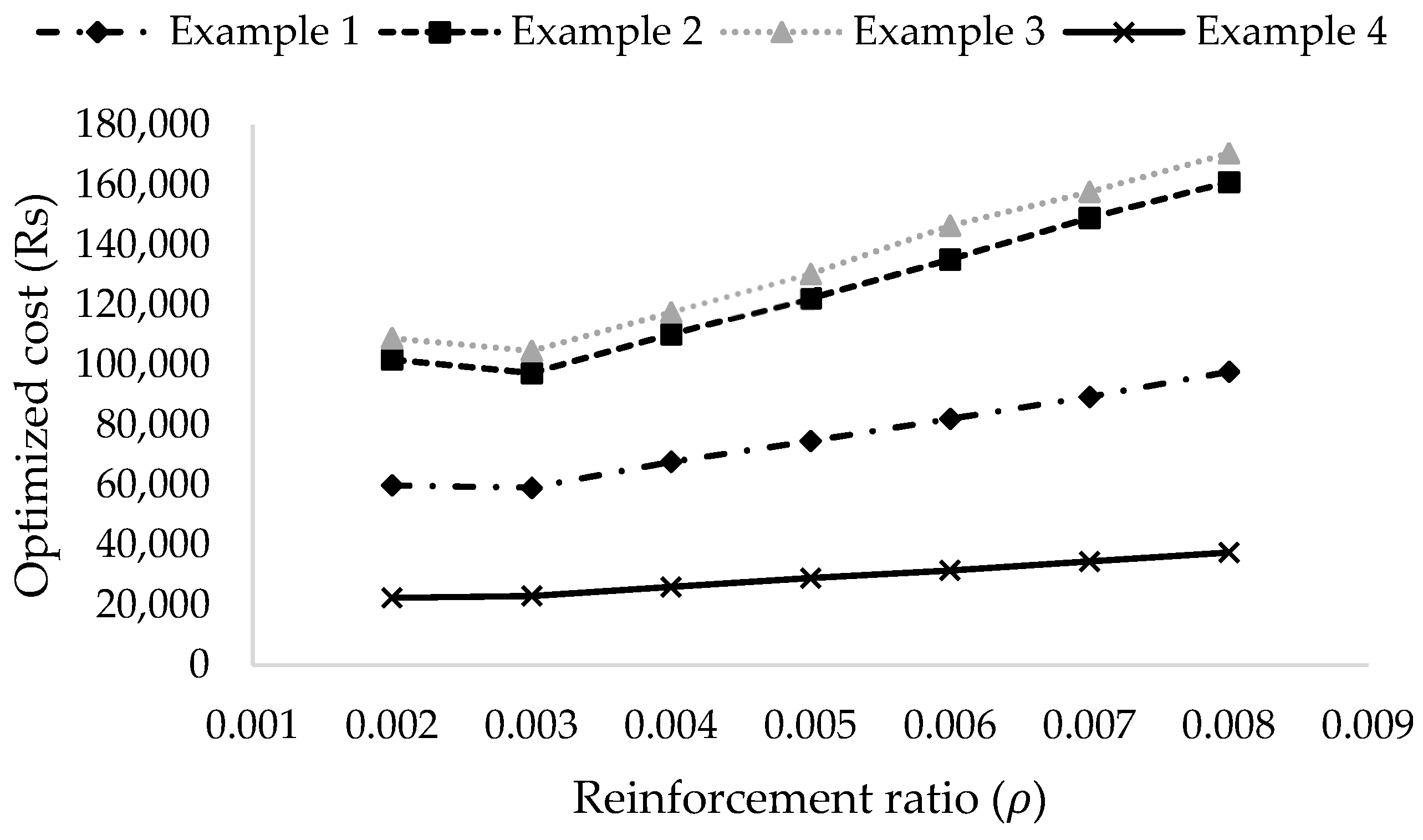
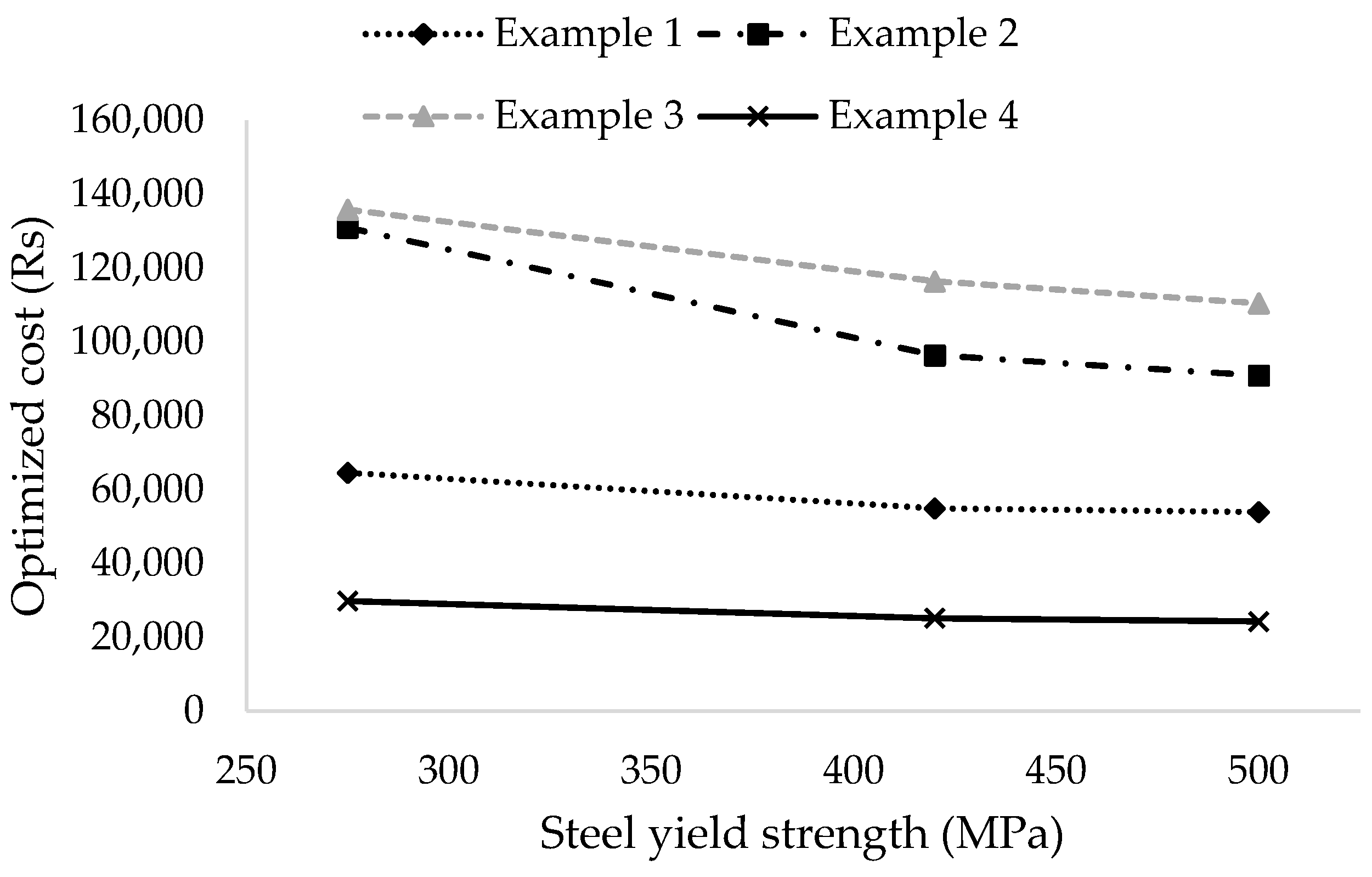
Figure 8,
Figure 9 and
Figure 10 further illustrate the effects of optimization and the distribution of costs of each cost component. By using the EA optimization for examples 1–4, the volume of concrete decreased by 35.12%, 47.62%, 19.54% and 23.32%, the area of footing decreased by 27.17%, 42.86%, 15.68% and 14.38% and the steel weight decreased by 20.63%, 28.24% 15.7% and 35.77 %, respectively. By using the GA optimization for examples 1–4, the volume of concrete decreased by 35.14%, 47.76%, 19.54% and 26.01%, the area of footing decreased by 27.17%, 43.05%, 15.69% and 17.32%, and the steel weight decreased by 20.64%, 32.21% 19.39% and 35.76 %, respectively. This trend provides an indication of the complex non-linear characteristic of the RC isolated footing design and hence, the reason to prefer the superior metaheuristic techniques for the optimization.
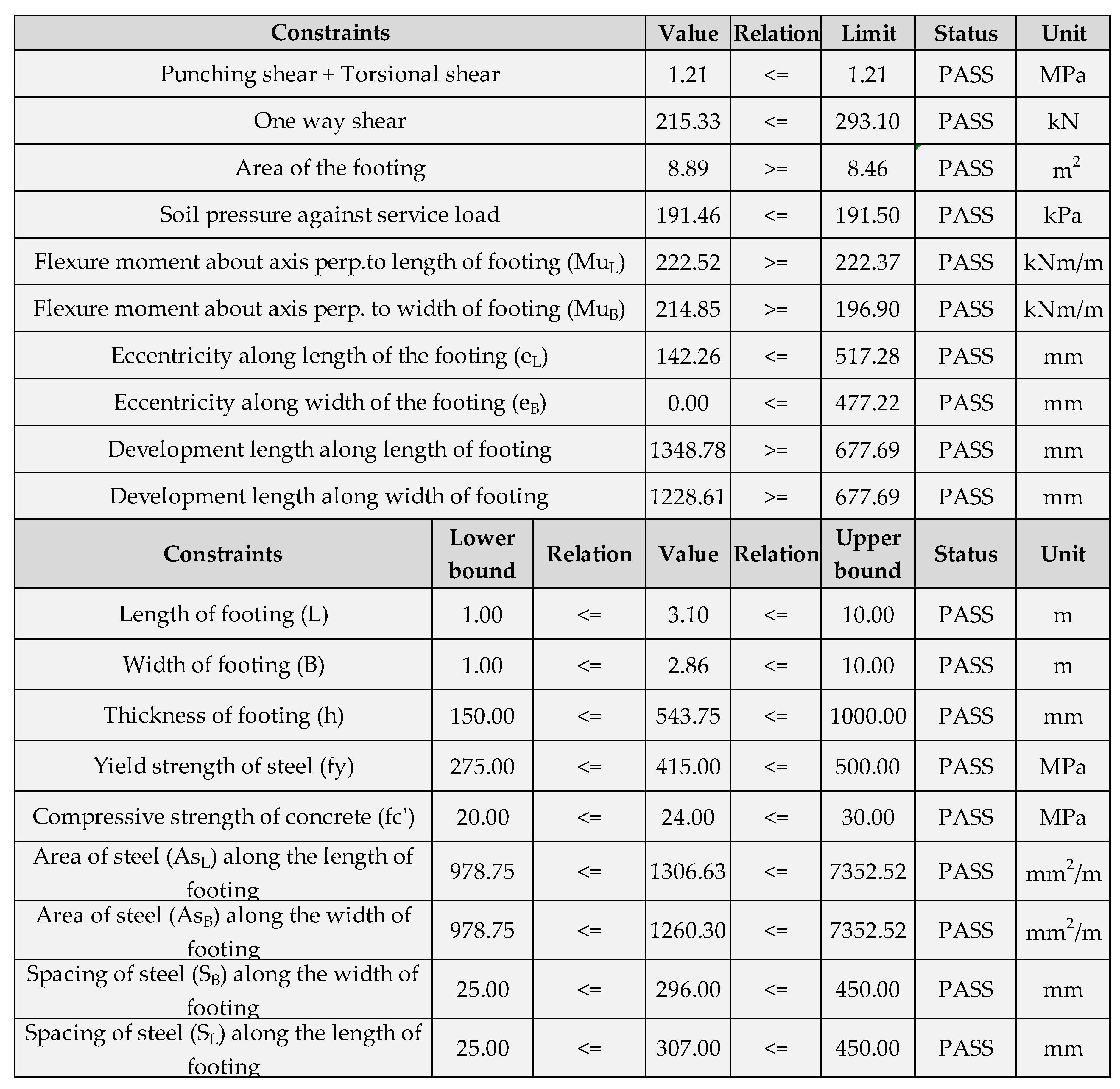
Two reports can be generated at the end of the algorithm. The answer report presents the non-binding and binding nature of each constraint and variable. The constraints with no slack are considered of a binding nature, as they limit the optimization of the variables. The population report describes the standard deviations of the mean value in each run. In example 4, soil pressure against the service load is of a binding nature for calculating the area of the footing. Relaxation of this constraint could result in more optimization. The tool has been modeled as a continuous problem and not as a discrete problem, because it was developed for achieving the highest percentage of optimization possible. This requires that the attained values of design variables undergo an engineer’s examination before practical implementation.