Structural Design Optimization of Flat Slab Hospital Buildings Using Genetic Algorithms
Abstract
:1. Introduction
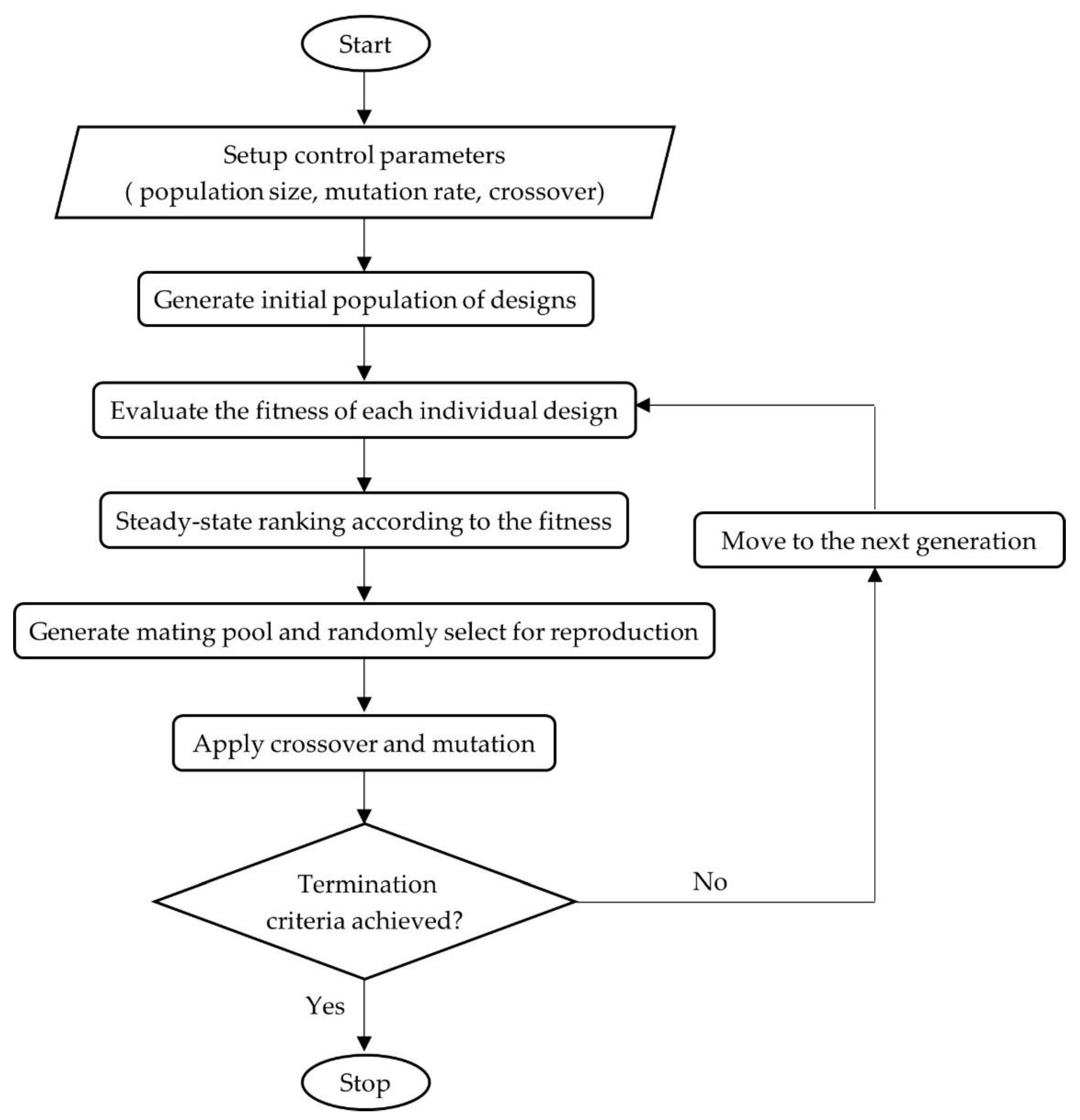
2. Optimization Algorithm
- Initial seed
- 2.
- Population size
- 3.
- Crossover rate
- 4.
- Mutation rate
- 5.
- Operators
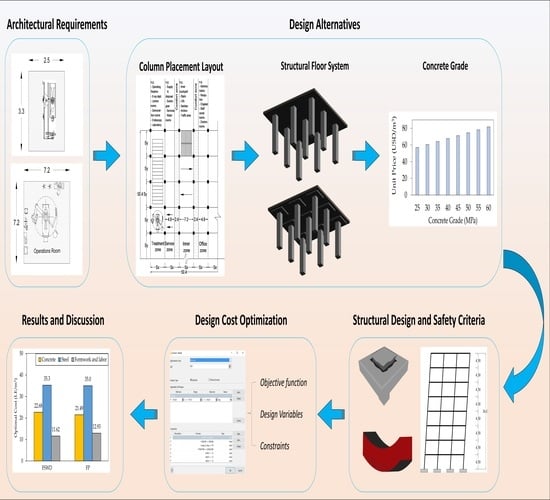
3. Optimized Building
3.1. Geometrical Considerations
3.2. Design Procedures
- -
- The building must have a regular plan layout;
- -
- The minimum number of bays in each direction is three;
- -
- The ratio of the longer span to the shorter span shall not exceed 1.3;
- -
- The maximum difference between the spans in a particular direction shall not exceed 10%.
3.3. Safety and Serviceability Criteria
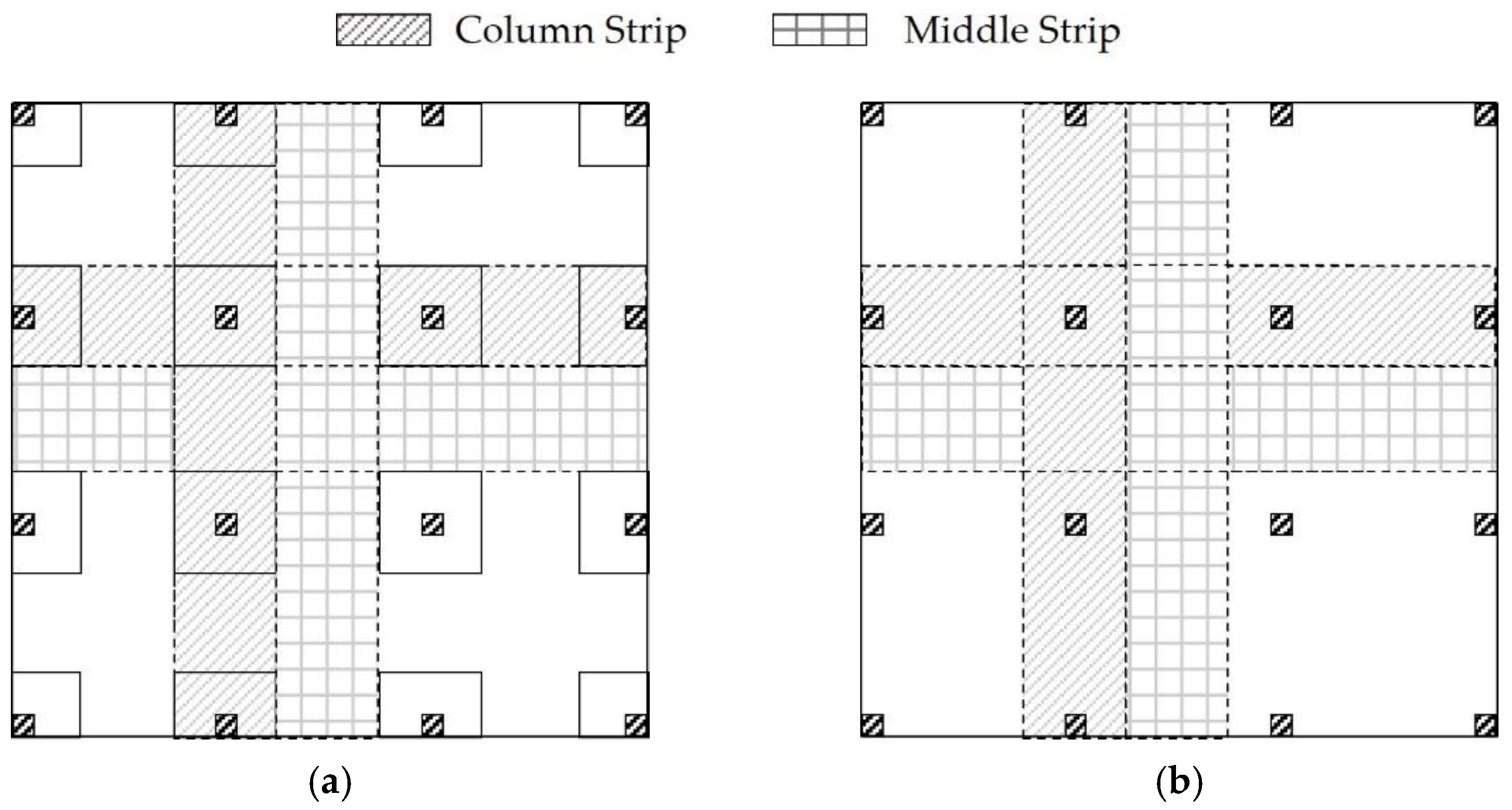
3.3.1. Punching Stresses
3.3.2. Deflection
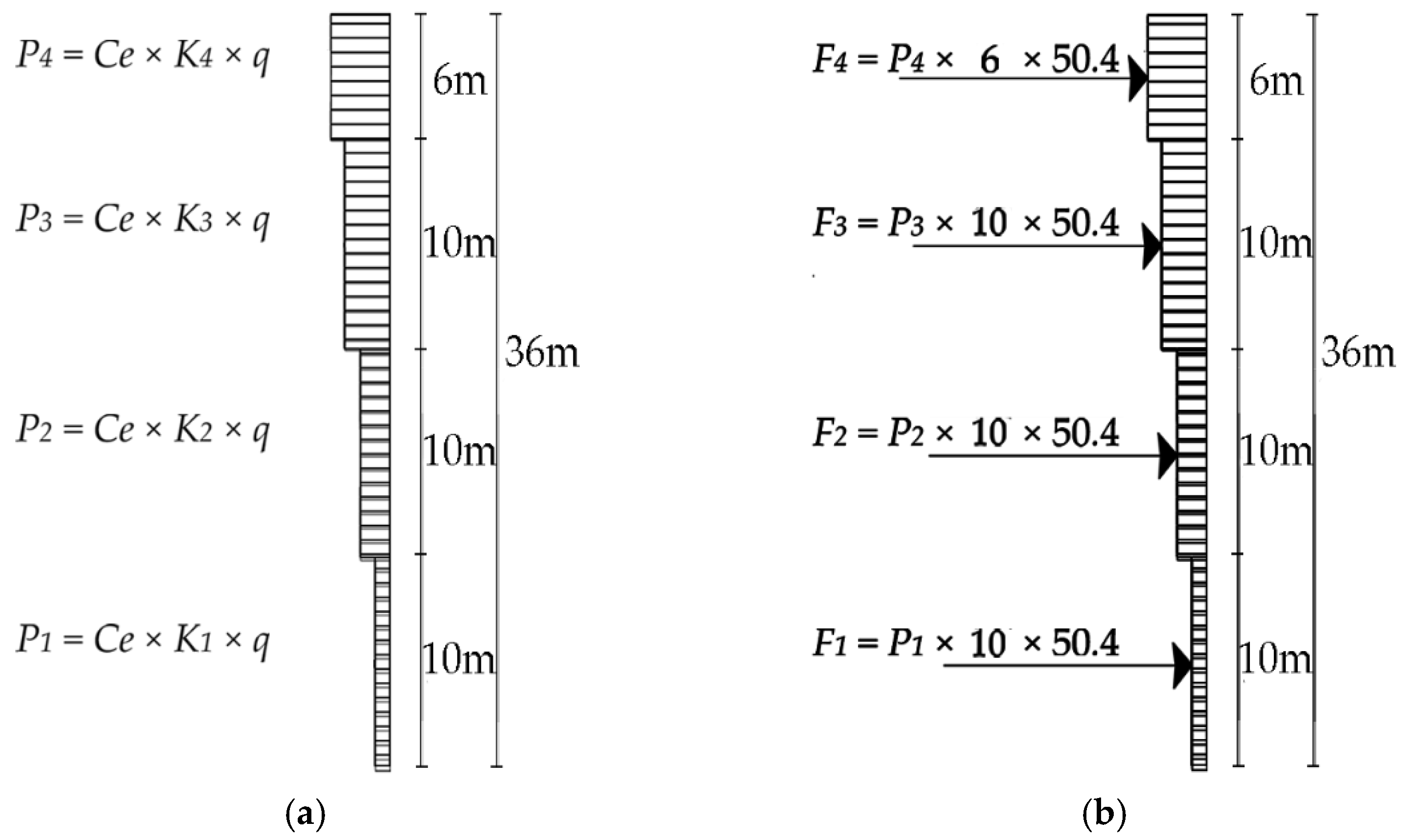
3.3.3. Stability Precautions
3.3.4. Maximum Drift
4. Problem Formulation
5. Results and Discussion
5.1. Effects of GA Control Parameters
5.2. Comparison between Design Alternatives
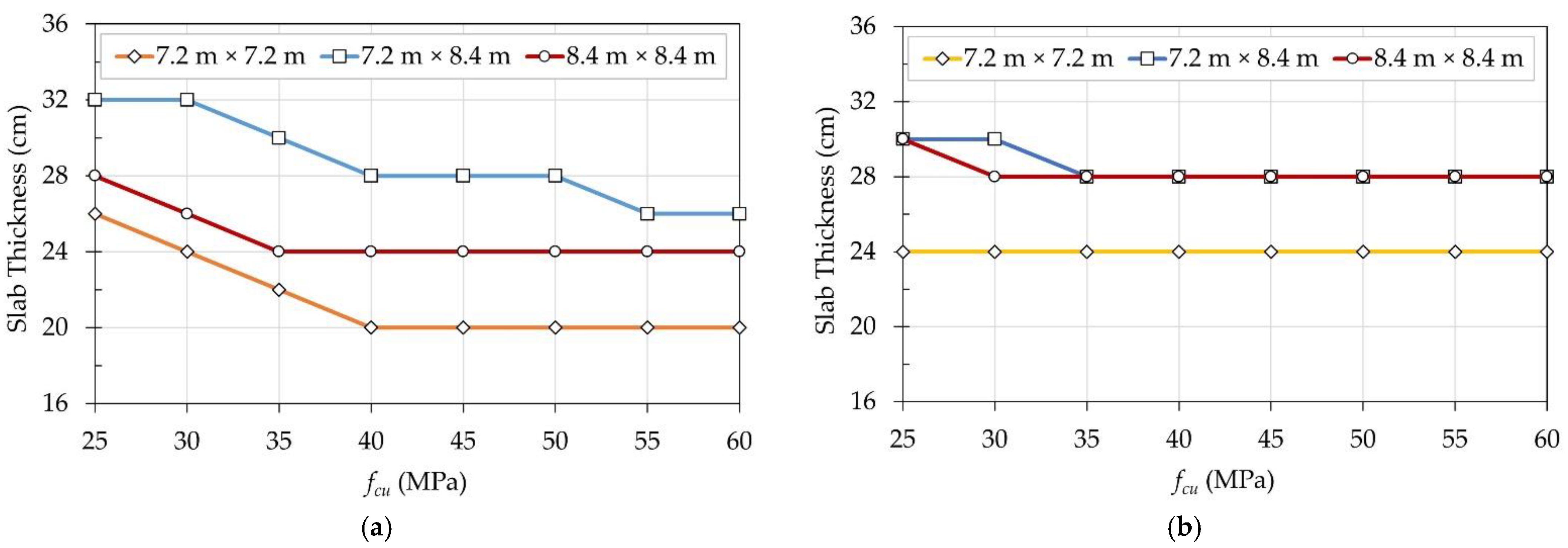
5.2.1. Effect of Compressive Strength
5.2.2. Effect of Slab Thickness
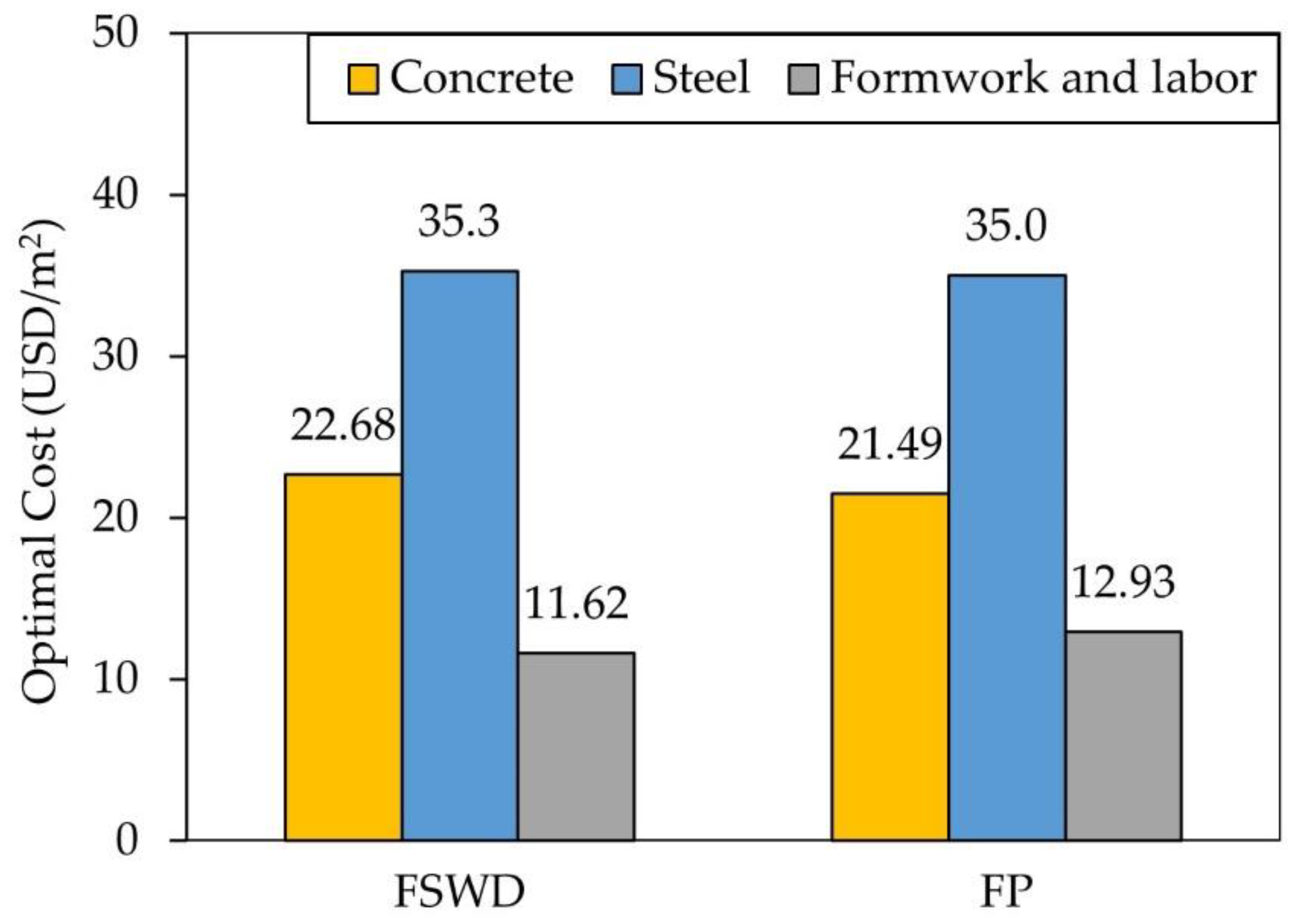
5.2.3. Optimal Parameters of the Best Design Alternatives
6. Conclusions
- -
- Slab thickness is the most significant variable in the optimal design of hospital buildings, regardless of the floor system;
- -
- Increasing fcu up to 45 MPa effectively reduces the building’s optimal cost only in the presence of drop panels. Otherwise, low concrete grades are preferred if no drop panels exist;
- -
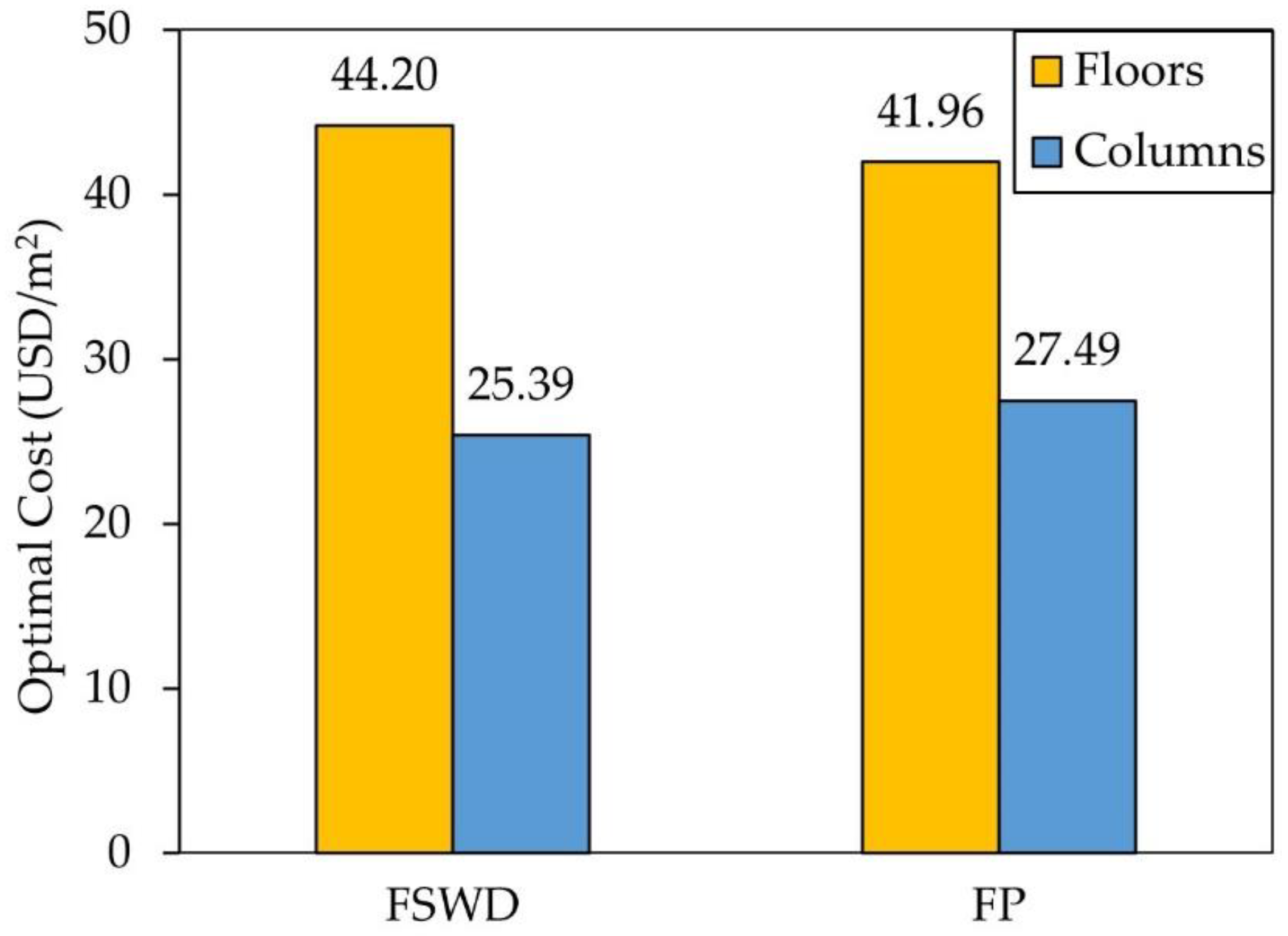
- For both systems, the construction cost of columns constitutes about 40% of the total optimal cost due to the special criteria for hospital buildings compared to residential and office buildings;
- -
- For both systems, the steel reinforcement quantities dominantly affect the total optimal cost.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| Design Alternative | Floor | Intermediate Columns | Edge Columns (x-Direction) | Edge Columns (y-Direction) | Corner Columns | Total Cost (USD/m2) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Floor System | Column Spacings (m) | Steel Bars | Steel Bars | Steel Bars | Steel Bars | |||||||||
| FSWD | 7.2 × 7.2 | 25 | 0.26 | 0.10 | 2.80 | 1.30 | 28T25 | 1.35 | 32T25 | 1.35 | 32T25 | 0.60 | 20T25 | 79.22 |
| FSWD | 7.2 × 8.4 | 25 | 0.32 | 0.08 | 3.40 | 1.35 | 32T25 | 1.50 | 32T28 | 1.50 | 32T28 | 0.70 | 20T28 | 87.57 |
| FSWD | 8.4 × 8.4 | 25 | 0.30 | 0.14 | 2.95 | 1.50 | 32T28 | 1.50 | 32T32 | 1.35 | 32T28 | 0.65 | 20T32 | 88.31 |
| FSWD | 7.2 × 7.2 | 30 | 0.24 | 0.12 | 2.60 | 1.15 | 28T22 | 1.35 | 32T25 | 1.35 | 32T25 | 0.60 | 20T25 | 75.32 |
| FSWD | 7.2 × 8.4 | 30 | 0.32 | 0.08 | 3.00 | 1.00 | 24T22 | 1.50 | 32T28 | 1.35 | 32T32 | 0.70 | 20T32 | 82.80 |
| FSWD | 8.4 × 8.4 | 30 | 0.26 | 0.10 | 2.90 | 1.00 | 24T25 | 1.40 | 32T32 | 1.35 | 32T32 | 0.60 | 20T32 | 79.21 |
| FSWD | 7.2 × 7.2 | 35 | 0.22 | 0.10 | 2.45 | 0.95 | 24T22 | 1.40 | 32T25 | 1.35 | 32T25 | 0.60 | 20T28 | 72.94 |
| FSWD | 7.2 × 8.4 | 35 | 0.30 | 0.08 | 3.10 | 1.00 | 24T22 | 1.35 | 32T28 | 1.40 | 32T32 | 0.65 | 20T32 | 82.44 |
| FSWD | 8.4 × 8.4 | 35 | 0.26 | 0.12 | 2.95 | 1.00 | 24T22 | 1.35 | 32T32 | 1.35 | 32T32 | 0.60 | 20T32 | 78.10 |
| FSWD | 7.2 × 7.2 | 40 | 0.20 | 0.14 | 2.40 | 0.75 | 20T18 | 1.35 | 32T28 | 1.35 | 32T28 | 0.60 | 20T28 | 69.82 |
| FSWD | 7.2 × 8.4 | 40 | 0.28 | 0.08 | 3.00 | 0.90 | 24T22 | 1.50 | 32T28 | 1.35 | 32T32 | 0.65 | 20T32 | 80.69 |
| FSWD | 8.4 × 8.4 | 40 | 0.24 | 0.10 | 3.00 | 0.90 | 24T22 | 1.35 | 32T32 | 1.35 | 32T32 | 0.60 | 20T32 | 78.25 |
| FSWD | 7.2 × 7.2 | 45 | 0.20 | 0.12 | 2.40 | 0.75 | 20T18 | 1.25 | 28T28 | 1.35 | 32T28 | 0.60 | 20T28 | 69.60 |
| FSWD | 7.2 × 8.4 | 45 | 0.28 | 0.08 | 3.00 | 0.90 | 24T22 | 1.50 | 32T28 | 1.35 | 32T32 | 0.65 | 20T32 | 82.13 |
| FSWD | 8.4 × 8.4 | 45 | 0.24 | 0.10 | 3.00 | 0.85 | 24T18 | 1.40 | 32T32 | 1.35 | 32T32 | 0.60 | 20T32 | 77.99 |
| FSWD | 7.2 × 7.2 | 50 | 0.20 | 0.12 | 2.50 | 0.70 | 20T16 | 1.35 | 32T28 | 1.35 | 32T28 | 0.60 | 20T28 | 71.21 |
| FSWD | 7.2 × 8.4 | 50 | 0.28 | 0.08 | 3.00 | 0.90 | 24T22 | 1.50 | 32T28 | 1.35 | 32T32 | 0.65 | 20T32 | 83.58 |
| FSWD | 8.4 × 8.4 | 50 | 0.24 | 0.10 | 3.00 | 0.85 | 24T18 | 1.40 | 32T32 | 1.35 | 32T32 | 0.60 | 20T32 | 79.22 |
| FSWD | 7.2 × 7.2 | 55 | 0.20 | 0.12 | 2.45 | 0.65 | 20T16 | 1.35 | 32T28 | 1.35 | 32T28 | 0.60 | 20T28 | 71.87 |
| FSWD | 7.2 × 8.4 | 55 | 0.26 | 0.10 | 2.80 | 1.35 | 32T25 | 1.40 | 32T25 | 1.45 | 32T28 | 0.60 | 20T28 | 89.85 |
| FSWD | 8.4 × 8.4 | 55 | 0.24 | 0.16 | 2.80 | 1.35 | 32T25 | 1.45 | 32T28 | 1.45 | 32T28 | 0.70 | 20T32 | 86.71 |
| FSWD | 7.2 × 7.2 | 60 | 0.20 | 0.14 | 2.50 | 0.90 | 24T22 | 1.35 | 32T25 | 1.35 | 32T25 | 0.65 | 20T28 | 76.94 |
| FSWD | 7.2 × 8.4 | 60 | 0.26 | 0.10 | 2.80 | 1.35 | 32T25 | 1.35 | 32T25 | 1.35 | 32T28 | 0.85 | 24T32 | 91.09 |
| FSWD | 8.4 × 8.4 | 60 | 0.24 | 0.10 | 2.85 | 1.50 | 32T28 | 1.40 | 32T28 | 1.35 | 32T28 | 0.70 | 20T32 | 91.41 |
| FP | 7.2 × 7.2 | 25 | 0.24 | - | - | 1.10 | 28T22 | 1.35 | 32T28 | 0.85 | 24T25 | 0.70 | 20T32 | 70.04 |
| FP | 7.2 × 8.4 | 25 | 0.30 | - | - | 1.10 | 28T28 | 1.15 | 28T32 | 1.35 | 32T32 | 0.60 | 20T32 | 82.18 |
| FP | 8.4 × 8.4 | 25 | 0.30 | - | - | 1.35 | 32T25 | 1.55 | 32T28 | 1.45 | 32T28 | 0.85 | 24T32 | 82.72 |
| FP | 7.2 × 7.2 | 30 | 0.24 | - | - | 1.00 | 24T22 | 1.35 | 32T28 | 0.80 | 20T28 | 0.85 | 24T32 | 69.45 |
| FP | 7.2 × 8.4 | 30 | 0.30 | - | - | 1.35 | 32T25 | 1.35 | 32T25 | 0.85 | 24T25 | 1.35 | 32T32 | 80.93 |
| FP | 8.4 × 8.4 | 30 | 0.28 | - | - | 1.35 | 32T25 | 1.50 | 32T28 | 1.40 | 32T28 | 0.85 | 24T32 | 81.24 |
| FP | 7.2 × 7.2 | 35 | 0.24 | - | - | 1.05 | 24T22 | 1.35 | 32T28 | 0.80 | 20T28 | 0.75 | 20T32 | 70.85 |
| FP | 7.2 × 8.4 | 35 | 0.28 | - | - | 1.35 | 32T25 | 1.35 | 32T28 | 0.80 | 20T28 | 0.80 | 20T32 | 79.13 |
| FP | 8.4 × 8.4 | 35 | 0.28 | - | - | 1.35 | 32T25 | 1.50 | 32T28 | 1.45 | 32T28 | 0.85 | 24T32 | 83.03 |
| FP | 7.2 × 7.2 | 40 | 0.24 | - | - | 0.85 | 24T25 | 1.35 | 32T28 | 1.35 | 32T28 | 0.60 | 20T28 | 75.56 |
| FP | 7.2 × 8.4 | 40 | 0.28 | - | - | 1.35 | 32T25 | 1.35 | 32T28 | 0.70 | 20T25 | 0.95 | 24T32 | 80.11 |
| FP | 8.4 × 8.4 | 40 | 0.28 | - | - | 1.35 | 32T25 | 1.55 | 32T28 | 1.45 | 32T28 | 0.85 | 24T32 | 84.84 |
| FP | 7.2 × 7.2 | 45 | 0.24 | - | - | 0.85 | 24T22 | 1.35 | 32T28 | 1.35 | 32T28 | 0.60 | 20T28 | 74.93 |
| FP | 7.2 × 8.4 | 45 | 0.28 | - | - | 1.35 | 32T25 | 1.35 | 32T28 | 0.65 | 20T25 | 1.00 | 24T32 | 81.46 |
| FP | 8.4 × 8.4 | 45 | 0.28 | - | - | 1.35 | 32T25 | 1.50 | 32T28 | 1.50 | 32T28 | 0.85 | 24T32 | 86.39 |
| FP | 7.2 × 7.2 | 50 | 0.24 | - | - | 0.85 | 24T22 | 1.35 | 32T28 | 1.35 | 32T28 | 0.60 | 20T28 | 76.19 |
| FP | 7.2 × 8.4 | 50 | 0.28 | - | - | 1.35 | 32T25 | 1.35 | 32T28 | 0.60 | 20T25 | 1.10 | 28T32 | 83.18 |
| FP | 8.4 × 8.4 | 50 | 0.28 | - | - | 1.35 | 32T25 | 1.55 | 32T28 | 1.50 | 32T28 | 0.85 | 24T32 | 88.22 |
| FP | 7.2 × 7.2 | 55 | 0.24 | - | - | 0.80 | 20T25 | 1.35 | 32T25 | 1.35 | 32T25 | 1.10 | 28T32 | 76.94 |
| FP | 7.2 × 8.4 | 55 | 0.28 | - | - | 1.35 | 32T25 | 1.35 | 32T28 | 0.60 | 20T22 | 1.10 | 28T32 | 84.13 |
| FP | 8.4 × 8.4 | 55 | 0.28 | - | - | 1.35 | 32T25 | 1.55 | 32T28 | 1.50 | 32T28 | 0.85 | 24T32 | 89.76 |
| FP | 7.2 × 7.2 | 60 | 0.24 | - | - | 0.80 | 20T25 | 1.35 | 32T28 | 1.35 | 32T28 | 0.60 | 20T32 | 78.91 |
| FP | 7.2 × 8.4 | 60 | 0.28 | - | - | 1.35 | 32T25 | 1.35 | 32T28 | 0.60 | 20T22 | 1.10 | 28T32 | 85.60 |
| FP | 8.4 × 8.4 | 60 | 0.28 | - | - | 1.35 | 32T25 | 1.55 | 32T28 | 1.55 | 32T28 | 0.85 | 24T32 | 91.64 |
References
- Gaspari, J.; Fabbri, K.; Gabrielli, L. A Study on Parametric Design Application to Hospital Retrofitting for Improving Energy Savings and Comfort Conditions. Buildings 2019, 9, 220. [Google Scholar] [CrossRef] [Green Version]
- Ismaeil, E.M.H.; Sobaih, A.E.E. Enhancing Healing Environment and Sustainable Finishing Materials in Healthcare Buildings. Buildings 2022, 12, 1676. [Google Scholar] [CrossRef]
- Gremigni, P.; Sommaruga, M.; Peltenburg, M. Validation of the Health Care Communication Questionnaire (HCCQ) to Measure Outpatients’ Experience of Communication with Hospital Staff. Patient Educ. Couns. 2008, 71, 57–64. [Google Scholar] [CrossRef] [PubMed]
- Laine, C.; Davidoff, F.; Lewis, C.E.; Nelson, E.C.; Nelson, E.; Kessler, R.C.; Delbanco, T.L. Important Elements of Outpatient Care: A Comparison of Patients’ and Physicians’ Opinions. Ann. Intern. Med. 1996, 125, 640–645. [Google Scholar] [CrossRef] [PubMed]
- Singh, H.; Haqq, E.D.; Mustapha, N. Patients’ Perception and Satisfaction with Health Care Professionals at Primary Care Facilities in Trinidad and Tobago. Bull. World Health Organ. 1999, 77, 356–360. [Google Scholar]
- Shyu, Y.-I.L.; Tang, W.-R.; Tsai, W.-C.; Liang, J.; Chen, M.-C. Emotional Support Levels Can Predict Physical Functioning and Health Related Quality of Life among Elderly Taiwanese with Hip Fractures. Osteoporos. Int. 2006, 17, 501–506. [Google Scholar] [CrossRef] [Green Version]
- Donabedian, A. Evaluating the Quality of Medical Care. Milbank Q. 2005, 83, 691–729. [Google Scholar] [CrossRef] [Green Version]
- Chandra, A.; Finlay, J.B.; Paul, D.P., 3rd. Overall Outpatient Satisfaction and Its Components: Perceived Changes at the Huntington VA Medical Center over Five Years. Hosp. Top. 2006, 84, 33–36. [Google Scholar] [CrossRef]
- Singer, S.; Götze, H.; Möbius, C.; Witzigmann, H.; Kortmann, R.-D.; Lehmann, A.; Höckel, M.; Schwarz, R.; Hauss, J. Quality of Care and Emotional Support from the Inpatient Cancer Patient’s Perspective. Langenbeck’s Arch. Surg. 2009, 394, 723–731. [Google Scholar] [CrossRef]
- Zhao, Y.; Mourshed, M. Patients’ Perspectives on the Design of Hospital Outpatient Areas. Buildings 2017, 7, 117. [Google Scholar] [CrossRef] [Green Version]
- Jiménez Mejía, K.; Barbero-Barrera, M.d.M.; Rodríguez Pérez, M. Evaluation of the Impact of the Envelope System on Thermal Energy Demand in Hospital Buildings. Buildings 2020, 10, 250. [Google Scholar] [CrossRef]
- Liu, A.; Ma, Y.; Miller, W.; Xia, B.; Zedan, S.; Bonney, B. Energy Analysis and Forecast of a Major Modern Hospital. Buildings 2022, 12, 1116. [Google Scholar] [CrossRef]
- Ma, Y.; Zedan, S.; Liu, A.; Miller, W. Impact of a Warming Climate on Hospital Energy Use and Decarbonization: An Australian Building Simulation Study. Buildings 2022, 12, 1275. [Google Scholar] [CrossRef]
- Andersen, A.R.; Nielsen, B.F.; Reinhardt, L.B. Optimization of Hospital Ward Resources with Patient Relocation Using Markov Chain Modeling. Eur. J. Oper. Res. 2017, 260, 1152–1163. [Google Scholar] [CrossRef] [Green Version]
- Helm, J.E.; Van Oyen, M.P. Design and Optimization Methods for Elective Hospital Admissions. Oper. Res. 2014, 62, 1265–1282. [Google Scholar] [CrossRef]
- Rady, M.; Mahfouz, S.Y.; Taher, S.E.-D.F. Optimal Design of Reinforced Concrete Materials in Construction. Materials 2022, 15, 2625. [Google Scholar] [CrossRef]
- Lee, D.; Kim, S.; Kim, S. Development of Hybrid Model for Estimating Construction Waste for Multifamily Residential Buildings Using Artificial Neural Networks and Ant Colony Optimization. Sustainability 2016, 8, 870. [Google Scholar] [CrossRef] [Green Version]
- Robati, M.; Mccarthy, T.J.; Kokogiannakis, G. Integrated Life Cycle Cost Method for Sustainable Structural Design by Focusing on a Benchmark Office Building in Australia. Energy Build. 2018, 166, 525–537. [Google Scholar] [CrossRef] [Green Version]
- Ženíšek, M.; Pešta, J.; Tipka, M.; Kočí, V.; Hájek, P. Optimization of RC Structures in Terms of Cost and Environmental Impact—Case Study. Sustainability 2020, 20, 8532. [Google Scholar] [CrossRef]
- Rady, M.; Mahfouz, S.Y. Effects of Concrete Grades and Column Spacings on the Optimal Design of Reinforced Concrete Buildings. Materials 2022, 15, 4290. [Google Scholar] [CrossRef]
- Sahab, M.G.; Ashour, A.F.; Toropov, V.V. Cost Optimisation of Reinforced Concrete Flat Slab Buildings. Eng. Struct. 2005, 27, 313–322. [Google Scholar] [CrossRef]
- The Ministry of Housing Utilities and Urban Communities. Egyptian Code for Design and Construction of Concrete Structures (ECP 203-2020), 4th ed.; Housing and Building National Research Center: Cairo, Egypt, 2020. [Google Scholar]
- The Ministry of Housing Utilities and Urban Communities. Egyptian Code for Calculating Loads and Forces in Structural Work and Masonry; Housing and Building National Research Center (HBRC): Cairo, Egypt, 2019. [Google Scholar]
- The Ministry of Housing Utilities and Urban Communities. Egyptian Guidelines for Hospitals and Healthcare Facilities (EGH 360-2010); Housing and Building National Research Center: Cairo, Egypt, 2010. [Google Scholar]
- Waheed, J.; Azam, R.; Riaz, M.R.; Shakeel, M.; Mohamed, A.; Ali, E. Metaheuristic-Based Practical Tool for Optimal Design of Reinforced Concrete Isolated Footings: Development and Application for Parametric Investigation. Buildings 2022, 12, 471. [Google Scholar] [CrossRef]
- Platt, B.S.; Mtenga, P.V. Parametric Optimization of Steel Floor System Cost Using Evolver. WIT Trans. Built Environ. 2007, 91, 119–128. [Google Scholar] [CrossRef] [Green Version]
- Farmakis, P.M.; Chassiakos, A.P. Genetic Algorithm Optimization for Dynamic Construction Site Layout Planning. Organ. Technol. Manag. Constr. Int. J. 2018, 10, 1655–1664. [Google Scholar] [CrossRef]
- Neufert, E.; Neufert, P. Architects’ Data; John Wiley & Sons: Hoboken, NJ, USA, 2012. [Google Scholar]
- Crosbie, M.; Callender, J. Time-Saver Standards for Architectural Design Data, 7th ed.; Watson, D., Ed.; McGraw Hill: New York, NY, USA, 1997. [Google Scholar]
- The Ministry of Housing Utilities and Urban Communities. The Monthly Bulletins of Average Retail Prices of Major Important Building Materials. Available online: http://www.mhuc.gov.eg/programs/index/2168 (accessed on 6 November 2022).








| Parameter | Value |
|---|---|
| Concrete unit weight | 25.0 kN/m3 |
| Steel unit weight | 78.5 kN/m3 |
| Concrete compressive strength | 25 MPa |
| High tensile steel strength | 420 MPa |
| Mild steel strength | 240 MPa |
| Floor covering load | 1.5 kPa |
| Live load | 2.0 kPa |
| Building side length in each direction | 30.0 m |
| Number of spans in each direction | 6 |
| Story height | 3.0 m |
| Parameter | Value |
|---|---|
| Minimum corridor width | 2.4 m |
| Minimum side length for regular rooms | 3.6 m |
| Minimum side length for special surgery rooms | 7.0 m |
| Bed’s gross area | 80 m2 |
| Minimum area for general surgery rooms | 30 m2 |
| Minimum area for special surgery rooms | 50 m2 |
| Parameter | Value |
|---|---|
| Zone | C |
| ) | 1.25 kg/m3 |
| Wind speed (v) | 33 m/s |
| ) | 1 |
| ) | 1 |
| ) | 1 |
| Gravitational acceleration (g) | 9.81 m/s2 |
| ) | 1.47 m/s2 |
| ) | 1.4 |
| Soil type | C |
| Soil type factor 1 (s) | 1.5 |
| ) | 0.25 |
| Response modification factor (R) | 5 |
| ) | 0.05 |
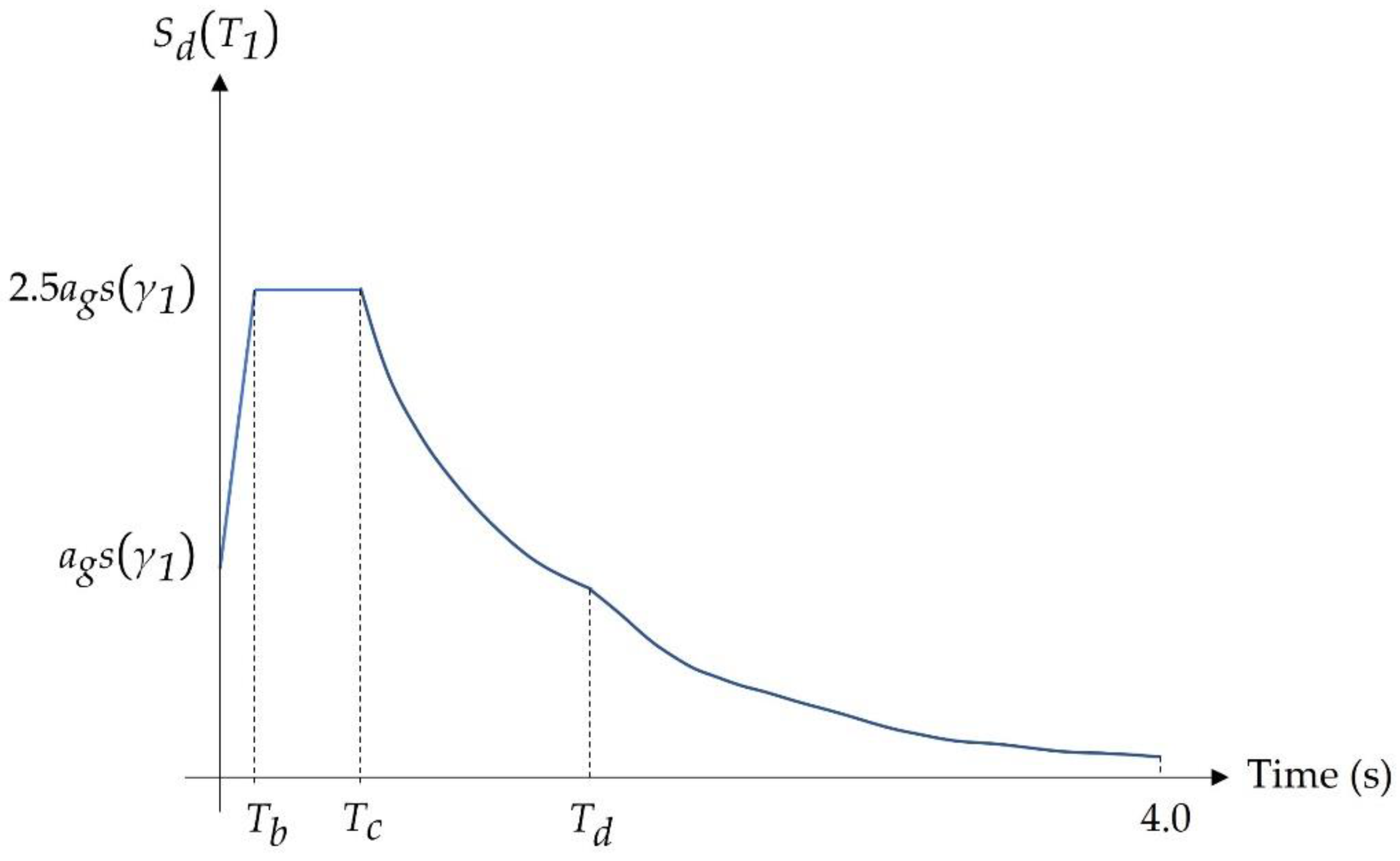
| Fundamental period | 0.73 s |
| Live load (L) | 4 kPa |
| Live load seismic coefficient (α) | 0.5 |
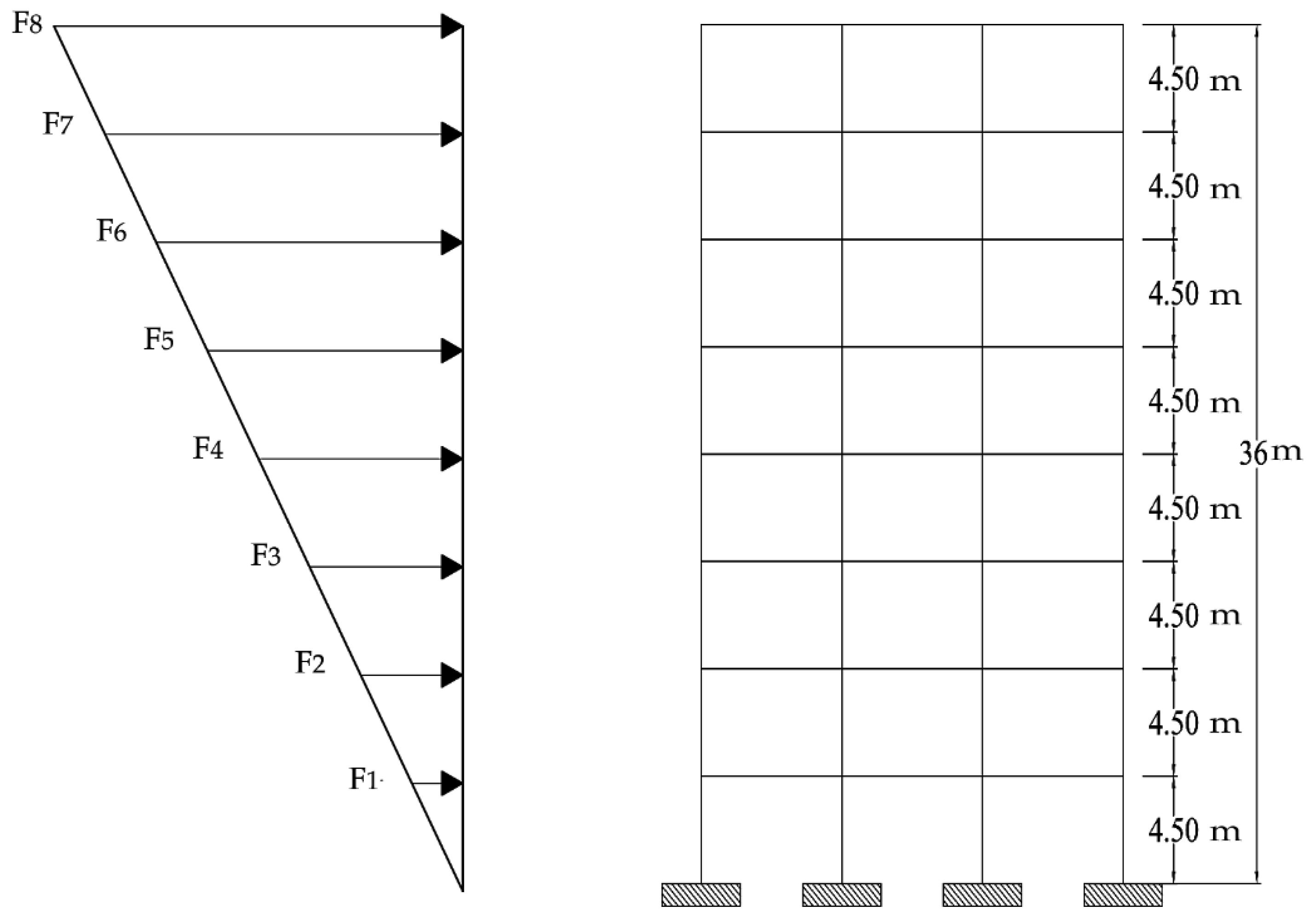
| Total building’s height (H) | 36 m |
| 25 | 57.03 |
| 30 | 60.56 |
| 35 | 64.09 |
| 40 | 67.67 |
| 45 | 71.15 |
| 50 | 74.67 |
| 55 | 78.20 |
| 60 | 81.73 |
| Variable | Increment (cm) | Cover Spacing (cm) |
|---|---|---|
| Slab thickness | 2 | 2 |
| Drop thickness | 2 | 2 |
| Drop width | 5 | 5 |
| Column width | 5 | 2.5 |
| Design Alternative | Floor | Intermediate Columns | Edge Columns (x-Direction) | Edge Columns (y-Direction) | Corner Columns | Total Cost (USD/m2) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Floor System | Column Spacings (m) | (m) | (m) | (m) | Steel Bars | (m) | Steel Bars | (m) | Steel Bars | (m) | Steel Bars | |||
| FSWD | 7.2 × 7.2 | 45 | 0.20 | 0.12 | 2.40 | 0.75 | 20T18 | 1.25 | 28T28 | 1.35 | 32T28 | 0.60 | 20T28 | 69.59 |
| FP | 7.2 × 7.2 | 30 | 0.24 | - | - | 1.00 | 24T22 | 1.35 | 32T28 | 0.80 | 20T28 | 0.85 | 24T32 | 69.44 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aidy, A.; Rady, M.; Mashhour, I.M.; Mahfouz, S.Y. Structural Design Optimization of Flat Slab Hospital Buildings Using Genetic Algorithms. Buildings 2022, 12, 2195. https://doi.org/10.3390/buildings12122195
Aidy A, Rady M, Mashhour IM, Mahfouz SY. Structural Design Optimization of Flat Slab Hospital Buildings Using Genetic Algorithms. Buildings. 2022; 12(12):2195. https://doi.org/10.3390/buildings12122195
Chicago/Turabian StyleAidy, Ahmed, Mohammed Rady, Ibrahim Mohsen Mashhour, and Sameh Youssef Mahfouz. 2022. "Structural Design Optimization of Flat Slab Hospital Buildings Using Genetic Algorithms" Buildings 12, no. 12: 2195. https://doi.org/10.3390/buildings12122195
APA StyleAidy, A., Rady, M., Mashhour, I. M., & Mahfouz, S. Y. (2022). Structural Design Optimization of Flat Slab Hospital Buildings Using Genetic Algorithms. Buildings, 12(12), 2195. https://doi.org/10.3390/buildings12122195