Effects of Different Frequency Sensitivity Models of a Viscoelastic Damper on Wind-Induced Response of High-Rise Buildings
Abstract
1. Introduction
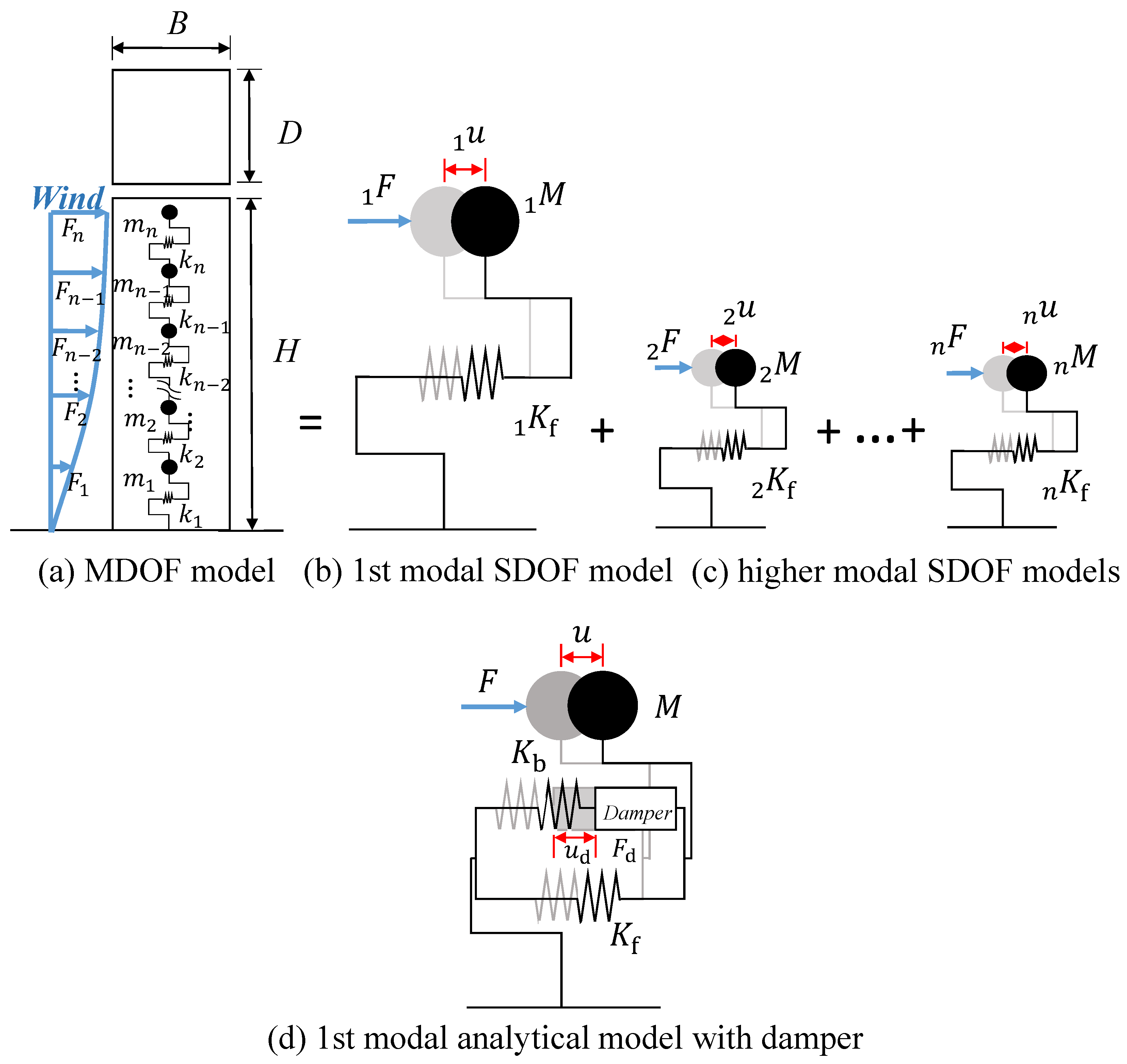
2. Target Building and Numerical Models
2.1. Target Building and the SDOF Model
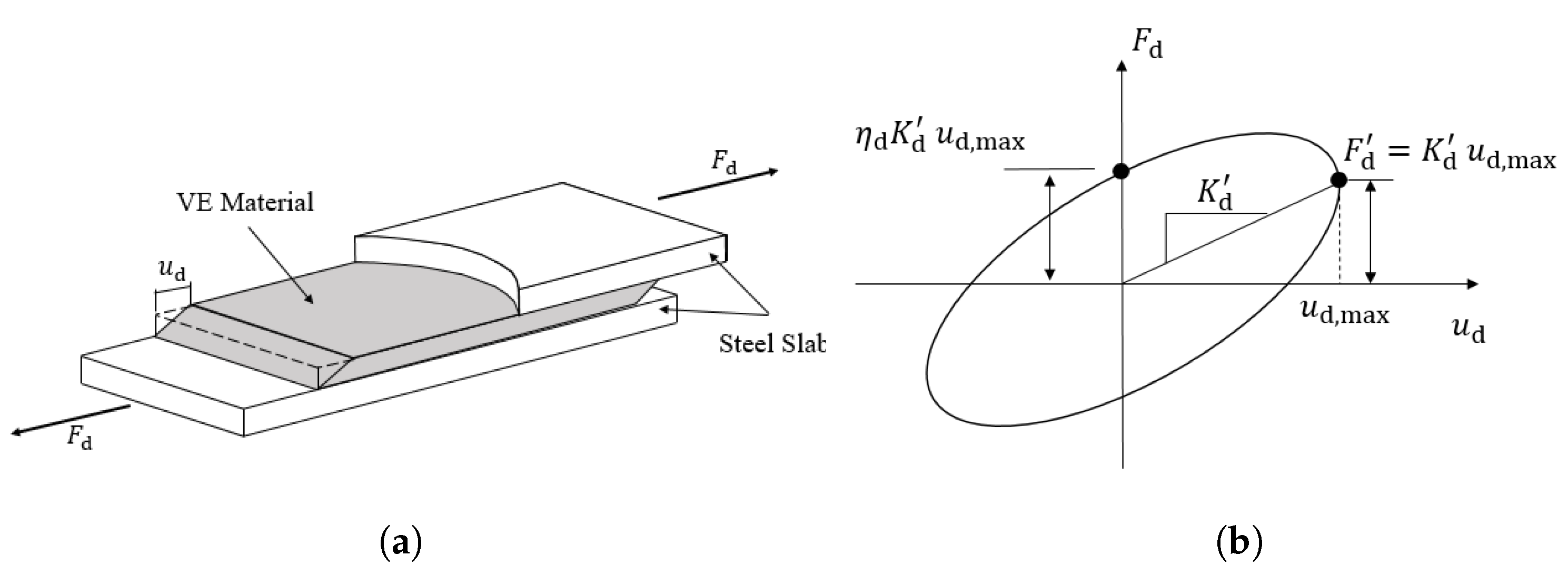
2.2. Basic Settings of Numerical Models with the VE Damper
2.3. FD Model and ID Models
2.3.1. FD Model
2.3.2. 4-Element Model
2.3.3. 6-Element Model
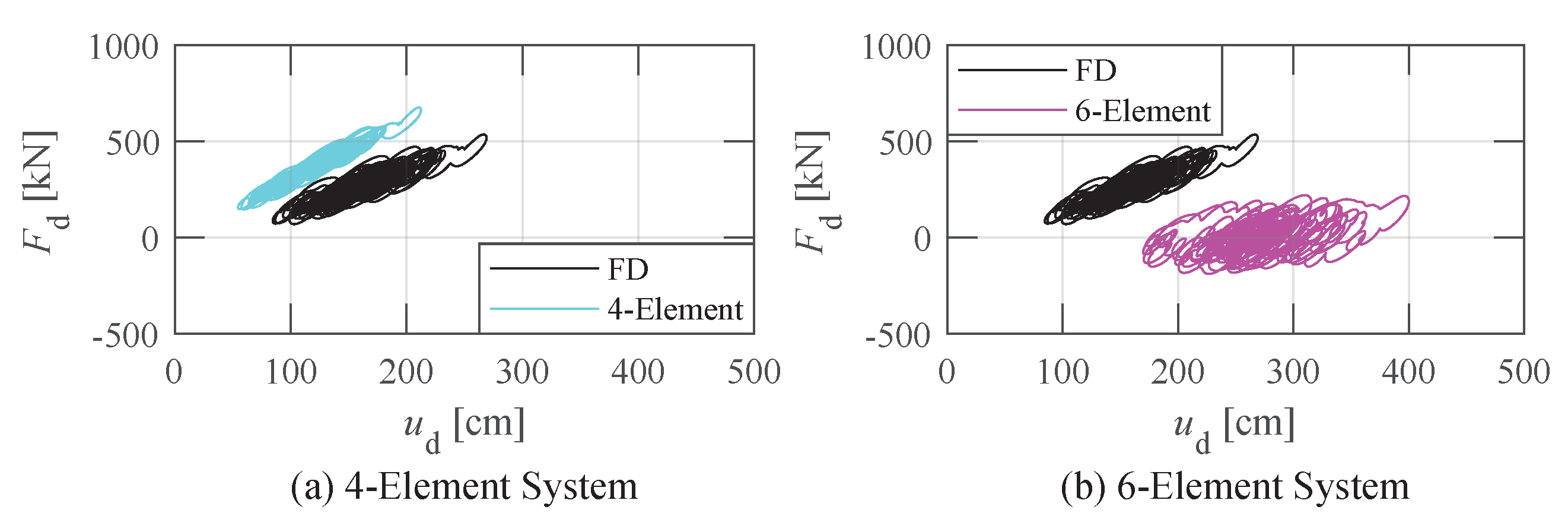
3. Characteristics of the VE Systems under the Steady-State Response
- -
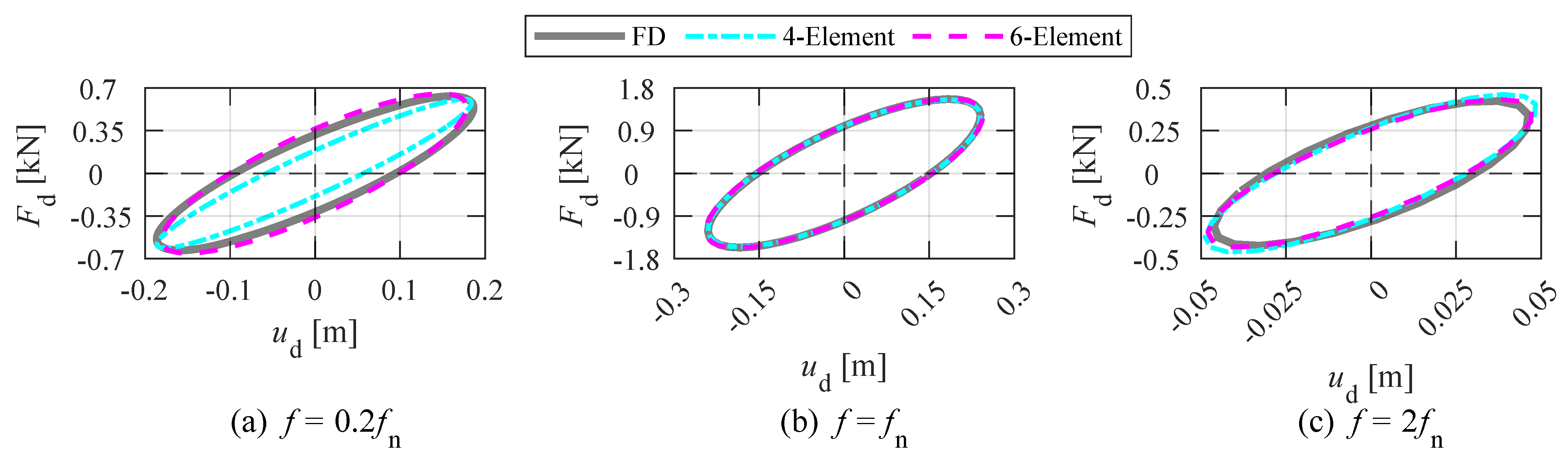
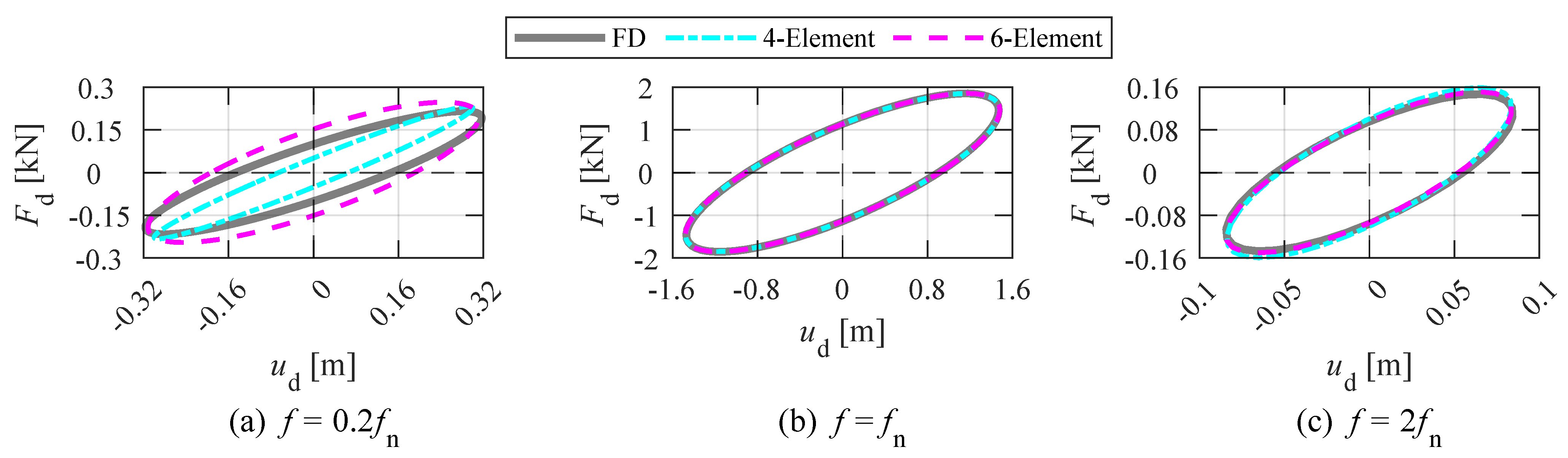
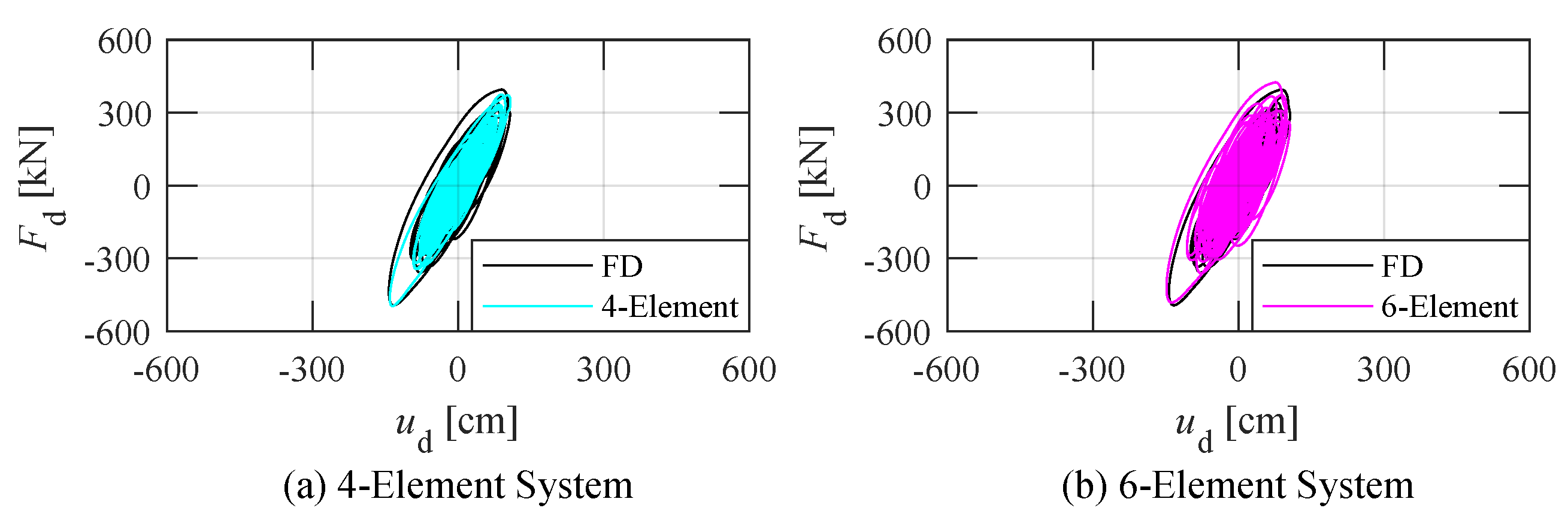
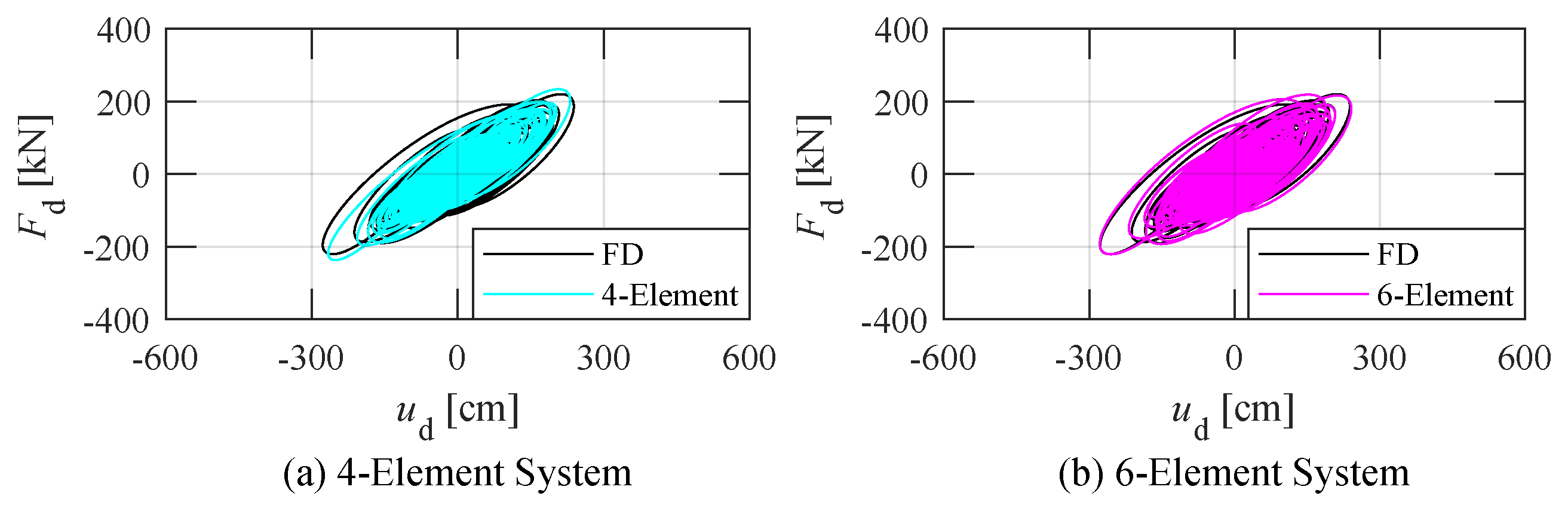
- When subjected to harmonic waves of , the hysteresis loop (Figure 8a) of the 4-element model is smaller than the FD model. While the hysteresis loop of the 6-element model is greater than the FD model. The massive difference in the hysteresis loop of the damper among three models when aligns with the relationship of frequency sensitivity in Figure 6.
- -
- -
4. Characteristics of the VE Systems under the Wind-Induced Response
4.1. Wind Force
4.2. Wind-Induced Response of FD Systems
- -
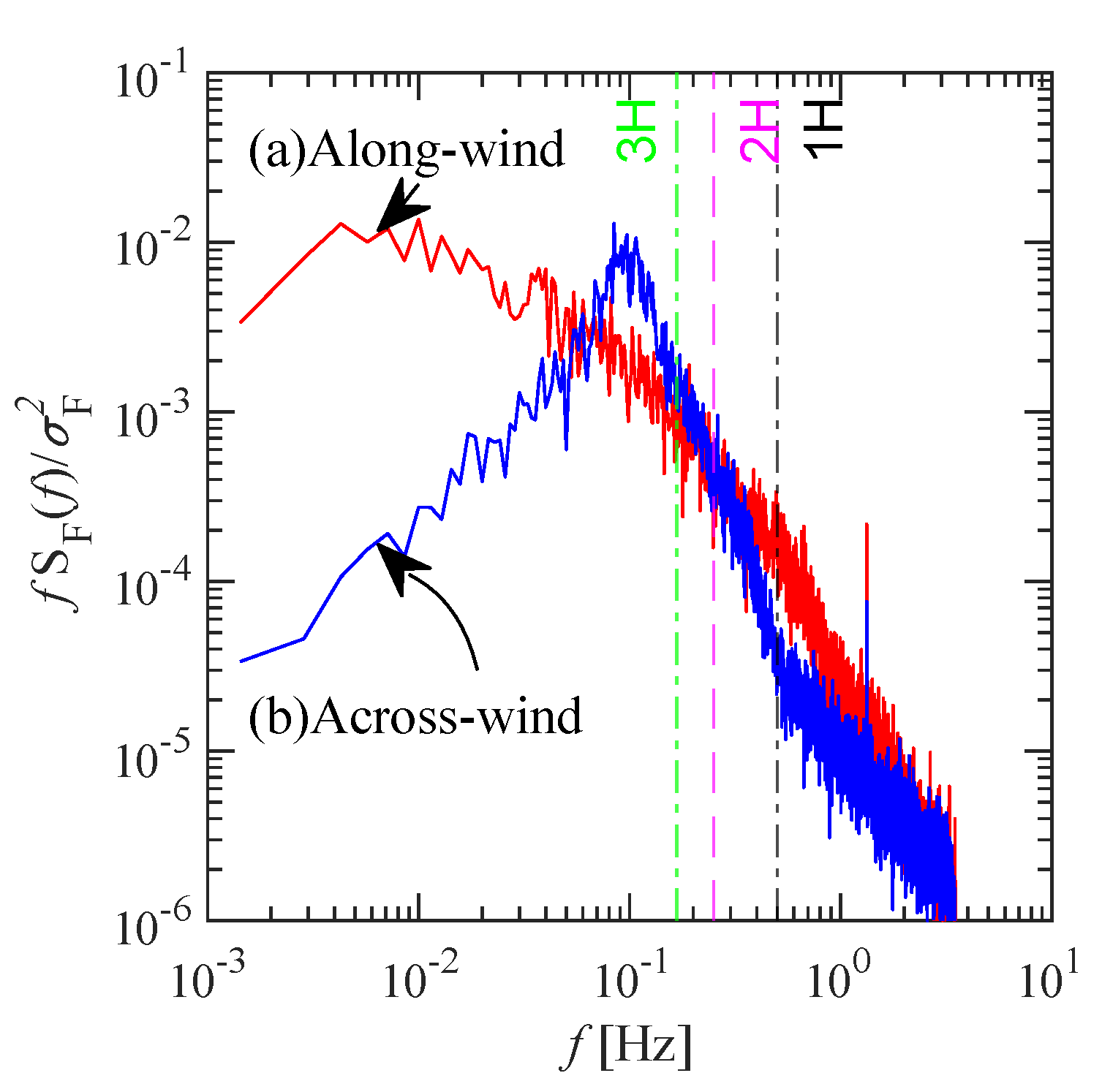
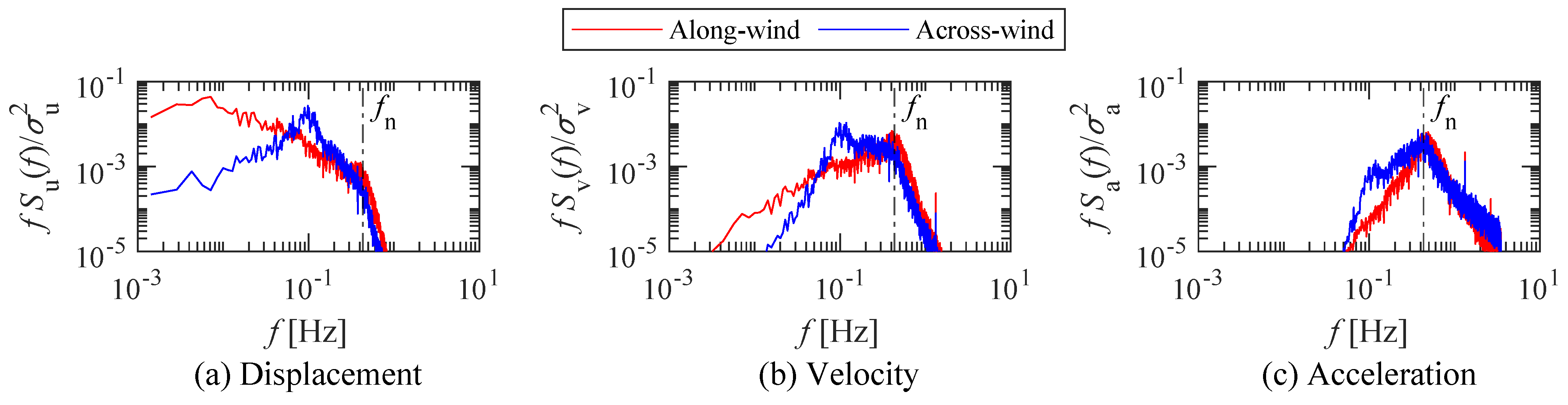
- In Figure 12a, the along-wind displacement has high power with wide-band frequencies in the low-frequency region. However, the across-wind displacement has high power around 1.0 Hz.
- -
- In Figure 12b, the along-wind velocity has high power close to the resonance frequency (). In contrast, the across-wind velocity spectrum has high power in a range from 1.0 Hz to the resonance frequency ().
- -
- In Figure 12c, the along-wind acceleration has a similar tendency with its velocity, having high power close to the resonance frequency (). Similarly, the across-wind acceleration has high power close to the resonance frequency.
- -
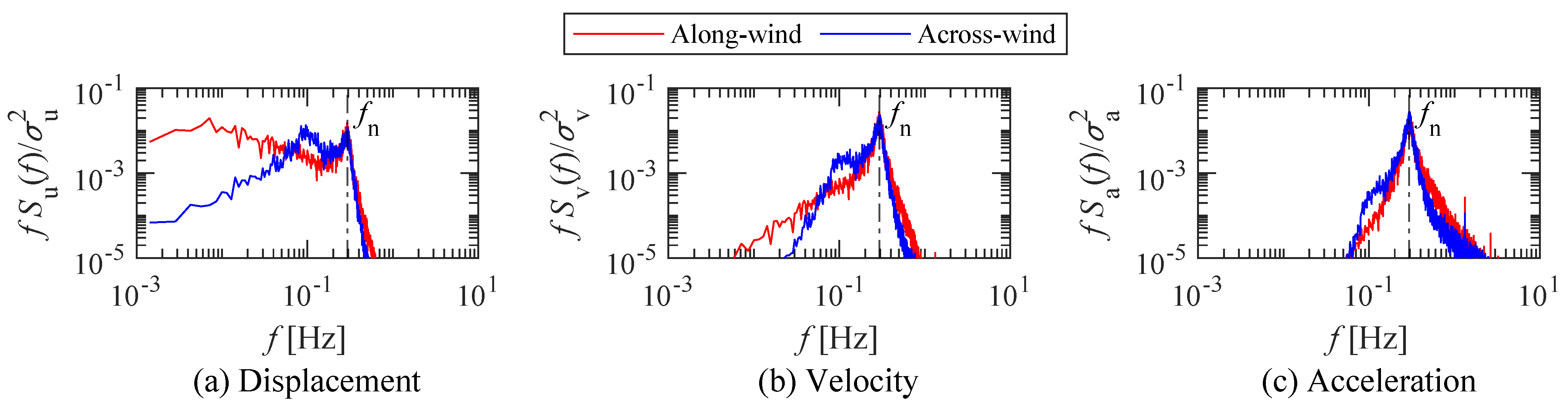
- In Figure 13a, the along-wind displacement has significantly high power close to the resonance frequency () and a wide band of the low-frequency region. However, the across-wind displacement has high power between 1.0 Hz and the resonance frequency ().
- -
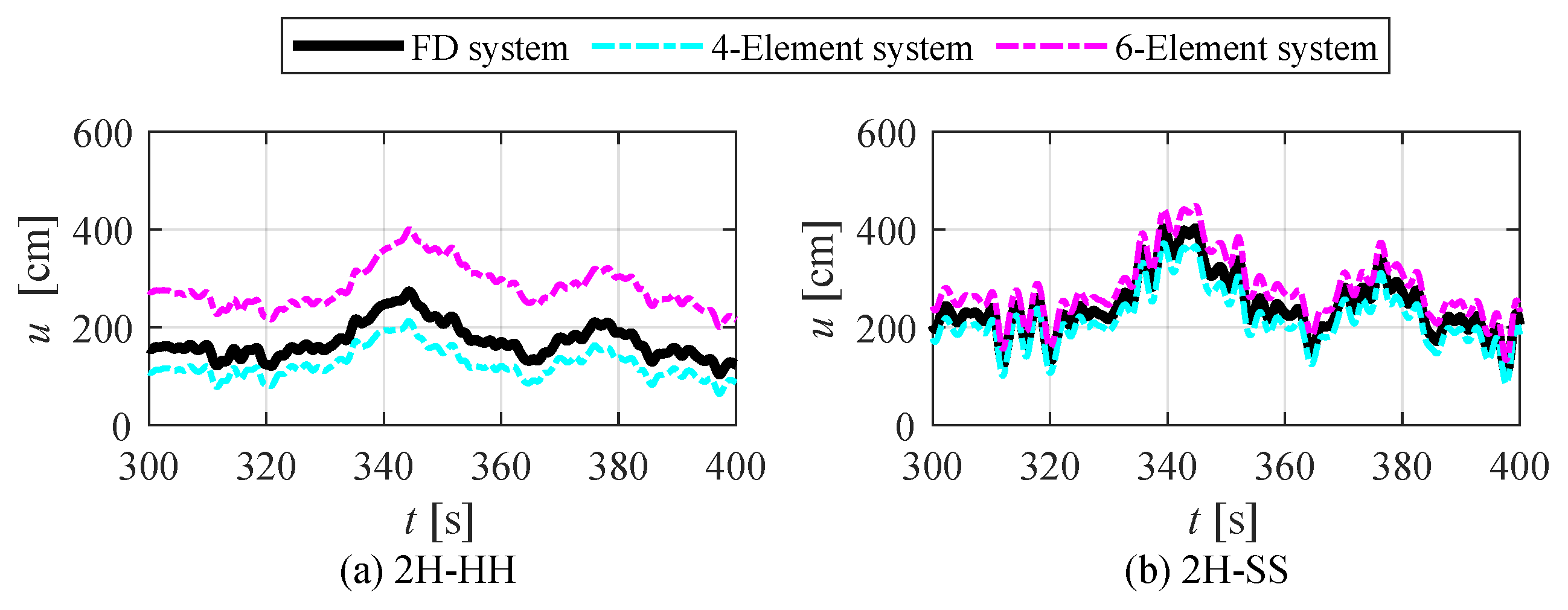
4.3. Response Comparison between ID Systems and FD System in Along-Wind
- -
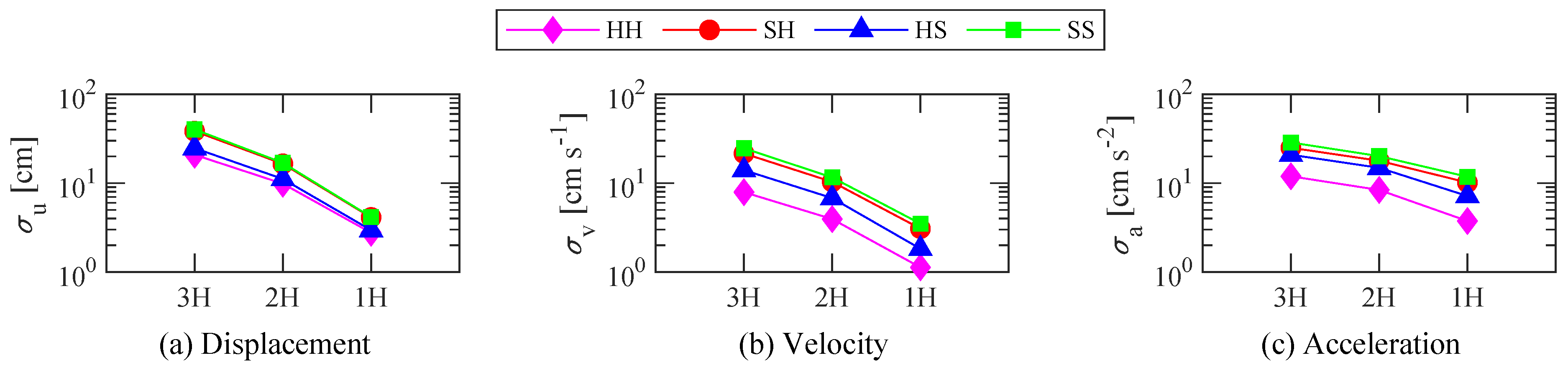
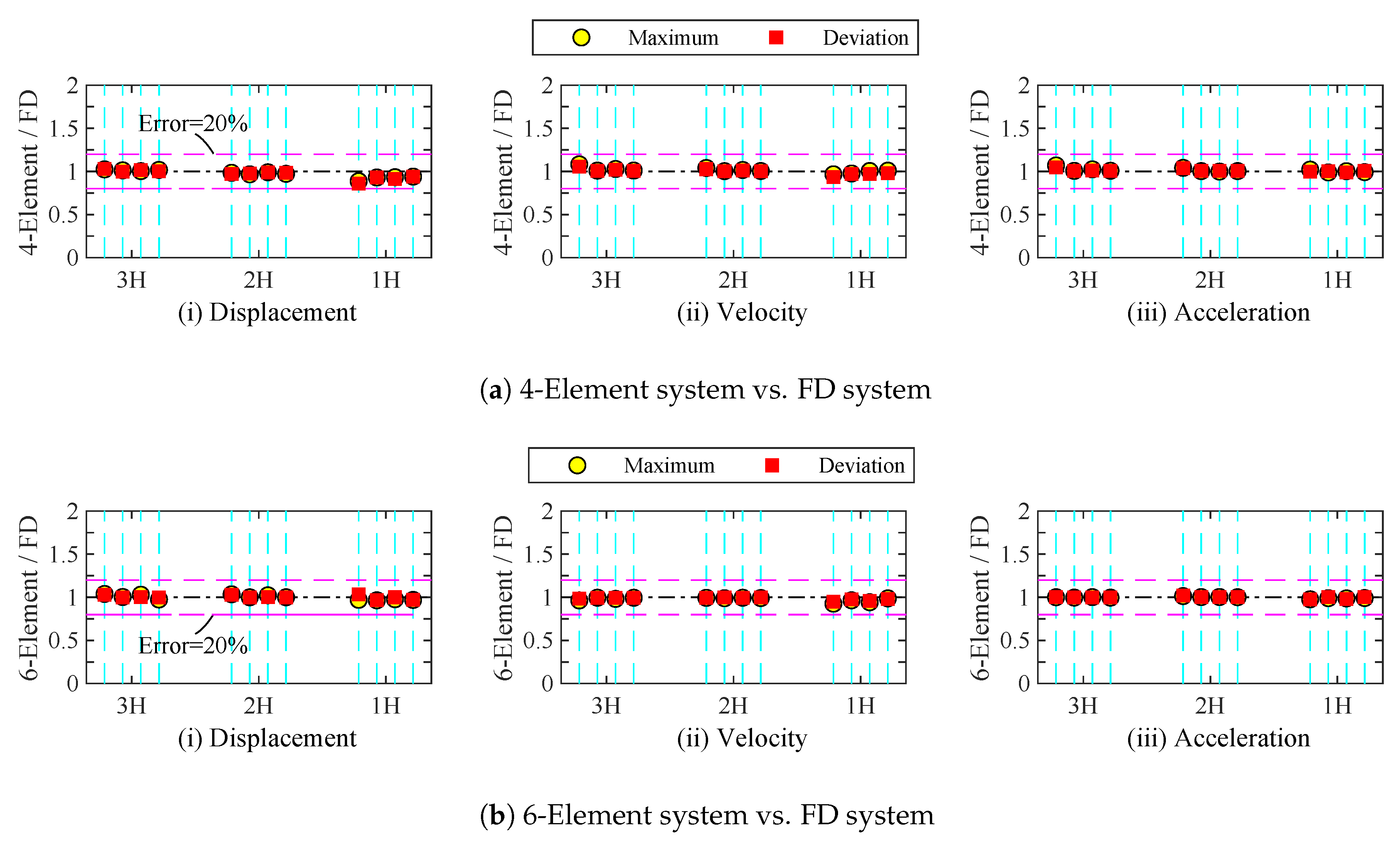
- The mean, maximum, and standard deviation of the along-wind displacement of the 4-element system is smaller than the FD system. It shows that the difference increases as the storage stiffness of the damper increases.
- -
- When the ratio of storage stiffness of the damper is 2.0 (as an added component is -HH or -HS), the difference of the mean, maximum, and standard deviation of the along-wind displacement between the 4-element system and the FD system is about .
- -
- The differences in the maximum and standard deviation of the along-wind velocity and acceleration of the 4-element system remain aligned with the FD system.
- -
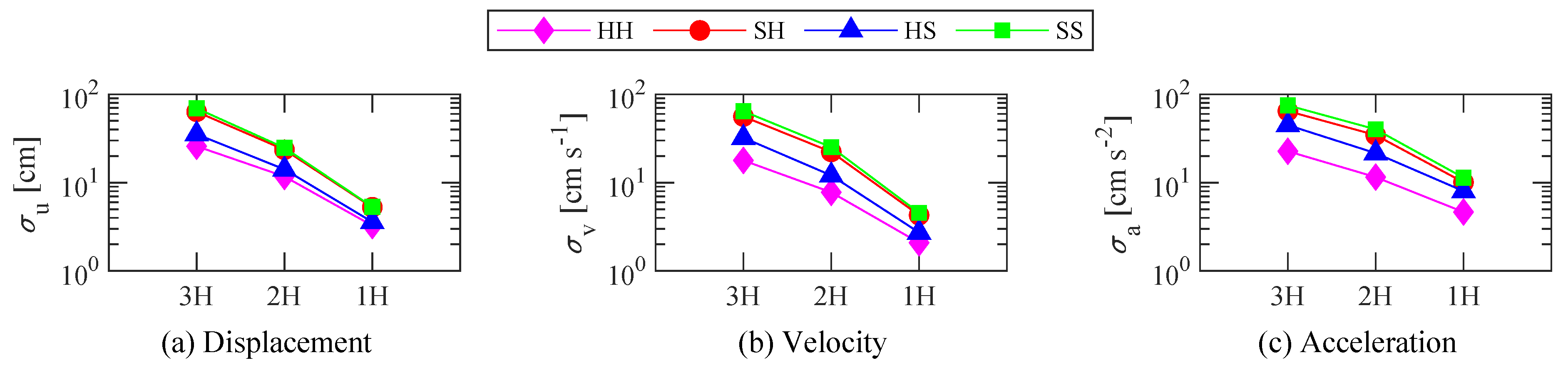
- The mean, maximum, and standard deviation of the along-wind displacement of the 6-element system is larger than the FD system. It shows that the difference increases as the storage stiffness of the damper increases.
- -
- When the ratio of storage stiffness of the damper is 2.0 (as an added component is -HH or -HS), the difference of the mean, maximum, and standard deviation of the along-wind displacement between the 6-element system and the FD system is over . In contrast, when the ratio of storage stiffness of the damper is 0.4 (as an added component is -SH or -SS), the difference of the mean, maximum, and standard deviation of the along-wind displacement between the 6-element system and the FD system is about .
- -
- The differences in the maximum and standard deviation of both along-wind velocity and acceleration of the 6-element system also remain aligned with the FD system.
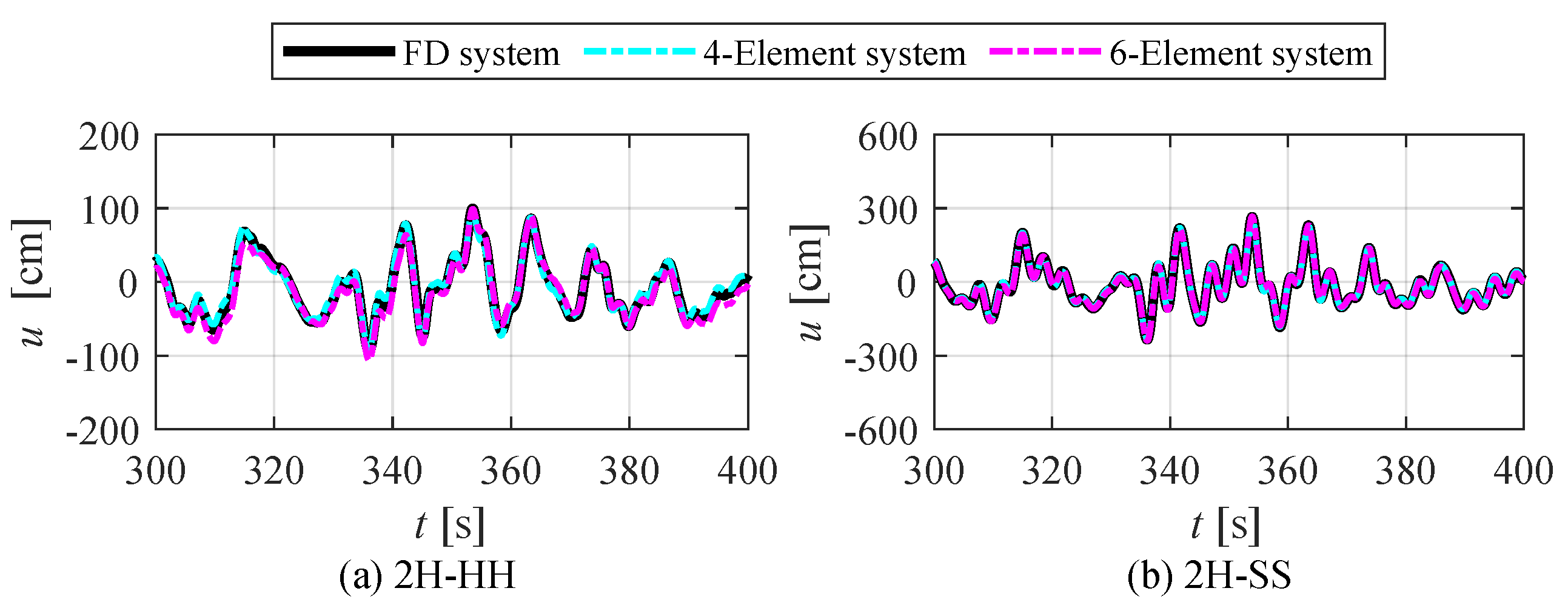
4.4. Response Comparison between ID Systems and FD System in Across-Wind
5. Conclusions
- -
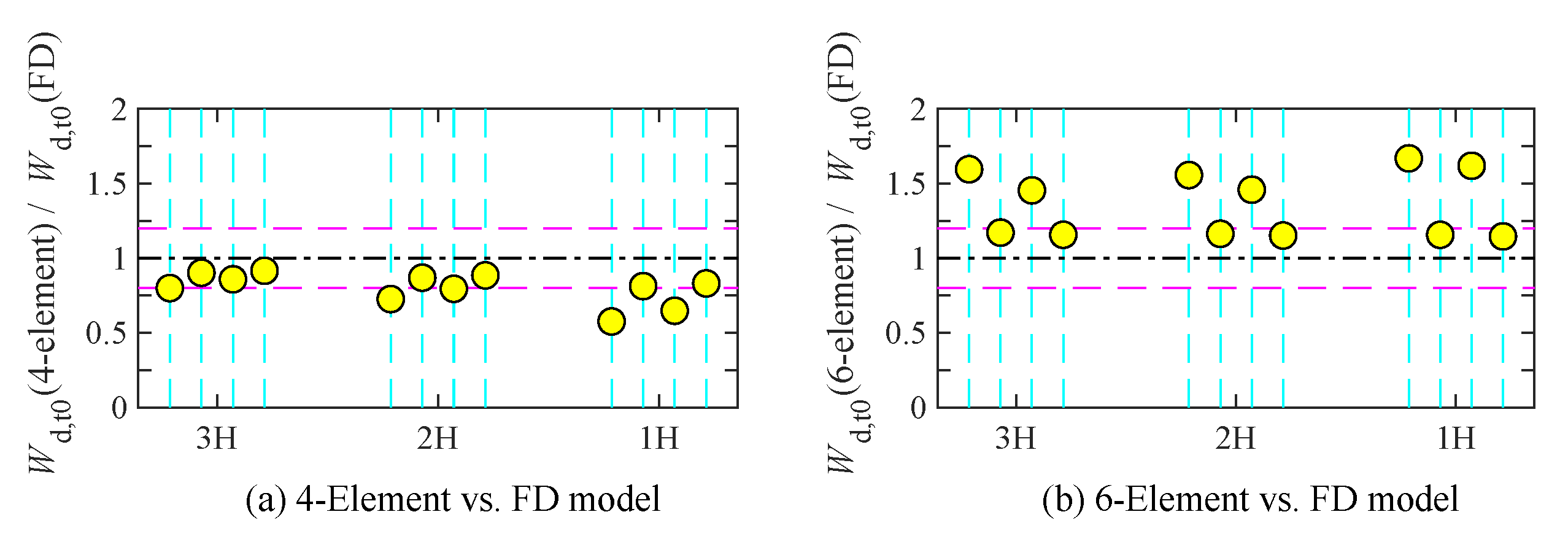
- The along-wind displacement of the 4-element and 6-element systems with the dampers of high storage stiffness has obvious differences with the FD system due to low frequency and the wide-band frequencies dominating the behavior of the VE system significantly. Furthermore, the frequency sensitivity of the 4-element and 6-element systems and the FD system have massive differences at low frequencies.
- -
- The along-wind displacement of the 4-element and 6-element systems with the dampers of low storage stiffness has better agreement with the FD system due to the resonance frequency dominating the behavior of the VE systems significantly, and the frequency sensitivity of VE systems having good agreements at the resonance frequency. Similarly, the hysteresis loops of the 4-element and 6-element systems with low storage stiffness align well with the FD system. The energy dissipation and the mean deformation of the 4-element and 6-element systems are also matching well with the FD system, respectively.
- -
- The responses and the hysteresis loops of the 4-element and 6-element systems have good agreements with the FD system due to the narrow-band frequencies being close to the resonance frequency along with the alignment of frequency sensitivity at resonance frequency dominating the across-wind response, which is more tremendous than the along-wind response.
- -
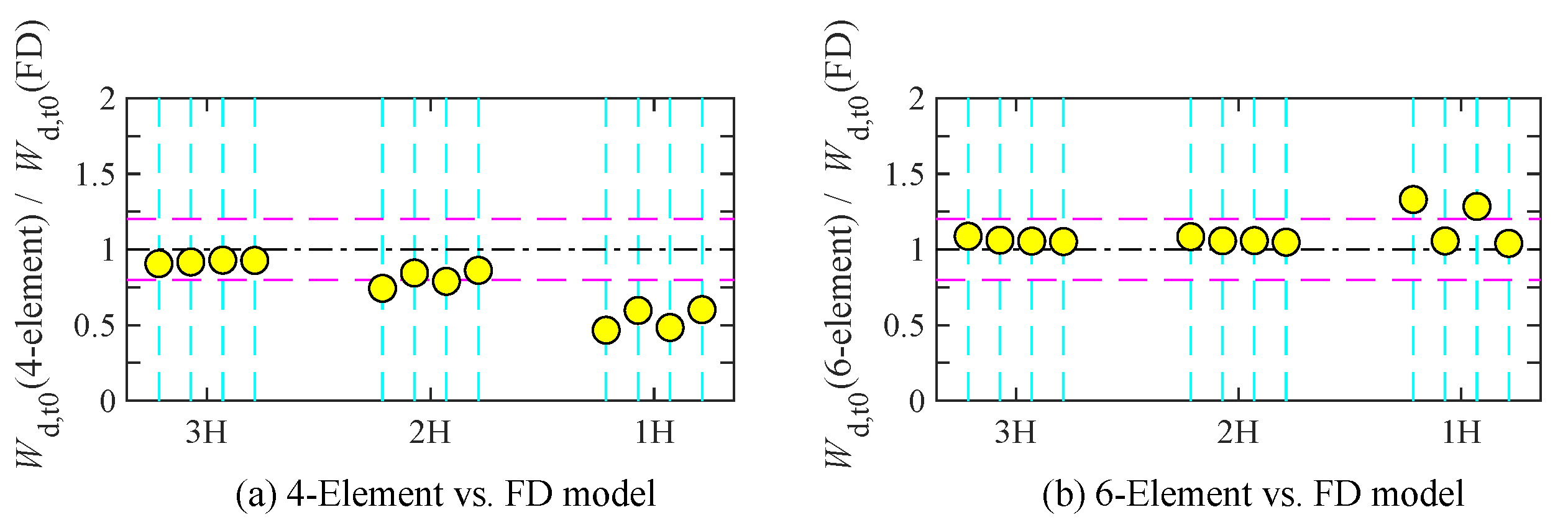
- The energy dissipation of the 6-element systems has better matching with the FD systems than the 4-element systems since the 6-element system has better agreement with the FD system at the resonance frequency than the 4-element system.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
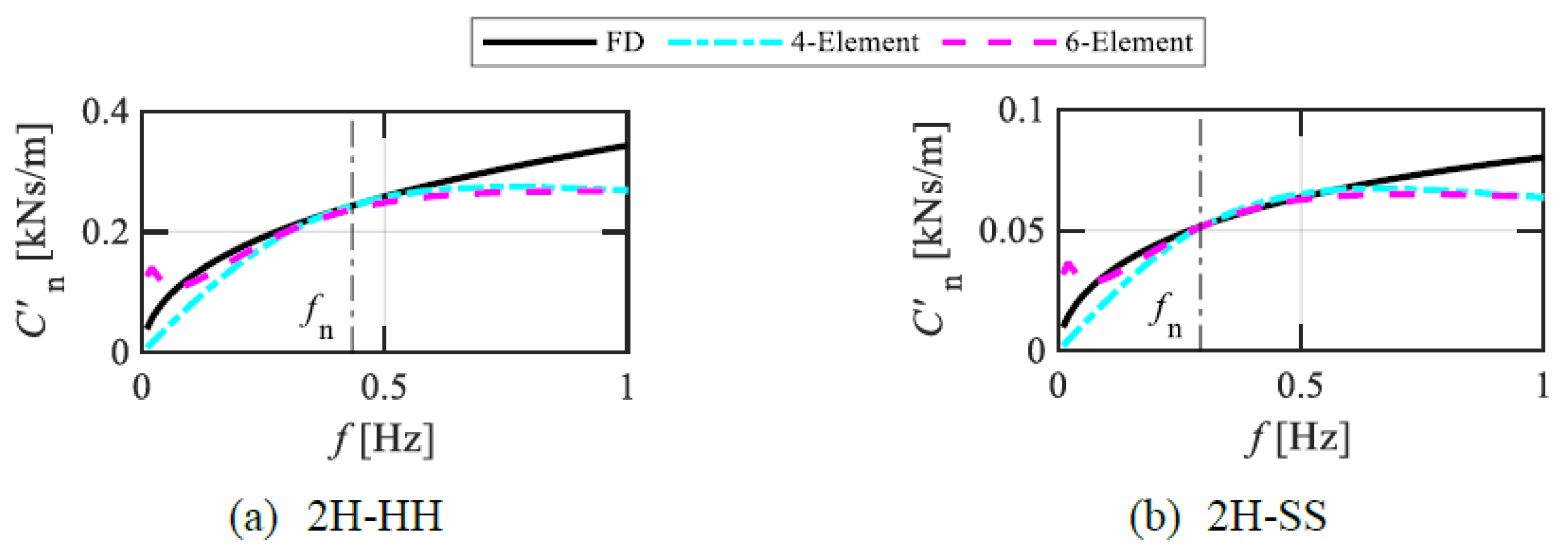
Appendix A. Frequency Sensitivity of the Damping Coefficient in the VE System
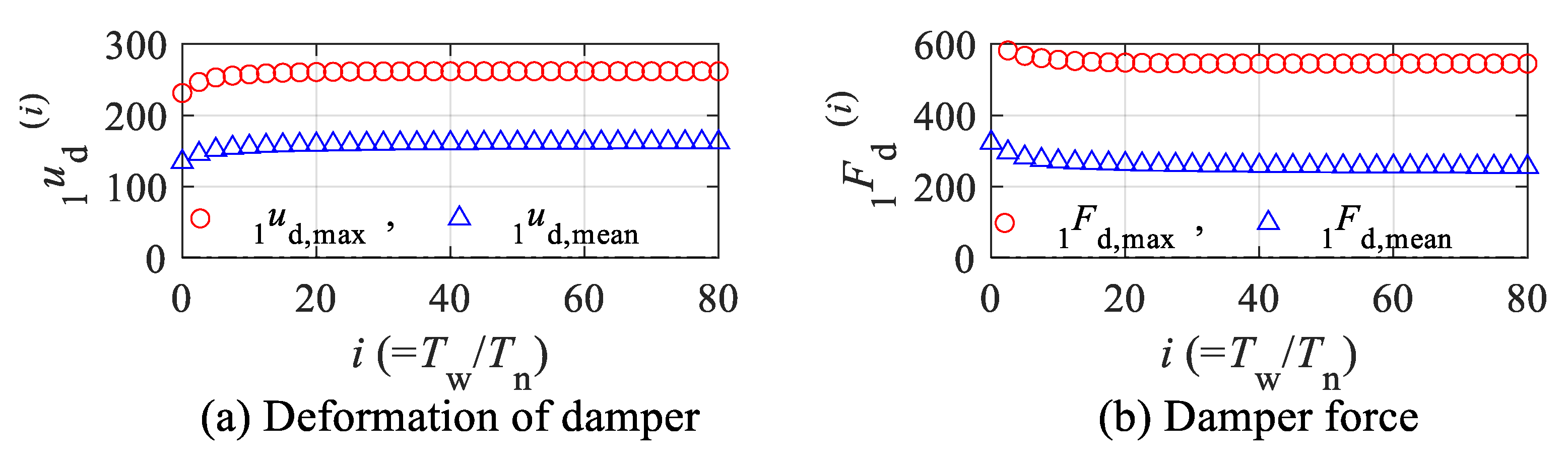
Appendix B. Numerical Integration Method of the Fractional Derivative Model [18,27]
Appendix C. Effect of Window Time
References
- Lin, P.; Ding, F.; Hu, G.; Li, C.; Xiao, Y.; Tse, K.; Kwok, K.; Kareem, A. Machine learning-enabled estimation of crosswind load effect on tall buildings. J. Wind. Eng. Ind. Aerodyn. 2022, 220, 104860. [Google Scholar] [CrossRef]
- Architectural Institute of Japan (AIJ). Guidelines for the Evaluation of Habitability to Building Vibration; AIJ: Tokyo, Japan, 2004. (In Japanese) [Google Scholar]
- Architectural Institute of Japan (AIJ). AIJ Recommendations for Loads on Buildings; AIJ: Tokyo, Japan, 2015. [Google Scholar]
- Simiu, E.; Yeo, D. Wind Effects on Structures: Modern Structural Design for Wind; John Wiley & Sons: Hoboken, NJ, USA, 2019. [Google Scholar]
- Boggs, D.; Dragovich, J. The nature of wind loads and dynamic response. Spec. Publ. 2006, 240, 15–44. [Google Scholar]
- The Japan Society of Seismic Isolation (JSSI). Manual for Design and Construction of Passively-Controlled Buildings, 3rd ed.; JSSI: Tokyo, Japan, 2013. (In Japanese) [Google Scholar]
- Samali, B.; Kwok, K. Use of viscoelastic dampers in reducing wind-and earthquake-induced motion of building structures. Eng. Struct. 1995, 17, 639–654. [Google Scholar] [CrossRef]
- Takewaki, I. Building Control with Passive Dampers: Optimal Performance-Based Design for Earthquakes; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Ghaemmaghami, A.R.; Kwon, O.S. Nonlinear modeling of MDOF structures equipped with viscoelastic dampers with strain, temperature and frequency-dependent properties. Eng. Struct. 2018, 168, 903–914. [Google Scholar] [CrossRef]
- Zhou, X.; Sun, T.; Sun, B.; Ma, N.; Ou, J. Vibration-Reduction Strategy for High-Rise Braced Frame Using Viscoelastic-Yielding Compounded BRB. Buildings 2022, 12, 1159. [Google Scholar] [CrossRef]
- Ito, M. Wind Engineering of Large Bridges in Japan; Routledge: London, UK, 2017; pp. 71–79. [Google Scholar]
- Song, Y.; Zhang, M.; Øiseth, O.; Rønnquist, A. Wind deflection analysis of railway catenary under crosswind based on nonlinear finite element model and wind tunnel test. Mech. Mach. Theory 2022, 168, 104608. [Google Scholar] [CrossRef]
- Holmes, J.D. Wind Loading of Structures; CRC Press: Boca Raton, FL, USA, 2007. [Google Scholar]
- Kareem, A.; Tamura, Y. Advanced Structural Wind Engineering; Springer: Berlin/Heidelberg, Germany, 2013; Volume 482. [Google Scholar]
- Nielsen, E.J.; Lai, M.L.; Soong, T.; Kelly, J.M. Viscoelastic damper overview for seismic and wind applications. In Proceedings of the Smart Structures and Materials 1996: Passive Damping and Isolation, SPIE, San Diego, CA, USA, 26–27 February 1996; Volume 2720, pp. 138–144. [Google Scholar]
- Sato, D.; Osabel, D.M.; Kasai, K. Evaluation method for practical application of viscoelastic damper using equivalent sinusoidal waveforms of long-duration random excitations in along-and across-wind directions. Eng. Struct. 2022, 254, 113735. [Google Scholar] [CrossRef]
- Chou, C.C.; Tseng, W.H.; Huang, C.H.; Tsuang, S.; Chang, L.M.; Chen, Y.H. A novel steel lever viscoelastic wall with amplified damper force-friction for wind and seismic resistance. Eng. Struct. 2020, 210, 110362. [Google Scholar] [CrossRef]
- Kasai, K.; Teramoto, M.; Okuma, K.; Tokoro, K. Constitutive rule for viscoelastic materials considering temperature, frequency, and strain sensitivities. J. Struct. Constr. Eng. 2001, 543, 77–86. (In Japanese) [Google Scholar] [CrossRef]
- Wang, S.J.; Zhang, Q.Y.; Yu, C.H. Effectiveness of damaged viscoelastic dampers in seismic protection of structures under main shocks and aftershocks. Eng. Struct. 2021, 242, 112424. [Google Scholar] [CrossRef]
- Min, K.W.; Kim, J.; Lee, S.H. Vibration tests of 5-storey steel frame with viscoelastic dampers. Eng. Struct. 2004, 26, 831–839. [Google Scholar] [CrossRef]
- Xu, Y.; Xu, Z.; Guo, Y.; Huang, X.; Dong, Y.; Li, Q. Dynamic Properties and Energy Dissipation Study of Sandwich Viscoelastic Damper Considering Temperature Influence. Buildings 2021, 11, 470. [Google Scholar] [CrossRef]
- Lewandowski, R. Influence of Temperature on the Dynamic Characteristics of Structures with Viscoelastic Dampers. J. Struct. Eng. 2019, 145, 04018245. [Google Scholar] [CrossRef]
- Kasai, K.; Osabel, D.M.; Sato, D. Dynamic response characterization and simplified analysis methods for viscoelastic dampers considering heat transfer. Earthq. Eng. Struct. Dyn. 2022, 1–24. [Google Scholar] [CrossRef]
- Dong, Y.R.; Xu, Z.D.; Guo, Y.Q.; Xu, Y.S.; Chen, S.; Li, Q.Q. Experimental study on viscoelastic dampers for structural seismic response control using a user-programmable hybrid simulation platform. Eng. Struct. 2020, 216, 110710. [Google Scholar] [CrossRef]
- Sato, D.; Kasai, K.; Tamura, T. Influence of frequency sensitivity of viscoelastic damper on wind-induced response. J. Struct. Constr. Eng. 2009, 74, 75–82. (In Japanese) [Google Scholar] [CrossRef]
- Zuo, Z.; Liu, L.; Zhou, Y.; Qin, J.; Cui, W. Acoustic Radiation Study of a Box Girder Viaduct Considering the Frequency-Dependent Viscoelasticity of the Rail Pad. Buildings 2022, 12, 1226. [Google Scholar] [CrossRef]
- Kasai, K.; Munshi, J.; Lai, M.; Maison, B. Viscoelastic Damper Hysteresis Model: Theory, Experiment, and Application ATC-17-1 Seminar. Appl. Technol. Counc. 1993, 2, 521–532. [Google Scholar]
- Duarte Ortigueira, M.; Tenreiro Machado, J. Fractional derivatives: The perspective of system theory. Mathematics 2019, 7, 150. [Google Scholar] [CrossRef]
- Ortigueira, M.D.; Machado, J.T. What is a fractional derivative? J. Comput. Phys. 2015, 293, 4–13. [Google Scholar] [CrossRef]
- Jones, D.I. Handbook of Viscoelastic Vibration Damping; John Wiley & Sons: Hoboken, NJ, USA, 2001. [Google Scholar]
- Lakes, R.; Lakes, R.S. Viscoelastic Materials; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
- Lewandowski, R.; Pawlak, Z. Response spectrum method for building structures with viscoelastic dampers described by fractional derivatives. Eng. Struct. 2018, 171, 1017–1026. [Google Scholar] [CrossRef]
- Oldham, K.; Spanier, J. The Fractional Calculus Theory and Applications of Differentiation and Integration to Arbitrary Order; Elsevier: Amsterdam, The Netherlands, 1974. [Google Scholar]
- Bagley, R.L.; Torvik, P. A theoretical basis for the application of fractional calculus to viscoelasticity. J. Rheol. 1983, 27, 201–210. [Google Scholar] [CrossRef]
- Tsai, C.; Lee, H. Applications of viscoelastic dampers to high-rise buildings. J. Struct. Eng. 1993, 119, 1222–1233. [Google Scholar] [CrossRef]
- Chang, K.; Soong, T.; Oh, S.T.; Lai, M. Seismic behavior of steel frame with added viscoelastic dampers. J. Struct. Eng. 1995, 121, 1418–1426. [Google Scholar] [CrossRef]
- Okuma, K.; Kasai, K. Global damping model of multi-mass system having elastic frame and viscoelastic damper. J. Struct. Constr. Eng. 2010, 75, 347–356. (In Japanese) [Google Scholar] [CrossRef]
- Hirai, H.; Yoshie, K.; Sato, D.; Suzuki, Y.; Kitamura, H. Characteristic of higher mode response of high-rise building under fluctuating wind force. AIJ J. Technol. Des. 2012, 18, 79–84. (In Japanese) [Google Scholar] [CrossRef][Green Version]
- Roncallo, L.; Solari, G.; Muscolino, G.; Tubino, F. Maximum dynamic response of linear elastic SDOF systems based on an evolutionary spectral model for thunderstorm outflows. J. Wind. Eng. Ind. Aerodyn. 2022, 224, 104978. [Google Scholar] [CrossRef]
- Marukawa, H.; Ohkuma, T.; Kitimura, H.; Yoshie, K.; Tsurumi, T.; Sato, D. 20097 Energy Input of Local Wind Forces for High-Rise Building Based on Wind Tunnel Test: Part. 2 Local Wind Force Characteristics of Rectangular High-Rise Buildings; AIJ: Tokyo, Japan, 2010; pp. 193–194. (In Japanese) [Google Scholar]
- Zhang, M.; Xu, F. Tuned mass damper for self-excited vibration control: Optimization involving nonlinear aeroelastic effect. J. Wind. Eng. Ind. Aerodyn. 2022, 220, 104836. [Google Scholar] [CrossRef]
- Kasai, K.; Okuma, K. Kelvin-type formulation and its accuracy for practical modeling of linear viscoelastic dampers (Part 1. One-mass system having damper and elastic/inelastic frame). J. Struct. Constr. Eng. 2001, 550, 71–78. [Google Scholar] [CrossRef]
- Kasai, K.; Fu, Y.; Watanabe, A. Passive control systems for seismic damage mitigation. J. Struct. Eng. 1998, 124, 501–512. [Google Scholar] [CrossRef]
- Fu, Y.; Kasai, K. Comparative study of frames using viscoelastic and viscous dampers. J. Struct. Eng. 1998, 124, 513–522. [Google Scholar] [CrossRef]

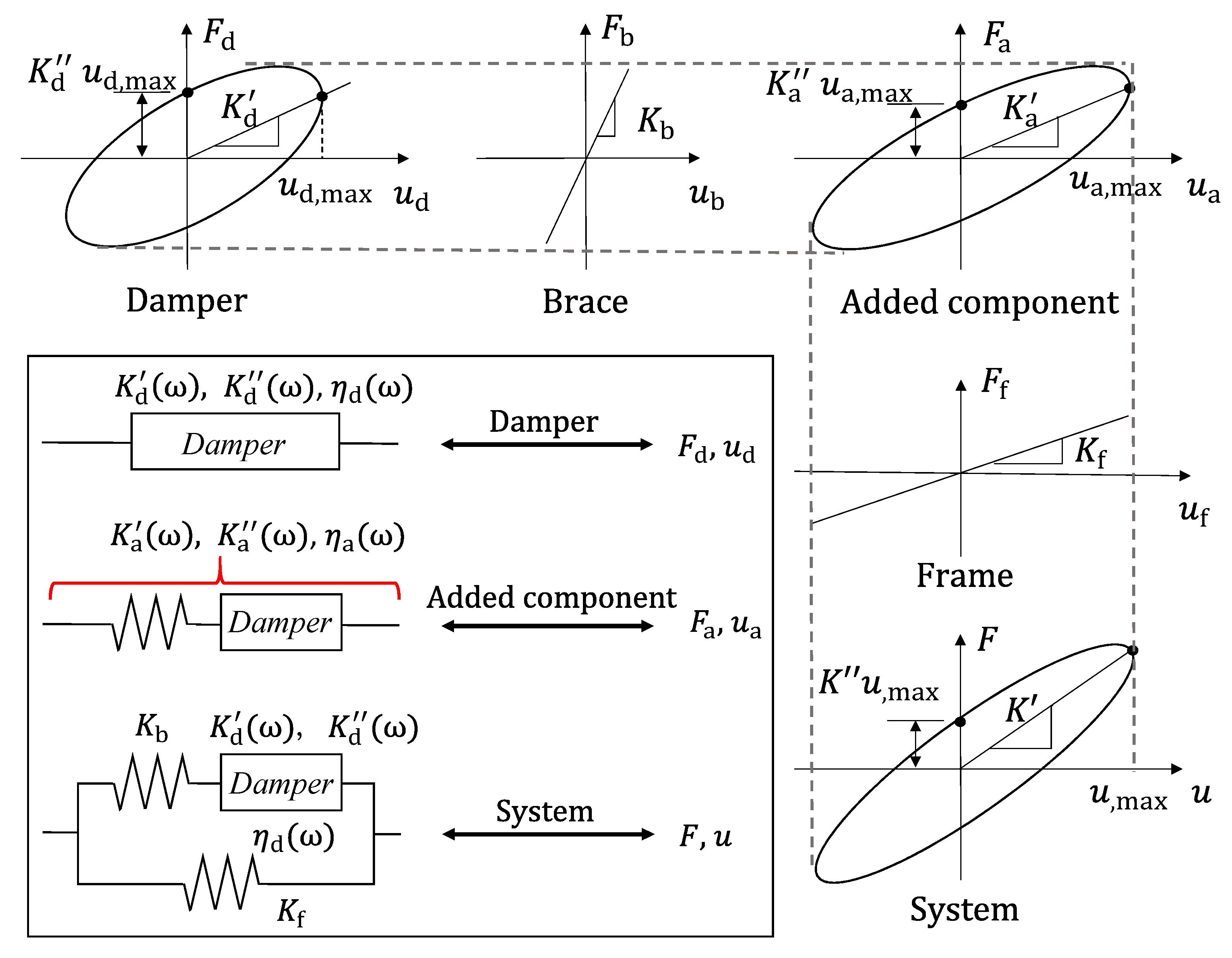









| System | Damper | Brace | |||
|---|---|---|---|---|---|
| 1H-HH | 2 s | Hard | Hard | ∞ | |
| 1H-SH | 2 s | Soft | Hard | ∞ | |
| 1H-HS | 2 s | Hard | Soft | ||
| 1H-SS | 2 s | Soft | Soft | ||
| 2H-HH | 4 s | Hard | Hard | ∞ | |
| 2H-SH | 4 s | Soft | Hard | ∞ | |
| 2H-HS | 4 s | Hard | Soft | ||
| 2H-SS | 4 s | Soft | Soft | ||
| 3H-HH | 6 s | Hard | Hard | ∞ | |
| 3H-SH | 6 s | Soft | Hard | ∞ | |
| 3H-HS | 6 s | Hard | Soft | ||
| 3H-SS | 6 s | Soft | Soft |
| FD Model | 4-Element Model | 6-Element Model | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Frame | System | |||||||||||||
| [Hz] | [m] | [] | [] | [] | [] | [] | [] | [] | [] | [] | [] | |||
| 1H-HH | ||||||||||||||
| 1H | 1H-SH | |||||||||||||
| (0.01 H) | 1H-HS | |||||||||||||
| 1H-SS | ||||||||||||||
| 2H-HH | ||||||||||||||
| 2H | 2H-SH | |||||||||||||
| (0.02 H) | 2H-HS | |||||||||||||
| 2H-SS | ||||||||||||||
| 3H-HH | ||||||||||||||
| 3H | 3H-SH | |||||||||||||
| (0.03 H) | 3H-HS | |||||||||||||
| 3H-SS | ||||||||||||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sato, D.; Chang, T.-W.; Chen, Y. Effects of Different Frequency Sensitivity Models of a Viscoelastic Damper on Wind-Induced Response of High-Rise Buildings. Buildings 2022, 12, 2182. https://doi.org/10.3390/buildings12122182
Sato D, Chang T-W, Chen Y. Effects of Different Frequency Sensitivity Models of a Viscoelastic Damper on Wind-Induced Response of High-Rise Buildings. Buildings. 2022; 12(12):2182. https://doi.org/10.3390/buildings12122182
Chicago/Turabian StyleSato, Daiki, Ting-Wei Chang, and Yinli Chen. 2022. "Effects of Different Frequency Sensitivity Models of a Viscoelastic Damper on Wind-Induced Response of High-Rise Buildings" Buildings 12, no. 12: 2182. https://doi.org/10.3390/buildings12122182
APA StyleSato, D., Chang, T.-W., & Chen, Y. (2022). Effects of Different Frequency Sensitivity Models of a Viscoelastic Damper on Wind-Induced Response of High-Rise Buildings. Buildings, 12(12), 2182. https://doi.org/10.3390/buildings12122182







