Building Energy Models at Different Time Scales Based on Multi-Output Machine Learning
Abstract
1. Introduction
- (1)
- This study compares the predictive performance of single-output and multi-output learning models in building energy analysis. This would provide guidelines on how to choose the single-output and multi-output models in creating machine learning models for building energy assessment.
- (2)
- This study explores the performance of two multi-output models (BASS and DNN) in which the main difference of the two models is whether to maintain output correlation. This would provide the guidelines on how to choose the learning models with or without considering output correlation.
- (3)
- The additive or accumulative features are investigated in creating various time scale models for building energy analysis. This would provide insight on the methods of obtaining building energy use from a smaller time scale to a larger time scale.
2. Method
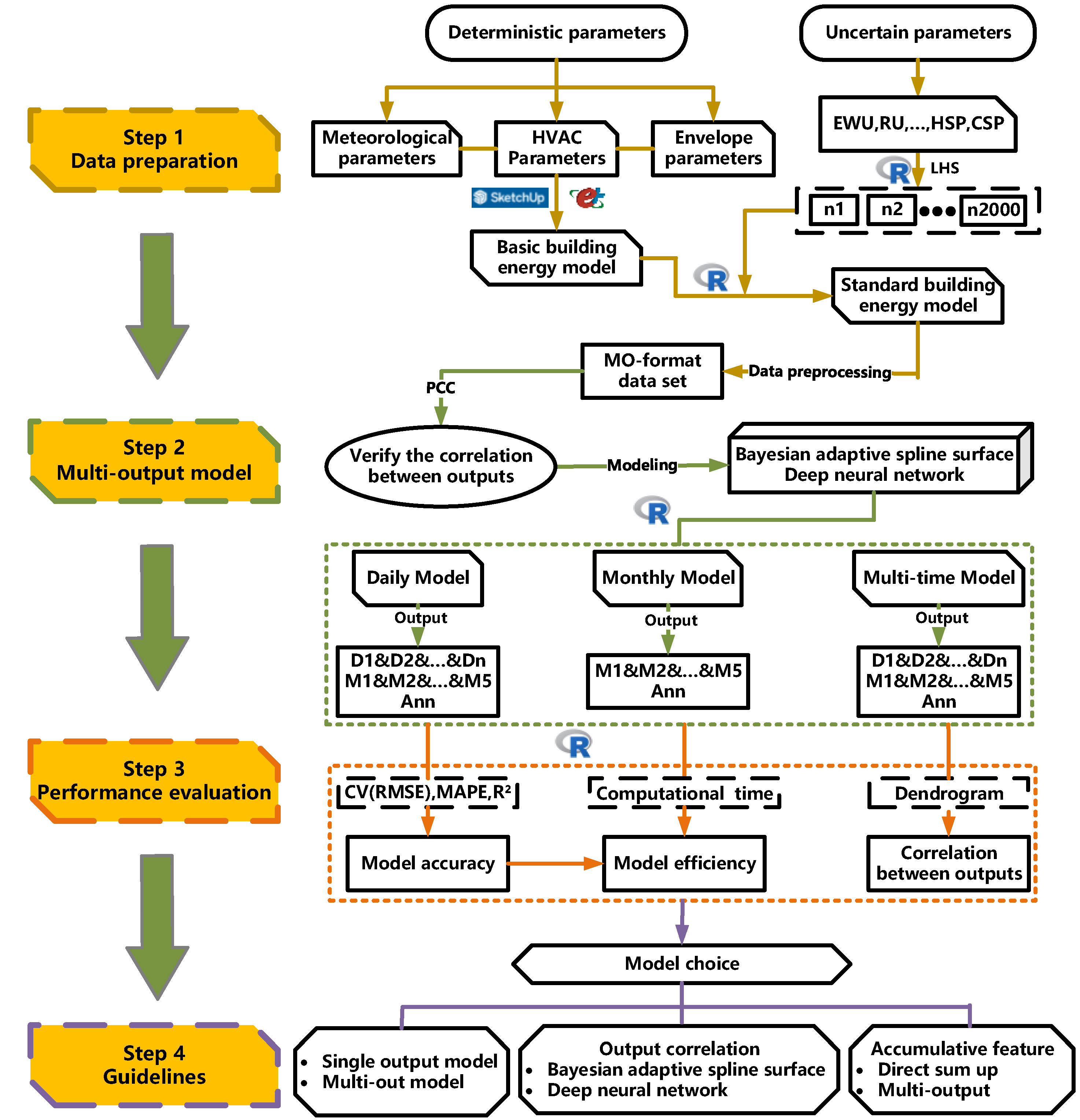
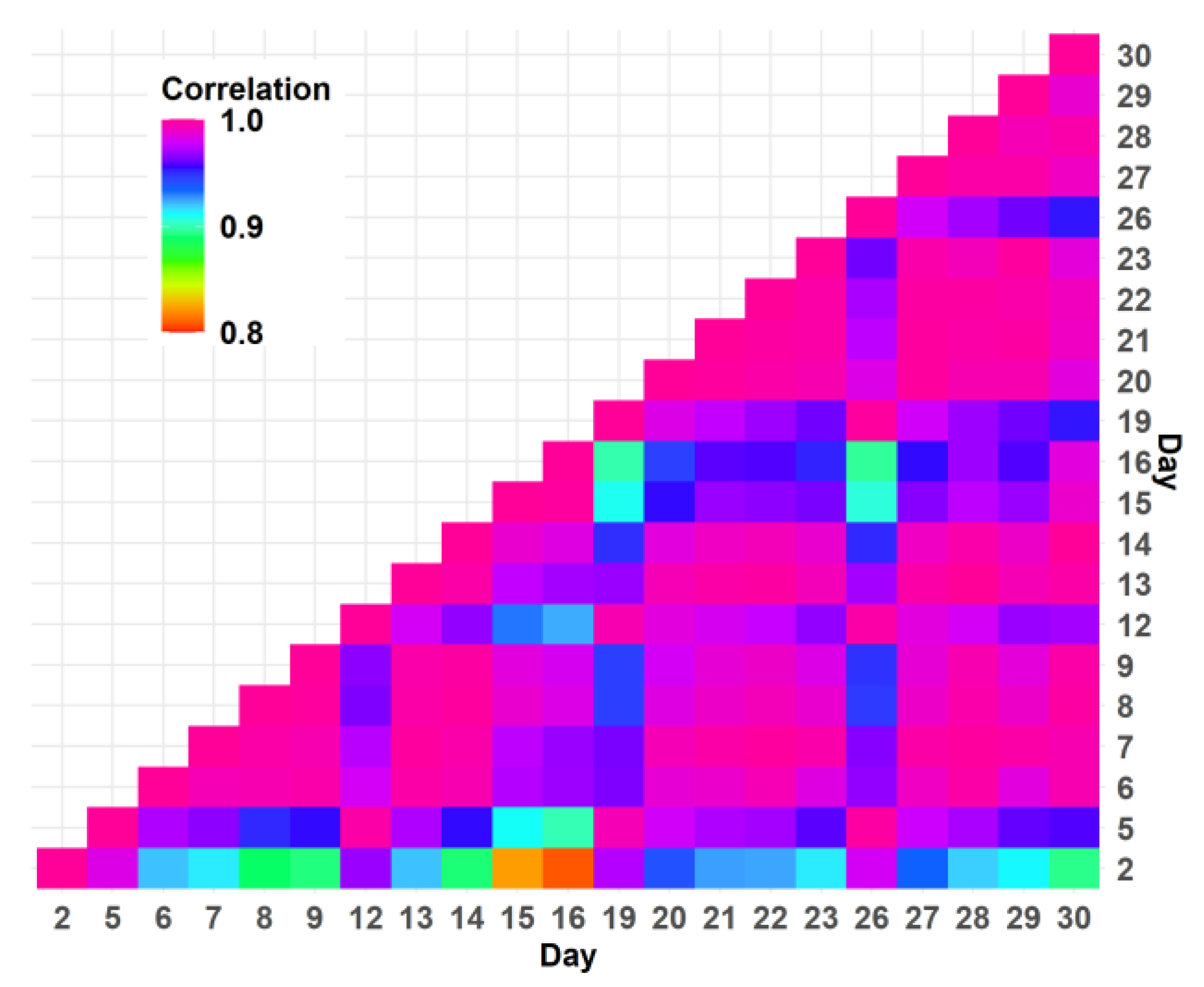
2.1. Data Preparation
2.2. Multi-Output Models
2.3. Performance Evaluation
3. Results and Discussion
3.1. Results of Model Hyperparameter Tuning
3.2. Results of Multi-Output Cooling Energy Models
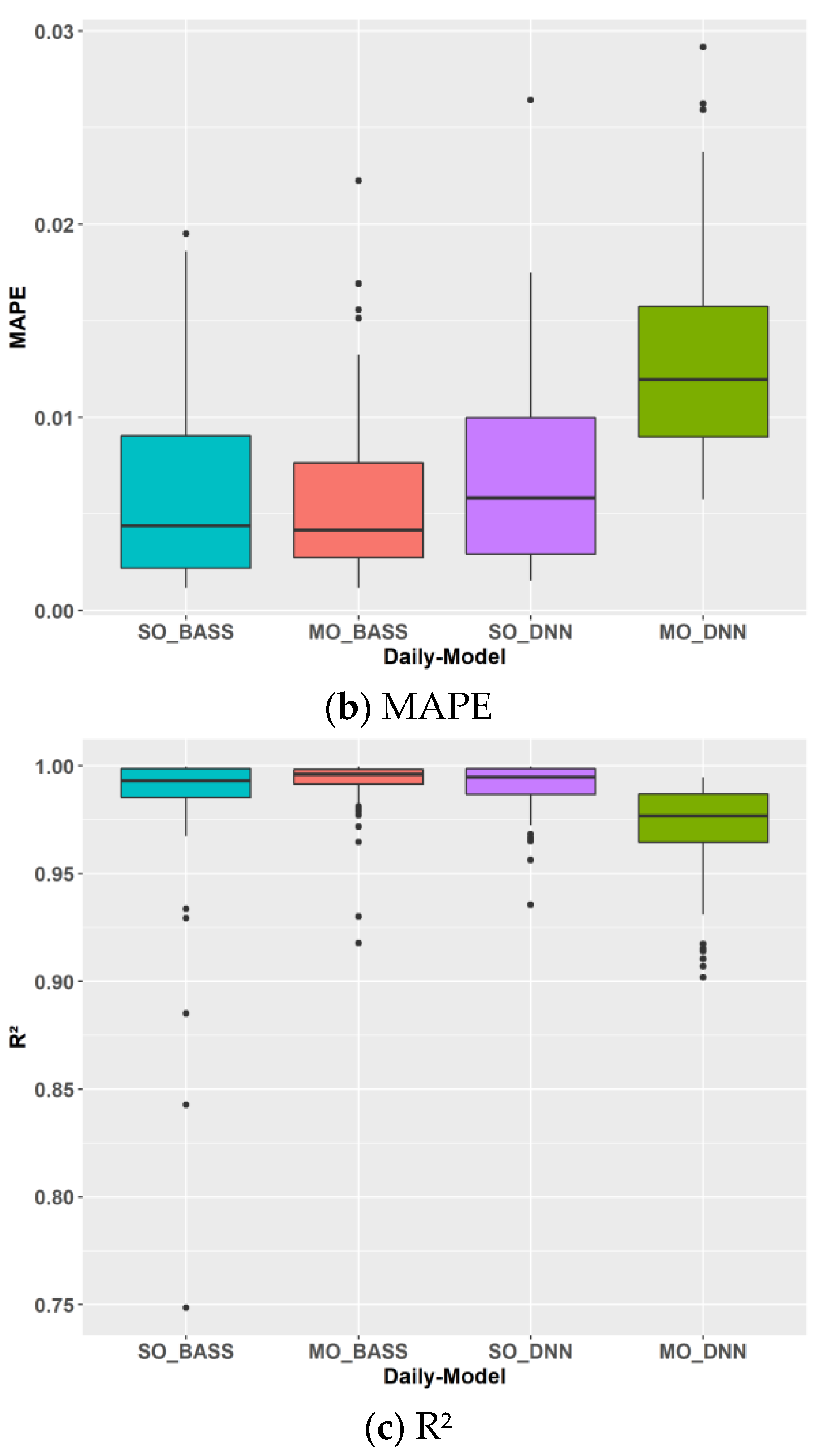
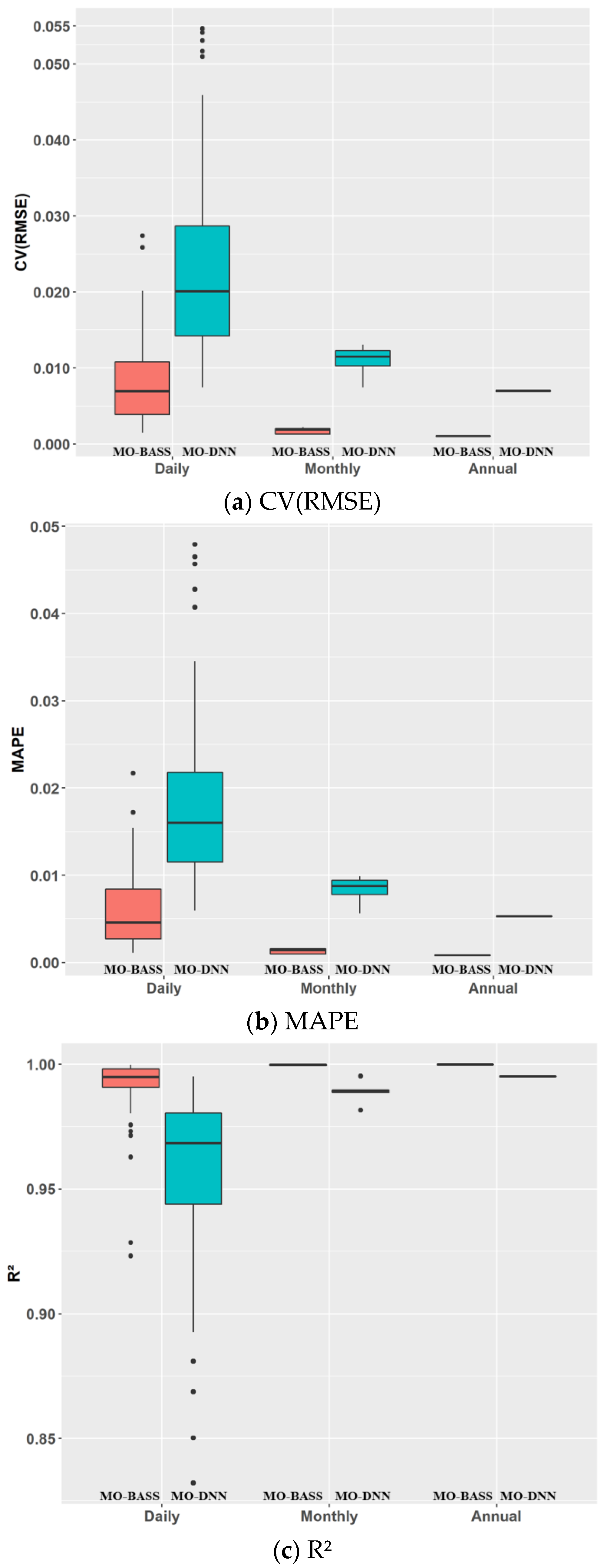
3.2.1. Daily Cooling Energy Models
3.2.2. Monthly Cooling Energy Models
3.2.3. Multi-Time Scale Cooling Energy Models
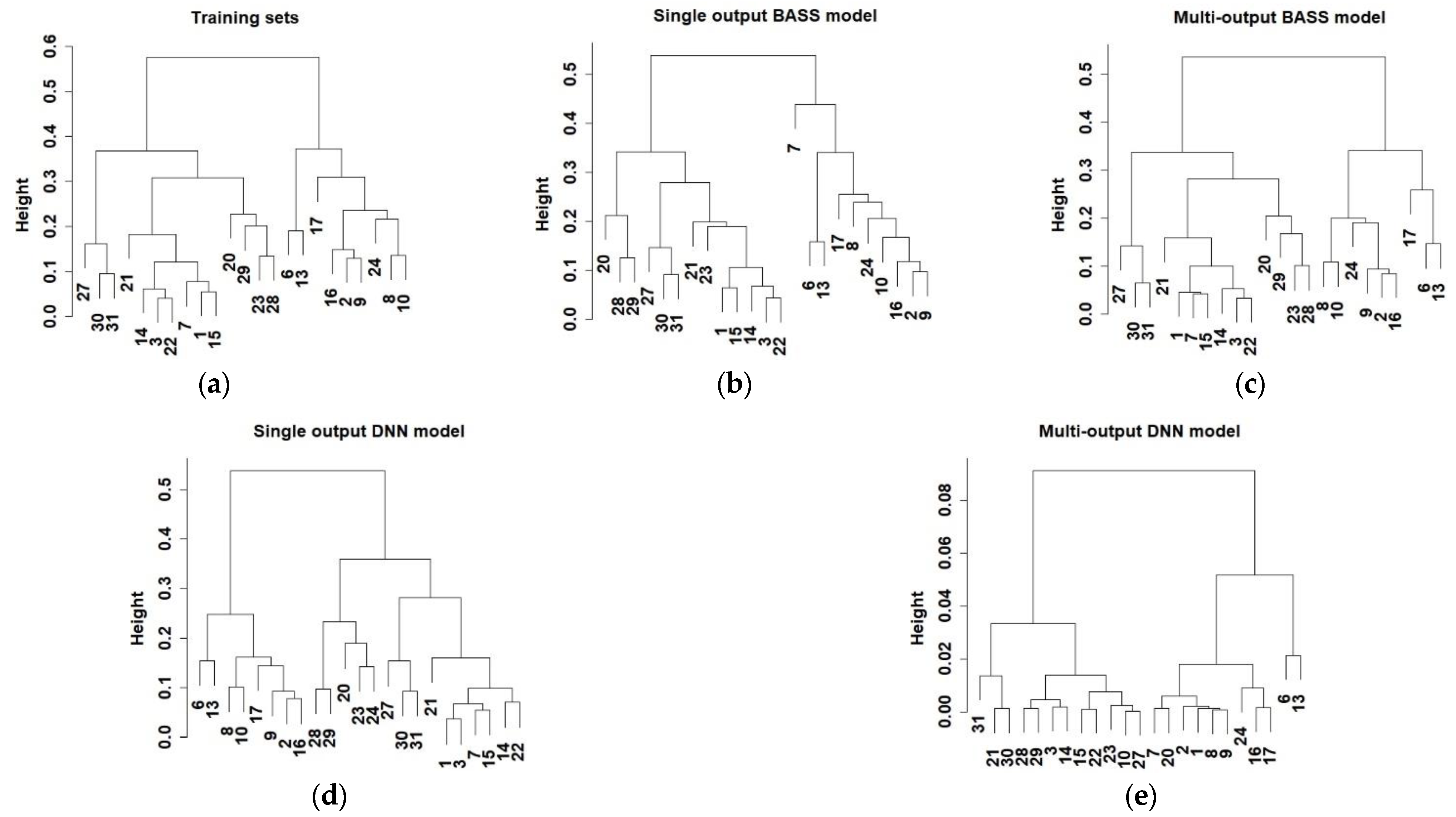
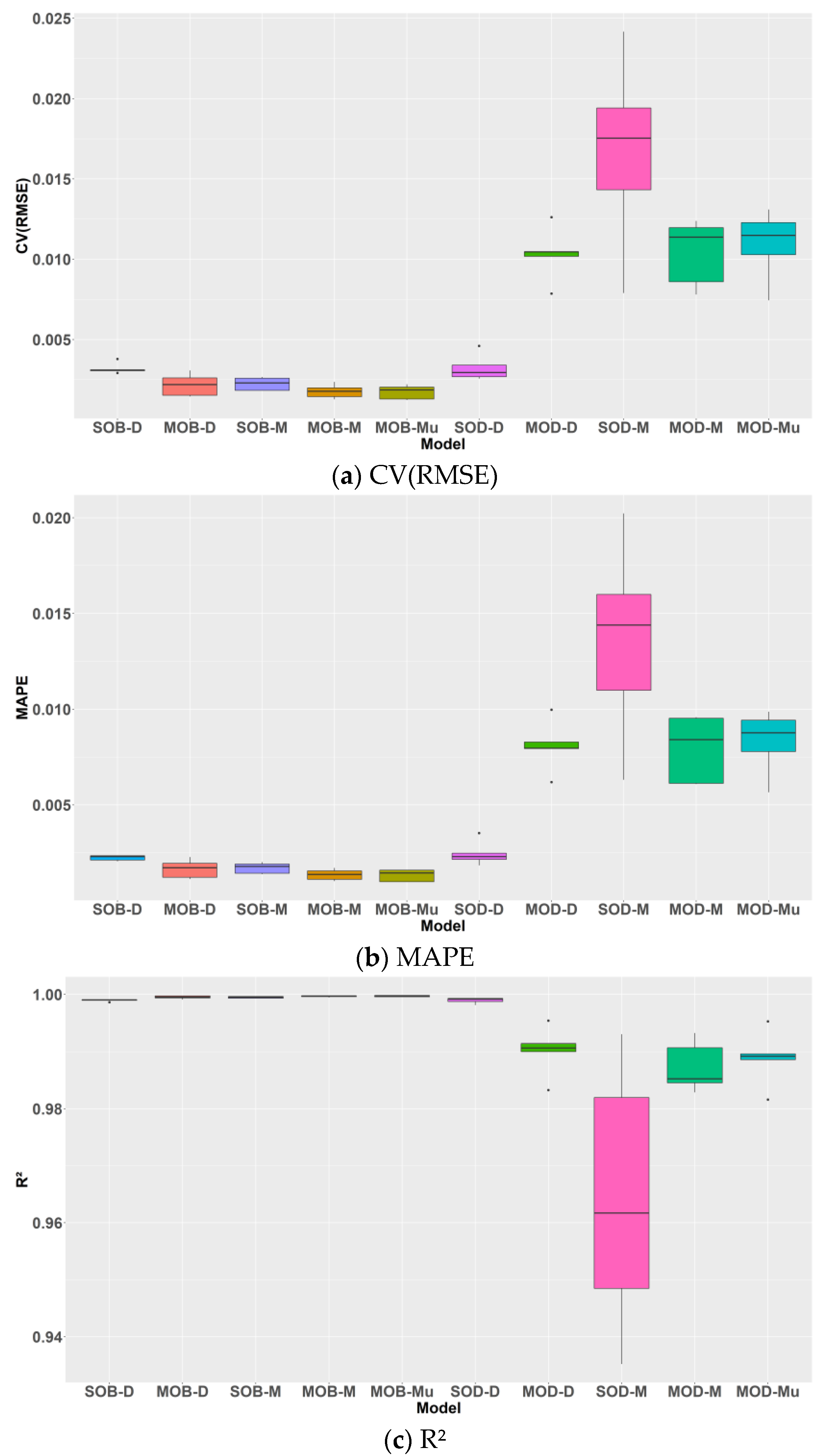
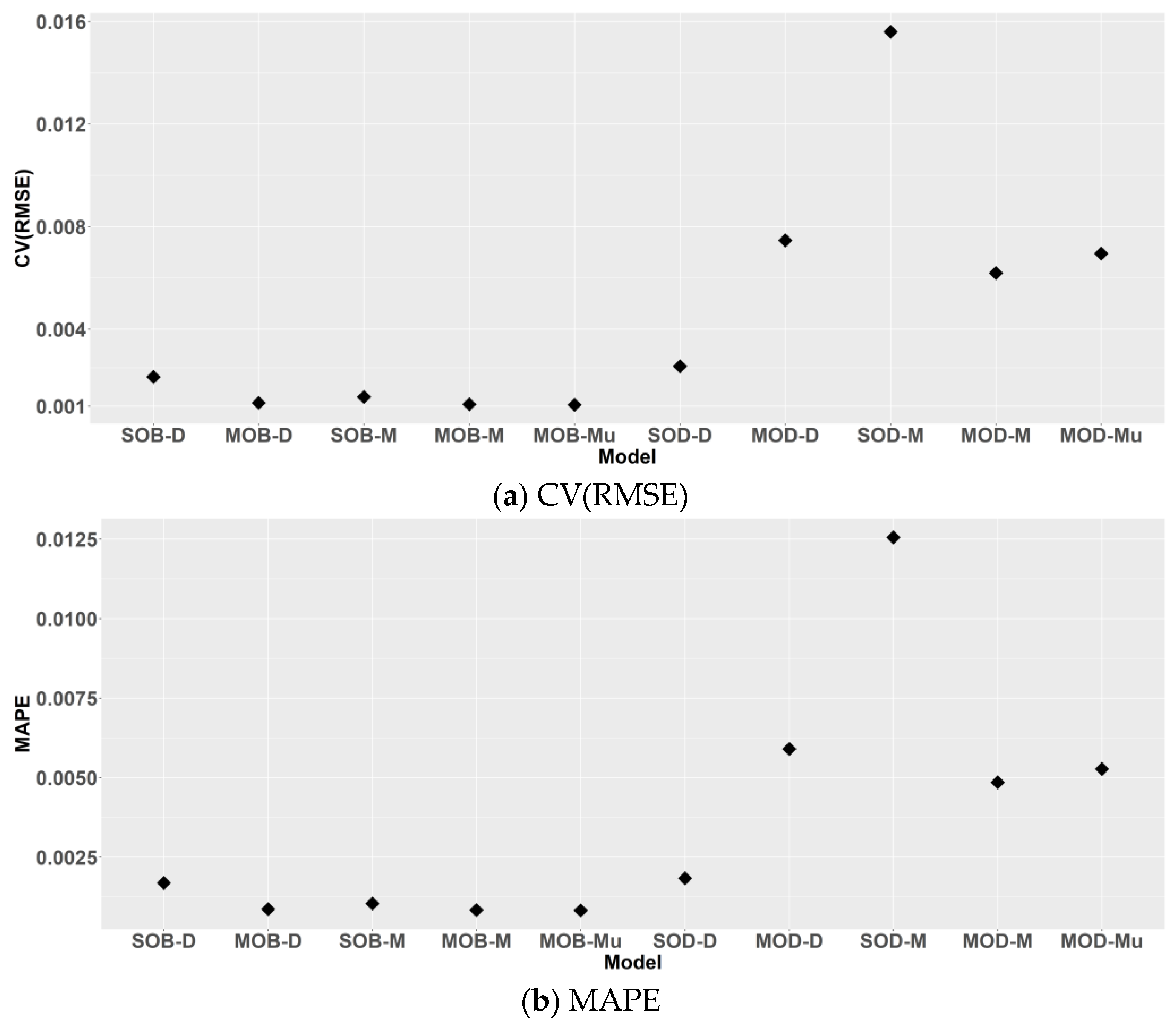
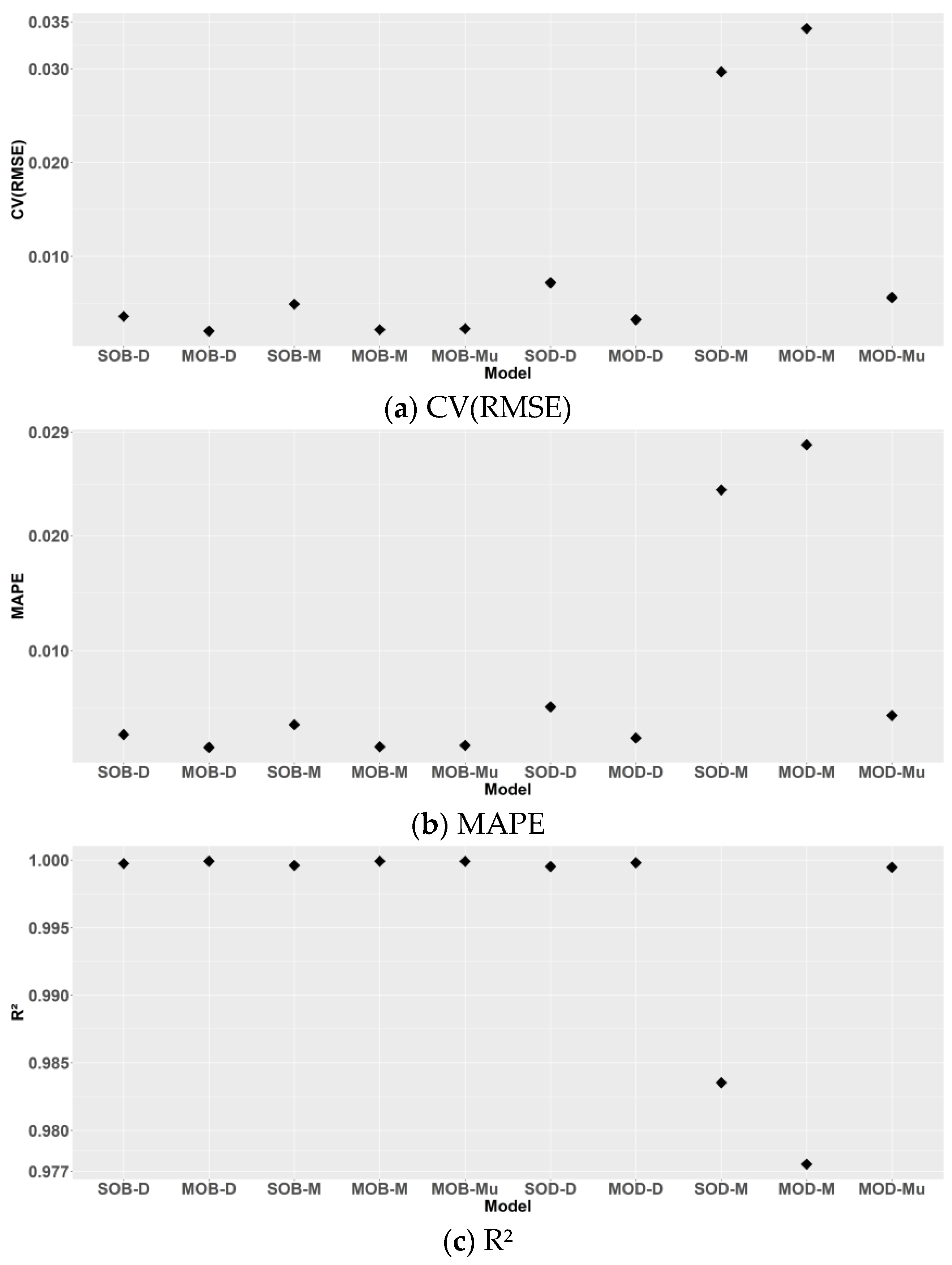
3.2.4. Performance Analysis of 10 Models for Monthly and Annual Cooling Energy
3.3. Results of Multi-Output Heating Energy Models
3.3.1. Daily Heating Energy Models
3.3.2. Monthly Heating Energy Models
3.3.3. Multi-Time Scale Heating Energy Models
3.3.4. Performance Analysis of Ten Models for Monthly and Annual Heating Energy
3.4. Guide and Application of Building Multi-Output Energy Models
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| ANN | artificial neural network |
| BASS | Bayesian adaptive spline surface |
| BIPV | building integrated photovoltaic |
| BMARS | Bayesian multivariate adaptive regression splines |
| CSP | cooling set-point |
| CSWD | Chinese standard weather data |
| CV(RMSE) | coefficient of variation of the root mean square error |
| DNN | deep neural network |
| DT | decision tree |
| ENMIM | ensemble model named evolutionary neural machine inference model |
| EPD | equipment power density |
| EWU | exterior wall U-value |
| GA-NMM | genetic algorithm-based numerical moment matching |
| GB | gradient boosting |
| HSP | heating set-point |
| HVAC | heating, ventilation, and air conditioning |
| INF | infiltration rate |
| KNN | K-nearest neighbor |
| lightGBM | light gradient boosting machine |
| LPD | lighting power density |
| LR | linear regression |
| LSSVR | least squares support vector regression |
| MAPE | mean absolute percentage error |
| MARS | multivariate adaptive regression splines |
| MIMO | multi-input multi-output |
| MO | multiple outputs |
| OPD | occupancy density |
| PCA | principal component analysis |
| PCC | Pearson’s correlation coefficient |
| PV | photovoltaic |
| R² | coefficient of determination |
| RBFNN | radial basis function neural network |
| RF | random forest |
| RU | roof U-value |
| SARIMA | seasonal autoregressive integrated moving average |
| SHGC | solar heat gain coefficient |
| SO | single output |
| SVM | support vector machine |
| WU | window U-value |
References
- UN Environment Programme (UNEP). 2021 Global Status Report for Buildings and Construction; UNEP: Nairobi, Kenya, 2021. [Google Scholar]
- Zhang, Y.; Teoh, B.K.; Wu, M.; Chen, J.; Zhang, L. Data-driven estimation of building energy consumption and GHG emissions using explainable artificial intelligence. Energy 2023, 262, 125468. [Google Scholar] [CrossRef]
- Al-Shargabi, A.A.; Almhafdy, A.; Ibrahim, D.M.; Alghieth, M.; Chiclana, F. Buildings’ energy consumption prediction models based on buildings’ characteristics: Research trends, taxonomy, and performance measures. J. Build. Eng. 2022, 54, 104577. [Google Scholar] [CrossRef]
- Guo, Y.-Y. Revisiting the building energy consumption in China: Insights from a large-scale national survey. Energy Sustain. Dev. 2022, 68, 76–93. [Google Scholar] [CrossRef]
- Mohapatra, S.K.; Mishra, S.; Tripathy, H.K.; Alkhayyat, A. A sustainable data-driven energy consumption assessment model for building infrastructures in resource constraint environment. Sustain. Energy Technol. Assess. 2022, 53, 102697. [Google Scholar] [CrossRef]
- Fathi, S.; Srinivasan, R.; Fenner, A.; Fathi, S. Machine learning applications in urban building energy performance forecasting: A systematic review. Renew. Sustain. Energy Rev. 2020, 133, 110287. [Google Scholar] [CrossRef]
- Zhang, L.; Wen, J.; Li, Y.; Chen, J.; Ye, Y.; Fu, Y.; Livingood, W. A review of machine learning in building load prediction. Appl. Energy 2021, 285, 116452. [Google Scholar] [CrossRef]
- Lei, L.; Chen, W.; Wu, B.; Chen, C.; Liu, W. A building energy consumption prediction model based on rough set theory and deep learning algorithms. Energy Build. 2021, 240, 110886. [Google Scholar] [CrossRef]
- Liu, Y.; Chen, H.; Zhang, L.; Wu, X.; Wang, X.-J. Energy consumption prediction and diagnosis of public buildings based on support vector machine learning: A case study in China. J. Clean. Prod. 2020, 272, 122542. [Google Scholar] [CrossRef]
- Alobaidi, M.H.; Chebana, F.; Meguid, M.A. Robust ensemble learning framework for day-ahead forecasting of household based energy consumption. Appl. Energy 2018, 212, 997–1012. [Google Scholar] [CrossRef]
- Wang, Z.; Hong, T.; Li, H.; Piette, M.A. Predicting city-scale daily electricity consumption using data-driven models. Adv. Appl. Energy 2021, 2, 100025. [Google Scholar] [CrossRef]
- Jetcheva, J.G.; Majidpour, M.; Chen, W.-P. Neural network model ensembles for building-level electricity load forecasts. Energy Build. 2014, 84, 214–223. [Google Scholar] [CrossRef]
- Ferrantelli, A.; Kuivjogi, H.; Kurnitski, J.; Thalfeldt, M. Office Building Tenants’ Electricity Use Model for Building Performance Simulations. Energies 2020, 13, 5541. [Google Scholar] [CrossRef]
- Wang, W.; Hong, T.; Xu, X.; Chen, J.; Liu, Z.; Xu, N. Forecasting district-scale energy dynamics through integrating building network and long short-term memory learning algorithm. Appl. Energy 2019, 248, 217–230. [Google Scholar] [CrossRef]
- Tran, D.-H.; Luong, D.-L.; Chou, J.-S. Nature-inspired metaheuristic ensemble model for forecasting energy consumption in residential buildings. Energy 2020, 191, 116552. [Google Scholar] [CrossRef]
- Tian, W.; Yang, S.; Li, Z.; Wei, S.; Pan, W.; Liu, Y. Identifying informative energy data in Bayesian calibration of building energy models. Energy Build. 2016, 119, 363–376. [Google Scholar] [CrossRef]
- Zhu, C.; Tian, W.; Yin, B.; Li, Z.; Shi, J. Uncertainty calibration of building energy models by combining approximate Bayesian computation and machine learning algorithms. Appl. Energy 2020, 268, 115025. [Google Scholar] [CrossRef]
- Koschwitz, D.; Frisch, J.; van Treeck, C. Data-driven heating and cooling load predictions for non-residential buildings based on support vector machine regression and NARX Recurrent Neural Network: A comparative study on district scale. Energy 2018, 165, 134–142. [Google Scholar] [CrossRef]
- Jahani, E.; Cetin, K.; Cho, I.H. City-scale single family residential building energy consumption prediction using genetic algorithm-based Numerical Moment Matching technique. Build. Environ. 2020, 172, 106667. [Google Scholar] [CrossRef]
- Lin, Q.; Liu, K.; Hong, B.; Xu, X.; Chen, J.; Wang, W. A data-driven framework for abnormally high building energy demand detection with weather and block morphology at community scale. J. Clean. Prod. 2022, 354, 131602. [Google Scholar] [CrossRef]
- Olu-Ajayi, R.; Alaka, H.; Sulaimon, I.; Sunmola, F.; Ajayi, S. Building energy consumption prediction for residential buildings using deep learning and other machine learning techniques. J. Build. Eng. 2022, 45, 103406. [Google Scholar] [CrossRef]
- Tian, W.; Zhu, C.; Sun, Y.; Li, Z.; Yin, B. Energy characteristics of urban buildings: Assessment by machine learning. Build. Simul. 2020, 14, 179–193. [Google Scholar] [CrossRef]
- Tian, W.; de Wilde, P.; Li, Z.; Song, J.; Yin, B. Uncertainty and sensitivity analysis of energy assessment for office buildings based on Dempster-Shafer theory. Energy Convers. Manag. 2018, 174, 705–718. [Google Scholar] [CrossRef]
- Wang, L.; Lee, E.W.M.; Hussian, S.A.; Yuen, A.C.Y.; Feng, W. Quantitative impact analysis of driving factors on annual residential building energy end-use combining machine learning and stochastic methods. Appl. Energy 2021, 299, 117303. [Google Scholar] [CrossRef]
- Singh, M.; Sharston, R. Quantifying the dualistic nature of urban heat Island effect (UHI) on building energy consumption. Energy Build. 2022, 255, 111649. [Google Scholar] [CrossRef]
- Luo, X.J.; Oyedele, L.O.; Ajayi, A.O.; Akinade, O.O. Comparative study of machine learning-based multi-objective prediction framework for multiple building energy loads. Sustain. Cities Soc. 2020, 61, 102283. [Google Scholar] [CrossRef]
- Liu, J.; Zhang, Q.; Dong, Z.; Li, X.; Li, G.; Xie, Y.; Li, K. Quantitative evaluation of the building energy performance based on short-term energy predictions. Energy 2021, 223, 120065. [Google Scholar] [CrossRef]
- Li, G.; Li, F.; Ahmad, T.; Liu, J.; Li, T.; Fang, X.; Wu, Y. Performance evaluation of sequence-to-sequence-Attention model for short-term multi-step ahead building energy predictions. Energy 2022, 259, 124915. [Google Scholar] [CrossRef]
- U.S. Department of Energy. EnergyPlus V22.1.0; U.S.Department of Energy: Washington, DA, USA, 2021.
- MOHURD (Ministry of Housing and Urban-Rural Development). China, Energy-Saving Design Standards for Public Buildings; China Building Industry Press: Beijing, China, 2015. [Google Scholar]
- MOHURD (Ministry of Housing and Urban-Rural Development). China, Technical Standards for Near-Zero Energy Buildings; China Building Industry Press: Beijing, China, 2019. [Google Scholar]
- Francom, D.; Sansó, B. BASS: An R Package for Fitting and Performing Sensitivity Analysis of Bayesian Adaptive Spline Surfaces. J. Stat. Softw. 2020, 94, 1–36. [Google Scholar] [CrossRef]
- An, N.; Zhao, W.; Wang, J.; Shang, D.; Zhao, E. Using multi-output feedforward neural network with empirical mode decomposition based signal filtering for electricity demand forecasting. Energy 2013, 49, 279–288. [Google Scholar] [CrossRef]
- Cohen-Addad, V.; Kanade, V.; Mallmann-Trenn, F.; Mathieu, C. Hierarchical Clustering: Objective Functions and Algorithms. J. Acm. 2019, 66, 1–42. [Google Scholar] [CrossRef]
- Kaminskyy, R.; Shakhovska, N.; Kryvinska, N.; Younas, M. Dendrograms-based disclosure method for evaluating cluster analysis in the IoT domain. Comput. Ind. Eng. 2021, 158, 107402. [Google Scholar] [CrossRef]
- Varshney, A.K.; Muhuri, P.K.; Lohani, Q.M.D. PIFHC: The Probabilistic Intuitionistic Fuzzy Hierarchical Clustering Algorithm. Appl. Soft Comput. 2022, 120, 108584. [Google Scholar] [CrossRef]


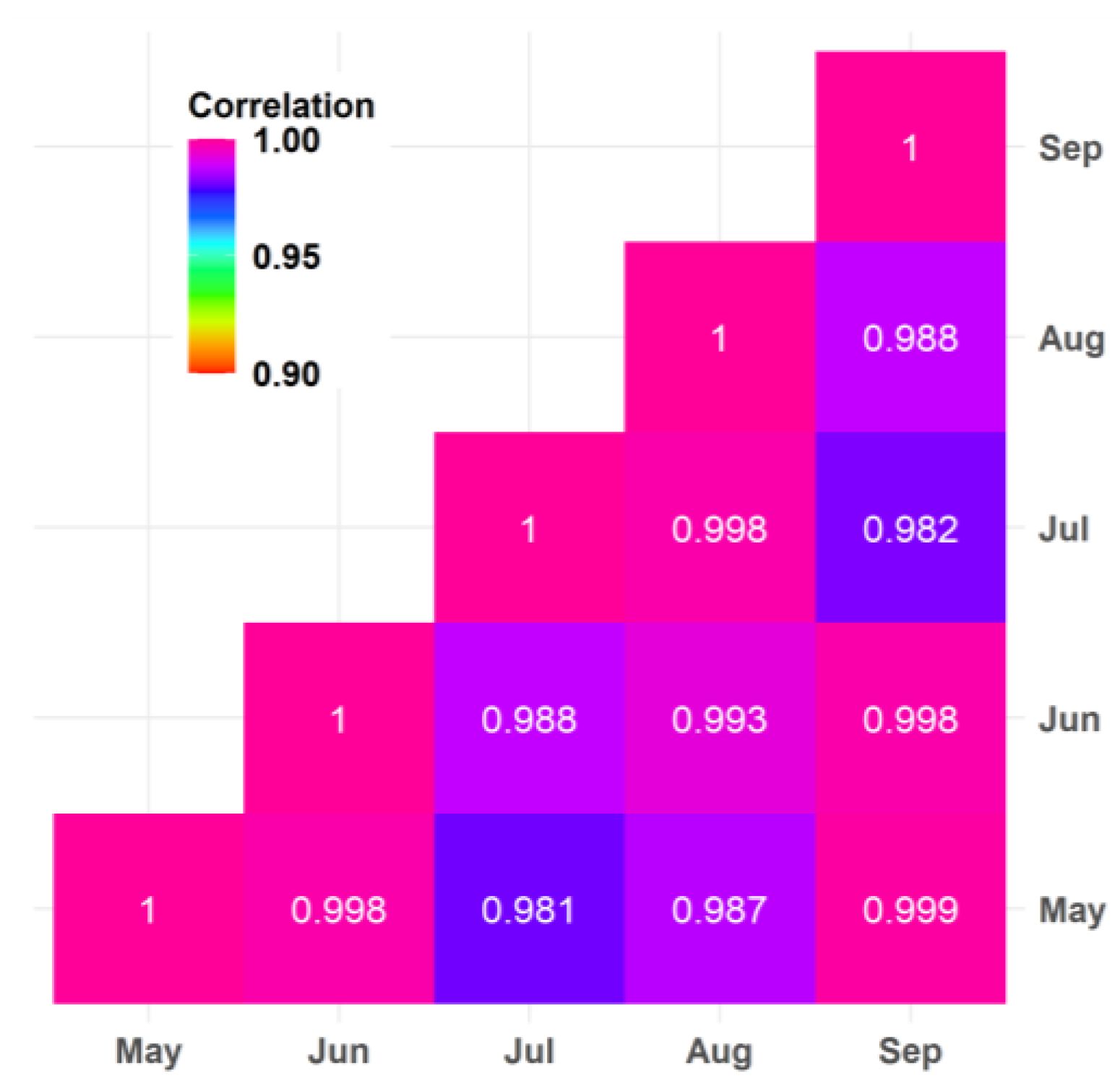
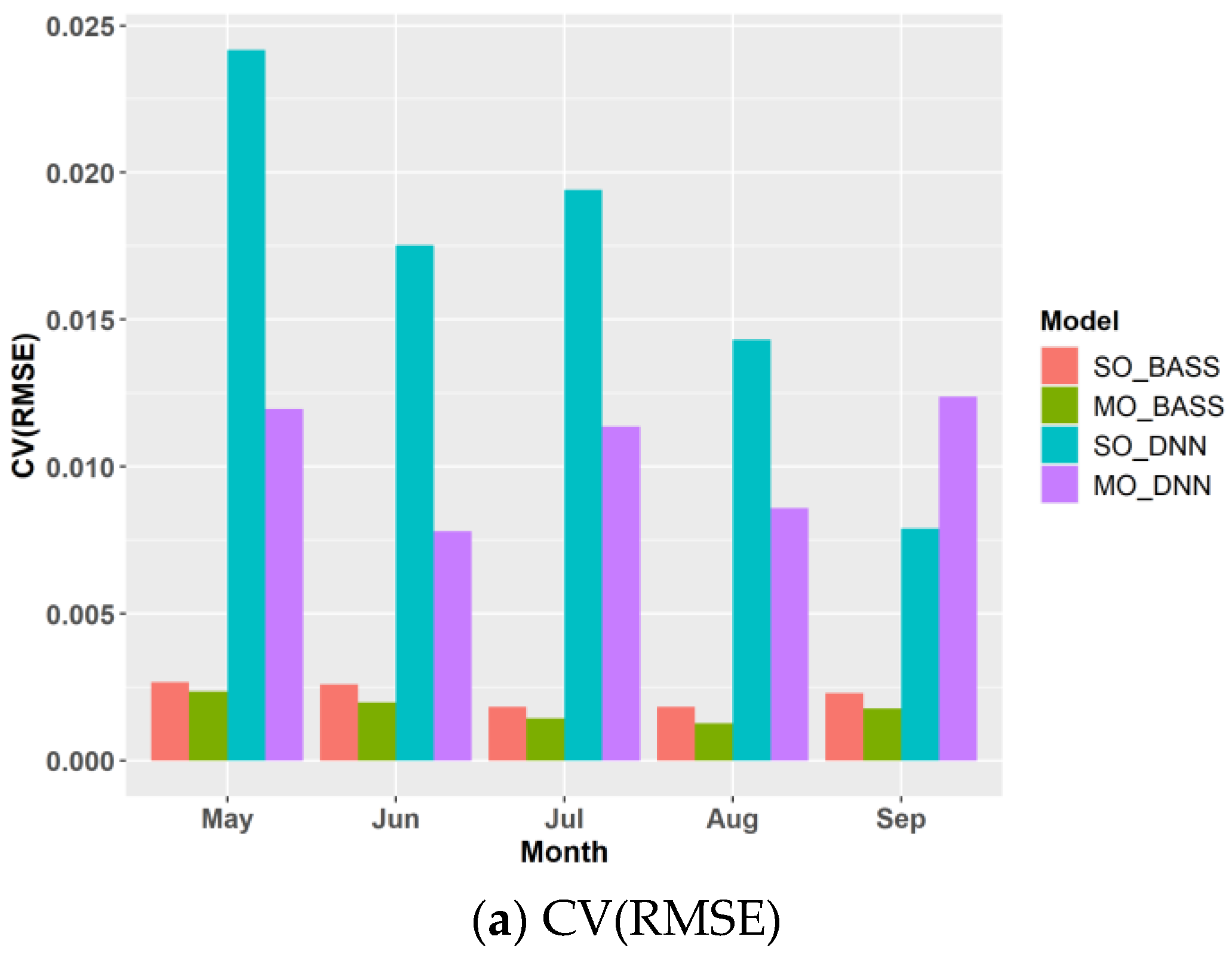
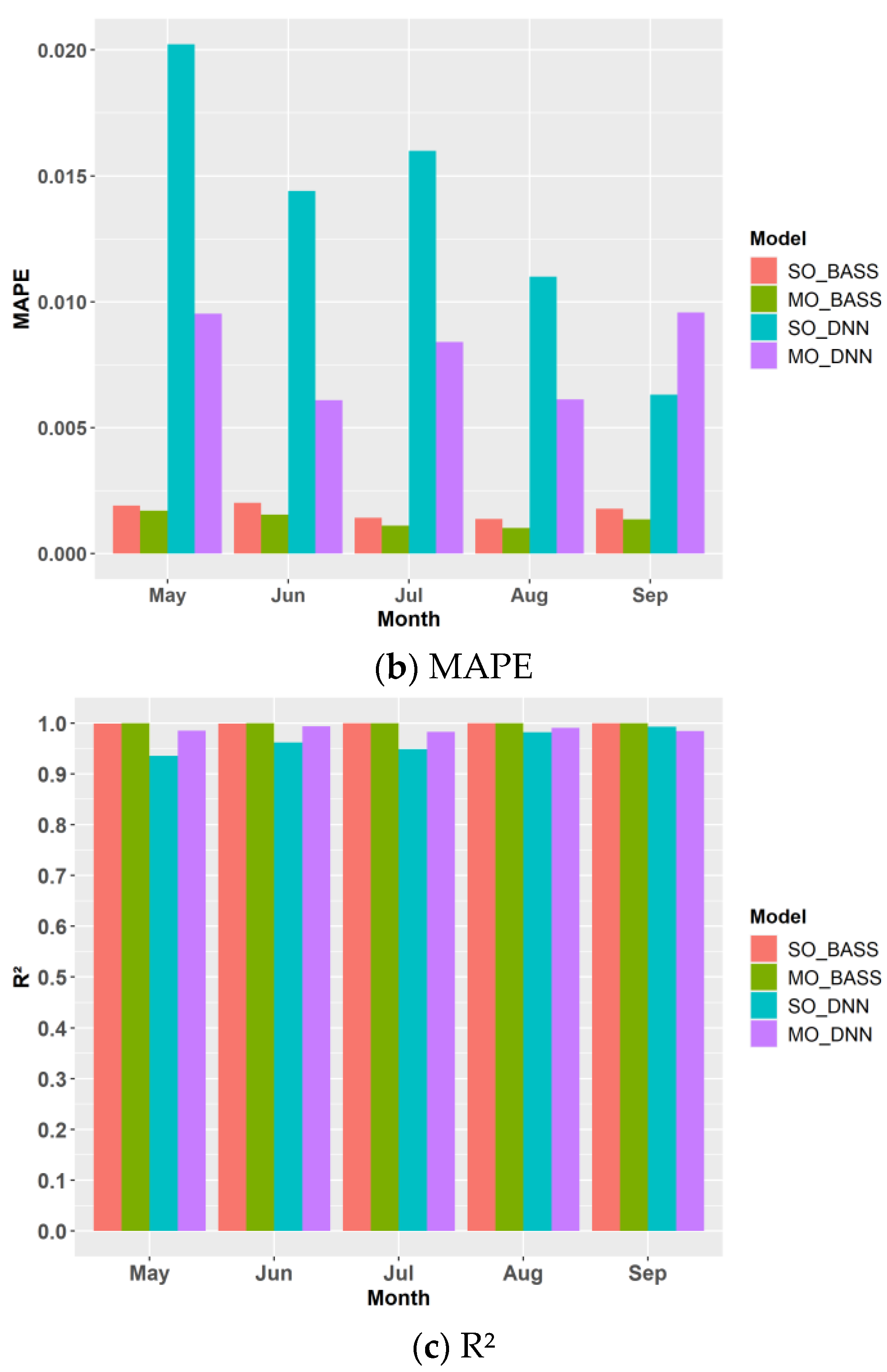
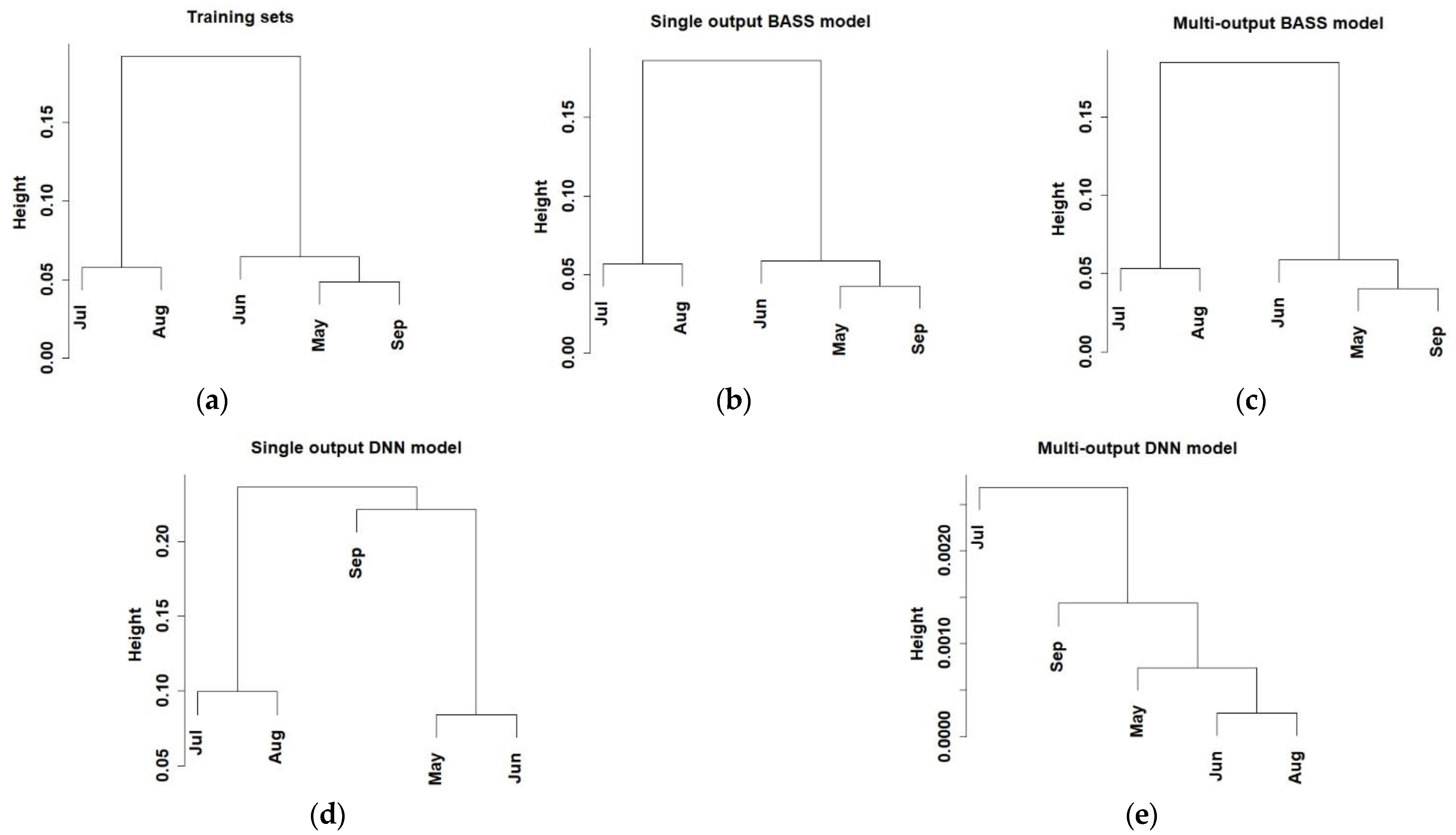

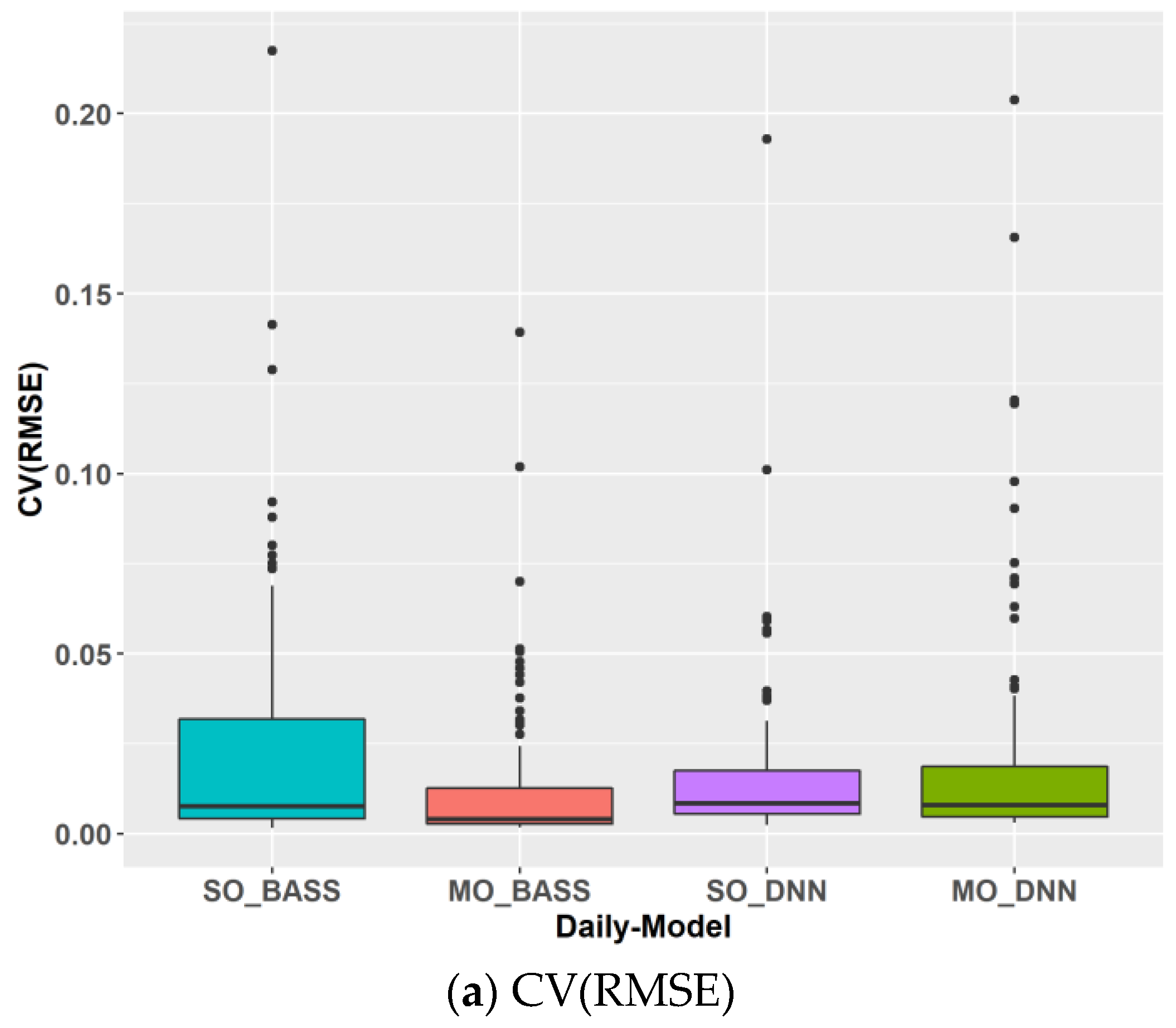
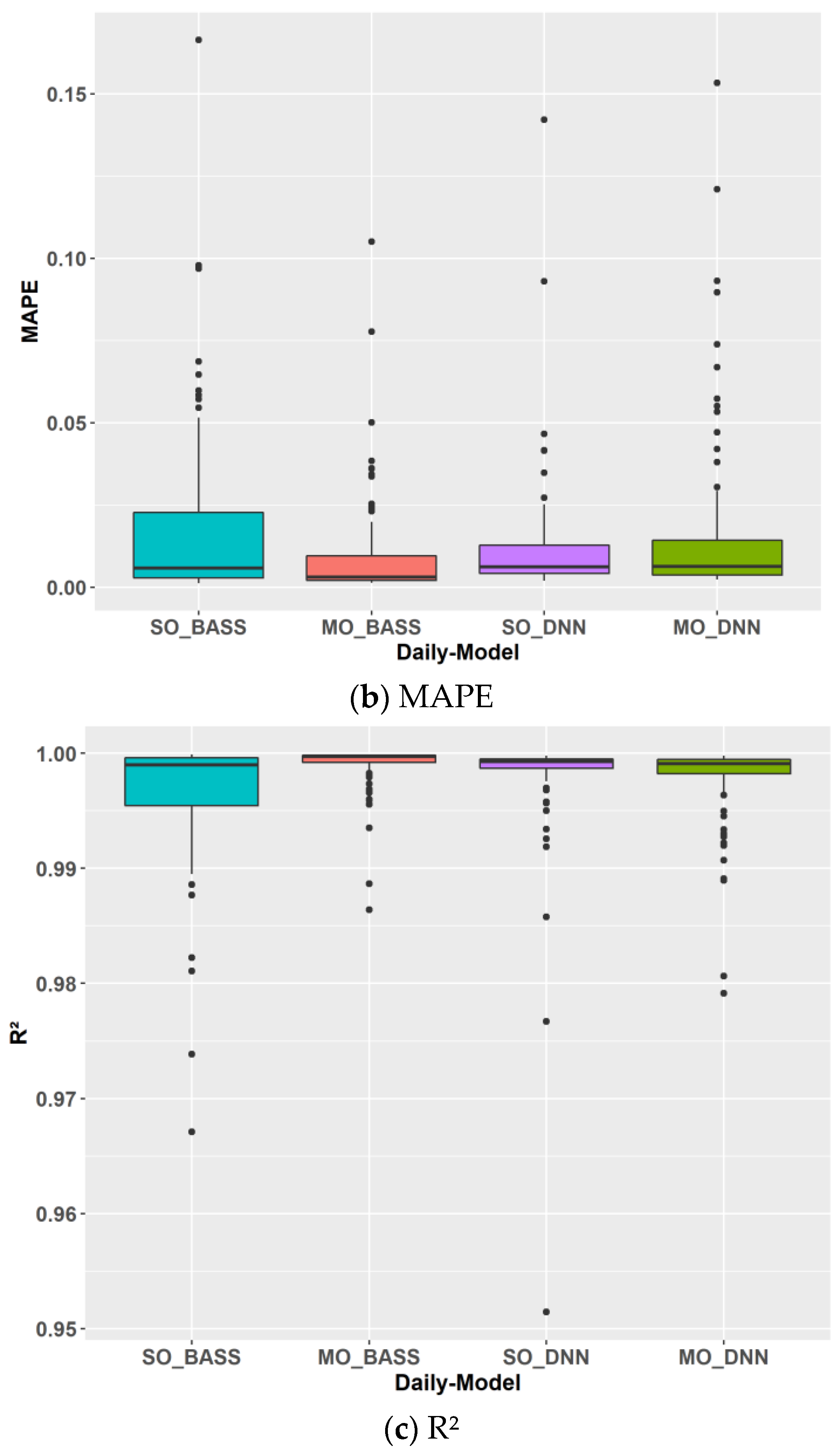
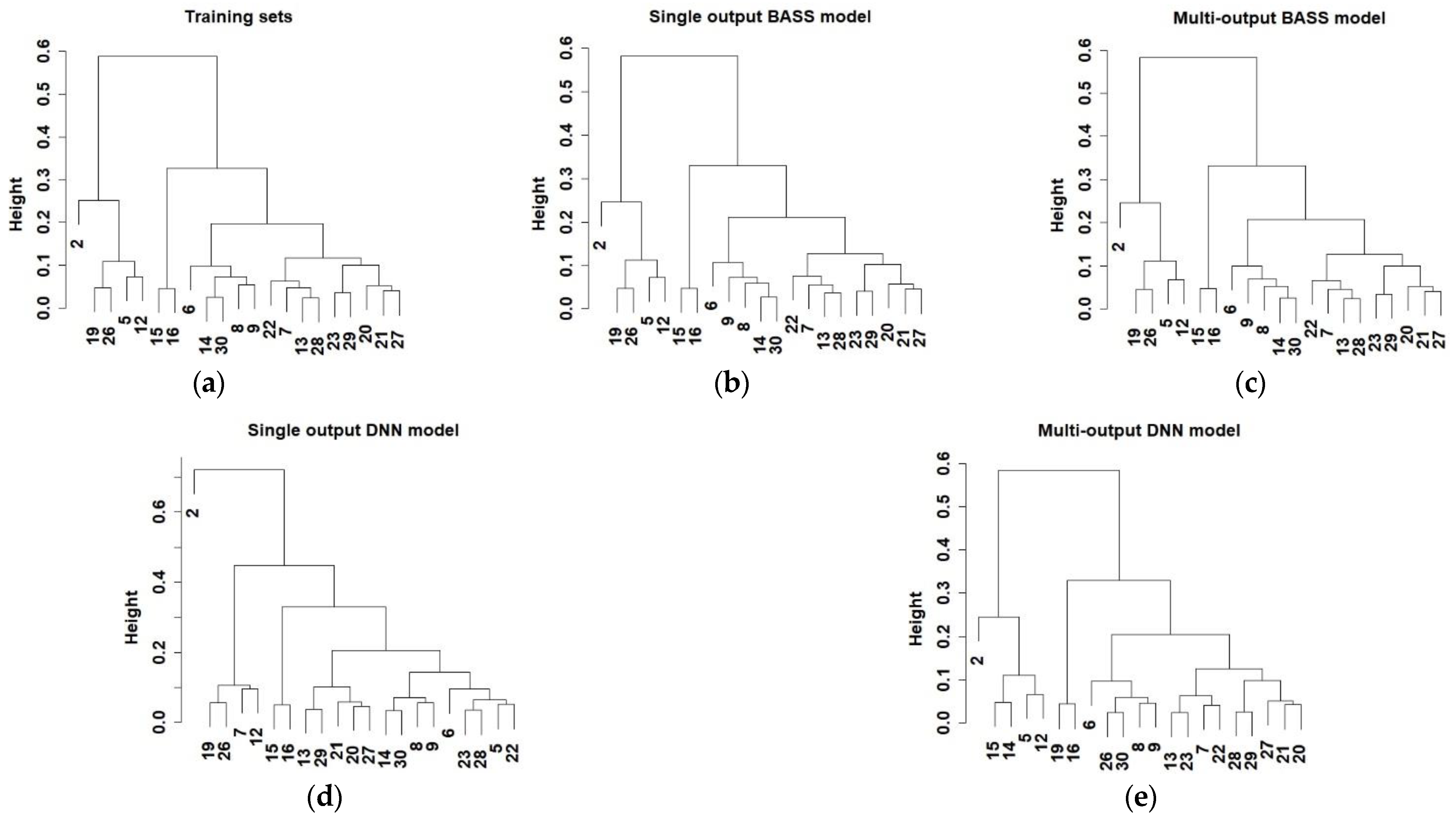
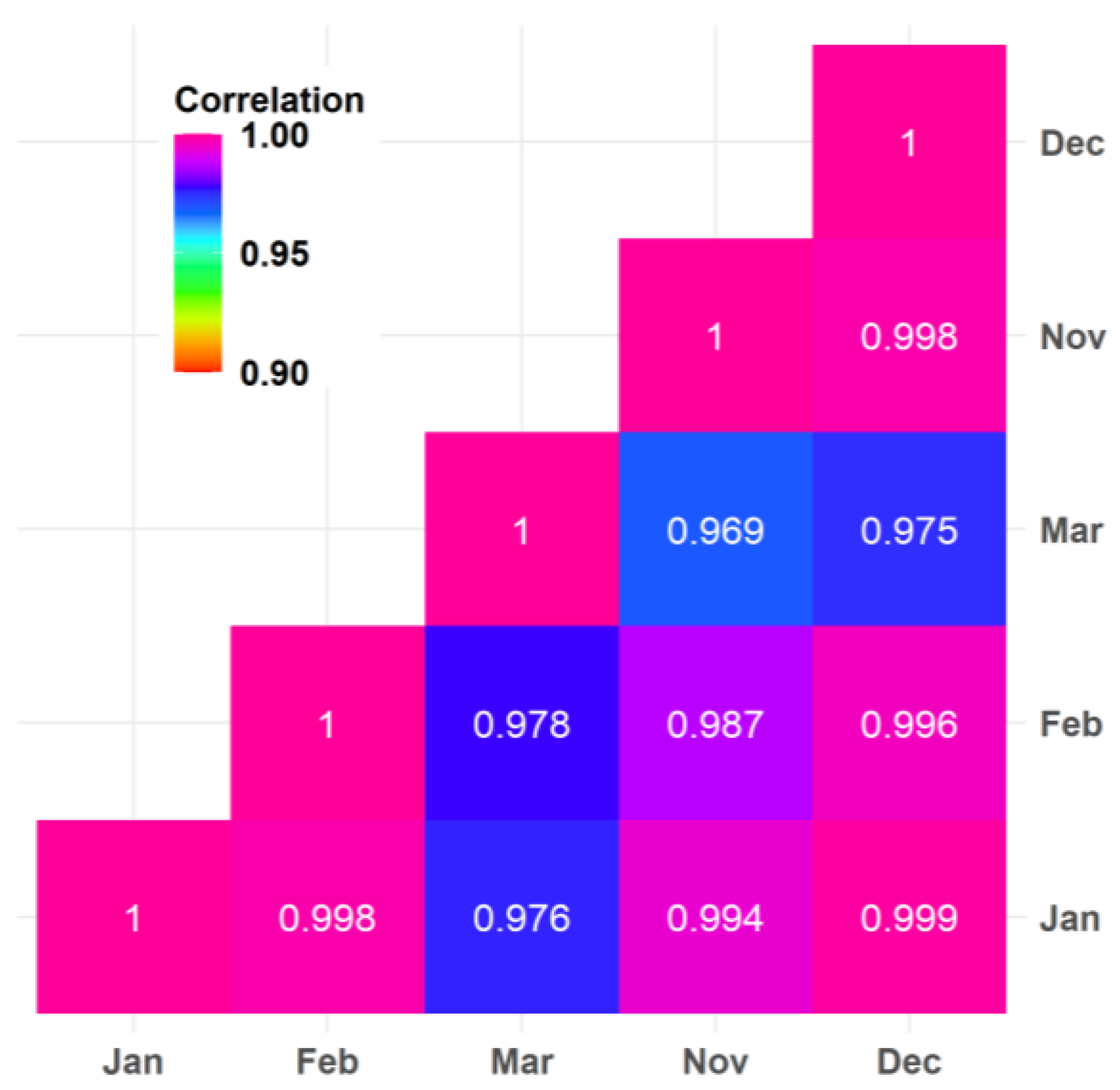

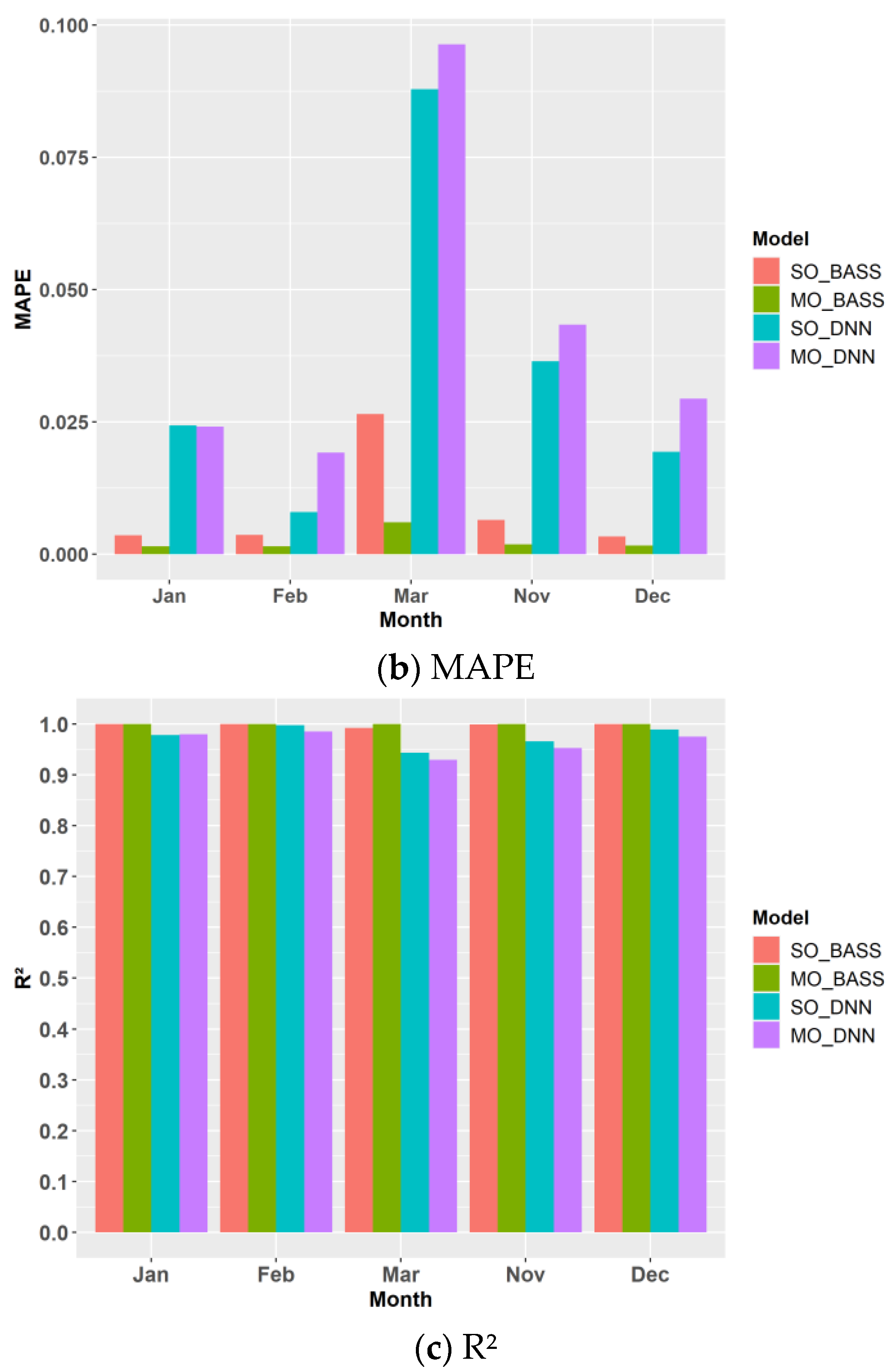
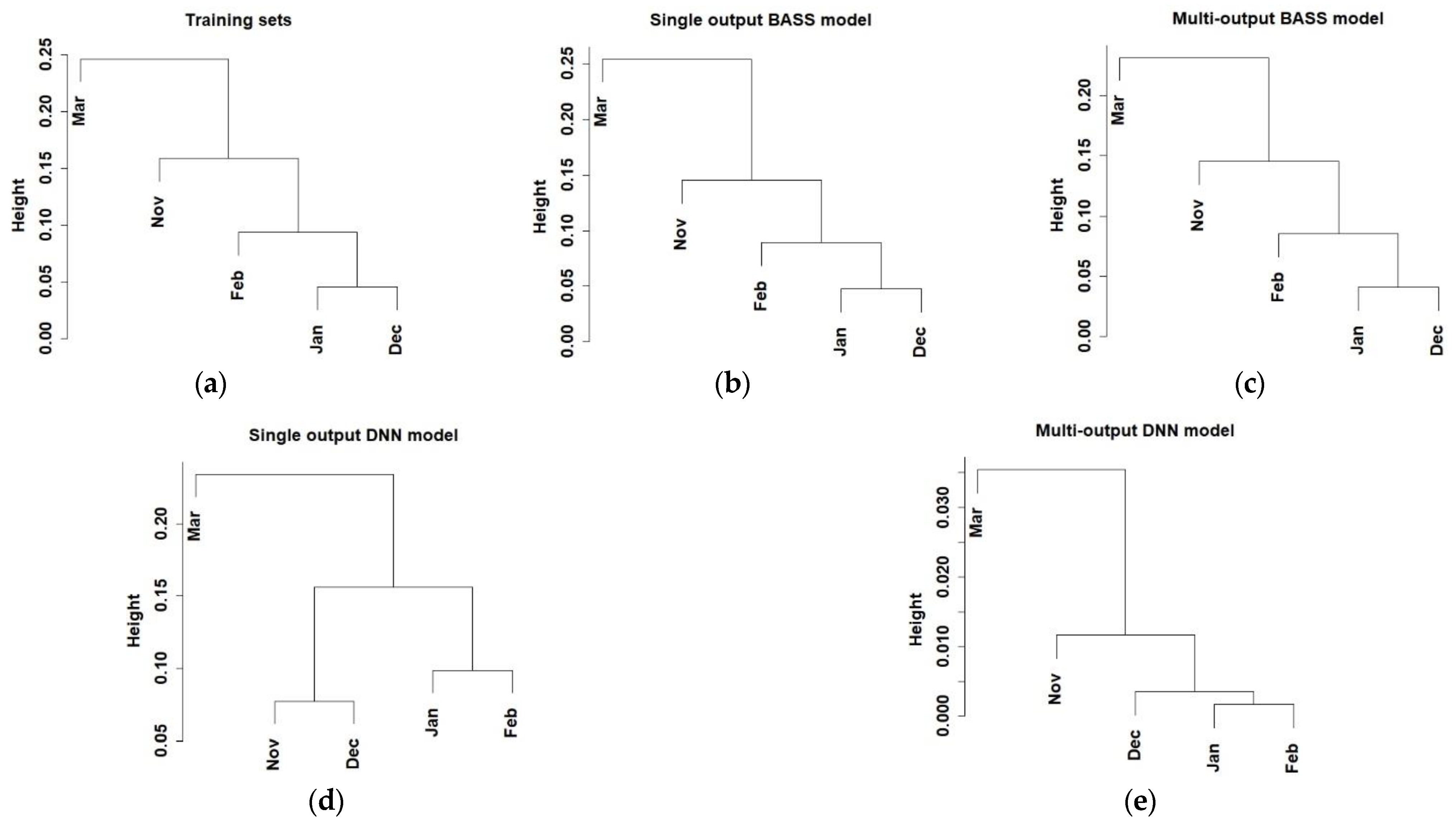
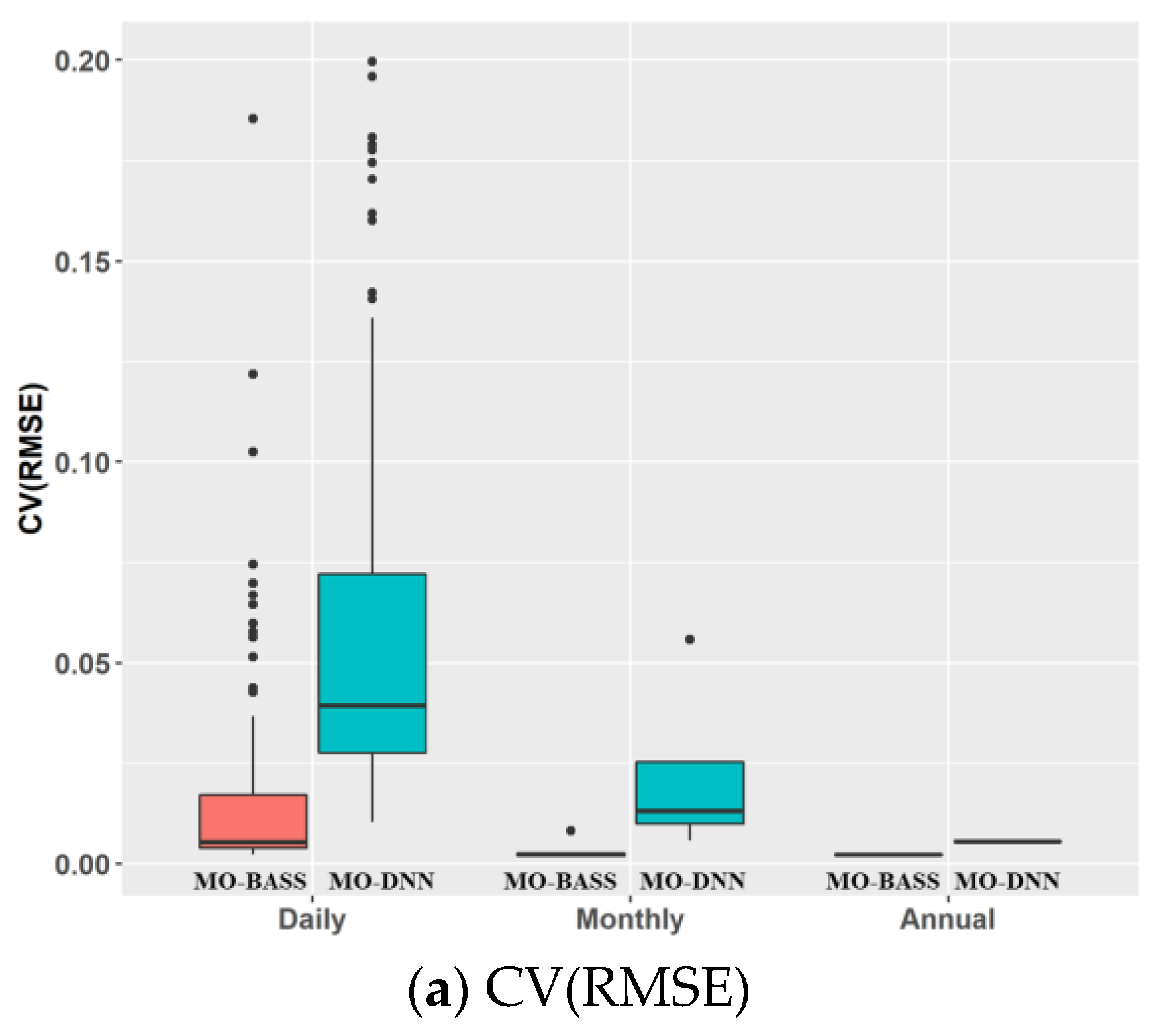
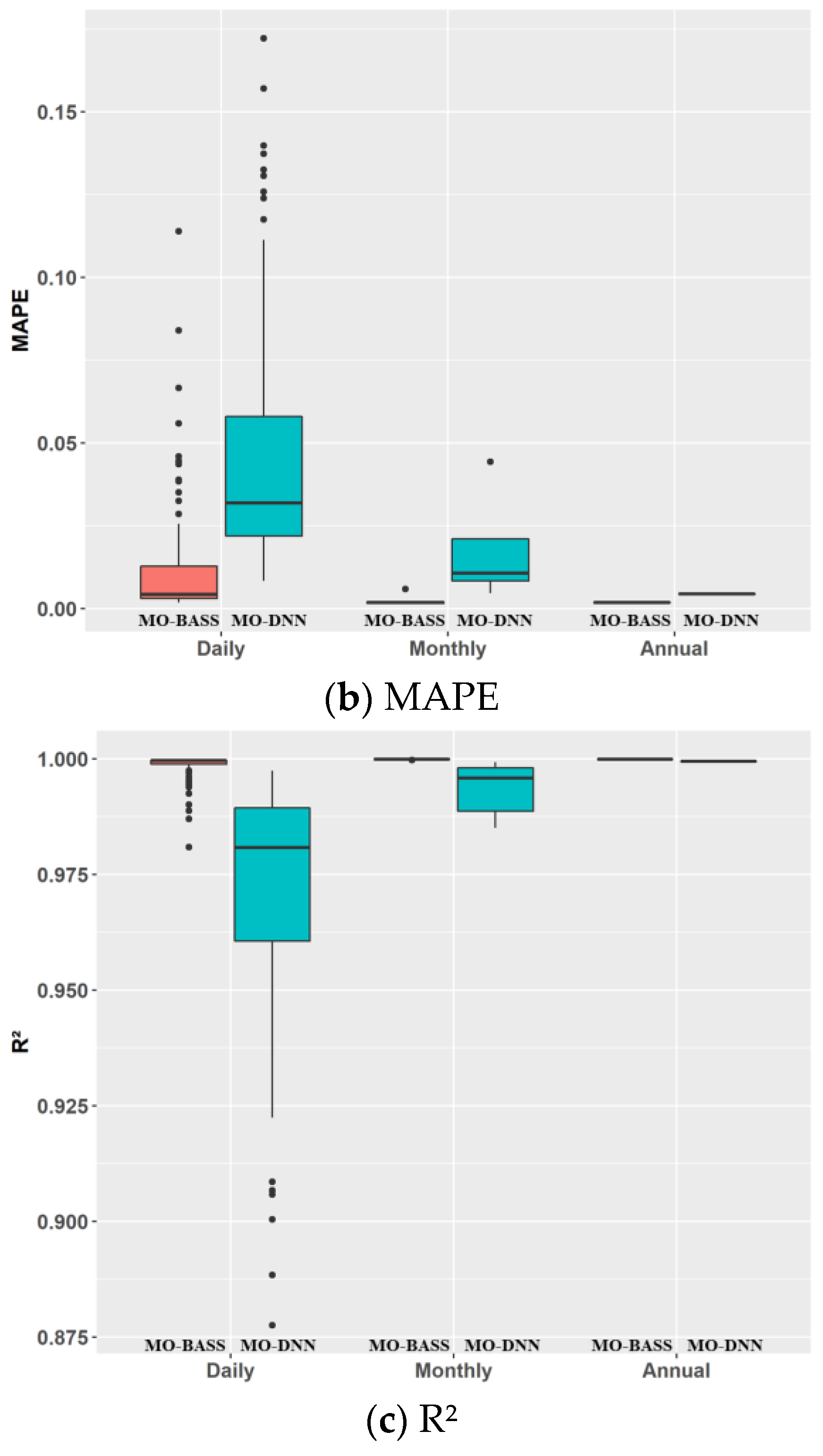

| No. | Parameters | Short Names | Range | Unit |
|---|---|---|---|---|
| 1 | Exterior wall U-value | EWU | 0.1–0.25 | W/(m2K) |
| 2 | Roof U-value | RU | 0.15–0.3 | W/(m2K) |
| 3 | Window U-value | WU | 1–2.4 | W/(m2K) |
| 4 | Solar heat gain coefficient | SHGC | 0.2–0.48 | - |
| 5 | Infiltration rate | INF | 0.5–0.8 | ACH |
| 6 | Lighting power density | LPD | 5–10 | W/m2 |
| 7 | Equipment power density | EPD | 9–15 | W/m2 |
| 8 | Occupancy density | OPD | 9–14 | m2/person |
| 9 | Heating set-point | HSP | 20–22 | °C |
| 10 | Cooling set-point | CSP | 24–26 | °C |
| Model | Hyperparameters | Daily | Monthly | Multi-Time | |||
|---|---|---|---|---|---|---|---|
| Cooling | Heating | Cooling | Heating | Cooling | Heating | ||
| SO-BASS | degree | 3 | 4 | 4 | - | ||
| nmcmc | 10,000 | ||||||
| MO-BASS | n.pc | 7 | 10 | 5 | 7 | ||
| degree | 3 | 4 | 4 | 3 | |||
| nmcmc | 10,000 | ||||||
| SO-DNN | activation | tanh,relu,liner | tanh,elu,relu,liner | - | |||
| number of hidden layers | 3 | ||||||
| output layer neurons | 1 | ||||||
| MO-DNN | activation | tanh,elu,relu,liner | |||||
| number of hidden layers | 4 | 3 | 4 | ||||
| output layer neurons | 105 | 102 | 5 | 111 | 108 | ||
| Models | Daily | Monthly | Multi-Time Scale |
|---|---|---|---|
| SO-BASS | 2032.2 | 98.7 | - |
| MO-BASS | 103.9 | 81.1 | 197.2 |
| SO-DNN | 3807.2 | 361.7 | - |
| MO-DNN | 137.3 | 72.2 | 236.3 |
| Machine Learning | Model | Description |
|---|---|---|
| BASS | SOB-D | Sum the daily energy from the single-output daily BASS models to obtain the monthly or annual energy |
| MOB-D | Sum the daily energy from the multi-output daily BASS models to obtain monthly or annual energy | |
| SOB-M | Monthly predictions or annual prediction (sum of monthly predictions) from the single-output monthly BASS models | |
| MOB-M | Monthly predictions or annual prediction (sum of monthly predictions) from the multi-output monthly BASS models | |
| MOB-Mu | Monthly or annual predictions from the multi-output multi-time scale BASS models | |
| DNN | SOD-D | Sum the daily energy from the single-output daily DNN models to obtain the monthly or annual energy |
| MOD-D | Sum the daily energy from the multi-output daily DNN models to obtain monthly or annual energy | |
| SOD-M | Monthly predictions or annual prediction (sum of monthly predictions) from the single-output monthly DNN models | |
| MOD-M | Monthly predictions or annual prediction (sum of monthly predictions) from the multi-output monthly DNN models | |
| MOD-Mu | Monthly or annual predictions from the multi-output multi-time scale DNN models |
| Model | Daily | Monthly | Multi-Time Scale |
|---|---|---|---|
| SO-BASS | 2293.0 | 128.8 | - |
| MO-BASS | 216.6 | 101.6 | 150.4 |
| SO-DNN | 3722.6 | 373.6 | - |
| MO-DNN | 69.7 | 65.4 | 165.9 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, G.; Tian, W.; Zhang, H.; Chen, B. Building Energy Models at Different Time Scales Based on Multi-Output Machine Learning. Buildings 2022, 12, 2109. https://doi.org/10.3390/buildings12122109
Li G, Tian W, Zhang H, Chen B. Building Energy Models at Different Time Scales Based on Multi-Output Machine Learning. Buildings. 2022; 12(12):2109. https://doi.org/10.3390/buildings12122109
Chicago/Turabian StyleLi, Guangchen, Wei Tian, Hu Zhang, and Bo Chen. 2022. "Building Energy Models at Different Time Scales Based on Multi-Output Machine Learning" Buildings 12, no. 12: 2109. https://doi.org/10.3390/buildings12122109
APA StyleLi, G., Tian, W., Zhang, H., & Chen, B. (2022). Building Energy Models at Different Time Scales Based on Multi-Output Machine Learning. Buildings, 12(12), 2109. https://doi.org/10.3390/buildings12122109











