Experimental and Parametric Study on Seismic Behavior of Steel Frame with ALC Panels
Abstract
1. Introduction
2. Details and Research
2.1. Design and Principle of The Pendulous Z-Panel Connector
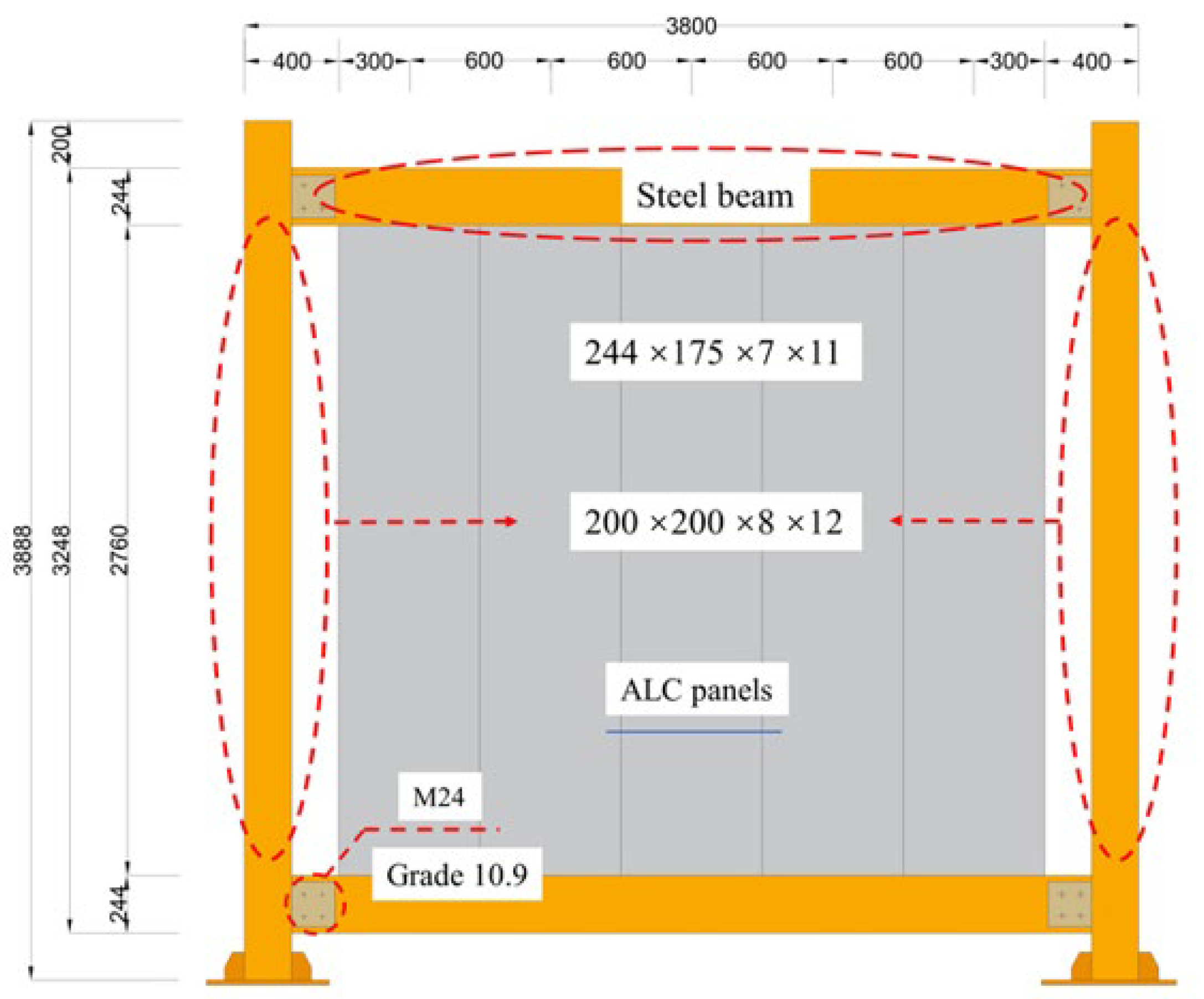
2.2. Test Specimens
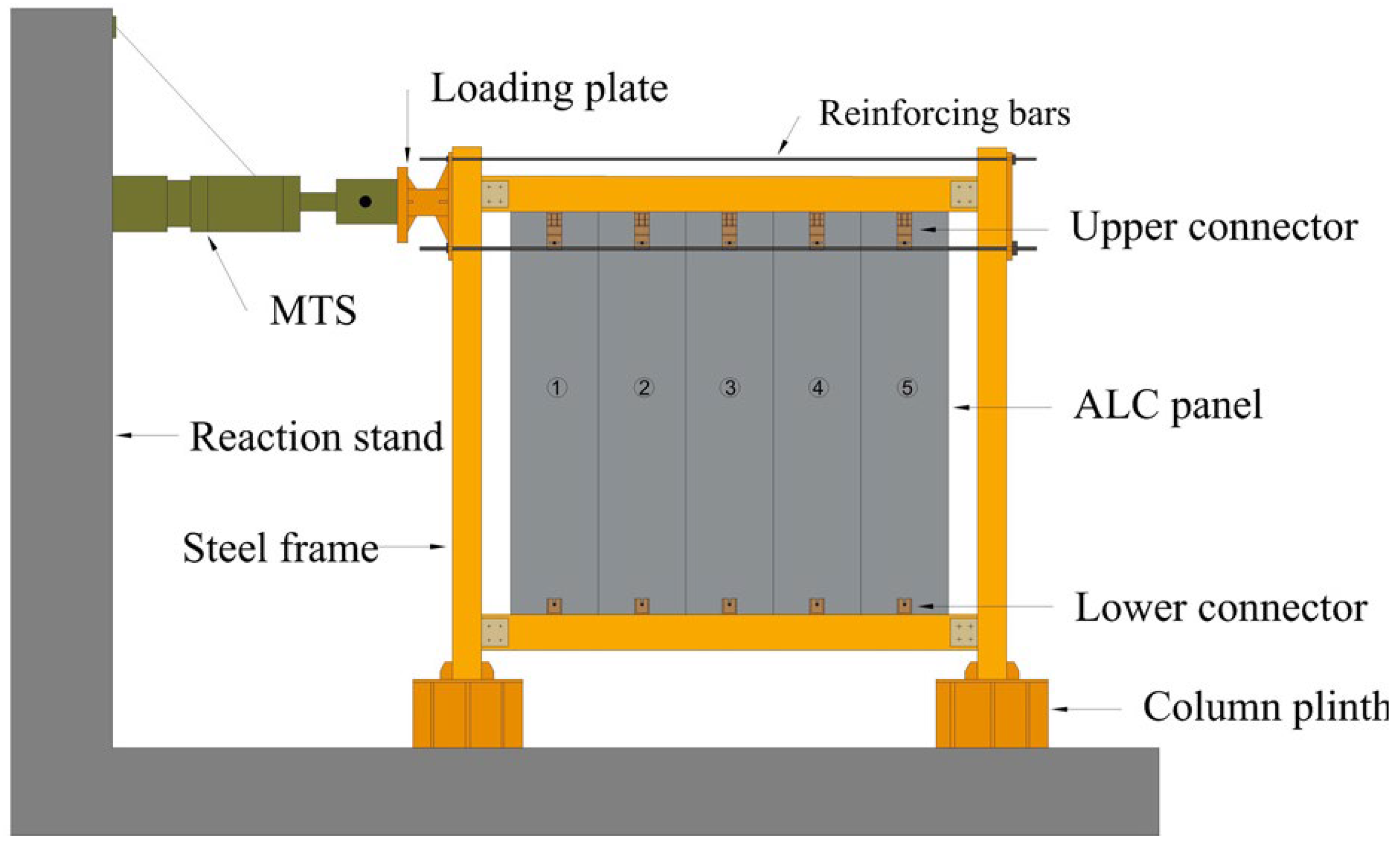
2.3. Experimental Device and Loading System
2.3.1. Experimental Device
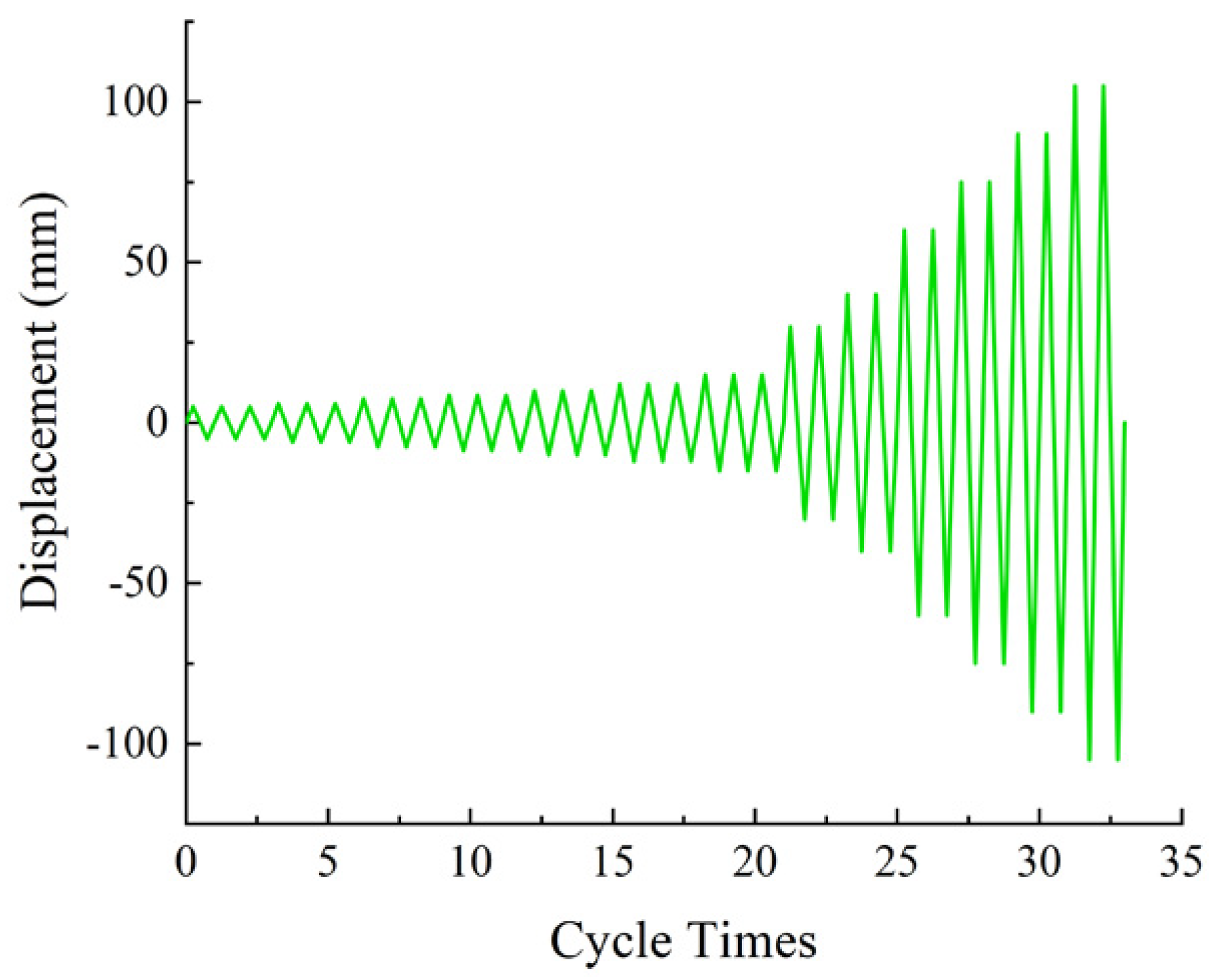
2.3.2. Loading System
2.4. Material Properties
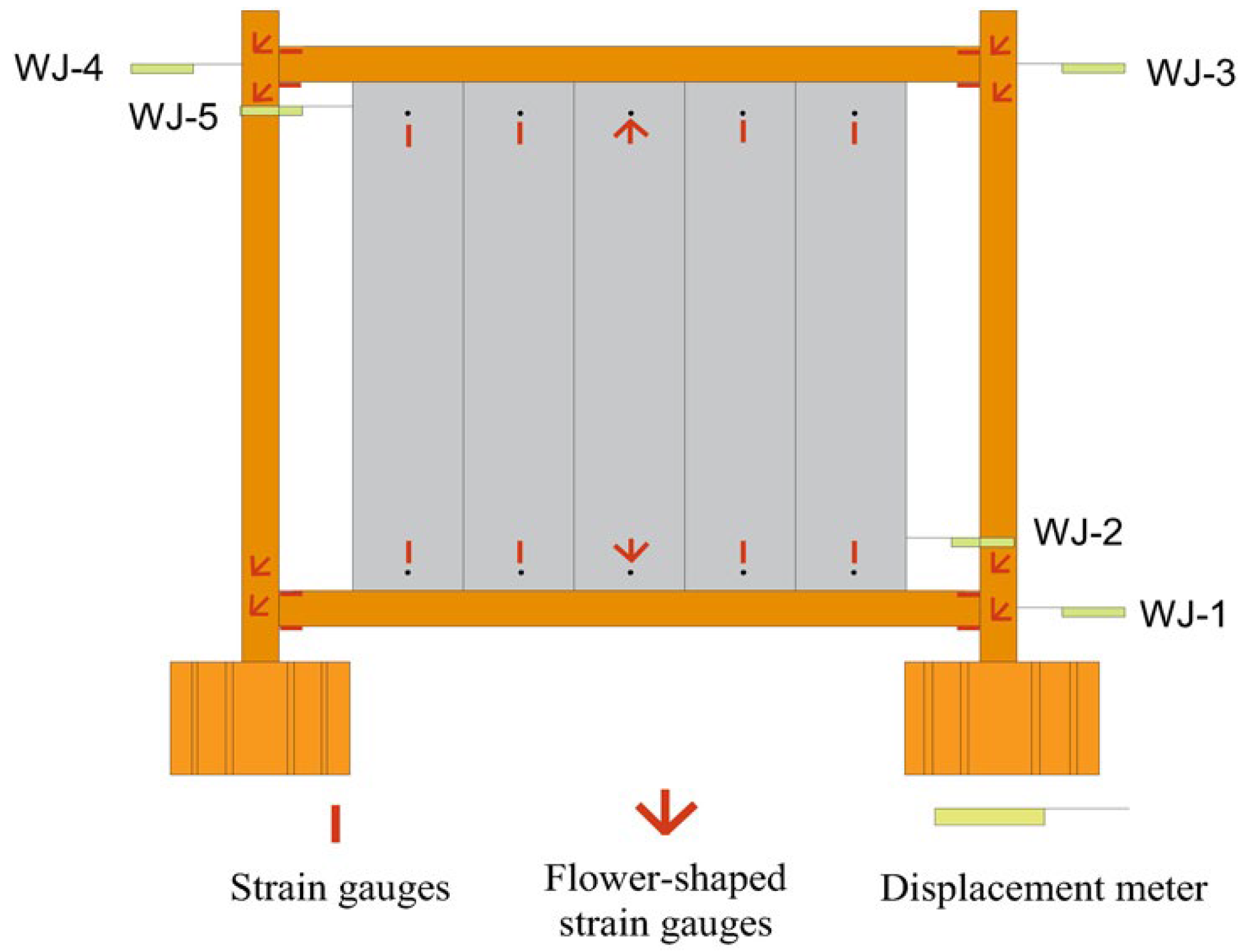
2.5. Measuring Point Arrangement
3. Experimental Investigation
3.1. Experimental Phenomenon
3.1.1. Specimen DC
3.1.2. Specimen DN
3.2. Experimental Results and Discussion
3.2.1. Hysteresis Curves
3.2.2. Coordinating Deformation Analysis
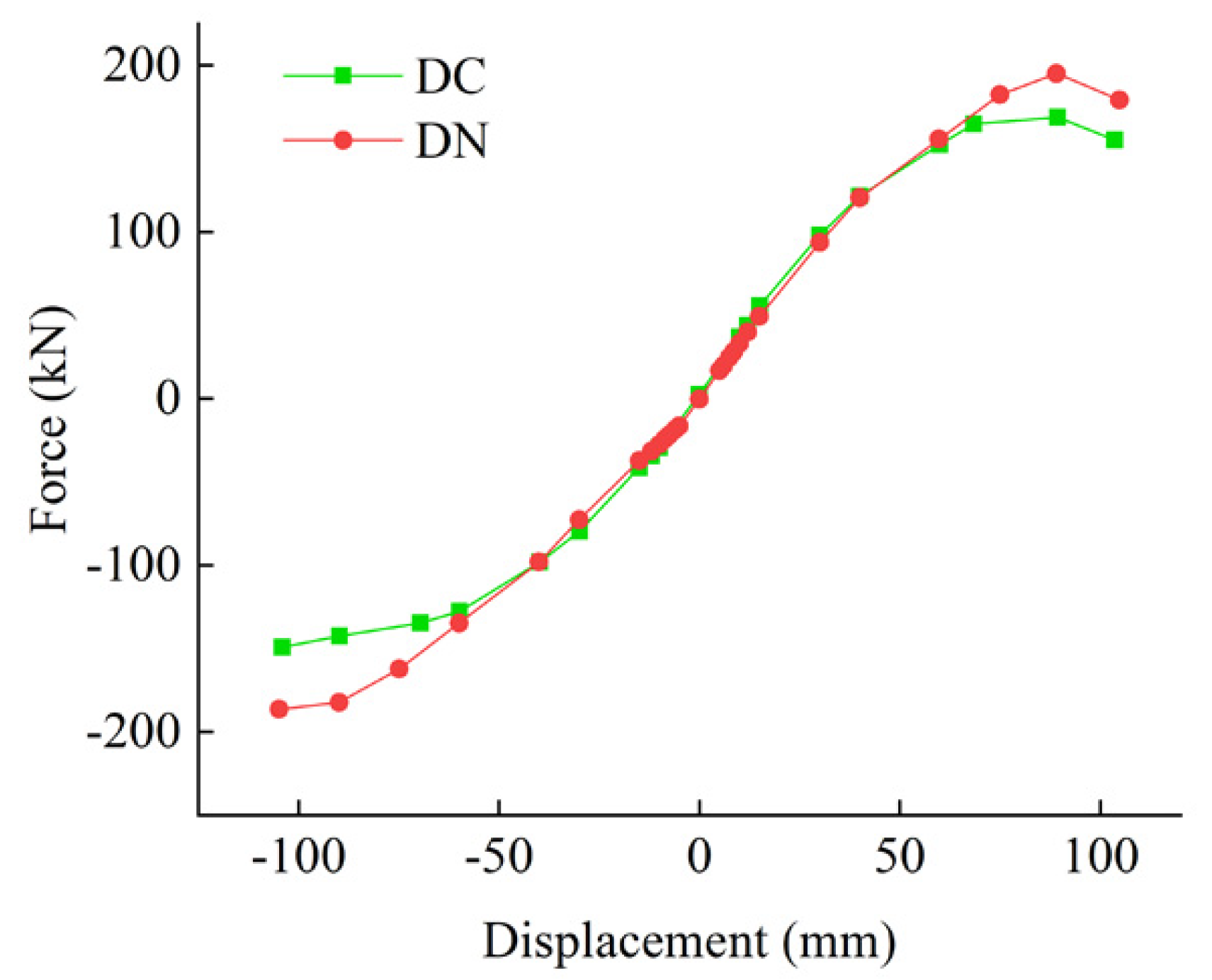
3.2.3. Comparison of Skeleton Curves
- (1)
- The structure is in the elastic stage during the initial loading stage, and the ALC panels bear lateral stiffness together with the steel frame. The skeleton curve of two groups of members is nearly linear.
- (2)
- With the increase in displacement, the bonding mortar between ALC panels fell off and the connector slipped, indicating that ALC panels gradually withdraw from the supply of stiffness. When the structure transitions to the elastic–plastic stage, the slope of the skeleton curve gradually decreases. At this stage, the load capacity of DN is slightly lower than that of DC because of the sliding mechanism of the new connector.
- (3)
- When the loading displacement reached 40 mm, the connecting bolt moved to the edge of the oblong hole. The ALC panels provide lateral stiffness again with the steel frames. The skeleton curve of DN exceeds that of DC. The ultimate load of the DN appears after the connectors reach the edge of the oblong hole, indicating that the Pendulous Z-plate connector improves the bearing capacity of the structure.
- (4)
- Table 4 shows the characteristic value of the skeleton curve. The displacement of the yield, load yield, ultimate displacement, and ultimate load of the structure can be obtained from the table. It can be observed that the yield load of DN is 11.61% higher than the yield load of DC, and the ultimate load of DN is 14.90% higher than the ultimate load of DC.
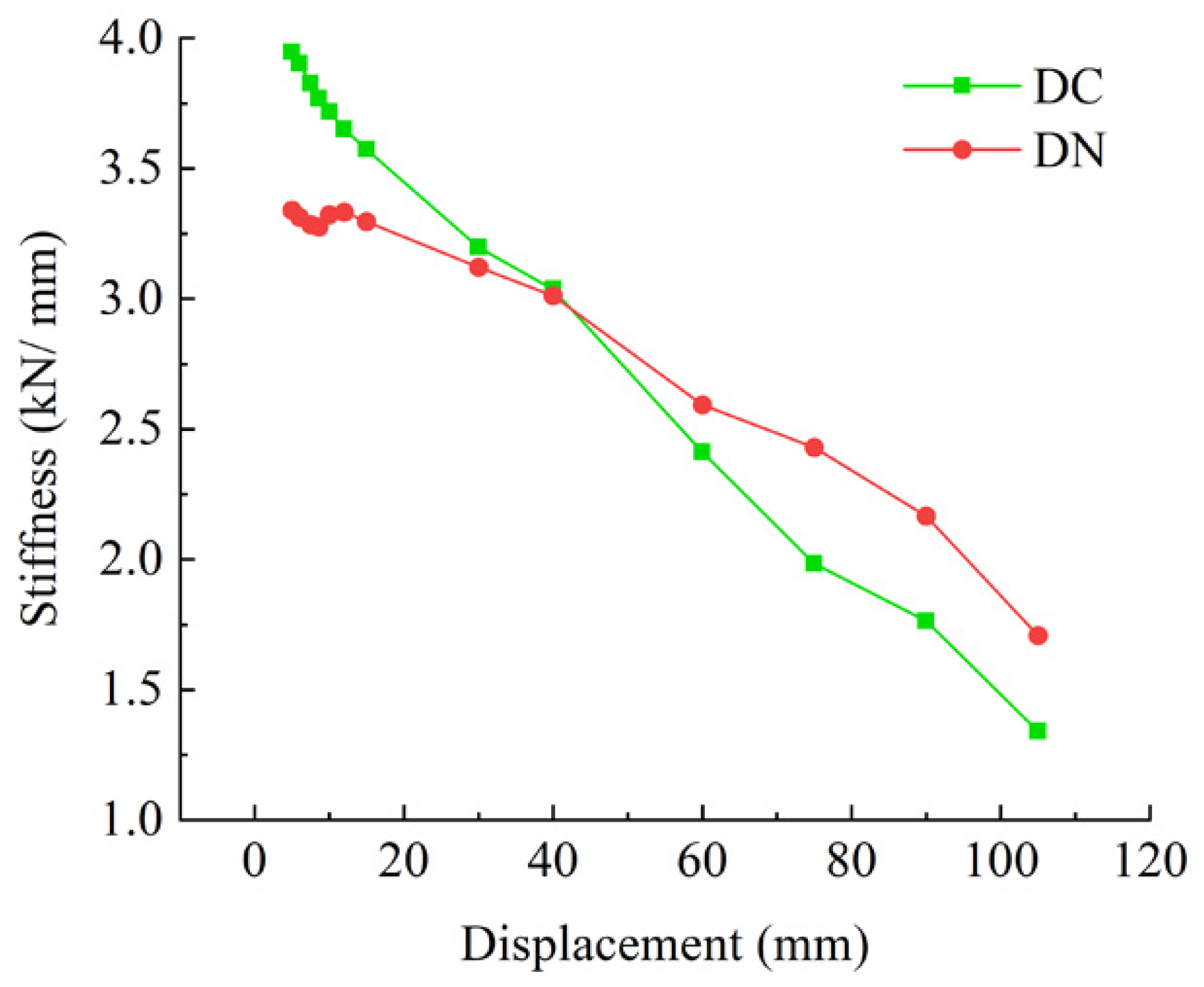
3.2.4. Degradation of Stiffness
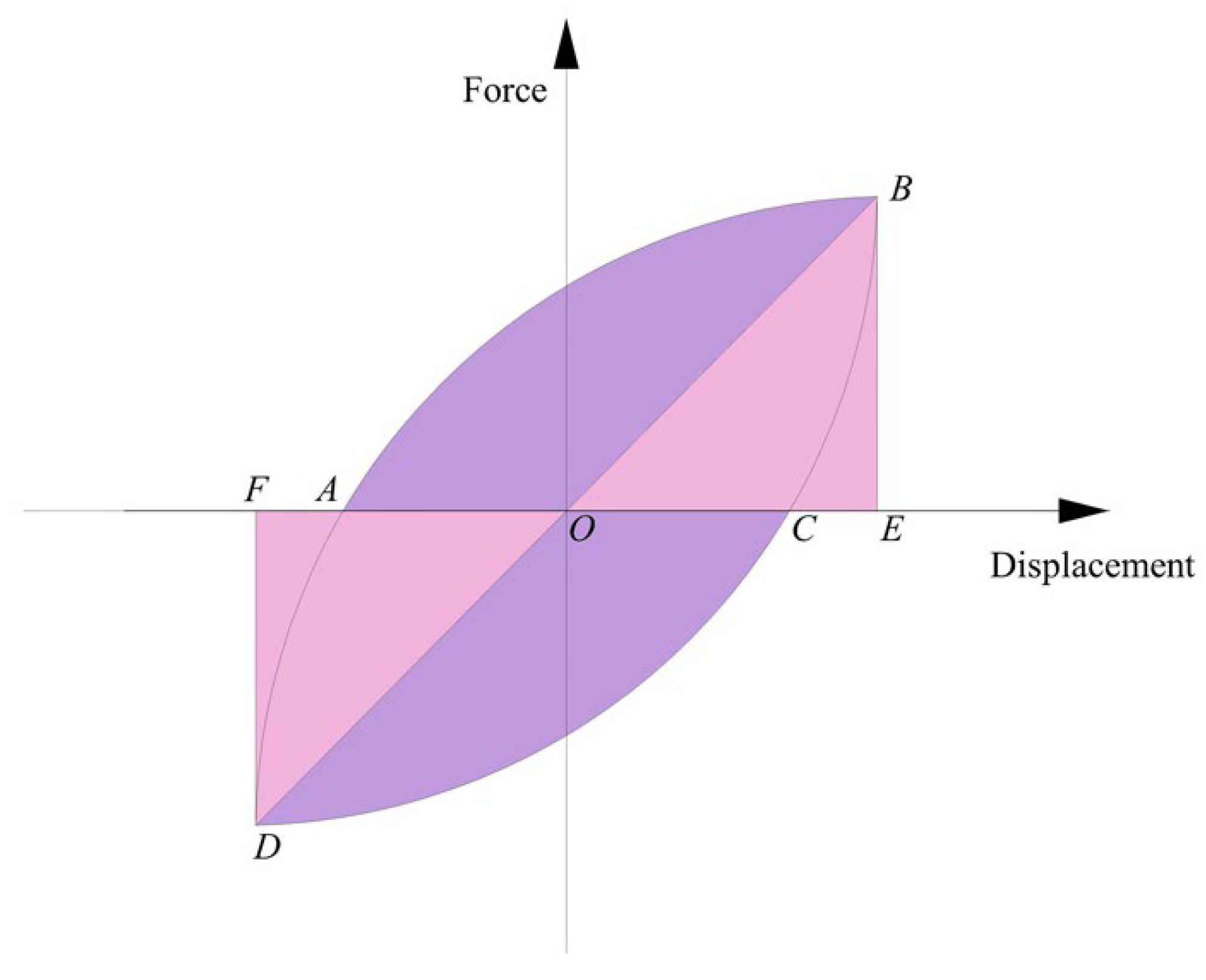
3.2.5. Energy Dissipation
4. Finite Element Analysis
4.1. Finite Element Model
4.2. Comparison of Simulation and Test Results
4.3. Parametric Study
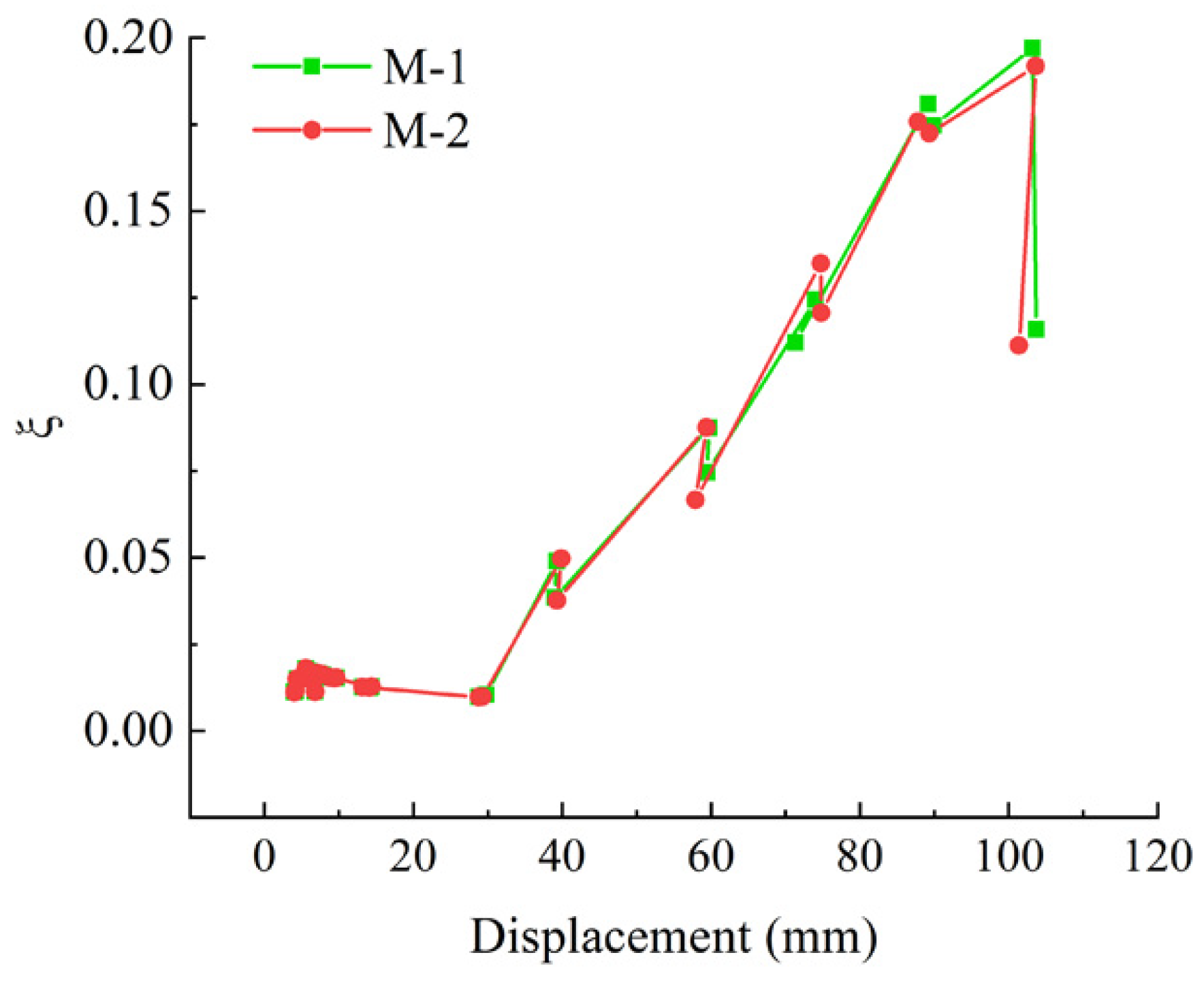
4.3.1. Degradation of Stiffness
- (1)
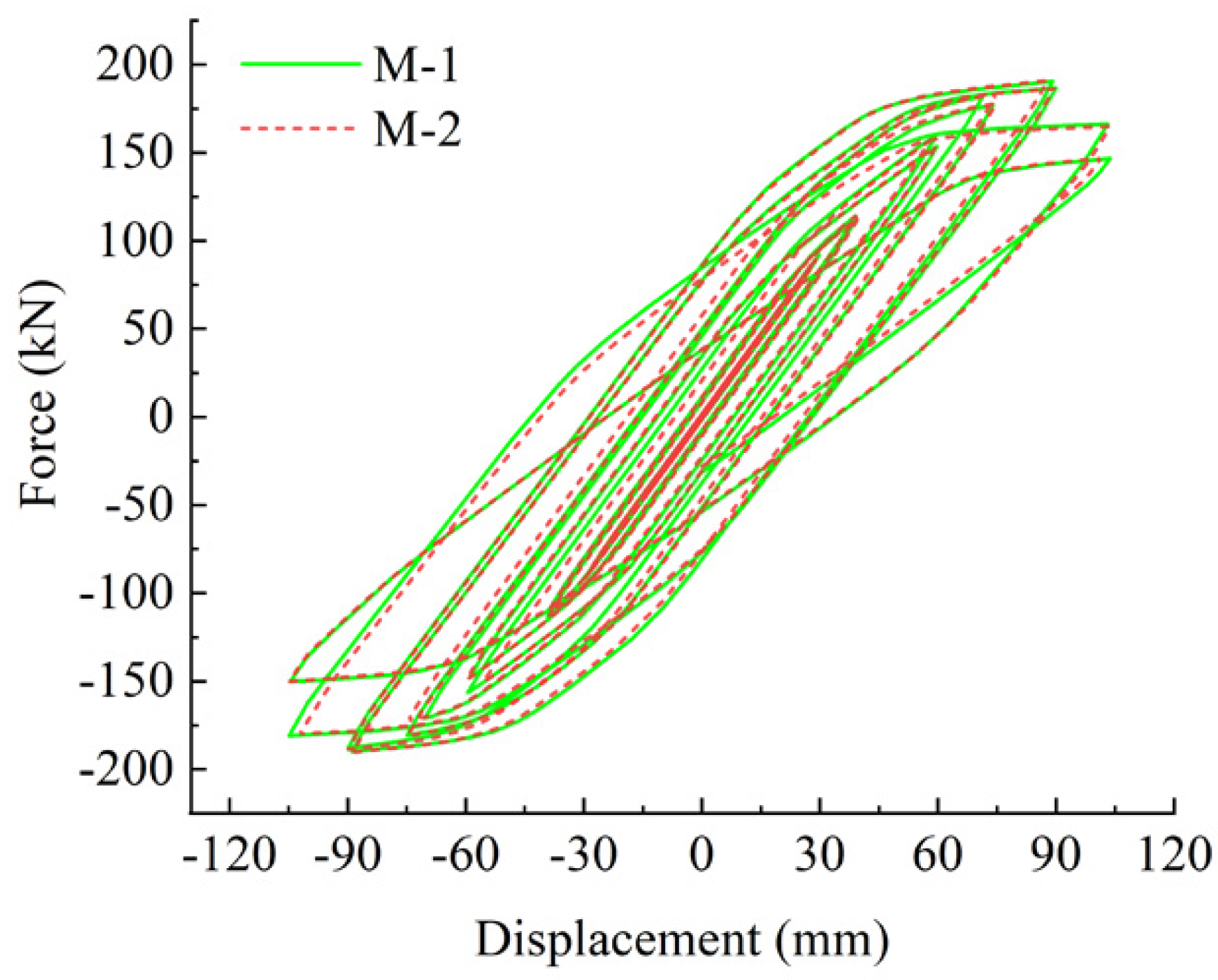
- The two groups of hysteresis curves show an inverse S-shape, and the area of the hysteresis loop increases with displacement, indicating that the two groups of specimens have good seismic behavior.
- (2)
- By comparing the hysteresis curves of the two groups, it is found that there is little difference between the hysteresis curves of the two groups of specimens. The hysteresis curves of M-1 are slightly fuller than those of M-2.
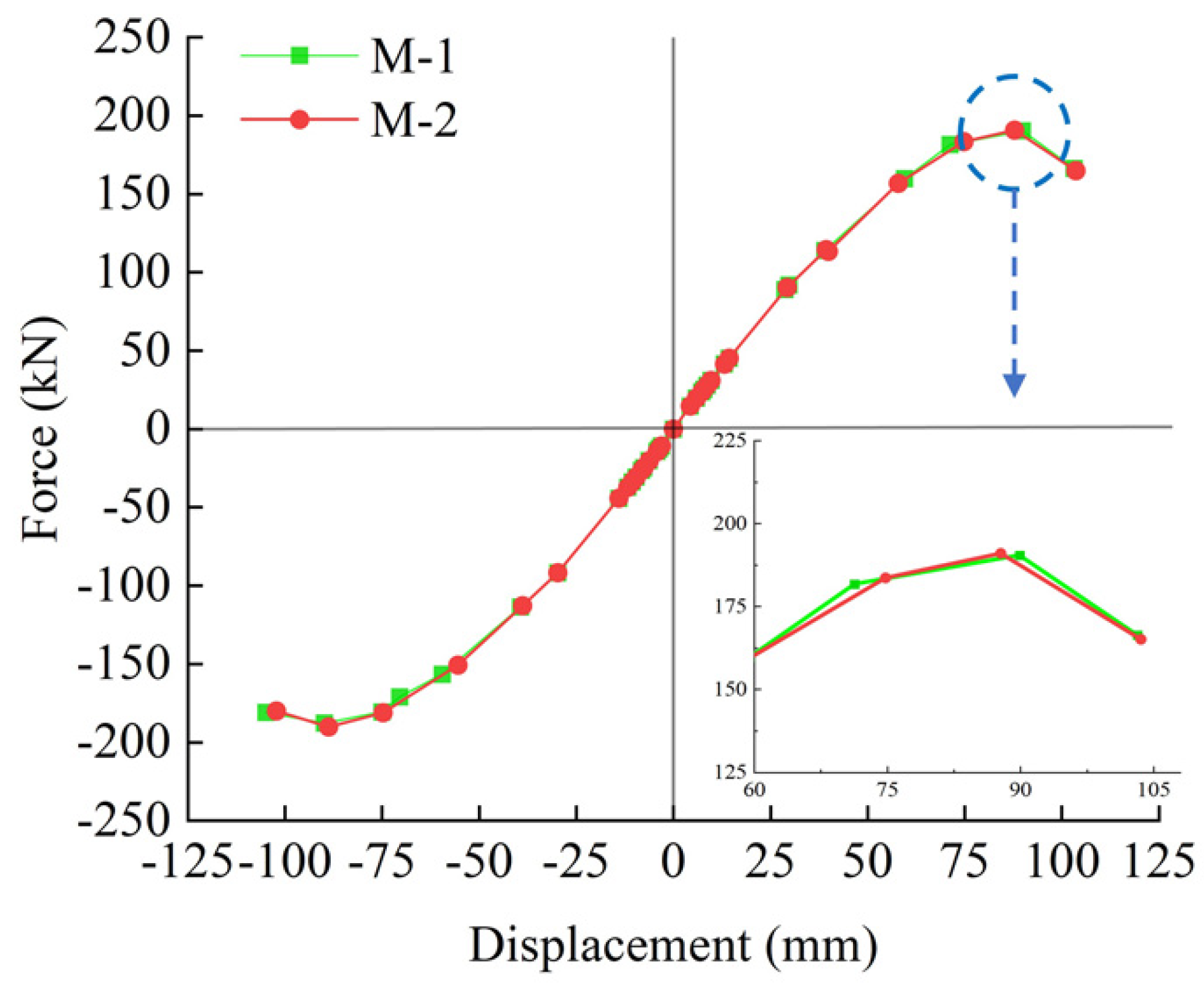
4.3.2. Skeleton Curves of Different Bolt Grades
4.3.3. Energy Dissipation of Different Bolt Grades
5. Conclusions
- (1)
- The test shows that both sets of the ALC panels provide lateral stiffness together with steel frames in a small earthquake. In the frequently occurring earthquake (displacement angle of 1/250), DN provides better coordinating deformation between the ALC panel and the steel frame than that DC. In the rarely occurring earthquake (displacement angle of 1/50), the new connector keeps the ALC panel from falling off. This new connection mode conforms to the design objectives and meets the seismic minimum standards.
- (2)
- Based on the results of the test data analysis, it was found that the new type connector has a higher bearing capacity and energy dissipation. The hysteresis curves of specimens both gradually approached the inverse S-shape, in which DN is fuller, indicating that its energy dissipation is better. In addition, in terms of skeleton curves, the yield-bearing capacity and ultimate load-carrying capacity of DN are higher by 11.61% and 14.90%, respectively, than those of DC, and the total energy dissipation of DN is increased by approximately 79.95% compared to DC.
- (3)
- In the aspect of simulation, the steel frame with the ALC panel model is established based on the test. Its findings show that the simulation results agree well with the test results. This finite element model can objectively reflect the loading features of the specimens.
- (4)
- A parametric study was conducted using finite element software to study the influence of bolt grades on the structural performance of the new connectors. The simulation results indicate that grade 5.6 bolts are not obviously different in the structural performance than grade 8.8 bolts, in which the loading-carrying capacity of grade 8.8 bolts increases slightly, and the fullness degree of hysteresis curve does not change obviously, and the difference of the energy dissipation is not particularly pronounced compared to the grade 5.6 bolts. In consideration of the engineering costs, grade 5.6 bolts are recommended.
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- De Matteis, G.; Landolfo, R. Diaphragm action of sandwich panels in pin-jointed steel structures: A seismic study. J. Earthq. Eng. 2000, 4, 251–275. [Google Scholar] [CrossRef]
- Guri, M.; Brzev, S.; Lluka, D. Performance of prefabricated large panel reinforced concrete buildings in the November 2019 Albania earthquake. J. Earthq. Eng. 2021, 26, 5799–5825. [Google Scholar] [CrossRef]
- Cao, X.Y.; Shen, D.; Feng, D.C.; Wang, C.L.; Qu, Z.; Wu, G. Seismic retrofitting of existing frame buildings through externally attached sub-structures: State of the art review and future perspectives. J. Build. Eng. 2022, 57, 104904. [Google Scholar] [CrossRef]
- Arslan, M.E.; Aykanat, B.; Subaşı, S.; Maraşlı, M. Cyclic behavior of autoclaved aerated concrete block infill walls strengthened by basalt and glass fiber composites. Eng. Struct. 2021, 240, 112431. [Google Scholar] [CrossRef]
- Ishida, T.; Tenderan, R.; Kohtaki, K.; Kishiki, S.; Iyama, J.; Hasegawa, T.; Seike, T.; Yamada, S. Experimental study on full-scale steel moment-resisting frames with nonstructural walls subjected to multiple earthquakes. Eng. Struct. 2021, 242, 112549. [Google Scholar] [CrossRef]
- Wang, J.; Li, B. Cyclic testing of square CFST frames with ALC panel or block walls. J. Constr. Steel Res. 2017, 130, 264–279. [Google Scholar] [CrossRef]
- Ye, M.; Jiang, J.; Chen, H.M.; Zhou, H.Y.; Song, D.D. Seismic behavior of an innovative hybrid beam-column connection for precast concrete structures. Eng. Struct. 2021, 227, 111436. [Google Scholar] [CrossRef]
- Getz, D.R.; Memari, A.M. Static and cyclic racking performance of autoclaved aerated concrete cladding panels. J. Archit. Eng. 2006, 12, 12–23. [Google Scholar] [CrossRef]
- Dal Lago, B.; Biondini, F.; Toniolo, G. Experimental tests on multiple-slit devices for precast concrete panels. Eng. Struct. 2018, 167, 420–430. [Google Scholar] [CrossRef]
- Binici, B.; Canbay, E.; Aldemir, A.; Demirel, I.O.; Uzgan, U.; Eryurtlu, Z.; Bulbul, K.; Yakut, A. Seismic behavior and improvement of autoclaved aerated concrete infill walls. Eng. Struct. 2019, 193, 68–81. [Google Scholar] [CrossRef]
- Latour, M.; Rizzano, G. Seismic behavior of cross-laminated timber panel buildings equipped with traditional and innovative connectors. Arch. Civ. Mech. Eng. 2017, 17, 382–399. [Google Scholar] [CrossRef]
- Furtado, A.; Rodrigues, H.; Arede, A.; Varum, H. Experimental investigation on the possible effect of previous damage, workmanship and test setup on the out-of-plane behaviour of masonry infill walls. J. Earthq. Eng. 2021, 26, 5647–5678. [Google Scholar] [CrossRef]
- Cao, X.Y.; Xiong, C.Z.; Feng, D.C.; Wu, G. Dynamic and probabilistic seismic performance assessment of precast prestressed reinforced concrete frames incorporating slab influence through three-dimensional spatial model. Bull. Earthq. Eng. 2022, 20, 6705–6739. [Google Scholar] [CrossRef]
- Cao, X.Y.; Feng, D.C.; Wang, Z.; Wu, G. Parametric investigation of the assembled bolt-connected buckling-restrained brace and performance evaluation of its application into structural retrofit. J. Build. Eng. 2022, 48, 103988. [Google Scholar] [CrossRef]
- Dai, X.M.; Zong, L.; Ding, Y.; Li, Z.X. Experimental study on seismic behavior of a novel plug-in self-lock joint for modular steel construction. Eng. Struct. 2019, 181, 143–164. [Google Scholar] [CrossRef]
- Palsson, H.; Goodno, B.J.; Craig, J.I.; Will, K.M. Cladding influence on dynamics response of tall buildings. Earthq. Eng. Struct. Dyn. 1984, 12, 215–228. [Google Scholar] [CrossRef]
- Aref, A.J.; Jung, W.Y. Energy-dissipating polymer matrix composite-infill wall system for seismic retrofitting. J. Struct. Eng. 2003, 129, 440–448. [Google Scholar] [CrossRef]
- Wang, X.; Liu, X.; Ma, L.; Zhou, X. Experimental research on seismic behavior of prefabricated ALC external panels. Steel Constr. 2017, 32, 26. [Google Scholar]
- Wilson, J.L.; Robinson, A.J.; Balendra, T. Performance of precast concrete load-bearing panel structures in regions of low to moderate seismicity. Eng. Struct. 2008, 30, 1831–1841. [Google Scholar] [CrossRef]
- Okazaki, T.; Nakashima, M.; Suita, K.; Matusmiya, T. Interaction between cladding and structural frame observed in a full-scale steel building test. Earthq. Eng. Struct. Dyn. 2007, 36, 35–53. [Google Scholar] [CrossRef]
- Zhang, C.; Ding, K.; He, S. Seismic performance of panel connectors with steel frame based on autoclaved lightweight concrete (ALC). Buildings 2022, 12, 372. [Google Scholar] [CrossRef]
- Wang, B.; Wang, J.; Wan, H.; Hou, H.; Wang, J. Research on capacity and connector structure of filling wall of high-rise steel structure building under cyclic loading. Constr. Steel Struct. Prog. 2015, 17, 44–50. [Google Scholar]
- PRC. GB 50011-2010; Code for Seismic Design of Buildings. China Building Industry Press: Beijing, China, 2011.
- PRC. GB/T 11969-2020; Test Methods of Autoclaved Aerated Concrete. China Building Industry Press: Beijing, China, 2021.
- PRC. GB/T 228.1-2020; Metallic Materials-Tensile Testing. China Building Industry Press: Beijing, China, 2011.
- Ding, K.; Zhang, Y. Experimental study on seismic performance of fabricated bolted joint under low-cycle reciprocating loads. Results Eng. 2021, 9, 100208. [Google Scholar] [CrossRef]
- Ma, Y.; Jia, J. The influence of different parameter on the seismic behavior of SRUHSC frame. Adv. Mater. Sci. Eng. 2017, 2017, e3495150. [Google Scholar] [CrossRef]
- Mahendran, M. Applications of finite element analysis in structural engineering. In Proceedings of the International Conference on Computer Aided Engineering, Indian institute of Technology Madras, Madras, Indian, 13–15 December 2007. [Google Scholar]
- Gad, E.F.; Chandler, A.M.; Duffield, C.F.; Stark, G. Lateral behavior of plasterboard-clad residential steel frames. J. Struct. Eng. 1999, 125, 32–39. [Google Scholar] [CrossRef]
- Ding, K.; Zhang, C.; He, S.; Liu, Y. Hysteresis behavior and design of the new autoclaved lightweight concrete (ALC) external panel connector with the steel frame. Adv. Mater. Sci. Eng. 2022, 2022, e8319044. [Google Scholar] [CrossRef]
- Ding, K.; Ye, Y.; Ma, W. Seismic performance of precast concrete beam-column joint based on the bolt connection. Eng. Struct. 2021, 232, 111884. [Google Scholar] [CrossRef]
- Tian, H.; Chen, Y. Experimental research and finite element analysis on lateral shearing behavior of ALC spliced-connection wallboard. J. Build. Struct. 2009, 30, 85–91. [Google Scholar]

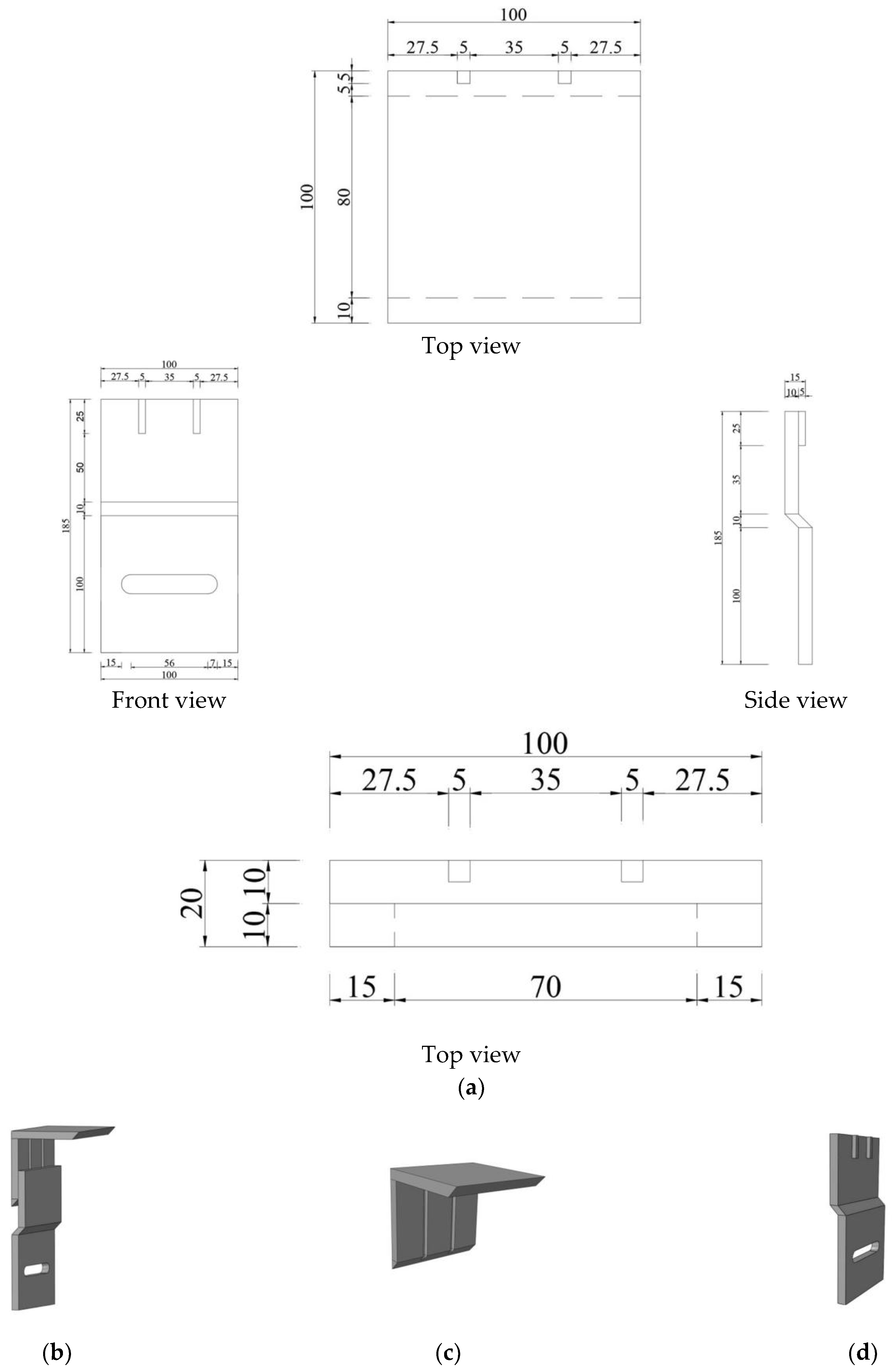







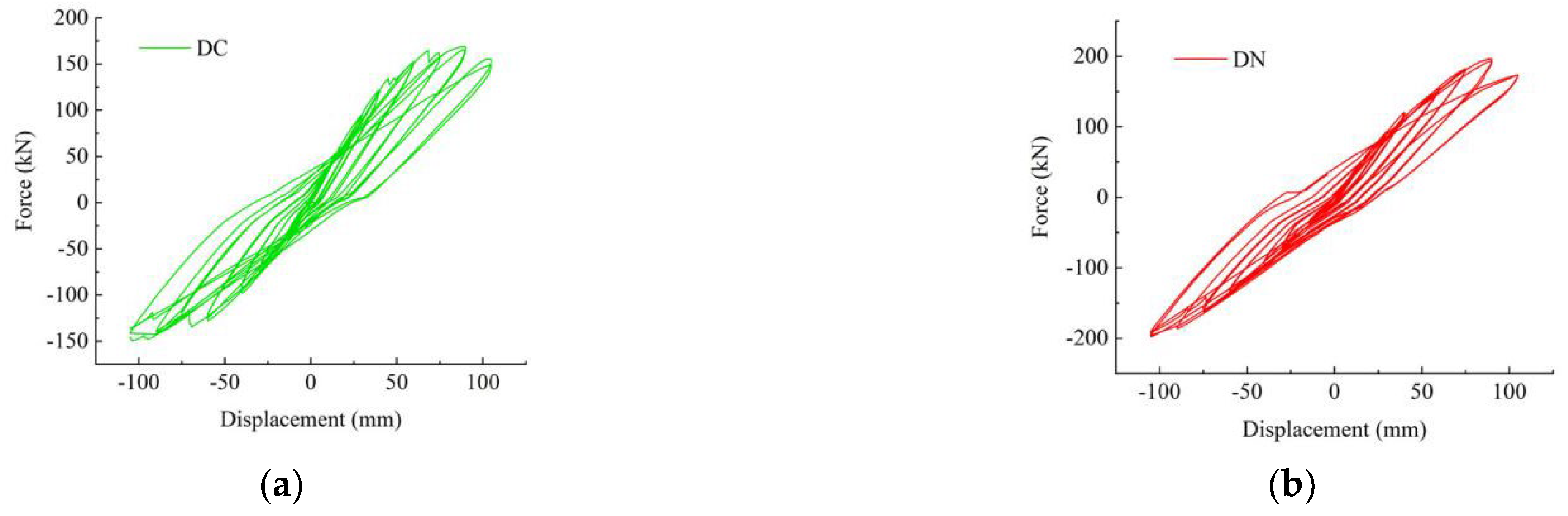





| Specimen | Connection Type |
|---|---|
| DC | L-hooked bolt connector |
| DN | The pendulous Z-plate connector |
| Specimens | Cross-Sectional Specifications |
|---|---|
| Frame column | HW 200 mm × 200 mm × 8 mm × 12 mm |
| Frame beam | HM 244 mm × 175 mm × 7 mm × 11 mm |
| Specimens | Thickness (mm) | Yield Stress (N/mm2) | Ultimate Stress (N/mm2) | Elongation Stress |
|---|---|---|---|---|
| Steel beam web | 7 | 275.3 | 411.3 | 22.3% |
| Steel column web | 8 | 278.2 | 409.8 | 20.8% |
| Steel beam flange | 11 | 263.4 | 401.6 | 25.2% |
| Steel column flange | 12 | 289.5 | 435.5 | 24.7% |
| The new connector | 10 | 376.6 | 510.1 | 19.6% |
| Loading Method | Yield Displacement (mm) | Yield Loading (kN) | Ultimate Displacement (mm) | Ultimate Loading (kN) |
|---|---|---|---|---|
| DC | 50.05 | 137.29 | 68.58 | 168.70 |
| DN | 58.82 | 153.23 | 88.35 | 193.83 |
| Specimen | Loading Displacement (mm) | Total Energy Dissipation (kN·mm) | The Equivalent Viscous Damping Coefficient | Energy Dissipation Coefficient |
|---|---|---|---|---|
| DC | 105 | 9633.25 | 0.10 | 0.62 |
| DN | 105 | 17,335.47 | 0.12 | 0.74 |
| Model Number | Bolt Diameter (mm) | Bolt Grade |
|---|---|---|
| M-1 | 14 | 5.6 |
| M-2 | 14 | 8.8 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ding, K.; Kong, X.; He, S.; Zong, D. Experimental and Parametric Study on Seismic Behavior of Steel Frame with ALC Panels. Buildings 2022, 12, 2070. https://doi.org/10.3390/buildings12122070
Ding K, Kong X, He S, Zong D. Experimental and Parametric Study on Seismic Behavior of Steel Frame with ALC Panels. Buildings. 2022; 12(12):2070. https://doi.org/10.3390/buildings12122070
Chicago/Turabian StyleDing, Kewei, Xiaoying Kong, Shulin He, and Da Zong. 2022. "Experimental and Parametric Study on Seismic Behavior of Steel Frame with ALC Panels" Buildings 12, no. 12: 2070. https://doi.org/10.3390/buildings12122070
APA StyleDing, K., Kong, X., He, S., & Zong, D. (2022). Experimental and Parametric Study on Seismic Behavior of Steel Frame with ALC Panels. Buildings, 12(12), 2070. https://doi.org/10.3390/buildings12122070







