Deep Learning-Enriched Stress Level Identification of Pretensioned Rods via Guided Wave Approaches
Abstract
1. Introduction
2. Guided Waves as NDE Approach for Prestressed Rods
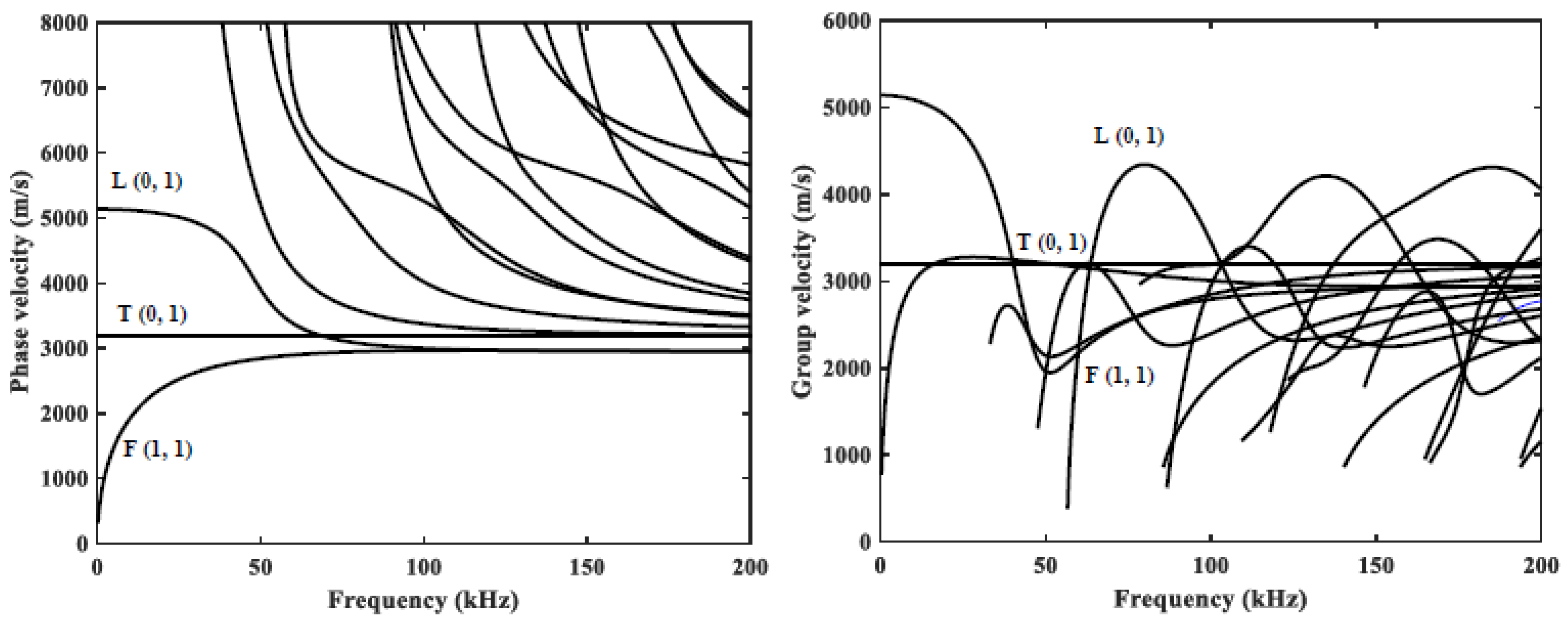
2.1. Governing Equations and Simulation of Guided Waves along a Rod
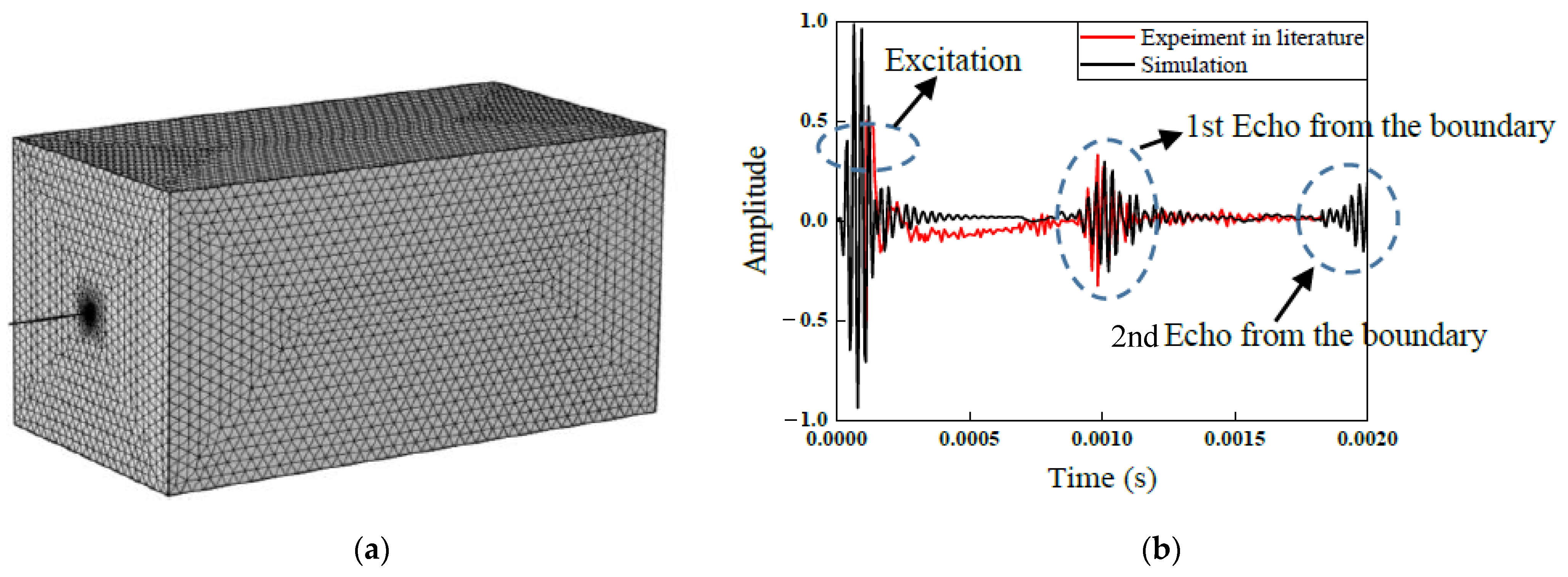
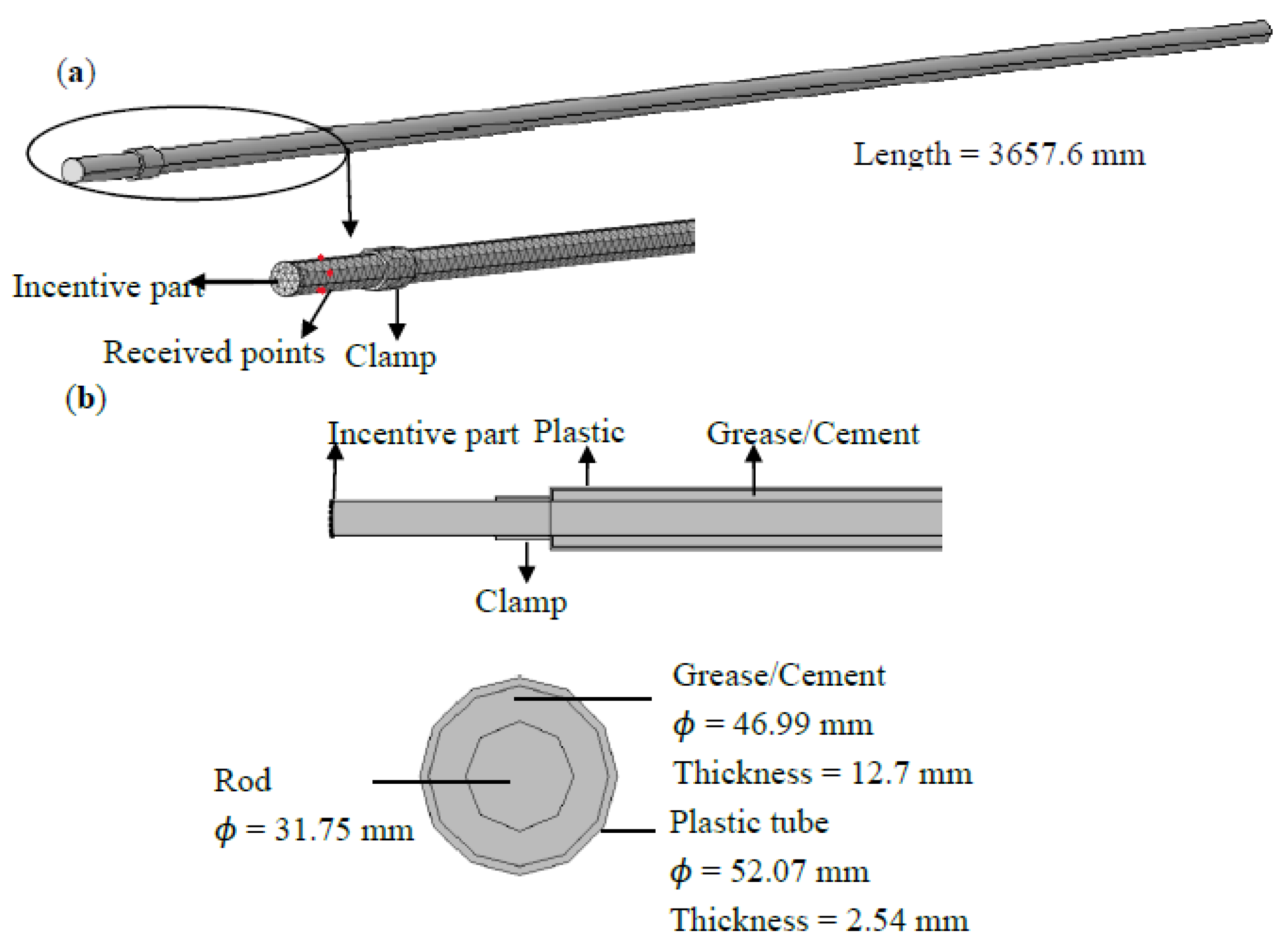
2.2. Calibration of the FE Analysis of the Ultrasonic Guided Waves through the Rod
2.3. Design of Scenarios
2.4. Data Collection and Augmentation
3. Deep Learning Framework
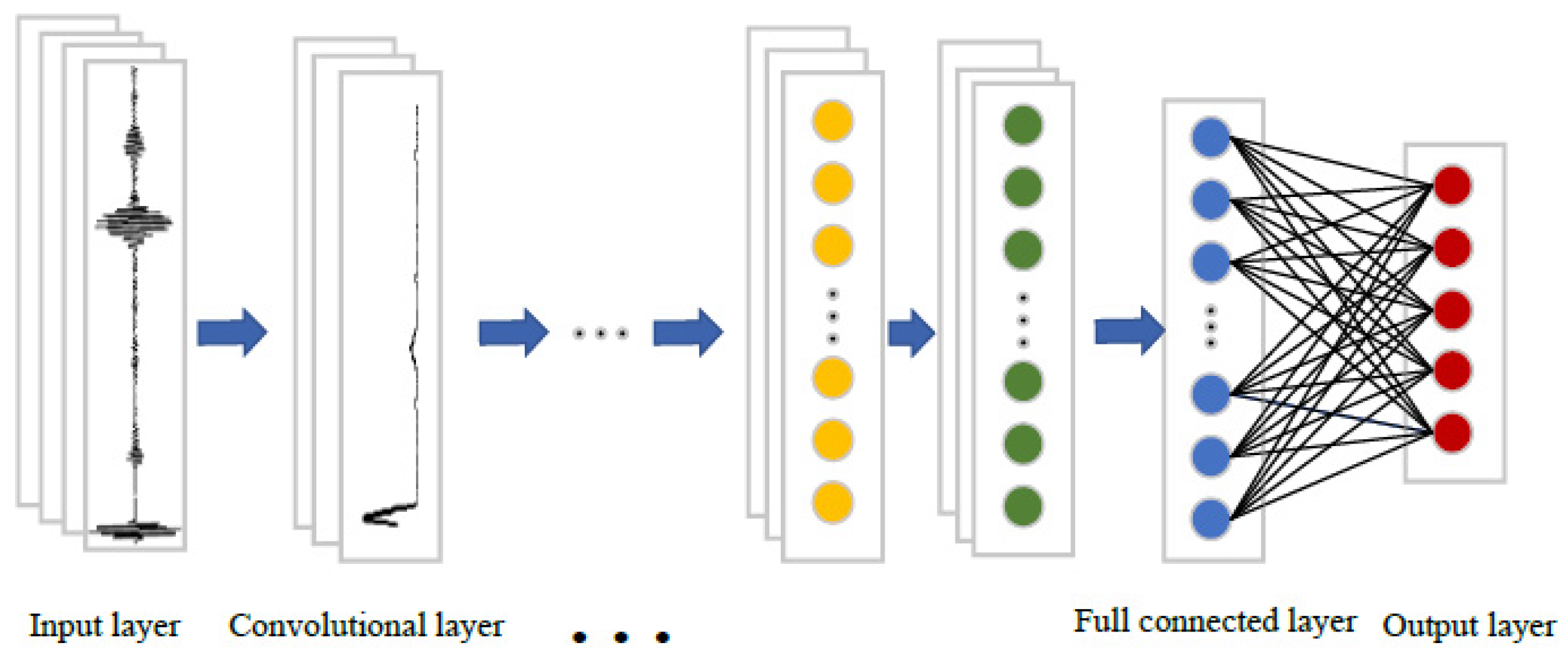
3.1. Introductions of CNN
3.2. CNN Architecture
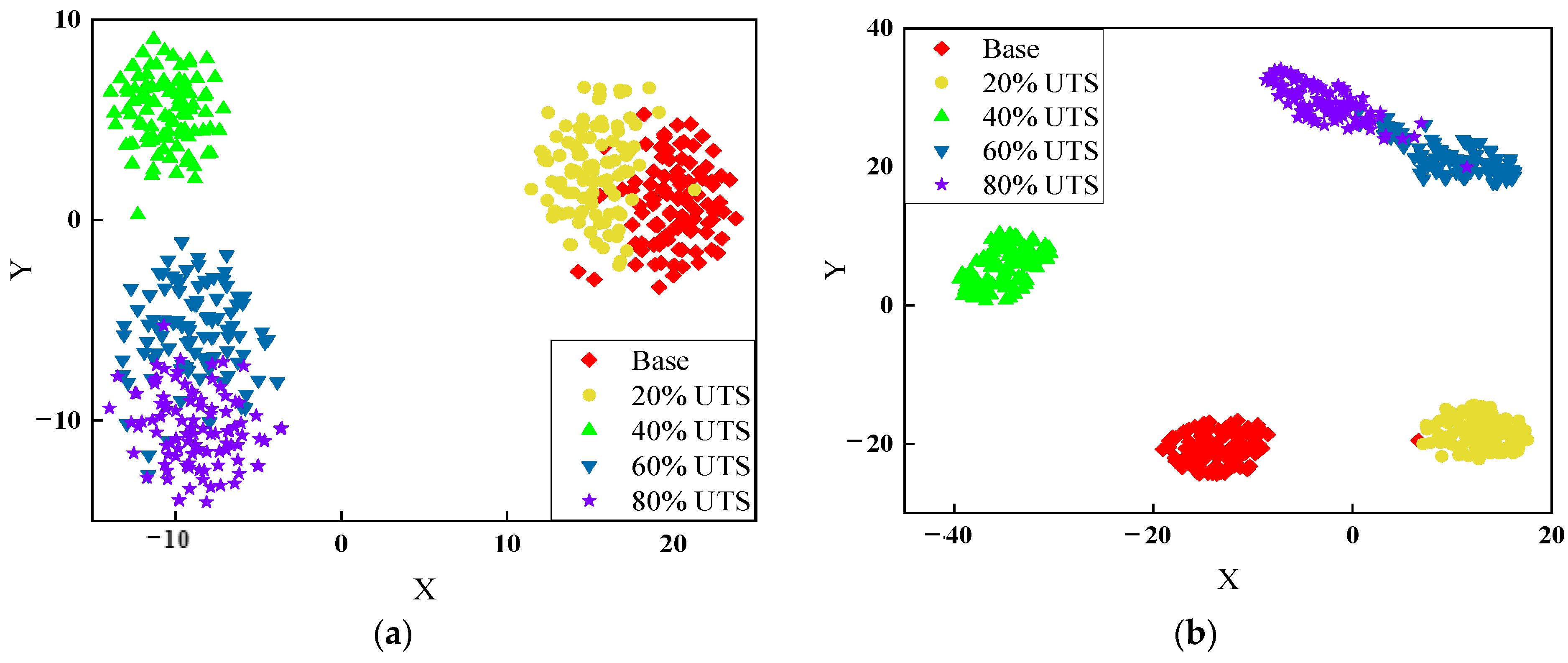
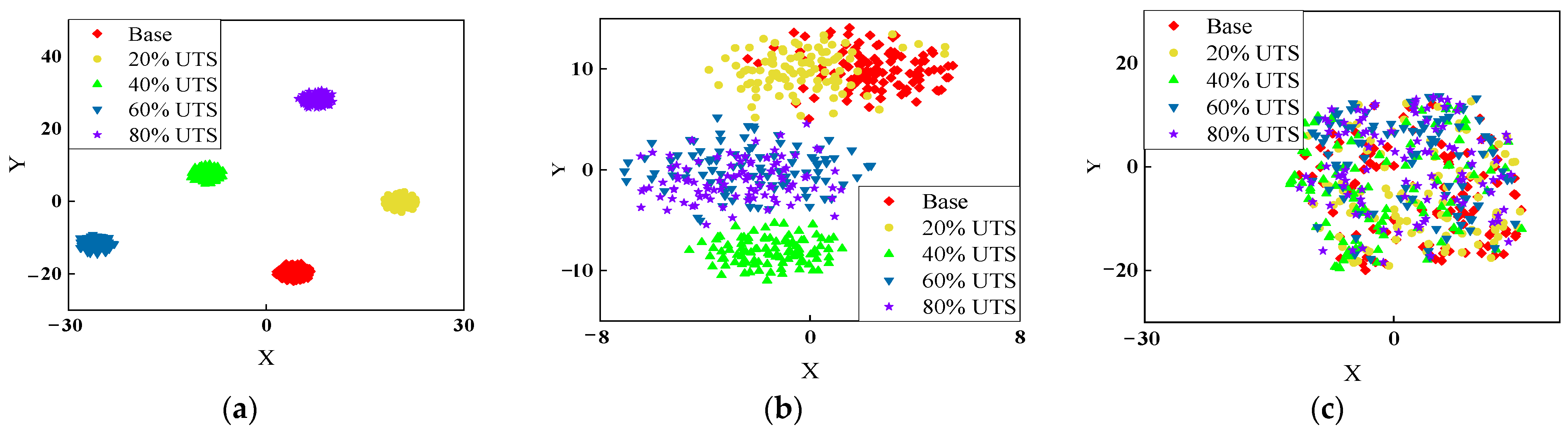
3.3. Feature Visualization with t-SNE
4. Results and Discussion
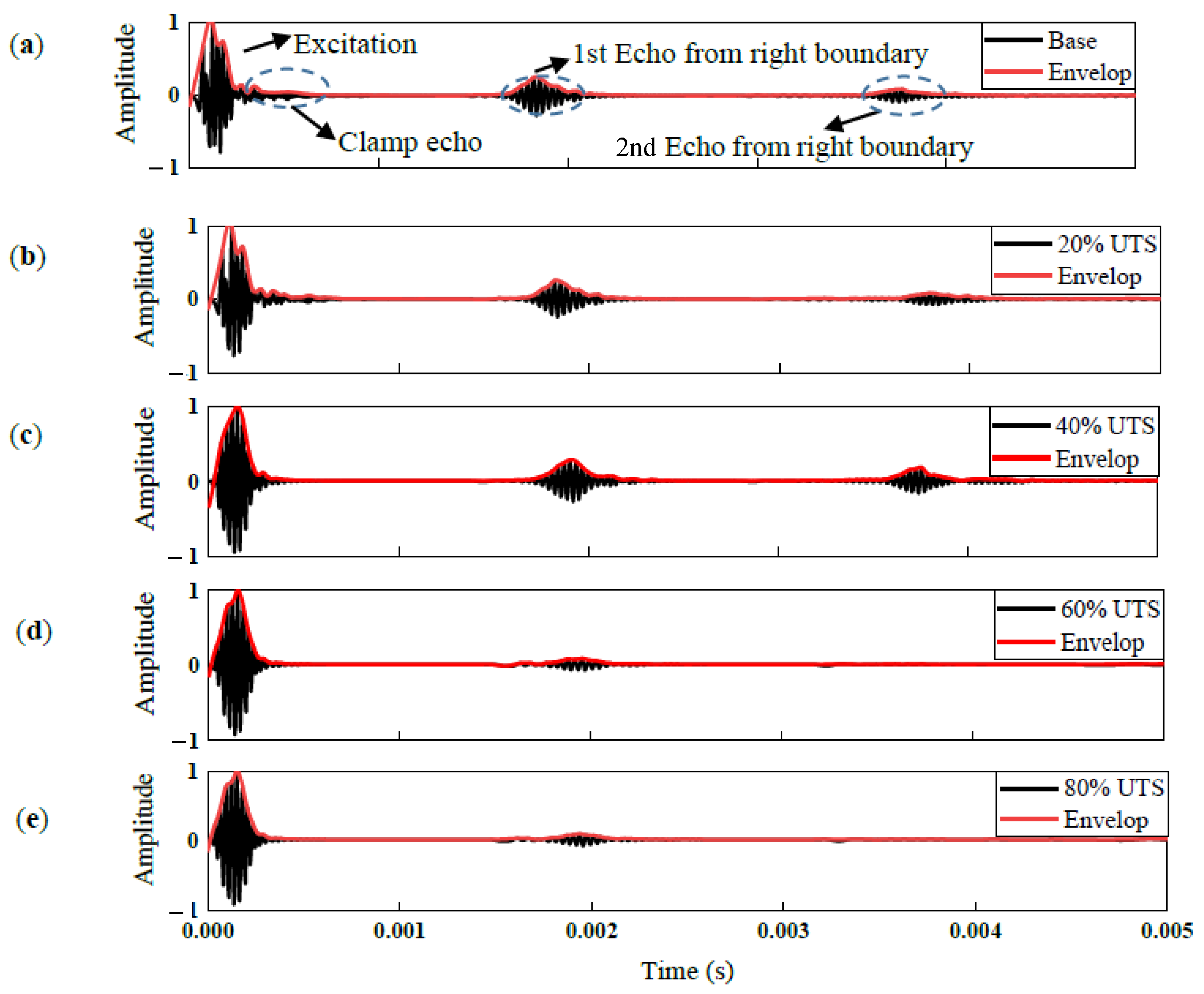
4.1. Feature Visualization
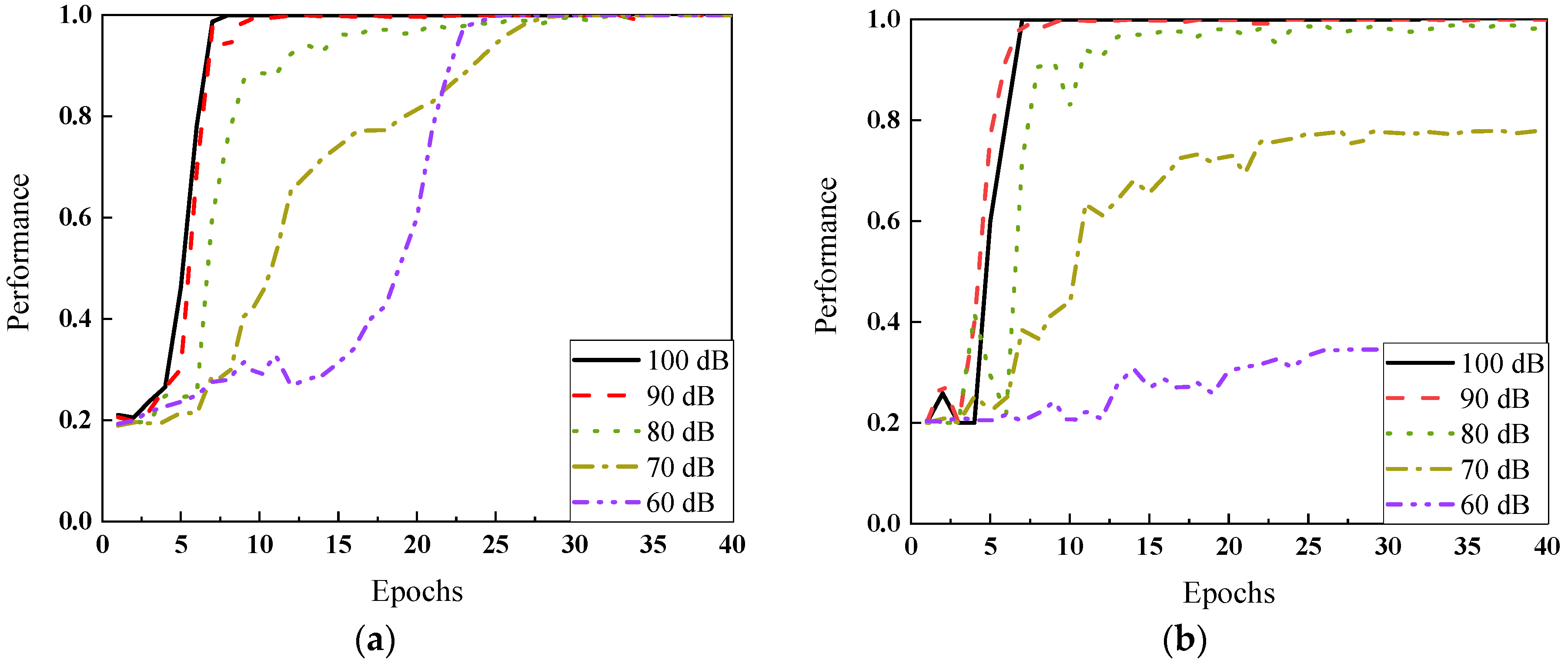
4.2. Classification for Prestress Levels of the Rod by CNN
4.3. Classification for Embedding Situation by CNN
5. Conclusions
- (a)
- The deep learning method effectively encoded the guided waves under complex uncertainties and assisted in stress level prediction and the embedded conditions of the rods, thereby showing potential for signal processing of NDE methods in structural health monitoring of PC structures.
- (b)
- The feature visualization method, t-SNE, provided an effective window that the different feature patterns could be clearly identified from visual two-dimensional plots. The distances between each feature point indicated the correlation among data. In addition, the impacts of noise interference on the data were observed with the use of this approach.
- (c)
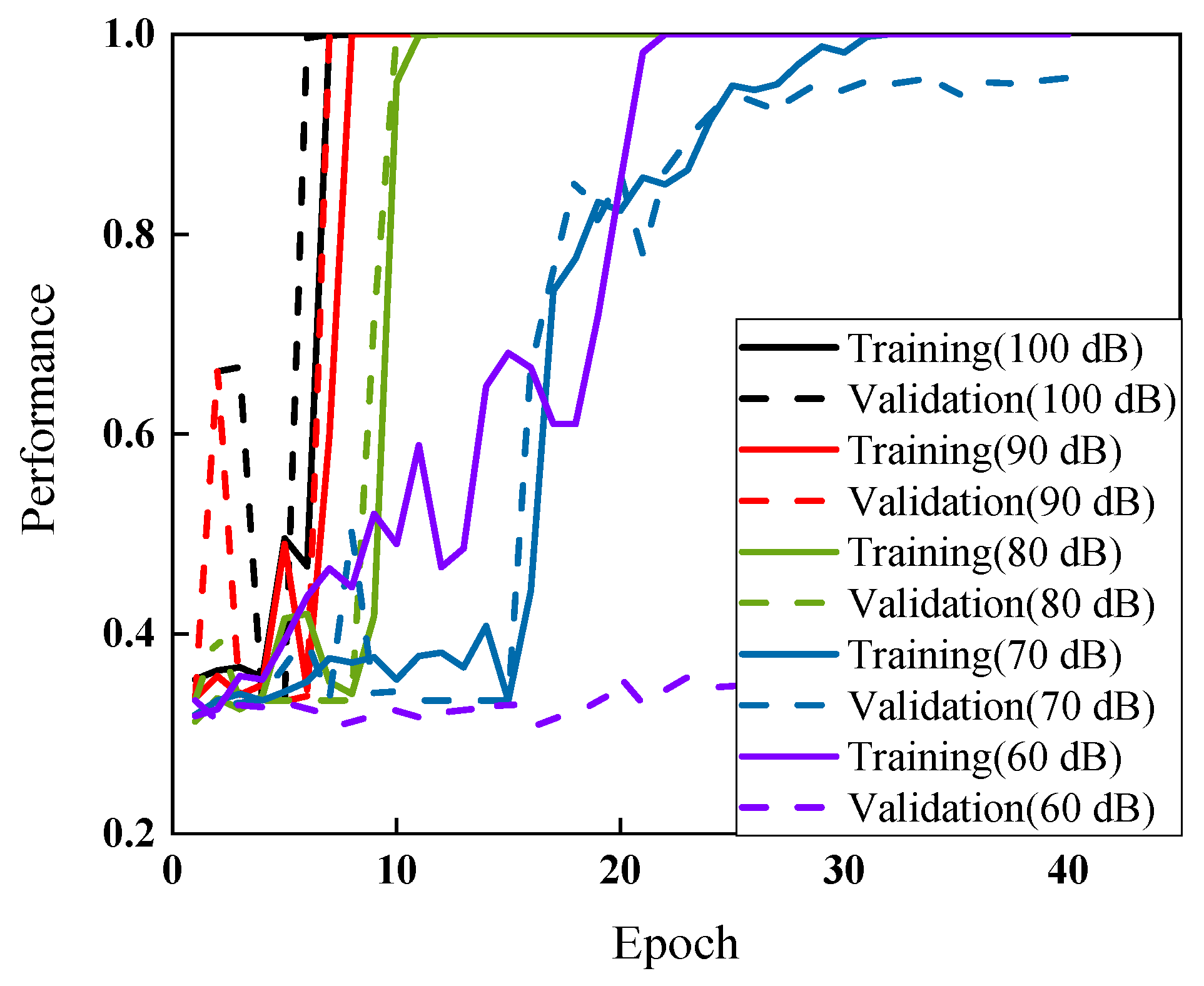
- The deep learning approach also exhibited high accuracy and robustness for data with high noise interference. The CNN classification for most cases could reach up to 100% when the noise levels were lower (80 dB–100 dB). However, with the energy of the noise (SNR = 70 dB) close to the signals, data classification exhibited a certain level of reduction, and the error rates were close to 80%. Particularly, when the noise increased to a much higher level (60 dB), all the signals were contaminated, and the effectiveness of the classification dropped.
- (d)
- The proposed method can also identify the embedding conditions. The identification is no less than 92% when the noise level is lower than 60 dB. However, the accuracy drops to 35% at 60 dB, which means it is difficult to distinguish the embedding conditions of rods.
Author Contributions
Funding
Conflicts of Interest
References
- Gui, G.; Pan, H.; Lin, Z.; Li, Y.; Yuan, Z. Data-driven support vector machine with optimization techniques for structural health monitoring and damage detection. KSCE J. Civ. Eng. 2017, 21, 523–534. [Google Scholar] [CrossRef]
- Tang, F.; Lin, Z.; Chen, G.; Yi, W. Three-dimensional corrosion pit measurement and statistical mechanical degradation analysis of deformed steel bars subjected to accelerated corrosion. Constr. Build. Mater. 2014, 70, 104–117. [Google Scholar] [CrossRef]
- Lin, Z.; Mostafa, F.; Wu, C.H.; Chen, G.; Bevans, W.J.; Gunasekaran, A.V.K.; Sedigh, S. Design, Construction, Laboratory and Field Testing of the Bridge on the Arnault Branch, Washington County, Missouri. In Center for Transportation Infrastructure and Safety/NUTC Program; Missouri University of Science and Technolog: Rolla, MO, USA, 2013. [Google Scholar]
- Bartoli, I.; Salamone, S.; Phillips, R.; Lanza di Scalea, F.; Sikorsky, C.S. Use of Interwire Ultrasonic Leakage to Quantify Loss of Prestress in Multiwire Tendons. J. Eng. Mech. 2011, 137, 324–333. [Google Scholar] [CrossRef]
- Chen, S.Z.; Wu, G.; Feng, D.C.J.M.S.; Processing, S. Damage detection of highway bridges based on long-gauge strain response under stochastic traffic flow. Mech. Syst. Signal Process. 2019, 127, 551–572. [Google Scholar] [CrossRef]
- Zhang, Z.; Pan, H.; Wang, X.; Tang, F.; Lin, Z. Ultrasonic guided wave approaches for pipeline damage diagnosis based on deep leaning. In Proceedings of the ASCE Pipelines 2022 Conference, Indianapolis, IN, USA, 31 July–3 August 2022. [Google Scholar]
- Zhang, Z.; Pan, H.; Wang, X.; Lin, Z. Machine learning-enabled Lamb wave approaches for damage detection. In Proceedings of the 2021 10th International Conference on Structural Health Monitoring of Intelligent Infrastructure, Porto, Portugal, 30 June–2 July 2021. [Google Scholar]
- Tang, F.; Lin, Z.; Qu, H. Investigation into corrosion-induced bond degradation between concrete and steel rebar with acoustic emission and 3D laser scan techniques. J. Infrastruct. Preserv. Resil. 2022, 3, 1–18. [Google Scholar] [CrossRef]
- Zhang, Y.M.; Wang, H.; Bai, Y.; Mao, J.X.; Xu, Y.C. Bayesian dynamic regression for reconstructing missing data in structural health monitoring. Struct. Health Monit. 2022, 21, 2097–2115. [Google Scholar] [CrossRef]
- Beard, M.; Lowe, M.; Cawley, P. Ultrasonic guided waves for inspection of grouted tendons and bolts. J. Mater. Civ. Eng. 2003, 15, 212–218. [Google Scholar] [CrossRef]
- Cobb, A.C.; Kwun, H.; Caseres, L.; Janega, G. Torsional guided wave attenuation in piping from coating, temperature, and large-area corrosion. NDT E Int. 2012, 47, 163–170. [Google Scholar] [CrossRef]
- Zhang, Z.; Pan, H.; Wang, X.; Lin, Z. Machine Learning-Enriched Lamb Wave Approaches for Automated Damage Detection. Sensors 2020, 20, 1790. [Google Scholar] [CrossRef]
- Zhang, Z.; Pan, H.; Wang, X.; Lin, Z. Deep Learning Empowered Structural Health Monitoring and Damage Diagnostics for Structures with Weldment via Decoding Ultrasonic Guided Wave. Sensors 2022, 22, 5390. [Google Scholar] [CrossRef]
- Sun, H.; Zhu, J. Nondestructive evaluation of steel-concrete composite structure using high-frequency ultrasonic guided wave. Ultrasonics 2020, 103, 106096. [Google Scholar] [CrossRef]
- Lanza di Scalea, F.; Rizzo, P.; Seible, F. Stress measurement and defect detection in steel strands by guided stress waves. J. Mater. Civ. Eng. 2003, 15, 219–227. [Google Scholar] [CrossRef]
- Ervin, B.L.; Kuchma, D.A.; Bernhard, J.T.; Reis, H. Monitoring corrosion of rebar embedded in mortar using high-frequency guided ultrasonic waves. J. Eng. Mech. 2009, 135, 9–19. [Google Scholar] [CrossRef]
- Chaki, S.; Bourse, G. Guided ultrasonic waves for non-destructive monitoring of the stress levels in prestressed steel strands. Ultrasonics 2009, 49, 162–171. [Google Scholar] [CrossRef]
- Treyssede, F.; Laguerre, L. Investigation of elastic modes propagating in multi-wire helical waveguides. J. Sound Vib. 2010, 329, 1702–1716. [Google Scholar] [CrossRef]
- Dubuc, B.; Ebrahimkhanlou, A.; Salamone, S. Higher order longitudinal guided wave modes in axially stressed seven-wire strands. Ultrasonics 2018, 84, 382–391. [Google Scholar] [CrossRef]
- Shoji, M. Ultrasonic Guided Wave Inspection of Anchor Rods Embedded in Soil. J. Nondestruct. Eval. 2019, 38, 96. [Google Scholar] [CrossRef]
- Pan, H.; Gui, G.; Lin, Z.; Yan, C. Deep BBN learning for health assessment toward decision-making on structures under uncertainties. KSCE J. Civ. Eng. 2018, 22, 928–940. [Google Scholar] [CrossRef]
- Lin, Z.; Pan, H.; Wang, X.; Li, M. Data-driven structural diagnosis and conditional assessment: From shallow to deep learning. In Proceedings of the Sensors and Smart Structures Technologies for Civil, Mechanical, and Aerospace Systems 2018, Denver, CO, USA, 4–8 March 2018; International Society for Optics and Photonics: Bellingham, WA, USA, 2018; p. 1059814. [Google Scholar]
- Abdeljaber, O.; Avci, O.; Kiranyaz, S.; Gabbouj, M.; Inman, D.J. Real-time vibration-based structural damage detection using one-dimensional convolutional neural networks. J. Sound Vib. 2017, 388, 154–170. [Google Scholar] [CrossRef]
- Fawaz, H.I.; Forestier, G.; Weber, J.; Idoumghar, L.; Muller, P.-A. Deep learning for time series classification: A review. Data Min. Knowl. Discov. 2019, 33, 917–963. [Google Scholar] [CrossRef]
- Pan, H.; Azimi, M.; Yan, F.; Lin, Z. Time-frequency-based data-driven structural diagnosis and damage detection for cable-stayed bridges. J. Bridge Eng. 2018, 23, 04018033. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, X.; Pan, H.; Lin, Z. Corrosion-induced damage identification in metallic structures using machine learning approaches. In Proceedings of the 2019 Defense TechConnect Innovation Summit, National Harbor, MD, USA, 7–10 October 2019. [Google Scholar]
- Cha, Y.J.; Choi, W.; Büyüköztürk, O. Deep learning-based crack damage detection using convolutional neural networks. Comput. Aided Civ. Infrastruct. Eng. 2017, 32, 361–378. [Google Scholar] [CrossRef]
- Cha, Y.J.; Choi, W.; Suh, G.; Mahmoudkhani, S.; Büyüköztürk, O. Autonomous structural visual inspection using region-based deep learning for detecting multiple damage types. Comput. Aided Civ. Infrastruct. Eng. 2018, 33, 731–747. [Google Scholar] [CrossRef]
- An, Y.-K.; Jang, K.; Kim, B.; Cho, S. Deep learning-based concrete crack detection using hybrid images. In Proceedings of the Sensors and Smart Structures Technologies for Civil, Mechanical, and Aerospace Systems 2018, Denver, CO, USA, 4–8 March 2018; International Society for Optics and Photonics: Bellingham, WA, USA, 2018; p. 1059812. [Google Scholar]
- Pan, H.; Zhang, Z.; Wang, X.; Lin, Z. Image-based damage conditional assessment of large-scale infrastructure systems using remote sensing and deep learning approaches. In Proceedings of the 2019 TechConnect World Innovation Conference, Boston, MA, USA, 17–19 June 2019. [Google Scholar]
- Guo, J.; Xie, X.; Bie, R.; Sun, L. Structural health monitoring by using a sparse coding-based deep learning algorithm with wireless sensor networks. Pers. Ubiquitous Comput. 2014, 18, 1977–1987. [Google Scholar] [CrossRef]
- Zhang, W.; Peng, G.; Li, C.; Chen, Y.; Zhang, Z. A new deep learning model for fault diagnosis with good anti-noise and domain adaptation ability on raw vibration signals. Sensors 2017, 17, 425. [Google Scholar] [CrossRef]
- Mahajan, H.; Banerjee, S. A machine learning framework for guided wave-based damage detection of rail head using surface-bonded piezo-electric wafer transducers. Mach. Learn. Appl. 2021, 7, 100216. [Google Scholar] [CrossRef]
- Tabian, I.; Fu, H.; Sharif Khodaei, Z. A Convolutional Neural Network for Impact Detection and Characterization of Complex Composite Structures. Sensors 2019, 19, 4933. [Google Scholar] [CrossRef]
- Zargar, S.A.; Yuan, F.-G. Impact diagnosis in stiffened structural panels using a deep learning approach. Struct. Health Monit. 2021, 20, 681–691. [Google Scholar] [CrossRef]
- Chree, C. The equations of an isotropic elastic solid in polar and cylindrical co-ordinates their solution and application. TCaPS 1889, 14, 250. [Google Scholar]
- Raghavan, A.; Cesnik, C.E. 3-D elasticity-based modeling of anisotropic piezocomposite transducers for guided wave structural health monitoring. J. Vib. Acoust. 2007, 129, 739–751. [Google Scholar] [CrossRef]
- Seco, F.; Martín, J.M.; Jiménez, A.; Pons, J.L.; Calderón, L.; Ceres, R. PCDISP: A tool for the simulation of wave propagation in cylindrical waveguides. In Proceedings of the 9th International Congress on Sound and Vibration, Orlando, FL, USA, 8–11 July 2002. [Google Scholar]
- Seco, F.; Jiménez, A.R. Modelling the generation and propagation of ultrasonic signals in cylindrical waveguides. Ultrason. Waves 2012, 1–28. [Google Scholar] [CrossRef]
- Beard, M.; Lowe, M. Non-destructive testing of rock bolts using guided ultrasonic waves. Int. J. Rock Mech. Min. Sci. 2003, 40, 527–536. [Google Scholar] [CrossRef]
- Haskins, R.W. Detection of Microcracks in Trunnion Rods Using Ultrasonic Guided Waves. 2015. Available online: https://apps.dtic.mil/sti/pdfs/ADA619008.pdf (accessed on 23 September 2022).
- Zhang, B.; Hong, X.; Liu, Y. Multi-task deep transfer learning method for guided wave-based integrated health monitoring using piezoelectric transducers. IEEE Sens. J. 2020, 20, 14391–14400. [Google Scholar] [CrossRef]
- Liang, X. Image-based post-disaster inspection of reinforced concrete bridge systems using deep learning with Bayesian optimization. Comput. Aided Civ. Infrastruct. Eng. 2019, 34, 415–430. [Google Scholar] [CrossRef]
- Zhang, Y.-M.; Wang, H.; Mao, J.-X.; Xu, Z.-D.; Zhang, Y.-F. Probabilistic framework with bayesian optimization for predicting typhoon-induced dynamic responses of a long-span bridge. J. Struct. Eng. 2021, 147, 04020297. [Google Scholar] [CrossRef]
- Gulgec, N.S.; Takáč, M.; Pakzad, S.N. Structural damage detection using convolutional neural networks. In Model Validation and Uncertainty Quantification, Volume 3; Springer: Cham, Switzerland, 2017; pp. 331–337. [Google Scholar]
- Maaten, L.v.d.; Hinton, G. Visualizing data using t-SNE. J. Mach. Learn. Res. 2008, 9, 2579–2605. [Google Scholar]




| Case | State | Prestressing Level (UTS) | Grout Material | Noise Level |
|---|---|---|---|---|
| 1 (no grout) | # 1 | zero | \ | 100 dB–60 dB |
| # 2 | 20% | \ | ||
| # 3 | 40% | \ | ||
| # 4 | 60% | \ | ||
| # 5 | 80% | \ | ||
| 2 (grease) | # 6 | zero | Grease | |
| # 7 | 20% | Grease | ||
| # 8 | 40% | Grease | ||
| # 9 | 60% | Grease | ||
| # 10 | 80% | Grease | ||
| 3 (cement) | # 11 | zero | Cement | |
| # 12 | 20% | Cement | ||
| # 13 | 40% | Cement | ||
| # 14 | 60% | Cement | ||
| # 15 | 80% | Cement |
| Name | Filters | Filter Size | Stride | Bias | Output Layer Size |
|---|---|---|---|---|---|
| Input layer | -- | -- | -- | -- | 1000 × 4 |
| Convolutional layer (C1) | 20 | 25 × 2 | 1 | 20 | 976 × 3 |
| Max pooling layer (P1) | 20 | 5 × 1 | 5 | -- | 195 × 3 |
| Convolutional layer (C2) | 40 | 25 × 3 | 1 | 40 | 171 × 1 |
| Max pooling layer (P1) | 40 | 5 × 1 | 5 | -- | 34 × 1 |
| Convolutional layer (C3) | 20 | 5 × 1 | 1 | 20 | 30 × 1 |
| ReLU | -- | -- | -- | -- | 30 × 1 |
| Fully connected layer (F1) | 5 | 30 × 1 | 1 | 5 | 5 |
| Softmax | -- | -- | -- | -- | 5 |
| 90 dB (100%) | 80 dB (98%) | |||||||||
| Base | 20% | 40% | 60% | 80% | Base | 20% | 40% | 60% | 80% | |
| Base | 100.0% | 0.0% | 0.0% | 0.0% | 0.0% | 99.0% | 0.0% | 0.0% | 0.0% | 0.0% |
| 20% | 0.0% | 100.0% | 0.0% | 0.0% | 0.0% | 1.0% | 100% | 0.0% | 0.0% | 0.0% |
| 40% | 0.0% | 0.0% | 100.0% | 0.0% | 0.0% | 0.0% | 0.0% | 100% | 0.0% | 0.0% |
| 60% | 0.0% | 0.0% | 0.0% | 100.0% | 0.0% | 0.0% | 0.0% | 0.0% | 98% | 7.0% |
| 80% | 0.0% | 0.0% | 0.0% | 0.0% | 100.0% | 0.0% | 0.0% | 0.0% | 2.0% | 93.0% |
| 70 dB (74%) | 60 dB (26.8%) | |||||||||
| Base | 75% | 27.0% | 0.0% | 0.0% | 0.0% | 28.0% | 27.0% | 20.0% | 12.0% | 15.0% |
| 20% | 25.0% | 71.0% | 1.0% | 0.0% | 0.0% | 28.0% | 22.0% | 17.0% | 15.0% | 12.0% |
| 40% | 0.0% | 0.0% | 98% | 0.0% | 0.0% | 20.0% | 16.0% | 34.0% | 17.0% | 22.0% |
| 60% | 0.0% | 1.0% | 1.0% | 63.0% | 37.0% | 14.0% | 14.0% | 12.0% | 23.0% | 15.0% |
| 80% | 0.0% | 1.0% | 0.0% | 37.0% | 63.0% | 10.0% | 21.0% | 17.0% | 33.0% | 36.0% |
| Case 2 (Grease as the Grout Material) | ||||||||||
| 90 dB (100%) | 80 dB (100%) | |||||||||
| Base | 20% | 40% | 60% | 80% | Base | 20% | 40% | 60% | 80% | |
| Base | 100.0% | 0.0% | 0.0% | 0.0% | 0.0% | 100.0% | 0.0% | 0.0% | 0.0% | 0.0% |
| 20% | 0.0% | 100.0% | 0.0% | 0.0% | 0.0% | 0.0% | 100.0% | 2.0% | 5.0% | 4.0% |
| 40% | 0.0% | 0.0% | 100.0% | 0.0% | 0.0% | 0.0% | 8.0% | 100.0% | 15.0% | 18.0% |
| 60% | 0.0% | 0.0% | 0.0% | 100.0% | 0.0% | 0.0% | 4.0% | 14.0% | 100.0% | 14.0% |
| 80% | 0.0% | 0.0% | 0.0% | 0.0% | 100.0% | 0.0% | 0.0% | 10.0% | 14.0% | 100.0% |
| 70 dB (78%) | 60 dB (46.6%) | |||||||||
| Base | 98% | 0.0% | 0.0% | 0.0% | 0.0% | 99% | 1% | 0% | 1% | 0% |
| 20% | 2.0% | 88% | 2.0% | 5.0% | 4.0% | 0% | 50% | 16% | 29% | 8% |
| 40% | 0.0% | 8.0% | 74% | 15.0% | 18.0% | 0% | 13% | 24% | 16% | 25% |
| 60% | 0.0% | 4.0% | 14.0% | 66% | 14.0% | 1% | 26% | 31% | 26% | 33% |
| 80% | 0.0% | 0.0% | 10.0% | 14.0% | 64.0% | 0% | 10% | 29% | 28% | 34% |
| Case 3 (Cement as the grout material) | ||||||||||
| 90 dB (100%) | 80 dB (94.4%) | |||||||||
| Base | 100.0% | 0.0% | 0.0% | 0.0% | 0.0% | 100.0% | 0.0% | 0.0% | 0.0% | 0.0% |
| 20% | 0.0% | 100.0% | 0.0% | 0.0% | 0.0% | 0.0% | 100.0% | 0.0% | 0.0% | 0.0% |
| 40% | 0.0% | 0.0% | 100.0% | 0.0% | 0.0% | 0.0% | 0.0% | 100.0% | 0.0% | 0.0% |
| 60% | 0.0% | 0.0% | 0.0% | 100.0% | 0.0% | 0.0% | 0.0% | 0.0% | 78.0% | 6.0% |
| 80% | 0.0% | 0.0% | 0.0% | 0.0% | 100.0% | 0.0% | 0.0% | 0.0% | 22.0% | 94.0% |
| 70 dB (76%) | 60 dB (41.6%) | |||||||||
| Base | 99.0% | 1.0% | 0.0% | 0.0% | 0.0% | 79.0% | 18.0% | 2.0% | 5.0% | 3.0% |
| 20% | 0.0% | 99.0% | 0.0% | 0.0% | 0.0% | 18.0% | 38.0% | 20.0% | 9.0% | 11.0% |
| 40% | 1.0% | 0.0% | 79.0% | 13.0% | 12.0% | 1.0% | 19.0% | 29.0% | 29.0% | 23.0% |
| 60% | 0.0% | 0.0% | 11.0% | 52.0% | 37.0% | 1.0% | 15.0% | 25.0% | 27.0% | 28.0% |
| 80% | 0.0% | 0.0% | 10.0% | 35.0% | 51.0% | 1.0% | 10.0% | 24.0% | 30.0% | 35.0% |
| 90 dB (100%) | 80 dB (100%) | |||||
| Unembedded | Cement | Grease | Unembedded | Cement | Grease | |
| Unembedded | 100.0% | 0.0% | 0.0% | 100.0% | 0.0% | 0.0% |
| Cement | 0.0% | 100.0% | 0.0% | 0.0% | 100.0% | 0.0% |
| Grease | 0.0% | 0.0% | 100.0% | 0.0% | 0.0% | 100.0% |
| 70 dB (92%) | 60 dB (35%) | |||||
| Unembedded | 84.0% | 0.0% | 7.0% | 37.0% | 24.0% | 39.0% |
| Cement | 1.0% | 99.0% | 0.0% | 28.0% | 43.0% | 36.0% |
| Grease | 15.0% | 1.0% | 93.0% | 35.0% | 33.0% | 25.0% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Z.; Tang, F.; Cao, Q.; Pan, H.; Wang, X.; Lin, Z. Deep Learning-Enriched Stress Level Identification of Pretensioned Rods via Guided Wave Approaches. Buildings 2022, 12, 1772. https://doi.org/10.3390/buildings12111772
Zhang Z, Tang F, Cao Q, Pan H, Wang X, Lin Z. Deep Learning-Enriched Stress Level Identification of Pretensioned Rods via Guided Wave Approaches. Buildings. 2022; 12(11):1772. https://doi.org/10.3390/buildings12111772
Chicago/Turabian StyleZhang, Zi, Fujian Tang, Qi Cao, Hong Pan, Xingyu Wang, and Zhibin Lin. 2022. "Deep Learning-Enriched Stress Level Identification of Pretensioned Rods via Guided Wave Approaches" Buildings 12, no. 11: 1772. https://doi.org/10.3390/buildings12111772
APA StyleZhang, Z., Tang, F., Cao, Q., Pan, H., Wang, X., & Lin, Z. (2022). Deep Learning-Enriched Stress Level Identification of Pretensioned Rods via Guided Wave Approaches. Buildings, 12(11), 1772. https://doi.org/10.3390/buildings12111772










