A GP-Based Hierarchical Objectives Decision-Making Method for Building Energy Efficiency Optimization
Abstract
1. Introduction
2. Literature Review
2.1. Methods for Multi-Objective Building Design
2.2. Comparison of GPM and MOO Models
- Converting the objectives into the weighted single objective which usually adopts the methods of weighted sum and weighted Tchebycheff [34]. In order to ensure that specific objectives have similar magnitudes, the normalization techniques must be implemented in advance. Wu et al. [35] introduced the weightings and net present value index to measure two specific objectives of energy saving after retrofitting.
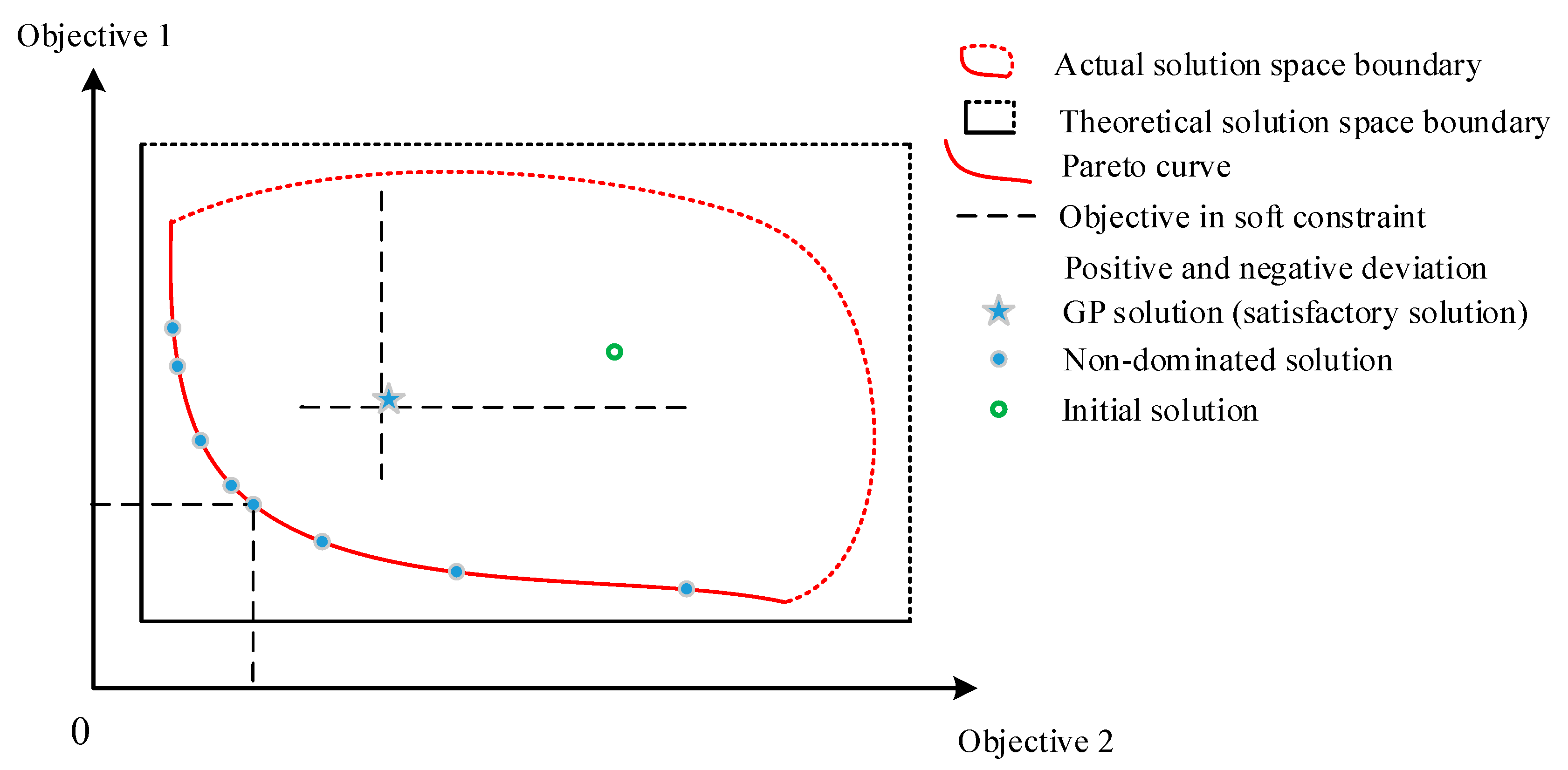
- Establishing the Pareto frontier as another approach to acquire the optimal solutions, which encompass a series of non-dominated solutions (Pareto optimality) according to the Pareto dominance concept [36]. Solutions on the Pareto frontier have no other feasible solution that can improve one specific solution without degrading at least one another [35]. The Pareto frontier has been employed by many studies to illustrate the trade-off variables and provide optional design schemes [6,22,35,37].
- In the construction project, there are some quantitative objectives, such as limited investment, relatively high energy efficiency, and limited construction period. These objectives are usually not equally important. A common verbal expression of the objectives is “the DMs desire to receive the Leadership in Energy and Environmental Design (LEED) gold certification on the basis of the limited investment”, which indicates that the cost is obviously of higher priority level than the sustainable indexes.
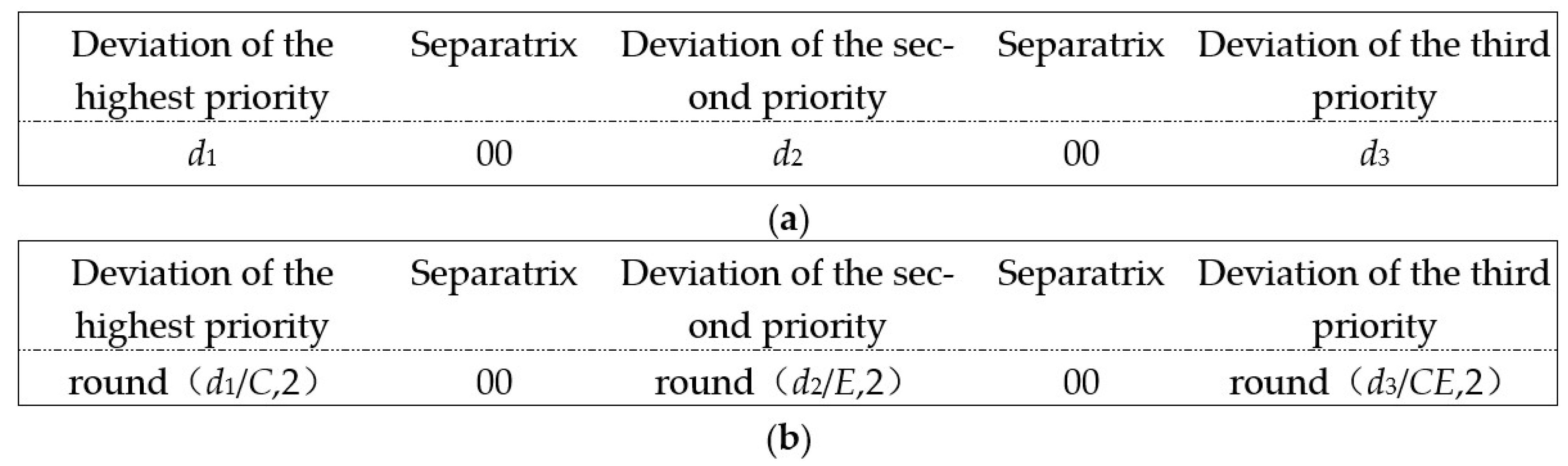
- The soft constraints introduced in the GPM approach ensure more flexibility in terms of delivering design requirements, and there are three total possible conditions to describe a soft constraint based on different usages: (a) when the negative deviational variable d- exists in a specific objective, it indicates that “the actual value is supposed to exceed the objective as far as possible”; (b) on the contrary, the existence of the positive deviational variable d+ means to make full use of the existing resources or reduce the use of excessive resource usage; and (c) the last condition that both d+ and d- exist underlines the shorter distance from the deviational variable to the objective rather than the specific approaching directions. The objective requires an exact match of both the actual value and the objective value.
- The hard constraints and the weighted constraints in the same priority level can be involved in the GPMs, expanding the application scenarios.
3. Research Methodology
3.1. Goal Programming Modeling
3.1.1. Brief Introduction
3.1.2. Development of Generalized Goal Programming Optimization Model
3.2. Optimization Procedure
3.2.1. Optimization Modeling
3.2.2. GPM Solution
3.2.3. GA Generation Loop
4. Case Study
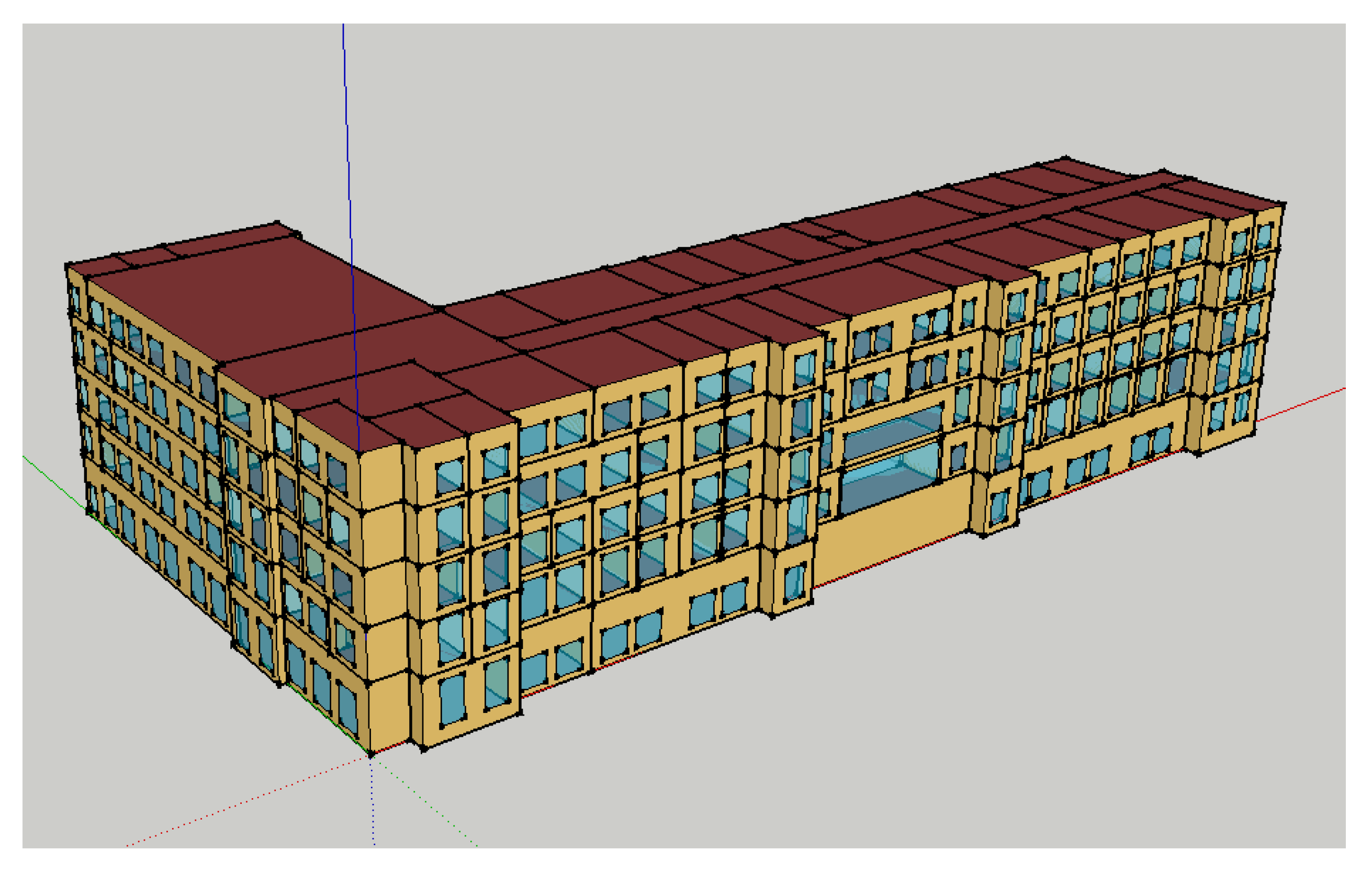
4.1. Case Introduction
4.2. Optimization with Five Scenarios
4.3. Programming
4.3.1. Python Programming Design
4.3.2. Python Code Basic Settings
4.4. Results and Discussion
4.4.1. Optimization Results for the Five Scenarios
4.4.2. Discussion
- Setting strict convergence conditions for each optimization objective in the GA iteration process;
- Setting a more flexible high priority level objective convergence threshold.
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Alpanda, S.; Peralta-Alva, A. Oil crisis, energy-saving technological change and the stock market crash of 1973–74. Rev. Econ. Dyn. 2010, 13, 824–842. [Google Scholar] [CrossRef]
- International Energy Agency (IEA). Key World Energy Statistics 2017; Organisation for Economic Co-operation and Development: Paris, France, 2017. [Google Scholar]
- International energy agency (IEA). World Energy Outlook. 2017. Available online: http://www.iea.org (accessed on 8 June 2020).
- Rebitzer, G. Integrating Life Cycle Costing and Life Cycle Assessment for Managing Costs and Environmental Impacts in Supply Chains. In Cost Management in Supply Chains; Physica: Heidelberg, Germany, 2002; pp. 127–146. [Google Scholar] [CrossRef]
- Hong, T.; Taylor-Lange, S.C.; D’Oca, S.; Yan, D.; Corgnati, S.P. Advances in research and applications of energy-related occupant behavior in buildings. Energy Build. 2016, 116, 694–702. [Google Scholar] [CrossRef]
- Liu, S.; Meng, X.; Tam, C. Building information modeling based building design optimization for sustainability. Energy Build. 2015, 105, 139–153. [Google Scholar] [CrossRef]
- Østergård, T.; Jensen, R.L.; Maagaard, S.E. Early Building Design: Informed decision-making by exploring multidimensional design space using sensitivity analysis. Energy Build. 2017, 142, 8–22. [Google Scholar] [CrossRef]
- Wang, C.; Cho, Y.K. Application of as-built data in building retrofit decision making process. Procedia Eng. 2015, 118, 902–908. [Google Scholar] [CrossRef][Green Version]
- Russell-Smith, S.V.; Lepech, M.D.; Fruchter, R.; Meyer, Y.B. Sustainable target value design: Integrating life cycle assessment and target value design to improve building energy and environmental performance. J. Clean. Prod. 2015, 88, 43–51. [Google Scholar] [CrossRef]
- Kaklauskas, A.; Zavadskas, E.K.; Raslanas, S. Multivariant design and multiple criteria analysis of building refurbishments. Energy Build. 2005, 37, 361–372. [Google Scholar] [CrossRef]
- Löhnert, G.; Dalkowski, A.; Sutter, W. Integrated Design Process: A Guideline for Sustainable and Solar-Optimised Building Design; International Energy Agency: Paris, France, 2003. [Google Scholar]
- Reed, B. The Integrative Design Guide to Green Building: Redefining the Practice of Sustainability; John Wiley & Sons: Hoboken, NJ, USA, 2009; Volume 43. [Google Scholar]
- Shao, Y. A systematic approach to energy efficiency improvements in buildings based on enterprise modeling method. In Proceedings of the SB13 Munich-Implementing Sustainability Changes, Munich, Germany, 24–26 April 2013; pp. 1283–1290. [Google Scholar]
- Antipova, E.; Boer, D.; Guillén-Gosálbez, G.; Cabeza, L.F.; Jiménez, L. Multi-objective optimization coupled with life cycle assessment for retrofitting buildings. Energy Build. 2014, 82, 92–99. [Google Scholar] [CrossRef]
- Mauro, G.M.; Hamdy, M.; Vanoli, G.P.; Bianco, N.; Hensen, J.L.M. A new methodology for investigating the cost-optimality of energy retrofitting a building category. Energy Build. 2015, 107, 456–478. [Google Scholar] [CrossRef]
- Abdou, N.; Mghouchi, Y.E.L.; Hamdaoui, S.; Asri, N.E.L.; Mouqallid, M. Multi-objective optimization of passive energy efficiency measures for net-zero energy building in Morocco. Build. Environ. 2021, 204, 108141. [Google Scholar] [CrossRef]
- Sharif, S.A.; Hammad, A. Simulation-based multi-objective optimization of institutional building renovation considering energy consumption, Life-Cycle Cost and Life-Cycle Assessment. J. Build. Eng. 2019, 21, 429–445. [Google Scholar] [CrossRef]
- Ascione, F.; Masi, R.F.D.; Rossi, F.D.; Ruggiero, S.; Vanoli, G.P. Optimization of building envelope design for nZEBs in Mediterranean climate: Performance analysis of residential case study. Appl. Energy 2016, 183, 938–957. [Google Scholar] [CrossRef]
- Kiss, B.; Szalay, Z. Modular approach to multi-objective environmental optimization of buildings. Autom. Constr. 2020, 111, 103044. [Google Scholar] [CrossRef]
- Hopfe, C.J.; Augenbroe, G.L.; Hensen, J.L. Multi-criteria decision making under uncertainty in building performance assessment. Build. Environ. 2013, 69, 81–90. [Google Scholar] [CrossRef]
- Ascione, F.; Bianco, N.; Stasio, C.D.; Mauro, G.M.; Vanoli, G.P. A new methodology for cost-optimal analysis by means of the multi-objective optimization of building energy performance. Energy Build. 2015, 88, 78–90. [Google Scholar] [CrossRef]
- Asadi, E.; da Silva, M.G.; Antunes, C.H.; Dias, L.; Glicksman, L. Multi-objective optimization for building retrofit: A model using genetic algorithm and artificial neural network and an application. Energy Build. 2014, 81, 444–456. [Google Scholar] [CrossRef]
- Bre, F.; Fachinotti, V.D. A computational multi-objective optimization method to improve energy efficiency and thermal comfort in dwellings. Energy Build. 2017, 154, 283–294. [Google Scholar] [CrossRef]
- Shi, X.; Tian, Z.; Chen, W.; Si, B.; Jin, X. A review on building energy efficient design optimization rom the perspective of architects. Renew. Sustain. Energy Rev. 2016, 65, 872–884. [Google Scholar] [CrossRef]
- Chegari, B.; Tabaa, M.; Simeu, E.; Moutaouakkil, F.; Medromi, H. Multi-objective optimization of building energy performance and indoor thermal comfort by combining artificial neural networks and metaheuristic algorithms. Energy Build. 2021, 239, 110839. [Google Scholar] [CrossRef]
- Delgarm, N.; Sajadi, B.; Kowsary, F.; Delgarm, S. Multi-objective optimization of the building energy performance: A simulation-based approach by means of particle swarm optimization (pso). Appl. Energy 2016, 170, 293–303. [Google Scholar] [CrossRef]
- Tuhus-Dubrow, D.; Krarti, M. Genetic-algorithm based approach to optimize building envelope design for residential buildings. Build. Environ. 2010, 45, 1574–1581. [Google Scholar] [CrossRef]
- Yu, W.; Li, B.; Jia, H.; Zhang, M.; Wang, D. Application of multi-objective genetic algorithm to optimize energy efficiency and thermal comfort in building design. Energy Build 2015, 88, 135–143. [Google Scholar] [CrossRef]
- Hamdy, M.; Hasan, A.; Siren, K. Applying a multi-objective optimization approach for design of low-emission cost-effective dwellings. Build. Environ. 2011, 46, 109–123. [Google Scholar] [CrossRef]
- Murray, S.N.; Walsh, B.P.; Kelliher, D.; O’Sullivan, D.T.J. Multi-variable optimization of thermal energy efficiency retrofitting of buildings using static modeling and genetic algorithms—A case study. Build. Environ. 2014, 75, 98–107. [Google Scholar] [CrossRef]
- Kusiak, A.; Xu, G.; Tang, F. Optimization of an HVAC system with a strength multi objective particle-swarm algorithm. Energy 2011, 36, 5935–5943. [Google Scholar] [CrossRef]
- Salas-Molina, F.; Rodriguez-Aguilar, J.A.; Pla-Santamaria, D. A stochastic goal programming model to derive stable cash management policies. J. Glob. Optim. 2019, 76, 333–346. [Google Scholar] [CrossRef]
- Bre, F.; Silva, A.S.; Ghisi, E.; Fachinotti, V.D. Residential building design optimisation using sensitivity analysis and genetic algorithm. Energy Build. 2016, 133, 853–866. [Google Scholar] [CrossRef]
- Steuer, R.E.; Choo, E.U. An interactive weighted Tchebycheff procedure for multiple objective programming. Math. Program. 1983, 26, 326–344. [Google Scholar] [CrossRef]
- Wu, Z.; Wang, B.; Xia, X. Large-scale building energy efficiency retrofit: Concept, model and control. Energy 2016, 109, 456–465. [Google Scholar] [CrossRef]
- Pierre, B. Pareto (Vilfredo)—Cours d’économie politique. Rev. Conomique 1965, 16, 811–812. [Google Scholar] [CrossRef]
- Li, X.; Malkawi, A. Multi-objective optimization for thermal mass model predictive control in small and medium size commercial buildings under summer weather conditions. Energy 2016, 112, 1194–1206. [Google Scholar] [CrossRef]
- Tamiz, M.; Jones, D.; Romero, C. Goal programming for decision making: An overview of the current state-of-the-art. Eur. J. Oper. Res. 1998, 111, 569–581. [Google Scholar] [CrossRef]
- Simon, H.A. Models of Man; Wiley: New York, NY, USA, 1955. [Google Scholar]
- Charnes, A.; Cooper, W.W. Management Models and Industrial Applications of Linear Programming; Wiley: New York, NY, USA, 1961. [Google Scholar]
- Lee, S.M. Goal Programming for Decision Analysis; Auerbach: Philadelphia, PA, USA, 1972. [Google Scholar]
- Ignizio, J.P. Goal Programming and Extensions (Lexington, Mass: DC Heath & Co); Lexington Books: Lexington, MA, USA, 1976. [Google Scholar]
- Romero, C. Handbook of Critical Issues in Goal Programming; Pergamon Press: Oxford, UK, 1991. [Google Scholar]
- Hamta, N.; Ehsanifar, M.; Sarikhani, J. Presenting a goal programming model in the time-cost-quality trade-off. Int. J. Constr. Manag. 2021, 21, 1–11. [Google Scholar] [CrossRef]
- Qian, S.D. Operations Research, 4th ed.; Tsinghua University Press: Beijing, China, 2012. [Google Scholar]
- De Kluyver, C.A. An exploration of various goal programming formulations-with application to advertising media scheduling. J. Oper. Res. Soc. 1979, 30, 167–171. [Google Scholar] [CrossRef]
- Masud, A.S.; Hwang, C.L. Interactive sequential goal programming. J. Oper. Res. Soc. 1981, 32, 391–400. [Google Scholar] [CrossRef]
- Al-Zubaydi, A.Y. Building models design and energy simulation with google sketchup and openstudio. J. Adv. Sci. Eng. Res. 2013, 3, 318–333. [Google Scholar]
- Hygh, J.S.; Decarolis, J.F.; Hill, D.B.; Ranjithan, S.R. Multivariate regression as an energy assessment tool in early building design. Build. Environ. 2012, 57, 165–175. [Google Scholar] [CrossRef]
- Geyer, P.; Schlüter, A. Automated metamodel generation for design space exploration and decision-making—A novel method supporting performance-oriented building design and retrofitting. Appl. Energy 2014, 119, 537–556. [Google Scholar] [CrossRef]
- Glodon Cost. GTJ2018 Operation Manual of Glodon BIM Civil Engineering Measurement Platform. 2018. Available online: https://max.book118.com/html/2019/0521/7200124063002026shtm (accessed on 14 May 2020).
- Goldberg, D.E. Genetic Algorithms in Search, Optimization and Machine Learning; Addison-Wesley Pub. Co.: Boston, MA, USA, 1989. [Google Scholar] [CrossRef]
- MOHURD. Thermal Design Code of Civil Buildings (GB 50176-2016); China Architecture & Building Press: Beijing, China, 2016.
- MOHURD. Code of Bills of Quantities and Valuation for Construction Works (GB 50500-2013); China Architecture & Building Press: Beijing, China, 2013.
- Carbon Emission Factor of the Building Materials. Available online: http://www.tanpaifang.com/tanjiliang/2019/0430/63792.html (accessed on 22 March 2020).

| People Density | Equipment Density | Usage Duration | Heating Room | Cooling Room | |
|---|---|---|---|---|---|
| Professor Office | Medium | Medium | Medium | Yes | Yes |
| Student Office | Large | Large | Long | Yes | Yes |
| Laboratory | Low | Low | Medium | Yes | Yes |
| Meeting Room | Large | Low | Short | Yes | Yes |
| Corridor | - | - | - | No | No |
| File Room | Low | Low | Short | Yes | Yes |
| No. | Density (kg/m3) | Conductivity (W/m·K) | Specific Heat (J/kg·K) | Thickness (m) | CUP (CNY/m3) | CEF (kg/m3) | |
|---|---|---|---|---|---|---|---|
| 1 | 800 | 0.54 | 1050 | [0.12, 0.37] | 355.85 | 321.99 | |
| 2 | 1400 | 0.58 | 1050 | 290.94 | 488.79 | ||
| 3 | 1800 | 0.87 | 1050 | 278.11 | 273 | ||
| 4 | 2300 | 1.453 | 1050 | 375.95 | 301.97 | ||
| 5 | 1280 | 1.12 | 1050 | 224.64 | 146 | ||
| 6 | 700 | 0.18 | 1050 | 423.73 | 230 | ||
| 7 | 2350 | 1.579 | 874 | 572 | 399.9 | ||
| 1 | 25 | 0.03 | 5350 | [0.02, 0.1] | 767.28 | 43.75 | |
| 2 | 18 | 0.041 | 2410 | 411.17 | 27.5 | ||
| 3 | 120 | 0.045 | 750 | 860.8 | 19.75 | ||
| 4 | 30 | 0.042 | 1380 | 889.9 | 154 | ||
| 5 | 30 | 0.033 | 1380 | 910.58 | 174 | ||
| 1 | 1800 | 0.93 | 1050 | [0.01, 0.05] | 937.37 | 377 | |
| 1 | 2300 | 1.453 | 1050 | [0.1, 0.25] | 379.95 | 301.97 | |
| 2 | 2350 | 1.579 | 874 | 591.13 | 399.9 | ||
| 1 | 25 | 0.03 | 5350 | [0.02, 0.1] | 589.62 | 43.75 | |
| 2 | 18 | 0.041 | 2410 | 376.62 | 27.5 | ||
| 3 | 120 | 0.045 | 750 | 484 | 102.4 | ||
| 4 | 30 | 0.42 | 1380 | 587.15 | 154 | ||
| 1 | 1800 | 0.93 | 1050 | [0.01, 0.05] | 937.37 | 377 | |
| 2 | 2100 | 1.28 | 1050 | 728.4 | 239.19 | ||
| 1 | 2300 | 1.453 | 1050 | [0.08, 0.25] | 379.95 | 301.97 | |
| 2 | 2350 | 1.579 | 874 | 591.13 | 399.9 | ||
| 1 | 25 | 0.03 | 5350 | [0.02, 0.1] | 767.28 | 43.75 | |
| 2 | 18 | 0.041 | 2410 | 511.17 | 27.5 | ||
| 3 | 120 | 0.045 | 750 | 860.8 | 102.4 | ||
| 4 | 30 | 0.042 | 1380 | 516.19 | 154 | ||
| 5 | 30 | 0.033 | 1380 | 910.58 | 174 | ||
| 1 | 1800 | 0.93 | 1050 | [0.01, 0.05] | 937.37 | 377 | |
| 2 | 2100 | 1.28 | 1050 | 728.4 | 239.19 | ||
| 1 | 2300 | 1.453 | 1050 | [0.08, 0.15] | 379.95 | 301.97 | |
| 2 | 2350 | 1.579 | 874 | 591.13 | 399.9 | ||
| 1 | 1800 | 0.93 | 1050 | [0.01, 0.05] | 937.37 | 377 | |
| 2 | 2100 | 1.28 | 1050 | 728.4 | 239.19 |
| No. | U-Factor (W/m2·K) | SHGC * | Thickness (m) | CUP (CNY/m2) | CEF (kg/m2) | |
|---|---|---|---|---|---|---|
| 1 | 5.818 | 0.8 | 0.0058 | 79.81 | 18.87 | |
| 2 | 5.604 | 0.76 | 0.012 | 126.56 | 34.98 | |
| 3 | 5.58 | 0.75 | 0.010 | 221.06 | 29.58 | |
| 4 | 3.109 | 0.72 | 0.018 | 126.56 | 34.98 | |
| 5 | 2.835 | 0.72 | 0.021 | 143.06 | 34.98 | |
| 6 | 2.7 | 0.72 | 0.024 | 148.06 | 34.98 | |
| 7 | 2.084 | 0.68 | 0.021 | 252.06 | 37.41 |
| Scenario 1 | Scenario 2 | Scenario 3 | Scenario 4 | Scenario 5 | |
|---|---|---|---|---|---|
| Model Expression |
| Objective (Unit) | Solution Boundary | Selected Objective Value | |
|---|---|---|---|
| Lower | Upper | ||
| C (CNY) | 815,673.9 | 4,014,919 | 2,000,000 |
| E (GJ) | 1243.47 | 2473.68 | 1600 (1200 and 400 in Scenario 4) |
| EC (kg) | 473,451.9 | 2,095,093 | 1,200,000 |
| Fitness Values of Best Individuals after Each GA Iteration Generation | Best in Scenario | 1 | 2 | 3 | 4 | 5 | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Generation 1 | Generation 2 | Generation 3 | Generation 4 | Generation 5 | Fitness value | 1,001,500.7 | 0.04 | 1200.31 | 1600.31 | 100.10 | ||
| Scenario 1 | 3,001,700.02 | 3,001,700.02 | 2,000,900.09 | 2,000,900.09 | 1,001,500.7 | Design Parameter Combination | 4 | 2 | 6 | 4 | 2 | |
| Scenario 2 | 300.1 | 0.23 | 0.23 | 0.23 | 0.04 | 0.34 | 0.158 | 0.297 | 0.167 | 0.297 | ||
| Scenario 3 | 1,000,900.26 | 1,000,400.29 | 1,000,400.29 | 1,000,400.29 | 1200.31 | 1 | 5 | 2 | 2 | 4 | ||
| Scenario 4 | 1800.55 | 1800.55 | 1800.55 | 1800.55 | 1600.31 | 0.029 | 0.026 | 0.095 | 0.027 | 0.084 | ||
| Scenario 5 | 100.32 | 100.32 | 100.32 | 100.10 | 100.10 | 1 | 1 | 2 | 1 | 2 | ||
| GA iteration convergence process | 0.01 | 0.042 | 0.01 | 0.047 | 0.011 | |||||||
 | 1 | 2 | 2 | 2 | 1 | |||||||
| 0.107 | 0.207 | 0.217 | 0.213 | 0.138 | ||||||||
| 5 | 1 | 4 | 5 | 4 | ||||||||
| 0.06 | 0.085 | 0.091 | 0.066 | 0.023 | ||||||||
| 2 | 2 | 2 | 2 | 2 | ||||||||
| 0.038 | 0.016 | 0.041 | 0.037 | 0.043 | ||||||||
| 2 | 1 | 1 | 2 | 1 | ||||||||
| 0.127 | 0.231 | 0.119 | 0.158 | 0.196 | ||||||||
| 1 | 2 | 4 | 4 | 2 | ||||||||
| 0.069 | 0.07 | 0.06 | 0.053 | 0.03 | ||||||||
| 1 | 1 | 2 | 2 | 1 | ||||||||
| 0.022 | 0.044 | 0.043 | 0.047 | 0.04 | ||||||||
| 1 | 3 | 2 | 2 | 2 | ||||||||
| 0.094 | 0.146 | 0.145 | 0.135 | 0.085 | ||||||||
| 2 | 1 | 2 | 1 | 1 | ||||||||
| 0.038 | 0.017 | 0.041 | 0.033 | 0.036 | ||||||||
| 7 | 5 | 5 | 7 | 3 | ||||||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, X.; Liu, S.; Sun, Y. A GP-Based Hierarchical Objectives Decision-Making Method for Building Energy Efficiency Optimization. Buildings 2022, 12, 52. https://doi.org/10.3390/buildings12010052
Li X, Liu S, Sun Y. A GP-Based Hierarchical Objectives Decision-Making Method for Building Energy Efficiency Optimization. Buildings. 2022; 12(1):52. https://doi.org/10.3390/buildings12010052
Chicago/Turabian StyleLi, Xiang, Sha Liu, and Yichao Sun. 2022. "A GP-Based Hierarchical Objectives Decision-Making Method for Building Energy Efficiency Optimization" Buildings 12, no. 1: 52. https://doi.org/10.3390/buildings12010052
APA StyleLi, X., Liu, S., & Sun, Y. (2022). A GP-Based Hierarchical Objectives Decision-Making Method for Building Energy Efficiency Optimization. Buildings, 12(1), 52. https://doi.org/10.3390/buildings12010052







