Seismic Analysis of the Bell Tower of the Church of St. Francis of Assisi on Kaptol in Zagreb by Combined Finite-Discrete Element Method
Abstract
:1. Introduction
2. FDEM Numerical Modelling
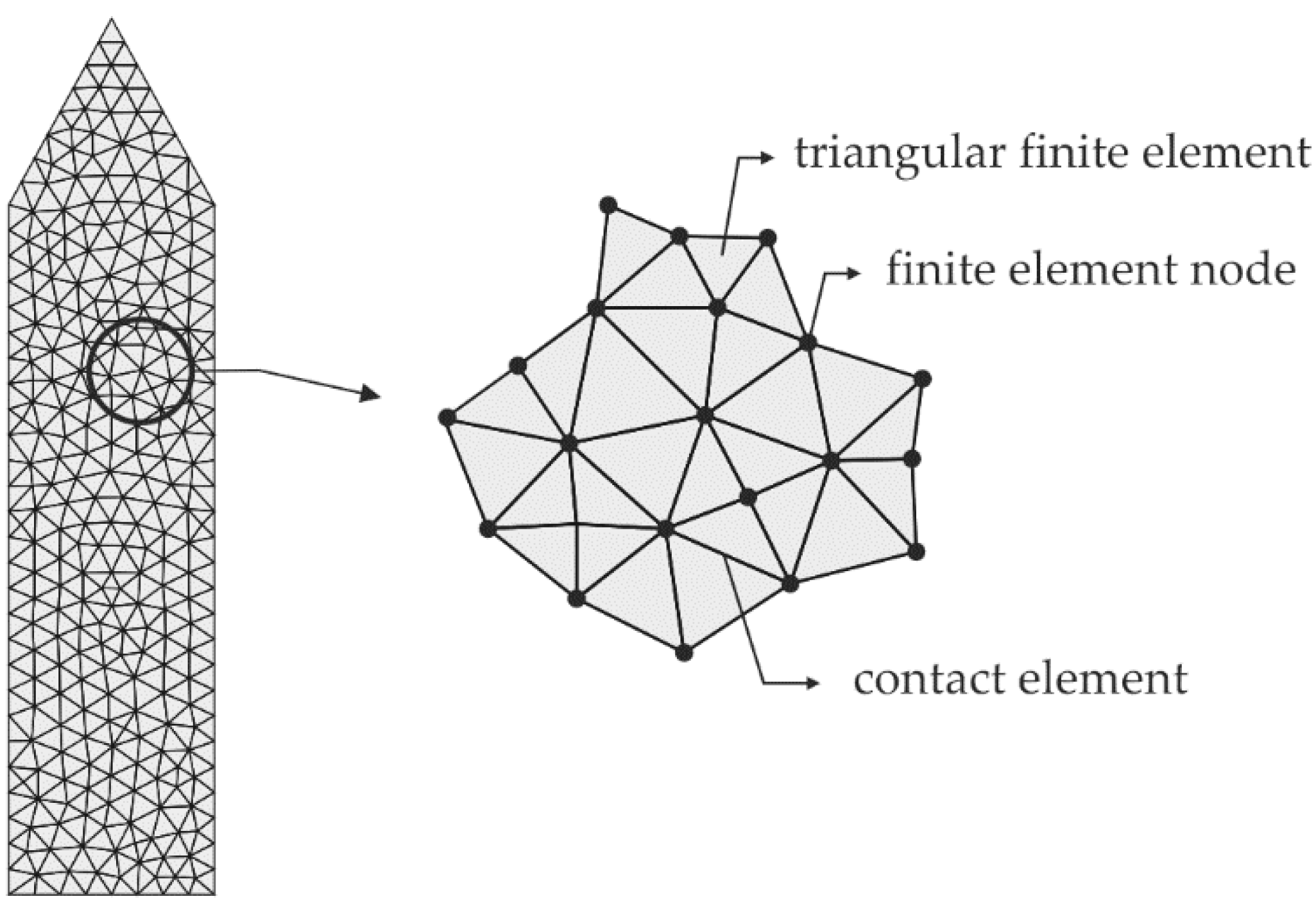
2.1. Discretisation of the Structure
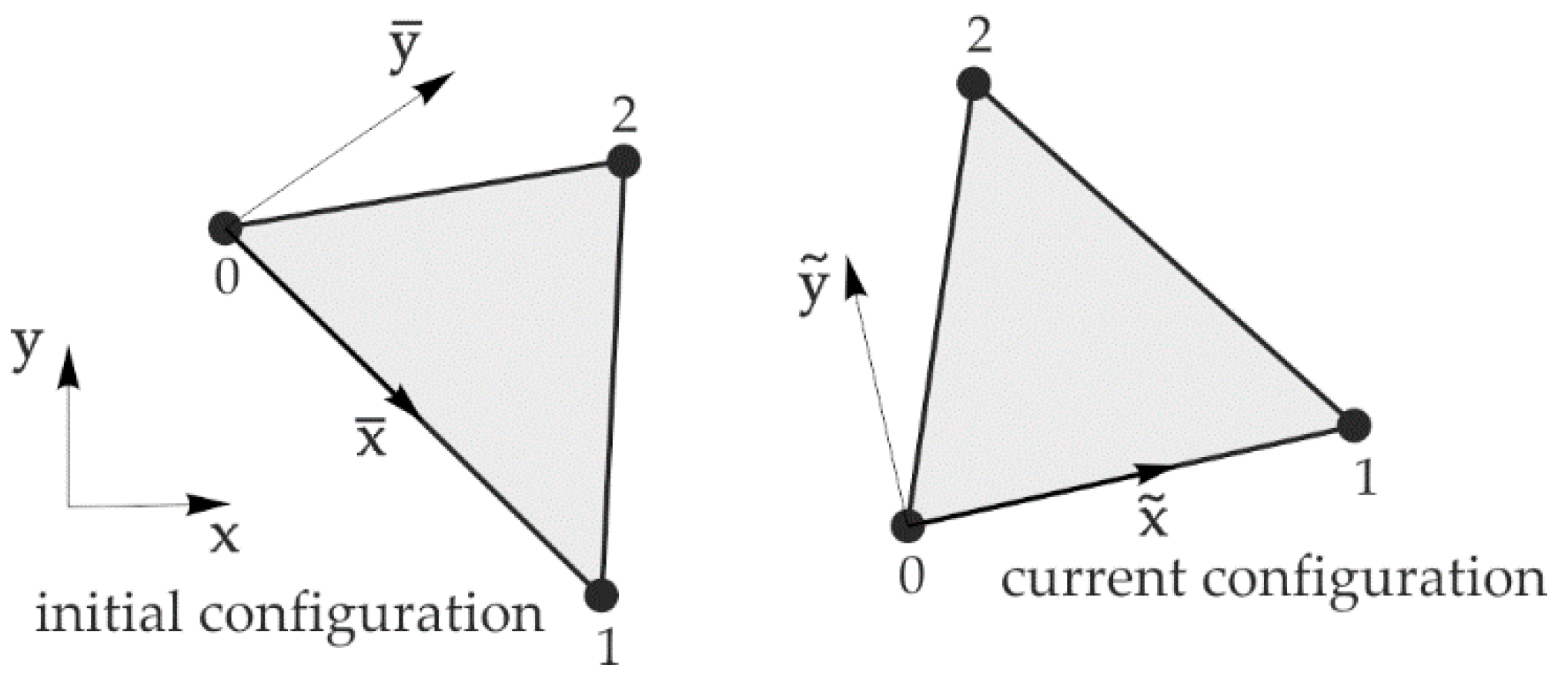
2.2. Deformability of Finite Elements
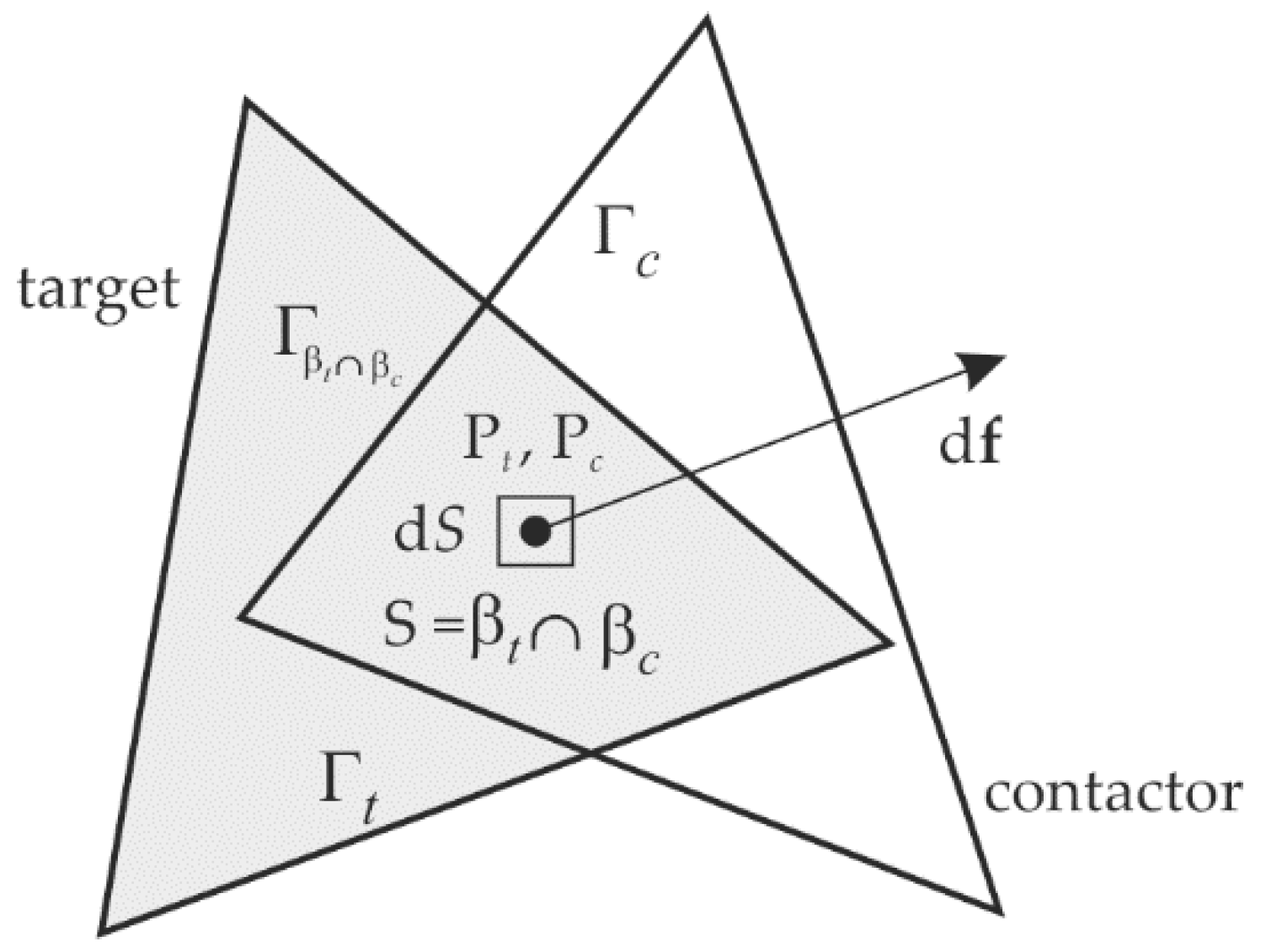
2.3. Contact Detection and Interaction
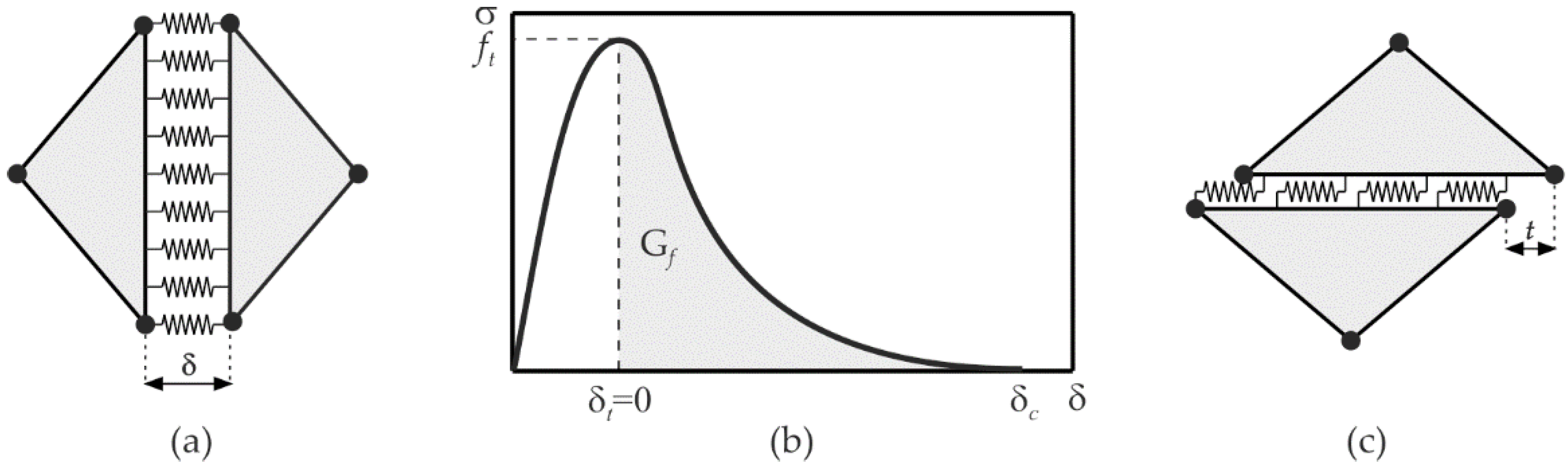
2.4. Fracture and Fragmentation
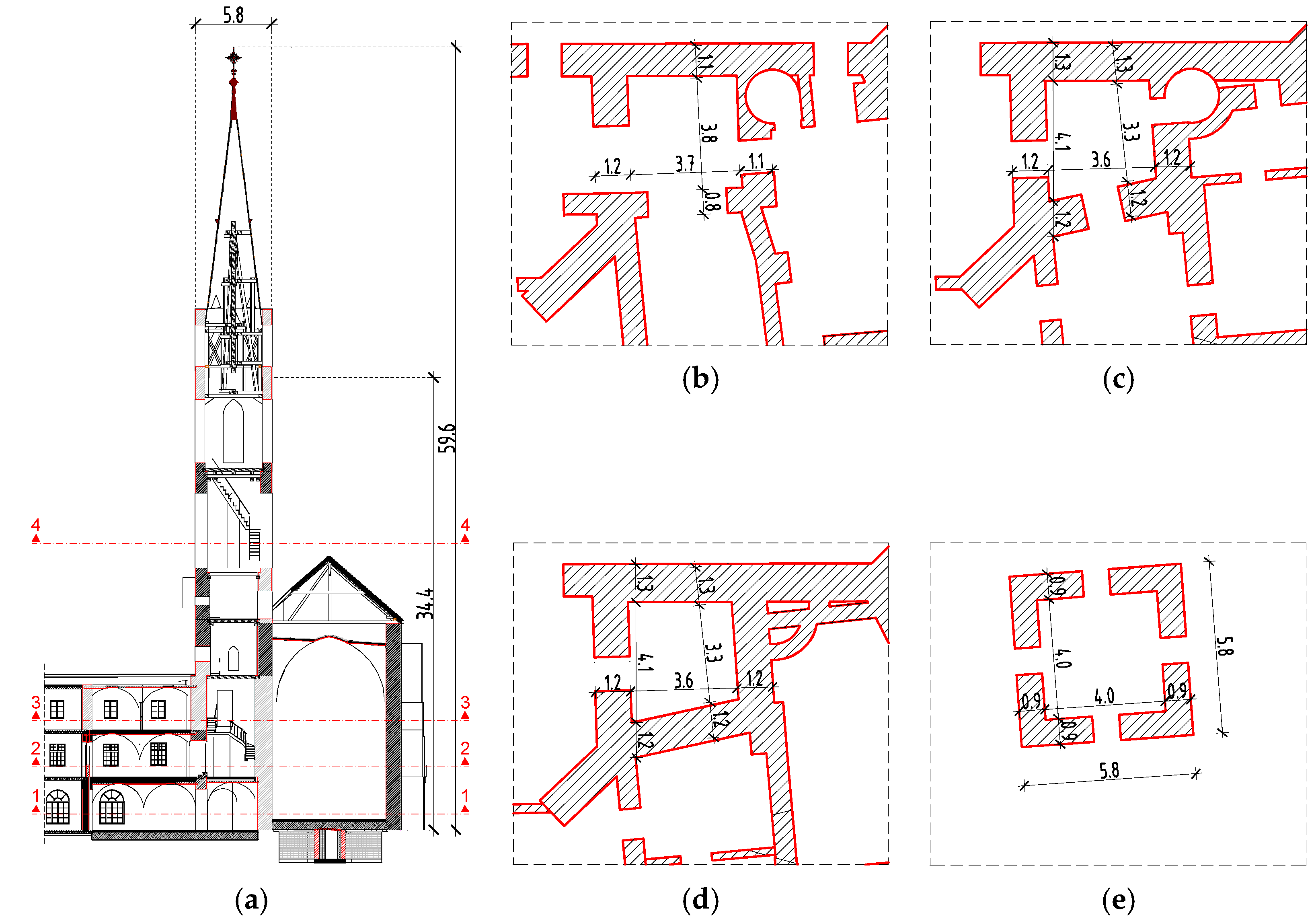
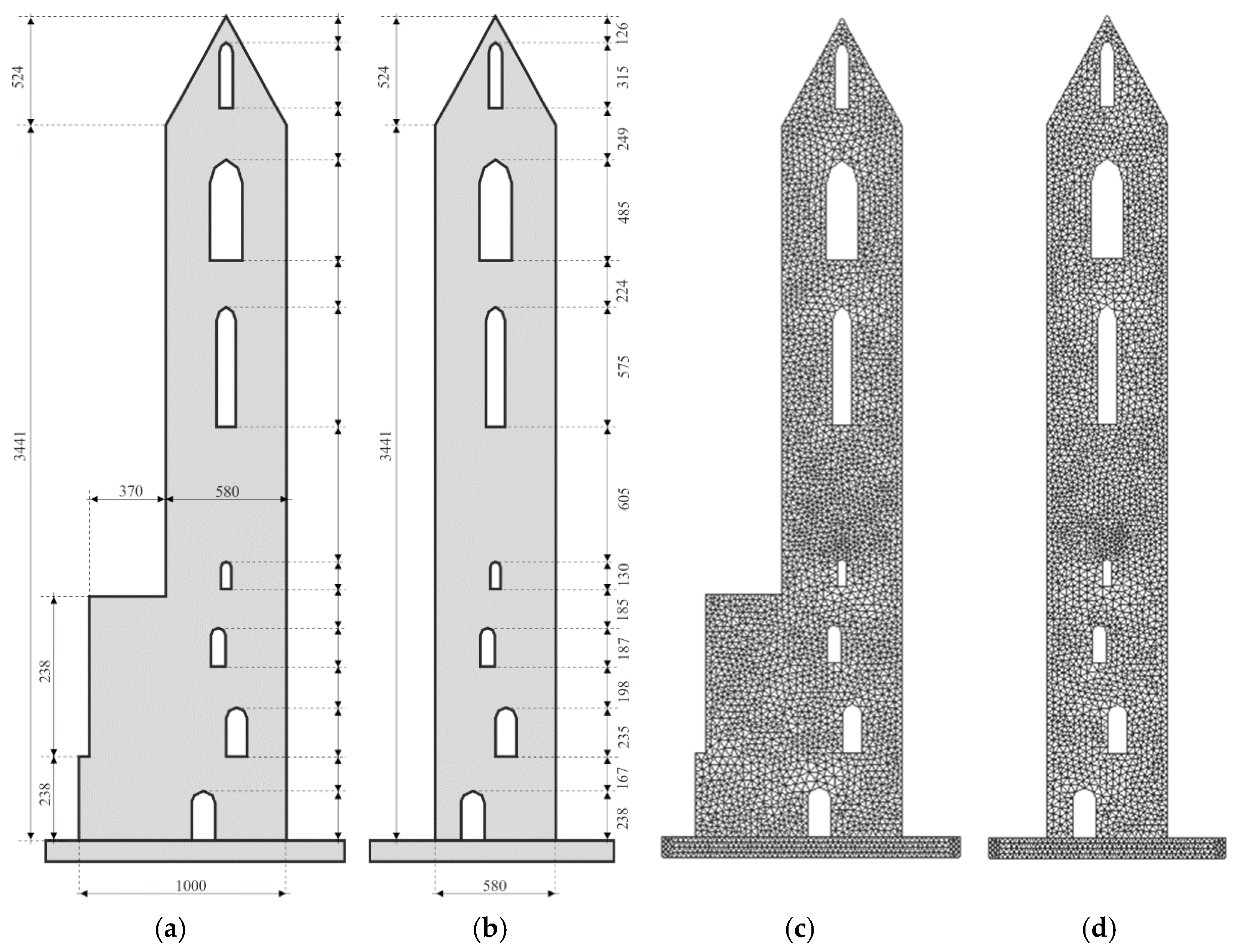
3. Description of the Structure and Numerical Model of Bell Tower
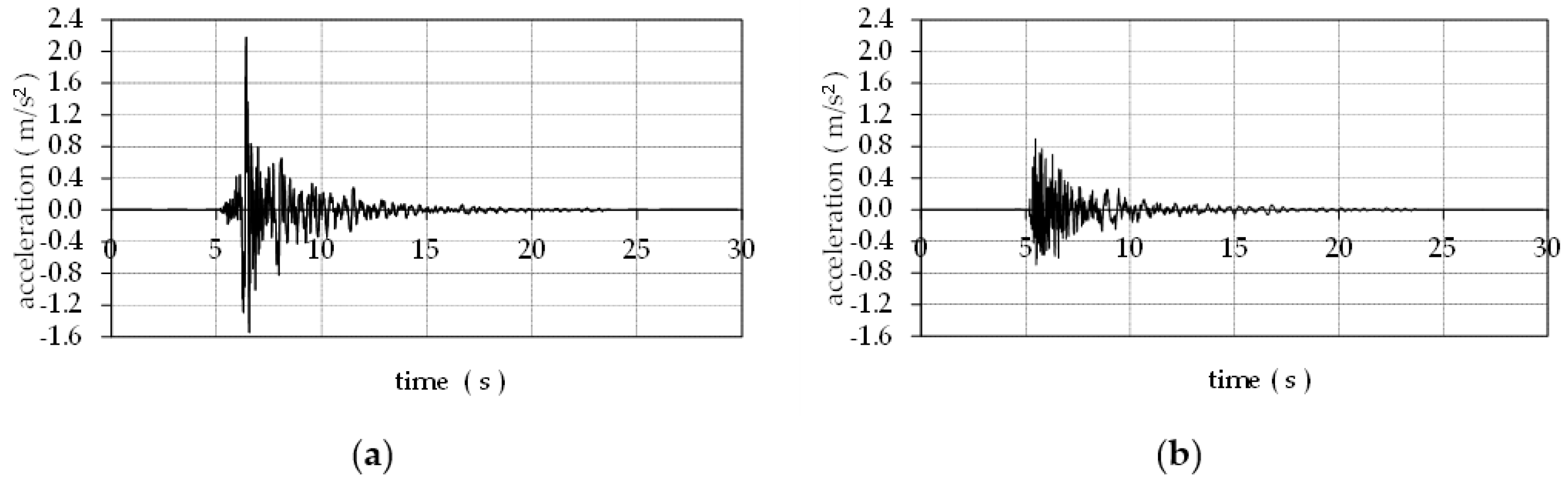
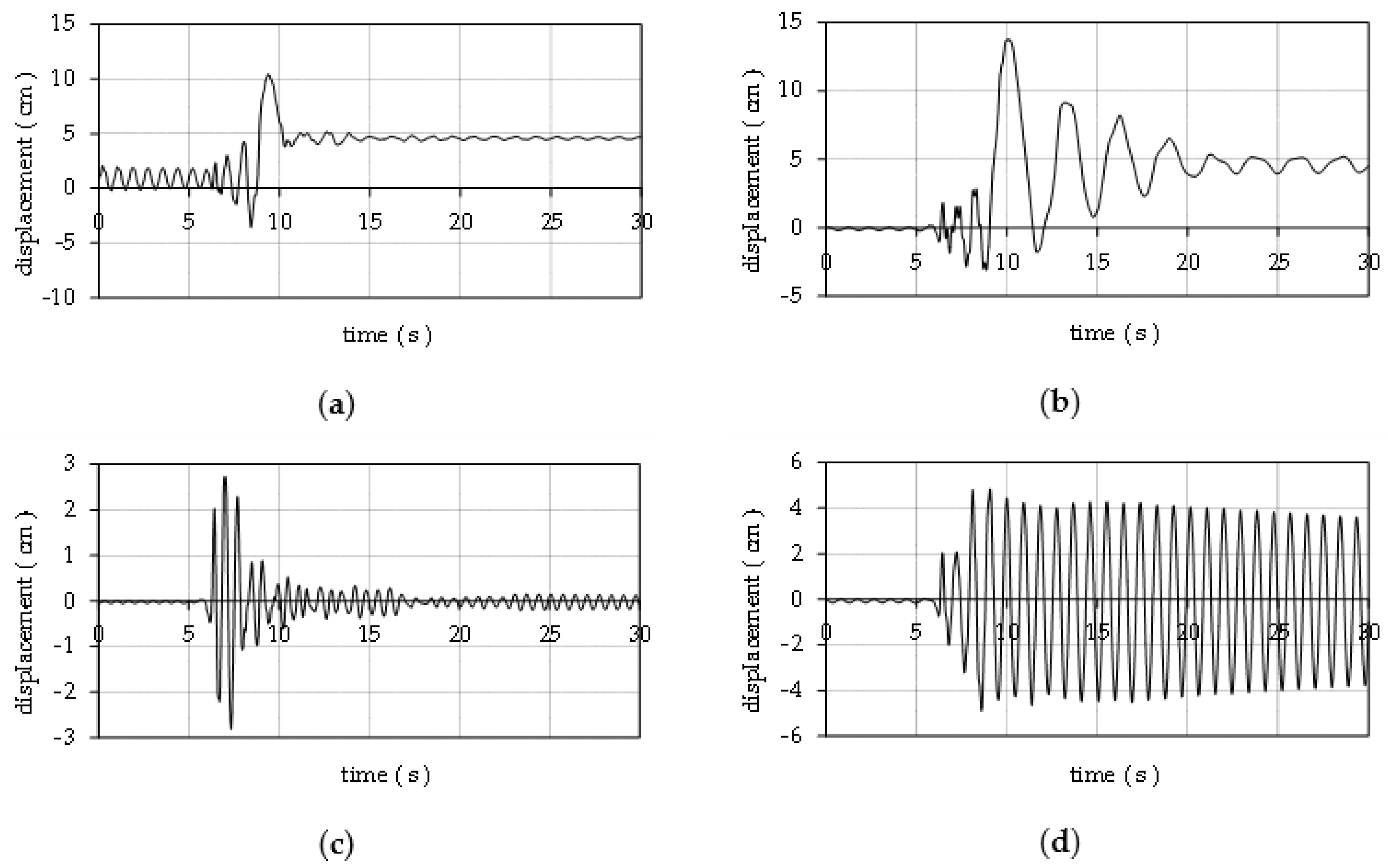
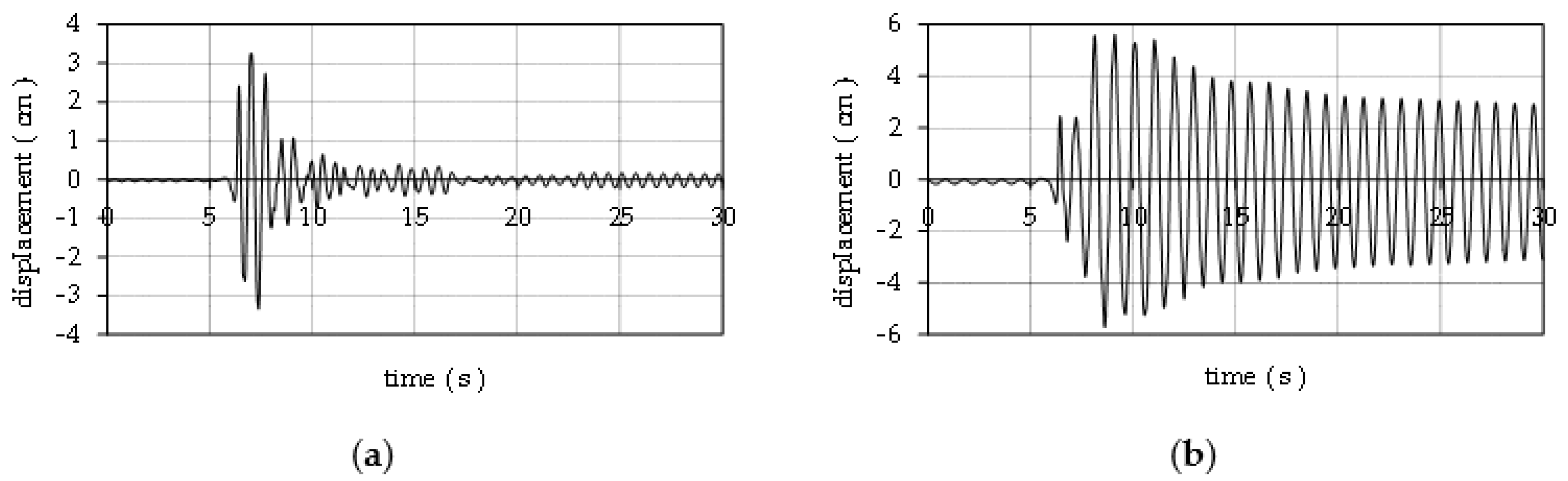
4. Results and Discussion
5. Conclusions
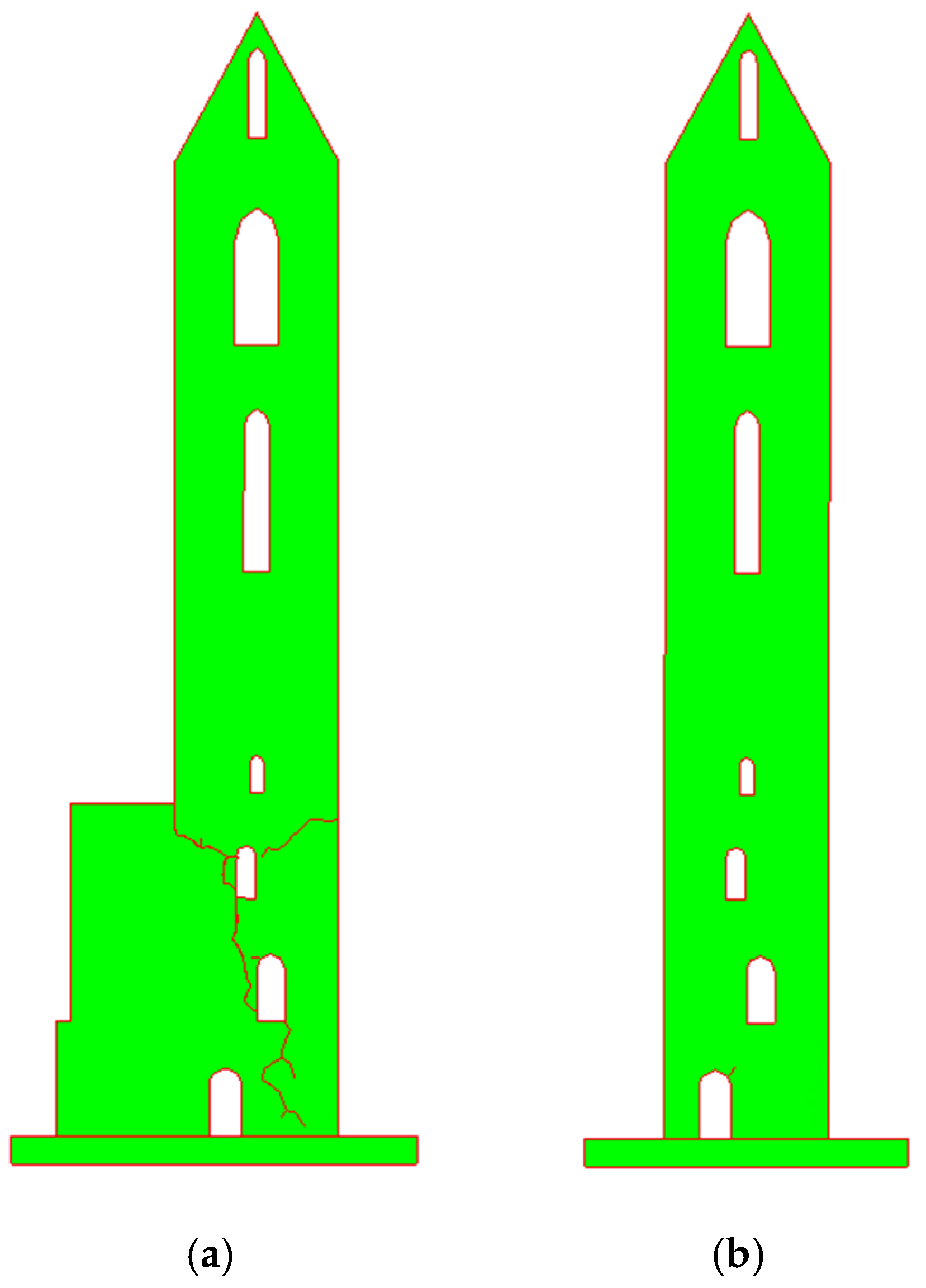
- The comparison of the crack pattern obtained with the numerical model and the ones which occurred on the bell tower during the earthquake in Zagreb on 22 March 2020 confirms that the adopted numerical model, based on the combined finite-discrete element method, is suitable for analysing the dynamic response of this and similar structures due to seismic activity.
- Very good matching of the crack pattern in the numerical model and on the actual structure confirms that the proposed modelling approach, which is based on the macro scale approach, is reliable enough to estimate the seismic resistance of this and similar structures. This finding may be significant since the macroscale approach is computationally very efficient for analysing the real-scale structure unlike the micro- and simplified microscale approach.
- The bell tower, with the corresponding geometry and assumed material properties, did not have the appropriate level of mechanical resistance and stability due to seismic activity as required by the technical regulations for building structures. This conclusion suggests the need to check the mechanical resistance and stability of similar structures that are expected to be exposed to seismic activity.
- The proposed recovery of the structure, which consists of 10 cm of reinforced sprayed concrete on the inside of the bell tower walls and the installation of carbon fabric on the outside of the bell tower walls, can achieve the required level of mechanical resistance and stability of the bell tower. This type of reconstruction could be considered suitable for similar structures, however, additional numerical analyses are required to make a more general conclusion.
- The bell tower, which would be completely detached from the structure but with the existing material properties, also does not have a sufficient level of mechanical resistance and stability to seismic activity.
- A completely detached, free-standing bell tower, with improved material properties after the proposed reconstruction, shows greater mechanical stability and resistance compared to the bell tower horizontally supported by the surrounding structure. This is because in this case the seismic energy introduced into the tower is mainly converted into kinetic energy due to the rocking motion unlike a horizontally supported tower where most of the seismic energy is converted into internal potential energy.
- For further research, it would be interesting to analyse the behaviour of the bell tower in a damaged state due to the activity of additional earthquakes and the behaviour of the bell tower with the same geometry which is made of dry-stone masonry and exposed to seismic loading.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ruggieri, S.; Tosto, C.; Rosati, G.; Uva, G.; Ferro, G.A. Seismic Vulnerability Analysis of Masonry Churches in Piemonte after 2003 Valle Scrivia Earthquake: Post-event Screening and Situation 17 Years Later. Int. J. Archit. Herit. 2020, 1–29. [Google Scholar] [CrossRef]
- Šodan, M.; Trogrlić, B.; Foretić, D.; Munjiza, A.; Balić, I.; Smoljanović, H. FDEM failure analysis: Bell tower of church of St. Francis of Assisi on Kaptol in Zagreb. In Proceedings of the 1st Croatian Conference on Earthquake Engineering—1CroCEE, Zagreb, Croatia, 22–24 March 2021; Lakusic, S., Atalic, J., Eds.; University of Zagreb, Faculty of Civil Engineering: Zagreb, Croatia, 2021; pp. 1569–1577. [Google Scholar]
- Peña, F.; Lourenço, P.B.; Mendes, N.; Oliveira, D.V. Numerical models for the seismic assessment of an old masonry tower. Eng. Struct. 2010, 32, 1466–1478. [Google Scholar] [CrossRef] [Green Version]
- Preciado, A. Seismic vulnerability and failure modes simulation of ancient masonry towers by validated virtual finite element models. Eng. Fail. Anal. 2015, 57, 72–87. [Google Scholar] [CrossRef]
- Shehu, R. Preliminary Assessment of the Seismic Vulnerability of Three Inclined Bell-towers in Ferrara, Italy. Int. J. Archit. Herit. 2020, 1–33. [Google Scholar] [CrossRef]
- Standoli, G.; Giordano, E.; Milani, G.; Clementi, F. Model Updating of Historical Belfries Based on Oma Identification Techniques. Int. J. Archit. Herit. 2021, 15, 132–156. [Google Scholar] [CrossRef]
- Ubertini, F.; Cavalagli, N.; Kita, A.; Comanducci, G. Assessment of a monumental masonry bell-tower after 2016 Central Italy seismic sequence by long-term SHM. Bull. Earthq. Eng. 2018, 16, 775–801. [Google Scholar] [CrossRef]
- Torelli, G.; D’Ayala, D.; Betti, M.; Bartoli, G. Analytical and numerical seismic assessment of heritage masonry towers. Bull. Earthq. Eng. 2020, 18, 969–1008. [Google Scholar] [CrossRef] [Green Version]
- Casolo, S.; Diana, V.; Uva, G. Influence of soil deformability on the seismic response of a masonry tower. Bull. Earthq. Eng. 2017, 15, 1991–2014. [Google Scholar] [CrossRef]
- Milani, G.; Casolo, S.; Naliato, A.; Tralli, A. Seismic Assessment of a Medieval Masonry Tower in Northern Italy by Limit, Nonlinear Static, and Full Dynamic Analyses. Int. J. Archit. Herit. 2012, 6, 489–524. [Google Scholar] [CrossRef]
- Casolo, S. A three-dimensional model for vulnerability analysis of slender medieval masonry towers. J. Earthq. Eng. 1998, 2, 487–512. [Google Scholar] [CrossRef]
- Casolo, S.; Milani, G.; Uva, G.; Alessandri, C. Comparative seismic vulnerability analysis on ten masonry towers in the coastal Po Valley in Italy. Eng. Struct. 2013, 49, 465–490. [Google Scholar] [CrossRef]
- Facchini, L.; Betti, M. Time-history analysis of slender masonry towers: A parametric study on the reliability of a simplified Bouc and Wen approach. Meccanica 2017, 52, 3181–3196. [Google Scholar] [CrossRef]
- Makris, N.; Alexakis, H. Limit equilibrium analysis of masonry buttresses and towers under lateral and gravity loads. Arch. Appl. Mech. 2015, 85, 1915–1940. [Google Scholar] [CrossRef]
- Munjiza, A. The Combined Finite-Discrete Element Method; John Wiley & Sons: Oxford, UK, 2004. [Google Scholar]
- Munjiza, A.; Knight, E.E.; Rouiger, E. Computational Mechanics of Discontinua; John Wiley & Sons: Oxford, UK, 2012. [Google Scholar]
- Munjiza, A.; Andrews, K.R.F. NBS contact detection algorithm for bodies of similar size. Int. J. Numer. Methods Eng. 1998, 43, 131–149. [Google Scholar] [CrossRef]
- Munjiza, A.; Andrews, K.R.F. Penalty function method for combined finite-discrete element system comprising large number of separate bodies. Int. J. Numer. Methods Eng. 2000, 49, 1377–1396. [Google Scholar] [CrossRef]
- Munjiza, A.; Andrews, K.R.F.; White, J.K. Combined single and smeared crack model in combined finite-discrete element method. Int. J. Numer. Methods Eng. 1999, 44, 41–57. [Google Scholar] [CrossRef]
- Munjiza, A.; John, N.W.M. Mesh size sensitivity of the combined FEM/DEM fracture and fragmentation algorithms. Eng. Fract. Mech. 2002, 69, 281–295. [Google Scholar] [CrossRef]
- Smoljanović, H.; Nikolić, Ž.; Živaljić, N. A combined finite-discrete numerical model for analysis of masonry structures. Eng. Fract. Mech. 2015, 136, 1–14. [Google Scholar] [CrossRef]
- Smoljanović, H.; Balić, I.; Trogrlić, B. Stability of regular stone walls under in-plane seismic loading. Acta Mech. 2015, 226, 1881–1896. [Google Scholar] [CrossRef]
- Balić, I.; Živaljić, N.; Smoljanović, H.; Trogrlić, B. Seismic resistance of dry stone arches under in-plane seismic loading. Struct. Eng. Mech. 2016, 58, 243–257. [Google Scholar] [CrossRef]
- Smoljanović, H.; Živaljić, N.; Nikolić, Ž.; Munjiza, A. Numerical analysis of 3D dry-stone masonry structures by combined finite-discrete element method. Int. J. Sol. Struct. 2018, 136–137, 150–167. [Google Scholar] [CrossRef]
- Munjiza, A.; Smoljanović, H.; Živaljić, N.; Mihanović, A.; Divić, V.; Uzelac, I.; Nikolić, Ž.; Balić, I.; Trogrlić, B. Structural applications of the combined finite-discrete element method. Comp. Part. Mech. 2020, 7, 1029–1046. [Google Scholar] [CrossRef]
- Xiang, J.; Munjiza, A.; Latham, J.P.; Guises, R. On the validation of DEM and FEM/DEM models in 2D and 3D. Eng. Comp. 2009, 26, 673–687. [Google Scholar] [CrossRef]
- Hillerborg, A.; Modeer, M.; Petersson, P.E. Analysis of crack formation and crack growth in concrete by means of fracture mechanics and finite elements. Cement Concrete Res. 1976, 6, 773–782. [Google Scholar] [CrossRef]
- Čopec, D. Restoration Intervention of Herman Bollé at the Franciscan Church on Kaptol in Zagreb. Master’s Thesis, Faculty of Civil Engineering, University of Zagreb, Zagreb, Croatia, 2014. (In Croatian). [Google Scholar]
- Foretić, D.; Foretić, I.; Foretić, F. A Snapshot of the Current Condition of the Franciscan Monastery—Map I; Foretić and Sons: Dugo Selo, Croatia, 2020. (In Croatian) [Google Scholar]
- Foretić, D.; Foretić, I.; Foretić, F. Franciscan Monastery Kaptol—Restoration Plan and Program; Foretić and Sons: Dugo Selo, Croatia, 2020. (In Croatian) [Google Scholar]
- Clementi, F.; Quagliarini, E.; Monni, F.; Giordano, E.; Lenci, S. Cultural Heritage and Earthquake: The Case Study of “Santa Maria Della Carità” in Ascoli Piceno. Open Civ. Eng. J. 2017, 11, 1079–1105. [Google Scholar] [CrossRef]
- Uroš, M.; Todorić, M.; Crnogorac, M.; Atalić, J.; Šavor Novak, M.; Lakušić, S. Earthquake Engineering—Renovation of Masonry Buildings; Faculty of Civil Engineering, University of Zagreb: Zagreb, Croatia, 2021. (In Croatian) [Google Scholar]





| Material Properties | Mortar | Carbon | Steel |
|---|---|---|---|
| Modulus of elasticity, Ec (MPa) | 30,000 | 210,000 | 210,000 |
| Tensile strength, ft (MPa) | 2.5 | 3850 | 500 |
| Shear strength, fs (MPa) | 5.0 | - | - |
| Material Properties | P1 | P2 |
|---|---|---|
| Modulus of elasticity, Ec (MPa) | 2250 | 3584 |
| Poisson’s ratio, ν | 0.3 | 0.3 0.670 |
| Tensile strength, ft (MPa) | 0.27 | 0.67 |
| Shear strength, fs (MPa) | 1.08 | 1.7 |
| Fracture energy in tension Gf,t (N/m) | 35 | 90 |
| Fracture energy in shear Gf,s (N/m) | 140 | 240 |
| Unit mass, ρ (kg/m3) | 1800 | 1800 |
| Numerical Model | Geometry | Material Properties |
|---|---|---|
| M1 | G1 (horizontally supported with the walls) | P1 (current properties before damage) |
| M2 | G2 (free tower resting on the base) | P1 (current properties before damage) |
| M3 | G1 (horizontally supported with the walls) | P2 (properties after structural repair) |
| M4 | G2 (free tower resting on the base) | P2 (properties after structural repair) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Balić, I.; Smoljanović, H.; Trogrlić, B.; Munjiza, A. Seismic Analysis of the Bell Tower of the Church of St. Francis of Assisi on Kaptol in Zagreb by Combined Finite-Discrete Element Method. Buildings 2021, 11, 373. https://doi.org/10.3390/buildings11080373
Balić I, Smoljanović H, Trogrlić B, Munjiza A. Seismic Analysis of the Bell Tower of the Church of St. Francis of Assisi on Kaptol in Zagreb by Combined Finite-Discrete Element Method. Buildings. 2021; 11(8):373. https://doi.org/10.3390/buildings11080373
Chicago/Turabian StyleBalić, Ivan, Hrvoje Smoljanović, Boris Trogrlić, and Ante Munjiza. 2021. "Seismic Analysis of the Bell Tower of the Church of St. Francis of Assisi on Kaptol in Zagreb by Combined Finite-Discrete Element Method" Buildings 11, no. 8: 373. https://doi.org/10.3390/buildings11080373






