Displacement-Based Seismic Assessment of the Likelihood of Failure of Reinforced Concrete Wall Buildings
Abstract
:1. Introduction
1.1. Probabilistic Displacement Based Assessment
1.2. Empirical Relationships between Seismic Intensity and Displacement Ductility Demand
2. Assessing the Likely Failure Mechanism for a RC Wall Building
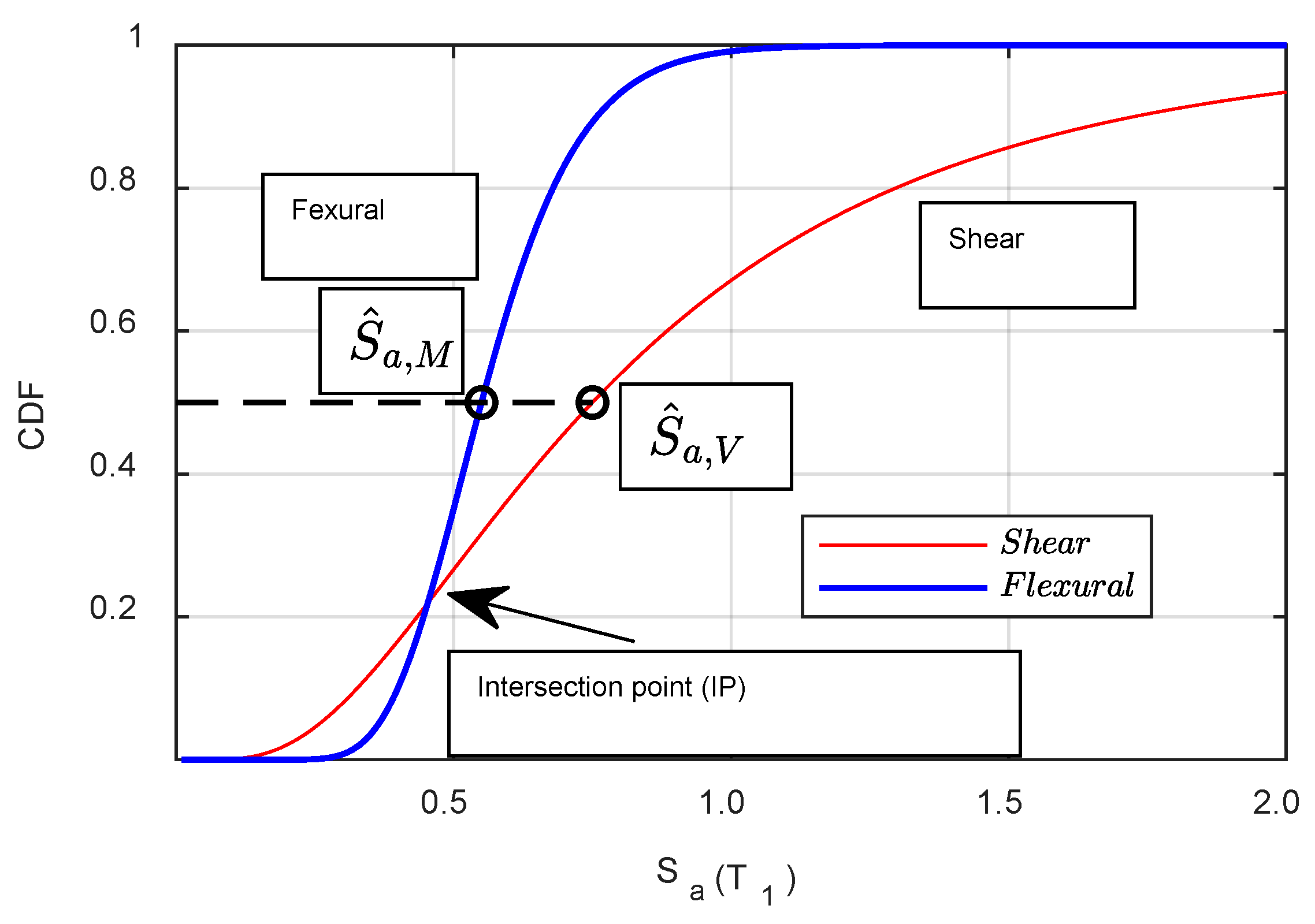
2.1. Flexural Plastic Hinging or a Wall Shear-Mechanism
2.2. Flexural Plastic Hinging or Foundation Overturning?
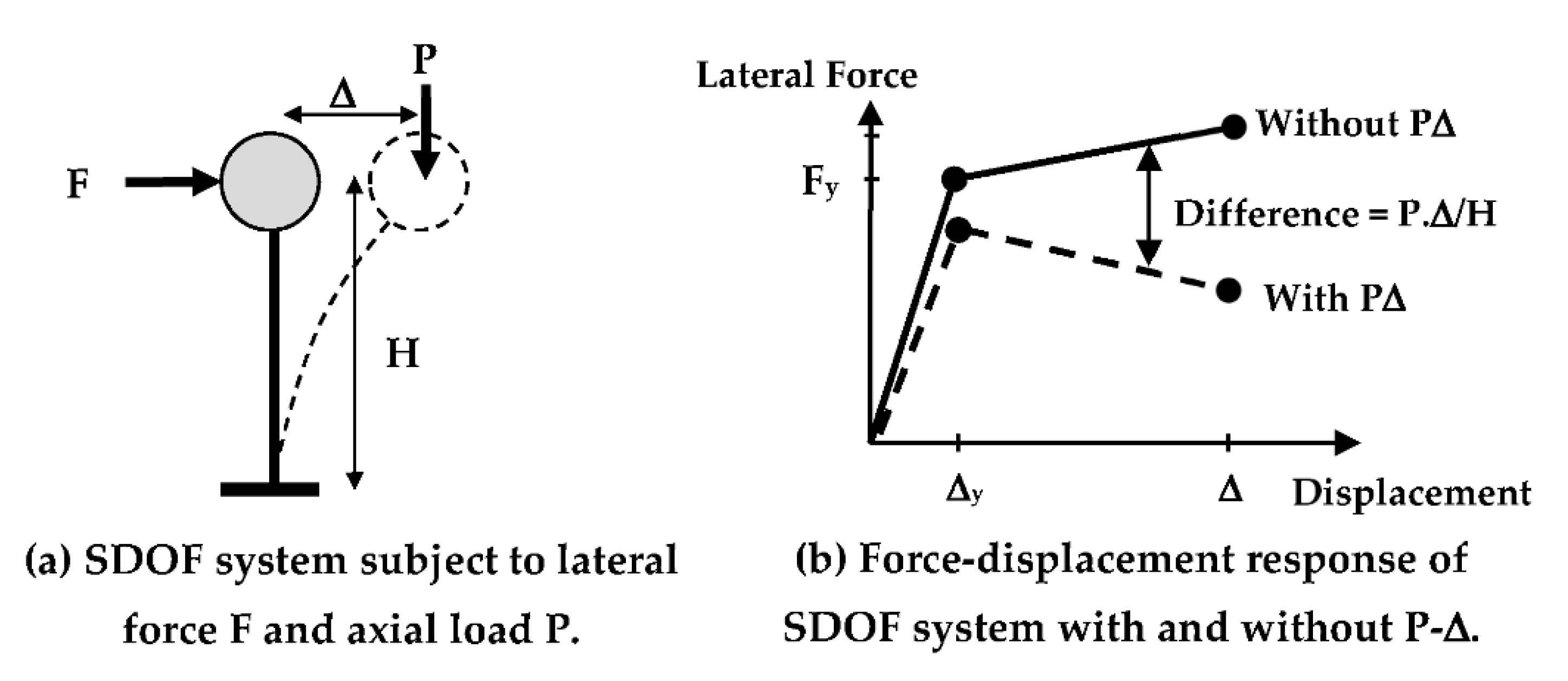
2.3. Influence of Uncertainties on the Expected Mechanism?
3. Identification of Limit State Deformation Capacity
3.1. Displacement Capacity for the Case of Flexural Hinging at Wall Base
3.2. Displacement Capacity for the Case of a Wall Shear Mechanism
3.3. Substitute Structure Characteristics
4. Quantification of the Limit State Median Intensity Capacity and Annual Probability of Failure
5. Quantifying the Annual Probability of Exceeding the Assessment Limit State
6. Gauging the Accuracy of Probabilistic Displacement-Based Assessment
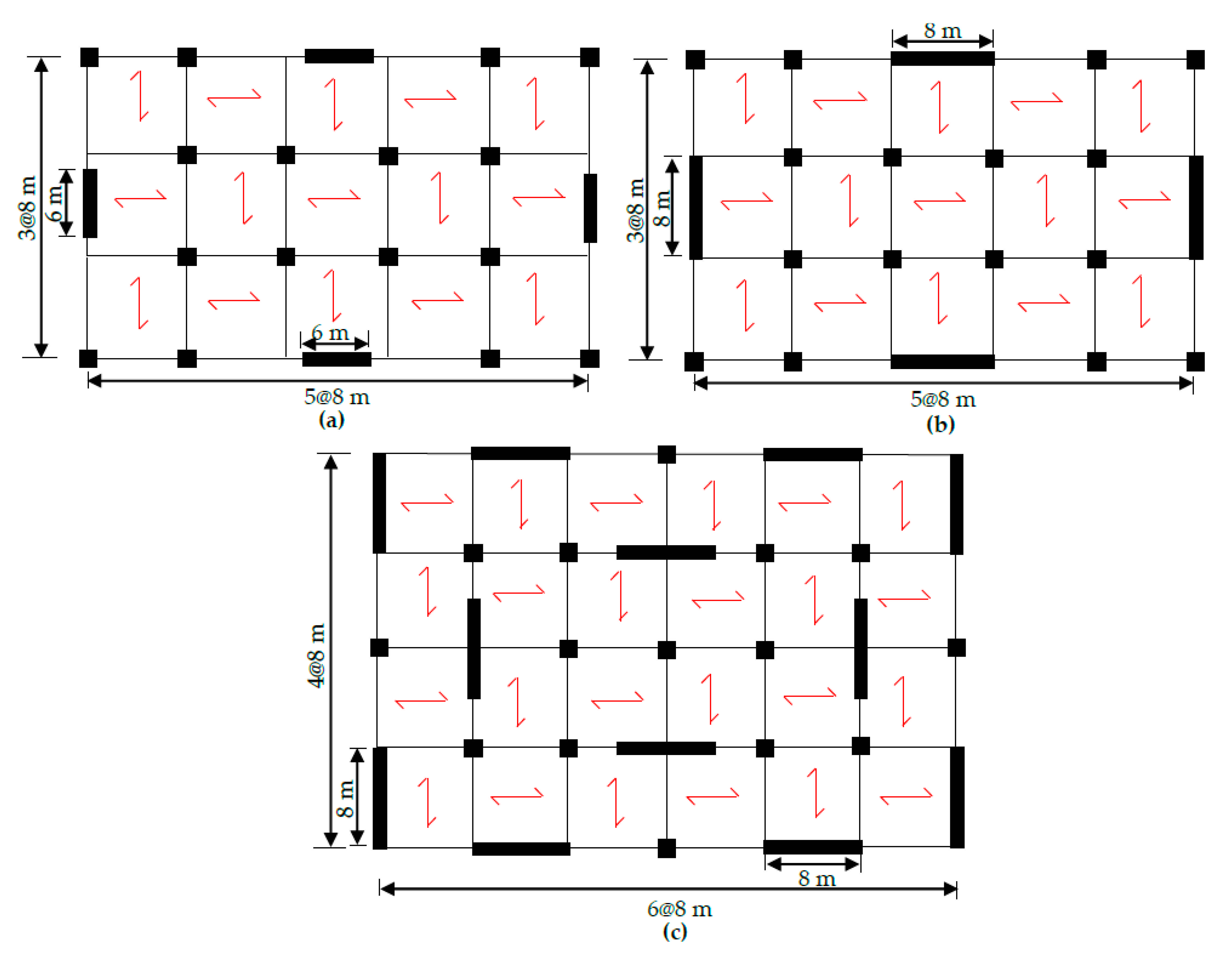
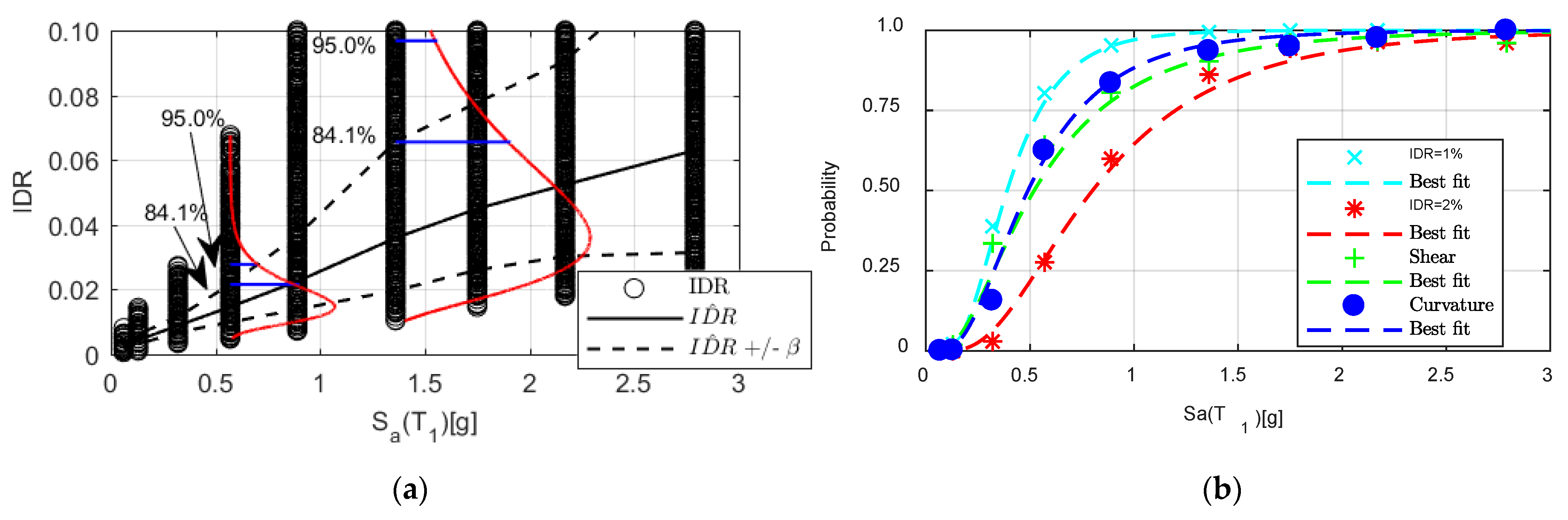
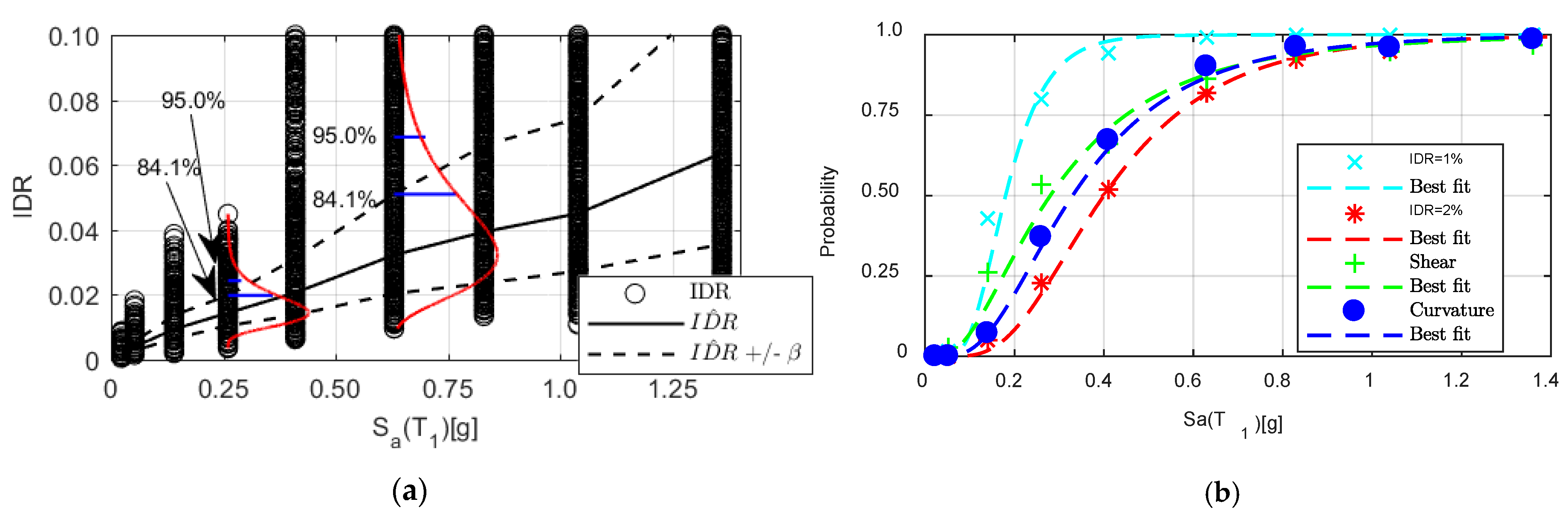
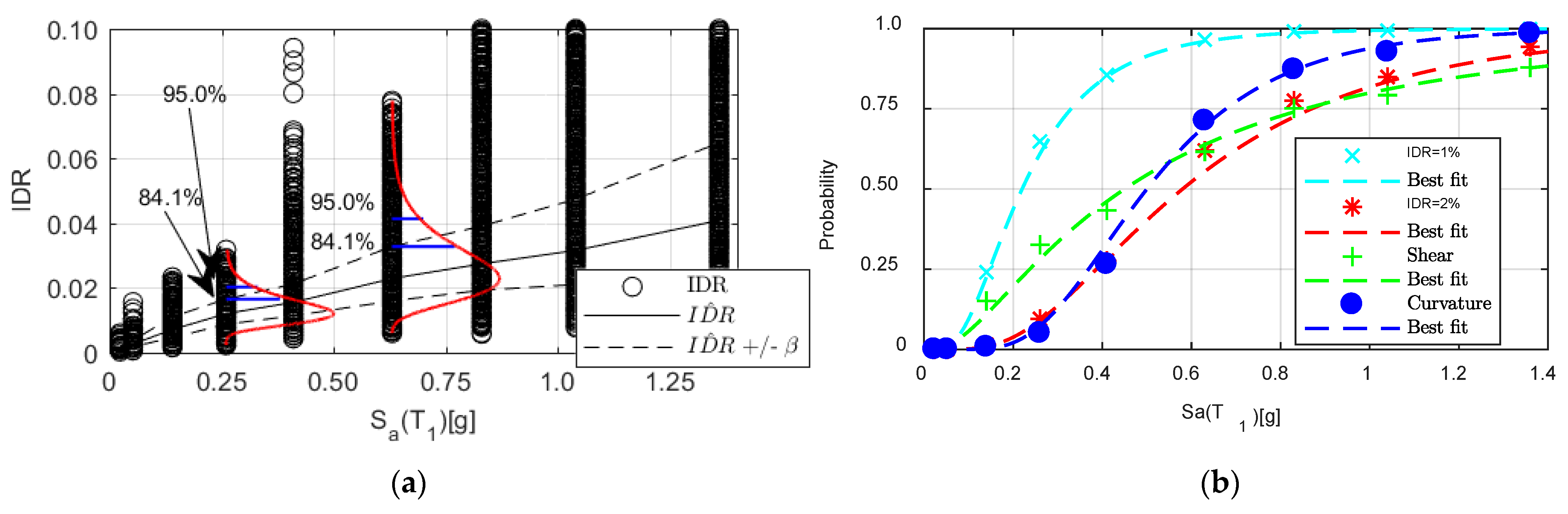
6.1. Rigorous Probabilistic Assessment of the Multi Story RC Wall Buildings
6.2. Simplified Probabilistic Assessment of the Multi Story RC Wall Buildings
7. Discussion
8. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
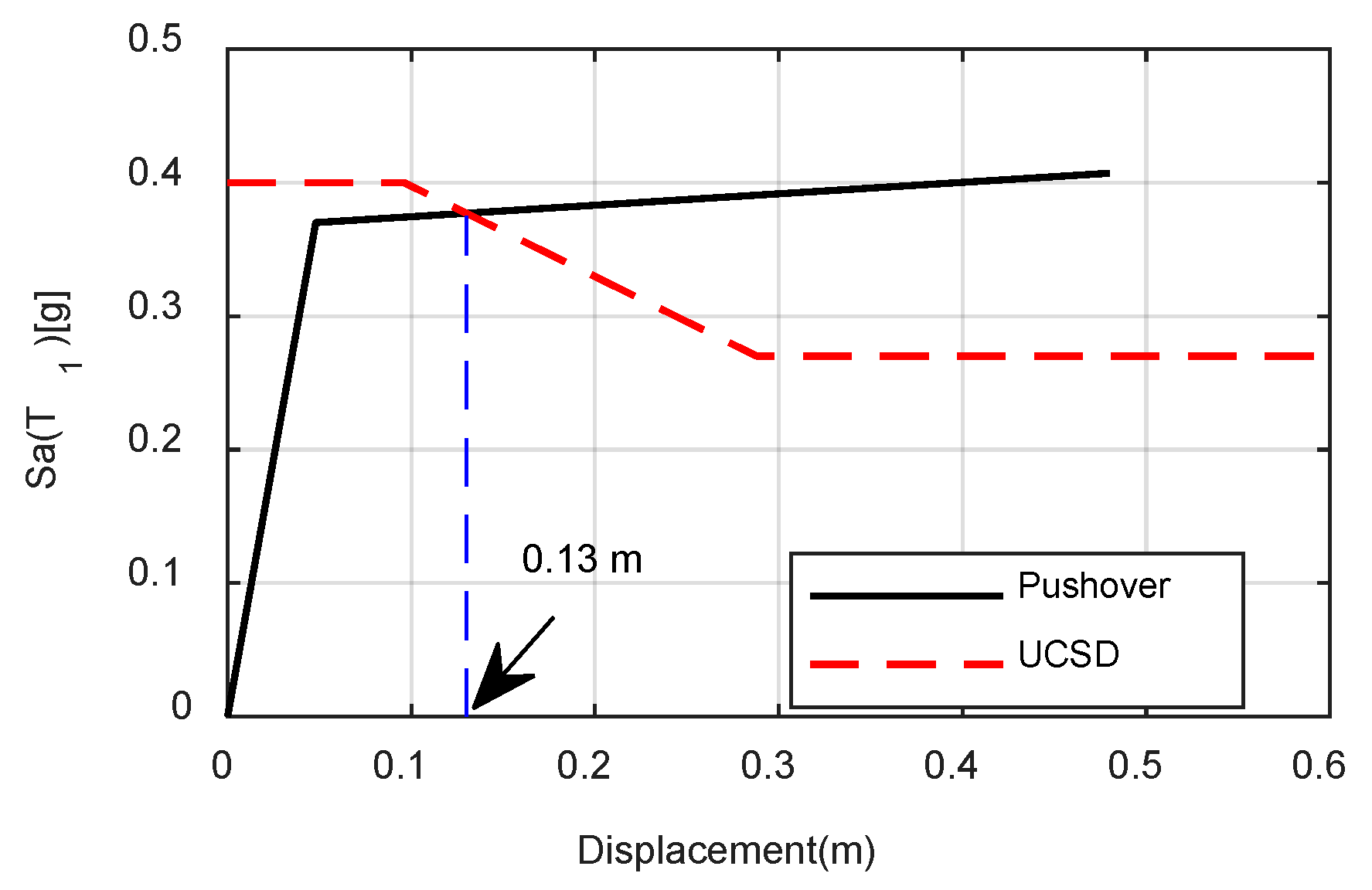
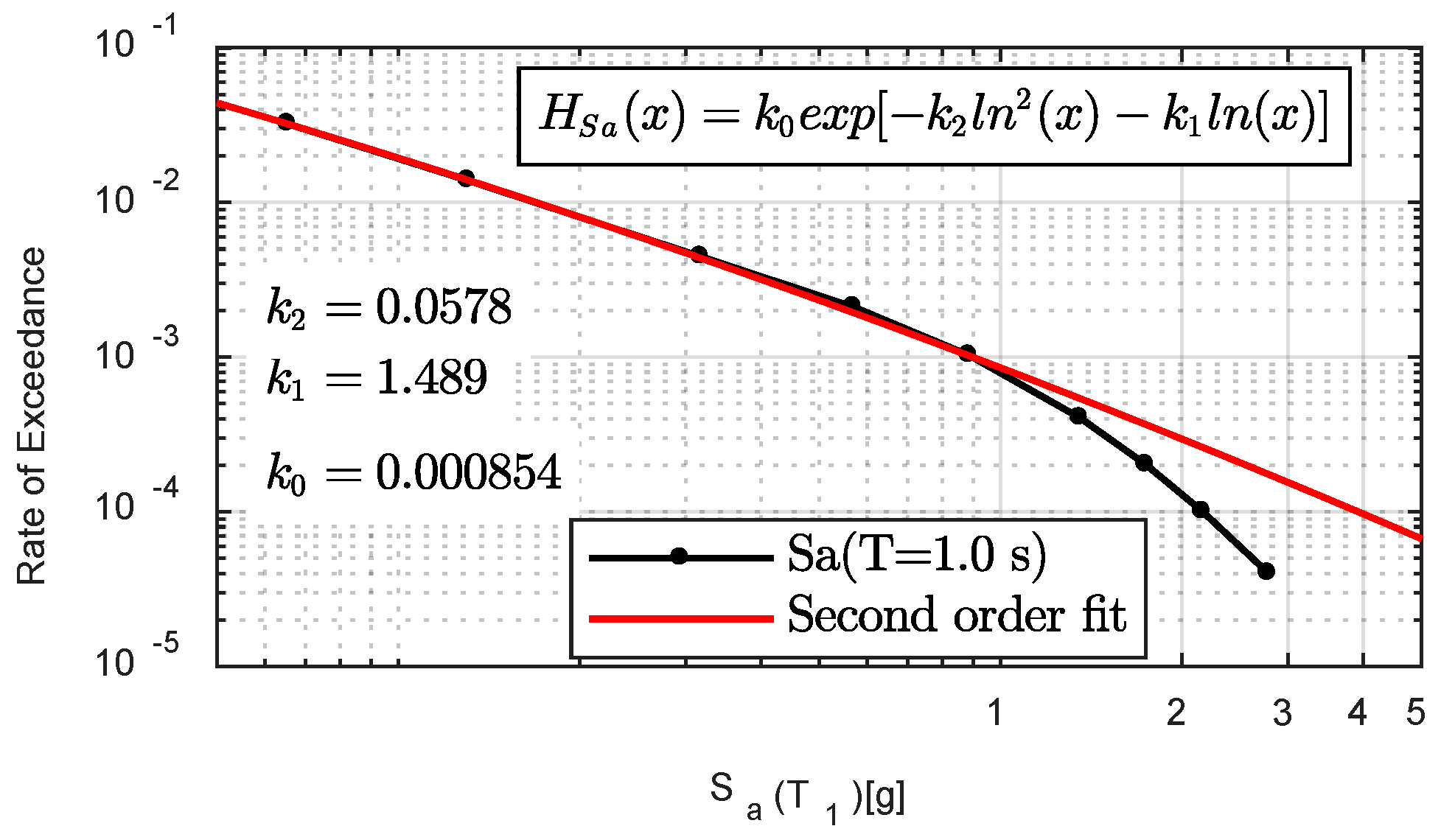
References
- CEN. Eurocode 8: Design of Structures for Earthquake Resistance-Part 1: General Rules, Seismic Actions and Rules for Buildings; CEN: Brussels, Belgium, 2005. [Google Scholar]
- FEMA. NEHRP Guidelines for the Seismic Rehabilitation of Buildings and Commentary; FEMA: Washington, DC, USA, 1997; pp. 273–274. [Google Scholar]
- NZSEE. The Seismic Assessment of Existing Buildings: Technical Guidelines for Engineering Assessments; Part C-Detailed Seismic Assessment; NZSEE: Wellington, New Zealand, 2017. [Google Scholar]
- Sullivan, T.J. Use of limit state loss versus intensity models for simplified estimation of expected annual loss. J. Earthq. Eng. 2016, 20, 954–974. [Google Scholar] [CrossRef]
- Sullivan, T.J.; Welch, D.P.; Calvi, G.M. Simplified seismic performance assessment and implications for seismic design. Earthq. Eng. Eng. Vib. 2014, 13, 95–122. [Google Scholar] [CrossRef]
- Welch, D.P.; Sullivan, T.J.; Calvik, G.M. Developing direct displacement-based procedures for simplified loss assessment in performance-based earthquake engineering. J. Earthq. Eng. 2014, 18, 290–322. [Google Scholar] [CrossRef]
- Vamvatsikos, D.; Aschheim, M.A. Performance-based seismic design via yield frequency spectra. J. Earthq. Eng. Struct. Dyn. 2016, 45, 1759–1778. [Google Scholar] [CrossRef]
- Priestley, M.; Calvi, G.M.; Kowalsky, M. Direct displacement-based seismic design of structures. In Proceedings of the NZSEE conference, Convention Centre, Palmerston North, New Zealand, 30 March 2007. [Google Scholar]
- Cornell, C.A.; Jalayer, F.; Hamburger, R.O.; Foutch, D.A. Probabilistic basis for 2000 SAC federal emergency management agency steel moment frame guidelines. J. Struct. Eng. 2002, 128, 526–533. [Google Scholar] [CrossRef] [Green Version]
- Fajfar, P.; Dolšek, M. A practice-oriented estimation of the failure probability of building structures. J. Earthq. Eng. Struct. Dyn. 2012, 41, 531–547. [Google Scholar] [CrossRef]
- Priestley, M.N.; Calvi, G.M.; Kowalsky, M.J. Displacement-Based Seismic Design of Structures; IUSS Press: Pavia, Italy, 2007. [Google Scholar]
- Orumiyehei, A.; Sullivan, T.J. Quantifying the Likelihood of Exceeding a Limit State via the Displacement-based Assessment Approach. J. Earthq. Eng. 2021, 1–19. [Google Scholar] [CrossRef]
- Sullivan, T.J.; Calvi, G.M. Developments in the Field of Displacement-Based Seismic Assessment, Research Report ROSE 2013/01; IUSS Press: Pavia, Italy, January 2013; pp. 1–531. ISBN 978-88-6198-090-7. [Google Scholar]
- Cardone, D.; Flora, A. Multiple inelastic mechanisms analysis (MIMA): A simplified method for the estimation of the seismic response of RC frame buildings. J. Eng. Struct. 2017, 145, 368–380. [Google Scholar] [CrossRef]
- Pampanin, S.; Bolognini, D.; Pavese, A. Performance-based seismic retrofit strategy for existing reinforced concrete frame systems using fiber-reinforced polymer composites. J. Compos. Struct. 2007, 11, 211–226. [Google Scholar] [CrossRef]
- Vamvatsikos, D. Derivation of new SAC/FEMA performance evaluation solutions with second-order hazard approximation. J. Earthq. Eng. Struct. Dyn. 2013, 42, 1171–1188. [Google Scholar] [CrossRef]
- Bakalis, K.; Vamvatsikos, D. Seismic Fragility Functions via Nonlinear Response History Analysis. J. Struct. Eng. 2018, 144, 04018181. [Google Scholar] [CrossRef]
- Veletsos, A.S.; Newmark, N.M. Effect of inelastic behavior on the response of simple systems to earthquake motions. In Proceedings of the 2nd World Conference Earthquake Engineering, Tokyo, Japan, 11–18 July 1960; pp. 895–912. [Google Scholar]
- Vamvatsikos, D.; Cornell, C.A. Incremental dynamic analysis. Earthq. Eng. Struct. Dyn. 2002, 31, 491–514. [Google Scholar] [CrossRef]
- Jalayer, F.; Cornell, C. Alternative non-linear demand estimation methods for probability-based seismic assessments. J. Earthq. Eng. Struct. Dyn. 2009, 38, 951–972. [Google Scholar] [CrossRef]
- Freeman, S. (Ed.) Evaluations of existing buildings for seismic risk-A case study of Puget Sound Naval Shipyard. In Proceedings of the 1st U.S. National Conference on Earthquake Engineering, Bremerton, WA, USA, 18–20 June 1975. [Google Scholar]
- Fajfar, P.; Gašperšič, P.; Drobnič, D. Seismic Design Methodologies for the Next Generation of Codes. In A Simplified Nonlinear Method for Seismic Damage Analysis of Structures; Routledge: Rotterdam, The Netherland, 1997. [Google Scholar]
- Federal Emergency Management Agency—FEMA. Recommended Seismic Design Criteria for New Steel Moment-Frame Buildings; Rep. No. FEMA-350; SAC Joint Venture: Washington, DC, USA, 2000. [Google Scholar]
- Jalayer, F.; Cornell, C.A. A Technical Framework for Probability-Based Demand and Capacity Factor (DCFD) Seismic Formats; Report No. RMS-RMS Program; PEER: Stanford, CA, USA, 2003. [Google Scholar]
- Miranda, E. Evaluation of site-dependent inelastic seismic design spectra. J. Struct. Eng. 1993, 119, 1319–1338. [Google Scholar] [CrossRef]
- Jalayer, F. Direct Probabilistic Seismic Anaysis: Implementing Non-Linear Dynamic Assessments. Ph.D. Thesis, Stanford University, Stanford, CA, USA, 2003. [Google Scholar]
- Stafford, P.J.; Sullivan, T.J.; Pennucci, D. Empirical correlation between inelastic and elastic spectral displacement demands. Earthq. Spectra 2016, 32, 1419–1448. [Google Scholar] [CrossRef] [Green Version]
- Priestley, M.N.; Calvi, G.M. Towards a capacity-design assessment procedure for reinforced concrete frames. Earthq. Spectra 1991, 7, 413–437. [Google Scholar] [CrossRef]
- Beyer, K.; Dazio, A.; Priestley, M.N. Seismic Design of Torsionally Eccentric Buildings with U-Shaped RC Walls; IUSS Press: Pavia, Italy, 2008. [Google Scholar]
- Pennucci, D.; Sullivan, T.J.; Calvi, G.M. Inelastic higher-mode response in reinforced concrete wall structures. Earthq. Spectra 2015, 31, 1493–1514. [Google Scholar] [CrossRef]
- Fox, M.J.; Sullivan, T.J.; Beyer, K. Evaluation of seismic assessment procedures for determining deformation demands in RC wall buildings. J. Earthq. Struct. 2015, 9, 911–936. [Google Scholar] [CrossRef] [Green Version]
- SANZ. Concrete Structures Standard; NZS 3101; Standards Association: Wellington, NZ, USA, 2006. [Google Scholar]
- Sullivan, T.J.; Salawdeh, S.; Pecker, A.; Corigliano, M.; Calvi, G.M. Soil-foundation-structure interaction considerations for performance-based design of RC wall structures on shallow foundations. In Soil-Foundation-Structure Interaction; CRC Press: Leiden, The Netherlands, 2010; pp. 193–200. [Google Scholar]
- Millen, M.D.; Pampanin, S.; Cubrinovski, M. An integrated performance-based design framework for building-foundation systems. J. Earthq. Eng. Struct. Dyn. 2021, 50, 718–735. [Google Scholar] [CrossRef]
- Sullivan, T.J.; Priestley, M.N.; Calvi, G.M. A Model Code for the Displacement-Based Seismic Design of Structures DBD12; IUSS Press: Pavia, Italy, 2012. [Google Scholar]
- Lupoi, G.; Franchin, P.; Lupoi, A.; Pinto, P.E. Seismic fragility analysis of structural systems. J. Eng. Mech. 2006, 132, 385–395. [Google Scholar] [CrossRef]
- Carr, A. RUAUMOKO, Software for Inelastic Dynamic Analysis; Department of Civil Engineering, University of Canterbury: Christchurch, New Zealand, 2021. [Google Scholar]
- Yeow, T.; Orumiyehei, A.; Sullivan, T.J.; MacRae, G.; Clifton, G.; Elwood, K. Seismic performance of steel friction connections considering direct-repair costs. Bull. Earthq. Eng. 2018, 16, 5963–5993. [Google Scholar] [CrossRef]
- Bradley, B.A. A generalized conditional intensity measure approach and holistic ground-motion selection. J. Earthq. Eng. Struct. Dyn. 2010, 39, 1321–1342. [Google Scholar] [CrossRef] [Green Version]
- O’Reilly, G.J.; Sullivan, T.J. Quantification of modelling uncertainty in existing Italian RC frames. J. Earthq. Eng. Struct. Dyn. 2017, 47, 1054–1074. [Google Scholar] [CrossRef]
- Gokkaya, B.U.; Baker, J.W.; Deierlein, G.G. Quantifying the impacts of modeling uncertainties on the seismic drift demands and collapse risk of buildings with implications on seismic design checks. J. Earthq. Eng. Struct. Dyn. 2016, 45, 1661–1683. [Google Scholar] [CrossRef]
- MathWorks, I. MATLAB: The Language of Technical Computing; Desktop Tools and Development Environment. Version 7. MathWorks: 2005. Available online: https://de.mathworks.com/company/aboutus/policies_statements/patents.html (accessed on 6 July 2021).
- Orumiyehei, A.; Sullivan, T.J. Assessment of the annual probability of failure for systems susceptible to two correlated failure mechanisms. In Proceedings of the 17th World Conference on Earthquake Engineering, Sendai, Japan, 27 September–2 October 2021. [Google Scholar]
- Baker, J.W. Efficient analytical fragility function fitting using dynamic structural analysis. Earthq. Spectra 2015, 31, 579–599. [Google Scholar] [CrossRef]
- Pennucci, D.; Sullivan, T.J.; Calvi, G.M. Performance-Based Seismic Design of Tall RC Wall Buildings; Iuss Press: Pavia, Italy, 2011. [Google Scholar]
- Priestley, M.N.; Seible, F.; Calvi, G.M. Seismic Design and Retrofit of Bridges; John Wiley & Sons: Ho boken, NJ, USA, 1996. [Google Scholar]
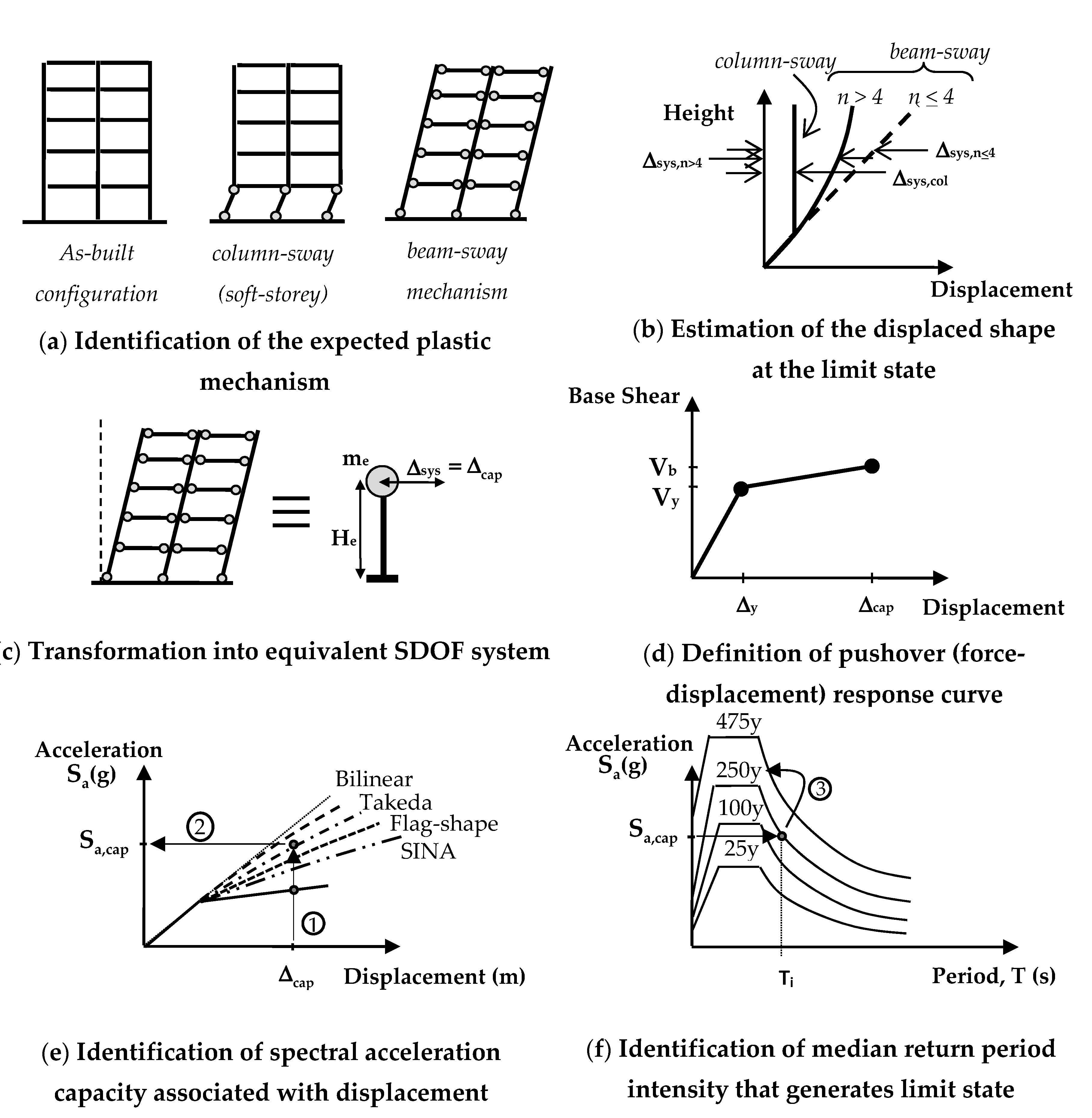
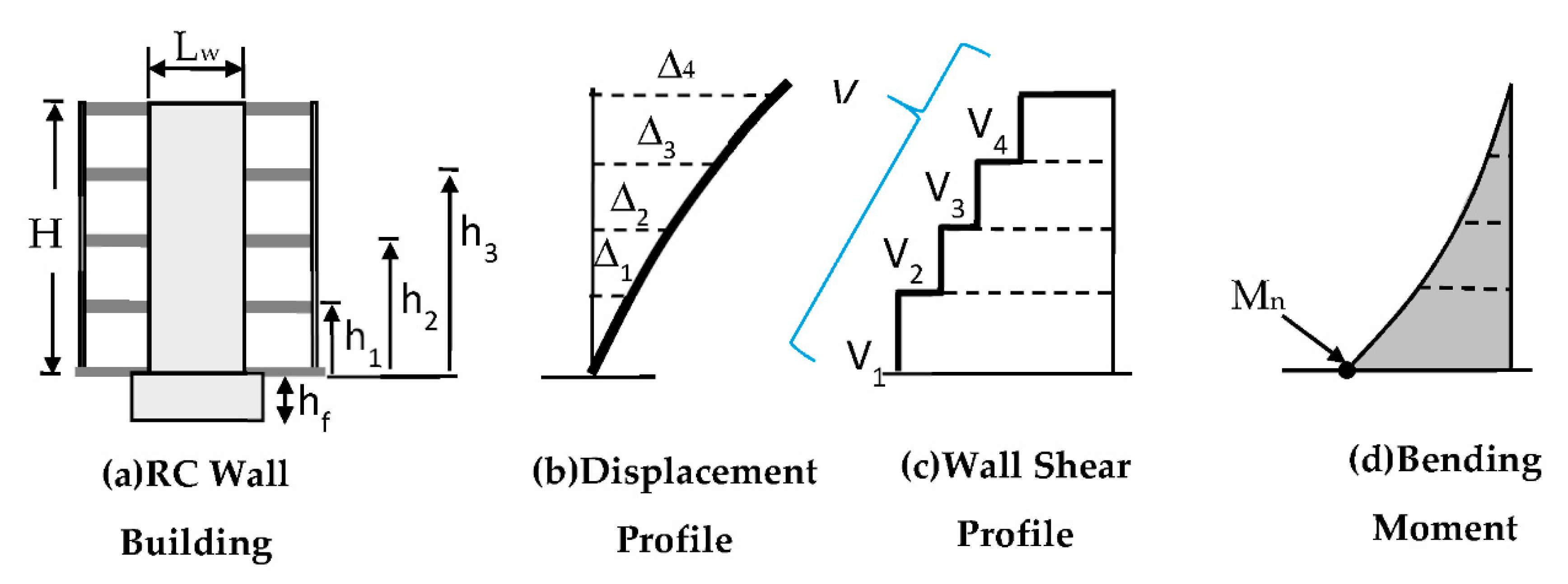

| Period | Bilinear | Takeda | Flag (λ = 5.67) | SINA | ||||
|---|---|---|---|---|---|---|---|---|
| T(s) | ||||||||
| 0. | 3.10 | 0.08 | 5.55 | 0.27 | 5.65 | 0.21 | 5.89 | 0.22 |
| 0.2 | 1.54 | 0.02 | 2.16 | 0.08 | 2.87 | 0.04 | 4.05 | 0.21 |
| 0.3 | 1.30 | 0.04 | 1.72 | 0.12 | 2.05 | 0.20 | 2.45 | 0.24 |
| 0.4 | 1.24 | 0.05 | 1.49 | 0.08 | 1.86 | 0.18 | 2.63 | 0.26 |
| 0.5 | 1.18 | 0.05 | 1.44 | 0.09 | 1.73 | 0.15 | 2.04 | 0.24 |
| 0.6 | 1.14 | 0.07 | 1.36 | 0.09 | 1.62 | 0.11 | 1.79 | 0.16 |
| 0.8 | 1.09 | 0.05 | 1.29 | 0.07 | 1.58 | 0.07 | 1.71 | 0.16 |
| 1.0 | 1.10 | 0.08 | 1.23 | 0.06 | 1.51 | 0.07 | 1.57 | 0.12 |
| 1.5 | 1.12 | 0.10 | 1.20 | 0.12 | 1.37 | 0.06 | 1.31 | 0.10 |
| 2.0 | 1.10 | 0.07 | 1.23 | 0.07 | 1.47 | 0.10 | 1.30 | 0.07 |
| 2.5 | 1.17 | 0.10 | 1.24 | 0.07 | 1.45 | 0.09 | 1.26 | 0.09 |
| 3.0 | 1.24 | 0.14 | 1.28 | 0.11 | 1.48 | 0.14 | 1.33 | 0.12 |
| Period | Bilinear | Takeda | Flag (λ = 5.67) | SINA | ||||
|---|---|---|---|---|---|---|---|---|
| T(s) | b | β | b | β | b | β | b | β |
| 0.2 ≤ T < 0.6 | 1.28 | 0.12 | 1.57 | 0.24 | 1.86 | 0.34 | 2.50 | 0.42 |
| 0.6 ≤ T ≤ 3.5 | 1.12 | 0.10 | 1.26 | 0.12 | 1.49 | 0.12 | 1.38 | 0.17 |
| Case Study * | My (kN·m) | β | Ieff (m4) | β | β | β | ||
|---|---|---|---|---|---|---|---|---|
| 4-story | 20,820 | 0.3 | 0.84 | 0.3 | 8.33 × 10−4 | 0.3 | 3.5 × 10−3 | 0.3 |
| 8-story | 41,677 | 0.3 | 2.24 | 0.3 | 6.25 × 10−5 | 0.3 | 2.62 × 10−3 | 0.3 |
| 12-story | 76,558 | 0.3 | 4.12 | 0.3 | 6.25 × 10−5 | 0.3 | 2.62 × 10−3 | 0.3 |
| Limit State | 4-Story | 8-Story | 12-Story | |||
|---|---|---|---|---|---|---|
| IDR = 0.01 | 0.39 | 0.50 | 0.18 | 0.40 | 0.22 | 0.60 |
| IDR = 0.02 | 0.80 | 0.45 | 0.40 | 0.50 | 0.58 | 0.70 |
| Shear failure | 0.52 | 0.70 | 0.28 | 0.70 | 0.45 | 0.95 |
| Curvature failure | 0.49 | 0.55 | 0.33 | 0.58 | 0.50 | 0.45 |
| Mechanism | APOE * 4-Story | APOE 8-Story | APOE 12-Story |
|---|---|---|---|
| IDR1 = 0.01 | 38 × 10−4 | 35 × 10−4 | 31 × 10−4 |
| IDR2 = 0.02 | 15 × 10−4 | 13 × 10−4 | 8 × 10−4 |
| Shear | 32 × 10−4 | 25 × 10−4 | 18 × 10−4 |
| Curvature | 31 × 10−4 | 18 × 10−4 | 9 × 10−4 |
| Limit States | 4-Story, Sa(T1) [g] | 8-Story, Sa(T1) [g] | 12-Story, Sa(T1) [g] | |||
|---|---|---|---|---|---|---|
| Simplified | MSA | Simplified | MSA | Simplified | MSA | |
| IDR = 0.01 | 0.39 | 0.39 | 0.20 | 0.18 | 0.30 | 0.22 |
| IDR = 0.02 | 0.78 | 0.80 | 0.39 | 0.40 | 0.57 | 0.58 |
| Shear | 0.58 | 0.52 | 0.34 | 0.28 | 0.50 | 0.45 |
| Curvature | 0.43 | 0.49 | 0.34 | 0.33 | 0.46 | 0.50 |
| Limit States | APOE * 4-Story | APOE 8-Story | APOE 12-Story | |||
|---|---|---|---|---|---|---|
| Simplified | Rigorous | Simplified | Rigorous | Simplified | Rigorous | |
| βAssumed | βRigorous | βAssumed | βRigorous | βAssumed | βRigorous | |
| IDR1 | 3.94 × 10−3 | 3.80 × 10−3 | 3.23 × 10−3 | 3.50 × 10−3 | 2.00 × 10−3 | 3.10 × 10−3 |
| IDR2 | 1.50 × 10−3 | 1.50 × 10−3 | 1.34 × 10−3 | 1.30 × 10−3 | 7.90 × 10−4 | 8.40 × 10−4 |
| Shear | 3.13 × 10−3 | 3.20 × 10−3 | 2.74 × 10−3 | 2.50 × 10−3 | 1.29 × 10−3 | 1.77 × 10−3 |
| Curvature | 3.60 × 10−3 | 3.10 × 10−3 | 1.75 × 10−3 | 1.80 × 10−3 | 1.11 × 10−3 | 9.00 × 10−4 |
| Limit States | APOE * 4-Story | APOE 8-Story | APOE 12-Story | |||
|---|---|---|---|---|---|---|
| Simplified | Rigorous | Simplified | Rigorous | Simplified | Rigorous | |
| βRigorous | βRigorous | βRigorous | βRigorous | βRigorous | βRigorous | |
| IDR1 | 4.10 × 10−3 | 3.80 × 10−3 | 3.13 × 10−3 | 3.50 × 10−3 | 2.16 × 10−3 | 3.10 × 10−3 |
| IDR2 | 1.50 × 10−3 | 1.50 × 10−3 | 1.39 × 10−3 | 1.30 × 10−3 | 1.02 × 10−3 | 8.40 × 10−4 |
| Shear | 2.95 × 10−3 | 3.20 × 10−3 | 2.60 × 10−3 | 2.50 × 10−3 | 1.68 × 10−3 | 1.77 × 10−3 |
| Curvature | 3.80 × 10−3 | 3.10 × 10−3 | 1.87 × 10−3 | 1.80 × 10−3 | 1.06 × 10−3 | 9.00 × 10−4 |
| Building | LS1 | LS2 | LS3 | LS4 | Simultaneous Failures and Retrofit | |||
|---|---|---|---|---|---|---|---|---|
| Retrofit None | Retrofit LS[1] | Retrofit LS(1,2) | Retrofit LS(1,2,3) | |||||
| 4-story | 4.10 × 10−3 | 1.5 × 10−3 | 2.95 × 10−3 | 3.35 × 10−3 | 11.8 × 10−3 | 7.78 × 10−3 | 6.29 × 10−3 | 3.35 × 10−3 |
| 8-story | 3.13 × 10−3 | 1.39 × 10−3 | 2.60 × 10−3 | 1.87 × 10−3 | 8.97 × 10−3 | 5.85 × 10−3 | 4.47 × 10−3 | 1.87 × 10−3 |
| 12-story | 2.16 × 10−3 | 1.02 × 10−3 | 1.68 × 10−3 | 1.06 × 10−3 | 5.91 × 10−3 | 3.76 × 10−3 | 2.75 × 10−3 | 1.06 × 10−3 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Orumiyehei, A.; Sullivan, T.J. Displacement-Based Seismic Assessment of the Likelihood of Failure of Reinforced Concrete Wall Buildings. Buildings 2021, 11, 295. https://doi.org/10.3390/buildings11070295
Orumiyehei A, Sullivan TJ. Displacement-Based Seismic Assessment of the Likelihood of Failure of Reinforced Concrete Wall Buildings. Buildings. 2021; 11(7):295. https://doi.org/10.3390/buildings11070295
Chicago/Turabian StyleOrumiyehei, Amirhossein, and Timothy J. Sullivan. 2021. "Displacement-Based Seismic Assessment of the Likelihood of Failure of Reinforced Concrete Wall Buildings" Buildings 11, no. 7: 295. https://doi.org/10.3390/buildings11070295
APA StyleOrumiyehei, A., & Sullivan, T. J. (2021). Displacement-Based Seismic Assessment of the Likelihood of Failure of Reinforced Concrete Wall Buildings. Buildings, 11(7), 295. https://doi.org/10.3390/buildings11070295





