Behaviour of Lightweight Concrete Wall Panel under Axial Loading: Experimental and Numerical Investigation toward Sustainability in Construction Industry
Abstract
1. Introduction
1.1. Sustainable Aspect of Agricultural Waste
1.2. Research on OPS Concrete
1.3. Concrete Wall Subjected to Axial Loading
1.4. Design Guide and Research of Concrete Wall
1.5. Research Significance
1.6. Objective
2. Experimental Program
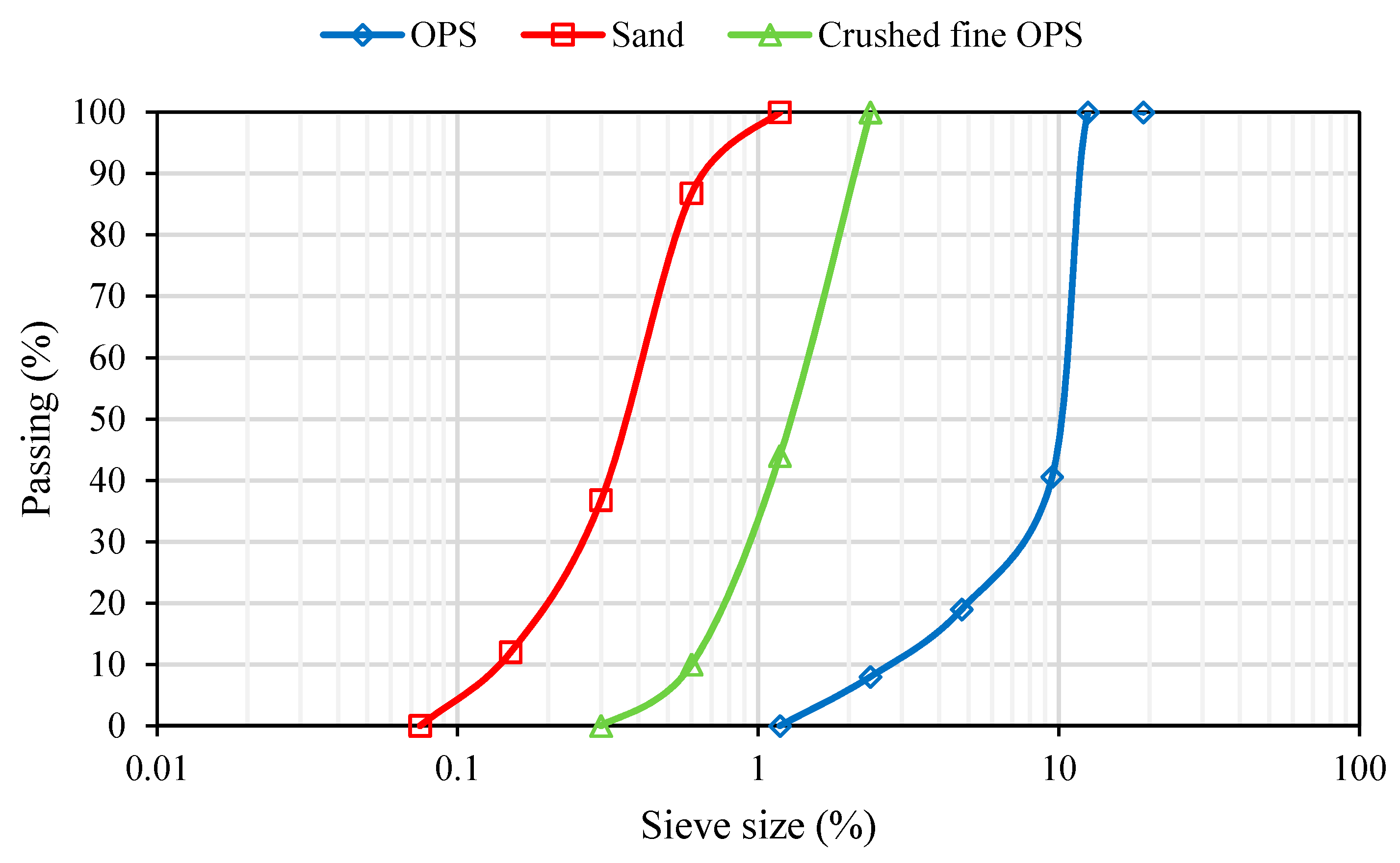
2.1. Materials
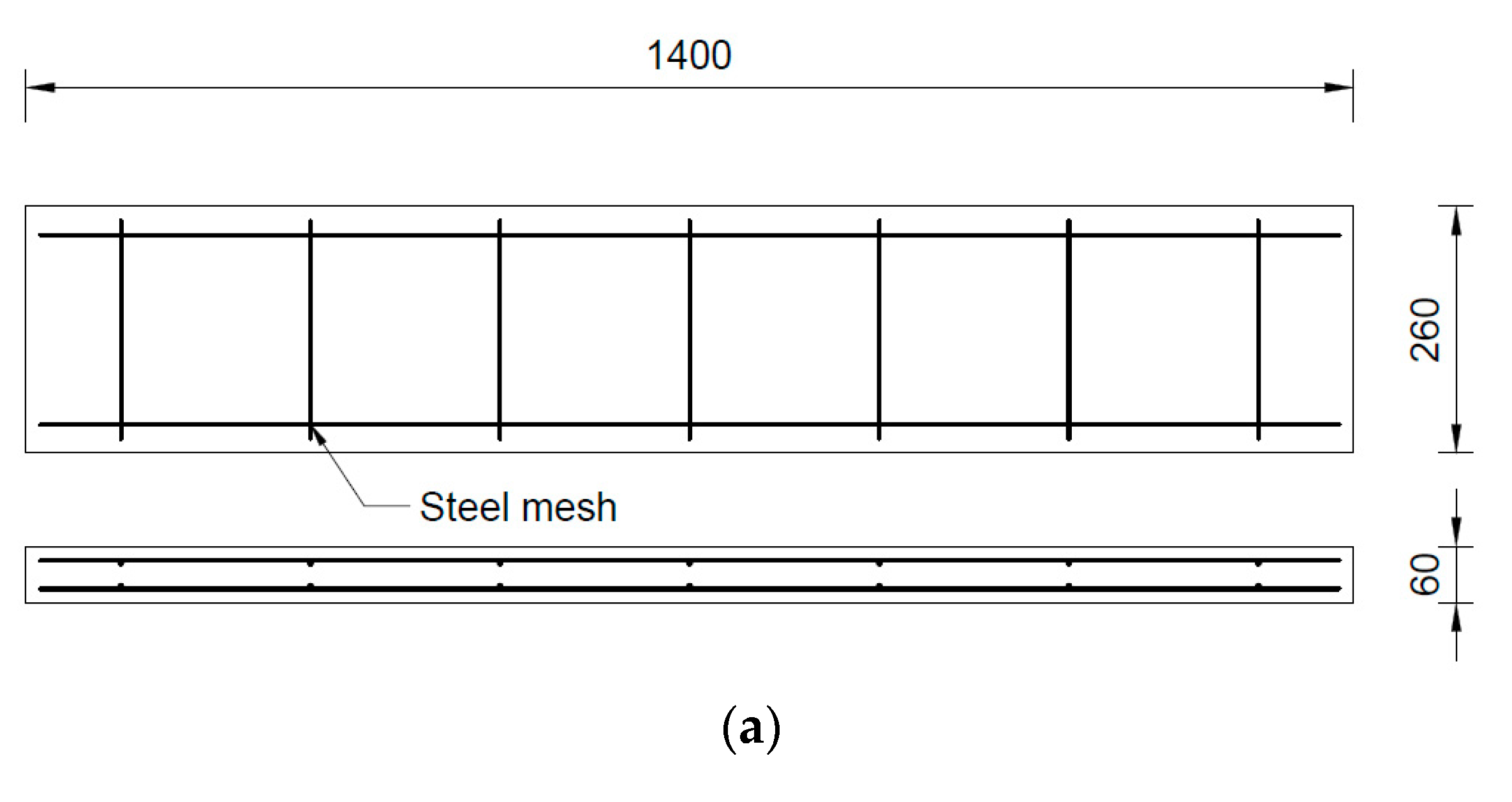
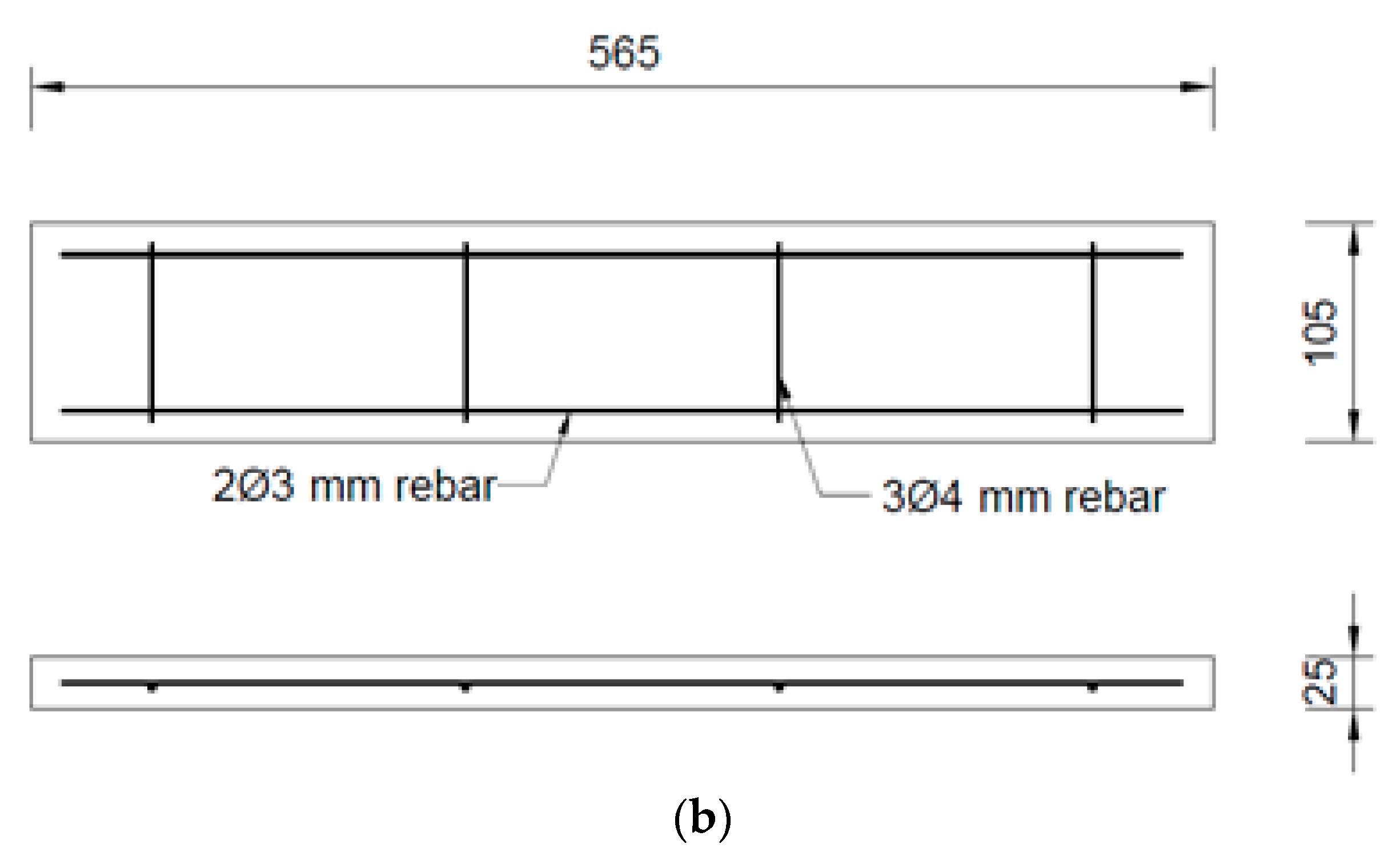
2.2. Wall Specimens
2.3. Experimental Setup and Instrumentation
3. Finite Element Model
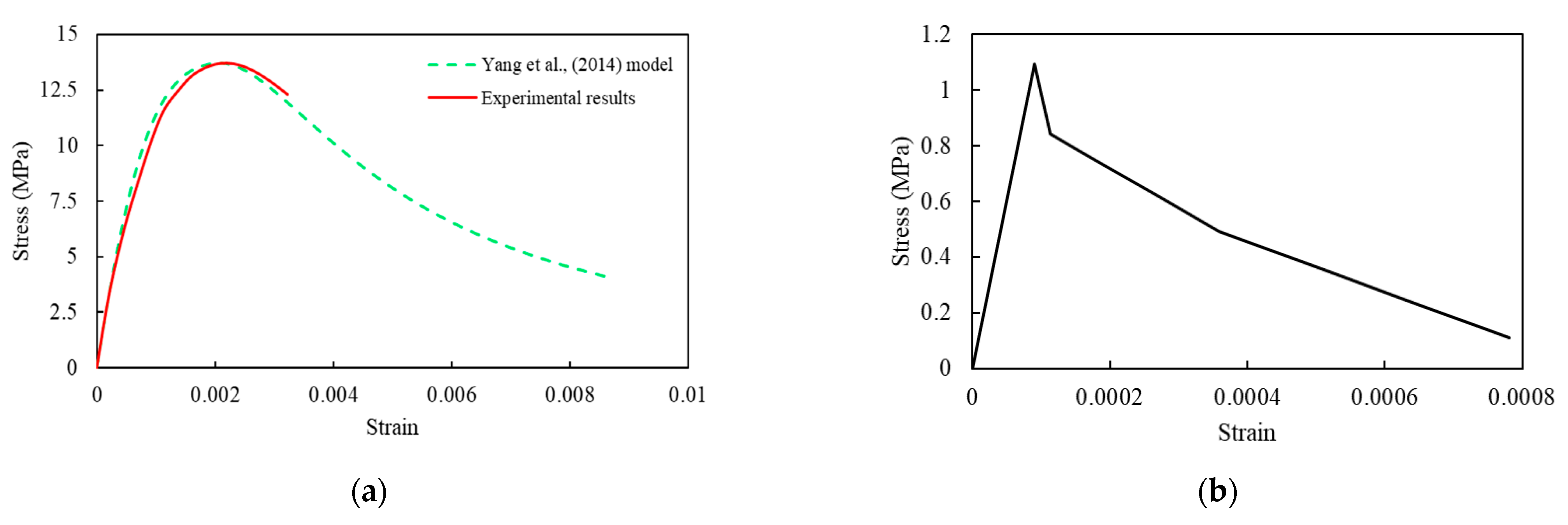
3.1. Material Model of Concrete
3.2. Material Model of Steel
3.3. Model Description
3.4. Summary
4. Results and Discussion
4.1. Experimental Results and Analysis
4.1.1. Failure Mode
4.1.2. Load Deflection
4.1.3. Deflection Corresponding to Ultimate Failure Load
4.1.4. Ultimate Failure Load
4.2. Effect of Specimen Size
4.3. FEA Model Validation
5. FEA Parametric Study
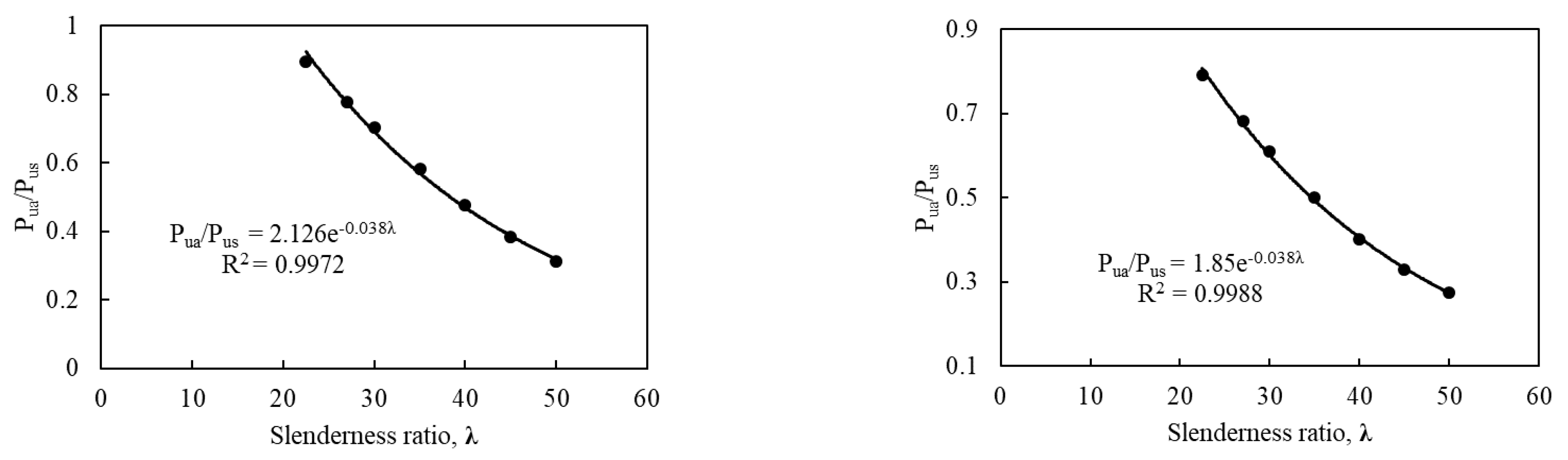
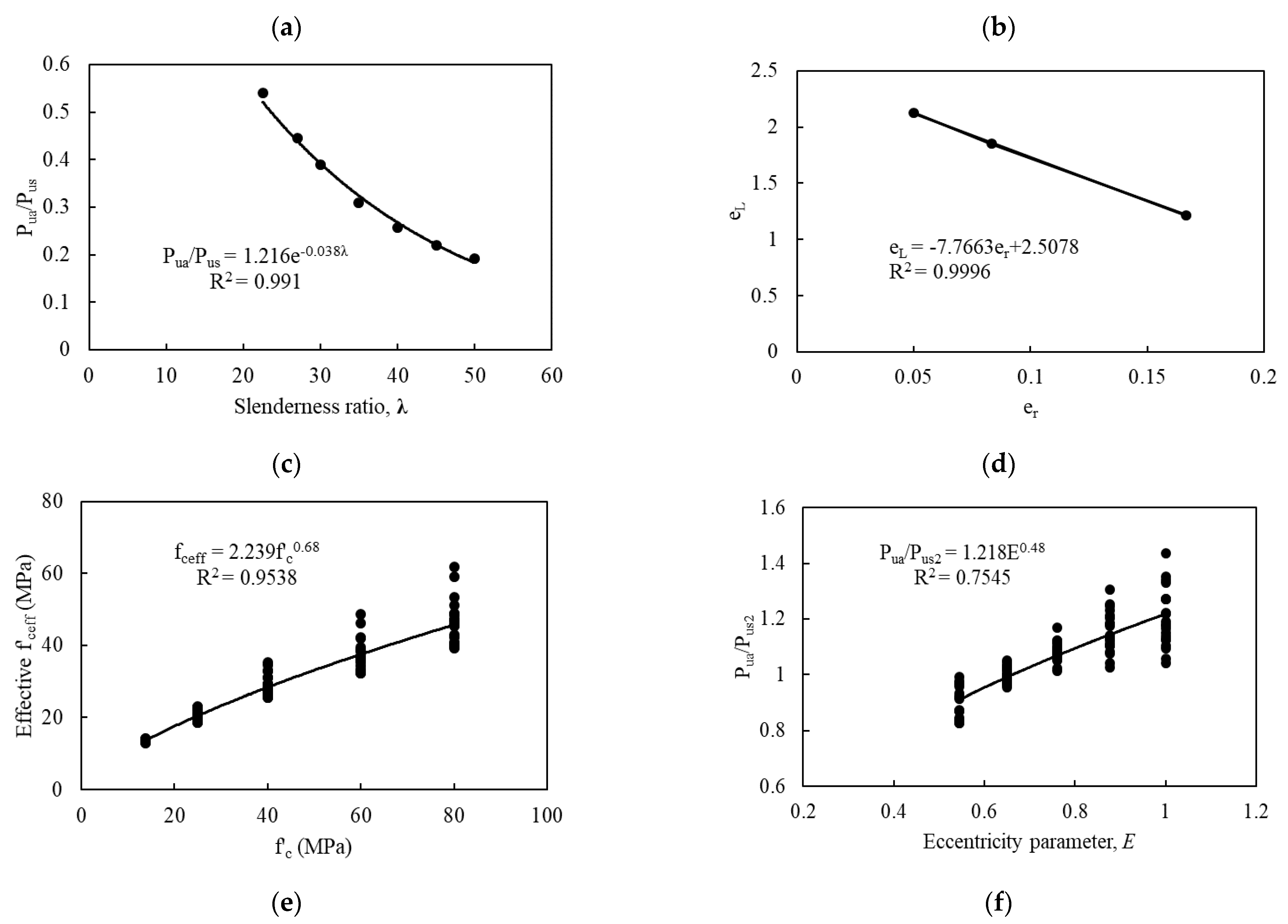
5.1. Effect of Slenderness Ratio
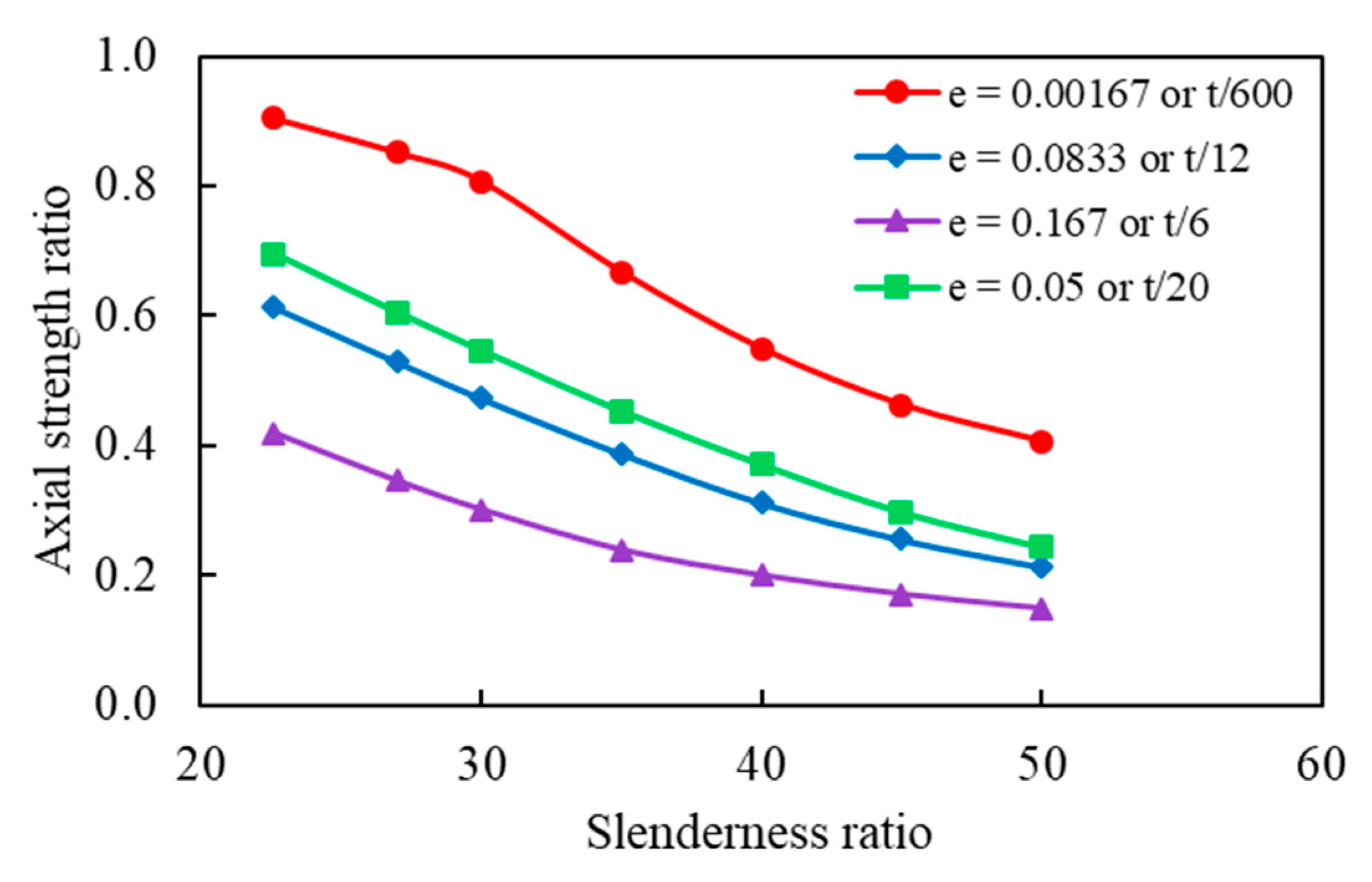
5.2. Effect of Eccentricity
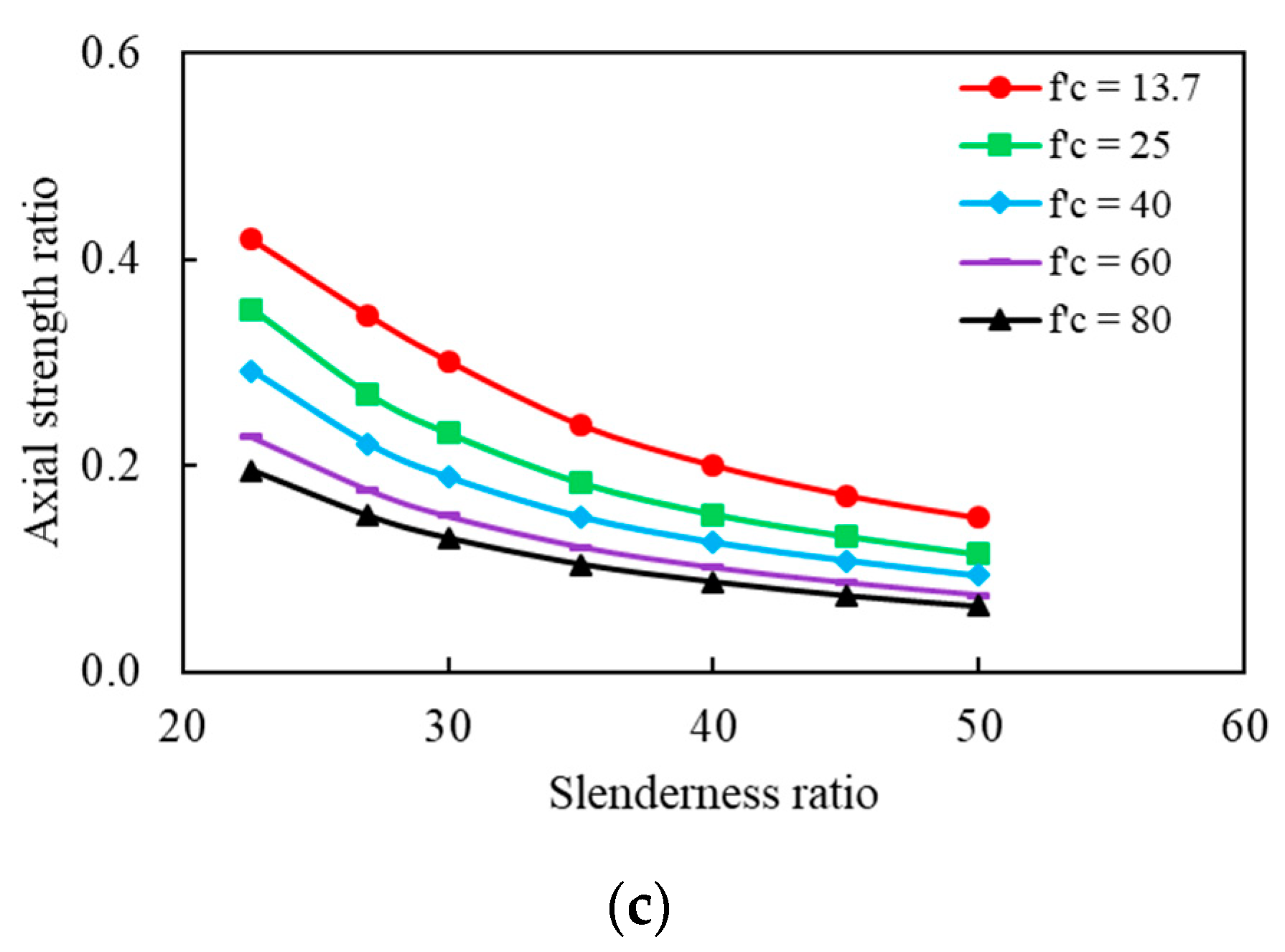
5.3. Effect of Compressive Strength
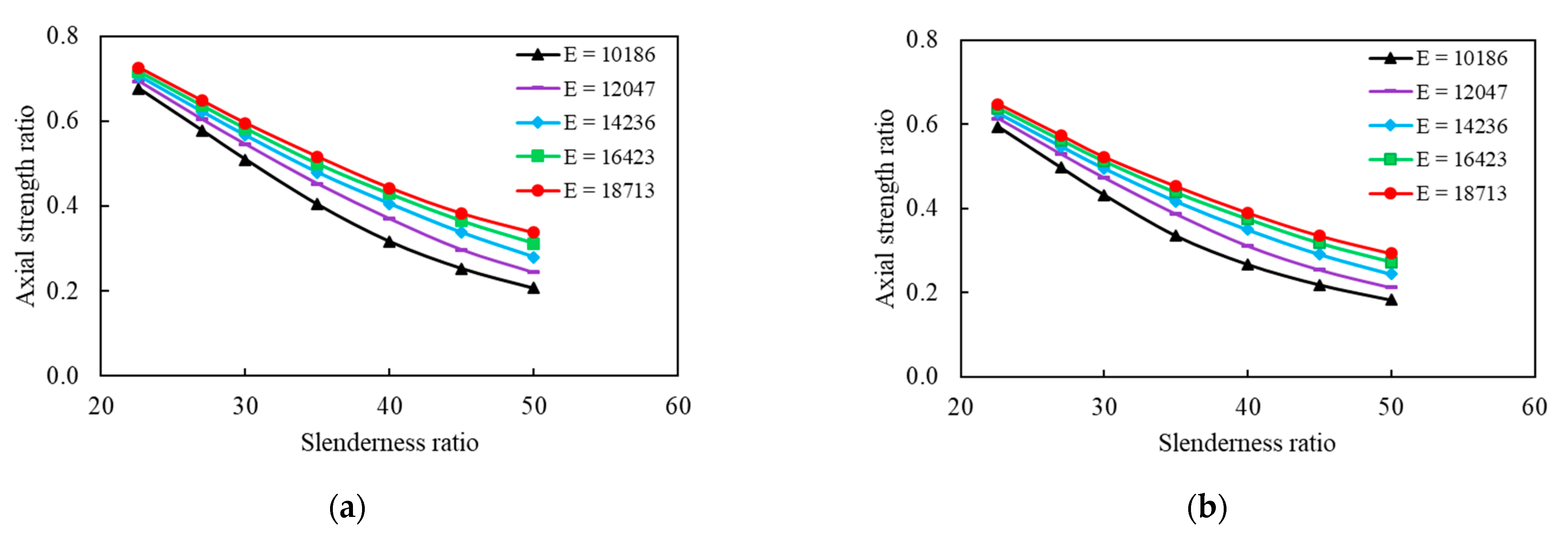
5.4. Effect of Elastic Modulus
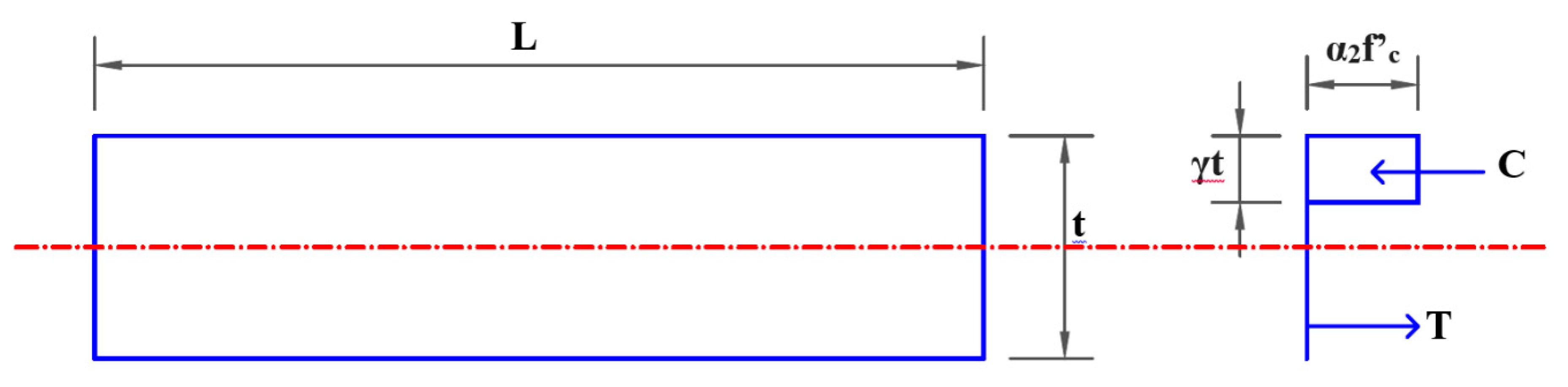
6. Proposed Design Equation
- The wall must contain minimum reinforcement in both vertical and horizontal directions as specified by the AS3600 standard;
- The loads are within the stress block of the section;
- The wall behaves as one-way wall under axial loading.
Equation Validation
7. Conclusions
- It is found that the axial load-deflection behavior of OPS-based LWSCC wall shows linear responses in the initial loading region, which are followed by nonlinear response up to ultimate failure load. The ultimate axial strength of lightweight wall decreases with an increase in the slenderness ratio.
- From the comparisons, it can be seen that the existing design equations from the standards provide conservative estimation with Pcal /Pexp ratios ranging from 0.36 to 0.91 and are not suitable for use in lightweight concrete wall. None of them takes into consideration the material properties of lightweight concrete.
- From the results of parametric study on the effects of slenderness ratio, it has been demonstrated that concrete wall is still capable of sustaining loading with a slenderness ratio more than 30, and the axial strength ratio decreases nonlinearly with the increase of slenderness ratio.
- Parametric study shows that the ultimate axial capacity increases nonlinearly with the increase of the compressive strength of concrete. Typically, the axial strength ratio can be decreased nonlinearly by 57% when compressive strength increases from 13.7 MPa to 80 MPa at constant eccentricity of t/6.
- From parametric study, the analysis has identified the elastic modulus as one of the key parameters determining the ultimate axial strength of concrete wall. Decrease in elastic modulus of concrete results in a reduced ultimate axial capacity of the wall and vice versa. Elastic modulus of concrete is the key parameter affecting the ultimate axial strength of lightweight concrete wall.
- A design equation based on the equivalent rectangular stress block concept and incorporated with statistical factors has been proposed, which takes into account the effects of the elastic modulus, slenderness ratio, eccentricity, and nonlinear compressive strength of concrete. The equation has been benchmarked against published data and found to be effective and versatile. With the consideration of concrete elastic modulus and relevant parameters, the proposed design equation is thought to be a more reliable and effective design aid for industrial application. The proposed design equation can be the basis for further development of the equation, taking into account more parameters such as wall openings and side restraints (two-way wall).
- Hence, considering its lightweight characteristics and self-compacting property, OPS-based LWSCC can be introduced as a sustainable solution for the construction industry to promote not only automation but also environmental conservation. The proposed design equation can serve as a practical design tool to provide insight into the strength of lightweight concrete wall used as an axial component for a sustainable building structure.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Specimen Details
| References | Specimen | H × L × t (mm) | f′c (MPa) | Steel Ratio | fsy (MPa) | Failure Load (kN) |
|---|---|---|---|---|---|---|
| Saheb and Desayi [28] | WAR1 | 600 × 900 × 50 | 17.864 | 0.00173 | 297 | 484.27 |
| WAR2 | 600 × 600 × 50 | 17.86 | 0.00 | 297 | 315.8 | |
| WAR3 | 600 × 400 × 50 | 17.86 | 0.00 | 297 | 198.29 | |
| WSR1 | 450 × 300 × 50 | 17.34 | 0.00 | 297 | 214.18 | |
| WSR2 | 600 × 400 × 50 | 17.34 | 0.00 | 297 | 254.1 | |
| WSR3 | 900 × 600 × 50 | 17.34 | 0.00 | 297 | 298.92 | |
| WSTV2 | 600 × 900 × 50 | 20.14 | 0.00 | 286 | 535.07 | |
| WSTV3 | 600 × 900 × 50 | 20.14 | 0.01 | 581 | 583.52 | |
| WSTH2 | 600 × 900 × 50 | 19.6 | 0.00173 | 297 | 538.01 | |
| Fragomeni and Mendis [35] | 2a | 1000 × 300 × 50 | 42.4 | 0.0025 | 450 | 231.8 |
| 2b | 1000 × 300 × 50 | 65.4 | 0.0025 | 450 | 263.5 | |
| 5a | 1000 × 500 × 40 | 35.7 | 0.0025 | 450 | 201.2 | |
| 5b | 1000 × 500 × 40 | 59.7 | 0.0025 | 450 | 269.2 | |
| 6b | 600 × 200 × 40 | 67.4 | 0.0031 | 450 | 178 | |
| Doh and Fragomeni [43] | OWNS3 | 1400 × 1400 × 40 | 52 | 0.0031 | 610 | 426.7 |
| OWNS4 | 1600 × 1600 × 40 | 51 | 0.0031 | 610 | 441.5 | |
| OWHS3 | 1400 × 1400 × 40 | 63 | 0.0031 | 610 | 441.5 | |
| OWHS4 | 1600 × 1600 × 40 | 75.9 | 0.0031 | 610 | 455.8 | |
| Ganesan, Indira and Santhakumar [36] | OPCAR1 | 600 × 320 × 40 | 33.832 | 0.0088 | 415 | 230.53 |
| GPCSR1 | 480 × 320 × 40 | 33.072 | 0.0088 | 415 | 256.18 | |
| GPCAR1 | 600 × 320 × 40 | 33.072 | 0.0088 | 415 | 211.89 |
References
- Mohammed, S.I.; Najim, K.B. Mechanical Strength, Flexural Behavior and Fracture Energy of Recycled Concrete Aggregate Self-Compacting Concrete. Structures. 2020, 23, 34–43. [Google Scholar] [CrossRef]
- Mo, K.H.; Thomas, B.S.; Yap, S.P.; Abutaha, F.; Tan, C.G. Viability of agricultural wastes as substitute of natural aggregate in concrete: A review on the durability-related properties. J. Clean. Prod. 2020, 275, 123062. [Google Scholar] [CrossRef]
- Ting, T.; Rahman, M.; Lau, H.; Ting, M. Recent development and perspective of lightweight aggregates based self-compacting concrete. Constr. Build. Mater. 2019, 201, 763–777. [Google Scholar] [CrossRef]
- Revilla-Cuesta, V.; Skaf, M.; Faleschini, F.; Manso, J.M.; Ortega-López, V. Self-compacting concrete manufactured with recycled concrete aggregate: An overview. J. Clean. Prod. 2020, 262, 121362. [Google Scholar] [CrossRef]
- Manzi, S.; Mazzotti, C.; Bignozzi, M.C. Self-compacting concrete with recycled concrete aggregate: Study of the long-term properties. Constr. Build. Mater. 2017, 157, 582–590. [Google Scholar] [CrossRef]
- Aslam, M.; Shafigh, P.; Jumaat, M.Z. Oil-palm by-products as lightweight aggregate in concrete mixture: A review. J. Clean. Prod. 2016, 126, 56–73. [Google Scholar] [CrossRef]
- Shafigh, P.; Jumaat, M.Z.; Mahmud, H. Mix design and mechanical properties of oil palm shell lightweight aggregate concrete: A review. Int. J. Phys. Sci. 2010, 5, 2127–2134. [Google Scholar]
- Zawawi, M.N.A.A.; Muthusamy, K.; Majeed, A.P.A.; Musa, R.M.; Budiea, A.M.A. Mechanical properties of oil palm waste lightweight aggregate concrete with fly ash as fine aggregate replacement. J. Build. Eng. 2020, 27, 100924. [Google Scholar] [CrossRef]
- Hamada, H.M.; Thomas, B.S.; Tayeh, B.; Yahaya, F.M.; Muthusamy, K.; Yang, J. Use of oil palm shell as an aggregate in cement concrete: A review. Constr. Build. Mater. 2020, 265, 120357. [Google Scholar] [CrossRef]
- Alengaram, U.J.; Al Muhit, B.A.; bin Jumaat, M.Z. Utilization of oil palm kernel shell as lightweight aggregate in concrete—A review. Constr. Build. Mater. 2013, 38, 161–172. [Google Scholar] [CrossRef]
- Nagaratnam, B.H.; Rahman, M.E.; Mirasa, A.K.; Mannan, M.A.; Lame, S.O. Workability and heat of hydration of self-compacting concrete incorporating agro-industrial waste. J. Clean. Prod. 2016, 112, 882–894. [Google Scholar] [CrossRef]
- Okpala, D. Palm kernel shell as a lightweight aggregate in concrete. Build. Environ. 1990, 25, 291–296. [Google Scholar] [CrossRef]
- Okafor, F.O. Palm kernel shell as a lightweight aggregate for concrete. Cem. Concr. Res. 1988, 18, 901–910. [Google Scholar] [CrossRef]
- Mannan, M.; Alexander, J.; Ganapathy, C.; Teo, D. Quality improvement of oil palm shell (OPS) as coarse aggregate in lightweight concrete. Build. Environ. 2006, 41, 1239–1242. [Google Scholar] [CrossRef]
- Chen, M.; Li, Z.-H.; Wu, J.-F.; Wang, J.-H. Shear behaviour and diagonal crack checking of shale ceramsite lightweight aggregate concrete beams with high-strength steel bars. Constr. Build. Mater. 2020, 249, 118730. [Google Scholar] [CrossRef]
- Teo, D.; Mannan, M.A.; Kurian, V.; Ganapathy, C. Lightweight concrete made from oil palm shell (OPS): Structural bond and durability properties. Build. Environ. 2007, 42, 2614–2621. [Google Scholar] [CrossRef]
- Shafigh, P.; Jumaat, M.Z.; Mahmud, H. Oil palm shell as a lightweight aggregate for production high strength lightweight concrete. Constr. Build. Mater. 2011, 25, 1848–1853. [Google Scholar] [CrossRef]
- Farahani, J.N.; Shafigh, P.; Alsubari, B.; Shahnazar, S.; Mahmud, H.B. Engineering properties of lightweight aggregate concrete containing binary and ternary blended cement. J. Clean. Prod. 2017, 149, 976–988. [Google Scholar] [CrossRef]
- Mannan, M.A.; Ganapathy, C. Engineering properties of concrete with oil palm shell as coarse aggregate. Constr. Build. Mater. 2002, 16, 29–34. [Google Scholar] [CrossRef]
- Alengaram, U.J.; Jumaat, M.Z.; Mahmud, H. Ductility behaviour of reinforced palm kernel shell concrete beams. Eur. J. Sci. Res. 2008, 23, 406–420. [Google Scholar]
- Fanijo, E.; Babafemi, A.J.; Arowojolu, O. Performance of laterized concrete made with palm kernel shell as replacement for coarse aggregate. Constr. Build. Mater. 2020, 250, 118829. [Google Scholar] [CrossRef]
- Alsalami, Z.H.A.; Harith, I.K.; Dhahir, M.K. Utilization of dates palm kernel in high performance concrete. J. Build. Eng. 2018, 20, 166–172. [Google Scholar] [CrossRef]
- Aslam, M.; Shafigh, P.; Nomeli, M.A.; Jumaat, M.Z. Manufacturing of high-strength lightweight aggregate concrete using blended coarse lightweight aggregates. J. Build. Eng. 2017, 13, 53–62. [Google Scholar] [CrossRef]
- Shafigh, P.; Jumaat, M.Z.; Mahmud, H.B.; Hamid, N.A.A. Lightweight concrete made from crushed oil palm shell: Tensile strength and effect of initial curing on compressive strength. Constr. Build. Mater. 2012, 27, 252–258. [Google Scholar] [CrossRef]
- Shafigh, P.; Nomeli, M.A.; Alengaram, U.J.; Mahmud, H.B.; Jumaat, M.Z. Engineering properties of lightweight aggregate concrete containing limestone powder and high volume fly ash. J. Clean. Prod. 2016, 135, 148–157. [Google Scholar] [CrossRef]
- Doh, J.-H.; Fragomeni, S.; Kim, J.-W. Brief review of studies on concrete wall panels in one and two way action. Int. J. Ocean. Eng. Technol. Spec. Sel. Pap. 2001, 4, 38–43. [Google Scholar]
- Delatte, N. Failure, Distress and Repair of Concrete Structures; Elsevier: Amsterdam, The Netherlands, 2009. [Google Scholar]
- Saheb, S.M.; Desayi, P. Ultimate strength of RC wall panels in one-way in-plane action. J. Struct. Eng. 1989, 115, 2617–2630. [Google Scholar] [CrossRef]
- Saheb, S.M.; Desayi, P. Ultimate strength of RC wall panels in two-way in-plane action. J. Struct. Eng. 1990, 116, 1384–1402. [Google Scholar] [CrossRef]
- Ganesan, N.; Indira, P.; Prasad, S.R. Strength and behavior of SFRSCC and SFRC wall panels under one-way in-plane action. In High Performance Fiber Reinforced Cement Composites 6; Springer: Berlin/Heidelberg, Germany, 2012; pp. 279–286. [Google Scholar]
- ACI Committee 318. Building Code Requirements for Structural Concrete (ACI 318-05) and Commentary (ACI 318R-05); American Concrete Institute: Farmington Hills, MI, USA, 2005. [Google Scholar]
- AS 3600-2018: Concrete Structures; Standards Australia Limited: Sydney, Australia, 2018.
- Institution, B.S. Eurocode 2: Design of Concrete Structures: Part 1-1: General Rules and Rules for Buildings; British Standards Institution: London, UK, 2004. [Google Scholar]
- Robinson, G.P.; Palmeri, A.; Austin, S.A. Design methodologies for one way spanning eccentrically loaded minimally or centrally reinforced pre-cast RC panels. Eng. Struct. 2013, 56, 1945–1956. [Google Scholar] [CrossRef][Green Version]
- Fragomeni, S.; Mendis, P. Improved axial load formulae for normal and high strength reinforced concrete walls. Aust. Civ. Eng. Trans. 1996, 38, 71. [Google Scholar]
- Ganesan, N.; Indira, P.; Santhakumar, A. Prediction of ultimate strength of reinforced geopolymer concrete wall panels in one-way action. Constr. Build. Mater. 2013, 48, 91–97. [Google Scholar] [CrossRef]
- Huang, Y.; Hamed, E.; Chang, Z.-T.; Foster, S.J. Theoretical and experimental investigation of failure behavior of one-way high-strength concrete wall panels. J. Struct. Eng. 2014, 141, 04014143. [Google Scholar] [CrossRef]
- Huang, Y.; Hamed, E. Buckling of one-way high-strength concrete panels: Creep and shrinkage effects. J. Eng. Mech. 2013, 139, 1856–1867. [Google Scholar] [CrossRef]
- Oberlender, G.D. Strength Investigation of Precast Reinforced Concrete Load-Bearing Wall Panels; The University of Texas at Arlington: Arlington, TX, USA, 1975. [Google Scholar]
- Seddon, A. Concrete Walls in Compression under Short-Term Axial and Eccentric Loads; IABSE (International Association for Bridge and Structural Engineering): Zürich, Switzerland, 1956. [Google Scholar]
- Pillai, S.U.; Parthasarathy, C. Ultimate strength and design of concrete walls. Build. Environ. 1977, 12, 25–29. [Google Scholar] [CrossRef]
- Zielinski, Z.; Troitski, M.; El-Chakieh, E. Bearing capacity tests on precast concrete thin-wall ribbed panels. PCI J. 1983, 28, 88–103. [Google Scholar] [CrossRef]
- Doh, J.-H.; Fragomeni, S. Evaluation of experimental work on concrete walls in one and two-way action. Aust. J. Struct. Eng. 2005, 6, 37–52. [Google Scholar] [CrossRef]
- Lim, J.C.; Ozbakkaloglu, T. Stress–strain model for normal-and light-weight concretes under uniaxial and triaxial compression. Constr. Build. Mater. 2014, 71, 492–509. [Google Scholar] [CrossRef]
- Cui, H.; Lo, T.Y.; Memon, S.A.; Xing, F.; Shi, X. Analytical model for compressive strength, elastic modulus and peak strain of structural lightweight aggregate concrete. Constr. Build. Mater. 2012, 36, 1036–1043. [Google Scholar] [CrossRef]
- Abdurra’uf, M.G.; Jaganathan, J.; Anwar, M.; Leung, H. Experimental studies and theoretical models for concrete columns confined with FRP composites: A review. World J. Eng. 2019, 16, 509–525. [Google Scholar]
- Hegger, J.; Dreßen, T.; Will, N. Zur Tragfähigkeit unbewehrter Betonwände. Beton-Und Stahlbetonbau 2007, 102, 280–288. [Google Scholar] [CrossRef]
- Hegger, J.; Dressen, T.; Will, N. Load-bearing capacity of plain concrete walls. Mag. Concr. Res. 2009, 61, 173–182. [Google Scholar] [CrossRef]
- Leabu, V.F. Problems and Performance of Precast Concrete Wall Panels. J. Proc. 1959, 56, 287–298. [Google Scholar]
- Kripanarayanan, K. Interesting Aspects of the Empirical Wall Design Equation. J. Proc. 1977, 74, 204–207. [Google Scholar]
- Mohamad, N.; Goh, W.I.; Abdullah, R.; Samad, A.A.A.; Mendis, P.; Sofi, M. Structural performance of FCS wall subjected to axial load. Constr. Build. Mater. 2017, 134, 185–198. [Google Scholar] [CrossRef]
- ASTM C150/C150M-12: Standard Specification for Portland Cement; ASTM International: West Conshohocken, PA, USA, 2012.
- Astm, C. Standard Specification for Fly Ash and Raw or Calcined Natural Pozzolan for Use as a Mineral Admixture in Portland Cement Concrete; ASTM International: West Conshohocken, PA, USA, 2003; p. 618. [Google Scholar]
- Ting, T.Z.H.; Rahman, M.E.; Lau, H.H. Sustainable lightweight self-compacting concrete using oil palm shell and fly ash. Constr. Build. Mater. 2020, 264, 120590. [Google Scholar] [CrossRef]
- ASTM C39/C39M-18, Standard Test Method for Compressive Strength of Cylindrical Concrete Specimens; ASTM International: West Conshohocken, PA, USA, 2018; Available online: www.astm.org (accessed on 1 November 2021).
- Standard Test Method for Splitting Tensile Strength of Cylindrical Concrete Specimens; ASTM International: West Conshohocken, PA, USA, 2011.
- Yang, K.-H.; Mun, J.-H.; Cho, M.-S.; Kang, T.H.-K. Stress-Strain Model for Various Unconfined Concretes in Compression. ACI Struct. J. 2014, 111, 819. [Google Scholar] [CrossRef]
- Systemes, D. Abaqus Theory Guide; Version 6.14; Simulia Corporation: Johnston, RI, USA, 2014. [Google Scholar]
- Wahalathantri, B.L.; Thambiratnam, D.; Chan, T.; Fawzia, S. A material model for flexural crack simulation in reinforced concrete elements using ABAQUS. In Proceedings of the First International Conference on Engineering, Designing and Developing the Built Environment for Sustainable Wellbeing, Brisbane, Australia, 27–29 April 2011. [Google Scholar]
- Hillerborg, A.; Modéer, M.; Petersson, P.-E. Analysis of crack formation and crack growth in concrete by means of fracture mechanics and finite elements. Cem. Concr. Res. 1976, 6, 773–781. [Google Scholar] [CrossRef]
- Nayal, R.; Rasheed, H.A. Tension stiffening model for concrete beams reinforced with steel and FRP bars. J. Mater. Civ. Eng. 2006, 18, 831–841. [Google Scholar] [CrossRef]
- Hui Fan, Y.; Pan Liu, P.; Shen, B.; Ma, K.; Wu, B.; Zheng, T.; Yang, F. Shear-bearing capacity analysis under static force for shear key of the reinforced concrete open-web sandwich slab applied to long-span structure. Int. J. Struct. Integr. 2020, 2, 195–213. [Google Scholar] [CrossRef]
- Ho, N.M.; Doh, J.H. Experimental and numerical investigations of axially loaded RC walls restrained on three sides. Struct. Des. Tall Spec. Build. 2018, 27, e1459. [Google Scholar] [CrossRef]
- Warner, R.F.; Rangan, B.; Hall, A.; Faulkes, K. Concrete Structures; Pearson Education Australia: Melbourne, Australia, 1998. [Google Scholar]
- Ho, N.M.; Doh, J.H. Prediction of ultimate strength of concrete walls restrained on three sides. Struct. Concr. 2019, 20, 942–954. [Google Scholar] [CrossRef]
- Bathe, K.-J.; Walczak, J.; Welch, A.; Mistry, N. Nonlinear analysis of concrete structures. Comput. Struct. 1989, 32, 563–590. [Google Scholar] [CrossRef]







| Chemicals | Cement (%) | Fly Ash (%) |
|---|---|---|
| 20.0 | 57.8 | |
| 5.2 | 20.0 | |
| 3.3 | 11.7 | |
| 63.2 | 3.28 | |
| 0.8 | 1.95 | |
| 2.4 | 0.08 | |
| - | 3.88 | |
| - | 2.02 | |
| - | 0.30 | |
| Loss on ignition | 2.5 | 0.32 |
| Physical Property | River Sand | OPS |
|---|---|---|
| Specific gravity | 2.64 | 1.19 |
| Water absorption (24 h) (%) | 1.1 | 18.11 |
| Aggregate impact value (AIV) (%) | - | 4.2 |
| Cement (kg/m3) | Fly Ash (kg/m3) | Water (kg/m3) | Sand (kg/m3) | OPS Aggregate (kg/m3) | SP (kg/m3) |
|---|---|---|---|---|---|
| 312 | 208 | 161.2 | 715 | 455 | 8.6 |
| Specimen | Height L (mm) | Width W (mm) | Thickness t (mm) | Average Compressive Strength (MPa) | Average Splitting Tensile Strength (MPa) | Nominal Density (kg/m3) |
|---|---|---|---|---|---|---|
| T25-AR1.8SR17 a | 425 | 235 | 25 | 16.4 | 1.5 | 1829 |
| T25-AR1.8SR23 a | 565 | 315 | 25 | |||
| T25-AR3.1SR23 a | 565 | 185 | 25 | |||
| T25-AR5.3SR23 a | 565 | 105 | 25 | |||
| T60-AR5.3SR23 b | 1400 | 260 | 60 | 13.7 | 1.1 | 1823 |
| Parameters | Values |
|---|---|
| Elastic modulus (MPa) | 12,047 |
| Poisson ratio | 0.2 |
| Density (kg/m3) | 1800 |
| Dilation angle | 31° |
| Eccentricity | 0.1 |
| 1.16 | |
| Kc | 0.667 |
| Viscosity | 0.001 |
| Fsy (MPa) | Fsu (MPa) | v |
|---|---|---|
| 299 | 374 | 0.3 |
| Specimens | Maximum Deflection, Δ (mm) | Specimen Height, H (mm) | Deflection Ratio, Δ/H |
|---|---|---|---|
| T25-AR1.8SR17 | 1.93 | 425 | 0.0045 |
| T25-AR1.8SR23 | 2.97 | 565 | 0.0053 |
| T25-AR3.1SR23 | 2.89 | 565 | 0.0051 |
| T25-AR5.3SR23 | 2.46 | 565 | 0.0044 |
| T60-AR5.3SR23 | 6.4 | 1400 | 0.0046 |
| Specimens | Average Failure Load Pexp (kN) | Standard Deviation of Test Results | Average Axial Strength Ratio Pexp/f′cAg | ACI Pcal (kN) | AS Pcal (kN) | Eurocode 2 Pcal (kN) |
|---|---|---|---|---|---|---|
| T25-AR1.8SR17 | 78 | 2.25 | 0.78 | 40.83 | 44.6 | 63.51 |
| T25-AR1.8SR23 | 85.59 | 1.8 | 0.64 | 39.81 | 46.42 | 66.33 |
| T25-AR3.1SR23 | 51.2 | 1.31 | 0.65 | 23.43 | 27.31 | 39.01 |
| T25-AR5.3SR23 | 27.32 | 0.6 | 0.68 | 10.46 | 12.52 | 18.06 |
| T60-AR5.3SR23 | 155.06 | 2.25 | 0.71 | 60.03 | 71.07 | 101.97 |
| Study | Specimen | Pexp (kN) | PFEA (kN) | PFEA/Pexp Ratio |
|---|---|---|---|---|
| Present Study | T25-AR1.8SR17 | 78 | 82.31 | 1.06 |
| T25-AR1.8SR23 | 85.59 | 88.53 | 1.03 | |
| T25-AR3.1SR23 | 51.2 | 53.55 | 1.05 | |
| T25-AR5.3SR23 | 27.32 | 28.55 | 1.05 | |
| T60-AR5.3SR23 | 155.06 | 159.68 | 1.03 | |
| Saheb and Desayi [28] | WSR1 | 214.18 | 192.4 | 0.90 |
| WSR2 | 254.1 | 246.87 | 0.97 | |
| WSR3 | 298.92 | 319.1 | 1.07 | |
| WSR4 | 373.65 | 409.67 | 1.10 | |
| WSTV4 | 704.14 | 787.66 | 1.12 | |
| WSTV7 | 463.28 | 430.94 | 0.93 | |
| WSTH6 | 348.74 | 362.97 | 1.04 | |
| Doh and Fragomeni [43] | OWNS3 | 426.7 | 462.25 | 1.08 |
| OWNS4 | 441.5 | 443.63 | 1.00 | |
| OWHS2 | 482.7 | 504 | 1.04 | |
| OWHS3 | 441.5 | 462.45 | 1.05 | |
| OWHS4 | 455.8 | 495.71 | 1.09 | |
| Mean | 1.04 | |||
| Standard Deviation | 0.06 | |||
| Specimen | ACI | AS | EC 2 | Equation (22) | |
|---|---|---|---|---|---|
| Pcal/Pexp | Pcal/Pexp | Pcal/Pexp | Pcal/Pexp | ||
| Present study | T25-AR1.8SR17 | 0.52 | 0.56 | 0.80 | 0.88 |
| T25-AR1.8SR23 | 0.46 | 0.54 | 0.77 | 1.00 | |
| T25-AR3.1SR23 | 0.45 | 0.53 | 0.75 | 0.97 | |
| T25-AR5.3SR23 | 0.38 | 0.46 | 0.66 | 0.94 | |
| T60-AR5.3SR23 | 0.39 | 0.46 | 0.66 | 0.97 | |
| Saheb and Desayi [28] | WAR1 | 0.78 | 0.68 | 0.75 | 1.06 |
| WAR2 | 0.80 | 0.70 | 0.77 | 1.08 | |
| WAR3 | 0.85 | 0.74 | 0.81 | 1.14 | |
| WSR1 | 0.62 | 0.54 | 0.64 | 0.88 | |
| WSR2 | 0.65 | 0.56 | 0.62 | 0.88 | |
| WSR3 | 0.66 | 0.57 | 0.52 | 0.89 | |
| WSTV2 | 0.80 | 0.70 | 0.76 | 1.03 | |
| WSTV3 | 0.73 | 0.64 | 0.70 | 0.94 | |
| WSTH2 | 0.78 | 0.67 | 0.74 | 1.01 | |
| Fragomeni and Mendis [35] | 2a | 0.92 | 0.79 | 0.67 | 0.87 |
| 2b | 1.25 | 1.07 | 0.91 | 0.92 | |
| 5a | 0.76 | 0.64 | 0.42 | 1.02 | |
| 5b | 0.95 | 0.80 | 0.52 | 0.96 | |
| 6b | 1.30 | 1.13 | 1.13 | 0.89 | |
| Doh and Fragomeni [43] | OWNS3 | N.A. | N.A. | N.A. | 1.10 |
| OWNS4 | N.A. | N.A. | N.A. | 0.99 | |
| OWHS3 | N.A. | N.A. | N.A. | 1.14 | |
| OWHS4 | N.A. | N.A. | N.A. | 1.11 | |
| Ganesan, Indira and Santhakumar [36] | OPCAR1 | 0.81 | 0.70 | 0.70 | 0.81 |
| GPCSR1 | 0.78 | 0.68 | 0.75 | 0.80 | |
| GPCAR1 | 0.86 | 0.74 | 0.75 | 0.87 | |
| Mean | 0.36 | 0.31 | 0.34 | 0.97 | |
| Standard Deviation | 1.05 | 0.97 | 0.96 | 0.10 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rahman, M.E.; Ting, T.Z.H.; Lau, H.H.; Nagaratnam, B.; Poologanathan, K. Behaviour of Lightweight Concrete Wall Panel under Axial Loading: Experimental and Numerical Investigation toward Sustainability in Construction Industry. Buildings 2021, 11, 620. https://doi.org/10.3390/buildings11120620
Rahman ME, Ting TZH, Lau HH, Nagaratnam B, Poologanathan K. Behaviour of Lightweight Concrete Wall Panel under Axial Loading: Experimental and Numerical Investigation toward Sustainability in Construction Industry. Buildings. 2021; 11(12):620. https://doi.org/10.3390/buildings11120620
Chicago/Turabian StyleRahman, Muhammad Ekhlasur, Timothy Zhi Hong Ting, Hieng Ho Lau, Brabha Nagaratnam, and Keerthan Poologanathan. 2021. "Behaviour of Lightweight Concrete Wall Panel under Axial Loading: Experimental and Numerical Investigation toward Sustainability in Construction Industry" Buildings 11, no. 12: 620. https://doi.org/10.3390/buildings11120620
APA StyleRahman, M. E., Ting, T. Z. H., Lau, H. H., Nagaratnam, B., & Poologanathan, K. (2021). Behaviour of Lightweight Concrete Wall Panel under Axial Loading: Experimental and Numerical Investigation toward Sustainability in Construction Industry. Buildings, 11(12), 620. https://doi.org/10.3390/buildings11120620








