Seismic Resistance of Timber Frames with Mud and Stone Infill Walls in a Chinese Traditional Village Dwelling
Abstract
:1. Introduction
2. Field Investigations
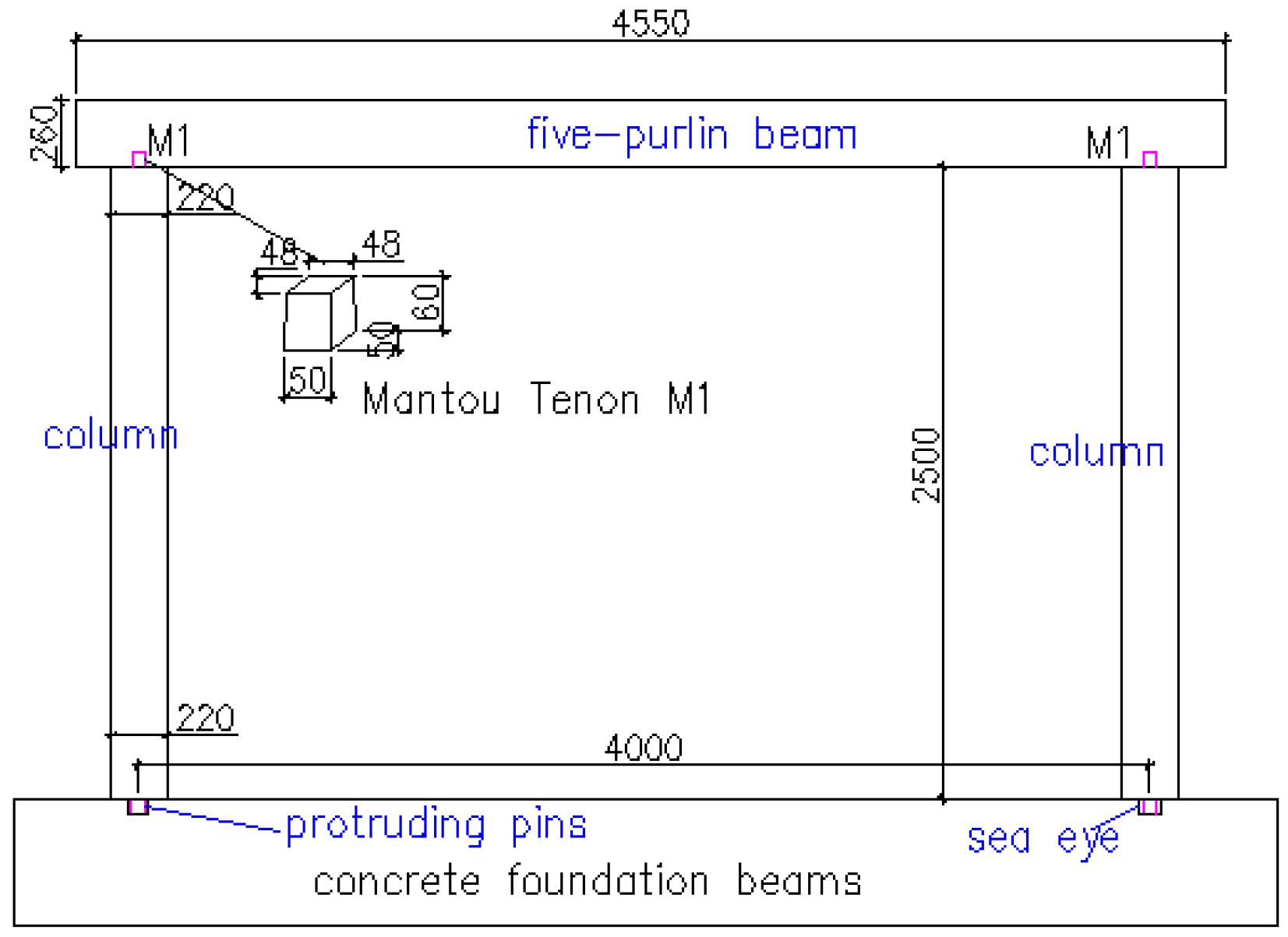
2.1. Foundation
2.2. Structural Walls
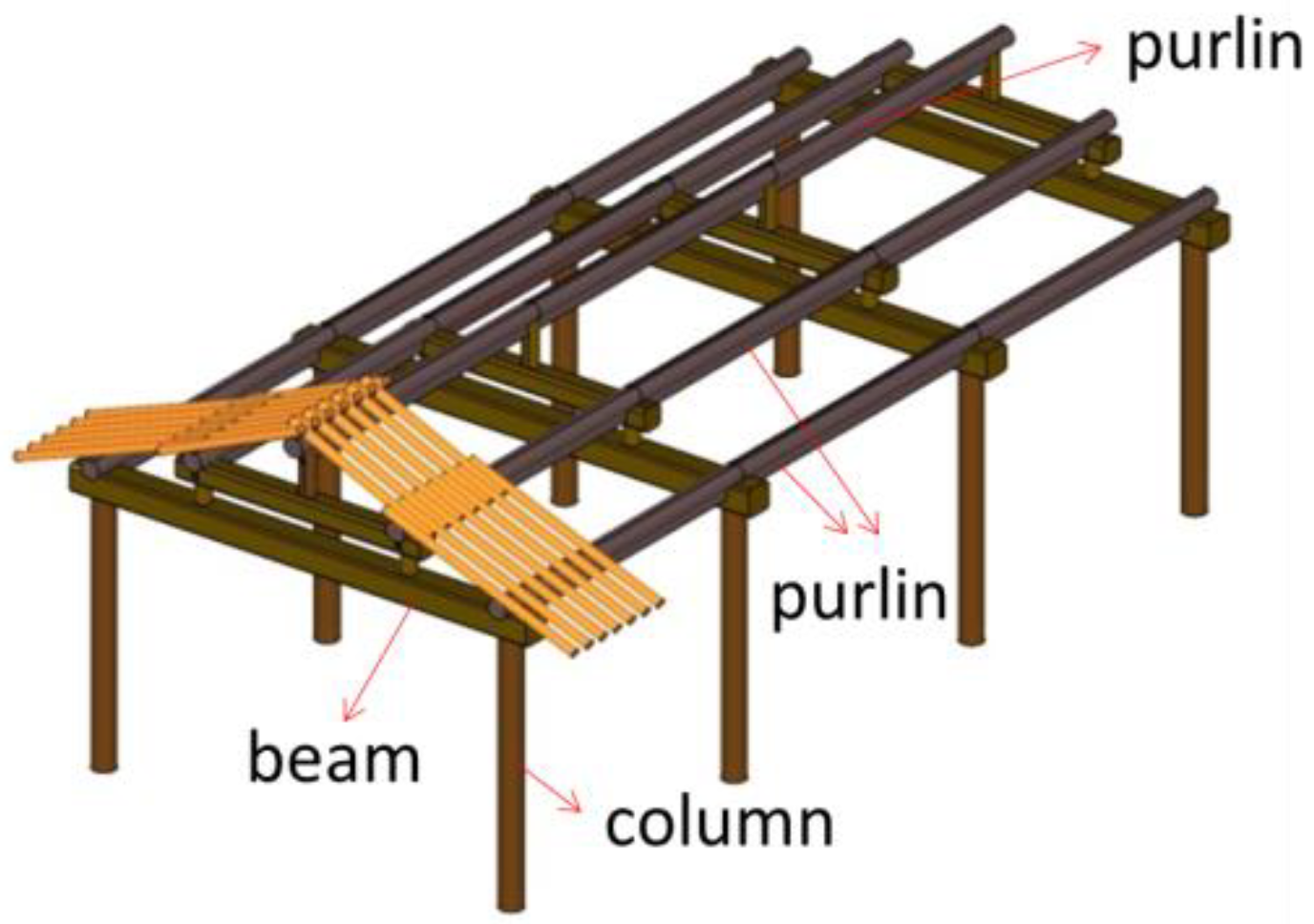
2.3. Roof Structure and Covering
3. Experimental Program
3.1. Test Configurations and Experimental Setup
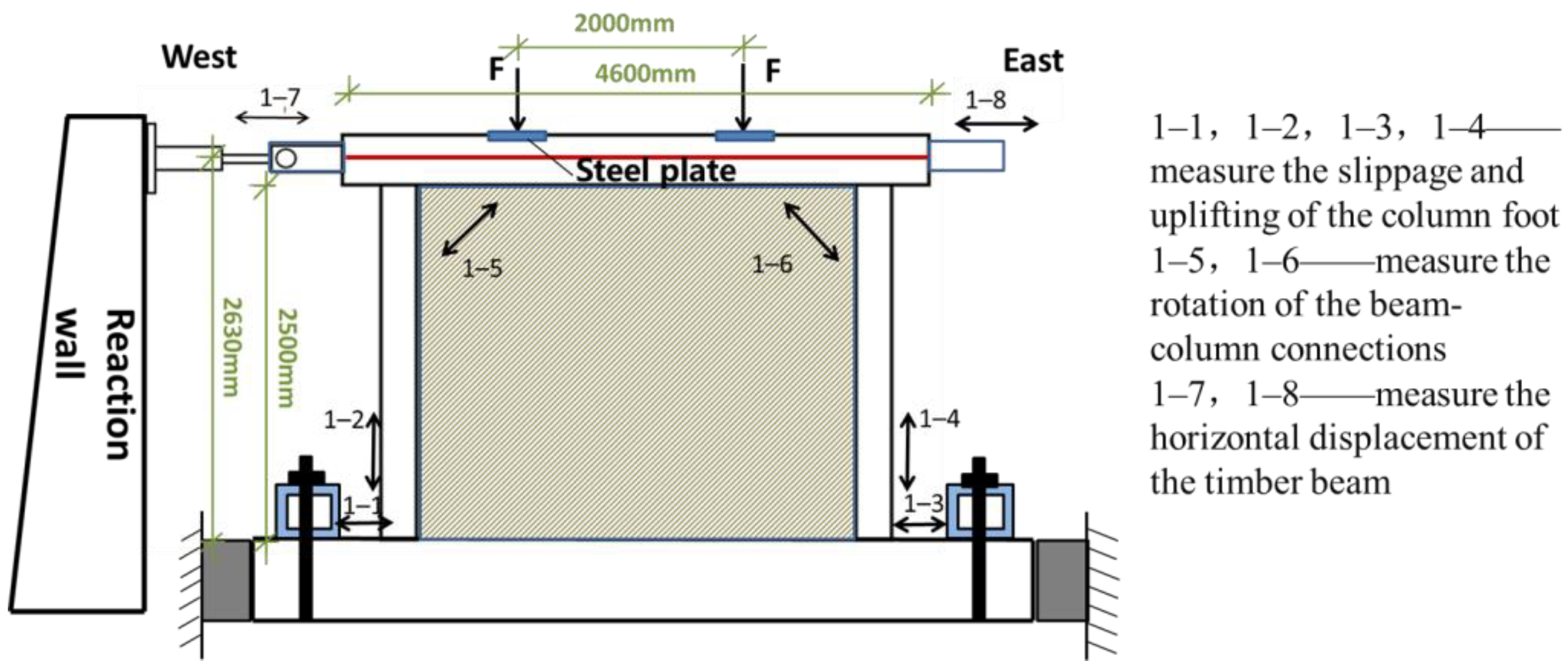


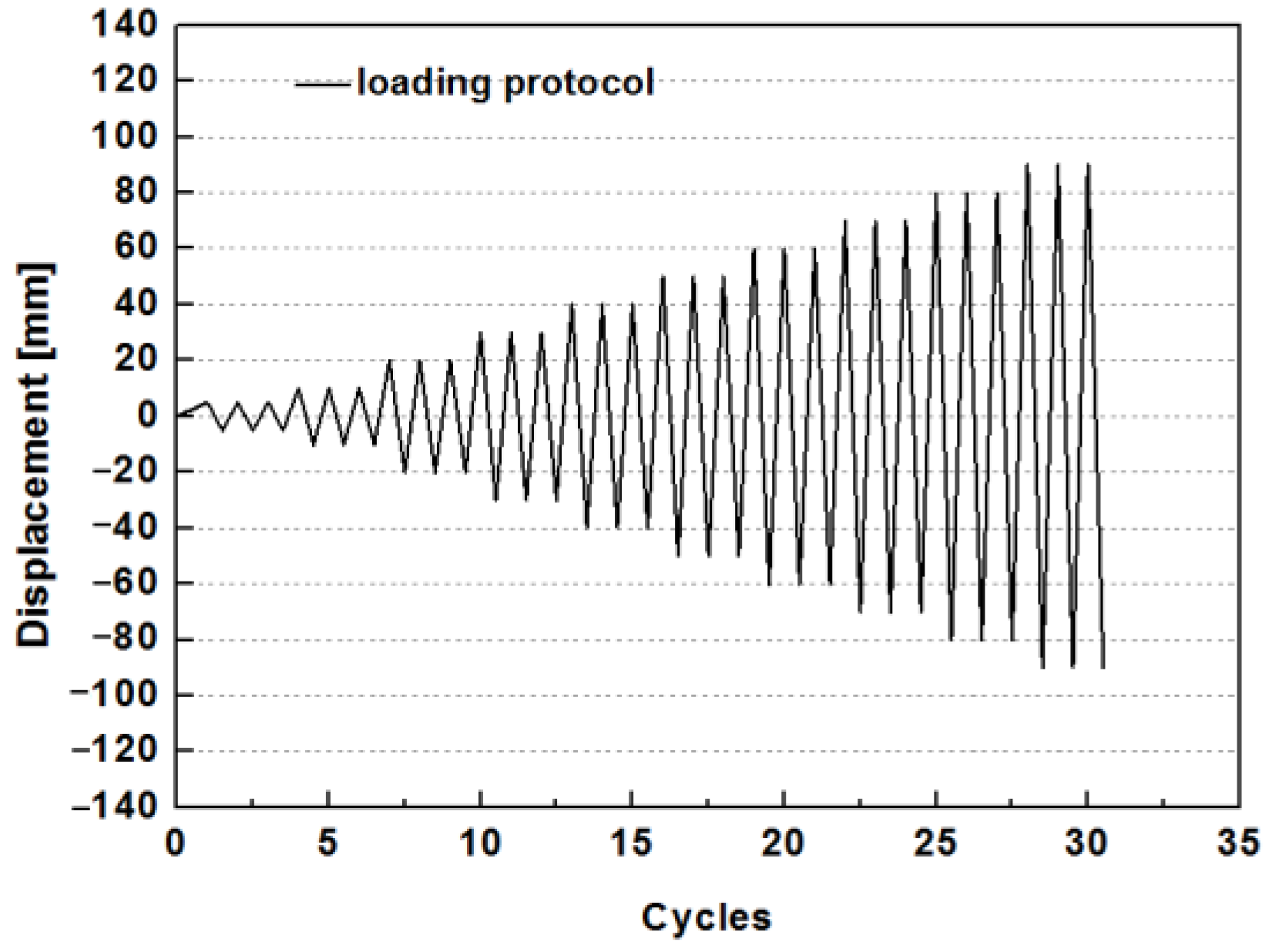
3.2. Loading Protocol
4. Experimental Results
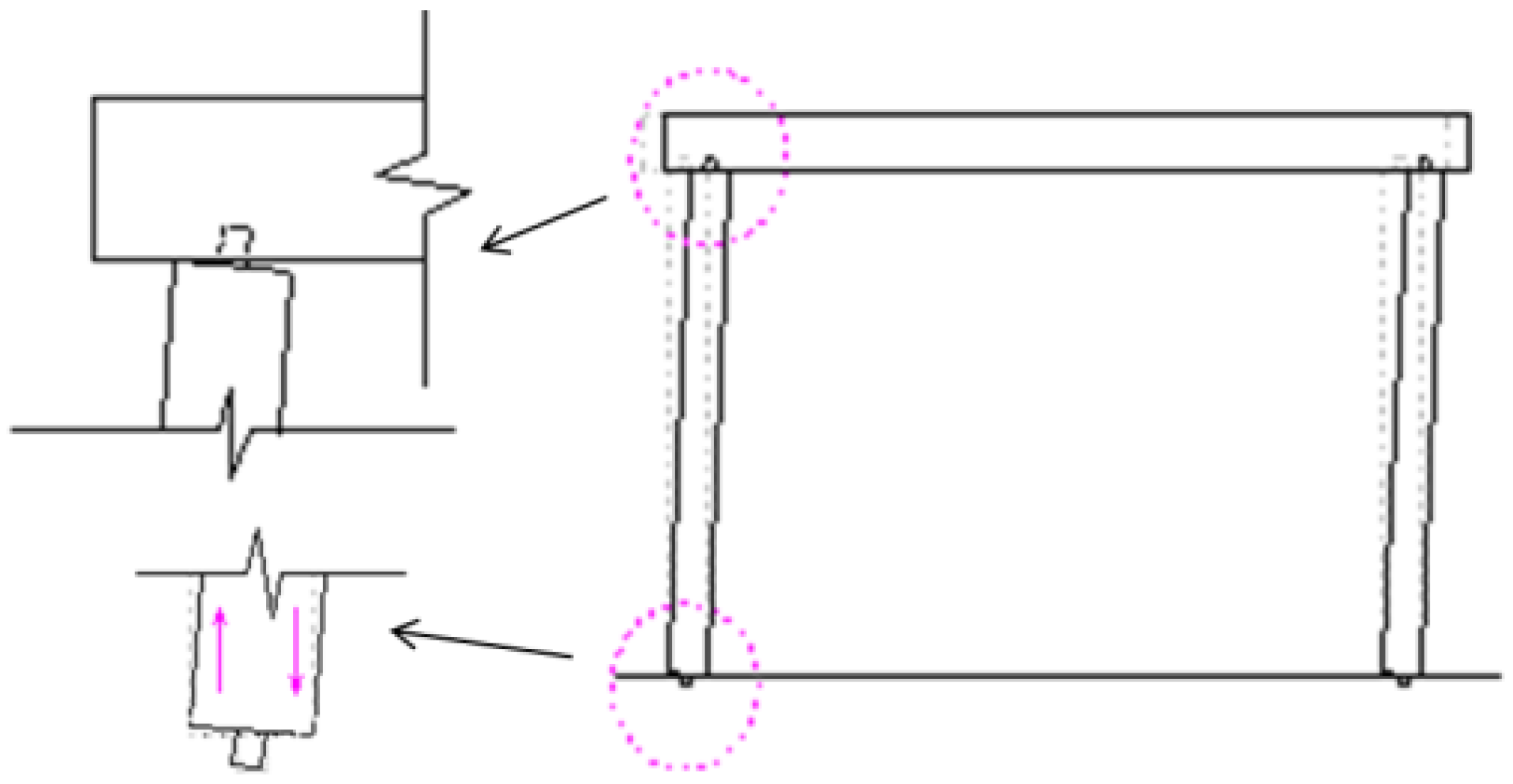
4.1. Experimental Phenomena
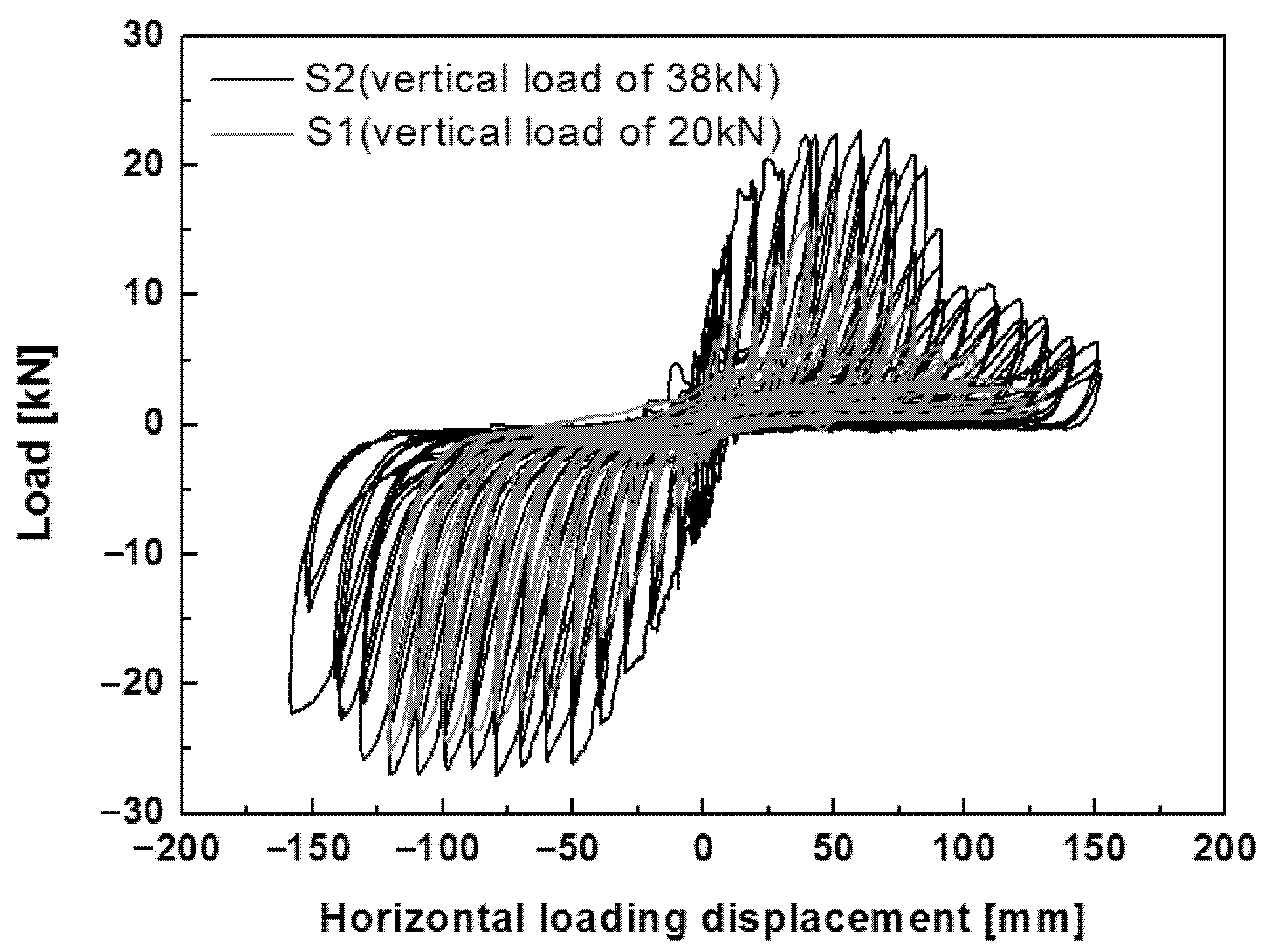
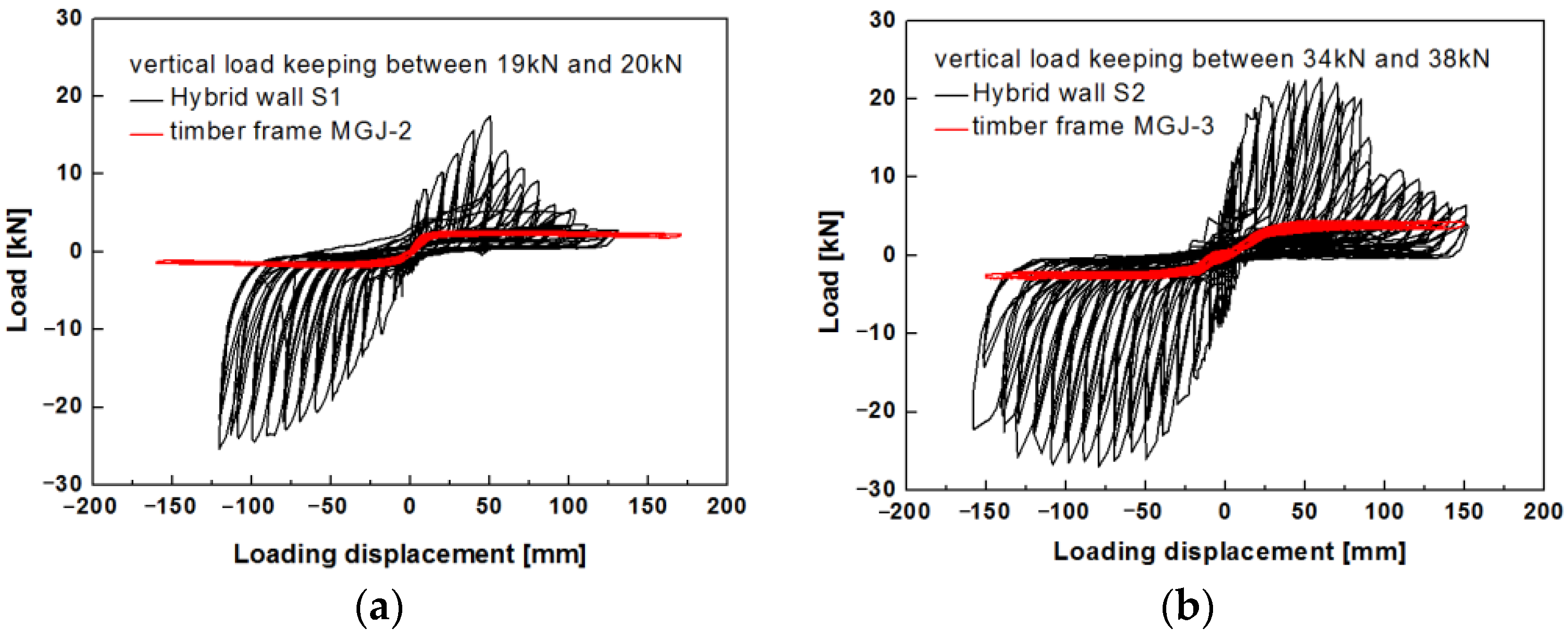
4.2. Typical Hysteresis Curves
4.3. Seismic Performance
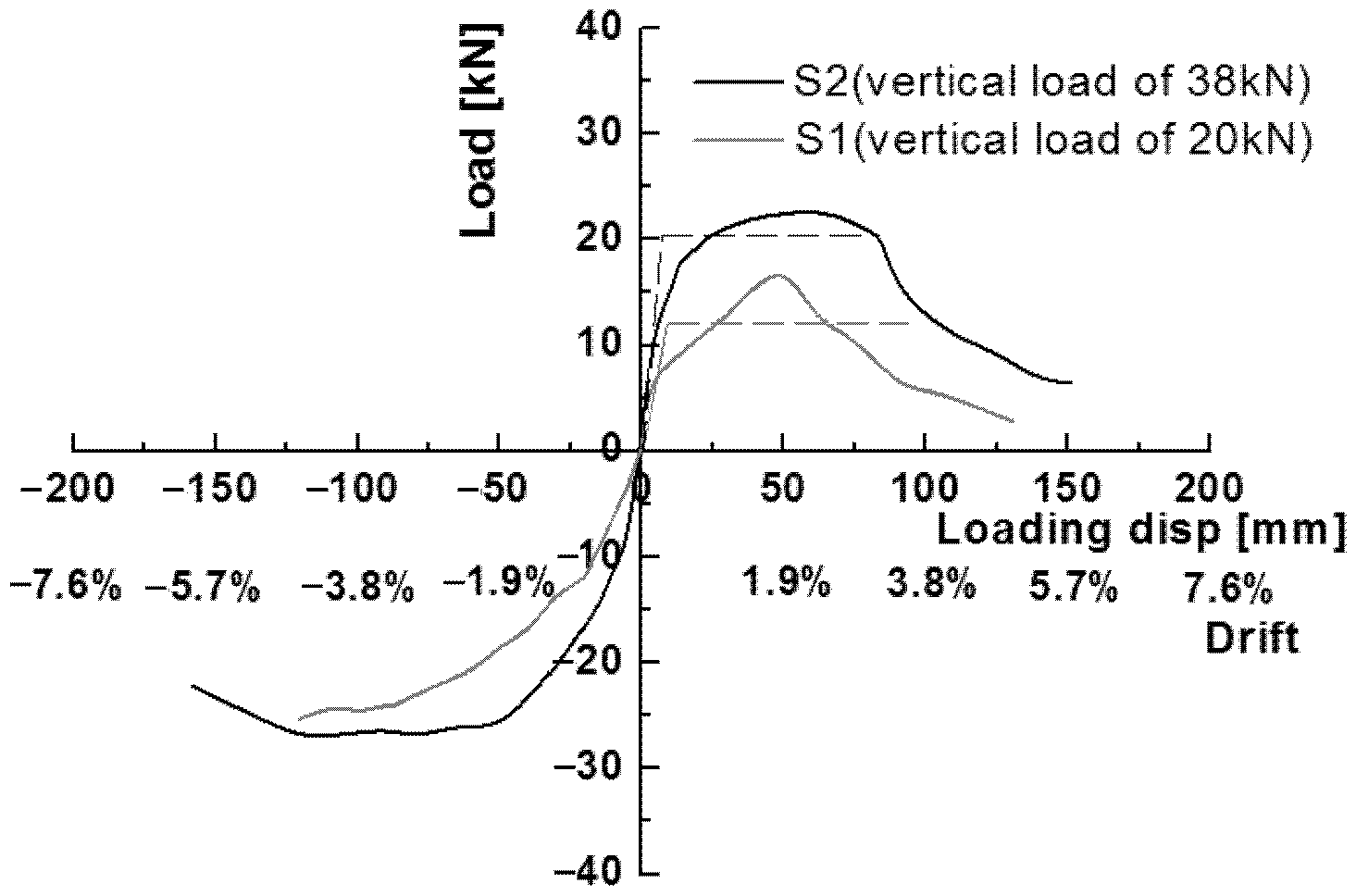
4.3.1. Idealized Bilinear Curves
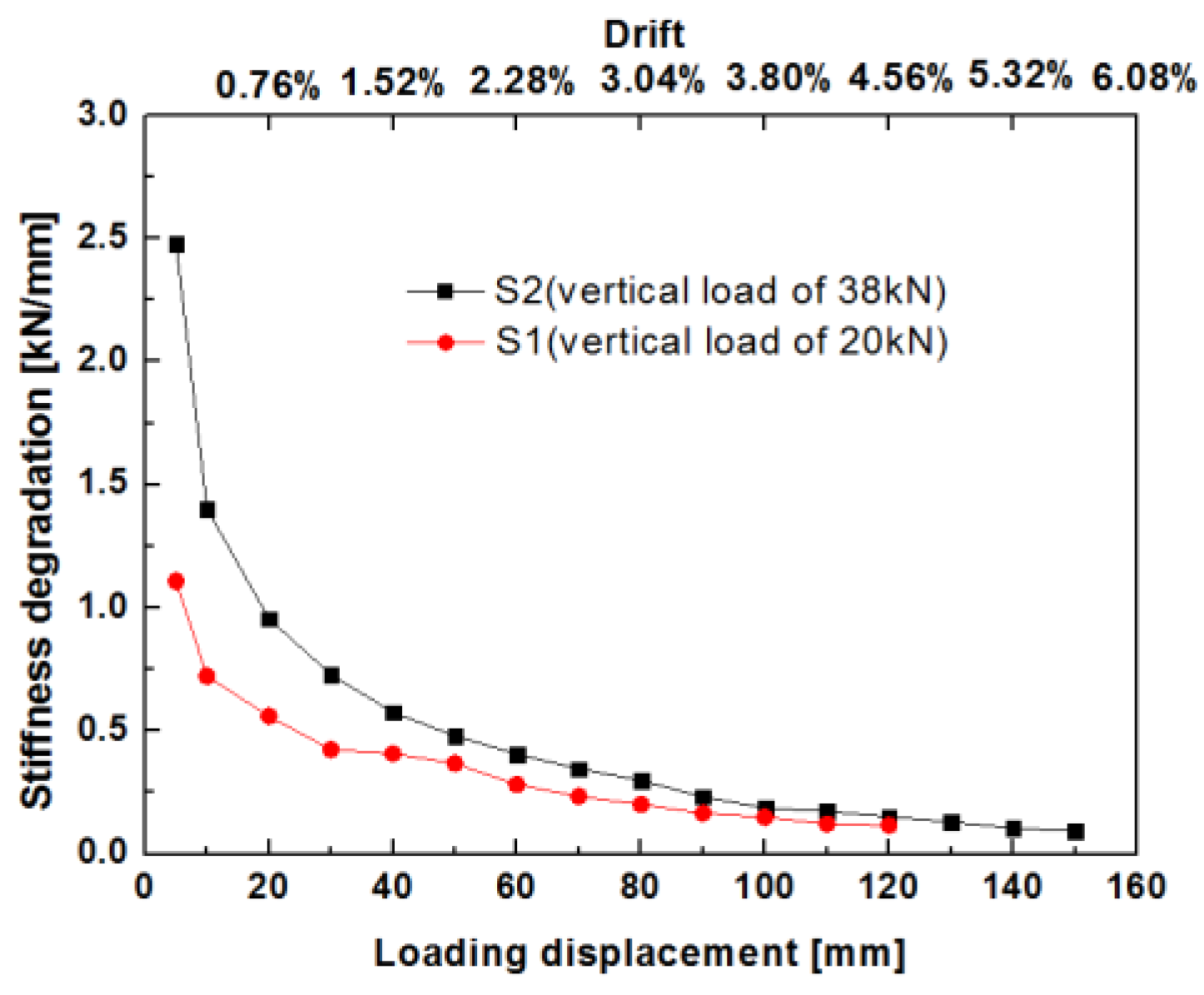
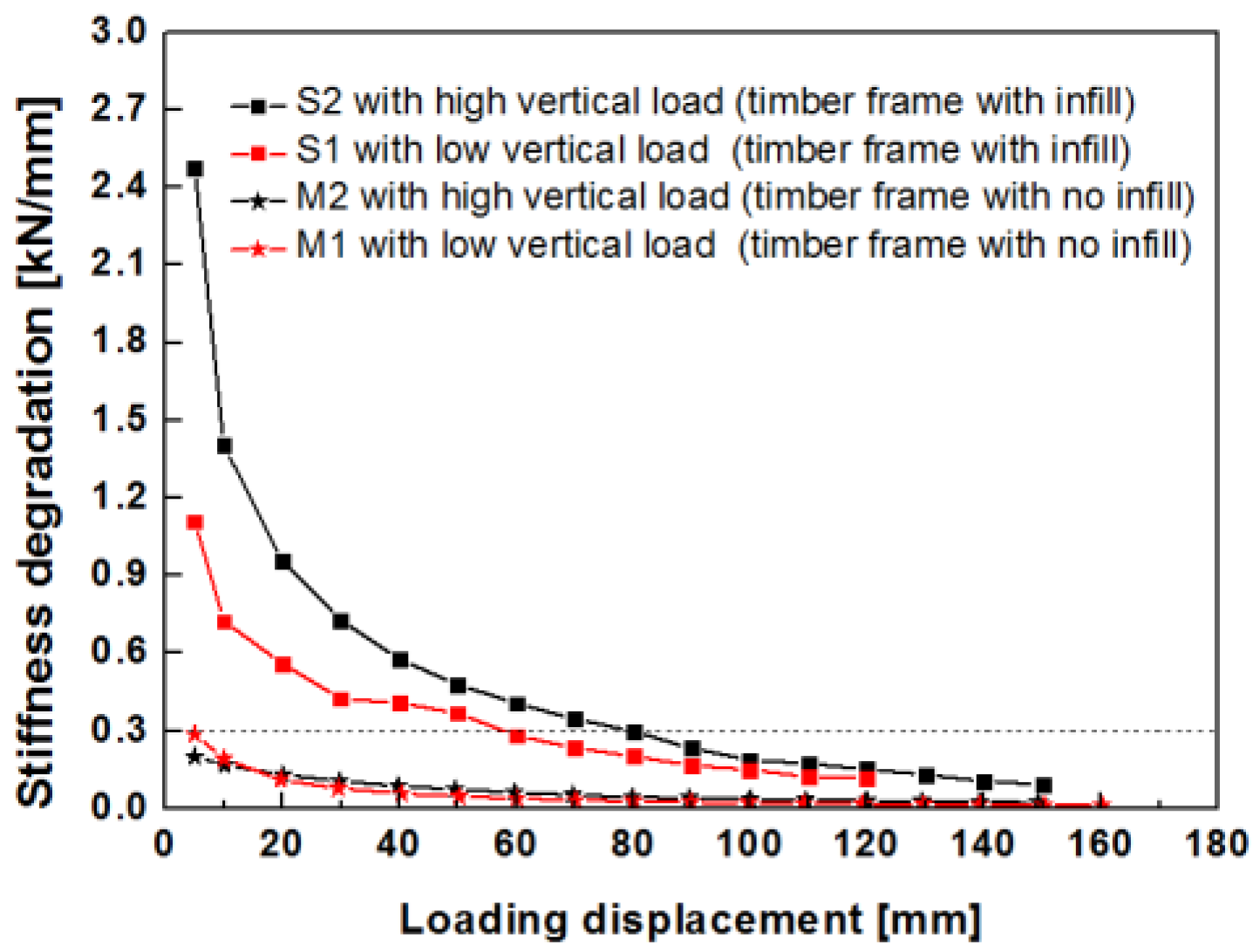
4.3.2. Stiffness Degradation Behavior
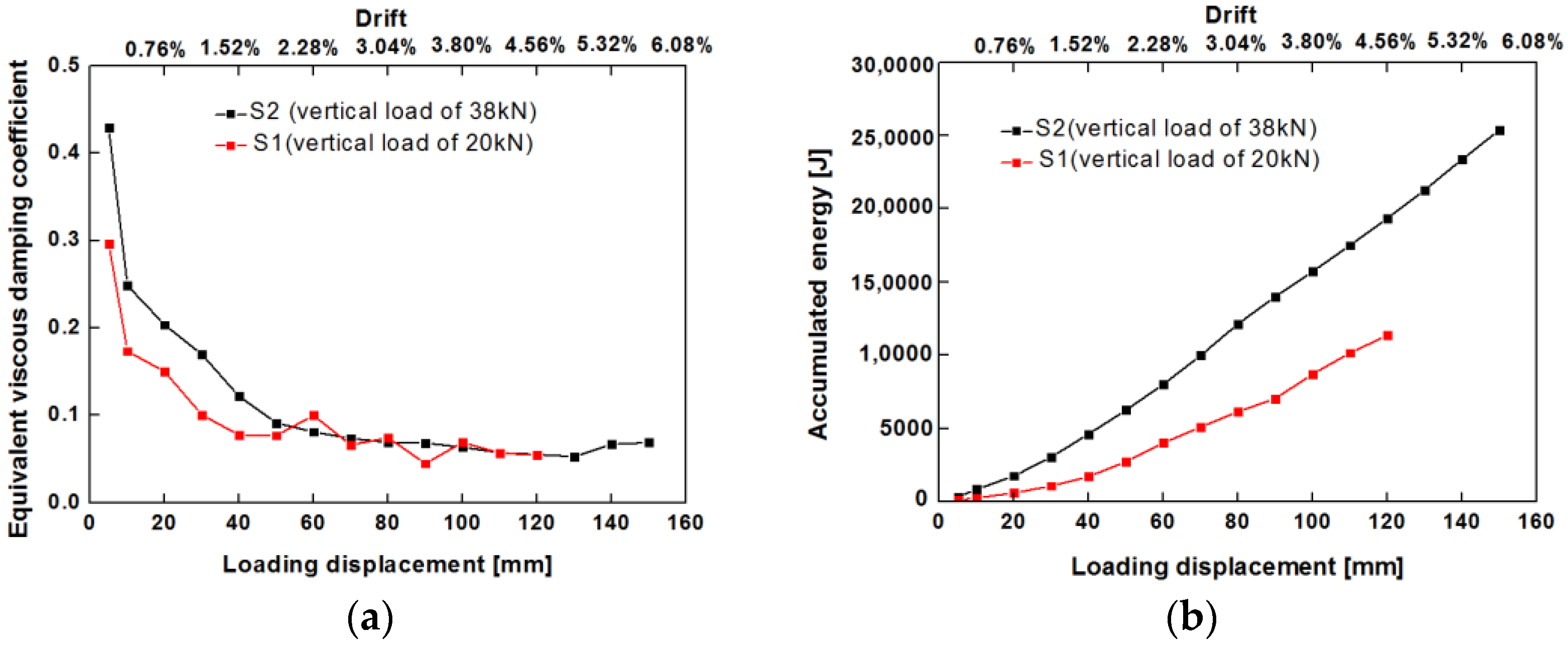
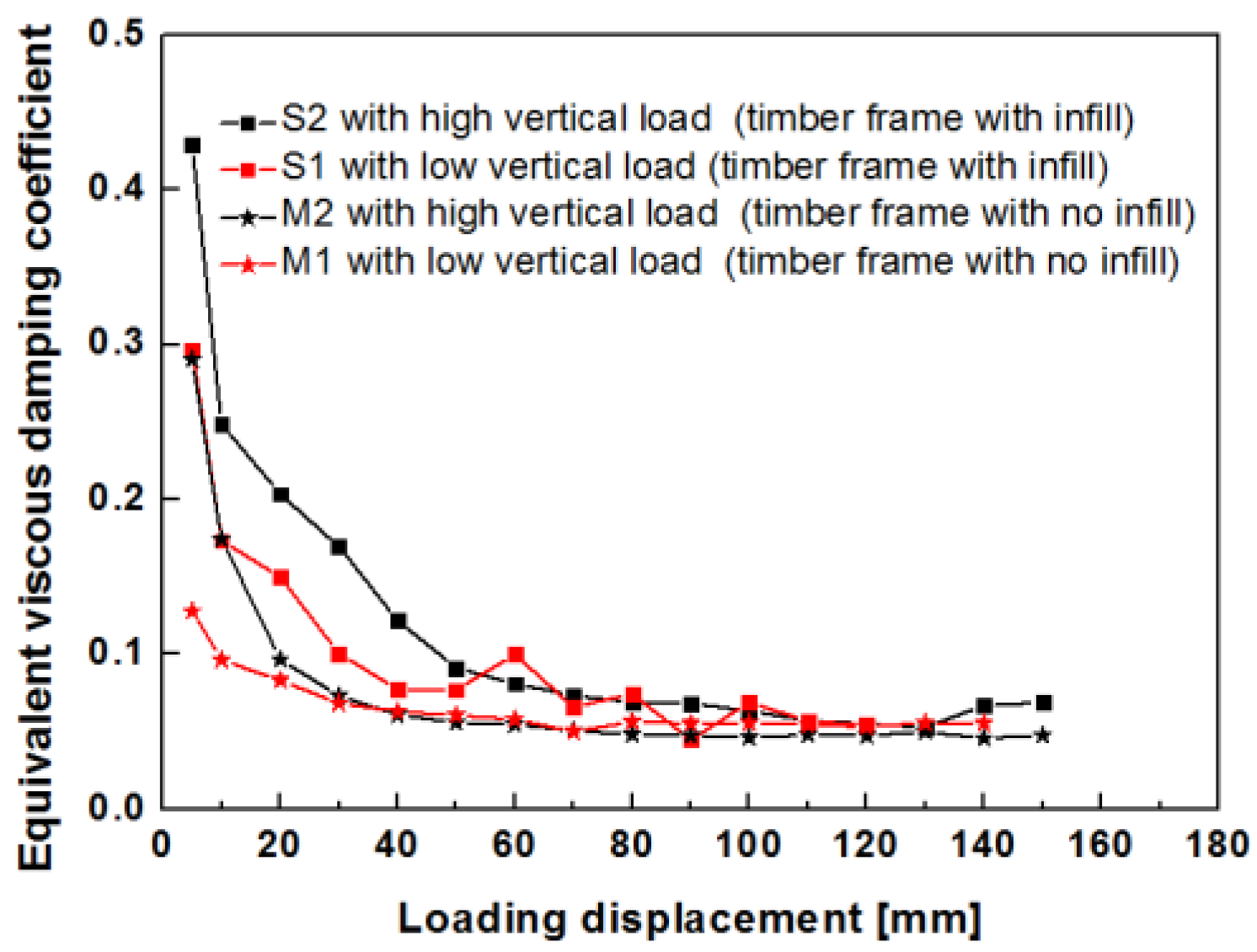
4.3.3. Energy Dissipation
4.4. Comparison with Experimental Results of Timber Frames with No Infill
5. Conclusions
- (1)
- The mud and stone infill considerably changed the lateral resistance responses of the walls. The timber frame with Mantou mortise and tenon joints acted as a rocking system, exhibiting weak lateral stiffness of less than 0.5 kN/mm and low strength of less than 5 kN with low energy dissipation. The cooperation between the timber frame and stone infill resulted in high lateral strength of over 20 kN, and the lateral stiffness was three times higher than that of the timber frame without infill. The timber frame with mud and stone infill also showed a high ductility factor (>10). The infill had a critical influence on the lateral performance of traditional village residence buildings, acting as the dominant resisting mechanism.
- (2)
- An increase in the vertical load resulted in an increase in the lateral resistance of the timber frame with infill walls. A larger applied vertical load resulted in higher lateral stiffness, higher lateral strength and greater energy dissipation capacity. Since different vertical loads were transferred at different positions, the lateral resistance at the internal transverse wall (24.87 kN) was larger than that at the external gable wall (21.46 kN), representing an increase of 16%. The lateral stiffness of the internal transverse wall (2.13 kN/mm) was greater than that of the external gable wall (0.96 kN/mm), representing a one-fold increase. The energy dissipation of the internal transverse wall was greater than that of the external gable wall.
- (3)
- The main in-plane failure mode of the timber frame with mud and stone infill included stones falling and infill collapse, but there was no damage to the timber frame. This response indicates that the wall might collapse during a seismic event, but the house would remain standing. The failure reason was that the wood column exerted pressure on the infill, resulting in shear damage of the infill wall in the thickness direction, due to the incompatibility of the deformation between the timber frame and stone infill.
- (4)
- These hybrid walls are different from Chuan-Dou timber frame with infilled timber panel with plentiful Fang similar to the tie beam. The infilled timber panel with plentiful Fang ensures the stability of Chuan-Dou timber structure, which is resilient enough in the earthquake. These hybrid walls are also different from timber frames consisting of diagonal bracing, tie beam and half-cross connections with mud and stone infill used in rural areas in Europe. The diagonal bracing, tie beam and half-cross connections provide better compatibility of the deformation between the wood frame and the infill.
- (5)
- More research is required to improve the deformation compatibility and strengthen the links between the timber frame and stone infill and prevent the out-of-plane collapse of the stone wall for traditional wood residences in northern China. We will focus on these topics in a future study.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Xie, Q.; Zhang, L.P.; Wang, L.; Zhou, W.; Zhou, T. Lateral performance of traditional Chinese timber frames: Experiments and analytical model. Eng. Struct. 2019, 186, 446–455. [Google Scholar] [CrossRef]
- Maeno, M.; Suzuki, Y.; Ohshita, T.; Kitahara, A. Seismic response characteristics of traditional wooden frame by full-scale dynamic and static tests. In Proceedings of the 13th World Conference on Timber Engineering (WCTE), Vancouver, BC, Canada, 1–6 August 2004; p. 1184. [Google Scholar]
- Chun, Q.; Yue, Z.; Pan, J.W. Experimental study on seismic characteristics of typical mortise-tenon joints of Chinese southern traditional timber frame buildings. Sci. China Technol. 2011, 54, 2404–2411. [Google Scholar] [CrossRef]
- Li, X.; Zhao, J.; Ma, G.; Chen, W. Experimental study on the seismic performance of a double-span traditional timber frame. Eng. Struct. 2015, 98, 141–150. [Google Scholar] [CrossRef]
- Li, X.; Zhao, J.; Ma, G.; Huang, S. Experimental study on the traditional timber mortise-tenon joints. Adv. Struct. Eng. 2015, 18, 2089–2102. [Google Scholar] [CrossRef]
- Li, S.; Zhou, Z.; Luo, H.; Milani, G.; Abruzzese, D. Behavior of traditional Chinese mortise-tenon joints: Experimental and numerical insight for coupled vertical and reversed cyclic horizontal loads. J. Build. Eng. 2020, 30, 101257. [Google Scholar] [CrossRef]
- Shen, Y.; Liu, H.; Zhou, J.; Chen, Z.; Wang, L.; Zhou, H. Experimental study on lateral performance of post-and-lintel timber frame in traditional residences. J.B. Univ. Technol. 2021, 47, 759–772. [Google Scholar] [CrossRef]
- Yao, K.; Zhao, H.T.; Ge, H.P. Experimental studies on the characteristic of mortise-tenon joint in historic timber buildings. Eng. Mech. 2006, 23, 168–173. (In Chinese) [Google Scholar] [CrossRef]
- Sui, Y.; Zhao, H.; Xue, J.; Zhang, H.; Xie, Q. Experimental study on characteristics of mortise-tenon joints in historic timber buildings. World Earthq. Eng. 2010, 26, 88–92. (In Chinese) [Google Scholar] [CrossRef]
- Gao, D.; Deng, H.; Liu, J.; Li, F.; Yang, Y. Pseudo-static experimental study on mortise and tenon joints of timber structures of Chinese Ming and Qing Dynasties. World Earthq. Eng. 2014, 30, 8–16. (In Chinese) [Google Scholar]
- Li, Y.Z.; Cao, S.Y.; Xue, J.Y. Analysis on mechanical behavior of dovetail mortise-tenon joints with looseness in traditional timber buildings. Struct. Eng. Mech. 2016, 60, 903–921. [Google Scholar] [CrossRef]
- Ma, L.; Xue, J.; Dai, W.; Zhang, X.; Zhao, X. Moment-rotation relationship of mortise-through-tenon connections in historic timber structures. Constr. Build. Mater. 2020, 232, 117285. [Google Scholar] [CrossRef]
- Chen, L.K.; Li, S.C.; Zhao, K.P.; Chen, Z.Y.; Song, T.; Zhang, L.; Jang, Z.J. Experimental and numerical investigation on seismic performance of one-way straight mortise-tenon joints based on a novel method to simulate damage of deteriorated ancient Chinese timber buildings. Perform. Constr. Facil. 2020, 34, 04019119. [Google Scholar] [CrossRef]
- Xie, Q.; Zheng, P.J.; Xiang, W.; Cui, Y.; Zhang, F. Experimental study on seismic behavior of damaged straight mortise-tenon joints of ancient timber buildings. J. Build. Struct. 2014, 35, 143–150. (In Chinese) [Google Scholar] [CrossRef]
- Xue, J.; Xia, H.; Li, Y.; Dai, W. Experiment study on seismic behavior of penetrated mortise-tenon joints under different degree of looseness in ancient buildings. J. Xi’an Univ. Arch. Technol. 2017, 49, 463–477. (In Chinese) [Google Scholar] [CrossRef]
- Xue, J.; Xu, D.; Ren, G.; Guo, R. Shake table test on seismic performance of column and tie wooden structure in traditional residence. China Civ. Eng. J. 2019, 52, 5–14. (In Chinese) [Google Scholar] [CrossRef]
- Wang, H.; Shang, S.; He, F.; Huang, S.; Deng, T.; Liu, D. Shaking table tests of Chinese traditional wood building and light wood framed building. J. Build. Struct. 2012, 33, 138–143. (In Chinese) [Google Scholar] [CrossRef]
- Xue, J.; Xu, D.; Guo, R. Shaking table tests and contrastive analysis for column-and-tie wooden buildings with and without infills. J. Vib. Shock. 2020, 39, 184–192. (In Chinese) [Google Scholar] [CrossRef]
- Xiong, H.; Wang, J.; Wu, L.; Chen, L. Experiment study on lateral resistance performance of Chuandou wooden frame structures. J. Build. Struct. 2018, 39, 122–129. (In Chinese) [Google Scholar] [CrossRef]
- Makarios, T.; Demosthenous, M. Seismic response of traditional buildings of Lefkas Island, Greece. Eng. Struct. 2006, 28, 264–278. [Google Scholar] [CrossRef]
- Ruggieri, N.; Zinno, R. Behavior of the Borbone constructive system under cyclic loading. In Proceedings of the 1st International Conference on Historic Earthquake-Resistant Timber Frames in the Mediterranean Area (Heart), Cosenza, Italy, 4–5 November 2013. [Google Scholar]
- Meireles, H.; Bento, R.; Cattari, S.; Lagomarsino, S. A hysteretic model for frontal walls in Pombalino buildings. Bull Earthq Eng. 2012, 10, 1481–1502. [Google Scholar] [CrossRef]
- Du, A.; Ferreira, J.G.; Guerreiro, L.; Branco, F.; Goncalves, A.M. Timbered masonry for earthquake resistance in Europe. Mater. Constr. 2012, 62, 615–628. [Google Scholar] [CrossRef]
- Langenbach, R. From “opus craticium” to the “Chicago frame”: Earthquake resistant traditional construction. Int. J. Archit. Herit. 2007, 1, 29–59. [Google Scholar] [CrossRef]
- Poletti, E.; Vasconcelos, G. Seismic behavior of traditional timber frame walls: Experimental results on unreinforced walls. B. Earthq. Eng. 2015, 13, 885–916. [Google Scholar] [CrossRef]
- Yasemin, D.A. Seismic resistance of traditional timber-frame hımış structures in Turkey: A brief overview. Int. Wood. Prod. J. 2017, 8, 21–28. [Google Scholar] [CrossRef] [Green Version]
- Gülkan, P.; Langenbach, R. The earthquake resistance of traditional timber and masonry dwellings in Turkey. In Proceedings of the 13th World Conference on Timber Engineering (WCTE), Vancouver, BC, Canada, 1–6 August 2004. [Google Scholar]
- Vintzileou, E.; Zagkotsis, A.; Repapis, C.; Zeris, C. Seismic behavior of the historical structural system of the island of Lefkada, Greece. Constr. Build. Mater. 2007, 21, 225–236. [Google Scholar] [CrossRef]
- Langenbach, R.; Kelley, S.; Sparks, P.; Rowell, K.; Hammer, M. Preserving Haiti’s Gingerbread Houses-2010 Earthquake Mission Report; World Monuments Fund: New York, NY, USA, 2011. [Google Scholar]
- Champagne, F.V.; Sieffert, Y.; Grange, S.; Polastri, A.; Daudeville, L. Experimental analysis of seismic resistance of timber-framed structures with stones and earth infill. Eng. Struct. 2014, 69, 102–115. [Google Scholar] [CrossRef]
- Dutu, A.; Niste, M.; Spatarelu, I.; Dima, D.I.; Kishiki, S. Seismic evaluation of Romanian traditional buildings with timber frame and mud masonry infills by in-plane static cyclic tests. Eng. Struct. 2018, 167, 655–670. [Google Scholar] [CrossRef]
- Cruz, H.; Pedro, J.; Stap, M.; Fronteira, A.M.D.; Machado, S. The Use of FRP in the Strengthening of Timber Reinforced Masonry Load-Bearing Walls. In Historical Constructions; Guimarães, Portugal, 2001; pp. 847–856. Available online: http://www.hms.civil.uminho.pt/sahc/2001/page%20847-856%20_128_.pdf (accessed on 21 October 2021).
- Vasconcelos, G.; Poletti, E.; Salavessa, E.; Jesus, A.M.; Loureno, P.B.; Pilaon, P. In-plane shear behavior of traditional timber walls. Eng. Struct. 2013, 56, 1028–1048. [Google Scholar] [CrossRef]
- Poletti, E.; Vasconcelo, G. Seismic behavior of traditional half-timbered walls: Cyclic tests and strengthening solutions. Struct. Anal. Hist. Constr. 2012, 32, 137–142. [Google Scholar]
- Ali, Q.; Schacher, T.; Ashraf, M.; Alam, B.; Naeem, A.; Ahmad, M.N.; Umar, M. In-plane behavior of full scale Dhajji Walls (Wooden Braced with Stone Infill) under quasi static loading. Earthq. Spectra 2012, 28, 835–858. [Google Scholar] [CrossRef]
- Dutu, A.; Sakata, H.; Yamazaki, Y.; Shindo, T. In-plane behavior of timber frames with masonry Infills under static cyclic loading. J. Struct. Eng. 2016, 142, 04015140. [Google Scholar] [CrossRef]
- Vasconcelos, G.; Lourengo, P.B. In-plane experimental behavior of stone masonry walls under cyclic loading. J. Struct. Eng. 2009, 135, 1269–1277. [Google Scholar] [CrossRef]
- Fang, D.P.; Iwasaki, S.; Yu, M.H.; Shen, Q.P.; Miyamoto, Y.; Hikosaka, H. Ancient Chinese timber architecture I: Experimental study. J. Struct. Eng. 2001, 127, 1348–1357. [Google Scholar] [CrossRef]
- JGJ/T 101-2015. Specification for Seismic Test of Buildings; China Architecture and Building Press: Beijing, China, 2015. [Google Scholar]
- Wang, F.; Zhao, K.; Zhang, J.; Yan, K. Influence of Different Types of Infill Walls on the Hysteretic Performance of reinforced concrete frames. Buildings 2021, 11, 310. [Google Scholar] [CrossRef]
- ASTM2126-11. Standard Test Methods for Cyclic (Reversed) Load Test for Shear Resistance of Walls for Buildings; ASTM International: West Conshohocken, PA, USA, 2011. [Google Scholar]
- Magenes, G.; Calvi, G.M. In-plane seismic response of brick masonry walls. Earthq. Eng. Struct. Dyn. 1997, 26, 1091–1112. [Google Scholar] [CrossRef]
- Gonalves, A.M.; Ferreira, J.G.; Guerreiro, L.; Branco, F. Experimental characterization of Pombalino “frontal” Wall cyclic behaviour. In Proceedings of the 15th World Conference on Earthquake Engineering, Lisbon, Portugal, 24–28 September 2012. [Google Scholar]























| Loading | Initial State | Yield Limit State | Strength Limit State | Failure Limit State | Ductility | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Direction | Ke [kN/mm] | Kemean [kN/mm] | Fy [kN] | Dy [mm] | Fp [kN] | Fpmean [kN] | Dp [mm] | Fu [kN] | Du [mm] | µ | |
| S1 | Positive | 1.33 | 0.96 | 12.02 | 9.04 | 17.58 | 21.46 | 50.66 | 14.06 | 94.49 | 10.45 |
| Negative | 0.59 | - | - | 25.34 | 86.81 | - | - | - | |||
| S2 | Positive | 2.98 | 2.13 | 20.47 | 6.86 | 22.74 | 24.87 | 60.05 | 18.19 | 84.26 | 12.28 |
| Negative | 1.19 | - | - | 26.99 | 79.62 | - | |||||
| Position | Vertical Load [kN] | Label | Ke [kN/mm] | Strength [kN] | |||||
|---|---|---|---|---|---|---|---|---|---|
| Positive | Negative | Mean | Positive | Negative | Mean | Increase | |||
| external transverse wall | 19–20 | M1 | 0.41 | 0.32 | 0.37 | 2.68 | 2.07 | 2.375 | 19.09 |
| S1 | 1.33 | 0.59 | 0.96 | 17.58 | 25.34 | 21.46 | |||
| internal transverse wall | 34–38 | M2 | 0.15 | 0.3 | 0.225 | 4. 47 | 3. 06 | 3.765 | 21.11 |
| S2 | 2.98 | 1.19 | 2.13 | 22.74 | 26.99 | 24.87 | |||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shen, Y.; Yan, X.; Yu, P.; Liu, H.; Wu, G.; He, W. Seismic Resistance of Timber Frames with Mud and Stone Infill Walls in a Chinese Traditional Village Dwelling. Buildings 2021, 11, 580. https://doi.org/10.3390/buildings11120580
Shen Y, Yan X, Yu P, Liu H, Wu G, He W. Seismic Resistance of Timber Frames with Mud and Stone Infill Walls in a Chinese Traditional Village Dwelling. Buildings. 2021; 11(12):580. https://doi.org/10.3390/buildings11120580
Chicago/Turabian StyleShen, Yinlan, Xingchen Yan, Piyong Yu, Hui Liu, Guofang Wu, and Wei He. 2021. "Seismic Resistance of Timber Frames with Mud and Stone Infill Walls in a Chinese Traditional Village Dwelling" Buildings 11, no. 12: 580. https://doi.org/10.3390/buildings11120580
APA StyleShen, Y., Yan, X., Yu, P., Liu, H., Wu, G., & He, W. (2021). Seismic Resistance of Timber Frames with Mud and Stone Infill Walls in a Chinese Traditional Village Dwelling. Buildings, 11(12), 580. https://doi.org/10.3390/buildings11120580







