Numerical Simulation and Parametric Analysis of Precast Concrete Beam-Slab Assembly Based on Layered Shell Elements
Abstract
1. Introduction
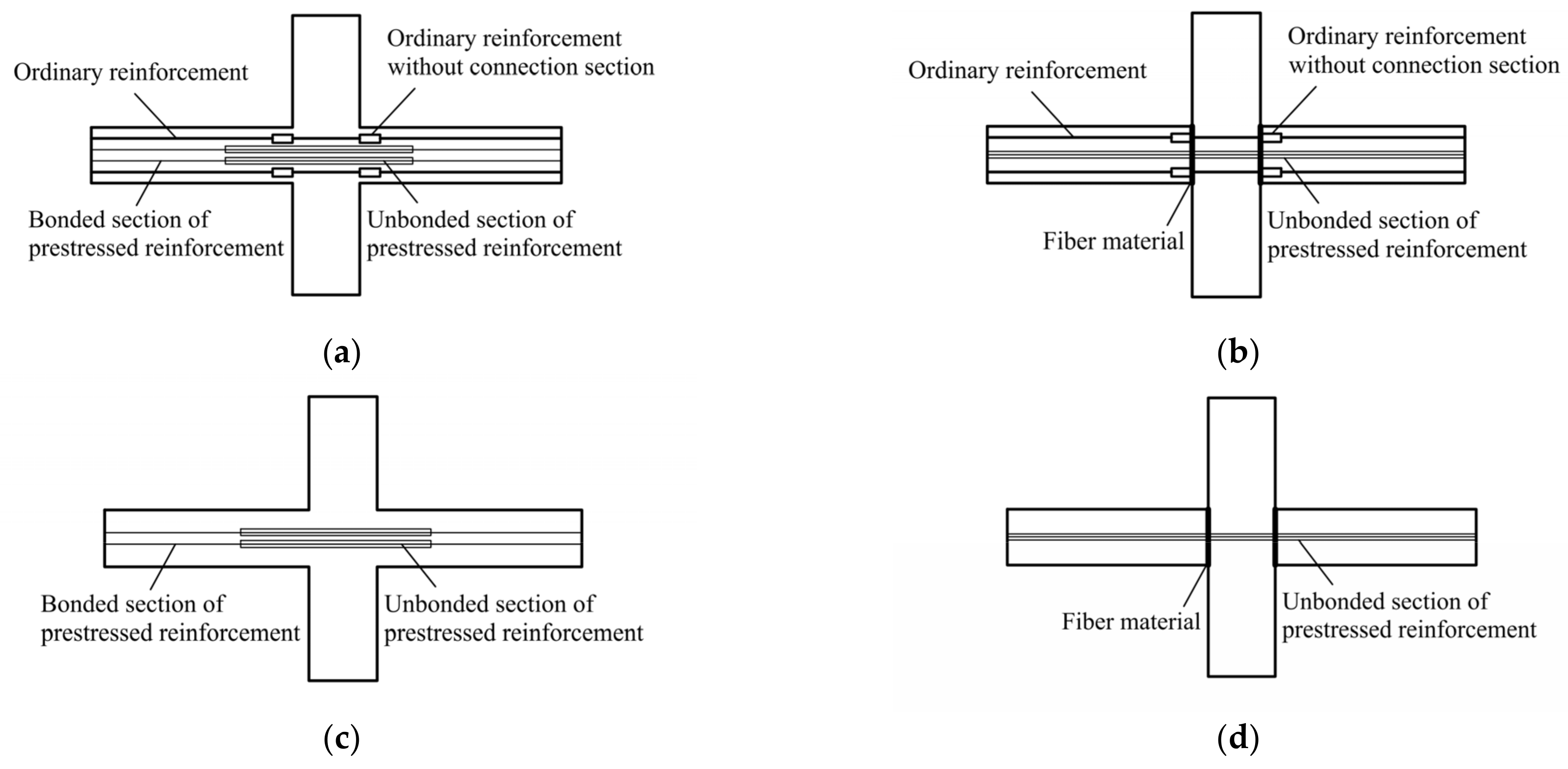
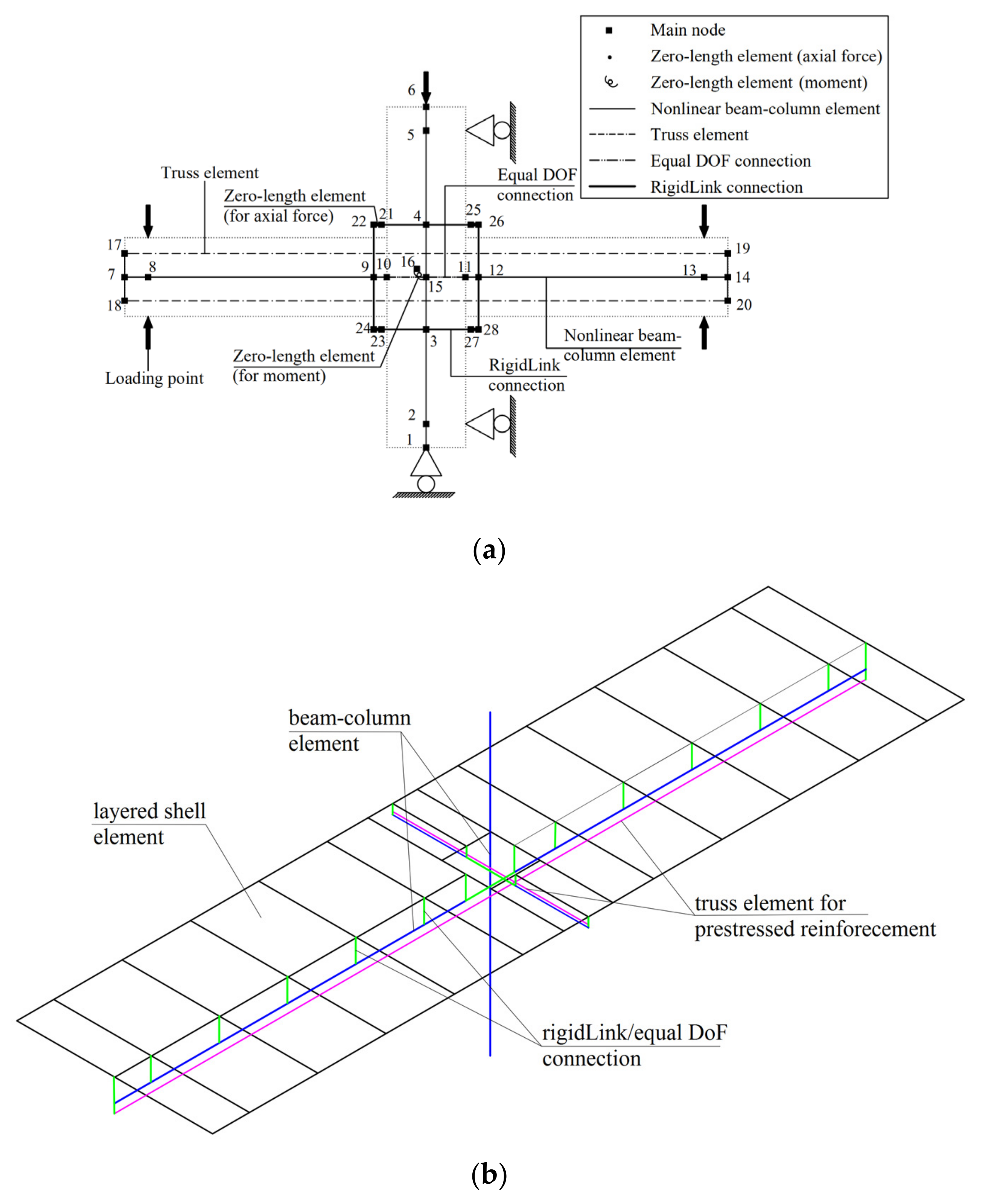
2. Modeling Strategy for Precast Beam–Slab Assembly Based on Layered Shell Element
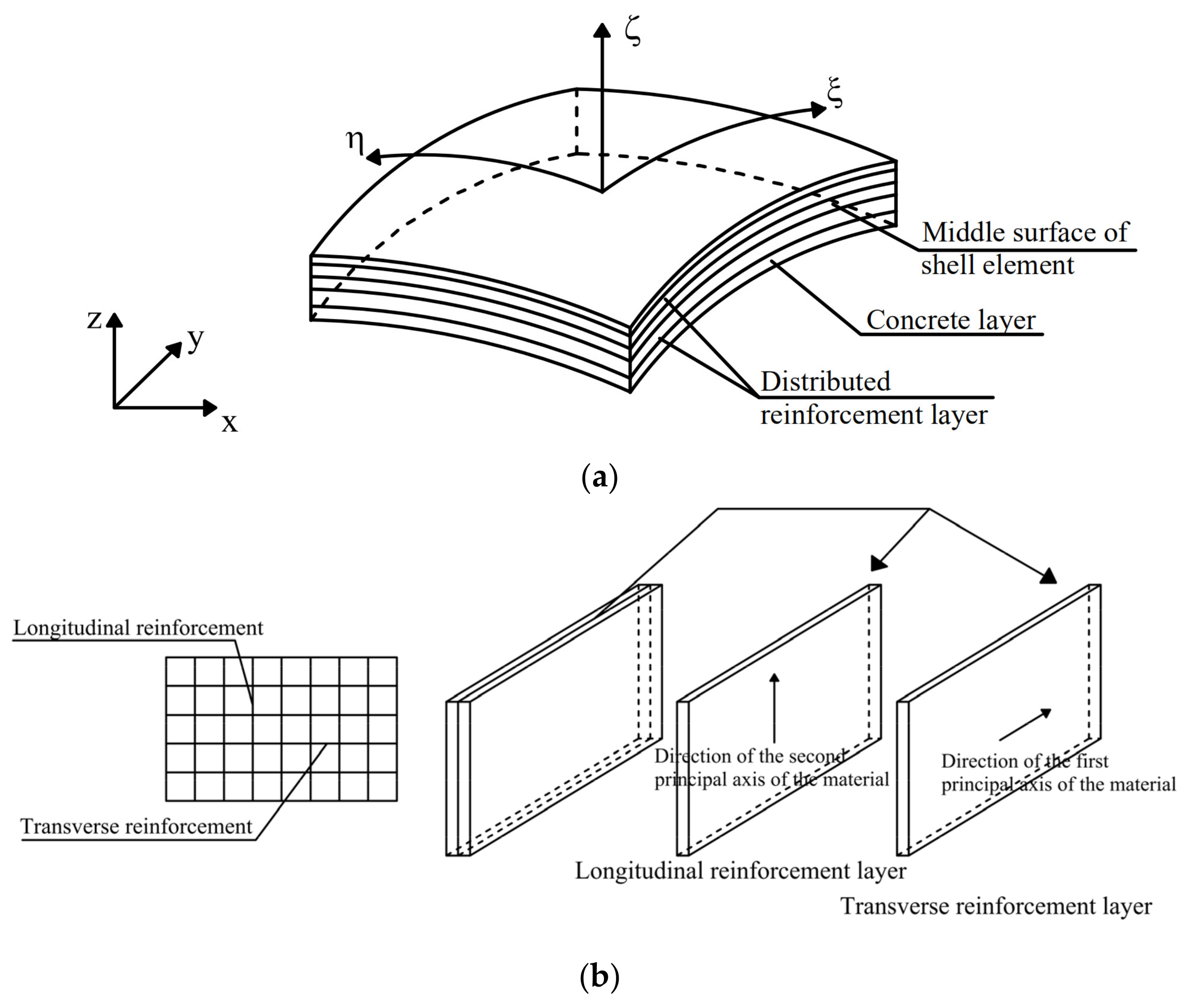
2.1. Layered Shell Element-Based Modeling Approach
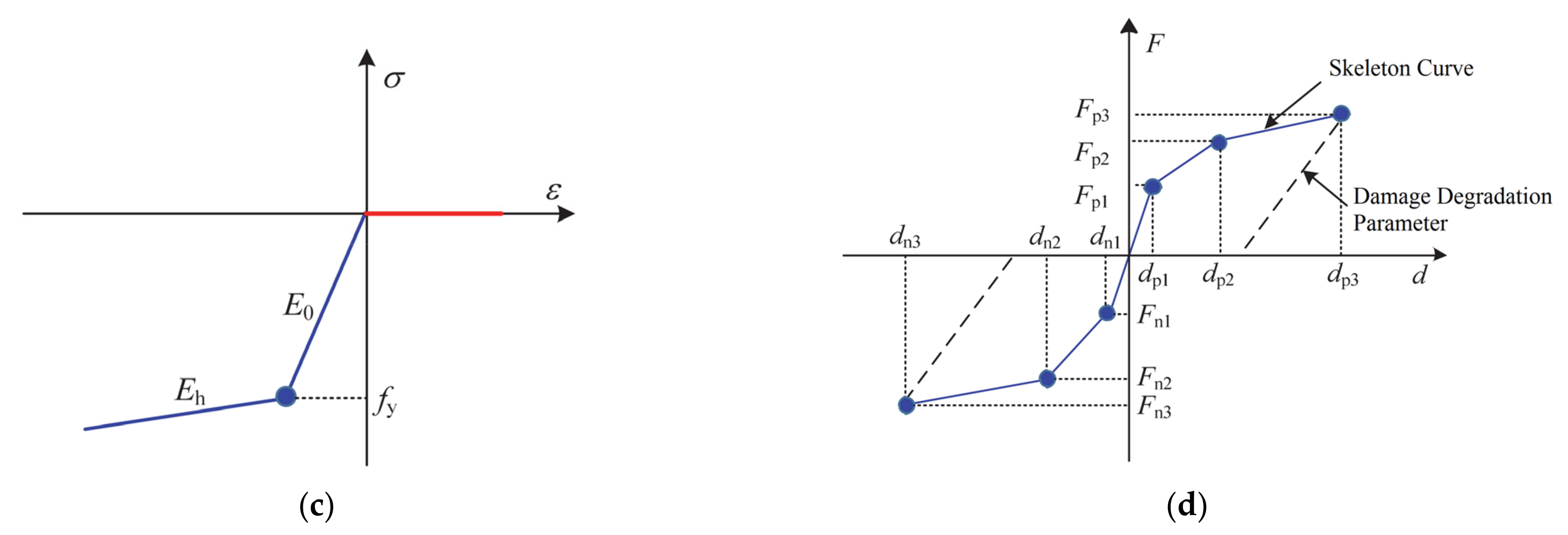
2.2. Material Models
3. Model Validation and Discussion
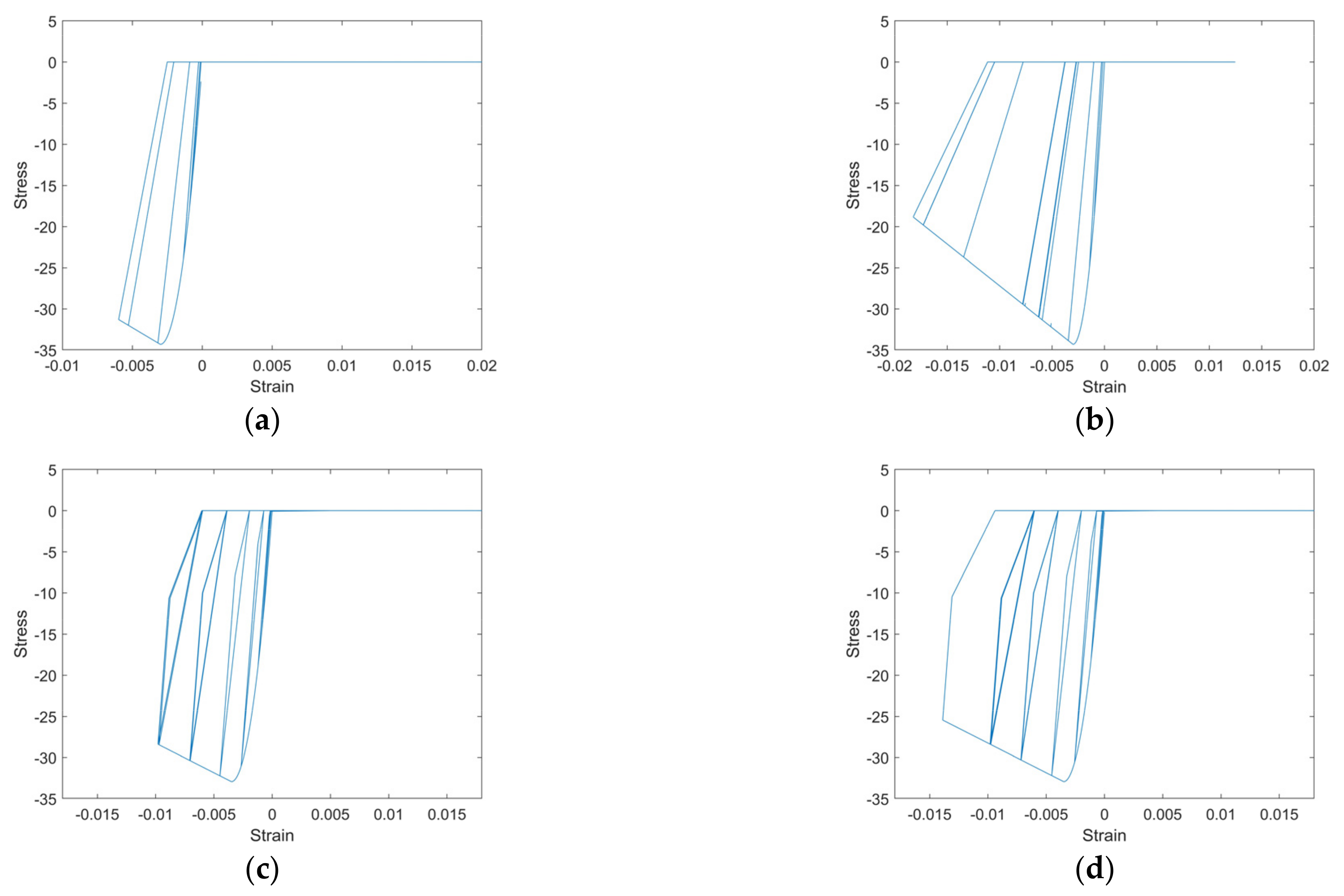
3.1. Cyclic Loading Test on Precast Beam–Slab Assembly
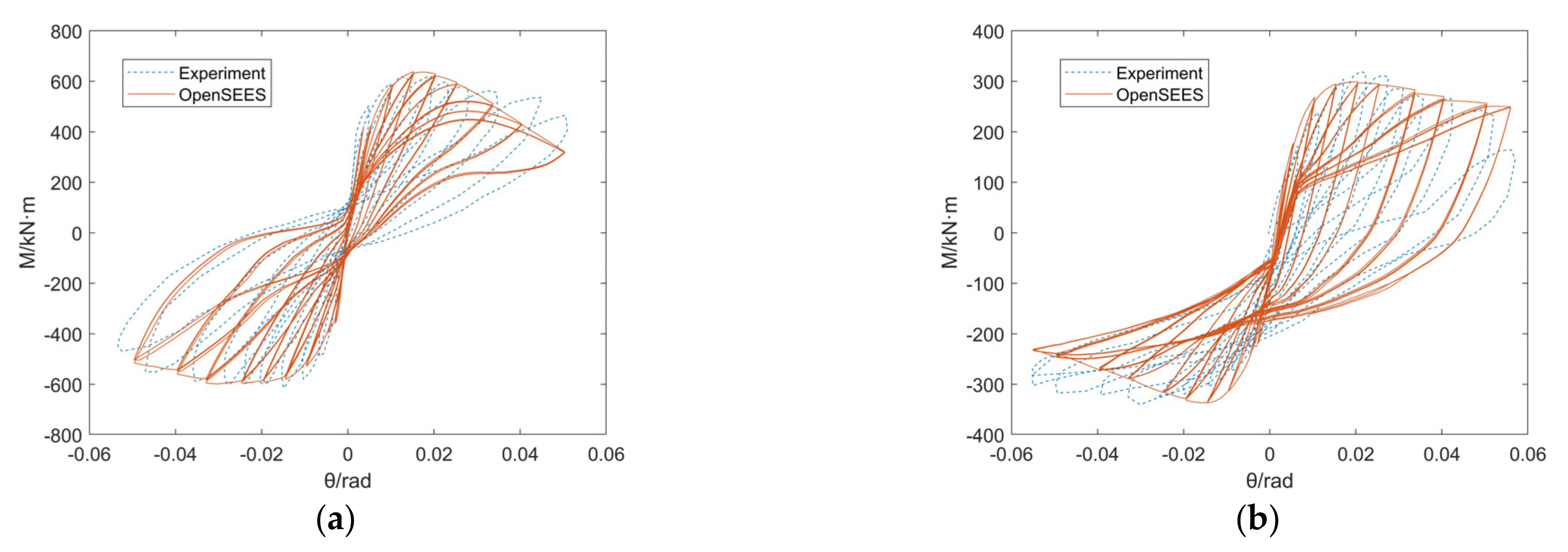
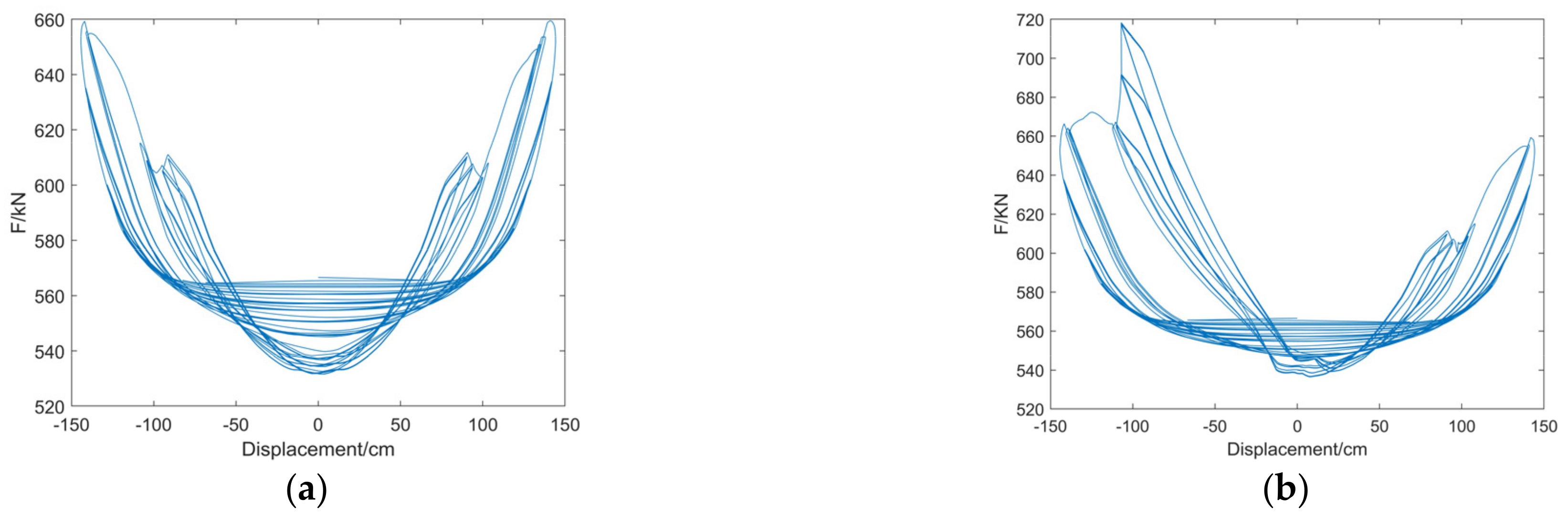
3.2. Numerical Results
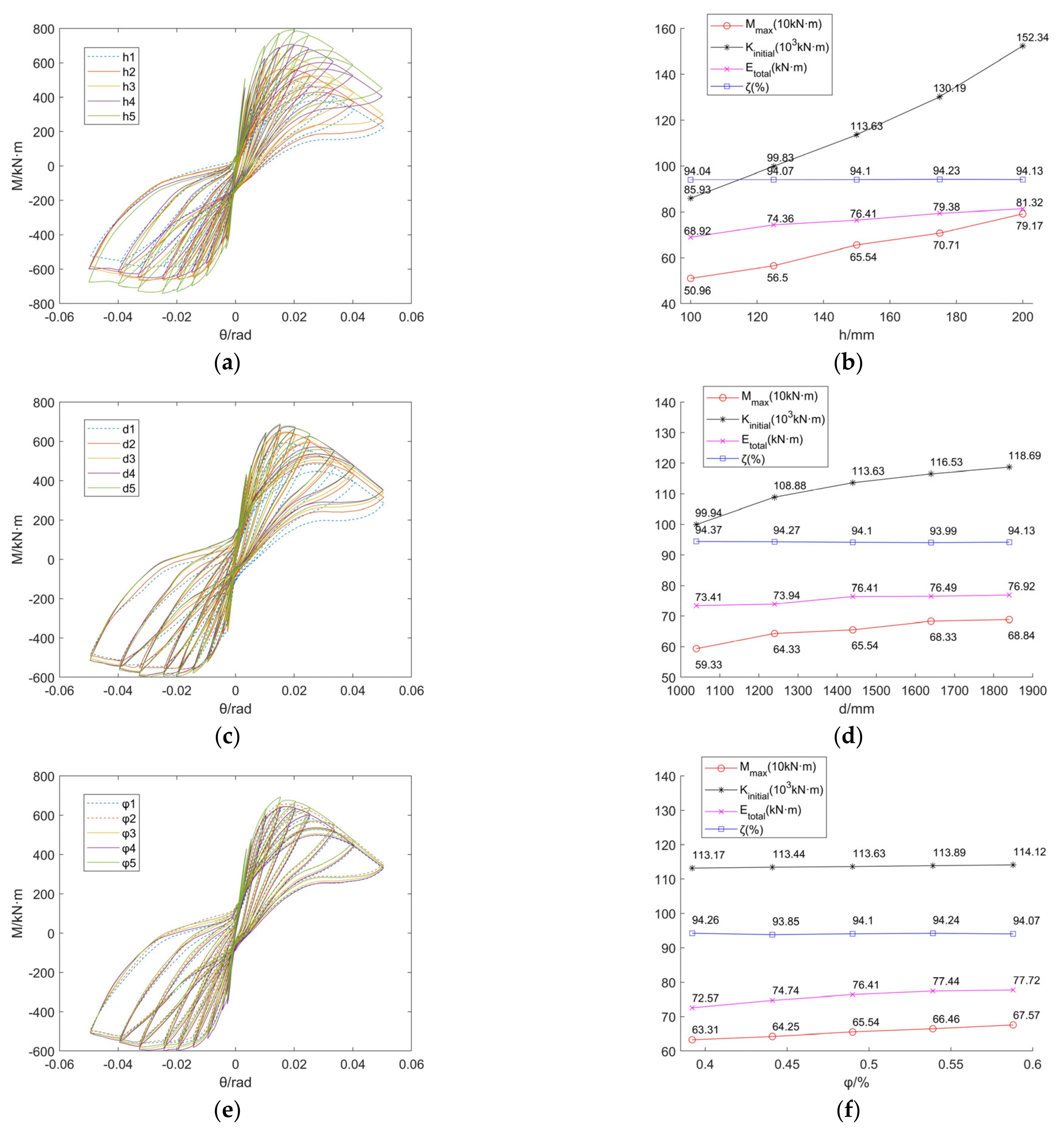
4. Parametric Analysis
4.1. Influence of Slab Thickness
4.2. Influence of Slab Width
4.3. Influence of Slab Reinforcement Ratio
5. Conclusions
- (1)
- This numerical simulation method can better predict the hysteretic performance of the prestressed assembled beam–slab joint. The simulation error of this method is less than 7.3% for the initial bearing capacity and 15.2% for the initial stiffness. Compared with the traditional solid model, the proposed model is computationally more efficient and better simulates the initial stiffness, loadbearing capacity, self-centering capability, energy dissipation capacity and stiffness degradation, as well as other mechanical performance indicators of the case study joints.
- (2)
- For the traditional two-dimensional modeling method, the influence of the floor is difficult to take into account. However, due to the consideration of the floor in this paper, the edge-joint specimen showed a very significant asymmetry, which affected the energy dissipation capacity, self-centering capability, initial stiffness, the mechanical behavior of the concrete at the beam end and the axial force of the prestressed steel bars. This certainly reflects the necessity of considering the influence of floor slabs in this type of nonlinear joint analysis.
- (3)
- With the increase of slab thickness from 100 mm to 200 mm, the initial stiffness, loadbearing capacity and energy dissipation capacity increased by 77.3%, 55.4% and 20.0%, respectively. In comparison, the trend was slower with the increase of slab width and when the width was close to the calculated value of the effective flange width; the influence on various indicators was less than 5.0%. However, the reinforcement ratio of the floor had little effect on the loadbearing capacity and stiffness of the joint, while it limitedly improved the energy dissipation capacity (with a maximum growth ratio of 7.1%). These three parameters had barely any effect on the stiffness degradation ratio of the joint.
- (4)
- Based on the research content and results of this paper, a simulation method that can be applied to “dry” connected structure was developed for reference in the future. In order to further increase the applicability of “dry” connected structures, special attention should be paid to the asymmetric effect of slabs on this kind of structure in future research.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| PC | Precast Concrete |
| PRESSS | Precast Seismic Structure Systems |
| UHPC | Ultra-High Performance Concrete |
| DOF | Degrees-Of-Freedom |
| OpenSees | Open System for Earthquake Engineering Simulation |
| fcʹ | peak compressive strength of concrete |
| ε0 | corresponding strain |
| ε3 | ultimate strain |
| fcu | the residual stress |
| Es | Young’s modulus |
| Eh | hardening modulus |
| θ | storey drift ratio |
| Etotal | total energy dissipation |
| ζ | the degradation ratio of secant stiffness |
| φ | reinforcement ratio of floor slab |
References
- Wu, G.; Feng, D. Research progress on the basic performance of fabricated concrete frame joints. J. Build. Struct. 2018, 39, 1–16. (In Chinese) [Google Scholar]
- Cheng, L.; Zhang, Y.; Li, W.; Zhang, P.; Li, H. Research on dry connection method of prefabricated concrete structure. North Archit 2019, 4, 13–16. (In Chinese) [Google Scholar]
- Priestley, M.J.N. The PRESSS program Current Status and Proposed Plans for PhaseIII. PCI J. 1996, 41, 22–40. [Google Scholar] [CrossRef]
- Geraldine, C.S.; LEW, H.S. Performance of precast concrete beam-to-column connections subject to cyclic loading. PCI J. 1991, 36, 56–67. [Google Scholar]
- Cai, J.; Feng, J.; Wang, Z.; Zhu, H. Research on seismic performance of prefabricated prestressed concrete assembled monolithic frame. J. Sun Yat Univ. (Nat. Sci. Ed.) 2009, 48, 136–140. (In Chinese) [Google Scholar]
- Guo, T.; Song, L.; Zhang, G.; Gu, Y. Experimental research on web-friction self-centering prestressed concrete frame beam-column joints. J. Civ. Eng. 2012, 45, 23–32. (In Chinese) [Google Scholar]
- Alver, N.; Selman, M.E.; Akgun, O.B. The effect of short cantilever beam formation on the structural behavior of precast posttensioned connections. Constr. Build. Mater. 2012, 35, 232–239. [Google Scholar] [CrossRef]
- Ercan Yuksel, H.; Faruk Karadogan, I.; Engin, B. Seismic behavior of two exterior beam- column connections made of normal-strength concrete developed for precast construction. Eng. Struct. 2015, 99, 157–172. [Google Scholar] [CrossRef]
- Zhang, C.; Zhou, Y.; Cai, X.; Meng, S. Experimental study on seismic performance of post- tensioned non-bonded hybrid assembled frame joints. J. Southeast Univ. 2016, 46, 1063–1069. (In Chinese) [Google Scholar]
- Han, C.; Li, Q.; Jiang, W. Experimental study on seismic performance of joints between prefabricated prestressed concrete beams and high-strength reinforced concrete columns. Vib. Shock 2017, 36, 248–253. (In Chinese) [Google Scholar]
- Liao, X.; Hu, X.; Ma, R.; Miao, D.; Xue, W. Experimental study on seismic performance of joints in assembled prestressed concrete frames with high axial compression ratio. J. Build. Struct. 2016, 37, 82–89. (In Chinese) [Google Scholar]
- Brunesi, E.; Peloso, S.; Pinho, R.; Nascimbene, R. Shake-Table Testing of a Full-Scale Two-Story Precast Wall-Slab-Wall Structure. Earthq. Spectra 2019, 35, 1583–1609. [Google Scholar] [CrossRef]
- Brunesi, E.; Peloso, S.; Pinho, R.; Nascimbene, R. Cyclic tensile testing of a three-way panel connection for precast wall-slab-wall structures. Struct. Concr. 2019, 20, 1307–1315. [Google Scholar] [CrossRef]
- Brunesi, E.; Peloso, S.; Pinho, R.; Nascimbene, R. Cyclic tensile testing of a full-scale two-storey reinforced precast concrete wall-slab-wall structure. Bull. Earthq. Eng. 2018, 16, 5309–5339. [Google Scholar] [CrossRef]
- Brunesi, E.; Nascimbene, R.; Peloso, S. Evaluation of the seismic Response of Precast Wall Connections: Experimental Observations and Numerical Modeling. J. Earthq. Eng. 2020, 24, 1057–1082. [Google Scholar] [CrossRef]
- Brunesi, E.; Nascimbene, R. Numerical web-shear strength assessment of precast prestressed hollow core slab units. Eng. Struct. 2015, 102, 13–30. [Google Scholar] [CrossRef]
- Valikhani, A.; Jahromi, A.J.; Mantawy, I.M.; Azizinamini, A. Numerical Modelling of concrete-to-UHPC Bond Strength. Materials 2020, 13, 1379. [Google Scholar] [CrossRef]
- Sucharda, O. Identification of Fracture Mechanic Properties of Concrete and Analysis of Shear Capacity of Reinforced Concrete Beams without Transverse Reinforcement. Materials 2020, 13, 2788. [Google Scholar] [CrossRef]
- Li, J.; Hao, H.; Wu, C. Numerical study of precast segmental column under blast loads. Eng. Struct. 2017, 134, 125–137. [Google Scholar] [CrossRef]
- Sousaa, R.; Batalhab, N.; Rodriguesc, H. Numerical simulation of beam-to-column connections in precast reinforced concrete buildings using fibre-based frame models. Eng. Struct. 2020, 203, 109845. [Google Scholar] [CrossRef]
- Cao, X.; Feng, D.; Wang, Z.; Wu, G. Research on numerical simulation method of assembled concrete frame joints based on OpenSEES. J. Civ. Eng. 2019, 52, 13–27. (In Chinese) [Google Scholar]
- Lu, X.; Xie, L.; Guan, H.; Huang, Y.; Lu, X. A shear wall element for nonlinear seismic analysis of super-tall buildings using OpenSees. Finite Elem. Anal. Des. 2015, 98, 14–25. [Google Scholar] [CrossRef]
- Lu, X.; Tian, Y.; Cen, S.; Guan, H.; Xie, L.; Wang, L. A high-performance quadrilateral flat shell element for seismic collapse simulation of tall buildings and its implementation in OpenSees. J. Earthq. Eng. 2018, 22, 1662–1682. [Google Scholar] [CrossRef]
- Hisham, M.; Yassin, M. Nonlinear Analysis of Prestressed Concrete Structures under Monotonic and Cycling Loads. Ph.D. Thesis, University of California, Berkeley, CA, USA, 1994. [Google Scholar]
- Scott, H.D.; Park, R.; Priestley, M.J.N. Stress-strain behavior of concrete confined by overlapping hoops at low and high strain rates. J. Am. Concr. Inst. 1982, 79, 13–27. [Google Scholar]
- Filippou, F.C.; Popov, E.P.; Bertero, V.V. Effects of Bond Deterioration on Hysteretic Behavior of Reinforced Concrete Joints; Report EERC 83-19; Earthquake Engineering Research. Available online: https://nehrpsearch.nist.gov/static/files/NSF/PB84192020.pdf (accessed on 1 December 2020).
- Kaya, M.; Arslan, A.S. Analytical modeling of post-tensioned precast beam-to-column connections. Mater. Des. 2009, 30, 3802–3811. [Google Scholar] [CrossRef]
- Pan, P.; Wang, H.; Guo, H.; Liu, K.; Wang, D.; Qi, H.; Geng, J. Research on seismic performance of post-tensioned non-bonded pre- stressed dry-connected beam-column joints. J. Build. Struct. 2018, 39, 47–55. (In Chinese) [Google Scholar]
- Ministry of Housing and Urban-Rural Development of the People’s Republic of China. Concrete Structure Design Code: GB50010-2010; China Building Industry Press: Beijing, China, 2015. (In Chinese) [Google Scholar]

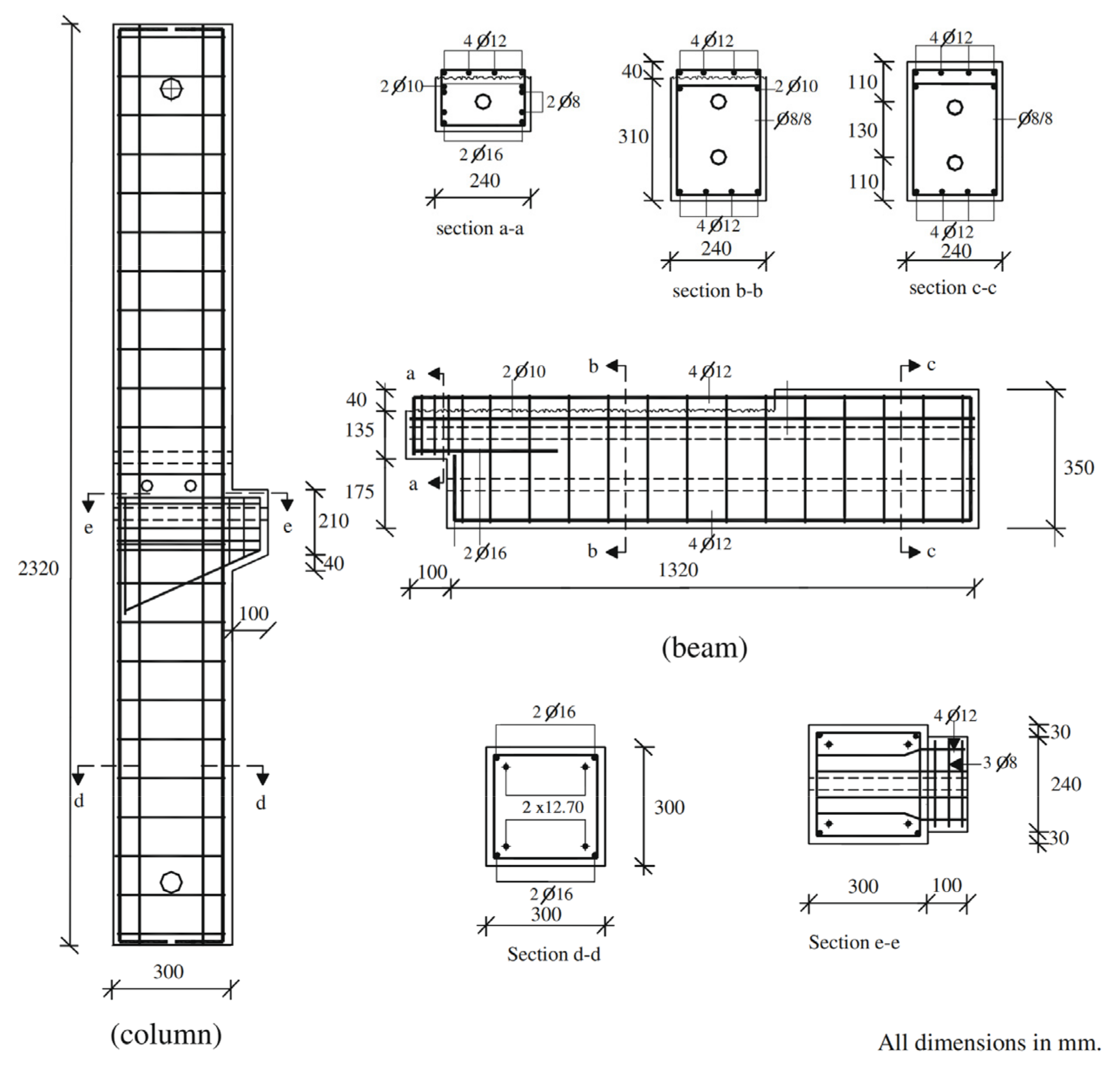
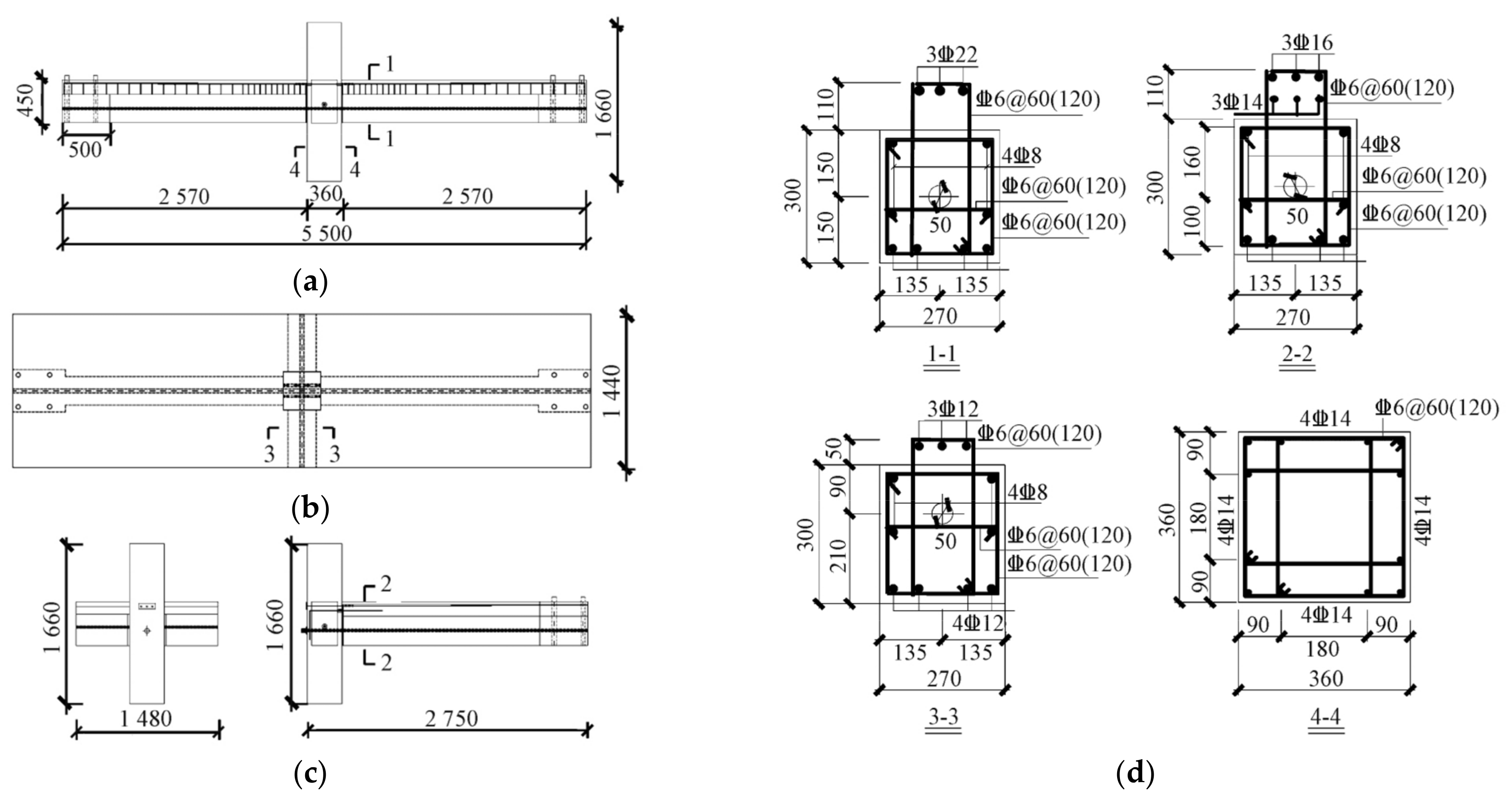

| Component | Specimen | Initial Prestress Strength (Mpa) | Ultimate Strength (Mpa) | ||
|---|---|---|---|---|---|
| Prestressed reinforcement(Steel02) | A2 | 730.6 | 1860.0 | ||
| B2 | 730.6 | 1860.0 | |||
| CP1 | 716.0 | 1790.0 | |||
| AP1 | 895.0 | 1790.0 | |||
| DP1 | 1074.0 | 1790.0 | |||
| Component | Specimen | fc’ | ε0 | fcu | ε3 |
| Concrete of beam and slab (Concrete02) | A2 | 26.8 | 0.025 | 5.4 | 0.0035 |
| B2 | 26.8 | 0.025 | 5.4 | 0.0035 | |
| CP1 | 42.5 | 0.04 | 8.5 | 0.004 | |
| AP1 | 42.6 | 0.04 | 8.52 | 0.004 | |
| DP1 | 41.0 | 0.04 | 8.2 | 0.004 | |
| Component | Specimen | Type of reinforcement | Diameter/mm | Yield strength | Hardening ratio |
| Reinforcement (Steel02/ElasticPPgap) | A2/B2 | HRB400 | 6/8/12/14/16/22 | 400.0 | 0.01 |
| CP1/AP1/DP1 | S500bs | 8 | 585.0 | 0.005 | |
| 10 | 505.0 | 0.005 | |||
| 12 | 522.0 | 0.005 | |||
| 14 | 540.0 | 0.005 | |||
| 16 | 485.0 | 0.005 | |||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Feng, D.-C.; Xiong, C.-Z.; Brunesi, E.; Parisi, F.; Wu, G. Numerical Simulation and Parametric Analysis of Precast Concrete Beam-Slab Assembly Based on Layered Shell Elements. Buildings 2021, 11, 7. https://doi.org/10.3390/buildings11010007
Feng D-C, Xiong C-Z, Brunesi E, Parisi F, Wu G. Numerical Simulation and Parametric Analysis of Precast Concrete Beam-Slab Assembly Based on Layered Shell Elements. Buildings. 2021; 11(1):7. https://doi.org/10.3390/buildings11010007
Chicago/Turabian StyleFeng, De-Cheng, Cheng-Zhuo Xiong, Emanuele Brunesi, Fulvio Parisi, and Gang Wu. 2021. "Numerical Simulation and Parametric Analysis of Precast Concrete Beam-Slab Assembly Based on Layered Shell Elements" Buildings 11, no. 1: 7. https://doi.org/10.3390/buildings11010007
APA StyleFeng, D.-C., Xiong, C.-Z., Brunesi, E., Parisi, F., & Wu, G. (2021). Numerical Simulation and Parametric Analysis of Precast Concrete Beam-Slab Assembly Based on Layered Shell Elements. Buildings, 11(1), 7. https://doi.org/10.3390/buildings11010007








