Impact of the Reinforcement Detailing on Seismic Performance of Isolated Non-structural Walls
Abstract
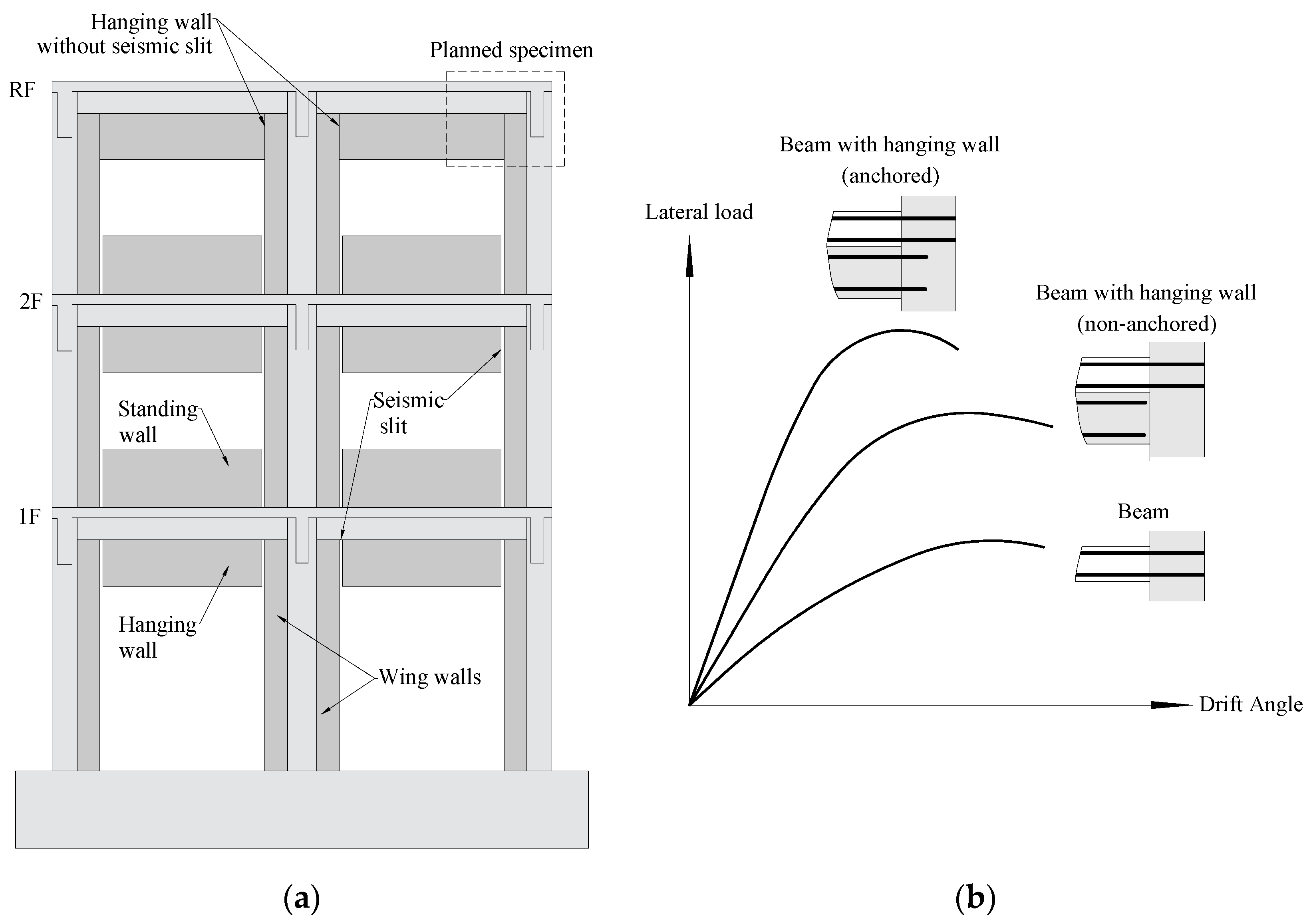
1. Introduction
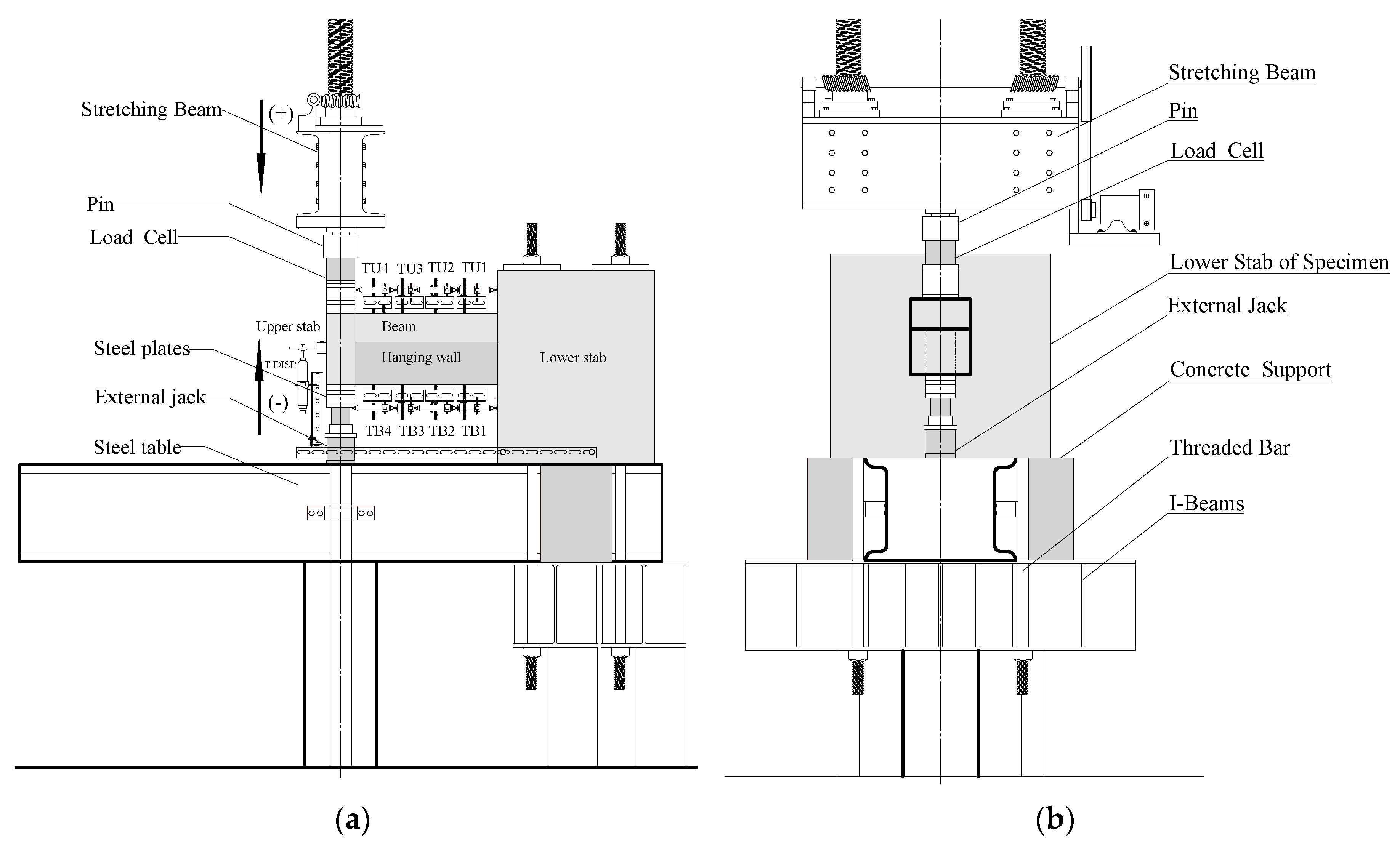
2. Experimental Study
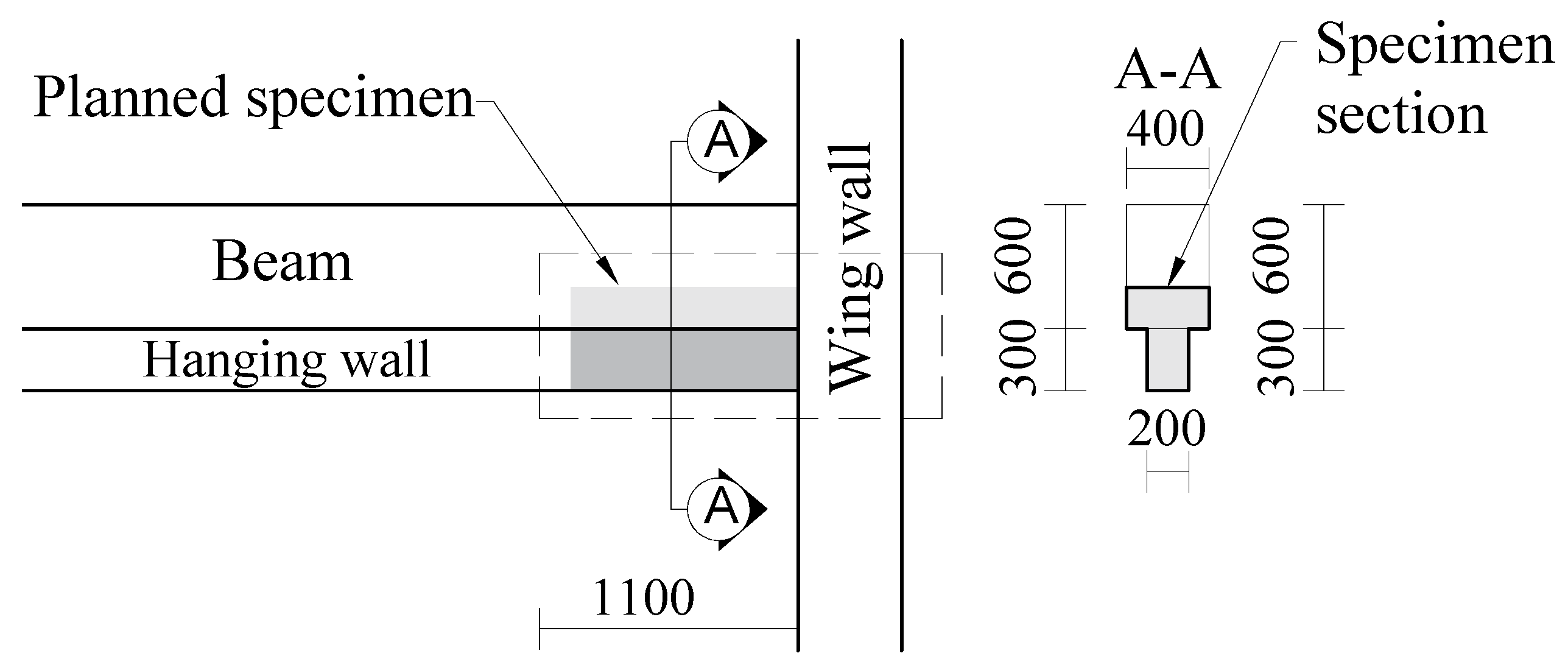
2.1. Test Specimen
2.2. Testing Program of the Specimen
3. Experimental Results
3.1. Damage Outline
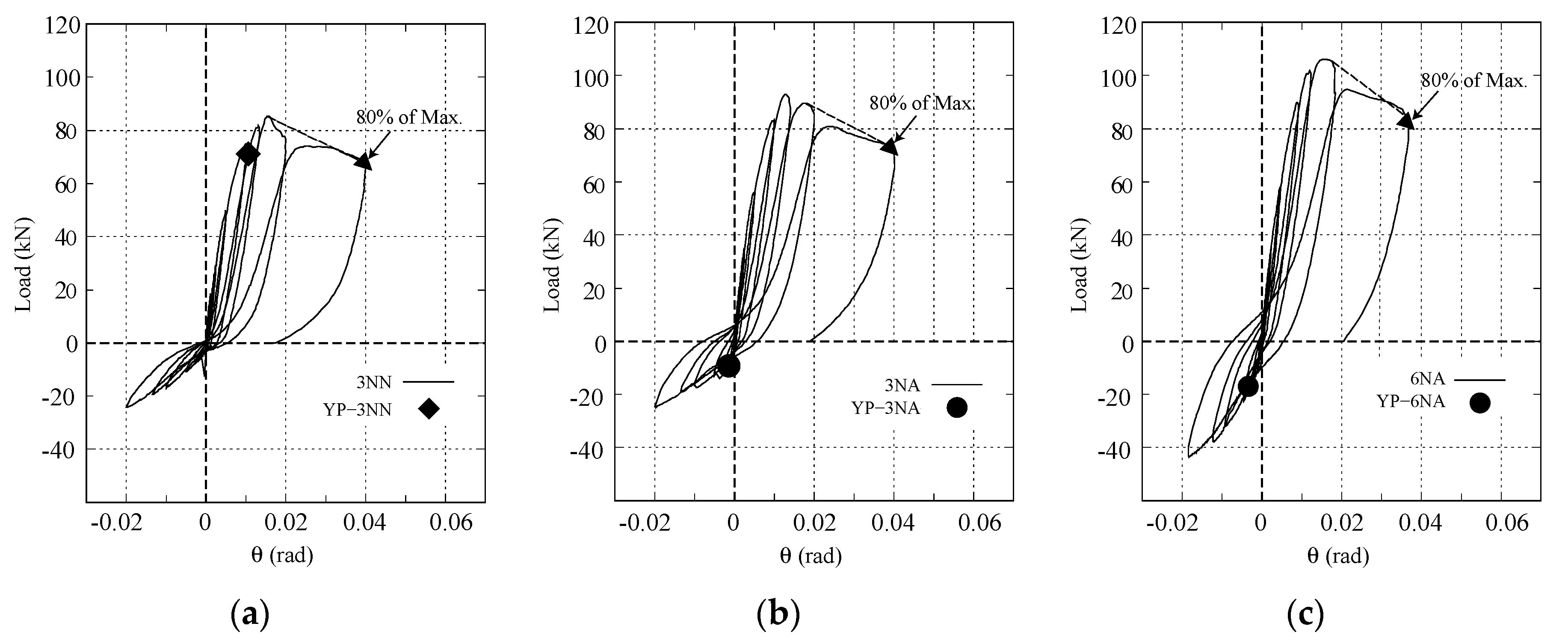
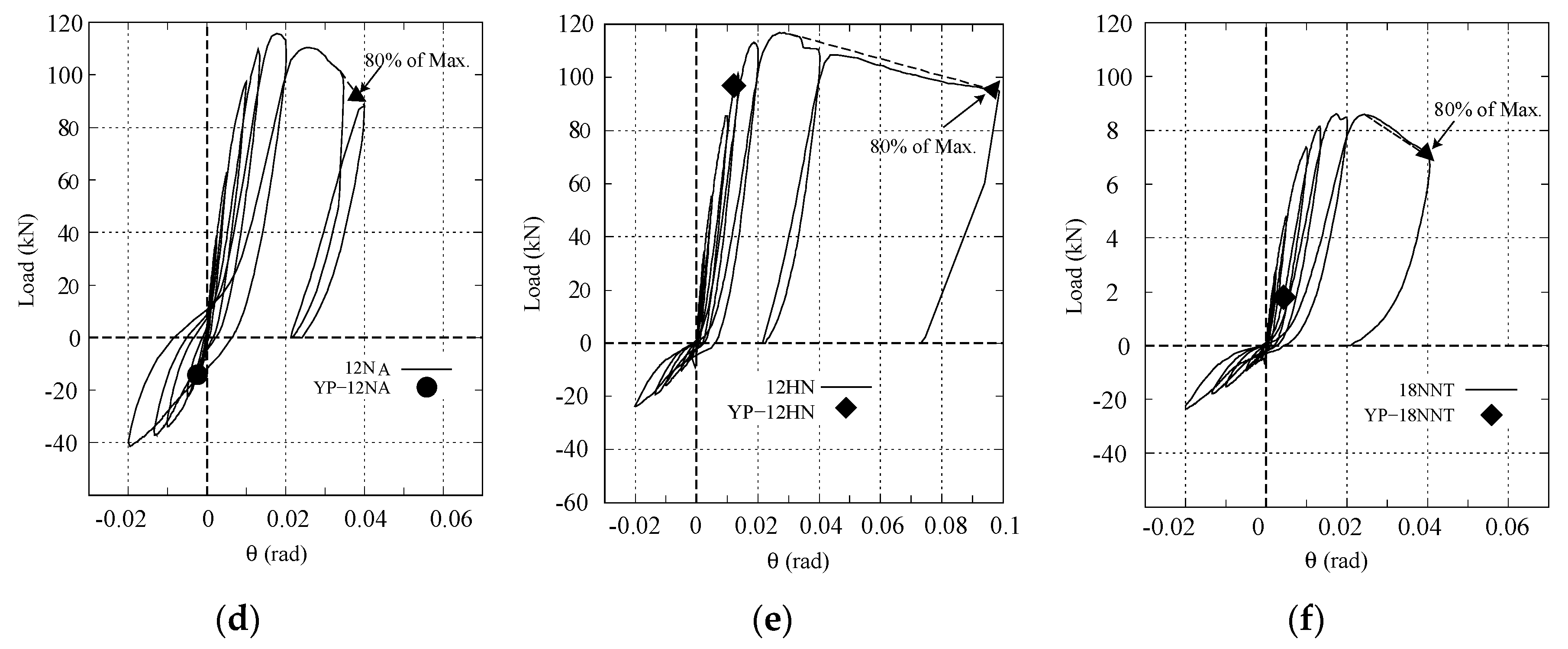
3.2. Load–Deflection Relation
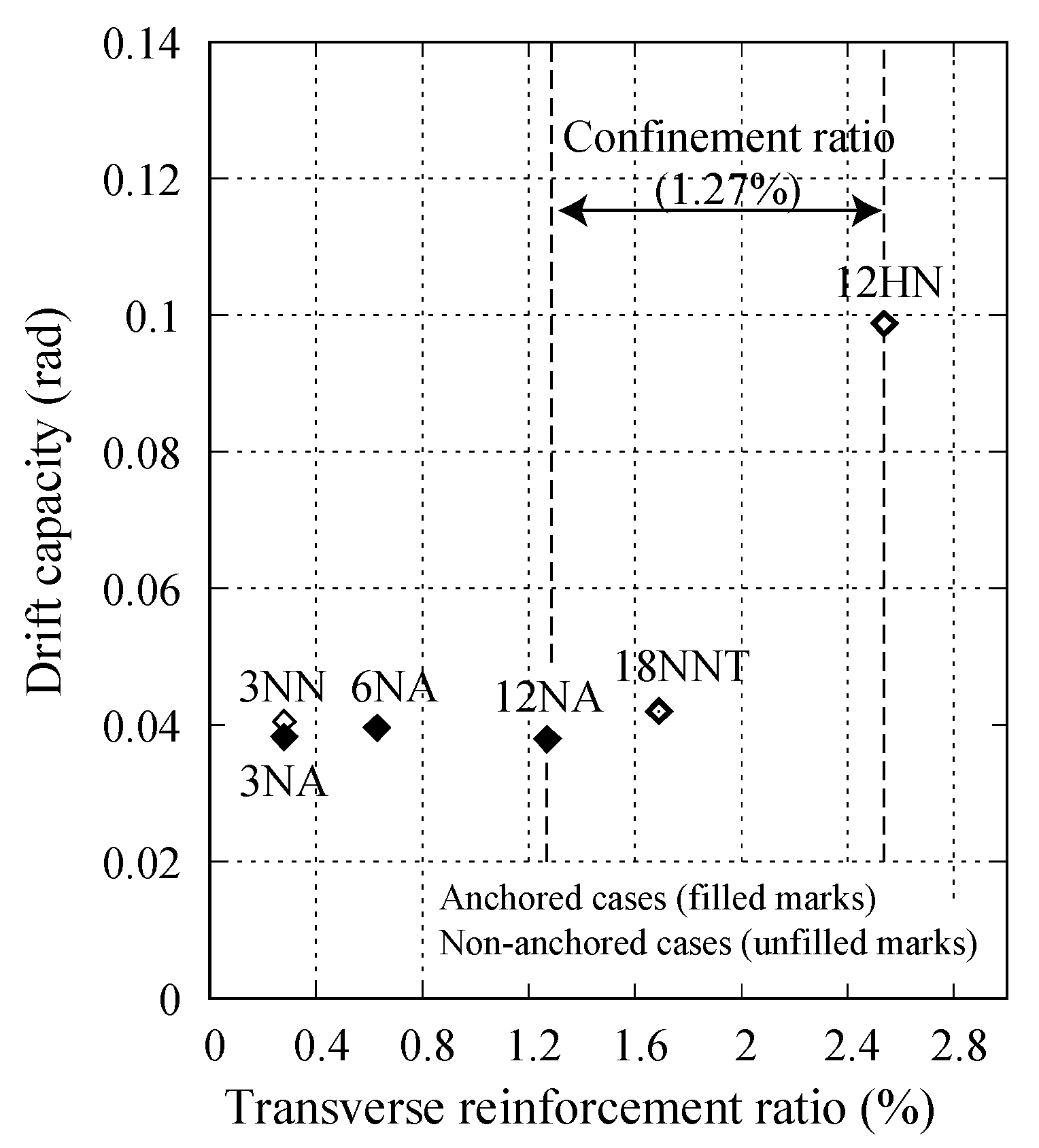
3.3. Drift Capacity
- There is a non-anchored detailing of longitudinal reinforcement;
- The amount of longitudinal reinforcement is equal or greater than transverse reinforcement;
- The confinements are placed at the critical zone of the wall.
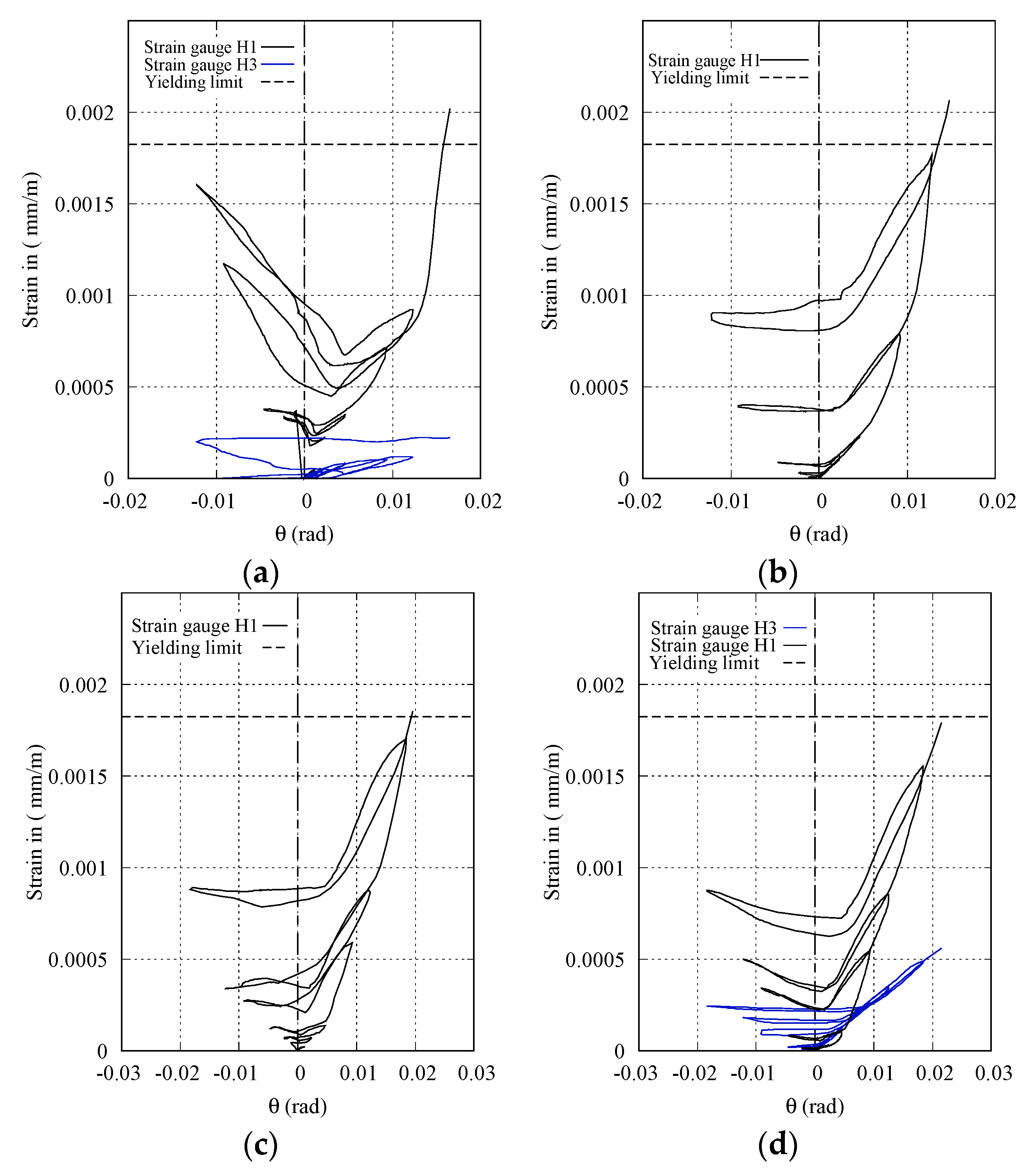
3.4. Strain–Drift Relationship of Trasnverse Reinforcements
4. Evaluation of the Experimental Results
4.1. Evaluation of the Strength
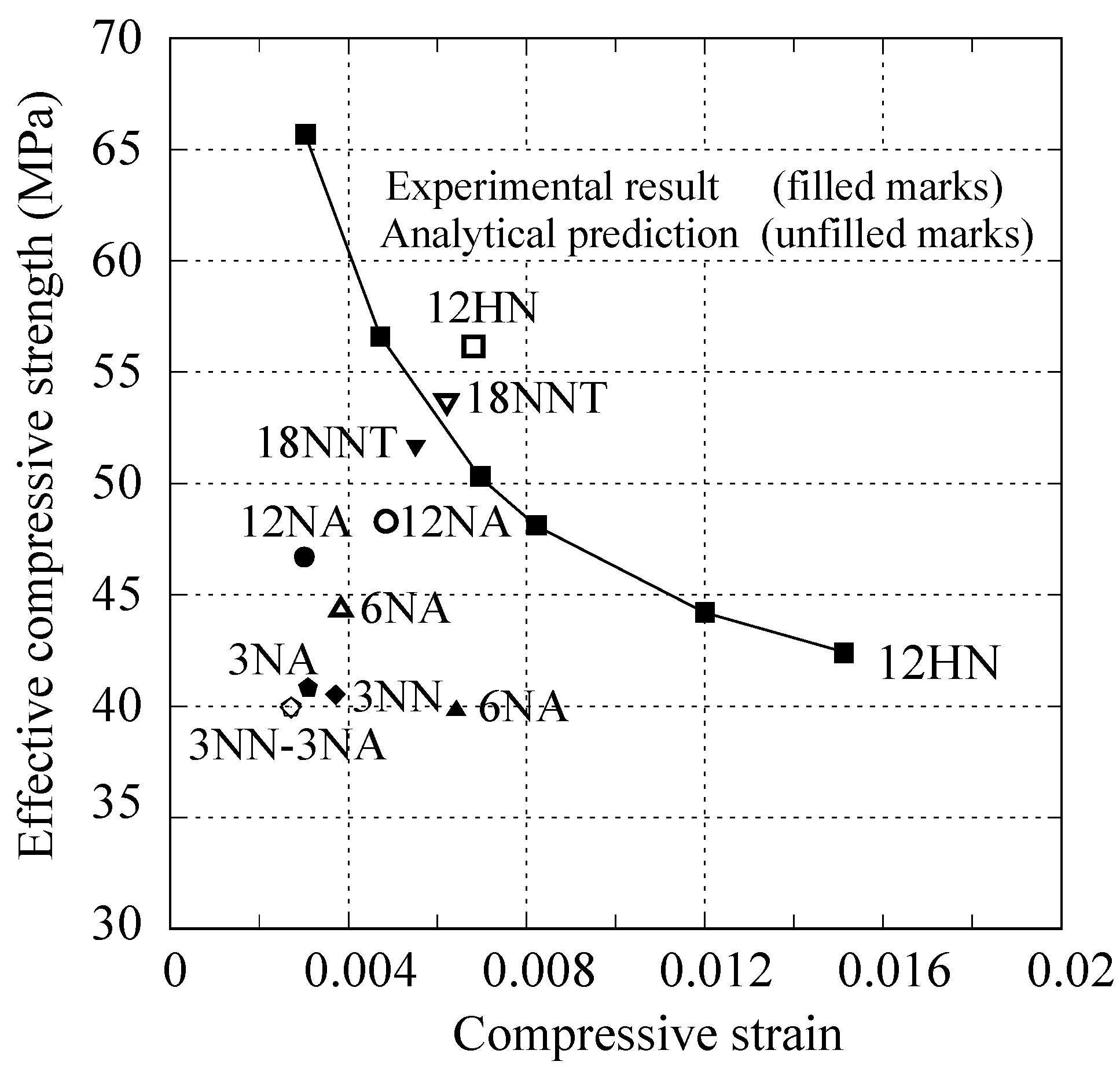
4.2. Evaluation of the Confinement and Reinforcement Detailing Impact
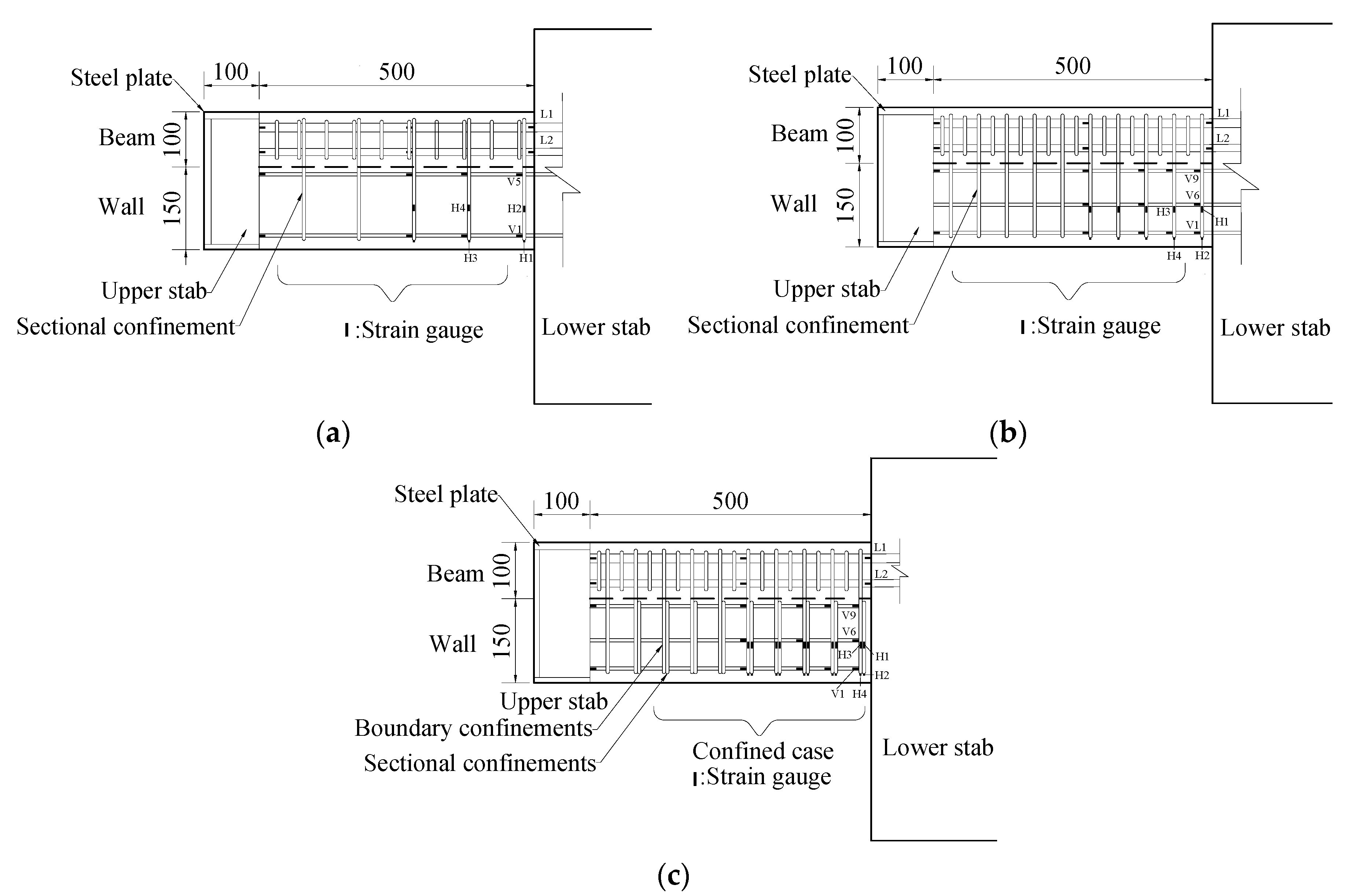
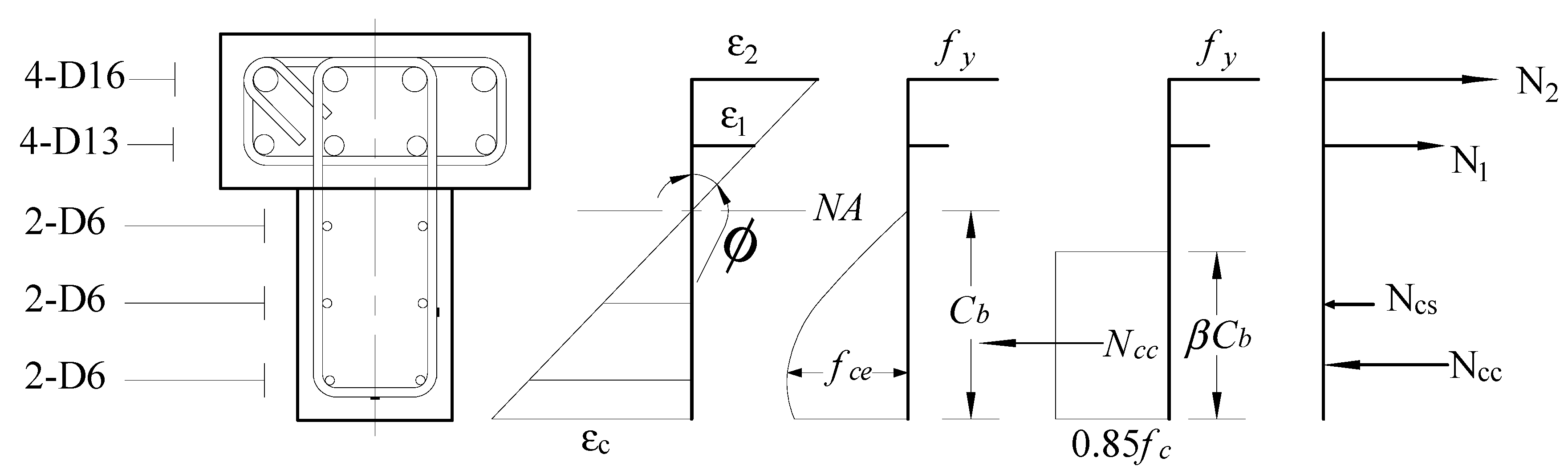
- To calculate internal forces, the stress incurred in every longitudinal reinforcement was calculated based on the strain gauge record pasted on the longitudinal reinforcement, as shown in Figure 4. The strain records from gauges V1, V5, L1, and L2 were used for stress analysis of specimens 3NN and 3NA, and the strain records from V1, V6, V9, L1, and L2 were used for the other specimens.
- The concrete compressive force Ncc was extrapolated using the equilibrium Equation (1).where NT (N1, N2) and NCS are tensile and compressive forces, respectively, as shown in Figure 13, determined according to the strain gauge records installed on the longitudinal bars.
- Neutral axis Cb was calculated using the curvature ϕ of the specimen. Curvature was calculated according to the strain gauge records L1 and L2 (ε1, ε2) installed on the D13 and D16 reinforcement bars (See Figure 4). Using neutral axis and curvature, the compressive strain at the extreme compression fiber was calculated.
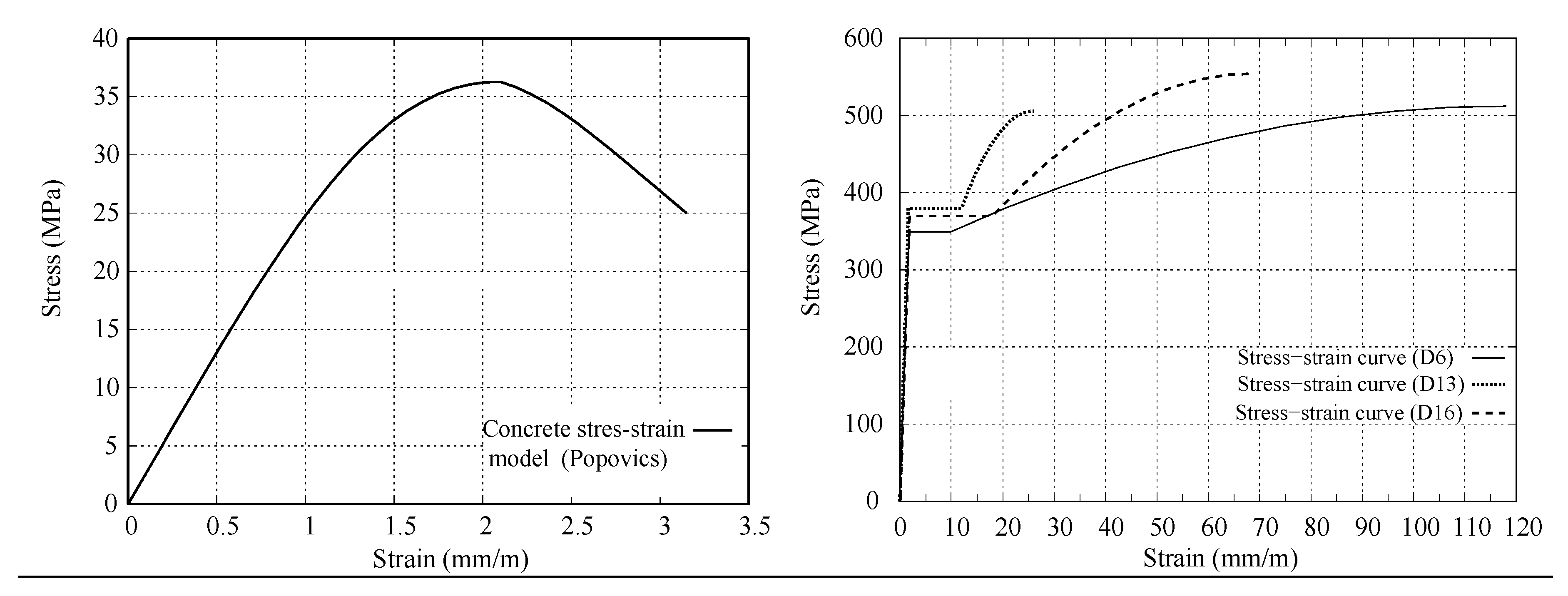
- Effective concrete compressive stress fce and compressive strain εcu was found using Equations (2) and (3):
4.3. Evaluation of the Stress Transition Mechanism
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Izumi, N.; Kashima, K.; Kusunoki, K.; Fukuyama, H. Outline of AIJ Standard for Lateral Load-carrying Capacity Calculation of Reinforced Concrete Structures (Draft). Concr. J. 2016, 54, 1155–1161. [Google Scholar] [CrossRef]
- Yoon, R.; Sanada, Y.; Akahori, T. Seismic Performance Evaluation of RC Moment-Resisting Frames with Typical Non-Structural Walls in Japan. J. Adv. Concr. Technol. 2017, 15, 544–557. [Google Scholar] [CrossRef][Green Version]
- Ju, R.-S.; Lee, H.-J.; Chen, C.-C.; Tao, C.-C. Experimental study on separating reinforced concrete infill walls from steel moment frames. J. Constr. Steel Res. 2012, 71, 119–128. [Google Scholar] [CrossRef]
- Kabeyasawa, T.; Kato, S.; Hosokawa, Y. Effect of spandrel and hanging walls on flexural capacity of reinforced concrete columns with wing walls. In Proceeding of the 10th U.S. National conference on Earthquake Engineering, Anchorage, AK, USA, 21–25 July 2014. [Google Scholar]
- Johnson, B. Anchorage Detailing Effects on Lateral Deformation Components of R/C Shear Walls. Master’s Thesis, University of Minnesota, Department of Civil Engineering, Minneapolis, MN, USA, 2010. [Google Scholar]
- American Concrete Institute. Building Code Requirements for Structural Concrete (ACI 318-14) and Commentary (ACI 318R-14); American Concrete Institute: Farmington Hills, MI, USA, 2014. [Google Scholar]
- Welt, T.S. Detailing for Compression in Reinforced Concrete Wall Boundary Elements: Experiments, Simulations, and Design Recommendations. Ph.D. Thesis, University of Illinois, Urbanna Champaign, IL, USA, 2015. [Google Scholar]
- Segura, C.L.; Wallace, J.W. Seismic Performance Limitations and Detailing of Slender Reinforced Concrete Walls. ACI Struct. J. 2018, 115, 849–860. [Google Scholar] [CrossRef]
- Walid, A.S.; Hibino, Y.; Kusunoki, K.; Tomohisa, M.; Sanada, Y.; Izumi, N.; Trevor, Z.Y.; Satoru, F. Structural performance of reinforced concrete members with monolithic non-structural wall under static and dynamic loads. Build. J. 2020. under review. [Google Scholar]
- Moehle, J.P.; Acevedo, C.; Creagh, A. Exploratory tests of wall boundary elements subjected to alternating tensile and compressive loadings. In Proceedings of the PEER Annual Meeting, San Francisco, CA, USA, 8–9 October 2010. [Google Scholar]
- Wallace, J.; Orakcal, K. ACI 318-99 Provisions for Seismic Design of Structural Walls. ACI Struct. J. 2002, 99, 499–508. [Google Scholar]
- Bentz, E.; Collins, M.P. Response 2000, Version 1.0.5; University of Toronto: Toronto, ON, Canada, 2001. [Google Scholar]
- Popovics, S. A numerical approach to the complete stress-strain curve of concrete. Cem. Concr. Res. 1973, 3, 583–599. [Google Scholar] [CrossRef]
- Mander, J.B.; Priestley, M.J.N.; Park, R. Theoretical Stress-Strain Model for Confined Concrete. J. Struct. Eng. 1988, 114, 1804–1826. [Google Scholar] [CrossRef]
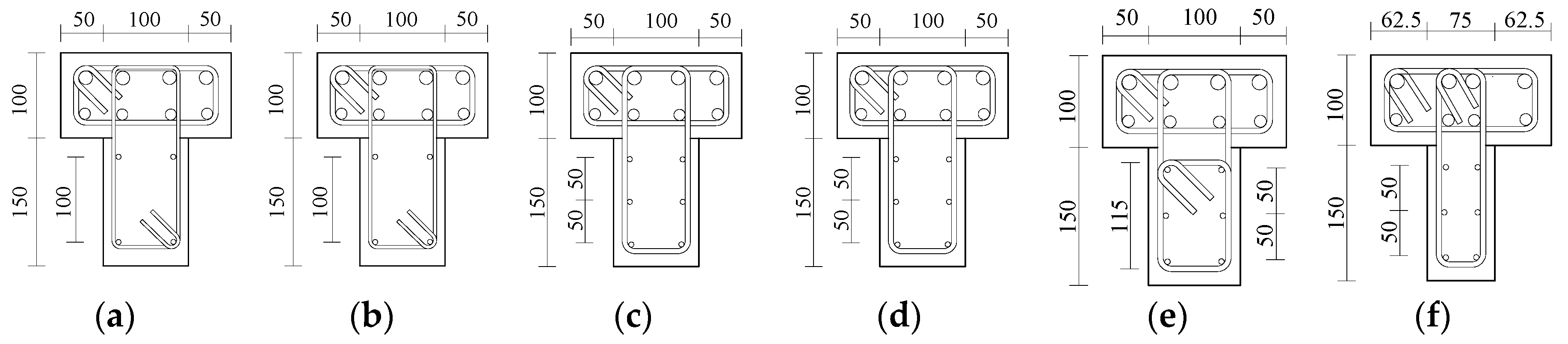




| ID | Cross Section | Transverse Reinforcement | Longitudinal Reinforcement | Boundary Confinement | Anchoring of Main Bar | Notice | |||
|---|---|---|---|---|---|---|---|---|---|
| Wall | Beam | Wall | Beam | Ratio | Depth (mm) | ||||
| 3NN | 100 × 150 | D4@100 (ρt = 0.28%) | D6@50 (ρt = 1.3%) | 4-D4 (ρl = 0.37%) | 4-D16 4-D13 (ρl = 6.51%) | No | |||
| 3NA | D4@100 (ρt = 0.28%) | D6@50 (ρt = 1.3%) | 4-D4 (ρl = 0.37%) | 4-D16 4-D13 (ρl = 6.51%) | - | - | Yes | Min. 1 | |
| 6NA | D6@100 (ρt = 0.63%) | D6@50 (ρt = 1.3%) | 6-D6 (ρl = 1.26%) | 4-D16 4-D13 (ρl = 6.51%) | Yes | Med. 2 | |||
| 12NA | D6@50 (ρt = 1.27%) | D6@50 (ρt = 1.3%) | 6-D6 (ρl = 1.26%) | 4-D16 4-D13 (ρl = 6.51%) | Yes | Max. 3 | |||
| 12HN | D6@50 (ρt = 1.27%) | D6@50 (ρt = 1.3%) | 6-D6 (ρl = 1.26%) | 4-D16 4-D13 (ρl = 6.51%) | 1.27% | 450 | No | Max. 3 | |
| 18NNT | 75 × 150 | D6@50 (ρl = 1.69%) | D6@50 (ρt = 1.3%) | 6-D6 (ρl = 1.69%) | 4-D16 4-D13 (ρl = 6.51%) | - | - | No | Slend. 4 |
| Compressive Strength f’c (MPa) | Strain at Peak (%) | Young’s Modulus (MPa) | Tensile Strength (Mpa) |
|---|---|---|---|
| 36.3 | 0.212 | 17,374.6 | 2.7 |
| Reinforcements | Young’s Modulus (GPa) | Yield Stress (MPa) | Ultimate Strength (MPa) |
|---|---|---|---|
| D4 | 178.8 | 356.7 | 503.5 |
| D6 | 185.6 | 338.3 | 501.7 |
| D13 | 201.3 | 380.6 | 506.2 |
| D16 | 203.4 | 383.8 | 568.9 |
| Specimen | Ultimate Strength Capacity Vexp 1 (kN) | Analytical Prediction Vana 2 (kN) | Vexp/Vana (%) |
|---|---|---|---|
| 3NN | 85.2 | 101.8 | 84 |
| 3NA | 92.8 | 104.9 | 88 |
| 6NA | 106.2 | 110.5 | 96 |
| 12NA | 115.8 | 110.5 | 105 |
| 12HN | 116.8 | 101.8 | 115 |
| 18NNT | 86.2 | 80.4 | 107 |
| Specimen | Drift Capacity (%) | Neutral Axis Depth (mm) | Effective Compressive Strength (MPa) | Ultimate Compressive Strain |
|---|---|---|---|---|
| 3NN | 0.040 | 144 | 40.8 | 0.0031 |
| 3NA | 0.038 | 150 | 40.5 | 0.0037 |
| 6NA | 0.040 | 161 | 39.8 | 0.0064 |
| 12NA | 0.037 | 134 | 48.3 | 0.0033 |
| 12HN | 0.099 | 148 | 50.3 | 0.0069 |
| 18NNT | 0.040 | 161 | 51.7 | 0.0055 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Safi, W.A.; Hibino, Y.; Kusunoki, K.; Sanada, Y.; Mukai, T. Impact of the Reinforcement Detailing on Seismic Performance of Isolated Non-structural Walls. Buildings 2020, 10, 89. https://doi.org/10.3390/buildings10050089
Safi WA, Hibino Y, Kusunoki K, Sanada Y, Mukai T. Impact of the Reinforcement Detailing on Seismic Performance of Isolated Non-structural Walls. Buildings. 2020; 10(5):89. https://doi.org/10.3390/buildings10050089
Chicago/Turabian StyleSafi, Walid Ahmad, Yo Hibino, Koichi Kusunoki, Yasushi Sanada, and Tomohisa Mukai. 2020. "Impact of the Reinforcement Detailing on Seismic Performance of Isolated Non-structural Walls" Buildings 10, no. 5: 89. https://doi.org/10.3390/buildings10050089
APA StyleSafi, W. A., Hibino, Y., Kusunoki, K., Sanada, Y., & Mukai, T. (2020). Impact of the Reinforcement Detailing on Seismic Performance of Isolated Non-structural Walls. Buildings, 10(5), 89. https://doi.org/10.3390/buildings10050089






