Abstract
Insulation systems for the floor, roof, and external walls play a prominent role in providing a thermal barrier for the building envelope. Design decisions made for the insulation material type and thickness can alleviate potential impacts on the embodied energy and improve the building thermal performance. This design problem is often addressed using a building information modelling (BIM)-integrated optimisation approach. However, one major weakness that lies in the current studies is that BIM is merely used as the source for design parameters input. This study proposes a BIM-based envelope insulation optimisation design tool using a common software Revit and its extension Dynamo to find the trade-off between the total embodied energy of the insulation system and the thermal performance of the envelope by considering the material type and thickness. In addition, the tool also permits data visualisation in a BIM environment, and automates subsequent material library mapping and instantiates the optimal insulation designs. The framework is tested on a case study based in Sydney, Australia. By analysing sample designs from the Pareto front, it is found that slight improvement in the thermal performance (1.3399 to 1.2112 GJ/m2) would cause the embodied energy to increase by more than 50 times.
1. Introduction and Literature Review
The construction industry plays a prominent role in addressing energy use and emissions. In 2018, it was responsible for 36% of the total energy consumed and 39% of process-related carbon dioxide emissions [1]. Energy ensued from buildings can be categorised into two types; energy consumed at the operational stage and the energy capital of all building materials, referred to as embodied energy [2]. However, “energy” and “operational energy” are usually used interchangeably, while the embodied energy of materials is often ignored [3]. The consequence is that energy savings in the operational stage are achieved at the price of the accumulation of embodied energy [4]. Embodied energy accounts for a significant part in the total energy requirement [5]. In a domestic context, Treloar [6] indicated that embodied energy is 20 to 50 times the annual operational energy for most buildings in Australia. One holistic approach for minimising environmental impacts posed by the built environment is by considering materials’ impact on the building performance and their embodied energy [7].
1.1. Insulation Design as a Multi-Objective Optimisation Problem
Design considerations in building envelope (roof, external walls, and floor) [8], building orientation and configuration, and passive thermal mechanisms have been extensively investigated to improve building performance [9]. Leveraging the insulation, which is a crucial design criterion for the building envelope, is believed to be an effective approach to alleviate adverse environmental impacts posed by the built environment [10]. A building envelope with a poorly designed insulation system could explain up to 40% of the total energy lost [11]. Insulation material effectiveness relates to its thermal conductivity, which is defined as W/m·K, representing the heat flow through a unit cross-section area of a one metre thick homogeneous material when the temperature gradient is equal to 1 K [12]. A lower thermal conductivity value means better intrinsic insulating performance. For any insulation installed in the building, the parameter thermal resistance (R-value) is more often used to express the insulation component’s resistance to conductive heat flow [13]. The R-value, expressed as m2·K/W is dependent on the thermal conductivity and the thickness of the insulation material with a higher R-value, indicating the greater effectiveness of the insulation layer. However, a thicker insulation inevitably leads to a higher embodied energy [14], and different insulation materials have distinct embodied energy impacts due to the raw materials used and the energy requirements for manufacturing and delivering the product [15].
Therefore, not fully understanding the embodied energy and thermal properties of insulation materials can be very problematic, especially when taking a closer look at the insulation materials in the market. For instance, in Europe, glass wool and mineral wool are the most used insulation materials in buildings, making up around 60% of the overall market. Expanded and extruded polystyrene and polyurethane also account for 27% of insulations in the market [16]. Among these insulation materials, polyurethane has the most ideal insulation performance with a thermal conductivity of around 0.025 W/m∙K [12], and the same parameter for mineral wool can go up to 0.071 W/m∙K [17]. However, when it comes to the embodied energy, mineral wool is reported to have much lower embodied energy (16.6 MJ/m3) compared to polyurethane (102.1 MJ/m3) [18].
In addition to this, the thickness of insulation materials used in buildings also affects the embodied energy and the thermal performance of the building [19]. In fact, Biswas et al. [10] pointed out that there is a positive linear relationship between the amount of insulation used and the embodied energy, and when the amount of insulation applied exceeds a certain level, there will not be any further energy reduction, but only the accumulation of embodied energy. In the literature, Dombaycı [20] obtained 46.6% and 41.53% reduction on energy consumption and emissions, respectively, through calculation by using insulation materials with their optimal thickness in the external wall. Some extended discussions on optimal insulation thickness also explore the performance of different insulation materials. Axaopoulos et al. [21] investigated the optimal thickness and the minimum embodied emissions per unit wall area as a single objective optimisation problem for three commonly used insulation materials, including extruded polystyrene, expanded polystyrene, and mineral wool, and reported an optimal thickness varying from 11.2 to 23.4 cm, together with a maximum of 72.2% reduction of annual embodied emissions when installing mineral wool. Similarly, a single optimisation problem proposed by Bojić et al. [22] concluded that when compared with other insulation materials, mineral wool yields the lowest annual total primary energy consumption, which is the sum of embodied energy and the operative primary energy for each year in this study, despite it having relatively high thermal conductivity compared to materials such as polyurethane, and the thickness utilised in the study was the greatest.
However, given the number of design options involved in a real design scenario, determining the optimal thickness by simple comparison across groups of insulation material can hardly suffice. As such, an envelope insulation design problem is examined in this study, which investigates the trade-off between the embodied energy and the thermal performance of the insulation design for the building envelope, namely, the floor, roof, and external walls, by considering material types and thickness at the same time.
1.2. A Building Information Modelling (BIM)-Integrated Optimisation Approach to Support Decision-Making
In respect of the envelope insulation design problem, design parameters are largely dependent on the envelope assemblies, which are inevitably associated with tedious construction documentation in the early design phase. Design decisions made at the early design stage have significant impacts on the sustainability performance of final deliveries [23]. As a response to this, a Building Information Modelling (BIM) integrated approach is regarded as most suitable due to the comprehensive design information that BIM can store [24,25]. Krygiel et al. [26] also argued that BIM can effectively leverage material selections to achieve building performance and environmental goals.
Within the realm of BIM-integrated studies, some utilise BIM as a pure information platform to derive material data, such as insulation type and thickness, in order to calculate a series of performance or environmental impact indicators [27], or give a score to the design based on pre-determined weightings [28]. To account for more dynamic operational conditions, some studies link energy simulation processes to the BIM model. Cho et al. [29] attempted to do so by transferring the BIM model information in the format of gbXML schema (Green Building XML) to an energy simulation tool, Ecotect [30], and conducted a parametric analysis on the insulation type. Similarly, Jalaei and Jrade [31] developed a Revit plugin that exports the design to gbXML format for energy simulation in Ecotect. After Ecotect was discontinued in 2015 [32], Kim et al. [33] presented a workflow that maps an external material database to the material information in a standard Industry Foundation Class format (IFC) file and creates a new file input for subsequent energy simulation. Nonetheless, the premise of these approaches is that designers can always make high quality decisions effectively based on their past experience.
Some studies focus on the area of combining the simulation with optimisation process in a BIM environment to investigate material selections. Bank et al. [34] designed a decision-making framework by integrating a BIM model with a System Dynamic (SD) decision-making software, where a simulation-based optimisation on BIM design parameters are carried out. SD is a computer modelling method that simulates the feedback structure in a system, namely the components and the resulting behaviours [35], and it is believed to be suitable for sustainability design problems with highly dynamic parameters that are time or space dependent [34]. In this framework, the linkage between the BIM model, the SD tool AnyLogic [36], and energy simulation tools requires proficiency in the use of Visual Basic or C# and Java. In addition, the use of SD is very limited in the construction industry [37], showing a lack of feasibility for further adoption of the proposed framework in practice. Similarly, a BIM-based thermal performance multidisciplinary design optimisation framework was proposed by Welle et al. [38], which delivered an automated workflow to address technical barriers such as interoperability issues between modelling and analytical software and poorly coordinated import-export procedures. This workflow also involves building up customised connections with the external energy simulation programme EnergyPlus [39] and Radiance [40].
More recently, common BIM software such as Revit [8] has incorporated energy simulation and Lifecycle Analysis (LCA) as its integrated plugins. An optimisation package is also available in Revit via its Visual Programming Language (VPL) platform, Dynamo [41]. However, at the early design stage, as suggested by Shadram et al. [42], LCA is more often carried out at a highly detailed level considering the scope of the analysis and its poor interoperability with other BIM-driven design process. As for the insulation design problem, Shadram and Mukkavaara [43] developed an optimisation framework utilising BIM for placing insulations focusing on the embodied energy and the operational energy, which is obtained from the simulation results, featuring modelling software Revit and Grasshopper [44], a VPL platform of Rhino [45]. Even so, this framework is still highly relying upon an external database as the material inventory and the core of the framework for simulation and optimisation is carried out by the non-BIM software [46], Grasshopper, whereas the intrinsic characteristic of BIM as a data platform to store model and project information is underappreciated.
BIM, as the building design information database [25,47], should be used more than a platform where material information is simply read as optimisation input. The BIM model needs to stay in sync with the optimal design model in the way that any parameter and project-specific information changes are properly documented. Furthermore, by visualising the data in the VPL platform [48] after the optimisation, it is believed that users can make more informed decisions [49]. Given that Revit is a BIM platform that is adopted by a majority of construction engineers and architects around the world [46], there is still a need for an automated optimisation-based BIM framework as a design decision support system for selecting the most suitable insulation material and thicknesses in building projects. The aim of this research is therefore to develop a BIM-based optimisation framework for the building envelope insulation system, emphasising on the embodied energy and thermal performance. A BIM-based insulation design framework using Revit [50] is proposed, to enhance the decision-making process for designing envelope insulation system accounting for its embodied energy and thermal performance. Embodied energy used in this study is defined as the total primary energy ensued from the material extraction, manufacturing, and transportation within a cradle-to-gate boundary [18]. The objective is to deliver an automatic workflow that (i) finds the trade-off between the embodied energy and thermal performance while considering the insulation type and thickness; and (ii) places the insulations in the model; and (iii) maps insulation material information to the BIM platform.
The remainder of this paper is organised as follows. Section two first presents the proposed optimisation framework, and then gives the mathematical description of the optimisation problem; this section also provides a detailed illustration of framework components together with tasks carried out. Following that, the proposed framework is applied on a realistic case study to showcase the feasibility of it. Conclusions are drawn at the end.
2. Materials and Methods
The proposed framework contributes to the research area of BIM-integrated optimisation by providing a decision-making system for building envelope insulation design, complete with automated material documentation procedures in the BIM model. In this section, the detailed framework components are presented.
2.1. The Proposed Framework
An optimised design-based building framework for insulation selection and dimensions that places emphasis on the embodied energy and the thermal energy performance of the envelope insulation system has been developed. The proposed framework integrates the multi-objective optimisation insulation design problem into a BIM modelling environment, enabling a seamless workflow for optimisation setup, data visualisation, model modification, and material documentations. As shown in Figure 1, the overview of the framework, which is further broken down into specific details to be outlined later, is comprised of four main components: (i) BIM Software; (ii) Envelop Insulation Optimisation; (iii) Visualisation, and (iv) Nomination of Insulation Design.
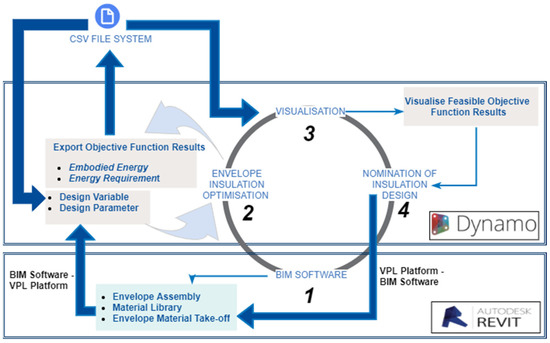
Figure 1.
An overview of building information modelling (BIM)-based Envelope Insulation System Optimisation Framework.
The BIM integration in this study is mainly two-fold. First, the intimacy between Dynamo and Revit allows the seamless transfer of optimisation parameters, such as existing envelope assemblies, quantity take-offs of each assembly layer, and the properties of assembly materials. This is achieved via the first module, BIM Software, where no manual work is required. However, it is expected that each envelope component is designed according to the construction specifications with correct assemblies and the material thermal information properly embedded. This allows Dynamo to extract the detailed assemblies of the building envelope and the quantities of the material used, as well as the corresponding material properties from Revit as the design parameters. Meanwhile, design variables, namely available insulation type and thickness to be tested, are exported to Dynamo from Comma-separated Value (CSV) files to initiate the optimisation. After the optimisation, Dynamo platform allows visualising all feasible design objective function results by interacting with the local directories specified by users where designated CSV files are stored and updating the envelope elements in Revit automatically via accessing Revit Application Programming Interface (API). Detailed explanations of these two integration processes are offered in Section 2.2 and Section 2.4 respectively.
In this framework, major data transfer paths between the building model and the VPL platform; and the VPL platform and local directories are highlighted in Figure 1. Key features of the data interaction paths design lies in the characteristics of the envelope insulation problem that the design parameters are uninsulated layers that are held as constants in the Revit model while the design variables also require corresponding visual presentation and information documentation in the BIM model. Different types of tasks performed within the other components of Figure 1 are discussed below.
2.2. Envelope Insulation Optimisation
The second component, the Optimisation Module, is illustrated in Figure 2. Data Transfer Node 1 is responsible for bridging Dynamo with other platforms to fetch information for the envelope optimization problem. It involves preparing two classes of optimisation inputs, the first of which aims to read available insulation type and thickness from CSV files. The second class is the material information of envelope assemblies from the BIM model. As suggested in Figure 2, these design parameters can be retrieved from three Revit dialogs. Figure 3 is an illustrative example of how the information for a wood finish timber floor is displayed in Revit.
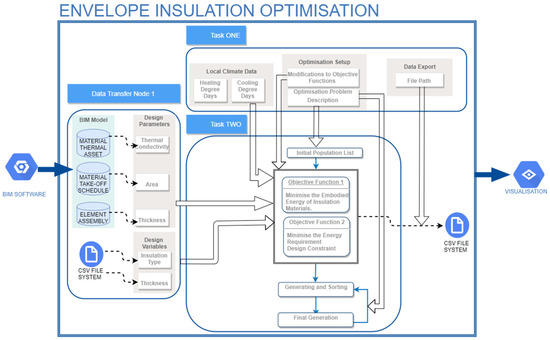
Figure 2.
Module Envelope Insulation Optimisation Workflow.
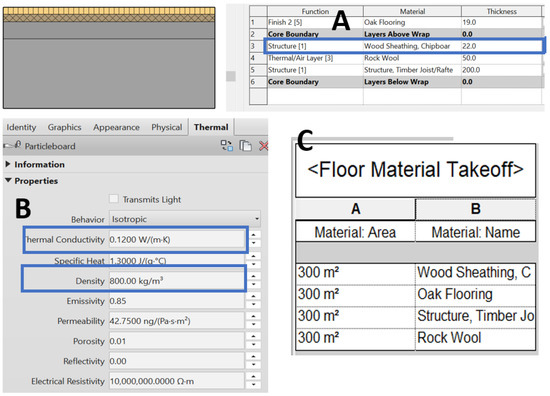
Figure 3.
Illustrative Example for a Wood Finish Timber Floor. (A) Layers of the floor; (B) properties of materials used; (C) quantity take-off.
Figure 3A,B are the BIM dialogs of the Element Assembly and Material Thermal Assets as shown in Data Transfer Node 1. For each layer of the envelope component, its function, material applied, and thickness nominated need to be defined. Thermal assets that are relevant to this study are thermal conductivity and density, as shown in Figure 3B, and they are associated with the material at each layer. The material assembly and properties hosted can be obtained using the Dynamo commands group A and B illustrated in Figure 4A,B. Command C generates the floor material take-off schedule shown in Figure 3. Note that it is important to insert an insulation layer at the model building stage. This allows the nominated insulation area shown in the schedule, which will provide more accurate results in the subsequent optimisation.

Figure 4.
Proposed Dynamo Workflow for Reading Data from the Revit Model. (A) Obtaining thickness; (B) collecting properties if material; (C) creating material take-off.
Task One in Figure 2 is where problem-specific parameters are specified, including the file path for exporting datapoints during the optimization process, optimisation setup, and the Heating Degree Days (HDD) and Cooling Degree Days (CDD) based on local climate data. These last two parameters are used to estimate the energy requirement when using a specific envelope system and are further discussed in the following section. Optimisation Problem Description refers to inputs of parameters that specify distinct optimisation scenario including population size, number of iterations, and variable ranges. Variable ranges correspond to the discrete list input of insulation type and thickness. Population size and iteration times refer to the total number of individuals included at each iteration and when the optimisation will stop. Any tailoring to objective functions is also included in Task One.
The core of this component, Task Two, employs Optimo [47], a Non-dominated Sorting Genetic Algorithm (NSGA-II) optimisation package of Dynamo to conduct the optimisation. NSGA-II is a multi-objective evolutionary algorithm in essence and utilises nondominated sorting techniques [51]. With necessary information supplied through the data interaction and Task One, the optimisation calculation process is carried out. The detailed mathematical equations formulated for the envelope insulation design problem are introduced in the following section.
Optimisation Mathematical Model
Table 1 summarises the notation set adopted to create the optimisation model proposed.

Table 1.
Notation Set.
In order to evaluate the primary design objectives, namely the embodied energy and the thermal performance, two sets of equations are formulated. The total embodied energy of the insulation system is calculated by summing up the embodied energy of the nominated insulation materials. The thermal performance is assessed by evaluating the energy requirement under static conditions using degree-days method, an approach commonly seen in insulation optimisation problems [20,52]. This method translates dynamic weather conditions into two local constant indicators, Heating Degree Days (HDD) and Cooling Degree Days (CDD), reflecting how much the daily average temperature deviates from a base comfortable thermal level over a certain period [53].
Within literature, one common approach to study the thermal resistance (R value) of wall assemblies, roof structure, and floor construction is by simple addition of the nominal thermal resistance value of each layer [8,54,55,56,57].
However, this method is established on the assumption that heat flow in every cross section of the assembly is homogeneous [58]. In some occasions such as when framing elements are used, thermal bridges will form, providing a faster heat transfer path [59]. In this study, isothermal plane method is employed to estimate the total R value of the building envelope. This approach adds up the effective thermal resistance of each layer of a building assembly, when more than one heat flow path is presented in one layer, which is common when there exists an opaque-cavity structure, the thermal resistance of each heat path will be calculated in proportion to the area [60].
The first objective function Embodied Energy (EE) aims to minimise the embodied energy per unit envelope area [21], which is defined in Equation (1):
where calculates the mass of the insulation material for envelope component . is the embodied energy coefficient given in MJ/Kg. The denominator denotes the total insulated area of the building envelope. indicates the total volume of insulation material used in component , which is calculated as shown in Equation (2):
where is the area of insulation material used in component , measured in square metres, and is the corresponding insulation thickness. Considering different envelop components might have different requirements on insulation thickness, specifies a range of thickness input for each component.
Equation (3) calculates the heat transfer rate where is the overall thermal transmittance and is the temperature difference:
Drawing upon this equation, Equation (4) utilises the degree-days approach to estimate the energy requirement [61,62]:
In Equation (4), the energy requirement is expressed in GJ/m2. HDD and CDD are the heating and cooling degree-days for a specified region respectively, and indicates the system efficiency. is the overall heat transfer coefficient and is defined in Equation (5):
is the heat transfer coefficient for a building envelope component. According to the Isothermal Plane method, it is defined as Equation (6) [60]:
In this equation, and are constants for the each envelop component , denoting the R-value for the inner and outer air film. is a binary parameter which equals 0 when component refers to the slab-on-ground floor system, and 1 otherwise [63]. The represents the total R-value of continuous layers, where only one heat flow path is identified, and therefore the resistance values are additive. indicates the thermal resistance of the parallel thermal path. and are the fractional area of heat flow path (excluding windows and doors) via the opaque and void section respectively for the envelope component [64]. Accordingly, and are the R-value of each path. In particular, denotes the thermal resistance of the insulation material .
One design constraint considered is related to the of the proposed insulation material. This is often regulated by local building codes [65,66,67]. This study adopts the maximum U-value allowed developed by the Australian national construction regulatory framework, the National Construction Code (NCC) [68], for different element assemblies on the building envelope. As a result, 0.24 W/m2·K, 1 W/m2·K and 0.36 W/m2·K are set as the upper bound for roof, floor and wall construction, respectively [67].
2.3. Visualisation
The optimal solutions produced by NSGA-II can be visualised in the form of a Pareto front when no further improvements can be made for any variable without harming other variables [69]. By visualising the Pareto-optimal design solutions, designers are able to select among a series of equally good design options more effectively [70]. The visualisation component in the proposed framework aims to provide visual presentation of the distribution of all feasible objective function values documented during the optimisation, such that whether the process has achieved its pareto optimality is made obvious to decision makers. Feasible designs are those that do not violate the design constraint. Figure 5 demonstrates the Dynamo setup for visualising datapoints. All feasible results for the objective function Embodied Energy will be plotted on the X-axis and the Energy Requirement result is visualised on the Y-axis.
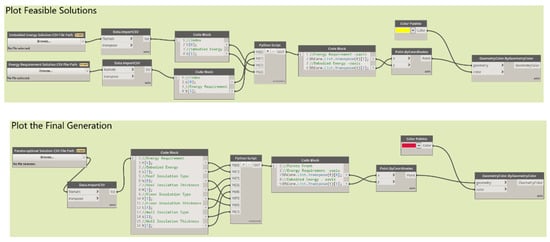
Figure 5.
Dynamo Workflow for Data Visualisation.
2.4. Nomination of Insulation Design
The aim of the fourth Module of the framework is to update the insulation design of the building envelope based on the decision made with reference to the visualised datapoints from the optimisation process and the Pareto-optimal solutions. Meanwhile, the material library will be maintained through a process that maps the optimal insulation materials. This is achieved mainly via three main steps; (i) selection of the optimal insulation design from the Pareto-optimal list, (ii) mapping the corresponding thermal properties into the material library, and (iii) instantiation of the solution in the BIM model. Figure 6 depicts the proposed workflow.
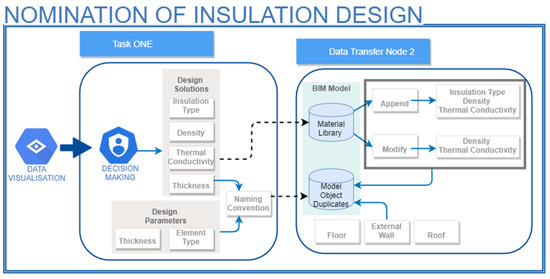
Figure 6.
Module Decision-Making Workflow.
Most building materials displayed in BIM models are not merely a graphical representation [71]. BIM software has a collection of material visuals and thermal and physical properties as its native material library, which can be easily modified and appended on a project basis. Data Transfer Node 2 first iterates materials from the final solution list determined by the designer and if the material is already present in the library, its thermal properties will be modified according to the optimisation result, otherwise a new insulation type will be created with the corresponding properties, namely density and thermal conductivity embedded. Python scripts are used to interact with the Revit material library using the Revit API. The scripts can be found in Appendix A. Another set of commands duplicates the external walls, roof, and floor in the current BIM document, and then assigns them with a new name that indicates the total thickness and the type of each envelope component, such as “Roof_110”, see Figure 7A, which also serves as the optimisation input. Figure 7B indicates the optimal insulation thickness determined by the designer.
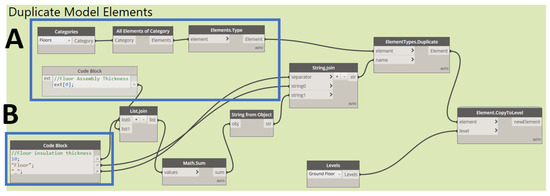
Figure 7.
Dynamo Workflow for Duplicating and Renaming Model Element. (A) Floor assembly thickness; (B) floor insulation thickness determined by the designer.
Finally, the optimal insulation material and thickness will be assigned to the renamed duplicates using two nodes from the Dynamo package Orchid [72]. Figure 8 gives an example of how a new type insulation material named ‘test1’ is populated in a drop-down list after mapping it to the material library via the Revit API. Accordingly, the thickness input should correspond to the optimal solution for the material ‘test1’. In addition, the element type and index can be fed by scripts shown in the previous graphs, as commands in Figure 7A have extracted the element type for each envelope component, and the index, representing where the insulation layer is inserted, has been specified in Figure 2A.
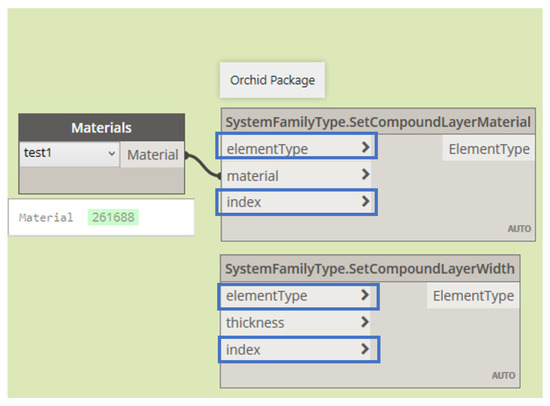
Figure 8.
Dynamo Nodes for Instantiating the Insulation Design.
2.5. Case Study
The developed framework was utilised on the envelope insulation design of a house located in Sydney, Australia. The case study has a total floor area of 59.4 m2 and is built on a slab-on-ground. The house has a pitched roof with ceiling lining under timber rafters and adopts the brick veneer external wall system, which is the most common wall construction method used in Australian dwellings [67]. Figure 9 and Figure 10 are the BIM model and the floor plan for the case study.
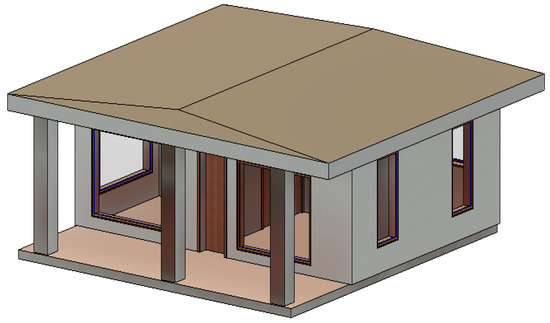
Figure 9.
3D BIM Model.
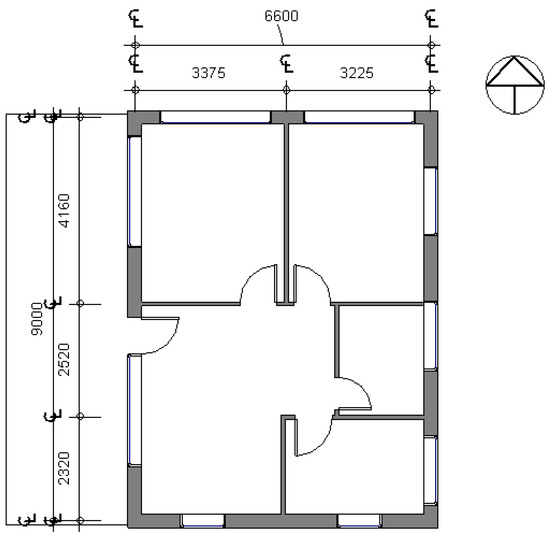
Figure 10.
Floor Plan, units in mm.
The building envelope system is shown in Table 2. The assemblies are presented in the following order: exterior side → interior side. Where no construction details are available in the drawings, sustainable design specifications offered in the Australian government website YourHome [73] were referred to as a general guideline.

Table 2.
Building Envelope Assembly Details.
The HDD and CDD in Sydney adopted in this study are 743 and 556, measured with a base temperature of 18 degrees [75]. The system efficiency was assumed to be 80% [76]. In addition, the area ratio of the framing component for the brick veneer wall system and roof is assumed to be 20% [77,78]. Therefore, and shown in Equation (7) are assumed to be 20% and 80% respectively for both external wall and roof.
A total of ten types of insulation were selected as optimisation input, including conventional insulation materials such as cellulose, mineral wool, a collective of insulation made of fibres [79], expanded purposes polystyrene (EPS), rock wool, one special type of mineral wool [79], polyurethane foam (PUR) [8], fibreglass batt [80] and emerging insulation like flax [81], recycled wool [82], and wood wool [8]. Their corresponding embodied energy coefficients following a cradle-to-ate approach, density and thermal conductivity were obtained from the Inventory of Carbon and Energy (ICE) database [18]. These design variables are presented in Table 3.

Table 3.
Insulation Types and Properties.
Insulation thickness tested are some common dimensions seen in the market and this information was gathered from local suppliers, see Table 4.

Table 4.
Insulation Thickness.
3. Results and Discussion
The optimisation programme has a mutation probability of 0.01 and a crossover possibility of 0.9. The crossover and mutation distribution indices are 20 [24]. The Pareto front was obtained at the 150th generation with a population size of 200. The calculation time took no more than 10 min on a personal computer with a 2.5 GHz processor and 8 GB of RAM.
Figure 11a gives a clear indication of the distribution of all feasible results in the Dynamo canvas that the black points from the final generation have formed the Pareto front. As a reminder, the horizontal axis represents the Embodied Energy function result, and on the vertical direction the value reflects the Energy Requirement function result. Note that in order to visualise this graph, geometry scaling was set as small in Dynamo, and a scale factor of 30 and 1/30 were applied to the Energy Requirement and Embodied Energy results respectively. For discussion purpose in this paper, the same group of results were also plotted on a 2-D scatter chart without geometry scaling to validate the Pareto optimality. This is illustrated in Figure 11b. In this graph, similarly, the lower the Energy Requirement value on the y-axis, the better the thermal performance of the insulation system. For instance, point A has demonstrated a unilateral focus on minimising the design objective Embodied Energy, while point H emphasised solely on reducing the Energy Requirement.

Figure 11.
(a) Case Study Data Visualisation in Dynamo, and (b) 2D Scatter Plot.
A total of 183 feasible solutions were obtained in the Pareto front. In addition to insulation design A and H, another six solutions have been identified in Figure 11b. The corresponding variables for solution A to H are listed Table 5. ER and EE are acronyms for the objective function Energy Requirement and Embodied Energy respectively.

Table 5.
Sample Design Solutions.
By contrasting designs A and H, it is noted that cellulose is opted for when considering the design objective Embodied Energy only as cellulose has the lowest embodied energy coefficient among all materials tested. In the meantime, design A is only associated with thinner insulation panels. However, the insulation dimension is bound by the design constraint on the system U value. From design A to H, there is a staggering difference in the Embodied Energy—this value of the design H is nearly 50 times of A. Insulation design B adopts the same material as A, while there is an increase in the thickness for floor insulation. Consequently, this leads to a 4.07% drop in Energy Requirement and a 16.56% increase in the embodied energy.
Moving towards designs with lower Energy Requirement, cellulose is replaced by fibreglass in design C, which has a slightly lower thermal conductivity. Thicker insulation panels were also proposed in this design. When comparing design C and D, it is noted that Embodied Energy doubled when rock wool is used in the floor assembly, even though it has better insulating properties and contains less embodied energy for a given mass. This is because rock wool’s density is tenfold that of fiberglass. Similarly, solution E proposes PUR for the floor insulation, and achieved a 1.44% reduction on the estimated energy demand, while the energy capital for the insulation system soared from 33.1118 MJ/m2 to 119.7994 MJ/m2 (i.e., the difference is around 250%). PUR is known for its effective insulation property, but it also has the highest embodied energy coefficient value among all materials input in the case study.
It is also observed in the table that design H improved the Energy Requirement by around 2.66% compared to design C at the expense of storing 10 times more embodied energy. Meanwhile, in the case of designs A and B, more energy reduction is only associated with a 16.56% increase in embodied energy. This can be explained by the change in insulation dimension from solution A to B.
Another thing to note is that for all designs displayed in the table, between any two solutions, the change observed in Embodied Energy is always more vigorous than the decrease or increase in Embodied Energy. For instance, the Energy Requirement falls around 3.3% from design B to C, while the Embodied Energy has increased nearly four times. Biswas et al. [10] reported that the environmental impact associated with the embodied energy of the insulation material is secondary compared to the effect on reducing operation energy. The previous study focuses on a lifecycle assessment of the insulation material, which is not within the scope of this study. In fact, it was highlighted by Hammond et al. [18] that most insulation materials can pay back their embodied energy during their lifetime, in spite of the fact that common materials in the market have very poor energy capital. The Energy Requirement and Embodied Energy comparison results in this case study are in part in line with this argument and reaffirm that further improvements on the embodied energy for insulation materials should still be made.
Flax insulation, woodwool, and recycled wool are not chosen in any of the design. This is because the input data, namely the embodied energy coefficient, thermal conductivity, and density selected did not demonstrate significant advantages over other traditional materials since each material in reality has a wide range of variations. For instance, the density of the flax insulation mat could vary from 5 to 100 Kg/m3, and its thermal conductivity was reported to be in the range of 0.035 to 0.075 W/m·K [17]. Therefore, there is no one-size-fits-all insulation design strategy and the envelope insulation design framework developed in this study permits dealing with two critical insulation design considerations, namely the material type and thickness, while considering the environmental impacts.
4. Conclusions
A BIM-based envelope insulation design framework was proposed in this study. The proposed framework integrates a common BIM platform, Revit, with an optimisation model that is built within Dynamo to deal with two insulation design aspects: the insulation type and thickness for the roof, external walls, and floor, while addressing the embodied energy of the insulation system and the thermal performance of the building envelope. A Dynamo package that employs NSGA-II algorithm was utilised to solve the problem. Two objective functions that represent the embodied energy per insulated area (MJ/m2) and the thermal energy requirement per envelope surface area (GJ/m2) were formulated. Some other key features of the BIM framework include:
- Plotting feasible objective function results on the Dynamo working canvas.
- Mapping insulation material properties into the Revit material library.
- Instantiating the optimal insulation design in the BIM model.
A case study was conducted using the developed tool and the results demonstrate that an improvement of the objective function Energy Requirement from 1.3399 to 1.2112 GJ/m2 led to a drastic increase in the embodied energy contained by the insulation materials—the value has expanded 50 times more from 6.7115 to 360.0903 MJ/m2. Some limitations of the results generated lie in the insulation materials selected for the case study. The emerging insulation materials, such as flax, woodwool, and recycled wool, seem to be less preferred according to the optimisation results, as the data input in this case study are only representative of the properties for each insulation material, but cannot generalise all possible material variations, which in fact result in a wide range of acceptable values when discussing the properties of a given insulation material. Fire safety of insulation materials was also not accounted for. This is a significant design requirement as the building envelope system can effectively prevent the spread of fire [87]. According to the optimisation results, PUR seems to be an ideal option, while during a fire this material would pose potential health threats [88]. Additionally, the Energy Requirement adopts degree-days calculation approach based on static Sydney weather conditions. This leads to another limitation of this study that the objective function results are restricted to Sydney, Australia only, and would vary significantly depending on the location of the property tested. It is therefore critical to reiterate that the purpose of this study is not to make recommendations on the suitable insulation design but to showcase the applicability of the proposed optimisation framework.
One major limitation identified in previous BIM-based simulation or optimisation framework is that BIM is often only used as the data input source. This work contributes to the research area of BIM-integrated studies by providing an automated envelope insulation optimisation workflow with material mapping, design instantiation, and data visualisation features.
The weakness of this study is that it does not consider the whole lifecycle stage of the insulation materials, where the cost factor would also play a prominent role in the insulation design [89]. Furthermore, some future work could investigate the possibility of optimising the overall wall, roof, and floor assemblies in the BIM environment. This would lead to additional complexities as some assembly layers become optional and there is also a need to account for the structural performance [90].
Author Contributions
Conceptualization, Z.C. and A.W.A.H.; methodology, Z.C. and A.W.A.H.; software, Z.C.; validation, Z.C. and A.W.A.H.; formal Analysis, Z.C.; investigation, Z.C. and A.W.A.H.; resources, Z.C. and A.W.A.H.; data curation, Z.C.; writing—original draft preparation, Z.C. and A.W.A.H.; writing—review and editing, Z.C., A.W.A.H., I.K. and A.A.; visualization, Z.C., A.W.A.H. and A.A.; supervision, A.W.A.H. and A.A.; project administration, A.W.A.H and I.K.; funding acquisition, A.W.A.H. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by UNSW Built Environment Limited APC Scheme.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. Dynamo Python Scripts Used for Revit Material Mapping
Figure A1 demonstrates using the Revit API method IsNameUnique to evaluate whether the optimal insulation material is already documented in the Revit material library.
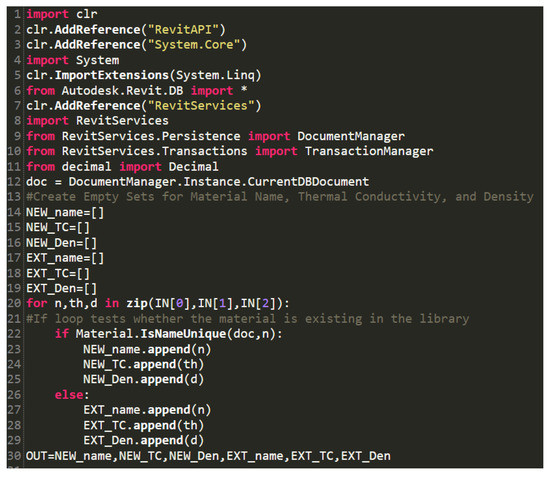
Figure A1.
Dynamo Python Script to Test If the Insulation Material is Already in the Revit Material Library.
The script in Figure A2 shows the procedure of updating the insulation material thermal conductivity and density in the Material Library based on the optimal design.
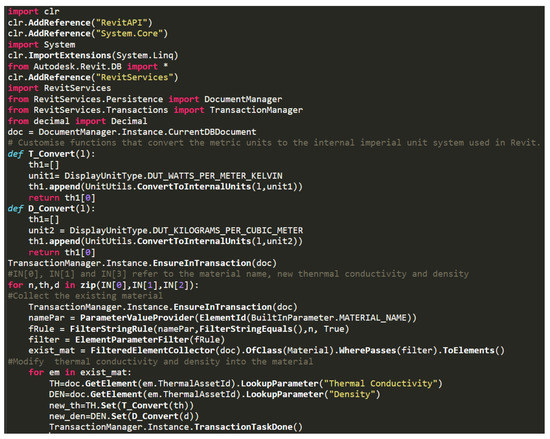
Figure A2.
Dynamo Python Script to Update Insulation Material Thermal Properties.
References
- International Energy Agency. 2019 Global Status Report for Buildings and Construction (p. 41). The Global Alliance for Buildings and Construction. 2019. Available online: http://wedocs.unep.org/bitstream/handle/20.500.11822/30950/2019GSR.pdf?sequence=1&isAllowed=y (accessed on 26 November 2020).
- Akbarnezhad, A.; Xiao, J. Estimation and Minimization of Embodied Carbon of Buildings: A Review. Buildings 2017, 7, 5. [Google Scholar] [CrossRef]
- Azari, R.; Abbasabadi, N. Embodied energy of buildings: A review of data, methods, challenges, and research trends. Energy Build. 2018, 168, 225–235. [Google Scholar] [CrossRef]
- Sierra-Pérez, J.; Rodríguez-Soria, B.; Boschmonart-Rives, J.; Gabarrell, X. Integrated life cycle assessment and thermodynamic simulation of a public building’s envelope renovation: Conventional vs. Passivhaus proposal. Appl. Energy 2018, 212, 1510–1521. [Google Scholar] [CrossRef]
- Thormark, C. A low energy building in a life cycle—Its embodied energy, energy need for operation and recycling potential. Build. Environ. 2002, 37, 429–435. [Google Scholar] [CrossRef]
- Treloar, G.J. Validation of the Use of Australian Input-Output Data for Building Embodied Energy Simulation. In Proceedings of the Eighth International Building Performance Simulation Association Conference on Building Simulation: For Better Building Design, Eindhoven, The Netherlands, 11–14 August 2003. [Google Scholar]
- Robati, M.; Daly, D.; Kokogiannakis, G. A method of uncertainty analysis for whole-life embodied carbon emissions (CO2-e) of building materials of a net-zero energy building in Australia. J. Clean. Prod. 2019, 225, 541–553. [Google Scholar] [CrossRef]
- Braulio-Gonzalo, M.; Bovea, M.D. Environmental and cost performance of building’s envelope insulation materials to reduce energy demand: Thickness optimisation. Energy Build. 2017, 150, 527–545. [Google Scholar] [CrossRef]
- Pacheco, R.; Ordóñez, J.; Martínez, G. Energy efficient design of building: A review. Renew. Sustain. Energy Rev. 2012, 16, 3559–3573. [Google Scholar] [CrossRef]
- Biswas, K.; Shrestha, S.S.; Bhandari, M.S.; Desjarlais, A.O. Insulation materials for commercial buildings in North America: An assessment of lifetime energy and environmental impacts. Energy Build. 2016, 112, 256–269. [Google Scholar] [CrossRef]
- Zheng, G.; Jing, Y.; Huang, H.; Gao, Y. Application of improved grey relational projection method to evaluate sustainable building envelope performance. Appl. Energy 2010, 87, 710–720. [Google Scholar] [CrossRef]
- Schiavoni, S.; D’Alessandro, F.; Bianchi, F.; Asdrubali, F. Insulation materials for the building sector: A review and comparative analysis. Renew. Sustain. Energy Rev. 2016, 62, 988–1011. [Google Scholar] [CrossRef]
- Office of Energy Efficiency & Renewable Energy. Insulation. Energy.Gov. Available online: https://www.energy.gov/energysaver/weatherize/insulation (accessed on 6 October 2020).
- Raouf, A.M.; Al-Ghamdi, S.G. Effect of R-values changes in the baseline codes: Embodied energy and environmental life cycle impacts of building envelopes. Energy Rep. 2020, 6, 554–560. [Google Scholar] [CrossRef]
- Crawford, R.H.; Stephan, A. The significance of embodied energy in certified passive houses. In Proceedings of the International Conference on Construction and Building Materials (ICCBM 2013), Hong Kong, China, 7–8 December 2013. [Google Scholar]
- Papadopoulos, A.M. State of the art in thermal insulation materials and aims for future developments. Energy Build. 2005, 37, 77–86. [Google Scholar] [CrossRef]
- Kymäläinen, H.-R.; Sjöberg, A.-M. Flax and hemp fibres as raw materials for thermal insulations. Build. Environ. 2008, 43, 1261–1269. [Google Scholar] [CrossRef]
- Hammond, G.; Jones, C.; Lowrie, F.; Tse, P. Building Services Research and Information Association, & University of Bath. In Embodied Carbon: The Inventory of Carbon and Energy (ICE); BSRIA: Bath, UK, 2011. [Google Scholar]
- Ürge-Vorsatz, D.; Khosla, R.; Bernhardt, R.; Chan, Y.C.; Vérez, D.; Hu, S.; Cabeza, L.F. Advances toward a Net-Zero Global Building Sector. Annu. Rev. Environ. Resour. 2020, 45. [Google Scholar] [CrossRef]
- Dombaycı, Ö.A. The environmental impact of optimum insulation thickness for external walls of buildings. Build. Environ. 2007, 42, 3855–3859. [Google Scholar] [CrossRef]
- Axaopoulos, I.; Axaopoulos, P.; Gelegenis, J.; Fylladitakis, E.D. Optimum external wall insulation thickness considering the annual CO2 emissions. J. Build. Phys. 2019, 42, 527–544. [Google Scholar] [CrossRef]
- Bojić, M.; Miletić, M.; Bojić, L. Optimization of thermal insulation to achieve energy savings in low energy house (refurbishment). Energy Convers. Manag. 2014, 84, 681–690. [Google Scholar] [CrossRef]
- Basbagill, J.; Flager, F.; Lepech, M.; Fischer, M. Application of life-cycle assessment to early stage building design for reduced embodied environmental impacts. Build. Environ. 2013, 60, 81–92. [Google Scholar] [CrossRef]
- Asl, M.R.; Zarrinmehr, S.; Bergin, M.; Yan, W. BPOpt: A framework for BIM-based performance optimization. Energy Build. 2015, 108, 401–412. [Google Scholar] [CrossRef]
- Wong, K.; Fan, Q. Building information modelling (BIM) for sustainable building design. Facilities 2013, 31, 138–157. [Google Scholar] [CrossRef]
- Krygiel, E.; Nies, B.; McDowell, S. Green BIM: Successful Sustainable Design with Building Information Modeling; John Wiley & Sons Incorporated: Hoboken, NJ, USA, 2008; Available online: http://ebookcentral.proquest.com/lib/unsw/detail.action?docID=362054 (accessed on 26 November 2020).
- Iddon, C.R.; Firth, S.K. Embodied and operational energy for new-build housing: A case study of construction methods in the UK. Energy Build. 2013, 67, 479–488. [Google Scholar] [CrossRef]
- Gbadamosi, A.-Q.; Mahamadu, A.-M.; Oyedele, L.O.; Akinade, O.O.; Manu, P.; Mahdjoubi, L.; Aigbavboa, C. Offsite construction: Developing a BIM-Based optimizer for assembly. J. Clean. Prod. 2019, 215, 1180–1190. [Google Scholar] [CrossRef]
- Cho, Y.K.; Alaskar, S.; Bode, T.A. BIM-Integrated Sustainable Material and Renewable Energy Simulation. Constr. Res. Congr. 2010, 288–297. [Google Scholar] [CrossRef]
- Autodesk. Preview of Autodesk Ecotect Analysis 2010|Search|Autodesk Knowledge Network. 2010. Available online: https://knowledge.autodesk.com/search-result/caas/video/youtube/watch-v-BKZ35xh4ofw.html (accessed on 26 November 2020).
- Jalaei, F.; Jrade, A. An Automated BIM Model to Conceptually Design, Analyze, Simulate, and Assess Sustainable Building Projects. J. Constr. Eng. 2014, 1–21. [Google Scholar] [CrossRef]
- Autodesk. Ecotect Analysis Discontinuation FAQ|Search|Autodesk Knowledge Network. Available online: https://knowledge.autodesk.com/search-result/caas/sfdcarticles/sfdcarticles/Ecotect-Analysis-Discontinuation-FAQ.html (accessed on 20 April 2016).
- Kim, H.; Shen, Z.; Kim, I.; Kim, K.; Stumpf, A.; Yu, J. BIM IFC information mapping to building energy analysis (BEA) model with manually extended material information. Autom. Constr. 2016, 68, 183–193. [Google Scholar] [CrossRef]
- Bank, L.C.; McCarthy, M.; Thompson, B.P.; Menassa, C.C. Integrating BIM with System Dynamics as a Decision-Making Framework for Sustainable Building Design and Operation; First International Conference on Sustainable Urbanization: Hong Kong, China, 2010. [Google Scholar]
- Stave, K.A. A System Dynamics Model to Facilitate Public Understanding of Water Management Options in Las Vegas, Nevada. J. Environ. Manag. 2003, 67, 303–313. [Google Scholar] [CrossRef]
- AnyLogic: Simulation Modeling Software Tools & Solutions for Business. 2020. Available online: https://www.anylogic.com/ (accessed on 26 November 2020).
- Thompson, B.P.; Bank, L.C. Use of system dynamics as a decision-making tool in building design and operation. Build. Environ. 2010, 45, 1006–1015. [Google Scholar] [CrossRef]
- Welle, B.; Haymaker, J.; Rogers, Z. ThermalOpt: A methodology for automated BIM-based multidisciplinary thermal simulation for use in optimization environments. Build. Simul. 2011, 4, 293–313. [Google Scholar] [CrossRef]
- National Renewable Energy Laboratory (NREL). EnergyPlus. 2020. Available online: https://energyplus.net/ (accessed on 26 November 2020).
- Larson, G.W.; Shakespeare, R.A. Rendering with Radiance. 2020. Available online: https://floyd.lbl.gov/radiance/book/index.html (accessed on 26 November 2020).
- Autodesk. Dynamo. Dynamo BIM. 2020. Available online: https://dynamobim.org/download/ (accessed on 26 November 2020).
- Shadram, F.; Johansson, T.D.; Lu, W.; Schade, J.; Olofsson, T. An integrated BIM-based framework for minimizing embodied energy during building design. Energy Build. 2016, 128, 592–604. [Google Scholar] [CrossRef]
- Shadram, F.; Mukkavaara, J. An integrated BIM-based framework for the optimization of the trade-off between embodied and operational energy. Energy Build. 2018, 158, 1189–1205. [Google Scholar] [CrossRef]
- Robert McNeel & Associates. Grasshopper—New in Rhino 6. 2018. Available online: https://www.rhino3d.com/6/new/grasshopper (accessed on 26 November 2020).
- Robert McNeel & Associates. Rhino Features. 2020. Available online: https://www.rhino3d.com/6/features (accessed on 26 November 2020).
- Kensek, K.M. Integration of Environmental Sensors with BIM: Case studies using Arduino, Dynamo, and the Revit API. Inf. De La Construcción 2014, 66, e044. [Google Scholar] [CrossRef]
- Asl, M.R.; Stoupine, A.; Zarrinmehr, S.; Yan, W. Optimo: A BIM-based multi-objective optimization tool utilizing visual programing for high performance building design. In Proceedings of the Conference of Education and Research in Computer Aided Architectural Design in Europe (ECAADe), Vienna, Austria, 16–18 September 2015; pp. 673–682. [Google Scholar]
- Lin, S.-H.; Gerber, D.J. Evolutionary energy performance feedback for design: Multidisciplinary design optimization and performance boundaries for design decision support. Energy Build. 2014, 84, 426–441. [Google Scholar] [CrossRef]
- Pilgrim, M.; Bouchlaghem, N.; Loveday, D.; Holmes, M. Towards the efficient use of simulation in building performance analysis: A user survey. Build. Serv. Eng. Res. Technol. 2003, 24, 149–162. [Google Scholar] [CrossRef]
- Autodesk. Revit|BIM Software|Autodesk Official Store. 2020. Available online: https://www.autodesk.com/products/revit/overview (accessed on 26 November 2020).
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Bolattürk, A. Determination of optimum insulation thickness for building walls with respect to various fuels and climate zones in Turkey. Appl. Therm. Eng. 2006, 26, 1301–1309. [Google Scholar] [CrossRef]
- Martínez, D.M.; Ebenhack, B.W.; Wagner, T.P. Chapter 8—Residential and commercial sector energy efficiency. In Energy Efficiency; Martínez, D.M., Ebenhack, B.W., Wagner, T.P., Eds.; Elsevier: Amsterdam, The Netherlands, 2019; pp. 227–269. [Google Scholar] [CrossRef]
- Bolattürk, A. Optimum insulation thicknesses for building walls with respect to cooling and heating degree-hours in the warmest zone of Turkey. Build. Environ. 2008, 43, 1055–1064. [Google Scholar] [CrossRef]
- Hasan, A. Optimizing insulation thickness for buildings using life cycle cost. Appl. Energy 1999, 63, 115–124. [Google Scholar] [CrossRef]
- Sisman, N.; Kahya, E.; Aras, N.; Aras, H. Determination of optimum insulation thicknesses of the external walls and roof (ceiling) for Turkey’s different degree-day regions. Energy Policy 2007, 35, 5151–5155. [Google Scholar] [CrossRef]
- Yu, J.; Tian, L.; Yang, C.; Xu, X.; Wang, J. Optimum insulation thickness of residential roof with respect to solar-air degree-hours in hot summer and cold winter zone of china. Energy Build. 2011, 43, 2304–2313. [Google Scholar] [CrossRef]
- Kośny, J.; Kossecka, E. Multi-dimensional heat transfer through complex building envelope assemblies in hourly energy simulation programs. Energy Build. 2002, 34, 445–454. [Google Scholar] [CrossRef]
- Dewsbury, M.; Wallis, L.; Fay, R.; Nolan, G. The Influence of Residential Framing Practices on Thermal Performance; ANZAScA: Lauceston, Australia, 2009; Volume 8. [Google Scholar]
- Natural Resources Canada. Tables for Calculating Effective Thermal Resistance of Opaque Assemblies. Available online: https://www.nrcan.gc.ca/energy/efficiency/housing/new-homes/energy-starr-new-homes-standard/tables-calculating-effective-thermal-resistance-opaque-assemblies/14176#a52 (accessed on 26 November 2020).
- Huang, Y.J.; Rosenfeld, A.H.; de Piedade, A.C.; Tseng, D. Energy efficiency in chinese apartment buildings: Parametric analysis with the DOE-2.1A computer program. In Proceedings of the First U.S.-China Conference on Energy, Resources, and Environment, Beijing, China, 7–12 November 1982. [Google Scholar]
- Kaynakli, O. A study on residential heating energy requirement and optimum insulation thickness. Renew. Energy 2008, 33, 1164–1172. [Google Scholar] [CrossRef]
- Australian Building Codes Board. National Construction Code NCC Volume One. 2016. Available online: https://ncc.abcb.gov.au/ncc-online/NCC/2016-A1/NCC-2016-Volume-One/Section-J-Energy-Efficiency/Specification-J16-Floor-Construction/1-Scope?inlineLink=%7B8210878D-AF74-4658-8AF1-90E3BD588813%7D (accessed on 26 November 2020).
- Lstiburek, J.; Baker, P. Measure Guideline: Incorporating Thick Layers of Exterior Rigid Insulation on Walls; U.S. Department of Energy’s Building America Program; Office of Energy Efficiency and Renewable Energy: Denver, CO, USA, 2015.
- American Society of Heating, Refrigerating and Air-Conditioning Engineers. ANSI/ASHRAE/IESNA Addenda to ANSI/ASHRAE/IESNA Standard 90.1-2007. 2008. Available online: https://www.ashrae.org/File%20Library/Technical%20Resources/Standards%20and%20Guidelines/Standards%20Addenda/90_1_2007_Supplement.pdf (accessed on 26 November 2020).
- Australian Bureau of Statistics. Environmental Issues: Energy Use and Conservation. 2008. Available online: https://www.ausstats.abs.gov.au/ausstats/subscriber.nsf/0/C70521268BC1B3D4CA25750E001131EF/$File/4602055001_mar%202008.pdf (accessed on 26 November 2020).
- Australian Building Codes Board. National Construction Code NCC Volume Two. 2019. Available online: https://ncc.abcb.gov.au/ (accessed on 26 November 2020).
- NCC|Australian Building Codes Board. 2020. Available online: https://ncc.abcb.gov.au/ (accessed on 26 November 2020).
- Hartikainen, M.; Miettinen, K.; Wiecek, M.M. Constructing a Pareto front approximation for decision making. Math. Methods Oper. Res. 2011, 73, 209–234. [Google Scholar] [CrossRef]
- Carlucci, S.; Cattarin, G.; Causone, F.; Pagliano, L. Multi-objective optimization of a nearly zero-energy building based on thermal and visual discomfort minimization using a non-dominated sorting genetic algorithm (NSGA-II). Energy Build. 2015, 104, 378–394. [Google Scholar] [CrossRef]
- Marios, T.; Kristoffer, N. Sustainable Design with Respect to LCA Using Parametric Design and BIM Tools. In Proceedings of the World Sustainable Built Environment Conference, Hong Kong, China, 5–7 June 2017. [Google Scholar]
- Jørgensen, E.F. What Is Orchid?—Dynamo Nodes. 2019. Available online: https://dynamonodes.com/2019/01/30/what-is-orchid/ (accessed on 26 November 2020).
- Department of Industry, Science, Energy and Resources. YourHome. 2020. Available online: https://www.yourhome.gov.au/ (accessed on 26 November 2020).
- Yumrutaş, R.; Ünsal, M.; Kanoğlu, M. Periodic solution of transient heat flow through multilayer walls and flat roofs by complex finite Fourier transform technique. Build. Environ. 2005, 40, 1117–1125. [Google Scholar] [CrossRef]
- Guan, L. Implication of global warming on air-conditioned office buildings in Australia. Build. Res. Inf. 2009, 37, 43–54. [Google Scholar] [CrossRef]
- Sustainability Victoria. Understand Heating Options for Your Home. 2020. Available online: https://www.sustainability.vic.gov.au/You-and-your-home/Save-energy/Heating/Choose-energy-efficient-heating (accessed on 26 November 2020).
- International Code Council Inc.; APA—The Engineered Wood Association. IECC Compliance Options for Wood-Frame Wall Assemblies. 2014. Available online: https://royomartin.com/wp-content/uploads/2017/01/IECC-Compliance-Options-for-Wood-Frame-Wall-Assemblies.pdf (accessed on 26 November 2020).
- Taitem Engineering. Multifamily Performance Program Technical Topic—New Buildings Calculating the U-Value of a Surface. 2008. Available online: https://www.taitem.com/wp-content/uploads/2011/01/TT-NC-Calculating-U-values-Nov-2008.pdf (accessed on 26 November 2020).
- Sirok, B.; Blagojevic, B.; Bullen, P. Mineral Wool: Production and Properties; Elsevier: Amsterdam, The Netherlands, 2008. [Google Scholar]
- Al-Homoud, M.S. Performance characteristics and practical applications of common building thermal insulation materials. Build. Environ. 2005, 40, 353–366. [Google Scholar] [CrossRef]
- Korjenic, A.; Petránek, V.; Zach, J.; Hroudová, J. Development and performance evaluation of natural thermal-insulation materials composed of renewable resources. Energy Build. 2011, 43, 2518–2523. [Google Scholar] [CrossRef]
- Corscadden, K.W.; Biggs, J.N.; Stiles, D.K. Sheep’s wool insulation: A sustainable alternative use for a renewable resource? Resour. Conserv. Recycl. 2014, 86, 9–15. [Google Scholar] [CrossRef]
- Bradford Gold Wall Batt Specifications. Bradford Insulation. 2020. Available online: https://www.bradfordinsulation.com.au/home-insulation/walls/gold-wall-batts/specifications (accessed on 26 November 2020).
- Knauf ClimaFoam® Insulation. Pricewise Insulation. 2020. Available online: https://pricewiseinsulation.com.au/product/knauf-climafoam-xps/ (accessed on 26 November 2020).
- Insulation Products|Knauf Insulation Australia. 2020. Available online: https://www.knaufinsulation.com.au/product (accessed on 26 November 2020).
- Bradford Insulation. Bradford Insulation for Homes with Metal Roofs—Specifications. 2020. Available online: https://www.bradfordinsulation.com.au/home-insulation/roofing/anticon/specifications (accessed on 26 November 2020).
- Pe, I.B.; Bjegovi, D.; Boström, L.; Milovanovi, B.; Hajdukovi, M. ETICS Fire Performance Test; Third ETICS Forum: Milan, Italy, 2015; Volume 10. [Google Scholar]
- Jelle, B.P. Traditional, state-of-the-art and future thermal building insulation materials and solutions—Properties, requirements and possibilities. Energy Build. 2011, 43, 2549–2563. [Google Scholar] [CrossRef]
- Wang, Y.; Huang, Z.; Heng, L. Cost-effectiveness assessment of insulated exterior walls of residential buildings in cold climate. Int. J. Proj. Manag. 2007, 25, 143–149. [Google Scholar] [CrossRef]
- Hammad, A.W.; Akbarnezhad, A.; Oldfield, P. Optimising embodied carbon and U-value in load bearing walls: A mathematical bi-objective mixed integer programming approach. Energy Build. 2018, 174, 657–671. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).