1. Introduction
Performances of public and private buildings in the last Italian seismic sequences have not been satisfactory since many structures and critical infrastructures like hospitals lost their serviceability, reporting significant damage up to the collapse [
1]. Strategies for interventions on large building stocks are available [
2] based on the results of comprehensive assessment programs put in place by the Italian Government through the Ordinance of the President of Council of Ministers (OPCM) 3274 [
3] regarding public buildings. More recently, financial incentive actions have been issued to promote the seismic/structural rehabilitation of private buildings paying attention to sustainable goals of modern societies in terms of energy efficiency. There are ideal conditions to invest in buildings’ renovation considering structural and energy upgrading needs of Italian buildings, with special attention to reinforced concrete (RC) ones, where most of the population lives.
The Italian RC residential stock is made of 3.7 million buildings according to the latest available Italian census [
4]. Overall, 55% of RC buildings were constructed before 1980 which is the year when a large part of the Italian territory became seismically classified. Hence, most of those buildings were designed without any seismic provision, with respect to gravity loads only. Further, a significant share of those RC frame buildings was realized using wide beams (having the depth equal to the slab thickness) for the internal spans, due to the architectural need of having a plane ceiling surface.
Several authors studied the performances of wide beams in RC frames [
5,
6,
7] finding some criticisms related to the reduced ductility in seismic conditions. In seismically designed buildings, the effect of reduced stiffness and strength of wide beams may be mitigated by a proper design of columns to fulfil requirements related to damage limitation states, for example, increasing the column cross section [
8,
9] to obtain a sufficient global stiffness. However, wide beams in gravity loads’ designed buildings or seismically designed with past codes have a reduced flexural strength that can be increased by a certain extent without changing the strength hierarchy with respect to columns, provided that an early joint shear failure can be excluded, as in most of the experimental tests carried out on non-seismically designed specimens [
10]. This means that columns are usually stronger than wide beams and a seismic upgrading in some cases can be obtained by only increasing the beams’ strength. However, considering the effect of slab on the beam flexural resistance, the additional increase due to a strengthening intervention only on the beam should be carefully evaluated in terms of strength hierarchy. Accounting for this, in [
11] an effort was made to optimize the beam’s detailing of newly constructed (code-conforming) interior wide beam–column joints in order to obtain a better performance under seismic actions. In [
12] an experimental program was carried out to investigate the cyclic behaviour of code-conforming exterior wide beam–column connections depending on the type of column (circular, rectangular) and the type of spandrel beam (shallow or deep).
Seismic upgrading solutions for wide beams must consider that the slab on both sides has the same thickness and installation of additional reinforcing elements cannot be made on the beam’s vertical sides, contrarily to what can be made in case of deep beams. In fact, other authors investigated the behaviour of wide beams strengthened with laminated CFRP (Carbon Fibre Reinforced Polymers) plates applied only on the bottom side, mainly intended as upgrading with respect to gravity loads [
13] even though such techniques were already extensively used for deep beam–column joints [
14,
15]. Additionally, in [
16] the research was focused on improving the flexural strength of reinforced concrete beams with near-surface mounted (NSM) CFRP bars using mechanical interlocking. The main goal was yet to improve the static monotonic loads’ resistance of RC wide beams. Some authors focused on checking the effectiveness of alternative materials for the flexural upgrading of RC beams using for example near-surface mounted aluminium alloy bars [
17] or basalt fibre fabric [
18]. In [
19] a strengthening system based on steel elements intended to shift the plastic hinge away from the joint core was developed.
This latter is more suitable for deep beam–column joints. A similar goal is pursued by haunch retrofit solutions [
20,
21,
22] that, by means of steel props and curbs connecting beam and column, can significantly improve concrete confinement and provide energy absorption due to their plastic deformation.
Some seismic strengthening systems were developed also through numerical simulations. In [
23] a finite element investigation was made to assess the potential effectiveness of CFRP laminates externally bonded to the beam in wide beam–column joints with an arrangement consistent with the real geometry and, then, feasible. Nevertheless, the experimental verification of applicability and effectiveness of (possibly) simple seismic strengthening techniques for wide beam–column joints is still necessary.
For these reasons, a part of a large experimental program carried out at the Laboratory of Structures of the University of Basilicata on beam–column joints was devoted to developing upgrading solutions for wide beam–column joints.
The experimental program was set to investigate the seismic performance of full-scale external beam–column joint specimen representative of subassemblies in existing RC frame buildings designed to either gravity or seismic loads. The experimental program is described in detail in [
24], which also report the analysis of test result and characterization of the seismic behaviour and damage mechanism on as-built specimens (i.e., not upgraded).
Non-satisfactory performances were observed due to the scarce capacity of dissipating seismic energy. In fact, bond-slip phenomena early affected the beam reinforcement located outside the column. Indeed, heavy pinching effects were observed as demonstrated by load–drift curves, as detailed in [
10,
24].
This means that seismic behaviour of wide beam–column joints is remarkably influenced by their geometry which is less efficient if compared to traditional joints with deep beams. The width of the beam, larger than the column one, causes remarkable decays of both strength and ductility due to the lack of anchorage for the beam rebars. Moreover, axial load has a role in the damage patterns, affecting the softening branch of the load–drift curve of wide beam–column joints as shown in [
24].
Therefore, by observing the damage mechanisms on the as-built specimens, two upgrading solutions were developed and applied to identical wide beam–column joint specimens. The techniques were derived from an upgrading technology, named CAM (Active Confining of Masonry) [
25] based on simple steel elements, tested by the authors on a deep beam–column joint [
26] with encouraging results. This paper describes the experimental program and discusses the results of the experimental tests in terms of effectiveness and applicability of CAM strengthening technique to wide beam–columns joints.
2. Steel Jacketing of RC Wide Beams
The CAM (Active Confinement of Masonry) technique was originally thought and developed for seismic upgrading interventions on masonry buildings. Afterwards, it was applied to RC elements [
27], to take advantage of its confining properties especially related to column elements [
25,
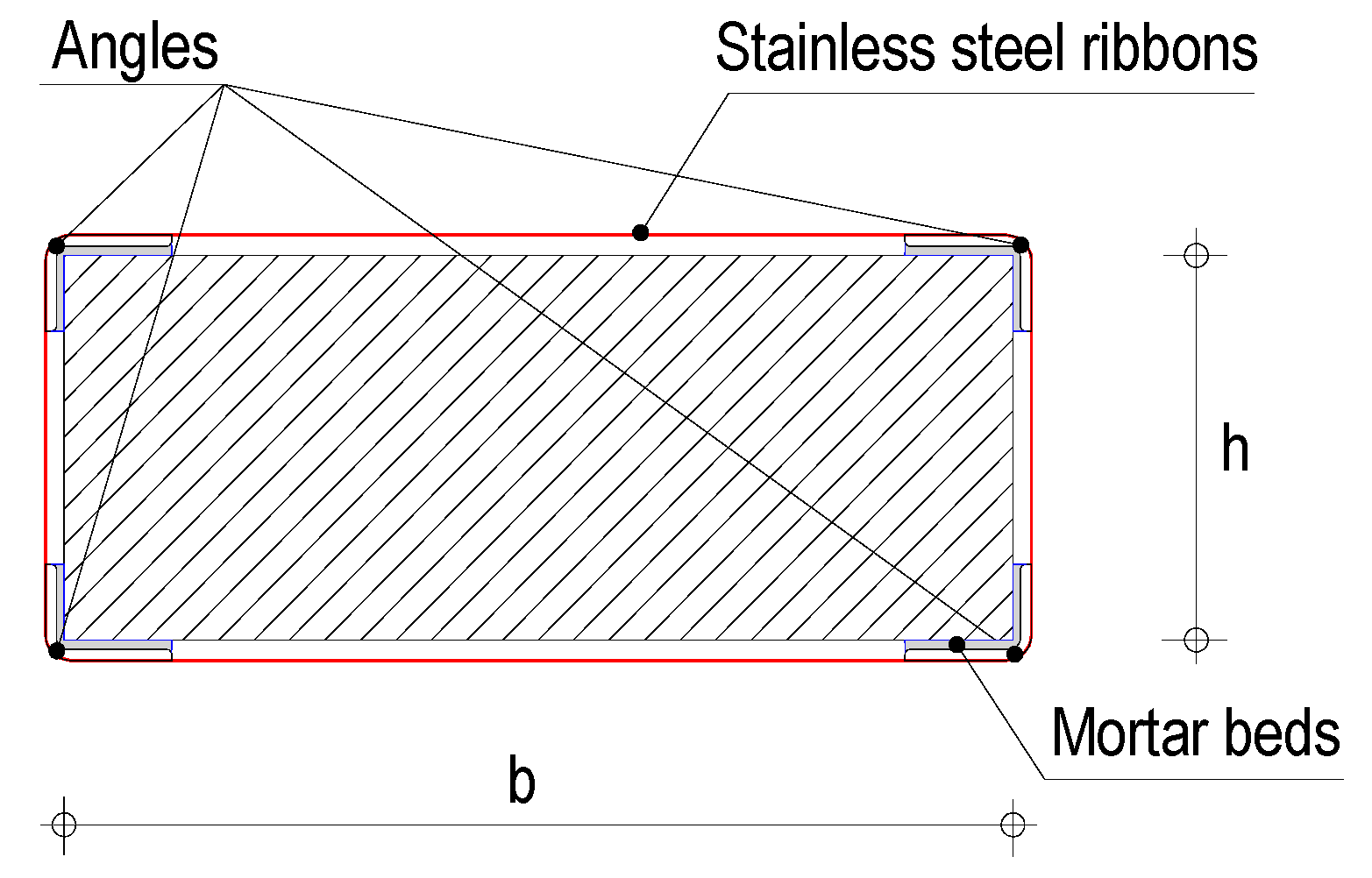
27] working as a jacketing system. In fact, CAM is a jacketing system composed by steel angles located at the cross-section corners (
Figure 1), enveloped by stainless steel ribbons able to provide confinement effects to the concrete and additional shear resistance as also suggested by EC8 [
28].
The effect of the wrapping ribbons is also intended to drastically reduce bond-slips of angles reducing global strength decays. However, in order to exploit the flexural strength increase, angles must be effectively connected to the framing members [
26].
Jacketing interventions through the CAM system differ from traditional ones for the presence of ribbons instead of steel plates connecting the angles. Ribbons are flexible, easy, and fast to apply during strengthening works [
29]. They are applied through a specific tool able to provide them with the required pre-stress. The presence of mortar beds between angles and corners of RC members is necessary to avoid stress concentrations and obtain an effective connection between them. Moreover, apparent corrosion problems [
30] related to the interaction of stainless and structural steel, are negligible due to the reduced contact surface between the different materials, which allows a proper life span [
31].
The proposal of applying the CAM system to wide beam–column joints is related to the fact that in both gravity loads designed and seismically designed RC frame buildings, generally speaking, the column is stronger than the beam (due to the small depth of the beam). This allows increasing the beam flexure strength (and the whole frame lateral load carrying capacity) without triggering detrimental column mechanisms [
10]. Therefore, upgrading interventions could be made, to some extent, by only acting on the beam, with feasible strengthening techniques.
The main design problem is the evaluation of the steel angles’ cross section working as additional longitudinal reinforcement for the beam with the condition of avoiding yielding phenomena in the column rebars, complying with capacity design principles.
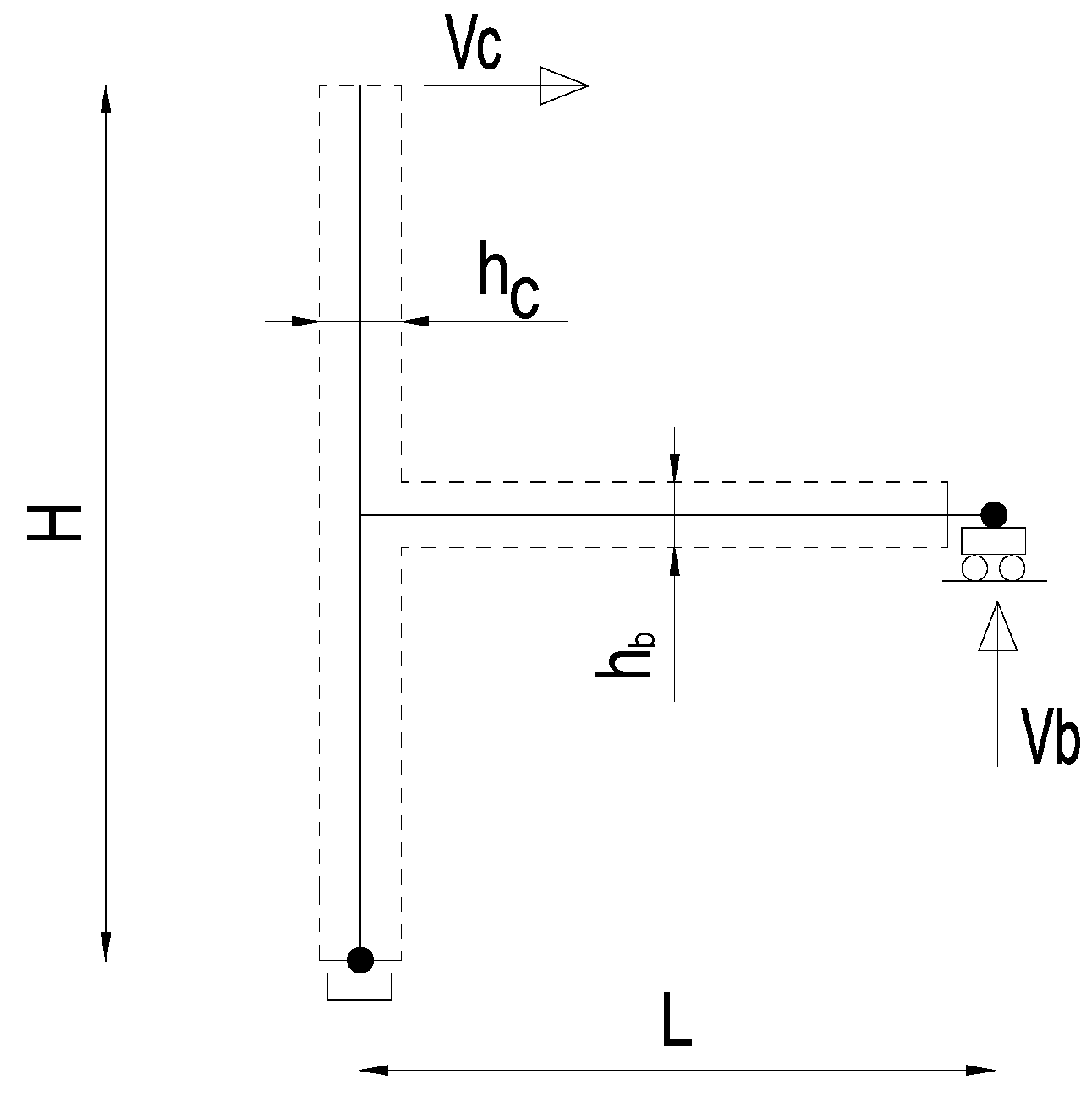
Referring to
Figure 2, the maximum column shear
Vc depends on the yielding moment of the column itself
Myc according to rotation equilibrium condition.
Then, the required beam’s resisting moment in the upgraded (u) condition can be computed as when and are small in comparison to, respectively, L and H.
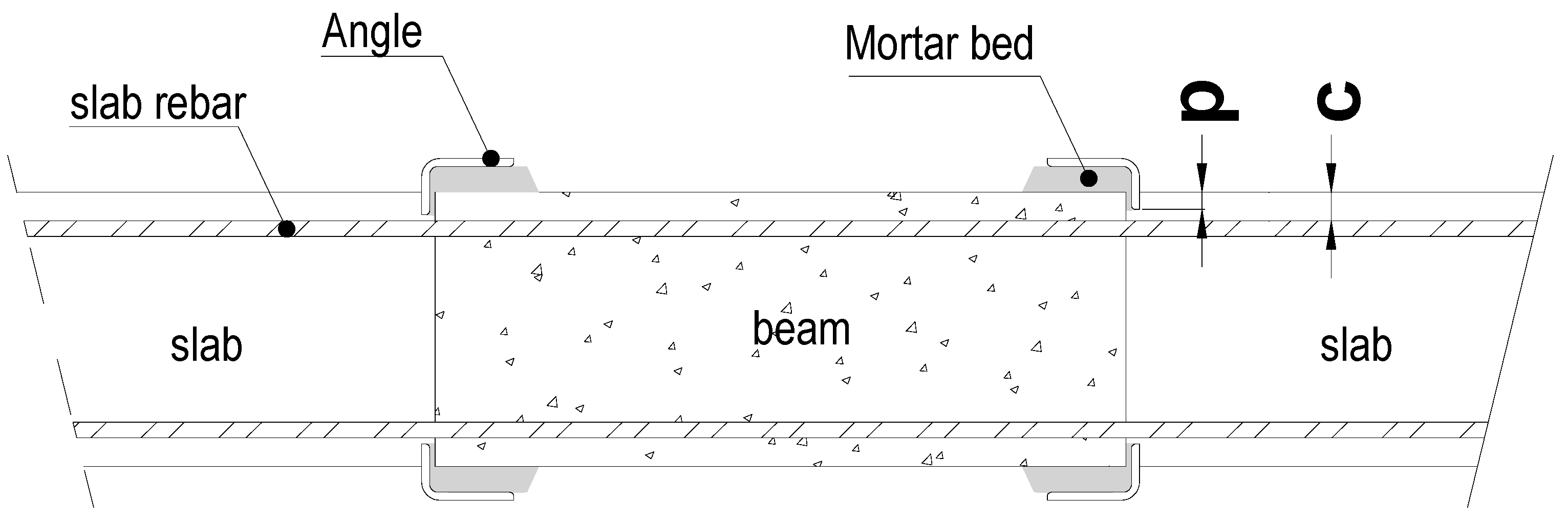
In real situations it is preferable to choose angles with different side sizes to obtain a feasible arrangement of the system. In fact, the beam is usually cast monolithically with slab and, therefore, placing the steel angles requires attention to the slab reinforcement crossing the beam.
Figure 3 shows the arrangement of angles in order to avoid interference between angles and slab reinforcement that needs to be surveyed before installing the strengthening system.
Layers of high-strength cement mortar (eventually fiber-reinforced) must be placed at each beam corner to work as supporting beds for angles and avoid excessive penetration of the vertical angles’ sides in the slab thickness. Therefore, the penetration
p inside the slab thickness must be smaller than the cover
c of the slab rebars, as shown in
Figure 3. Mortar beds are also able to evenly distribute the pressure between angles and the beam corners.
Finally, it is worth noting that the installation of the stainless-steel ribbons requires the presence of vertical holes in the slab to connect the upper and lower sides of the beam.
3. Experimental Program
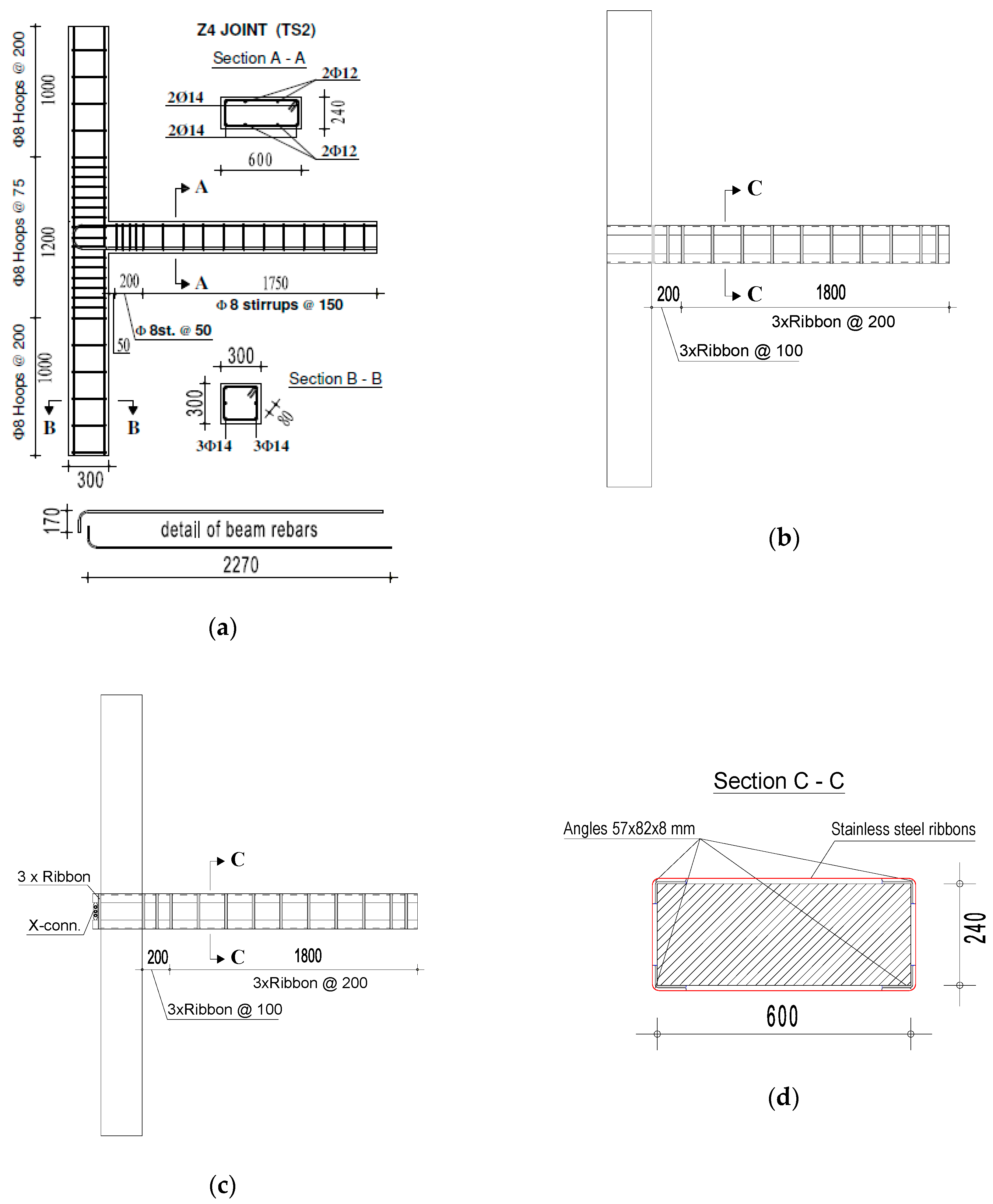
For the scope of this study, three identical samples (
Figure 4a) are considered: one representing the unstrengthened case (named TS2, no upgrading was applied), two additional specimens (named TS9 and TS10) equipped with different versions of CAM applied to the beam.
The exterior beam–column joint prototype (
Figure 4a) belongs to an internal frame of an RC 4-storeys building having story height of 3.2 m. The wide beam has width equal to 600 mm and depth of 240 mm while the column has square cross Section 300 × 300 mm
2. The beam is provided with four rebars at both the top and the bottom of the cross section, two of which are anchored in the column core and the remaining are out of the confined beam–column joint.
Electromagnetic scanning investigation on specimens allowed to check the position of steel cages compared to the design provision. Few differences were found about the concrete cover size of the beam longitudinal rebars. Larger cover values for the top and the bottom (80 and 40 mm, respectively) rebars were found for all the three specimens.
The specific axial load was set equal to ν = 0.15, where ν = N/( (N is the axial load, b and h are width and height of the column section, and fcm is the mean cylinder compressive strength of concrete).
The subassemblies details matched those prescribed for structures located in the lowest seismicity zone (Z4), where the design peak ground acceleration ag is equal to 0.05 g. Although the specimens were seismically designed, steel reinforcement was almost the minimum requested by the seismic code.
The materials’ mechanical properties (concrete and steel) of the three specimens, were assessed before the seismic tests. Cubic concrete samples were collected during casting and subjected to standard compression tests. The mean cylinder strength was
fcm equal to 21.5 MPa with negligible variation among the three specimens. As for the steel, the mean value of yielding stress was
fy = 480 MPa, while the failure stress was found to be equal to
ft = 590 MPa. Ductility of steel was characterized by the failure strain
εu = 11.4%. Hence, the used steel matched the class B450C according to the current Italian structural code [
32] and the hot rolled steel of class C according to EC2 [
33]. The adopted stainless steel for ribbons was of class C1000 according to UNI-EN 10088-4 [
29] with yielding stress
fys = 240 MPa and failure stress
ftk = 540 MPa.
The idea of upgrading only on the beam was based on the observation that the as-built specimen previously tested showed a weak beam-strong column mechanism [
10]. Therefore, it is possible to increase only the beam strength while guaranteeing that the column remains “strong” in the upgraded condition, according to
Section 2. The two different versions of the upgrading system do not differ in terms of angles cross section area but only in terms of confinement ribbons arrangement as shown later. Then, the design of steel angles is made in the same way as follows.
Remembering that and considering the material properties, geometry and detailing reported above, the required beam resisting moment is = 190 kNm. The maximum resisting moment of the beam in the as-built condition is the sagging one (causing tensile stresses in the bottom rebars) equal to MRd = 61 kNm.
The area of structural steel to be added under the shape of angles to increase MRd up to MRd−u can be computed by the ultimate limit state method. In doing this, it must be considered that structural steel (class S355 according to EC3) of angles has a yielding stress fyk = 355 MPa smaller than the yielding stress of rebars fy = 480 MPa with a ratio ρy = fy/fyk = 1.35.
The required angles’ area is Aa = 16.44 cm2 that multiplied by ρy leads to an effective area Aa,eff = 22.00 cm2 corresponding to two angles 57 × 82 × 8 mm that must be placed at bottom corners of the beam. The same elements are placed at the top corners.
Figure 4b and
Figure 5 show the configuration of TS9 upgrading system. The angles have dimensions 57 × 82 × 8 mm and are made of steel class S355 with yielding stress equal to
fyk = 355 MPa.
They are laid on the beam corners and enveloped with assemblies of three superimposed stainless-steel ribbons, with spacing variable in the range 100–200 mm. The ribbons are provided with 19 × 0.9 mm section and are prestressed at about 150 MPa by means of an automated tool. It is worth noting that no ribbons are placed in the beam–column intersection region. In correspondence to the back end of the beam, steel plates welded to the angles (
Figure 5b) provide some passive confinement effect and further anchorage to the angles in case of slippage phenomena.
In
Figure 4c and
Figure 6, TS10 strengthening configuration is shown, being similar to that one of TS9 specimen.
The only important change is related to ribbons placed at the back end of the beam. As can be seen, angles are enveloped by three additional superimposed ribbons providing an active confinement action in a high stress region, when subjected to seismic loads. To allow these ribbons to be placed, angles were 60 mm longer with respect to the back end of the beam (
Figure 4c and
Figure 6a).
Further, to avoid overstressing of steel angles, on the beam’s back end X-shaped steel devices were placed (
Figure 6b).
These latter can yield in case of bond-slip affecting angles, in order to limit force applicable to the beam back ends.
Test Apparatus
In order to simulate seismic loads, experimental tests were performed applying horizontal displacements at the upper end of the column (
Figure 7).
The boundary conditions were devoted to obtaining stresses distributions like those in moment resisting frames when subjected to seismic loads. All the tests were made by holding always the same value of axial load on the column (equal to 15% of the ultimate value, i.e., N = 290 kN), which was applied by a hydraulic jack placed in vertical position. The apparatus for the application of axial load was realized to have at every time the same inclination of the column, in order to avoid dangerous p-delta effects. Tests were cyclic quasi static, and displacement controlled according to a rate of 4 mm/s. The total drift in terms of ratio between displacement and height of the subassemblies, was equal to 0.06, 0.25, 0.50, 0.75, 1.00, 1.25, 1.50, 2.00, 2.50, 3.00, 3.50, 4.00%. To monitor the specimens’ behaviour, three load cells recorded the axial load acting on the column, the beam reaction, and the horizontal force exerted by the actuator on the upper end of the column.
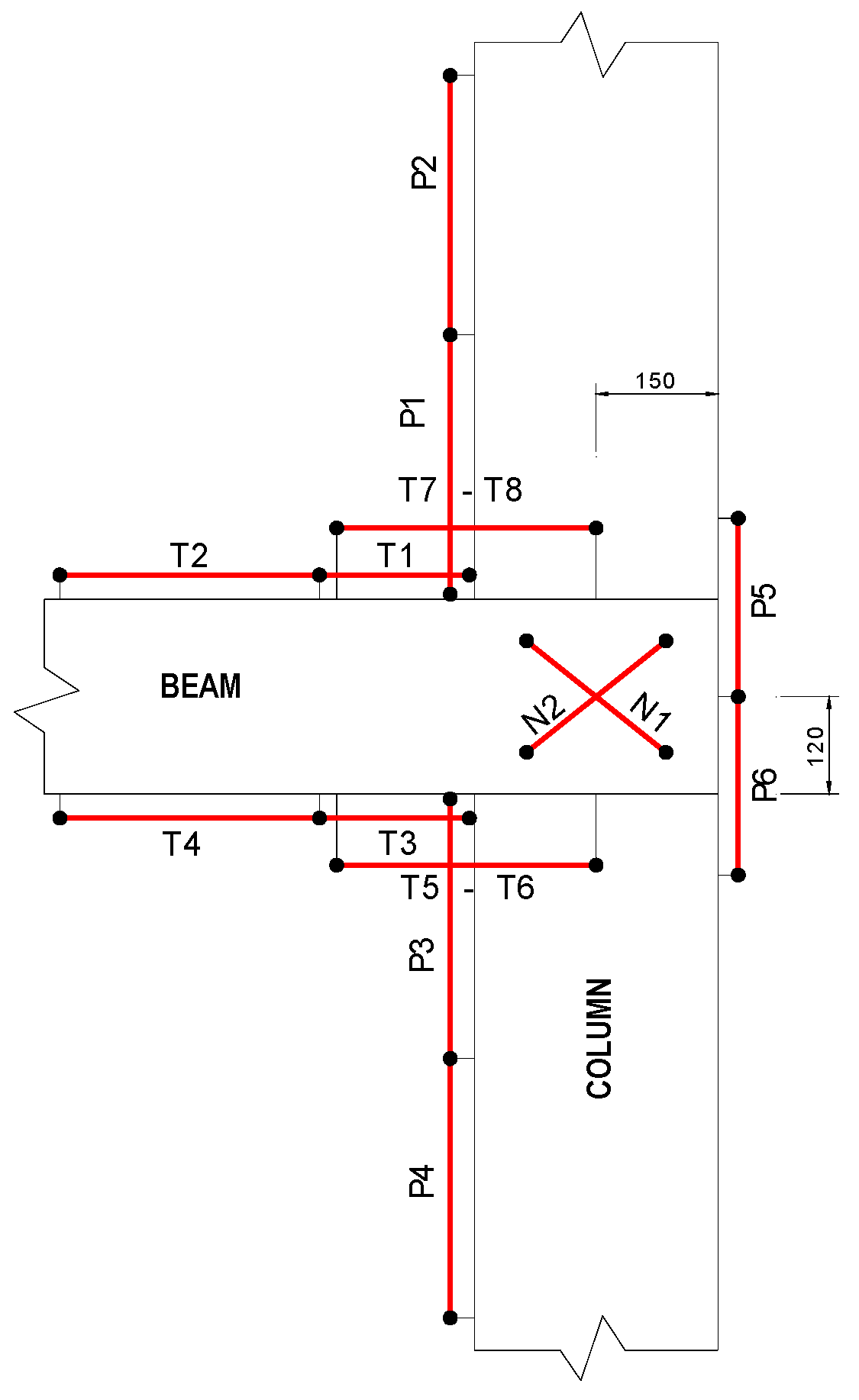
Deformations were monitored through six transducers (LVDTs) placed on the column (P1–P6 in
Figure 8), 8 on the beam (T1–T8), and 4 on the beam sides into the column depth (N1–N4).
Further information related to the test apparatus can be found in [
10].
4. Analysis of Results
This section is devoted to illustrating and discussing the damage mechanisms observed during the experiments as well as quantifying the seismic performance increase in terms of lateral load-carrying capacity and energy dissipation provided by the upgraded specimens.
4.1. Damage Mechanisms
Even though a brittle post-peak behaviour was observed for all the specimens, being the damage essentially concentrated on the beam, a strong column-weak beam post-elastic behaviour was observed in accordance with the code prescriptions.
Figure 9 shows the cracks on one side of the subassemblies after the tests imposing a drift equal to 3%.
Two sub-vertical cracks are observed in TS2 (unstrengthened) specimen, highlighting damage effects related to flexure stresses on the beam. Because of the upgrading intervention, TS9 and TS10 did not show this kind of damage.
Concerning the sides of the beam within the beam–column intersection, all specimens were affected by inclined cracks due to high shear stresses generated by beam rebars, the absence of the confining effect due to the compressive axial load, and of specific confining reinforcement. The latter is mainly responsible of the load drop after the peak in all the specimens. In fact, damage on beam’s sides did not allow the beam rebars (and angles in upgraded specimens) working properly, causing a strength degradation.
Although similar crack patterns were observed, significant differences were found in their extent.
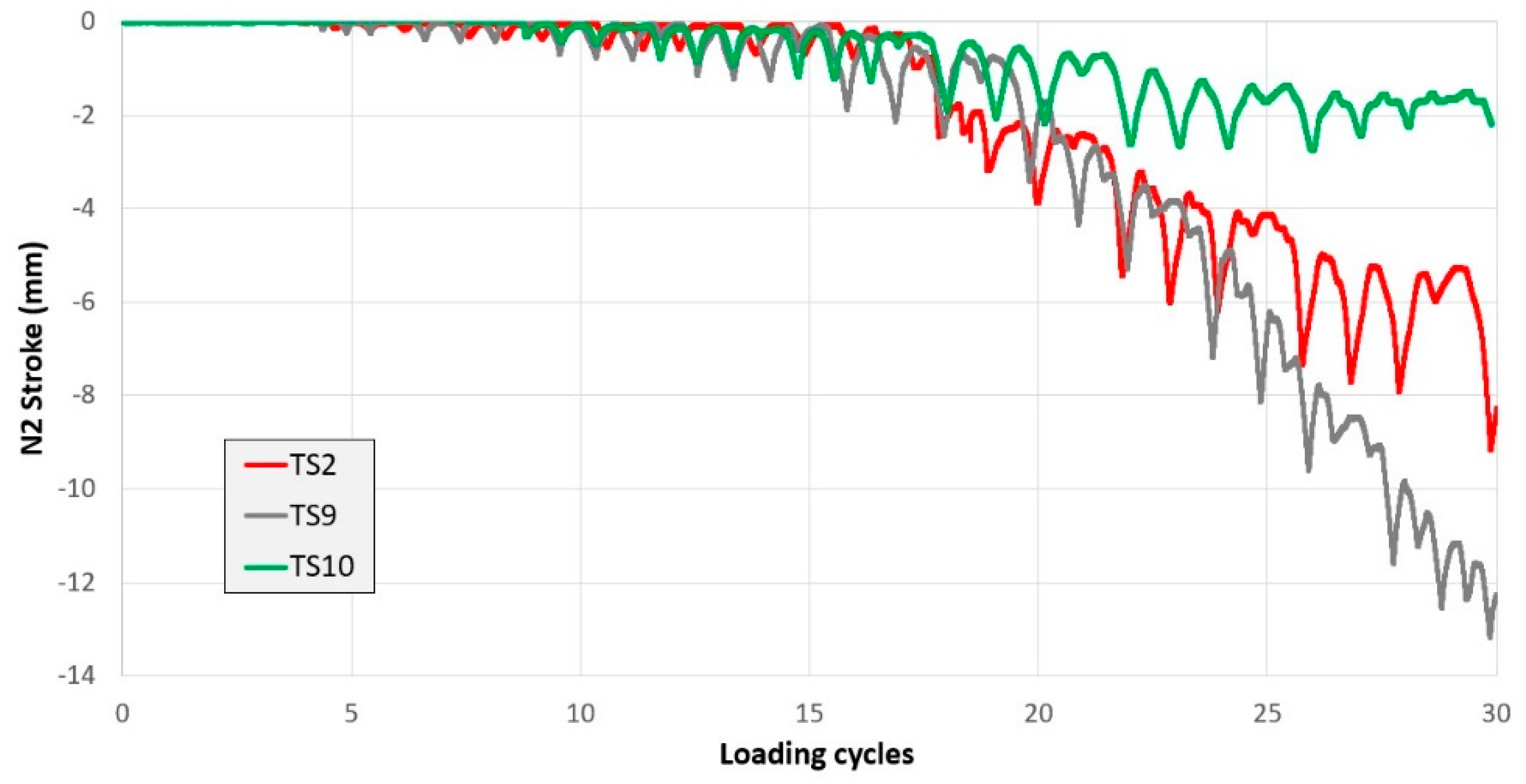
Figure 10 displays the stroke of LVDT named N2 (see
Figure 8) representing the diagonal deformation of the beam side as function of the number of loading cycles performed between drift values of 0.50% and 4% (three cycles are carried out for each drift amplitude with 30 cycles in total) where stroke values (elongation/shortening measured by the LVDT) were not negligible.
As can be seen, TS2 and TS9 specimens show the largest stroke values indicating a high crack opening that reach 13.5 mm for TS9 and 9.0 mm for TS2 with a marked divergent trend. The diagonal deformation in the examined region of TS9 is even larger than that of TS2 due to the increased resisting moment of the beam in absence of an effective concrete confinement where rebars and angles are anchored.
On the contrary, specimen TS10 shows significantly better results with a maximum diagonal deformation of about 2.5 mm with much less divergence of the crack opening, indicating that the rear stainless-steel ribbons have a great influence on the damage extent. This is even more surprising considering that TS10 provides better seismic performance of TS9 and, obviously, TS2. This is confirmed by the side views in
Figure 9 where TS10 shows less damage than other specimens with fewer cracks of small opening while TS2 shows spalling phenomena and TS9 has more cracks and a near spalled region at the rear end of the beam.
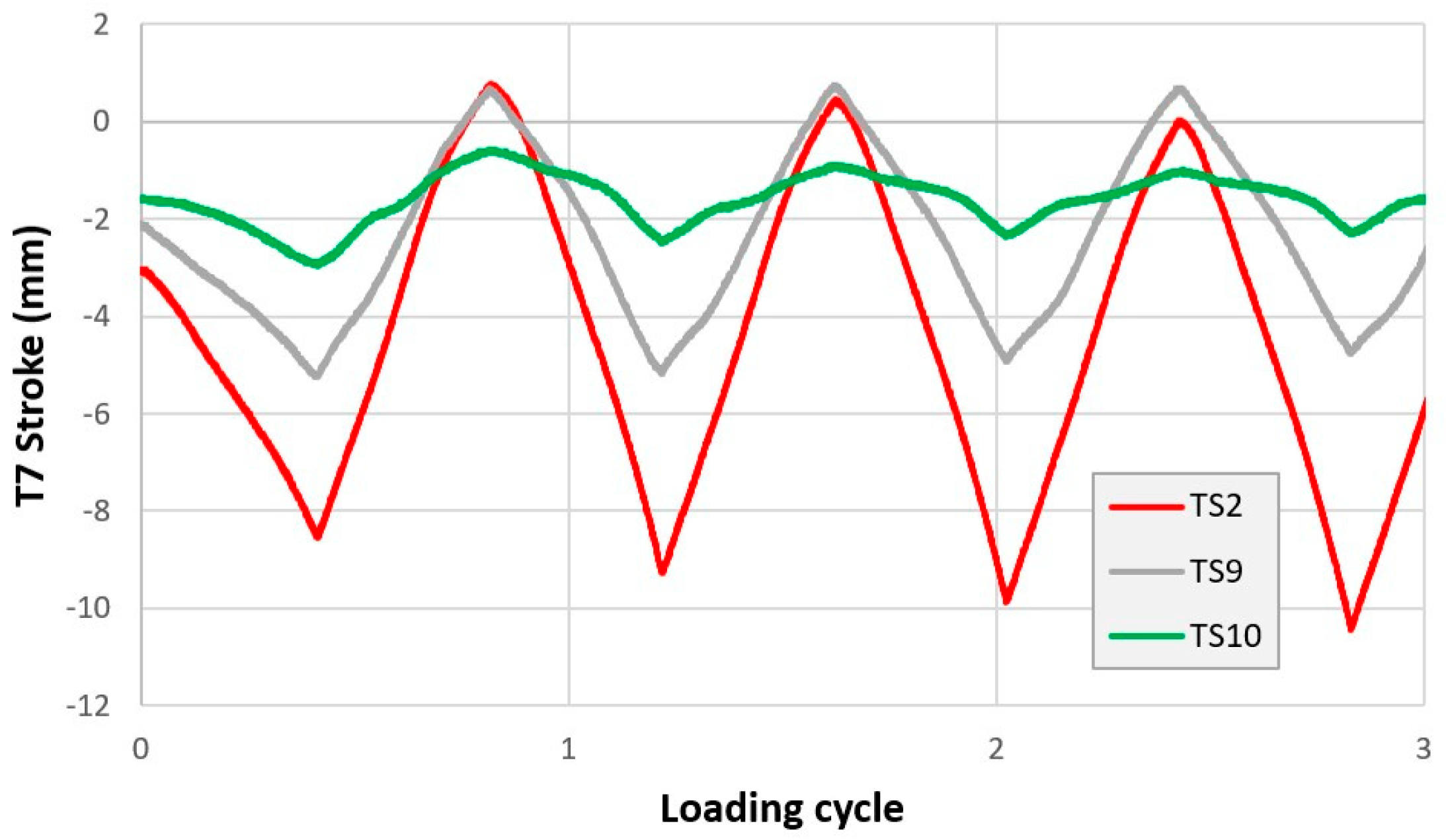
To better understand these aspects,
Figure 11 shows the stroke recorded by LVDT “T7” (negative values are elongations) being proportional to the beam deformation at interface with column, during the tests on the three specimens at a drift value equal to 3.0%.
As can be seen, specimen TS9 shows a smaller beam rotation compared to TS2, which is counterbalanced by the larger diagonal deformation previously highlighted. Moreover, TS10 shows a furtherly smaller beam rotation than TS9. This means that, based on the same total imposed drift (3.0%), TS10 experiences a larger column deformation. In agreement with the latter, looking to the column members, TS2 shows absence of cracks, while TS9 and TS10 show some cracks due to the higher flexural strength of the beam, determining higher moment stresses in columns and related deformations.
4.2. Seismic Performances
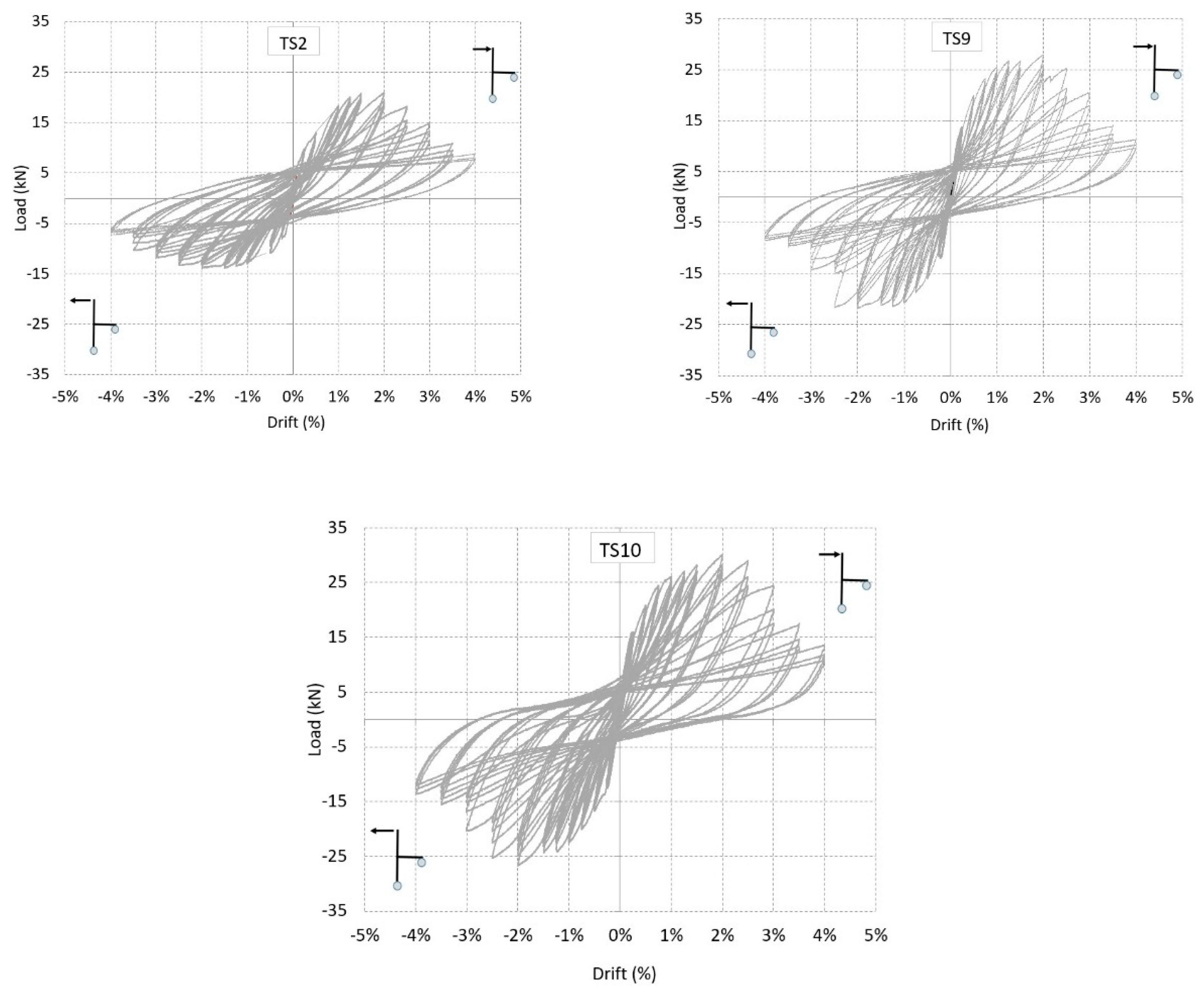
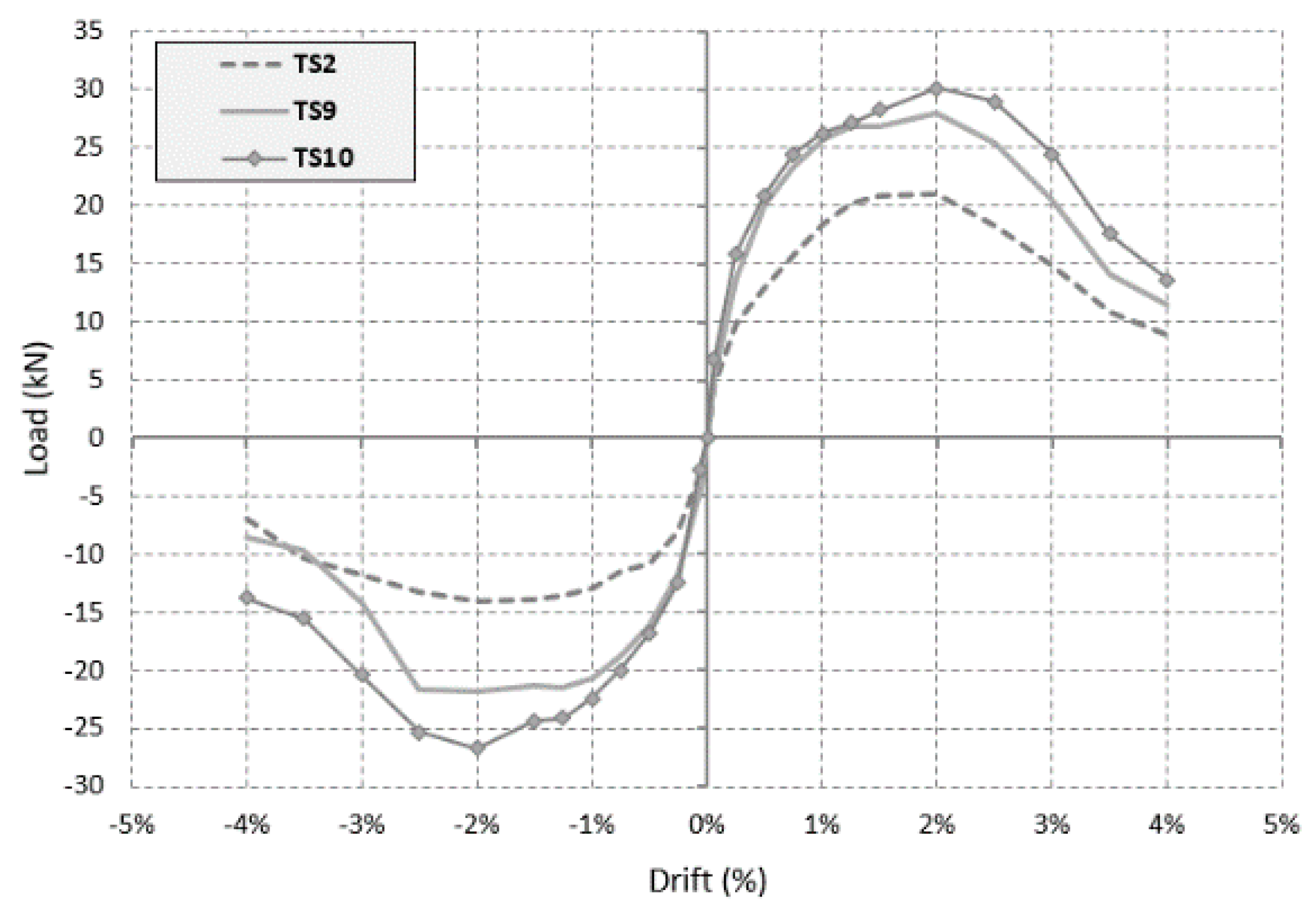
The seismic behaviour of investigated specimens is firstly evaluated in terms of load–drift envelopes (i.e., lateral load vs. drift). To this end, the main results (depicted in
Figure 12) are also summarized in
Table 1, in terms of maximum and minimum load values
Fmax and
Fmin, respectively (positive loading is such that the beam is subjected to sagging moment, i.e., tensile stress in the bottom rebars); drift values at which
Fmax and
Fmin are achieved, namely
d(
Fmax) and
d(
Fmin); ultimate positive (
du+) and negative (
du-) drift values.
Further, the ratio between maximum,
Fmax/
Fmax_TS2, and minimum,
Fmin/
Fmin_TS2, loads observed in the upgraded subassemblies compared to that of specimen TS2 are reported in
Table 1. Firstly, it must be noted that behaviour of the three specimens is not symmetric, with significant differences between max and min load values. This depends on the difference in terms of the beam rebars’ concrete cover as mentioned before. However, asymmetry is smaller for upgraded specimens.
The ultimate drift
du was conventionally evaluated according to [
34] as that drift value where a strength decay of 20% is found compared to the maximum force.
Table 1 also shows that the increase of the maximum load values due to the upgrading systems is significant. For positive loads, subassemblies TS9 and TS10 show increases of 33% and 43% compared to TS2, respectively.
For negative load, the capacity increase is even larger and equal to 56% for TS9 and 92% for TS10. Looking at
Figure 13, significant force increments for the strengthened specimens can be noted also for low drift values (less than 1.0%).
This latter is due to the delayed cracking of the beam’s cross section and has significant benefits in terms of whole stiffness. Therefore, the strengthened specimens are expected to behave much better also with respect to damage limitation states providing an appreciable reduction of damage to non-structural components (e.g., infills).
In terms of ultimate deformation capacity du, small differences between unstrengthened and strengthened specimens are observed: ultimate drift values do not exceed 3.2% and the maximum value is achieved by TS2 specimen for negative loads.
It can be noted that the response of the two upgraded subassemblies (TS9 and TS10) is similar until the drift is below 1.0%. Afterwards, the heavier damage in the angles’ anchorage zone influenced the flexural resistance of the beam and, therefore, the capacity of TS9 subassembly.
Due to this, the load carrying capacity of specimen TS9 rapidly reduces (especially for negative loading), because of the reduced efficiency of upper steel angles. This did not happen to TS10 specimen, due to the presence of additional ribbons placed at the back end of the beam, able to strongly reduce bond-slip effects and providing beneficial confinement to the beam–column intersection.
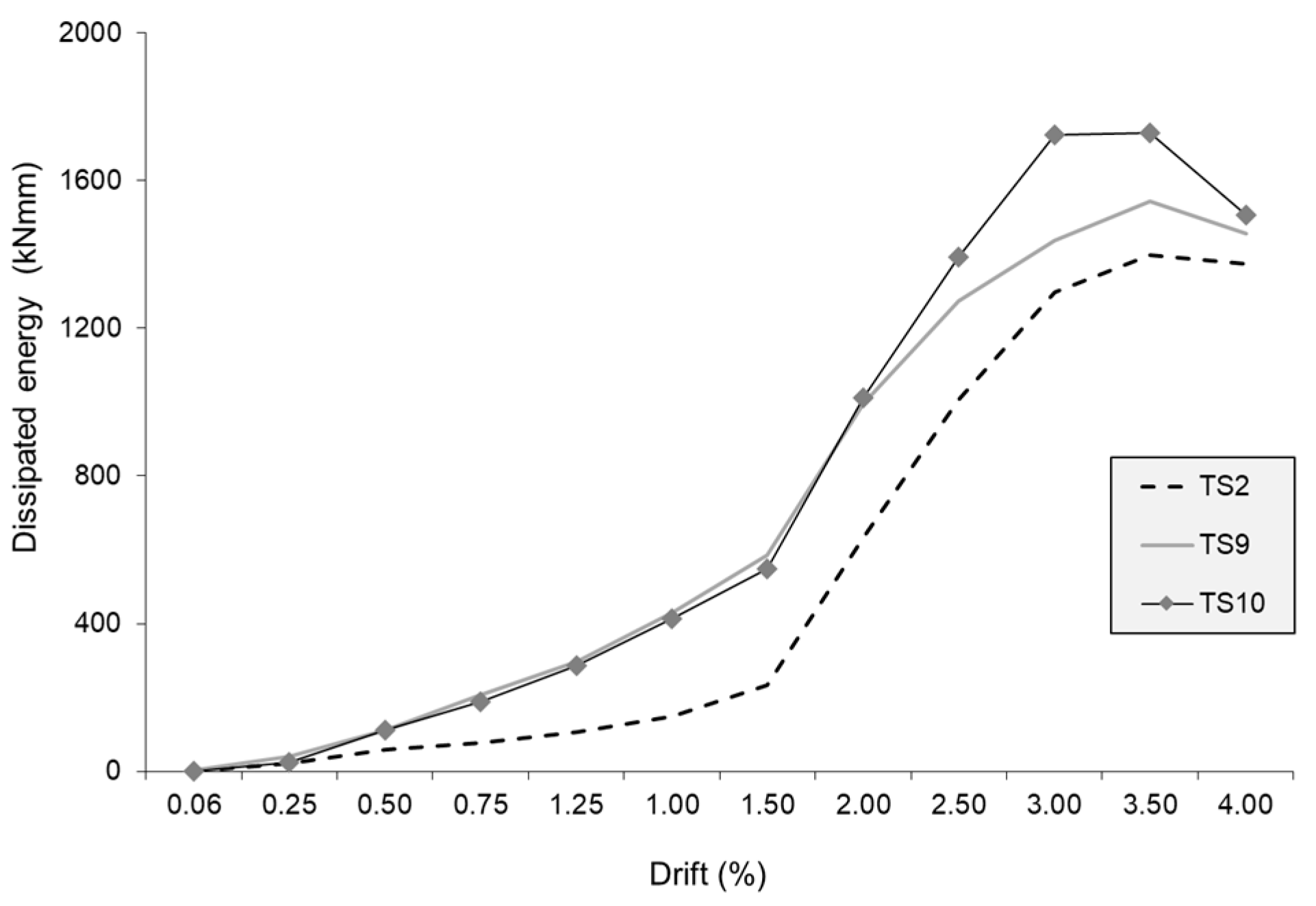
Figure 14 shows the dissipated energy computed as the average value among the three load cycles performed at each drift level.
The strengthened specimens dissipate much more energy than the benchmark specimen (TS2), even for low drift values (less than 1.50%). Above 2.0% drift, the dissipated energy significantly increases for all the specimens due to yielding of beam longitudinal rebars. Energy of TS9 starts to differ from TS10 due to the above-mentioned heavier damage, although it remains higher than that of TS2. From the energy dissipation point of view, the strengthening solution of specimen TS10 shows better performances and clearly points out the importance of providing an active confinement also in the rear part of the beam whenever possible.
4.3. Design Recommendations
Experimental results clearly show that the proposed retrofit solutions are effective in increasing the seismic performance of investigated specimens without modifying strength hierarchy between beam and column, although this should be always object of careful evaluations in order to avoid detrimental effects. The solution proposed for specimen TS10 shows that it is of paramount importance using measures to provide confining effects in the rear part of the beam, where steel angles are anchored. This can have a beneficial influence on the post-peak behaviour and energy dissipation, making this solution preferable compared to that one applied to specimen TS9. From a design perspective, for the beam–column joints here studied, the beam resisting moment in the upgraded condition
has been computed in order to not exceed the value needed to yield the column member. This latter derived from simple equilibrium conditions. Therefore, the area of steel angles can be calculated in order to achieve a resisting moment of the beam equal to
. In doing this, using the Ultimate Limit State calculations for RC sections in case of flexure, it is necessary to remember that angles are usually made of ordinary steel while ribbed reinforcing bars are of a different grade normally provided with different strength (see
Section 3). It means that a homogenization coefficient should be used to convert angles area in rebars area.
Finally, to propose a complete upgrading solution, details of application have also been reported, paying attention to the real feasibility of the strengthening solution. Careful evaluation of the slab rebars’ concrete cover must be performed before starting to apply the strengthening techniques, and high-strength concrete beds must be realized to position angles in the right way and avoid stress concentrations. The proposed strengthening solution can significantly upgrade seismic capacity of wide beam–column joints even though design calculation should be based on a Knowledge Level 3 (KL3, [
28,
32]), i.e., the maximum. This is because the details and material properties of RC members and, especially of the column, should be free of uncertainties, in order to obtain reliable design calculations, avoiding weak-column behaviour.
5. Conclusions
The main aim of this study is to explore the possibility of applying the steel jacketing technique to strengthen wide beams in RC frame buildings by using the well-known CAM system. Specifically, the proposed approach is based on exploiting the exceedance of flexural strength that columns typically have with respect to framing wide beams. This allows upgrading only the beams, resulting in a simpler and cheaper seismic strengthening.
After a description of the design procedure, the results of experimental tests on three full scale RC wide beam–column joints are presented and discussed, pointing out the performances of two versions of CAM-like jacketing system purposely arranged in configurations suitable for wide beams.
Test results show that:
Seismic performances of strengthened specimens (in both TS9 and TS10 configuration) significantly improved, especially in terms of lateral load carrying capacity;
Strengthened specimens show higher stiffness and therefore are expected to behave better also with respect to damage limitation states, thus providing a remarkable damage reduction to non-structural components (e.g., infills);
Upgraded specimen TS10 shows lower damage without nearly spalled regions that were found instead for specimen TS9. This is also confirmed by the diagonal deformation measured on the beam sides, whose values were much lower for TS10 specimen;
Consequently, the strengthening arrangement adopted for TS10 is more effective due to the active confinement provided in the rear part of the beam. This determines peak load increases equal to 43% and 92% for positive and negative loading direction, respectively. TS9 provides lower peak load increases equal to 33% and 56% due to the earlier damage and consequent strength degradation;
The strengthened specimens show remarkable increases also in terms of dissipated energy even for low drift values and, once again, the solution applied to specimen TS10 appears better than TS9.
In summary, the upgrading solution for RC wide beam–column joints here proposed is feasible and effective. When needed, strengthening only beam members is practicable, even though a careful evaluation of the capacity design principles is required to guarantee the strong-column condition according to the proposed design method and recommendations. In case column members were not provided with enough flexural strength, some intervention should be carried out also on them, however the intervention details here provided for wide beams remain valid and generally applicable. Future research developments, based on experimental tests and/or numerical simulations, can help to improve applicability and effectiveness of the proposed technique. Mainly, they would consist of: (i) investigating on the role of the adjacent RC slab, (ii) limiting damage at beam sides due to anchorage action of steel angles.