Experimental Study of Thermal Buoyancy in the Cavity of Ventilated Roofs
Abstract
1. Introduction
1.1. Pitched Wooden Roofs
1.2. Driving Forces
1.3. Previous Research
1.4. Knowledge Gap
1.5. Objectives and Scope
- How are the temperature conditions in the air cavity related to the air cavity design?
- How is the airflow through the cavity influenced by the air cavity design?
- To what degree may thermal buoyancy drive airflow in the air cavity?
2. Theoretical Framework
3. Methods
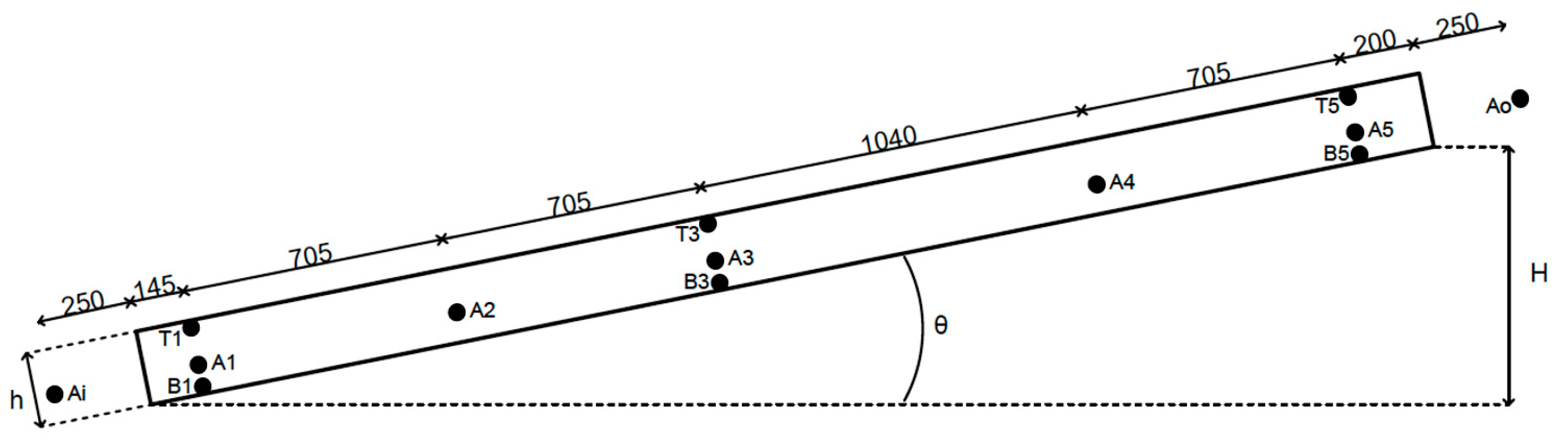
3.1. Laboratory Model
3.2. Experimental Procedure
3.3. Test Setups
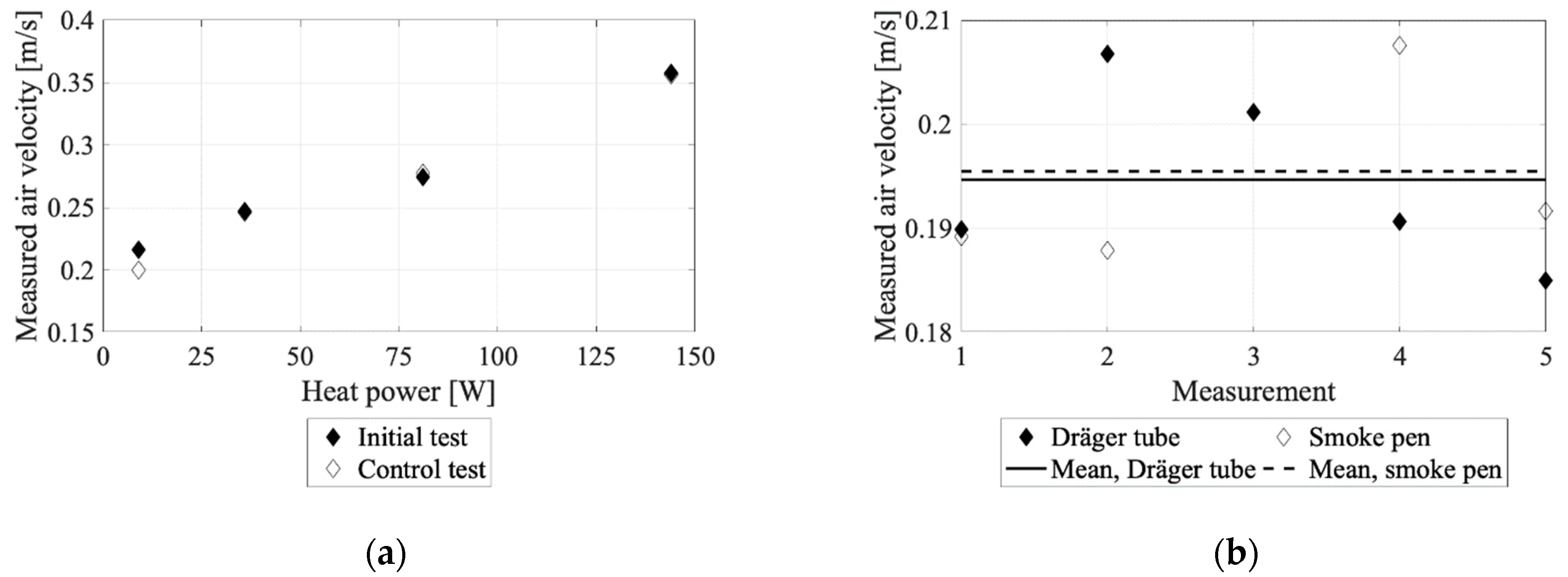
3.4. Validation of Experimental Test Regime
4. Experimental Results
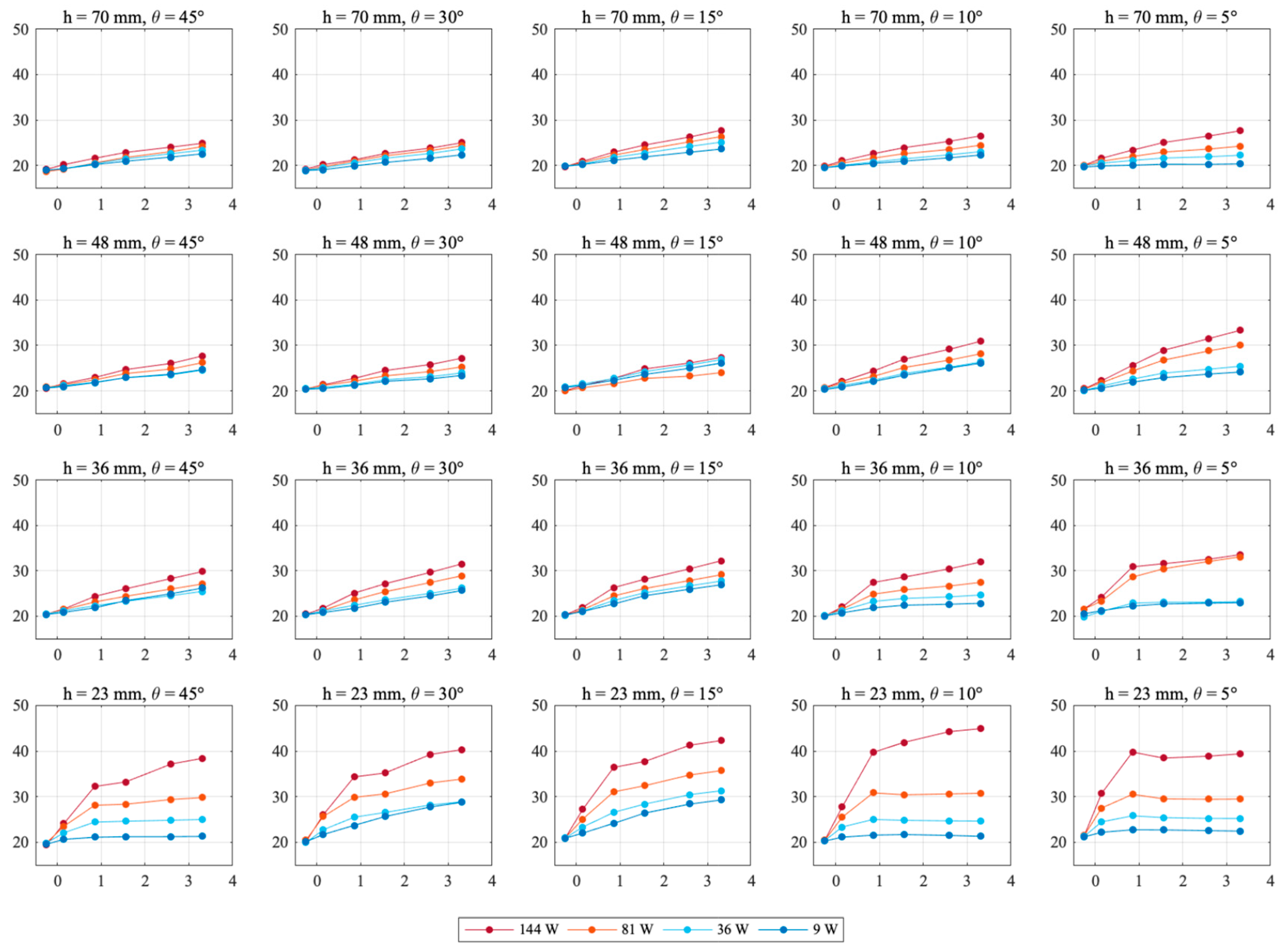
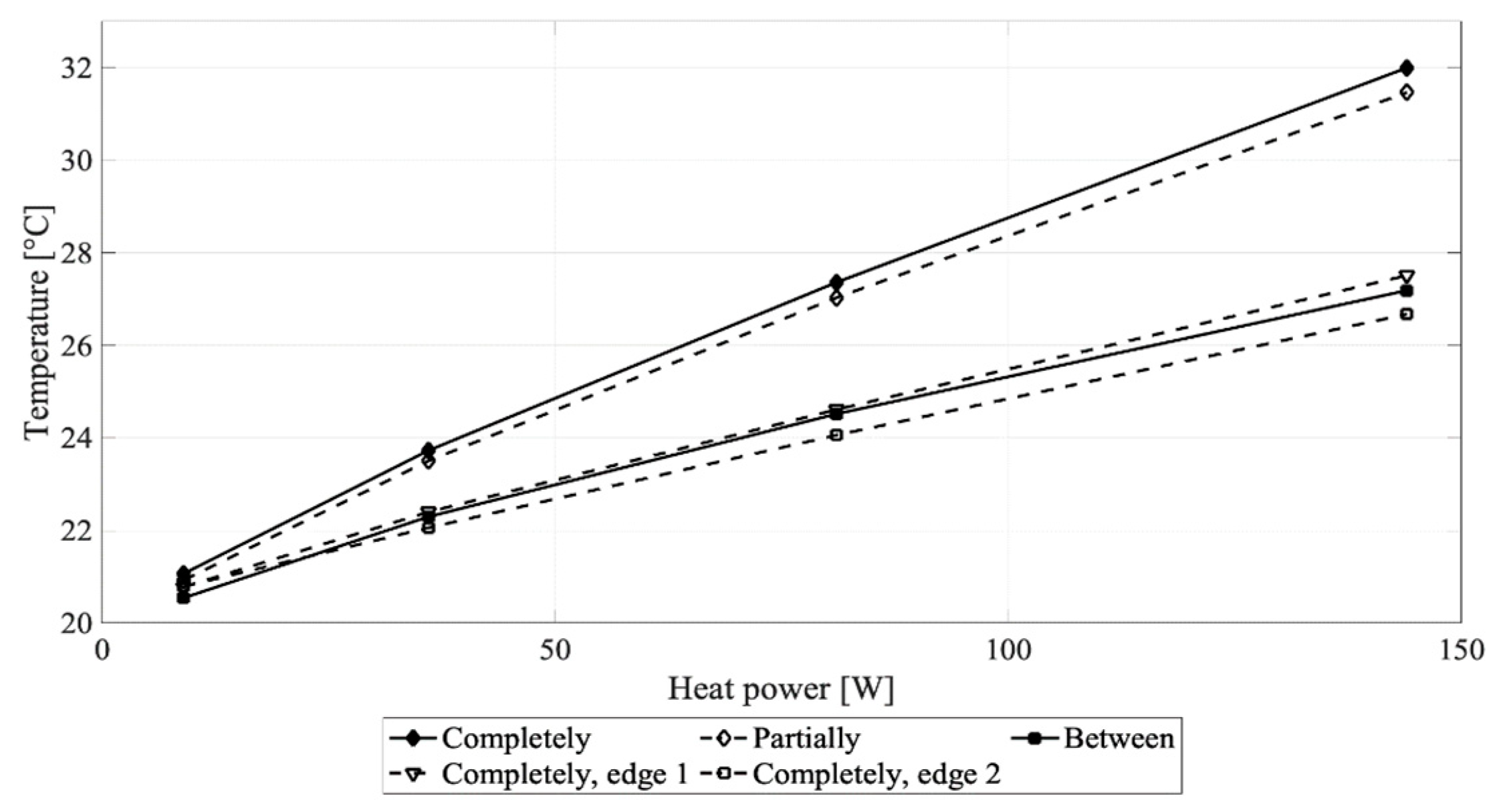
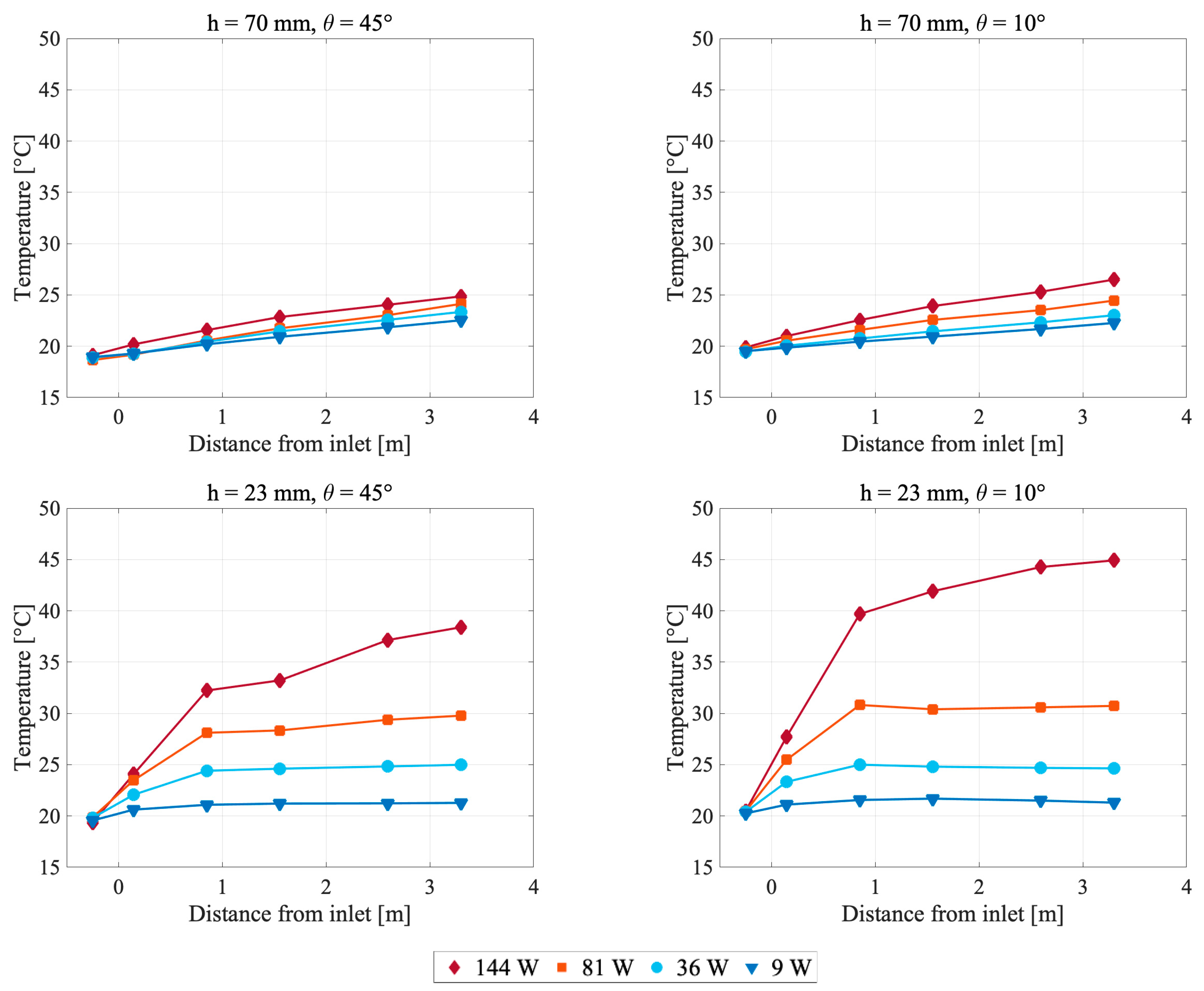
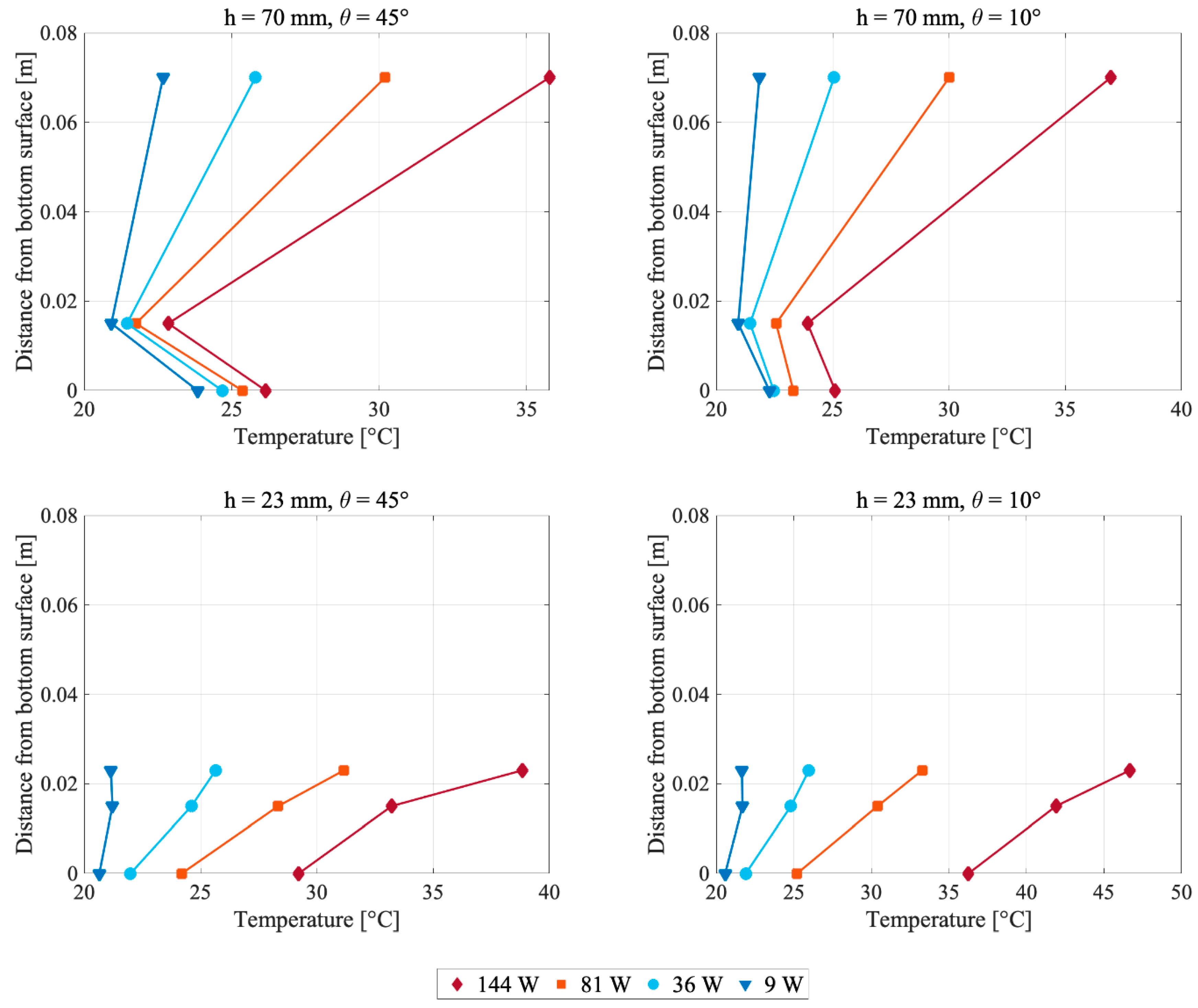
4.1. Temperature Conditions
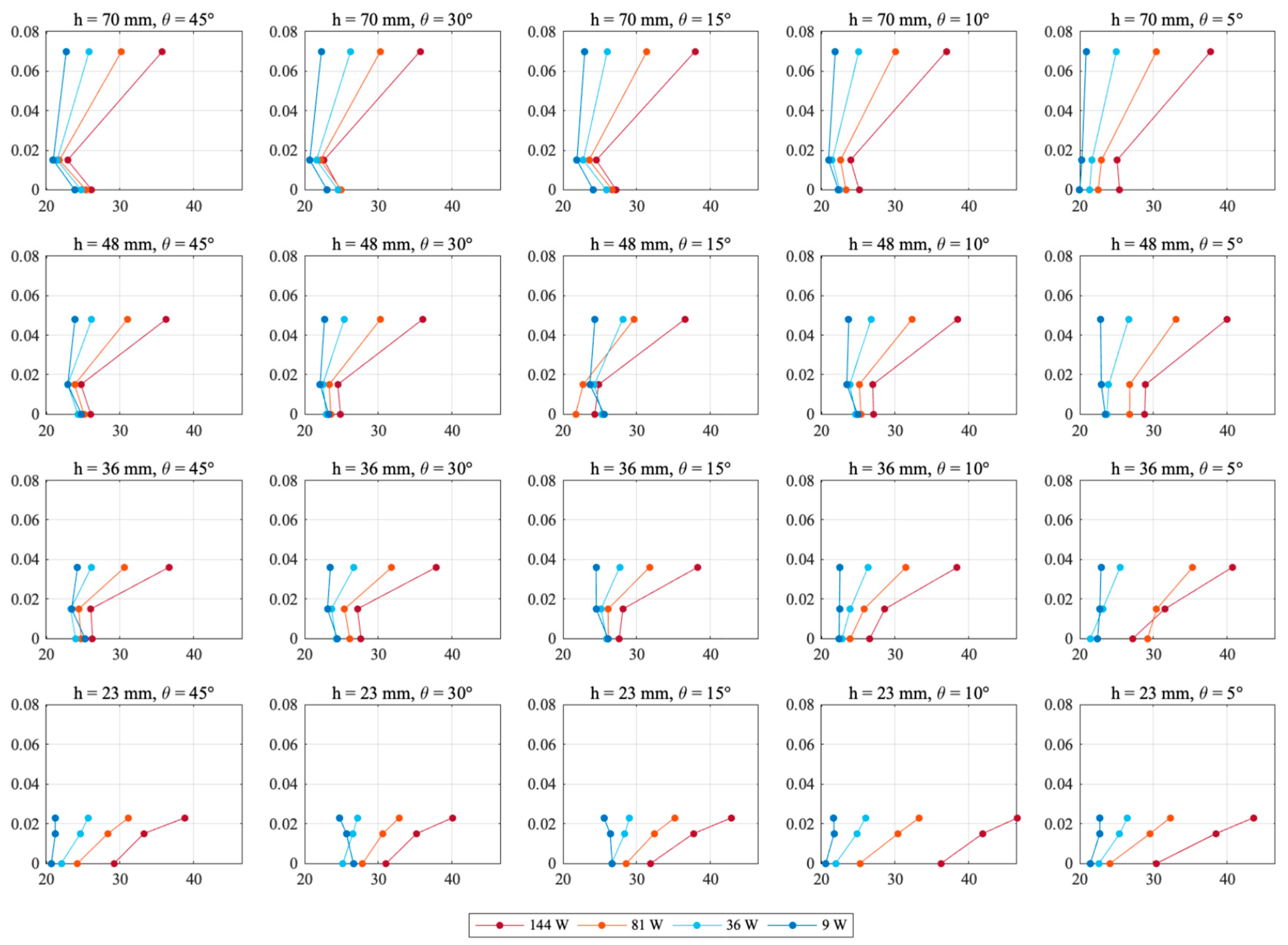
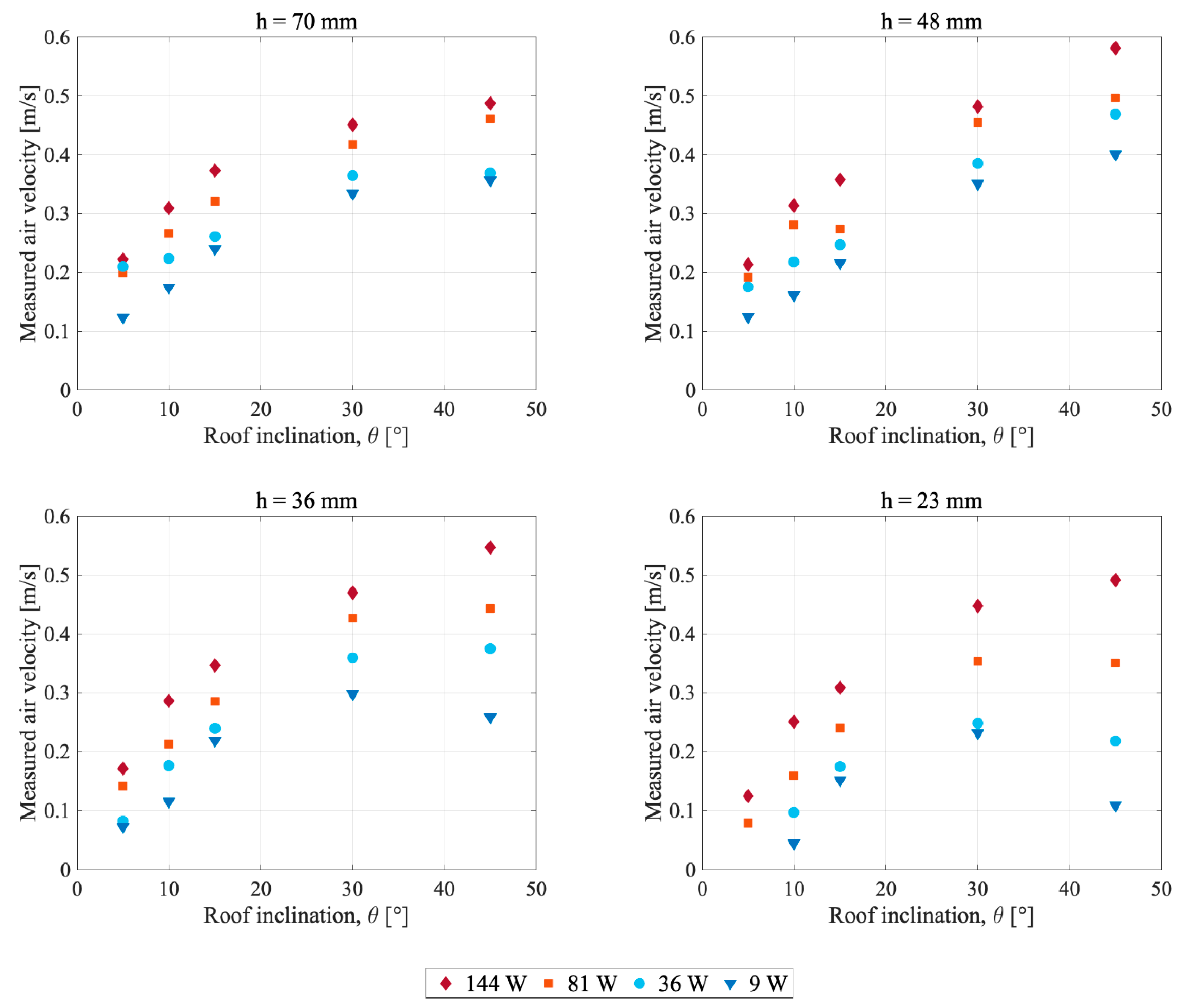
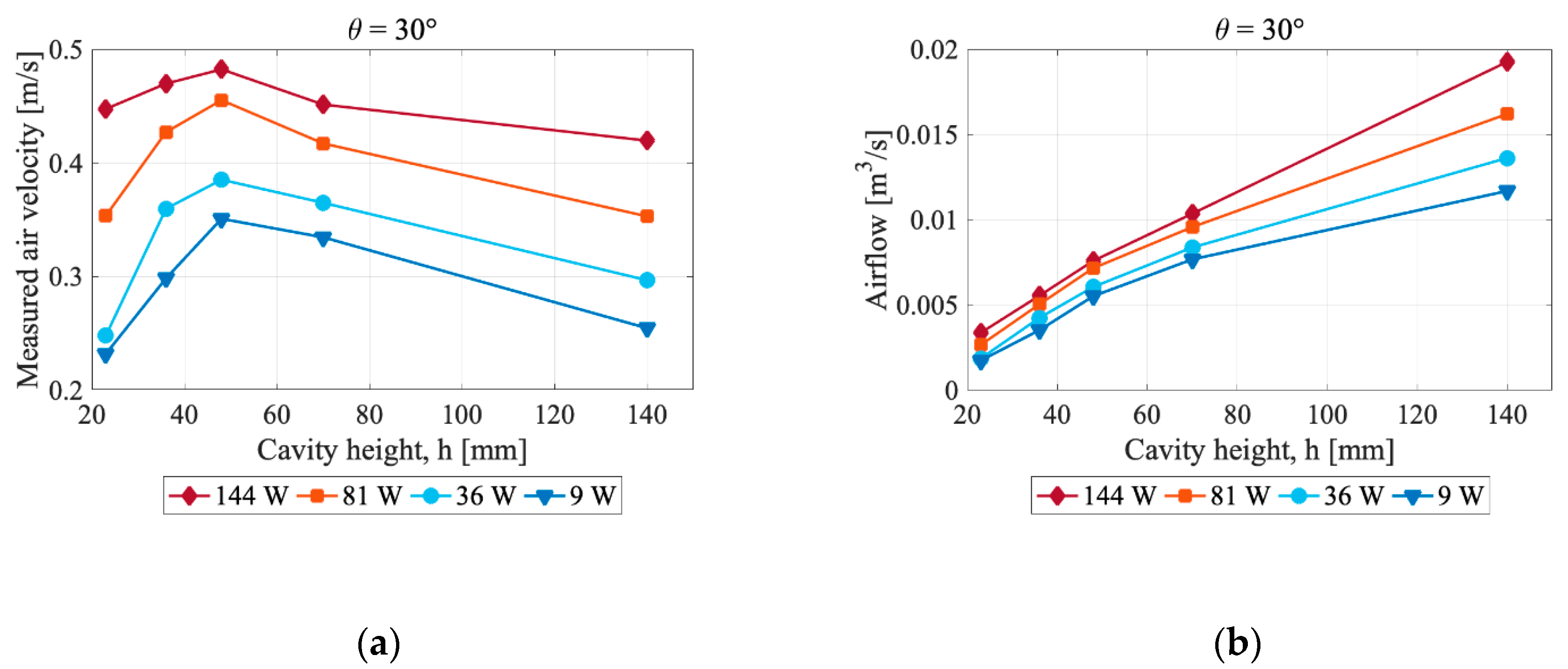
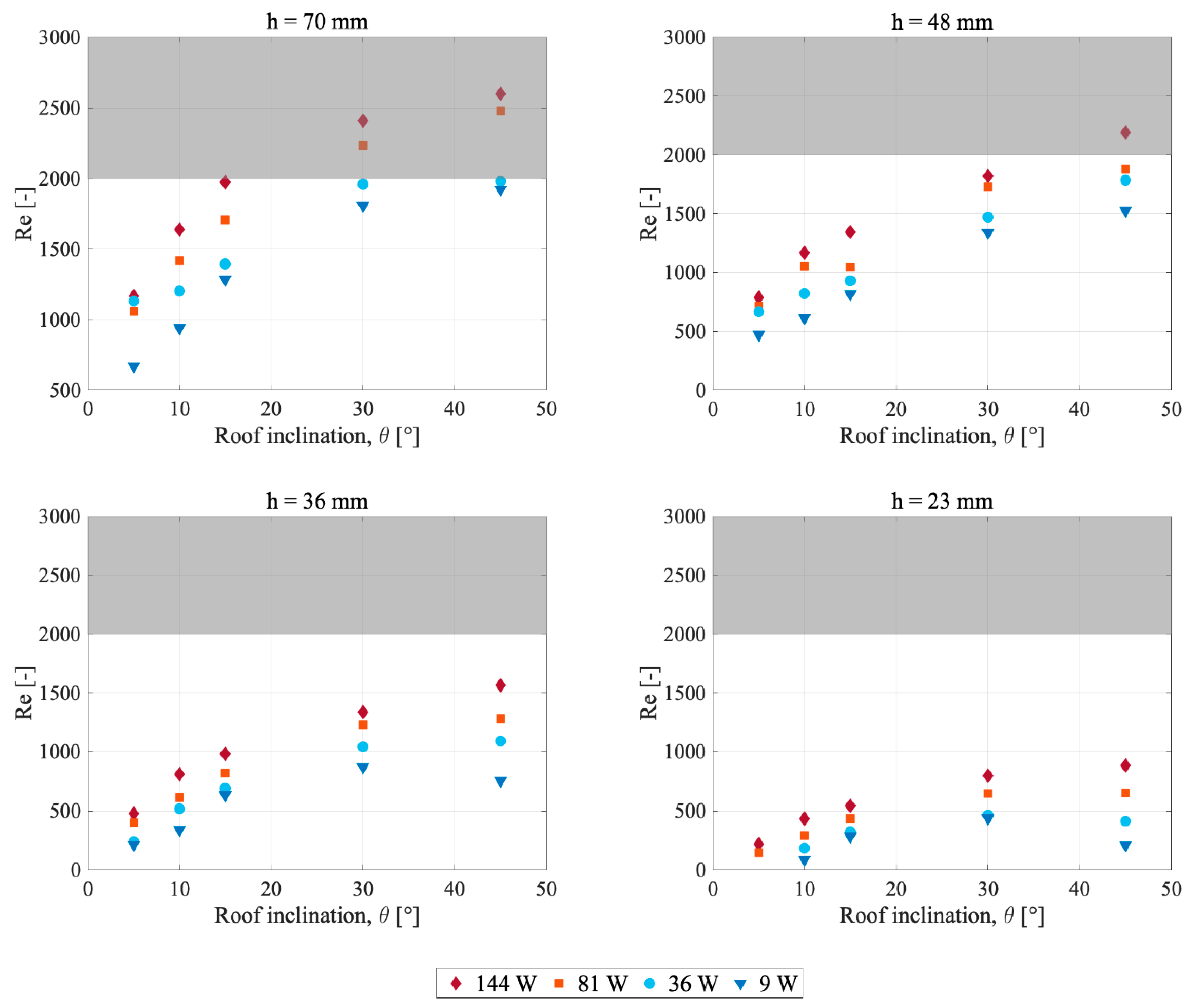
4.2. Air Velocity and Flow Conditions
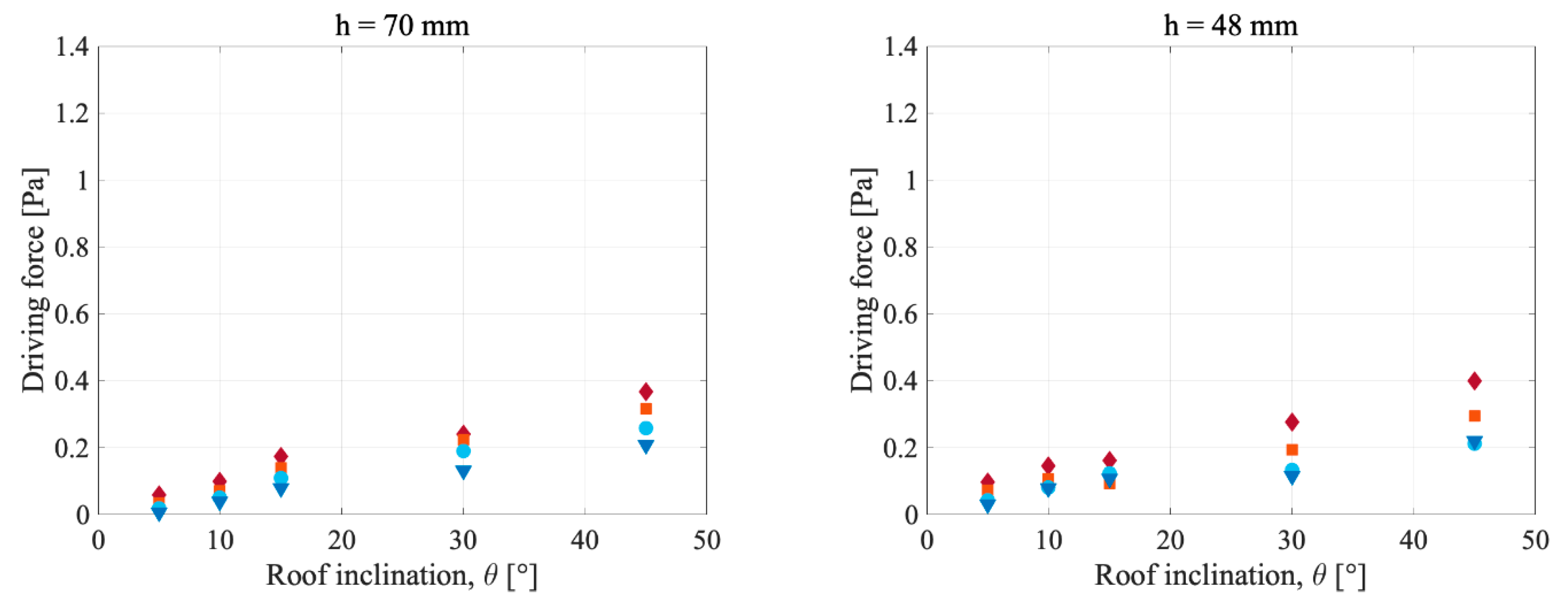
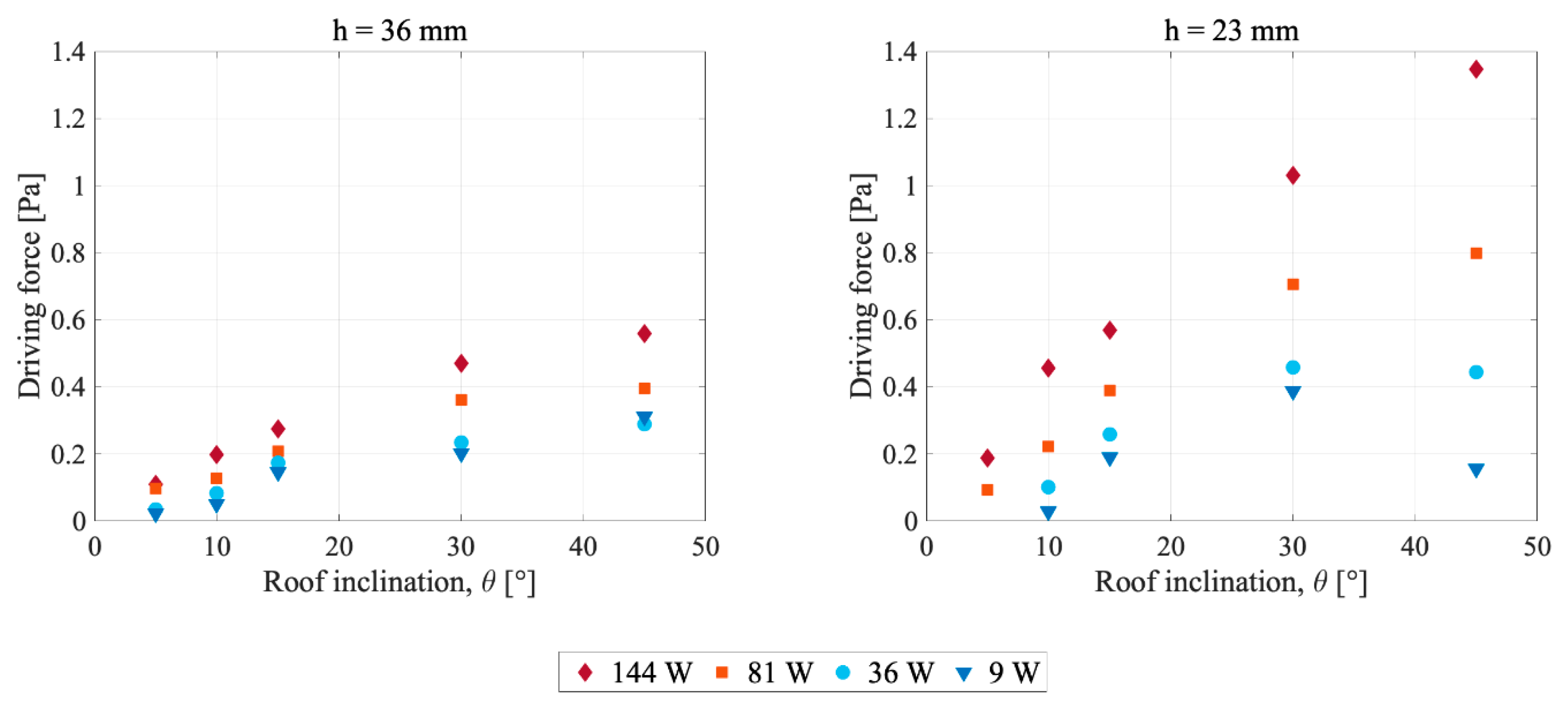
4.3. Driving Force
5. Analysis of Measurements
5.1. Temperature Conditions
5.1.1. Temperature Profile along the Cavity
5.1.2. Temperature Profile across the Cavity
5.1.3. Influence of Air Cavity Design and Heat Power Level
5.1.4. Heat Power Level Related to Local Climate
5.2. Air Velocity and Flow Conditions
5.2.1. Flow Characteristics
5.2.2. Influence of Air Cavity Design and Heat Power Level
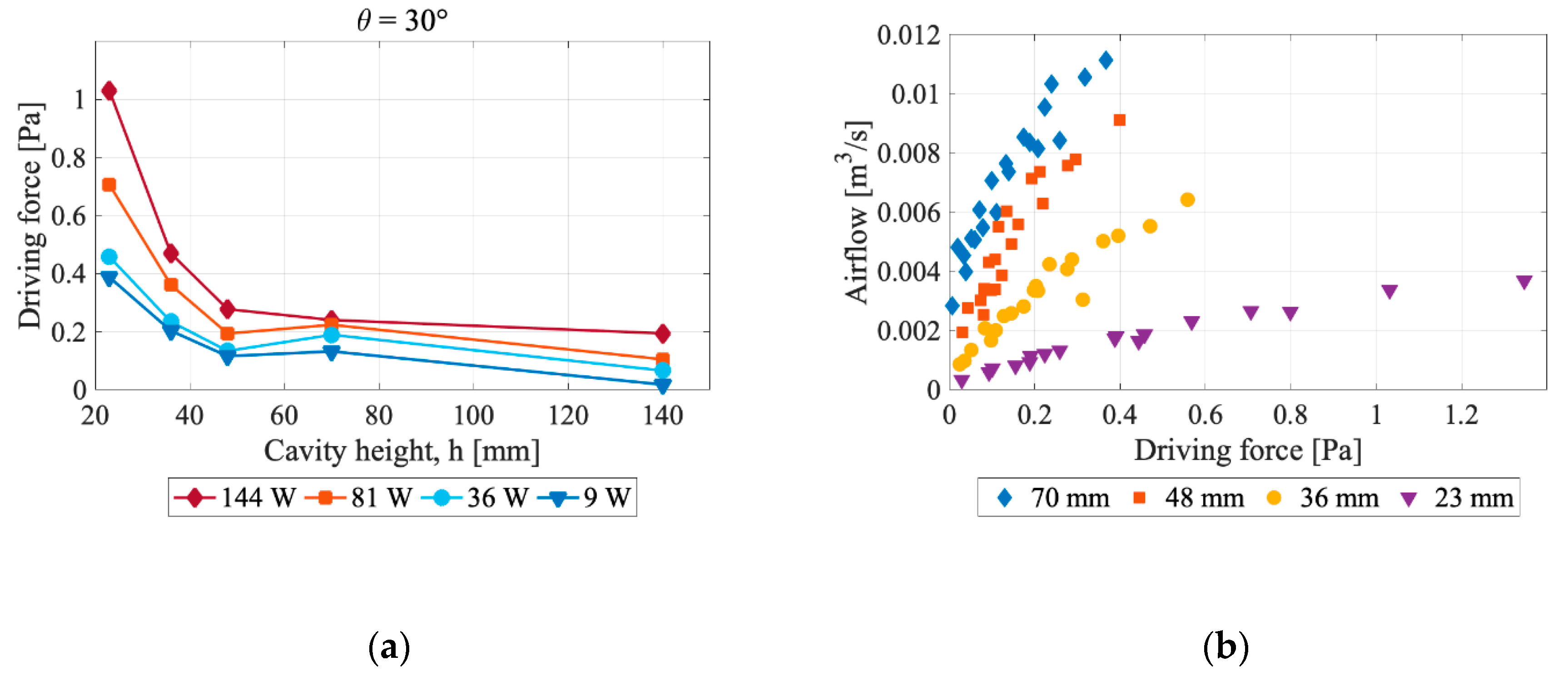
5.3. Driving Force
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
References
- Edvardsen, K.; Ramstad, T. Trehus Håndbok 5 [Wooden Houses. Handbook 5]; SINTEF Building and Infrastructure: Oslo, Norway, 2014. [Google Scholar]
- Gullbrekken, L.; Kvande, T.; Jelle, B.P.; Time, B. Norwegian pitched roof defects. Buildings 2016, 6, 24. [Google Scholar] [CrossRef]
- Blom, P. Venting of attics and pitched, insulated roofs. J. Therm. Envel. Build. Sci. 2001, 25, 32–50. [Google Scholar] [CrossRef]
- Blom, P. Ventilasjon av isolerte, skrå tretak [Venting of Insulated, Pitched Roofs]. Ph.D. Thesis, Norwegian Technical University, Trondheim, Norway, 1990. [Google Scholar]
- Norton, B.; Eames, P.C.; Mallick, T.K.; Huang, M.J.; McCormack, S.J.; Mondol, J.D.; Yohanis, Y.G. Enhancing the performance of building integrated photovoltaics. Sol. Energy 2011, 85, 1629–1664. [Google Scholar] [CrossRef]
- Shukla, A.K.; Sudhakar, K.; Baredar, P. A comprehensive review on design of building integrated photovoltaic system. Energy Build. 2016, 128, 99–110. [Google Scholar] [CrossRef]
- Zhang, T.; Tan, Y.; Yang, H.; Zhang, X. The application of air layers in building envelopes: A review. Appl. Energy 2016, 165, 707–734. [Google Scholar] [CrossRef]
- Roels, S.; Langmans, J. Highly insulated pitched roofs resilient to air flow patterns: Guidelines based on a literature review. Energy Build. 2016, 120, 10–18. [Google Scholar] [CrossRef]
- Bøhlerengen, T. Isolerte skrå tretak med lufting mellom vindsperre og undertak [Insulated pitched wooden roofs ventilated between the underlayer roof and the wind barrier]. In SINTEF Building Research Design Guides 525.101; SINTEF: Oslo, Norway, 2007. [Google Scholar]
- Bøhlerengen, T. Isolerte skrå tretak med kombinert undertak og vindsperre [Insulated pitched wooden roofs with combined underlayer roof and wind barrier]. In SINTEF Building Research Design Guides 525.102; SINTEF: Oslo, Norway, 2012. [Google Scholar]
- Gullbrekken, L.; Uvsløkk, S.; Kvande, T.; Petterson, K.; Time, B. Wind pressure coefficients for roof ventilation purposes. J. Wind Eng. Ind. Aerodyn. 2018, 175, 144–152. [Google Scholar] [CrossRef]
- Walker, T.S.; Forest, T.W. Field measurements of ventilation rates in attics. Build. Environ. 1995, 30, 333–347. [Google Scholar] [CrossRef]
- Falk, J.; Sandin, K. Ventilated rainscreen cladding: Measurements of cavity air velocities, estimation of air change rates and evaluation of driving forces. Build. Environ. 2013, 59, 164–176. [Google Scholar] [CrossRef]
- Ciampi, M.; Leccese, F.; Tuoni, G. Energy analysis of ventilated and microventilated roofs. Sol. Energy 2005, 79, 183–192. [Google Scholar] [CrossRef]
- Villi, G.; Pasut, W.; De Carli, M. CFD modelling and thermal performance analysis of a wooden ventilated roof structure. Build. Simul. 2009, 2, 215–228. [Google Scholar] [CrossRef]
- Susanti, L.; Homma, H.; Matsumoto, H.; Suzuki, Y.; Shimizu, M. Numerical simulation of natural ventilation of a factory roof cavity. Energy Build. 2010, 42, 1337–1343. [Google Scholar] [CrossRef]
- Susanti, L.; Homma, H.; Matsumoto, H. A naturally ventilated cavity roof as potential benefits for improving thermal environment and cooling load of a factory building. Energy Build. 2011, 43, 211–218. [Google Scholar] [CrossRef]
- Gagliano, A.; Patania, F.; Nocera, F.; Ferlito, A.; Galesi, A. Thermal performance of ventilated roofs during summer period. Energy Build. 2012, 49, 611–618. [Google Scholar] [CrossRef]
- Li, D.; Zheng, Y.; Liu, C.; Qi, H.; Liu, X. Numerical analysis on thermal performance of naturally ventilated roofs with different influencing parameters. Sustain. Cities Soc. 2016, 22, 86–93. [Google Scholar] [CrossRef]
- Bianco, V.; Diana, A.; Manca, O.; Nardini, S. Thermal behavior evaluation of ventilated roof under summer and winter conditions. Int. J. Heat Technol. 2017, 35, 353–360. [Google Scholar] [CrossRef]
- Bortolini, M.; Bottarelli, M.; Piva, S. Summer thermal performance of ventilated roofs with tiled coverings. J. Phys. Conf. Ser. 2017, 796, 012023. [Google Scholar] [CrossRef]
- Bianco, V.; Diana, A.; Manca, O.; Nardini, S. Numerical investigation of an inclined rectangular cavity for ventilated roofs applications. Therm. Sci. Eng. Prog. 2018, 6, 426–435. [Google Scholar] [CrossRef]
- De With, G.; Cherry, N.; Haig, J. Thermal benefits of tiled roofs with above-sheathing ventilation. J. Build. Phys. 2008, 33, 171–194. [Google Scholar] [CrossRef]
- Tong, S.; Li, H. An efficient model development and experimental study for the heat transfer in naturally ventilated inclined roofs. Build. Environ. 2014, 81, 296–308. [Google Scholar] [CrossRef]
- Biwole, P.H.; Woloszyn, M.; Pompeo, C. Heat transfers in a double-skin roof ventilated by natural convection in summer time. Energy Build. 2008, 40, 1487–1497. [Google Scholar] [CrossRef]
- Hofseth, V. Studie av luftede trekonstruksjoner [Study of Ventilated Roof Constructions]. Master’s Thesis, Norwegian University og Science and Technology, Trondheim, Norway, 2004. [Google Scholar]
- Susanti, L.; Homma, H.; Matsumoto, H.; Suzuki, Y.; Shimizu, M. A laboratory experiment on natural ventilation through a roof cavity for reduction of solar heat gain. Energy Build. 2008, 40, 2196–2206. [Google Scholar] [CrossRef]
- Lee, S.; Park, S.H.; Yeo, M.S.; Kim, K.W. An experimental study on airflow in the cavity of a ventilated roof. Build. Environ. 2008, 44, 1431–1439. [Google Scholar] [CrossRef]
- Chami, N.; Zoughaib, A. Modeling natural convection in a pitched thermosyphon system in building roofs and experimental validation using particle image velocimetry. Energy Build. 2010, 42, 1267–1274. [Google Scholar] [CrossRef]
- Nusser, B.; Teibinger, M. Experimental investigations about the air flow in the ventilation layer of low pitched roofs. In Proceedings of the 2nd Central European Symposium on Building Physics, Vienna, Austria, 9–11 September 2013. [Google Scholar]
- Sandberg, M.; Moshfegh, B. Ventilated-solar roof air flow and heat transfer investigation. Renew. Energy 1998, 15, 287–292. [Google Scholar] [CrossRef]
- Khedari, J.; Yimsamerjit, P.; Hirunlabh, J. Experimental investigation of free convection in roof solar collector. Build. Environ. 2002, 37, 455–459. [Google Scholar] [CrossRef]
- Bunnag, T.; Khedari, J.; Hirunlabh, J.; Zeghmati, B. Experimental investigation of free convection in an open-ended inclined rectangular channel heated from the top. Int. J. Ambient Energy 2004, 25, 151–162. [Google Scholar] [CrossRef]
- Zhai, X.Q.; Dai, Y.J.; Wang, R.Z. Experimental investigation on air heating and natural ventilation of a solar air collector. Energy Build. 2005, 37, 373–381. [Google Scholar] [CrossRef]
- Sandberg, M.; Moshfegh, B. The investigation of fluid flow and heat transfer in a vertical channel heated from one side by PV elements. Part II. Experimental study. Renew. Energy 1996, 8, 254–258. [Google Scholar] [CrossRef]
- Gullbrekken, L.; Uvsløkk, S.; Geving, S.; Kvande, T. Local loss coefficients inside air cavity of ventilated pitched roofs. J. Build. Phys. 2017, 42, 197–219. [Google Scholar] [CrossRef]
- Hagentoft, C.-E. Introduction to Building Physics; Studentlitteratur AB: Lund, Sweden, 2001. [Google Scholar]
- Kronvall, J. Air Flows in Building Components. Ph.D. Thesis, Lund University, Lund, Sweden, 1980. [Google Scholar]
- Geving, S.; Thue, J.V. Fukt i Bygninger [Moisture in Buildings]; Norges Byggforskningsinstitutt: Oslo, Norway, 2002. [Google Scholar]
- Cengel, Y.A.; Cimbala, J.M. Fluid Mechanics, Fundamentals and Applications, 3rd ed.; McGraw Hill Education: Boston, MA, USA, 2014. [Google Scholar]
- ASHRAE. 2005 ASHRAE Handbook: Fundamentals; American Society of Heating, Refrigerating and Air-Conditioning Engineers: Atlanta, GA, USA, 2005. [Google Scholar]
- Hansen, H.E.; Kjerulf-Jensen, P.; Stampe, O.B. Varme-og Klimateknik, Grundbog, 4th ed.; Danvak ApS: København, Denmark, 2013. [Google Scholar]
- Arfvidsson, J.; Harderup, L.-E.; Samuelson, I. Fukthandbok: Praktik och teori [Moisture Handbook: Practice and Theory], 4th ed.; AB Svensk Byggtjänst: Stockholm, Sweden, 2017. [Google Scholar]
- Gullbrekken, L.; Kvande, T.; Time, B. Ventilated wooden roofs: Influence of local weather conditions-measurements. In Proceedings of the 11th Nordic Symposium on Building Physics, Trondheim, Norway, 11–14 June 2017; pp. 777–782. [Google Scholar]

© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bunkholt, N.S.; Säwén, T.; Stockhaus, M.; Kvande, T.; Gullbrekken, L.; Wahlgren, P.; Lohne, J. Experimental Study of Thermal Buoyancy in the Cavity of Ventilated Roofs. Buildings 2020, 10, 8. https://doi.org/10.3390/buildings10010008
Bunkholt NS, Säwén T, Stockhaus M, Kvande T, Gullbrekken L, Wahlgren P, Lohne J. Experimental Study of Thermal Buoyancy in the Cavity of Ventilated Roofs. Buildings. 2020; 10(1):8. https://doi.org/10.3390/buildings10010008
Chicago/Turabian StyleBunkholt, Nora Schjøth, Toivo Säwén, Martina Stockhaus, Tore Kvande, Lars Gullbrekken, Paula Wahlgren, and Jardar Lohne. 2020. "Experimental Study of Thermal Buoyancy in the Cavity of Ventilated Roofs" Buildings 10, no. 1: 8. https://doi.org/10.3390/buildings10010008
APA StyleBunkholt, N. S., Säwén, T., Stockhaus, M., Kvande, T., Gullbrekken, L., Wahlgren, P., & Lohne, J. (2020). Experimental Study of Thermal Buoyancy in the Cavity of Ventilated Roofs. Buildings, 10(1), 8. https://doi.org/10.3390/buildings10010008




